Индуктивность — проводник — Большая Энциклопедия Нефти и Газа, статья, страница 1

Индуктивность — проводник

Cтраница 1

Индуктивность проводников Ь зависит от их формы и размеров.  [1]

Индуктивность проводника в данной среде определяется исключительно его размерами и формой. Индуктивность прямолинейного провода невелика. Индуктивность того же провода в форме витка значительно больше. При одинаковых размерах катушек ( длин и диаметров) их индуктивность пропорциональна квадрату числа витков. Индуктивность катушки прямо пропорциональна магнитной проницаемости ia сердечника.  [2]

Индуктивность проводника зависит от его формы, размеров, а также от свойств окружающей среды. Если сила тока изменяется со временем, то изменяется и магнитный поток, сцепленный с контуром. Изменение магнитного потока, в свою очередь, вызывает появление в проводнике индукционного тока.

Так как индукционный ток вызван изменением силы тока в самом проводнике, то данное явление возникновения индукционного тока называется самоиндукцией, а возникающая эдс — эдс самоиндукции. Самоиндукция является частным случаем явления электромагнитной индукции.  [3]

Индуктивность проводника в данной среде определяется исключительно его размерами и формой. Индуктивность прямолинейного провода невелика. Индуктивность того же провода в форме витка значительно больше. При одинаковых размерах катушек ( длин и диаметров) их индуктивность пропорциональна квадрату числа витков. Индуктивность катушки прямо пропорциональна магнитной проницаемости ia сердечника.  [4]

Индуктивность проводника численно равна магнитному потоку, создаваемому током в 1 ампер, протекающему по данному проводнику.  [5]

Индуктивность проводника характеризует его размеры и форму, а также магнитную проницаемость среды, окружающей проводник. Индуктивность проводника остается постоянной, если не изменяется его форма, размеры и магнитная проницаемость окружающей его среды.  [6]

Индуктивность проводников проявляется только при прохождении через них изменяющегося со временем тока. В этой работе индуктивность определяется методом мостика, питаемого переменным током.  [7]

Индуктивность проводника L называется еще коэффи циентом самоиндукции.  [8]

Индуктивность проводников I, зависит от их формы и размеров.  [9]

Индуктивность L проводника определяется его формой, размерами, взаимным расположением отдельных его частей, средой, в которой происходит замыкание магнитного потока.  [10]

Индуктивность проводников L зависит от их формы и размеров.  [11]

Индуктивность проводника конечного сечения складывается из внешней и н д у к-тивности.  [13]

Если индуктивность проводника, соединяющего экран с шасси ( корпусом), велика, то экран может не уменьшить, а увеличить емкостную паразитную связь.  [15]

Страницы:      1    2    3    4

От чего зависит индуктивность проводника в вакууме Индуктивность L зависит от формы т размеров проводник

Работа добавлена на сайт samzan.ru: 2015-07-05

Билет 17

1. От чего зависит индуктивность проводника в вакууме?

Индуктивность L зависит от формы т размеров проводника, а также магнитной проницаемости среды

2. Как изменится период свободных колебаний в колебательном контуре, если индуктивность катушки и электроемкость конденсатора увеличить в 2 раза?

. Период увеличится в 2 раза

3. Что такое дифракция? Приведите примеры проявления (использования) дифракции в жизни.

Явление отклонения световых волн от прямолинейного распространения при прохождении отверстий и вблизи краёв экранов называется дифракцией (огибание светом встречных препятствий).

4. Чему равно максимальное число электронов, находящихся в состояниях, определяемых главным квантовым числом?

n	Количество электронов в состояниях	Максимальное количество электронов
	s(l=0)	p(l=1)	d(l=2)	f(l=3)	g(l=4)
1	2	—	—	—	—	2
2	2	6	—	—	—	8
3	2	6	10	—	—	18
4	2	6	10	14	—	32
5	2	6	10	14	18	50

5. Чему равна магнитная индукция  поля кругового тока? Укажите направление вектора магнитной индукции в центре кругового витка с током. Ток течет против часовой стрелки.

Рассм.рис.6

,  

Направление вектора магнитной индукции будет направлено вертикально вверх.

6. Волновое уравнение.

или

где v – фазовая скорость,

оператор Лапласа

7. Запишите выражение для массы фотона.

8. Записать закон радиоактивного распада

: N-число ядер оставшихся к времени t, -число ядер в t=0, первоначальное количество ядер., -постоянная радиоактивного распада, t-время распада.

9. Какой магнитный поток пронизывает плоскую поверхность площадью 50 см2 при индукции поля  0,2 Тл, если эта поверхность расположена под углом 60º к вектору индукции?

Дано:S=50 см2, B=0.

2 Tл, α=600 

Найти: Ф

Решение: Ф=B*S*cos α=5*10-3 Вб

10. Чему равна величина  магнитной индукции в вакууме, если в среде с магнитной проницаемостью μ= 100  это же поле имеет магнитную индукцию 10-2 Тл.

11. В цепь включены конденсатор емкостью 2 мкФ и катушка индуктивностью 0,5 Гн. При какой частоте тока в этой цепи будет резонанс?

w0=103Гц

12.

1.  Через катушку, индуктивность которой L=10-3 Гн, проходит ток  I=1 А. Чему равен магнитный поток сквозь катушку?

Дано:L=10-3 Гн, I = 1А

Найти: Ф    Решение:

14. .На сколько изменится энергия электрона в атоме водорода при излучении атомом фотона с длиной волны ?

    

15.

16. Уравнение колебаний заряда в колебательном контуре имеет вид (мкКл). Чему равна ёмкость конденсатора, если индуктивность катушки 0,5 Гн?

=1/;c=1/L2;c=200мкФ

1.  Монохроматический пучок света с длиной волны 490 нм, падая по нормали к поверхности, производит световое давление 4,9 мкПа. Какое число фотонов падает в единицу времени на единицу площади этой поверхности? Коэффициент отражения света 0,25.

1.  .Пучок электронов движется вдоль оси х со скоростью , которая определена с точностью 0,01%.

Найти неопределенность координаты электрона.(

Переходя от неравенства к равенству, получим    

1.  Найти кинетическую энергию протона, движущегося по дуге окружности радиусом R в магнитном поле индукцией В. Заряд протона q, масса m.

Дано:  R, B, q, m

Найти: Wk       Решение: W=m*v2/2, R=m*V/q*B, V=R*q*B/m, W=1/2*R2*q2B2/m

dB

Рис. 6

I

От чего зависит индукция — Мастер Фломастер

Эл.ток создает собственное магнитное поле. Магнитный поток через контур пропорционален индукции магнитного поля (Ф

B), индукция пропорциональна силе тока в проводнике
(B

I), следовательно магнитный поток пропорционален силе тока (Ф

ЭДС самоиндукции зависит от скорости изменения силы тока в эл.цепи, от свойств проводника
(размеров и формы) и от относительной магнитной проницаемости среды, в которой находится проводник.

Физическая величина, показывающая зависимость ЭДС самоиндукции от размеров и формы проводника и от среды, в которой находится проводник, называется коэффициентом самоиндукции или индуктивностью.

Индуктивность — физ. величина, численно равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1 Ампер за 1 секунду.

Также индуктивность можно рассчитать по формуле:

где Ф — магнитный поток через контур, I — сила тока в контуре.

Единицы измерения индуктивности в системе СИ:

Индуктивность катушки зависит от: числа витков, размеров и формы катушки и от относительной магнитной проницаемости среды

Индуктивность взаимная — величина, характеризующая магнитную связь двух или более электрических цепей (контуров). Если имеется два проводящих контура , то часть линий магнитной индукции, создаваемых током в первом контуре, будет пронизывать площадь, ограниченную вторым контуром (т. е. будет сцеплена с контуром 2).

Магнитный поток Ф₁₂ через контур 2, созданный током I₁ в контуре 1, прямо пропорционален току:

Коэффициент пропорциональности M₁₂ зависит от размеров и формы контуров 1 и 2, расстояния между ними, их взаимного расположения, а также от магнитной проницаемости окружающей среды и называется взаимной индуктивностью или коэффициентом взаимной индукции контуров 1 и 2. В системе СИ И. в. измеряется в Генри.

Трансформаторная ЭДС. Принцип действия трансформатора основан на явлении электромагнитной индукции. Линии индукции магнитного поля, создаваемого переменным током в первичной обмотке, благодаря наличию сердечника практически без потерь пронизывают витки вторичной обмотки. Поскольку магнитный поток во вторичной обмотке изменяется со временем (т.к. в первичной обмотке переменный ток), то согласно закону Фарадея в ней возбуждается ЭДС индукции. Трансформатор может работать только на переменном токе, т.к. магнитный поток, созданный постоянным током, не изменяется с течением времени.

Пусть первичная обмотка трансформатора подключена к источнику тока с переменной ЭДС E₁ и с действующим значением напряжения U₁. На вторичной обмотке ЭДС E₂ и напряжение U₂.

Из законов Ома следует, что напряжение на обмотке равно

(1)

где r — сопротивление обмотки. При изготовлении трансформатора сопротивление первичной обмотки r₁ делают очень малым, поэтому часто им можно пренебречь.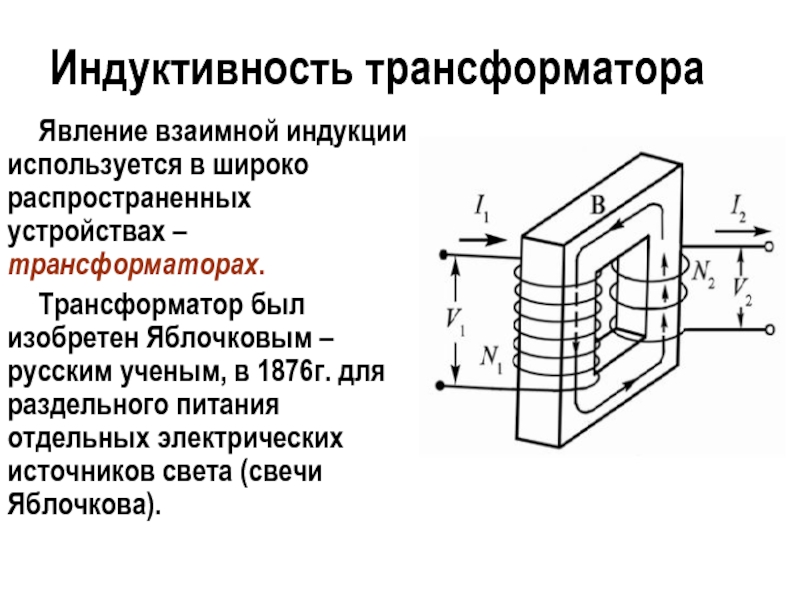 Тогда

Если пренебречь потерями магнитного потока в сердечнике, то в каждом витке вторичной обмотки будет индуцироваться точно такая же ЭДС индукции e₁, как и ЭДС индукции e₂ в каждом витке первичной обмотки, т.е. e₁ = e₂. Следовательно, отношение ЭДС в первичной E₁ и вторичной E₂ обмотках равно отношению числа витков в них:

(2)

Трансформаторный ток. Токи обмоток обратно пропорциональны числам витков (I₁/I₂ приблиз = w₁/w₂ = 1/n). С увеличением тока активно-индуктивного приемника вторичное напряжение несколько снижается.

Рис.1.11. К определению магнитного потока рассеяния в катушке с ферромагнитным сердечником

часть магнитного потока катушки замыкается не по сердечнику, а по воздуху. Эта часть потока носит название потока рассеивания Ф_р (рис. 1.11). Таким образом, полный поток, сцепленный с витками катушки равен

.

(1.14)

На основании закона Ома для магнитной цепи (1.7) можно написать выражение для потока рассеяния:

.

Так как , то .То есть поток рассеяния , в отличие от потока в сердечнике, совпадает по фазе с током и связан с ним линейной зависимостью. Следовательно, на векторной диаграмме вектор потока будет совпадать с вектором тока (рис.1.12).

Рис.1.12. Векторная диаграмма магнитных потоков, ЭДС и токов катушки с ферромагнитным сердечником

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Студент — человек, постоянно откладывающий неизбежность. 10253 — | 7245 — или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Магнитное взаимодействие движущихся электрических зарядов согласно представлениям теории поля объясняется следующим образом: всякий движущийся электрический заряд создает в окружающем пространстве магнитное поле, способное действовать на другие движущиеся электрические заряды.

В — физическая величина, являющаяся силовой характеристикой магнитного поля. Она называется магнитной индукцией (или индукцией магнитного поля).

Магнитная индукция — векторная величина. Модуль вектора магнитной индукции равен отношению максимального значения силы Ампера, действующей на прямой проводник с током, к силе тока в проводнике и его длине:

Единица магнитной индукции. В Международной системе единиц за единицу магнитной индукции принята индукция такого магнитного поля, в котором на каждый метр длины проводника при силе тока 1 А действует максимальная сила Ампера 1 Н. Эта единица называется тесла (сокращенно: Тл), в честь выдающегося югославского физика Н. Тесла:

Движение проводника с током в магнитном поле показывает, что магнитное поле действует на движущиеся электрические заряды. На проводник действует сила Ампера F_А = IBlsin a , а сила Лоренца действует на движущийся заряд:

где a — угол между векторами B и v .

Движение заряженных частиц в магнитном поле. В однородном магнитном поле на заряженную частицу, движущуюся со скоростью перпендикулярно линиям индукции магнитного поля, действует сила_м , постоянная по модулю и направленная перпендикулярно вектору скорости.Под действием магнитной силы частица приобретает ускорение, модуль которого равен:

В однородном магнитном поле эта частица движется по окружности. Радиус кривизны траектории, по которой движется частица, определяется из условияоткуда следует,

Радиус кривизны траектории является величиной постоянной, поскольку сила, перпендикулярная вектору скорости, меняется только ее направление, но не модуль. А это и означает, что данная траектория является окружностью.

Период обращения частицы в однородном магнитном поле равен:

Последнее выражение показывает, что период обращения частицы в однородном магнитном поле не зависит от скорости и радиуса траектории ее движения.

Если напряженность электрического поля равна нулю, то сила Лоренца _л равна магнитной силе _м :

Явление электромагнитной индукции открыл Фарадей, который установил, что в замкнутом проводящем контуре возникает электрический ток при любом изменении магнитного поля, пронизывающего контур.

Магнитный поток Ф (поток магнитной индукции) через поверхность площадью S — величина, равная произведению модуля вектора магнитной индукции на площадь S и косинус угла а между вектором и нормалью к поверхности:

Ф=BScos

В СИ единица магнитного потока 1 Вебер (Вб) — магнитный поток через поверхность площадью 1 м 2 , расположенную перпендикулярно направлению однородного магнитного поля, индукция которого равна 1 Тл:

Электромагнитная индукция-явление возникновения электрического тока в замкнутом проводящем контуре при любом изменении магнитного потока, пронизывающего контур.

Возникающий в замкнутом контуре, индукционный ток имеет такое направление, что своим магнитным полем противодействует тому изменению магнитного потока, которым он вызван (правило Ленца).

ЗАКОН ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ

Опыты Фарадея показали, что сила индукционного тока I_i в проводящем контуре прямо пропорциональна скорости изменения числа линий магнитной индукции , пронизывающих поверхность, ограниченную этим контуром.

Поэтому сила индукционного тока пропорциональна скорости изменения магнитного потока через поверхность, ограниченную контуром:

Известно, что если в цепи появился ток, это значит, что на свободные заряды проводника действуют сторонние силы. Работа этих сил по перемещению единичного заряда вдоль замкнутого контура называется электродвижущей силой (ЭДС). Найдем ЭДС индукции ε_i.

По закону Ома для замкнутой цепи

Так как R не зависит от , то

ЭДС индукции совпадает по направлению с индукционным током, а этот ток в соответствии с правилом Ленца направлен так, что созданный им магнитный поток противодействует изменению внешнего магнитного потока.

Закон электромагнитной индукции

ЭДС индукции в замкнутом контуре равна взятой с противоположным знаком скорости изменения магнитного потока, пронизывающего контур:

Опыт показывает, что магнитный поток Ф , связанный с контуром, прямо пропорционален силе тока в этом контуре:

Индуктивность контура L — коэффициент пропорциональности между проходящим по контуру током и созданным им магнитным потоком.

Индуктивность проводника зависит от его формы, размеров и свойств окружающей среды.

Самоиндукция — явление возникновения ЭДС индукции в контуре при изменении магнитного потока, вызванном изменением тока, проходящего через сам контур.

Самоиндукция — частный случай электромагнитной индукции.

Индуктивность — величина, численно равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока в нем на единицу за единицу времени. В СИ за единицу индуктивности принимают индуктивность такого проводника, в котором при изменении силы тока на 1 А за 1 с возникает ЭДС самоиндукции 1 В. Эта единица называется генри (Гн):

ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ

Явление самоиндукции аналогично явлению инерции. Индуктивность при изменении тока играет ту же роль, что и масса при изменении скорости тела. Аналогом скорости является сила тока.

Значит энергию магнитного поля тока можно считать величиной, подобной кинетической энергии тела :

Предположим, что после отключения катушки от источника,ток в цепи убывает со временем по линейному закону.

ЭДС самоиндукции имеет в этом случае постоянное значение:

где I — начальное значение тока, t — промежуток времени, за который сила тока убывает от I до 0.

За время t в цепи проходит электрический заряд q = I_cpt . Так как I_cp = (I + 0)/2 = I/2 , то q=It/2 . Поэтому работа электрического тока:

Эта работа совершается за счет энергии магнитного поля катушки. Таким образом, снова получаем:

Пример. Определите энергию магнитного поля катушки, в которой при токе 7,5 А магнитный поток равен 2,3*10 -3 Вб. Как изменится энергия поля, если сила тока уменьшиться вдвое?

Энергия магнитного поля катушки W ₁ = LI ₁ 2 /2. По определению, индуктивность катушки L = Ф/I ₁. Следовательно,

Ответ: энергия поля равна 8,6 Дж; при уменьшении тока вдвое она уменьшится в 4 раза.

Магнитная индукция () — это векторная физическая величина, характеризующий магнитное поле. За направление вектора магнитной индукции принимается:

1. направление от южного полюса S к северному полюсу N магнитной стрелки, свободно устанавливающейся в магнитном поле, или

2. направление положительной нормали к замкнутому контуру с током на гибком подвесе, свободно устанавливающемся в магнитном поле. Положительной считается нормаль, направленная в сторону перемещения острия буравчика (с правой нарезкой), рукоятку которого вращают по направлению тока в рамке.

Ясно, что направления 1) и 2) совпадают, что было установлено еще опытами Ампера.

Что касается величины магнитной индукции (т. е. ее модуля) В, которая могла бы характеризовать силу действия поля, то экспериментами было установлено, что максимальная сила F, с которой ноле действует на проводник с током (помещенный перпендикулярно линиям индукции магнитного поля), зависит от силы тока I в проводнике и от его длины Δl (пропорциональна им). Однако сила, действующая на элемент тока (единичной длины и силы тока), зависит только от самого поля, т. е. отношение для данного поля является величиной постоянной (аналогично отношению силы к заряду для электрического поля). Эту величину и определяют как магнитную индукцию:

.

Индукция магнитного поля в данной точке равна отношению максимальной силы, действующей на проводник с током, к длине проводника и силе тока в проводнике, помещенном в эту точку.

Чем больше магнитная индукция в данной точке поля, тем с большей силой будет действовать поле в этой точке на магнитную стрелку или движущийся электрический заряд.

Единицей магнитной индукции в СИ является тесла (Тл), названная в честь хорватского электротехника Николы Теслы. Как видно из формулы, .

ИНДУКТИВНОСТЬ — это… Что такое ИНДУКТИВНОСТЬ?

ИНДУКТИВНОСТЬ

ИНДУКТИВНОСТЬ

свойство магнитного поля, создаваемого током проводника, при изменениях величины этого тока возбуждать в проводнике так наз. электродвижущую силу самоиндукции. Энергия возникающих при этом в проводнике индукционных токов образуется за счет энергии окружающего проводник магнитного поля. И. зависит от размеров и формы проводника и не зависит от его материала. Она велика для проводников, свитых в виде спирали, обмоток и разного рода приборов. Наибольшей И. обладают катушки с железным сердечником внутри, как, напр., обмотки электромагнитов и трансформаторов. И. зависит от числа витков этих обмоток (возрастая с его увеличением) и от материала стальных сердечников. Измеряется в генри.

Технический железнодорожный словарь. — М.: Государственное транспортное железнодорожное издательство. Н. Н. Васильев, О. Н. Исаакян, Н. О. Рогинский, Я. Б. Смолянский, В. А. Сокович, Т. С. Хачатуров. 1941.

.

Синонимы:

• ИНДУКТИВНОЕ СОПРОТИВЛЕНИЕ
• ИНДУКТОР

Смотреть что такое «ИНДУКТИВНОСТЬ» в других словарях:

• Индуктивность — Размерность L2MT−2I−2 Единицы измерения СИ Гн СГС …   Википедия

• ИНДУКТИВНОСТЬ — (от лат. inductio наведение, побуждение), величина, характеризующая магн. св ва электрич. цепи. Ток, текущий в проводящем контуре, создаёт в окружающем пр ве магн. поле, причём магнитный поток Ф, пронизывающий контур (сцепленный с ним), прямо… …   Физическая энциклопедия

• ИНДУКТИВНОСТЬ — ИНДУКТИВНОСТЬ, физическая величина, характеризующая магнитные свойства электрических цепей и равная отношению потока Ф магнитной индукции, пересекающего поверхность, ограниченную проводящим контуром, к силе тока в этом контуре, создающем Ф; в СИ… …   Современная энциклопедия

• индуктивность — индуктивность; статическая индуктивность; отрасл. коэффициент самоиндукции Скалярная величина, характеризующая связь потокосцепления самоиндукции с током в рассматриваемой электрической цепи, равная отношению потокосцепления самоиндукции этой… …   Политехнический терминологический толковый словарь

• индуктивность — Скалярная величина, равная отношению потокосцепления самоиндукции элемента электрической цепи к электрическому току в нем. [ГОСТ Р 52002 2003] Тематики электротехника, основные понятия Синонимы собственная индуктивность …   Справочник технического переводчика

• Индуктивность — ИНДУКТИВНОСТЬ, физическая величина, характеризующая магнитные свойства электрических цепей и равная отношению потока Ф магнитной индукции, пересекающего поверхность, ограниченную проводящим контуром, к силе тока в этом контуре, создающем Ф; в СИ… …   Иллюстрированный энциклопедический словарь

• ИНДУКТИВНОСТЬ — физическая величина, характеризующая магнитные свойства электрических цепей и равная отношению потока Ф магнитной индукции, пересекающего поверхность, ограниченную проводящим контуром, к силе тока в этом контуре, создающем Ф; в СИ измеряется в… …   Большой Энциклопедический словарь

• ИНДУКТИВНОСТЬ — ИНДУКТИВНОСТЬ, свойство электрической цепи или элемента цепи, создающий ЭЛЕКТРОДВИЖУЩУЮ СИЛУ (ЭДС) при изменении электрического тока. В системе СИ единицей измерения служит ГЕНРИ. Самоиндукция (обозначение L) имеет место при протекании тока по… …   Научно-технический энциклопедический словарь

• ИНДУКТИВНОСТЬ — ИНДУКТИВНОСТЬ, индуктивности, мн. нет, жен. (книжн. спец.). отвлеч. сущ. к индуктивный. Ииндуктивность доказательств. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 …   Толковый словарь Ушакова

• ИНДУКТИВНОСТЬ — мера магнитной энергии, возникающей вокруг данной цепи, когда через нее проходит определенный электрический ток. Наличие индуктивности всегда тормозит процесс изменений тока. Самойлов К. И. Морской словарь. М. Л.: Государственное Военно морское… …   Морской словарь

Явление самоиндукции и ее закономерности

Его можно предложить учащимся, как частный случай электромагнитной индукции, с использованием простейшей схемы замкнутого контура, в который включен генератор переменного тока. Сила тока в цепи такого генератора изменяется по закону синуса, что на графике выглядит так:

1. Формулируем проблему №1: Что должно наблюдаться в контуре, по которому течет переменный ток?

Для этого рассуждаем и одновременно составляем логическую цепочку:

Переменная ЭДС генератора создает в контуре изменяющийся  по величине и направлению переменный ток ~ I, создающий переменный собственный магнитный   поток ~ Фсобств, который пересекает контур, наводит в нем ЭДС самоиндукции . По закону Фарадея:

На «глазах» учащихся вырастает логическая цепочка 1, которую они составляют сознательно, понимают что новое явление – это частный случай явления электромагнитной индукции и сами формируют понятие самоиндукции, закономерности этого явления и вводят новое физическое понятие – индуктивность проводника, составляют формулу закона Фарадея для самоиндукции. А затем последовательно, пошагово раскрывают и уточняют, что наводится собственным магнитным потоком

(прямо пропорционален)

(прямо пропорционален)

То есть, скорость изменения собственного магнитного потока прямо пропорциональна скорости изменения тока в контуре.

Введя коэффициент пропорциональности L, запишем:

И тогда логическая цепочка запишется так:

Определение явления   самоиндукции

Это тоже закон Фарадея, который надо читать так:

Величина , возникшей в контуре при изменении тока в нем, прямо пропорциональна и зависит от L – индуктивности контура.

2. Формулируем проблему № 2: Понятие  индуктивности контура – это новая характеристика проводника, которой он обладает в электромагнитном поле.

Ее физический смысл:

под индуктивностью проводника L надо понимать такую , которая возникает в нем, если изменение тока в нем будет происходить на 1А за каждую секунду.

Следовательно, чем больше при , тем больше L проводника.

3. Упражнение: Индуктивность проводника L = 2Гн. Что это означает?

– Что при 

4. Обратить внимание на следующие правила:

1) все проводники обладают омическим сопротивлением:

2) все проводники в переменном электромагнитном поле обладают индуктивностью.

3) индуктивность проводника зависит от его формы и конструкции:

а)

б) у соленоида индуктивность зависит от числа витков, чем больше n, тем больше L.

в) у соленоида с сердечником индуктивность зависит от материала сердечника: Fe, Ni, Co.

где: n – число витков на 1 ед.длины, V – объем соленоида.

5. Итак, индуктивность – новое свойство проводника.

Оно созвучно с мерой инертности по отношению к изменению тока в контуре. Чем больше индуктивность проводника L_s, тем изменение силы тока в проводнике происходит медленнее.

6. Вопрос на развитие физической логики: что же будет происходить в данном контуре?

 должен препятствовать изменению силы тока в цепи, и поэтому изменение силы тока в контуре будет отставать от изменения  на клеммах контура по фазе.

будет тормозить нарастание тока в контуре и тормозить его убывание по правилу Ленца.

7. Роль в технике: действует в каждое мгновение при изменении тока в цепи, например, в момент включения и выключения освещения, холодильника, и т.д. Особенно опасно ее действие в момент размыкания рубильников в цепи, содержащих большие индуктивности. поддерживает убывание тока и может во много раз превысить напряжение сети. Тогда при размыкании цепи возникают экстратоки (искры), которые плавят рубильник. Чтобы погасить экстратоки, рубильники помещают в масло, гасящее искру. Правило устройств электроустановок учитывает это опасное свойство. Энергия тока и созданного им магнитного поля вначале запасается в контуре в виде , а потом, в момент размыкания всегда выделяется в виде мощной искры.

Разберем явление самоиндукции, наблюдаемое в контуре Б:

1) В момент замыкания цепи:

, которая тормозит нарастание тока

2) В момент размыкания:

, которая тормозит нарастание тока

8.  играет положительную роль в радиотехнике для получения электромагнитных колебаний. Без нее была бы невозможна радиосвязь и телевидение.

При решении расчетных задач на явление самоиндукции я использую ту же систему алгоритмизации, что и при прохождении темы «Электромагнитная индукция», изложенной в личном кабинете.

Общий анализ самоиндукции:

1)

2) Фсобств = L ^.I

Расчет индуктивностей.

Общее выражение для взаимной индуктивности двух контуров произвольной формы

Расчет индуктивностей. Общее выражение для взаимной индуктивности двух контуров произвольной формы (рис. 3.5), выполненных из немагнитного материала и расположенных в воздухе, выглядит следующим образом:

где V₁ и V₂ – объемы пространства, занимаемого первым и вторым контуром; r – расстояние от элемента объема dv₁ первого контура до элемента объема dv₂ второго контура; – вектор плотности тока в точках элемента объема dv₁; – вектор плотности тока в точках элемента объема dv₂.

Как было отмечено выше, при m = const взаимная индуктивность не зависит от токов в контурах. Наличие токов в последнем выражении не противоречит этому положению, поскольку при постоянных токах их можно внести под знаки интегралов, и тогда в подынтегральном выражении получим отношение плотности тока к соответствующему току, которое определяется только формой проводника.

Общее выражение для собственной индуктивности контура можно получить, пользуясь общим выражением для взаимной индуктивности двух контуров. Для этого необходимо представить два совершенно одинаковых контура, сближающихся до полного слияния так, что один из них занимает объем другого. После такого слияния, по существу, уже остается только один контур. Из выражения для М₂₁ нетрудно получить выражение для L такого контура, положив I₁ = I₂ = I и V₁ = V₂ = V. Имеем

причем – плотность тока в элементе dv; – плотность тока в элементе dv^/ одного и того же проводника; r – расстояние между этими элементами объема. Интегрирование производится дважды по всему объему проводника V. Формулы для индуктивности весьма упрощаются для контуров из линейных проводников, поперечные размеры сечений которых весьма малы. При вычислении собственной индуктивности таких проводников ее подразделяют на внутреннюю (L_ВТ) и внешнюю (L_ВШ) и общую индуктивность определяют путем их суммирования.

Ниже приведены выражения для индуктивностей простейших систем.

Индуктивность тонкого цилиндрического проводника длиной l и радиусом R (длина много больше радиуса)

.

Индуктивность отрезка цилиндрического проводника длиной l и радиусом R

Индуктивность двухпроводной линии на длине l

.

Здесь D – расстояние между проводами; R – радиус проводов (R << D).

Индуктивность параллельных цилиндров длиной l, с радиусами R₁ и R₂ и расстоянием между осями D

.

Индуктивность круглого кольца радиусом r из тонкого цилиндрического провода диаметром d

Если провод выполнен из неферромагнитного материала, то

Индуктивность прямоугольной рамки из тонкого круглого провода

Здесь а и b – длины сторон рамки; d – диагональ рамки; r – радиус провода (r << а; r << b).

Индуктивность проводников.

Нужна помощь в написании работы?

Пусть есть виток, по которому течёт ток. Этот ток создаёт собственное магнитное поле, следовательно, можно посчитать магнитный поток  в этом витке .

Нельзя ли при некоторых условиях записать формулу проще Магнитный поток зависит от тока (закон Био-Савара) и от геометрии витка (круглый, квадратный и т.д.). Попробуем описать поток так ;  — некоторое число характеризующее геометрию витка.  — индуктивность проводника.

;

 .

Т.е. при наличии тока  проводник может деформировать самого себя. Если проводник жёсток то , тогда

.

Пример: Найдём индуктивность катушки о которой известно: длина ;  — число витков. Пусть .

Внимание!

Если вам нужна помощь в написании работы, то рекомендуем обратиться к профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные корректировки и доработки. Узнайте стоимость своей работы.

Найдём магнитный поток в контуре L , который охватывает всю катшку и одним ребром уходит на бесконечность. Тогда .

.

; .

Пусть площадь сечения — . B – однородно.

,

.

Замечание: На краях поле не однородно, но т.к.  то пренебрегаем этой погрешностью, т.е. краевые эффекты считаем незначительными.

Поможем написать любую работу на аналогичную тему

Получить выполненную работу или консультацию специалиста по вашему учебному проекту

Узнать стоимость Поделись с друзьями

Индуктивность

• Изучив этот раздел, вы сможете описать:
• • Единица индуктивности.
• • Факторы, влияющие на индуктивность.
• • Напряжение и э.д.с.
• • Самоиндукция.
• • Обратный э.м. и его эффекты.

Индуктивность

Ток, генерируемый в проводнике изменяющимся магнитным полем, пропорционален скорости изменения магнитного поля.Этот эффект называется ИНДУКТИВНОСТЬЮ и обозначается символом L. Он измеряется в единицах, называемых генри (H), названных в честь американского физика Джозефа Генри (1797-1878). Один генри — это величина индуктивности, необходимая для создания ЭДС в 1 вольт в проводнике, когда ток в проводнике изменяется со скоростью 1 ампер в секунду. Генри — довольно крупная единица измерения для использования в электронике, чаще всего используются миллигенри (мГн) и микрогенри (мкГн). Эти единицы описывают одну тысячную и одну миллионную генри соответственно.

Хотя генри обозначается символом (заглавной) H, имя Генри применяется к единице индуктивности с использованием строчной буквы h. Форма множественного числа генри может быть генри или генри; Американский национальный институт стандартов и технологий рекомендует использовать в публикациях США генри.

Факторы, влияющие на индуктивность.

Величина индуктивности в катушке индуктивности зависит от:

• а. Количество витков провода в индукторе.
• г.Материал сердечника.
• г. Форма и размер сердечника.
• г. Форма, размер и расположение проволоки, из которой состоят катушки.

Поскольку индуктивность (в генри) зависит от множества переменных величин, ее довольно сложно рассчитать точно; были разработаны многочисленные формулы, учитывающие различные особенности конструкции. Также в этих формулах часто необходимо использовать специальные константы и таблицы данных преобразования для работы с необходимой степенью точности.Использование компьютерных программ и систем автоматизированного проектирования несколько облегчило ситуацию. Однако внешние эффекты, вызванные другими компонентами и проводкой рядом с индуктором, также могут повлиять на его значение индуктивности после его сборки в цепь, поэтому, когда требуется точное значение индуктивности, одним из подходов является расчет приблизительного значения и разработка индуктор так, чтобы он был регулируемым.

Типичная формула для аппроксимации значения индуктивности катушки индуктивности приведена ниже.Эта конкретная версия предназначена для расчета индуктивности «соленоида, намотанного одним слоем витков бесконечно тонкой ленты, а не проволоки, и с равномерно и близко расположенными витками».

Рис. 3.2.1 Миниатюрный индуктор переменного тока.

Где:

• L — индуктивность в генри.
• d — диаметр рулона в метрах.
• n — количество витков в катушке.
• l — длина змеевика в метрах.

Для катушек, не соответствующих в точности указанным выше спецификациям, необходимо учитывать дополнительные факторы. На рис. 3.2.1 показан один из способов получения достаточно точной индуктивности, используемый в некоторых ВЧ и ВЧ схемах. Миниатюрная катушка индуктивности намотана на пластмассовый каркас, в который достаточно ввинчен ферритовый (железная пыль) сердечник, чтобы обеспечить сердечник с нужной индуктивностью.

Напряжение и э.д.с.

Напряжение , индуцированное в проводнике, называется e.м.ф. (электродвижущая сила), потому что ее источником является изменяющееся магнитное поле вокруг проводника и вне его. Любое внешнее напряжение (в том числе создаваемое внешней батареей или источником питания) называется э.д.с., в то время как напряжение (разность потенциалов или п.о.) на внутреннем компоненте в цепи называется напряжением.

Задний э.д.с.

Обратная ЭДС (также называемая ЭДС счетчика) — это ЭДС, создаваемая через индуктор изменяющимся магнитным потоком вокруг проводника, вызванным изменением тока в индукторе.Его значение можно рассчитать по формуле:

Где:

• E — наведенная обратная ЭДС. в вольтах
• L — индуктивность катушки в генри.
• ΔI — изменение силы тока в амперах.
• Δt — время изменения тока в секундах.

Примечания:

Δ (греч. D — дельта) обозначает различие или изменение свойства.

Итак, формула описывает обратную ЭДС как зависимость от индуктивности (в генри), умноженную на скорость изменения тока (в амперах в секунду).

Знак минус перед L указывает, что полярность наведенной обратной ЭДС будет обратной по сравнению с изменяющимся напряжением на проводнике, которое первоначально вызвало изменение тока и, как следствие, изменение магнитного поля.

Помните, что при работе с практическими значениями милли или микрогенри все значения, используемые в формуле, должны быть преобразованы в стандартные значения генри-ампер и секунд, как описано в нашем буклете «Советы по математике».

Пример

Поскольку значение обратной ЭДС зависит от скорости изменения тока, оно будет наибольшим, когда произойдет самое быстрое изменение.Например, скорость изменения чрезвычайно высока всякий раз, когда ток через катушку индуктивности отключается; тогда изменение может быть от максимума до нуля всего за несколько миллисекунд.

Представьте, что катушка индуктивности 200 мГн, подключенная к источнику питания 9 В, пропускает ток силой 2 ампера. Когда ток отключается, он падает до нуля через 10 мсек. Какой будет обратная ЭДС, генерируемая на катушке?

E = 200 мГн x 2 А / 10 мс

или

E = 200 x 10 ^-3 x 2/10 x 10 ^-3

= 40 вольт

Значит, обратная ЭДС, возникающая при выключении, более чем в 4 раза превышает напряжение питания!

Эти высоковольтные импульсы, возникающие при отключении индуктивного компонента, такого как двигатель или катушка реле, могут потенциально вызвать повреждение выходного транзистора или интегральной схемы, переключающей устройство.Поэтому существенная защита обеспечивается включением диода в выходной каскад, как показано на рис. 3.2.2 и 3.2.3

Задняя защита от ЭДС

Рис. 3.2.2 Задний Э.

д.с. Защитный диод.

Защитный диод на рис. 3.2.2, подключенный к катушке индуктивности, обычно имеет обратное смещение, поскольку напряжение на его катоде, подключенном к шине питания + V, будет более положительным, чем его анод на коллекторе транзистора. Однако при выключении на индукторе появляется большой всплеск напряжения противоположной полярности из-за схлопывающегося магнитного поля.Во время этого скачка напряжения коллектор транзистора может находиться под более высоким потенциалом, чем питание, за исключением того, что если это произойдет, диод станет смещенным в прямом направлении и предотвратит повышение напряжения коллектора выше, чем на шине питания.

Рис. 3.2.3 Защитные диоды в ULN2803.

На рис. 3.2.3 показан популярный I.C. (ULN2803) для переключения индуктивных нагрузок. Выходы восьми инвертирующих усилителей защищены диодом, общие катоды которого подключены к положительной шине питания + V на выводе 10.

Самоиндукция

Принцип работы самоиндукции зависит от двух взаимосвязанных действий, происходящих одновременно, и от каждого из этих действий в зависимости от другого.

Действие 1.

Любой проводник, в котором изменяется ток, будет создавать вокруг себя изменяющееся магнитное поле.

Действие 2.

Любой проводник в ИЗМЕНЯЕМОМ магнитном поле будет иметь изменяющуюся ЭДС, наведенную в него.Величина этой наведенной ЭДС и величина индуцированного тока, который она производит в проводнике, будут зависеть от скорости изменения магнитного поля; чем быстрее изменяется поток поля, тем больше будет наведенная ЭДС. и его последующий ток.

Эффект индукции индуктором эдс в самом себе называется самоиндукцией (но часто его называют просто индукцией). Когда катушка индуктивности индуцирует ЭДС в отдельную соседнюю катушку индуктивности, это называется взаимной индукцией и является свойством, используемым трансформаторами.

Изменяющееся магнитное поле, создаваемое вокруг проводника изменяющимся током в проводнике, вызывает изменение ЭДС в этом проводнике. Эта изменяющаяся ЭДС, в свою очередь, создает переменный ток, текущий в направлении, противоположном исходному току. Таким образом, изменения в этом токе противодействуют изменениям в исходном токе.

Таким образом, действие 2 ограничивает изменения, происходящие из-за действия 1. Если исходный ток увеличивается, индуцированный ток замедляет скорость увеличения.Точно так же, если исходный ток уменьшается, индуцированный ток замедляет скорость уменьшения. Общий результат этого — уменьшение амплитуды переменного тока через катушку индуктивности и, таким образом, уменьшение амплитуды переменного напряжения на катушке индуктивности.

Поскольку сила магнитного поля, создаваемого исходным током, зависит от скорости (скорости) изменения тока, индуктор уменьшает поток переменного тока (AC) больше на высоких частотах, чем на низких.Этот ограничивающий эффект, создаваемый наведенной ЭДС, будет сильнее на более высоких частотах, потому что на высоких частотах ток и, следовательно, поток изменяются быстрее. Этот эффект получил название «Индуктивное реактивное сопротивление».

Индуктивное реактивное сопротивление.

Реактивное сопротивление создает сопротивление потоку переменного тока. Как и сопротивление, оно измеряется в Ом, но поскольку сопротивление имеет одно и то же значение на любой частоте, а сопротивление переменному току в индукторах зависит от частоты, его нельзя назвать сопротивлением.Вместо этого он называется Reactance (X). Конденсаторы также обладают свойством реактивного сопротивления, но они по-разному реагируют на частоту, поэтому существует два типа реактивного сопротивления; индукторы имеют индуктивное реактивное сопротивление (X _L ), а конденсаторы — емкостное реактивное сопротивление (X _C ).

[решено] Индуктивность катушки зависит от того, какое из следующих значений f

Вопрос:

Бесплатная практика с пробными тестами из тестовой тетради

Опции:

1. Тип обмотки


2. Количество витков


3. Материал проводника


4. Все вышеперечисленное

Правильный ответ:

Вариант 4 (Решение ниже)

Этот вопрос ранее задавали в

MPSC Помощник инженера EE Mains 2019 — Документ 2

Решение:

Скачать вопрос с решением PDF ››

Концепт :

Индуктивность катушки определяется как:

\ (L = \ frac {{μ {N ^ 2} A}} {l} \)

N = количество витков в катушке

A = Площадь поперечного сечения

l = длина змеевика

μ = магнитная проницаемость катушки

Заявка:

Из приведенного выше выражения индуктивность зависит от

Количество витков в катушке:

• При прочих равных условиях большее количество витков провода в катушке приводит к большей индуктивности; чем меньше витков провода в катушке, тем меньше индуктивность.
• Больше витков провода означает, что катушка будет генерировать большее количество силы магнитного поля (измеряется в ампер-витках) для данного количества тока катушки.

Площадь змеевика:

• При прочих равных условиях большая площадь катушки (при измерении в продольном направлении через катушку в поперечном сечении сердечника) приводит к большей индуктивности; меньшая площадь катушки приводит к меньшей индуктивности.
• Большая площадь катушки представляет меньшее сопротивление формированию потока магнитного поля для данной величины силы поля (ампер-витки).

Длина рулона:

• При прочих равных условиях, чем больше длина катушки, тем меньше индуктивность; чем короче длина катушки, тем больше индуктивность.
• Более длинный путь для потока магнитного поля приводит к большему сопротивлению формированию этого потока для любой заданной величины силы поля (ампер-витков).

Основной материал:

• При прочих равных условиях, чем больше магнитная проницаемость сердечника, вокруг которого намотана катушка, тем больше индуктивность; чем меньше проницаемость сердечника, тем меньше индуктивность.
• Материал сердечника с большей магнитной проницаемостью приводит к большему потоку магнитного поля для любой заданной величины силы поля (ампер-витков).

Скачать вопрос с решением PDF ››

Сопротивление проводника — Energy Education

Рис. 1. Нить накаливания загорается из-за сопротивления проводящего провода. ^[1]

Сопротивление проводника — это свойство проводника при определенной температуре, и оно определяется как величина сопротивления протеканию электрического тока через проводящую среду. ^[2] Сопротивление проводника зависит от площади поперечного сечения проводника, длины проводника и его удельного сопротивления. Важно отметить, что электрическая проводимость и удельное сопротивление обратно пропорциональны, а это означает, что чем больше проводимость, тем меньше сопротивление.

Сопротивление проводника можно рассчитать при температуре 20 ° C по следующей формуле: ^[3]

[математика] \ R = \ frac {\ rho L} {A} [/ математика]

где:

• [math] R [/ math] — сопротивление в омах (Ом)
• [math] \ rho [/ math] — удельное сопротивление материала в омметрах (Ом · м)
• [math] L [/ math] — длина проводника в метрах (м)
• [math] A [/ math] — площадь поперечного сечения проводника в метрах в квадрате (м ² )

Эта формула говорит нам, что сопротивление проводника прямо пропорционально [математике] \ rho [ / math] и [math] L [/ math], и обратно пропорционально [math] A [/ math].Поскольку сопротивление некоторого проводника, например отрезка провода, зависит от столкновений внутри самого провода, сопротивление зависит от температуры. С повышением температуры сопротивление провода увеличивается, так как столкновения внутри провода увеличиваются и «замедляют» протекание тока. Величина изменения определяется температурным коэффициентом. ^[4] Положительный температурный коэффициент приводит к увеличению сопротивления с повышением температуры, тогда как отрицательный температурный коэффициент приводит к уменьшению сопротивления с повышением температуры.Поскольку проводники обычно демонстрируют повышенное удельное сопротивление с повышением температуры, они имеют положительный температурный коэффициент. Наиболее распространенные типы резисторов — это переменные резисторы и постоянные резисторы.

Используя сопротивление проводника, можно создать свет в лампе накаливания. В лампочке накаливания есть проволочная нить определенной длины и ширины, обеспечивающая определенное сопротивление. Если это сопротивление правильное, ток, протекающий через провод, замедляется ровно настолько, без остановки из-за слишком большого сопротивления, что нить накала нагревается до точки, в которой она начинает светиться. ^[5]

Подробнее о сопротивлении проводника см. HyperPhysics.

PhET: Сопротивление в проводе

Университет Колорадо любезно разрешил нам использовать следующую симуляцию Фета. Изучите моделирование, чтобы увидеть, как изменяется сопротивление проводника в зависимости от геометрии и удельного сопротивления:

Для дальнейшего чтения

Для получения дополнительной информации см. Соответствующие страницы ниже:

Список литературы

Параметры линии передачи Сопротивление и индуктивность

Линии передачи моделируются с помощью параметров сопротивления, индуктивности, емкости и проводимости.Сопротивление и индуктивность вместе называются импедансом линии передачи. Параллельная емкость и проводимость также называется проводимостью. Здесь мы не собираемся выводить формулы, а только для разработки некоторых концепций о параметрах линии передачи. Это поможет нам понять моделирование линии передачи и анализ энергосистемы. В этой статье мы обсудим сопротивление и индуктивность линии. В следующей статье мы обсудим емкость и проводимость линии.

Сопротивление

Жилы линий электропередачи имеют небольшое сопротивление. Для коротких линий важную роль играет сопротивление. По мере увеличения линейного тока возрастают омические потери (потери I ² R). Когда ток превышает определенное значение, тепло, выделяемое из-за омических потерь, начинает плавить проводник, и проводник становится длиннее, что приводит к большему провисанию. Ток, при котором это состояние проводника необратимо, называется тепловым пределом проводника.Короткие воздушные линии должны эксплуатироваться в пределах этого лимита.
Сопротивление R провода длиной l и сечением a определяется по формуле

  l.
                 R = ρ ----
                         а
  

Здесь ρ — постоянное удельное сопротивление материала проводника. В линиях электропередачи обычно используются проводники ACSR со спирально скрученными жилами.Таким образом, фактическая длина проводника примерно на 2% больше, чем длина проводника ACSR. Таким образом, из приведенной выше формулы сопротивление линии на 2% больше, чем длина проводника. Другим важным фактором является то, что при увеличении частоты тока плотность тока увеличивается по направлению к поверхности проводника, а плотность тока в центре проводника становится меньше. Это означает, что больше тока течет к поверхности проводника и меньше — к центру. Это хорошо известный скин-эффект.Даже на промышленной частоте (60/50 Гц) из-за этого скин-эффекта эффективная площадь поперечного сечения проводника меньше. Опять же из приведенного выше уравнения ясно, что сопротивление проводника больше для более высокой частоты. Таким образом, сопротивление проводника переменному току больше, чем сопротивление постоянному току. Еще одним фактором, влияющим на сопротивление проводника, является температура. Сопротивление линейно зависит от температуры. Производители указывают сопротивление проводника, и следует использовать данные производителя.
Индуктивность

Для линий средней и большой протяженности индуктивность (реактивное сопротивление) преобладает над сопротивлением. Величина тока, протекающего в проводнике, связана с другим параметром — индуктивностью. Мы знаем, что магнитное поле связано с проводником с током. В линии передачи переменного тока этот ток изменяется синусоидально, поэтому соответствующее магнитное поле, которое пропорционально току, также изменяется синусоидально.Это изменяющееся магнитное поле индуцирует в проводнике ЭДС (или индуцированное напряжение). Эта ЭДС (или напряжение) противодействует току, протекающему в линии. Эта ЭДС эквивалентно отображается параметром, известным как индуктивность. Значение индуктивности зависит от относительной конфигурации проводника и магнитного поля. Индуктивность на простом языке — это поток, связанный с проводником, деленный на ток, протекающий в проводнике. При расчете индуктивности учитываются потоки внутри и снаружи проводника.Полученная таким образом индуктивность и есть полная индуктивность. Далее, если не упомянуто исключительно, индуктивность означает полную индуктивность, обусловленную внутренней и внешней потокосцеплением проводника. Символ L используется повсеместно для обозначения индуктивности. L измеряется в Генри (H). Обычно он выражается в меньших единицах, миллигенри (мГн). Производители обычно указывают значение индуктивности на километр или милю.
Следует отметить, что во всех приведенных ниже формулах индуктивность L выражается в Генри на единицу длины, а не просто в Генри.Здесь изображено несколько случаев.

• Для однофазной линии см. Рис-A. Индуктивность проводника

L = 2 * 10 ^-7 ln (D / r ₁ ^‘)

Здесь D — расстояние между центрами проводников.

r ₁ ^‘ = r ₁ * e ^{— (1/4)} = 0,7788 r ₁

r1 — фактический радиус проводника.

Для однофазной линии обратный путь также имеет индуктивность, скажем, L ‘.Если обратный провод имеет радиус r2, то

L ^‘ = 2 * 10 ^-7 ln (D / r ₂ ^‘ )

Следовательно, общая индуктивность однофазной цепи Lt = L + L ‘
переставляя, получаем

L _t = 4 * 10 ^-7 ln [D / √ (r ₁ ^‘ . R ₂ ^‘)]

• Для трехфазной цепи, у которой три круглых проводника находятся в углах равностороннего треугольника (Рис-B (i)), здесь применяется приведенная выше формула для однофазного случая.В этом случае индуктивность на фазу L равна:
.

Если Знаменатель переименован в Ds, то

L = 2 * 10 ^-7 ln (D / D _s )

Здесь Ds = r ‘

Как уже было сказано, r’ в 0,7788 раз больше фактического радиус (r) проводника.

• Для трехфазной цепи, в которой три круглых проводника расположены произвольно (Рис-B (ii)), а проводники переставлены, тогда

L = 2 * 10 ^-7 ln [∛ (D ₁ .Д ₂ . D ₃ ) / D _s ]

Начиная с однофазной линии, можно заметить, что все три уравнения для индуктивности фазного проводника аналогичны. Помните, что эта формула для трехфазной линии недействительна для неперемещенных линий.

Наблюдая формулу для однофазных и трехфазных линий, мы можем обобщить формулу для индуктивности фазной линии в виде

L = 2 * 10 ^-7 ln (D / D _s )

Где
D = среднее геометрическое расстояние (GMD)
D _s = средний геометрический радиус (GMR)

В однофазном случае GMD — это просто расстояние между центрами двух проводников.
В трехфазном случае для проводников, равноудаленных друг от друга, GMD — это расстояние между любыми двумя фазными проводниками.
В трехфазном случае для линейных проводников произвольно помещается GMD = ∛ (D ₁ D ₂ D ₃ )

Во всех трех случаях D _s = r ‘.

• Из вышесказанного можно сделать вывод, что GMD — это эквивалентное расстояние между проводниками. Когда два или более проводов на фазу используются, как в жгутах проводов, необходимо рассчитать GMD.Здесь вычисляются расстояния от каждого проводника в одной фазе до каждого проводника в другой фазе. Если, например, в однофазной линии есть 4 проводника в одной фазе и 3 проводника в другой фазе (Рис-C), то у нас будет 12 номеров расстояний между проводниками. Я показал только четыре дистанции.

GMD = [D ₁ . D ₂ …….. D ₁₂ ] ^1/12

Итак, здесь GMD — это корень 12-й степени из произведения 12 чисел расстояний.

• GMR рассчитывается для каждой фазы отдельно. Каждая из фаз может иметь разные значения GMR в зависимости от размера и расположения проводника. GMR следует рассчитывать, когда каждая фаза состоит из более чем одного проводника на фазу, как в приведенном выше примере. Для расчета GMR, когда используются два или более проводников на фазу, определяется первое произведение всех групп (одна группа для каждого проводника), где каждая группа является произведением возможных расстояний от одного проводника до других проводников, включая r ‘этого проводника.В приведенном выше примере GMR для линии с 3 проводниками на фазу составляет
.

GMR = [(r ₁ ^‘ .D ₁₂ .D ₁₃ ) (r ₂ ^‘ .D ₂₃ .D ₂₁ ) (r ₃ ^‘. D ₃₁ .D ₃₂ )] ^1/9

Следует отметить, что D ₁₂ = D ₂₁ , D ₁₃ = D ₃₁ и D ₂₃ = D ₃₂

Для трех проводов на фазу (тройной провод)
GMR = ∛ (Ds * d ² )

Для четырех проводов на фазу (четырехжильный провод)
GMR = 1.09 ∜ (Ds * d ³ )


Как рассчитать GMD трехфазной линии с жгутом проводов? В качестве примера см. Рис. E, где трехфазные пучки (тройная проводимость) размещены горизонтально на опорах электропередачи. В этом случае расстояние между проводниками (D) принимается как расстояние между центрами жгутов проводов.

Итак, GMD = ∛ (D.D.2D)

Вы также можете рассчитать, учитывая расстояние от каждого связанного провода одной фазы до других проводов двух других фаз. Но рассчитанная GMD не сильно отличается от нашей простой формы, приведенной выше. Это связано с тем, что D значительно больше d.

• Для проводов ACSR GMR указывается производителем.Если этот GMR называется Ds. Например, если два таких проводника ACSR (сдвоенный провод) используются в пучке для каждой фазы. GMR схемы фазовых проводов вычисляется, предполагая, что подаваемое GMR (или Ds) является эквивалентным радиусом проводника ACSR.

Следовательно, если d — это расстояние между центрами двух проводников ACSR, аналогично формулам в
Фиг.-D,

GMR = [(D _s .d). (D _s .d)] ^1/4 = √ (D _s . d)

• Мы обсудим индуктивность и емкость для двойной цепи после обсуждения емкости линии в следующей статье.

Обычно не всегда удается расположить фазовые линии на опорах равномерно. Чтобы сделать индуктивность и емкость всех трех фаз почти равными, проводники меняются местами.Это означает, что проводники меняют положение после 1/3 длины линии. Путем перестановки индуктивность и емкость всех трех фазных линий становятся почти равными. Это помогает уравновесить трехфазные напряжения на приемном конце линии. Хотя приведенные выше формулы получены с учетом транспонирования, те же формулы также используются для неперемещенных случаев для получения приблизительных значений.

Емкость и проводимость линии передачи

Факторы, от которых зависит емкость проводника

Емкость проводника прямо пропорциональна площади пластин, а емкость обратно пропорциональна расстоянию между пластинами.

Факторы, от которых зависит емкость проводника.

Согласно определению емкости C = Q / V. Таким образом, для фиксированного количества зарядов факторы, от которых изменяется потенциал проводника, емкость также будет изменяться в зависимости от этих факторов. Причины изменения следующие:

(a) Площадь проводника: Чем больше увеличивается площадь, тем больше увеличивается емкость. Мы знаем, что для сферического проводника C = 4πε ₀ ε _r r.Таким образом, с увеличением r увеличивается и площадь, а также увеличивается ее емкость C. Это вообще верно для всех проводников.

(b) Среда, окружающая проводник: Емкость проводника зависит от диэлектрической проницаемости окружающей его среды. Емкость проводника больше, чем у среды с более высокой диэлектрической проницаемостью, а емкость будет меньше для среды с более низкой диэлектрической проницаемостью. Если емкость проводника в воздушной среде или в вакууме равна C ₀ , а для среды с диэлектрической проницаемостью ε _r — C _k , то из уравнения (емкость конденсатора) можно показать, что,

ε _r = C _k / C ₀

= [Емкость проводника в любой среде / Емкость этого проводника в воздухе или в вакууме]

(c) Расстояние между пластинами : Уменьшение емкости из-за увеличения расстояния между пластинами параллельного пластинчатого конденсатора и обратное верно, когда расстояние уменьшается.

(d) Наличие проводника с любым другим проводником или заземленным проводником: Если существует какой-либо другой неизменный или заземленный проводник с заряженным проводником, то из-за электрической индукции емкость экспериментального проводника увеличится. Но если аналогично заряженное тело присутствует рядом с заряженным проводником, емкость экспериментального проводника будет уменьшаться, а если присутствует противоположно заряженное тело, то емкость увеличится.

Существует несколько факторов, от которых зависит сопротивление, а именно: Сопротивление проводника в первую очередь зависит от материала, из которого он сделан.Сопротивление — это не что иное, как противодействие на пути свободных электронов проводника.

• Удельное сопротивление: Сопротивление зависит от удельного сопротивления, которое является константой пропорциональности и зависит от природы вещества и температуры.
• Температура: Температура является жизненно важным фактором при определении сопротивления проводника. С повышением температуры значение удельного сопротивления увеличивается, поэтому сопротивление увеличивается.Таким образом, в случае повышения температуры сопротивление уменьшается.
• Длина: Сопротивление прямо пропорционально длине. Таким образом, с увеличением длины увеличивается значение сопротивления.
• Удельная проводимость: Это свойство указывает, сколько вещество будет проводить. Это свойство зафиксировано для фиксированного материала.
• Площадь поперечного сечения: Сопротивление обратно пропорционально площади поперечного сечения.Чем больше площадь поперечного сечения, тем меньше сопротивление. Таким образом, с увеличением площади поперечного сечения значение сопротивления уменьшается. Точно так же длина прямо пропорциональна длине проводника. Чем больше длина, тем больше сопротивление.

7.14: Индуктивность коаксиальной структуры

Давайте теперь определим индуктивность коаксиальной структуры, показанной на рисунке \ (\ PageIndex {1} \). Индуктивность этой структуры представляет интерес по ряду причин, в частности, для определения характеристического импеданса коаксиальной линии передачи, как описано в разделе 3.10.

Рисунок \ (\ PageIndex {1} \): Определение индуктивности коаксиальной линии.

Для наших настоящих целей мы можем смоделировать структуру, как показано на рисунке \ (\ PageIndex {1} \). Эта модель состоит из двух концентрических идеально проводящих цилиндров радиусов \ (a \) и \ (b \), разделенных однородным материалом с проницаемостью \ (\ mu \). Чтобы облегчить анализ, разместим ось \ (+ z \) вдоль общей оси концентрических цилиндров, чтобы цилиндры можно было описать как поверхности \ (\ rho = a \) и \ (\ rho = b \ ).

Ниже мы найдем индуктивность, принимая ток \ (I \) на внутреннем проводнике и интегрируя по результирующему магнитному полю, чтобы получить магнитный поток \ (\ Phi \) между проводниками. Затем индуктивность может быть определена как отношение потока отклика к току источника.

Прежде чем мы начнем, обратите внимание, что вывод, который мы собираемся сделать, аналогичен выводу емкости коаксиальной структуры, рассмотренной в разделе 5.24. Читателю может быть полезно ознакомиться с этим разделом, прежде чем пытаться сделать это.

Первый шаг — найти магнитное поле внутри конструкции. Это относительно просто, если мы можем пренебречь краевыми полями, поскольку тогда внутреннее поле можно считать постоянным по отношению к \ (z \). Этот анализ также применим к случаю, когда длина \ (l \) относится к одному короткому участку гораздо более длинной конструкции; в этом случае мы получим индуктивность на длину , а не полную индуктивность конструкции. Обратите внимание, что последнее — именно то, что нам нужно для модели эквивалентной схемы с сосредоточенными элементами (раздел 3.4).

Для определения индуктивности мы используем определение: \ [L \ треугольник \ frac {\ Phi} {I} \ label {m0125_eIndDef} \] Ток \ (I \), текущий в направлении \ (+ z \) на внутренний проводник создает магнитное поле внутри коаксиальной структуры. Напряженность магнитного поля для этого сценария была определена в разделе 7.5, где мы нашли \ [{\ bf H} = \ hat {\ phi} \ frac {I} {2 \ pi \ rho} ~~, ~~ a \ le \ rho \ le b \] Читатель должен заметить, что в этом разделе мы рассматривали просто линию тока; не коаксиальная структура.Итак, на каком основании мы утверждаем, что поле внутри коаксиальной структуры одинаково? Это следствие закона Ампера (раздел 7.14): \ [\ oint _ {\ mathcal C} {\ bf H} \ cdot d {\ bf l} = I_ {encl} \] Если в этой новой задаче мы укажем то же круговой путь \ (\ mathcal {C} \) с радиусом больше \ (a \) и меньше \ (b \), тогда заключенный ток будет просто \ (I \). Наличие внешнего проводника не меняет радиальную симметрию проблемы, и больше ничего не остается, что могло бы изменить исход.Это стоит отметить для справки в будущем:

Магнитное поле внутри коаксиальной структуры, состоящей из концентрических проводников, несущих ток \ (I \), идентично магнитному полю линейного тока \ (I \) в свободном пространстве.

Нам понадобится плотность магнитного потока (\ ({\ bf B} \)) в отличие от \ ({\ bf H} \), чтобы получить магнитный поток. Это просто, поскольку они связаны проницаемостью среды; то есть \ ({\ bf B} = \ mu {\ bf H} \). Таким образом: \ [{\ bf B} = \ hat {\ phi} \ frac {\ mu I} {2 \ pi \ rho} ~~, ~~ a \ le \ rho \ le b \]

Затем мы получаем \ (\ Phi \) путем интегрирования по плотности магнитного потока \ [\ Phi = \ int _ {\ mathcal S} {{\ bf B} \ cdot d {\ bf s}} \] где \ ( \ mathcal {S} \) — это любая открытая поверхность, через которую должны проходить все силовые линии магнитного поля внутри конструкции.{b} \ frac {d \ rho} {\ rho} \ right) \\
& = \ frac {\ mu I l} {2 \ pi} \ ln \ left (\ frac {b} {a} \ right )
\ конец {выровнено}

Заключение: \ [L \ треугольник \ frac {\ Phi} {I} = \ frac {\ left (\ mu Il / 2 \ pi \ right) \ ln \ left (b / a \ right)} {I} \] Обратите внимание, что множители \ (I \) в числителе и знаменателе сокращаются, оставляя: \ [\ boxed {L = \ frac {\ mu l} {2 \ pi} \ ln \ left (\ frac {b} {a} \ right)} \] Обратите внимание, что это размерно правильный, имея единицы H. Также обратите внимание, что это выражение зависит только от материалов (через \ (\ mu \)) и геометрии (через \ (l \), \ (a \) и \ (b \)).Примечательно, что , а не , зависит от тока, что подразумевает нелинейное поведение.

Чтобы восстановить соединение с параметрами модели линии передачи с сосредоточенными элементами (разделы 3.4 и 3.10), мы просто разделим на \ (l \), чтобы получить параметр длины на единицу: \ [\ boxed {L ‘= \ frac { \ mu} {2 \ pi} \ ln \ left (\ frac {b} {a} \ right)} \ label {m0125_eLp} \], который имеет ожидаемые единицы H / m.

Пример \ (\ PageIndex {1} \): Индуктивность коаксиального кабеля RG-59

Коаксиальный кабель

RG-59 состоит из внутреннего проводника радиусом \ (0.292 \) мм, внешний проводник с радиусом \ (1.855 \) мм и полиэтиленовый (немагнитный диэлектрик) промежуточный материал. Оцените индуктивность на длину RG-59.

Решение

Из постановки задачи, \ (a = 0,292 \) мм, \ (b = 1,855 \) мм и \ (\ mu \ cong \ mu_0 \), поскольку промежуточный материал немагнитный. Используя уравнение \ ref {m0125_eLp}, мы находим \ (L ‘\ cong 370 \) nH / m.

Авторы и авторство

Индуктивность, единица измерения, характеристики, материалы сердечника

Когда кусок провода формируется в катушку, как показано на рисунке 1, он становится основным индуктором.Термины катушка и индуктор используются как синонимы. Как показано на рисунке, ток через катушку создает электромагнитное поле. Магнитные силовые линии вокруг каждой петли (витка) в обмотке катушки эффективно дополняют силовые линии вокруг соседних петель, образуя сильное электромагнитное поле внутри и вокруг катушки. Чистое направление всего электромагнитного поля создает северный и южный полюсы.

Рисунок 1: Катушка индуктивности с воздушной катушкой

Чтобы понять формирование общего электромагнитного поля в катушке, рассмотрим взаимодействие электромагнитных полей вокруг двух соседних контуров.Каждая магнитная силовая линия вокруг соседних петель отклоняется в единую внешнюю траекторию, когда петли сближаются. Этот эффект проклят, потому что магнитные силовые линии находятся в противоположных направлениях между соседними петлями и, следовательно, нейтрализуются, когда петли находятся близко друг к другу. Общее электромагнитное поле для двух контуров показано в части (b). Этот эффект является аддитивным для многих близко расположенных контуров в катушке, то есть каждый дополнительный контур увеличивает электромагнитное поле.Для простоты показаны только отдельные силовые линии, хотя их много.

Собственная индуктивность

: при прохождении тока через катушку индуктивности создается электромагнитное поле. При изменении тока меняется и электромагнитное поле. Увеличение тока расширяет электромагнитное поле, а уменьшение тока уменьшает его. Следовательно, изменяющийся ток создает изменяющееся электромагнитное поле вокруг индуктора. В свою очередь, изменяющееся электромагнитное поле вызывает индуцированное напряжение на катушке в направлении, противодействующем изменению тока.Это свойство называется самоиндуктивностью, но обычно его называют просто индуктивностью, что символизирует L.

Индуктивность — это мера способности катушки устанавливать наведенные напряжения в результате изменения ее тока, и это индуцированное напряжение направлено против изменения тока.

Единица индуктивности

Генри (Гн) — основная единица индуктивности. По определению, индуктивность катушки равна одному генри, когда ток через катушку, изменяющийся со скоростью один ампер в секунду, индуцирует на катушке один вольт.Во многих практических приложениях чаще всего используются миллигенри (мГн) и микрогенри (мкГн).

Наведенное напряжение зависит от

L и di / dt

Индуктивность (L) катушки и скорость изменения тока (di / dt) во времени определяют индуцированное напряжение (V _ind ). Изменение тока вызывает изменение электромагнитного поля, которое, в свою очередь, индуцирует напряжение на катушке, как вы знаете. индуцированное напряжение прямо пропорционально L и di / dt, как указано в следующей формуле.

V _ind = L (di / dt)

Формула показывает, что чем больше индуктивность, тем больше индуцированное напряжение. Кроме того, это означает, что чем быстрее изменяется ток катушки (больше di / dt), тем больше индуцированное напряжение.

Физические характеристики индукторов

Следующие параметры важны для определения индуктивности катушки. Возможность материала сердечника, количества витков провода, длины сердечника и его поперечного сечения.

Основной материал

Как обсуждалось выше, индуктор представляет собой катушку с проволокой, которая окружает магнитный или немагнитный материал, называемый сердечником. Примерами магнитных материалов являются железо, никель, сталь, кобальт или сплавы. Эти материалы обладают проницаемостью, которая в сотни или тысячи раз превышает проницаемость вакуума, и классифицируются как ферромагнитные. Ферромагнитный сердечник обеспечивает лучший путь для магнитных силовых линий и, таким образом, позволяет создавать более сильное магнитное поле.Примеры немагнитных материалов: воздух, медь, пластик и стекло. проницаемость этих материалов такая же, как и для вакуума.

Физические параметры

Количество витков провода, длина и площадь поперечного сечения сердечника являются факторами при установке значения индуктивности. Индуктивность обратно пропорциональна длине сердечника и прямо пропорциональна площади поперечного сечения. Кроме того, индуктивность напрямую связана с количеством витков в квадрате.Это соотношение выглядит следующим образом:

L = (N ² мкА) / I

где L — индуктивность в генри (Гн), N — количество витков провода, µ — проницаемость в генри на метр (Гн / м), A — площадь поперечного сечения в метрах в квадрате и длина жилы в метрах. (м).

.

Сопротивление обмотки

Когда катушка из определенного материала, например, изолированный медный провод, этот провод имеет определенное сопротивление на единицу длины.Когда для создания катушки используется много витков провода, общее сопротивление может быть значительным. Это внутреннее сопротивление называется сопротивлением постоянному току или сопротивлением обмотки (R _W ).

Хотя это сопротивление распределено по длине провода, оно эффективно проявляется последовательно с индуктивностью катушки, как показано на рисунке 5. Во многих приложениях сопротивление обмотки может быть достаточно малым, чтобы его можно было игнорировать, и катушку рассматривать как идеальный индуктор. В других случаях необходимо учитывать сопротивление.

Рисунок 5: Сопротивление обмотки индуктора

Емкость обмотки

Когда два проводника расположены рядом, между ними всегда есть некоторая емкость. Таким образом, когда много витков провода расположены близко друг к другу в катушке. Определенная паразитная емкость, называемая конденсатором обмотки (C _W ), является естественным побочным эффектом. Во многих приложениях эта емкость обмотки очень мала и не оказывает существенного влияния. В других случаях, особенно на высоких частотах, это может стать весьма важным.

Эквивалентная схема индуктора с сопротивлением обмотки (R _W ) и емкостью обмотки (C _W ) показана на рисунке 6.