Явление самоиндукции. Индуктивность проводников.

При любом изменении тока в проводнике его собственное магнитное поле также изменяется. Вместе с ним изменяется и поток магнитной индукции, пронизывающий поверхность, охваченную контуром проводника. В результате в этом контуре индуцируется ЭДС. Это явление называется явлением самоиндукции.

В соответствии с законом Био-Савара-Лапласа индукция магнитного поля В пропорциональна силе тока I в проводнике. Отсюда следует, что поток магнитной индукции и сила тока I также пропорциональны друг другу:

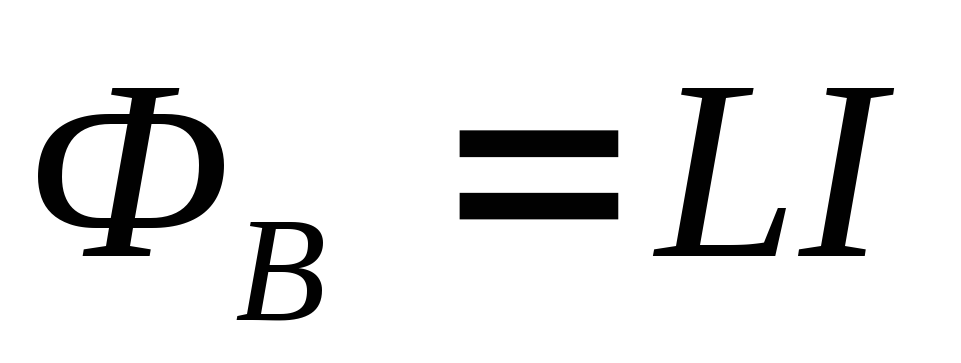
Коэффициент пропорциональности L называют

индуктивностью проводника. За единицу индуктивности в СИ принимают индуктивность такого проводника, у которого при силе тока 1А создается поток магнитной индукции, равный 1Вб. Эту единицу называют Генри, Гн.

Индуктивность проводника зависит от его формы и размеров, а также от магнитных свойств окружающей его среды (магнитной проницаемости μ). Заметим при этом, что линейная зависимость между иI остается справедливой и в том случае, когда μ зависит от напряженности магнитного поля Н, а значит, от I (например, ферромагнитная среда). В этом случае индуктивность

L также зависит от I.

Согласно основному закону электромагнитной индукции, ЭДС самоиндукции, возникающая при изменении силы тока в проводнике, есть:

.

Или, записав , будем иметь:.

В том случае, когда среда не является ферромагнитной L=const, тогда:

Последняя формула дает возможность определить индуктивность L как коэффициент пропорциональности между скоростью изменения силы тока в проводнике и возникающей вследствие этого ЭДС самоиндукции.

Пример вычисления индуктивности. Индуктивность соленоида.

Согласно основному соотношению, связывающему между собой ток I и поток , индуктивность проводника определяется выражением: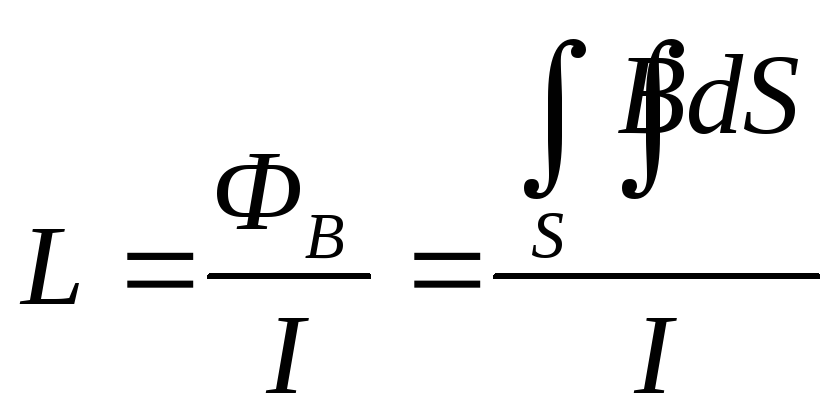

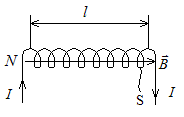
Применим эту формулу для расчета индуктивности прямого длинного соленоида.

Имеем:

.

Рисунок 5.3. Прямой длинный соленоид

Поток магнитной индукции через один виток катушки 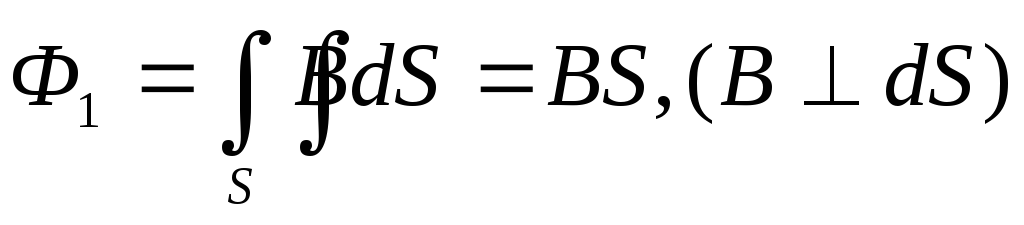; через все N витков поток равен:

.

Поделив это выражение на I , находим искомую индуктивность соленоида:_, где — число витков на единицу длины;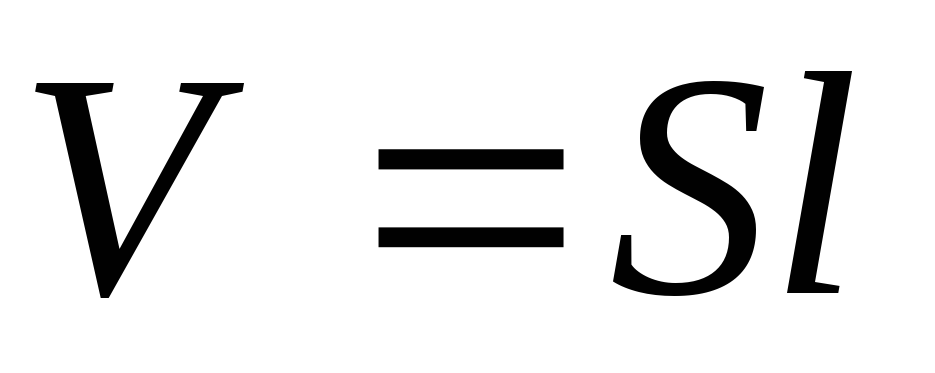— объем соленоида.

Если магнитная проницаемость сердечника зависит от

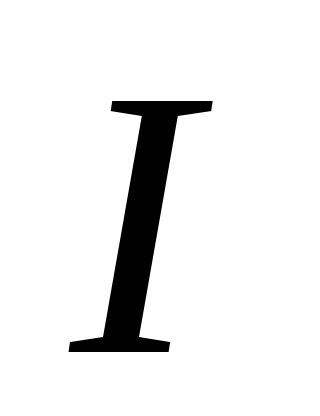(силы тока), что имеет место, когда сердечником соленоида является, например, железный или ферритовый стержень, тобудет зависеть от . Это свойство индуктивности используют, в частности, в различных устройствах релейной защиты электрических цепей при токовых перегрузках.

Переходные процессы в электрических цепях, содержащих индуктивность. Экстратоки замыкания и размыкания.

При всяком изменении силы тока в каком-либо контуре в нем возникает ЭДС самоиндукции, которая вызывает появление в этом контуре

дополнительных токов, называемых экстратоками. По правилу Ленца экстратоки, возникающие в проводниках вследствие самоиндукции, всегда направлены так, чтобы воспрепятствовать изменению тока, текущего в цепи. В схеме опыта, приведенной на рисункепри замыкании ключа (положение 1) в катушке возникает экстраток замыкания, направление которого противоположно нарастающему току батареи. При этом часть экстратока замыкания ответвляется на батарею, а часть на гальванометр, где его направление совпадает с направлением тока батареи – гальванометр дает дополнительный отброс вправо.

Рисунок 5.4. Электрическую цепь, состоящая из источника ЭДС ,

катушки индуктивности L и сопротивления R.: 1 – замыкание ключа: _, 2 — размыкание ключа:

При размыкании ключа (положение 2) магнитный поток в катушке начнет исчезать. В ней возникнет экстраток размыкания, который будет препятствовать убыванию магнитного потока, то есть будет направлен в катушке в ту же сторону, что и убывающий ток. При этом экстраток размыкания теперь целиком проходит через гальванометр, где его направление

противоположно направлению первоначального тока – гальванометр дает отброс влево.

Установление и исчезновение тока в цепи, содержащей индуктивность, происходит не мгновенно, а постепенно. Рассмотрим электрическую цепь, состоящую из источника ЭДС , катушки индуктивностиL и сопротивления R. При размыкании ключа в образующейся замкнутой цепи помимо ЭДС

будет действовать ЭДС самоиндукции. По второму правилу Кирхгофа можем написать:или в виде

.

Решением полученного дифференциального уравнения, полагая, что в начальный момент времени t = 0 ток отсутствовал I(0)=0, является функция:

,

где

.

График этой функции приведен на рис.3 (кривая 1). Видим, что установление тока в цепи происходит не мгновенно, а с некоторым запаздыванием. Характерное время называетсявременем ретардации (запаздывания, задержки).

Рисунок 5.5. Установление и исчезновение тока в цепи, содержащей индуктивность.

При замыкании ключа образуется контур, содержащий только индуктивность L и сопротивление R (источник ЭДС

при этом блокируется). Теперь в цепи действует только ЭДС самоиндукции, и по закону Ома: или в виде

.

Решением этого уравнения, считая, что в начальный момент времени t = 0 ток имел максимальное значение, равное , является функция:

.

График ее приведен на рис. 5.5 (кривая 2). Видим, что исчезновение тока в цепи происходит не мгновенно, но с запаздыванием.

Характерное врем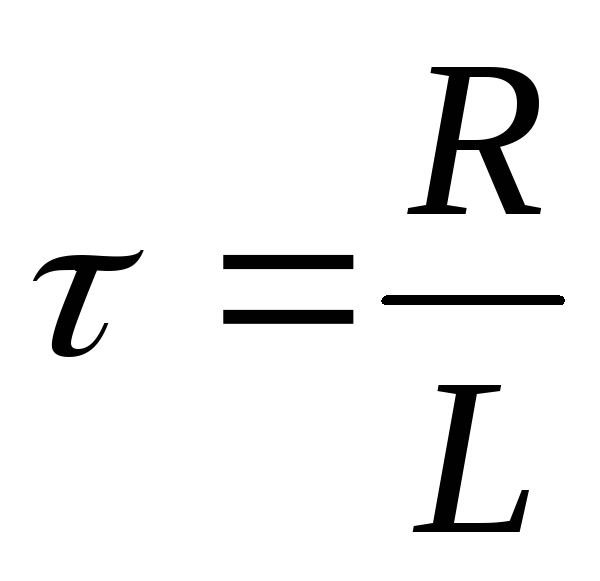я называется в этом случаевременем релаксации (восстановления).

Расчёт индуктивности. Часть 1 | HomeElectronics

Всем доброго времени суток! В прошлой статье я рассказывал о таком явлении как электромагнитная индукция и ЭДС возникающая при самоиндукции и взаимной индукции. Устройства, в основе которых лежат данные явления и процессы, называются индуктивными элементами (катушки колебательных контуров, трансформаторы, дроссели, реакторы). В качестве одного из основных параметров данных элементов выступает индуктивность L(также имеет название коэффициента самоиндукции). О том, как рассчитать данный параметр пойдёт речь в данной статье.

Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.

Методы расчёта индуктивностей

Индуктивностью (обозначается L) или коэффициентом самоиндукции называется коэффициент пропорциональности между потокосцеплением (обозначается Ψ­_L) и электрическим током, который возбуждает данное потокосцепление.

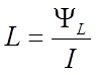
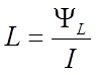
В простых случаях индуктивность можно рассчитать, применяя формулы для вычисления магнитной индукции B₀ (закон Био-Савара-Лапласа), магнитного потока Φ и потокосцепления Ψ­_L

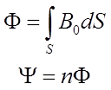
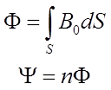
где S – площадь поверхности ограниченная контуром, который создает магнитную индукцию;

n – количество контуров с током, которые пронизывает магнитный поток.

Однако это в идеальном случае, в реальности говоря о токе I, который протекает по проводнику, необходимо отметить, что его распределение по сечению проводника не всегда равномерно, вследствие возникновения скин-эффекта при переменном токе. В результате этого эффекта плотность электрического тока распределяется неравномерно, происходит её уменьшение от внешнего слоя проводника к его центру. Уменьшение плотности тока также происходит неравномерно и зависит от частоты переменного тока. Для оценки скин-эффекта ввели понятие толщины скин-слоя ∆, которая показывает, на каком расстоянии от поверхности проводника плотность тока падает в е = 2,718 раз. Толщину скин-слоя можно вычислить по выражению

где δ – глубина проникновения переменного тока или толщина скин-слоя;

μ – магнитная проницаемость вещества;

γ – удельная электрическая проводимость материала проводника;

ω – круговая частота переменного тока, ω = 2πf.

Поэтому непосредственный способ вычисления индуктивности практически не применяется.

На практике применяется выражения для индуктивности, выведенные с некоторыми допущениями, погрешности вычисления индуктивности по этим выражениями составляет порядка нескольких процентов.

Так как индуктивные элементы довольно разнообразны, их можно разделить на три группы:

индуктивные элементы без сердечников;

индуктивные элементы с замкнутыми сердечниками;

индуктивные элементы с сердечниками, имеющие воздушный зазор.

Самые простые по конструкции являются индуктивные элементы без сердечников, поэтому рассмотрим их в первую очередь. Простейшим из таких элементов является прямой провод.

Индуктивность прямолинейного провода круглого сечения

При расчёте индуктивности необходимо разделять индуктивность на постоянном токе и индуктивность на высокой частоте. Под высокой частотой следует понимать такую частоту, на которой толщина скин-слоя меньше размеров поперечного сечения провода. В случае если толщина скин-слоя больше поперечных размеров провода, то можно вести расчёт для постоянного тока.

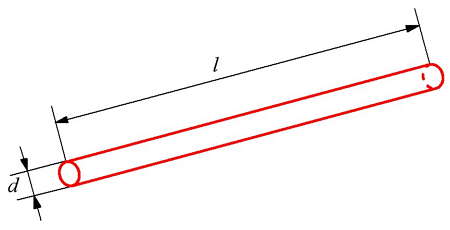
Определение индуктивности прямого провода. l – это длина проводника, d = 2r – диаметр проводника.

В случае постоянного тока или тока низкой частоты индуктивность составит

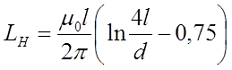
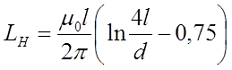
где μ₀ – магнитная постоянная, μ₀ = 4π•10^-7 Гн/м;

l – длина провода, м;

d – диаметр провода, м.

Как я уже говорил, на величину индуктивности влияет частота переменного тока, поэтому в случае необходимости рассчитать индуктивность на любой частоте применяется следующее выражение

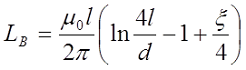
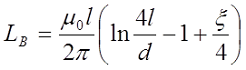
где ξ – коэффициент, вносящий поправку на распространение переменного тока по сечению провода. Данный коэффициент зависит от величины k*r, где

d = 2r – диаметр поперечного сечения провода, м.

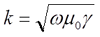
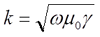
где ω – угловая частота переменного тока, ω = 2πf;

μ₀ – магнитная постоянная, μ₀ = 4π•10^-7 Гн/м;

γ – удельная проводимость вещества проводника.

Тогда если k*r < 3, то

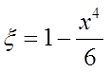
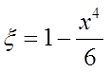
если k*r > 3, то

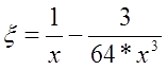
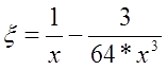
где

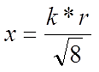
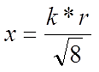
Пример. Необходимо рассчитать индуктивность прямолинейного провода круглого сечения из меди (γ = 5,81*10⁷ См/м) диаметром d = 2 мм и длиной l = 4 м, при постоянном токе и токе частотой f = 50 кГц.

На постоянном токе

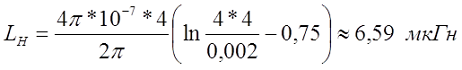
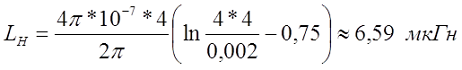
На частоте 50 кГц

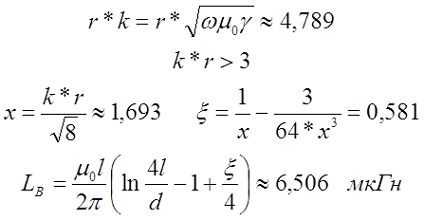
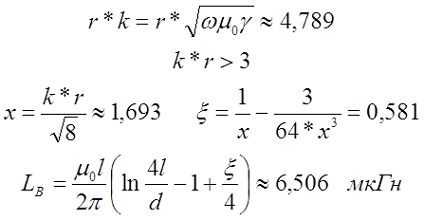
Индуктивность кругового кольца круглого сечения

Теперь рассмотрим, какова будет индуктивность если провод свернуть в кольцо. Такой индуктивный элемент будет иметь вид

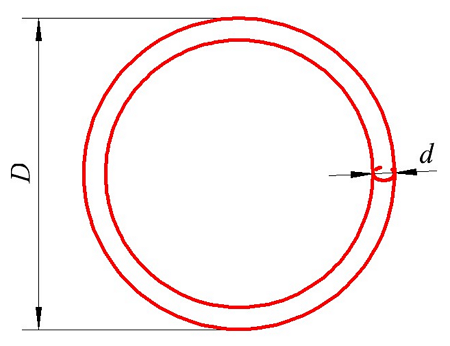
Определение индуктивности кругового витка. D – диаметр кольца (витка), d – диаметр провода, из которого сделано кольцо (виток).

При этом его индуктивность можно вычислить по следующему выражению

для  постоянного тока

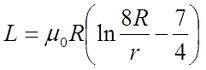
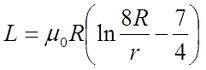
где R – радиус витка, м, R = D/2;

r – радиус провода, м, r = d/2;

μ₀ – магнитная постоянная, μ₀ = 4π•10^-7 Гн/м.

Так же как и для проводника существует выражение для индуктивности кругового витка на любой частоте

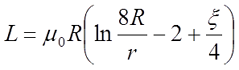
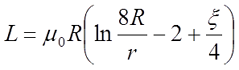
где ξ – коэффициент, вносящий поправку на распространение переменного тока по сечению провода. Определяется также как и для прямого проводника.

Пример. В качестве примера рассчитаем индуктивность такого же провода, как и в первом примере, только свёрнутом в кольцо. В этом случае диаметр провода d = 2 мм, а диаметр кольца D = l/π = 4/3,142 ≈ 1,273 м, провод выполнен из меди (γ = 5,81*10⁷ См/м).

Для постоянного тока индуктивность составит

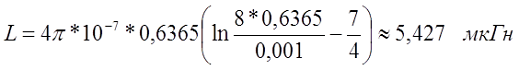
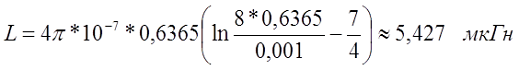
На частоте 50 кГц

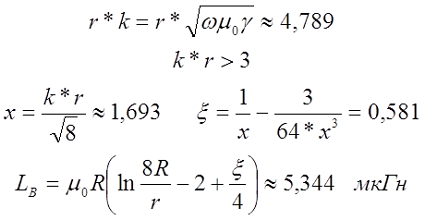
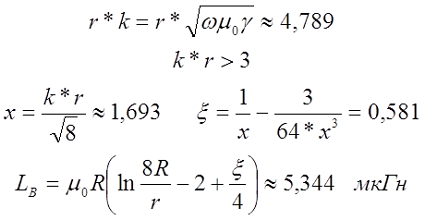
В следующей части я продолжу рассмотрение расчётов индуктивности для различных индуктивных элементов.

Теория это хорошо, но без практического применения это просто слова.Здесь можно всё сделать своими руками.

2. В чём суть электромагнитной индукции? Индуктивность проводника, единицы его измерения. Выведите формулу индуктивности бесконечно длинного соленоида.

Явление электромагнитной индукции заключается в том, что в замкнутом проводящем контуре при изменении потока магнитной индукции, охватываемого этим контуром, возникает электрический ток. Индуктивность контура (L) – коэффициент пропорциональности. ,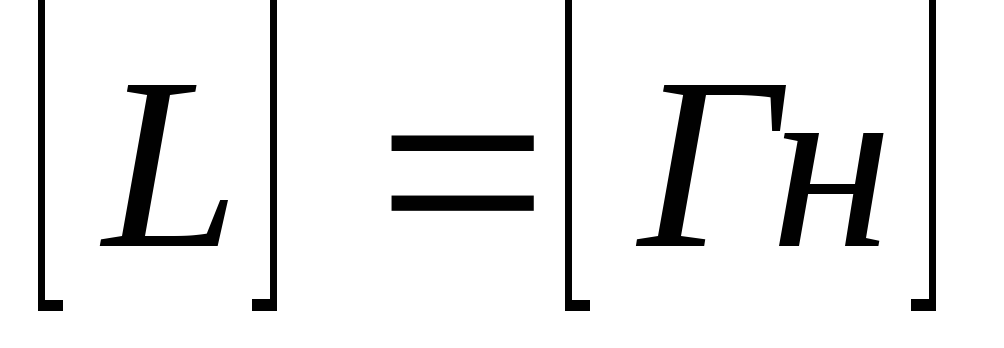. 1Гн – индуктивность такого контура, магнитый поток самоиндукции которого при токе в 1А = 1Вб. 1Гн=1Вб/А=1В*С/А. Индуктивность длинного соленоида. Полный магнитный поток через соленоид.

Билет №19

1. Опишите поведение проводника в электрическом поле. Покажите, что напряжённость внутри любой полости проводника=0, а силовые линии эл.ст. поля вблизи поверхности проводника перпендикулярны этой поверхности.

Небольшая цил. Пов-ть, одно из оснований расположено внутри, другое – вне проводника.Поток вектора D ч/з внутр. Пов-ть = 0. Ч/з внешнюю пов-ть поток смещения DdS. Внутри цилиндра содержится сторонний заряд δdS. По т.Гаусса получим D=δ => E= δ/ε₀ε. Вблизи выступов эквапотенц-ые пов-ти распол-ся гуще, значит, и напряженность поля здесь больше => плотность зарядов на выступах особенно велика. К такому же выводу м/о прийти учтя, что из-за взаимного отталкивания заряды стремятся расположиться как м/о дальше друг от друга. Вблизи углублений в проводнике эквапотенциальные пов-ти расположены реже => напряженность меньше => плотность меньше. Вывод: плотность зарядов при данном потенциале опр-ся кривизной пов-ти; растет с увеличением полож-ой кривизны и убывает с увеличением отриц. кривизны.

Если поместить проводник во внешнее эл.-ст. поле заряды проводника начнут перемещаться. Это будет продолжаться до тех пор, пока не установится равновесие распределение зарядов, при котором Eвнутр. Проводника=0. Если бы это было так, то в проводнике возникло бы упор. движение зарядов без затраты энергии от вн. источника, что противоречит закону сохранения энергии.

Т.к. поле внутри проводника отсутствует, то поверхность проводника является эквивалентной => Е направлен по нормали к поверхности. Если бы это было не так, то под действием заряды начали бы перемещаться по поверхности проводника, что противоречит равновесному распределению зарядов.

2. Выведите формулу для силы взаимодействия двух параллельных бесконечно длинных проводников с током. Дайте определение единицы силы тока – Ампера.

Ампер – сила не изменяющегося тока, который при прохождении по двум параллельным прямоугольным проводником бесконечной длины и ничтожно малого поперечного сечения, расположенном в вакууме на расстоянии 1м один от другого, создаёт между этими проводниками силу, равную 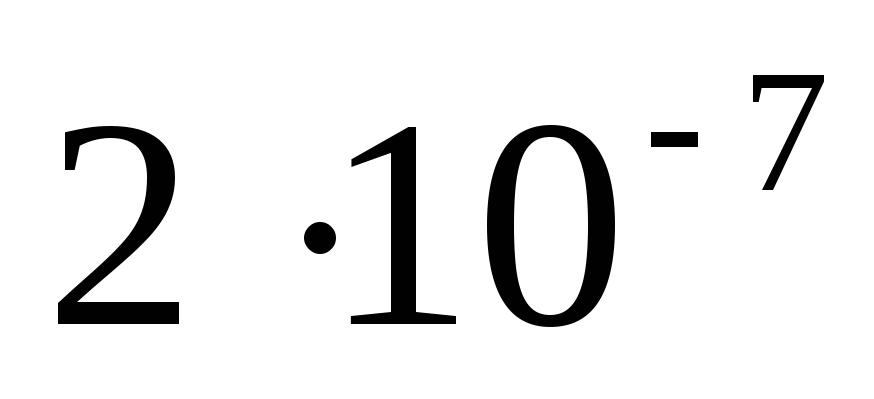Н на каждый метр длины. Два параллельных тока одинакового направления притягиваются, разного – отталкиваются.

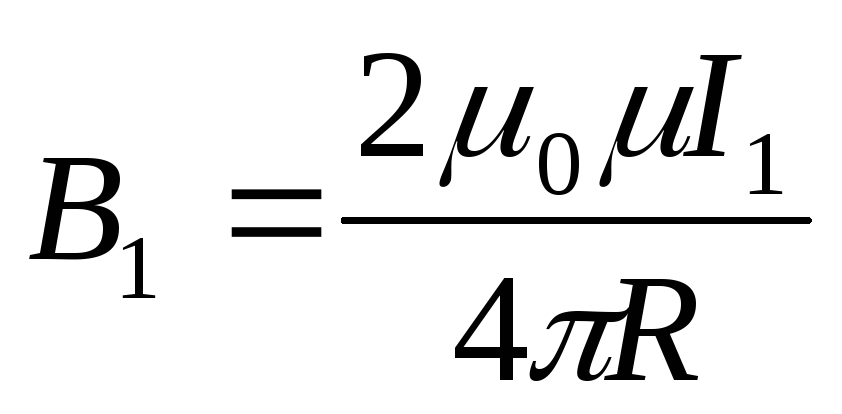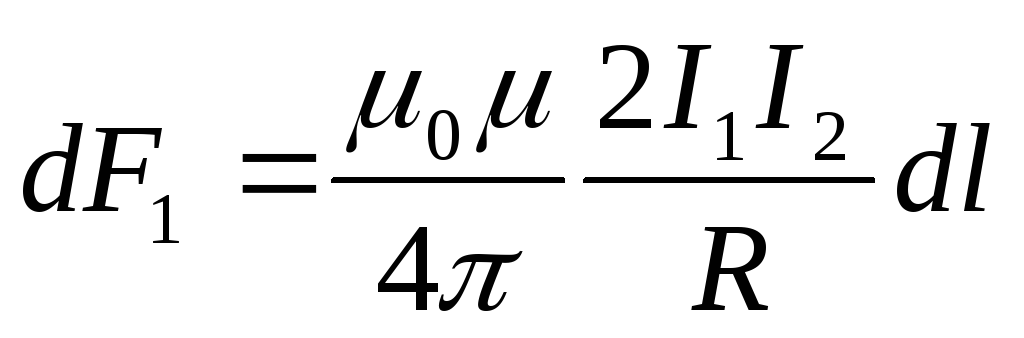. По закону Ампера: ,. Рассуждая аналогично получаем:.

Билет №20

Какие вещества относятся к сегментоэлекрикам? В чём особенность их строения? Перечислите и объясните свойства сегметоэлектриков.

Сегментоэлектрики – диэлектрики, обладающие в определённом интервале температур спонтанной поляризованностью, т.е. поляризованностью в отсутствии внешнего поля (сегнетова соль, титанат бария). При отсутствии вн. поля сегнетоэлектрик состоит из доменов, областей с различными направлениями поляризованности. В целом дипольный момент диэлектрика=0. При внесении сегнетоэл. во вн.эл. поле происходит переориентация дипольных моментов по полю. После прекращения действия поля сумма эл. поля доменов будет поддерживать их некоторую ориентацию. Свойства: 1) При T> т. Кюри cв-ва исчезают. 2) , Х сегментоэл. зависит отполя.3) Р(Е) нелинейная – представляет собой петлю ГИСТЕРЕЗИСА.

2. Выведите дифференциальное уравнение затухающих колебаний в эл. контуре. Запишите его решение. Раскройте физический смысл коэффициента затухания, логарифмического декремента затухания, добротности контура.

Конденсатор предварительно заряжен. По второму закону Кирхгофа: ,,,.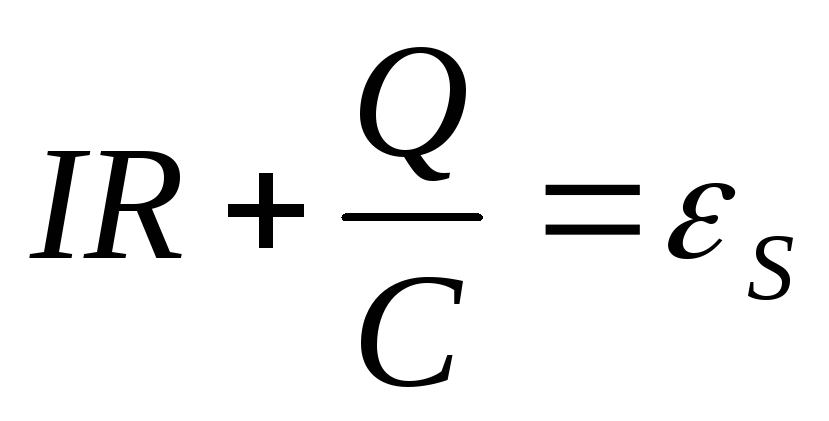

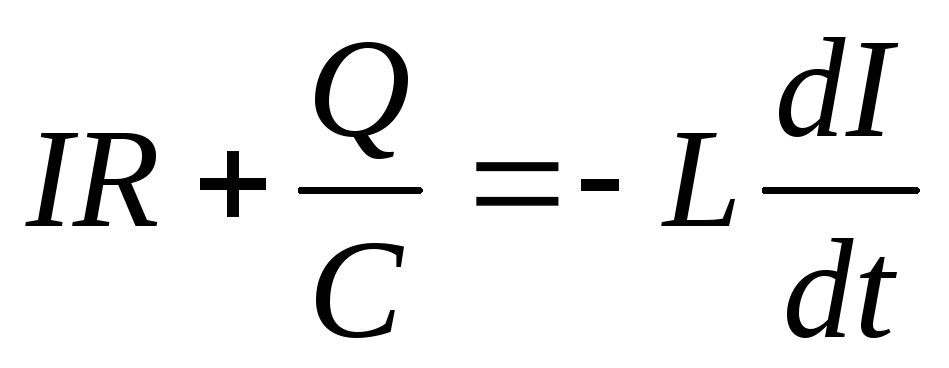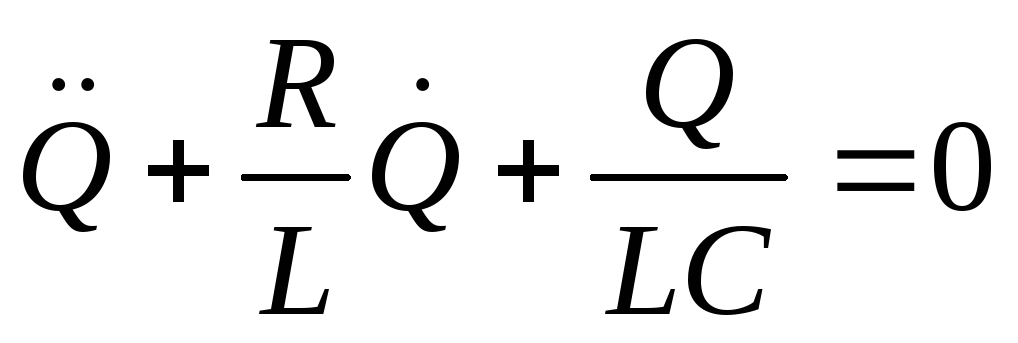Обозначим — коэффициент затухания.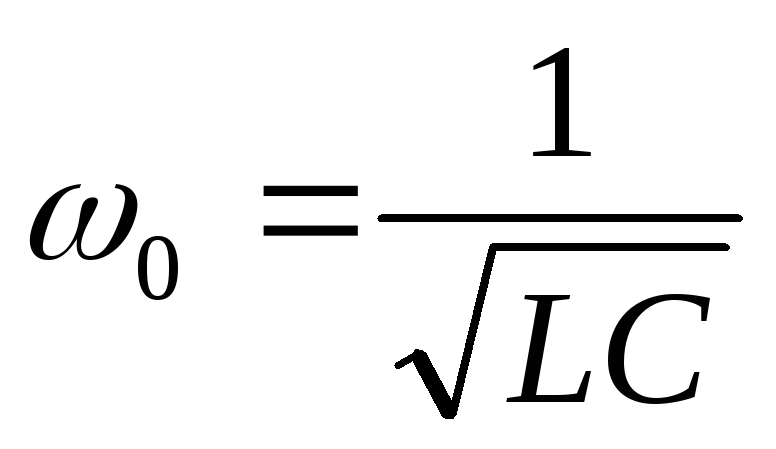— собственная частота.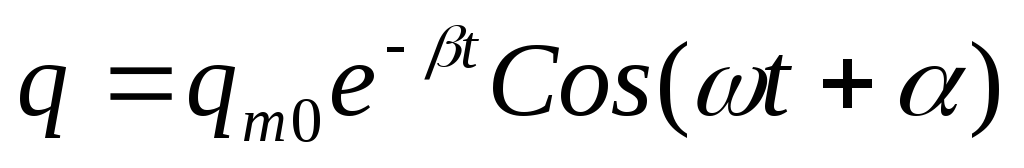,,,,,,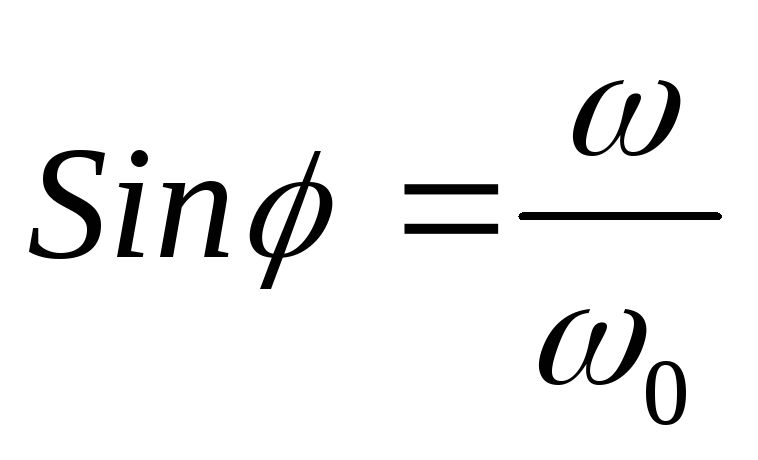-изменение амплитуды затухающих колебаний. Логарифмический декремент затухания:— время, за которое амплитуда уменьшается в е раз.-связь междуи.— коэффициент затухания — в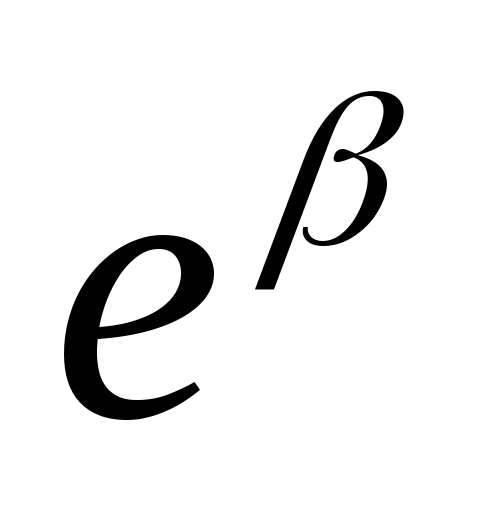— раз уменьшается амплитуда в единицу времени.

Добротность пропорциональна числу колебаний Ne, совершаемых системой за время релаксации.

Билет №21

1.Докажите, что на границе двух диэлектриков тангенциальная составляющая вектора претерпевают разрывов, а тангенциальная составляющая остаётся без изменения.

— напряжённость электрического поля. ,-направлен по касательным и силовым линиям.-вектор электрического смещения.. Построим вблизи границы раздела двух диэлектриков небольшой замкнутый прямоугольный контур.

По теореме о циркуляции вектора 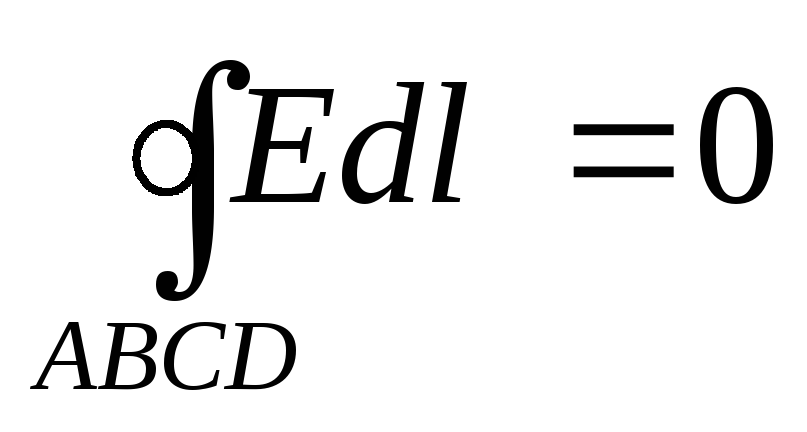,. Интегралы по участкамDA и BC ничтожно малы. =>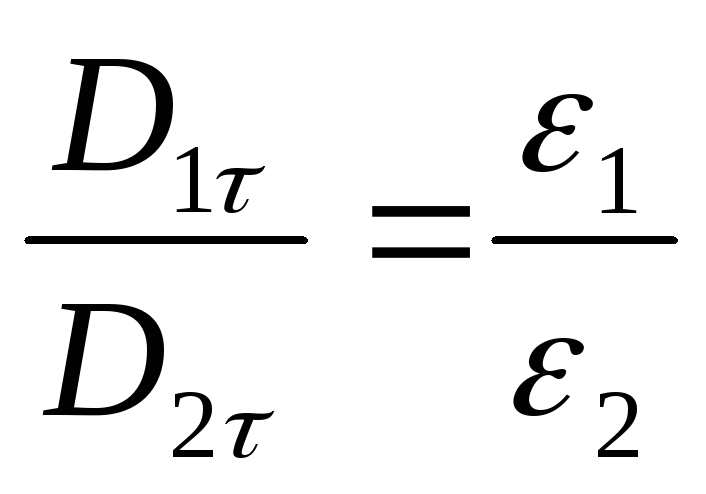. Таким образом тангенциальная составляющаяне претерпевает разрыв. На границе раздела двух диэлектриков построим прямой цилиндр, высота которого ничтожно мала. Основания настолько малы, что в пределах каждого из ниходинаков. По теореме Гаусса:,=>. Таким образом нормальная составляющаяне претерпевает разрыв.

Самоиндукция. Индуктивность. Энергия магнитного поля тока

Самоиндукция. Индуктивность. Энергия магнитного поля тока

«Физика — 11 класс»

Самоиндукция.

Если по катушке идет переменный ток, то:
магнитный поток, пронизывающий катушку, меняется во времени,
а в катушке возникает ЭДС индукции .
Это явление называют самоиндукцией.

По правилу Ленца при увеличении тока напряженность вихревого электрического поля направлена против тока, т.е. вихревое поле препятствует нарастанию тока.
При уменьшения тока напряженность вихревого электрического поля и ток направлены одинаково, т.е.вихревое поле поддерживает ток.

На вышеприведенном рисунке:
при замыкании ключа первая лампа вспыхивает практически сразу, а вторая — с заметным запозданием, т.к. ЭДС самоиндукции в цепи второй лампы велика, и сила тока не сразу достигает своего максимального значения.

При размыкании ключа в катушке L возникает ЭДС самоиндукции, которая поддерживает уменьшающийся ток.
В момент размыкания через гальванометр идет ток размыкания, направленный против начального тока до размыкания.
Сила тока при размыкании может быть больше начального тока, т.е. ЭДС самоиндукции больше ЭДС источника тока.

Индуктивность

Величина индукции магнитного поля, создаваемого током, пропорционален силе тока, а магнитный поток пропорционален магнитной индукции.

Следовательно

Ф = LI

где L — индуктивность контура (иначе коэффициентом самоиндукции), т.е. это коэффициент пропорциональности между током в проводящем контуре и магнитным потоком.

Используя закон электромагнитной индукции, получаем равенство

Индуктивность — это физическая величина, численно равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока в нем на 1 А за 1 с.

Индуктивность зависит от размеров проводника, его формы и магнитных свойств среды, в которой находится проводник, но не зависит от силы тока в проводнике.

Индуктивность катушки (соленоида) зависит от количества витков в ней.

Единицу индуктивности в СИ называется генри (1Гн).
Индуктивность проводника равна 1 Гн, если в нем при равномерном изменении силы тока на 1 А за 1 с возникает ЭДС самоиндукции 1 В.

Аналогия между самоиндукцией и инерцией.

Явление самоиндукции подобно явлению инерции в механике.

В механике:
Инерция приводит к тому, что под действием силы тело приобретает определенную скорость постепенно.
Тело нельзя мгновенно затормозить, как бы велика ни была тормозящая сила.

В электродинамике:
При замыкании цепи за счет самоиндукции сила тока нарастает постепенно.
При размыкании цепи самоиндукция поддерживает ток некоторое время, несмотря на сопротивление цепи.

Явление самоиндукции выполняет очень важную роль в электротехнике и радиотехнике.

Энергия магнитного поля тока

По закону сохранения энергии энергия магнитного поля, созданного током, равна той энергии, которую должен затратить источник тока (например, гальванический элемент) на создание тока.
При размыкании цепи эта энергия переходит в другие виды энергии.

При замыкании цепи ток нарастает.
В проводнике появляется вихревое электрическое поле, действующее против электрического поля, созданного источником тока.
Чтобы сила тока стала равной I, источник тока должен совершить работу против сил вихревого поля.
Эта работа идет на увеличение энергии магнитного поля тока.

При размыкании цепи ток исчезает.
Вихревое поле совершает положительную работу.
Запасенная током энергия выделяется.
Это обнаруживается, например, по мощной искре, возникающей при размыкании цепи с большой индуктивностью.

Энергия магнитного поля, созданного током, проходящим по участку цепи с индуктивностью L, определяется по формуле

Магнитное поле, созданное электрическим током, обладает энергией, прямо пропорциональной квадрату силы тока.

Плотность энергии магнитного поля (т. е. энергия единицы объема) пропорциональна квадрату магнитной индукции: w_м ~ В²,
аналогично тому как плотность энергии электрического поля пропорциональна квадрату напряженности электрического поля w_э ~ Е².

Источник: «Физика — 11 класс», учебник Мякишев, Буховцев, Чаругин

Электромагнитная индукция. Физика, учебник для 11 класса — Класс!ная физика

Электромагнитная индукция. Магнитный поток — Направление индукционного тока. Правило Ленца — Закон электромагнитной индукции — ЭДС индукции в движущихся проводниках. Электродинамический микрофон — Вихревое электрическое поле — Самоиндукция. Индуктивность. Энергия магнитного поля тока — Электромагнитное поле — Примеры решения задач — Краткие итоги главы

Помогите решить / разобраться (Ф)

jast321

Формулы для расчёта индуктивности провода гораздо сложнее, чем Вы тут представили.

В частности, заметьте: в вашей формуле 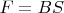величина 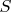не может быть площадью поперечного сечения проводника. Ведь эта формула применима только к любой такой площадке 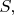которая перпендикулярна магнитному полю 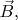и в каждой точке которой, к тому же, величина поля 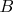одинаковая. Но магнитное поле прямого провода везде (но далеко от прочих участков провода, которые как-то изогнуты и подключены к источнику тока) направлено параллельно плоскости поперечного сечения прямого провода, а величина поля 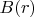на расстоянии от оси провода зависит от этого расстояния.

Магнитный поток для формулы 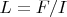надо вычислять как интеграл по элементам площади плоскости, содержащей ось провода, учитывая, что 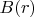тем больше, чем ближе элемент площади расположен к поверхности провода. При одном и том же токе 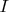c уменьшением радиуса провода 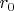поле 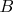вблизи поверхности провода возрастает пропорционально 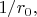поэтому возрастает и поток, и, соответственно, возрастает индуктивность.

Индуктивность провода можно определить и по-другому — как коэффициент 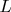в формуле для энергии магнитного поля 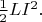Тогда картина станет ещё понятнее: у поверхности тонкого провода поле 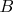больше, чем у поверхности более толстого провода с таким же током, поэтому больше энергия поля и, соответственно, больше индуктивность тонкого провода, чем в случае с более толстым проводом.

Индуктивность — Википедия

Материал из Википедии — свободной энциклопедии

Индуктивность микрополосковой линии является распределённой и характеризуется значением индуктивности на единицу длины.

Индукти́вность (или коэффициент самоиндукции) — коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, и полным магнитным потоком, называемым также потокосцеплением, создаваемым этим током через поверхность^[1], краем которой является этот контур^[2][3][4].

Индуктивность является электрической инерцией, подобной механической инерции тел. А вот мерой этой электрической инерции как свойства проводника может служить ЭДС самоиндукции. Характеризуется свойством проводника противодействовать появлению, прекращению и всякому изменению электрического тока в нём.

В формуле

Ψ=LI{\displaystyle \displaystyle \Psi =LI}

Ψ{\displaystyle \displaystyle \Psi } — потокосцепление, I{\displaystyle I} — сила тока в контуре, L{\displaystyle L} — индуктивность.

• Нередко говорят об индуктивности прямого длинного провода (см.). В этом и в других случаях (в особенности таких, к которым не применимо квазистационарное приближение), когда замкнутый контур непросто адекватно и однозначно указать, приведённое выше определение требует особых уточнений; отчасти полезным для этого оказывается упоминаемый ниже подход, связывающий индуктивность с энергией магнитного поля.

Через индуктивность выражается ЭДС самоиндукции в контуре, возникающая при изменении в нём тока^[4]:

Ei=−dΦdt=−LdIdt{\displaystyle {\mathcal {E}}_{i}=-{\frac {d\Phi }{dt}}=-L{\frac {dI}{dt}}}

Индуктивность | Полезные статьи — Кабель.РФ

Индуктивность L — величина, равная отношению потокосцепления, связанного с контуром, к силе тока, протекающего по нему:

<

Индуктивность складывается из внутренней индуктивности (жилы кабеля и провода) L _в и наружной, междужильной, индуктивности L _и

Единица индуктивности генри (гн) — индуктивность контура, с которым сцеплен магнитный поток 1 вб, когда по контуру течет ток 1 а, или индуктивность контура, в котором возникает э. д. с. самоиндукции 1 в при изменении тока в нем на 1 а в 1 сек.

Индуктивность одножильного кабеля, а также внешняя индуктивность коаксиального кабеля

Индуктивность коаксиального кабеля

Общая индуктивность коаксиального кабеля с медными внутренним и внешним проводниками

У многопроволочного внутреннего проводника диаметр равен

Индуктивность внутреннего проводника спирального радиочастотного кабеля (задержки), выполненного в виде спирали поверх сердечника с магнитной проницаемостью μ

Индуктивность двухжильного кабеля:

а) неэкранированного (рис. 2-2)

б) экранированного (рис. 2-3)

в) с учетом магнитного потока внутри жил

где Q(x) — коэффициент, зависящий от вихревых токов, и радиуса жилы r (табл. 2-2). С возрастанием частоты передаваемого тока общая индуктивность цепи уменьшается, а внешняя индуктивность не зависит от частоты.

Индуктивность двухпроводной линии (см. рис. 2-2), когда μ = 1,

Индуктивность одиночного провода

Зависимость индуктивности кабеля от частоты приведена на рис. 1-1. При больших сечениях токопроводящих жил, а также при высоких частотах происходит уплотнение тока у периферии жилы, благодаря чему снижается напряженность магнитного поля внутри токопроводящей жилы. Для определения индуктивности одиночного провода пользуются так же формулой

Для трехжильного кабеля или трех одножильных кабелей, расположенных по вершинам равностороннего треугольника (см. рис. 2-2,б) индуктивность каждой жилы также можно определить по (2-16). В случае трехжильного кабеля с секторными жилами за r принимают радиус эквивалентной по сечению круглой жилы, а за а — расстояние между серединами малых хорд секторов в поперечном сечении кабеля. В случае расположения трех одножильных кабелей в одной плоскости (рис. 2-2,в) индуктивность среднего кабеля определяют по приведенной выше формуле, но за а принимается расстояние между осями двух соседних кабелей. Индуктивность -крайних кабелей

 

где I _а и I _с — силы тока в крайних кабелях.

Приведенные формулы для подсчета индуктивности справедливы в случае небронированных кабелей. При наличии в непосредственной близости к кабелю магнитных материалов (например, проволочная или ленточная броня) индуктивность таких кабелей соответственно возрастает; в этом случае

где μ- магнитная проницаемость брони кабеля; D ₁ и D ₂ — диаметры кабеля под броней и поверх нее, мм.

В трехжильном кабеле в каждый момент времени сумма величин тока, в трех жилах равна нулю. Результирующий магнитный поток в пространстве, окружающем жилы на некотором удалении от них практически также, равен нулю. Поэтому в трехжильных кабелях, влиянием магнитной брони на индуктивность пренебрегают.

Индуктивность искусственной цепи, образованной из четверки (Ч) в кабелях дальней связи,

при четверке типа двойной пары (ДП)

Индуктивное сопротивление x _L — сопротивление, которое оказывает переменному току проводник, обладающий индуктивностью L: