что это такое и от чего зависит
В радиотехнике часто приходится сталкиваться с индуктивным сопротивлением. Его источником являются катушки. Они представляют собой двухполюсник, намотанный медным эмалированным проводом (обычно это ПЭТВ) на ферритовый или железный сердечник. Подобные детали встречаются в широком перечне оборудования: от древних советских радиоприёмников до материнских плат ПК последних моделей.

Катушки индуктивности
Формулы, зависимости и виды индуктивности
Электрическая индуктивность L – это величина, равная коэффициенту пропорциональности между током I, протекающим в замкнутом контуре, и создаваемым им магнитным потоком, иначе называемым потокосцеплением Y:
Y = LI.
Если к выводам катушки на некоторое время приложить напряжение, то в ней начнёт протекать ток I и формироваться магнитное поле. Чем меньше индуктивность L, тем быстрее протекает данный процесс. В итоге рассматриваемый двухполюсник накопит некоторое количество потенциальной энергии. При отключении питания он будет стремиться её вернуть. В результате на выводах катушки образуется ЭДС самоиндукции E, которая многократно превышает изначально приложенное напряжение. Подобная технология ранее использовалась в магнето систем зажигания ДВС, а сейчас широко встречается в повышающих DC-DC преобразователях.
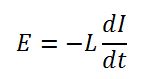
Формула ЭДС самоиндукции, здесь t – это время, в течение которого ток I уменьшится до нуля
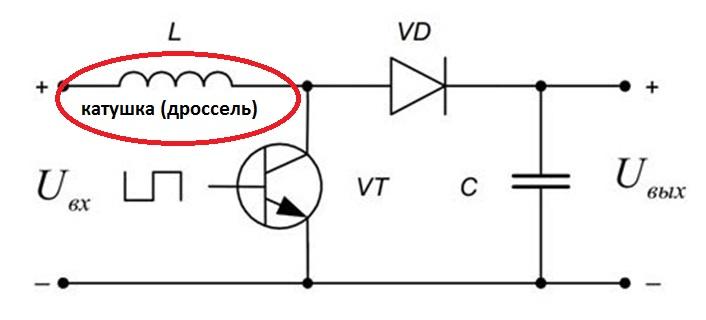
Простой DC-DC повышающий преобразователь
Катушка (она же – дроссель) – это радиодеталь с ярко выраженной индуктивностью, ведь именно для этого её и создавали. Однако подобным свойством обладают в принципе все элементы. Например, конденсатор, резистор, кабель, просто кусок провода и даже тело человек также имеют некоторую индуктивность. В расчетах ВЧ схем это обязательно принимается во внимание.
Важно! Проводя измерение индуктивности специализированным прибором, стоит помнить, что нельзя держаться руками за оба его вывода. В противном случае показания могут измениться и будут неверными. Вызвано это включением в измеряемую цепь тела человека с его собственной индуктивностью.
Сопротивление катушки переменному току
Гораздо интереснее дела обстоят с индуктивностью в контуре переменного тока. Любая катушка содержит в себе две составляющие сопротивления:
- Активную;
- Индуктивную.
При постоянном токе учитывается только первый фактор, а при переменном – оба. Формула индуктивного сопротивления XL катушки имеет следующий вид:
XL = 2pfL,
где:
- p = 3.14;
- f – частота переменного тока, Гц;
- L – индуктивность катушки, Гн.
Полное сопротивление катушки Z, называемое импедансом, определяется, исходя из активной R и индуктивной XL составляющих.
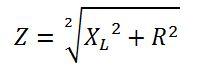
Импеданс катушки
Важно! Если катушка установлена в печатную плату, то для проверки её следует отпаять. В таком случае индуктивность будет измеряться независимо от других компонентов, что существенно повысит точность показаний прибора.
Расчёт индуктивного сопротивления катушки
Любая индуктивность, в т.ч. катушка, оказывает переменному току некоторое сопротивление. Как его рассчитать, было описано выше. Из формулы XL=2pfL видно, что сопротивление дросселя в первую очередь зависит от частоты протекающего по нему тока и его индуктивности. При этом с обоими параметрами связь прямо пропорциональная.
Частота – это характеристика внешней среды, индуктивность катушки зависит от ряда её геометрических свойств:
L=u0urN2S/l,
где:
- u0 – магнитная проницаемость вакуума – 4p*10-7 Гн/м;
- ur – относительная проницаемость сердечника;
- N – количество витков дросселя;
- S – его поперечное сечение в м2;
- l – длина катушки в метрах.
Располагая вышеописанными формулами и информацией о материале и размерах катушки, можно достаточно точно прикинуть её индуктивное сопротивление без каких-либо измерительных приборов.
Дополнительная информация. Некоторые цифровые мультиметры имеют режим замера индуктивности. Подобная функция встречается редко, однако иногда оказывается очень полезной. Поэтому при выборе прибора стоит обратить внимание на то, способен ли он измерять индуктивность.
Где применяется катушка (дроссель, индуктивность)
Дроссели имеют примитивную конструкцию: просто намотанный витками на каком-либо сердечнике проводник. В то же время в таком приборе нечему ломаться. Также у дросселей широчайший функционал и десятки применений. Из всего этого следует, что в какой бы точке города ни находился человек, в радиусе 1 км от него всегда будут тысячи катушек индуктивности, настолько они распространены.
Катушка как электромагнит
Самое простое применение катушки – это электромагнит. С подобным применением каждый сталкивается, заходя в подъезд. Сила, удерживающая дверь на месте и препятствующая несанкционированному доступу чужака, берётся из электромагнита. Он находится сверху.
Электрический ток, проходя по виткам катушки, создаёт вокруг неё переменное электромагнитное поле. Оно возбуждает в металлическом «бруске», расположенном на двери, вихревые токи, которые так же создают магнитное поле. В результате получаются два управляемых магнита. Они притягиваются друг к другу. Тем самым дверь надёжно удерживается на месте.
Другое применение электромагнитов в быту – индукционные плиты. Катушка наводит в металлической посуде переменный высокочастотный ток. Он, в свою очередь, своим тепловым действием разогревает кастрюлю. В промышленности нечто подобное используется для разогрева и плавки металлов. Только в таком случае применяются на порядки более высокие мощности и другие частоты тока.

Индукционный нагрев металла
Индуктивность как фильтр
Импульсные блоки питания, электрические двигатели и диммеры для регулировки яркости ламп накаливания выбрасывают в сеть большое количество искажений и помех. Вызвано это неравномерностью потребляемого тока. Для борьбы с подобными сетевыми шумами применяются специальные фильтры на основе конденсаторов и дросселей.
Данный узел представляет собой небольшую катушку из медного эмалированного провода диаметром 0,2-2 мм. Обмотка наматывается на ферритовый сердечник. Чаще всего он изготовлен в форме кольца, немного реже встречаются так называемые «гантельки».
Подобные фильтры имеются в компьютерных блоках питания, компактных люминесцентных лампах (иногда не ставят, экономят), на выходах сварочных инверторов.
Также фильтр может быть звуковым. Его задача – срезать определённый диапазон частот. Индуктивные свойства этого прибора таковы, что он хорошо проводит низкие частоты, а высокие – приглушает. Поэтому дроссели используют для того, чтобы до динамиков дошёл только бас. По факту ослаблено будут слышны и другие частоты. Для более эффективной работы фильтра нужны дополнительные детали: конденсаторы и операционные усилители.

Самодельный звуковой фильтр
Катушка как источник ЭДС
Китайская промышленность удивила школьников 2000-х новой игрушкой – вечным фонариком. Его не нужно было заряжать. Фонарик работал от катушки индуктивности, около которой под действием движения рук перемещался магнит. Он наводил в обмотке переменную ЭДС, которая питала осветительный прибор.
Подобное явление объясняется законом электромагнитной индукции. Если проводник (рамка) находится в переменном электромагнитном поле, то в нём начинает наводиться электродвижущая сила. Иными словами, появляется напряжение.
Закон этот совсем неигрушечный, ведь он используется в работе генераторов на подавляющем большинстве электростанций, в том числе любые ТЭЦ, ГЭС, АЭС и ветряки. По подобному принципу работают динамомашины, питающие фары велотранспорта.
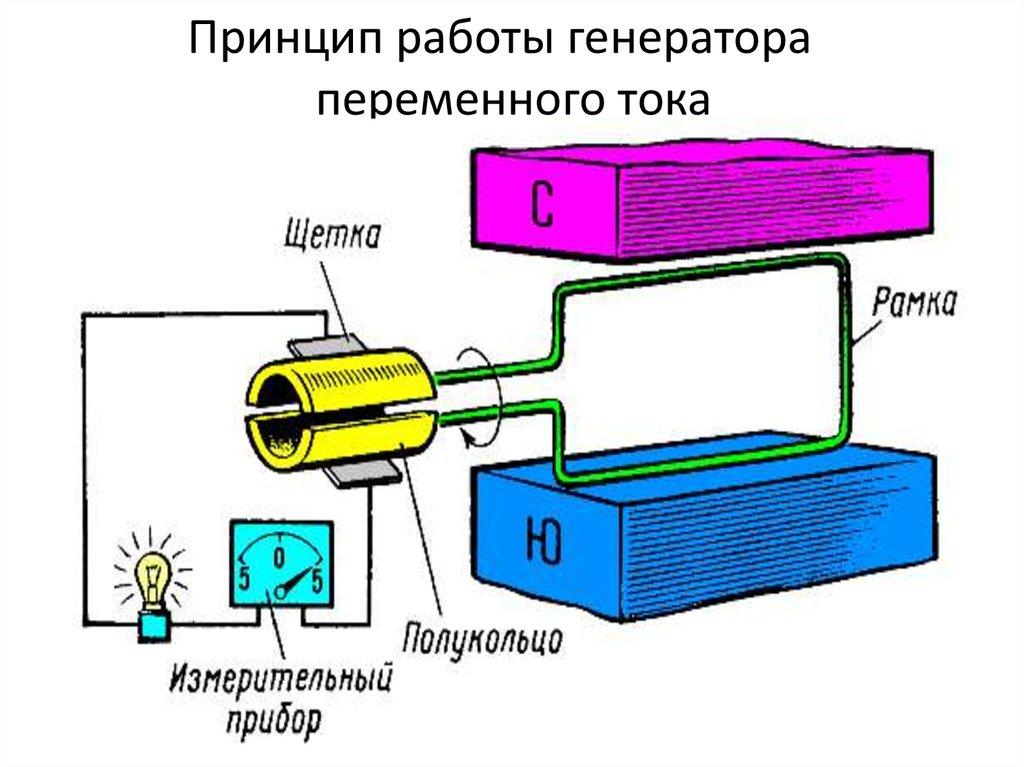
Принцип работы генератора
Две катушки – трансформатор
Ещё одно распространённое применение – это электрический трансформатор. Конструктивно он состоит из двух и более катушек, расположенных на одном железном или ферритовом сердечнике. Подобный агрегат работает только с переменным напряжением. Если на первичную обмотку подать ток, то он создаст в сердечнике магнитный поток. Он, в свою очередь, наведёт ЭДС во вторичной обмотке. Напряжения во входной и выходной катушках прямо зависят от количества их витков.
Таким образом, можно трансформировать 220 В из розетки в 12 В, необходимых для питания небольшой стереосистемы, или преобразовать 10 000 вольт в 220 для передачи от подстанции к жилым домам. Подобным методом можно добиться и повышения напряжения, т.е. превратить 12 В обратно в 220.
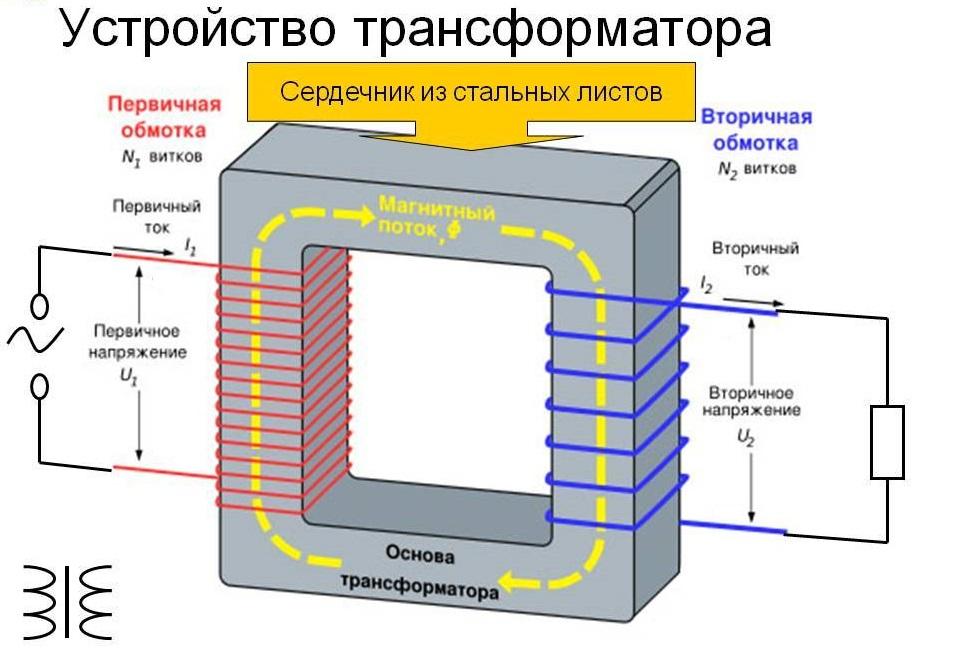
Устройство трансформатора
Катушка индуктивности — элемент колебательного контура
Сейчас это уже редкость, но раньше для подстройки нужной радиостанции использовали колебательный контур. Он состоит из двух элементов, включенных параллельно: катушки индуктивности и переменного конденсатора. Работая в паре, они способны выделить из множества окружающих сигналов именно тот, который требуется. При попадании на антенну приёмника нужной частоты электромагнитных волн колебательный контур входит в резонанс. Процесс сопровождается лавинообразным увеличением ЭДС. Частота, на которой это происходит, зависит от индуктивности катушки и ёмкости конденсатора.
Катушка индуктивности – дроссель ДРЛ ламп
Несмотря на то, что освещение улиц и промышленных предприятий стремительно переходит на LED светильники, по СНГ всё ещё осталось огромное количество мест, где используются устаревшие дуговые ртутные люминесцентные лампы типа ДРЛ. Более всего они распространены в мелких городах и на второстепенных улицах. Их можно узнать по характерному холодно-белому свету и долгому розжигу.
ДРЛ лампы не способны работать без пускорегулирующего дросселя. Он обладает высоким индуктивным сопротивлением и призван ограничить пусковой ток осветительного прибора. Дроссели для ламп подбираются, исходя из их мощности. Наиболее распространённые номиналы – 250, 400 и 1000 Вт. Информация о мощности указывается на самом дросселе. Там же можно найти схемы включения.
Из вышесказанного можно подчеркнуть, что катушка индуктивности является консервативным и давно освоенным на практике электронным компонентом. Однако спрос на его применение по-прежнему не спадает. Поэтому знания, необходимые для расчета катушек и их правильного включения, необходимы каждому специалисту, имеющему дело с электроникой.
Видео
Катушка индуктивности (дроссель). | Электрознайка. Домашний Электромастер.
При прохождении тока по проводнику, вокруг него образуется магнитное поле. В свою очередь, образовавшееся вокруг проводника, магнитное поле начинает взаимодействовать с током протекающим по проводнику. Эти взаимодействия выражаются в законах о самоиндукции, взаимоиндукции и индуктивности.
Чем длиннее провод, тем больше его индуктивность. Если свернуть этот провод в катушку, то магнитное поле каждого витка складывается в общее магнитное поле катушки.
Чем больше витков в катушке, тем больше магнитный поток Ф проходящий через нее, тем больше ее индуктивность.
Индуктивность (коэффициент самоиндукции) – физическая величина, характеризующая магнитные свойства электрической цепи ( проводящего контура).
Коэффициент пропорциональности между силой электрического тока I в контуре и создаваемым им магнитным потоком Ф через контур.
L = Ф / I. где: L — индуктивность в генри, Гн.
Ф — магнитный поток проходящий через катушку.
I — ток в витках катушки, в амперах.
Индуктивность катушки зависит от количества витков, формы каркаса, магнитной проницаемости среды, где установлена катушка. Для увеличения индуктивности катушки в нее вставляют сердечник из ферромагнитного материала (сталь, феррит, альсифер и др.).
Изменять индуктивность катушки можно разными способами:
- изменяя количество витков;
- раздвигая или сжимая витки;
- вводя в катушку ферромагнитный или диамагнитный сердечник;
- разбивая катушку на секции а затем включая их встречно, параллельно или последовательно;
- вводя подмагничивание постоянным током;
- подводя или отводя короткозамкнутый выток к торцу катушки.
Катушка индуктивности, при прохождении через нее переменного тока, оказывает ему индуктивное сопротивление. Объясняется это тем, что проходящий по ней переменный ток создает ток самоиндукции, который направлен навстречу основному току.
Величина индуктивного (реактивного) сопротивления зависит от частоты переменного тока и от индуктивности катушки (дросселя).
X = 2 · π · f · L.
где: Х – индуктивное сопротивление Ом;
f — частота переменного тока Гц;
π — 3,14
L — индуктивность Гн.
Индуктивное сопротивление катушки во много раз больше ее активного сопротивления.
Активное сопротивление R катушки равно ее омическому сопротивлению при постоянном токе и составляет от долей Ома до единиц Ом (зависит от диаметра провода).
Индуктивное (реактивное) сопротивление катушки велико и составляет от 100 до 10000 Ом и более и не зависит от диаметра провода.
Если включить индуктивность к источнику напряжения, то ток в цепи вследствие возникновения ЭДС самоиндукции будет медленно возрастать от нуля до максимума.
Ток в цепи индуктивности отстает от напряжения на 90 градусов.
Индуктивность катушки. От чего она зависит и как её можно измерить?
Катушка индуктивности – электронный компонент, представляющий собой винтовую либо спиральную конструкцию, выполненную с применением изолированного проводника. Основным свойством катушки индуктивности, как понятно из названия – индуктивность. Индуктивность – это свойство преобразовать энергию электрического тока в энергию магнитного поля. Величина индуктивности для цилиндрической или кольцевой катушки равна
Где ψ — потокосцепление, µ0 = 4π*10-7 – магнитная постоянная, N – количество витков, S – площадь поперечного сечения катушки.
Также катушке индуктивности присущи такие свойства как небольшая ёмкость и малое активное сопротивление, а идеальная катушка и вовсе их лишена.
Электрический ток способствует накоплению энергии в магнитном поле катушки. Если отключить подачу электричества, накопленная энергия будет возвращена в электрическую цепь. Значение напряжения при этом в цепи катушки возрастает многократно. Величина запасаемой энергии в магнитном поле равна примерно тому значению работы, которое необходимо получить, чтобы обеспечить появление необходимой силы тока в цепи. Значение энергии, запасаемой катушкой индуктивности можно рассчитать с помощью формулы.
Реактивное сопротивление
При протекании переменного тока, катушка обладает кроме активного, еще и реактивным сопротивлением, которое находится по формуле
По формуле видно, что в отличие от конденсатора, у катушки с увеличением частоты, реактивное сопротивление растет, это свойство применяется в фильтрах частот.
При построении векторных диаграмм важно помнить, что в катушке, напряжения опережает ток на 90 градусов.
Добротность катушки
Еще одним важным свойством катушки является добротность. Добротность показывает отношение реактивного сопротивления катушки к активному.
Чем выше добротность катушки, тем она ближе к идеальной, то есть она обладает только главным своим свойством – индуктивностью.
Катушка индуктивности в электрической цепи для переменного тока имеет не только собственное омическое сопротивление, но имеет реактивное сопротивлениепеременному току, нарастающее при увеличении частоты, поскольку при изменении тока в катушке возникает ЭДС самоиндукции, препятствующая этому изменению.
Катушка индуктивности обладает реактивным сопротивлением, модуль которого , где — индуктивность катушки, — циклическая частота протекающего тока. Соответственно, чем больше частота тока, протекающего через катушку, тем больше её сопротивление.
Сопротивление потерь[править | править вики-текст]
В катушках индуктивности помимо основного эффекта взаимодействия тока и магнитного поля наблюдаются паразитные эффекты, вследствие которых импеданс катушки не является чисто реактивным. Наличие паразитных эффектов ведёт к появлению потерь в катушке, оцениваемых сопротивлением потерь . Потери складываются из потерь в проводах, диэлектрике, сердечнике и экране:
где — потери в проводах,
— потери в диэлектрике,
— потери в сердечнике,
— потери на вихревые токи
Температурный коэффициент индуктивности (ТКИ)[править | править вики-текст]
ТКИ — это параметр, характеризующий зависимость индуктивности катушки от температуры.
Температурная нестабильность индуктивности обусловлена целым рядом факторов: при нагреве увеличивается длина и диаметр провода обмотки, увеличивается длина и диаметр каркаса, в результате чего изменяются шаг и диаметр витков; кроме того при изменении температуры изменяются диэлектрическая проницаемость материала каркаса, что ведёт к изменению собственной ёмкости катушки. Очень существенно влияние температуры на магнитную проницаемость ферромагнетика сердечника:
2. Катушка индуктивности в цепи переменного тока | 3. Реактивное сопр. и импеданс — Индуктивность | Часть2
2. Катушка индуктивности в цепи переменного тока
Катушка индуктивности в цепи переменного тока
Катушка индуктивности в цепи переменного тока ведет себя не так, как резистор. Если резисторы просто противостоят потоку электронов (напряжение на них прямопропорционально току), то катушки индуктивности противостоят изменению проходящего через них тока (напряжение на них прямопропоционально скорости изменения тока). Согласно Закону Ленца, индуцированное напряжение всегда имеет такую полярность, которая пытается сохранить текущее значение силы тока. То есть, если величина тока возрастает, то индуцированное напряжение будет «тормозить» поток электронов; если величина тока уменьшается, то полярность напряжения развернется и будет «помогать» электронному потоку оставаться на прежнем уровне. Такое противостояние изменению величины тока называется реактивным сопротивлением.
Математическая взаимосвязь между напряжением на катушке индуктивности и скоростью изменения тока через нее выглядит следующим образом:
Отношение di/dt представляет собой скорость изменения мгновенного тока (i) с течением времени, и измеряется в амперах в секунду. Индуктивность (L) измеряется в Генри, а мгновенное напряжение (u) — в вольтах. Чтобы показать, что происходит с переменным током, давайте проанализируем простую индуктивную схему:
Простая индуктивная цепь: ток катушки отстает от напряжения на 90o.
Если мы построим график тока и напряжения для этой простой цепи, то он будет выглядеть примерно так:
Как вы помните, изменение напряжения на катушке индуктивности является реакцией на изменение тока, проходящего через нее. Отсюда можно сделать вывод, что мгновенное напряжение равно нулю всякий раз, когда мгновенное значение тока находится в пике (нулевое изменение, или нулевой наклон синусоидальной волны тока), и мгновенное напряжение равно своему пиковому значению всякий раз, когда мгновенный ток находится в точках максимального изменения (точки самого крутого наклона волны тока, в которых она пересекает нулевую линию). Все это приводит к тому, что волна напряжения на 90o не совпадает по фазе с волной тока. На графике видно, как волна напряжения дает «фору» волне тока: напряжение «ведет» ток, а ток «запаздывает» за напряжением.
Ели мы на этот график нанесем значения мощности нашей схемы, то все станет еще более интересным:
Поскольку мгновенная мощность представляет собой произведение мгновенного напряжения и мгновенного тока (p = iu), она будет равна нулю, если мгновенное напряжение или ток будут равны нулю. Всякий раз, когда мгновенные значения тока и напряжения имеют положительные значения (выше нулевой линии), мощность так же будет положительна. Аналогично примеру с резистивной цепью, мощность примет положительное значение и в том случае, если мгновенный ток и напряжение будут иметь отрицательные значения (ниже нулевой линии). Однако, вследствие того, что волны напряжения и тока не совпадают по фазе на 90o, бывают случаи, когда ток положителен, а напряжение отрицательно (или наоборот), в результате чего появляются отрицательные значения мгновенной мощности.
Но, что такое отрицательная мощность? Отрицательная мощность означает, что катушка индуктивности отдает энергию обратно в цепь. Положительная же мощность означает, что катушка индуктивности поглощает энергию из цепи. Так как положительные и отрицательные циклы питания равны по величине и продолжительности, в течение полного цикла катушка индуктивности отдает обратно в схему столько же энергии, сколько она потребляет из нее. В практическом смысле это означает, что реактивное сопротивление катушки не рассеивает никакой энергии, чем оно и отличается от сопротивления резистора, рассеивающего энергию в виде тепла. Однако, все вышесказанное справедливо только для идеальных катушек индуктивности, провода которых не имеют никакого сопротивления.
Сопротивление катушки индуктивности, изменяющее силу тока, интерпретируется как сопротивление переменному току в целом, у которого по определению постоянно меняется мгновенная величина и направление. Это сопротивление переменному току похоже на обычное сопротивление, но отличается от него тем, что всегда приводит к фазовому сдвигу между током и напряжением, а так же рассеивает нулевую мощность. Из-за указанных различий, данное сопротивление носит несколько иное название — реактивное сопротивление. Реактивное сопротивление, как и обычное, измеряется в Омах, только обозначается оно символом Х, а не R. Для большей конкретики, реактивное сопротивление катушки индуктивности обычно обозначают заглавной буквой Х с буквой L в качестве индекса: XL.
Поскольку напряжение на катушке индуктивности пропорционально скорости изменения тока, оно будет больше для быстро меняющихся токов, и меньше — для токов с более медленным изменением. Это означает, что реактивное сопротивление любой катушки индуктивности (в Омах) прямопропорционально частоте переменного тока. Точная формула расчета реактивного сопротивления выглядит следующим образом:
Если на катушку индуктивностью 10 мГн воздействовать частотами 60, 120 и 2500 Гц, то ее реактивное сопротивление примет следующие значения:
| Частота (Гц) | Реактивное сопротивление (Ом) |
|---|---|
| 60 | 3.7699 |
| 120 | 7.5398 |
| 2500 | 157.0796 |
В уравнении реактивного сопротивления выражение “2πf” имеет важное значение. Оно означает число в радианах в секунду, характеризующее «вращение» переменного тока (один полный цикл переменного тока представляет собой одно полное круговое вращение). Радиан — это единица измерения углов: в одном полном круге есть 2π радиан, точно так же, как в нем есть 360o. Если генератор переменного тока двухполюсный, то он произведет один полный цикл для каждого полного оборота вала, что будет означать 2π радиан или 360o. Если постоянную 2π умножить на частоту в герцах (циклах в секунду), то результатом будет число в радианах в секунду, известное как угловая (циклическая) частота переменного тока.
Помимо выражения 2πf, угловая частота переменного тока может обозначаться строчной греческой буквой ω (Омега). В этом случае формула XL = 2πfL может быть написана как XL = ωL.
Необходимо понимать, что угловая частота является выражением того, насколько быстро проходит полный цикл волны, равный 2π радиан. Она необязательно представляет фактическую скорость вала генератора, производящего переменный ток. Если генератор имеет более двух полюсов, его угловая частота будет кратной скорости вращения вала. По этой причине ω иногда выражается в единицах электрических радиан в секунду, чтобы отличить ее от механического движения.
При любом способе выражения угловой частоты очевидно, что она прямопропорциональна реактивному сопротивлению катушки индуктивности. При увеличении частоты переменного тока (или скорости вращения вала генератора), катушка индуктивности будет оказывать большее сопротивление прохождению тока и наоборот. Переменный ток в простой индуктивной цепи равен напряжению (в Вольтах) поделенному на реактивное сопротивление катушки индуктивности (в Омах). Как видите, это аналогично тому что переменный или постоянный ток в простой резистивной цепи равен напряжению (в Вольтах) поделенному на сопротивление (в Омах). В качестве примера давайте рассмотрим следующую схему:
Однако, мы должны иметь в виду, что напряжение и ток имеют разные фазы. Как было сказано ранее, напряжение имеет фазовый сдвиг +90o по отношению к току (рисунок ниже). Если представить фазовые углы напряжения и тока математически (в виде комплексных чисел), то мы увидим, что сопротивление катушки индуктивности переменному току обладает следующим фазовым углом:
Ток на катушке индуктивности отстает от напряжения на 90o.
Математически можно сказать, что фазовый угол сопротивления катушки индуктивности переменному току составляет 90o. Фазовый угол реактивного сопротивления току очень важен при анализе цепей. Особенно эта важность проявляется при анализе сложных цепей переменного тока, где реактивные и простые сопротивления взаимодействуют друг с другом. Он также окажется полезным для представления сопротивления любого компонента электрическому току с точки зрения комплексных чисел (а не скалярных величин сопротивления и реактивного сопротивления).
2. Катушки индуктивности и расчеты | 14. Катушки индуктивности | Часть1
2. Катушки индуктивности и расчеты
Катушки индуктивности и расчеты
Катушки индуктивности, в отличии от проводников, не обладают стабильным сопротивлением. Однако, для них существует определенная математическая зависимость между напряжением и током:
Как видите, эта формула похожа на аналогичную формулу «Закона Ома» для конденсатора. Она связывает одну переменную (в нашем случае напряжение на катушке индуктивности) со скоростью изменения другой переменной (тока через катушку). И напряжение (u) и скорость изменения тока здесь (di/dt) мгновенны: они берутся в определенный момент времени. Величина скорости изменения тока (di/dt) выражается в амперах в секунду, и имеет положительное значение при увеличении тока, и отрицательное значение при его уменьшении.
Поведение катушки индуктивности (по аналогии с конденсатором) тесно связано с переменной времени. Если не учитывать внутреннее сопротивление катушки индуктивности (ради чистоты эксперимента мы принимаем его равным нулю), то напряжение на ее выводах будет зависеть от изменения тока во времени.
Давайте предположим, что мы подключили идеальную катушку индуктивности (имеющую нулевое сопротивление провода) к цепи, позволяющей измерить ток через эту катушку при помощи потенциометра:
Если механизм потенциометра находится в одном положении (ползунок неподвижен), то соединенный последовательно с ним амперметр зарегистрирует постоянный (неизменный) ток, а подключенный к катушке индуктивности вольтметр покажет 0 вольт. Так как ток в этом случае постоянен, скорость его изменения (di/dt) будет равна нулю. Посмотрев внимательно на вышеприведенное уравнение можно сделать вывод, что при нулевом значении du/dt мгновенное напряжение на катушке так же будет равно нулю. С точки зрения физики, если ток будет постоянным (неизменным), то постоянным будет и произведенное катушкой индуктивности магнитное поле. При отсутствии изменений магнитного потока (dΦ/dt = 0 Вебер в секунду) индуцированное напряжение будет равно нулю.
Если ползунок потенциометра медленно перемещать вверх, то его сопротивление будет медленно уменьшаться. Ток в цепи при этом будет возрастать, что можно увидеть по медленному отклонению стрелки амперметра:
Если ползунок потенциометра перемещать с постоянной скоростью, то ток в цепи будет нарастать равномерно, а значит, отношение di/dt будет иметь фиксированное значение. Это значение, умноженное на индуктивность (так же имеющую фиксированную величину), даст нам постоянное напряжение некоторой величины. С точки зрения физики, постепенное увеличение тока приведет к росту магнитного поля. Увеличивающийся магнитный поток поля создаст в катушке индуцированное напряжение, выраженное уравнением Фарадея: e = N(dΦ/dt). Это напряжение принимает такую полярность, которая пытается противодействовать изменению тока. Другими словами, полярность напряжения, индуцированного в результате увеличения тока, будет ориентирована против направления этого тока, чтобы сохранить его величину на прежнем уровне. Это явление демонстрирует более общий принцип физики, известный как Правило Ленца, который гласит: Индукционный ток всегда имеет такое направление, что он ослабляет действие причины, возбуждающей этот ток.
В этом случае катушка индуктивности выступает в качестве нагрузки. Она имеет отрицательную полярность индуцированного напряжения со стороны входа потока электронов, и положительную полярность — со стороны выхода.
Если мы будем двигать ползунок потенциометра в том же направлении, но с различной скоростью, то получим следующий график:
Обратите внимание: напряжение на катушке индуктивности в любой момент времени пропорционально скорости изменения (наклону линии) тока. Когда линия тока на графике растёт быстро (крутой подъем), напряжение имеет большое значение. Когда линия тока растет медленно (пологий подъем), напряжение имеет маленькое значение. В одном месте графика можно увидеть строго горизонтальный отрезок линии тока (нулевой наклон, представляющий период времени, когда ползунок потенциометра не двигался вообще), при котором напряжение упало до нулевой отметки.
Если мы будем двигать ползунок потенциометра вниз, то его сопротивление увеличится, а ток в цепи уменьшится (отрицательное значение для di/dt). Катушка индуктивности всегда выступает против любого изменения тока, полярность индуцированного ей напряжения будет противоположна направлению этого изменения:
Величина производимого катушкой индуктивности напряжения конечно же зависит от скорости уменьшения тока. Как гласит Закон Ленца, индуцированное напряжение будет противоположно изменению тока. При уменьшении тока полярность напряжения будет ориентирована таким образом, чтобы попытаться сохранить величину этого тока на прежнем уровне. В данном случае катушка выступает в качестве источника. Она имеет положительную полярность индуцированного напряжения со стороны входа потока электронов, и отрицательную полярность — со стороны выхода. Чем быстрее уменьшается ток, тем больше напряжения будет производить катушка индуктивности за счет высвобождения накопленной энергии.
Запомните, величина индуцированного идеальной катушкой индуктивности напряжения прямо пропорциональна скорости изменения протекающего через нее тока. Единственным различием между эффектами снижения увеличения тока является полярность индуцированного напряжения. При одинаковой скорости уменьшения/увеличения тока, величина напряжения будет одинаковой. Например, при скорости изменения тока (di/dt) -2 ампера в секунду будет произведено такое же количество индуцированного напряжения, как и при di/dt +2 ампера в секунду, только полярность этих напряжений будет противоположной.
Если ток через катушку индуктивности изменяется очень быстро, то она произведет очень высокое напряжение. В качестве примера давайте рассмотрим следующую схему:
В этой схеме лампа подключена параллельно катушке индуктивности. Переключатель используется для управления током в цепи, а питание подается от 6-вольтовой батареи. При включении выключателя, катушка индуктивности окажет кратковременное сопротивление изменению тока от нуля до некоторой величины, на ее выводах сгенерируется небольшое напряжение. Так как для ионизации газа внутри неоновой лампы необходимо напряжение порядка 70 вольт, шести вольт источника питания, а тем более низкого мгновенного напряжения катушки индуктивности в момент включения выключателя будет явно недостаточно, чтобы зажечь эту лампу:
Если выключатель разомкнуть, то в цепи мгновенно возникнет очень высокое сопротивление (сопротивление воздушного зазора между контактами). Это сопротивление спровоцирует почти мгновенное уменьшение тока. Математически, значение di/dt будет очень большим отрицательным числом. Такое быстрое изменение тока (с некоторой величины до нуля, в короткий промежуток времени) приведет к возникновению очень высокого напряжения на катушке индуктивности (пытающегося противодействовать понижению тока). Этого напряжения, как правило, более чем достаточно чтобы зажечь неоновую лампу, хотя бы на короткое время, пока ток не упадет до нуля:
Для достижения максимального эффекта, индуктивность катушки должна быть как можно больше (по крайней мере один Генри).
Обсуждение:Катушка индуктивности — Википедия
Оказывает ли индуктивная катушка сопротивление постоянному току, Rk=0 217.8.236.160 05:10, 6 февраля 2011 (UTC)
- Идеальная теоретическая — нет. Реальная практическая — да, это один из основных параметров неидеальности катушки. ASDFS 08:05, 6 февраля 2011 (UTC)
Свойства нужно выкинуть их преамбулы, есть раздел «Характеристики» где тоже наличиствует чушь:
ЭДС самоиндукции равна по модулю и противоположна по знаку напряжению на концах катушки
- |ε|=−ε=U{\displaystyle |\varepsilon |=-\varepsilon =U}
Д.Ильин 15:44, 15 ноября 2012 (UTC)
Называть катушку индуктивности (компонент) индуктивностью (величина, параметр) — безграмотно, если это не жаргон профессионалов. Ср.: резистор называть сопротивлением. Д.Ильин 15:59, 15 ноября 2012 (UTC)
(Это верно только для колебательного контура на частоте резонанса, к свойствам катушки отношения не имеет.)
Бог с Вами, ASDFS, откройте любой учебник ТОЭ (раздел «векторные диаграммы») и Вы поймете, что неправы. Напомню, сдвиг фаз определен для двух меандров равной частоты скважности 2, но если возбуждать меандром напряжения К.И., то никакого сдвига не будет.
Д.Ильин 14:11, 16 ноября 2012 (UTC)
- Расшифруйте вторую фразу — я не понял. Что касается сабжа, то поясните мне, балбесу, на пальцах: вот у нас соединены КИ 1мкГн и источник тока 1Гц 1А. Так что там у нас с фазами будет? ASDFS 15:45, 16 ноября 2012 (UTC)
- Меандр – многозначный термин, пока его многозначность в руВП не отражена, спасибо, навели, восполню при очередном кураже этот пробел.
- 1. Река в Малой Азии – сильно петляет, течет на все стороны света, от этого произошел другой термин:
- 2. Меандр (орнамент) очень часто встречается в эллинских античных предметах искусства – непрерывная линия состоящая из ортогональных отрезков, если двигаться по этой линии, то путь тоже будет во все стороны света. Вы ее неоднократно видели, вероятно, не зная, что это меандр.
- 3. Меандр (электроника, электротехника), более века как устоявшийся своего рода жаргон, отец, — кажется, Хевисайд – обычно, прямоугольное колебание с плоскими вершинами и короткими фронтами, иногда – волнистая печатная дорожка с прямоугольными изгибами.
- Скважность – отношение периода к длительности импульса, например, положительного, в меандре при скважности 2 длительности импульса и паузы равны. Для двух меандров равной частоты и не обязательно равной скважности можно ввести понятие фазового сдвига. При этом период принимается равным 2*пи, сдвиг фаз – запаздывание нарастающего фронта 1-го колебания относительно нарастающего фронта 2-го колебания, выраженный в радианах (или градусах).
- При возбуждении КИ меандром напряжения, ток в ней будет представлять собой пилообразное колебание, причем изломы этого колебания будут совпадать по времени с фронтами возбуждения, поэтому здесь говорить о фазовом сдвиге некорректно, или только с оговорками (сдвиг=0).
- Разберем Ваш пример: идеальная КИ 1 мкГн, 1 А, 1 Гц, гармонический ток. Модуль_импеданса = реактивному_сопротивлению = омега*L = 2*пи*f*10^-6 = 6.28*1*10^-6* = 6.28*10^-6 Ом. = 6.28 мкОм. При возбуждении током: модуль_напряжения_на_КИ = модуль_тока*Модуль_импеданса = 1*6.28*10^-6 = 6.28 мкВ, но вектор напряжения (в терминах вращающихся векторов) все равно ортогонален вектору тока, иными словами, напряжения отстает по фазе от тока на пи/2. Подчеркну, речь шла об идеальной КИ, практически, изготовить КИ, чтобы ее активное сопротивление составляло доли мкОм (приближенно смоделировать Ваш утрированный пример) очень трудно, габариты ее будут с большую кастрюлю, или применить сверхпроводники.
- Немного просмотрел Ваш вклад в ВП, вполне все грамотно и корректно, — напрасно себя балбесом именуете…
- Извините за задержку с ответом, возился со ст. Cray. С уважением, Д.Ильин 15:53, 17 ноября 2012 (UTC)
- Блестяще! Не слышал такого прекрасного образчика риторики уж лет 25, со времен Горбачева. Безупречно! Столько текста вокруг да около и ни слова по теме — это сильно. Моя Вам уважуха. ASDFS 16:10, 17 ноября 2012 (UTC)
- Извините за задержку с ответом, возился со ст. Cray. С уважением, Д.Ильин 15:53, 17 ноября 2012 (UTC)
- Без словесного поноса я Вам написал 16.11.12, для профессионала той фразы можно было бы и не писать (да он и не станет удалять про сдвиг фаз), но и написанную, Вы ее не поняли. Поэтому, я, увидев, что Вы начинающий электронщик, дружелюбно разжевал тему, в том числе и Ваш пример. Теперь поясните мне, что конкретно в моем посте бла-бла-бла а ля Горбачев? Что не по теме? Впрочем, можете не напрягаться, более никогда не стану Вас утомлять своей назойливой риторикой. Но просьба, не правьте, плохо зная предмет, а то у вас сдвиг фаз пи/2 оказывается только в колебательных контурах — просто восхитительно, а я-то, недоучка, уже массу лет заблуждался… Д.Ильин 16:51, 17 ноября 2012 (UTC)
- 16.11.12 сдвиг фаз определен для двух меандров равной частоты
скважности 2, но если возбуждать меандром напряжения К.И., то никакого сдвига не будет. Первая часть фразы про то что сдвиг фаз это разница временных параметров двух идентичных сигналов. Кэп Очевидность согласен. Вторая часть — утверждение без пояснений что ежели прямоугольный сигнал подать на КИ то сдвига фаз не будет. Сегодня вы вроде бы разъяснили — будет треугольник тока. Типа раз там прямоугольник а тут треугольник — сдвиг фаз не смотрим потому как формы сигналов неидентичны. Я правильно Вас расшифровал? P.S. Если считаете что я неправ — верните правку на место, я согласен что плохо понимаю этот вопрос. ASDFS 18:03, 17 ноября 2012 (UTC)
- 16.11.12 сдвиг фаз определен для двух меандров равной частоты
Продифференцируйте: U(t)=−LdIdt{\displaystyle U(t)=-L{dI \over dt}}, при I = Io*sin(омега*t), или проинтегрируйте U(t) = Uo*sin(омега*t), и Вы запомните про сдвиги фаз тока и напряжения в КИ на всю жизнь, как навык езды на велосипеде. Кстати, и формулу реактивного сопротивления, продифференцировав, увидите.
Что каксается ст. КИ — там еще конь не валялся, еще улучшать и улучшать, пока некогда, займусь позднее. Мною движет ее высокая важность. Д.Ильин 19:43, 17 ноября 2012 (UTC)
…Если считаете что я неправ — верните правку на место… Не я считаю, Фарадей с Максвеллом так считают, в гробу ворочаются, видя безграмотнсть.
…Верните правку… — еще чего хотите? может мне еще сплясать на стриптизерном шесте? Вы сделали некорректное удаление — Вам и восстанавливать. Славная позиция, кто-то обкакается, а старик должен подтирать задницы.
Д.Ильин 15:48, 21 ноября 2012 (UTC)
Последовательное соединение катушек[править код]
Пожалуйста объясните неспециалисту. Довожу до ума двухполосные колонки и столкнулся с тем, что две КИ соединённые последовательно воздействуют на резуемую частоту гораздо (на порядок сильнее) чем можно предположить из приведённых в статье формул: XL=ωL{\displaystyle ~X_{L}=\omega L} (зависимость сопротивления от частоты и индуктивности) и L=∑i=1NLi{\displaystyle L=\sum _{i=1}^{N}L_{i}} (при последовательном соединении катушек общая индуктивность равна сумме индуктивностей всех соединённых катушек). Берём катушку на 0.4mH, она подавляет частоту 4 кГц примерно в 10 раз (-10 дБ), берём на 0.8mH — понижение 4 кГц в 20 раз (-13 дБ). Того же (понижения в 20 раз) можно ожидать и от двух последовательно соединённых КИ по 0.4mH, но нет! Они режут 4 кГц практически в 100 раз (на замерах -19-20 дБ). Проверка на Multisim (EWB) тоже не сильно расходится с практикой. Рассуждаем логически: пусть данная катушка (так и есть в реале) практически не влияет на 50 Гц и режет 4 кГц в десять раз. Проходя через вторую катушку 50 Гц не меняется, а 4 кгц уменьшается ещё в 10 раз! Расхождение с формулой пятикратное. Где я ошибаюсь (а со мной и уважаемая EWB)? Sergoman 17:22, 14 марта 2014 (UTC)
длина средней линии сердечника[править код]
Пожалуйста дайте определение «длина средней линии сердечника«. Неспециалистам неясно что это такое.
Все ли виды перечислены в статье?[править код]

Если взять катушку, поместить в неё магнитный сердечник и начинать двигать его вдоль оси катушки, что произойдёт? В статье такой вид и примененеие не описано. Как пример — вот такой фонарик. 37.113.180.61 01:05, 9 сентября 2019 (UTC)
Также упущен такой момент, как катушки электромагнитов (подробнее) и трансформаторов. Да и про вихревые токи вроде ничего не написано. 37.113.180.61 01:09, 9 сентября 2019 (UTC)
от напряжения или от силы тока?
L=M0*M*N^2V/l^2, где М -магнитная проницаемость материала сердечника. М0=4Pi*10^-7, N- число витков соленоида, V- объем l- длина катушки в системе СИ
От конструкции, от провода, от сердечника
от количества витков от материала сердечника
Диаметр, сердечник, число витков, в меньшей степени диаметр провода….



