Приветствую всех на нашем сайте!
Мы продолжаем изучать электронику с самых основ, и темой сегодняшней статьи будет катушка индуктивности. Забегая вперед скажу, что сначала мы обсудим теоретические аспекты, а несколько будущих статей посвятим целиком и полностью рассмотрению различных электрических схем, в которых используются катушки индуктивности, а также элементы, которые мы изучили ранее в рамках нашего курса – резисторы и конденсаторы.
Устройство и принцип работы катушки индуктивности.
Как уже понятно из названия элемента – катушка индуктивности, в первую очередь, представляет из себя именно катушку 🙂 То есть большое количество витков изолированного проводника. Причем наличие изоляции является важнейшим условием – витки катушки не должны замыкаться друг с другом. Чаще всего витки наматываются на цилиндрический или тороидальный каркас:
Важнейшей характеристикой катушки индуктивности является, естественно, индуктивность, иначе зачем бы ей дали такое название 🙂 Индуктивность – это способность преобразовывать энергию электрического поля в энергию магнитного поля. Это свойство катушки связано с тем, что при протекании по проводнику тока вокруг него возникает магнитное поле:
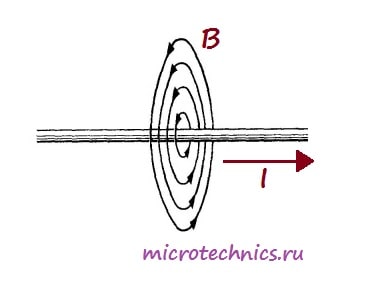
А вот как выглядит магнитное поле, возникающее при прохождении тока через катушку:
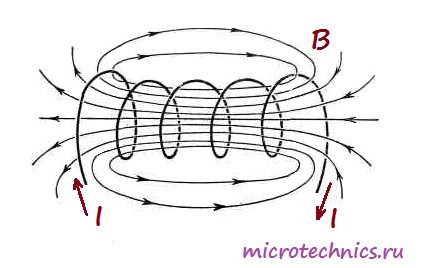
В общем то, строго говоря, любой элемент в электрической цепи имеет индуктивность, даже обычный кусок провода. Но дело в том, что величина такой индуктивности является очень незначительной, в отличие от индуктивности катушек. Собственно, для того, чтобы охарактеризовать эту величину используется единица измерения Генри (Гн). 1 Генри – это на самом деле очень большая величина, поэтому чаще всего используются мкГн (микрогенри) и мГн (милигенри). Величину индуктивности катушки можно рассчитать по следующей формуле:
L = \frac{\mu_0\thinspace \mu S N^2}{l}
Давайте разберемся, что за величину входят в это выражение:
- \mu_0 – магнитная проницаемость вакуума. Это табличная величина (константа) и равна она следующему значению: \mu_0 = 4 \pi \cdot 10^{-7}\medspace\frac{Гн}{м}
- \mu – магнитная проницаемость магнитного материала сердечника. А что это за сердечник и для чего он нужен? Сейчас выясним. Дело все в том, что если катушку намотать не просто на каркас (внутри которого воздух), а на магнитный сердечник, то индуктивность возрастет многократно. Посудите сами – магнитная проницаемость воздуха равна 1, а для никеля она может достигать величины 1100. Вот мы и получаем увеличение индуктивности более чем в 1000 раз
- S – площадь поперечного сечения катушки
- N – количество витков
- l – длина катушки
Из формулы следует, что при увеличении числа витков или, к примеру, диаметра (а соответственно и площади поперечного сечения) катушки, индуктивность будет увеличиваться. А при увеличении длины – уменьшаться. Таким образом, витки на катушке стоит располагать как можно ближе друг к другу, поскольку это приведет к уменьшению длины катушки.
С устройством катушки индуктивности мы разобрались, пришло время рассмотреть физические процессы, которые протекают в этом элементе при прохождении электрического тока. Для этого мы рассмотрим две схемы – в одной будем пропускать через катушку постоянный ток, а в другой -переменный!
Катушка индуктивности в цепи постоянного тока.
Итак, в первую очередь, давайте разберемся, что же происходит в самой катушке при протекании тока. Если ток не изменяет своей величины, то катушка не оказывает на него никакого влияния. Значит ли это, что в случае постоянного тока использование катушек индуктивности и рассматривать не стоит? А вот и нет 🙂 Ведь постоянный ток можно включать/выключать, и как раз в моменты переключения и происходит все самое интересное. Давайте рассмотрим цепь:
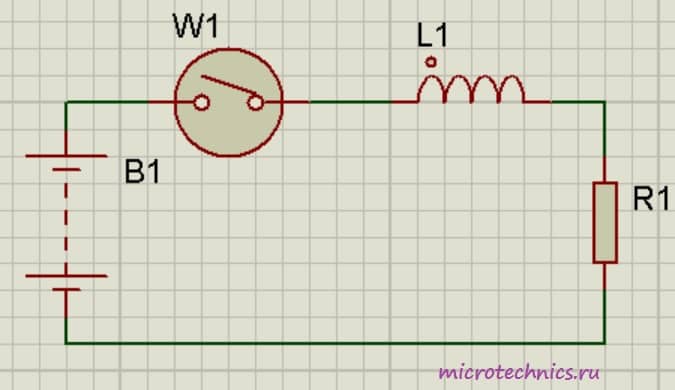
Резистор выполняет в данном случае роль нагрузки, на его месте могла бы быть, к примеру, лампа. Помимо резистора и индуктивности в цепь включены источник постоянного тока и переключатель, с помощью которого мы будем замыкать и размыкать цепь. Что же произойдет в тот момент когда мы замкнем выключатель?
Ток через катушку начнет изменяться, поскольку в предыдущий момент времени он был равен 0. Изменение тока приведет к изменению магнитного потока внутри катушки, что, в свою очередь, вызовет возникновение ЭДС (электродвижущей силы) самоиндукции, которую можно выразить следующим образом:
\varepsilon_s = -\frac{d\Phi}{dt}
Возникновение ЭДС приведет к появлению индукционного тока в катушке, который будет протекать в направлении, противоположном направлению тока источника питания. Таким образом, ЭДС самоиндукции будет препятствовать протеканию тока через катушку (индукционный ток будет компенсировать ток цепи из-за того, что их направления противоположны). А это значит, что в начальный момент времени (непосредственно после замыкания выключателя) ток через катушку I_L будет равен 0. В этот момент времени ЭДС самоиндукции максимальна. А что же произойдет дальше? Поскольку величина ЭДС прямо пропорциональна скорости изменения тока, то она будет постепенно ослабевать, а ток, соответственно, наоборот будет возрастать. Давайте посмотрим на графики, иллюстрирующие то, что мы обсудили:
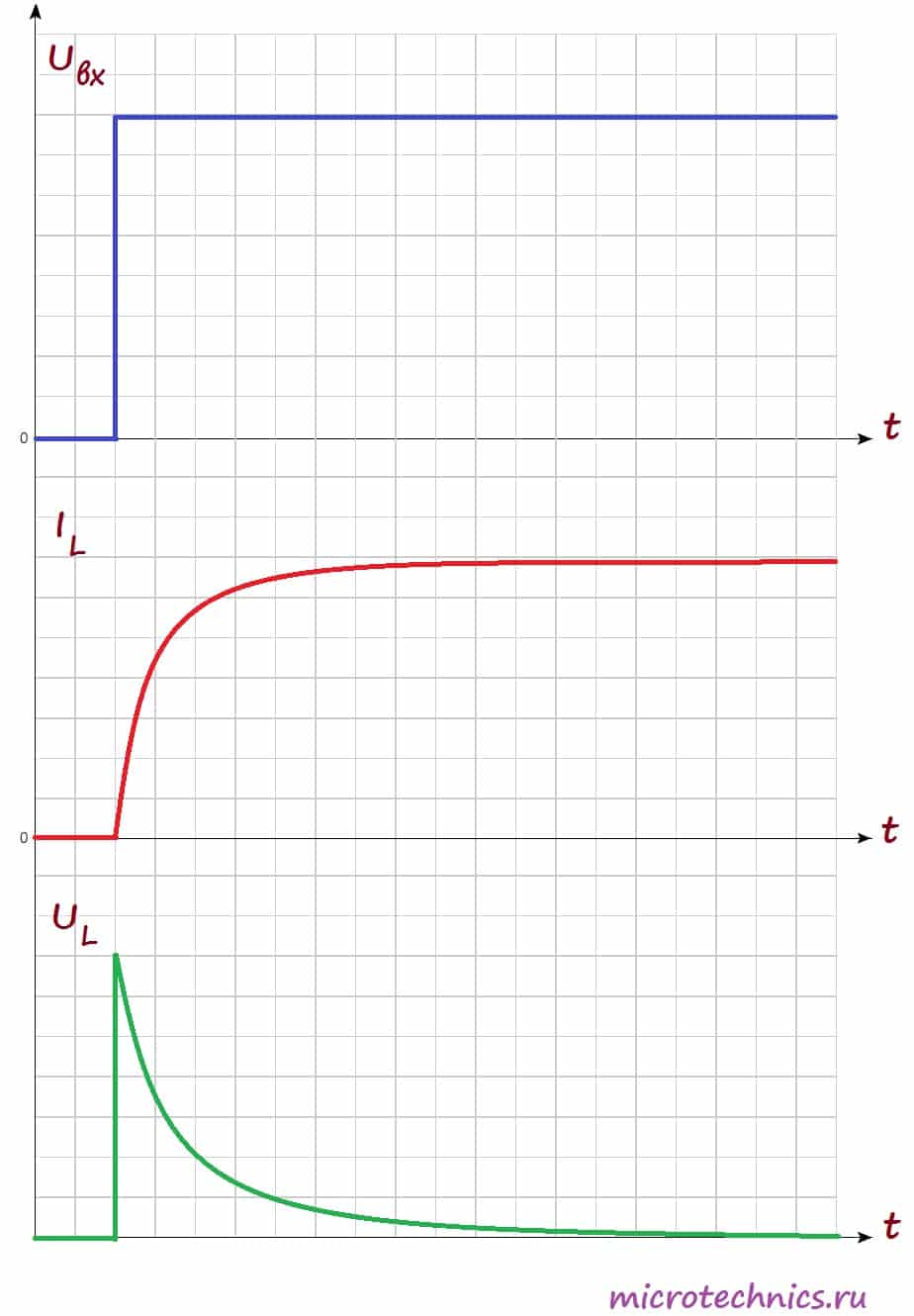
На первом графике мы видим входное напряжение цепи – изначально цепь разомкнута, а при замыкании переключателя появляется постоянное значение. На втором графике мы видим изменение величины тока через катушку индуктивности. Непосредственно после замыкания ключа ток отсутствует из-за возникновения ЭДС самоиндукции, а затем начинает плавно возрастать.
Напряжение на катушке наоборот в начальный момент времени максимально, а затем уменьшается. График напряжения на нагрузке будет по форме (но не по величине) совпадать с графиком тока через катушку (поскольку при последовательном соединении ток, протекающий через разные элементы цепи одинаковый). Таким образом, если в качестве нагрузки мы будем использовать лампу, то они загорится не сразу после замыкания переключателя, а с небольшой задержкой (в соответствии с графиком тока).
Аналогичный переходный процесс в цепи будет наблюдаться и при размыкании ключа. В катушке индуктивности возникнет ЭДС самоиндукции, но индукционный ток в случае размыкания будет направлен в том же самом направлении, что и ток в цепи, а не в противоположном, поэтому запасенная энергия катушки индуктивности пойдет на поддержание тока в цепи:
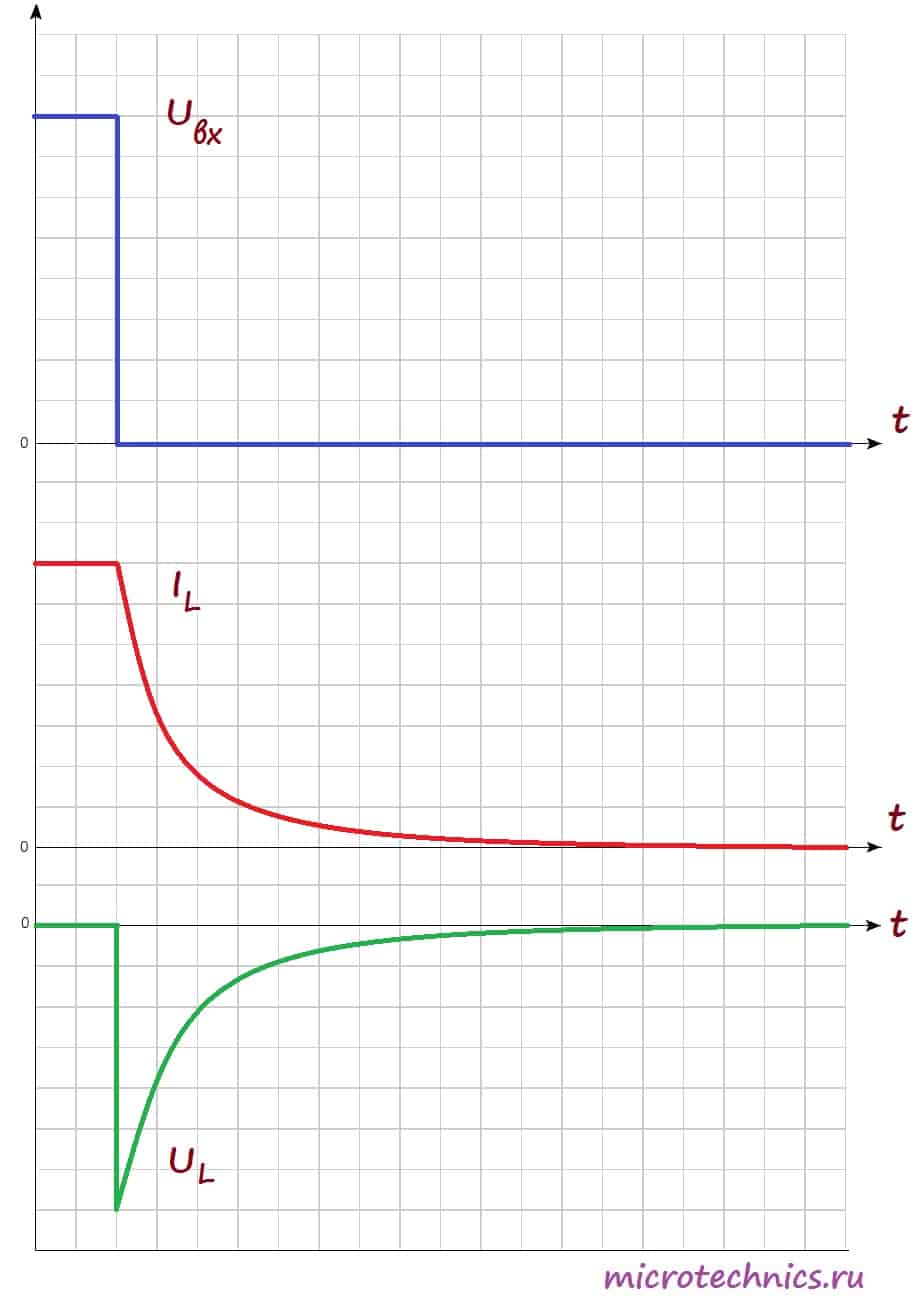
После размыкания ключа возникает ЭДС самоиндукции, которая препятствует уменьшению тока через катушку, поэтому ток достигает нулевого значения не сразу, а по истечении некоторого времени. Напряжение же в катушке по форме идентично случаю замыкания переключателя, но противоположно по знаку. Это связано с тем, что изменение тока, а соответственно и ЭДС самоиндукции в первом и втором случаях противоположны по знаку (в первом случае ток возрастает, а во втором убывает).
Кстати, я упомянул, что величина ЭДС самоиндукции прямо пропорциональна скорости изменения силы тока, так вот, коэффициентом пропорциональности является ни что иное как индуктивность катушки:
\varepsilon_s = -L\medspace\frac{dI}{dt}
На этом мы заканчиваем с катушками индуктивности в цепях постоянного тока и переходим к цепям переменного тока.
Катушка индуктивности в цепи переменного тока.
Рассмотрим цепь, в которой на катушку индуктивности подается переменный ток:
Давайте посмотрим на зависимости тока и ЭДС самоиндукции от времени, а затем уже разберемся, почему они выглядят именно так:
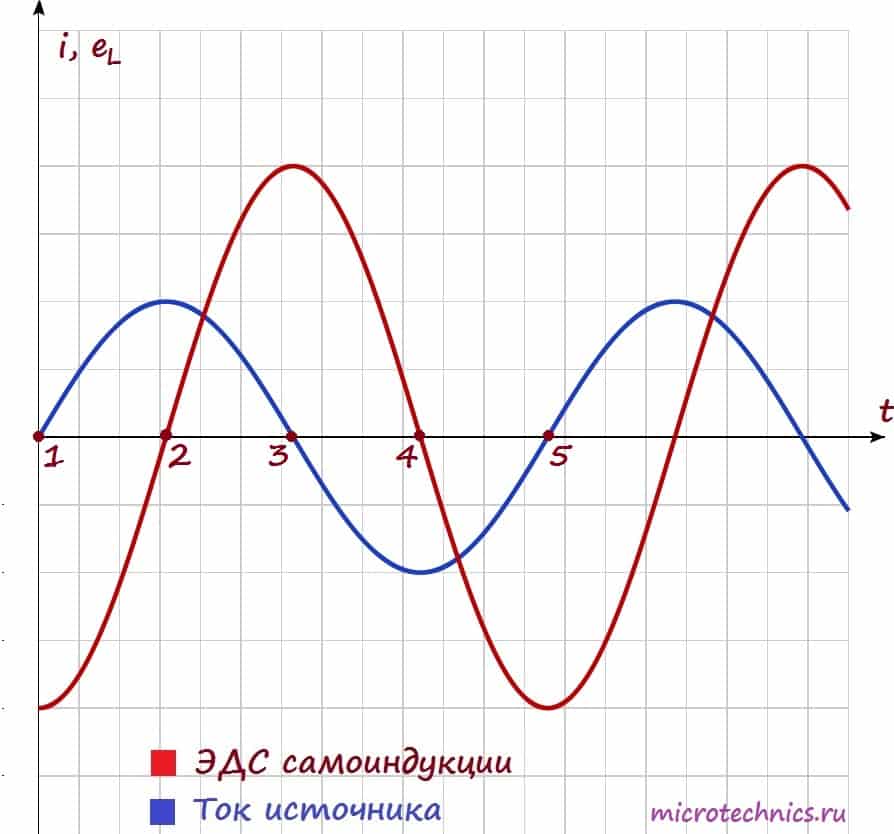
Как мы уже выяснили ЭДС самоиндукции у нас прямо пропорциональна и противоположна по знаку скорости изменения тока:
\varepsilon_L = -L\medspace\frac{dI}{dt}
Собственно, график нам и демонстрирует эту зависимость! Смотрите сами – между точками 1 и 2 ток у нас изменяется, причем чем ближе к точке 2, тем изменения меньше, а в точке 2 в течении какого-то небольшого промежутка времени ток и вовсе не изменяет своего значения. Соответственно скорость изменения тока максимальна в точке 1 и плавно уменьшается при приближении к точке 2, а в точке 2 равна 0, что мы и видим на графике ЭДС самоиндукции. Причем на всем промежутке 1-2 ток возрастает, а значит скорость его изменения положительна, в связи с этим на ЭДС на всем этом промежутке напротив принимает отрицательные значения.
Аналогично между точками 2 и 3 – ток уменьшается – скорость изменения тока отрицательная и увеличивается – ЭДС самоиндукции увеличивается и положительна. Не буду расписывать остальные участки графика – там все процессы протекают по такому же принципу 🙂
Кроме того, на графике можно заметить очень важный момент – при увеличении тока (участки 1-2 и 3-4) ЭДС самоиндукции и ток имеют разные знаки (участок 1-2: \varepsilon < 0, i > 0, участок 3-4: \varepsilon > 0, i < 0). Таким образом, ЭДС самоиндукции препятствует возрастанию тока (индукционные токи направлены “навстречу” току источника).
А на участках 2-3 и 4-5 все наоборот – ток убывает, а ЭДС препятствует убыванию тока (поскольку индукционные токи будут направлены в ту же сторону, что и ток источника и будут частично компенсировать уменьшение тока).
И в итоге мы приходим к очень интересному факту – катушка индуктивности оказывает сопротивление переменному току, протекающему по цепи. А значит она имеет сопротивление, которое называется индуктивным или реактивным и вычисляется следующим образом:
X_L = w\medspace L
Где w – круговая частота: w = 2 \pi f. [/latex]f[/latex] – это частота переменного тока. Таким образом, чем больше частота тока, тем большее сопротивление будет ему оказывать катушка индуктивности. А если ток постоянный (f = 0), то реактивное сопротивление катушки равно 0, соответственно, она не оказывает влияния на протекающий ток.
Давайте вернемся к нашим графикам, которые мы построили для случая использования катушки индуктивности в цепи переменного тока. Мы определили ЭДС самоиндукции катушки, но каким же будет напряжение u? Здесь все на самом деле просто! По 2-му закону Кирхгофа:
u + \varepsilon_L = 0
А следовательно:
u = – \varepsilon_L
Построим на одном графике зависимости тока и напряжения в цепи от времени:
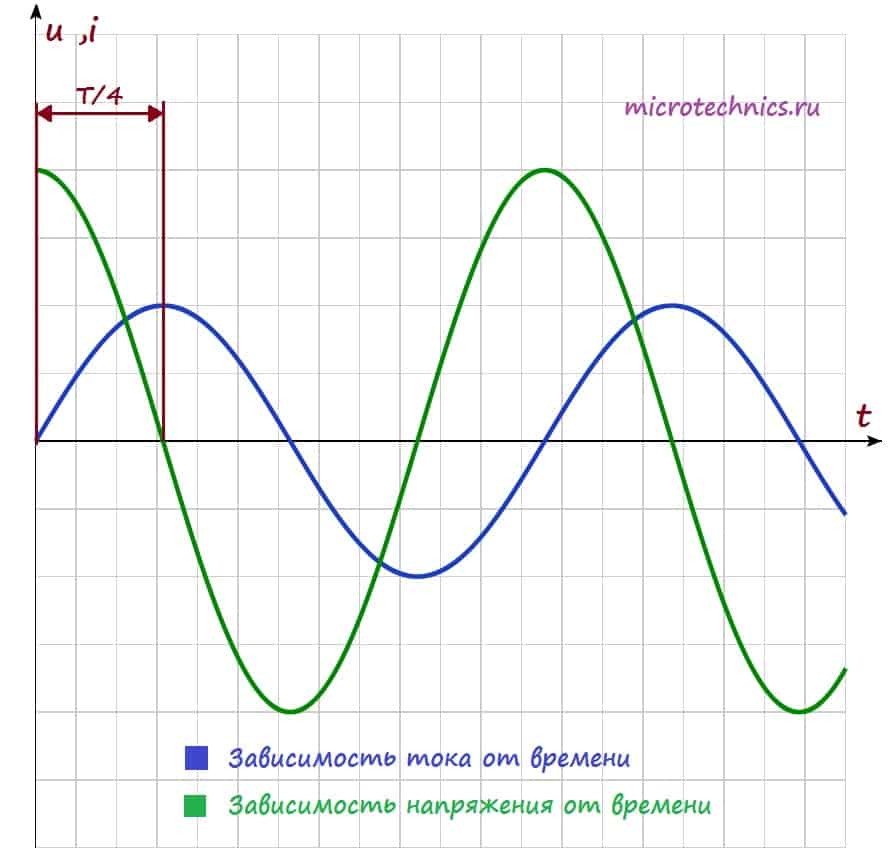
Как видите ток и напряжение сдвинуты по фазе (ссылка) друг относительно друга, и это является одним из важнейших свойств цепей переменного тока, в которых используется катушка индуктивности:
При включении катушки индуктивности в цепь переменного тока в цепи появляется сдвиг фаз между напряжением и током, при этом ток отстает по фазе от напряжения на четверть периода.
Вот и с включением катушки в цепь переменного тока мы разобрались!
На этом, пожалуй, закончим сегодняшнюю статью, она получилась уже довольно объемной, поэтому разговор о катушках индуктивности мы продолжим в следующий раз. Так что до скорых встреч, будем рады видеть вас на нашем сайте!
Один из важных элементов электротехники и электроники – индуктивность. В этой статье рассказывается о том, что это такое, и от чего зависит эта величина.
Катушки индуктивности
Что такое индуктивность
При изменении силы тока в проводнике наводится ЭДС самоиндукции. Соотношение между скоростью изменения тока и ЭДС – это коэффициент самоиндукции, или индуктивность проводника.
Это также коэффициент, отображающий связь между электрическим током, текущим в проводнике или обмотке, и магнитным потоком, который он создаёт.
Если этот провод намотать на катушку, то магнитное поле возрастёт. Это связано с явлением самоиндукции. Она увеличивается также при наличии внутри обмотки сердечника с высокой магнитной проницаемостью.
Обозначается этот параметр буквой «L». Кроме того, также в схемах обозначается катушка индуктивности или дроссель.
Единица измерения индуктивности катушки – 1 генри (Гн). Такой индуктивностью обладает дроссель, в котором при изменении тока на 1 ампер за 1 секунду наводится ЭДС в 1 вольт.
Так называют также саму катушку, главным качеством которой является индуктивное сопротивление.
Важно! Катушка, кроме индуктивного, обладает активным сопротивлением. Соотношение между ними называется «добротность».
Что такое индуктивность
Самоиндукция
Принцип работы катушки индуктивности можно сравнить с инерцией. При начале движения поезда энергия тратится на его разгон, а при торможении запасённая кинетическая энергия не позволяет остановиться составу мгновенно.
При появлении тока в проводнике вокруг него появляется поле. Часть энергии, протекающей по проводу, расходуется на его создание, и ток достигает максимума только после создания магнитного поля.
При отключении питания поле будет поддерживать ток до исчерпания энергии, заключённой в этом поле.
Магнитное поле проводника
При изменении магнитного потока, проходящего через площадь, ограниченную контуром, в проводниках, образующих этот контур, наводится ЭДС. Ток, протекающий по проводам, создаёт вокруг них магнитное поле, изменения которого, в свою очередь, наводят в этих проводах электродвижущую силу. Это ЭДС самоиндукции.
Самоиндукция направлена против источника напряжения и противодействует изменениям силы тока в цепи. Поэтому ток в индуктивности не может измениться мгновенно.
Величина ЭДС индукции зависит от скорости изменения магнитного потока. Но так как изменения тока в обмотке приводят к изменениям магнитного поля, то величина самоиндукции зависит от скорости его изменения. Она появляется и существует только при изменениях силы и направления тока. В сети переменного напряжения он отстаёт по фазе от напряжения. Это можно увидеть на экране осциллографа.
Через некоторое время после включения магнитный поток достигает своего максимума, перестаёт противодействовать росту тока, и параметры цепи начинают определяться активным сопротивлением обмотки.
При отключении поле начинает поддерживать ток в цепи. Это приводит к росту напряжения на выводах катушки и искрению контактов.
Влияние числа витков и способа намотки
Если прямой проводник свернуть в кольцо, то получится катушка индуктивности. При подключении к ней постоянного напряжения в ней появляются северный и южный магнитные полюса. При этом устройство превращается в электромагнит. Чем больше витков в бобине и чем больше ток, протекающий через неё, тем больше магнитное поле. Поэтому магнитный поток, создаваемый обмоткой, определяется как произведение силы тока на число витков и измеряется в ампер-витках.
При включении прибора в сеть переменного напряжения в таком устройстве магнитные поля отдельных витков усиливают друг друга путём взаимоиндукции.
Магнитное поле катушки с током
Основным параметром катушки является индуктивность. На неё влияет то, как намотано это устройство:
- Число витков. Чем больше витков, тем выше индуктивность. Это связано с тем, что витки наводят ЭДС друг в друге, чем поддерживают её;
- Длина катушки и расстояние между витками. Чем больше длина и расстояние между витками, тем меньше индуктивность из-за уменьшенного влияния магнитного поля проводов друг на друга;
- Площадь сечения обмотки. Чем больше сечение катушки, тем выше индуктивность. Это вызвано меньшим сопротивлением в контуре большего размера магнитному потоку.
Интересно. Индуктор в индукционных электроплитах мотается в виде плоской катушки – «корзины».
Материал сердечника
Кроме числа витков и размеров катушки, на формирование магнитного потока влияет магнитная проницаемость сердечника, вокруг которого она намотана. У разных материалов она различная. Кроме того, имеет значение поперечное сечение сердечника, а также его форма: если он замкнут в кольцо или другую геометрическую фигуру, то поток на всём пути следования проходит по сердечнику с большей проницаемостью, чем воздух, и оказывает большее влияние на соседние витки, что повышает индуктивность катушки с сердечником.
Интересно. Аналогичное влияние оказывает длина магнитопровода: чем он длиннее, тем индуктивность ниже.
Катушка на ферритовом сердечнике
Современные магнитные материалы
Сердечники могут изготавливаться из различных материалов, исходя из рабочей частоты и силы тока:
- Электротехническая сталь. Применяется в сетях постоянного напряжения в реле и электромагнитах. Использование в устройствах переменного напряжения недопустимо из-за вихревых токов и связанных с этим больших потерь при нагреве;
- Трансформаторная сталь. Для уменьшения потерь и нагрева сердечники устройств для переменного напряжения собираются из пластин трансформаторной стали. Однако при рабочей частоте, превышающей 1 кГц, и больших токах намагничивания потери становятся слишком большими, поэтому при таких частотах этот материал не используется;
- Железоникелевые сплавы. Имеют высокую проницаемость при малых полях и низкий предел насыщения. Работают при частотах до 100кГц и используются в магнитофонных головках, датчиках и подобных механизмах;
- Пермаллои. Железоникелевые сплавы с высокой проницаемостью. Для придания различных свойств легируются другими металлами;
- Аморфные и нанокристаллические материалы. Имеют большой диапазон рабочих частот и применяются в электросчётчиках, импульсных трансформаторах в блоках питания и как замена пермаллоев. Имеют, по сравнению с ними, большую рабочую частоту и индукцию насыщения;
- Магнитодиэлектрики. У этих материалов диапазон частот в десятки мГц, но малая проницаемость и предел насыщения, поэтому работают только в слабых полях. Используются в высокочастотной технике: в магнитопроводах, дросселях и катушках;
- Ферриты и ферритовые сердечники. У этого материала минимальные вихревые токи, и они могут работать на максимальных рабочих частотах, но имеют малый предел насыщения. Параметры зависят от температуры и ухудшаются (стареют) со временем. У каждой марки есть критическая частота, свыше которой возрастают потери. Это определяет их область применения.
При повышении рабочей частоты материалов уменьшается предел насыщения. Кроме того, свойства магнитопроводов меняются при изменении частоты и насыщенности магнитного потока. Поэтому не рекомендуется использовать материал сердечников в непредназначенных для него условиях.
Вариометр
В некоторых случаях необходимо менять параметры устройства. Это делается разными способами:
- Изменением положения сердечника. В подстроечных элементах небольшого размера это делается отвёрткой, вращая которую магнитопровод можно выдвинуть из обмотки;
- Изменением числа витков. В конструкциях небольшого размера это выполняется при помощи переключателей, в крупногабаритных устройствах по виткам передвигается ползунок с контактами;
- Изменением положения частей катушки относительно друг друга. Если части катушки отодвигать друг от друга, то индуктивность уменьшится, и, наоборот, при приближении она возрастёт. Аналогичный эффект получится, если части катушки без сердечника намотаны на каркасах разного диаметра, и одна вращается внутри другой. Поворотом можно добиться взаимной нейтрализации магнитного потока и, как следствие, уменьшения индуктивности.
Вариометр – катушка с переменной индуктивностью
Знание того, от чего зависит индуктивность, и принципа её работы, а также, зачем в ней нужен сердечник из магнитопроницаемого материала, поможет изготовить катушку индуктивности своими руками.
Видео
Оцените статью:Большинство проводящих материалов (металлов) является парамагнитными или ферромагнитными, в то время как большинство непроводящих материалов (неметаллов) является диамагнитными. Любой проводник обладает некоторой индуктивностью в ответ на изменение величины или направления протекания тока. Даже обычный прямой провод имеет индуктивность, хотя она достаточно мала, чтобы пренебрегать ею. Если провод свернуть в петлю — его индуктивность увеличится. Чем больше сделать таких одинаковых витков, тем большая индуктивность будет присуща проводу. Индуктивность одиночной петли или катушки из провода может быть многократно увеличена с помощью подходящего ферромагнитного сердечника.
Простейшими катушками индуктивности являются катушки с воздушным сердечником (рисунок 1). Они сделаны путем намотки провода вокруг пластмассового, деревянного или любого не ферромагнитного сердечника. Индуктивность катушки зависит от числа витков, радиуса и общей формы, также она пропорциональна числу витков и диаметру катушки. Индуктивность обратно пропорциональна длине провода для заданного диаметра катушки и числу витков. Итак, чем ближе будут витки, тем больше будет индуктивность. Электропроводность катушек индуктивности зависит от материала и толщины провода. Потери (в виде тепла) в значительной степени зависят от материала, используемого в качестве сердечника.
Рис. 1. Пример катушки индуктивности с воздушным сердечником
Катушки с воздушным сердечником имеют небольшую индуктивность, которая может составлять максимум 1 мГн. Катушки с воздушным сердечником могут быть рассчитаны так, что будут пропускать через себя ток практически неограниченной величины при условии использования проводника большой длины, смотанного в катушку большого радиуса. Такие катушки индуктивности практически не вносят потерь, так как воздух не рассеивает много энергии в виде тепла. Чем выше частота переменного тока, тем меньше индуктивность, необходимая для получения значительных эффектов. Таким образом, катушки индуктивности с воздушным сердечником вполне подходят для применения в высокочастотных цепях переменного тока благодаря отсутствию потерь, способности пропускать через себя большие токи и достаточным значениям индуктивности.
При использовании железных или ферритовых сердечников индуктивность может быть значительно увеличена. Однако порошкообразный, железный или ферритовый сердечник вносит значительные потери электрической энергии в виде тепла. Использование ферромагнитных сердечников также ограничивает максимальную величину рабочего тока катушек индуктивности. В ферромагнитных сердечниках насыщение происходит при протекании максимального рабочего тока. При увеличении тока сверх этого критического значения индуктивность может начать уменьшаться. При больших токах ферромагнитные сердечники могут достаточно сильно нагреваться, что может привести к их разрушению и необратимому существенному изменению номинальной индуктивности катушки.
Соленоид против катушек индуктивности
Соленоиды часто путают с катушками индуктивности. Соленоиды — это катушки проводов, которые предназначены для использования в качестве электромагнитов. Многие индукторы также являются катушками проводов, но они предназначены для обеспечения индуктивности в электрической цепи. Катушки индуктивности цилиндрической формы также называют соленоидными катушками, но только из-за их конструкции, схожей с конструкцией соленоида. Тем не менее, они не предназначены для использования в качестве электромагнита. Соленоиды специально используются в качестве электромагнитов и обычно имеют подвижный или статический сердечник. Обычно соленоиды используются в качестве электромагнитов в электрических звонках, электродвигателях, работающих на постоянном токе, и в реле.
Соленоидные катушки как индуктивности
Простейшими и наиболее распространенными индуктивностями являются соленоидные катушки. Эти индуктивности представляют собой цилиндрические катушки, намотанные вокруг диамагнитного или ферромагнитного сердечника. Они являются самыми простыми с точки зрения проектирования и изготовления.
Соленоидная, или цилиндрическая катушка может быть легко использована для подстройки величины индуктивности, если в конструкцию интегрировать механизм перемещения ферромагнитного сердечника катушки внутрь и наружу. Путем перемещения сердечника внутрь катушки и обратно можно изменять ее эффективную магнитную проницаемость и, следовательно, величину индуктивности. Это называется настройкой магнитной проницаемости и используется для подстройки частот в радиочастотных схемах.
Сердечник можно сделать подвижным, прикрепив его к винтовому валу и закрепив гайкой на другом конце катушки. Когда вал винта вращается по часовой стрелке — сердечник перемещается внутрь катушки, увеличивая эффективную магнитную проницаемость и, следовательно, величину индуктивности. Когда вал винта вращается против часовой стрелки — сердечник выдвигается, уменьшая эффективную магнитную проницаемость и, следовательно, величину индуктивности.
Тороиды как катушки индуктивности
Сегодня еще одной наиболее распространенной формой катушек индуктивности является тороид. Тороиды имеют кольцевой ферромагнитный сердечник, на который намотан провод. Тороиды нуждаются в меньшем числе витков и физически меньше при той же величине индуктивности и рабочей величине тока, по сравнению с соленоидными катушками (рисунок 2). Другим важным преимуществом тороидов является то, что магнитный поток находится внутри сердечника, что позволяет избежать нежелательной взаимной индуктивности.
Рис. 2. Сильноточные тороидальные катушки индуктивности
Однако намотать провод на тороид сложно. Регулировать магнитную проницаемость тороида еще сложнее. Проектирование катушек с тороидальным сердечником и переменной величиной индуктивности требует реализации громоздкой и сложной конструкции. В цепях, где требуется взаимная индуктивность, катушки должны быть намотаны на один и тот же сердечник в случае, если тороид используется в качестве катушки индуктивности.
Индуктивности на основе чашеобразных Р-сердечников*
В типичных катушках индуктивности — соленоидных и тороидных — провод намотан вокруг ферромагнитного сердечника. Катушки индуктивности на основе чашеобразных сердечников – это другой тип индуктивностей, в котором обмотка катушки находится внутри ферромагнитного сердечника. Чашеобразный ферромагнитный сердечник имеет форму двух половин в виде чаш со специальным цилиндрическим выступом (керном) на дне одной из половин, на котором размещается обмотка. Обе половины имеют отверстия, из которых извлекается провод катушки. Вся сборка скрепляется болтом и гайкой.
Катушки данного типа, как и тороиды, обладают большой индуктивностью и электропроводностью при небольших габаритах и меньшем числе витков. Магнитный поток, как и в случае с тороидами, остается внутри. Таким образом, нет нежелательной взаимной индуктивности с сердечниками. Опять же, как и в случае с тороидами, очень трудно варьировать величину индуктивности катушек данного типа. Изменять величину индуктивности в катушках индуктивности на основе Р-сердечников возможно только путем изменения числа витков и при использовании отводов в разных точках катушки.
*- В литературе также встречается термин “Р-сердечник закрытого типа”. В ГОСТ 19197-73 данному типу сердечников присвоено название – “броневой”.
Линия передачи как индуктивность
В цепях постоянного тока катушки индуктивности ведут себя почти так же, как и обычный провод, обладая незначительным сопротивлением, но не более того. Таким образом, они находят применение преимущественно в электрических цепях переменного тока. В аудиосхемах в качестве индуктивностей обычно используются тороиды, катушки на основе круглых чашеобразных сердечников или аудиотрансформаторы. Номинал индуктивности, применяемый в таких электрических цепях, варьируется от нескольких мГн до 1 Гн. Катушки индуктивности вместе с конденсаторами используются в аудиосхемах для подстройки. В настоящее время микросхемы практически полностью вытеснили катушки индуктивности и конденсаторы в аудиосистемах и других подобных областях применения.
При увеличении частоты должны использоваться индуктивности с сердечниками меньшей проницаемости. На нижнем конце радиочастотного спектра используются те же катушки индуктивности, что и в аудиоприложениях. На частотах до нескольких МГц весьма распространены катушки индуктивности с тороидальным сердечником. Для частот 30…100 МГц предпочтительны катушки с воздушным сердечником. Для частот более 100 МГц в линии передачи используются высокочастотные индуктивности и специальные трансформаторы. Линии передачи малой длины (четверть длины волны сигнала или меньше) сами могут быть использованы в качестве индуктивности для подстройки частоты радиосигналов. Линия передачи, используемая в качестве подобной индуктивности, обычно представляет собой коаксиальный кабель.
Индуктивности в цепях постоянного тока
Катушки индуктивности практически бесполезны в цепях постоянного тока. Однако можно предположить, что катушка индуктивности, подключенная к цепи постоянного тока, может быть полезна для понимания принципов ее работы и особенностей поведения пульсирующих напряжений постоянного тока. Предположим, что обычная катушка индуктивности подключена к источнику напряжения через ключ. При замыкании ключа на индуктивность подается напряжение, вызывающее быстрое изменение протекающего через нее тока. Когда приложенное напряжение увеличивается от нуля до пикового значения (за короткое время), индуктивность противодействует изменяющемуся через нее току, индуцируя напряжение, противоположное по полярности приложенному напряжению. Индуцированное напряжение при подаче питания на катушку индуктивности называется обратной ЭДС и определяется по формуле 1:
VL = – L*(di/dt), (1)
где:
- VL – напряжение (обратная ЭДС), индуцированная на катушке;
- L – индуктивность катушки;
- di/dt – скорость изменения тока во времени.
Согласно приведенной формуле 1, внезапное изменение тока через катушку индуктивности дает бесконечное напряжение, что физически невозможно. Таким образом, ток через катушку индуктивности не может измениться мгновенно. Ток сталкивается с влиянием индуктивности при каждом небольшом изменении его величины и медленно возрастает до своего пикового постоянного значения. Итак, в начальный момент времени катушка индуктивности представляет собой разрыв цепи, когда переключатель замкнут. Обратная ЭДС наводится на катушку индуктивности до тех пор, пока изменяется значение протекающего через нее тока. Индуцированная обратная ЭДС всегда остается равной и противоположной возрастающему приложенному напряжению. Когда напряжение и ток от источника приближаются к постоянному значению, обратная ЭДС падает до нуля, а катушка индуктивности начинает вести себя как обычный провод. При подаче напряжения на катушку индуктивности мощность, запасенная ею, определяется по формуле 2:
P = V * I = L*i*di/dt, (2)
где:
- P – электрическая мощность, запасенная в катушке;
- V – величина пикового напряжения на катушке индуктивности;
- I – величина пикового тока, протекающего через катушку индуктивности.
Энергия, запасенная индуктивностью при подаче напряжения, определяется по формуле 3:
W = ∫P.dt = ∫L*i*(di/dt)dt = (1/2)LI2, (3)
где:
- W – электрическая энергия, запасенная в катушке индуктивности в виде магнитного поля;
- I – максимальное значение тока, протекающего через катушку.
Когда происходит отключение источника напряжения (путем размыкания ключа), напряжение на индуктивности падает с постоянного пикового значения до нуля. В отличие от конденсаторов, при отключении источника напряжения напряжение на индуктивности не поддерживается. Фактически оно уже упало до нуля, тогда как ток, проходящий через него стал постоянным. Теперь, когда приложенное напряжение падает от пикового постоянного значения до нуля, ток, протекающий через катушку индуктивности, также падает с постоянного пикового значения до нуля. Катушка противодействует падению тока, вызывая прямую ЭДС в направлении приложенного напряжения. Из-за индуцированной прямой ЭДС ток, проходящий через катушку индуктивности, падает до нуля с более медленной скоростью. Как только ток уменьшается до нуля, прямая ЭДС также падает до нуля.
Таким образом, при подаче напряжения питания электрическая энергия преобразовывалась в магнитное поле в катушке индуктивности, что было очевидно по обратной ЭДС, индуцированной на ней. При отключении напряжения питания та же самая электрическая энергия возвращается индуктором в цепь в форме прямой ЭДС. Всякий раз, когда напряжение на катушке индуктивности увеличивается, возникает обратная ЭДС, а всякий раз, когда напряжение на катушке уменьшается, возникает прямая ЭДС.
На практике обратная или прямая ЭДС, которая наводится на катушке индуктивности, во много раз больше приложенного напряжения. Если источник индуктивности подключен к источнику напряжения или катушка индуктивности подключена к цепи постоянного тока без какой-либо защиты, электрическая энергия, возвращаемая при размыкании переключателя, выделяется в виде скачка напряжения или искры на контактах переключателя. Если индуктивность или ток в цепи достигают достаточно больших значений, то энергия выделяется в форме дуги или искры на контакте переключателя и может даже сжечь или расплавить его. Этого можно избежать, используя резистор и конденсатор, соединенные в RC-цепь и включенные последовательно с контактом переключателя. Такая RC-цепь называется снабберной и позволяет электрической энергии, выделяемой катушкой индуктивности, заряжать и разряжать конденсатор, поэтому она не повреждает другие компоненты. Во многих электрических цепях для сохранения компонентов схемы от обратной или прямой ЭДС катушек индуктивности или соленоидов используются защитные диоды.
Катушка индуктивности в цепи переменного тока
Катушка индуктивности противодействует любому изменению тока, который протекает через нее, а переменный ток, в свою очередь, отстает на 90° от напряжения. В начальный момент времени, когда напряжение источника подается на катушку, ток через нее протекает максимальный, но в противоположном направлении. При подаче напряжения ток протекает через катушку индуктивности из-за индуцированной обратной ЭДС, которая противоположна приложенному напряжению. Индуцированное на катушке напряжение всегда равно и противоположно по знаку приложенному напряжению в любой момент времени. Когда приложенное напряжение возрастает от нуля до пикового значения, ток через катушку падает от максимума до нуля.
Когда прикладываемое напряжение падает от максимального значения до нуля, то на катушке индуцируется прямая ЭДС, заставляя ток противоположного направления расти от нуля до пикового значения. Когда приложенное напряжение меняет полярность и возрастает до пикового значения, ЭДС снова индуцируется на катушке, вызывая падение обратного тока от пикового значения до нуля. Когда приложенное напряжение снова падает до нуля в обратном направлении, в катушке индуцируется прямая ЭДС, заставляющая ток снова расти от нуля до максимального значения в противоположном направлении. Это продолжается для каждого цикла протекания переменного тока.
Индуктивное сопротивление
Противодействие протекающему току из-за наличия индуктивности называется индуктивным сопротивлением. Амплитуда тока через катушку индуктивности обратно пропорциональна частоте приложенного напряжения. Поскольку напряжение на катушке (обратная или прямая ЭДС) пропорционально индуктивности, то амплитуда тока также обратно пропорциональна величине индуктивности. Итак, противодействие току из-за наличия индуктивности в виде индуктивного сопротивления определяется по формуле 4:
XL = 2πfL= ωL (4)
Соответственно, пиковая амплитуда тока, проходящего через катушку индуктивности, определяется по формуле 5:
Ipeak = Vpeak/XL= Vpeak/ ωL, (5)
где:
- Ipeak – пиковое значение переменного тока, протекающего через катушку индуктивности;
- Vpeak – пиковое значение переменного напряжения, приложенного к катушке;
- XL – индуктивное сопротивление.
Как резистивное и емкостное сопротивление, так и единица индуктивного сопротивления измеряется в омах. Следует отметить, что в электрических цепях нет потерь энергии из-за наличия емкостного или индуктивного сопротивления, что нельзя сказать об обычном резистивном сопротивлении. Тем не менее, реактивное сопротивление может ограничивать уровни тока через конденсатор или катушку индуктивности.
Применение катушек индуктивности
Катушки индуктивности используются в электрических цепях переменного тока. Они обычно применяются в аналоговых схемах, схемах обработки сигналов и в системах телекоммуникаций, а также используются вместе с конденсаторами для создания фильтров различных топологий. В телекоммуникационных системах индуктивности применяются в составе специальных фильтров, которые нужны для подавления возможных бросков напряжения и предотвращения утечки информации через линии системы электропитания.
Трансформаторы, которые используются для повышения или понижения напряжения переменного тока, состоят из двух катушек индуктивности, объединенных в единую конструкцию определенным образом. Индуктивности также используются для временного хранения электрической энергии в цепях выборки-хранения и источниках бесперебойного питания. В цепях электропитания катушки индуктивности (где они называются фильтрующими дросселями) используются для сглаживания пульсирующих токов.
Поведение индуктивности при прохождении через нее сигнала можно определить следующим образом:
- Всякий раз, когда приложенное к катушке индуктивности напряжение увеличивается, катушка генерирует обратную ЭДС, в результате чего ток через нее падает с максимального значения до нуля или даже ниже этого уровня. Всякий раз, когда прикладываемое напряжение уменьшается, катушка создает прямую ЭДС, в результате чего ток через нее повышается с нуля или текущего уровня до максимального значения или даже до более высокого.
- Обратная или прямая ЭДС сохраняется на катушке индуктивности до тех пор, пока приложенное напряжение, а следовательно и ток через нее изменяются. Когда приложенное напряжение достигает определенного постоянного значения, обратная или прямая ЭДС падает до нуля, и постоянный ток протекает через катушку индуктивности без какого-либо противодействия, как в обычном соединительном проводе.
- Из-за наличия индуктивности скорость изменения тока в цепи замедляется. Если сигнал переменный, то ток всегда будет отставать от напряжения на 90° из-за наличия индуктивности.
- Благодаря индуктивному или емкостному сопротивлению потери энергии отсутствуют. Энергия, запасенная катушкой индуктивности в форме магнитного поля или конденсатором в форме электростатического поля, возвращается обратно в цепь, как только приложенное напряжение падает до нуля или меняет полярность. Однако из-за реактивного сопротивления пиковый уровень тока (амплитуда сигнала) ограничен.
Источник: https://www.engineersgarage.com
Индуктивность: формула, единица измерения
Индуктивность – это элемент цепи, где происходит накопление энергии от магнитного поля. Так происходит запас поля или его преобразование в иные виды энергий. Самым идеальным примером служит катушка индуктивности. В ней происходит запасание поля и его дальнейшее преобразование в энергию других видов, в том числе и тепловую. Способность накапливать магнитное поле и является индуктивностью. Индуктивность напрямую связана с электромагнитной индукцией, статья о которой, также есть на нашем сайте. В данной статье будет описано данное физическое явление, как оно происходит, а также как используется на практике, в чем измеряется и как можно рассчитать физические характеристики. Дополнениями служат два ролика и одна статья, по выбранной теме.
Что такое индуктивность.
Индуктивность в цепи переменного тока
Прохождение электрического тока по проводнику или катушке сопровождается появлением магнитного поля. Рассмотрим электрическую цепь переменного тока, в которую включена катушка индуктивности, имеющая небольшое количество витков проволоки сравнительно большого сечения, активное сопротивление которой можно считать практически равным нулю. Под действием э. д. с. генератора в цепи протекает переменный ток, возбуждающий переменный магнитный поток. Этот поток пересекает «собственные» витки катушки и в ней возникает электродвижущая сила самоиндукции
Электродвижущая сила самоиндукции, согласно правилу Ленца, всегда противодействует причине, вызывающей ее. Так как э. д. с. самоиндукции всегда противодействует изменениям переменного тока, вызываемым э. д. с. генератора, то она препятствует прохождению переменного тока. При расчетах это учитывается по индуктивному сопротивлению, которое обозначается XL и измеряется в омах.
Измерение катушки индуктивности мультиметром
Таким образом, индуктивное сопротивление катушки XL, зависит от величины э. д. с. самоиндукции, а следовательно, оно, как и э. д. с. самоиндукции, зависит от скорости изменения тока в катушке (от частоты ω) и от индуктивности катушки L
XL = ωL,
- где XL— индуктивное сопротивление, ом;
- ω — угловая частота переменного тока, рад/сек;
- L— индуктивность катушки, гн.
Так как угловая частота переменного тока ω = 2πf, то индуктивное сопротивление
XL = 2πf L, (59)
где f — частота переменного тока, гц.
Индуктивностью называется идеализированный элемент электрической цепи, в котором происходит запасание энергии магнитного поля. Запасания энергии электрического поля или преобразования электрической энергии в другие виды энергии в ней не происходит.
Пример. Катушка, обладающая индуктивностью L = 0,5 гн, присоединена к источнику переменного тока, частота которого f = 50 гц. Определить:
1) индуктивное сопротивление катушки при частоте f = 50 гц;
2) индуктивное сопротивление этой катушки переменному току, частота которого f = 800 гц.
Решение. Индуктивное сопротивление переменному току при f = 50 гц
XL = 2πf L = 2 · 3,14 · 50 · 0,5 = 157 ом.
При частоте тока f = 800 гц
XL = 2πf L = 2 · 3,14 · 800 · 0,5 = 2512 ом.
Индуктивность сварочной дуги
Приведенный пример показывает, что индуктивное сопротивление катушки повышается с увеличением частоты переменного тока, протекающего по ней. По мере уменьшения частоты тока индуктивное сопротивление убывает. Для постоянного тока, когда ток в катушке не изменяется и магнитный поток не пересекает ее витки, э. д. с. самоиндукции не возникает, индуктивное сопротивление катушки XL равно нуло. Катушка индуктивности для постоянного тока представляет собой лишь сопротивление
Выясним, как изменяется з. д. с. самоиндукции, когда по катушке индуктивности протекает переменный ток. Известно, что при неизменной индуктивности катушки э. д. с. самоиндукции зависит от скорости изменения силы тока и она всегда направлена навстречу причине, вызвавшей ее.
В первую четверть периода сила тока возрастает от нулевого до максимального значения. Электродвижущая сила самоиндукции ес, согласно правилу Ленца, препятствует увеличению тока в цепи. Поэтому на графике (пунктирной линией) показано, что ес в это время имеет отрицательное значение. Во вторую четверть периода сила тока в катушке убывает до нуля. В это время э. д. с. самоиндукции изменяет свое направление и увеличивается, препятствуя убыванию силы тока. В третью четверть периода ток изменяет свое направление и постепенно увеличивается до максимального значения; э. д. с. самоиндукции имеет положительное значение и далее, когда сила тока убывает, э. д. с. самоиндукции опять меняет свое направление и вновь препятствует уменьшению силы тока в цепи.
Индуктивность
Из сказанного следует, что ток в цепи и э. д. с. самоиндукции не совпадают по фазе. Ток опережает э. д. с. самоиндукции по фазе на четверть периода или на угол φ = 90°. Необходимо также иметь в виду, что в цепи с индуктивностью, не содержащей г, в каждый момент времени электродвижущая сила самоиндукции направлена навстречу напряжению генератора U. В связи с этим напряжение и э. д. с. самоиндукции ес также сдвинуты по фазе друг относительно друга на 180°.
Из изложенного следует, что в цепи переменного тока, содержащей только индуктивность, ток отстает от напряжения, вырабатываемого генератором, на угол φ = 90° (на четверть периода) и опережает э. д. с. самоиндукции на 90°. Можно также сказать, что в индуктивной цепи напряжение опережает по фазе ток на 90°. Построим векторную диаграмму тока и напряжения для цепи переменного тока с индуктивным сопротивлением. Для этого отложим вектор тока I по горизонтали в выбранном нами масштабе.
Чтобы на векторной диаграмме показать, что напряжение опережает по фазе ток на угол φ = 90°, откладываем вектор напряжения U вверх под углом 90°. Закон Ома для цепи с индуктивностью можно выразить так:
Следует подчеркнуть, что имеется существенное отличие между индуктивным и активным сопротивлением переменному току. Когда к генератору переменного тока подключена активная нагрузка, то энергия безвозвратно потребляется активным сопротивлением.
Если же к источнику переменного тока присоединено индуктивное сопротивление r = 0, то его энергия, пока сила тока возрастает, расходуется на возбуждение магнитного поля. Изменение этого поля вызывает возникновение э. д. с. самоиндукции. При уменьшении силы тока энергия, запасенная в магнитном поле, вследствие возникающей при этом э. д. с. самоиндукции возвращается обратно генератору.
- В первую четверть периода сила тока в цепи с индуктивностью возрастает и энергия источника тока накапливается в магнитном поле. В это время э. д. с. самоиндукции направлена против напряжения.
- Когда сила тока достигнет максимального значения и начинает во второй четверти периода убывать, то э. д. с. самоиндукции, изменив свое направление, стремится поддержать ток в цепи. Под действием э. д. с. самоиндукции энергия магнитного поля возвращается к источнику энергии — генератору. Генератор в это время работает в режиме двигателя, преобразуя электрическую энергию в механическую.
- В третью четверть периода сила тока в цепи под действием э. д. с. генератора увеличивается, и при этом ток протекает в противоположном направлении. В это время энергия генератора вновь накапливается в магнитном поле индуктивности.
- В четвертую четверть периода сила тока в цепи убывает, а накопленная в магнитном поле энергия при воздействии э. д. с. самоиндукции вновь возвращается генератору.
Таким образом, в первую и третью четверть каждого периода генератор переменного тока расходует свою энергию в цепи с индуктивностью на создание магнитного поля, а во вторую и четвертую четверть каждого периода энергия, запасенная в магнитном поле катушки в результате возникающей э. д. с. самоиндукции, возвращается обратно генератору.
Интересно по теме: Как проверить стабилитрон.
Из этого следует, что индуктивная нагрузка в отличие от активной в среднем не потребляет энергию, которую вырабатывает генератор, а в цепи с индуктивностью происходит «перекачивание» энергии от генератора в индуктивную нагрузку и обратно, т. е. возникают колебания энергии. Из сказанного следует, что индуктивное сопротивление является реактивным. В цепи, содержащей реактивное сопротивление, происходят колебания энергии от генератора к нагрузке и обратно.
Индуктивность и емкость в цепи переменного тока
Изменения силы тока, напряжения и э. д. с. в цепи переменного тока происходят с одинаковой частотой, но фазы этих изменений, вообще говоря, различны. Поэтому если начальную фазу силы тока условно принять за нуль, то начальные фазы напряжения и э. д. с. соответственно будут иметь некоторые значения ϕ и ψ. При таком условии мгновенные значения силы тока, напряжения и э. д. с. будут выражаться следующими формулами:
i = Iм sin ωt
u = Uм sin (ϕ + ωt),
e = Ɛm sin (ψ + ωt).
Сопротивление цепи, которое обусловливает безвозвратные потери электрической энергии на тепловое действие тока, называют активным. Это сопротивление для тока низкой частоты можно считать равным сопротивлению R этого же проводника постоянному току и находить по формуле:
R=(pl/S)(1 + at).
В цепи переменного тока, имеющей только активное сопротивление, например в лампах накаливания, нагревательных приборах и т. п., сдвиг фаз между напряжением и током равен нулю, т. е. ϕ=0. Это означает, что ток и напряжение в такой цепи изменяются в одинаковых фазах, а электрическая энергия полностью расходуется на тепловое действие тока.
График и схема подключения
Включение в цепь переменного тока катушки с индуктивностью L проявляется как увеличение сопротивления цепи. Объясняется это тем, что при переменном токе в катушке все время действует э. д. с. самоиндукции, ослабляющая ток. Сопротивление XL, которое обусловливается явлением самоиндукции, называют индуктивным сопротивлением. Так как э. д. с. самоиндукции тем больше, чем больше индуктивность цепи и чем быстрее изменяется ток, то индуктивное сопротивление прямо пропорционально индуктивности цепи L и круговой частоте переменного тока ω:
ХL = ωL.
Влияние индуктивного сопротивления на силу тока в цепи наглядно иллюстрируется опытом, изображенным на рис. 26.6. При опускании ферромагнитного сердечника в катушку лампа гаснет, а при его удалении вновь загорается. Это объясняется тем, что индуктивность катушки сильно возрастает при введении в нее сердечника. Следует отметить, что напряжение на индуктивном сопротивлении опережает по фазе ток.
Постоянный ток не проходит через конденсатор, так как между его обкладками находится диэлектрик. Если конденсатор включить в цепь постоянного тока, то после зарядки конденсатора ток в цепи прекратится.
Катушки индуктивности
Пусть конденсатор включен в цепь переменного тока. Заряд конденсатора (q=CU) вследствие изменения напряжения непрерывно изменяется, поэтому в цепи течет переменный ток. Сила тока будет тем больше, чем больше емкость конденсатора и чем чаще происходит его перезарядка, т. е. чем больше частота переменного тока. Сопротивление, обусловленное наличием электроемкости в цепи переменного тока, называют емкостным сопротивлением Хс. Оно обратно пропорционально емкости С и круговой частоте ω;
Хс = 1/ωС
Из сравнения формул (26.11) и (26.12) видно, что катушки индуктивности представляют собой очень большое сопротивление для тока высокой частоты и небольшое для тока низкой частоты, а конденсаторы — наоборот. Напряжение на емкостном сопротивлении Ха отстает по фазе от тока. Индуктивное XL и емкостное Хс сопротивления называют реактивными. В теории переменного тока доказывается, что при последовательном включении индуктивного и емкостного сопротивлений общее реактивное сопротивление равно их разности:
X = XL—XC
и имеет индуктивный характер при XL > Хс и емкостный характер при XL < Xc.
В заключение заметим, что средняя активная мощность переменного тока, показывающая, сколько энергии за единицу времени передается электрическим током данному участку цепи, определяется формулой:
P = IU cos ϕ.
Мощность, затрачиваемая только на тепловое действие тока, выражается формулой:
Р = I2R
Для увеличения активной мощности переменного тока нужно повышать cos ϕ. (Объясните, почему наибольшее значение cos ϕ имеет при XL=XC.)
Индуктивность
Устройство катушки
Более близким к идеализированному элементу — индуктивности — является реальный элемент электронной цепи — индуктивная катушка. В отличие от индуктивности в индуктивной катушке имеют место также запасание энергии электронного поля и преобразование электронной энергии в другие виды энергии, а именно в термическую. Количественно способность реального и идеализированного частей электронной цепи припасать энергию магнитного поля характеризуется параметром, именуемым индуктивностью.
Таким макаром термин «индуктивность» применяется как заглавие идеализированного элемента электронной цепи, как заглавие параметра, количественно характеризующего характеристики этого элемента, и как заглавие основного параметра индуктивной катушки.
Связь меж напряжением и током в индуктивной катушке определяется законом электрической индукции, из которого следует, что при изменении магнитного потока, пронизывающего индуктивную катушку, в ней наводится электродвижущая сила е, пропорциональная скорости конфигурации потокосцепления катушки ψ и направленная таким макаром, чтоб вызываемый ею ток стремился воспрепятствовать изменению магнитного потока:
e = — dψ / dt
В системе единиц СИ магнитный поток и потокосцепление выражают в веберах (Вб).
Интересно почитать: инструкция как прозвонить транзистор.
Магнитный поток Ф, пронизывающий любой из витков катушки, в общем случае может содержать две составляющие: магнитный поток самоиндукции Фси и магнитный поток наружных полей Фвп: Ф — Фси + Фвп.
1-ая составляющая представляет собой магнитный поток, вызванный протекающим по катушке током, 2-ая — определяется магнитными полями, существование которых не связано с током катушки — магнитным полем Земли, магнитными полями других катушек и неизменных магнитов. Если 2-ая составляющая магнитного потока вызвана магнитным полем другой катушки, то ее именуют магнитным потоком взаимоиндукции.
Потокосцепление катушки ψ, так же как и магнитный поток Ф, может быть представлено в виде суммы 2-ух составляющих: потокосцепления самоиндукции ψси, и потокосцепления наружных полей ψвп
ψ= ψси + ψвп
Наведенная в индуктивной катушке ЭДС е, в свою очередь, может быть представлена в виде суммы ЭДС самоиндукции, которая вызвана конфигурацией магнитного потока самоиндукции, и ЭДС, вызванной конфигурацией магнитного потока наружных по отношению к катушке полей:
e = eси + eвп,
тут еси — ЭДС самоиндукции, евп — ЭДС наружных полей.
Если магнитные потоки наружных по отношению к индуктивной катушке полей равны нулю и катушку пронизывает только поток самоиндукции, то в катушке наводится только ЭДС самоиндукции.
Заключение
Рейтинг автора
Автор статьи
Инженер по специальности «Программное обеспечение вычислительной техники и автоматизированных систем», МИФИ, 2005–2010 гг.
Написано статей
Более подробно об индуктивности рассказано в статье Что такое катушка индуктивности. Если у вас остались вопросы, можно задать их в комментариях на сайте. Также в нашей группе ВК можно задавать вопросы и получать на них подробные ответы от профессионалов.
Также в нашей группе ВК можно задавать вопросы и получать на них подробные ответы от профессионалов. Для этого приглашаем читателей подписаться и вступить в группу. В завершение статьи хочу выразить благодарность источникам, откуда мы черпали информацию во время подготовки материала:
www.jasic.ua
www.tkexp.ru
www.elektrica.info
www.electricalschool.info
www.tehnar.net.ua
www.tehinfor.ru
ПредыдущаяТеорияЧто такое электромагнитная индукция?
СледующаяТеорияЧто такое анод и катод, в чем их практическое применение
ИНДУКТИВНОСТЬ — Студопедия
Эл.ток создает собственное магнитное поле. Магнитный поток через контур пропорционален индукции магнитного поля (Ф ~ B), индукция пропорциональна силе тока в проводнике
(B ~ I), следовательно магнитный поток пропорционален силе тока (Ф ~ I).
ЭДС самоиндукции зависит от скорости изменения силы тока в эл.цепи, от свойств проводника
(размеров и формы) и от относительной магнитной проницаемости среды, в которой находится проводник.
Физическая величина, показывающая зависимость ЭДС самоиндукции от размеров и формы проводника и от среды, в которой находится проводник, называется коэффициентом самоиндукции или индуктивностью.
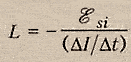
Индуктивность — физ. величина, численно равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1 Ампер за 1 секунду.
Также индуктивность можно рассчитать по формуле:
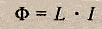
где Ф — магнитный поток через контур, I — сила тока в контуре.
Единицы измерения индуктивности в системе СИ:
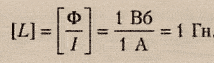
Индуктивность катушки зависит от: числа витков, размеров и формы катушки и от относительной магнитной проницаемости среды
( возможен сердечник).
Индуктивность взаимная — величина, характеризующая магнитную связь двух или более электрических цепей (контуров). Если имеется два проводящих контура , то часть линий магнитной индукции, создаваемых током в первом контуре, будет пронизывать площадь, ограниченную вторым контуром (т. е. будет сцеплена с контуром 2).
Магнитный поток Ф12 через контур 2, созданный током I1 в контуре 1, прямо пропорционален току:
Коэффициент пропорциональности M12 зависит от размеров и формы контуров 1 и 2, расстояния между ними, их взаимного расположения, а также от магнитной проницаемости окружающей среды и называется взаимной индуктивностью или коэффициентом взаимной индукции контуров 1 и 2. В системе СИ И. в. измеряется в Генри.
Трансформаторная ЭДС. Принцип действия трансформатора основан на явлении электромагнитной индукции. Линии индукции магнитного поля, создаваемого переменным током в первичной обмотке, благодаря наличию сердечника практически без потерь пронизывают витки вторичной обмотки. Поскольку магнитный поток во вторичной обмотке изменяется со временем (т.к. в первичной обмотке переменный ток), то согласно закону Фарадея в ней возбуждается ЭДС индукции. Трансформатор может работать только на переменном токе, т.к. магнитный поток, созданный постоянным током, не изменяется с течением времени.
Пусть первичная обмотка трансформатора подключена к источнику тока с переменной ЭДС E1 и с действующим значением напряжения U1. На вторичной обмотке ЭДС E2 и напряжение U2.
Из законов Ома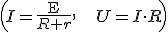 
следует, что напряжение на обмотке равно
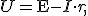(1)
где r — сопротивление обмотки. При изготовлении трансформатора сопротивление первичной обмотки r1 делают очень малым, поэтому часто им можно пренебречь. Тогда
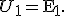
Если пренебречь потерями магнитного потока в сердечнике, то в каждом витке вторичной обмотки будет индуцироваться точно такая же ЭДС индукции e1, как и ЭДС индукции e2 в каждом витке первичной обмотки, т.е. e1 = e2. Следовательно, отношение ЭДС в первичной E1 и вторичной E2 обмотках равно отношению числа витков в них:
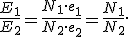(2)
Трансформаторный ток. Токи обмоток обратно пропорциональны числам витков (I1/I2 приблиз = w1/w2 = 1/n). С увеличением тока активно-индуктивного приемника вторичное напряжение несколько снижается.
Поток рассеивания.
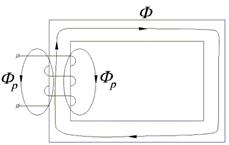
Рис.1.11. К определению магнитного потока рассеяния в катушке с ферромагнитным сердечником
часть магнитного потока катушки замыкается не по сердечнику, а по воздуху. Эта часть потока носит название потока рассеивания Фр (рис. 1.11). Таким образом, полный поток, сцепленный с витками катушки равен
 . | (1.14) |
На основании закона Ома для магнитной цепи (1.7) можно написать выражение для потока рассеяния:
 . |
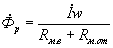Так как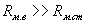 
, то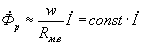 
.То есть поток рассеяния 
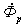, в отличие от потока 
в сердечнике, совпадает по фазе с током и связан с ним линейной зависимостью. Следовательно, на векторной диаграмме вектор потока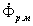 
будет совпадать с вектором тока 
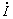(рис.1.12).
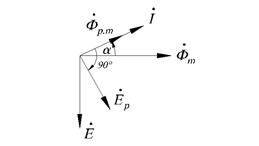
Рис.1.12. Векторная диаграмма магнитных потоков, ЭДС и токов катушки с ферромагнитным сердечником
Введение
Думаю, что многие из читателей видели хотя бы один ролик на популярных видеосервисах, где электричество передается через пустое пространство при помощи индуктивных катушек.
В этой статье мы хотим обратиться к первоосновам процесса беспроводной передачи энергии с помощью магнитного поля. Начав с рассмотрения простейшей индуктивной катушки, и вычисления ее индуктивности, мы постепенно перейдем к теории электрических цепей, в рамках которой, будет показан и обоснован способ передачи максимальной мощности при прочих равных условиях. Итак, начнем.
Магнитное поле одиночного витка с током
Рассмотрим магнитное поле одиночного витка с током. Найдем магнитное поле витка в любой точке пространства. Почему необходимо подобное рассмотрение? Потому что почти во всех книгах, по крайней мере в тех, которые удалось отыскать автору статьи, решение данной задачи ограничивается нахождением лишь одной компоненты магнитного поля и лишь вдоль оси витка — $inline$B_z(z)$inline$, в то время как мы отыщем закон для магнитного поля во всем пространстве.
Иллюстрация к закону Био-Савара-Лапласа
Для нахождения магнитного поля, воспользуемся законом Био-Савара-Лапласа (смотри Википедия — Закон Био-Савара-Лапласа). На рисунке видно, что центр системы координат $inline$O$inline$ совпадает с центром витка. Контур окружности витка обозначен как $inline$C$inline$, а радиус окружности — как $inline$a$inline$.По витку течет ток $inline$I$inline$. $inline$\vec{r}$inline$ — это переменная-радиус-вектор из начала координат в произвольную точку витка. $inline$\vec{r}_0$inline$ — это радиус-вектор в точку наблюдения. Еще нам понадобится полярный угол $inline$\varphi$inline$ — угол между радиус-вектором $inline$\vec{r}$inline$ и осью $inline$OX$inline$. Расстояние от оси витка до точки наблюдения обозначим за $inline$\rho$inline$. И наконец, $inline$\mathrm{d}\vec{r}$inline$ — элементарное приращение радиус-вектора $inline$\vec{r}$inline$.
Согласно закону Био-Савара-Лапласа, элемент контура с током $inline$\mathrm{d}\vec{r}$inline$ создает элементарный вклад в магнитное поле, который дается формулой
$$display$$\mathrm{d}\vec{B}(\vec{r}_0)=\frac{\mu_0 I}{4\pi} \cdot \frac{[\,\mathrm{d}\vec{r} \times (\vec{r}_0-\vec{r})]}{|\vec{r}_0-\vec{r}|^3}$$display$$
Теперь остановимся подробнее на переменных и выражениях, входящих в формулу. С учетом аксиальной симметрии задачи можем записать
$$display$$\vec{r}_0 = (\rho\cos{\varphi}, \rho\sin{\varphi}, z) \overset{\varphi = 0}{\rightarrow} (\rho, 0, z)$$display$$
$$display$$\vec{r} = (a\cos{\varphi}, a\sin{\varphi}, 0)$$display$$
$$display$$\mathrm{d}\vec{r} = (-a\sin{\varphi}, a\cos{\varphi}, 0)\,\mathrm{d}\varphi$$display$$
$$display$$\vec{r}_0-\vec{r} = (\rho -a\cos{\varphi}, -a\sin{\varphi}, z)$$display$$
$$display$$[\mathrm{d}\vec{r} \times (\vec{r}_0-\vec{r})] = \begin{vmatrix} \vec{e}_x& \vec{e}_y& \vec{e}_z\\ -a\sin{\varphi}\,\mathrm{d}\varphi& a\cos{\varphi}\,\mathrm{d}\varphi& 0\\ \rho -a\cos{\varphi}& -a\sin{\varphi}& z \end{vmatrix} = (az\cos{\varphi}, az\sin{\varphi}, a^2 -a\rho\cos{\varphi})\,\mathrm{d}\varphi$$display$$
$$display$$|\vec{r}_0-\vec{r}|^3 = \left(\rho^2 + a^2 + z^2 -2\rho a\cos{\varphi}\right)^{\frac{3}{2}}$$display$$
Для того чтобы найти результирующее магнитное поле, нужно проинтегрировать по всему контуру витка, то есть
$$display$$\vec{B}(\vec{r}_0) = \int_C{\,\mathrm{d}\vec{B}(\vec{r}_0)}$$display$$
После подстановки всех выражений и некоторых тождественных преобразований получаем выражения для аксиальной и радиальной компоненты магнитного поля соответственно
$$display$$B_z(\rho, z) = \frac{\mu_0 I}{4\pi} \int_0^{2\pi}{\frac{\left( a^2 -\rho a\cos{\varphi}\right)\,\mathrm{d}\varphi}{\left(\rho^2 + a^2 + z^2 -2\rho a\cos{\varphi}\right)^{\frac{3}{2}}}}$$display$$
$$display$$B_r(\rho, z) = \frac{\mu_0 I}{4\pi} \int_0^{2\pi}{\frac{a\,z\,\cos{\varphi}\,\mathrm{d}\varphi} {\left(\rho^2 + a^2 + z^2 -2\rho a\cos{\varphi}\right)^{\frac{3}{2}}}}$$display$$
Для нахождения абсолютного значения магнитного поля необходимо просуммировать компоненты по теореме Пифагора $inline$B = \sqrt{B_r^2 + B_z^2}$inline$.
Продемонстрируем полученное решение на примере витка радиуса $inline$a = 0.1$inline$ (м) и $inline$I=1$inline$ (А).
Амплитуда аксиальной компоненты магнитного поля
Амплитуда радиальной компоненты магнитного поля
Абсолютная амплитуда магнитного поля
Заметим, что для витка произвольной формы, на больших расстояниях $inline$z\gg a$inline$, т.е. много больше характерного размера витка, поведение магнитного поля будет стремиться к найденному решению.
Подсказка…Для подобных вычислений и построения графиков удобно использовать MathCad 15
Катушка индуктивности. Магнитно-связанные катушки
Теперь, когда мы знаем решение для магнитного поля одного витка, можем найти индуктивность катушки, состоящей из $inline$n$inline$ витков. По определению индуктивность — это коэффициент пропорциональности между током в витке и магнитным потоком через площадь сечения витка. Мы пользуемся здесь идеальной моделью катушки, которая безразмерна по направлению своей оси симметрии. Конечно же, на практике такого не бывает. Однако, как приближенные, полученные формулы будут достаточно хороши. Хотя катушки и считаются безразмерными вдоль $inline$OZ$inline$, необходимо задаться ненулевым радиусом сечения провода. Обозначим его $inline$\delta$inline$, и пример равным $inline$\delta=0,1$inline$ (мм). Иначе при интегрировании магнитного потока подынтегральное выражение обратится в бесконечность.
Индуктивно связанные катушки
На рисунке изображены две магнитно связанные катушки. Пусть первая катушка имеет радиус $inline$a_1$inline$ и содержит $inline$n_1$inline$ витков, а вторая — $inline$a_2$inline$ и $inline$n_2$inline$ соответственно. Тогда для нахождения собственных индуктивностей необходимо вычислить магнитный поток каждой катушки через свое собственное сечение.
$$display$$\Phi = \iint_S{\vec{B}\cdot\vec{\,\mathrm{d}S}} = \int_0^{2\pi}{\int_0^{a-\delta}{B_z(\rho,z)\rho\,\mathrm{d}\rho\,\mathrm{d}\varphi}} = 2\pi\int_0^{a-\delta}{B_z(\rho,z)\rho\,\mathrm{d}\rho}$$display$$
Поскольку в катушке много витков, найдем величину, называемую потокосцепление, дважды умножив на количество витков
$$display$$\Psi = \frac{1}{2}n^2\mu_0 I \int_0^{a-\delta}{\int_0^{2\pi}{\frac{\left( a^2 — \rho a\cos{\varphi}\right)\,\mathrm{d}\varphi}{\left(\rho^2 + a^2 + z^2 -2\rho a\cos{\varphi}\right)^{\frac{3}{2}}}}\rho\,\mathrm{d}\rho}$$display$$
По определению, индуктивность это коэффициент пропорциональности $inline$L$inline$ в формуле $inline$\Psi = LI$inline$. Таким образом, получим собственные индуктивности катушек
$$display$$L_1 = \frac{1}{2}n_1^2\mu_0 \int_0^{a_1-\delta}{\int_0^{2\pi}{\frac{\left( a_1^2 — \rho a_1\cos{\varphi}\right)\,\mathrm{d}\varphi}{\left(\rho^2 + a_1^2 -2\rho a_1\cos{\varphi}\right)^{\frac{3}{2}}}}\rho\,\mathrm{d}\rho}$$display$$
$$display$$L_2 = \frac{1}{2}n_2^2\mu_0 \int_0^{a_2-\delta}{\int_0^{2\pi}{\frac{\left( a_2^2 — \rho a_2\cos{\varphi}\right)\,\mathrm{d}\varphi}{\left(\rho^2 + a_2^2 -2\rho a_2\cos{\varphi}\right)^{\frac{3}{2}}}}\rho\,\mathrm{d}\rho}$$display$$
Пусть центры катушек разделены расстоянием $inline$d$inline$, лежат на одной оси, и их плоскости витков сориентированы параллельно. Для нахождения взаимной индуктивности, нужно вычислить потокосцепление, образуемое одной катушкой через сечение другой, то есть
$$display$$\Psi_{12} = \frac{1}{2}n_1 n_2\mu_0 I \int_0^{a_2-\delta}{\int_0^{2\pi}{\frac{\left( a_1^2 — \rho a_1\cos{\varphi}\right)\,\mathrm{d}\varphi}{\left(\rho^2 + a_1^2 + z^2 -2\rho a_1\cos{\varphi}\right)^{\frac{3}{2}}}}\rho\,\mathrm{d}\rho}$$display$$
Тогда взаимная индуктивность катушек дается выражением
$$display$$M_{12} = \frac{1}{2}n_1 n_2\mu_0 \int_0^{a_2-\delta}{\int_0^{2\pi}{\frac{\left( a_1^2 — \rho a_1\cos{\varphi}\right)\,\mathrm{d}\varphi}{\left(\rho^2 + a_1^2 + d^2 -2\rho a_1\cos{\varphi}\right)^{\frac{3}{2}}}}\rho\,\mathrm{d}\rho}$$display$$
Насколько известно автору, такие интегралы можно взять только численно.
Заметим, что как правило $inline$\Psi_{12} = \Psi_{21}$inline$ и $inline$M_{12} = M_{21} = M$inline$. Коэффициентом связи катушек называется величина
$$display$$k = \frac{M}{\sqrt{L_1L_2}}$$display$$
Исследуем зависимость коэффициента связи катушек от расстояния. Для этого рассмотрим две одинаковые катушки с радиусом витков $inline$a_1 = a_2 = 0.1$inline$ (м) и количеством витков $inline$n_1 = n_2 = 100$inline$. При этом собственная индуктивность каждой из катушек составит $inline$L_1 = L_2 = 8.775$inline$ (мГн).
Коэффициент связи катушек от расстояния между ними
График не изменится, если одинаково изменить число витков в обеих катушках, либо одинаково изменить радиус обеих катушек. Коэффициент связи удобно выражать в процентах. Из графика видно, что даже при расстоянии между катушками в 1 (мм) коэффицент связи меньше 100%. Коэффициент падает до 10% на расстоянии порядка 60 (мм), и до 1% на 250 (мм).
Беспроводная передача энергии
Итак, нам известны индуктивности и коэффициент связи. Теперь воспользуемся теорией электрических цепей переменного тока для поиска оптимальных параметров, при которых передаваемая мощность оказалась бы максимальной. Для понимания этого параграфа читатель должен быть знаком с понятием электрического импеданса, а также с законами Кирхгофа и законом Ома. Как известно из теории цепей, две индуктивно-связанные катушки образуют воздушный трансформатор. Для анализа трансформаторов удобна Т-образная схема замещения.
Воздушный трансформатор и его эквивалентная схема
Передающую катушку слева будем условно называть «трасмиттер», а принимающую катушку справа — «ресивер». Между катушками коэффициент связи $inline$k$inline$. На стороне ресивера находится потребитель, представленный нагрузкой $inline$z_L$inline$. Нагрузка в общем случае может быть комплексной. Входное напряжение на стороне трансмиттера $inline$u_1$inline$, а входной ток — $inline$i_1$inline$. Напряжение, передаваемое на ресивер — $inline$u_2$inline$, и передаваемый ток $inline$i_2$inline$. Полный импеданс на стороне трансмиттера обозначим как $inline$z_1$inline$, а полный импеданс на стороне ресивера $inline$z_2$inline$.
Предполагается, что на вход схемы подается синусоидальное напряжение $inline$u_1 = u_{1m}\sin{\omega t}$inline$.
Обозначим $inline$R_{coil\,1}, R_{coil\,2}, L_{coil\,1}, L_{coil\,2}, M$inline$ — сопротивления и индуктивности катушек (две собственные и одна взаимная) соответственно. Тогда, согласно теории трансформатора
$$display$$z_1 = R_{coil\,1} + j\omega (L_{coil\,1} — M)$$display$$
$$display$$z_2 = R_{coil\,2} + j\omega(L_{coil\,2} — M) + R_{load} + j X_{load}$$display$$
С другой стороны, согласно нашим обозначениям
$$display$$z_1 = r_1 + j x_1$$display$$
$$display$$z_2 = r_2 + j x_2$$display$$
где $inline$r_1, r_2$inline$ — полные активные сопротивления на стороне трансмиттера и ресивера соответственно, и $inline$x_1, x_2$inline$ — полные реактивные сопротивления.
Импеданс связи равен $inline$z_3 = j \omega M = j x_3$inline$.
Найдем входной ток цепи
$$display$$i_1 = \frac{u_1}{z_1 + z_2 || z_3}$$display$$
где знак $inline$||$inline$ обозначает параллельное соединение сопротивлений. Тогда напряжение, переданное на ресивер
$$display$$u_2 = u_1 — i_1 z_1 = u_1\left(1 — \frac{z_1}{z_1 + z_2 || z_3}\right)$$display$$
И наведенный ток
$$display$$i_2 = \frac{u_2}{z_2} = \frac{u_1}{z_2}\left(1 — \frac{z_1}{z_1 + z_2 || z_3}\right)$$display$$
Можем найти комплексную мощность, переданную в ресивер
$$display$$s_2 = u_2 i_2^* = p_2 + jq_2$$display$$
Таким образом имеем выражение для комплексной мощности
$$display$$s_2 = |u_1|^2 z_2 \left|\frac{z_3}{z_1z_2+z_1z_3+z_2z_3}\right|^2$$display$$
Выражение для активной компоненты мощности
$$display$$p_2 = |u_1|^2 r_2 \left|\frac{z_3}{z_1z_2+z_1z_3+z_2z_3}\right|^2$$display$$
Выражение для реактивной компоненты мощности
$$display$$q_2 = |u_1|^2 x_2 \left|\frac{z_3}{z_1z_2+z_1z_3+z_2z_3}\right|^2$$display$$
В большинстве практических задач требуется передать максимальную активную мощность, поэтому
$$display$$p_2 \rightarrow \mathrm{max} \Rightarrow \left|\frac{z_3}{z_1z_2+z_1z_3+z_2z_3}\right|^2 \rightarrow \mathrm{max}$$display$$
Либо, что то же самое
$$display$$\left|z_1 + z_2 + \frac{z_1z_2}{z_3}\right|^2 \rightarrow \mathrm{min}$$display$$
$$display$$\left|r_1 + jx_1 + r_2 + jx_2 +\frac{(r_1 + jx_1)( r_2 + jx_2)}{jx_3}\right|^2 \rightarrow \mathrm{min}$$display$$
$$display$$\frac{1}{x_3^2}|(r_1x_3 + r_2x_3 + r_1x_2 + r_2x_1) + j(x_1x_3 + x_2x_3 + x_1x_2 — r_1r_2)|^2 \rightarrow \mathrm{min}$$display$$
Для удобства введем функцию
$$display$$f(x_1,x_2) = (r_1x_3 + r_2x_3 + r_1x_2 + r_2x_1) + j(x_1x_3 + x_2x_3 + x_1x_2 — r_1r_2)$$display$$
и исследуем ее на наличие экстремумов
$$display$$|f(x_1,x_2)|^2 \rightarrow \mathrm{min}$$display$$
Откуда получаем систему из двух уравнений
$$display$$\frac{\partial|f|^2}{\partial x_1} = 2\mathbb{Re}(f)r_2 + 2\mathbb{Im}(f)(x_2 + x_3) = 0$$display$$
$$display$$\frac{\partial|f|^2}{\partial x_2} = 2\mathbb{Re}(f)r_1 + 2\mathbb{Im}(f)(x_1 + x_3) = 0$$display$$
Эта система имеет пять решений, два из которых нефизичны, так как приводят к мнимым значениям величин, которым полагается быть действительными. Три других физических решения приведены ниже вместе с соответствующими формулами для мощности
Решение 1
$$display$$x_1 = -x_3,\quad x_2 = -x_3$$display$$
Мощность
$$display$$p_2 = \frac{|u_1|^2\,x_3^2\,r_2}{\left(r_1r_2 + x_3^2\right)^2}, \quad q_2 = -\frac{|u_1|^2\,x_3^3}{\left(r_1r_2 + x_3^2\right)^2}$$display$$
Решение 2 и 3
$$display$$x_1 = \frac{1}{r_2}\left(\sqrt{r_1r_2\left(x_3^2-r_1r_2\right)}-r_2x_3\right), \quad x_2 = \frac{1}{r_1}\left(\sqrt{r_1r_2\left(x_3^2-r_1r_2\right)}-r_1x_3\right)$$display$$
$$display$$x_1 = -\frac{1}{r_2}\left(\sqrt{r_1r_2\left(x_3^2-r_1r_2\right)}+r_2x_3\right), \quad x_2 = -\frac{1}{r_1}\left(\sqrt{r_1r_2\left(x_3^2-r_1r_2\right)}+r_1x_3\right)$$display$$
Мощность для решений 2 и 3
$$display$$p_2 = \frac{|u_1|^2}{4\,r_1}, \quad q_2 = \frac{|u_1|^2\,x_2}{4\,r_1\,r_2}$$display$$
Решение 2 и 3 нужно использовать, когда реактивное сопротивление связи достаточно велико
$$display$$x_3^2 > r_1r_2$$display$$
Когда же это не так, нужно использовать решение 1. Чаще всего в реальных ситуациях $inline$x_3$inline$ окажется мало, поэтому рассмотрим решение 1 несколько подробнее.
Решение 1: $inline$x_1 = -x_3,\quad x_2 = -x_3$inline$. И соответствующая ему активная мощность дается формулой
$$display$$p_2 = \frac{|u_1|^2\,x_3^2\,r_2}{\left(r_1r_2 + x_3^2\right)^2}$$display$$
Из формулы мощности видно, что мощность зависит от реактивного сопротивления связи $inline$x_3 = 2\pi\,f\,k\,\sqrt{L_{coil\,1}L_{coil\,2}}$inline$, а значит и от частоты передачи $inline$f$inline$, и от геометрии взаимного расположения катушек, которая учитывается коэффициентом связи $inline$k$inline$.
Как заметили внимательные читатели, зависимость $inline$p_2(x_3)$inline$ — нелинейная. Функция $inline$p_2(x_3)$inline$ достигает максимума при $inline$x_3 = \sqrt{r_1r_2}$inline$.
Исследование формулы мощности $inline$p_2(x_3)$inline$ на экстремумы
Максимальная активная мощность при $inline$x_3 = \sqrt{r_1r_2}$inline$ равна
$$display$$p_2 = \frac{|u_1|^2}{4\,r_1}$$display$$
Таким образом, вышеозначенная формула представляет абсолютный теоретический предел переданной активной мощности при любых условиях. При этом для реактивной мощности, переданной в ресивер, имеем
$$display$$q_2=\frac{|u_1|^2}{\sqrt{r_1r_2}}$$display$$
Численное моделирование
Продемонстрировать работу всей вышеизложенной теории можно, выполнив симуляцию SPICE модели нашего устройства из двух связанных катушек.
SPICE модель двух индуктивно-связанных катушек
Симуляция выполнена для коэффициента связи $inline$k = 1$inline$%, что соответствует 25 см удаления между катушками. Параметры катушек те же, что и в предыдущем параграфе, принятые для построения графика $inline$k$inline$.
Получается, что реактивные сопротивления каждой из катушек необходимо скомпенсировать конденсаторами $inline$С_1$inline$ и $inline$С_2$inline$. То есть настроить каждый из контуров (передающий и принимающий) в резонанс на заданной частоте. Если предположить, что величина нагрузки действительная, то величины емкостей могут быть найдены из формул
$$display$$C_1 = \frac{1}{\omega^2 L_1}, \quad C_2 = \frac{1}{\omega^2 L_2}$$display$$
Ниже приведены два графика для переданного напряжения и переданной мощности во времени на частоте $inline$f=10$inline$ (кГц).
Переданное напряжение
Переданная мощность
Из рисунков видно, что на расстоянии 25 (см) переданное напряжение оказалось приблизительно в 2.5 меньше входного, а переданная пиковая мощность — приблизительно в 4 раза меньше мощности, потребляемой от входа, что согласуется с полученными формулами.
В заключении опишем, какие меры можно предпринять для увеличения передаваемой мощности:
- увеличить количество витков в катушках $inline$n_1, n_2$inline$
- увеличить радиус витков $inline$a_1, a_2$inline$
- увеличить частоту передачи $inline$f$inline$
- уменьшить расстояние между катушками $inline$d$inline$
- ввести магнитный сердечник, принадлежащий обеим катушкам (замкнутый либо открытый)
- ввести незамкнутый магнитный сердечник, принадлежащий лишь катушке-ресиверу
Пожалуй, написание этой статьи накладывает на автора обязательство изготовить и протестировать такую систему из двух катушек в лабораторных условиях, но это уже совсем другая история. Благодарю за внимание.
Литература
- Сивухин, Д. В. «Общий курс физики. Т. 3: Электричество и магнетизм.» (1990).
- Бессонов, Лев Алексеевич. Теоретические основы электротехники. Электромагнитное поле. Общество с ограниченной ответственностью Издательство ЮРАЙТ, 2012.
- Лаврентьев, М. А., and Б. В. Шабат. «Теория функций комплексной переменной.» (1972).