Индуктивность — это… Что такое Индуктивность?

        физическая величина, характеризующая магнитные свойства электрической цепи. Ток, текущий в проводящем контуре, создаёт в окружающем пространстве магнитное поле, причём Магнитный поток Ф, пронизывающий контур (сцепленный с ним), прямо пропорционален силе тока I :                  Коэффициент пропорциональности L называется И. или коэффициентом самоиндукции контура. И. зависит от размеров и формы контура, а также от магнитной проницаемости (См. Магнитная проницаемость) окружающей среды. В Международной системе единиц (См. Международная система единиц) (СИ) И. измеряется в Генри, в СГС системе единиц (См. СГС система единиц) (Гаусса) И. имеет размерность длины и поэтому единица И. называется сантиметром (1 гн = 10⁹ см).          Через И. выражается эдс самоиндукции (См. Самоиндукция) в контуре, возникающая при изменении в нём тока:         

        (ΔI — изменение тока за время Δt).

При заданной силе тока И. определяет энергию W магнитного поля тока:

        

        Чем больше И., тем больше магнитная энергия, накапливаемая в пространстве вокруг контура с током. Если провести аналогию между электрическими и механическими явлениями, то магнитную энергию следует сопоставить с кинетической энергией тела Т = mv²/2 (где m — масса тела, v — скорость его движения), при этом И. будет играть роль массы, а ток — роль скорости. Таким образом, И. определяет инерционные свойства тока.

         Практически участки цепи со значительной И. выполняют в виде индуктивности катушек (См. Индуктивности катушка). Для увеличения

L применяют катушки с железными сердечниками, но в этом случае, в силу зависимости магнитной проницаемости μ ферромагнетиков (См. Ферромагнетики) от напряжённости поля, а следовательно, и от силы тока, И. становится зависящей от I. И. длинного соленоида из N витков, имеющего площадь поперечного сечения S и длину l, в среде с магнитной проницаемостью μ равна (в единицах СИ): L = μμ₀N ²S/l, где μ₀ — Магнитная постоянная, или магнитная проницаемость вакуума.

         Лит.: Калашников С. Г., Электричество, М., 1970 (Общий курс физики, т. 2), гл. 9.

         Г. Я. Мякишев.

В чем измеряется электромагнитная индукция

Взаимосвязь электрических и магнитных полей

Электрические и магнитные явления изучались давно, вот только никому не приходило в голову каким-то образом связать эти исследования между собой. И только в 1820 году было обнаружено, что проводник с током действует на стрелку компаса. Это открытие принадлежало датскому физику Хансу Кристиану Эрстеду. Впоследствии его именем была названа единица измерения напряженности магнитного поля в системе СГС: русское обозначение Э (Эрстед), англоязычное – Oe. Такую напряженность магнитное поле имеет в вакууме при индукции в 1 Гаусс.

Это открытие наводило на мысль о том, что из электрического тока можно получить магнитное поле. Но вместе с тем возникали мысли и по поводу обратного преобразования, а именно, как из магнитного поля получить электрический ток. Ведь многие процессы в природе обратимы: из воды получается лед, который можно снова растопить в воду.

На изучение этого очевидного сейчас закона физики после открытия Эрстеда ушло целых двадцать два года. Получением электричества из магнитного поля занимался английский ученый Майкл Фарадей. Делались различной формы и размеров проводники и магниты, искались варианты их взаимного расположения. И только, видимо, случайно ученый обнаружил, что для получения на концах проводника ЭДС необходимо еще одно слагаемое – движение магнита, т.е. магнитное поле должно быть обязательно переменным.

Сейчас это никого уже не удивляет. Именно так работают все электрические генераторы, – пока его чем-то вращают, электроэнергия вырабатывается, лампочка светит. Остановили, перестали вращать, и лампочка погасла.

Электромагнитная индукция

Таким образом, ЭДС на концах проводника возникает лишь в том случае, если его определенным образом перемещать в магнитном поле. Или, точнее говоря, магнитное поле обязательно должно изменяться, быть переменным. Это явление получило название электромагнитной индукции, по-русски электромагнитное наведение: в этом случае говорят, что в проводнике наводится ЭДС. Если к такому источнику ЭДС подключить нагрузку, то в цепи будет протекать ток.

Величина наведенной ЭДС зависит от нескольких факторов: длины проводника, индукции магнитного поля B, и в немалой степени от скорости перемещения проводника в магнитном поле. Чем быстрее вращать ротор генератора, тем напряжение на его выходе выше.

Замечание: электромагнитную индукцию (явление возникновение ЭДС на концах проводника в переменном магнитном поле) не следует путать с магнитной индукцией – векторной физической величиной характеризующей собственно магнитное поле.

Три способа получения ЭДС

Индукция

Этот способ был рассмотрен в первой части статьи. Достаточно перемещать проводник в магнитном поле постоянного магнита, или наоборот перемещать (практически всегда вращением) магнит около проводника. Оба варианта однозначно позволят получить переменное магнитное поле. В этом случае способ получения ЭДС называется индукцией. Именно индукция используется для получения ЭДС в различных генераторах. В опытах Фарадея в 1831 году магнит поступательно перемещался внутри катушки провода.

Взаимоиндукция

Это название говорит о том, что в этом явлении принимают участие два проводника. В одном из них протекает изменяющийся ток, который создает вокруг него переменное магнитное поле. Если рядом находится еще один проводник, то на его концах возникает переменная же ЭДС.

Такой способ получения ЭДС называется взаимоиндукцией. Именно по принципу взаимоиндукции работают все трансформаторы, только проводники у них выполнены в виде катушек, а для усиления магнитной индукции применяются сердечники из ферромагнитных материалов.

Если ток в первом проводнике прекратится (обрыв цепи), или станет пусть даже очень сильным, но постоянным (нет никаких изменений), то на концах второго проводника никакой ЭДС получить не удастся.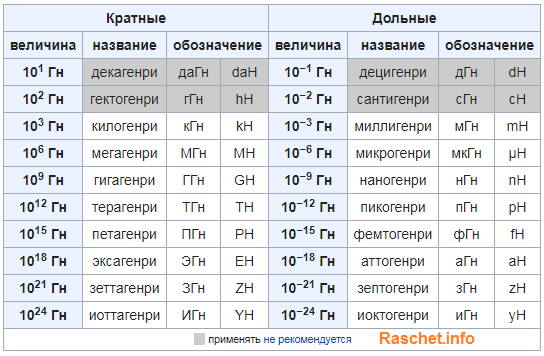 Вот почему трансформаторы работают только на переменном токе: если к первичной обмотке подключить гальваническую батарейку, то на выходе вторичной обмотки никакого напряжения однозначно не будет.

ЭДС во вторичной обмотке наводится только при изменении магнитного поля. Причем, чем сильнее скорость изменения, именно скорость, а не абсолютная величина, тем больше будет наведенная ЭДС.

Самоиндукция

Если убрать второй проводник, то магнитное поле в первом проводнике будет пронизывать не только окружающее пространство, но и сам проводник. Таким образом, под воздействием своего поля в проводнике наводится ЭДС, которая называется ЭДС самоиндукции.

Явления самоиндукции в 1833 году изучал русский ученый Ленц. На основании этих опытов удалось выяснить интересную закономерность: ЭДС самоиндукции всегда противодействует, компенсирует внешнее переменное магнитное поле, которое вызывает эту ЭДС. Эта зависимость называется правилом Ленца (не путать с законом Джоуля – Ленца).

Знак «минус» в формуле как раз и говорит о противодействии ЭДС самоиндукции причинам ее породившим. Если катушку подключить к источнику постоянного тока, ток будет возрастать достаточно медленно. Это очень заметно при «прозвонке» первичной обмотки трансформатора стрелочным омметром: скорость движения стрелки в сторону нулевого деления шкалы заметно меньше, чем при проверке резисторов.

При отключении катушки от источника тока ЭДС самоиндукции вызывает искрение контактов реле. В случае, когда катушка управляется транзистором, например катушка реле, то параллельно ей ставится диод в обратном направлении по отношению к источнику питания. Это делается для того, чтобы защитить полупроводниковые элементы от воздействия ЭДС самоиндукции, которая может в десятки и даже сотни раз превышать напряжение источника питания.

Для проведения опытов Ленц сконструировал интересный прибор. На концах алюминиевого коромысла закреплены два алюминиевых же кольца. Одно кольцо сплошное, а в другом был сделан пропил. Коромысло свободно вращалось на иголке.

При введении постоянного магнита в сплошное кольцо оно «убегало» от магнита, а при выведении магнита стремилось за ним. Те же самые действия с разрезанным кольцом никаких движений не вызывали. Это объясняется тем, что в сплошном кольце под воздействием переменного магнитного поля возникает ток, который создает магнитное поле. А в разомкнутом кольце тока нет, следовательно, нет и магнитного поля.

Немаловажная деталь этого опыта в том, что если магнит будет введен в кольцо и останется неподвижным, то никакой реакции алюминиевого кольца на присутствие магнита не наблюдается. Это лишний раз подтверждает, что ЭДС индукции возникает только в случае изменения магнитного поля, причем величина ЭДС зависит от скорости изменения. В данном случае просто от скорости перемещения магнита.

То же можно сказать и о взаимоиндукции и самоиндукции, только изменение напряженности магнитного поля, точнее скорость его изменения зависит от скорости изменения тока. Для иллюстрации этого явления можно привести такой пример.

Пусть через две достаточно большие одинаковые катушки проходят большие токи: через первую катушку 10А, а через вторую целых 1000, причем в обеих катушках токи линейно возрастают. Предположим, что за одну секунду ток в первой катушке изменился с 10 до 15А, а во второй с 1000 до 1001А, что вызвало появление ЭДС самоиндукции в обеих катушках.

Но, несмотря на такое огромное значение тока во второй катушке, ЭДС самоиндукции будет больше в первой, поскольку там скорость изменения тока 5А/сек, а во второй всего 1А/сек. Ведь ЭДС самоиндукции зависит от скорости возрастания тока (читай магнитного поля), а не от его абсолютной величины.

Индуктивность

Магнитные свойства катушки с током зависят от количества витков, геометрических размеров. Значительного усиления магнитного поля можно добиться введением в катушку ферромагнитного сердечника. О магнитных свойствах катушки с достаточной точностью можно судить по величине ЭДС индукции, взаимоиндукции или самоиндукции. Все эти явления были рассмотрены выше.

Характеристика катушки, которая рассказывает об этом, называется коэффициентом индуктивности (самоиндукции) или просто индуктивностью. В формулах индуктивность обозначается буквой L, а на схемах этой же буквой обозначаются катушки индуктивности.

Единица измерения индуктивности – генри (Гн). Индуктивностью 1Гн обладает катушка, в которой при изменении тока на 1А в секунду вырабатывается ЭДС 1В. Это величина достаточно большая: индуктивностью в один и более Гн обладают сетевые обмотки достаточно мощных трансформаторов.

Поэтому достаточно часто пользуются величинами меньшего порядка, а именно милли и микро генри (мГн и мкГн). Такие катушки применяются в электронных схемах. Одно из применений катушек – колебательные контура в радиоустройствах.

Также катушки используются в качестве дросселей, основное назначение которых пропустить без потерь постоянный ток при этом ослабив переменный (фильтры в источниках питания). Как правило, чем выше рабочая частота, тем меньшей индуктивности требуются катушки.

Индуктивное сопротивление

Если взять достаточно мощный сетевой трансформатор и померить мультиметром сопротивление первичной обмотки, то окажется, что оно всего несколько Ом, и даже близко к нулю. Выходит, что ток через такую обмотку будет очень большим, и даже стремиться к бесконечности. Кажется, короткое замыкание просто неизбежно! Так почему же его нет?

Одним из основных свойств катушек индуктивности является индуктивное сопротивление, которое зависит от индуктивности и от частоты переменного тока, который подведен к катушке.

Нетрудно видеть, что с увеличением частоты и индуктивности индуктивное сопротивление увеличивается, а на постоянном токе вообще становится равным нулю. Поэтому при измерении сопротивления катушек мультиметром измеряется только активное сопротивление провода.

Конструкция катушек индуктивности весьма разнообразна и зависит от частот, на которых работает катушка. Например, для работы в дециметровом диапазоне радиоволн достаточно часто используются катушки, выполненные печатным монтажом. При массовом производстве такой способ очень удобен.

Индуктивность катушки зависит от ее геометрических размеров, сердечника, количества слоев и формы. В настоящее время выпускается достаточное количество стандартных катушек индуктивности похожих на обычные резисторы с выводами. Маркировка таких катушек выполняется цветными кольцами. Также существуют катушки для поверхностного монтажа, применяемые в качестве дросселей. Индуктивность таких катушек составляет несколько миллигенри.

Поделитесь этой статьей с друзьями:

Вступайте в наши группы в социальных сетях:

В этой статье мы постараемся разобраться в том, что такое магнитная индукция, как она связана с магнитным полем, какое отношение имеет магнитная индукция к току, и как действует на ток. Вспомним основные правила, определяющие направление индукционных линий, а также отметим некоторые формулы, которые помогут в решении задач магнитостатики.

Силовой характеристикой магнитного поля в выбранной точке пространства является магнитная индукция В. Эта векторная величина определяет силу, с которой магнитное поле действует на движущуюся в нем заряженную частицу. Если заряд частицы равен q, ее скорость равна v, а индукция магнитного поля в данной точке пространства равна В, то на частицу в данной точке со стороны магнитного поля действует сила, равная:

Таким образом, В — это вектор, величина и направление которого таковы, что сила Лоренца, действующая на движущийся заряд со стороны магнитного поля равна:

Здесь альфа — это угол между вектором скорости и вектором магнитной индукции. Вектор силы Лоренца F перпендикулярен вектору скорости и вектору магнитной индукции. Его направление для случая движения положительно заряженной частицы в однородном магнитном поле определяется правилом левой руки:

«Если левую руку расположить так, чтобы вектор магнитной индукции входил в ладонь, а четыре вытянутых пальца были направлены по направлению движения положительно заряженной частицы, то отогнутый на 90 градусов большой палец покажет направление силы Лоренца».

Поскольку ток в проводнике является движением заряженных частиц, то магнитную индукцию можно определить и как отношение максимального механического момента, действующего со стороны однородного магнитного поля на рамку с током, к произведению силы тока в рамке на площадь рамки:

Магнитная индукция — фундаментальная характеристика магнитного поля, как напряженность для электрического поля . В системе СИ магнитная индукция измеряется в тесла (Тл), в системе СГС — в гауссах (Гс). 1 тесла = 10000 гаусс. 1 Тл — это индукция такого однородного магнитного поля, в котором на рамку площадью 1 м2, по которой течет ток в 1 А, действует максимальный вращающий механический момент сил, равный 1 Н • м.

Кстати, индукция магнитного поля Земли на широте 50° в среднем составляет 0,00005 Тл, а на экваторе — 0,000031 Тл. Вектор магнитной индукции всегда направлен по касательной к магнитной силовой линии.

Контур, помещенный в однородное магнитное поле, пронизывается магнитным потоком Ф, – потоком вектора магнитной индукции. Величина магнитного потока Ф зависит от направления вектора магнитной индукции относительно контура, от его величины, и от площади контура, пронизываемого линиями магнитной индукции. Если вектор В будет перпендикулярен площади контура, то магнитный поток Ф, пронизывающий контур, будет максимальным.

Сам термин индукция происходит от латинского «индукцио», что означает «наведение» (например, навести на мысль – то есть вызвать мысль). Синонимы: наведение, возникновение, образование. Не путать с явлением электромагнитной индукции.

Проводник с током имеет вокруг себя магнитное поле. Открыл магнитное поле электрического тока в 1820 году датский физик Ханс Кристиан Эрстед. Для определения направления силовых линий индукции магнитного поля В электрического тока I, текущего по прямолинейному проводнику, пользуются правилом правого винта или буравчика:

«Направление вращения рукоятки буравчика показывает направление линий магнитной индукции В, а поступательное движение буравчика тогда соответствует направлению тока в проводнике. »

При этом величина магнитной индукции B на расстоянии R от проводника с током I может быть найдена про формуле:

где магнитная постоянная:

Если линии напряженности электростатического поля Е начинаясь на положительных зарядах, заканчиваются на отрицательных, то линии магнитной индукции B замкнуты всегда. В отличие от электрических зарядов, магнитных зарядов, которые бы создавали полюса подобно электрическим зарядам, в природе не обнаружено.

Теперь несколько слов о постоянных магнитах. Еще в начале 19 века, французский исследователь и физик-естествоиспытатель Андре-Мари Ампер выдвинул гипотезу о молекулярных токах. Согласно Амперу, движения электронов вокруг атомных ядер порождают элементарные токи, которые в свою очередь создают вокруг себя элементарные магнитные поля. И если кусок ферромагнетика поместить во внешнее магнитное поле, то эти микроскопические магнитики сориентируются во внешнем поле, и кусок ферромагнетика станет магнитом.

Вещества с большим значением остаточной намагниченности, такие как сплав неодим-железо-бор, позволяют сегодня получать мощные постоянные магниты. Неодимовые магниты теряют не более 1-2 % своей намагниченности за 10 лет. Но их можно легко размагнитить, нагрев до температуры +70°C и более.

Надеемся, что данная статья помогла Вам получить общее представление о том, что такое магнитная индукция и откуда на возникает.

Причиной электродвижущей силы может стать изменение магнитного поля в окружающем пространстве. Это явление называетсяэлектромагнитной индукцией. Величина ЭДС индукции в контуре определяется выражением

где — поток магнитного поля через замкнутую поверхность , ограниченную контуром. Знак «−» перед выражением показывает, что индукционный ток, созданный ЭДС индукции, препятствует изменению магнитного потока в контуре (см. правило Ленца).

41. Индуктивность, ее единица СИ. Индуктивность длинного соленоида.

Индукти́вность (или коэффициент самоиндукции) — коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, и магнитным потоком, создаваемым этим током через поверхность [1] , краем которой является этот контур. [2][3][4] .

— магнитный поток, — ток в контуре, — индуктивность.

Нередко говорят об индуктивности прямого длинного провода(см.). В этом случае и других (особенно – в не отвечающих квазистационарному приближению) случаях, когда замкнутый контур непросто адекватно и однозначно указать, приведенное выше определение требует особых уточнений; отчасти полезным для этого оказывается подход (упоминаемый ниже), связывающий индуктивность с энергией магнитного поля.

Через индуктивность выражается ЭДС самоиндукции в контуре, возникающая при изменении в нём тока [4] :

.

Из этой формулы следует, что индуктивность численно равна ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1 А за 1 с.

При заданной силе тока индуктивность определяет энергию магнитного поля, создаваемого этим током [4] :

.

Обозначение и единицы измерения

В системе единиц СИ индуктивность измеряется в генри [7] , сокращенно Гн, в системе СГС — в сантиметрах (1 Гн = 10 9 см) [4] . Контур обладает индуктивностью в один генри, если при изменении тока на один ампер в секунду на выводах контура будет возникать напряжение в один вольт. Реальный, не сверхпроводящий, контур обладает омическим сопротивлением R, поэтому на нём будет дополнительно возникать напряжение U=I*R, где I — сила тока, протекающего по контуру в данное мгновение времени.

Символ , используемый для обозначения индуктивности, был взят в честь Ленца Эмилия Христиановича (Heinrich Friedrich Emil Lenz) [ источник не указан 1017 дней ] . Единица измерения индуктивности названа в честь Джозефа Генри (Joseph Henry) [8] . Сам термин индуктивность был предложен Оливером Хевисайдом (Oliver Heaviside) в феврале 1886 года [ источник не указан 1017 дней ] .

Электрический ток, который течет в замкнутом контуре, создает вокруг себя магнитное поле, индукция которого, согласно закону Био-Савара-Лапласа, пропорциональна току. Сцепленный с контуром магнитный поток Ф поэтому прямо пропорционален току I в контуре: (1) где коэффициент пропорциональности L называетсяиндуктивностью контура. При изменении в контуре силы тока будет также изменяться и сцепленный с ним магнитный поток; значит, в контуре будет индуцироваться э.д.с. Возникновение э.д.с. индукции в проводящем контуре при изменении в нем силы тока называетсясамоиндукцией. Из выражения (1) задается единица индуктивности генри (Гн): 1 Гн — индуктивность контура, магнитный поток самоиндукции которого при токе в 1 А равен 1 Вб: 1 Гн = 1 Вб/с = 1 В

Вычислим индуктивность бесконечно длинного соленоида. Полный магнитный поток сквозь соленоид (потокосцепление) равен μ_{μ(N 2 I/l)S . Подставив в (1), найдем (2) т. е. индуктивность соленоида зависит от длиныl солениода, числа его витков N, его , площади S и магнитной проницаемости μ вещества, из которого изготовлен сердечник соленоида. Доказано, что индуктивность контура зависит в общем случае только от геометрической формы контура, его размеров и магнитной проницаемости среды, в которой он расположен, и можно провести аналог индуктивности контура с электрической емкостью уединенного проводника, которая также зависит только от формы проводника, его размеров и диэлектрической проницаемости среды. Найдем, применяя к явлению самоиндукции закон Фарадея, что э.д.с. самоиндукции равна Если контур не претерпевает деформаций и магнитная проницаемость среды остается неизменной (в дальнейшем будет показано, что последнее условие выполняется не всегда), то L = const и(3) где знак минус, определяемый правилом Ленца, говорит о том, чтоналичие индуктивности в контуре приводит к замедлению изменения тока в нем. Если ток со временем увеличивается, то (dI/dt 0 т. е. ток самоиндукции направлен навстречу току, обусловленному внешним источником, и замедляет его увеличение. Если ток со временем уменьшается, то (dI/dt>0) и ξs >1), обладающей боль­шой индуктивностью, э.д.с. самоиндукции может во много раз превышать э.д.с. источника тока, включенного в цепь. Таким образом, необходимо учитывать, что контур, содержащий индуктивность, нельзя резко размыкать, так как это (возникнове­ние значительных э.д.с. самоиндукции) может привести к пробою изоляции и выводу из строя измерительных приборов. Если в контур сопротивление вводить постепенно, то э.д.с. самоиндукции не достигнет больших значений.}

43. Явление взаимной индукции. Трансформатор.

Рассмотрим два неподвижных контура (1 и 2), которые расположены достаточно близко друг от друга (рис. 1). Если в контуре 1 протекает ток I₁, то магнитный поток, который создавается этим током (поле, создающее этот поток, на рисунке изображено сплошными линиями), прямо пропорционален I₁. Обозначим через Ф₂₁ часть потока,пронизывающая контур 2. Тогда (1) где L₂₁ — коэффициент пропорциональности.

Если ток I₁ меняет свое значение, то в контуре 2 индуцируется э.д.с. ξ_i2 , которая по закону Фарадея будет равна и противоположна по знаку скорости изменения магнитного потока Ф₂₁, который создается током в первом контуре и пронизыващет второй: Аналогичным образом, при протекании в контуре 2 тока I₂ магнитный поток (его поле изображено на рис. 1 штрихами) пронизывает первый контур. Если Ф₁₂ — часть этого потока, который пронизывает контур 1, то Если ток I₂ меняет свое значение, то в контуре 1 индуцируется э.д.с. ξ_i1 , которая равна и противоположна по знаку скорости изменения магнитного потока Ф₁₂, который создается током во втором контуре и пронизывает первый: Явление возникновения э.д.с. в одном из контуров при изменении силы тока в другом называется взаимной индукцией. Коэффициенты пропорциональности L₂₁ и L₁₂ называются взаимной индуктивностью контуров. Расчеты, которые подтверждены опытом, показывают, что L₂₁ и L₁₂ равны друг другу, т. е. (2) Коэффициенты пропорциональности L₁₂ и L₂₁ зависят от размеров, геометрической формы, взаимного расположения контуров и от магнитной проницаемости среды, окружающей контуры. Единица взаимной индуктивности та же, что и для индуктивности, — генри (Гн). Найдем взаимную индуктивность двух катушек, которые намотаны на общий тороидальный сердечник. Этот случай имеет большое практическое значение (рис. 2). Магнитная индукция поля, которое создавается первой катушкой с числом витков N₁, током I₁ и магнитной проницаемостью μ сердечника, B = μμ_{(N1I1/l) где l — длина сердечника по средней линии. Магнитный поток сквозь один виток второй катушки Ф2 = BS = μμ(N1I1/l)S}

Значит, полный магнитный поток (потокосцепление) сквозь вторичную обмотку, которая содержит N₂ витков, Поток Ψ создается током I₁, поэтому, используя (1), найдем (3) Если рассчитать магнитный поток, который создавается катушкой 2 сквозь катушку 1, то для L₁₂ получим выражение в соответствии с формулой (3). Значит, взаимная индуктивность двух катушек, которые намотаны на общий тороидальный сердечник,

Трансформа́тор (от лат. transformo — преобразовывать) — это статическое электромагнитное устройство, имеющее две или более индуктивно связанных обмоток на каком-либо магнитопроводе и предназначенное для преобразования посредствомэлектромагнитной индукции одной или нескольких систем (напряжений) переменного тока в одну или несколько других систем (напряжений) переменного тока без изменения частоты системы (напряжения) переменного тока

Катушка индуктивности.

Параметры. Виды. Обозначение на схемах

Здравствуйте, уважаемые читатели сайта sesaga.ru. Катушка индуктивности относится к числу элементов, без которых не получится построить приемник, телевизор, радиоуправляемую модель, передатчик, генератор сигналов, модемный преобразователь, сетевой фильтр и т.п.

Катушку индуктивности или просто катушку можно представить в виде нескольких витков провода намотанного в спираль. Ток проходя по каждому витку спирали создает в них магнитное поле, которое пересекаясь с соседними витками наводит в них э.д.с самоиндукции. И чем провод длиннее и большее число витков он образует, тем самоиндукция больше.

Индуктивность

По своей сути индуктивность является электрической инерцией и ее основное свойство состоит в том, чтобы оказывать сопротивление всякому изменению протекающего тока. Если через катушку пропускать определенный ток, то ее индуктивность будет противодействовать как уменьшению, так и увеличению протекающего тока.

В отличие от конденсатора, который пропускает переменный и не пропускает постоянный ток, катушка индуктивности свободно пропускает постоянный ток и оказывает сопротивление переменному току, потому что он изменяется быстрее, чем может изменяться магнитное поле.

И чем больше индуктивность катушки и чем выше частота тока, тем оказываемое сопротивление сильнее. Это свойство катушки применяют, например, в приемной аппаратуре, когда требуется в электрической цепи преградить путь переменному току.

Индуктивность измеряется в генри (Гн), миллигенри (1мГн = 10ˉ3 Гн), микрогенри (1мкГн = 10ˉ6 Гн), наногенри (1нГн = 10ˉ9 Гн) и обозначается латинской буквой L.

Общие свойства катушек индуктивности

В зависимости от требуемой индуктивности и частоты, на которой катушка будет работать, она может иметь самые различные исполнения.

Для высоких частот это может быть простая катушка состоящая из нескольких витков провода или же катушка с сердечником из ферромагнитного материала и иметь индуктивность от нескольких наногенри до нескольких десятков миллигенри. Такие катушки применяются в радиоприемной, передающей, измерительной аппаратуре и т.п.

Катушки, работающие на высоких частотах, можно разделить на катушки контуров, катушки связи и дроссели высокой частоты. В свою очередь катушки контуров могут быть с постоянной индуктивностью и переменной индуктивностью (вариометры).

По конструктивному признаку высокочастотные катушки разделяются на однослойные и многослойные, экранированные и неэкранированные, катушки без сердечников и катушки с магнитными и немагнитными сердечниками, бескаркасные, цилиндрические плоские и печатные.

Для работы в цепи переменного тока низкой частоты, на звуковых частотах, во входных фильтрах блоков питания, в цепях питания осветительного электрооборудования применяются катушки с достаточно большой индуктивностью. Их индуктивность достигает десятки и даже сотни генри, а в обмотках могут создаваться большие напряжения и протекать значительные токи.

Для увеличения индуктивности при изготовлении таких катушек применяют магнитопроводы (сердечники), собранные из отдельных тонких изолированных пластин сделанных из специальных магнитных материалов – электротехнических сталей, пермаллоев и др.

Применение наборных магнитопроводов обусловлено тем, что под действием переменного магнитного поля в сплошном магнитопроводе, который можно рассматривать как множество короткозамкнутых витков, образуются вихревые токи, которые нагревают магнитопровод, бесполезно потребляя часть энергии магнитного поля. Изоляция же между слоями стали оказывается на пути вихревых токов и значительно снижает потери.

Катушки с магнитопроводами из изолированных пластин можно разделить на

дроссели и трансформаторы.

Основные параметры катушек индуктивности

Свойства катушек могут быть охарактеризованы четырьмя основными параметрами: индуктивностью, добротностью, собственной емкостью и стабильностью.

1. Индуктивность.

Индуктивность (коэффициент самоиндукции) является основным электрическим параметром и характеризует величину энергии, запасаемой катушкой при протекании по ней электрического тока. Чем больше индуктивность катушки, тем больше энергии она запасает в своем магнитном поле.

Индуктивность зависит от размеров каркаса, формы, числа витков катушки, диаметра и марки провода, а также от формы и материала магнитопровода (сердечника).

В радиолюбительских схемах, как правило, величину индуктивности не указывают, так как радиолюбителя интересует не эта величина, а количество витков провода в катушке, диаметр и марка провода, способ намотки (внавал, виток к витку, крест на крест, секционная намотка) и размеры каркаса катушки.

2. Добротность.

Добротность (Q) характеризуется качеством работы катушки индуктивности в цепях переменного тока и определяется как отношение реактивного сопротивления катушки к ее активному сопротивлению потерь.

Активное сопротивление включает в себя сопротивление провода обмотки катушки; сопротивление, вносимое диэлектрическими потерями в каркасе; сопротивление, вносимое собственной емкостью и сопротивления, вносимые потери в экраны и сердечники.

Чем меньше активное сопротивление, тем выше добротность катушки и ее качество. В большинстве случаев добротность катушки определяют резонансные свойства и к.п.д. контура.
Современные катушки средних размеров имеют добротность около 50 – 300.

3. Собственная емкость.

Катушки индуктивности обладают собственной емкостью, которая увеличивается по мере увеличения числа витков и размеров катушки. Между соседними витками существует межвитковая емкость, из-за которой некоторая часть тока проходит не по проводу, а через емкость между витками, отчего сопротивление между выводами катушки уменьшается.

Все дело в том, что общее напряжение, приложенное к катушке, разделяется на межвитковые напряжения из-за чего между витками образуется электрическое поле, вызывающее скопление зарядов. Витки, разделенные слоями изоляции, образуют обкладки множества маленьких конденсаторов, через которые протекает часть тока, из общей емкости которых и складывается собственная емкость катушки. Таким образом катушка обладает не только индуктивными но и емкостными свойствами.

Собственная емкость является вредным параметром и ее стремятся уменьшить применением специальных форм каркаса и способом намотки провода.

4. Стабильность.

Стабильность катушки характеризуется изменением ее параметров под воздействием температуры, влажности и во времени.

Изменение индуктивности под влиянием температуры характеризуют температурным коэффициентом индуктивности (ТКИ), равным относительному изменению индуктивности при изменении температуры на 1°С. ТКИ катушки определяется способом намотки и качеством диэлектрика каркаса.

Влажность вызывает увеличение собственной емкости и диэлектрических потерь, а также понижает стабильность катушки. Для защиты от действия влажности применяется герметизация или пропитка и обволакивание обмотки негигроскопичными составами.

Такие катушки обладают более низкой добротностью и большой собственной емкостью, но при этом они более устойчивы к воздействию влаги.

Катушки индуктивности с магнитопроводами

Для получения малогабаритных катушек различного назначения применяют магнитопроводы (сердечники), которые изготавливают из магнитодиэлектриков и ферритов. Катушки с магнитопроводами имеют меньшее число витков при заданной индуктивности, малую длину провода и небольшие размеры.

Ценным свойством катушек с магнитопроводами является возможность их подстройки, т.е. изменения индуктивности в небольших пределах путем перемещения внутри катушки специального цилиндрического подстроечника, состоящего из феррита с напрессованной на него резьбовой втулкой.

Магнитодиэлектрики представляют собой измельченное вещество, содержащее в своем составе железо (ферромагнетик), частицы которого равномерно распределены в массе диэлектрика (бакелита или аминопласта). Наиболее широко применяют магнитопроводы из альсифера (сплав алюминия, кремния и железа) и карбонильного железа.

Ферриты представляют собой твердые растворы окислов металлов или их солей, прошедшие специальную термическую обработку (обжиг). Получающееся при этом вещество – полупроводниковая керамика – обладает очень хорошими магнитными свойствами и малыми потерями даже на очень высоких частотах.

Основным достоинством ферритов является высокая магнитная проницаемость, которая позволяет существенно уменьшить размеры катушек.

В старых принципиальных схемах магнитопроводы из магнитодиэлектриков и ферритов обозначались одинаково – утолщенной штриховой линией (рис. а). Впоследствии стандарт ЕСКД оставил этот символ для магнитопроводов из магнитодиэлектрика, а для ферритовых ввел обозначение, ранее применявшееся только для магнитопроводов низкочастотных дросселей и трансформаторов – сплошную жирую линию (рис. б). Однако согласно последней редакции ГОСТ 2.723.68 (март 1983г.) магнитопроводы катушек изображают линиями нормальной толщины (рис. в).

Катушки, индуктивность которых можно изменять с помощью магнитопровода, на электрических схемах указываются при помощи знака подстроечного регулирования, который вводится в ее условное обозначение.

Изменение индуктивности обозначают двумя способами: либо знаком подстроечного регулирования пересекающим обозначения катушки и магнитопровода (рис. а), либо только пересечением магнитопровода с изображением его над катушкой (рис. б).

Экранированные катушки индуктивности

Для устранения паразитных связей, обусловленных внешним электромагнитным полем катушки и влияния на катушку окружающего пространства, ее экранируют, т.е. помещают в замкнутом металлическом экране.

Однако под влиянием экрана изменяются основные электрические параметры катушки: уменьшаются индуктивность и добротность, увеличивается сопротивление и собственная емкость.

Изменение параметров катушки тем больше, чем ближе к ее виткам расположен экран, т.е. изменение параметров зависит от соотношения между размерами катушки и размерами самого экрана.

Для высокочастотных катушек экраны выполняются в виде круглых или прямоугольных стаканов из алюминия, меди или латуни с толщиной стенок 0,3 – 0,5 мм.

Чтобы на схемах обозначить экранированную катушку, ее условное обозначение помещают в знак экранирования, который соединяют с корпусом.

Также необходимо отметить, что экранировать необходимо лишь катушки большого размера, диаметр которых составляет более 15 – 20 мм.

Катушки диаметром не более 4 – 5 мм создают магнитное поле в относительно небольшом пространстве и при удалении таких катушек от других деталей на расстояние в 4 – 5 раз больше их диаметра опасных связей, как правило, не возникает, поэтому они не нуждаются в специальном экранировании.

Обозначение катушек с отводами и начала обмотки

В радио и электротехнической аппаратуре, например, в приемниках или импульсных преобразователях напряжения, иногда используют не всю индуктивность катушки, а только некоторую ее часть. Для таких случаев катушки изготавливают с отводом или отводами.

При разработке некоторых конструкций иногда необходимо строго соблюсти начало и конец обмотки катушки или трансформатора. Чтобы указать, какой из концов обмотки является началом, а какой – концом, у вывода начала обмотки ставят жирную точку.

Для подстройки катушек на частотах свыше 15…20 МГц часто применяют магнитопроводы из немагнитных материалов (меди, алюминия и т.п.). Возникающие в таком магнитопроводе под действием магнитного поля катушки вихревые токи создают свое поле, противодействующее основному, в результате чего индуктивность катушки уменьшается.

Немагнитный магнитопровод-подстроечник обозначают так же, как и ферритовый, но рядом указывают химический символ металла, из которого он изготовлен. На рисунке изображен подстроечник, изготовленный из меди.

Вот и все, что хотел рассказать о катушках индуктивности.
Удачи!

Литература:
1. В. А. Волгов «Детали и узлы радиоэлектронной аппаратуры».
2. В. В. Фролов «Язык радиосхем».
3. М. А. Сгут «Условные обозначения и радиосхемы».

Определяем добротность и частоту собственного резонанса катушки индуктивности

Как ни странно, в катушках индуктивности нас в первую очередь интересует индуктивность. Измерить индуктивность не сложно. Готовые RLC-метры стоят недорого. Если RLC-метра нет, но есть осциллограф, индуктивность можно определить с его помощью. Также нормальный антенный анализатор без труда измеряет как индуктивность, так и емкость. Но у катушек индуктивности есть еще по крайней мере два важных свойства — частота собственного резонанса и добротность. Давайте разберемся, почему эти свойства важны и как их измерить.

Суть проблемы

Катушки индуктивности, существующие в реальном мире, можно описать при помощи следующей модели:

Здесь L — это индуктивность катушки. Катушка мотается неким проводником, а реальный проводник имеет отличные от нуля потери. Резистор Rs (он же ESR, equivalent series resistance) как раз отображает эти потери. Конденсатор Cp — это паразитная емкость между витками катушки.

Можно заметить, что индуктивность L и конденсатор Cp образуют параллельный колебательный контур. У этого контура есть резонансная частота. Она и называется частотой собственного резонанса катушки (self-resonant frequency). Ниже этой частоты катушка ведет себя, как катушка. Однако выше она начинает вести себя больше как конденсатор. Определив частоту собственного резонанса, мы поймем, на каких частотах может быть использована катушка.

Rs имеет сложную природу, и работать с ним напрямую неудобно. Поэтому вместо того, чтобы говорить об Rs, говорят о добротности (quality factor или Q). Добротность — это безразмерная величина, характеризующая скорость затухания колебаний в колебательной системе. Чем больше Q, тем меньше затухания.

Для катушек индуктивности добротность определяется, как отношение реактивного сопротивления к Rs:

Реактивное сопротивление является функцией от частоты. Rs на самом деле тоже зависит от частоты. В мире любительского радио обычно говорят о Q на рабочих частотах катушки. Предполагается, что на этом интервале частот добротность меняется незначительно.

Стоит упомянуть, что различают холостую добротность (unloaded Q) и нагруженную добротность (loaded Q). В рамках этой статьи под добротностью понимается исключительно холостая добротность. Нагруженная добротность возникает, когда катушку помещают в конкретную электрическую цепь.

Испытуемый

Попробуем определить частоту собственного резонанса и добротность такой катушки:

Катушка намотана проводом МГТФ площадью сечения 0.35 кв.мм на трубе ПВХ с внешним диаметром 25 мм. Для принудительного шага я мотал два параллельных провода. Затем один провод постепенно отматывался, а второй фиксировался лаком. Длина намотки составила 30 мм, индуктивность — 2 мкГн.

Такой способ намотки был использован с целью получить не самую позорную добротность. За годы экспериментов радиолюбители выработали хорошие практики, позволяющие максимизировать добротность. Основные рекомендации:

• Толстый проводник предпочтительнее тонкого;
• Любой диэлектрик в качестве каркаса катушки или изолятора проводника уменьшает добротность;
• Charles Michaels, W7XC (SK) рекомендует в катушках с воздушным диэлектриком использовать отношение длины катушки к ее диаметру (L/D) не более 2:1. Здесь речь идет о намотке виток к витку;
• Если же катушка мотается на каркасе, рекомендуется L/D = 1:1;
• Tom Rauch, W8JI рекомендует использовать расстояние между витками, равное толщине проводника и L/D от 1 до 4;

Кое-какие подробности можно найти в 9-ой главе книги ON4UN’s Low Band DXing, 5th Edition, в разделе 3.7.2 Making or Buying High-Q Loading Coils. Отмечу, что просто следовать этим советам недостаточно. Если ваша задача — получить как можно большую добротность, нужно брать конкретные доступные материалы, мотать катушки и измерять.

На самом деле, мной было намотано пять катушек пятью разными способами. Приведенная выше имела максимальную добротность.

Ищем собственный резонанс

Для определения частоты собственного резонанса было решено воспользоваться анализатором спектра. С тем же успехом подойдет осциллограф с генератором сигналов, или RTL-SDR с генератором шума. Но анализатор спектра удобнее.

Для подключения катушки между следящим генератором и входом анализатора было использовано такое приспособление:

Экраны BNC-разъемов соединены между собой, а жилы идут к «банановым» коннекторам. К этим коннекторам и подключается катушка.

В итоге получаем такую АЧХ:

Перед нами частоты от 1 до 201 МГц, цена деления по горизонтали — 20 МГц. Собственный резонанс, если верить графику, пришелся где-то на 150 МГц. Ниже аттенюация сигнала увеличивается с ростом частоты. Так и должна работать катушка. Выше аттенюация уменьшается с ростом частоты. Это поведение конденсатора.

Какие выводы отсюда можно сделать? Катушку можно использовать на частотах где-то до 37 МГц. На частотах, приближающихся к частоте собственного резонанса, использовать катушки нельзя. Причина заключается в том, что добротность падает по мере приближения к частоте собственного резонанса. На частоте собственного резонанса добротность равна нулю. Рекомендуется использовать катушки на частотах в 4+ раза ниже частоты собственного резонанса.

Определяем добротность

Для определения добротности воспользуемся подходом из статьи Fixture for Measuring Inductor Q with your Antenna Analyzer [PDF], которую написал Phil Salas, AD5X. По инструкции из статьи было изготовлено такое устройство:

Идея довольно простая. Антенный анализатор подключается к BNC разъему, а катушка подключается к «банановым» коннекторам. В первом положении тумблера антенный анализатор измеряет эквивалент нагрузки 50 Ом. Для эквивалента нагрузки было использовано 20 соединенных параллельно резисторов 1 кОм ± 1%. Во втором положении измеряется последовательный колебательный контур, образованный этим же резистором 50 Ом, измеряемой катушкой и КПЕ.

На резонансной частоте последовательный LC-контур представляет собой КЗ, и мы увидим чисто активное сопротивление около 50 Ом:

В данном случае (первый график) резонанс попал на 9.3185 МГц. Антенный анализатор видит 50.4 Ом. Переключаем тумблер в другое положение. Видим сопротивление резистора без контура. Оно составило 49.8 Ом (второй график). Есть также небольшая реактивность в 0.4j. Ею мы пренебрежем, поскольку это всего лишь:

>>> from math import pi
>>> F = 9_318_500
>>> 0.4/(2*pi*F)
6.83178378888857e-09

… 6.8 нГн, почти в 300 раз меньше измеряемых 2 мкГн.

Смотрите, что получается. С контуром было 50.4 Ом, а без контура — 49.8 Ом. Разница в 0.6 Ом включает в себя Rs катушки, а также потери на конденсаторе. Но конденсаторы обладают существенно большей добротностью (> 1000), чем катушки. Поэтому разница в 0.6 Ом приходится преимущественно на Rs катушки.

Теперь у нас есть все необходимое для вычисления добротности:

>>> from math import pi
>>> F = 9_318_500
>>> L = 2.0/1000/1000
>>> Rs = 50.4 — 49.8
>>> Xl = 2*pi*F*L
>>> Q = Xl/Rs
>>> Q
195.16620761650944

Добротность порядка 200 — это неплохой результат. Обычные покупные катушки для сквозного монтажа имеют добротность в пределах 100. Не удивительно, что бывалые радиолюбители предпочитают мотать катушки самостоятельно. Случайная самодельная катушка из медной проволоки будет иметь добротность уже порядка 100-150. Согласно Low Band DXing, после некоторой практики можно легко делать катушки с добротностью ~400. В качестве потолка в различных источниках приводится Q от 800 до 1000.

Домашнее задание: Смотайте катушку с индуктивностью побольше, порядка 70 мкГн. Для такой катушки вам понадобится каркас около 70 мм и 30 витков эмалированной проволоки диаметром 0.9 мм. Каким вышел Rs? Куда попала частота собственного резонанса? Сравните с приведенными выше результатами.

Внимательный читатель может поинтересоваться, а почему номинал резистора был выбран именно 50 Ом? Это сделано лишь по той причине, что ошибка измерения антенного анализатора при таком сопротивлении минимальна. В теории, с тем же успехом можно использовать любое другое сопротивление, лишь бы оно было чисто активным.

Заключение

Допустим, мы спаяли генератор или фильтр, и он работает не так, как ожидалось. Причина может заключаться к собственном резонансе катушек. Слишком большие потери в согласующем устройстве? Причина может быть в низкой добротности компонентов. Теперь мы имеем больше шансов правильно диагностировать такие проблемы, или еще лучше — вообще избегать их.

Дополнение: Измеряем параметры кварцевых резонаторов

Метки: Электроника.

Катушка индуктивности. Обозначение на схеме и примеры её использования в электронике.

Обозначение, параметры и разновидности катушек индуктивности

Одним из самых известных и необходимых элементов аналоговых радиотехнических схем является катушка индуктивности. В цифровых электронных схемах индуктивные элементы практически потеряли свою актуальность и применяются только в устройствах питания как сглаживающие фильтры.

Катушки индуктивности на принципиальных схемах обозначаются латинской буквой “L” и имеют следующее изображение.

Разновидностей катушек индуктивности существуют десятки. Они бывают высокочастотные, низкочастотные, с подстроечными сердечниками и без них. Бывают катушки с отводами, катушки, рассчитанные на большие напряжения. Вот так, например, выглядят бескаркасные катушки.

Катушки для СВЧ аппаратуры называются микрополосковыми линиями. Они даже внешне не похожи на катушки. С катушками индуктивности связан такой эффект как резонанс и гениальный Никола Тесла получал на резонансных трансформаторах миллионы вольт.

Основной параметр катушки это её индуктивность. Величина индуктивности измеряется в Генри (Гн, англ. – «H»). Это достаточно большая величина и поэтому на практике применяют меньшие значения (мГн, mH – миллигенри и мкГн, μH– микрогенри) соответственно 10^-3 и 10^-6 Генри. Величина индуктивности катушки указывается рядом с её условным изображением (например, 100 μH). Чтобы не запутаться в микрогенри и миллигенри, советую узнать, что такое сокращённая запись численных величин.

Многие факторы влияют на индуктивность катушки. Это и диаметр провода, и число витков, а на высоких частотах, когда применяют бескаркасные катушки с небольшим числом витков, то индуктивность изменяют, сближая или раздвигая соседние витки.

Часто для увеличения индуктивности внутрь каркаса вводят сердечник из ферромагнетика, а для уменьшения индуктивности сердечник должен быть латунным. То есть можно получить нужную индуктивность не увеличением числа витков, что ведёт к увеличению сопротивления, а использовать катушку с меньшим числом витков, но использовать ферритовый сердечник. Катушка индуктивности с сердечником изображается на схемах следующим образом.

В реальности катушка с сердечником может выглядеть так.

Также можно встретить катушки индуктивности с подстроечным сердечником. Изображаются они вот так.

Катушка с подстроечным сердечником вживую выглядит так.

Такая катушка, как правило, имеет сердечник, положение которого можно регулировать в небольших пределах. При этом величина индуктивности также меняется. Подстроечные катушки индуктивности применяются в устройствах, где требуется одноразовая подстройка. В дальнейшем индуктивность не регулируют.

Наряду с подстроечными катушками можно встретить и катушки с регулируемой индуктивностью. На схемах такие катушки обозначаются вот так.

В отличие от подстроечных катушек, регулируемые катушки индуктивности допускают многократную регулировку положения сердечника, а, следовательно, и индуктивности.

Ещё один параметр, который встречается достаточно часто это добротность контура. Под добротностью понимается отношение между реактивным и активным сопротивлением катушки индуктивности. Добротность обычно бывает в пределах 15 – 350.

На основе катушки индуктивности и конденсатора выполнен самый необходимый узел радиотехнических устройств, колебательный контур. На схеме изображён входной контур простого радиоприёмника рассчитанного на работу в диапазонах средних и длинных волн.

В настоящее время в этих диапазонах станций практически нет. Катушка индуктивности L1 имеет достаточно большое число витков, чтобы перекрыть диапазон по максимуму. Для улучшения приёма к первой обмотке L1 подключается внешняя антенна. Это может быть простой кусок проволоки длиной в пределах двух метров.

Благодаря большому числу витков в индуктивности L1 присутствует целый спектр частот и как минимум пять — шесть работающих радиостанций. Две индуктивности L1 и L2 намотанные на одном каркасе представляют собой высокочастотный трансформатор. Для того чтобы выделить на катушке индуктивности L2 станцию, работающую, допустим на частоте 650 КГц необходимо с помощью переменного конденсатора C1 настроить колебательный контур на данную частоту.

После этого выделенный сигнал можно подавать на базу транзистора усилителя высокой частоты. Это одно из применений катушки индуктивности. Точно на таком же принципе построены выходные каскады радио- и телевизионных передатчиков только наоборот. Антенна не принимает слабый сигнал, а отдаёт в пространство ЭДС.

Примеров использования катушки индуктивности великое множество. На рисунке изображён весьма несложный, но хорошо зарекомендовавший себя в работе сетевой фильтр.

Фильтр состоит из двух дросселей (катушек индуктивности) L1 и L2 и двух конденсаторов С1 и С2. на старых схемах дроссели могут обозначаться как Др1 и Др2. Сейчас это редкость. Катушки индуктивности намотаны проводом ПЭЛ-0,5 – 1,5 мм. на каркасе диаметром 5 миллиметров и содержат по 30 витков каждая. Очень хорошо параллельно сети 220V подключить варистор. Тогда защита от бросков сетевого напряжения будет практически полной. В качестве конденсаторов лучше не использовать керамические, а поискать старые, но надёжные МБМ на напряжение не менее 400V.

Вот так выглядит дроссель входного фильтра компьютероного блока питания ATX.

Как видно, он намотан на кольцеобразном сердечнике. На схеме он обозначается следующим образом. Точками отмечены места начала намотки провода. Это бывает важно, так как это влият на направление магнитного потока.

Выходные выпрямители современного импульсного блока питания всегда конструируют по двухполупериодным схемам. Широко известный выпрямительный диодный мост, у которого большие потери практически не используют. В двухполупериодных выпрямителях используют сборки из двух диодов Шоттки. Самая важная особенность выпрямителей в импульсных блоках питания это фильтры, которые начинаются с дросселя (индуктивности).

Напряжение, снимаемое с выхода выпрямителя обладающего индуктивным фильтром, зависит кроме амплитуды ещё и от скважности импульсов, поэтому очень легко регулировать выходное напряжение, регулируя скважность входного. Процесс регулирования скважности импульсов называют широтно-импульсной модуляцией (ШИМ), а в качестве управляющей микросхемы используют ШИМ контроллер.

Поскольку амплитуда напряжения на входах всех выпрямителей изменяется одинаково, то стабилизируя одно напряжение, ШИМ контроллер стабилизирует все. Для увеличения эффекта, дроссели всех фильтров намотаны на общем магнитопроводе.

Именно таким образом устроены выходные цепи компьютерного блока питания формата AT и ATX. На его печатной плате легко обнаружить дроссель с общим магнитопроводом. Вот так он выглядит на плате.

Как уже говорилось, этот дроссель не только фильтрует высокочастотные помехи, но и играет важную роль в стабилизации выходных напряжений +12, -12, +5, -5. Если выпаять этот дроссель из схемы, то блок питания будет работать, но вот выходные напряжения будут «гулять» причём в очень больших пределах – проверено на практике.

Так магнитопровод у такого дросселя общий, а катушки индуктивности электрически не связаны, то на схемах такой дроссель обозначают так.

Здесь цифра после точки (L1.1; L1.2 и т.д.) указывает на порядковый номер катушки на принципиальной схеме.

Ещё одно очень хорошо известное применение катушки индуктивности это использование её в системах зажигания транспортных средств. Здесь катушка индуктивности работает как импульсный трансформатор. Она преобразует напряжение 12V с аккумулятора в высокое напряжение порядка нескольких десятков тысяч вольт, которого достаточно для образования искры в свече зажигания.

Когда через первичную обмотку катушки зажигания протекает ток, катушка запасает энергию в своём магнитном поле. При прекращении прохождения тока в первичной обмотке пропадающее магнитное поле индуцирует во вторичной обмотке мощный короткий импульс напряжением 25 – 35 киловольт.

Импульсный трансформатор из тех же катушек индуктивности является основным узлом хорошо известного устройства для самообороны как электорошокер. Схем может быть несколько, но принцип один: преобразование низкого напряжения от небольшой батарейки или аккумулятора в импульс слабого тока, но очень высокого напряжения. У серьёзных моделей напряжение может достигать 75 – 80 киловольт.

Главная &raquo Радиоэлектроника для начинающих &raquo Текущая страница

Также Вам будет интересно узнать:

 

Размерность — индуктивность — Большая Энциклопедия Нефти и Газа, статья, страница 1

Размерность — индуктивность

Cтраница 1

Размерность индуктивности в системе CGSM равна размерности длины и поэтому CGSM-единица индуктивности получила название сантиметр. CGSM магнитный поток, пронизывающий этот контур, равен 1 мкс.  [1]

Размерность индуктивности L — мкГн; емкое.  [3]

Размерностью индуктивности в системе СГС является длина [ L ]; единицей измерения индуктивности в этой системе служит сантиметр. Индуктивность, равная 1 см, в 10 раз меньше 1 гн: 1 ед.  [4]

Таким образом, размерность индуктивности в системе CQS-M совпадает с размерностью длины. Единицей индуктивности в системе CGS-M является сантиметр.  [5]

Показать, что г 2С имеет размерность индуктивности, ] / L / C — размерность сопротивления; L / r — размерность емкости.  [7]

Из (64.3) следует, что размерность цо равна размерности индуктивности, деленной на размерность длины.  [8]

Из (64.3) следует, что размерность р 0 равна размерности индуктивности, деленной на размерность длины.  [9]

Очевидно, что ( a — f — Ъх) имеет размерность индуктивности. Величина этой индуктивности является в данном случае линейной функцией положения якоря соленоида.  [10]

Постоянные Н, входящие в выражение сопротивлений реактивных двухполюсников, имеют размерность индуктивности для двухполюсников классов I и IV и размерность, обратную емкости, для классов II и III. Для нахождения постоянной Я надо определить характер сопротивления двухполюсника ( индуктивный или емкостный) при частоте, превышающей наибольшую резонансную.  [11]

В системе СГСМ за единицу индуктивности принимается 1 сантиметр, так как размерность индуктивности контура в этой системе единиц оказывается равной размерности длины.  [12]

Из сравнения (98.1) с (93.1) видно, что размерность Li та же, что и размерность индуктивности, и поэтому взаимная индуктивность измеряется в тех же единицах, что и индуктивность.  [13]

Из сравнения (110.1) с (105.1) видно, что размерность L12 — та же, что и размерность индуктивности, и поэтому коэффициент взаимной индукции измеряется в тех же единицах, что и индуктивность.  [15]

Страницы:      1    2

Катушка индуктивности | Виды катушек, практические опыты

Что такое катушка индуктивности

Что вы себе представляете под словом “катушка” ? Ну… это, наверное, какая-нибудь “фиговинка”, на которой намотаны нитки, леска, веревка, да что угодно! Катушка индуктивности представляет из себя точь-в-точь то же самое, но вместо нитки, лески или чего-нибудь еще там намотана обыкновенная медная проволока в изоляции.

Изоляция может быть из бесцветного лака, из ПВХ-изоляции и даже из матерчатой. Тут фишка такая, что хоть и провода в катушке индуктивности очень плотно прилегают к друг другу, они все равно изолированы друг от друга. Если будете мотать катушки индуктивности своими руками, ни в коем случае не вздумайте брать обычный медный голый провод!

Индуктивность

Любая катушка индуктивности обладает индуктивностью. Индуктивность катушки измеряется в Генри (Гн), обозначается буковкой L и замеряется с помощью LC – метра.

Что такое индуктивность?  Если через  провод пропустить электрический ток, то он вокруг себя создаст магнитное поле:

где

В – магнитное поле, Вб

I – сила тока, А

А давайте возьмем и намотаем в спиральку этот провод и подадим на его концы напряжение

И у нас получится вот такая картина с магнитными силовыми линиями:

Грубо говоря, чем больше линий магнитного поля пересекут площадь этого соленоида, в нашем случае площадь цилиндра, тем больше будет магнитный поток (Ф). Так как через катушку течет электрический ток, значит, через нее проходит ток с  Силой тока (I), а коэффициент между магнитным потоком и силой тока называется индуктивностью и вычисляется по формуле:

С научной же точки зрения, индуктивность – это способность извлекать энергию из источника электрического тока и сохранять ее в виде магнитного поля. Если ток в катушке увеличивается, магнитное поле вокруг катушки расширяется, а если ток уменьшается , то магнитное поле сжимается.

Самоиндукция

Катушка индуктивности обладает также очень интересным свойством. При подаче на катушку постоянного напряжения, в катушке возникает на короткий промежуток времени противоположное напряжение.

Это противоположное напряжение называется ЭДС самоиндукции. Эта ЭДС зависит от значения индуктивности катушки. Поэтому, в момент подачи напряжения на катушку сила тока в течение долей секунд плавно меняет свое значение от 0 до некоторого значения, потому что напряжение, в момент подачи электрического тока, также меняет свое значение от ноля и до установившегося значения. Согласно Закону Ома:

где

I – сила тока в катушке , А 

U – напряжение в катушке, В 

 R – сопротивление катушки, Ом

Как мы видим по формуле, напряжение меняется от нуля и до напряжения, подаваемого в катушку, следовательно и ток тоже будет меняться от нуля и до какого то значения. Сопротивление катушки для постоянного тока также постоянное.

[quads id=1]

И второй феномен в катушке индуктивности заключается в том, что если мы разомкнем цепь катушка индуктивности – источник тока, то у нас ЭДС самоиндукции будет суммироваться к напряжению, которое мы уже подали на катушку.

То есть как только мы разрываем цепь, на катушке напряжение в этот момент может быть  в разы больше, чем было до размыкания  цепи, а сила тока в цепи катушки будет тихонько падать, так как ЭДС самоиндукции будет поддерживать убывающее напряжение.

Сделаем первые выводы о работе катушки индуктивности при подаче на нее постоянного тока. При подаче на катушку электрического тока, сила тока будет плавно увеличиваться, а при снятии электрического тока с катушки, сила тока будет плавно убывать до нуля. Короче говоря, сила тока в катушке мгновенно измениться не может.

Типы катушек индуктивности

Катушки индуктивности делятся в основном на два класса: с магнитным и  немагнитным сердечником. Снизу  на фото катушка с немагнитным сердечником.

Но где у нее сердечник? Воздух – это немагнитный сердечник :-).  Такие катушки также могут быть намотаны на какой-нибудь цилиндрической бумажной трубочке. Индуктивность катушек с немагнитным  сердечником используется, когда индуктивность не превышает 5 миллигенри.

А вот катушки индуктивности с сердечником:

В основном используют сердечники из феррита и железных пластин. Сердечники повышают индуктивность катушек в разы. Сердечники в виде кольца (тороидальные) позволяют получить большую индуктивность, нежели просто сердечники из цилиндра.

Для катушек средней индуктивности используются ферритовые сердечники:

Катушки с большой индуктивностью делают как трансформатор с железным сердечником, но с одной обмоткой, в отличие от трансформатора.

Дроссель

Также есть особый вид катушек индуктивностей. Это так называемые дроссели. Дроссель – это катушка индуктивности, задача которой состоит в том, чтобы создать в цепи большое сопротивление для переменного тока, чтобы подавить токи высоких частот.

Постоянный ток через дроссель проходит без проблем. Почему это происходит, можете прочитать в этой статье. Обычно дроссели включаются в цепях питания усилительных устройств. Дроссели предназначены для защиты источников питания от попадания в них высокочастотных сигналов (ВЧ-сигналов). На низких частотах (НЧ) они используются в фильтрах цепей питания и обычно имеют металлические или ферритовые сердечники. Ниже на фото силовые дроссели:

Также существует еще один особый вид дросселей – это сдвоенный дроссель. Он представляет из себя две встречно намотанных катушки индуктивности. За счет встречной намотки и взаимной индукции он более эффективен. Сдвоенные дроссели получили широкое распространение в качестве входных фильтров блоков питания, а также в звуковой технике.

Что влияет на индуктивность?

От каких факторов зависит индуктивность катушки? Давайте проведем несколько опытов.  Я намотал катушку с немагнитным сердечником. Ее индуктивность настолько мала, что LC – метр мне показывает ноль.

Имеется ферритовый сердечник

Начинаю вводить катушку в сердечник на самый край

LC-метр  показывает 21 микрогенри.

Ввожу катушку на середину феррита

35 микрогенри. Уже лучше.

Продолжаю вводить катушку на правый край феррита

20 микрогенри. Делаем вывод, самая большая индуктивность на цилиндрическом феррите возникает в его середине.  Поэтому, если будете мотать на цилиндрике, старайтесь мотать в середине феррита. Это свойство используется для плавного изменения индуктивности  в переменных катушках индуктивности:

где

1 – это каркас катушки

2 – это витки катушки

3 – сердечник, у которого сверху пазик под маленькую отвертку. Вкручивая или выкручивая сердечник, мы тем самым изменяем индуктивность катушки.

Экспериментируем дальше. Давайте попробуем сжимать и разжимать витки катушки. Для начала ставим ее в середину и начинаем сжимать витки

Индуктивность стала почти 50 микрогенри!

А давайте-ка попробуем расправим витки по всему ферриту

13 микрогенри. Делаем вывод: для максимальной индуктивности мотать катушку надо “виток к витку”.

Убавим витки катушки в два раза. Было 24 витка, стало 12.

Совсем маленькая индуктивность. Убавил количество витков в 2 раза, индуктивность уменьшилась в 10 раз.  Вывод: чем меньше количество витков – тем меньше индуктивность и наоборот. Индуктивность меняется не прямолинейно виткам.

[quads id=1]

Давайте поэкспериментируем с ферритовым кольцом.

Замеряем индуктивность

15 микрогенри

Отдалим витки катушки друг от друга

Замеряем снова

Хм, также 15 микрогенри. Делаем вывод: расстояние от витка до витка  не играет никакой роли в катушке индуктивности тороидального исполнения.

Мотнем побольше витков. Было 3 витка, стало 9.

Замеряем

Офигеть! Увеличил количество витков  в 3 раза, а индуктивность увеличилась в 12 раз! Вывод: индуктивность меняется не прямолинейно виткам.

Если верить формулам для расчета индуктивностей, индуктивность зависит от “витков в квадрате”. Эти формулы я здесь выкладывать не буду, потому как не вижу надобности. Скажу только, что индуктивность зависит еще от таких параметров, как сердечник (из какого материала он сделан), площадь поперечного сечения сердечника, длина катушки.

Обозначение на схемах

Последовательное и параллельное соединение катушек индуктивности

При последовательном соединении индуктивностей, их общая индуктивность будет равняться сумме индуктивностей.

А при параллельном соединении получаем вот так:

При соединении индуктивностей должно выполняться правило, чтобы они были пространственно разнесены на плате. Это связано с тем, что при близком расположении друг друга их магнитные поля будут влиять с друг другом, и поэтому показания индуктивностей будут неверны. Не ставьте на одну железную ось две и более тороидальных катушек.  Это может привести к неправильным показаниям общей индуктивности.

Резюме

Катушка индуктивности играет в электронике очень большую роль, особенно в приемопередающей аппаратуре. На катушках индуктивности строятся также различные фильтры для электронной радиоаппаратуры, а в электротехнике ее используют также в качестве ограничителя скачка силы тока.

Ребята из Паяльника забабахали очень неплохой видос про катушку индуктивности. Советую посмотреть в обязательном порядке:

Измерение емкости и индуктивности с помощью осциллографа и функционального генератора

В большинстве лабораторий имеется достаточный запас цифровых мультиметров для измерения сопротивления постоянному току, но когда речь идет об измерении индуктивности, емкости и импеданса, это не всегда легко найти измеритель LCR.

Счетчики

LCR работают, подавая на устройство напряжение переменного тока. при испытании, и измеряя результирующий ток, как по амплитуде, так и по фаза относительно сигнала переменного напряжения. Емкостный импеданс будет иметь форма волны тока, которая опережает форму волны напряжения.Индуктивный импеданс будет имеют форму волны тока, которая отстает от формы волны напряжения. К счастью, если у вас есть осциллограф и генератор функций в вашей лаборатории, вы можете использовать аналогичный метод для измерения многочастотного импеданса с хорошим Результаты. Этот подход также может быть адаптирован для использования в качестве учебной лаборатории. упражнение.

Рисунок 1. Импеданс смоделирован как конденсатор или индуктор с эквивалентным последовательным сопротивлением.

Что такое импеданс?

Импеданс — это полное сопротивление току в цепь переменного тока.Он состоит из сопротивления (реального) и реактивного сопротивления. (мнимый) и обычно представляется в сложных обозначениях как Z = R + jX , где R — сопротивление, а X — реактивное сопротивление.

Реальные компоненты состоят из проводов, соединений, проводники и диэлектрические материалы. Эти элементы вместе составляют характеристики импеданса компонента, и это полное сопротивление изменяется в зависимости от частота тестового сигнала и уровень напряжения, наличие напряжения смещения постоянного тока или текущие и окружающие факторы, такие как рабочие температуры или высота.Из этих потенциальных влияний частота тестового сигнала часто оказывается определяющей. наиболее значимый фактор.

В отличие от идеальных компонентов, настоящие компоненты не являются чисто индуктивные или емкостные. Все компоненты имеют последовательное сопротивление, которое Параметр R в его импедансе. Но у них также есть несколько участников реактивное сопротивление. Например, конденсатор имеет последовательную индуктивность, которая становится больше проявляется на высоких частотах. Когда мы измеряем реальный конденсатор, серия индуктивность (ESL) будет влиять на показания емкости, но мы не сможем измерять его как отдельный, самостоятельный компонент.

Методы измерения импеданса

Метод I-V, описанный в этом примечании по применению, просто один из многих методов измерения импеданса. Другие включают мостовой метод. и резонансный метод.

Метод I-V использует значение напряжения и тока на тестируемое устройство (DUT) для расчета неизвестного импеданса, Z _x . Текущий измеряется путем измерения падения напряжения на прецизионном резисторе последовательно с тестируемым устройством, как показано на рисунке 2.Уравнение 1 показывает, как можно использовать схему. найти Z _x . Уравнение 1:

Теоретическая точность

В этом документе мы будем использовать Tektronix AFG2021. произвольный / функциональный генератор и осциллограф Tektronix серии MDO4000 для выполнения измерение. Полоса пропускания AFG2021 в 20 МГц хорошо подходит для этого. измерение. Точность усиления постоянного тока MDO4000 составляет 2% при настройке 1 мВ / дел. 1,5% при других вертикальных настройках. Как вы можете видеть в уравнении 1, Точность измерения напряжения осциллографом является наиболее важным фактором общая точность теста.

На основании уравнения 1 теоретическая точность этого метод измерения должен составлять около 4% при настройке MDO4000 1 мВ / дел и 3% при других настройках.

Так как частота дискретизации осциллографа очень велика. выше, чем частота стимулов, используемых в этих тестах, ошибка вклад фазовых измерений будет незначительным.

Рисунок 3. Испытательная установка для оценка конденсатора, как в Примере 1.

Тестовый пример

В следующих двух примерах представлены конденсатор / индуктор / Измерение ESR с помощью осциллографа и функционального генератора.

Использованное оборудование:

• AFG2021 Генератор произвольных функций / функций
Осциллограф
• MDO4104C
• А 1 кОм прецизионный резистор
• Подлежащие испытаниям конденсаторы и катушки индуктивности
• Два пробника напряжения Tektronix TPP1000

Для этого применения большинство осциллографов и функций генераторы дадут приемлемые результаты, так как тестовые частоты ниже 100 кГц. Однако мы воспользуемся статистикой измерений на MDO4000. Серии в этом примере.

Рисунок 4. Осциллограммы напряжения и измерения, сделанные в узлах A1 и A2.

Пример 1: керамический конденсатор 10 мкФ

Установите испытательную схему, как показано на рисунке 3. Примечание. что R _ESR и C связаны с испытываемым керамическим конденсатором, и что R _fg — это выходное сопротивление 50 Ом. генератор функций.

Установите функциональный генератор на выход 1,9 В. амплитуда, синусоида 100 Гц.Вы можете использовать ручку AFG2021 или клавиатуру для установить напряжение и частоту. Отрегулируйте настройку вертикального масштаба осциллографа, чтобы использовать как можно большую часть дисплея — используя как можно больше диапазон, насколько это возможно, вы улучшите точность своего напряжения измерения.

Используйте осциллограф для проверки узлов A1 и A2. Рисунок 4 показывает результирующую форму волны.

Выберите средний режим сбора данных осциллографа. и установите количество средних значений на 128. Это уменьшит влияние случайных шум по вашим измерениям.Настройте осциллограф на измерение канала 1 частота, фаза между каналом 2 и каналом 1, амплитуда канала 1 и амплитуда канала 2, как показано на рисунке 4. Если ваш осциллограф предлагает статистику измерений, такую ​​как серия MDO4000, запишите средние значения для вашего расчеты. В противном случае запишите самые последние значения.

Из измерительной установки мы знаем:

• Частота стимула, f = 100 Гц
• Прецизионный резистор, Rref = 1 кОм

Из измерений, выполненных на осциллографе и показанных на рисунке 4:

• Амплитуда напряжения, измеренная при A1, В _A1 = 1.929 В
• Амплитуда напряжения, измеренная при A2, В _A2 = 0,310 В
• Разность фаз между напряжением, измеренным в точке A2 относительно A1, θ = -79,95 °

Обратите внимание, что в узле A1 напряжение имеет фазовый угол 0 °, то есть он находится в фазе с выходом функционального генератора. На А2 напряжение равно сдвинуты вперед на фазовый угол θ.

Полное сопротивление тестируемого конденсатора можно найти используя уравнение 1.

Импеданс можно выразить в полярной форме, где величина определяется уравнением 2.

Уравнение 2:

Угол импеданса определяется вычитанием двух углы:

Уравнение 3:

Для теста в нашем примере мы можем использовать уравнение 2 и уравнение 3, чтобы найти величину и угол импеданса конденсатор тестируемый:

Теперь мы можем преобразовать импеданс в прямоугольную форму. найти сопротивление и емкость.

Используя приведенные выше уравнения, мы можем решить для ESR и Емкость ИУ:

Уравнения 4 и 5:

Используя уравнение 4 и уравнение 5, мы можем вычислить ESR и емкость для тестируемого конденсатора:

— пользователем Область применения / FG — пользователем USB VNA — пользователем LCR — пользователем Область применения / FG — пользователем USB VNA — пользователем LCR Частота емкость (мкФ) емкость (мкФ) емкость (мкФ) СОЭ (Ом) СОЭ (Ом) СОЭ (Ом) 10 Гц 10.3 10,4 НЕТ 28,3 32,8 НЕТ 30 Гц 10,1 10,4 НЕТ 9,1 7,8 НЕТ 100 Гц 9.8 10,3 10,22 2,4 3,2 2,3 300 Гц 9,8 10,1 НЕТ 0,7 1,1 НЕТ 1 кГц 9.7 9,8 9,96 0,3 0,3 0,21 Таблица 1. Сравнительная таблица примера 1. LCR в руководстве указано, что точность составляет 0,05%, а в руководстве по USB VNA указано, что точность измерения составляет 0,05%. 2% точность.

В таблице 1 сравниваются результаты, полученные с помощью осциллографа. и генератор функций для результатов, достигаемых с помощью недорогого ВАЦ и традиционный измеритель LCR.Измеритель LCR, используемый в этом случае, поддерживает только тест частоты 100 Гц и 1 кГц, которые являются общими частотами тестирования компонентов. Вы заметите, что эти три метода достаточно хорошо коррелируют.

Значения пассивных компонентов указаны с особым частоту, и измерители LCR часто имеют более одной тестовой частоты для эта причина. В таблице 1 показаны результаты с использованием осциллографа / функции. комбинация генераторов на пяти разных частотах. Вы можете увидеть эффект паразитная индуктивность в испытательной цепи при увеличении испытательной частоты — измеренная емкость падает с увеличением испытательной частоты.См. Раздел о «Диапазон измерения» для получения дополнительной информации о тестовых частотах.

Для достижения наилучших результатов вам необходимо сохранить значение прецизионного резистора (R _ref ) достаточно низкий, чтобы дать значительную волну напряжения в узле A2. Резистор также должно быть больше 50 Ом, иначе выходное сопротивление функционального генератора будет учитываться при измерении.

Рисунок 5. Испытательная установка для оценка катушки индуктивности как в Примере 2.

Пример 2: индуктор 10 мГн

Схема и процедура проверки практически идентичны те, которые использовались для проверки конденсатора в Примере 1.

Используйте функциональный генератор для вывода 1,9 В. амплитуда синусоидальной волны 10 кГц. Сигнал подается на опорный резистор и испытуемый индуктор.

Используйте осциллограф для проверки узлов A1 и A2. Рисунок 6 показаны две результирующие формы волны.

Рисунок 6. Осциллограммы напряжения и измерения взяты в узлах A1 и A2.

Выберите средний режим сбора данных осциллографа. и установите количество средних значений на 128. Это уменьшит влияние случайных шум по вашим измерениям.Настройте осциллограф на измерение канала 1 частота, фаза между каналом 2 и каналом 1, амплитуда канала 1 и амплитуда канала 2, как показано на рисунке 6. Если ваш осциллограф предлагает статистику измерений, такую ​​как серия MDO4000, запишите средние значения для вашего расчеты. В противном случае запишите самые последние значения.

Из измерительной установки мы знаем:

• Частота стимула, f = 10 кГц
• Прецизионный резистор, R _ref = 1 кОм

Из измерений, выполненных на осциллографе и показанных на рисунке 6:

Амплитуда напряжения, измеренная при A1, В _A1 = 1.832 В

Амплитуда напряжения, измеренная при A2, В _A2 = 0,952 В

Разность фаз между напряжением измеряется в точке A2 относительно A1, θ = 56,03 °

Обратите внимание, что в узле A1 напряжение имеет фазовый угол 0 °, то есть он находится в фазе с выходом функционального генератора. На А2 напряжение равно сдвинуты вперед на фазовый угол θ.

Мы можем использовать те же уравнения для расчета импеданса ИУ, которое мы использовали для измерения конденсатора в примере 1. Импеданс может быть выраженным в полярной форме, где величина и угол импеданса равны предоставлено:

Теперь мы можем преобразовать в прямоугольную форму сопротивление, чтобы найти сопротивление и индуктивность

Используя приведенные выше уравнения, мы можем решить для ESR и Индуктивность ИУ:

Уравнения 6 и 7:

Используя уравнения 6 и 7, мы можем рассчитать СОЭ и индуктивность испытуемой катушки индуктивности:

	— пользователем Область применения / FG	по USB ВНА	по LCR	— пользователем Область применения / FG	по USB ВНА	по LCR
Частота	индуктивность (мГн)	индуктивность (мГн)	индуктивность (мГн)	СОЭ (Ом)	СОЭ (Ом)	СОЭ (Ом)
10 Гц	12	10.3	НЕТ	20,5	20,8	НЕТ
100 Гц	10,1	10,4	10,31	20,6	20,9	20,9
1 кГц	10,3	10.2	10,1	20,5	22	21,5
10 кГц	10	9,8	9,76	29,8	31,5	29,4

Таблица 2. Сравнительная таблица примера 2.

Опять же, в таблице 2 сравниваются достигнутые результаты с осциллографа и генератора функций для результатов, достигаемых с помощью недорогого ВАЦ и традиционный измеритель LCR.Эти три метода хорошо коррелируют.

Таблица 2 также показывает результаты, полученные с помощью осциллографа / комбинация функционального генератора на четырех различных частотах. См. Раздел в разделе «Диапазон измерений» для получения дополнительной информации о тестовых частотах.

Еще раз, вам, возможно, придется поэкспериментировать со стоимостью _рэнд , чтобы получить лучшее Результаты.

Рисунок 7. Емкость / частота коробка.	Рисунок 8.Индуктивность / частота коробка.

Диапазон измерения

Существуют практические ограничения на частоту стимула и значения конденсатора или индуктора ИУ для этого метода измерения импеданса.

На рисунке 7 показан блок емкости / частоты. Если емкость значение и частота тестирования указаны в рамке, тогда вы сможете измерить это. В заштрихованной области точность измерения будет около 3%, а за пределами заштрихованной области точность падает примерно до 5%.Эти неопределенности предположим, что вы позаботились о том, чтобы использовать весь экран осциллографа, усреднено 128 периодов сигналов и использовано среднее значение амплитуды и фазы для выполнения расчетов.

Аналогичный блок индуктивности / частоты показан на рисунке. 8 для испытания индуктора.

Заключение

Если у вас нет измерителя LCR в вашей лаборатории, или вы хочу продемонстрировать поведение конденсаторов и катушек индуктивности при синусоидальном стимула, осциллографа и генератора функций могут помочь вам сделать простой, прозрачное измерение импеданса.Вы можете рассчитывать на емкость и индуктивность значения с погрешностью 3% -5%. Чтобы воспользоваться этим методом, вы нужен только функциональный генератор с хорошим диапазоном частот и амплитуд, осциллограф с хорошими характеристиками и функциями, которые мы обсуждали, несколько прецизионные резисторы, а также калькулятор или электронную таблицу.

[Решено] Индуктивность измеряется с помощью

.

Вопрос:

Бесплатная практика с тестами из тестовой тетради

Опции:

1. Мост Кельвина


2. Мост Вина


3. Мост Шеринга


4. Мост Максвелла

Правильный ответ:

Вариант 4 (Решение ниже)

Этот вопрос ранее задавали в

Официальный документ GATE EE 2021

Решение:

Скачать вопрос с решением PDF ››

Индуктивность может быть измерена мостом Максвелла

Тип моста	Название моста	Используется для измерения	Важно
Мосты постоянного тока	Мост Уитстона	Среднее сопротивление
	Мост Кори Фостера	Среднее сопротивление
	Двойной мост Кельвина	Очень низкое сопротивление
	Мост мегаом	Высокое сопротивление
	мегомметр	Высокое сопротивление изоляции	Сопротивление кабелей
Мосты переменного тока	Индуктивный мост Максвелла	Индуктивность	Не подходит для измерения Q
	Индуктивно-емкостный мост Максвелла	Индуктивность	Подходит для катушки средней добротности (1
	Hay’s Bridge	Индуктивность	Подходит для катушки с высокой добротностью (Q> 10), самый медленный мост
	Мост Андерсона	Индуктивность	5-точечный мост, точный и самый быстрый мост (Q
	Мост Оуэна	Индуктивность	Используется для измерения катушек с низкой добротностью
	Мост взаимной индуктивности Хевисайда	Взаимная индуктивность
	Модификация Кэмпбелла моста Хевисайд	Взаимная индуктивность
	Мост Де-Саути	Емкость	Подходит для идеального конденсатора
	Мост Шеринга	Емкость	Используется для измерения относительной диэлектрической проницаемости
	Мост Вейна	Емкость и частота	Анализатор гармонических искажений, используемый как режекторный фильтр, используемый в аудио и высокочастотных приложениях

Скачать вопрос с решением PDF ››

Простой метод измерения неизвестных индукторов

Простой метод измерения неизвестных индукторов

Простой и быстрый способ измерить индуктивность неизвестного силового дросселя

(при условии, что у вас есть функциональный генератор и осциллограф).

Рональд Деккер

---

1. Введение

При любой возможности я всегда спасаю (силовые) катушки индуктивности от старых печатных плат и импульсных источников питания. Хороший ассортимент индукторов разного номинала всегда пригодится во время экспериментов, особенно с повышающими преобразователями и т.п. Я уверен, что должна существовать система, с помощью которой производители этих катушек индуктивности маркируют их значением индуктивности, но пока мне не удалось ее обнаружить. На некоторых индукторах напечатаны номера, а другие отмечены цветными точками, что в любом случае является катастрофой, потому что я дальтоник.Чтобы быстро определить значение индуктивности этих катушек индуктивности, я использую простой метод, который, я уверен, заинтересует других разработчиков индукторов. Вам понадобятся функциональный генератор 0–100 кГц с выходом 50 Ом и осциллограф.

2. Пошаговое описание метода

Поскольку большинство людей будет больше интересоваться методом, чем лежащей в его основе теорией, давайте начнем с пошагового описания:

1. Подключите 50-омный выход функционального генератора к осциллографу и выберите синусоидальный сигнал.
2. Установите частоту генератора примерно на 20 кГц.
3. Отрегулируйте выходное напряжение генератора на пиковое значение 1 В.
4. Подключите неизвестную индуктивность параллельно к осциллографу (рис. 2.1). Это уменьшит амплитуду сигнала.
5. Теперь отрегулируйте только частоту генератора так, чтобы амплитуда на осциллографе была ровно половиной от исходного значения (0,5 В пикового значения).

   Я выполняю шаги с 3 по 5 следующим образом: На шаге 3 я сначала устанавливаю вертикальную чувствительность осциллографа на 0.2 В / дел. Затем я регулирую амплитуду генератора сигналов так, чтобы синусоидальная волна точно помещалась между отметками 25% и 75% на экране (рис. 2.1A). Амплитуда сейчас ровно 1 В. Затем я подключаю катушку индуктивности (шаг 4) и увеличиваю вертикальную чувствительность до 0,1 В / дел. На шаге 5 я теперь регулирую частоту так, чтобы синусоидальная волна снова точно попадала между отметками 25% и 75% (рис. 2.1B). Амплитуда синусоиды теперь составляет 0,5 В.

6. Наконец, считайте частоту и рассчитайте индуктивность, исходя из L = 4.57 / ф. С L в Генри и f в Гц. Вы также можете предпочесть L = 4570 / f с L в uH и f в кГц.

Рисунок 2.1 Измерение неизвестных катушек индуктивности.

3. Как это работает и немного теории

Катушка индуктивности в сочетании с внутренним последовательным сопротивлением в генераторе образуют цепь делителя напряжения (рис. 3.1). Без подключенной катушки индуктивности падение напряжения на резисторе 50 Ом незначительно, и осциллограф отображает внутреннее напряжение генератора.При подключенной катушке индуктивности ток через катушку индуктивности вызовет падение напряжения на резисторе 50 Ом, что приведет к падению амплитуды сигнала на экране осциллографа. Ток через катушку индуктивности зависит как от частоты, так и от индуктивности. Для сигналов постоянного тока (0 Гц) индуктор представляет собой короткое замыкание. Для очень высоких частот ток через катушку индуктивности незначителен. Кроме того, для данной частоты, чем выше индуктивность, тем меньше ток.

Рисунок 3.1 Принципиальная схема

Точное соотношение между напряжением внутреннего генератора и напряжением, измеренным осциллографом, может быть рассчитано
с помощью простой теории сетей:
В этой формуле L представляет собой индуктивность, R — сопротивление (50 Ом), а omega — радиальную частоту (= 2 * pi * f с f в Гц).
Теперь вопрос в том, для какой частоты (Vscope / Vgen) = 0,5:
Итак, наконец:
В которой L — индуктивность в Генри, а f — частота в Гц.
Этот метод хорошо работает только для катушек индуктивности с низким последовательным сопротивлением
и индуктивностью в диапазоне, скажем, от 10 до нескольких сотен мкГн.

4. Включая последовательное сопротивление.

Хорошая особенность веб-сайта в том, что люди время от времени вносят очень полезный вклад. Карен Ортон (Великобритания) усовершенствовала предложенный выше метод для индукторов со значительным сопротивлением. Просто сначала измерьте сопротивление постоянным током и используйте его в приведенной ниже формуле. В остальном процедура в точности такая, как описано выше.

Вот математика собственными руками Каренса:

Индуктивность измеряется в AOhm BFarad CHenry DNone класс 10 физика CBSE

Совет: Все электрические единицы обычно представлены в системе международных единиц (система СИ).
Эти единицы СИ эквивалентны некоторым производным единицам, таким как единица сопротивления в производной форме — вольт на единицу ампер, которая может быть эквивалентна ому в системе СИ. Обычно единицы СИ основаны на именах их ученых.

Полный ответ:
Все электрические единицы, используемые для измерения электрического выражения, обычно основаны на системе единиц СИ. Некоторые электрические единицы являются фундаментальными единицами, например, ток. Единица измерения тока — Ампер. Некоторые электрические единицы являются производными от основных единиц, таких как Вольт. Вольт — производная единица измерения разности потенциалов. Некоторые производные единицы эквивалентны имени своего ученого, которое можно назвать единицей СИ. Единица индуктивности — Генри, основанная на имени ученого.
Единица заряда, т.е. кулон всегда выражается в системе СИ.
Единица измерения сопротивления в СИ — Ом.
Так как выражение для закона Ома можно записать как —
\ [R = \ dfrac {V} {I} \]
Так как единица измерения разности потенциалов в системе СИ V — это вольт, а единица измерения тока I — ампер.
Таким образом, единица сопротивления R может быть выражена как —
\ [R = \ dfrac {Volt} {Ampere} \]
Что может быть записано в системе СИ как,
\ [R = Ohm \]
Итак, наконец, единица измерения сопротивления в системе СИ. это Ом.
Единица измерения конденсатора в системе СИ — Фарад.
Так как выражение для емкости можно записать как —
\ [C = \ dfrac {Ch \ arg e} {потенциал \ _difference} \]
\ [C = \ dfrac {q} {V} \]
Поскольку, единица СИ заряда q является кулоновским, а единица измерения разности потенциалов в системе СИ V — вольт.
Таким образом, единица емкости C может быть выражена как —
\ [C = \ dfrac {кулон} {вольт} \]
Это может быть выражено как —
\ [C = Farad \]
Итак, наконец, единица измерения емкости в системе СИ — Фарад.
единица индуктивности в СИ — Генри.
Так как выражение для индуктивности может быть выражено как-
\ [L = \ dfrac {Electric \ _flux} {Current} \]
\ [L = \ dfrac {\ phi} {I} \]
SI Единица измерения электрического потока Единица тока Вебера и СИ — Ампер.
Таким образом, единица собственной индуктивности L может быть выражена как —
\ [L = \ dfrac {Weber} {Ampere} \]
Это может быть выражено как —
\ [L = Henry \]
Итак, наконец, единица индуктивности в СИ — Генри.

Вариант B правильный.

Примечание:
Единицы СИ также могут быть выражены в степени 10, для этой цели некоторые термины определены вместе с такими единицами, как мА, представляют миллиампер. МА представляет собой мегаампер. Мегаампер больше милиампера. Подобно nH представляет собой наногенри.Так много других терминов используется с единицами, чтобы упоминать их в большем и меньшем количестве.

Измерения емкости и индуктивности с помощью цифровых мультиметров в формате PXI

Конденсаторы

Конденсатор — это электронный компонент, способный накапливать энергию в виде заряда. Каждый конденсатор состоит из двух пластин из проводящего материала, разделенных диэлектриком, которым может быть воздух, бумага, пластик, оксид или любой другой изолятор. Диэлектрическая постоянная, или K, изолятора представляет его способность накапливать заряд.В таблице 2 показаны значения K для различных диэлектрических материалов.

Диэлектрик	Диэлектрическая проницаемость ( K )
Вакуум	1
Воздух	1.0001
Тефлон	2,0
Полипропилен	2.1
Полистирол	2,5
Поликарбонат	2,9
Полиэстер	3,2
FR-4	3,8–5,0
Стекло	4,0–8,5
Слюда	6.5–8,7
Керамика	От 6 до нескольких тысяч
Оксид алюминия	7
Оксид тантала	11

Таблица 2 . Значения K для различных диэлектрических материалов

Электрические свойства изоляторов изменяются в зависимости от таких факторов, как температура, частота, напряжение и влажность.Эта вариативность и механическая конструкция конденсатора создают далеко не идеальное устройство. Лучшее представление реальных конденсаторов показано в эквивалентной модели на рисунке 4, которая может помочь вам понять различные паразитные элементы, присутствующие в реальном компоненте. Эти паразитные элементы влияют на импеданс конденсатора на разных испытательных частотах.

Рисунок 4 . Модель различных паразитных элементов в реальном компоненте, которые могут повлиять на конденсатор

Параллельное сопротивление, R _p , обычно имеет большое значение, и его влияние существенно только при измерении конденсаторов с малыми значениями.Эквивалентное последовательное сопротивление R _s , хотя и небольшое значение, важно для конденсаторов с большими номиналами, где полное сопротивление мало по сравнению с R _s и где рассеивается большая мощность. Последовательная индуктивность, L _s , представляет собой спад общей индуктивности и емкости на более высоких частотах. На низких частотах емкость зависит от частоты и уровня тестового сигнала из-за изменений диэлектрических свойств. На рисунке 5 показан алюминиевый электролитический конденсатор емкостью 2,2 мкФ, 100 В, измеренный на различных частотах.Ошибка относится к измерению с использованием испытательного сигнала переменного тока 1 В _{среднеквадратичное значение} переменного тока на частоте 1 кГц.

Рисунок 5 . Алюминиевый электролитический конденсатор на 100 В, 2,2 мкФ, измерения на разных частотах

Эти факторы приводят к тому, что конденсаторы имеют разные значения при различных условиях температуры, частоты и уровня сигнала.

Катушки индуктивности

Катушка индуктивности — это электронный компонент, способный накапливать энергию в виде тока.Каждый индуктор состоит из проводящей катушки, которую можно обернуть без сердечника или вокруг магнитного материала. Проницаемость материала сердечника является мерой напряженности магнитного поля, которое может быть индуцировано в нем. Электрические свойства сердечников изменяются в зависимости от таких факторов, как температура, частота, ток и т. Д. Эта вариативность и механическая конструкция индуктора создают далеко не идеальное устройство. Лучшее представление реальных катушек индуктивности показано в эквивалентной модели на рисунке 6, которая может помочь вам понять различные паразитные элементы, присутствующие в реальном компоненте.Эти паразитные элементы влияют на импеданс катушки индуктивности на разных испытательных частотах.

Рисунок 6 . Модель различных паразитных элементов в реальном компоненте, которые могут повлиять на индуктор

Последовательное сопротивление R _s представляет собой резистивные потери в проводнике. Параллельная емкость, C _p , является эквивалентным емкостным эффектом между витками катушки, а параллельное сопротивление, R _p , представляет собой сумму всех потерь, связанных с материалом сердечника.Воздушным сердечникам требуется намного больше витков в катушке для достижения высоких значений индуктивности. Таким образом, воздушные сердечники часто непрактичны для применения из-за их большого размера и веса. Кроме того, воздушные сердечники обычно имеют большую емкость обмотки и последовательное сопротивление с высоким значением индуктивности. Не все паразиты влияют на стоимость индуктора, но некоторые паразиты более заметны, чем другие, в зависимости от конструкции катушки, геометрии индуктора, калибра провода и характеристик сердечника.Значение индуктивности и величина каждого типа паразита по отношению к другим типам паразита определяют частотную характеристику. Геометрия некоторых компонентов может увеличить чувствительность компонентов к внешним факторам, и эта повышенная чувствительность может повлиять на стоимость индуктора. Индукторы с открытым магнитным потоком более чувствительны к металлическим материалам, которые находятся в непосредственной близости, потому что такие материалы изменяют магнитное поле. Тороидальные индукторы удерживают поток внутри сердечника и менее чувствительны к внешним проводникам в непосредственной близости.На Рисунке 7 показан поток, связанный с этими типами катушек индуктивности:

Рисунок 7 . Типы индукционного потока

На рисунке 8 индуктор с воздушным сердечником 5 мГн измерен на разных частотах. Ошибка относится к измерению с тестовым сигналом 1 В _rms при 1 кГц. Этот тип индуктора имеет высокую емкость обмотки из-за размера и количества витков, необходимых для его конструкции. Следовательно, этот тип индуктивности измеряет, как если бы индуктивность сильно зависела от частоты.

Рисунок 8 . Индуктор с воздушным сердечником, 5 мГн, измерения на разных частотах

Ожидается, что некоторые ферритовые сердечники сильно различаются в зависимости от уровня тестового сигнала. На рисунке 9 индуктор с ферритовым сердечником емкостью 100 мкГн испытывается при различных уровнях тестового сигнала. Ошибка относится к измерению с тестовым сигналом 1 мА _rms при 1 кГц.

Рисунок 9 . Индуктор с ферритовым сердечником 100 мкГн протестирован при различных уровнях тестового сигнала

Все эти факторы могут сочетаться и приводить к тому, что индукторы имеют разные значения при различных условиях температуры, частоты и уровня сигнала.

Тестовый сигнал

Цифровые мультиметры

PXIe-4082 используют источник переменного тока в качестве возбуждения для измерений емкости и индуктивности. Форма волны тока представляет собой очень стабильную прямоугольную волну с ограничениями по гармоникам. Метод измерения извлекает многотоновую информацию, содержащуюся в тестовом сигнале, для определения емкости или индуктивности тестируемого устройства. Частота и уровень тестового сигнала и извлеченных из него тонов показаны в таблицах 3 и 4:

Емкость
Диапазон	Фундаментальный		Третья гармоника		Эффективный тестовый сигнал
	Частота	Текущий	Частота	Текущий	Частота	Текущий
300 пФ	1 кГц	0.5 мкА	3 кГц	0,16 мкА	3 кГц	0,16 мкА
1 нФ	1 кГц	1 мкА	3 кГц	0,33 мкА	3 кГц	0,33 мкА
10 нФ
100 нФ	1 кГц	10 мкА	3 кГц	3.3 мкА	3 кГц	3,3 мкА
1 мкФ	1 кГц	100 мкА	3 кГц	33 мкА	1 кГц	100 мкА
10 мкФ	1 кГц	1 мА	3 кГц	330 мкА	1 кГц	1 мА
100 мкФ	91 Гц	1 мА	273 Гц	330 мкА	91 Гц	1 мА
1000 мкФ
10,000 мкФ

Индуктивность
Диапазон	Фундаментальный		Третья гармоника		Эффективный тестовый сигнал
	Частота	Текущий	Частота	Текущий	Частота	Текущий
10 мкГн
100 мкГн
1 мГн	1 кГц	1 мА	3 кГц	330 мкА	3 кГц	330 мкА
10 мГн	1 кГц	10 мкА	3 кГц	3.3 мкА	3 кГц	3,3 мкА
100 мГн	91 Гц	100 мкА	273 Гц	33 мкА	273 Гц	33 мкА
1 выс.	91 Гц	10 мкА	273 Гц	3,3 мкА	273 Гц	3.3 мкА
5 выс.	91 Гц	1 мкА	273 Гц	0,33 мкА	273 Гц	0,33 мкА

Таблицы 3 и 4 . Частота и уровень тестового сигнала и извлеченных из него тонов

Дигитайзер измеряет полное сопротивление ИУ на двух частотах (тонах). По этим двум измерениям рассчитываются потери (входные, кабельные и DUT).Используя рассчитанные потери, программа вычисляет емкость или индуктивность на одной из двух частот (эффективная частота). Эффективный тестовый сигнал включен в качестве эталона. Это сигнал, который дает сопоставимое значение емкости или индуктивности при измерении однотональным методом измерения. Из-за паразитов и материалов, используемых в конструкции реальных компонентов, измеренное значение емкости или индуктивности может отличаться от одного прибора к другому. При измерении конденсаторов с лучшими диэлектрическими свойствами вы наблюдаете гораздо меньшую разницу в показаниях между различными приборами.Это наблюдение также применимо к катушкам индуктивности с лучшими магнитными свойствами. В таблице 5 приведены примеры диэлектриков с хорошими и плохими частотными характеристиками.

Диэлектрики с хорошими частотными характеристиками	Диэлектрики с низкими частотными характеристиками
Тефлон Слюда Полипропилен Поликарбонат Керамический COG	Оксид тантала Оксид алюминия Керамика Y5U

Таблица 5 .Примеры диэлектриков с хорошими и плохими частотными характеристиками

Из-за величины необходимого тока намагничивания вы можете увидеть увеличение чувствительности к изменениям частоты и другим факторам зависимости в индукторах с сердечниками большего размера, например, используемых в трансформаторах и силовых индукторах.

Температурные эффекты

Температура может иметь большое влияние на импеданс ИУ. Обычно конденсаторы имеют большие температурные коэффициенты (колебания от 5 до 80 процентов во всем диапазоне температур, в зависимости от используемого конденсатора), за исключением керамических конденсаторов COG, которые могут иметь только 0.003% / ° C отклонение. Индукторы, особенно с сердечником, отличным от воздуха, могут сильно изменяться в зависимости от температуры. Дрейф температуры окружающей среды и температуры тестируемого устройства (например, из-за обращения) может привести к ошибке в измерениях. Контролируйте изменения температуры окружающей среды, чтобы уменьшить количество ошибок.

Кабельная проводка

Чтобы уменьшить вариации паразитных параметров системы, NI рекомендует использовать коаксиальный кабель или экранированные витые пары с экраном, используемым в качестве пути возврата тока и подключенным к входу LO цифрового мультиметра. Эта конфигурация делает компенсацию ОТКРЫТО / КОРОТКОЕ более практичной и помогает уменьшить наводку шума.Для ручного измерения деталей для поверхностного монтажа можно использовать пинцет. Цифровой мультиметр PXIe-4082 может компенсировать импеданс, создаваемый испытательными приборами. Для получения дополнительной информации см. Ниже раздел «Компенсация при открытии / коротком замыкании». Уменьшите механические отклонения (например, перемещение или изгиб кабелей или изменение крепления) между двумя последовательными измерениями, чтобы сохранить повторяемость. Используйте высококачественный кабель, например Belden 83317, доступный на сайте belden.com. NI рекомендует кабели с тефлоновой, полипропиленовой или полиэтиленовой изоляцией.Для получения дополнительной информации о требованиях к кабелям см. Межкомпонентные соединения и кабели. Очень хорошие характеристики были достигнуты при использовании этого кабеля длиной до 25 футов при измерениях емкости и индуктивности за счет выполнения компенсации ОТКРЫТО / КОРОТКОЕ перед измерением.

Шумоподавитель

Чтобы свести к минимуму шумоподавление, держите кабели, установку и тестируемое устройство вдали от любых источников электромагнитного шума, таких как двигатели, трансформаторы и электронно-лучевые трубки (ЭЛТ). Избегайте источников частот около 91 Гц, 1 кГц, 10 кГц и соответствующих гармоник, потому что эти частоты являются частотами токов возбуждения, используемых NI 4082.Используйте экранированный кабель (рекомендуется использовать разъемы BNC и коаксиальный кабель) для прокладки кабелей и для подключения внешнего проводника к входу LO цифрового мультиметра.

Индуктивность — определение — глоссарий

Основной характеристикой катушки является индуктивность, которая возникает из-за последовательного соединения множества отдельных проводников. Провод намотан на несущий сердечник. Если сердечник выполнен из ферромагнитного материала, то катушки — из железного сердечника.Катушка с воздушным сердечником не имеет намагничивающегося сердечника. Можно выделить два основных типа катушек: цилиндрическая катушка, открытая с обеих сторон, и замкнутая кольцевая катушка.

Катушка обладает омическим сопротивлением, которое зависит от материала лидера, длины лидера и его поперечного сечения. Когда электрический ток течет через катушку, она создает магнитное поле. Катушка цилиндра, подключенная к постоянному напряжению, в конечном итоге работает как стержневой магнит. Магнитное поле зависит от ядерного материала катушки, количества витков и геометрии катушки.Все размеры вместе образуют индуктивность катушки.

Переменный ток уменьшает магнитное поле в катушке. Катушка забирает энергию, накапливает ее в магнитном поле и снова доставляет, толкая энергию вперед и назад, без какого-либо эффекта. Эта энергия называется реактивной энергией и реактивным сопротивлением сопротивления. Если сердечник сделан из железа, то в результате продолжающегося перемагничивания возникают вихревые токи. Это нагревает ядро, что приводит к дальнейшей потере энергии. Катушка с потерями в стали потребляет больше тока, чем рассчитывается по реактивному сопротивлению.Сопротивление потерь в стали соответствует действующему сопротивлению в эквивалентной электрической цепи, которая включается параллельно реактивному сопротивлению.

На индуктивное реактивное сопротивление влияет частота переменного напряжения и его индуктивность. Индуктивное реактивное сопротивление тем больше, чем больше индуктивность катушки и чем выше частота приложенного переменного напряжения. Символ индуктивности — «L», а единица измерения обозначена как «H» в честь физика Джозефа Генри. Катушка имеет индуктивность 1 Генри, если сила тока изменяется равномерно за 1 секунду на 1 ампер, а напряжение индуцируется 1 В.

Можно легко измерить индуктивность с помощью точного измерителя LCR.

«Назад

для измерения индуктивности

На протяжении многих лет я пытался измерить индуктивность полезным, точным и осмысленным способом.
An индуктор как практический элемент схемы с использованием реальных физических материалов внезапно принимает характер, личность и поведение, которое сложно и запутанно. Настоящая мотивация для этой статьи это накопившееся за многие годы разочарование спецификация индуктивностей в различных радиолюбительских журналах, особенно отличные статьи ARRL в QST и вездесущий Справочник ARRL.Меня всегда очень злит, когда индуктор указан как столько витков на сердечнике Amidon blah-blah, или в старину мля типа катушки Миллера. Эти устройства редко встречались доступны в розницу в Австралии, а если и были, то очень чрезмерно завышены в цене, и никогда не будет имеется в наличии. Авторы статей практически никогда не указывали конструкция индуктивности …. Генри, только когда X включает Амидон мля ядро! Этот недосмотр помешал стартовому множества небольших проектов.Я отказываюсь платить глупые цены, требуемые за фирменные ядра!

Настоящие индукторы, сделанные из настоящих материалов демонстрируют сильную зависимость от желаемой частоты срабатывания. В очень широкий выбор материалов сердечника из ферритовой или железной пыли, просто добавляет путаницы. Тогда существует сейчас, широкая доступность различных немаркированных и неуказанных ферритов сердечники доступны как излишки. Ядра имеют в основном четыре различных операционные типы.

1. Годен только для подавления радиочастот (до 1 МГц, если вам повезет)
2. Хорошо до примерно 4 МГц
3. Хорошо примерно до 30 МГц
4. Хорошо примерно до 100 МГц

типа 1 можно найти во всем современном электронном оборудовании.Никогда не пытайтесь использовать один из них в качестве основы индуктора, хотя они могут все еще демонстрируют полезные свойства на частоте 1,8 МГц.
тип 2 обычно встречается в импульсных источниках питания в больших количествах.
тип 3 — это то, что действительно нужно радиолюбителям, и они относительно редки. , что индуктор с воздушным сердечником работает лучше.

на проблема здесь — катушка Q. Катушка индуктивности с ферритовым сердечником неизменно имеет меньше Q, чем у любой катушки с воздушным сердечником.(note1) Это правда, что ядро ​​ториода по своей природе самозащитный, но катушка с воздушным сердечником изогнута в тор ! Я заметил, что в индийских радиожурналах радиолюбителей их катушки намотаны на пластиковые шайбы! Они получают самозащиту, себя Поддержки и без налога на амидон и выше Q в придачу!

Так вот моя проблема. Мой мусорный ящик был переполнен таинственными катушками и сердечники, извлеченные из давно мертвых потребительских товаров длительного пользования. Кем они были хорош для ?

Я пробовал разные методы, чтобы быстро охарактеризовать таинственная катушка.Мои первые попытки использовали мост Максвелла, очаровательный дизайн, учитывая, что теория первого порядка предполагает, что это не Частота Зависимая. Это практически верно, но только под условия, при которых паразитная емкость пренебрежимо мала и частота измерения ниже 100 кГц. Мост Максвелла также легко Измерьте Q. Интересующие нас индуктивности для радиолюбителей, обычно 100 мкГн. до 0,1 мкГн выходят за пределы полезного диапазона физически реализуемых мосты. Максимальная частота, которая полезна с максвеллом мост составляет около 5 МГц, но нулевой мост кажется только слабо связано с измеряемой индуктивностью!

Другой мой Метод заключался в использовании моего шумового моста.Это быстро обнаруживает максимальная полезная частота таинственного ядра. Метод здесь — намотать несколько бифилярных витков в качестве балуна 4: 1 и измерьте импеданс, когда К балуну подключен резистор 200 Ом. Бесполезное ядро ​​не может преобразуйте это сопротивление в реальное значение 50 Ом + реактивное сопротивление 0 Ом. Если это не 50 Ом и имеет значительную реактивную составляющую, тогда сердечник бесполезен для рч, и особенно бесполезен для сердечников балуна. Однако измерить индуктивность с помощью этого метод, потому что я должен откалибровать реактивную шкалу шума мост, а это утомительная процедура; и я не обязательно верю в моих калибровках!

Коммерческие измерители индуктивности с прямым считыванием сдавайся ниже 100уХ.Профессиональные автоматические мосты LCR другое дело, по крайней мере, можно указать частоту измерения и тогда будьте уверены в результате. Они совершенно выходит за рамки моего бюджета, и они не ходят на фестивали Ham.

Другой метод, который я пробовал с некоторым успехом, — использовать два терминала осциллятор, как и генератор MC1628 ecl, с переменной 100 пФ конденсатор и просто измерьте частоту, на которой загадочный индуктор колеблется. Метод не может выявить добротность катушки индуктивности.Это может достаточно надежно измерять очень малые индуктивности, вплоть до 0,1 мкГн. В при таком низком значении они неизменно являются воздушным сердечником и имеют «высокую» добротность. Генератор MC1628 ecl не всегда начинает колебаться при всех возможные комбинации L и C. Обычно метод надежен со всеми индукторами с воздушным сердечником или настраиваемыми индукторами от 200 мкГн до 0,1 мкГн. Погрешности измерения являются результатом паразитные сопротивления.
Тороидальные индукторы с ферритовым сердечником все еще хлопотно. иногда осциллятор запускается, а часто нет.Там по-прежнему нет индикации Q. Может показаться, что это работает на вашей частоте Интересно, но Q может быть настолько низким, что его использование в фильтрах будет невозможно.

Так что же делать.

Я забочусь о ферритовых сердечниках, поэтому мне действительно нужна точная индуктивность и надежное указание добротности.

Этот метод действительно работает, потому что мы измеряем частоту параллельного резонанса таинственный индуктор и конденсатор, в которые я верю! В схема до смешного проста, вряд ли стоит усилий рисование схемы.Загадочный индуктор помещен в параллельно с серебряным слюдяным конденсатором 2700 пФ, вот и все! я рекомендуют использовать для этого случая конденсаторы из серебряной слюды. У них очень высокая добротность и очень низкий дрейф, и ни один из патология, которую могут иметь керамические конденсаторы. Не используйте «аудио» конденсаторы типа «greencaps»
и по возможности избегайте керамических конденсаторов. Если вам необходимо использовать керамический рассчитаны на высокое напряжение, так как они будут иметь хорошую добротность и отсутствие пьезо электрическая паразитарная фенонема, которую керамика низкого напряжения может экспонат.