что это, как рассчитать, формулы и примеры

Трансформатор, как элемент радиотехники и электротехники, работает на основе электромагнитной индукции. Говоря об индуктивности трансформатора, имеют в виду индуктивность обмоток и взаимоиндукцию между ними.

Каждая из обмоток представляет некоторое количество витков провода, намотанных на ферромагнитный сердечник, то есть обыкновенную катушку индуктивности.

Трудность в определении параметров катушки заключается в том, что они изменяются в зависимости от нескольких параметров и их сочетания:

• токи в обмотках;
• уровень намагниченности магнитопровода;
• магнитные характеристики сердечника;
• взаимодействие между соседними обмотками;
• наличия постоянной составляющей тока.

Конструкция и принцип действия силового трансформатора

В основе конструкции любого трансформатора находятся следующие элементы:

1. Сердечник из ферромагнитного материала.
2. Первичная и вторичные обмотки. В случае автотрансформатора одна обмотка выполняет обе функции.

В сетях переменного тока промышленной частоты (50 или 60Гц) в качестве ферромагнитного материала используется сталь, обработанная по специальной технологии. На высоких частотах часто делаются трансформаторы без сердечника, поскольку для нормальной работы достаточно взаимосвязи межу катушками.

Принцип работы:

• в первичной обмотке, подключенной в цепь питания, создается переменное электрическое поле;
• под действием поля первичной катушки в сердечнике создается переменное магнитное поле;
• в силу электромагнитной индукции во всех обмотках наблюдается ЭДС индукции.

ЭДС индукции в первичной обмотке направлена противоположно поданному напряжению, поэтому они взаимно компенсируются. В результате, при отсутствии нагрузки через первичную обмотку протекает сравнительно небольшой ток холостого хода.

Наличие тока вторичной цепи аналогично вызывает дополнительный магнитный поток, а он – ЭДС самоиндукции в первичное катушке. В результате компенсация первичного напряжения снижается и растет ток в первичной цепи.

Физическое понятие индуктивности обмоток

Индуктивность представляет собой коэффициент пропорциональности между током, создаваемым замкнутым электрическим контуром, и магнитным потоком, который создается этим контуром.

Более понятной формулировкой будет та, которая говорит о величине ЭДС самоиндукции в замкнутом контуре, которая возникает при изменении силы тока за единицу времени. То есть, понятие индуктивности справедливо для изменяющегося тока.

При постоянном токе говорить об индуктивности бессмысленно.

В идеальном трансформаторе все электромагнитное поле, создаваемое обмотками, замкнуто в магнитном сердечнике. В реальных конструкциях существует поле рассеяния, величина которого зависит от способа выполнения катушки и конструктивных особенностей сердечника. Чем больше толщина намотки, тем большая часть электромагнитного поля замыкается вне магнитопровода.

Этому способствует также качество сборки магнитопровода. Зазоры между пластинами способствуют резкому увеличению рассеивания. В связи с этим наилучшими свойствами обладают О-образные сердечники.

Формулы и измерение

Формулы для расчета индуктивности катушек довольно сложны и имеет различный вид для различных типов исполнения обмоток:

• линейный проводник;
• одновитковая катушка;
• плоская катушка;
• соленоидальная обмотка;
• тороидальная форма.

Наибольшие сложности возникают при расчетах многовитковых многослойных катушек, то есть тех, которые составляют обмотку трансформаторов.

В подавляющем большинстве случаев точный расчет невозможен, поэтому приходится использовать примерные данные и уточнять их после проведения измерений.

Формулы  для расчета индуктивности трансформатора основаны на расчетах соленоида:

L=µ_{µN²S/l, где}

µ0 – магнитная постоянная;

µ – магнитная проницаемость сердечника;

N – количество витков;

S – площадь одного витка;

l – длина обмотки.

Для измерения индуктивности существует несколько методик и приборов, созданных на их основе. В большинстве случаев измерение производится путем вычислений индуктивного сопротивления катушки при подаче образцового напряжения заданной частоты и измеренного значения тока через обмотку.

В специализированных приборах вычисления производятся автоматически, и пользователь только считывает показания шкалы прибора, выраженные в единицах индуктивности – Гн, мГн или мкГн.

Как измерить в домашних условиях

Приборы для непосредственного измерения индуктивности имеют высокую стоимость и редко используются в домашних условиях. С приемлемой точностью результаты можно получить, используя обычные приборы для измерения переменного тока: амперметр и вольтметр. Также необходим омметр.

Порядок действий следующий:

1. При помощи омметра определяют активное сопротивление обмотки R.
2. Подключают трансформатор последовательно с амперметром в сеть.
3. Параллельно обмотке подключают вольтметр.
4. По показаниям приборов определяют полное сопротивление трансформатора: Z=U/I
5. Индуктивное сопротивление находят, вычитая из полного сопротивления активное: X_L=Z-R
6. Индуктивность определяется по формуле: L=X_L/(2πf), где π – число пи 3.14, f – частота измерений.

Как правило, активное сопротивление намотки значительно (на несколько порядков) меньше индуктивного, поэтому можно его не учитывать. Именно поэтому, включение трансформатора в цепь постоянного напряжения вызывает короткое  замыкание. Ток обмотки при этом будет ограничиваться только активным сопротивлением.

Пример расчета

К примеру, требуется рассчитать индуктивность первичной обмотки трансформатора питания. Путем измерений определено:

1. Сопротивление обмотки 3 Ом.
2. Напряжение сети 220 В.
3. Частота питающего напряжения 50 Гц.
4. Ток холостого хода 05 А.

Полное сопротивление:

Z=U/I=220/0.05=4400 Ом

Активное сопротивление меньше полного в 10000 раз и его можно не учитывать.

Определяем индуктивность:

L=X_L/(2πf) =4400/ (2∙3.14∙50) =14 Гн.

Индуктивности обмоток трансформатора и электромагнитное рассеяние

Дата публикации: 29 июля 2013.
Категория: Трансформаторы.

Индуктивности обмоток

В трансформаторах со стальным магнитопроводом магнитная проницаемость стали µ во время цикла перемагничивания непостоянна. Поэтому в течение этого цикла непостоянны также собственные L и взаимные М индуктивности обмоток трансформатора. В результате такого непостоянства µ при подключении трансформатора к сети с синусоидальным напряжем в его намагничивающем токе i₀ возникают высшие гармоники (смотрите статью «Явления, возникающие при намагничивании магнитопроводов трансформаторов»).

Рисунок 1. Магнитные потоки трансформатора при одностороннем намагничивании (i1 ≠ 0, i2 = 0)

При работе трансформатора на ток i₀ накладывается ток нагрузки, по отношению к которому ток i₀ и, в особенности, его высшие гармоники малы. Поэтому при исследовании режимов работы трансформатора указанными гармониками можно пренебречь и учитывать только основную гармонику тока i₀. Это равносильно допущению, что во время цикла перемагничивания µ, L и M постоянны. Влияние насыщения магнитопровода при этом можно учесть, принимая в расчет при разных режимах работы трансформатора, при разных амплитудах потока магнитопровода, значения µ, L и M для данного режима работы. В соответствии с изложенным будем полагать, что µ, L и M постоянны.

Рассмотрим индуктивности и индуктивные сопротивления обмоток, обусловленные магнитным потоком магнитопровода Ф_с, все силовые линии которого полностью замыкаются по замкнутому магнитопроводу и поэтому сцепляются со всеми витками первичной и вторичной обмоток (рисунок 1).

Пусть поток Ф_с создается током первичной обмотки i₁, когда ток вторичной обмотки i₂ = 0. Значения Ф_с и i₁ могут быть известны, например, из данных расчета магнитной цепи или из опыта. Тогда собственная индуктивность первичной обмотки от потока в магнитопроводе

Lс1 = w1 × Фс / i1.

(1)

Величину L_с1 можно выразить также через магнитное сопротивление магнитопровода

(2)

где l_k, S_k и µ_k соответственно означают длину, площадь сечения и магнитную проницаемость k-го участка магнитной цепи. При этом

Фc = F1 / Rµc = w1× i1 / Rµc.

(3)

и после подстановки этого значения Ф_с в выражение (1) получим

Отметим, что значение R_µc также может быть определено по данным расчета магнитной цепи или из данных опыта по соотношению (3).

Аналогично индуктивность вторичной обмотки от потока магнитопровода

а взаимная индуктивность первичной и вторичной обмоток от потока магнитопровода

Mс = w1 × w2 / Rµс

(6)

Картина магнитного поля, замыкающегося целиком по магнитопроводу, одинакова независимо от того, какой из обмоток это поле создается. Поэтому и магнитное сопротивление потоку Ф_с одинаково для поля обеих обмоток и в равенства (4), (5) и (6) входит одинаковая величина R_µс. Вследствие этого также

(7)

Кроме потока Ф_с, ток первичной обмотки i₁ создает также поток Ф_в1 (рисунок 1), силовые линии которого замыкаются частично по воздуху или через трансформаторное масло. Потокосцеплениям Ψ_в1 и Ψ_в12 этого потока с первичной и вторичной обмотками соответствует собственная индуктивность первичной обмотки

L_в1 = Ψ_в1 / i₁

и взаимная индуктивность двух обмоток

M_в12 = Ψ_в12 / i₁.

Точно так же при питании вторичной обмотки током i₂ создается поток Ф_в2, замыкающийся частично по воздуху. Потокосцеплениям Ψ_в2 и Ψ_в21 этого потока с вторичной и первичной обмотками соответствует собственная индуктивность вторичной обмотки

L_в2 = Ψ_в2 / i₂

и взаимная индуктивность двух обмоток

M_в21 = Ψ_в21 / i₂.

При этом, согласно принципу взаимности,

M_в12 = M_в21 = M_в

Поля потоков Ф_в1 и Ф_в2 имеют гораздо более сложный характер, чем поле потока Ф_с. Отдельные магнитные линии этих потоков сцепляются с неполными и разными числами витков первичной и вторичной обмоток. Поэтому в отличие от L_с2 [смотрите соотношение (7)]

(8)

Полные собственные индуктивности первичной и вторичной обмоток

L11 = Lс1 + Lв1;   L22 = Lс2 + Lв2,

(9)

и полная взаимная индуктивность

Первые слагаемые равенств (9) и (10) значительно больше вторых, так как потоки через воздух относительно малы.

Понятие об электромагнитном рассеянии

Полнота электромагнитной связи двух индуктивно связанных цепей характеризуется коэффициентом связи этих цепей

(11)

Как известно из курса теоретических основ электротехники, в реальных условиях всегда c < 1.

Если бы в трансформаторе отсутствовали потоки Ф_в1 и Ф_в2, замыкающиеся по воздуху, то L₁₁ = L_c1, L₂₂ = L_c2, M = M_c, и в этом случае в соответствии с равенствами (4), (5), (6) и (11)

Таким образом, неполнота электромагнитной связи в трансформаторе, выражаемая неравенством c < 1, обусловлена наличием потоков Ф_в1 и Ф_в2 или, точнее, неодинаковым их сцеплением с обеими обмотками. Условие c = 1 было бы достигнуто только в том случае, если бы удалось полностью совместить первичную и вторичную обмотки, что фактически невозможно.
Явление неполной электромагнитной связи называется электромагнитным рассеянием.

Наряду с соотношением (11) целесообразно ввести в рассмотрение коэффициент электромагнитного рассеяния

(12)

Чем меньше c и чем больше σ, тем больше рассеяние.

Ввиду того что явление рассеяния обусловлено неодинаковостью или неполнотой сцепления потоков Ф_в1 и Ф_в2, проходящих по воздуху, с обеими обмотками, эти потоки называют часто также потоками рассеяния, однако это название до некоторой степени условно, так как потоки Ф_в1 и Ф_в2 обусловливают также явление взаимной индукции, поскольку M_в ≠ 0. Степень неполноты электромагнитной связи, или величина электромагнитного рассеяния, оказывает большое влияние на многие технические показатели и характеристики трансформаторов и вращающихся электрических машин.

В трансформаторах с ферромагнитным магнитопроводом потоки Ф_в1 и Ф_в2 относительно малы.

Поэтому электромагнитная связь в трансформаторах чрезвычайно высока, а рассеяние мало.

В силовых трансформаторах, например, c = 0,998 – 0,9995 и соответственно σ = 0,001 –  0,004.

Вследствие этого значение σ, определяемое по формуле (12), представляет собой разность весьма близких величин и вычисление σ по этой формуле связано с очень большими погрешностями, так как L₁₁, L₂₂ и M в практических устройствах не могут быть рассчитаны или определены из опыта с достаточной степенью точности. Поэтому возникает необходимость в непосредственном определении параметров, характеризующих электромагнитное рассеяние.

Источник: Вольдек А. И., «Электрические машины. Учебник для технических учебных заведений» – 3-е издание, переработанное – Ленинград: Энергия, 1978 – 832с.

Индуктивность трансформатора

      Итак, явление взаимной индукции используется в широко распространенных устройствах – трансформаторах.

      Трансформатор был изобретен Яблочковым, русским ученым, в 1876 г. для раздельного питания отдельных электрических источников света (свечи Яблочкова).

      Рассчитаем взаимную индуктивность двух катушек  и , намотанных на общий сердечник (рис. 5.5).

      Когда в первой катушке идет ток , в сердечнике возникает магнитная индукция  и магнитный поток Ф через поперечное сечение S.

Рис. 5.5.

      Магнитное поле тороида можно рассчитать по формуле

      Через вторую обмотку проходит полный магнитный поток , сцепленный со второй обмоткой:

здесь  – потокосцепление, которое можно найти по формуле:

      По определению, взаимная индуктивность двух катушек равна:

      К первичной обмотке подключена переменная ЭДС . По закону Ома ток в этой цепи будет определяться алгебраической суммой внешней ЭДС и ЭДС индукции.

где  – сопротивление обмотки.

        – делают малым (медные провода) и . Тогда

      Во второй обмотке, по аналогии, , отсюда

,

(5.4.1)

      Если пренебречь потерями, т.е. предположить, что , то

,

(5.4.2)

Коэффициент трансформации будет равен:    

---

2. Взаимная индукция. Трансформатор

Явление взаимной индукции заключается в наведении ЭДС индукции в проводнике, находящемся вблизи цепи переменного тока.

Из закона электромагнитной индукции Фарадея следует, что ЭДС взаимной индукции равна

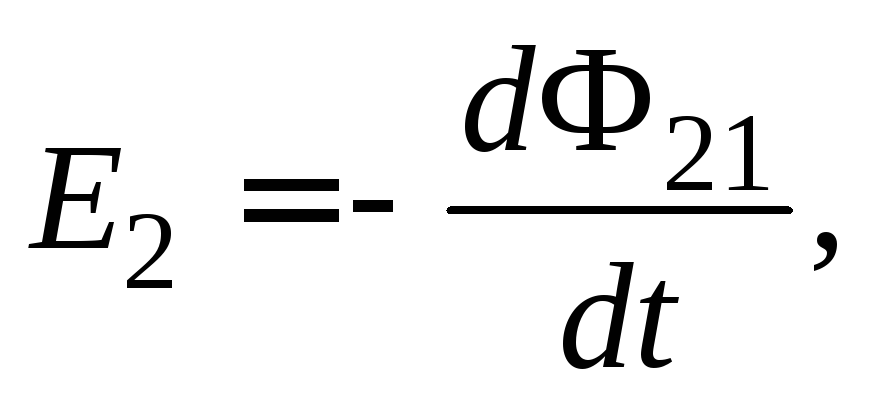(16.1)

где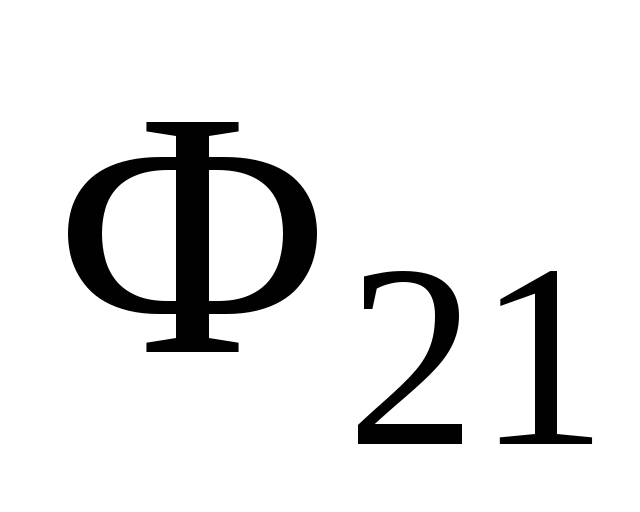

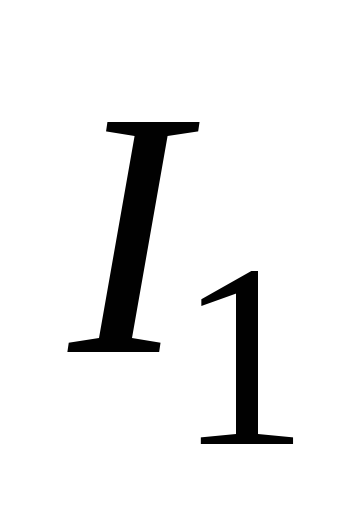– магнитный поток через поверхность, ограниченную вторым контуром, обусловленный магнитным полем тока, протекающего в первом контуре (рис. 16.1).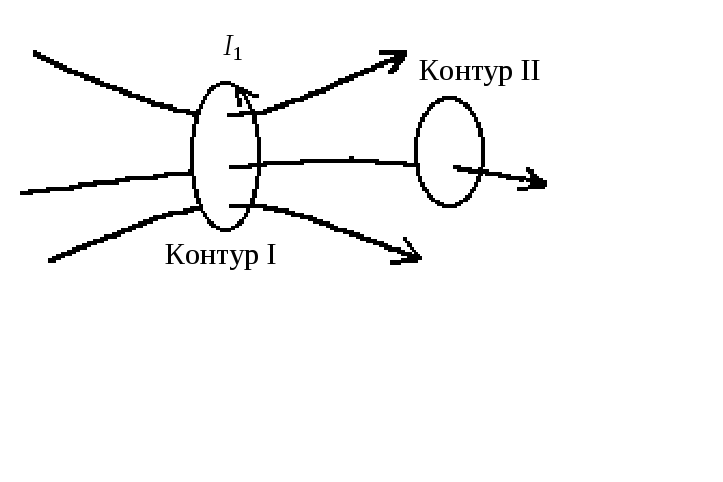

Рис. 16.1

Чем больше сила тока 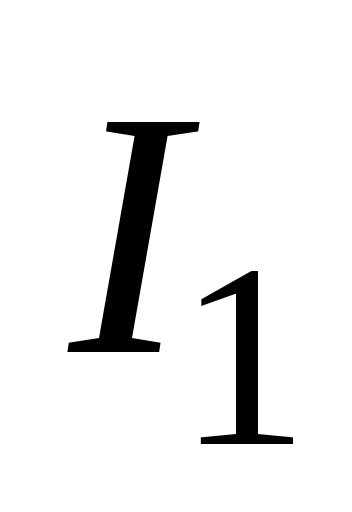в первом контуре, тем больше магнитный поток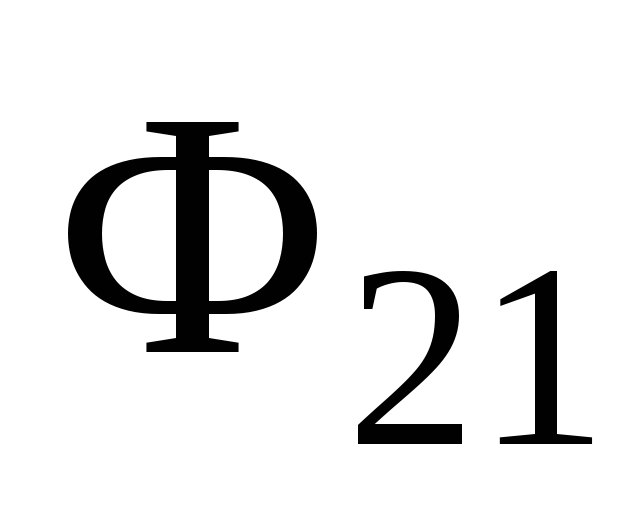, обусловленный этим током. Поэтому, так же как и при самоиндукции, этот магнитный поток пропорционален силе тока

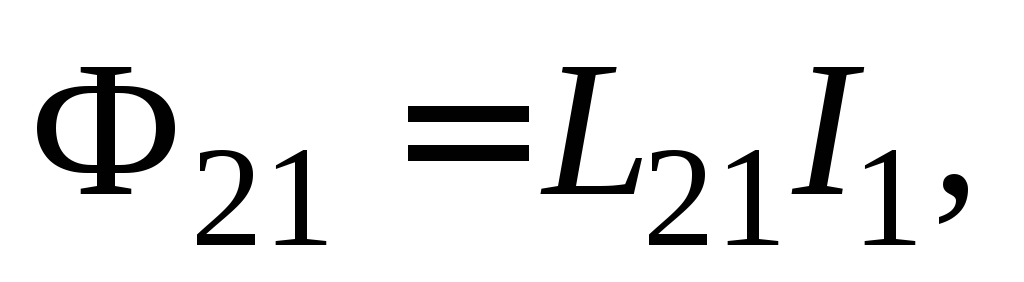(16.2)

где, как говорилось выше, коэффициент пропорциональности 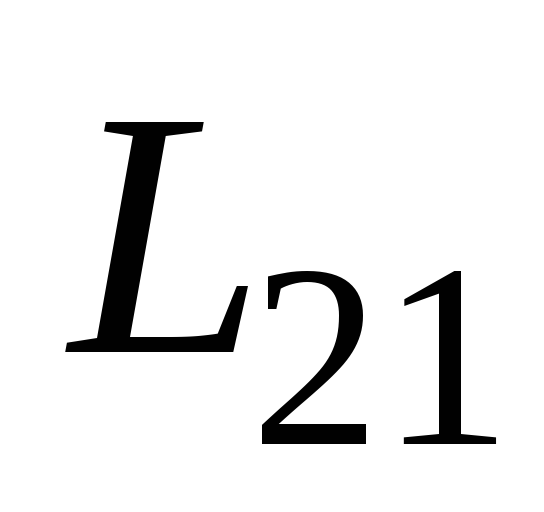называется взаимной индуктивностью (статической взаимной индуктивностью) второго и первого контуров. Этот коэффициент зависит от геометрических размеров, формы, количества витков, взаимного расположения первого и второго контуров, от магнитной проницаемости среды, в которой они находятся.

Если источник тока отключить от первого контура и подключить ко второму, создав ток , то для магнитного потока через площадь первого контура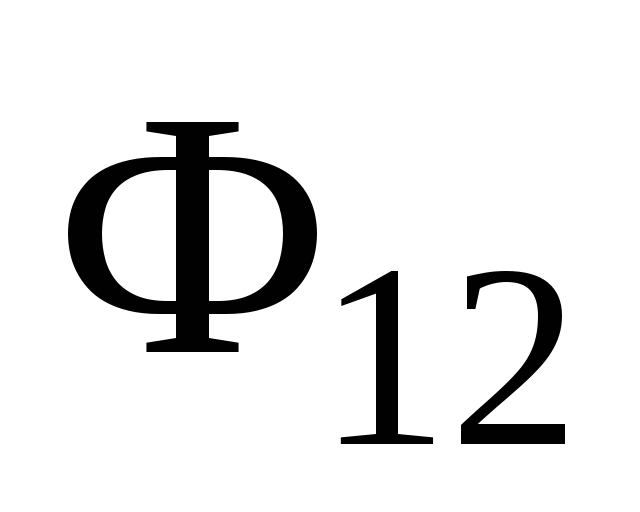можно записать аналогичную формулу

.

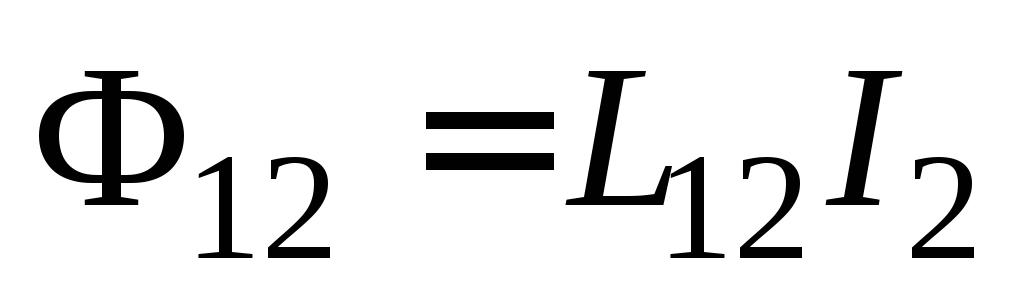Пусть контуры находятся в неферромагнитной среде, тогда, как можно показать, для них выполняется так называемая теорема взаимности, согласно которой коэффициенты взаимной индуктивности равны друг другу численно и имеют одинаковые знаки

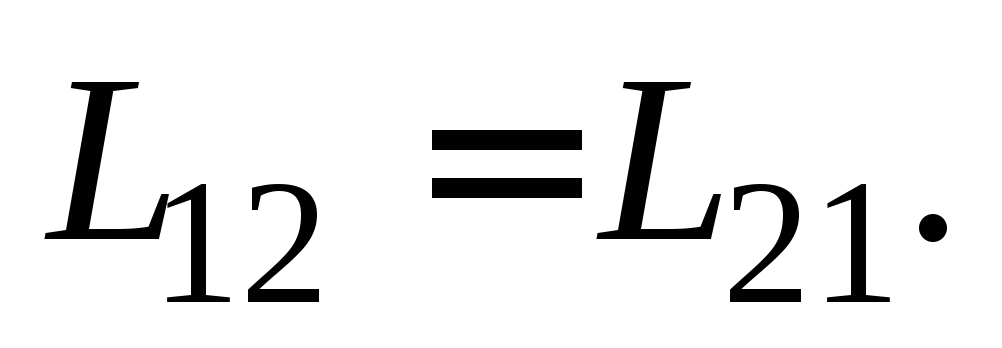
Если же среда ферромагнитная, причем режим перемагничивания среды выходит за пределы обратимого процесса, то 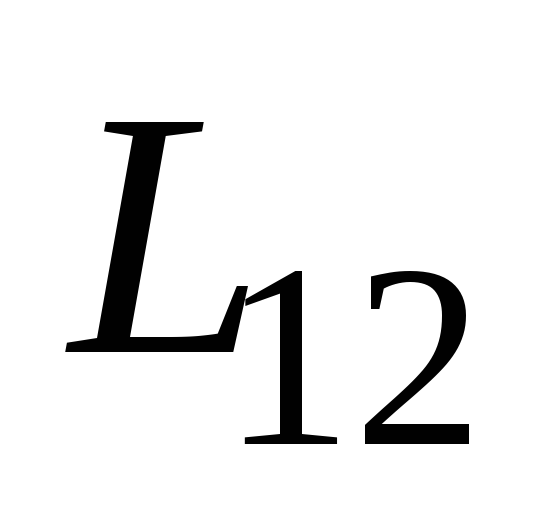и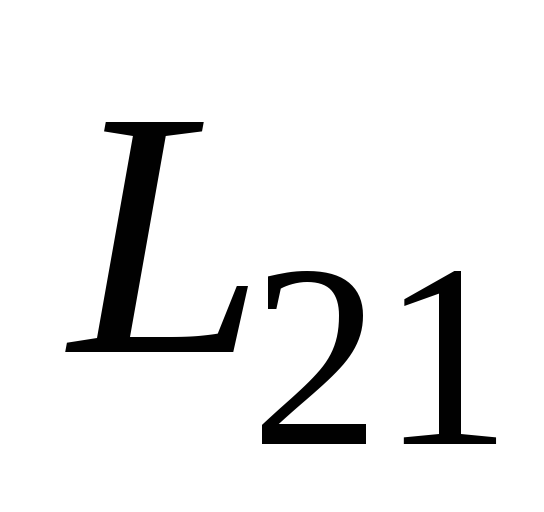зависят не только от вышеперечисленных параметров, но и от величины токов в контурах. В этом случае теорема взаимности не выполняется.

Заменив в законе Фарадея (16.1) магнитный поток его выражением (16.2) и полагая 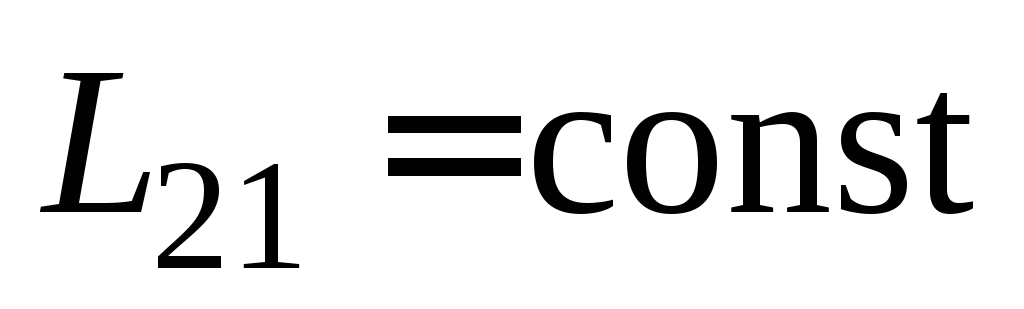, получим

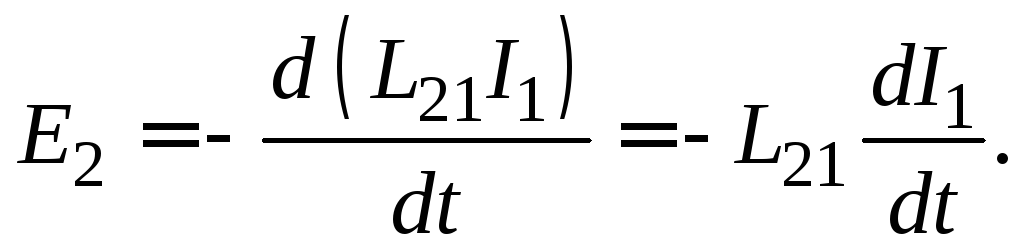(16.3)

Если первый и второй контуры находятся в ферромагнитной среде, то можно пользоваться формулой, по виду аналогичной формуле (16.3):

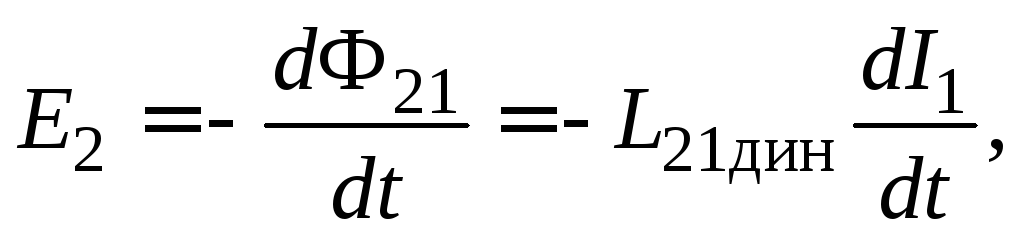(16.4)

где – так называемая динамическая взаимная индуктивность второго и первого контуров.

На явлении взаимной индукции основано действие трансформаторов, которые применяются для повышения или понижения напряжения переменного электрического тока.

Трансформатор (рис. 16.2) состоит из двух или нескольких соленоидальных обмоток, расположенных близко друг от друга и чаще всего закрепленных на общем ферромагнитном сердечнике. Концы пер-вичной обмотки присоединены к источнику переменного тока, а кон- цы вторичной обмотки включены в цепь потребителя электрической энергии.

Переменное магнитное поле тока 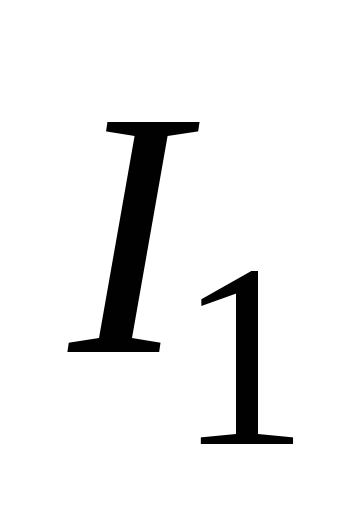, протекающего в первичной обмотке трансформатора, вызывает появление ЭДС взаимной индукции во вторичной обмотке. Магнитное поле первичной обмотки практически полностью локализовано в ферромагнитном сердечнике, играющем роль магнитной цепи. Поэтому применение в трансформаторе такого замкнутого сердечника, общего для обеих обмоток, позволяет резко увеличить магнитный поток взаимной индукции и взаимную индуктивность.

Определим статическую и динамическую взаимные индуктивности обмоток трансформатора.

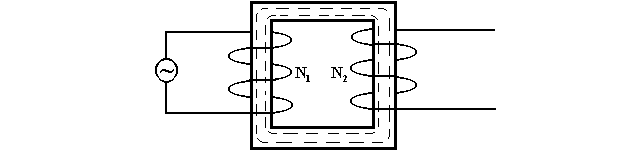
N₁

N₂

Рис. 16.2

Пусть Ф – магнитный поток в сердечнике. Тогда магнитный поток через 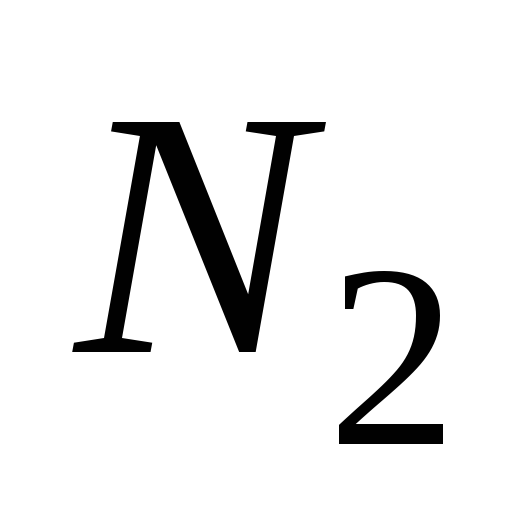витков вторичной обмотки равен

Следовательно, из формул (16.2) и (16.4) получим

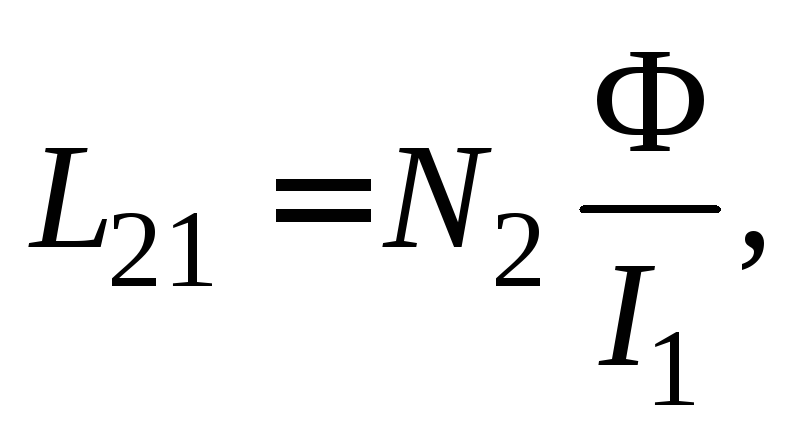
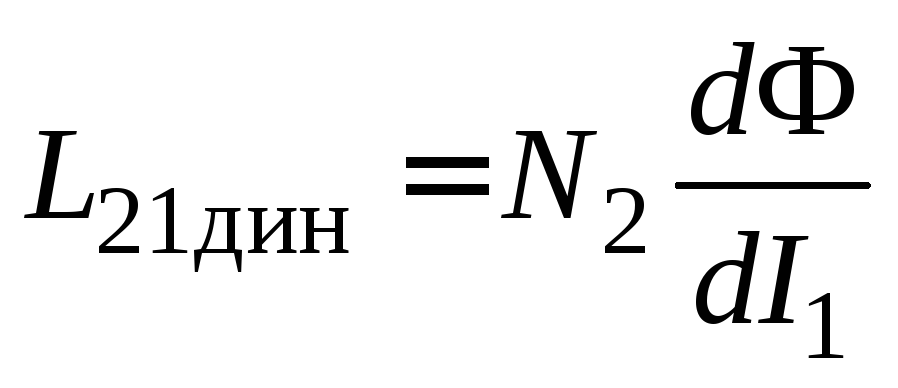. (16.5)

Статическая и динамическая индуктивности первичной обмотки трансформатора в режиме холостого хода, соответствующего разомкнутому состоянию вторичной цепи 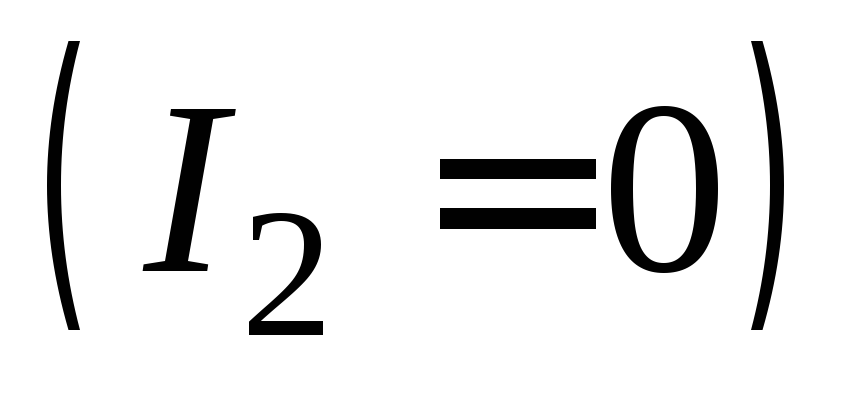,равны

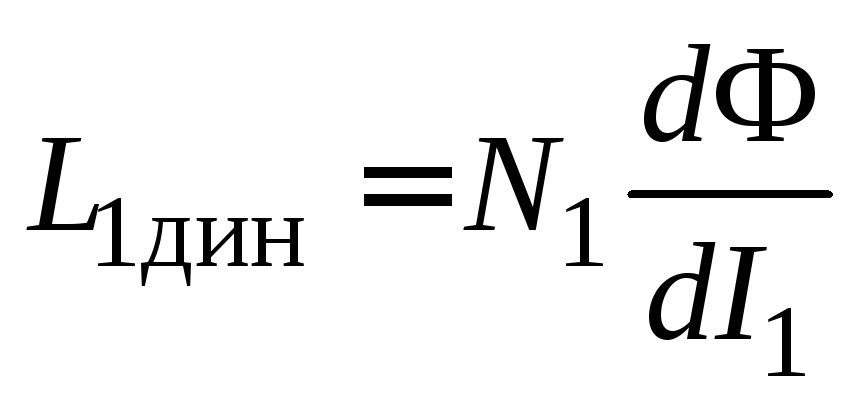. (16.6)

ЭДС самоиндукции в первичной обмотке можно выразить формулой

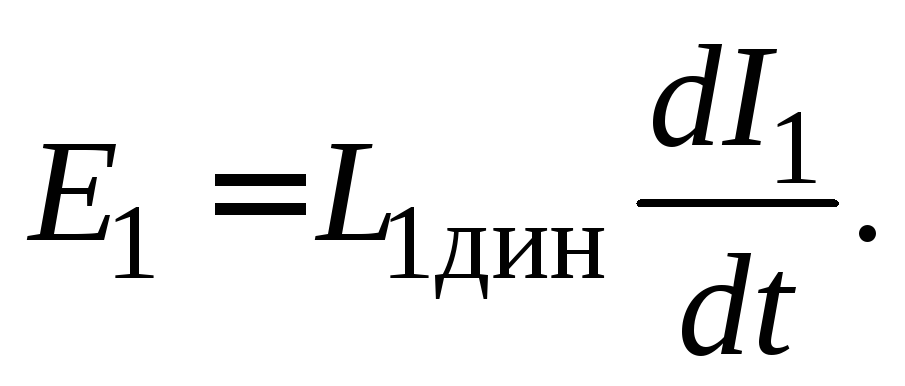
Найдем отношение абсолютных значений напряжени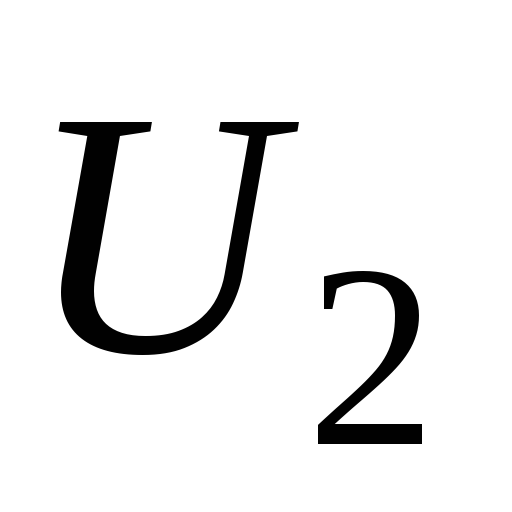й и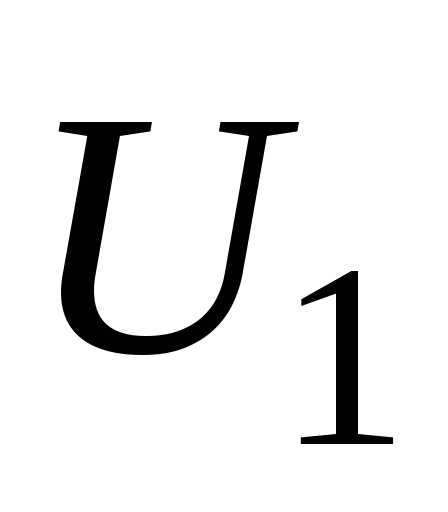на концах вторичной и первичной обмоток при холостом ходе, называемое коэффициентом трансформации.

При разомкнутой вторичной обмотке (холостой ход) 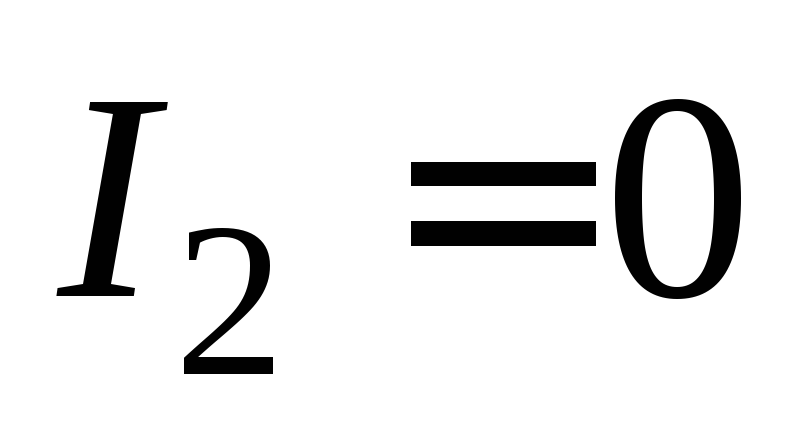. В этом случае напряжение на ее концах численно равно ЭДС взаимной индукции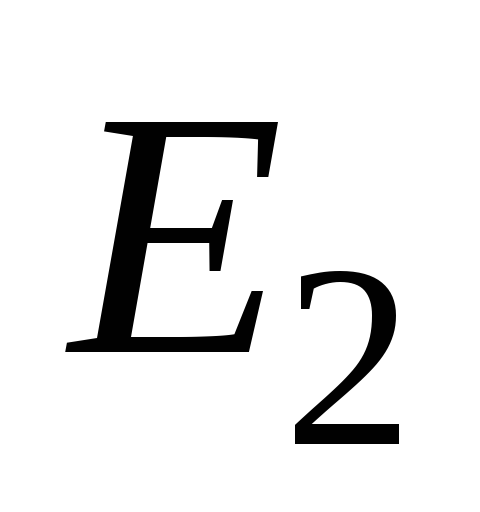

(16.7)

На концах первичной обмотки напряжение 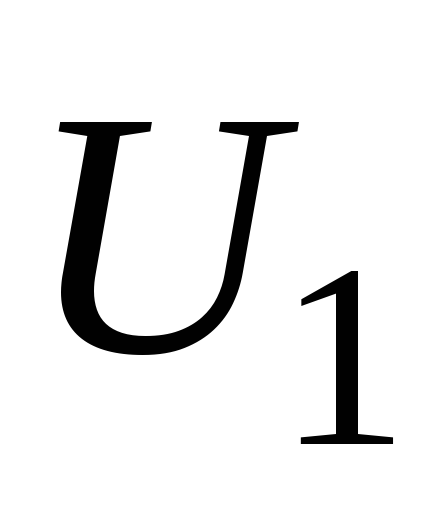, как можно показать с помощью закона Ома, равно

(16.8)

где 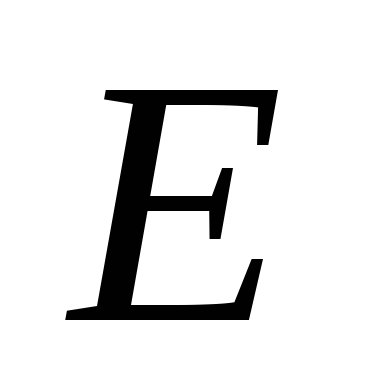– ЭДС источника тока;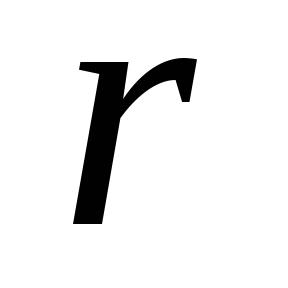– внутреннее сопротивление источника тока, подключенного к первичной обмотке трансформатора.

Сила тока в первичной обмотке согласно закону Ома для замкнутой цепи определяется формулой

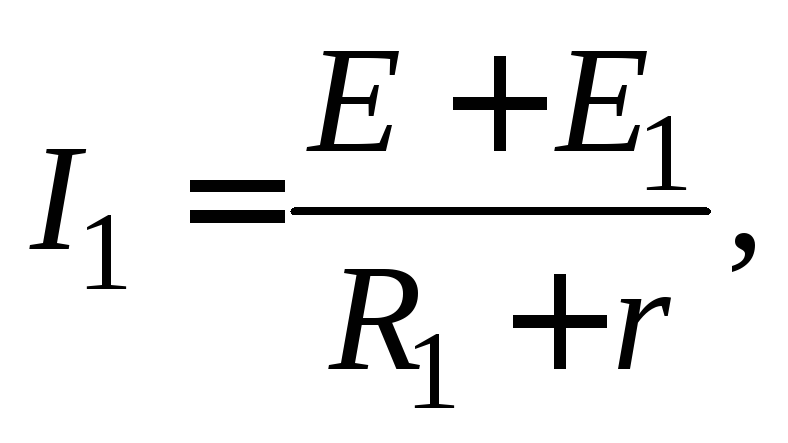
где – ЭДС самоиндукции в первичной обмотке;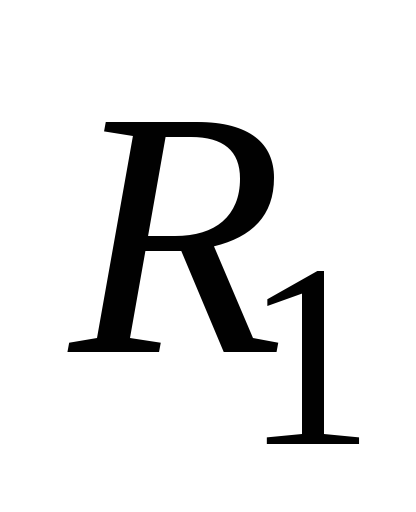– сопротивление первичной обмотки.

Выражая 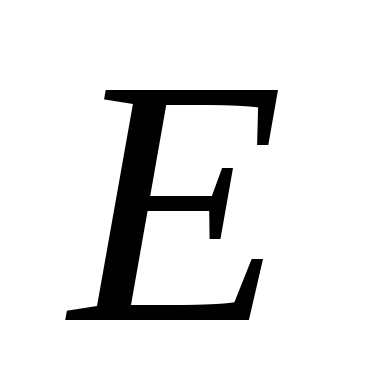и подставляя в (16.8), получаем

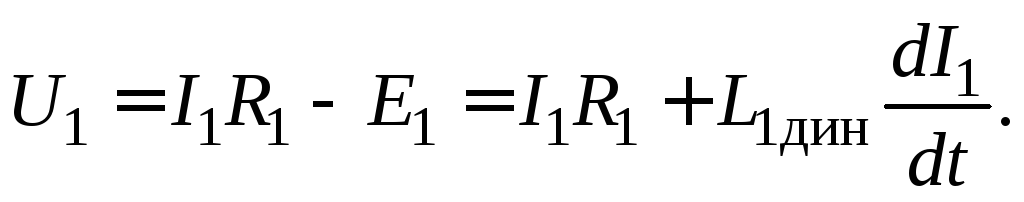
Как правило, для трансформаторов первый член в правой части пренебрежимо мал по сравнению со вторым. Поэтому приближенно можно считать, что

(16.9)

Зная 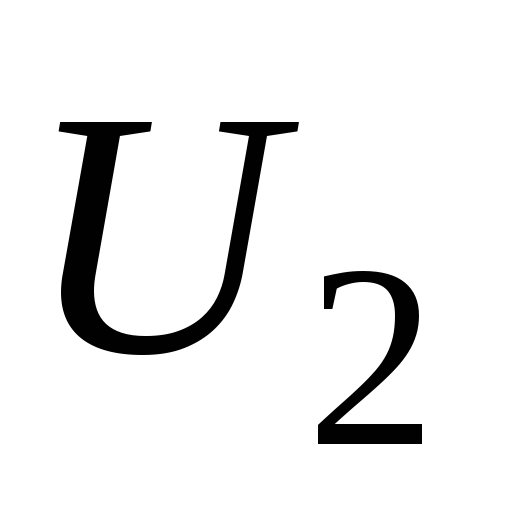и, используя формулы (5),(6),(7),(9), находим коэффициент трансформации

. (16.10)

О трансформаторе импульсном замолвите слово / Habr

Несмотря не то, что не так давно проскакивали довольно неплохо написанные статьи о расчете трансформатора импульсного источника питания, я предложу вашему вниманию свою методику, и не просто голую методику, а максимально прозрачное описание принципов, в ней использующихся.

Картинок не будет, будет около 18 несложных формул и много текста. Всех желающих приобщиться прошу на борт.

Я хочу поведать вам о том, как расчитать такого хитрого зверя, как импульсный трансформатор обратноходового источника питания. Обратноходовик, или FlyBack — это, наверное, самая популярная топология импульсного преобразователя. По моему мнению, в ИИП есть два очень важных и тонких момента — это трансформатор и петля обратной связи. В данной статье я хочу показать один из возможных наборов несложных математических уравнений, решая которые мы можем получить данные вполне реального трансформатора для флайбэка.

В интернете, в различных авторских статьях, или в AppNotes различных производетелей, можно найти различные методики расчета, которые зачастую максимально «сжаты», так, что из формул совершенно не понятно, как они получается. Я хочу сделать упор не на точность, а на максимальную наглядность и прозрачность производимых расчетов, так чтобы вы поняли, «почему так».

Далее постараюсь писать кратко и емко, так, чтобы вы смогли сесть и посчитать сразу после прочтения статьи. Эпюры напряжений и токов в обратноходовом источнике рисовать не буду, считаю, что вы достаточно подготовлены для того, что бы такие термины, как «индуктивность рассеяния», «отраженное напряжение», «пиковое значение тока через силовой ключ», «размагничивание магнитопровода» вам понятны.

Итак, считать будем трансформатор обратноходового источника питания, без корректора коэфициента мощности, как наиболее распространенный, да и «расчётка» моя пока только под него заточена.

Отдельно сделаю примечание, что подразумевается т.н. квазирезонансный режим работы преобразователя, когда накачка энергии в трансформатор начинается сразу после полного размагничивания магнитопровода. Т.е. т.н. «коэффициент безразрывности тока» =1, т.е. как только вся энергия вытекла через вторичную обмотку(и рассеялась в снабберной цепи), сразу включаем ключ и накачиваем снова. Такой режим в последнее время очень популярен в обратноходовых источниках питания, т.к. позволяет чуток поднять КПД.

Заранее оговорюсь — нижеприведенная методика весьма груба, но она «железобетонно» работает, многократно проверена на реальных трансформаторах в реальных источниках питания.

Для начала скачайте расчетку, откройте, пробегитесь глазами. В нее уже «вбиты» значения для расчета трансформатора источника питания, с выходной мощностью 100Вт.

Расчетка: к сожалению, по какой-то неведомой мне причине, публичная ссылка не отображается.
Возможно публикация публичных ссылок противоречит правилам. Надеюсь на то, что модераторы услышат этот крик души и снизошлют на меня персональную настройку фильтра, а пока можете переписать в Эксель, или маткад, все нижеприводимые формулы и получить годный результат.

Итак, поехали. Для того, чтобы начать расчет нам потребуется задаться несколькими исходными параметрами (все они выделены зеленым цветом в расчетке), а именно:

1. Выходная мощность источника питания для которого делаем трансформатор (POUTmax).
2. Выходное напряжение источника (Uout)(1).
3. Выходное напряжение служебной обмотки (Ubias)(2).
4. Минимальное напряжение питающей сети (UACmin)(3).
5. Максимальное напряжение в сети (UACmax)(3).
6. Уровень пульсаций на фильтрующем конденсаторе сетевого выпрямителя (Urpl)(4).
7. Ожидаемый КПД трансформатора (берите 0,85 и не прогадаете) (ŋ).
8. Частота работы преобразователя (5).
9. Пиковое значение тока протекающего через ключ коммутирующий первичную обмотку (ILPRpeak) (6).

(1) Если выходные напряжения достаточно низкие- учитывайте прямое падение напряжения на диоде.
(2) В подавляющем большинстве конструкций источников питания, требуется третья обмотка, от которой будет питаться управляющая микросхема.
(3) Всегда берите с запасом, т.е. если указан диапазон 180-264, берите от 160 до 280.
(4) Этот параметр зачастую можно только угадать, берите 10% от постоянной составляющей на нем и не ошибетесь, по факту полученного рабочего прототипа «подрихтуете» расчет.
(5) Частота к преобразователях с ожиданием размагничивания сердечника- плавающая, берем «с потолка» такую, которую хотим получить при полной нагрузке.
(6) Я надеюсь вы в курсе, что форма тока треугольная, что коммутирует ключ, что такое ключ и т.п.

Итак, первая формула:
Начнем с определения индуктивности первичной обмотки, Lpr.

Lpr=(1000×2×POUTmax)/(ŋ×F×ILPRpeak^2 )     	(1)

Для упрощения я выкину КПД, и множитель 1000, который нужен только для приведения результата к микроГенри от Генри, получится нижеследующее уравнение:

Lpr=(2×POUTmax)/(F×ILPRpeak^2 )     		(1.1)

На первый взгляд совершенно непонятно как так получается. Давайте попробуем ее преобразовать. Перенеся множители справа-налево, получим.

(Lpr×ILPRpeak^2)/2=POUTmax/F       (1.2)

Преобразуем правую часть, получим:

(Lpr×ILPRpeak^2)/2=POUTmax×T	(1.3)

Итак, в левой части у нас энергия содержащаяся в индуктивности (учебник физики, если не понятно). В правой части имеем мощность которая расходуется за период работы преобразователя. Т.е. энергия запасенная в индуктивности первичной обмотки (на этапе накачки, от начала периода до размыкания ключа) равна мощности передаваемой в нагрузку за весь период T (от начала накачки, до полного исчерпания энергии в трансформаторе и начала нового импульса).

В установившемся режиме то, что закачали в трансформатор из сети, должно равняться тому, что слили в нагрузку. Т.е. все рассуждения предполагают, что наш источник уже работает, а не стартует.

Оставим-же пока эту формулу (1), мы потом воспользуемся ею в расчётке, я лишь хотел продемонстрировать как она так получается.
Теперь о параметрах. Присмотримся к формуле. Зафиксировав (выбрав на свое усмотрение) три из четырех неизвестных, мы можем получить значение четвертой.

Мощность (POUTmax), мы уже задали.

Частота, ее можно просто выбрать по своему желанию. Не мудрствуя лукаво тыкнем скажем 50кГц и не проиграем. Лезть за 150кГц не стоит, так как потери на переключение станут неоправданно высокими, да еще скинэффект, не нужно это нам во флайбэке.

Пиковое значение тока через первичную обмотку, и одновременно ключ- ILPRPeak, это параметр на нервах которого мы будем играть. Выбирая его значение ILPRPeak, мы изменяем Lpr, а вместе с ней еще много чего другого. В моей расчетке будем менять ILPRpeak и наблюдать за другими ячейками таблицы, в которых будут находится результаты других формул. Опять-же, ближе к реальности, для 100Вт источника можно задаться для начала ILPRpeak= 3…4A.

Просто попробуйте подставить в ячейку различные числа, и вы увидите, как изменятся другие производные параметры. В частности, выбирая пиковый ток «первички», мы смотрим на «отраженное» напряжение, и исходим из соображений наличествующих у нас ключей. Так же этот параметр влияет на пиковое значение тока «вторички», что тоже важно, ибо во флайбэках токи имеют форму прямоугольного треугольника, и пиковые значения в разы превышают действующие, т.е. если ток нагрузки 5А, то пиковое может быть и 50, ориентируйтесь на наличествующие диоды и потери в меди обмотки.

Вторая формула:

UDCmin=UACmin×1.41-Urpl     	(2)

Тут упрощать нечего, думаю понятно, что мы получаем самое худшее значение постоянного напряжения, с учетом просадки на буферном конденсаторе, что стоит за сетевым выпрямителем, или за ККМ.

Ton=(Lpr×ILPRpeak)/UDCmin    	(3)

В формуле (3) мы вычисляем, сколько времени должен быть открыт ключ, чтоб ток в индуктивности, при приложении к ней нашего самого худшего UDCmin вырос от нуля до желаемого ILPRpeak.

T=1/F×1000  		(4) 

Частотой мы задались ранее, период посчитали в (4). На 1000 умножаем потому, что желаемую частоту мы записали в кГц а не в 1000-х Герц.

Toff=T-Ton    	(5)

Оставшаяся часть периода, которая будет посвящена передаче энергии в нагрузку, вычисляется по формуле (5).

Q=Toff/Ton    (6)

Максимальный коэффициент заполнения для худшего напряжения в сети и максимальной просадки на фильтрующем конденсаторе вычисляем в (6).

Urv=UDCmin×Ton/Toff    	(7)

«Отраженное» напряжение. Наш трансформатор, хоть и обратноходовый, но таки трансформатор, а значит коэффициент трансформации к нему так-же применим. Если на нашей вторичной обмотке во время протекания тока через выпрямительный диод, апряжение (например) 12.7В, то через соотношение количества витков это напряжение трансформируется в первичную обмотку (ведь магнитный поток «омывает» одновременно все обмотки).

Формула (7), немного хитрая, попробуем ее «раскрутить». Получим:

UDCmin×Ton=Urv×Toff 		(7.1)

(7.1) Демонстрирует один очень важный момент, называемый в народе «равенство вольт*секундных интервалов». Возможно справедливость утверждения (7.1) не очевидна, или не сразу понятна, пока используем полученное с помощью (7) численное значение как есть, в его правомерности не сомневайтесь.

UVTmax=UACmax×1.41+Urv 	(8)

Надеюсь вы хорошо понимаете, что на обратном ходу, первичная обмотка, для постоянного напряжения, что на фильтрующем конденсаторе- просто кусок проволоки, т.е. если наш фильтрующий конденсатор все еще заряжен до 310В, то при разомкнутом силовом ключе, протекании тока через вторичную обмотку, постоянка попросту «проходит» через первичку и прикладывается к ключу, но вместе с ней, к ключу добавляется еще отраженное напряжение. И самое печальное, что оно суммируется с постоянкой. И это без учета выброса от индуктивности рассеяния, имейте это ввиду, в расчетке данное обстоятельство специально выделено красным шрифтом.

Тогда (8) показывает, какое напряжение будет приложено к силовому ключу на обратном ходу. Можно сразу прибавить к максимальному напряжению, на которое расчитан ключ, еще сверху вольт этак 200 и не ошибетесь. Макетирование покажет реальную амплитуду выброса напряжения порожденного индуктивностью рассеяния.

Теперь можем посчитать коэффициент трансформации трансформатора, например таким образом:

Kfb=Uout/Urv 	(9)

Я называю этот коэффициент трансформации «обратным», т.к. считается он задом наперед. Теперь классический коэффициент трансформации, который можно получить:

K=1/Kfb 	(10)

Далее посчитаем максимальное напряжение, которое будет приложено к выпрямительному диоду на прямом ходу преобразователя. Думаю вы хорошо понимаете, что оно будет складываться из напряжения на фильтрующем конденсаторе нагрузки, которое в рабочем режиме, можно считать постоянным, и трансформированного, через коэффициент трансформации, напряжения приложенного к первичной обмотке.

UVDmax=Uout+(VACmax×1.41)/K  	(11)

И не забываем, что выбросы от паразитных индуктивностей обмоток трансформатора, действуют и на диод в т.ч. Если речь идет о источниках с высокими выходными напряжениями, берите запас по напряжению минимум 200В. Для низковольтных, как минимум 1.5, и внимательно смотрите осциллографом на выпрямитель.

Далее.

Lsec=Lpr/K^2   (12)

Из (12) получаем индуктивность вторичной обмотки трансформатора. Правило которое используется в формуле гласит, что «индуктивности обмоток трансформатора соотносятся как квадраты их витков», т.к. выражение можно представить как:

Lsec/Lpr=N2^2/N1^2   (12.1)  ( N2^2/N1^2 =K^2)

Далее посчитаем пиковый ток вторичной обмотки. Готовьтесь получить тут достаточно большие цифры, потому, что это «обратноход», и ток у него во «вторичке» — треугольный, и пиковое значение может быть ощутимо больше тока нагрузки.

ILSECpeak=√(1000×2×POUTmax)/(F×ŋ×Lsec) 	(13)

Данная формула преобразуется точно также как и первая формула для ILPRpeak.

ILSECrms=ILSECpeak√(1-Q)/3 	(14)

В (14) вычисляется действующее значение тока через вторичную обмотку трансформатора. Обяснить почему корень из (1-Q)/3 я не могу, вероятно это можно объяснить построив эпюры и прибегнув к геометрии. Тут же прикинем и действующее значение тока первичной обмотки.

ILPRrms=ILPRmax√Q/3 	(15)

Итак, индуктивности, токи, частоты посчитали. А как выбрать магнитопровод, спросите вы, как расчитать немагнитный зазор? Для начала мы его «прикинем», основываясь на своем жизненном опыте, а «загнав» его параметры в расчетку, поглядев посчитанную индукцию, можно выбрать другой магнитопровод. Вот захотелось мне источник мощностью 100Вт, с выходным напряжением 12В. Беру я «с потолка» магнитопровод типоразмера PQ2620.

Из его Datasheet выписываю Ae, предполагаемый зазор, и Коэффициент индуктивности для данного зазора (в даташитах Epcos, часто приводится таблица со стандартными зазорами для данного магнитопровода, и значениях Al и эквивалентной проницаемости). Если-же данных о коэфициенте Al для желаемого вами зазора, нет, придется его(зазор) изготовить, намотать пробные 100 витков, и посчитать по простой формуле Al=√(L/N^2), где L- измеренное значение индуктивности на сердечнике с пропиленным вами зазором, N — количество витков, что вы набросали(рекомендую мотать пробных 100 витков).

Объяснять что Такое Ae, G, и Al не буду, предполагая, что вы и сами знаете, зачем нужен зазор в магнитопроводе, и что такое Al. Также в расчетку можно вписать эквивалентную проницаемость сердечника с зазором, но она там не используется, чисто для красоты). В формуле (16) считаем необходимое количество витков.

Npr=√Lpr/Al 	(16)

Один из самых важных параметров для трансформатора- пиковое значение потока магнитной индукции.

B=(Lpr×ILPRpeak)/(Npr×Ae) 	(17)

Превышать значение 0,3 я категорически не рекомендую, а 0,4 это уже катастрофа. Так совпало, что данный магнитопровод вроде как вполне подходит под наши нужды. Индукция меньше 0,3Тл, так и хочется его заложить под наши нужды. К сожалению, расчетка не содержит формул для расчета заполненности окна магнитопровода медью, поэтому дать по ней окончательный вердикт — нельзя.

Если же индукция больше 0,3Тл, можем или выбрать более крупный магнитопровод, или увеличить зазор. Увеличив зазор мы получим уже другое значение Al и соотв. значение потока индукции.

Вообще, жизненный опыт показывает, что лучше не лезть в зазоры более 1.5мм., ибо им свойственны свои паразитные явления, такие как выпучивание линий магнитного поля, разогрев витков находящихся вблизи зазора, до температур, при которых им может настать «хана», короче от 0.2мм до 1.5мм. Меньше 0.2- температурное расширение материала может существенно изменить параметры трансформатора. Больше 1.5мм — написал выше.

Выбирая магнитопровод, а именно сравнивая различные модели, только по поперечному сечению керна (Ae), можно упустить из виду то, что длина магнитной линии тоже влияет на Al при том-же сечении, и зазоре.

Например магнитопровод PQ2620 имеет площадь сечения керна 122мм.кв, а ETD34 только 97мм.кв., но длины магнитных линий этих магнитопроводов различны, и через ETD34 можно так-же успешно прокачать 100Вт, как и через PQ2620. Я к тому, что берите и подставляйте в расчетку все феррриты, что находятся вблизи тех размеров, что, как вам кажется, могут прокачать желаемую мощность.
После расчета магнитной индукции в расчетке идет расчет количества витков вторичной обмотки и вспомогательной обмотки, на них специально останавливаться не буду, методология та-же, что и ранее.

Я надеюсь написанное выше будет вам полезно. Разработка ИИП это огромный пласт прикладной науки, и сия «расчетка» лишь маленький листик одного из талмудов, в котором собран весь опыт человечества, но она крайне полезна в прикладном плане, для разработки простеньких «флайбэков».

Моя «расчетка» (а на самом деле не моя, а унаследованная от идейного вдохновителя) довольно примитивный инструмент, поэтому я могу порекомендовать использовать сборник программ Владимира Денисенко, что легко находятся через поисковик. Тех, кто «рубит» в «силовой» теме, и имеет что сказать- вэлкам в коменты. Любая критика приветствуется!

Что непонятно — спрашивайте, я дополню статью более детальными объяснениями.

43. Явление взаимной индукции. Трансформатор.

Рассмотрим два неподвижных контура (1 и 2), которые расположены достаточно близко друг от друга (рис. 1). Если в контуре 1 протекает ток I₁, то магнитный поток, который создавается этим током (поле, создающее этот поток, на рисунке изображено сплошными линиями), прямо пропорционален I₁. Обозначим через Ф₂₁ часть потока,пронизывающая контур 2. Тогда   (1) 

где L₂₁ — коэффициент пропорциональности. 

Если ток I₁ меняет свое значение, то в контуре 2 индуцируется э.д.с. ξ_i2 , которая по закону Фарадея будет равна и противоположна по знаку скорости изменения магнитного потока Ф₂₁, который создается током в первом контуре и пронизыващет второй:   

Аналогичным образом, при протекании в контуре 2 тока I₂ магнитный поток (его поле изображено на рис. 1 штрихами) пронизывает первый контур. Если Ф₁₂ — часть этого потока, который пронизывает контур 1, то   

Если ток I₂ меняет свое значение, то в контуре 1 индуцируется э.д.с. ξ_i1 , которая равна и противоположна по знаку скорости изменения магнитного потока Ф₁₂, который создается током во втором контуре и пронизывает первый:   

Явление возникновения э.д.с. в одном из контуров при изменении силы тока в другом называется взаимной индукцией. Коэффициенты пропорциональности L₂₁ и L₁₂ называются взаимной индуктивностью контуров. Расчеты, которые подтверждены опытом, показывают, что L₂₁ и L₁₂ равны друг другу, т. е. 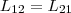  (2) 

Коэффициенты пропорциональности L₁₂ и L₂₁ зависят от размеров, геометрической формы, взаимного расположения контуров и от магнитной проницаемости среды, окружающей контуры. Единица взаимной индуктивности та же, что и для индуктивности, — генри (Гн). 

Н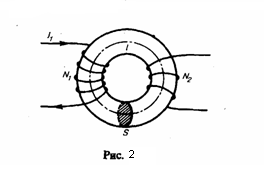айдем взаимную индуктивность двух катушек, которые намотаны на общий тороидальный сердечник. Этот случай имеет большое практическое значение (рис. 2). Магнитная индукция поля, которое создавается первой катушкой с числом витков N₁, током I₁ и магнитной проницаемостью μ сердечника, B = μμ₀(N₁I₁/l) где l — длина сердечника по средней линии. Магнитный поток сквозь один виток второй катушки Ф₂ = BS = μμ₀(N₁I₁/l)S 

Значит, полный магнитный поток (потокосцепление) сквозь вторичную обмотку, которая содержит N₂ витков,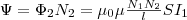   

Поток Ψ создается током I₁, поэтому, используя (1), найдем 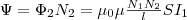  (3) 

Если рассчитать магнитный поток, который создавается катушкой 2 сквозь катушку 1, то для L₁₂ получим выражение в соответствии с формулой (3). Значит, взаимная индуктивность двух катушек, которые намотаны на общий тороидальный сердечник,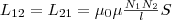   

Трансформа́тор (от лат. transformo — преобразовывать) — это статическое электромагнитное устройство, имеющее две или более индуктивно связанных обмоток на каком-либо магнитопроводе и предназначенное для преобразования посредствомэлектромагнитной индукции одной или нескольких систем (напряжений) переменного тока в одну или несколько других систем (напряжений) переменного тока без изменения частоты системы (напряжения) переменного тока

Закон Фарадея

См. также: Электромагнитная индукция

ЭДС, создаваемая во вторичной обмотке, может быть вычислена по закону Фарадея, который гласит, что:

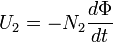
Где

U₂ — Напряжение на вторичной обмотке,

N₂ — число витков во вторичной обмотке,

Φ — суммарный магнитный поток, через один виток обмотки. Если витки обмотки расположены перпендикулярно линиям магнитного поля, то поток будет пропорционален магнитному полю B и площади S через которую он проходит.

ЭДС, создаваемая в первичной обмотке, соответственно:

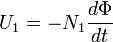
Где

U₁ — мгновенное значение напряжения на концах первичной обмотки,

N₁ — число витков в первичной обмотке.

Поделив уравнение U₂ на U₁, получим отношение^[6]:

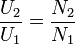
1. Взаимоиндукция — основа работы трансформаторов | 9. Трансформаторы | Часть2

1. Взаимоиндукция — основа работы трансформаторов

Взаимоиндукция — основа работы трансформаторов

Давайте предположим, что мы намотали катушку изолированного провода вокруг замкнутого ферромагнитного материала и возбудили ее от источника переменного напряжения:

 

Изолированная обмотка на замкнутом ферромагнетике обладает индуктивным реактивным сопротивлением, ограничивающим переменный ток

 

Мы ожидаем, что катушка индуктивности с железным сердечником будет противостоять приложенному напряжению своим индуктивным реактансом, ограничивающим ток через катушку согласно уравнениям, X_L = 2πfL и I=U/X (или I=U/Z). Чтобы лучше понять этот пример, мы должны более детально рассмотреть взаимодействие напряжения, тока и магнитного потока в устройстве.

Второй закон Кирхгофа нам говорит, что Алгебраическая сумма всех напряжений любой замкнутой цепи должна равняться нулю. В нашем примере, мы применим этот фундаментальный закон электричества для описания соответствующих напряжений источника питания и катушки индуктивности. Здесь (как и в любой цепи, состоящей из одного источника питания и одной нагрузки) напряжение на нагрузке должно равняться напряжению, подаваемому от источника питания, при условии нулевого падения напряжения на сопротивлении соединительных проводов. Другими словами, нагрузка (катушка индуктивности) должна произвести напряжение, противостоящее напряжению источника и равное ему по величине. Алгебраическая сумма этих двух напряжений цепи должна равняться нулю. Откуда же берется это противостоящее напряжение? Если бы нагрузкой был обычный резистор (рисунок (б) выше), то падение напряжения на нем происходило бы от потери электрической энергии (за счет «трения» электронов, проходящих через сопротивление). В идеальной катушке индуктивности (в которой отсутствует сопротивление провода), противостоящее напряжение возникает за счет другого механизма — реакции на изменение магнитного потока в железном сердечнике. Когда переменный ток изменяется, магнитный поток также изменяется. Изменение потока вызывает возникновение встречной ЭДС.

Майкл Фарадей открыл математическую связь между магнитным потоком (Ф) и наведенным напряжением в следующем уравнении:

 

 

Мгновенное напряжение (падение напряжения в любой момент времени) на катушке равно количеству витков провода этой катушки вокруг сердечника (N), умноженному на мгновенную скорость изменения магнитного потока (dΦ/dt). Графически это выглядит как последовательность синусоидальных волн (предполагается, что используется синусоидальный источник напряжения), в которой волна потока на 90^o отстает от волны напряжения:

 

Магнитный поток отстает от приложенного напряжение на 90 °, поскольку поток пропорционален скорости изменения dΦ/dt.

 

Магнитный поток в ферромагнитном материале аналогичен току в проводнике: он должен быть мотивирован некоторой силой. В электрических цепях такой силой является напряжение (электродвижущая сила или ЭДС). В магнитных «схемах» этой силой является магнитодвижущая сила, или МДС. Магнитодвижущая сила (МДС) и магнитный поток (Φ) связаны друг с другом таким свойством магнитных материалов, как магнитное сопротивление (обозначается буквой «R»):

 

 

В нашем примере, МДС, необходимая для создания переменного магнитного потока (Φ), должна создаваться переменным током, проходящим через катушку. Магнитодвижущая сила, созданная электромагнитной катушкой, равна величине проходящего через данную катушку тока (в амперах), умноженному на число витков этой катушки вокруг сердечника (единица СИ для МДС — ампер-виток). Поскольку математическая зависимость между магнитным потоком и МДС, так же, как и математическая зависимость между МДС и током, прямо пропорциональна (в обоих уравнениях скорость изменения отсутствует), ток через катушку будет в одной фазе с волной потока:

 

 

Волна переменного тока, проходящего через катушку индуктивности, отстает от волны приложенного напряжения на 90^o по той простой причине, что это необходимо для создания переменного магнитного потока, скорость изменения которого вызывает напряжение, противоположное по фазе приложенному. Благодаря своей функции создания магнитодвижущей (намагничивающей) силы для сердечника, этот ток иногда называют током намагничивания.

Стоит отметить, что ток, проходящий через катушку индуктивности с железным сердечником, не является абсолютно синусоидальным благодаря нелинейной кривой намагничивания В(Н) железа. Фактически, если используется недорогая катушка индуктивности с небольшим количеством железа, плотность магнитного потока может достигнуть таких высоких уровней (приближающихся к насыщению), при которых волна тока намагничивания будет выглядеть примерно так:

 

 

 

Когда плотность потока приближается к насыщению, форма волны тока намагничивания становится искаженной.

 

Когда ферромагнитный материал приближается к магнитному насыщению (насыщению магнитного потока), для обеспечения равного увеличения магнитного потока (Ф) требуются непропорционально большие уровни магнитодвижущей силы (МДС). Поскольку МДС пропорциональна проходящему через катушку току (МДС = NI, где «N» — число витков провода в катушке, а «I» — ток через неё), большое увеличение МДС, необходимое для нужного увеличения потока, приводит к большому увеличению тока катушки. Таким образом, ток катушки резко возрастает на пиках (для поддержания неискаженной формы волны потока), что объясняет колоколообразные полупериоды его волны в вышеприведенном графике.

Ситуация еще более осложняется потерями энергии внутри железного сердечника. Эффекты гистерезиса и вихревых токов усугубляют дальнейшее искажение и усложнение волны тока, делая ее еще менее синусоидальной и изменяя ее фазу (она отстает от приложенного напряжения немного меньше, чем на 90^o). Этот ток катушки, возникающий из суммы всех магнитных эффектов в сердечнике (намагниченность, гистерезисные потери, потери на вихревые токи и т.д.), называется током намагничивания. Искажение тока намагничивания железного сердечника катушки может быть минимизировано, если он спроектирован и работает при очень низких плотностях потока. Иначе говоря, для этого требуется сердечник с большой площадью поперечного сечения, что делает катушку громоздкой и дорогостоящей. Ради простоты мы предположим, что в нашем примере сердечник далек от насыщения и не имеет потерь, что приводит к синусоидальному току намагничивания.

В разделе Катушки индуктивности мы с вами уже видели, что если волна тока на 90^o не совпадает по фазе с волной напряжения, то это создает условие, при котором катушка индуктивности попеременно поглощает энергию и возвращает ее обратно в цепь. Если катушка индуктивности идеальна (в ней отсутствует сопротивление провода, отсутствуют потери в магнитном сердечнике и т.д.), она будет рассеивать нулевую мощность. 

А теперь давайте рассмотрим то же самое индуктивное устройство, только с двумя катушками, намотанными вокруг одного железного сердечника. Первая катушка здесь будет называться первичной обмоткой, а вторая — вторичной:

 

 

Если вторичная обмотка испытывает такое же изменение магнитного потока, как и первичная (а так и должно быть, при условии идеальной локализации магнитного потока через общий сердечник) и имеет такое же количество витков вокруг сердечника, то в ней будет индуцироваться напряжение, равное приложенному по величине и по фазе. На следующем графике волна индуцированного (наведенного) напряжения имеет немного меньшую амплитуду, чем волна напряжения источника. Это сделано для того, чтобы отличить одно напряжение от другого:

 

 

Этот эффект называется взаимоиндукцией: возникновение напряжения в одной катушке в ответ на изменение тока в другой катушке.  Взаимоиндукция измеряется в Генри и обозначается заглавной буквой «M»:

 

 

Во вторичной обмотке тока не будет, поскольку она разомкнута. Однако, если мы подключим к ней нагрузочный резистор, через обмотку пойдет переменный ток, и он будет синфазен с индуцированным напряжением (поскольку напряжение на резисторе и ток через него всегда синфазны друг с другом).

 

 

Можно предположить, что ток вторичный обмотки вызовет дополнительный магнитный поток в сердечнике. На самом деле это не так. Если в сердечнике возникнет больше магнитного потока, то это приведет к увеличению напряжения, индуцированного напряжением первичной обмотки (помните, что u = dФ/dt). Такого не может быть, поскольку индуцированное первичной обмоткой напряжение должно иметь одну и ту же величину, и фазу, чтобы находиться в балансе с приложенным напряжением в соответствии со вторым законом Кирхгофа. Следовательно, ток вторичной обмотки не может влиять на магнитный поток в сердечнике. Однако, этот ток изменит суммарную МДС в магнитопроводе.

При движении электронов по проводу всегда возникает магнитодвижущая сила. Обычно, в соответствии с «магнитным Законом Ома» (МДС = ФR), магнитодвижущая сила сопровождается магнитным потоком. В нашем случае, однако, дополнительный поток не допустим, а это значит, что единственным условием существования МДС вторичной обмотки является произведенная первичной обмоткой противодействующая МДС, которая имеет такую же величину, но противоположную фазу. И это происходит на самом деле: переменный ток, возникающий в первичной обмотке (на 180^o несовпадающий по фазе с током вторичной обмотки) создает противодействующую МДС и предотвращает дополнительный поток в сердечнике. Знаки полярности и стрелки направления тока добавлены к иллюстрации для уточнения фазовых соотношений:

 

 

Если вы считаете этот процесс немного запутанным, не беспокойтесь. Динамика трансформатора — сложный вопрос. Важно понимать следующее: когда переменное напряжение подается на первичную обмотку, в сердечнике возникает магнитный поток, индуцирующий переменное напряжение во вторичной обмотке (синфазное с напряжением источника). Любой ток, проходящий через вторичную обмотку (при подключении нагрузки), индуцирует соответствующий ток в первичной обмотке, забирая его из источника.

Обратите внимание на то, что первичная обмотка ведет себя как нагрузка по отношению к источнику переменного напряжения, а вторичная обмотка ведет себя как источник относительно резистора. Вместо того, чтобы энергия поочередно поглощалась и возвращалась в цепь первичной обмотки, эта энергия теперь переходит во вторичную обмотку, с которой она подается на диссипативную (энергоемкую) нагрузку. Конечно, существует и дополнительный ток первичной обмотки (отстающий от приложенного напряжения на 90^o), которого достаточно для намагничивания сердечника и создания напряжения, необходимого для баланса с источником (ток намагничивания).

Такой тип устройств называется трансформаторами, поскольку они преобразует электрическую энергию в магнитную энергию, а затем снова в электрическую. Так как работа трансформатора зависит от электромагнитной индукции между двумя неподвижными катушками, а также от магнитного потока переменной величины и «полярности», все трансформаторы обязательно являются устройствами переменного тока. Условное обозначение трансформатора представляет собой две катушки индуктивности, разделенные общим магнитным сердечником:

 

 

На этом условном обозначении легко различимы две катушки индуктивности. Пара вертикальных линий представляют собой общий для обеих катушек железный сердечник. Несмотря на то, что многие трансформаторы имеют сердечники из ферромагнитных материалов, существуют и такие, которые  сердечников не имеют вовсе, составляющие их катушки магнитно связаны друг с другом по воздуху.

На следующей фотографии показан силовой трансформатор такого типа, который используется в газоразрядных источниках освещения. Здесь хорошо видны две катушки индуктивности, намотанные вокруг железного сердечника.

 

Как видите, провода обоих катушек имеют медно-красное лаковое покрытие. Верхняя катушка по размеру больше нижней, она содержит большее количество витков провода вокруг сердечника. Катушки индуктивности в трансформаторах очень часто упоминаются как обмотки. В рассмотренном нами примере силовая катушка (подключенная к источнику напряжения) называется первичной обмоткой, а несиловая — вторичной обмоткой. 

На фотографии ниже показан поперечный разрез трансформатора. Здесь вы можете увидеть железный сердечник в разрезе и две обмотки. Первичная и вторичная обмотки в этом трансформаторе так же отличаются по размеру и имеют разное количество витков. Диаметр проводов у первичной и вторичной обмоток тоже разный. Причину различия диаметра проводов в обмотках мы рассмотрим несколько позже. Кроме того, железный сердечник данного трансформатора сделан из множества тонких пластин (ламинаций), а не из сплошного куска железа. Причина этого также будет объяснена позже.

 

 

Работу простого трансформатора легко продемонстрировать при помощи программы SPICE. Для этого мы представим первичную и вторичную обмотки симулируемого трансформатора в виде пары «взаимосвязанных» катушек индуктивности (рисунок ниже). Коэффициент связи магнитного поля, приведенный в конце строки «k» SPICE описания цепи, в нашем примере устанавливается очень близким к идеальному (1.000). Этот коэффициент описывает, насколько тесно две катушки индуктивности «связаны» магнитно. Чем лучше магнитная связь между двумя катушками, тем эффективнее будет передача энергии между ними.

 

 

transformer
v1 1 0 ac 10 sin
rbogus1 1 2 1e-12 
rbogus2 5 0 9e12  
l1 2 0 100      
l2 3 5 100     
** This line tells SPICE that the two inductors  
** l1 and l2 are magnetically “linked” together
k l1 l2 0.999          
vi1 3 4 ac 0      
rload 4 5 1k    
.ac lin 1 60 60 
.print ac v(2,0) i(v1)  
.print ac v(3,5) i(vi1) 
.end    

 

Примечание: резисторы Rbogus необходимы для правильной работы программы SPICE. Первый из них разрывает непрерывную цепь между источником напряжения и L₁ (непрерывная цепь в этом случае недопустима программой SPICE). Второй обеспечивает необходимое заземление вторичной цепи (на узел под номером 0), поскольку SPICE не может функционировать с незаземленными цепями.

 

freq          v(2)        i(v1)       
6.000E+01     1.000E+01   9.975E-03   Primary winding
 
freq          v(3,5)      i(vi1)      
6.000E+01     9.962E+00   9.962E-03   Secondary winding

 

Обратите внимание, что при одинаковой индуктивности обеих обмоток (по 100 Генри каждая), переменные напряжения и токи на них почти равны. Разница между токами первичной и вторичной обмоток — это ток намагничивания, о котором говорилось ранее: запаздывающий на 90^о ток, необходимый для намагничивания сердечника. Этот ток обычно очень мал по сравнению с вызванным нагрузкой первичным током, поэтому, первичный и вторичный токи практически равны. То, что вы видите здесь, вполне типично для эффективности трансформаторов. Эффективность менее 95% считается плохой для современных конструкций силовых трансформаторов, в которых передача энергии происходит без движущихся частей или других компонентов, подверженных износу.

Если мы уменьшим сопротивление нагрузки, чтобы получить больший ток во вторичной обмотке (при том же напряжении), то мы увидим ответное увеличение тока в первичной обмотке. Несмотря на то, что источник переменного напряжения напрямую не подключен к сопротивлению нагрузки (скорее, он электромагнитно «связан»), величина тока, потребляемого от источника, будет почти такой же, как и величина тока, которая потреблялась бы напрямую связанной с источником нагрузкой. Рассмотрите внимательно два следующих SPICE моделирования, которые покажут вам процессы, происходящие при разных значениях нагрузочных резисторов:

 

transformer   
v1 1 0 ac 10 sin
rbogus1 1 2 1e-12       
rbogus2 5 0 9e12
l1 2 0 100      
l2 3 5 100      
k l1 l2 0.999   
vi1 3 4 ac 0    
** Note load resistance value of 200 ohms
rload 4 5 200        
.ac lin 1 60 60 
.print ac v(2,0) i(v1)  
.print ac v(3,5) i(vi1) 
.end    

freq          v(2)        i(v1)       
6.000E+01     1.000E+01   4.679E-02
 
freq          v(3,5)      i(vi1)      
6.000E+01     9.348E+00   4.674E-02

 

Обратите внимание на почти равные значения первичного и вторичного токов. Если в нашем первом моделировании оба тока были приблизительно 10 мА, то теперь их величина составляет около 47 мА. Во втором моделировании оба тока ближе к обоюдному равенству, поскольку ток намагничивания остается таким же, как и раньше, а ток нагрузки увеличивается. Обратите также внимание на уменьшение вторичного напряжения при увеличении нагрузки (увеличении силы тока). Давайте попробуем другое моделирование с еще более низким значением сопротивления нагрузки (15 Ом):

 

transformer   
v1 1 0 ac 10 sin
rbogus1 1 2 1e-12       
rbogus2 5 0 9e12
l1 2 0 100      
l2 3 5 100      
k l1 l2 0.999   
vi1 3 4 ac 0    
rload 4 5 15    
.ac lin 1 60 60 
.print ac v(2,0) i(v1)  
.print ac v(3,5) i(vi1) 
.end    

freq          v(2)        i(v1)       
6.000E+01     1.000E+01   1.301E-01
 
freq          v(3,5)      i(vi1)      
6.000E+01     1.950E+00   1.300E-01

 

Ток нагрузки теперь составляет 0,13 А или 130 мА, что существенно выше, чем в предыдущем моделировании. Первичный ток здесь очень близок по величине ко вторичному, но обратите внимание, как значительно вторичное напряжение упало по отношению к первичному (1,95 вольт на вторичной обмотке против 10 вольт на первичной обмотке). Причина этого заключается в несовершенстве конструкции нашего трансформатора: поскольку первичная и вторичная обмотки не полностью связаны друг с другом (коэффициент k составляет 0,999 вместо 1,000), в трансформаторе присутствует индуктивность рассеяния (паразитная индуктивность). Иными словами, некоторая часть магнитного поля не связана со вторичной обмоткой, а следовательно, не может связывать с ней передаваемую энергию:

 

Индуктивность рассеяния обусловлена магнитным потоком, который не охватывает обе обмотки.

 

Следовательно, этот поток рассеяния просто сохраняет и возвращает энергию в исходную цепь через самоиндукцию, эффективно действуя как последовательный импеданс как в первичных, так и во вторичных цепях. Напряжение падает через данный последовательный импеданс, что приводит к уменьшению напряжению нагрузки: напряжение на нагрузке «проседает» по мере увеличения тока нагрузки.

 

Эквивалентная схема показывает индуктивность рассеяния в качестве последовательных катушек индуктивности, независимых от «идеального трансформатора».

 

Если мы изменим конструкцию трансформатора, и сделаем лучшую магнитную связь между первичной и вторичной обмотками, то напряжения на первичной и вторичной обмотках будут намного ближе к равенству:

 

transformer  
v1 1 0 ac 10 sin
rbogus1 1 2 1e-12       
rbogus2 5 0 9e12
l1 2 0 100 
l2 3 5 100
** Coupling factor = 0.99999 instead of 0.999
k l1 l2 0.99999   
vi1 3 4 ac 0    
rload 4 5 15    
.ac lin 1 60 60 
.print ac v(2,0) i(v1)  
.print ac v(3,5) i(vi1) 
.end    

freq          v(2)        i(v1)       
6.000E+01     1.000E+01   6.658E-01

freq          v(3,5)      i(vi1)      
6.000E+01     9.987E+00   6.658E-01

 

Из этого моделирования видно, что вторичное напряжение снова становится равным первичному, а вторичный ток равен первичному. К сожалению, построить такой трансформатор в реальности очень трудно. Компромиссом здесь может быть только уменьшение индуктивности как первичной, так и вторичной обмоток. Смысл такого действия заключается в том, что меньшая индуктивность обмоток приводит к меньшей индуктивности рассеяния (которая вызывает проблемы при любой степени неэффективности магнитной связи). В результате, напряжение нагрузки у нас становится ближе к идеальному (при той же нагрузке и с таким же коэффициентом связи):

 

transformer
v1 1 0 ac 10 sin
rbogus1 1 2 1e-12       
rbogus2 5 0 9e12
** inductance = 1 henry instead of 100 henrys   
l1 2 0 1
l2 3 5 1
k l1 l2 0.999   
vi1 3 4 ac 0    
rload 4 5 15    
.ac lin 1 60 60 
.print ac v(2,0) i(v1)  
.print ac v(3,5) i(vi1) 
.end    

freq          v(2)        i(v1)       
6.000E+01     1.000E+01   6.664E-01

freq          v(3,5)      i(vi1)      
6.000E+01     9.977E+00   6.652E-01

 

Таким образом, уменьшив индуктивность первичной и вторичной обмоток, мы смогли привести напряжение на нагрузке (имеющей большую величину, а следовательно, и большой ток) почти к идеальному значению (9,997 вольт). В этот момент у вас может возникнуть вопрос: «Если уменьшение индуктивности — это все, что необходимо для достижения почти идеальной производительности трансформатора с большой нагрузкой, то зачем нужно беспокоиться об эффективной магнитной связи? Если невозможно построить трансформатор с совершенной магнитной связью, но легко сделать обмотки с низкой индуктивностью, то почему бы просто не делать все трансформаторы с низкой индуктивностью обмоток? (ведь они имеют высокую эффективность даже при плохой магнитной связи)».

Ответ на данный вопрос можно найти в следующем SPICE моделировании, в котором используются те же низкие индуктивности обмоток трансформатора, но на этот раз с более «легкой» нагрузкой (меньший ток) — 1 кОм вместо 15 Ом:

 

transformer 
v1 1 0 ac 10 sin
rbogus1 1 2 1e-12       
rbogus2 5 0 9e12
l1 2 0 1
l2 3 5 1
k l1 l2 0.999   
vi1 3 4 ac 0    
rload 4 5 1k    
.ac lin 1 60 60 
.print ac v(2,0) i(v1)  
.print ac v(3,5) i(vi1) 
.end    

freq          v(2)        i(v1)       
6.000E+01     1.000E+01   2.835E-02

freq          v(3,5)      i(vi1)      
6.000E+01     9.990E+00   9.990E-03

 

При низких значениях индуктивности обмоток трансформатора, первичные и вторичные напряжения близки к взаимному равенству, чего нельзя сказать о первичных и вторичных токах. В нашем конкретном случае первичный ток имеет величину 28,35 мА, в то время как величина вторичного тока составляет только 9,990 мА (вторичный ток почти в три раза меньше первичного). С чем это может быть связано? При малом значении индуктивности первичной обмотки, индуктивное сопротивление так же имеет малую величину, а, следовательно, гораздо больший ток намагничивания. Значительное количество тока, проходящего через первичную обмотку, работает только на намагничивание сердечника, а не на передачу полезной энергии вторичной обмотке и нагрузке.

Идеальный трансформатор (с одинаковыми первичной и вторичной обмотками) имел бы одинаковые напряжения и токи в обоих обмотках при любой нагрузке. В идеальном мире, трансформаторы передавали бы электроэнергию от первичной обмотки ко вторичной так гладко, как если бы нагрузка была подключена непосредственно к первичному источнику питания, без трансформатора вообще. Однако, такая идеальность может быть достигнута только при идеальном сочетании магнитного потока между первичной и вторичной обмотками. Поскольку в реальном мире этого достичь невозможно, трансформаторы проектируются для работы в определенных ожидаемых диапазонах напряжений и нагрузок (чтобы максимально приблизить их к идеалу). На данный момент вам важно усвоить, что основной принцип работы трансформатора заключается в передаче энергии от первичной ко вторичной цепи при помощи индуктивной связи.