Магнитное поле соленоида
Соленоидом называется совокупность N одинаковых витков изолированного проводящего провода, равномерно намотанных на общий каркас или сердечник. По виткам проходит одинаковый ток. Магнитные поля, созданные каждым витком в отдельности, складываются по принципу суперпозиции. Индукция магнитного поля внутри соленоида велика, а вне его — мала. Для бесконечно длинного соленоида индукция магнитного поля вне соленоида стремится к нулю. Если длина соленоида во много раз больше диаметра его витков, то соленоид можно практически считать бесконечно длинным. Магнитное поле такого соленоида целиком сосредоточено внутри него и является однородным (рис.6).
Величину
индукции магнитного поля внутри
бесконечно длинного соленоида можно
определить, используя теорему
о циркуляции вектора 
 по произвольному замкнутому контуру
равна алгебраической сумме токов,
охватываемых контуром, умноженной на
магнитную постоянную μо:
по произвольному замкнутому контуру
равна алгебраической сумме токов,
охватываемых контуром, умноженной на
магнитную постоянную μо: 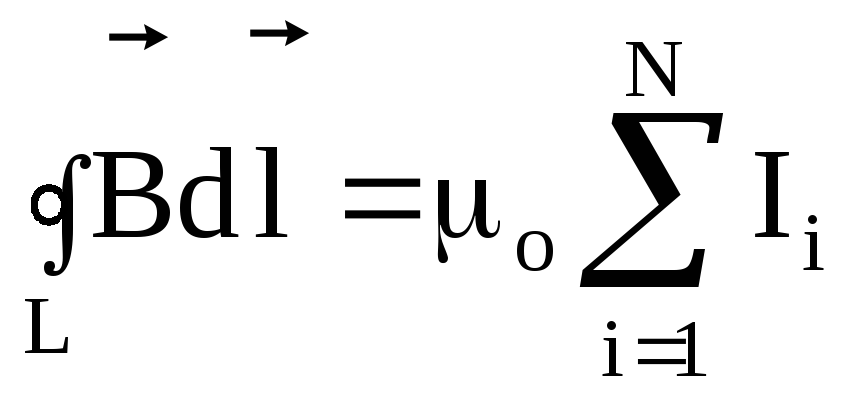 ,
(20)
,
(20)
где μ0 = 4π 10-7 Гн/м.
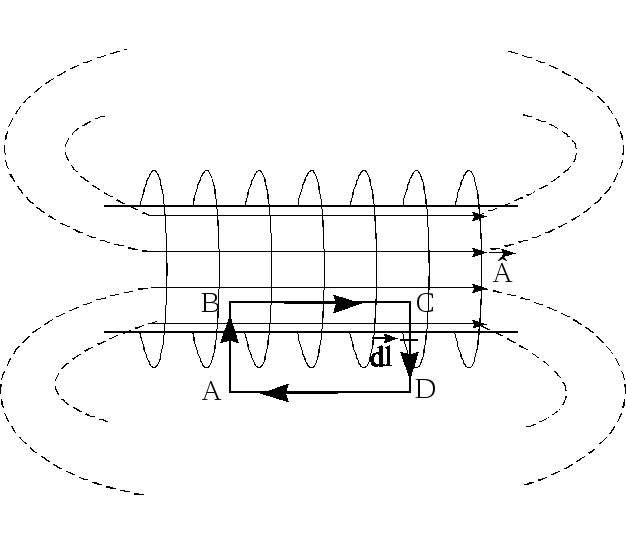
Рис.6. Магнитное поле соленоида
Для
определения величины магнитной индукции
В внутри соленоида выберем замкнутый
контур ABCD
прямоугольной формы, где 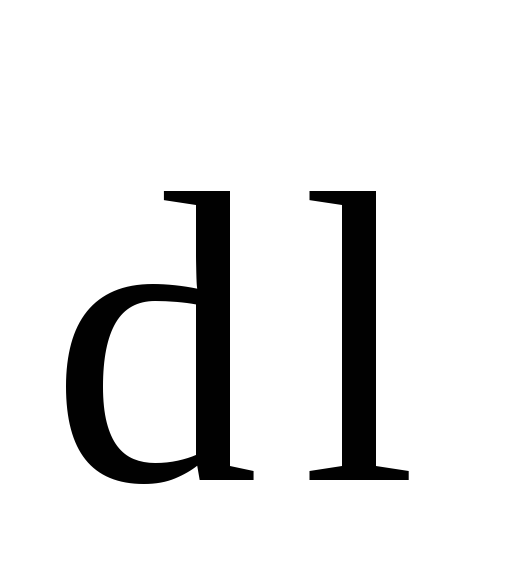
Тогда
циркуляция вектора  по замкнутому контуруABCD,
охватывающему N
витков, равна:
по замкнутому контуруABCD,
охватывающему N
витков, равна:
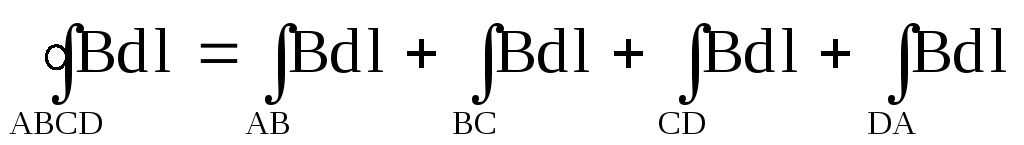 (21)
(21)
На
участках AB
и CD
произведение 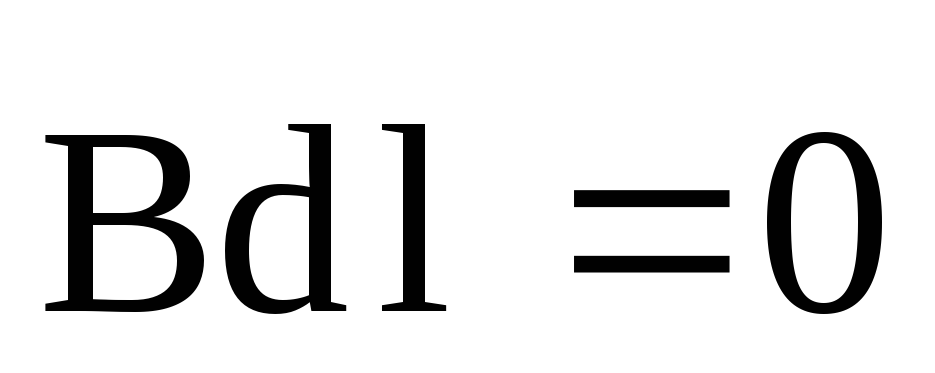
 и
и взаимно перпендикулярны. Поэтому
взаимно перпендикулярны. Поэтому  .
(22)
.
(22)
На
участке DA
вне соленоида интеграл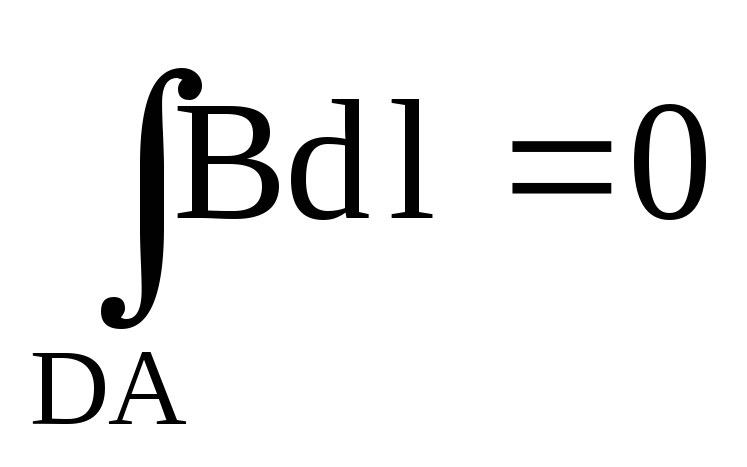 ,
так как магнитное поле вне контура
равно нулю.
,
так как магнитное поле вне контура
равно нулю.
Тогда формула (21) примет вид:
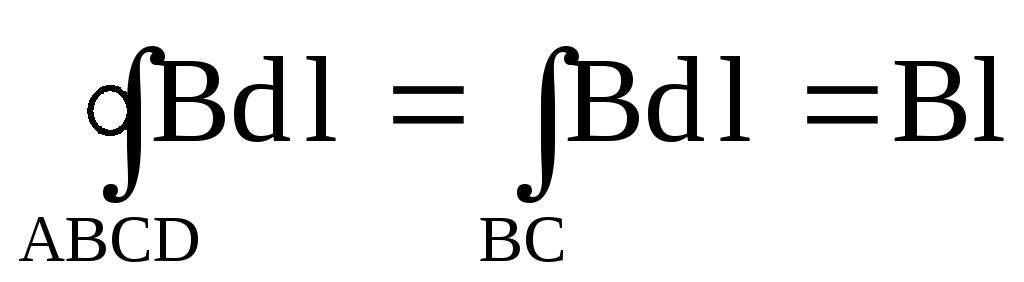 ,
(23)
,
(23)
где l – длина участка BC. Сумма токов, охватываемых контуром, равна
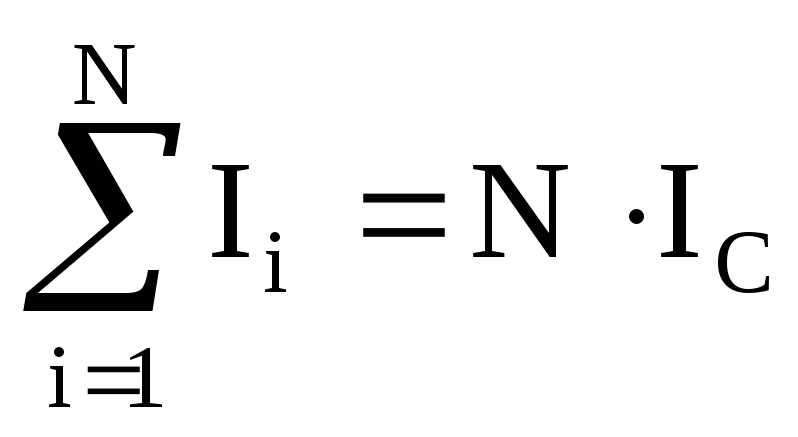 ,
(24)
,
(24)
где Ic – сила тока соленоида; N – число витков, охватываемых контуром ABCD.
Подставив (23) и (24) в (20), получим:
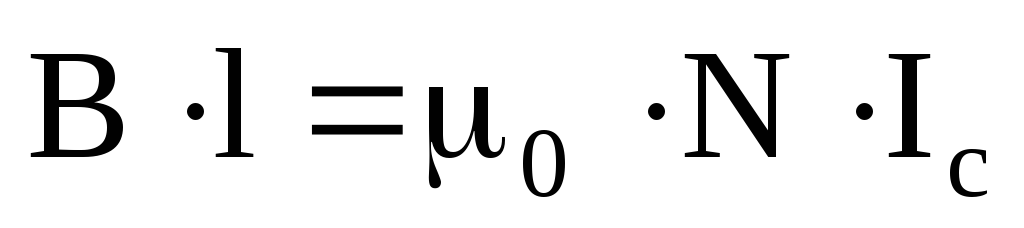 . (25)
. (25)
Из (25) получим выражение для индукции магнитного поля бесконечно длинного соленоида:
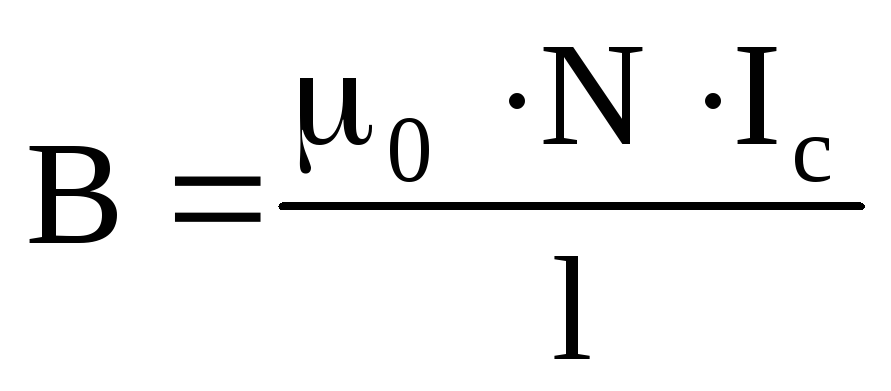 .
(26)
.
(26)
Так как число витков на единицу длину соленоида n равно:
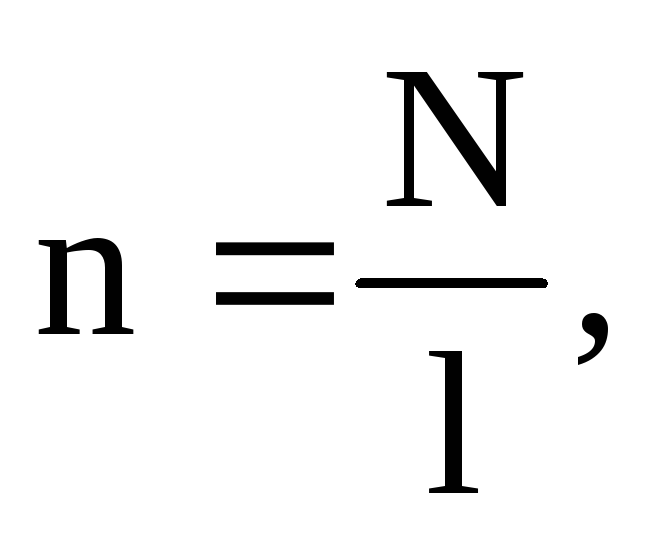 (27)
(27)
то окончательно получим:
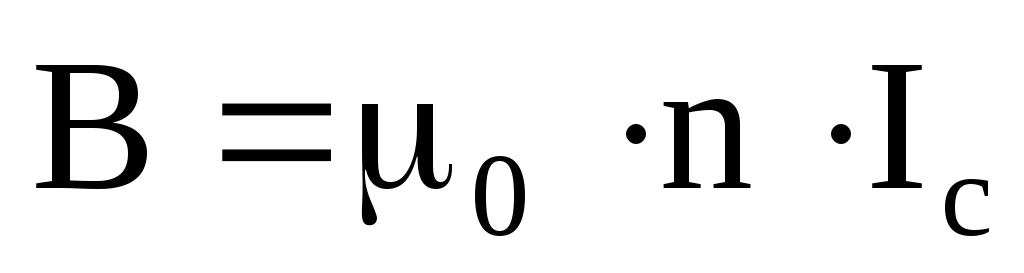 .
(28)
.
(28)
Если внутрь соленоида помещен сердечник, то формула (28) для В примет вид:
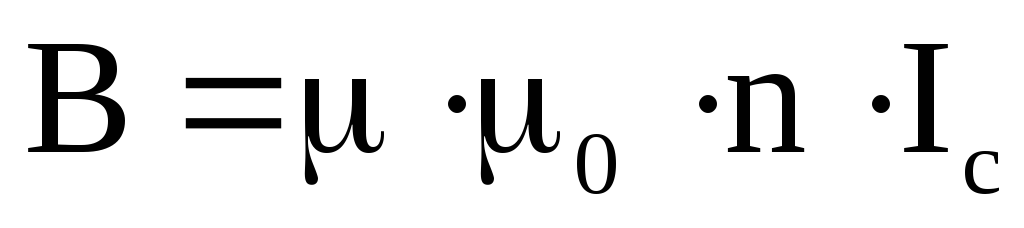
где — магнитная проницаемость материала сердечника.
Таким образом, индукция В магнитного поля соленоида определяется током соленоида Ic, числом витком n на единицу длины соленоида и магнитной проницаемостью материала сердечника.
Цилиндрический магнетрон
Магнетроном называется двухэлектродная электронная лампа (диод), содержащая накаливаемый катод и холодный анод и помещенная во внешнее магнитное поле.
Анод
диода имеет форму цилиндра радиусом 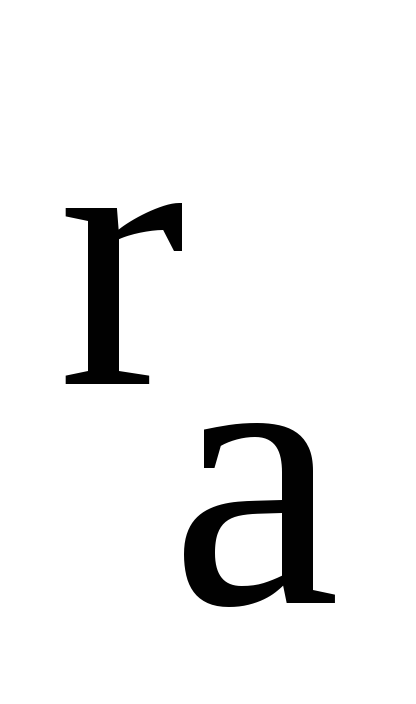
 ,
вдоль оси которого расположена нить
накала, как правило, изготавливаемая
из вольфрама (рис.7).
,
вдоль оси которого расположена нить
накала, как правило, изготавливаемая
из вольфрама (рис.7). Раскалённый
катод в результате явления термоэлектронной
эмиссии испускает термоэлектроны,
которые образуют вокруг катода электронное
облако. При подаче анодного напряжения  (рис.8),
электроны начинают перемещаться от
катода к аноду вдоль радиусов, что
приводит к возникновению анодного тока
(рис.8),
электроны начинают перемещаться от
катода к аноду вдоль радиусов, что
приводит к возникновению анодного тока

Рис.7. Схема диода
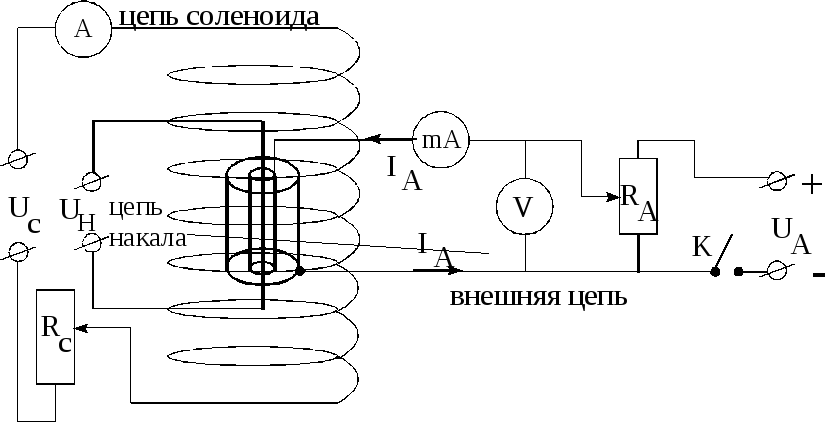 Рис.8.
Электрическая схема цепи
Рис.8.
Электрическая схема цепи
Величина анодного напряжения регулируется потенциометром RA. Чем больше анодное напряжение, тем большее количество электронов за единицу времени достигает анода, следовательно, тем больше анодный ток.
Напряжённость электрического поля Е между катодом и анодом такая же, как и в цилиндрическом конденсаторе:
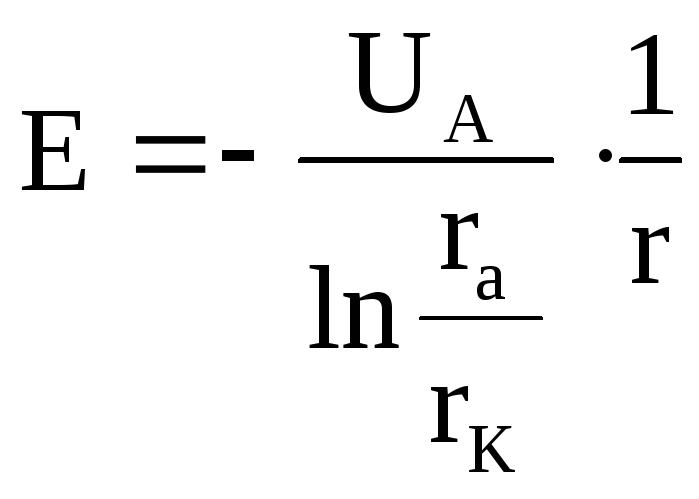 ,
(30)
,
(30)
где r – расстояние от оси катода до данной точки пространства между катодом и анодом.
Из формулы (30) следует, что напряжённость поля Е обратно пропорциональна расстоянию r до оси катода. Следовательно, напряженность поля максимальна у катода.
Так как
rк <<ra, (31)
то
значение логарифма ln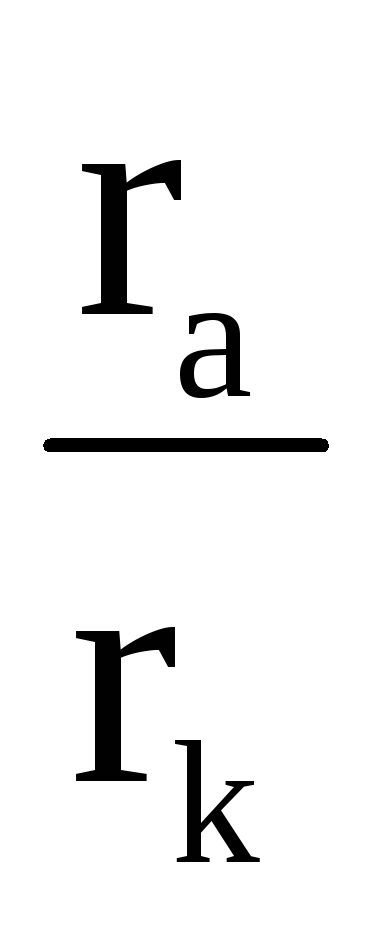
Внешнее магнитное поле, в которое помещён диод, создаётся соленоидом (рис.8). Длина соленоида l много больше диаметра его витков, поэтому поле внутри соленоида можно считать однородным. Ток в цепи соленоида изменяется с помощью потенциометра RC (рис.8) и регистрируется амперметром.
Характер движения электронов в зависимости от величины поля соленоида показан на рис.9. Если ток в цепи соленоида отсутствует, то индукция магнитного поля В = 0. Тогда электроны движутся от катода к аноду практически по радиусам.
Увеличение тока в цепи соленоида приводит к возрастанию величины В. При этом, траектории движения электронов начинают искривляться, однако все электроны достигают анода. В анодной цепи будет течь ток такой же, как и в отсутствии магнитного поля.
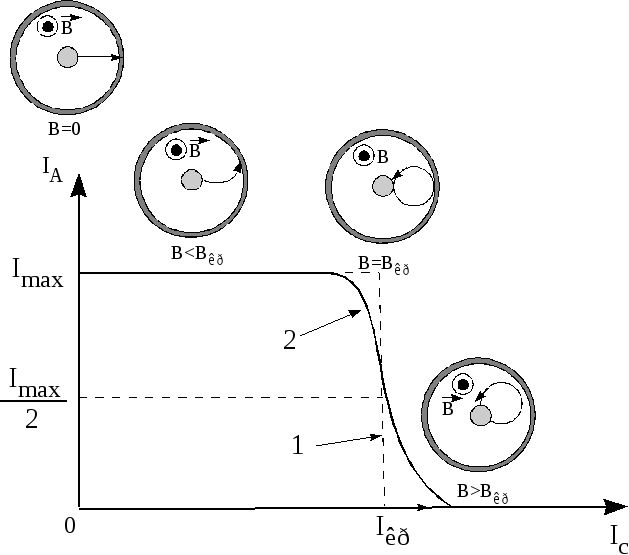
Рис.9. Зависимость анодного тока IA от величины тока соленоида Ic в идеальном (1) и реальном (2) случаях, а также характер движения электронов в зависимости от величины поля соленоида.
При некотором значении тока в соленоиде радиус окружности, по которой движется электрон, становится равным половине расстояния между катодом и анодом:
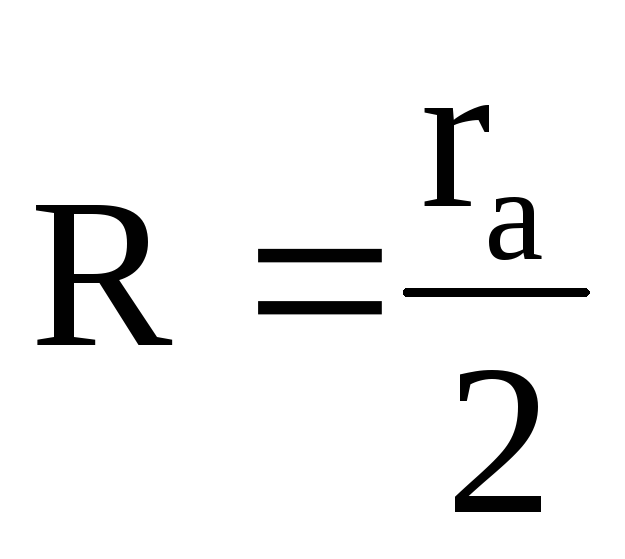 ..
(32)
..
(32)
Электроны в этом случае касаются анода и уходят к катоду (рис.9). Такой режим работы диода называется критическим. При этом по соленоиду течёт критический ток Iкр, которому соответствует критическое значение индукции магнитного поля В = Вкр.
При
В = Вкр анодный ток в идеальном случае должен
скачком уменьшиться до нуля. При В > В
Однако на практике, вследствие некоторого разброса скоростей электронов и нарушения соосности катода и соленоида, анодный ток уменьшается не скачком, а плавно (рис.9, кривая 2). При этом значение силы тока соленоида, соответствующее точке перегиба на кривой 2, считается критическим Iкр. Критическому значению тока соленоида соответствует анодный ток, равный:
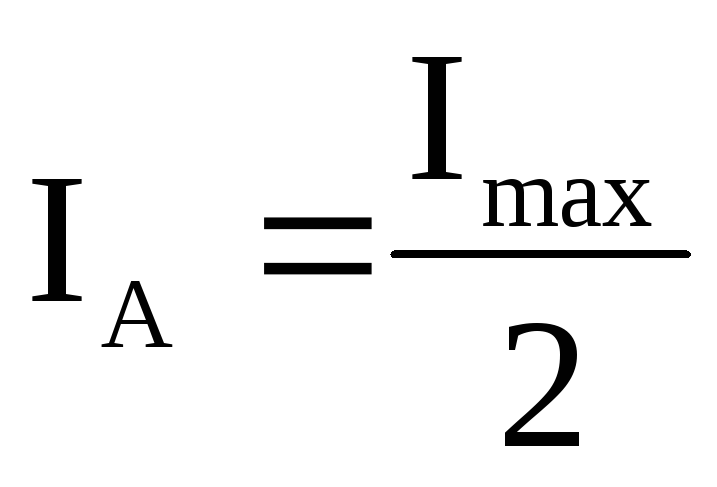 ,
(33)
,
(33)
где 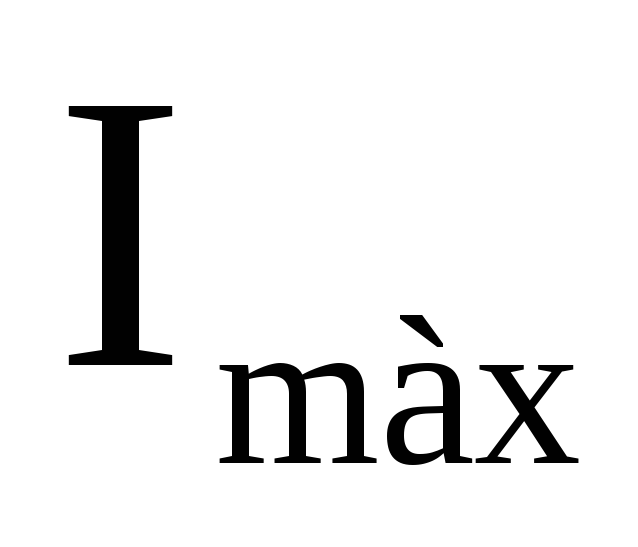 – максимальное значение анодного тока
при В = 0.
– максимальное значение анодного тока
при В = 0.
Зависимость анодного тока IA от величины индукции магнитного поля В (или от тока в соленоиде) при постоянном анодном напряжении и постоянном накале называется сбросовой характеристикой магнетрона.
Магнитное поле соленоида
Применим теорему о циркуляции вектора для вычисления простейшего магнитного поля – бесконечно длинного соленоида, представляющего собой тонкий провод, намотанный плотно виток к витку на цилиндрический каркас (рис. 2.11).
Рис. 2.11
Соленоид можно представить в виде системы одинаковых круговых токов с общей прямой осью.
Бесконечно длинный соленоид симметричен любой, перпендикулярной к его оси плоскости. Взятые попарно (рис. 2.12), симметричные относительно такой плоскости витки создают поле, в котором вектор перпендикулярен плоскости витка, т.е. линии магнитной индукции имеют направление параллельное оси соленоида внутри и вне его.
Рис. 2.12
Из параллельности вектора оси соленоида вытекает, что поле как внутри, так и вне соленоида должно быть однородным.
Возьмём воображаемый прямоугольный контур 1–2–3–4–1 и разместим его в соленоиде, как показано на рисунке 2.13.
Рис. 2.13
Второй и четвёртый интегралы равны нулю, т.к. вектор перпендикулярен направлению обхода, т.е .
Возьмём участок 3–4 – на большом расстоянии от соленоида, где поле стремится к нулю; и пренебрежём третьим интегралом, тогда
где – магнитная индукция на участке 1–2 – внутри соленоида, – магнитная проницаемость вещества.
Если отрезок 1–2 внутри соленоида, контур охватывает ток:
где n – число витков на единицу длины, I – ток в соленоиде (в проводнике).
Тогда магнитная индукция внутри соленоида:
| , | (2.7.1) |
Вне соленоида:
и , т.е. .
Бесконечно длинный соленоид аналогичен плоскому конденсатору – и тут, и там поле однородно и сосредоточено внутри.
Произведение nI – называется число ампер витков на метр.
У конца полубесконечного соленоида, на его оси магнитная индукция равна:
| , | (2.7.2) |
Практически, если длина соленоида много больше, чем его диаметр, формула (2.7.1) справедлива для точек вблизи середины, формула (2.7.2) для точек около конца.
Если же катушка короткая, что обычно и бывает на практике, то магнитная индукция в любой точке А, лежащей на оси соленоида, направлена вдоль оси (по правилу буравчика) и численно равна алгебраической сумме индукций магнитных полей создаваемых в точке А всеми витками. В этом случае имеем:
· В точке, лежащей на середине оси соленоида магнитное поле будет максимальным:
| , | (2.7.3) |
где L – длина соленоида, R – радиус витков.
· В произвольной точке конечного соленоида (рис. 2.14) магнитную индукцию можно найти по формуле
| , | (2.7.4) |
Рис. 2.14
На рисунке 2.15 изображены силовые линии магнитного поля : а) металлического стержня; б) соленоида; в) железные опилки, рассыпанные на листе бумаги, помещенной над магнитом, стремятся вытянуться вдоль силовых линий; г) магнитные полюсы соленоида.
Рис. 2.15
12.7. Магнитное поле соленоида
С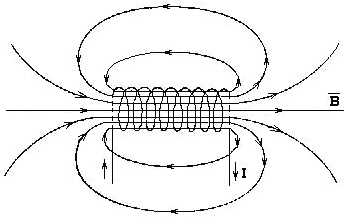 оленоид
представляет собой провод, навитый
равномерно в виде спирали на общий
цилиндрический каркас (см.
рис.
12.14).
Произведение (IN)
числа витков однослойной намотки
соленоида на силу тока, обтекающего
витки, называется числом ампер-витков.
оленоид
представляет собой провод, навитый
равномерно в виде спирали на общий
цилиндрический каркас (см.
рис.
12.14).
Произведение (IN)
числа витков однослойной намотки
соленоида на силу тока, обтекающего
витки, называется числом ампер-витков.
Рис. 12.14
Соленоиды
предназначены для создания в небольшом
объеме пространства достаточно сильного
магнитного поля. При плотной намотке
витков поле соленоида эквивалентно
полю системы круговых параллельных
токов с общей осью. Если диаметр d витков
соленоида во много раз меньше его длины
(d
l), то соленоид считается бесконечно
длинным (или тонким). Магнитное поле
такого соленоида практически целиком
сосредоточено внутри, причем вектор
магнитной индукции  внутри направлен
вдоль оси соленоида и связан с направлением
тока правилом правого винта.
внутри направлен
вдоль оси соленоида и связан с направлением
тока правилом правого винта.
Р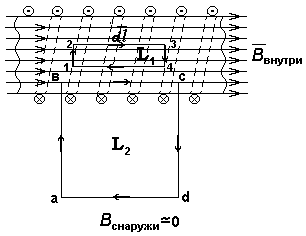 ис.
12.15
ис.
12.15
Рассмотрим
воображаемый замкнутый контур 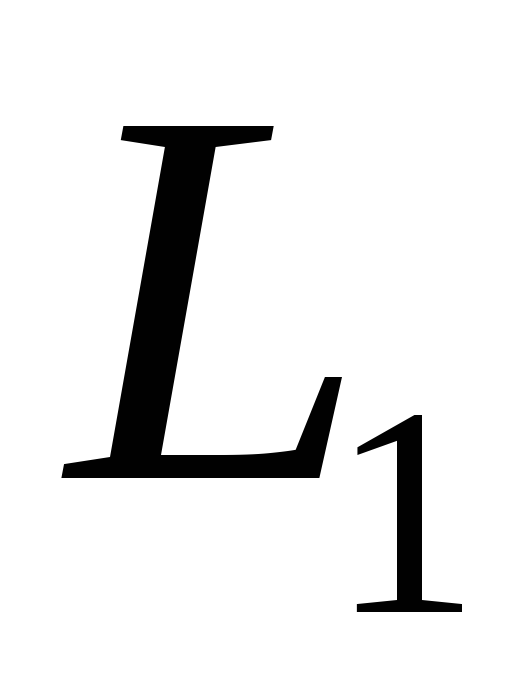 внутри соленоида (рис.
12.15). Этот
контур не охватывает токов, поэтому по
теореме о циркуляции
внутри соленоида (рис.
12.15). Этот
контур не охватывает токов, поэтому по
теореме о циркуляции
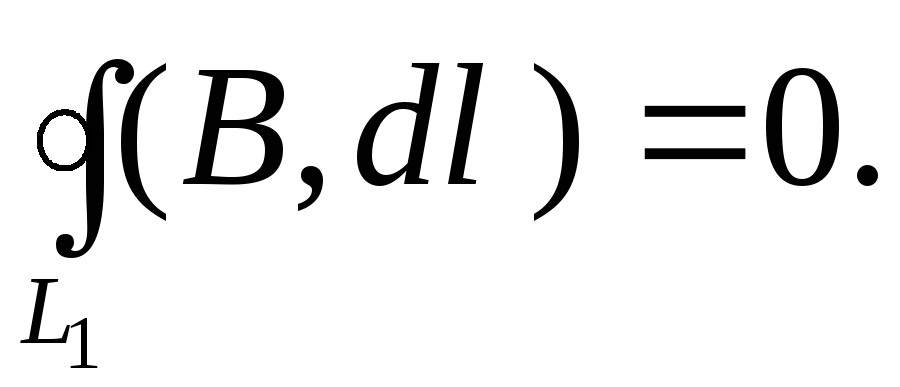
Разобьем
этот круговой интеграл на четыре
интеграла (по сторонам контура) и учтем,
что на отрезках (1-2) и (3-4) вектор  перпендикулярен
перпендикулярен ,
поэтому скалярное произведение (
,
поэтому скалярное произведение ( ,
, )
здесь обращается в ноль. Индукция поля
во всех точках отрезка (2-3) одинакова и
равна
)
здесь обращается в ноль. Индукция поля
во всех точках отрезка (2-3) одинакова и
равна 23,
а на отрезке (4-1)
23,
а на отрезке (4-1)  41,
причем l23 =
l41 = l.
41,
причем l23 =
l41 = l.
Таким образом, обойдя контур по часовой стрелке, получим
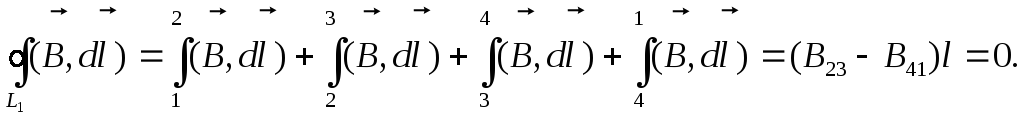
Так как l 0, то В23 = В41 = В внутри.
Поскольку контур внутри соленоида был выбран произвольно, то полученный результат справедлив для любых внутренних точек соленоида, то есть поле внутри соленоида однородное:
 внутри = const.
внутри = const.
Чтобы найти величину индукции этого поля, рассмотрим контур L2 (а –b –c –d –а ), охватывающий N витков с током (рис. 12.15). Согласно теореме о циркуляции (и на основании предыдущих рассуждений), получим соотношение
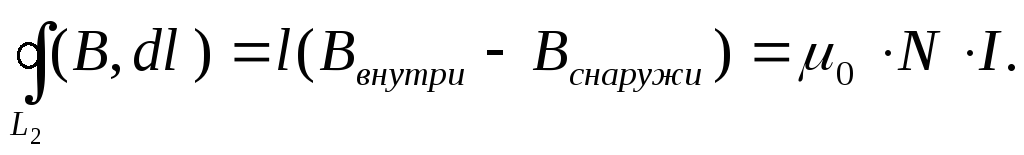
Поле
снаружи бесконечно длинного соленоида
очень слабое ( снаружи =0), им можно
пренебречь, следовательно,
снаружи =0), им можно
пренебречь, следовательно,
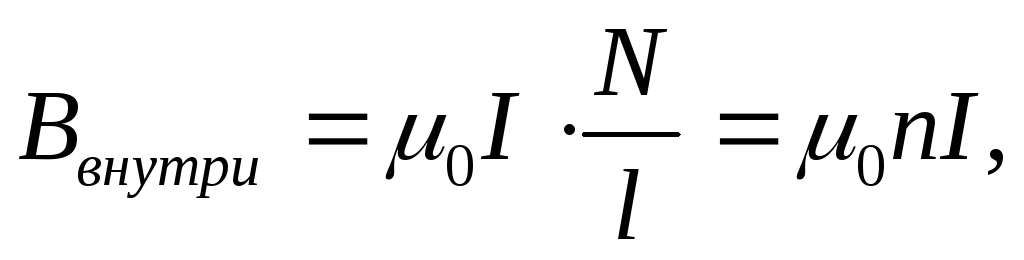 (12.35)
(12.35)
где n=N/l — число витков, приходящихся на единицу
длины соленоида.
Таким образом, индукция магнитного поля внутри бесконечно длинного соленоида одинакова по величине и направлению и пропорциональна числу ампер-витков, приходящихся на единицу длины соленоида.
Симметрично расположенные витки вносят одинаковый вклад в магнитную индукцию на оси соленоида, поэтому у конца полубесконечного соленоида на его оси магнитная индукция равна половине того значения, которое дает формула (12.35), т.е.
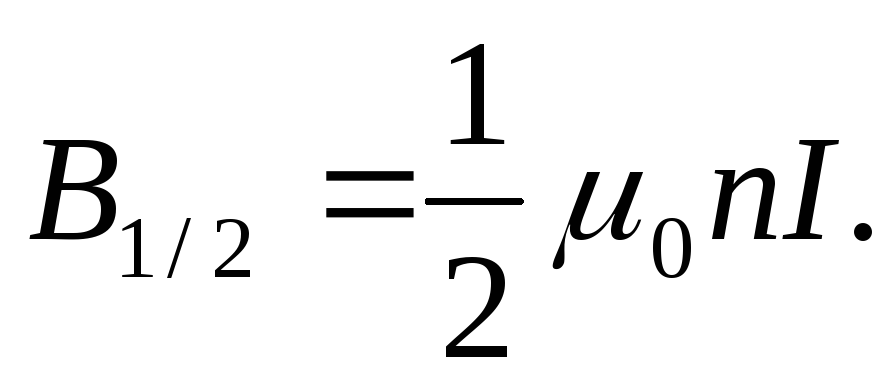 (12.36)
(12.36)
Практически, если (l d), то формула (12.35) справедлива для точек в средней части соленоида, а формула (12.36) – для точек на оси вблизи его концов.
Применяя закон Био-Савара-Лапласа, можно найти магнитную индукцию поля соленоида конечной длины (рис. 12.16) в произвольной точке А на его оси:
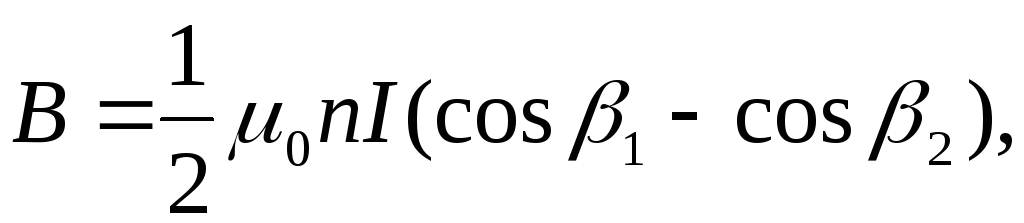 (12.37)
(12.37)
г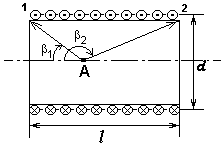 де
де — углы между осью соленоида и радиус-
вектором, проведенным из рассматриваемой
точки к концам соленоида.
— углы между осью соленоида и радиус-
вектором, проведенным из рассматриваемой
точки к концам соленоида.
Рис. 12.16
Поле
такого соленоида неоднородное, величина
индукции зависит от положения точки А и длины соленоида. Для бесконечно
длинного соленоида 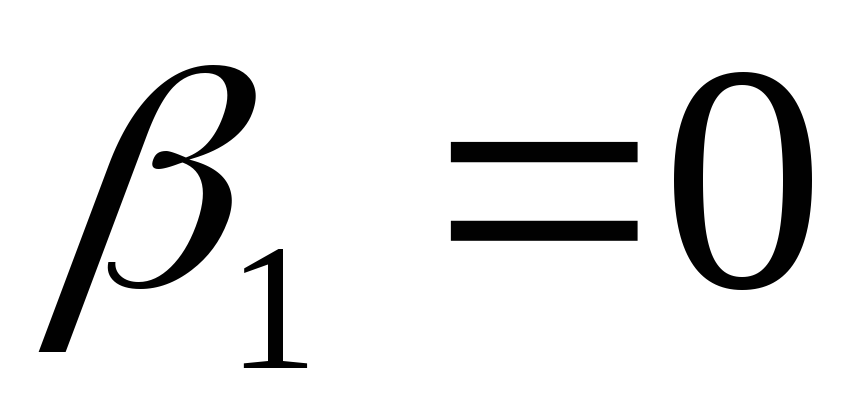 ,
,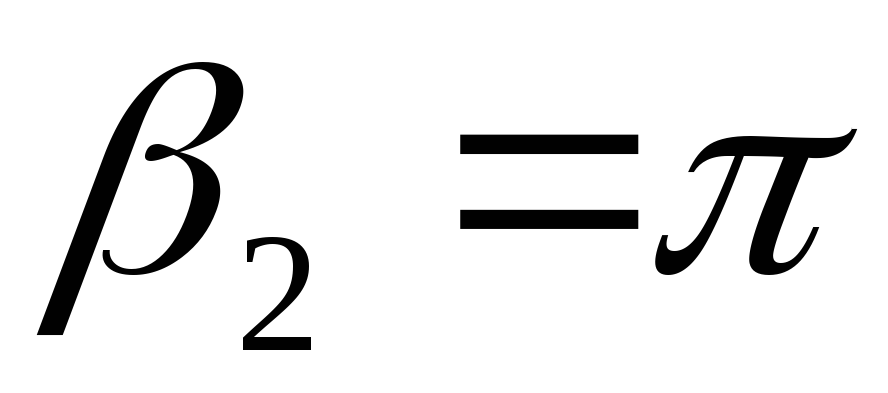 ,
и формула (12.37) переходит в формулу
(12.35).
,
и формула (12.37) переходит в формулу
(12.35).
Электричество и магнетизм
Если длина соленоида много больше его диаметра (l >> 2R), мы возвращаемся к формуле для поля в бесконечно длинном соленоиде (6.20). Относительная разница этих двух значений равна
По условию эта разница мала: , то есть мало отношение диаметра соленоида к его длине: 2R/l << 1. Поэтому можно воспользоваться формулой разложения квадратного корня
Отсюда
или
Подставляя численное значение d, находим, что разница будет менее половины процента при выполнении соотношения
Иными словами, соленоид может рассматриваться как бесконечно длинный, если его длина в двадцать или более раз превышает радиус.
Пример 2. Найти магнитное поле Ве в крайней торцевой точке оси соленоида конечной длины l. Сравнить с результатом предыдущего примера.
Решение. Магнитное поле в торцевой точке оси соленоида конечной длины l дается тем же интегралом (6.19), но теперь пределы интегрирования будут выглядеть иначе
|
(6.22) |
Отношение полей в средней и крайней точках оси соленоида равно
Это отношение всегда меньше единицы (то есть поле на торце меньше поля в середине соленоида). При l >> R имеем
Этот результат легко понять. Представим себе бесконечный соленоид, который мысленно рассекаем пополам в точке наблюдения. Можно считать, что поле в этой точке создается двумя одинаковыми «полубесконечными» соленоидами, расположенными по разные стороны от нее. Ясно, что при удалении одного из них точка наблюдения становится торцом оставшегося «полубесконечного» соленоида, а магнитная индукция в ней уменьшиться именно в два раза.
Это — так называемый краевой эффект. Пример демонстрирует, что недостаточно выполнения соотношения l >> R, чтобы пользоваться формулами для бесконечно длинного соленоида; надо еще, чтобы точка наблюдения находилась далеко от его концов.
На рис. 6.25 представлен опыт по исследованию распределения силовых линий магнитного поля вокруг соленоида. Поле соленоида, ось которого лежит в плоскости пластинки, сосредоточено в основном внутри соленоида. Силовые линии внутри имеют вид параллельных прямых вдоль оси катушки, а поле снаружи практически отсутствует.
Рис. 6.25. Визуализация силовых линий магнитного поля
Видео 6.1. Силовые линии магнитного поля проводников с током различной формы: прямой ток, соленоид, один виток.
Исследование магнитногого поля соленоида
Цель работы: экспериментальное определение значений магнитной индукции на оси соленоида и сравнение их с расчетными значениями.
Приборы и оборудование: соленоид, амперметр, источник постоянного тока, измерительная катушка, баллистический гальванометр, миллиамперметр.
Теоретическое введение
Соленоид
представляет собой катушку, по виткам
которой течет ток. Этот ток создает
магнитное поле. О причинах возникновения
магнитного поля и его свойствах прочитайте
в работе 26. Наиболее простой вид картины
силовых линий будет в случае бесконечно
длинного соленоида. Опыт показывает,
что чем длиннее соленоид, тем меньше
индукция магнитного поля вне его. Для
бесконечно длинного соленоида магнитное
поле снаружи отсутствует вообще, а
внутри его линии вектора  направлены вдоль его оси, причем линии
вектора
направлены вдоль его оси, причем линии
вектора составляют
с направлением тока правовинтовую
систему.
составляют
с направлением тока правовинтовую
систему.
Магнитное поле в точках на оси соленоида конечной длины можно рассчитать, используя закон Био-Савара-Лапласа:
Индукция
магнитного поля  ,
созданного длинным проводом произвольной
конфигурации, по которому течет токI , равна
векторной сумме индукций магнитных
полей
,
созданного длинным проводом произвольной
конфигурации, по которому течет токI , равна
векторной сумме индукций магнитных
полей  ,
созданных каждым элементом длины
,
созданных каждым элементом длины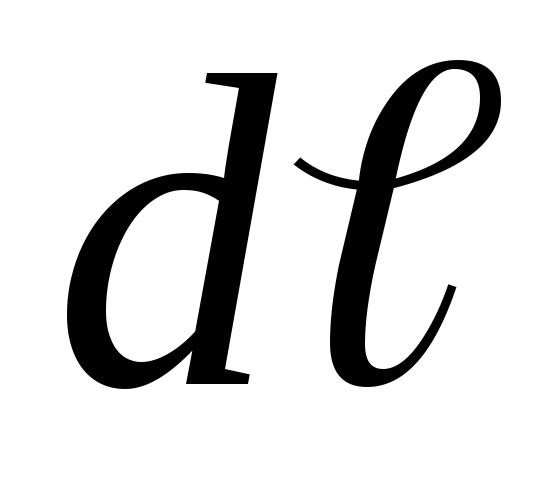 этого провода
этого провода
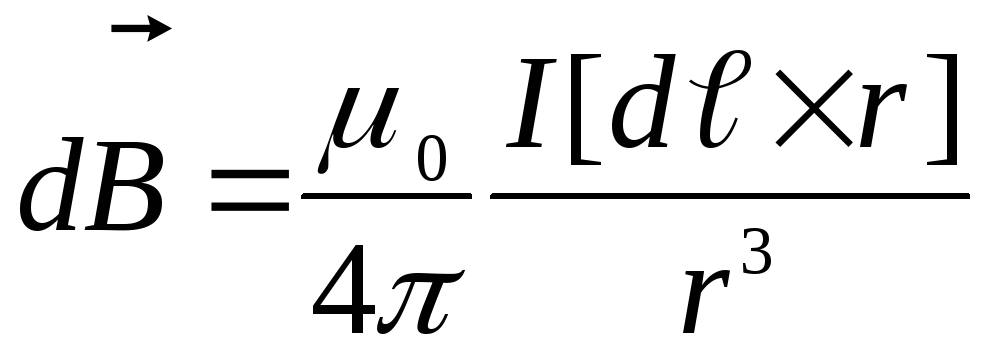 ,
(1)
,
(1)
где 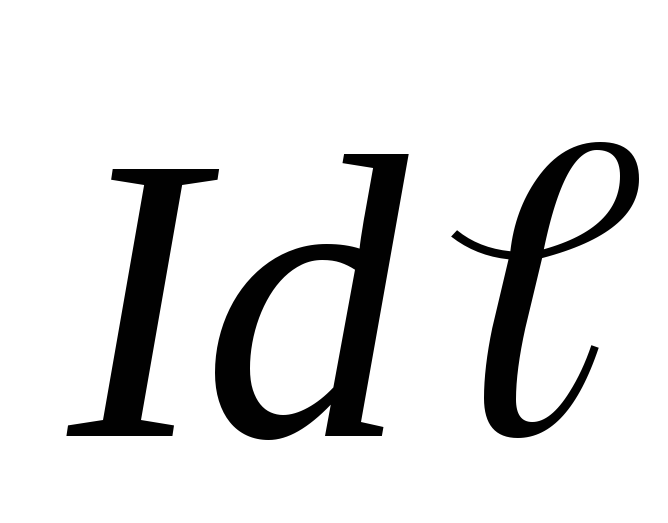 – элемент тока,
– элемент тока, – радиус-вектор, проведенный от этого
элемента до точки, в который определяем
магнитное поле. Как видно из формулы,
поле перпендикулярно плоскости, в
которой лежат радиус-вектор и элемент
тока. Модуль индукции, создаваемой
элементом тока находится по формуле
– радиус-вектор, проведенный от этого
элемента до точки, в который определяем
магнитное поле. Как видно из формулы,
поле перпендикулярно плоскости, в
которой лежат радиус-вектор и элемент
тока. Модуль индукции, создаваемой
элементом тока находится по формуле
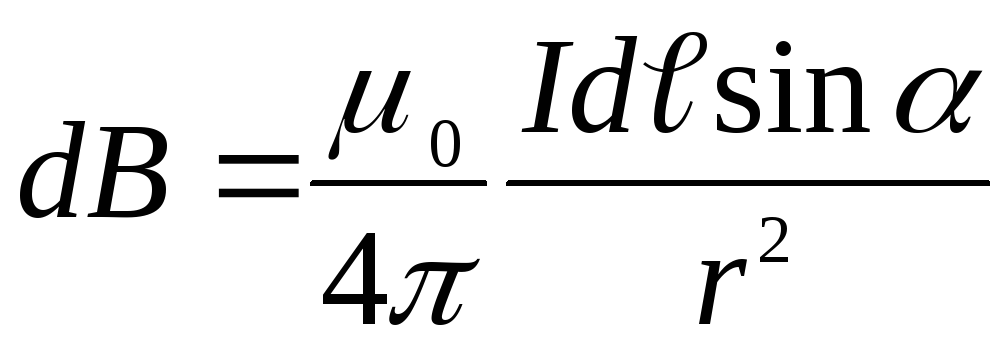 ,
(2)
,
(2)
где  – угол между радиус-вектором и элементом
тока.
– угол между радиус-вектором и элементом
тока.
Использование этого закона дает формулу
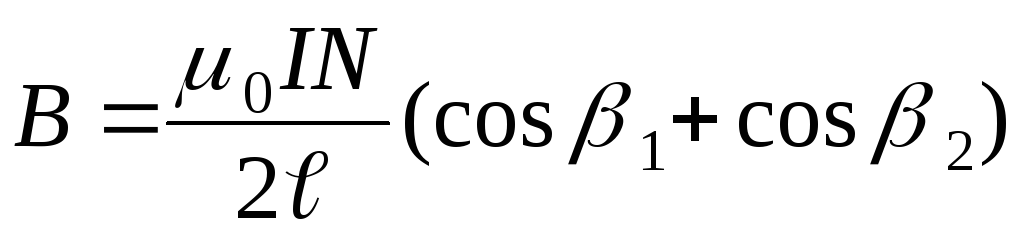 ,
(3)
,
(3)
где I – ток в соленоиде, N – полное число витков в соленоиде, 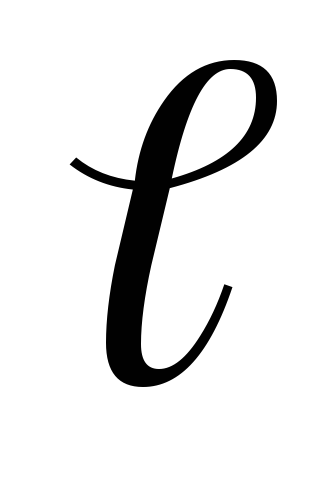 – его длина,r— радиус
соленоида, а – расстояние от края соленоида до той
точки, в которой определяется значение
магнитной индукции,
– его длина,r— радиус
соленоида, а – расстояние от края соленоида до той
точки, в которой определяется значение
магнитной индукции,
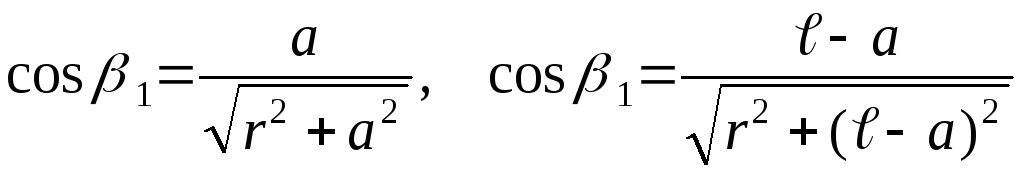 .
(4)
.
(4)
Если
длина катушки в 5 раз превосходит ее
диаметр, то магнитное поле на оси ее
почти совпадает с полем бесконечно
длинного соленоида. Для определения
магнитного поля на оси бесконечно
длинного соленоида удобнее воспользоваться
теоремой о
циркуляции вектора  .
.
Циркуляция
вектора индукции магнитного поля  по
любому замкнутому контуру равна
алгебраической сумме всех токов,
охватываемых этим контуром, умноженной
на магнитную постоянную
по
любому замкнутому контуру равна
алгебраической сумме всех токов,
охватываемых этим контуром, умноженной
на магнитную постоянную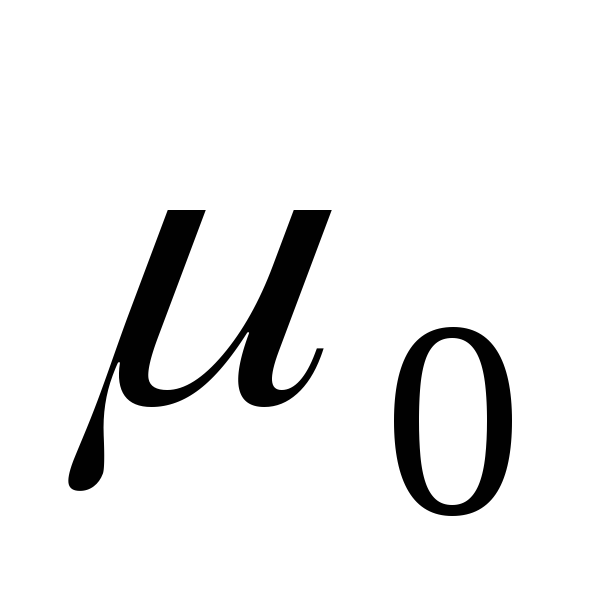
 ,
,
где 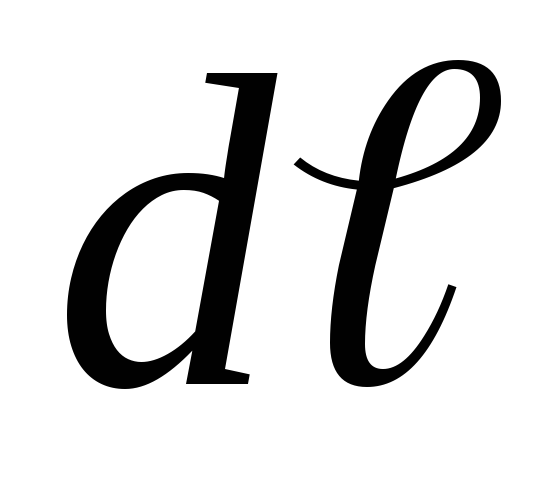 – элемент длины контура, по которому
считают циркуляцию.
– элемент длины контура, по которому
считают циркуляцию.
Следует
помнить, что 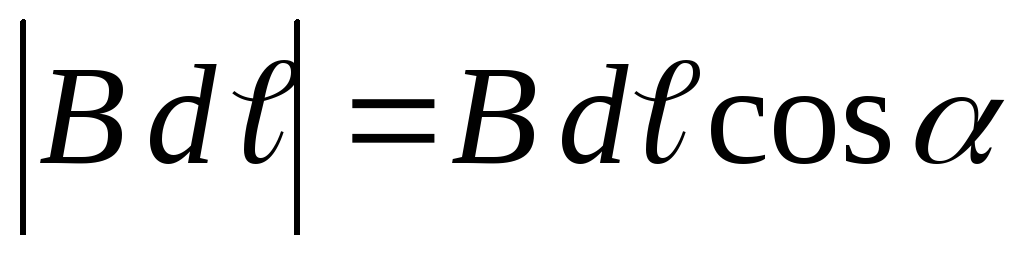 ,
где
,
где – угол между векторами
– угол между векторами и
и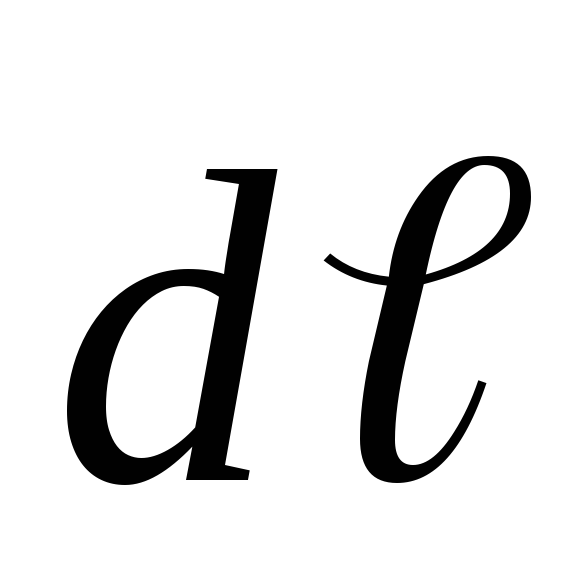 .
.
Если токи текут в разных направлениях, то положительным считают тот, направление которого связано с направлением обхода контура правилом правого винта.
Из
симметрии магнитного поля соленоида
следует, что контур, по которому будем
считать циркуляцию  ,следует
выбрать прямоугольный. Тогда на участке
1–2 угол
,следует
выбрать прямоугольный. Тогда на участке
1–2 угол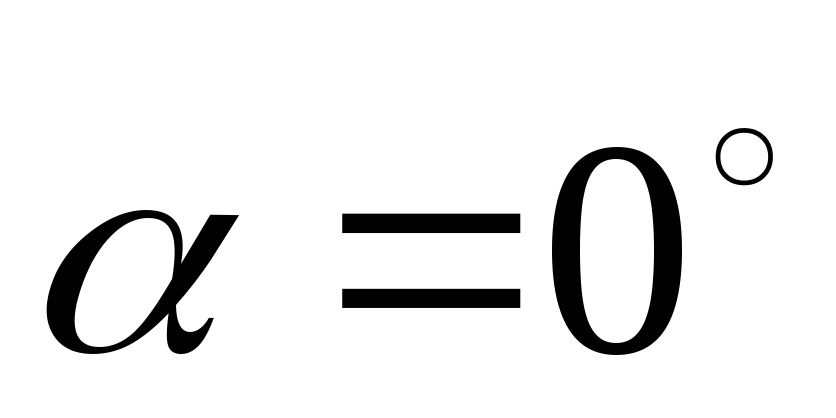 ,
а на участках 2–3 и 4–1 угол
,
а на участках 2–3 и 4–1 угол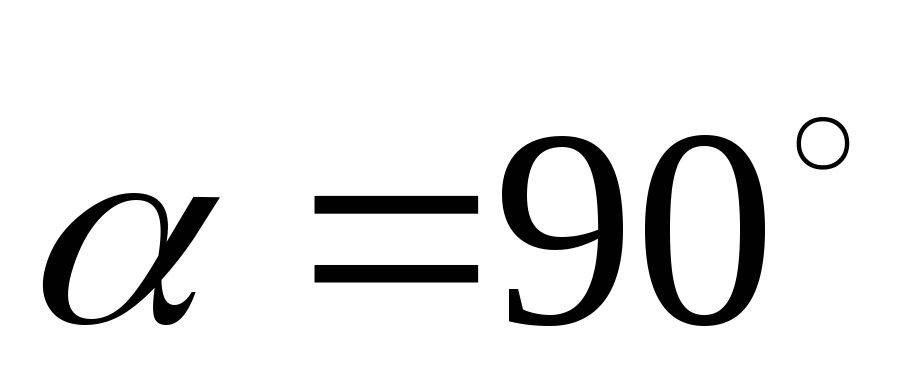 .
На участке 3–4 (вне соленоида) индукция
магнитного поля
.
На участке 3–4 (вне соленоида) индукция
магнитного поля .
Тогда выражение (4) преобразуется в
.
Тогда выражение (4) преобразуется в
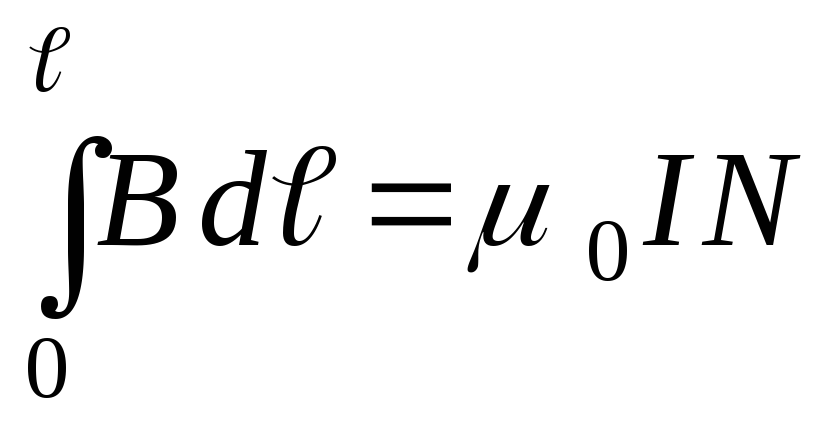 ,
,
где N – число витков соленоида, охваченных выбранным контуром.
Из
выражения (4) следует 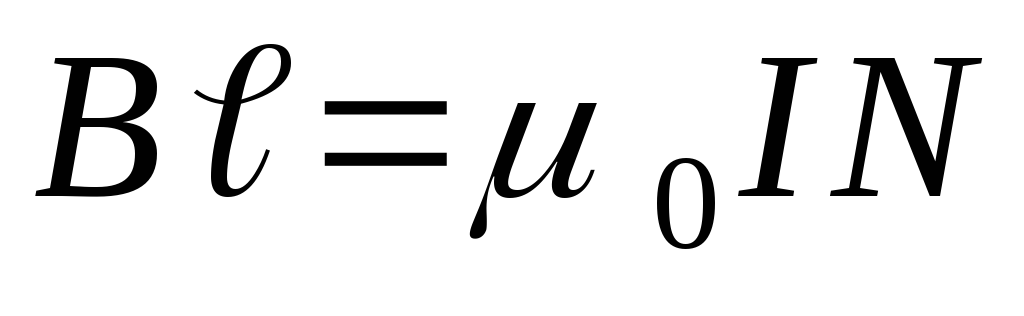 или
или
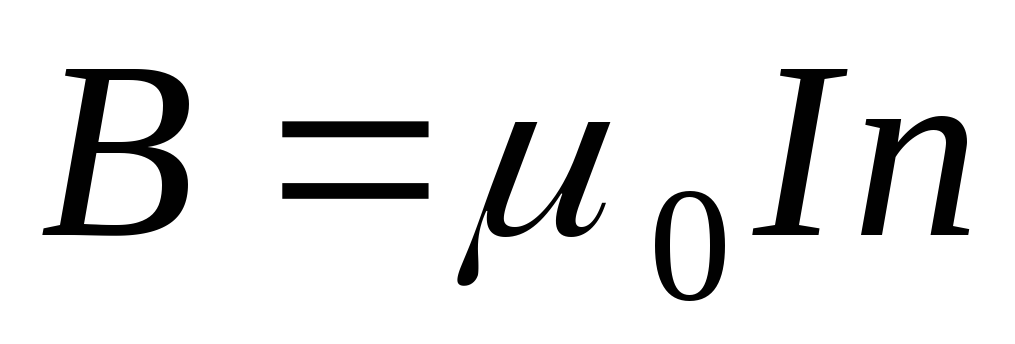 ,
,
где 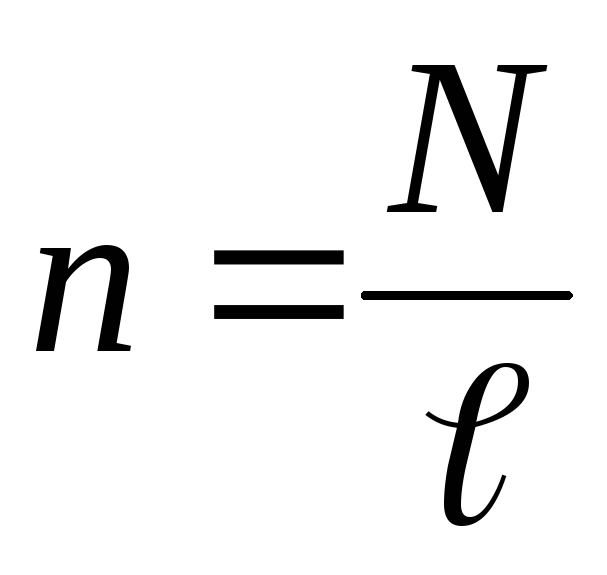 – число витков, приходящихся на единицу
длины соленоида.
– число витков, приходящихся на единицу
длины соленоида.
Экспериментальное
изучение распределения магнитной
индукции поля внутри соленоида
предлагается провести с помощью установки
состоящей из источника постоянного
тока G;
соленоида L1 магнитное
поле которого исследуется; маленькой
измерительной катушки L2, которая
введена в соленоид и может перемещаться
вдоль его оси; баллистического
гальванометра Р2,
соединенного с катушкой L2; выключателя S и миллиамперметра P1,
с помощью которого можно измерить ток
в соленоиде. При измерении индукции
магнитного поля измерительную катушку
устанавливают в какой-либо точке на оси
соленоида. В момент замыкания кнопки S цепи соленоида L1 ток в нем возрастает от 0 до постоянного
значения I . При этом
магнитный поток через витки катушки L2 изменяется
от 0 до 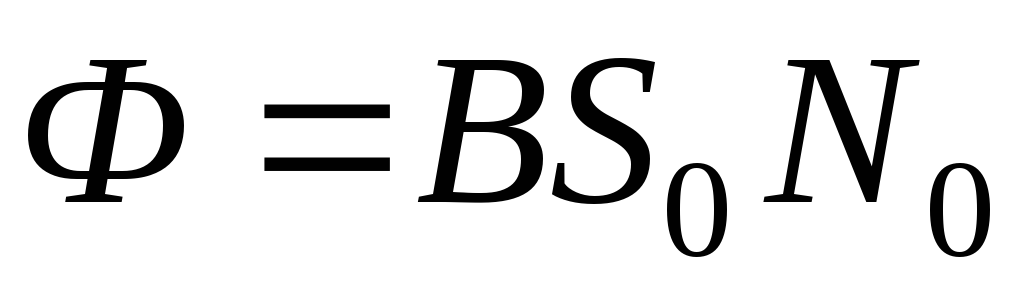 ,
где
,
где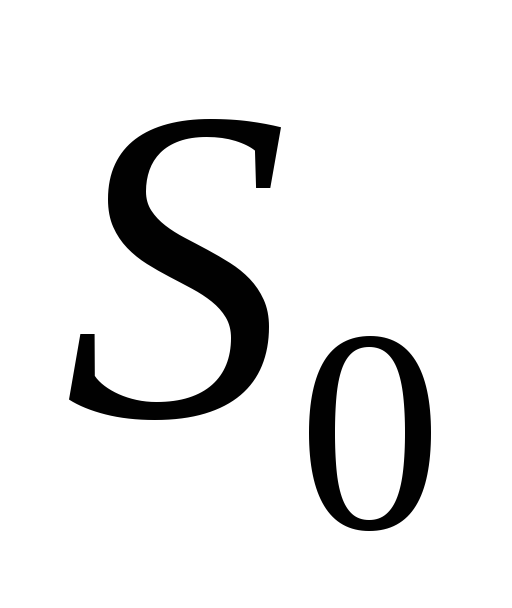 — площадь сечения соленоида,
— площадь сечения соленоида, 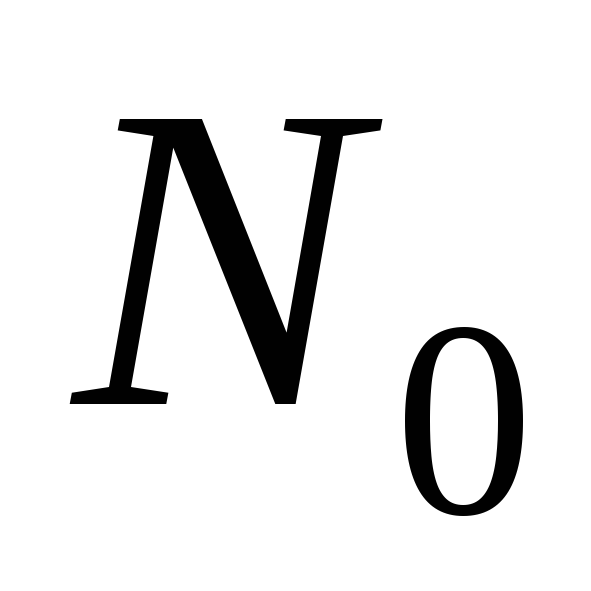 –число
витков в катушке L2. Изменение магнитного потока приводит
к возникновению в катушке L2 электродвижущей силы индукции
–число
витков в катушке L2. Изменение магнитного потока приводит
к возникновению в катушке L2 электродвижущей силы индукции 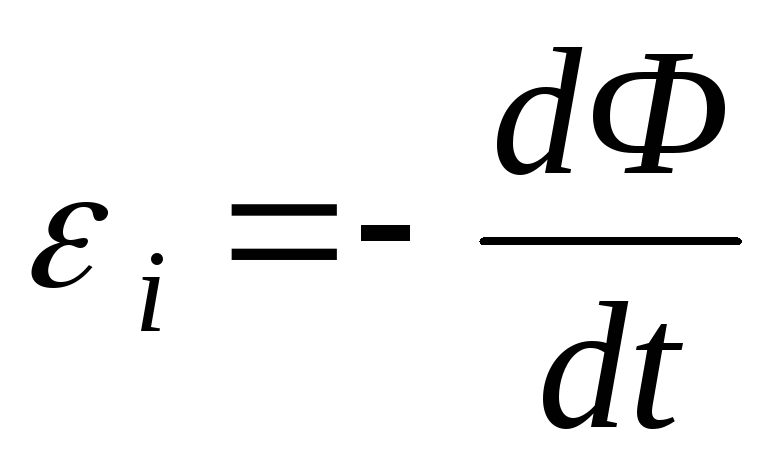 и появлению в цепи катушкиL2 индукционного
тока i. В результате
этого световой зайчик гальванометра
смещается на угол
и появлению в цепи катушкиL2 индукционного
тока i. В результате
этого световой зайчик гальванометра
смещается на угол  ,
пропорциональный количеству электричества
,
пропорциональный количеству электричества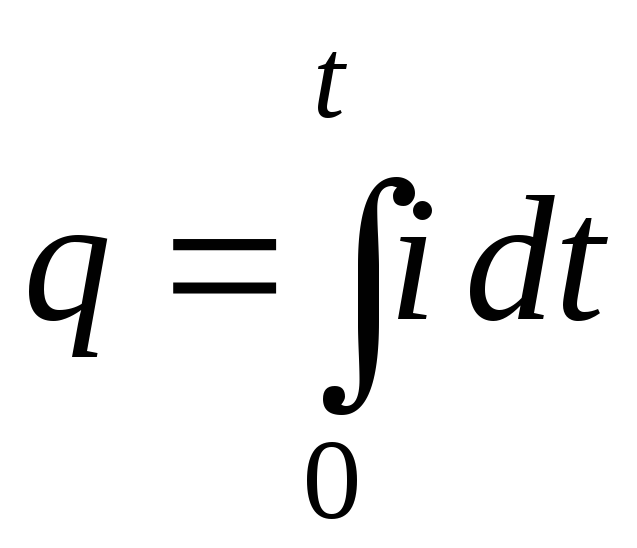 ,
протекшего через измерительную часть
установки. Этот угол равен
,
протекшего через измерительную часть
установки. Этот угол равен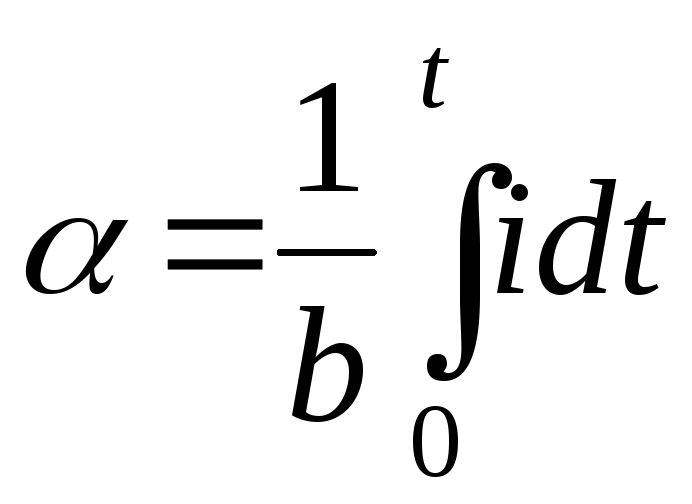 ,
гдеb – баллистическая
постоянная гальванометра.
,
гдеb – баллистическая
постоянная гальванометра.
Если
полное сопротивление цепи электрической
катушки L2 равно R , то ток в ней  и поэтому
и поэтому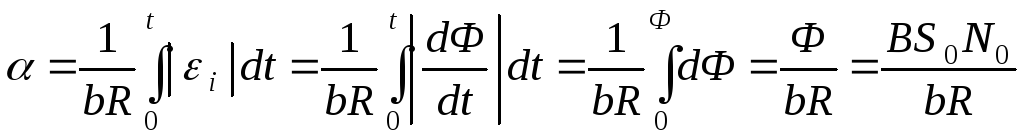 .
.
Тогда
для магнитной индукции имеем 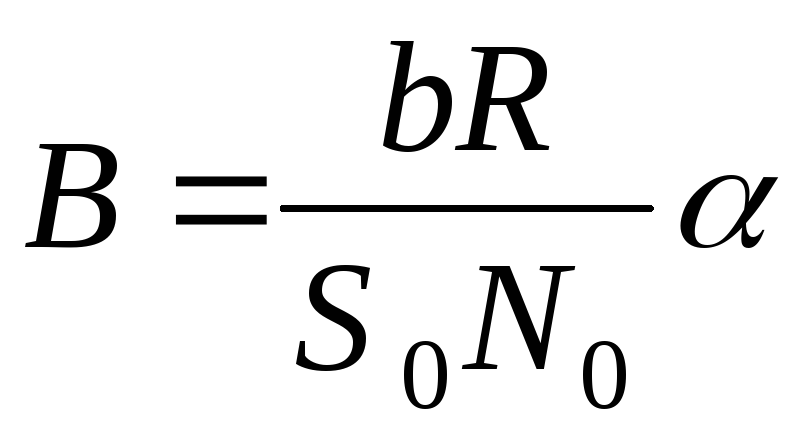 или
или
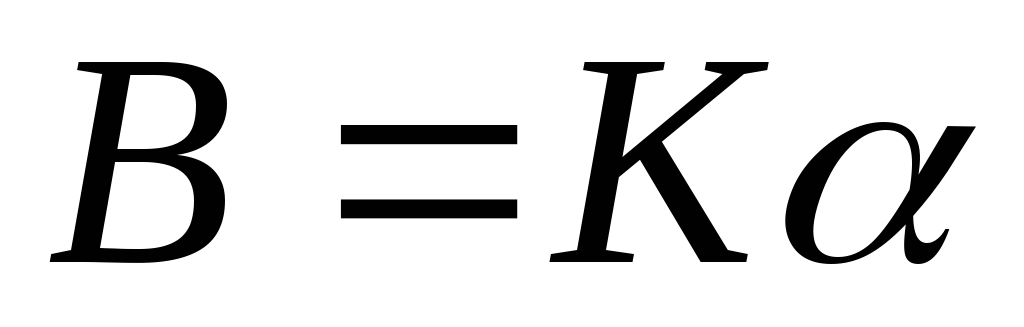 ,
(6)
,
(6)
где
постоянная 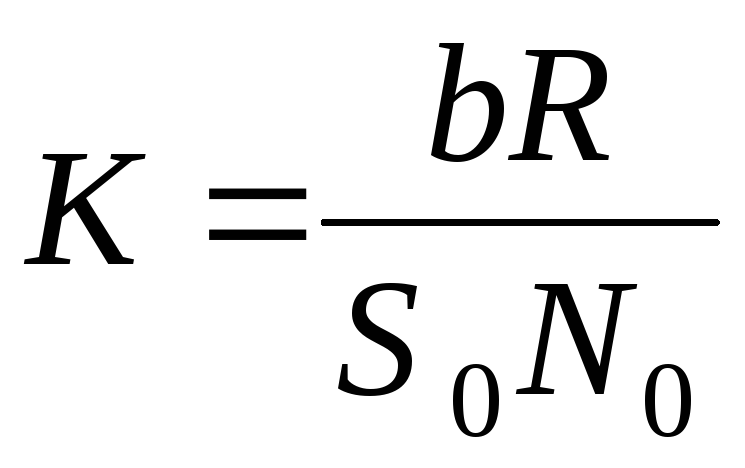 принимается за цену деления баллистического
гальванометра. По формуле (6) определяются
экспериментальные значения магнитной
индукции поля на оси соленоида.
принимается за цену деления баллистического
гальванометра. По формуле (6) определяются
экспериментальные значения магнитной
индукции поля на оси соленоида.
Порядок выполнения работы
Ознакомиться с установкой и включить ее в сеть (220 В).
Ручкой на установке поместить измерительную катушку L2 у одного из концов соленоида, определив ее положение а с помощью указателя на шкале.
Нажать на кнопку S , измерить отброс светового зайчика
 с
помощью указателя по шкале гальванометра.
с
помощью указателя по шкале гальванометра.Такие же измерения а и
 проделать
для других положений катушкиL2, перемещая
ее каждый раз на 1 см вдоль оси соленоида.
проделать
для других положений катушкиL2, перемещая
ее каждый раз на 1 см вдоль оси соленоида.По формуле (6) найти экспериментальные значения магнитной индукции, воспользовавшись значением К, указанным на установке.
Для тех же, что и в предыдущем случае, значений а рассчитать по формулам (3) и (4) теоретические значения магнитной индукции в соленоиде.
Данные измерений и вычислений занести в таблицу.
Построить графики
 по результатам, полученным из опыта и
по теоретическим расчетам.
по результатам, полученным из опыта и
по теоретическим расчетам.
Таблица
а, м
 ,
дел
,
дел ,
Тл
,
Тл

 ,
Тл
,
Тл
Контрольные вопросы
Что такое магнитное поле? Какими свойствами оно обладает? Имеет ли источники, вихри?
Дайте определение
 .
Что такое линии индукции магнитного
поля?
.
Что такое линии индукции магнитного
поля?На что и как действует магнитное поле?
Сформулируйте теорему о циркуляции вектора
 и используйте ее для расчета магнитной
индукции внутри бесконечно длинного
соленоида.
и используйте ее для расчета магнитной
индукции внутри бесконечно длинного
соленоида.Сформулируйте закон Био-Савара и принцип суперпозиции.
Что такое магнитный поток? В чем состоит явление электромагнитной индукции. Как используется это явление в данной работе? На какой угол отклонится зайчик баллистического гальванометра, если долго держать нажатой кнопку S ?
По кольцу радиуса R течет ток I. Используя закон Био-Савара, определить магнитную индукцию в точке на оси кольцо, на расстоянии а от центра кольца.
Литература
1. Савельев И.В. Курс общей физики –2-е изд. — М.: Наука. 1982, т.2 гл. “Магнитное поле в вакууме”
2. Ремизов А.Н. Медицинская и биологическая физика.– М: Высшая школа, 1987, глава 16, параграфы 16.1, 16.5; глава 17, параграф 17.1.
ЛАБОРАТОРНАЯ РАБОТА 28
ОПРЕДЕЛЕНИЕ ИНДУКТИНОСТИ ТОРОИДА С ФЕРРИТОВЫМ
МАГНИТОПРОВОДОМ
Цель работы: изучение зависимости индуктивности тороида от силы тока.
Приборы: амперметр, вольтметр, тороид.
Теоретическое введение
Тороидальная катушка (тороид) представляет собой провод, навитый на каркас (магнитопровод), имеющий форму тор (рис. 1). При пропускании тока по плотно навитому проводу образуется магнитное поле, напряженность Н которого вне тороида практически равна нулю, а внутри вычисляется по формуле
Н = IN/l = In, (1)
где I – сила тока, N – полное число витков, n – число витков, приходящееся на единицу длины тороида. Формула (1) справедлива для тороида, длина которого l (l = 2r) значительно больше, чем диаметр магнитопровода. Можно принять магнитное поле внутри такого тороида однородным.
Индукция магнитного поля В = 0Н или с учетом (1)
В = 0nI, (2)
где – относительная магнитная проницаемость среды (вещества магнитопровода), 0 – магнитная постоянная.
Поток магнитной индукции, сцепленной с тороидом
Ф = Ф0N,
где Ф0 = ВS – поток через один виток тороида площадью S = d2/4.
Учитывая равенство (2), получаем
Ф = 0nISN = 0n2lSI. (3)
Если
каркас тороида немагнитный,
то поле  ,
а значит и полный магнитный потокФ будут пропорциональны силе тока I,
и можно записать
,
а значит и полный магнитный потокФ будут пропорциональны силе тока I,
и можно записать
Ф = LI, (4)
где L – коэффициент, называемый индуктивностью тороида. L – физическая величина, численно равная магнитному потоку, сцепленному со всеми витками, когда ток, создающий этот поток, равен единице.
Единицей индуктивности в СИ является генри (Гн). Магнитный поток измеряется в веберах (Вб), причем 1Гн = 1Вб/А.
Сопоставляя выражения (3) и (4), получаем индуктивность тороида
L = 0n2Sl. (5)
Все вышеизложенное справедливо и для бесконечно длинного соленоида.
При измерении силы тока в тороиде возникает ЭДС индукции, которую называют ЭДС самоиндукции
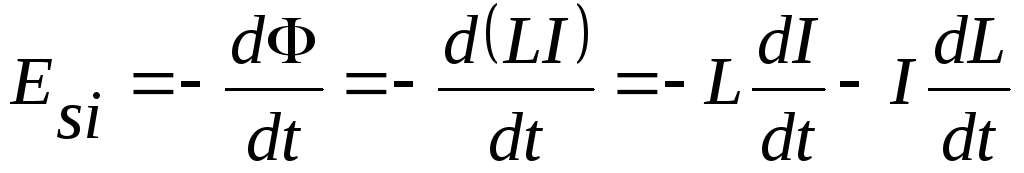 .
(6)
.
(6)
Если при изменениях силы тока индуктивность остается постоянной (что возможно, когда магнитопровод немагнитный), то ЭДС самоиндукции
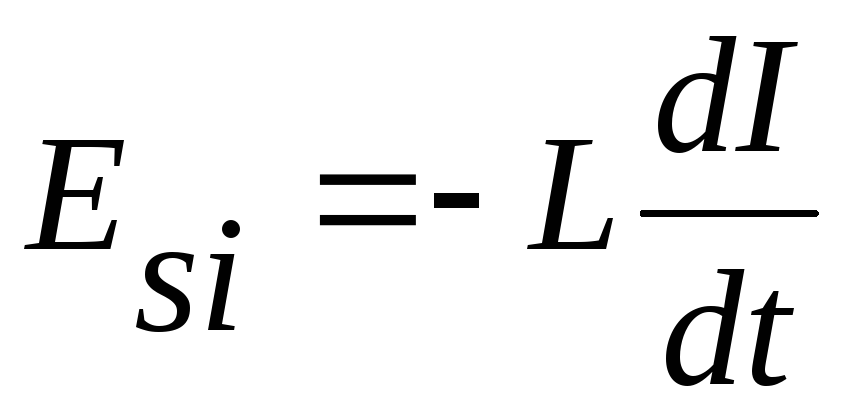 .
(7)
.
(7)
Соотношение (7) дает возможность определить индуктивность как коэффициент пропорциональности между скоростью изменения силы тока в контуре и возникающей вследствие этого ЭДС самоиндукции. Однако такое определение правомерно лишь в случае, когда L = const.
В присутствии ферромагнетикаL будет функцией отI(черезН). Следовательно,dL/dtв формуле (6) можно записать как (dL/dt)(dI/dt). Тогда
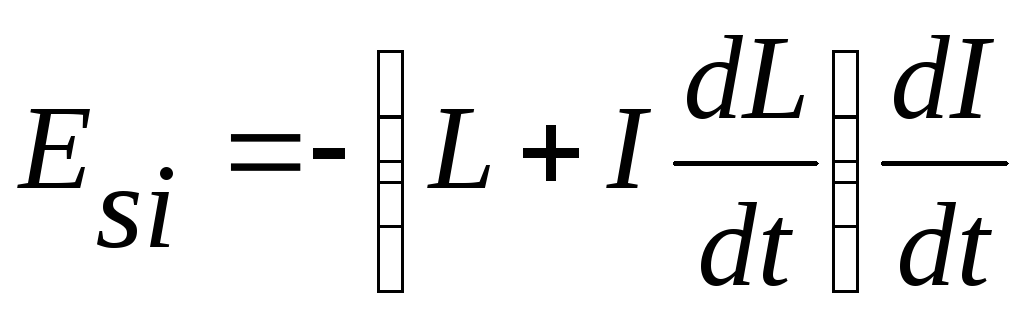 .
(8)
.
(8)
Отсюда видно, что при наличии ферромагнетика коэффициент пропорциональности между Еsi и dI/dt отнюдь не равен L, как было указано в соотношении (7).
Если магнитопровод тороида изготовлен из ферроипгнитного материала (железа, никеля, кобальта и их сплавов и соединений), то относительная магнитная проницаемость является сложной функцией от напряженности Н магнитного поля в тороиде (рис.2):
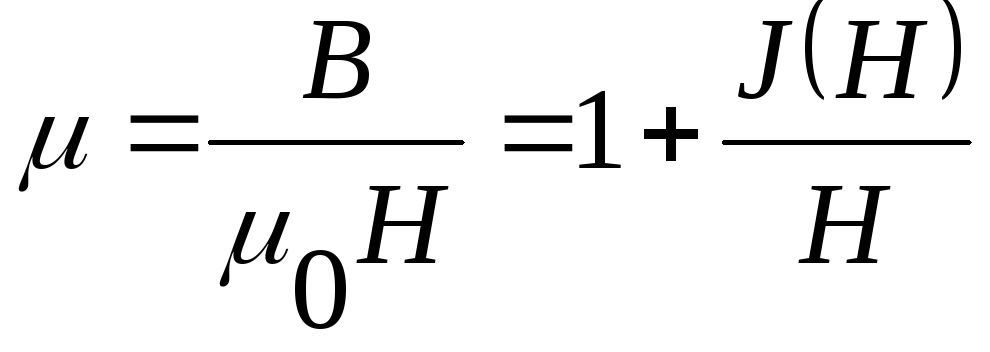 .
(9)
.
(9)
где J – намагниченность, т.е. магнитный момент единицы объема ферромагнетика. Начиная с некоторого значения Н, численное значение вектора намагниченности практически остается постоянным и равным JН. Это объясняется следующим образом.
При определенных условиях в кристаллах могут возникать так называемые обменные силы, которые заставляют магнитные моменты атомов устанавливаться параллельно друг другу. В результате возникают области (размером 1–10 мкм) спонтанного, т.е. самопроизвольного намагничивания. Эти области называются доменами. В пределах каждого домена ферромагнетик намагничен до насыщения и имеет определенный магнитный момент. Направления этих моментов для различных доменов различны, поэтому при отсутствии внешнего поля суммарный момент образца равен нулю и образец в целом представляется макроскопически не намагниченным.
При включении внешнего магнитного поля домены, ориентированные по полю, растут за счет доменов, ориентированных против поля. Очевидно, что магнитное насыщение наступает тогда, когда векторы магнитных моментов всех доменов устанавливаются параллельно внешнему магнитному полю.
В относительно слабых полях В растет быстрее Н вследствие быстрого роста J, поэтому увеличивается до max (рис. 2). В сильных полях наступает насыщение намагниченности (J = JН = const), поэтому при дальнейшем росте Н отношение J/H 0 и магнитная проницаемость согласно формуле (9) начинает убывать, стремясь к единице. Следовательно, в сильных магнитных полях индукция В возрастает с увеличением Н по линейному закону (рис. 3).
Если после того, как ферромагнетик намагничен (даже не до насыщения), внешнее магнитное поле устранить, начнется распад крупных доменов на более мелкие. Однако полного хаоса при этом не возникнет и достигнутая намагниченность частично сохранится. Это используют при изготовлении постоянных магнитов. Отметим еще одно свойство ферромагнетиков. Для каждого ферромагнитного вещества существует температура (точка Кюри), выше которой ферромагнитные свойства полностью исчезают и вещество становится парамагнетиком.
В медицине ферромагнетики находят разнообразное применение: исправление грудной клетки у детей, магнитные заглушки для предотвращения выделений из искусственного наружного свища ободочной кишки, для удаления железных частичек из глаз и др.
Итак, ферромагнетиков является функцией напряженности (или тока, так как Н I). Из формулы (5) видно, что индуктивность тороида зависит от его геометрических размеров и относительной магнитной проницаемости среды. Следовательно, в присутствии ферромагнетика L тороида зависит от I так же, как от Н. Для немагнитных магнитопроводов = const, поэтому L = const при изменении тока.
В данной работе в качестве магнитопровода в тороиде используется феррит – материал с магнитными свойствами ферромагнетика, но с низкой (или нулевой) проводимостью.
При прохождении постоянного тока через обмотку тороида он оказывает активное сопротивление R, обусловленное электрическими свойствами проводника, длиной и сечение провода. Если по тороиду пропустить переменный ток, то полное сопротивление тороида возрастает.
Эффективная сила тока в цепи, содержащей индуктивность, емкость и активное сопротивление, определяется формулой
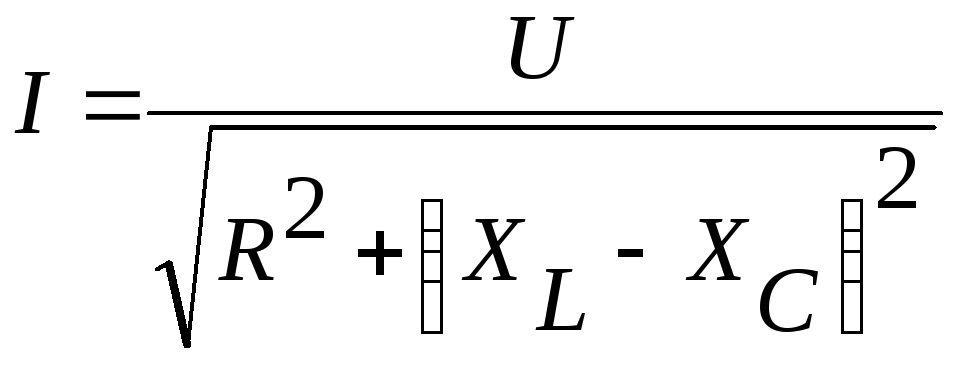 .
(10)
.
(10)
где U – эффективное напряжение, XL = L – индуктивное сопротивление, XC = 1/С – емкостное
сопротивление, 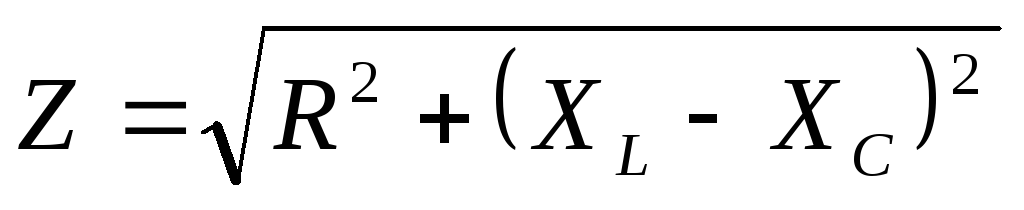 –
полное сопротивление цепи (импеданс), – циклическая
частота.
–
полное сопротивление цепи (импеданс), – циклическая
частота.
Так как для исследуемого тороида активное сопротивление R мало по сравнению с индуктивным сопротивлением XL, а емкостное сопротивление XC практически отсутствует, то формулу (10) можно записать в виде I = U/L, откуда
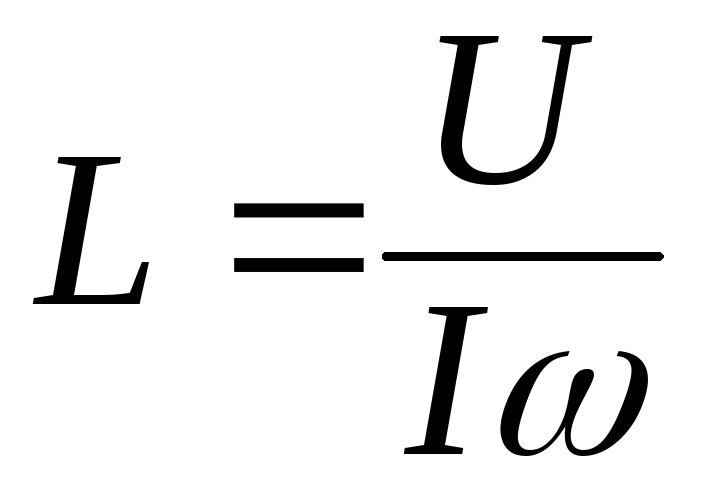 ,
(11)
,
(11)
где = 2, а = 50 Гц.
3. Магнитное поле соленоида.
Е
 Рисунок
7
– Магнитное
поле соленоида
Рисунок
7
– Магнитное
поле соленоида
Индукция магнитного поля на оси соленоида вычисляется по формуле:
 ,
,
г
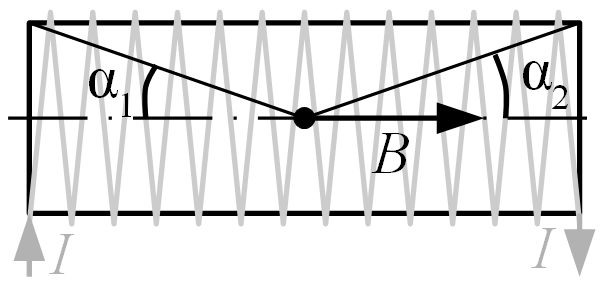 Рисунок
8 – К расчету магнитного поля соленоида
Рисунок
8 – К расчету магнитного поля соленоида
В случае достаточно длинного соленоида (ℓ>> R) углы α1и α2для точек в середине соленоида стремятся к нулю и индукцию магнитного поля можно вычислить по формуле для бесконечного соленоида:
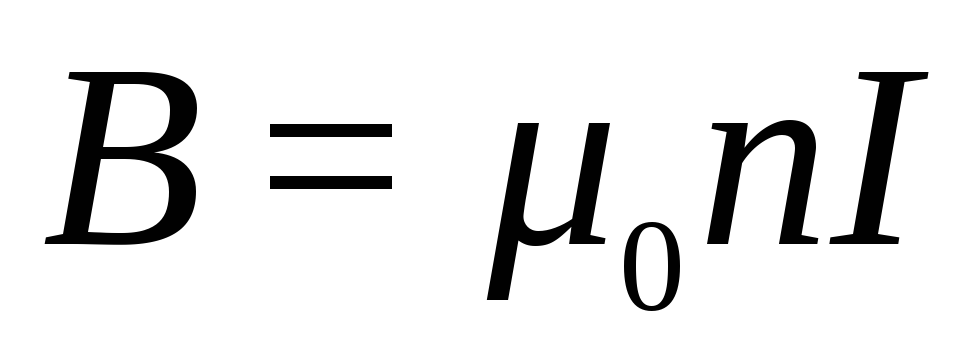 . (6)
. (6)
Простые соленоиды позволяют получать поля с индукцией до 0,2 Тл, соленоиды с охлаждаемыми обмотками – до 10 Тл, сверхпроводящие соленоиды позволяют получать поля с индукцией несколько десятков тесла.
4. Магнитное поле катушек Гельмгольца.
Катушки Гельмгольца – это две короткие катушки, расположенные на расстоянии, равном их радиусу.
Если катушки соединены последовательно (их магнитные поля направлены в одну сторону), то в области между катушками создается почти однородное магнитное поле. Если катушки включены встречно, магнитная индукция равна нулю в центре между ними и равномерно возрастает от центра к катушке (магнитное поле постоянного градиента: dB/dx = const; рис.9).
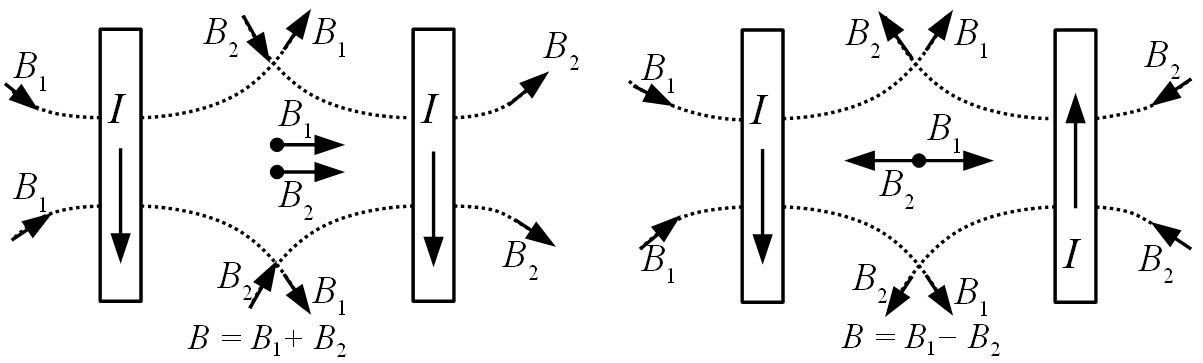 Рисунок
9 – Магнитное поле катушек Гельмгольца
при последовательном (слева) и встречном
(справа) включении
Рисунок
9 – Магнитное поле катушек Гельмгольца
при последовательном (слева) и встречном
(справа) включении
4. Использование индукционного эталонного датчика для измерения индукции магнитного поля
В основе принципа измерения магнитного поля индукционным датчиком лежит закон электромагнитной индукции. Индукционный эталонный датчик представляет собой измерительную катушку, параметры которой заранее известны. Эту катушку помещают в область пространства, где необходимо измерить магнитное поле.
Закон электромагнитной индукции:при изменении магнитного потока,
пронизывающего замкнутый контур ( ),
в нем возникает ЭДС индукции:
),
в нем возникает ЭДС индукции:
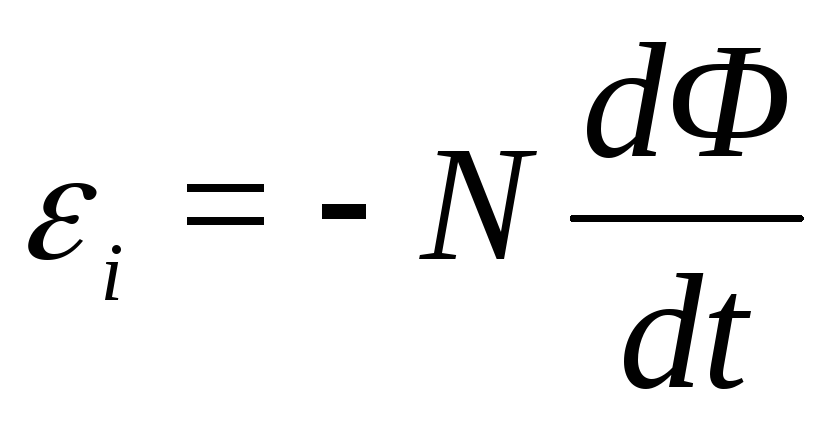 ,
,
где N– число витков.
Под действием ЭДС индукции в контуре возникает индукционный ток:
I = εi/R,
где R– сопротивление контура.
Изменение магнитного потока можно получить путем изменения тока в системе, создающей магнитное поле. В работе исследуемые токовые системы подключаются к источнику синусоидального тока.
Индукционный датчик (рис.10) представляет собой катушку 1 из N0 = 250 витков (площадьS0 = 2,5 см2), закрепленную на кронштейне 2, установленном в стойке 3 на рейтере 4, который может перемещаться по рельсу 5. Под рельсом закреплена линейка 6 для отсчета координаты метки на рейтере. Катушка может поворачиваться вокруг осиОО, перпендикулярной оси кронштейна; угол поворота отсчитывается по шкале 7. При ослаблении винта 8 кронштейн может поворачиваться вокруг осиO‘O‘. Поэтому катушка может принимать произвольную ориентацию. Датчик регистрирует составляющую магнитного поляВ, параллельную оси катушки.
С
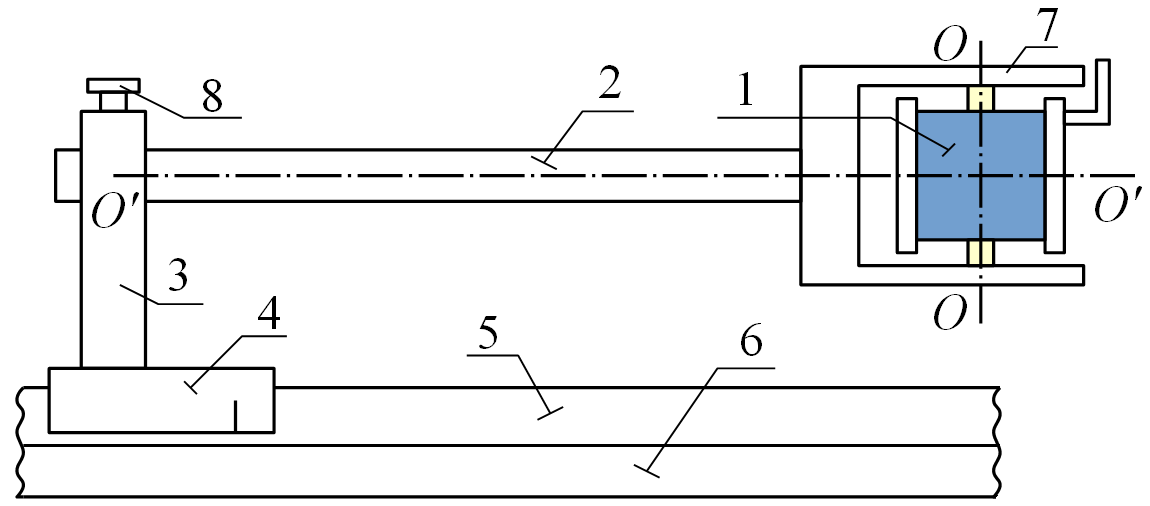 Рисунок
10 – Индукционный эталонный датчик
Рисунок
10 – Индукционный эталонный датчик
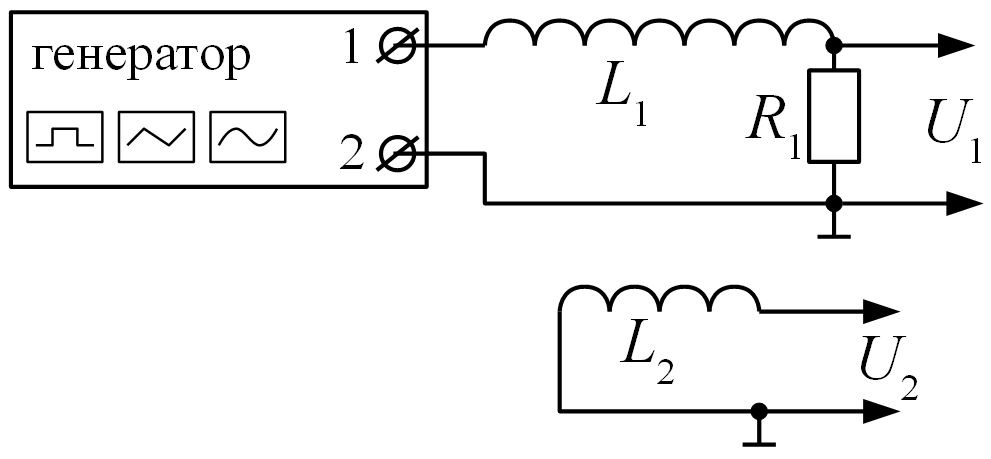 Рисунок
11 – Схема измерения магнитного поля
Рисунок
11 – Схема измерения магнитного поля
В
 Рисунок
12 – К определению величины ΔU
Рисунок
12 – К определению величины ΔU
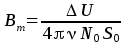 , (7)
, (7)
где ν – частота, N0 = 250 витков,S0 = 2,5 см2= 2,5·10-4м2.
2006 Г.
Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
Нижегородский Государственный Технический Университет
Выксунский филиал
Кафедра ОиОПД
Магнитное поле соленоида.
Датчик Холла
Лабораторная работа № 2-6
г. Выкса
Составили: В.П.Маслов, И.И.Рожков, О.Д.Честнова, Р.В.Щербаков.
Дана методика определения индукции магнитного поля соленоида на основе закона Био-Савара-Лапласа и с применением датчика Холла.
Научный редактор А.А. Радионов
Цель работы: ознакомиться с определением индукции магнитного поля соленоида на основе закона Био-Савара-Лапласа и с применением датчика Холла.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Закон Био-Савара-Лапласа. Вывод формулы для напряженности и индукции магнитного поля на оси кругового витка с током.
В
пространстве, окружающем проводники с
током, движущиеся заряды, магниты,
возникает магнитное поле, которое можно
обнаружить по воздействию его на другой
проводник с током или магнитную стрелку.
Магнитное поле в каждой точке пространства
количественно может быть описано с
помощью вектора напряженности магнитного
поля 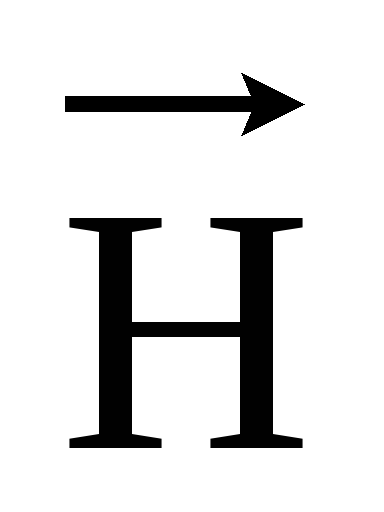 или
с помощью вектора индукции магнитного
поля
или
с помощью вектора индукции магнитного
поля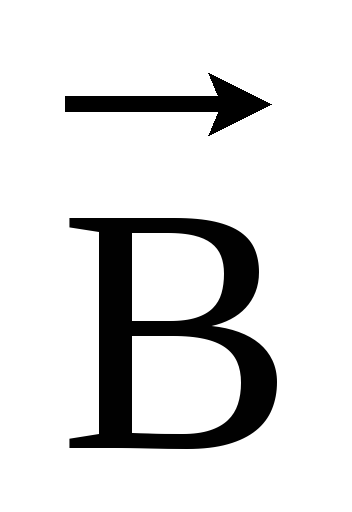 .
В вакууме векторы
.
В вакууме векторы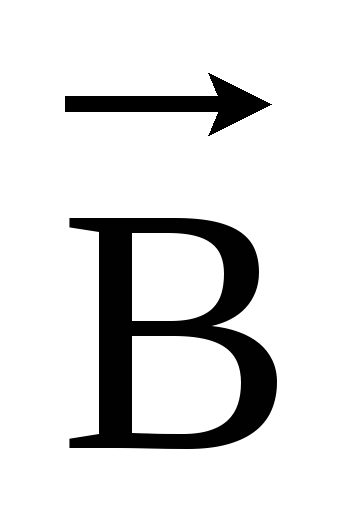 и
и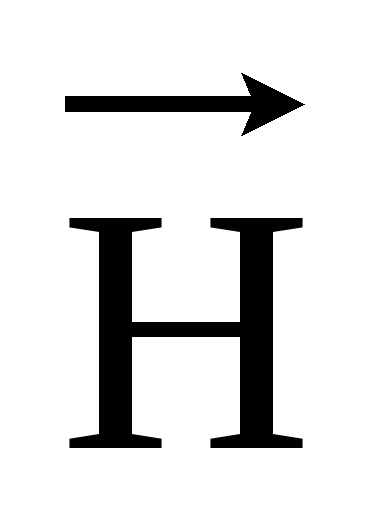 связаны
соотношением:
связаны
соотношением:
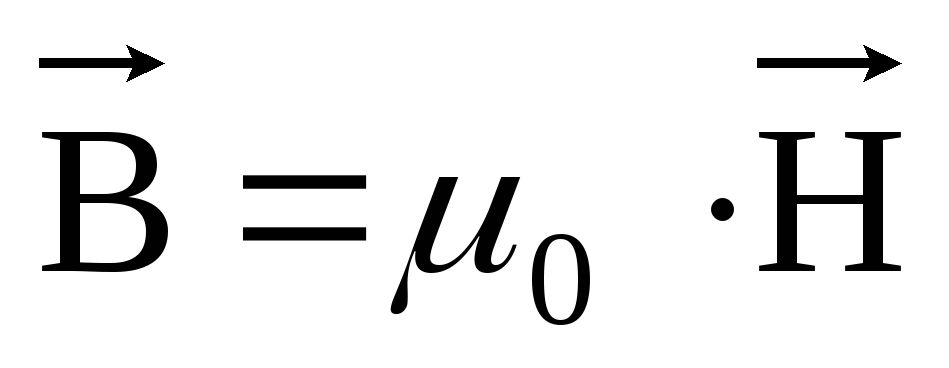 , (1)
, (1)
где μ0 = 4π·10-7 Гн/м — магнитная постоянная.
Единицы
измерения 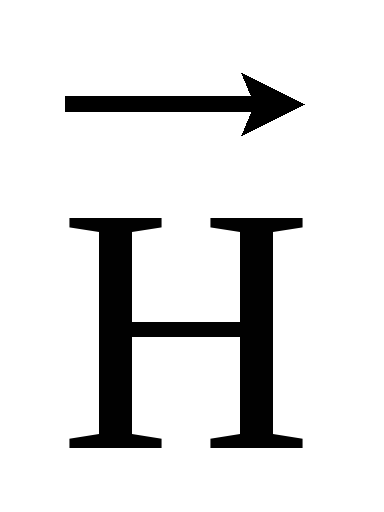 и
и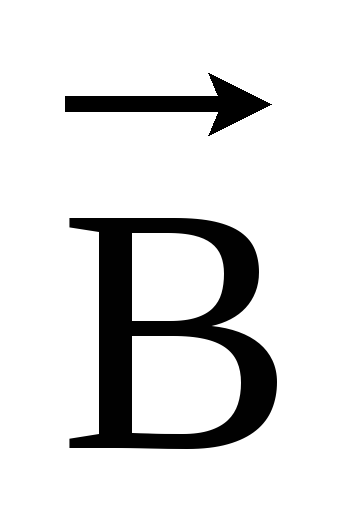 А/м и
Тл соответственно. В среде с магнитной
проницаемостью μ
А/м и
Тл соответственно. В среде с магнитной
проницаемостью μ
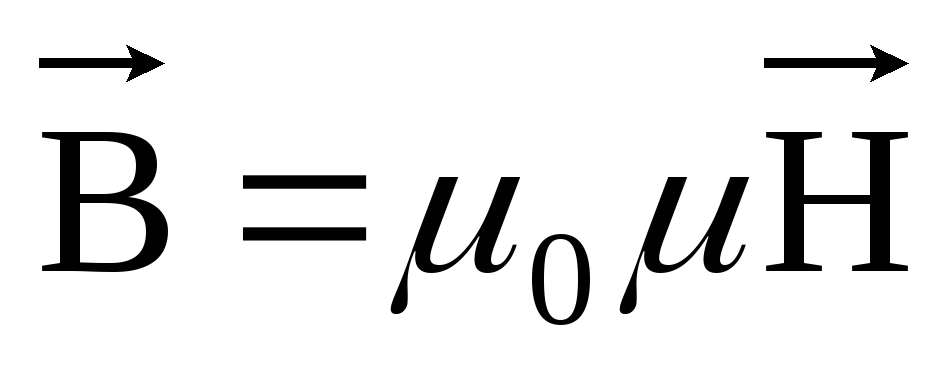
Для
вычисления напряженности и индукции
магнитного поля, используют закон
Био-Савара-Лапласа, согласно которому
элементарная напряженность магнитного
поля 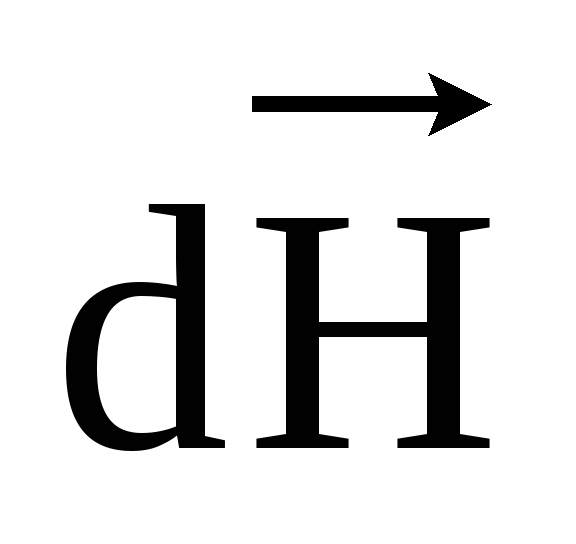 ,
создаваемая элементом проводника с
током
,
создаваемая элементом проводника с
током в некоторой точке пространства на
расстоянии
в некоторой точке пространства на
расстоянии 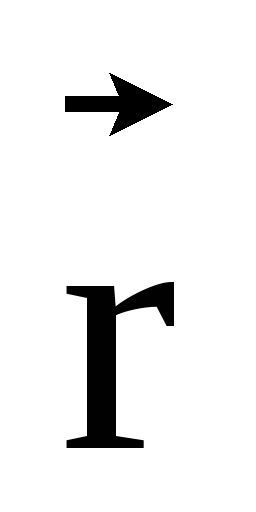 ,
определяется выражением
,
определяется выражением
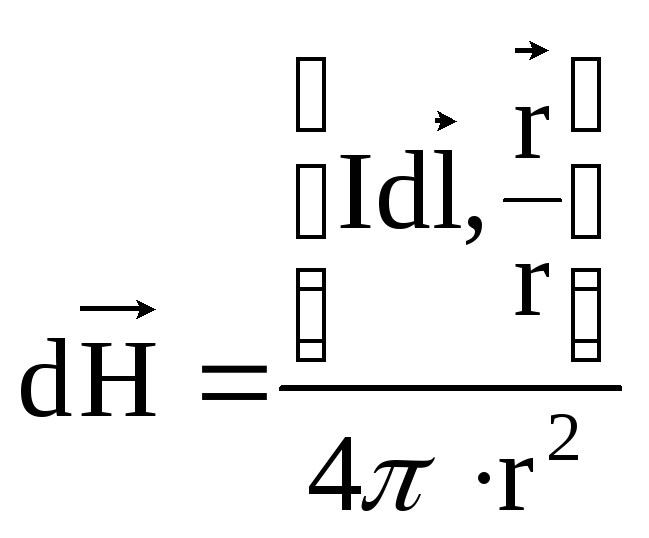 , (2)
, (2)
где 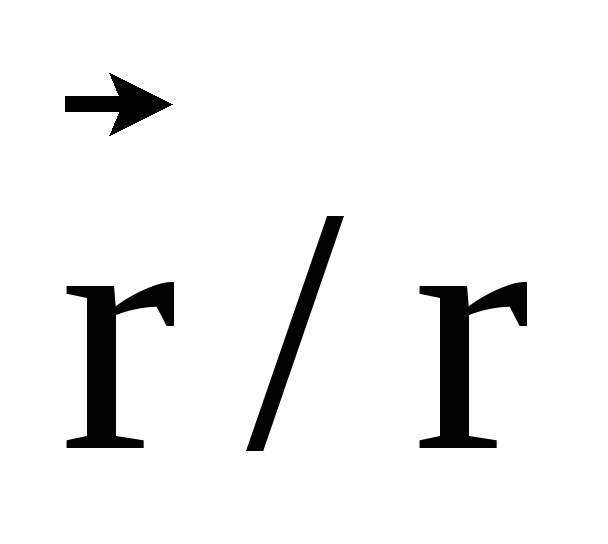 — единичный вектор вдоль
— единичный вектор вдоль .
.
Модуль вектора
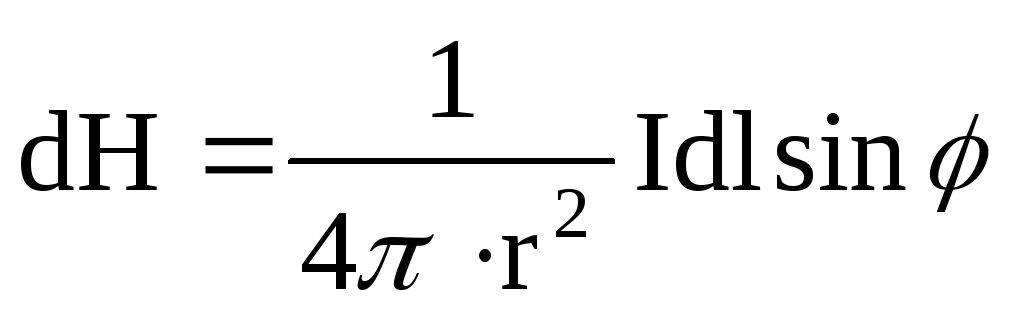 ,
,
где φ – угол между
векторами  и
и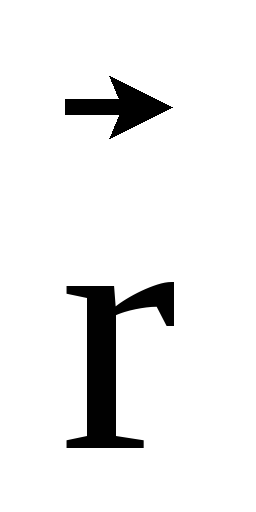 .
.
Для
нахождения результирующей напряженности,
создаваемой проводником конечных
размеров, надо воспользоваться принципом
суперпозиции магнитных полей и найти
векторную сумму элементарных напряженностей
от
всех элементов проводника.
Применим формулу (2) для вычисления
напряженности магнитного поля на оси
кругового витка с током (рис. 1).
проводника.
Применим формулу (2) для вычисления
напряженности магнитного поля на оси
кругового витка с током (рис. 1).
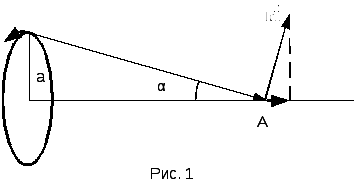
На
рис. 1 компонента dH1,
созданная элементом тока  ,
согласно (2) определяется как
,
согласно (2) определяется как
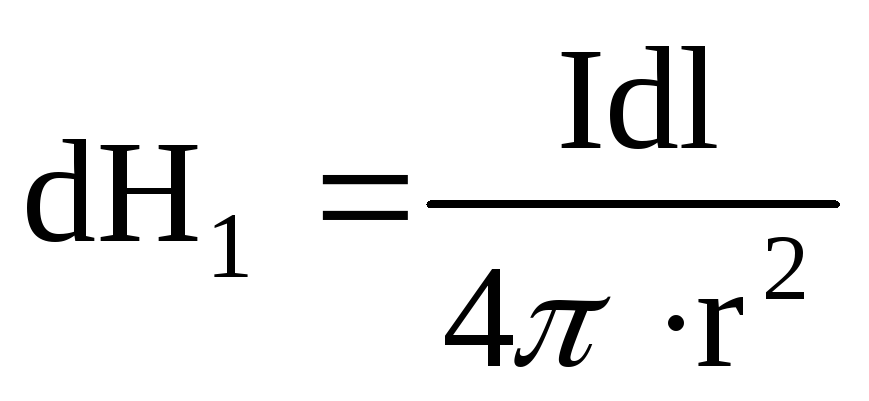 ,
,
где
учтено, что угол между 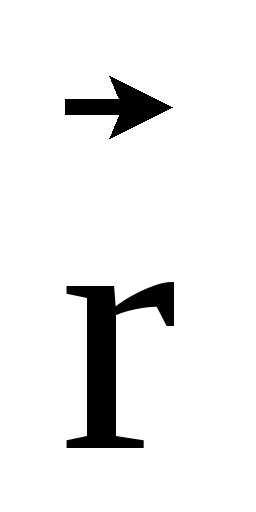 и
и прямой. Из симметрии элементов
прямой. Из симметрии элементов витка по отношению к точке А видно, что
результирующая напряженность магнитного
поля направлена вдоль оси так, что
витка по отношению к точке А видно, что
результирующая напряженность магнитного
поля направлена вдоль оси так, что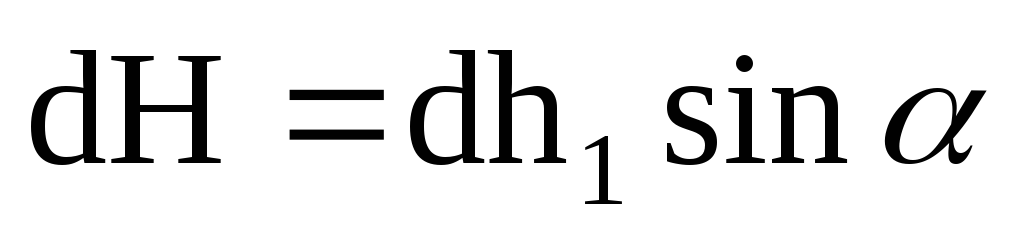 ,
то есть
,
то есть
 .
.
В правой части последней формулы все-величины, кроме dl, постоянны (для данной точки А), поэтому интегрирование no dl дает
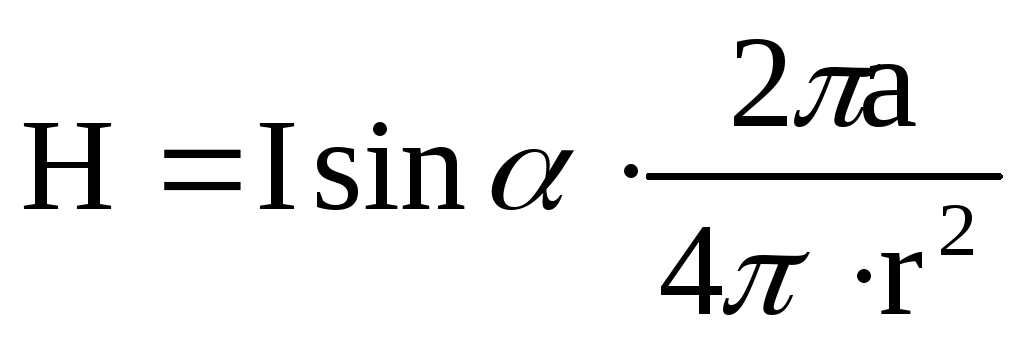 ,
,
или согласно рис. 1
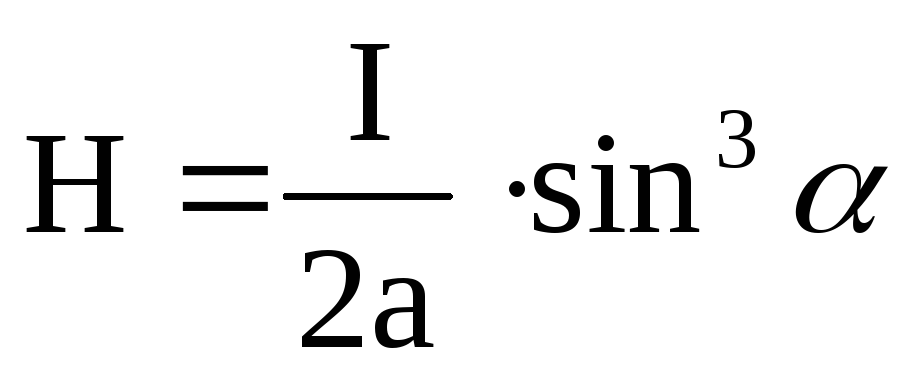 (3)
(3)
Величину 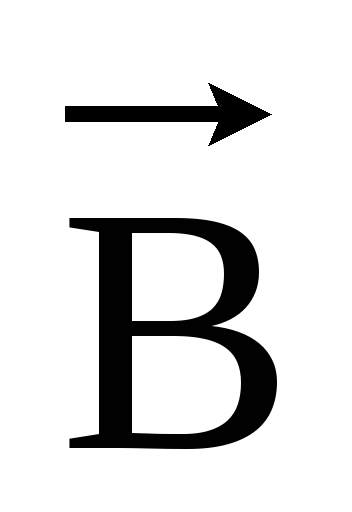 можно найти по формуле (1).
можно найти по формуле (1).
Вывод формулы для напряженности и индукции магнитного поля на оси соленоида (на расстоянии z от средней точки на оси)
Пусть на единицу длины соленоида приходится в витков (рис.2), тогда участок dz содержит ndz витков, которые, согласно (3), в точке А на оси создадут напряженность
 . (4)
. (4)
На рис. 2 L — длина соленоида, а — радиус витков обмотки, 0 -центральная точка на оси соленоида. ОА=z — координата точки А.
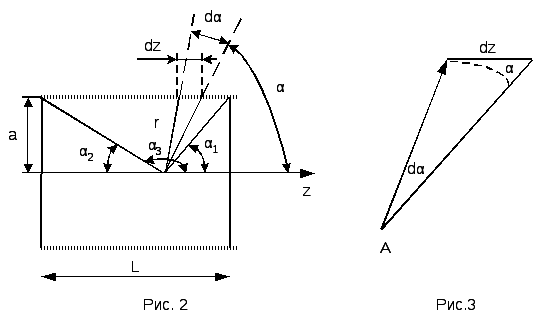
На
рис. 3 отдельно изображены элементы dz,
радиус-вектор  и углы α и dα.
Из геометрических построений рис.2 и 3
следует:
и углы α и dα.
Из геометрических построений рис.2 и 3
следует:
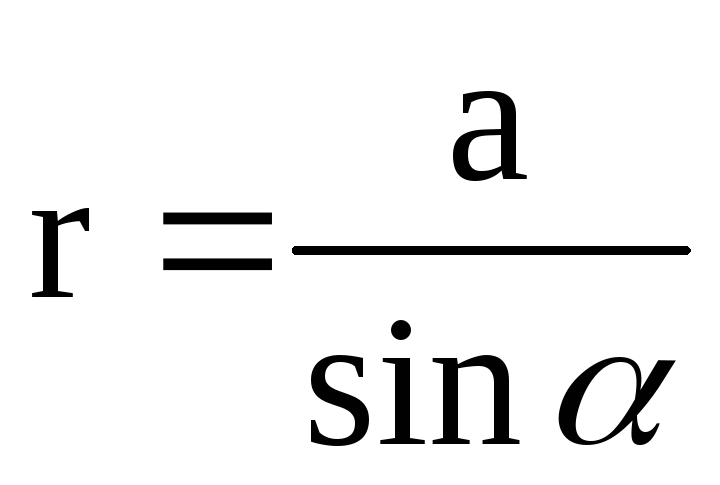 ;
; 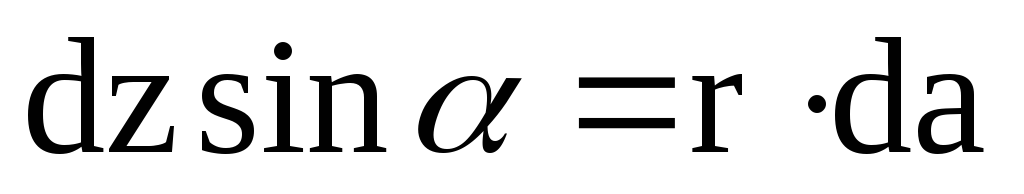 ;
;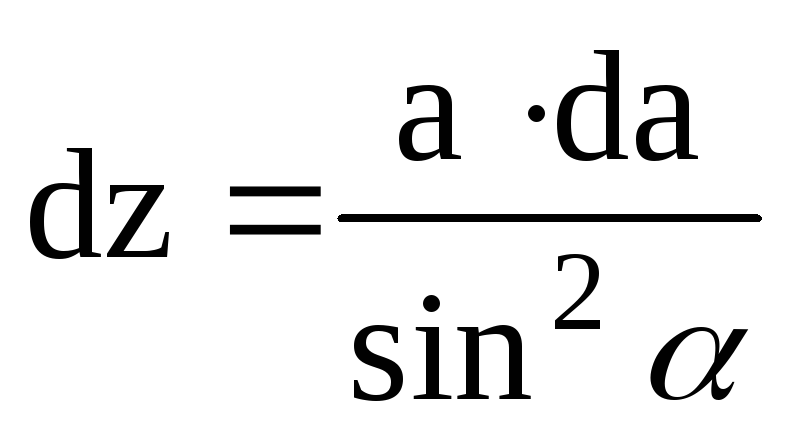 .
.
Подставим эти соотношения в (4) и проинтегрируем по α в пределах от α1 до α3:
 .
.
Учитывая,
что 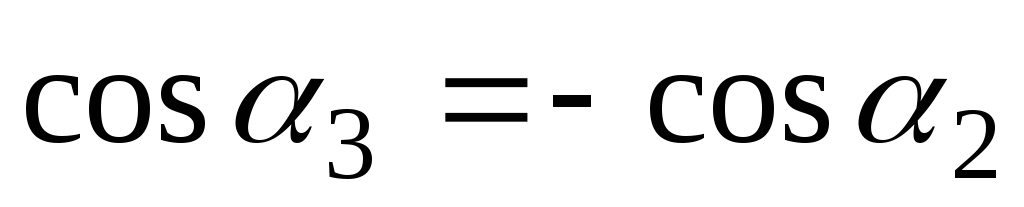 ,
получим
,
получим
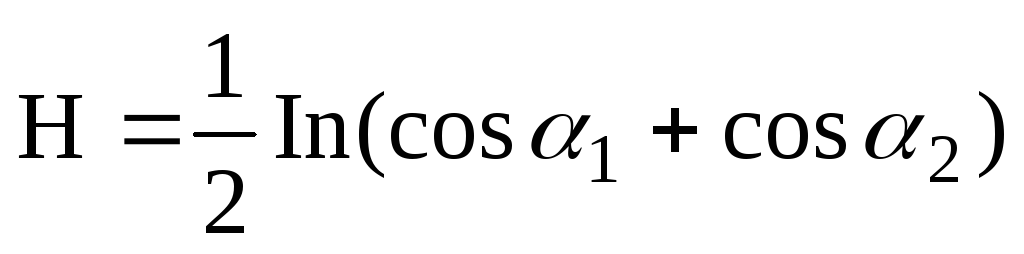 (5)
(5)
В случае бесконечно длинного соленоида (l>>α) в центральной точке 0 α1→0, α2→0,
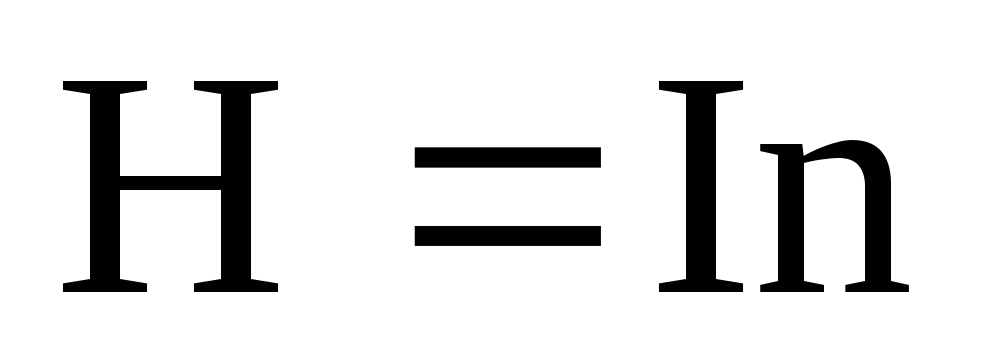 . (6)
. (6)
Из (5) также следует, что при переходе от центра к краю полубесконечного соленоида (на краю z=0,5L, α1=π/2, α2→0) напряженность уменьшается вдвое:
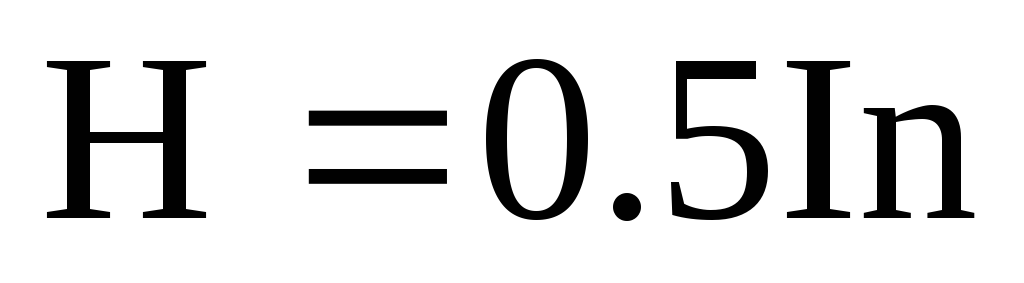 . (7)
. (7)
Индукцию, магнитного поля получим, добавив к выражениям (5), (б), (7) формулу (1). Отметим, что вывод формулы (6) для бесконечно длинного соленоида получается существенно проще на основе закона полного тока.




 с
помощью указателя по шкале гальванометра.
с
помощью указателя по шкале гальванометра. проделать
для других положений катушкиL2, перемещая
ее каждый раз на 1 см вдоль оси соленоида.
проделать
для других положений катушкиL2, перемещая
ее каждый раз на 1 см вдоль оси соленоида.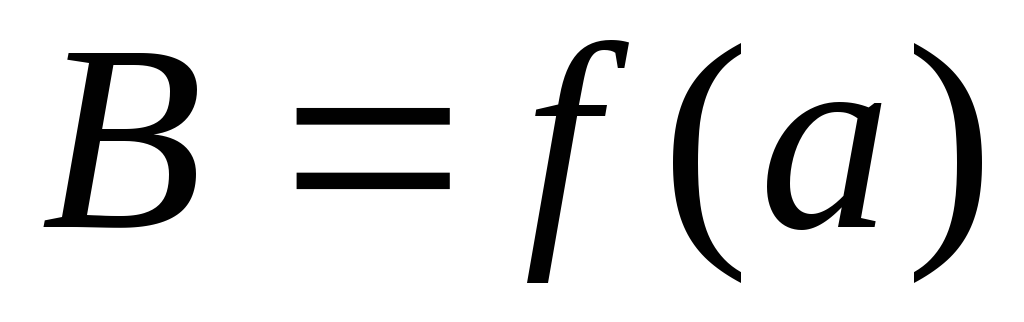 по результатам, полученным из опыта и
по теоретическим расчетам.
по результатам, полученным из опыта и
по теоретическим расчетам. ,
дел
,
дел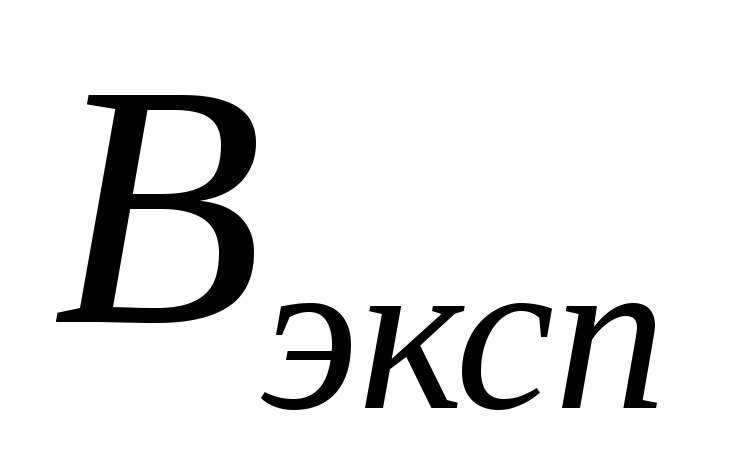 ,
Тл
,
Тл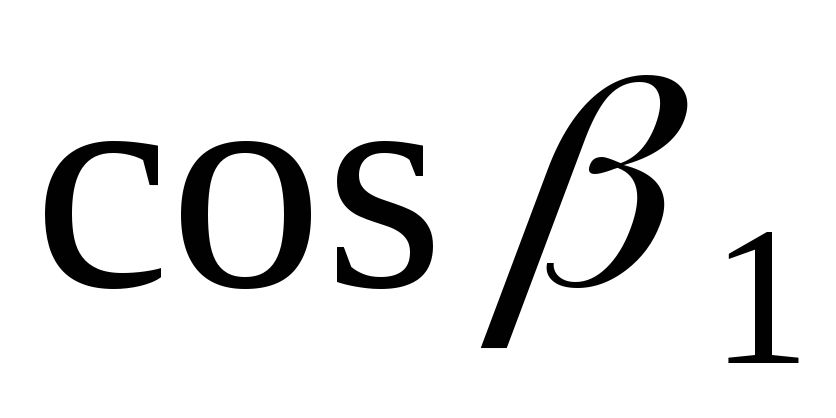
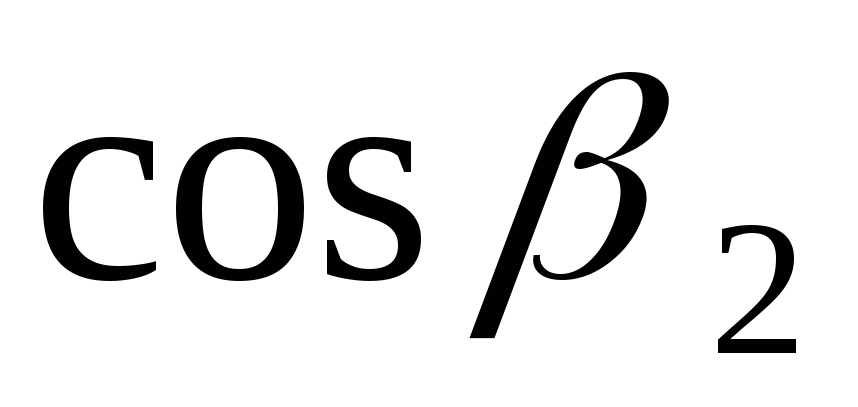
 ,
Тл
,
Тл .
Что такое линии индукции магнитного
поля?
.
Что такое линии индукции магнитного
поля? и используйте ее для расчета магнитной
индукции внутри бесконечно длинного
соленоида.
и используйте ее для расчета магнитной
индукции внутри бесконечно длинного
соленоида.