Насыщение ферритового сердечника — торроидального и Ш-образного. Онлайн калькуляторы.
Итак, мы решили поразвлечься и всерьёз сваять что-нибудь стоящее своими руками, как то: индуктивный фильтр для блока питания,
дроссель для усилительного каскада, выходной трансформатор для однотактного УНЧ, или фиг его знает — чего ещё похуже…
Что объединяет этих жертв нашего волеизъявления?
Каждое из перечисленных моточных изделий содержит магнитомягкий магнитопровод, и через каждое из них протекает
постоянный ток. И если к переменному току, даже значительных величин, магнитопровод относится
сдержанно-положительно, то к постоянке питает явную антипатию и может резко войти в насыщение от её переизбытка.
При насыщении сердечника его относительная магнитная проницаемость резко уменьшается, что влечёт за собой пропорциональное
уменьшение индуктивности изделия.
На этой странице порассуждаем о тороидальных магнитопроводах из ферритов, распылённого железа, электротехнической стали и их способности противостоять постоянному току.
Для наглядности рассмотрим график зависимости B от H, называемый петлёй гистерезиса, для распространённого, где-то даже народного, феррита марки N87 фирмы EPCOS.
Здесь:
H — напряжённость магнитного поля, а
B — магнитная индукция в сердечнике.
Зависимость приведена при температуре изделия +25 гр.С.
Интересующие нас параметры из datasheet-а производителя:
Начальная магнитная проницаемость —
µ = 2200,
Магнитная индукция насыщения при H=1200 А/м —
Bнас = 0,490 Т.
Если внимательно присмотреться к графику, то легко заметить, что в области малых и средних индукций зависимость практически
линейна и её наклон примерно равен µ. Именно на этот участок в большинстве случаев и должен
приходиться диапазон рабочих индукций.
Так что давайте без лишних прелюдий и телодвижений сделаем фундаментальный вывод — для нормальной работы катушки, намотанной на магнитопроводе, рабочие значения магнитной индукция в сердечнике не должны превышать величину 0,75 — 0,8 от значения справочной характеристики Bнас (Bs).
Переходим к незамысловатым формулам!
Магнитная индукция в сердечнике равна:
B = µ×µ0×n×I/l, где:
µ — магнитная проницаемость сердечника,
µ0 = 4π×10-7 (Гн/м) — физическая константа, называемая магнитной постоянной,
n — количество витков обмотки,
I — ток в обмотке,
l — средняя длина магнитного контура.
Поскольку рабочий режим магнитопровода мы выбираем в линейной области петли гестерезиса, то в качестве значения µ можно использовать паспортную характеристику начальной магнитной проницаемости сердечника.
Теперь можно рисовать калькулятор для расчёта магнитной индукции в катушке с учетом выбранного типа сердечника и конкретного количества витков обмотки.
Для удобства восприятия, помещу сюда и значение индуктивности полученного моточного изделия. Формулы для вычислений этого параметра
выглядят следующим образом:
L=0,0002×µ×h×n2×ln(Dвнешн/Dвнутр)
при соблюдении условия
Dвнешн/Dвнутр>1,75,
L=0,0004×µ×h×n
ТАБЛИЦА РАСЧЁТА МАГНИТНОЙ ИНДУКЦИИ В КАТУШКЕ С ТОРОИДАЛЬНЫМ СЕРДЕЧНИКОМ.
Увы, но значительных токов через катушки на ферритовых кольцах, или торах из трансформаторной стали нам пропустить не удастся —
нужны танцы с бубнами в виде немагнитных воздушных зазоров.
Другое дело — сердечники из распылённого железа, представляющие собой магнитопровод с немагнитными зазорами, технологически
распределёнными по всему объёму магнитопровода. Их очевидный плюс — высокая индукция насыщения, минус — малые величины магнитной
проницаемости.
В связи с этим, в некоторых случаях (в основном на низких частотах) предпочтительным является использование именно сердечников
из ферритов (или железа) с пропилом для создания малого воздушного зазора.
Данная мера позволяет в значительной мере увеличить величину допустимых токов через катушку без ввода магнитопровода в режим насыщения.
Длина этого воздушного зазора позволяет регулировать как величину
максимально-допустимой напряжённости магнитного поля в сердечнике, так и параметр изменившейся магнитной проницаемости, называемой
эквивалентной магнитной проницаемостью сердечника с зазором — µэф. Значение этого
параметра вычисляется по формуле:
µ
µ — начальная магнитная проницаемость сердечника,
l — средняя длина магнитного контура,
lз — длина воздушного зазора (толщина пропила).
Давайте посчитаем этот параметр.
РАСЧЁТ ЭКВИВАЛЕНТНОЙ МАГНИТНОЙ ПРОНИЦАЕМОСТИ СЕРДЕЧНИКА С ЗАЗОРОМ.
Таблица даёт приблизительную, но, в большинстве своём, приемлемую точность расчёта при величинах длины воздушного зазора 0,2-2 мм.
Для Ш-образных сердечников в качестве внутреннего и внешнего диаметров следует вводить справочную характеристику длины магнитного контура le.
Определив ниже магнитную проницаемость сердечника с зазором, следует ввести это значение в предыдущий калькулятор и заново произвести вычисления магнитной индукции и индуктивности катушки.
Для наглядности приведу два графика петли гистерезиса Ш-образного ферритового сердечника марки N87 без немагнитного
воздушного зазора и с зазором около 1 мм. Феррит ETD 59/31/22, достаточно крупный, с средней длиной магнитного контура
le = 139 мм.
Механизмы влияния зазора у Ш-образных и тороидальных сердечников абсолютно идентичны.
Эквивалентная магнитная проницаемость сердечника с зазором уменьшилась и составила величину 160 единиц.
Соответственно, уменьшился и наклон петли, позволяя сердечнику работать при гораздо больших значениях напряжённости
магнитного поля вдали от области магнитной индукции насыщения сердечника.
Линейная область петли гистерезиса также заметно увеличилась, что позволяет увеличить максимальные рабочие значения магнитной индукция в сердечнике вплоть до 0,85-0,9 от значения справочной характеристики Bнас (Bs).
Магнитное поле катушки с током — урок. Физика, 8 класс.
Практический интерес представляет собой магнитное поле катушки с током.
Катушка получится, если плотно, виток к витку, намотать провод в достаточно длинную спираль (рис. 1). В катушке может быть несколько десятков, сотен или даже тысяч витков.
Соленоид (от греч. solen — «канал», «труба» и eidos — «подобный») — разновидность катушки с током. Обычно под термином «соленоид» подразумевается цилиндрическая обмотка из провода, причём длина такой обмотки многократно превышает её диаметр.
Рис. 1
На рис. 2 изображена катушка, состоящая из большого числа витков провода, намотанного на деревянный каркас.
Обрати внимание!
Когда в катушке есть ток, железные опилки притягиваются к её концам, при отключении тока они отпадают.
Рис. 2
Если катушку с током подвесить на тонких и гибких проводниках, то она установится так же, как магнитная стрелка компаса: один конец катушки будет обращён к северу, другой — к югу.
Значит, катушка с током, как и магнитная стрелка, имеет два полюса — северный и южный (рис. 3).
Рис. 3
Вокруг катушки с током имеется магнитное поле. Его, как и поле прямого тока, можно обнаружить при помощи опилок (рис. 4).
Обрати внимание!
Магнитные линии магнитного поля катушки с током являются также замкнутыми кривыми.
Принято считать, что вне катушки они направлены от северного полюса катушки к южному (см. рис. 4).
Рис. 4
Катушки с током широко используют в технике в качестве магнитов. Они удобны тем, что их магнитное действие можно изменять (усиливать или ослаблять) в широких пределах. Рассмотрим способы, при помощи которых можно это делать.
На рис. 2 изображён опыт, в котором наблюдается действие магнитного поля катушки с током. Если заменить катушку другой, с большим числом витков проволоки, то при той же силе тока она притянет больше железных предметов.
Магнитное действие катушки с током тем сильнее, чем больше число витков в ней.
Включим в цепь, содержащую катушку, реостат (рис. 5) и при помощи него будем изменять силу тока в катушке.
При увеличении силы тока действие магнитного поля катушки с током усиливается, при уменьшении — ослабляется.
Рис. 5
Оказывается также, что магнитное действие катушки с током можно значительно усилить, не меняя число её витков и силу тока в ней. Для этого надо ввести внутрь катушки железный стержень (сердечник) (рис. 6).
Железо, введённое внутрь катушки, усиливает магнитное действие катушки.
Рис. 6
Направление магнитного поля тока связано с направлением тока в катушке.
Определить направление линий магнитного поля катушки с током можно при помощи правила правой руки, или правила правого буравчика.
Принято считать, что та сторона катушки или витка с током, откуда линии магнитного поля выходят, — это и есть северный магнитный полюс (\(N\)), а сторона, куда линии входят, — это южный магнитный полюс (\(S\)) (рис. 7).
Рис. 7
1. Магнитное поле и индуктивность | 14. Катушки индуктивности | Часть1
1. Магнитное поле и индуктивность
Магнитное поле и индуктивность
Вокруг всякого проводника, по которому течет ток, возникает магнитное поле. Такой эффект называется электромагнетизмом. Магнитные поля оказывают влияние на выравнивание электронов в атомах, и могут вызывать физическую силу, способную развиваться в пространстве. Как и электрические поля, магнитные поля могут занимать совершенно пустое пространство, и воздействовать на материю на расстоянии.
Магнитное поле обладает двумя основными характеристиками: магнитодвижущей силой и магнитным потоком. Общее количество поля или его эффект называется магнитным потоком, а сила, которая формирует этот магнитный поток в пространстве, называется магнитодвижущей силой. Эти две характеристики примерно аналогичны электрическому напряжению (магнитодвижущая сила) и электрическому току (магнитный поток) в проводнике. Магнитный поток, в отличие от электрического тока (который существует только там, где есть свободные электроны), может распространяться в абсолютно пустом пространстве. Пространство оказывает сопротивление магнитному потоку точно так же, как проводник оказывает сопротивление электрическому току. Величина магнитного потока равна магнитодвижущей силе, поделенной на сопротивление среды.
Магнитное поле имеет отличия от электрического поля. Если электрическое поле зависит от имеющегося количества разноименных зарядов (чем больше электрических зарядов одного вида на одном проводнике, и противоположного, на другом, тем больше будет электрическое поле между этими проводниками), то магнитное поле создается потоком электронов (чем интенсивнее движение электронов, тем больше вокруг них магнитного поля).
Устройство, способное запасать энергию магнитного поля, называется катушкой индуктивности. Форма катушки создает гораздо более сильное магнитное поле, чем обычный прямолинейный проводник. Конструкционной основой катушки индуктивности является диэлектрический каркас, на который наматывается провод в виде спирали (существуют так же и бескаркасные катушки). Обмотка может быть как однослойной, так и многослойной. Для увеличения индуктивности применяют магнитные сердечники. Помещенный внутрь катушки сердечник концентрирует магнитное поле и тем самым увеличивает ее индуктивность.
Условные обозначения катушек индуктивности на электрических схемах выглядят следующим образом:
Поскольку электрический ток создает вокруг катушки концентрированное магнитное поле, магнитный поток этого поля приравнивается к хранилищу энергии (сохранение которой происходит за счет кинетического движения электронов через катушку). Чем больше ток в катушке, тем сильнее магнитное поле, и тем больше энергии будет хранить катушка индуктивности.
Так как катушки индуктивности сохраняют кинетическую энергию движущихся электронов в виде магнитного поля, в электрической цепи они ведут себя совершенно иначе, чем резисторы (которые просто рассеивают энергию в виде тепла). Способность накапливать энергию в зависимости от тока позволяет катушке индуктивности поддерживать этот ток на постоянном уровне. Иными словами, она сопротивляется изменениям тока. Когда ток через катушку увеличивается или уменьшается, она производит напряжение, полярность которого противоположна этим изменениям.
Для сохранения большего количества энергии, ток через катушку индуктивности должен быть увеличен. В этом случае напряженность магнитного поля увеличится, что приведет к возникновению напряжения согласно принципу электромагнитной самоиндукции. И наоборот, для высвобождения энергии из катушки, проходящий через нее ток должен быть уменьшен. В этом случае напряженность магнитного поля уменьшится, что приведет к возникновению напряжения противоположной полярности.
Вспомните Первый закон Ньютона, который гласит что всякое тело продолжает удерживаться в состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние. С катушками индуктивности ситуация примерно аналогичная: «электроны, движущиеся через катушку стремятся оставаться в движении, а покоящиеся электроны имеет тенденцию оставаться в покое». Гипотетически, короткозамкнутая катушка индуктивности будет сколь угодно долго поддерживать постоянную скорость потока электронов без внешней помощи:
На практике же, катушка индуктивности способна поддерживать постоянный ток только при использовании сверхпроводников. Сопротивление обычных проводов приведет к неизбежному затуханию потока электронов (без внешнего источника энергии).
Когда ток через катушку увеличивается, он создает напряжение, полярность которого противоположна потоку электронов. В этом случае катушка индуктивности выступает в качестве нагрузки. Она, как говорится, «заряжается», поскольку все большее количество энергии сохраняется в ее магнитном поле. На следующем рисунке обратите внимание на полярность напряжения по отношению к направлению тока:
И наоборот, когда ток через катушку уменьшается, на ее выводах возникает напряжение, полярность которого соответствует потоку электронов. В этом случае катушка индуктивности выступает в качестве источника питания. Она высвобождает энергию магнитного поля в остальную часть схемы. Обратите внимание на полярность напряжения по отношению к направлению тока:
Если ненамагниченную катушку индуктивности подключить к источнику питания, то в первоначальный момент времени она будет сопротивляться потоку электронов пропуская все напряжение источника. Как только ток начнет возрастать, сила магнитного поля, созданного вокруг катушки, будет увеличиваться поглощая энергию источника питания. В конечном итоге ток достигнет максимального значения и прекратит свой рост. В этот момент катушка прекращает поглощать энергию от источника питания и напряжение на ее выводах падает до минимального уровня (в то время как ток остается на максимальном уровне). Таким образом, при сохранении большего количества энергии, ток через катушку индуктивности увеличивается, а напряжение на ее выводах падает. Заметьте, такое поведение полностью противоположно поведению конденсатора, в котором увеличение количества запасенной энергии приводит к увеличению напряжения на его выводах. Если конденсаторы используют запасенную энергию на поддержание постоянной величины напряжения, то катушки индуктивности такую энергию используют на поддержание постоянной величины тока.
Тип материала, из которого изготавливается провод катушки, оказывает значительное влияние на магнитный поток (а следовательно и на количество запасаемой энергии) создаваемый заданной величиной тока. Влияет на магнитный поток и материал, из которого изготавливается сердечник катушки индуктивности: ферромагнитный материал (например железо) создаст более сильный поток, чем немагнитный материал (например алюминий или воздух).
Способность катушки индуктивности извлекать энергию из источника электрического тока и сохранять ее в виде магнитного поля называется индуктивностью. Индуктивность так же является мерой сопротивления изменениям тока. Для обозначения индуктивности используется символ «L», а измеряется она в Генри, сокращенно «Гн»
Магнитное поле. Электромагнитная индукция. Часть 3. Электромагнитная индукция
Как же всё-таки возникает ток на электростанции? Оказывается, если вдвигать постоянный магнит в катушку, в катушке возникнет ток. Чтобы это увидеть, можно подключить катушку к гальванометру.
Рис. 13 – Возникновение тока в катушке при движении магнита
Что такое гальванометр?
Если не вдаваться в особенности строения гальванометра, то это прибор, стрелка которого отклоняется при протекании через него тока. Он с его помощью можно измерить силу тока, причем очень маленькую, десятки микроампер. Можно проградуировать его шкалу в единицах напряжения. Чтобы это был полноценный амперметр или вольтметр, нужно добавить определенное внутреннее сопротивление прибора. Нас же сейчас интересует гальванометр не столько как измерительный прибор, сколько как индикатор, мы обнаруживаем сам факт, что ток протекает.
Если выдвигать магнит из катушки, ток тоже возникнет и его направление будет противоположным тому, который возникал при движении магнита в катушку. Причем обратите внимание, ток протекает в катушке именно в процессе движения магнита – когда движение прекращается, ток пропадает. Эта деталь мешала обнаружить этот ток его первооткрывателю Фарадею, подробнее об опыте Фарадея вы можете узнать в ответвлении.
Опыт Фарадея
Когда обнаружили, что вокруг проводника с током возникает магнитное поле, у ученых того времени возникла мысль: а не может ли из-за магнитного поля возникнуть ток в проводнике? Ведь стало понятно, что связь между ними какая-то есть. Майкл Фарадей пытался обнаружить такое возникновение тока, спровоцированное магнитным полем. Он подключал катушку к гальванометру, помещал в неё постоянный магнит и следил за стрелкой гальванометра.
В то время приборы были не такими помехозащищёнными, точными и надежными, как сейчас, поэтому, по одной из версий, гальванометр находился далеко от катушки, возможно даже в соседней комнате, чтобы никакие вибрации не создавали помехи. Поэтому, когда Фарадей помещал магнит в катушку, именно во время движения магнита в катушке возникал ток, и стрелка гальванометра отклонялась. Но когда магнит останавливался и ученый подходил к гальванометру, протекание тока уже прекращалось.
Считается, что обнаружить явление электромагнитной индукции помог ученик Фарадея, который находился возле гальванометра в момент, когда Фарадей помещал в катушку магнит, и заметил отклонение стрелки.
Это явление назвали электромагнитной индукцией, а возникающий при этом ток – индукционным.
Возникновение этого тока не должно нас удивлять при том, что мы уже знаем об электромагнитном поле. Мы изучили силу, которая действует на движущийся электрический заряд в магнитном поле. Но движение относительно, и заряд движется в магнитном поле или источник магнитного поля движется относительно заряда – это может быть одна и та же ситуация при рассмотрении в разных системах отсчета. И возможна ситуация, когда электроны будут двигаться в магнитном поле вместе с проводником, а сила, с которой на них действует магнитное поле, будет заставлять их двигаться вдоль проводника, то есть создаст электрический ток. Так что это еще одно проявление электромагнитного взаимодействия зарядов в атомах магнита и свободных зарядов в проводнике.
Для описания этого явления ввели удобный математический инструмент – магнитный поток через выбранную площадь. Что это за выбранная площадь? Мы рассматриваем возникновение тока в замкнутом контуре, и в этом случае ток будет зависеть от магнитного потока через площадь контура.
Так вот, магнитный поток – это по определению произведение магнитной индукции 
на площадь 
, поток через которую вычисляется, и на косинус угла между вектором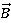 
и перпендикуляром к площади. Обозначать магнитный поток договорились большой греческой буквой 
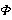, запишем:
Единицу измерения магнитного потока назвали вебер:
Теперь легко описать электромагнитную индукцию: при изменении магнитного потока через замкнутый контур в нем возникает ток, пропорциональный скорости изменения магнитного потока:
Коэффициентом пропорциональности здесь будет сопротивление всего контура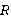 
. Это может быть суммарное сопротивление проводов, если контур состоит только из проводов, или сопротивление проводов плюс приборов, если в цепь включены какие-то приборы, как тот же гальванометр:
И вот что удобно: эта модель универсальна для разных случаев электромагнитной индукции. Магнит вдвигают в катушку – изменяется индукция магнитного поля через площадь одного витка, легко вычислить магнитный поток через виток, а так как это катушка, то умножаем магнитный поток через один виток на количество витков в катушке. Магнит выдвигают из катушки – опять изменяется и опять легко вычислить изменение магнитного потока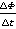 
, а значит и индукционный ток. Виток поворачивают в магнитном поле – изменяется угол между вектором 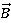и перпендикуляром к площади витка, а значит – изменение магнитного потока и индукционный ток легко посчитать. Мы можем изменить форму и площадь витка – и снова наша модель применима, изменение площади витка означает изменение магнитного потока через эту площадь.
Модуль тока мы определили. А как определить его направление? В опыте с магнитом, катушкой и гальванометром ток был направлен то в одну, то в другую сторону, в зависимости от того, в какую сторону движется магнит и каким полюсом. Эти направления должны подчиняться какой-то закономерности. Эту закономерность обнаружил ученый Эмилий Ленц, и она названа в его честь правилом Ленца.
Возникающий при изменении магнитного потока электрический ток направлен так, чтобы его магнитное поле противодействовало тому изменению магнитного потока, которое вызвало этот ток.
Давайте разберемся на примере, определим направление индукционного тока, который возникает, если вставить в него постоянный магнит северным полюсом вниз.
Магнитный поток создается магнитным полем, индукция которого направлена вниз. Магнитный поток увеличивается, так как при неизменной площади витков и при отсутствии вращения увеличивается магнитная индукция. По правилу Ленца магнитное поле должно противодействовать этому увеличению, поэтому магнитное поле тока в катушке будет направлено противоположно магнитному полю магнита, то есть вверх. По правилу буравчика определяем, в каком направлении течет ток, если вектор магнитной индукции его магнитного поля направлен вверх.
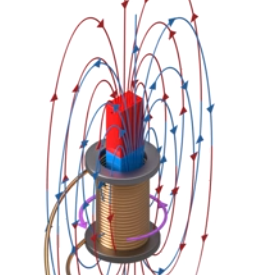
Рис. 14 – Направление индукционного тока в катушке при погружении в нее магнита
А если затем этот магнит вытащить из катушки? Линии индукции магнитного поля по-прежнему направлены вниз, магнитный поток через катушку уменьшается. По правилу Ленца магнитное поле индукционного тока будет противодействовать этому уменьшению, то есть это магнитное поле будет как бы поддерживать уменьшающееся поле магнита, оно будет с ним со направлено, будет тоже направлено вниз.
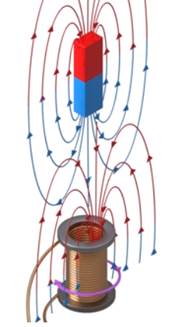
Рис. 15 — Направление индукционного тока в катушке при отдалении от нее магнита
Самоиндукция
Изменяющееся магнитное поле (количественно это удобнее выразить через магнитный поток) создаёт электрический ток в проводнике, это явление электромагнитной индукции. Давайте рассмотрим катушку, в которой мы увеличиваем силу тока. Ток в катушке создает магнитное поле катушки. Так как мы увеличиваем силу тока, то будет увеличиваться и индукция магнитного поля.
И что мы имеем: изменяющееся магнитное поле вокруг катушки. Можно даже вычислить магнитный поток через катушку, и этот магнитный поток будет изменяться. А при изменении магнитного потока в катушке должен возникать индукционный ток! Давайте разберемся, куда он может быть направлен. Изобразим направление тока в катушке и по правилу буравчика магнитное поле катушки. Оно увеличивается, значит, по правилу Ленца, магнитное поле индукционного тока должно быть направлено противоположно нарастающему полю. Найдем направление индукционного тока, он будет направлен против того изначального нарастающего тока. Такое явление, когда изменение магнитного поля катушки создает индукционный ток в этой же катушке, назвали самоиндукцией.
Конечно, неудобно рассматривать два тока, протекающие одновременно в одной катушке, мы рассмотрим их сумму. Так как токи направлены в противоположные стороны, то индукционный ток будет вычитаться из начального тока. Полностью прекратиться протекание тока или его нарастание не может, потому что тогда не будет изменяться магнитное поле и не будет возникать «сдерживающий» индукционный ток. А вот замедление нарастания тока происходит. Ток в катушке не только медленнее нарастает из-за самоиндукции, но и медленнее убывает. Можете в качестве упражнения проследить за процессами в катушке при уменьшении тока.
Токи самоиндукции могут вредить электроприборам в моменты их включения и выключения, и это нужно учитывать при их проектировании. Но вот это явление инерционности, что ток не нарастает и не убывает мгновенно, можно и использовать, нам оно еще пригодится.
Расчёт магнитной индукции многослойной катушки.
В общем случае магнитная индукция проводников с током любой формы находится по закону Био — Савара — Лапласа и принципу суперпозиции магнитных полей. Если многослойную катушку индуктивности представить как набор круговых токов расположенных на одной оси и имеющих одинаковое направление то модуль индукции магнитного поля в точке на оси этих круговых токов будет равен сумме модулей индукций создаваемых каждым током в отдельности:Рисунок 1 — Нахождение магнитной индукции круговых токов
Направление индукции магнитного поля определяется по правилу правого винта. Направление магнитной индукции совпадает с направлением магнитного потока, пример определения этого направления можно посмотреть в статье «обозначение индуктивно связанных катушек».
Рисунок 2 — Круговой ток
Модуль индукции магнитного поля на оси кругового тока на расстоянии z от центра определяется по формуле:
Где: μ — магнитная проницаемость материала, μ0 =4·π·10-7 Гн/м — магнитная постоянная, I — ток, R — радиус кругового тока, z — расстояние от центра кругового тока. Эта формула выведена из закона Био — Савара — Лапласа.
Рисунок 3 — Катушка индуктивности в виде набора круговых токов
Для расчёта магнитной индукции катушки аппроксимированной круговыми токами в точке на её оси можно воспользоваться программой: canvas не поддерживается браузером.Индуктивность. Самоиндукция. Энергия магнитного поля тока. Примеры решения задач по физике. 10-11 класс
Индуктивность. Самоиндукция. Энергия магнитного поля тока. Примеры решения задач по физике. 10-11 класс
Задачи по физике — это просто!
Не забываем, что решать задачи надо всегда в системе СИ!
А теперь к задачам!
Элементарные задачи из курса школьной физики на расчет индуктивности, самоиндукции, энергии магнитного поля тока.
Задача 1
Какова индуктивность витка проволоки, если при токе 6 А создается магнитный поток 12 мВб?
Задача 2
В катушке из 150 витков течет ток 7,5 А, и при этом создается магнитный поток 20 мВб.
Какова индуктивность катушки?
Задача 3
Через соленоид, индуктивность которого 0,4 мГн и площадь поперечного сечения 10 см2, проходит ток 0,5 А.
Какова индукция поля внутри соленоида, если он содержит 100 витков?
Задача 4
Определить индуктивность контура с током 1,2 А, если контур ограничивает площадь 20 см2, а магнитная индукция поля равна 0,8 Тл, причем вектор магнитной индукции направлен под углом 30o к плоскости контура.
Задача 5
Какая ЭДС самоиндукции возбуждается в обмотке электромагнита с индуктивностью 0,4 Гн при изменении силы тока на 5 А за 0,02 секунды?
Задача 6
Определить энергию магнитного поля катушки, если ее индуктивность 0,2 Гн, а ток в ней 12 А.
Задача 7
Какой должна быть сила тока в катушке с индуктивностью 0,5 Гн, чтобы энергия магнитного поля оказалась равной 1 Дж?
Задача 8
Найти энергию магнитного поля соленоида, индуктивность которого 0,02 Гн, а магнитный поток через него составляет 0,4 Вб.