Формула индукции магнитного поля, B
Направлением вектора магнитной индукции считают направление на север магнитной стрелки, которая может свободно вращаться в магнитном поле. Такое же направление имеет положительная нормаль к замкнутому контуру, по которому течет ток. Положительная нормаль имеет направление, совпадающее с направлением перемещения правого винта (буравчика), если его вращают по направлению тока в контуре.
Модуль вектора магнитной индукции можно установить, используя силу, которая действует на проводники с током, помещенные в магнитное поле (силу Ампера). Тогда модуль вектора равен частному от деления максимальной силы (), с которой магнитное поле оказывает воздействие на отрезок проводника с током (I) к произведению силы тока на длину проводника ():
Рассматривая силу Лоренца, которая действует на заряженную частицу, движущуюся в магнитном поле, получают формулу для магнитной индукции в виде:
где – модуль силы Лоренца; q – заряд частицы, движущейся со скоростью v в магнитном поле; – это угол между векторами и . Направления , векторов и связаны между собой правилом левой руки.
Формулой, которая определяет величину вектора магнитной индукции в данной точке магнитного поля, считают так же следующее выражение:
где – максимальный вращающий момент, действующий на рамку, которая обладает магнитным моментом , равным единице, если нормаль к рамке перпендикулярна направлению поля. Вращающий момент (M), действующий на контур с током I в однородном магнитном поле можно вычислить как:
где S – площадь, которую обтекает ток I. Следует помнить, что максимальный вращающий момент получается тогда, когда плоскость контура параллельна линиям магнитной индукции поля ().
Принцип суперпозиции магнитных полей
Если магнитное поле получается в результат наложения нескольких магнитных полей то, магнитная индукция поля (), может быть найдена как векторная сумма магнитных индукций отдельных полей ():
Закон Био-Савара-Лапласа, как формула для вычисления величины индукции магнитного поля
Закон Био-Савара – Лапласа является одним из распространенных законов, который позволяет вычислить вектор магнитной индукции () в любой точке магнитного поля, создаваемого в вакууме элементарным проводником с током:
где I – сила тока; – вектор элементарный проводник по модулю он равен длине проводника, при этом его направление совпадает с направлением течения тока; – радиус-вектор, который проводят от элементарного проводника к точке, в которой находят поле; – магнитная постоянная. Вектор является перпендикулярным к плоскости, в которой расположены и , конкретное направление вектора магнитной индукции определяют при помощи правила буравчика (правого винта).
Для однородного и изотропного магнетика, заполняющего пространство, вектор магнитной индукции в вакууме( и в веществе (), при одинаковых условиях, связывает формула:
где – относительная магнитная проницаемость вещества.
Частные случаи формул для вычисления модуля вектора магнитной индукции
Формула для вычисления модуля вектора индукции в центре кругового витка с током (I):
где R – радиус витка.
Модуль вектора магнитной индукции поля, которое создает бесконечно длинный прямой проводник с током:
где r – расстояние от оси проводника до точки, в которой рассматривается поле.
В средней части соленоида магнитная индукция поля вычисляется при помощи формулы:
где n – количество витков соленоида на единицу длины; I – сила тока в витке.
Примеры решения задач по теме «Индукция магнитного поля»
Магнитная индукция, магнитный поток: определение, формулы, смысл
 Магнитная индукция (обозначается символом В) – главная характеристика магнитного поля (векторная величина ), которая определяет силу воздействия на перемещающийся электрический заряд (ток) в магнитном поле, направленной в перпендикулярном направлении скорости движения.
Магнитная индукция (обозначается символом В) – главная характеристика магнитного поля (векторная величина ), которая определяет силу воздействия на перемещающийся электрический заряд (ток) в магнитном поле, направленной в перпендикулярном направлении скорости движения.
Магнитная индукция определяется способностью влиять на объект с помощью магнитного поля. Эта способность проявляется при перемещении постоянного магнита в катушке, в результате чего в катушке индуцируется (возникает) ток, при этом магнитный поток в катушке также увеличивается.
Физический смысл магнитной индукции
Физически это явление объясняется следующим образом. Металл имеет кристаллическую структуру (катушка состоит из металла). В кристаллической решетке металла расположены электрические заряды — электроны. Если на металл не оказывать ни какое магнитное воздействие, то заряды (электроны) находятся в покое и никуда не движутся.
Если же металл попадает под действие переменного магнитного поля (из-за перемещения постоянного магнита внутри катушки — именно перемещения), то заряды начинают двигаться под действием этого магнитного поля.
В результате чего в металле возникает электрический ток. Сила этого тока зависит от физических свойств магнита и катушки и скорости перемещения одного относительно другого.
При помещении металлической катушки в магнитное поле заряженные частицы металлический решетки (в кашутке) поворачиваются на определенный угол и размещаются вдоль силовых линий магнитного поля.
Чем выше сила магнитного поля, тем больше количество частиц поворачиваются и тем более однородным будет являться их расположение.
Магнитные поля, ориентированные в одном направлении не нейтрализуют друг друга, а складываются, формируя единое поле.
Формула магнитной индукции
где, В — вектор магнитной индукции, F — максимальная сила действующая на проводник с током, I — сила тока в проводнике, l — длина проводника.


Магнитный поток
Магнитный поток это скалярная величина, которая характеризует действие магнитной индукции на некий металлический контур.
Магнитная индукция определяется числом силовых линий, проходящих через 1 см2 сечения металла.
Магнитометры, используемые для ее измерения, называют теслометрами.
Единицей измерения магнитной индукции в системе СИ является Тесла (Тл).
После прекращения движение электронов в катушке сердечник, если он выполнен из мягкого железа, теряет магнитные качества. Если он изготовлен из стали, то он имеет способность некоторое время сохранять свои магнитные свойства.

Формула магнитной индукции, B
Формулы определяющие величину вектора магнитной индукции получают, используя выражение для силы Ампера, силы Лоренца и применяя понятие вращающего момента.
Формула величины вектора магнитной индукции
Формулой, которая определяет величину вектора магнитной индукции в конкретной точке магнитного поля можно считать следующее выражение:
где – максимальный вращающий момент, действующий на рамку, которая обладает магнитным моментом , равным единице, если нормаль к рамке перпендикулярна направлению поля.
При помощи силы Ампера величина вектора магнитной индукции задана как:
где модуль равен пределу отношения величины силы (), с которой магнитное поле действует на бесконечно малый проводник с током, к силе тока (I) умноженной на длину этого проводника (), если длина проводника стремится к нулю. Как известно кроме величины вектор магнитной индукции имеет направление. В данном случае перпендикулярен к направлению силы и перпендикулярен направлению элемента проводника. Если рассматривать вращение из конца вектора магнитной индукции по кратчайшему расстоянию от направления силы к направлению тока, оно должно идти против часовой стрелки.
Используя силу Лоренца, получают формулу для магнитной индукции в виде:
где – модуль силы Лоренца; q – заряд частицы, движущейся со скоростью v в магнитном поле; – это угол между векторами и . Направления , векторов и связаны между собой правилом левой руки.
Закон Био-Савара-Лапласа
Данный закон предоставляет нам возможность вычислить вектор магнитной индукции () в любой точке магнитного поля, которое создается в вакууме элементарным проводником с током:
где I – сила тока; – вектор элементарный проводник по модулю он равен длине проводника, при этом его направление совпадает с направлением течения тока; – радиус-вектор, который проводят от элементарного проводника к точке, в которой находят поле; – магнитная постоянная. Вектор является перпендикулярным к плоскости, в которой расположены и , конкретное направление вектора магнитной индукции определяют при помощи правила буравчика (правого винта).
Для однородного и изотропного магнетика, заполняющего пространство, вектор магнитной индукции в вакууме( и в веществе (), при одинаковых условиях, связывает формула:
где – относительная магнитная проницаемость вещества.
Частные случаи формул для вычисления величины вектора магнитной индукции
Формула для вычисления модуля вектора индукции в центре кругового витка с током (I):
где R – радиус витка.
Модуль вектора магнитной индукции поля, которое создает бесконечно длинный прямой проводник с током:
где r – расстояние от оси проводника до точки, в которой рассматривается поле.
В средней части соленоида магнитная индукция поля вычисляется при помощи формулы:
где n – количество витков соленоида на единицу длины; I – сила тока в витке.
Принцип суперпозиции
Магнитная индукция поля (), которое является наложением нескольких полей, находится как векторная сумма магнитных индукций отдельных полей ():
Примеры решения задач по теме «Магнитная индукция»
Магнитная индукция
ЭЛЕКТРИЧЕСКОЕ ПОЛЕ — существует вокруг электрического заряда, материально. Основное свойство электрического поля: действие с силой на эл.заряд, внесенный в него. Электростатическое поле— поле неподвижного эл.заряда, не меняется со временем. Напряженность электрического поля. — количественная характеристика эл. поля. — это отношение силы, с которой поле действует на внесенный точечный заряд к величине этого заряда. — не зависит от величины внесенного заряда, а характеризует электрическое поле!
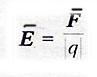
Направление вектора напряженности совпадает с направлением вектора силы, действующей на положительный заряд, и противоположно направлению силы, действующий на отрицательный заряд.
Напряженность поля точечного заряда:
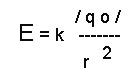 где
q0 — заряд, создающий электрическое
поле.
В любой точке поля напряженность
направлена всегда вдоль прямой,
соединяющей эту точку и q0.
где
q0 — заряд, создающий электрическое
поле.
В любой точке поля напряженность
направлена всегда вдоль прямой,
соединяющей эту точку и q0.
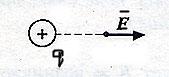
3
ПРИНЦИП СУПЕРПОЗИЦИИ ( НАЛОЖЕНИЯ ) ПОЛЕЙ
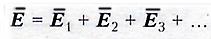
Если в данной точке пространства различные электрически заряженные частицы 1, 2, 3… и т.д. создают электрические поля с напряженностью Е1, Е2, Е3 … и т.д., то результирующая напряженность в данной точке поля равна геометрической сумме напряженностей.
Силовые линии эл. поля — непрерывные линии, касательными к которым являются векторы напряженности эл.поля в этих точках. Однородное эл.поле — напряженность поля одинакова во всех точках этого поля. Свойства силовых линий: не замкнуты (идут от + заряда к _ ), непрерывны, не пересекаются, их густота говорит о напряженности поля (чем гуще линии, тем больше напряженность).
Графически надо
ЭЛЕКТРИЧЕСКОЕ ПОЛЕ заряженного шара.
Есть заряженный проводящий шар радиусом R.
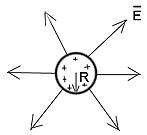
— заряд равномерно рапределен лишь по поверхности шара! Напряженность эл. поля снаружи:
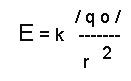
Напряженность внутри шара: Е = 0
12
ЭЛЕКТРОЕМКОСТЬ — характеризует способность двух проводников накапливать электрический заряд. — не зависит от q и U. — зависит от геометрических размеров проводников, их формы, взаимного расположения, электрических свойств среды между проводниками.
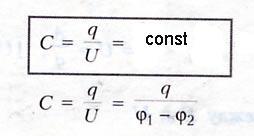 Единицы
измерения в СИ: ( Ф — фарад )
Единицы
измерения в СИ: ( Ф — фарад )
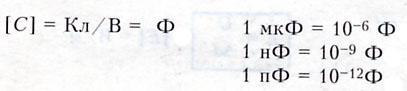
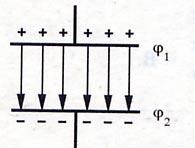
КОНДЕНСАТОРЫ
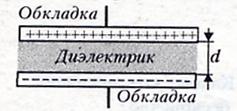
— электротехническое устройство, накапливающее заряд ( два проводника, разделенных слоем диэлектрика ).
 где
d много меньше размеров проводника. Обозначение
на электрических схемах:
где
d много меньше размеров проводника. Обозначение
на электрических схемах:
 Все
электрическое поле сосредоточено внутри
конденсатора.
Заряд конденсатора —
это абсолютное значение заряда одной
из обкладок конденсатора.
Все
электрическое поле сосредоточено внутри
конденсатора.
Заряд конденсатора —
это абсолютное значение заряда одной
из обкладок конденсатора.
Виды конденсаторов: 1. по виду диэлектрика: воздушные, слюдяные, керамические, электролитические 2. по форме обкладок: плоские, сферические. 3. по величине емкости: постоянные, переменные (подстроечные).
Электроемкость плоского конденсатора
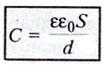 где
S — площадь пластины (обкладки) конденсатора
d
— расстояние между пластинами
eо —
электрическая постоянная
e —
диэлектрическая проницаемость диэлектрика
где
S — площадь пластины (обкладки) конденсатора
d
— расстояние между пластинами
eо —
электрическая постоянная
e —
диэлектрическая проницаемость диэлектрика
Включение конденсаторов в электрическую цепь
параллельное
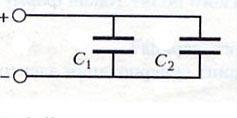
последовательное
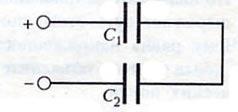
Тогда общая электроемкость (С):
при параллельном включении
.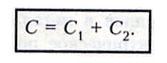 при
последовательном включении
при
последовательном включении
ЭНЕРГИЯ ЗАРЯЖЕННОГО КОНДЕНСАТОРА
Конденсатор — это система заряженных тел и обладает энергией. Энергия любого конденсатора:
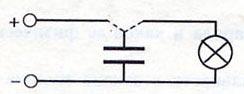
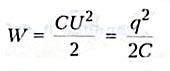 где
С — емкость конденсатора
q — заряд
конденсатора
U — напряжение на обкладках
конденсатора
Энергия конденсатора
равна работе, которую совершит
электрическое поле при сближении пластин
конденсатора вплотную,
или равна
работе по разделению положительных и
отрицательных зарядов , необходимой
при зарядке конденсатора.
где
С — емкость конденсатора
q — заряд
конденсатора
U — напряжение на обкладках
конденсатора
Энергия конденсатора
равна работе, которую совершит
электрическое поле при сближении пластин
конденсатора вплотную,
или равна
работе по разделению положительных и
отрицательных зарядов , необходимой
при зарядке конденсатора.
ЭНЕРГИЯ ЭЛЕКТРИЧЕСКОГО ПОЛЯ КОНДЕНСАТОРА
Энергия
конденсатора приблизительно равна
квадрату напряженности эл. поля внутри
конденсатора.
Плотность энергии эл.
поля конденсатора: 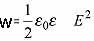
14
Электри́ческий ток — направленное (упорядоченное) движение заряженных частиц[1][2][3]. Такими частицами могут являться: в металлах —электроны, в электролитах — ионы (катионы и анионы), в газах — ионы и электроны, в вакууме при определенных условиях — электроны, вполупроводниках — электроны и дырки (электронно-дырочная проводимость). Иногда электрическим током называют также ток смещения, возникающий в результате изменения во времени электрического поля].
Сила
тока — физическая
величина 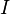 ,
равная отношению количества
заряда
,
равная отношению количества
заряда 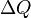 ,
прошедшего через некоторую поверхность
за время
,
прошедшего через некоторую поверхность
за время 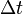 ,
к величине этого промежутка времени[1]:
,
к величине этого промежутка времени[1]:
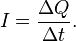
В качестве рассматриваемой поверхности часто используется поперечное сечение проводника.
Сила тока в Международной системе единиц (СИ) измеряется в амперах (русское обозначение: А; международное: A), ампер является одной из семиосновных единиц СИ. 1 А = 1 Кл/с.
По закону
Ома сила
тока 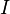 для
участка цепи прямо пропорциональна
приложенному напряжению
для
участка цепи прямо пропорциональна
приложенному напряжению 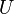 к
участку цепи и обратно
пропорциональнасопротивлению
к
участку цепи и обратно
пропорциональнасопротивлению 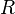 проводника этого
участка цепи:
проводника этого
участка цепи:
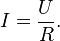
Носителями
заряда, движение которых, приводит к
возникновению тока, являются заряженные
частицы, в роли которых обычно
выступаютэлектроны, ионы или дырки.
Сила тока зависит от заряда 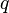 этих
частиц, их концентрации
этих
частиц, их концентрации 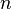 ,
средней скорости упорядоченного движения
частиц
,
средней скорости упорядоченного движения
частиц 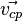 ,
а также площади
,
а также площади 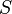 и
формы поверхности, через которую течёт
ток.
и
формы поверхности, через которую течёт
ток.
Если 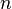 и
и 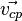 постоянны
по объёму проводника, а интересующая
поверхность плоская, то выражение для
силы тока можно представить в виде
постоянны
по объёму проводника, а интересующая
поверхность плоская, то выражение для
силы тока можно представить в виде
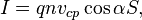
где 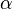 —
угол между скоростью частиц
и вектором
нормали к
поверхности.
—
угол между скоростью частиц
и вектором
нормали к
поверхности.
В
более общем случае, когда сформулированные
выше ограничения не выполняются,
аналогичное выражение можно записать
только для силы тока 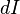 ,
протекающего через малый элемент
поверхности площадью
,
протекающего через малый элемент
поверхности площадью 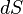 :
:
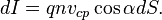
Тогда выражение для силы тока, протекающего через всю поверхность, записывается в виде интеграла по поверхности
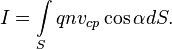
В металлах заряд переносят электроны, соответственно в этом случае выражение для силы тока имеет вид
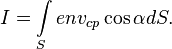
где e — элементарный электрический заряд.
Вектор 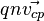 называют плотностью
электрического тока.
Как следует из сказанного выше, его
величина равна силе тока, протекающей
через малый элемент поверхности единичной
площади, расположенный перпендикулярно
скорости
называют плотностью
электрического тока.
Как следует из сказанного выше, его
величина равна силе тока, протекающей
через малый элемент поверхности единичной
площади, расположенный перпендикулярно
скорости 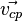 ,
а направление совпадает с направлением
упорядоченного движения заряженных
частиц[2].
,
а направление совпадает с направлением
упорядоченного движения заряженных
частиц[2].
Для измерения силы тока используют специальный прибор — амперметр (для приборов, предназначенных для измерения малых токов, также используются названия миллиамперметр, микроамперметр, гальванометр). Его включают в разрыв цепи в том месте, где нужно измерить силу тока. Основные методы измерения силы тока: магнитоэлектрический, электромагнитный и косвенный (путём измерения вольтметром напряжения на известном сопротивлении).
В случае переменного тока различают мгновенную силу тока, амплитудную (пиковую) силу тока и эффективную силу тока (равную силе постоянного тока, который выделяет такую же мощность).
Пло́тность то́ка — векторная физическая величина, имеющая смысл силы тока, протекающего через элемент поверхности единичной площади[1]. Например, при равномерном распределении плотности тока и всюду ортогональности её плоскости сечения, через которое вычисляется или измеряется ток, величина вектора плотности тока:
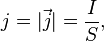
где I — сила тока через поперечное сечение проводника площадью S (также см.рисунок).
Иногда речь может идти о скалярной[2] плотности тока, в таких случаях под ней подразумевается именно та величина j, которая приведена в формуле.
В общем случае:
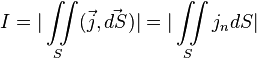 ,
,
где 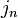 —
нормальная (ортогональная) составляющая
вектора плотности тока по отношению к
элементу поверхности площадью
—
нормальная (ортогональная) составляющая
вектора плотности тока по отношению к
элементу поверхности площадью 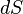 ;
вектор
;
вектор 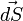 —
специально вводимый вектор элемента
поверхности, ортогональный элементарной
площадке и имеющий абсолютную величину,
равную её площади, позволяющий записать
подынтегральное выражение как обычное
скалярное произведение.
—
специально вводимый вектор элемента
поверхности, ортогональный элементарной
площадке и имеющий абсолютную величину,
равную её площади, позволяющий записать
подынтегральное выражение как обычное
скалярное произведение.
Как видим из этого определения, сила тока есть поток вектора плотности тока через некую заданную фиксированную поверхность.
В
простейшем предположении, что все
носители тока (заряженные частицы)
двигаются с одинаковым вектором
скорости 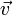 и
имеют одинаковые заряды
и
имеют одинаковые заряды 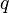 (такое
предположение может иногда быть
приближенно верным; оно позволяет лучше
всего понять физический смысл плотности
тока), а концентрация их
(такое
предположение может иногда быть
приближенно верным; оно позволяет лучше
всего понять физический смысл плотности
тока), а концентрация их 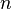 ,
,
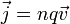
или
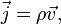
где 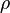 —
плотность заряда этих носителей.
—
плотность заряда этих носителей.
Направление
вектора 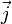 соответствует
направлению вектора скорости
соответствует
направлению вектора скорости 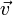 ,
с которой движутся заряды,
создающие ток, если q положительно.
,
с которой движутся заряды,
создающие ток, если q положительно.
В
реальности даже носители одного типа
движутся вообще говоря и как правило с
различными скоростями. Тогда под 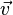 следует
понимать среднюю скорость.
следует
понимать среднюю скорость.
В сложных системах (с различными типами носителей заряда, например, в плазме или электролитах)
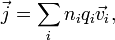
то
есть вектор плотности тока есть сумма
плотностей тока по всем типам подвижных
носителей; где 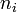 — концентрация
частиц каждого
типа,
— концентрация
частиц каждого
типа, 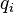 —
заряд частицы данного типа,
—
заряд частицы данного типа, 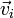 —
вектор средней скорости частиц этого
типа.
—
вектор средней скорости частиц этого
типа.
Выражение для общего случая может быть записано также через сумму по всем индивидуальным частицам:
15
Зако́н О́ма — эмпирический физический закон, определяющий связь электродвижущей силы источника или электрического напряжения с силой тока и сопротивлением проводника. Экспериментально установлен в 1826 году, и назван в честь его первооткрывателя Георга Ома.
В
своей оригинальной форме он был записан
его автором в виде : 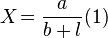 ,
,
Здесь X —
показания гальванометра,
т.е в современных обозначениях сила
тока I, a —
величина, характеризующая свойства
источника тока, постоянная в широких
пределах и не зависящая от величины
тока, то есть в современной терминологии
электродвижущая сила (ЭДС)  , l —
величина, определяемая длиной соединяющих
проводов, чему в современных представлениях
соответствует сопротивление внешней
цепи R и,
наконец, b параметр,
характеризующий свойства всей установки,
в котором сейчас можно усмотреть учёт
внутреннего сопротивления источника
тока r[1].
, l —
величина, определяемая длиной соединяющих
проводов, чему в современных представлениях
соответствует сопротивление внешней
цепи R и,
наконец, b параметр,
характеризующий свойства всей установки,
в котором сейчас можно усмотреть учёт
внутреннего сопротивления источника
тока r[1].
В таком случае в современных терминах и в соответствии с предложенной автором записи формулировка Ома (1) выражает
Закон Ома для полной цепи:
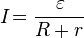 ,
(2)
,
(2)
где:
 — ЭДС источника
напряжения,
— ЭДС источника
напряжения, — сила
тока в
цепи,
— сила
тока в
цепи, — сопротивление всех
внешних элементов цепи,
— сопротивление всех
внешних элементов цепи, — внутреннее
сопротивление источника
напряжения.
— внутреннее
сопротивление источника
напряжения.
Из закона Ома для полной цепи вытекают следствия:
При r<<R сила тока в цепи обратно пропорциональна её сопротивлению. А сам источник в ряде случаев может быть назван источником напряжения
При r>>R сила тока от свойств внешней цепи (от величины нагрузки) не зависит. И источник может быть назван источником тока.
Часто[2] выражение:
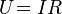 (3)
(3)
(где 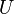 есть напряжение или падение
напряжения,
или, что то же, разность
потенциалов между
началом и концом участка проводника)
тоже называют «Законом Ома».
есть напряжение или падение
напряжения,
или, что то же, разность
потенциалов между
началом и концом участка проводника)
тоже называют «Законом Ома».
Таким образом, электродвижущая сила в замкнутой цепи, по которой течёт ток в соответствии с (2) и (3) равняется:
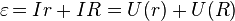 (4)
(4)
То есть сумма падений напряжения на внутреннем сопротивлении источника тока и на внешней цепи равна ЭДС источника. Последний член в этом равенстве специалисты называют «напряжением на зажимах», поскольку именно его показывает вольтметр, измеряющий напряжение источника между началом и концом присоединённой к нему замкнутой цепи. В таком случае оно всегда меньше ЭДС.
К другой записи формулы (3), а именно:
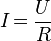 (5)
(5)
применима другая формулировка:
| Сила тока в участке цепи прямо пропорциональна напряжению и обратно пропорциональна электрическому сопротивлению данного участка цепи. |
|
Выражение (5) можно переписать в виде:
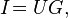 (6)
(6)
где коэффициент пропорциональности G назван проводимость или электропроводность. Изначально единицей измерения проводимости был «обратный Ом» — Mо[3], в Международной системе единиц (СИ) единицей измерения проводимости является си́менс (русское обозначение: См; международное: S), величина которого равна обратному ому.
ЗАКОН ДЖОУЛЯ -ЛЕНЦА
При прохождениии тока по проводнику проводник нагревается, и происходит теплообмен с окружающей средой, т.е. проводник отдает теплоту окружающим его телам.
Количество теплоты, выделяемое проводником с током в окружающую среду, равно произведению квадрата силы тока, сопротивления проводника и времени прохождения тока по проводнику.
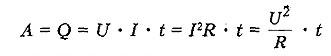
По закону сохранения энергии количество теплоты, выделяемое проводником численно равно работе, которую совершает протекающий по проводнику ток за это же время.
В системе СИ:
[Q] = 1 Дж
19
МАГНИТНОЕ ПОЛЕ
— это особый вид материи, посредством которой осуществляется взаимодействие между движущимися электрически заряженными частицами.
СВОЙСТВА ( стационарного) МАГНИТНОГО ПОЛЯ
Постоянное (или стационарное) магнитное поле — это магнитное поле, неизменяющееся во времени .
1. Магнитное поле создается движущимися заряженными частицами и телами, проводниками с током, постоянными магнитами.
2. Магнитное поле действует на движущиеся заряженные частицы и тела, на проводники с током, на постоянные магниты, на рамку с током.
3. Магнитное поле вихревое, т.е. не имеет источника.
— это силовая характеристика магнитного поля.
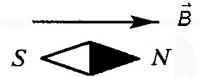
Вектор магнитной индукции направлен всегда так, как сориентирована свободно вращающаяся магнитная стрелка в магнитном поле.
Единица измерения магнитной индукции в системе СИ:
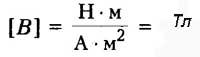
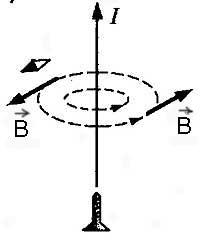
Направление линий магнитной индукции
— определяется по правилу буравчика или по правилу правой руки.
Правило буравчика ( в основном для прямого проводника с током):
Если направление поступательного движения буравчика совпадает с направлением тока в проводнике, то направление вращения ручки буравчика совпадает с направлением линий магнитного поля тока.
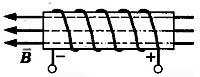
Правило правой руки ( в основном для определения направления магнитных линий внутри соленоида):
Если обхватить соленоид ладонью правой руки так, чтобы четыре пальца были направлены вдоль тока в витках, то отставленный большой палец покажет направление линий магнитного поля внутри соленоида.
Существуют другие возможные варианты применения правил буравчика и правой руки.
Сила ампера
— это сила, с которой магнитное поле действует на проводник с током.
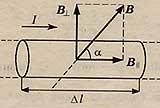

Модуль силы Ампера равен произведению силы тока в проводнике на модуль вектора магнитной индуции, длину проводника и синус угла между вектором магнитной индукции и направлением тока в проводнике.
Сила Ампера максимальна, если вектор магнитной индукции перпендикулярен проводнику.
Если вектор магнитной индукции параллелен проводнику, то магнитное поле не оказывает никакого действия на проводник с током, т.е. сила Ампера равна нулю.
Направление силы Ампера определяется по правилу левой руки:
Если левую руку расположить так, чтобы перпендикулярная проводнику составляющая вектора магнитной индукции входила в ладонь, а 4 вытянутых пальца были направлены по направлению тока, то отогнутый на 90 градусов большой палец покажет направление силы, действующий на проводник с током.
Примеры:
 или
или 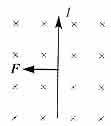
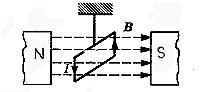
Действие магнитного поля на рамку с током
Однородное магнитное поле ориентирует рамку (т.е. создается вращающий момент и рамка поворачивается в положение, когда вектор магнитной индукции перпендикулярен плоскости рамки).
Неоднородное магнитное поле ориентирует + притягивает или отталкивает рамку с током. Так, в магнитном поле прямого проводника с током (оно неоднородно) рамка с током ориентируется вдоль радиуса магнитной линии и притягивается или отталкивается от прямого проводника с током в зависимости от направления токов.
22
Магнитный момент витка с током это физическая величина, как и любой другой магнитный момент, характеризует магнитные свойства данной системы. В нашем случае систему представляет круговой виток с током. Этот ток создает магнитное поле, которое взаимодействует с внешним магнитным полем. Это может быть как поле земли, так и поле постоянного или электромагнита.
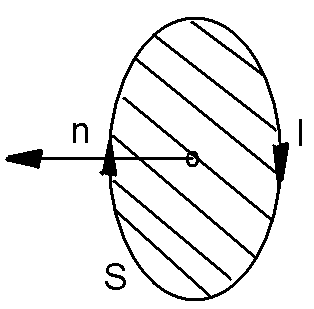
Рисунок — 1 круговой виток с током
Круговой виток с током можно представить в виде короткого магнита. Причем этот магнит будет направлен перпендикулярно плоскости витка. Расположение полюсов такого магнита определяется с помощью правила буравчика. Согласно которому северный плюс будет находиться за плоскостью витка, если ток в нем будет двигаться по часовой стрелке.
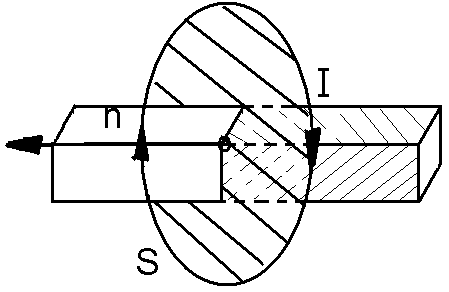
Рисунок— 2 Воображаемый полосовой магнит на оси витка
На этот магнит, то есть на наш круговой виток с током, как и на любой другой магнит, будет воздействовать внешнее магнитное поле. Если это поле будет однородным, то возникнет вращающий момент, который будет стремиться развернуть виток. Поле буде поворачивать виток так чтобы его ось расположилась вдоль поля. При этом силовые линии самого витка, как маленького магнита, должны совпасть по направлению с внешним полем.
Если же внешнее поле будет не однородным, то к вращающему моменту добавится и поступательное движение. Это движение возникнет вследствие того что участки поля с большей индукцией будут притягивать наш магнит в виде витка больше чем участки с меньшей индукцией. И виток начнет двигаться в сторону поля с большей индукцией.
Величину магнитного момента кругового витка с током можно определить по формуле.
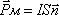
Конспект «Магнитное поле. Теория, формулы, схемы»
Подобно тому, как покоящийся электрический заряд действует на другой заряд посредством электрического поля, электрический ток действует на другой ток посредством магнитного поля. Действие магнитного поля на постоянные магниты сводится к действию его на заряды, движущиеся в атомах вещества и создающие микроскопические круговые токи.
Учение об электромагнетизме основано на двух положениях:
- магнитное поле действует на движущиеся заряды и токи;
- магнитное поле возникает вокруг токов и движущихся зарядов.
Взаимодействие магнитов
Постоянный магнит (или магнитная стрелка) ориентируется вдоль магнитного меридиана Земли. Тот его конец, который указывает на север, называется северным полюсом (N), а противоположный конец — южным полюсом (S). Приближая два магнита друг к другу, заметим, что одноименные их полюсы отталкиваются, а разноименные — притягиваются (рис. 1).

Если разделить полюса, разрезав постоянный магнит на две части, то мы обнаружим, что каждая из них тоже будет иметь два полюса, т. е. будет постоянным магнитом (рис. 2). Оба полюса — северный и южный, — неотделимые друг от друга, равноправны.
Магнитное поле, создаваемое Землей или постоянными магнитами, изображается, подобно электрическому полю, магнитными силовыми линиями. Картину силовых линий магнитного поля какого-либо магнита можно получить, помещая над ним лист бумаги, на котором насыпаны равномерным слоем железные опилки. Попадая в магнитное поле, опилки намагничиваются — у каждой из них появляется северный и южный полюсы. Противоположные полюсы стремятся сблизиться друг с другом, но этому мешает трение опилок о бумагу. Если постучать по бумаге пальцем, трение уменьшится и опилки притянутся друг к другу, образуя цепочки, изображающие линии магнитного поля.
На рис. 3 показано расположение в поле прямого магнита опилок и маленьких магнитных стрелок, указывающих направление линий магнитного поля. За это направление принято направление северного полюса магнитной стрелки.
Опыт Эрстэда. Магнитное поле тока
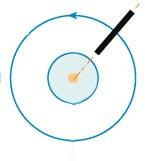
В начале XIX в. датский ученый Эрстэд сделал важное открытие, обнаружив действие электрического тока на постоянные магниты. Он поместил длинный провод вблизи магнитной стрелки. При пропускании по проводу тока стрелка поворачивалась, стремясь расположиться перпендикулярно ему (рис. 4). Это можно было объяснить возникновением вокруг проводника магнитного поля.
Магнитные силовые линии поля, созданного прямым проводником с током, представляют собой концентрические окружности, расположенные в перпендикулярной к нему плоскости, с центрами в точке, через которую проходит ток (рис. 5). Направление линий определяется правилом правого винта:
Если винт вращать по направлению линий поля, он будет двигаться в направлении тока в проводнике.
Силовой характеристикой магнитного поля является вектор магнитной индукции B. В каждой точке он направлен по касательной к линии поля. Линии электрического поля начинаются на положительных зарядах и оканчиваются на отрицательных, а сила, действующая в этом поле на заряд, направлена по касательной к линии в каждой ее точке. В отличие от электрического, линии магнитного поля замкнуты, что связано с отсутствием в природе «магнитных зарядов».
Магнитное поле тока принципиально ничем не отличается от поля, созданного постоянным магнитом. В этом смысле аналогом плоского магнита является длинный соленоид — катушка из провода, длина которой значительно больше ее диаметра. Схема линий созданного им магнитного поля, изображенная на рис. 6, аналогична таковой для плоского магнита (рис. 3). Кружочками обозначены сечения провода, образующего обмотку соленоида. Токи, текущие по проводу от наблюдателя, обозначены крестиками, а токи противоположного направления — к наблюдателю — обозначены точками. Такие же обозначения приняты и для линий магнитного поля, когда они перпендикулярны плоскости чертежа (рис. 7 а, б).

Направление тока в обмотке соленоида и направление линий магнитного поля внутри него также связаны правилом правого винта, которое в этом случае формулируется так:
Если смотреть вдоль оси соленоида, то текущий по направлению часовой стрелки ток создает в нем магнитное поле, направление которого совпадает с направлением движения правого винта (рис. 8)

Исходя из этого правила, легко сообразить, что у соленоида, изображенного на рис. 6, северным полюсом служит правый его конец, а южным — левый.
Магнитное поле внутри соленоида является однородным — вектор магнитной индукции имеет там постоянное значение (B = const). В этом отношении соленоид подобен плоскому конденсатору, внутри которого создается однородное электрическое поле.
Сила, действующая в магнитном поле на проводник с током
Опытным путем было установлено, что на проводник с током в магнитном поле действует сила. В однородном поле прямолинейный проводник длиной l, по которому течет ток I, расположенный перпендикулярно вектору поля B, испытывает действие силы: F = I l B.
Направление силы определяется правилом левой руки:
Если четыре вытянутых пальца левой руки расположить по направлению тока в проводнике, а ладонь — перпендикулярно вектору B, то отставленный большой палец укажет направление силы, действующей на проводник (рис. 9).
 Следует отметить, что сила, действующая на проводник с током в магнитном поле, направлена не по касательной к его силовым линиям, подобно электрической силе, а перпендикулярна им. На проводник, расположенный вдоль силовых линий, магнитная сила не действует.
Следует отметить, что сила, действующая на проводник с током в магнитном поле, направлена не по касательной к его силовым линиям, подобно электрической силе, а перпендикулярна им. На проводник, расположенный вдоль силовых линий, магнитная сила не действует.
Уравнение F = IlB позволяет дать количественную характеристику индукции магнитного поля.
Отношение  не зависит от свойств проводника и характеризует само магнитное поле.
не зависит от свойств проводника и характеризует само магнитное поле.
Модуль вектора магнитной индукции B численно равен силе, действующей на расположенный перпендикулярно к нему проводник единичной длины, по которому течет ток силой один ампер.
В системе СИ единицей индукции магнитного поля служит тесла (Тл):

Магнитное поле. Таблицы, схемы, формулы
(Взаимодействие магнитов, опыт Эрстеда, вектор магнитной индукции, направление вектора, принцип суперпозиции. Графическое изображение магнитных полей, линии магнитной индукции. Магнитный поток, энергетическая характеристика поля. Магнитные силы, сила Ампера, сила Лоренца. Движение заряженных частиц в магнитном поле. Магнитные свойства вещества, гипотеза Ампера)




Дополнительные материалы по теме: Электромагнитные явления
Конспект по теме «Магнитное поле. Теория, формулы, схемы».
Следующая тема «Электромагнитная индукция»
связь магнитного потока и ВМИ
Один из параметров магнитного поля – его силовая характеристика. Она обозначает, с какой силой поле влияет на движущиеся в нём заряженные частицы. Это значение из разряда векторных величин, носит название магнитная индукция B→.
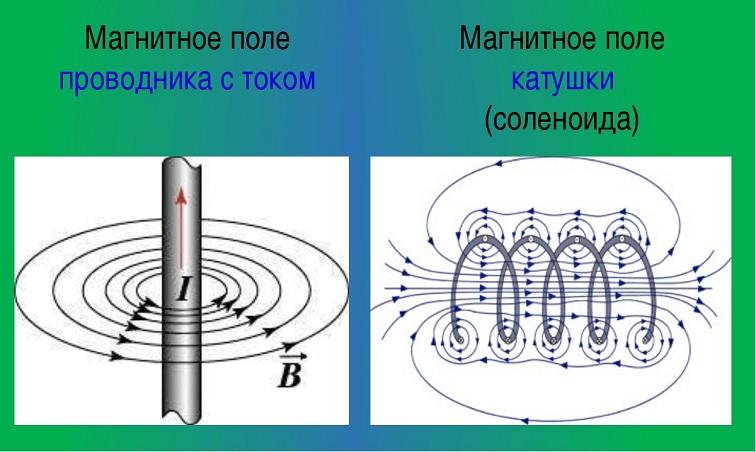
Индукция B→ проводника с током и соленоида
Физический смысл магнитной индукции (МИ)
Возможность действовать на предмет магнитным полем (МП) определяет сущность настоящей индукции. Она появляется в момент перемещения в катушке индуктивности магнита постоянной природы. Результатом такого движения является появление тока, с одновременным увеличением магнитного потока. Поскольку обмотка у катушки металлическая, а структура металла – кристаллическая решётка, то можно объяснить физические свойства этого явления.
Электроны, находящиеся в этой решётке, при отсутствии магнитного воздействия находятся в покое. Движения никакого нет. Оно начинается в тот момент, когда электроны попадают под воздействие переменного МП (поле изменяется при перемещении постоянного магнита).
Значение возникающего в катушке тока зависит от диаметра жилы и количества витков, физических характеристик магнита и скорости его движения.
Единица размерности в системе Си рассматриваемой характеристики – тесла. Она обозначается буквами Тл.
Важно! Электроны в решётке, после попадания катушки в МП, разворачиваются под некоторым углом и выстраиваются вдоль силовых линий МП. Количество ориентированных частиц и однородность их размещения зависимы от величины поля.
Вектор – это вектор индукции магнитного поля (градиентный параметр МП).
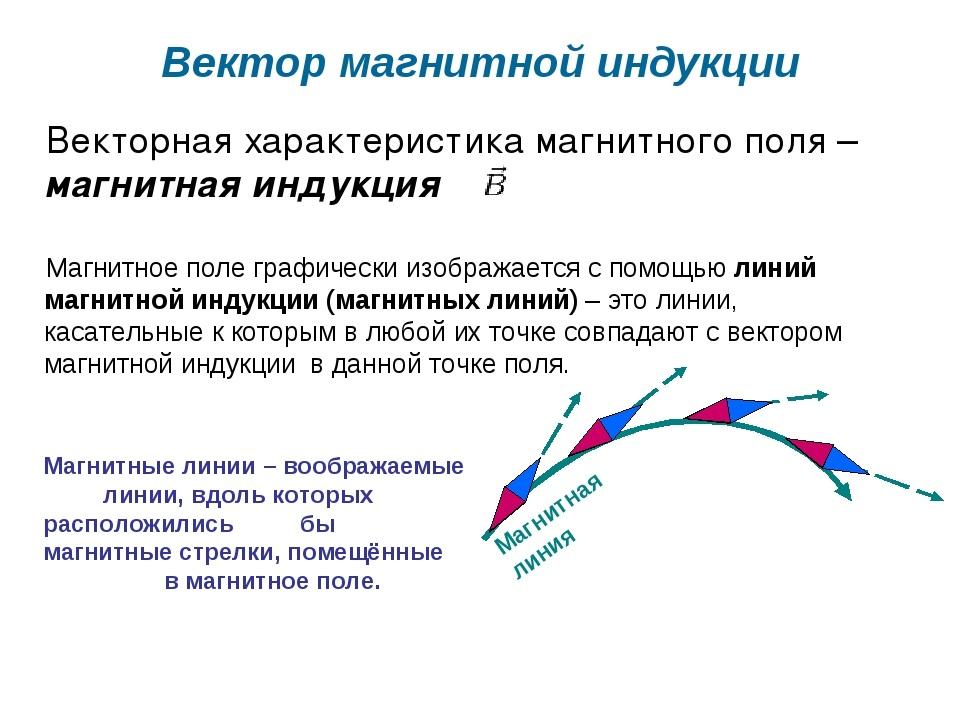
Вектор магнитной индукции
Направление вектора МИ
Направление магнитных полей может указать стрелка магнита, помещаемая в эти поля. Она будет крутиться до тех пор, пока не остановится. Северный конец стрелки покажет, куда ориентирован B→ орт того или иного поля.
Таким же образом ведёт себя рамка с током, имеющая возможность без помех ориентироваться в МП. Направленность вектора индукции указывает ориентацию нормали к такому замкнутому электромагнитному контуру.
Внимание! Здесь используют правило буравчика (правого винта). Если винт вращать так, как направлен ток в рамке, то поступательное продвижение винта совпадёт с направлением положительной нормали.
В некоторых случаях, чтобы найти направление, применяют правило правой руки.

Определение направления B→
Наглядное отображение линий МИ
Линию, к которой можно провести касательную, совпадающую с B→, называют линией магнитной индукции (МИ). С помощью таких линий можно визуально отобразить магнитное поле. Это сомкнутые контурные чёрточки, которые охватывают токи. Их густота всегда пропорциональна величине B→ в конкретной точке МП.
Информация. Когда имеют дело с МП прямого движения заряженных частиц, то эти линии изображаются в виде концентрических окружностей. Они имеют свой центр, расположенный на прямой линии с током, и находятся в плоскостях, расположенных под прямым углом к нему.
С направлением магнитных линий также можно определиться, пользуясь правилом буравчика.
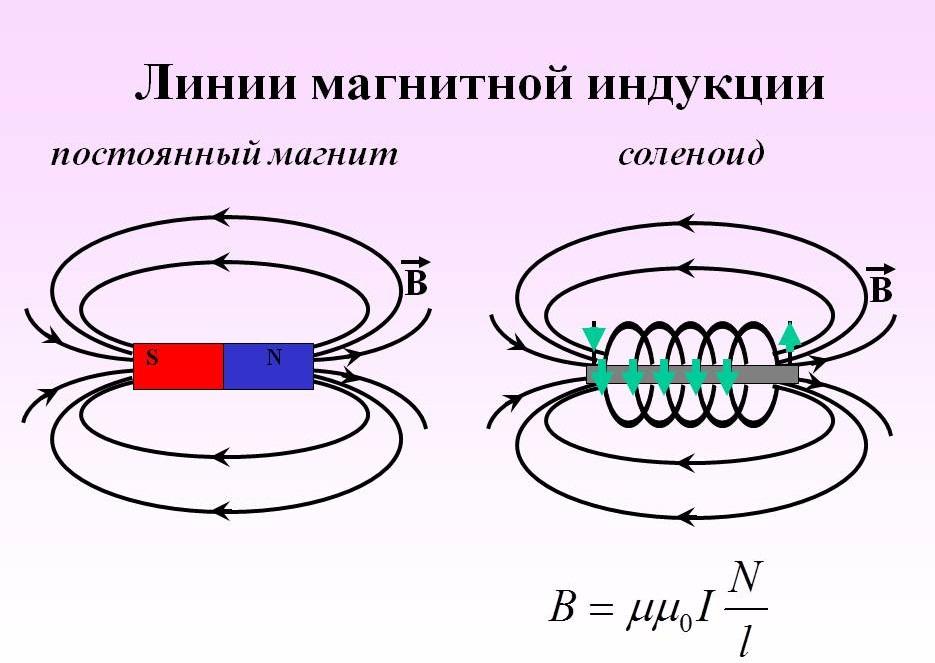
Графическое обозначение линий МИ
Модуль вектора магнитной индукции
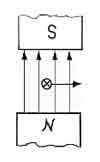
Чтобы определить величину вектора МИ, нужно узнать его модуль. Как определяется модуль вектора магнитной индукции (градиент)? Это можно понять на примере небольшой модели. Если поместить в поле подковообразного магнита горизонтально подвешенный проводник, то МП магнита будет действовать только на участок, расположенный в междуполюсном промежутке. Сила F→, действующая на этот участок, будет направлена под прямым углом к линиям индукции и самому проводнику. Она достигает своего максимума, когда орт МИ располагается перпендикулярно проводнику.
Значение модуля B→ будет равно отношению максимального значения этой силы F→ к произведению длины отрезка ∆L на силу движения зарядов (I), а именно:
B = Fm/I*∆L.
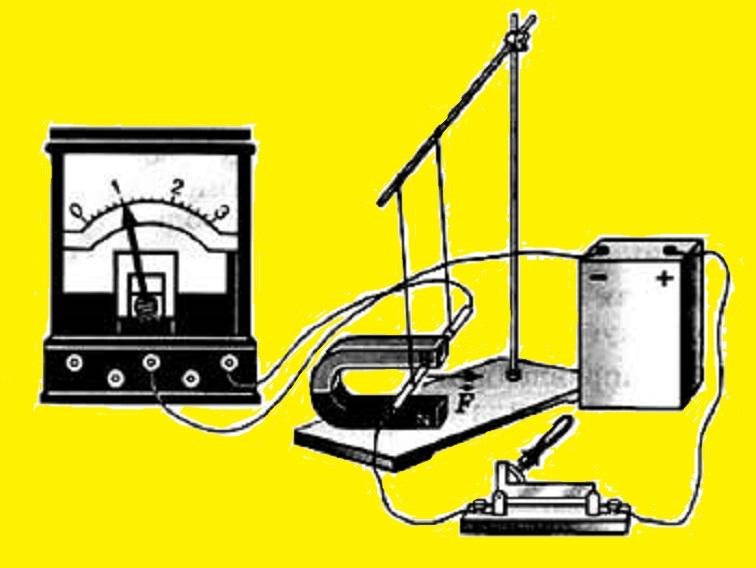
Электрическая модель для определения модуля B→
Основные формулы для вычисления вектора МИ
Вектор магнитной индукции, формула которого B = Fm/I*∆L, можно находить, применяя другие математические вычисления.
Закон Био-Савара-Лапласа
Описывает правила нахождения B→ магнитного поля, которое создаёт постоянный электроток. Это экспериментально установленная закономерность. Био и Савар в 1820 году выявили её на практике, Лапласу удалось сформулировать. Этот закон является основополагающим в магнитостатике. При практическом опыте рассматривался неподвижный провод с малым сечением, через который пропускали электроток. Для изучения выбирался малый участок провода, который характеризовался вектором dl. Его модуль соответствовал длине рассматриваемого участка, а направление совпадало с направлением тока.
Интересно. Лаплас Пьер Симон предложил считать током даже движение одного электрона и на этом утверждении, с помощью данного закона, доказал возможность определения МП продвигающегося точечного заряда.
Согласно этому физическому правилу, каждый сегмент dl проводника, по которому протекает электрический ток I, образовывает в пространстве вокруг себя на промежутке r и под углом α магнитное поле dB:
dB = µ0 *I*dl*sin α /4*π*r2,
где:
- dB – магнитная индукция, Тл;
- µ0 = 4 π*10-7 – магнитная постоянная, Гн/м;
- I – сила тока, А;
- dl – отрезок проводника, м;
- r – расстояние до точки нахождения магнитной индукции, м;
- α – угол, образованный r и вектором dl.
Важно! Согласно закону Био-Савара-Лапласа, суммируя векторы магнитных полей отдельных секторов, можно определить МП нужного тока. Оно будет равно векторной сумме.
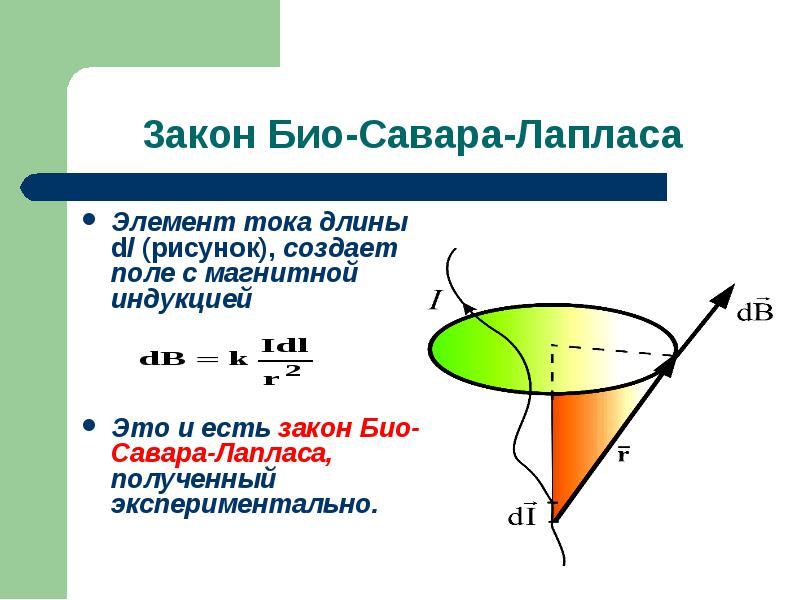
Закон Био-Савара-Лапласа
Существуют формулы, описывающие этот закон для отдельных случаев МП:
- поля прямого перемещения электронов;
- поля кругового движения заряженных частиц.
Формула для МП первого типа имеет вид:
В = µ* µ0*2*I/4*π*r.
Для кругового движения она выглядит так:
В = µ*µ0*I/4*π*r.
В этих формулах µ – это магнитная проницаемость среды (относительная).
Рассматриваемый закон вытекает из уравнений Максвелла. Максвелл вывел два уравнения для МП, случай, где электрическое поле постоянно, как раз рассматривают Био и Савар.
Принцип суперпозиции
Для МП существует принцип, согласно которому общий вектор магнитной индукции в определённой точке равен векторной сумме всех векторов МИ, созданных разными токами в данной точке:
B→= B1→+ B2→+ B3→… + Bn→
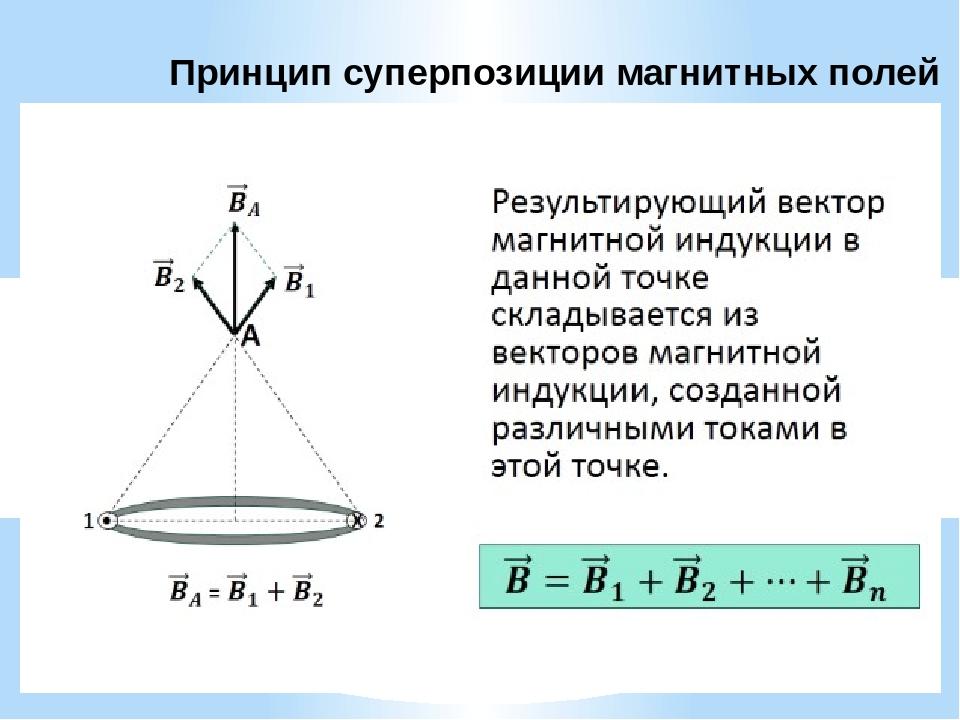
Принцип суперпозиции
Теорема о циркуляции
Изначально в 1826 году Андре Ампер сформулировал данную теорему. Он разобрал случай с постоянными электрическими полями, его теорема применима к магнитостатике. Теорема гласит: циркуляция МП постоянного электричества по любому контуру соразмерна сумме сил всех токов, которые пронизывают этот контур.
Стоит знать! Тридцать пять лет спустя Д. Максвелл обобщил это утверждение, проведя параллели с гидродинамикой.
Другое название теоремы – закон Ампера, описывающий циркуляцию МП.
Математически теорема записывается следующим образом.

Математическая формула теоремы о циркуляции
где:
- B→– вектор магнитной индукции;
- j→ – плотность движения электронов.
Это интегральная форма записи теоремы. Здесь в левой части интегрируют по некоторому замкнутому контуру, в правой части – по натянутой поверхности на полученный контур.
Магнитный поток
Одна из физических величин, характеризующих уровень МП, пересекающего любую поверхность, – магнитный поток. Обозначается буквой φ и имеет единицу измерения вебер (Вб). Эта единица характерна для системы СИ. В СГС магнитный поток измеряется в максвеллах (Мкс):
108 Мкс = 1 Вб.
Магнитный поток φ определяет величину МП, пронизывающую определённую поверхность. Поток φ зависит от угла, под которым поле пронизывает поверхность, и силы поля.
Формула для расчёта имеет вид:
φ = |B*S| = B*S*cosα,
где:
- В – скалярная величина градиента магнитной индукции;
- S – площадь пересекаемой поверхности;
- α – угол, образованный потоком Ф и перпендикуляром к поверхности (нормалью).
Внимание! Поток Ф будет наибольшим, когда B→ совпадёт с нормалью по направлению (угол α = 00). Аналогично Ф = 0, когда он проходит параллельно нормали (угол α = 900).
Магнитный поток
Вектор магнитной индукции, или магнитная индукция, указывает направление поля. Применяя простые методы: правило буравчика, свободно ориентирующуюся магнитную стрелку или контур с током в магнитном поле, можно определить направление действия этого поля.
Видео
Электромагнитная индукция – FIZI4KA

Явление электромагнитной индукции
Электромагнитная индукция – явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.
Явление электромагнитной индукции было открыто М. Фарадеем.
Опыты Фарадея
- На одну непроводящую основу были намотаны две катушки: витки первой катушки были расположены между витками второй. Витки одной катушки были замкнуты на гальванометр, а второй – подключены к источнику тока. При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.
- Первая катушка была подключена к источнику тока, вторая, подключенная к гальванометру, перемещалась относительно нее. При приближении или удалении катушки фиксировался ток.
- Катушка замкнута на гальванометр, а магнит движется – вдвигается (выдвигается) – относительно катушки.


Опыты показали, что индукционный ток возникает только при изменении линий магнитной индукции. Направление тока будет различно при увеличении числа линий и при их уменьшении.
Сила индукционного тока зависит от скорости изменения магнитного потока. Может изменяться само поле, или контур может перемещаться в неоднородном магнитном поле.
Объяснения возникновения индукционного тока
Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна ЭДС. Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.
Электроны в неподвижном проводнике могут приводиться в движение только электрическим полем. Это электрическое поле порождается изменяющимся во времени магнитным полем. Его называют вихревым электрическим полем. Представление о вихревом электрическом поле было введено в физику великим английским физиком Дж. Максвеллом в 1861 году.
Свойства вихревого электрического поля:
- источник – переменное магнитное поле;
- обнаруживается по действию на заряд;
- не является потенциальным;
- линии поля замкнутые.
Работа этого поля при перемещении единичного положительного заряда по замкнутому контуру равна ЭДС индукции в неподвижном проводнике.
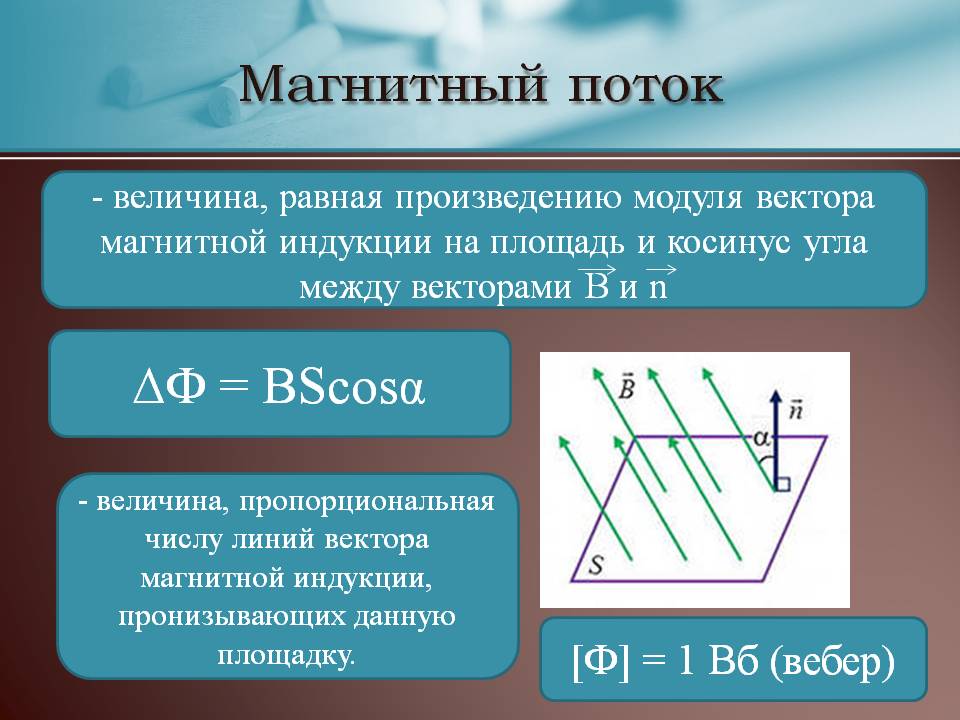
Магнитный поток
Магнитным потоком через площадь \( S \) контура называют скалярную физическую величину, равную произведению модуля вектора магнитной индукции \( B \), площади поверхности \( S \), пронизываемой данным потоком, и косинуса угла \( \alpha \) между направлением вектора магнитной индукции и вектора нормали (перпендикуляра к плоскости данной поверхности):




Обозначение – \( \Phi \), единица измерения в СИ – вебер (Вб).
Магнитный поток в 1 вебер создается однородным магнитным полем с индукцией 1 Тл через поверхность площадью 1 м2, расположенную перпендикулярно вектору магнитной индукции:


Магнитный поток можно наглядно представить как величину, пропорциональную числу магнитных линий, проходящих через данную площадь.
В зависимости от угла \( \alpha \) магнитный поток может быть положительным (\( \alpha \) < 90°) или отрицательным (\( \alpha \) > 90°). Если \( \alpha \) = 90°, то магнитный поток равен 0.
Изменить магнитный поток можно меняя площадь контура, модуль индукции поля или расположение контура в магнитном поле (поворачивая его).
В случае неоднородного магнитного поля и неплоского контура магнитный поток находят как сумму магнитных потоков, пронизывающих площадь каждого из участков, на которые можно разбить данную поверхность.
Закон электромагнитной индукции Фарадея
Закон электромагнитной индукции (закон Фарадея):
ЭДС индукции в замкнутом контуре равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную контуром:
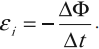
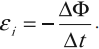
Знак «–» в формуле позволяет учесть направление индукционного тока. Индукционный ток в замкнутом контуре имеет всегда такое направление, чтобы магнитный поток поля, созданного этим током сквозь поверхность, ограниченную контуром, уменьшал бы те изменения поля, которые вызвали появление индукционного тока.
Если контур состоит из \( N \) витков, то ЭДС индукции:


Сила индукционного тока в замкнутом проводящем контуре с сопротивлением \( R \):
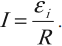
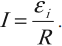
При движении проводника длиной \( l \) со скоростью \( v \) в постоянном однородном магнитном поле с индукцией \( \vec{B} \) ЭДС электромагнитной индукции равна:
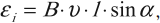
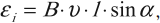
где \( \alpha \) – угол между векторами \( \vec{B} \) и \( \vec{v} \).
Возникновение ЭДС индукции в движущемся в магнитном поле проводнике объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.
Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю.
Количество теплоты в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.
Важно!
Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам:
- магнитный поток изменяется вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле;
- вторая причина изменения магнитного потока, пронизывающего контур, – изменение во времени магнитного поля при неподвижном контуре. В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея.
Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной:
- в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца;
- в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.
Правило Ленца
Направление индукционного тока определяется по правилу Ленца: индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток.
Алгоритм решения задач с использованием правила Ленца:
- определить направление линий магнитной индукции внешнего магнитного поля;
- выяснить, как изменяется магнитный поток;
- определить направление линий магнитной индукции магнитного поля индукционного тока: если магнитный поток уменьшается, то они сонаправлены с линиями внешнего магнитного поля; если магнитный поток увеличивается, – противоположно направлению линий магнитной индукции внешнего поля;
- по правилу буравчика, зная направление линий индукции магнитного поля индукционного тока, определить направление индукционного тока.
Правило Ленца имеет глубокий физический смысл – оно выражает закон сохранения энергии.
Самоиндукция
Самоиндукция – это явление возникновения ЭДС индукции в проводнике в результате изменения тока в нем.
При изменении силы тока в катушке происходит изменение магнитного потока, создаваемого этим током. Изменение магнитного потока, пронизывающего катушку, должно вызывать появление ЭДС индукции в катушке.
В соответствии с правилом Ленца ЭДС самоиндукции препятствует нарастанию силы тока при включении и убыванию силы тока при выключении цепи.


Это приводит к тому, что при замыкании цепи, в которой есть источник тока с постоянной ЭДС, сила тока устанавливается через некоторое время.
При отключении источника ток также не прекращается мгновенно. Возникающая при этом ЭДС самоиндукции может превышать ЭДС источника.
Явление самоиндукции можно наблюдать, собрав электрическую цепь из катушки с большой индуктивностью, резистора, двух одинаковых ламп накаливания и источника тока. Резистор должен иметь такое же электрическое сопротивление, как и провод катушки.
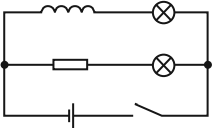

Опыт показывает, что при замыкании цепи электрическая лампа, включенная последовательно с катушкой, загорается несколько позже, чем лампа, включенная последовательно с резистором. Нарастанию тока в цепи катушки при замыкании препятствует ЭДС самоиндукции, возникающая при возрастании магнитного потока в катушке.
При отключении источника тока вспыхивают обе лампы. В этом случае ток в цепи поддерживается ЭДС самоиндукции, возникающей при убывании магнитного потока в катушке.
ЭДС самоиндукции \( \varepsilon_{is} \), возникающая в катушке с индуктивностью \( L \), по закону электромагнитной индукции равна:


ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в катушке.
Индуктивность
Электрический ток, проходящий по проводнику, создает вокруг него магнитное поле. Магнитный поток \( \Phi \) через контур из этого проводника пропорционален модулю индукции \( \vec{B} \) магнитного поля внутри контура, а индукция магнитного поля, в свою очередь, пропорциональна силе тока в проводнике.
Следовательно, магнитный поток через контур прямо пропорционален силе тока в контуре:


Индуктивность – коэффициент пропорциональности \( L \) между силой тока \( I \) в контуре и магнитным потоком \( \Phi \), создаваемым этим током:
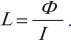
Индуктивность зависит от размеров и формы проводника, от магнитных свойств среды, в которой находится проводник.
Единица индуктивности в СИ – генри (Гн). Индуктивность контура равна 1 генри, если при силе постоянного тока 1 ампер магнитный поток через контур равен 1 вебер:
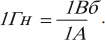
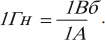
Можно дать второе определение единицы индуктивности: элемент электрической цепи обладает индуктивностью в 1 Гн, если при равномерном изменении силы тока в цепи на 1 ампер за 1 с в нем возникает ЭДС самоиндукции 1 вольт.
Энергия магнитного поля
При отключении катушки индуктивности от источника тока лампа накаливания, включенная параллельно катушке, дает кратковременную вспышку. Ток в цепи возникает под действием ЭДС самоиндукции.
Источником энергии, выделяющейся при этом в электрической цепи, является магнитное поле катушки.
Для создания тока в контуре с индуктивностью необходимо совершить работу на преодоление ЭДС самоиндукции. Энергия магнитного поля тока вычисляется по формуле:
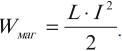
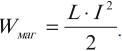
Основные формулы раздела «Электромагнитная индукция»


Алгоритм решения задач по теме «Электромагнитная индукция»:
1. Внимательно прочитать условие задачи. Установить причины изменения магнитного потока, пронизывающего контур.
2. Записать формулу:
- закона электромагнитной индукции;
- ЭДС индукции в движущемся проводнике, если в задаче рассматривается поступательно движущийся проводник; если в задаче рассматривается электрическая цепь, содержащая источник тока, и возникающая на одном из участков ЭДС индукции, вызванная движением проводника в магнитном поле, то сначала нужно определить величину и направление ЭДС индукции. После этого задача решается по аналогии с задачами на расчет цепи постоянного тока с несколькими источниками.
3. Записать выражение для изменения магнитного потока и подставить в формулу закона электромагнитной индукции.
4. Записать математически все дополнительные условия (чаще всего это формулы закона Ома для полной цепи, силы Ампера или силы Лоренца, формулы кинематики и динамики).
5. Решить полученную систему уравнений относительно искомой величины.
6. Решение проверить.
Электромагнитная индукция
3 (60%) 2 votes




 — ЭДС источника
напряжения,
— ЭДС источника
напряжения, — сила
тока в
цепи,
— сила
тока в
цепи,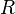 — сопротивление всех
внешних элементов цепи,
— сопротивление всех
внешних элементов цепи, — внутреннее
сопротивление источника
напряжения.
— внутреннее
сопротивление источника
напряжения.

