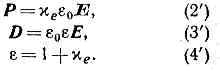Электрическая индукция — Википедия
Материал из Википедии — свободной энциклопедии
Электри́ческая инду́кция (электри́ческое смеще́ние) — векторная величина, равная сумме вектора напряжённости электрического поля и вектора поляризации.
В СИ: D=ε0E+P{\displaystyle \mathbf {D} =\varepsilon _{0}\mathbf {E} +\mathbf {P} }.
В СГС: D=E+4πP{\displaystyle \mathbf {D} =\mathbf {E} +4\pi \mathbf {P} }.
Величина электрической индукции в системе СГС измеряется в СГСЭ или СГСМ единицах, а в Международной системе единиц (СИ) — в кулонах, деленных на м² (L−2TI). В рамках СТО векторы D{\displaystyle \mathbf {D} } и H{\displaystyle \mathbf {H} } (напряжённость магнитного поля) объединяются в единый тензор, аналогичный тензору электромагнитного поля.
Уравнения для вектора индукции в СГС имеют вид (2-я пара уравнений Максвелла)
- divD=4πρ{\displaystyle \mathrm {div} \,\mathbf {D} =4\pi \rho }
- rotH=4πcj+1c∂D∂t{\displaystyle \mathrm {rot} \,\mathbf {H} ={4\pi \over c}\mathbf {j} +{1 \over c}{\frac {\partial \mathbf {D} }{\partial t}}}
В СИ
- divD=ρ{\displaystyle \mathrm {div} \,\mathbf {D} =\rho }
- rotH=j+∂D∂t{\displaystyle \mathrm {rot} \,\mathbf {H} =\mathbf {j} +{\frac {\partial \mathbf {D} }{\partial t}}}
Здесь ρ{\displaystyle \rho } — плотность свободных зарядов, а j{\displaystyle \mathbf {j} } — плотность тока свободных зарядов. Введение вектора D{\displaystyle \mathbf {D} }, таким образом, позволяет исключить из уравнений Максвелла неизвестные молекулярные токи и поляризационные заряды.
Материальные уравнения[править | править код]
Для полного определения электромагнитного поля уравнения Максвелла необходимо дополнить материальными уравнениями
- Di=∑j=13εijEj{\displaystyle \mathbf {D} _{i}=\sum \limits _{j=1}^{3}\varepsilon _{ij}\mathbf {E} _{j}}
Величины εij{\displaystyle \varepsilon _{ij}} образуют тензор диэлектрической проницаемости. В принципе, он может зависеть как от точки внутри тела, так и от частоты колебаний электромагнитного поля. В изотропных средах тензор диэлектрической проницаемости сводится к скаляру, называемому также диэлектрической проницаемостью. Материальные уравнения для D{\displaystyle \mathbf {D} } приобретают простой вид
- D=εE{\displaystyle \mathbf {D} =\varepsilon \mathbf {E} }
Возможны среды, для которых зависимость между D{\displaystyle \mathbf {D} } и E{\displaystyle \mathbf {E} } является нелинейной (в основном — сегнетоэлектрики).
Граничные условия[править | править код]
На границе двух веществ скачок нормальной компоненты Dn{\displaystyle D_{n}} вектора D{\displaystyle \mathbf {D} } определяется поверхностной плотностью свободных зарядов:
: limϵ→0(∂D∂n(r+ϵn)−∂D∂n(r−ϵn))=4πσ(r){\displaystyle \lim _{\epsilon \to 0}\left({\frac {\partial \mathbf {D} }{\partial n}}(\mathbf {r} +\epsilon \mathbf {n} )-{\frac {\partial \mathbf {D} }{\partial n}}(\mathbf {r} -\epsilon \mathbf {n} )\right)=4\pi \sigma (\mathbf {r} )} (в СГС)
- limϵ→0(∂D∂n(r+ϵn)−∂D∂n(r−ϵn))=σ(r){\displaystyle \lim _{\epsilon \to 0}\left({\frac {\partial \mathbf {D} }{\partial n}}(\mathbf {r} +\epsilon \mathbf {n} )-{\frac {\partial \mathbf {D} }{\partial n}}(\mathbf {r} -\epsilon \mathbf {n} )\right)=\sigma (\mathbf {r} )} (в СИ)[источник не указан 1422 дня]
Здесь ∂D∂n=(n;∇)D{\displaystyle {\tfrac {\partial \mathbf {D} }{\partial n}}=(\mathbf {n} ;\nabla )\mathbf {D} } — нормальная производная, r{\displaystyle \mathbf {r} } — точка на поверхности раздела, n{\displaystyle \mathbf {n} } — вектор нормали к этой поверхности в данной точке, σ(r){\displaystyle \sigma (\mathbf {r} )} — поверхностная плотность свободных зарядов. Уравнение не зависит от выбора нормали (внешней или внутренней). В частности, для диэлектриков уравнение означает, что нормальная компонента вектора D{\displaystyle \mathbf {D} } непрерывна на границе сред. Простого уравнения для касательной составляющей D{\displaystyle \mathbf {D} } записать нельзя, она должна определяться из граничных условий для E{\displaystyle \mathbf {E} } и материальных уравнений.
ЭЛЕКТРИЧЕСКАЯ ИНДУКЦИЯ — это… Что такое ЭЛЕКТРИЧЕСКАЯ ИНДУКЦИЯ?
- ЭЛЕКТРИЧЕСКАЯ ИНДУКЦИЯ
- ЭЛЕКТРИЧЕСКАЯ ИНДУКЦИЯ
-
(D), векторная величина, характеризующая электрич. поле и равная сумме двух векторов разл. природы: напряжённости электрического поля Е — гл. хар-ки поля и поляризации среды Р, к-рая определяет электрич. состояние в-ва в этом поле. В Гаусса системе единицD=E+4pP, (1)
в СИ
D=e0E+P, (1′)
где e0 — размерная константа, наз. электрической постоянной или диэлектрич. проницаемостью вакуума.
В изотропном в-ве, не обладающем сегнетоэлектрич. св-вами, при слабых полях вектор поляризации прямо пропорц. напряжённости поля. В системе Гаусса
Р=cеЕ, (2)
где cе — пост. безразмерная величина, наз. диэлектрической восприимчивостью. Для сегнетоэлектриков cе зависит от Е, и связь между Р и Е становится нелинейной.
Подставив выражение (2) в (1), получим:
D =(1+4pce)E=eE. (3)
Величина
e=1+4pcе (4)
наз. диэлектрической проницаемостью в-ва.
В системе СИ

Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.
-
— физическое векторное поле D(t, r)- компонента макроскопич. электромагнитного поля в сплошной среде. См. Электрическое поле.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.
- ЭЛЕКТРИЧЕСКАЯ ЁМКОСТЬ
- ЭЛЕКТРИЧЕСКАЯ ПОСТОЯННАЯ
Смотреть что такое «ЭЛЕКТРИЧЕСКАЯ ИНДУКЦИЯ» в других словарях:
ЭЛЕКТРИЧЕСКАЯ ИНДУКЦИЯ (D) — величина, характеризующая электрическое поле в веществе наряду с напряженностью (Е): D = eЕ, где e диэлектрическая проницаемость вещества. Поток электрической индукции через замкнутую поверхность определяется свободными зарядами, находящимися… … Большой Энциклопедический словарь
ЭЛЕКТРИЧЕСКАЯ ИНДУКЦИЯ — (обозначение D), плотность ЭЛЕКТРИЧЕСКОГО ПОТОКА на единицу площади … Научно-технический энциклопедический словарь
Электрическая индукция — Не следует путать с явлением электростатической индукции. Не следует путать с явлением электромагнитной индукции. Электрическая индукция Размерность L−2TI Едини … Википедия
электрическая индукция — (D), величина, характеризующая электрическое поле в веществе наряду с напряжённостью (Е):D = εE, где ε диэлектрическая проницаемость вещества. Поток электрической индукции через замкнутую поверхность определяется свободными зарядами,… … Энциклопедический словарь
электрическая индукция — elektrinio srauto tankis statusas T sritis Standartizacija ir metrologija apibrėžtis Vektorinis dydis D, apibūdinantis elektrinį lauką. Vakuume D = ε₀E; dielektrike D = ε₀E + P; čia ε₀ – elektrinė konstanta, E – elektrinio lauko stipris, P –… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
электрическая индукция
Электрическая индукция — или электростатическая индукция см. Индукция … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
ЭЛЕКТРИЧЕСКАЯ ИНДУКЦИЯ — то же, что электрическое смещение … Естествознание. Энциклопедический словарь
ИНДУКЦИЯ — (лат. inductio, от in в, и duco веду). 1) возбуждение электричества в проволоке посредством приближения её к электризованному телу. 2) метод мышления, иначе наз. наведение, при котором из частных положений выводят общее заключение. Словарь… … Словарь иностранных слов русского языка
ИНДУКЦИЯ — ИНДУКЦИЯ, индукции, жен. (лат. inductio наведение). 1. Метод мышления, при котором из частных суждений выводится общее (филос.). 2. Возбуждение электрической и магнитной энергии под влиянием магнитного поля или приближением заряженного… … Толковый словарь Ушакова
Конспект «Электромагнитная индукция» — УчительPRO
«Электромагнитная индукция»
Электромагнитная индукция — это явление, которое заключается в возникновении электрического тока в замкнутом проводнике в результате изменения магнитного поля, в котором он находится. Это явление открыл английский физик М. Фарадей в 1831 г. Суть его можно пояснить несколькими простыми опытами.
Описанный в опытах Фарадея принцип получения переменного тока используется в индукционных генераторах, вырабатывающих электрическую энергию на тепловых или гидроэлектростанциях. Сопротивление вращению ротора генератора, возникающее при взаимодействии индукционного тока с магнитным полем, преодолевается за счет работы паровой или гидротурбины, вращающей ротор. Такие генераторы преобразуют механическую энергию в энергию электрического тока.
Вихревые токи, или токи Фуко
Если массивный проводник поместить в переменное магнитное поле, то в этом проводнике благодаря явлению электромагнитной индукции возникают вихревые индукционные токи, называемые токами Фуко.
Вихревые токи возникают также при движении массивного проводника в постоянном, но неоднородном в пространстве магнитном поле. Токи Фуко имеют такое направление, что действующая на них в магнитном поле сила тормозит движение проводника. Маятник в виде сплошной металлической пластинки из немагнитного материала, совершающий колебания между полюсами электромагнита, резко останавливается при включении магнитного поля.
Во многих случаях нагревание, вызываемое токами Фуко, оказывается вредным, и с ним приходится бороться. Сердечники трансформаторов, роторы электродвигателей набирают из отдельных железных пластин, разделенных слоями изолятора, препятствующего развитию больших индукционных токов, а сами пластины изготовляют из сплавов, имеющих высокое удельное сопротивление.
Электромагнитное поле
Электрическое поле, созданное неподвижными зарядами, является статическим и действует на заряды. Постоянный ток вызывает появление постоянного во времени магнитного поля, действующего на движущиеся заряды и токи. Электрическое и магнитное поля существуют в этом случае независимо друг от друга.
Явление электромагнитной индукции демонстрирует взаимодействие этих полей, наблюдаемое в веществах, в которых есть свободные заряды, т. е. в проводниках. Переменное магнитное поле создает переменное электрическое поле, которое, действуя на свободные заряды, создает электрический ток. Этот ток, будучи переменным, в свою очередь порождает переменное магнитное поле, создающее электрическое поле в том же проводнике, и т. д.
Совокупность переменного электрического и переменного магнитного полей, порождающих друг друга, называется электромагнитным полем. Оно может существовать и в среде, где нет свободных зарядов, и распространяется в пространстве в виде электромагнитной волны.
Классическая электродинамика — одно из высших достижений человеческого разума. Она оказала огромное влияние на последующее развитие человеческой цивилизации, предсказав существование электромагнитных волн. Это привело в дальнейшем к созданию радио, телевидения, телекоммуникационных систем, спутниковых средств навигации, а также компьютеров, промышленных и бытовых роботов и прочих атрибутов современной жизни.
Краеугольным камнем теории Максвелла явилось утверждение, что источником магнитного поля может служить одно только переменное электрическое поле, подобно тому, как источником электрического поля, создающим в проводнике индукционный ток, служит переменное магнитное поле. Наличие проводника при этом не обязательно — электрическое поле возникает и в пустом пространстве. Линии переменного электрического поля, аналогично линиям магнитного поля, замкнуты. Электрическое и магнитное поля электромагнитной волны равноправны.
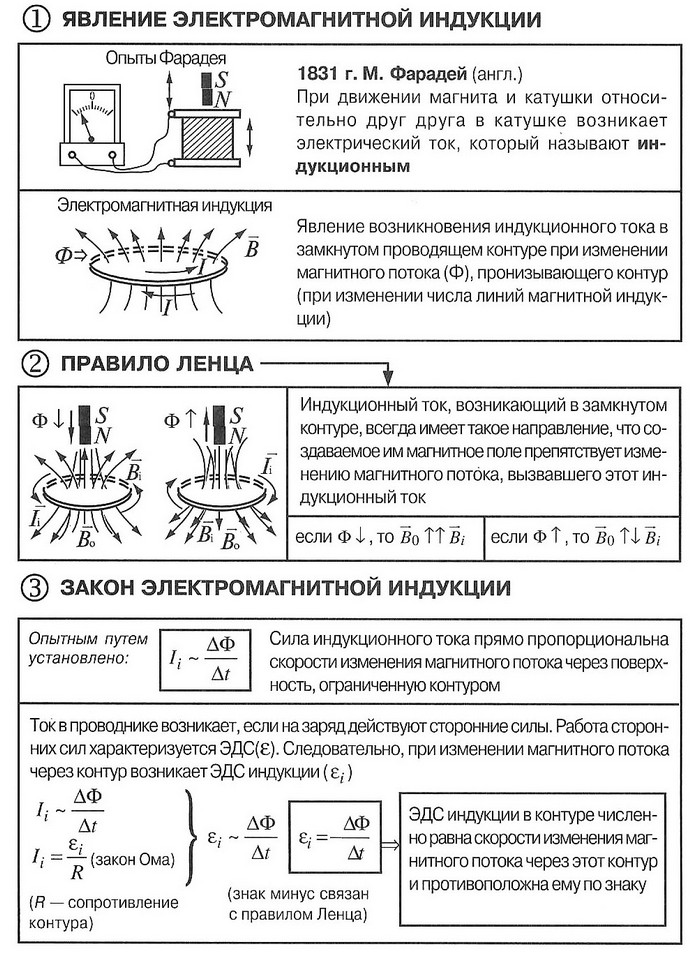
Электромагнитная индукция в схемах и таблицах
(Явление электромагнитной индукции, опыты Фарадея, правило Ленца, закон электромагнитной индукции, вихревое электрическое поле, самоиндукция, индуктивность, энергия магнитного поля тока)

Дополнительные материалы по теме:
Конспект урока по физике в 11 классе «Электромагнитная индукция».
Следующая тема: «».
Электрическая индукция — Википедия. Что такое Электрическая индукция
Электри́ческая инду́кция (электри́ческое смеще́ние) — векторная величина, равная сумме вектора напряжённости электрического поля и вектора поляризации.
В СИ: D=ε0E+P{\displaystyle \mathbf {D} =\varepsilon _{0}\mathbf {E} +\mathbf {P} }.
В СГС: D=E+4πP{\displaystyle \mathbf {D} =\mathbf {E} +4\pi \mathbf {P} }.
Величина электрической индукции в системе СГС измеряется в СГСЭ или СГСМ единицах, а в Международной системе единиц (СИ) — в кулонах на м² (L−2TI). В рамках СТО векторы D{\displaystyle \mathbf {D} } и H{\displaystyle \mathbf {H} } (напряжённость магнитного поля) объединяются в единый тензор, аналогичный тензору электромагнитного поля.
Определяющие уравнения
Уравнения для вектора индукции в СГС имеют вид (2-я пара уравнений Максвелла)
- divD=4πρ{\displaystyle \mathrm {div} \,\mathbf {D} =4\pi \rho }
- rotH=4πcj+1c∂D∂t{\displaystyle \mathrm {rot} \,\mathbf {H} ={4\pi \over c}\mathbf {j} +{1 \over c}{\frac {\partial \mathbf {D} }{\partial t}}}
В СИ
- divD=ρ{\displaystyle \mathrm {div} \,\mathbf {D} =\rho }
- rotH=j+∂D∂t{\displaystyle \mathrm {rot} \,\mathbf {H} =\mathbf {j} +{\frac {\partial \mathbf {D} }{\partial t}}}
Здесь ρ{\displaystyle \rho } — плотность свободных зарядов, а j{\displaystyle \mathbf {j} } — плотность тока свободных зарядов. Введение вектора D{\displaystyle \mathbf {D} }, таким образом, позволяет исключить из уравнений Максвелла неизвестные молекулярные токи и поляризационные заряды.
Материальные уравнения
Для полного определения электромагнитного поля уравнения Максвелла необходимо дополнить материальными уравнениями, связывающими векторы D{\displaystyle \mathbf {D} } и E{\displaystyle \mathbf {E} } (а также H{\displaystyle \mathbf {H} } и B{\displaystyle \mathbf {B} }) в веществе. В вакууме эти векторы совпадают, а в веществе связь между ними зачастую предполагают линейной:
- Di=∑j=13εijEj{\displaystyle \mathbf {D} _{i}=\sum \limits _{j=1}^{3}\varepsilon _{ij}\mathbf {E} _{j}}
Величины εij{\displaystyle \varepsilon _{ij}} образуют тензор диэлектрической проницаемости. В принципе, он может зависеть как от точки внутри тела, так и от частоты колебаний электромагнитного поля. В изотропных средах тензор диэлектрической проницаемости сводится к скаляру, называемому также диэлектрической проницаемостью. Материальные уравнения для D{\displaystyle \mathbf {D} } приобретают простой вид
- D=εE{\displaystyle \mathbf {D} =\varepsilon \mathbf {E} }
Возможны среды, для которых зависимость между D{\displaystyle \mathbf {D} } и E{\displaystyle \mathbf {E} } является нелинейной (в основном — сегнетоэлектрики).
Граничные условия
На границе двух веществ скачок нормальной компоненты Dn{\displaystyle D_{n}} вектора D{\displaystyle \mathbf {D} } определяется поверхностной плотностью свободных зарядов:
: limϵ→0(∂D∂n(r+ϵn)−∂D∂n(r−ϵn))=4πσ(r){\displaystyle \lim _{\epsilon \to 0}\left({\frac {\partial \mathbf {D} }{\partial n}}(\mathbf {r} +\epsilon \mathbf {n} )-{\frac {\partial \mathbf {D} }{\partial n}}(\mathbf {r} -\epsilon \mathbf {n} )\right)=4\pi \sigma (\mathbf {r} )} (в СГС)
- limϵ→0(∂D∂n(r+ϵn)−∂D∂n(r−ϵn))=σ(r){\displaystyle \lim _{\epsilon \to 0}\left({\frac {\partial \mathbf {D} }{\partial n}}(\mathbf {r} +\epsilon \mathbf {n} )-{\frac {\partial \mathbf {D} }{\partial n}}(\mathbf {r} -\epsilon \mathbf {n} )\right)=\sigma (\mathbf {r} )} (в СИ)[источник не указан 965 дней]
Здесь ∂D∂n=(n;∇)D{\displaystyle {\tfrac {\partial \mathbf {D} }{\partial n}}=(\mathbf {n} ;\nabla )\mathbf {D} } — нормальная производная, r{\displaystyle \mathbf {r} } — точка на поверхности раздела, n{\displaystyle \mathbf {n} } — вектор нормали к этой поверхности в данной точке, σ(r){\displaystyle \sigma (\mathbf {r} )} — поверхностная плотность свободных зарядов. Уравнение не зависит от выбора нормали (внешней или внутренней). В частности, для диэлектриков уравнение означает, что нормальная компонента вектора D{\displaystyle \mathbf {D} } непрерывна на границе сред. Простого уравнения для касательной составляющей D{\displaystyle \mathbf {D} } записать нельзя, она должна определяться из граничных условий для E{\displaystyle \mathbf {E} } и материальных уравнений.
Литература
См. также
Электрическая индукция — это… Что такое Электрическая индукция?
Электри́ческая инду́кция (электри́ческое смеще́ние) — векторная величина, равная сумме вектора напряжённости электрического поля и вектора поляризации.
В СИ: .
В СГС: .
Величина электрической индукции в системе СГС измеряется в СГСЭ или СГСМ единицах, а в СИ — в кулонах на м² (L−2TI). В рамках СТО векторы и объединяются в единый тензор, аналогичный тензору электромагнитного поля.
Определяющие уравнения
Уравнения для вектора индукции в СГС имеют вид (2ая пара уравнений Максвелла)
Здесь — плотность свободных зарядов, а — плотность тока свободных зарядов. Введение вектора , таким образом, позволяет исключить из уравнений Максвелла неизвестные молекулярные токи и поляризационные заряды.
Материальные уравнения
Для полного определения электромагнитного поля уравнения Максвелла необходимо дополнить материальными уравнениями, связывающими векторы и (а также и ) в веществе. В вакууме эти векторы совпадают, а в веществе связь между ними зачастую предполагают линейной:
Величины образуют тензор диэлектрической проницаемости. В принципе, он может зависеть как от точки внутри тела, так и от частоты колебаний электромагнитного поля. В изотропных средах тензор диэлектрической проницаемости сводится к скаляру, называемому также диэлектрической проницаемостью. Материальные уравнения для приобретают простой вид
Возможны среды, для которых зависимость между и является нелинейной (в основном — сегнетоэлектрики).
Граничные условия
На границе двух веществ скачок нормальной компоненты вектора определяется поверхностной плотностью свободных зарядов:
- (в СГС)
- (в СИ)
Здесь — нормальная производная, — точка на поверхности раздела, — вектор нормали к этой поверхности в данной точке, — поверхностная плотность свободных зарядов. Уравнение не зависит от выбора нормали (внешней или внутренней). В частности, для диэлектриков уравнение означает, что нормальная компонента вектора непрерывна на границе сред. Простого уравнения для касательной составляющей записать нельзя, она должна определяться из граничных условий для и материальных уравнений.
Литература
См. также
13. Вектор электрической индукции
Вектор электрической индукции D (называемый также электрическим смещением) является суммой двух векторов различной природы:напряжённости электрического поля Е — главной характеристики этого поля — и поляризации Р, которая определяет электрическое состояние вещества в этом поле. В системе Гаусса: D= E +4pP
Теорема Гаусса
Поток напряженности электрического поля, проходящий через замкнутую поверхность, пропорционален суммарному электрическому заряду, содержащемуся внутри этой поверхности.
14. Электрическая емкость. Конденсаторы. Энергия электрического поля.
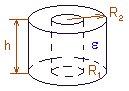
| Электроемкость. Конденсаторы. Энергия электростатического поля. Электроемкостью (емкостью) C уединенного изолированного проводника называется физическая величина, равная отношению изменения заряда проводника q к изменению его потенциала: C = q/. Электроемкость уединенного проводника зависит только от его формы и размеров, а также от окружающей его диэлектрической среды (). Единица измерения емкости в системе СИ называется Фарадой. Фарада (Ф) — это емкость такого уединенного проводника, потенциал которого повышается на 1 Вольт при сообщении ему заряда в 1 Кулон. 1 Ф = 1 Кл/1 В. Конденсатором называют систему двух разноименно заряженных проводников, разделенных диэлектриком (например, воздухом). Свойство конденсаторов накапливать и сохранять электрические заряды и связанное с ними электрическое поле характеризуется величиной, называемой электроемкостью конденсатора. Электроемкость конденсатора равна отношению заряда одной из пластин Q к напряжению между ними U: C = Q/U. В зависимости от формы обкладок, конденсаторы бывают плоскими, сферическими и цилиндрическими. Формулы для расчета емкостей этих конденсаторов приведены в таблице.
|
Основные законы и определения физических величин
Ампера закон – закон взаимодействия двух проводников с токами; параллельные проводники с токами одного направления притягиваются, а с токами противоположного направления – отталкиваются.
Взаимной индукции явление – если контуры неподвижны и ферромагнетиков вблизи них нет, то при изменении силы тока в одном из контуров в другом контуре возникает электродвижущая сила индукции.
Джоуля–Ленца закон – закон, описывающий тепловое действие электрического тока. Согласно закону Джоуля–Ленца количество теплоты, выделяющееся в проводнике при прохождении по нему постоянного тока, прямо пропорционально квадрату силы тока, сопротивлению проводника и времени прохождения.
Диэлектрики –
вещества, неспособные проводить
электрический ток. Идеальных изоляторов
в природе не существует. Все вещества
хотя бы в ничтожной степени проводят
электрический ток, однако диэлектрики
проводят ток в  раз
хуже, чем вещества, называемые проводниками.
Причина в том, что в отличие от проводников
в диэлектриках нет свободных зарядов.
раз
хуже, чем вещества, называемые проводниками.
Причина в том, что в отличие от проводников
в диэлектриках нет свободных зарядов.
Закон сохранения заряда: заряд электрически замкнутой системы, то есть системы, через поверхность которой не переносятся заряженные частицы, не изменяется, какие бы процессы в ней не происходили.
Источники тока – устройства, служащие для поддержания в проводнике долговременного электрического тока. Они преобразуют химическую, тепловую, световую и другие виды энергии в электрическую.
Кирхгофа
правило (первое) –
если условиться считать подходящие к
узлу токи положительными, а исходящие
– отрицательными, то алгебраическая
сумма сил токов в узле равна нулю:  ,
где n –
число проводов, сходящихся в узле.
,
где n –
число проводов, сходящихся в узле.
Кирхгофа правило (второе) – в любом замкнутом контуре, произвольно выбранном в разветвленной цепи, алгебраическая сумма произведений сил токов, текущих через сопротивления соответствующих участков цепи, равна алгебраической сумме электродвижущих сил, действующих в этом контуре.
Конденсатор – устройство, способное при небольшом относительно окружающих тел потенциале накапливать на себе большие заряды. Конденсаторы делают в виде двух проводников, расположенных близко друг к другу. Образующие конденсатор проводники называются обкладками конденсатора.
Кулона
закон –
основной закон электростатики, выражающий
зависимость силы взаимодействия двух
неподвижных точечных зарядов от
расстояния между ними: два неподвижных
точечных заряда взаимодействуют с
силой, прямо пропорциональной произведению
величин этих зарядов и обратно
пропорциональной квадрату расстояния
между ними и диэлектрической проницаемости
среды, в которой находятся заряды: 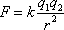 .
Величина
.
Величина 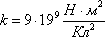 численно
равна силе, действующей между двумя
точечными неподвижными зарядами по
1 Кл каждый, находящимися в вакууме
на расстоянии 1 м друг от друга.
Точечность зарядов, о взаимодействии
которых идет речь, означает, что линейные
размеры тел, на которых сосредоточены
эти заряды, пренебрежимо малы по сравнению
с расстоянием между ними.
численно
равна силе, действующей между двумя
точечными неподвижными зарядами по
1 Кл каждый, находящимися в вакууме
на расстоянии 1 м друг от друга.
Точечность зарядов, о взаимодействии
которых идет речь, означает, что линейные
размеры тел, на которых сосредоточены
эти заряды, пренебрежимо малы по сравнению
с расстоянием между ними.
Кюри точка (температура Кюри) – температура фазового перехода II рода, связанного со скачкообразным изменением магнитных или электрических свойств вещества (например, переход из ферромагнитного состояния в парамагнитное, переход в сегнетоэлектрическое состояние).
Левой руки правило – правило, определяющее направление силы, которая действует на находящийся в магнитном поле проводник с током (или движущуюся заряженную частицу). Оно гласит: если левую руку расположить так, чтобы вытянутые пальцы показывали направление тока (скорости частицы), а силовые линии магнитного поля (линии магнитной индукции) входили в ладонь, то отставленный большой палец укажет направление силы, действующей на проводник (положительную частицу).
Ленца правило – правило, определяющее направление индукционных токов, возникающих при электромагнитной индукции. Согласно правилу Ленца индукционный ток всегда имеет такое направление, что его собственный магнитный поток компенсирует изменения внешнего магнитного потока, вызвавшие этот ток. Правило Ленца – следствие закона сохранения энергии.
Магнетики – вещества, существенно изменяющие значение магнитного поля, в которое они помещены.
Магнитная индукция – векторная величина, характеризующая магнитное поле и определяющая силу, действующую на движущуюся заряженную частицу со стороны магнитного поля в заданной точке. Модуль и направление вектора магнитной индукции определяются по влиянию магнитного поля на проводник или на рамку с током, помещенную в заданную точку магнитного поля.
Магнитная проницаемость вещества – физическая величина, показывающая, во сколько раз вектор магнитной индукции в однородной среде отличается от вектора магнитной индукции в той же точке пространства в вакууме. В зависимости от значения магнитной проницаемости вещества подразделяются на парамагнетики, диамагнетики и ферромагнетики.
Магнитная
составляющая силы Лоренца –
сила, действующая на один заряд в
магнитном поле. Величина силы Лоренца
равна 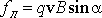 ,
где a – угол между направлением скорости
заряда
,
где a – угол между направлением скорости
заряда 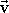 и
вектором магнитной индукции
и
вектором магнитной индукции 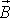 .
Если вектор
.
Если вектор 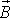 перпендикулярен
перпендикулярен 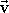 ,
то магнитная составляющая силы Лоренца
равна
,
то магнитная составляющая силы Лоренца
равна  .
Направление силы Лоренца определяется
для положительных зарядов по правилу
левой руки. Сила Лоренца всегда
перпендикулярна к скорости, поэтому
работы не совершает, а это означает, что
в постоянном магнитном поле энергия
движущейся частицы остается неизменной.
.
Направление силы Лоренца определяется
для положительных зарядов по правилу
левой руки. Сила Лоренца всегда
перпендикулярна к скорости, поэтому
работы не совершает, а это означает, что
в постоянном магнитном поле энергия
движущейся частицы остается неизменной.
Магнитное поле – одна из форм электромагнитного поля. Магнитное поле создается движущимися электрическими зарядами, орбитальными магнитными моментами и спиновыми магнитными моментами электронов, протонов и др.
Магнитные бури – возмущения магнитного поля Земли; могут длиться несколько суток; вызываются воздействием усиленных потоков солнечной плазмы (солнечного ветра) на магнитосферу Земли.
Напряжение (падение напряжения) – величина, численно равная работе, совершаемой электрическими и сторонними силами при перемещении единичного положительного заряда на данном участке цепи.
Напряженность
электрического поля –
силовая характеристика электрического
поля. Напряженность – это векторная
величина, равная в каждой точке отношению
силы 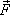 ,
действующей на пробный заряд
,
действующей на пробный заряд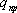 ,
помещенный в эту точку поля, к величине
этого заряда:
,
помещенный в эту точку поля, к величине
этого заряда: 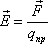 .
Направление вектора напряженности
совпадает с направлением силы, действующей
на положительный заряд.
.
Направление вектора напряженности
совпадает с направлением силы, действующей
на положительный заряд.
Ома закон – один из основных законов электрического тока: сила постоянного электрического тока на участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна его сопротивлению. В случае замкнутой цепи закон Ома формулируется следующим образом: сила постоянного электрического тока в цепи прямо пропорциональна электродвижущей силе источника тока и обратно пропорциональна полному сопротивлению электрической цепи.
Плотность тока – величина, равная заряду, проходящему за единицу времени через единичную площадку, перпендикулярную направлению движения зарядов. Плотность тока является векторной величиной.
Принцип
суперпозиции магнитных полей:
если магнитное поле создано несколькими
проводниками с токами, то вектор магнитной
индукции 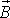 в
какой-либо точке этого поля равен
векторной сумме магнитных индукций,
созданных в этой точке каждым током в
отдельности:
в
какой-либо точке этого поля равен
векторной сумме магнитных индукций,
созданных в этой точке каждым током в
отдельности: 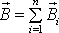 .
.
Принцип
суперпозиции электрических
полей: напряженность
поля  ,
создаваемого совокупностью заряженных
тел, равна сумме напряженностей полей
,
создаваемого совокупностью заряженных
тел, равна сумме напряженностей полей  ,
создаваемых каждым из тел в отдельности:
,
создаваемых каждым из тел в отдельности: 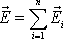 .
.
Пробный заряд – положительный точечный заряд, который вносится в данное электромагнитное поле для измерения его характеристик. Этот заряд должен быть достаточно мал, чтобы не нарушать положение зарядов – источников исследуемого поля и, следовательно, не искажать существующее поле.
Проводимость – электрическая характеристика проводника, которая определяется его физическими свойствами и геометрическими размерами.
Проводники – вещества, хорошо проводящие электрический ток благодаря наличию в них большого количества подвижных заряженных частиц.
Самоиндукции явление – возникновение электродвижущей силы индукции в случае, когда изменяющийся магнитный поток через замкнутый контур создается переменным током в самом контуре.
Сила
Ампера –
сила, действующая на проводник с током
в магнитном поле. Максимальное значение
силы, действующей на элемент проводника
длиной 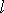 ,
равно
,
равно 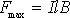 .
Оно достигается в том случае, когда угол
a между вектором
.
Оно достигается в том случае, когда угол
a между вектором 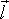 ,
направление которого совпадает с
направлением тока, и вектором магнитной
индукции равен
,
направление которого совпадает с
направлением тока, и вектором магнитной
индукции равен  .
При других значениях этого угла сила
Ампера равна
.
При других значениях этого угла сила
Ампера равна  .
Направление силы Ампера определяется
по правилу левой руки: если магнитные
силовые линии входят в ладонь, а четыре
выпрямленных пальца совпадают с
направлением тока, то отогнутый большой
палец указывает направление силы.
.
Направление силы Ампера определяется
по правилу левой руки: если магнитные
силовые линии входят в ладонь, а четыре
выпрямленных пальца совпадают с
направлением тока, то отогнутый большой
палец указывает направление силы.
Сила тока – количественная характеристика электрического тока, равная величине заряда, переносимого через рассматриваемую поверхность в единицу времени.
Силовые
линии электрического поля –
линии, касательные к которым в каждой
точке поля совпадают с направлением
вектора напряженности 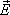 .
Густота линий выбирается таким образом,
чтобы количество линий, пронизывающих
единицу поверхности, перпендикулярной
к линиям площадки, было бы равно модулю
вектора напряженности.
.
Густота линий выбирается таким образом,
чтобы количество линий, пронизывающих
единицу поверхности, перпендикулярной
к линиям площадки, было бы равно модулю
вектора напряженности.
Теорема Гаусса для магнитных полей: полный магнитный поток через произвольную замкнутую поверхность равен нулю. Равенство нулю магнитного потока через замкнутую поверхность является следствием того факта, что в природе нет магнитных зарядов, и магнитные поля образуются только электрическими зарядами.
Теорема
Гаусса для электрических полей:
поток вектора напряженности электрического
поля через произвольную замкнутую
поверхность, охватывающую заряд q,
равен  .
Если внутри поверхности находится n зарядов,
то, согласно принципу суперпозиции
полей, полный поток будет складываться
из потоков напряженностей полей всех
зарядов и будет равен
.
Если внутри поверхности находится n зарядов,
то, согласно принципу суперпозиции
полей, полный поток будет складываться
из потоков напряженностей полей всех
зарядов и будет равен 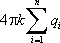 ,
где под
,
где под  подразумевается
алгебраическая сумма всех зарядов,
охватываемых замкнутой поверхностью.
подразумевается
алгебраическая сумма всех зарядов,
охватываемых замкнутой поверхностью.
Потенциалом
электрического поля в
данной точке называется отношение
потенциальной энергии, которой обладает
пробный заряд, помещенный в данную точку
поля, к этому заряду: 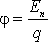 .
Потенциал численно равен потенциальной
энергии, которой обладал бы в данной
точке поля единичный положительный
заряд. Потенциал поля, создаваемого
системой зарядов, равен алгебраической
сумме потенциалов, создаваемых каждым
из зарядов в отдельности.
.
Потенциал численно равен потенциальной
энергии, которой обладал бы в данной
точке поля единичный положительный
заряд. Потенциал поля, создаваемого
системой зарядов, равен алгебраической
сумме потенциалов, создаваемых каждым
из зарядов в отдельности.
Теорема
о циркуляции для магнитных полей –
циркуляция вектора магнитной индукции 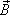 по
произвольному контуру равна произведению
магнитной постоянной на алгебраическую
сумму сил токов, пронизывающих контур,
по которому берется циркуляция. Если
контур не охватывает ток, то циркуляция
вектора
по
произвольному контуру равна произведению
магнитной постоянной на алгебраическую
сумму сил токов, пронизывающих контур,
по которому берется циркуляция. Если
контур не охватывает ток, то циркуляция
вектора 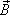 равна
нулю.
равна
нулю.
Теория близкодействия, противоположная по своей сути теории дальнодействия. Согласно теории близкодействия действие тел друг на друга на расстоянии всегда должно объясняться присутствием некоторых промежуточных агентов, передающих действие.
Точечный заряд – заряженное тело, размеры которого пренебрежимо малы по сравнению с расстояниями до других зарядов рассматриваемой системы. Точечный заряд такая же физическая идеализация, как и материальная точка в механике.
Эквипотенциальная поверхность – поверхность, во всех точках которой потенциал электрического поля имеет одинаковые значения.
Электризация трением – возникновение на теле заряда при контакте с другим телом, состоящим из другого вещества.
Электрическая
емкость –
отношение величины заряда уединенного
проводника к его потенциалу 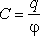 ,
то есть ёмкость численно равна заряду,
сообщение которого проводнику повышает
его потенциал на единицу. Емкость зависит
только от размеров и формы проводника,
а также от свойств среды, в которую
помещен проводник.
,
то есть ёмкость численно равна заряду,
сообщение которого проводнику повышает
его потенциал на единицу. Емкость зависит
только от размеров и формы проводника,
а также от свойств среды, в которую
помещен проводник.
Электрический
диполь –
совокупность равных по величине, но
противоположных по знаку двух точечных
зарядов —q и +q, сдвинутых
друг относительно друга на некоторое
расстояние l.
Вектор 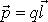 называется
электрическим моментом диполя или
дипольным моментом, здесь вектор
называется
электрическим моментом диполя или
дипольным моментом, здесь вектор  –
радиус-вектор, проведенный от отрицательного
заряда к положительному (плечо диполя).
Если длина
–
радиус-вектор, проведенный от отрицательного
заряда к положительному (плечо диполя).
Если длина 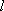 пренебрежимо
мала по сравнению с расстоянием от
диполя до точки наблюдения, то диполь
называется точечным.
пренебрежимо
мала по сравнению с расстоянием от
диполя до точки наблюдения, то диполь
называется точечным.
Электрический
заряд –
физическая величина, определяющая
интенсивность электромагнитных
взаимодействий. В природе носителями
электрического заряда являются
элементарные частицы. Носителем
элементарного, то есть наименьшего,
отрицательного заряда является электрон,
заряд которого  ,
а масса
,
а масса .
.
Электрический ток – направленное движение электрических зарядов.
Электродвижущая
сила –
физическая величина, равная работе
сторонних сил при перемещении единичного
положительного заряда на данном участке
цепи: 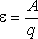 .
Электродвижущая сила – важнейшая
энергетическая характеристика источника.
.
Электродвижущая сила – важнейшая
энергетическая характеристика источника.
Электродинамика – раздел физики, в котором изучаются свойства электрических зарядов и явления, обусловленные их взаимодействием.
Электромагнитной индукции закон (формулировка Максвелла): всякое изменение магнитного поля вызывает появление вихревого электрического поля.
Электромагнитной индукции закон (формулировка Фарадея) – закон, описывающий явление возникновения электрического тока в проводящем контуре при изменении магнитного потока через поверхность, натянутую на контур: электродвижущая сила индукции прямо пропорциональна скорости изменения магнитного потока.
Электростатика – раздел электродинамики, изучающий взаимодействие и электрические поля покоящихся электрических зарядов.
Электростатическая индукция – явление возникновения противоположных зарядов на концах изолированного проводника при внесении его в электрическое поле. Если проводник разрезать на две части, то одна из них окажется заряженной положительно, а другая – отрицательно. Если проводник вынести из электрического поля, не разрезая, то он снова окажется нейтральным.
01. Электромагнитная индукция – это явление возникновения электрического тока в замкнутом проводящем контуре при изменении магнитного потока, проходящего через него.
Электромагнитная индукция была открыта Фарадеем в 1831 г.
Для демонстрации этого явления возьмем неподвижный магнит и проволочную катушка, концы которой соединим с гальванометром. Если катушку приблизить к одному из полюсов магнита, то во время движения стрелка гальванометра отклоняется – в катушке возбуждается электрический ток. При движении катушки в обратном направлении направление тока меняется на противоположное. То же самое происходит, если повернуть магнит на 180 градусов, не меняя направления движения катушки.
Возбуждение электрического тока при движении проводника в магнитном поле объясняется действием силы Лоренца, возникающий при движении проводника.
Рассмотрим
случай, когда два параллельных провода
АВ и CD
замкнуты, справа –
разомкнуты. Вдоль проводов может свободно
скользить проводящий мостик BC.
Когда мостик движется вправо со скоростью
v,
вместе с ним движутся электроны и
положительные ионы. На каждый движущий
заряд в магнитном поле действует сила
Лоренца 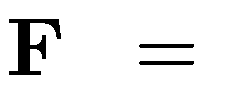
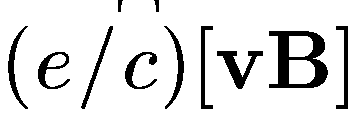 .
На положительные ион она действует
вниз, на отрицательные вверх. В результате
электроны начнут перемещаться по мостику
вверх, т.е. по нему потечет электрический
ток, направленный вниз. Перераспределившись
заряды создадут электрическое поле,
которое возбудит токи и в остальных
участках контура ABCD.
.
На положительные ион она действует
вниз, на отрицательные вверх. В результате
электроны начнут перемещаться по мостику
вверх, т.е. по нему потечет электрический
ток, направленный вниз. Перераспределившись
заряды создадут электрическое поле,
которое возбудит токи и в остальных
участках контура ABCD.
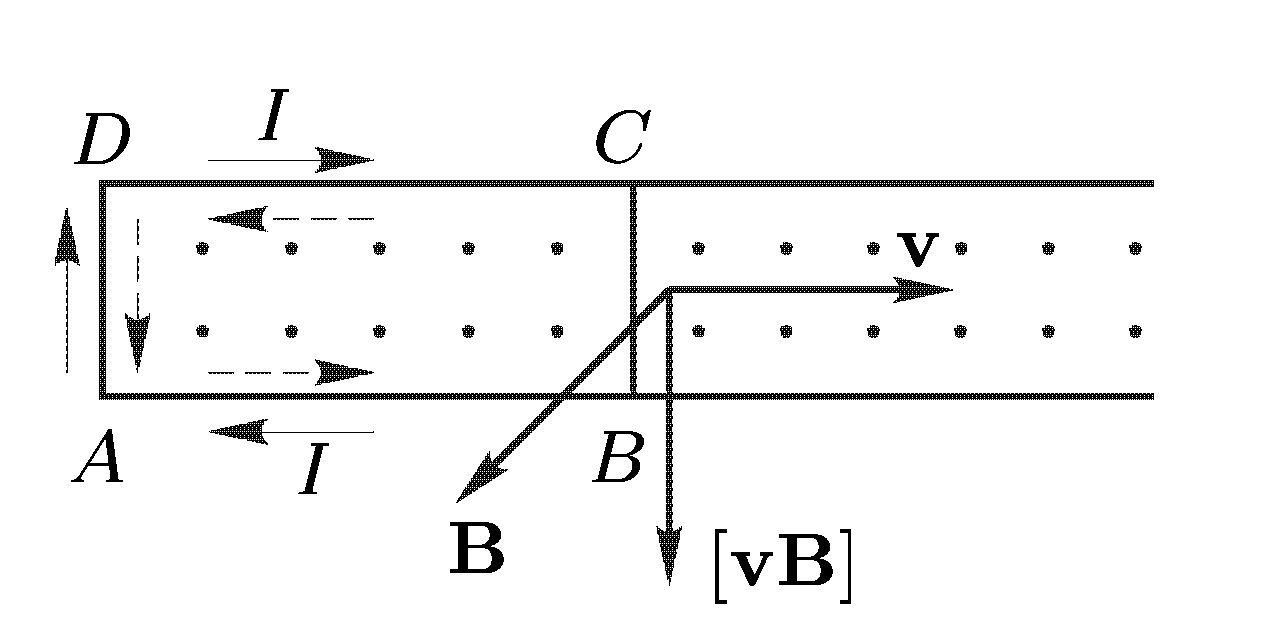
Сила Лоренца F в опыте играет роль сторонней силы, возбуждающей электрический ток.
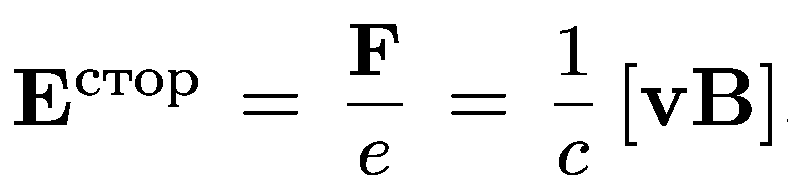
02. Электродвижущая сила индукции (ЭДС) — скалярная физическая величина, характеризующая работу сторонних сил в источниках постоянного или переменного тока.
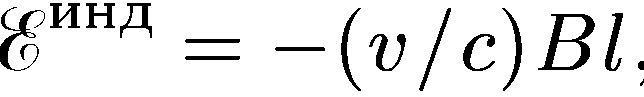
Знак
минус поставлен потому, что стороннее
поле  направлено
против положительного обхода контура.
направлено
против положительного обхода контура.
Величина
lv
есть приращение площади контура ABCD
в единицу времени, или скорость приращении
этой площади. Поэтому  равна
равна 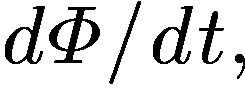
Основной закон электромагнитной индукции.(Дифференциальная форма закона электромагнитной индукции)
При движении замкнутого провода в магнитном поле в нем возбуждается электродвижущая сила, пропорциональная скорости приращения магнитного потока, пронизывающего контур провода.
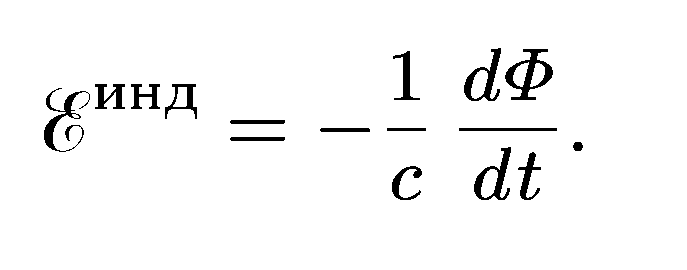
03. Правило Ленца (принцип Ле Шателье)
Индукционный ток всегда имеет такой направление, что он ослабляет действие причины, возбуждающий этот ток.
Возьмем
в магнитном поле замкнутый проволочный
виток, положительное направление обхода
которого составляет с направлением
поля правовинтовую систему. Допустим,
что магнитный поток Ф возрастает. Тогда,
согласно формуле  ,
величина будет отрицательна, а индукционный ток
в витке потечет в отрицательном
направлении. Такой ток, ослабляя внешнее
магнитное поле, будет препятствовать
возрастанию магнитного потока.
,
величина будет отрицательна, а индукционный ток
в витке потечет в отрицательном
направлении. Такой ток, ослабляя внешнее
магнитное поле, будет препятствовать
возрастанию магнитного потока.
Пусть
теперь магнитный поток Ф убывает. Тогда
величина 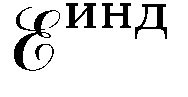 станет положительной, а индукционный
ток в витке потечет в положительном
направлении и будет препятствовать
убыванию магнитного поля и магнитного
потока.
станет положительной, а индукционный
ток в витке потечет в положительном
направлении и будет препятствовать
убыванию магнитного поля и магнитного
потока.
04. Индуктивность проводов.
Рассмотрим
тонкий замкнутый провод, по которому
течет постоянный ток I.
Внутри провода параллельно его оси
проведем произвольный замкнутый
математический контур s
и установим на нем положительное
направление. Если в пространстве нет
ферримагнитных тел, то величина
B(магнитное
поле тока) и Ф(магнитный поток) будут
пропорционально току.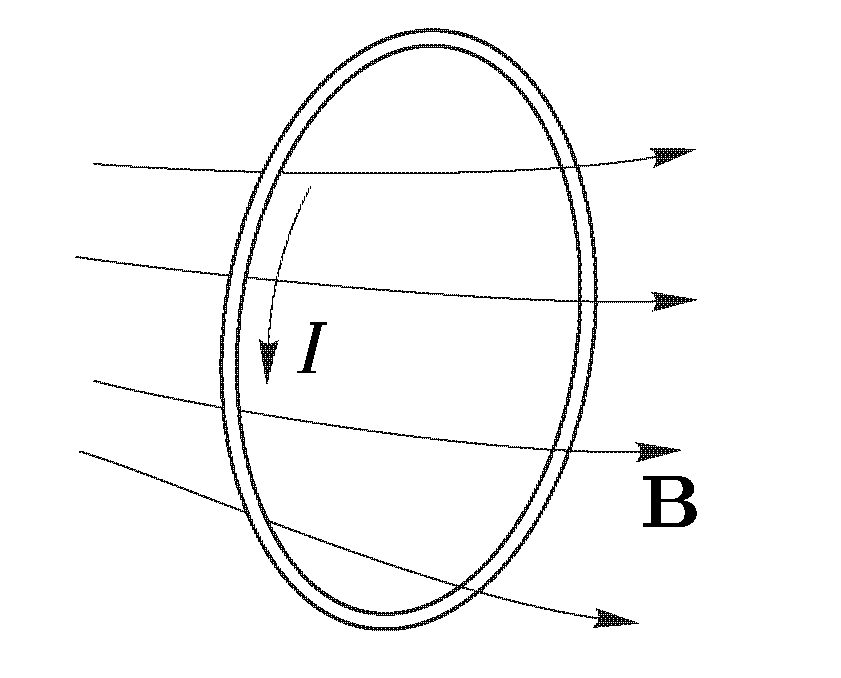
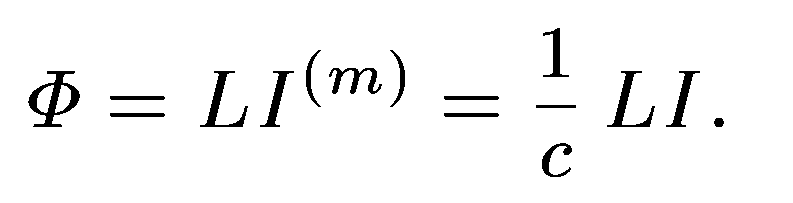 здесь
здесь 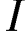 — сила тока в гауссовской системе единиц,
а
— сила тока в гауссовской системе единиц,
а 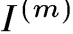 — сила тока в системе СГСМ.
— сила тока в системе СГСМ.
— самоиндукция, или коэффициент самоиндукции провода. Он не зависит от силы тока, определяется только размерами и конфигурацией самого провода.
Пример:
Вычислим индуктивность соленоида. Пусть 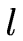 — длина соленоида,
— длина соленоида, 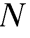 — общее число витков,
— общее число витков, 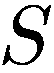 — площадь одного витка.
— площадь одного витка.
Индукция
магнитного поля внутри соленоида 
Магнитный
поток через один виток равен 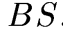 ,
я через
,
я через 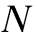 витков —
витков — 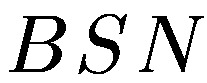 т.е.
т.е. 
Получим
индуктивность 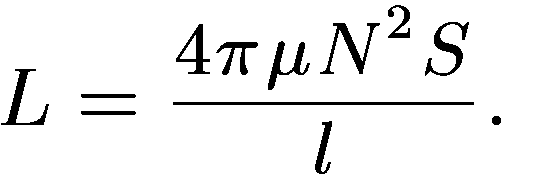 (
в сантиметрах)
(
в сантиметрах)
Магнитный поток — это поток Ф вектора магнитной индукции B через конечную поверхность S. За единицу магнитного потока принимают максвелл.
Максвелл есть магнитный поток, создаваемый магнитным полем в один гаусс через перпендикулярную к нему площадь в один квадратный сантиметр.