20____ Г.

Литература

Основная литература

1. Трофимова Т.И. Курс физики. 11-е изд., стер. — М.: Академия, 2006.— 560 с. Учебное пособие (9-е издание, переработанное и дополненное), 2004 г.

2. Трофимова Т.И.Основы физики: учеб. пособие. кн.3.Электродинамика. -М.: Высшая школа, 2007. -270 с 4.

3. Трофимова Т.И., Фирсов А.В. Курс физики. Задачи и решения. Учеб. пособие для втузов/.- М.: Издат. Центр «Академия», 2004.-592.

4. Трофимова Т.И. Павлова З.Г. Сборник задач по курсу физики с решениями. М.: Высш. шк., 2002.

ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

§1. Закон Кулона. Взаимодействие заряженных тел.

Закон Кулона: сила F взаимодействия двух точечных зарядов про­порциональна произведению этих зарядов q

1 и q₂, обратно пропор­циональна квадрату расстояния r между ними и направлена вдоль линии соединяющей эти заряды:

,

где ε — диэлектрическая проницаемость среды (показывает, во сколь­ко раз сила взаимодействия двух зарядов в данной среде меньше, чем в вакууме), ε_о — электрическая постоянная, .

Следует подчеркнуть, что формула верна только для точечных зарядов. В случае использования реальных тел, области в которых разделены заряды разбиваются на малые элементы, сила взаимодействия между которыми может быть рассчитана по закону Кулона.

Закон сохранения зарядов.В любой замкнутой системе заряженных тел алгебраическая сумма зарядов остается постоянной:

q₁+q₂+…+q_n=const,

где n — число заряженных тел в системе.

Возможно лишь перераспределение заряда между телами замкнутой системы.

§ 2. Напряженность и индукция электрического поля. Поток напряженности и индукции. Сила, действующая на заряд в электрическом поле. Циркуляция напряженности.

1. Напряженность электрического поля есть величина, равная отношениюсилы

, действующей на положительный пробный заряд q помещенный в данную точку поля, к этому заряду

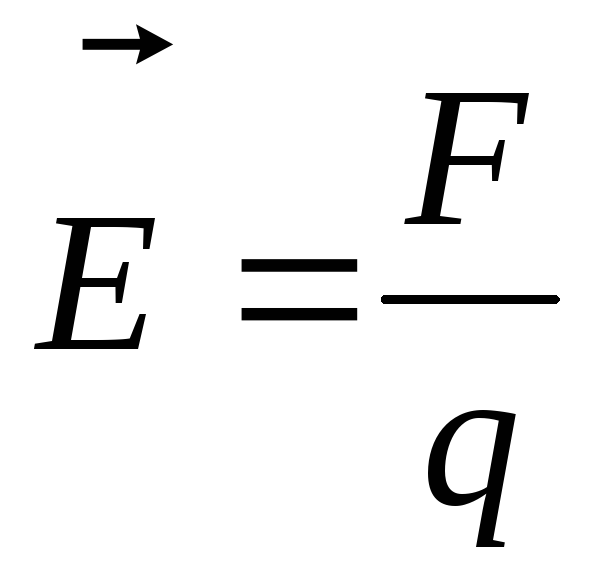
Напряженность поля численно равна силе, действующей на еди­ничный точечный положительный заряд, помещенный в данную точку.

2. Сила действующая на точечный заряд q, помещенный в электри­ческое поле,

выражается формулой

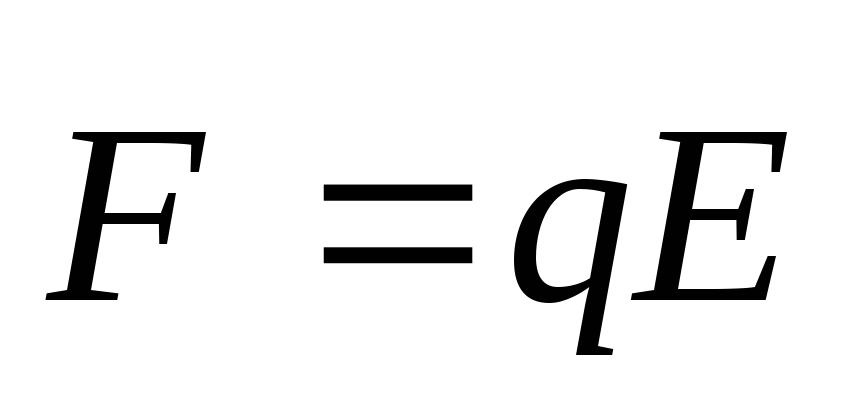
3. Для графического изображения поля вводится понятие силовой линии, т. е.

линии, в каждой точке которой касательная совпадает с направлением вектора напряженности поля. Условно принято силовые линии проводить с такой густотой, чтобы число силовых линий пронизывающих единицу площади нормальной к силовым линиям, равнялось напряженности поля. При таком условии число силовых линий, пронизывающих элементарную площадку dS, выражается формулой:

dN = E cos α dS = E_n

dS,

где α — угол, образуемый силовой линией с нормалью к площадке, E_n — проекция вектора напряженности Е на нормаль к плоскости S.

Интегрируя это выражение по всей поверхности S, получим число силовых линий N пронизывающих всю поверхность:

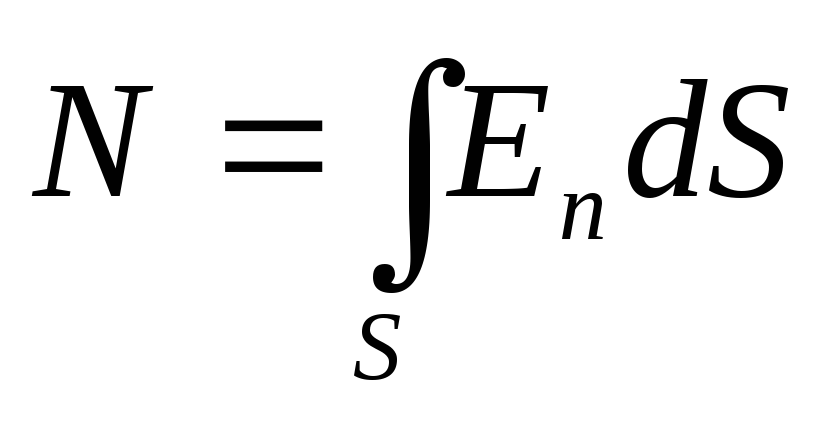
4. Потоком вектора напряженности Е через поверхность S называется выражение

В случае замкнутой поверхности

где интегрирование ведется по всей замкнутой поверхности.

5. Теорема Остроградского — Гаусса. Поток вектора напряженности N_Е через

любую замкнутую поверхность, охватывающую заряды q₁, q₂, …, q_n равен алгебраической сумме зарядов внутри этой поверхности:

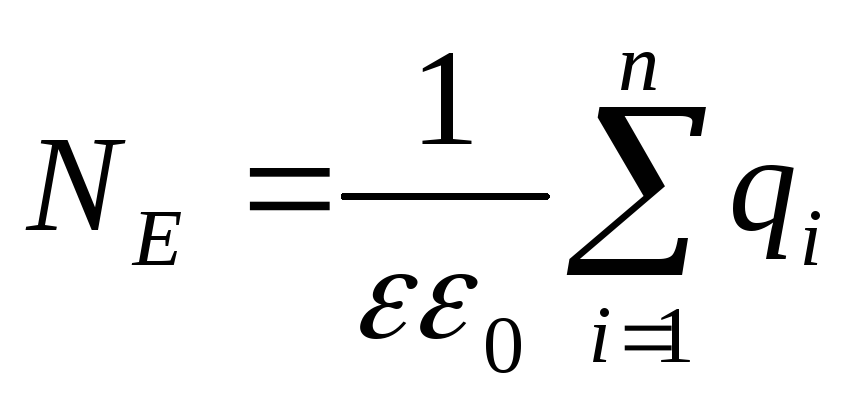
6. Напряженность электрического поля, создаваемого точечным зарядом q на

расстоянии r от заряда, выражается формулой:

Напряженность электрического поля, создаваемого металличе­ской заряженной сферой радиуса R на расстоянии r от центра сферы:

а) внутри сферы (r<R),

q=0, следовательно, E=0;

б) на поверхности сферы (r=R)E=,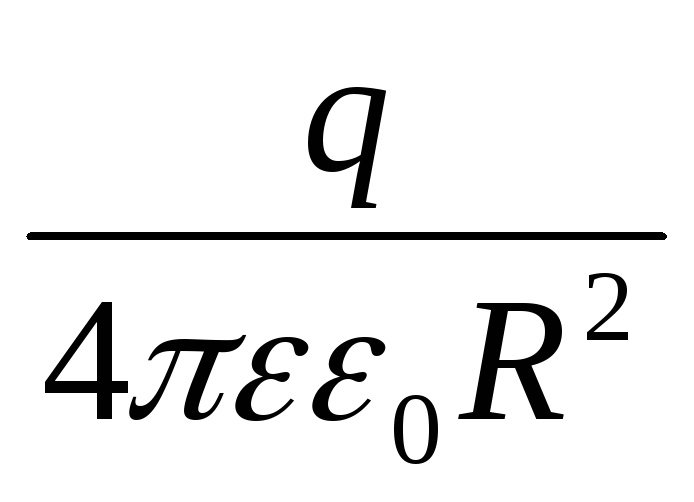

в) вне сферы (r > R) E=, где q — заряд сферы.

7. Если электрическое поле создано двумя и более точечными зарядами, то для

нахождения напряженности поля и других его характеристик следует использовать принцип суперпозиции (наложения) электрических полей, согласно которому напряженность результирующего поля равна векторной (геометрической) сумме напряженностей полей, создаваемых отдельными зарядами:

=₁+

₂+…+_n

В случае двух электрических полей с напряжённостями E₁ и E₂ абсолютное значение вектора напряженности суперпозиции полей в некоторой точке

где α— угол между векторами ₁ и

₂.

8. Напряженность поля, создаваемого бесконечно длинной равно­мерно заряженной

нитью на расстоянии r от ее оси,

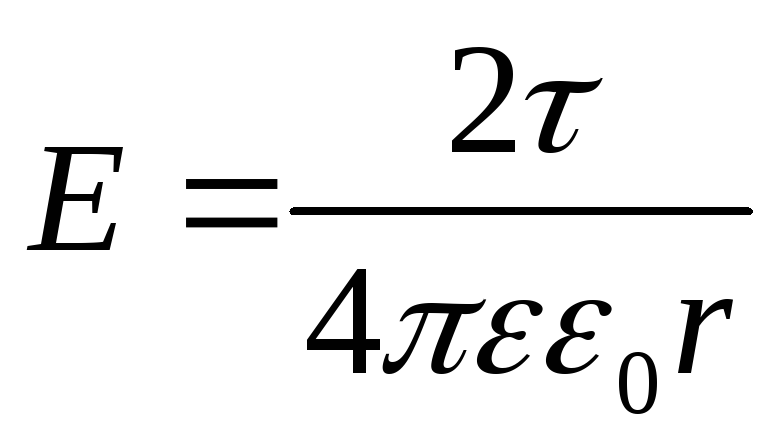
где τ — линейная плотность заряда.

Линейная плотность заряда есть физическая величина, численно равная заряду, приходящемуся на единицу длины нити (цилиндра):

9. Напряженность поля, создаваемого бесконечной равномерно заряженной

плоскостью E=

где — поверхностная плотность заряда.

Поверхностная плотность заряда есть физическая величина, численно равная заряду, приходящемуся на единицу площади:

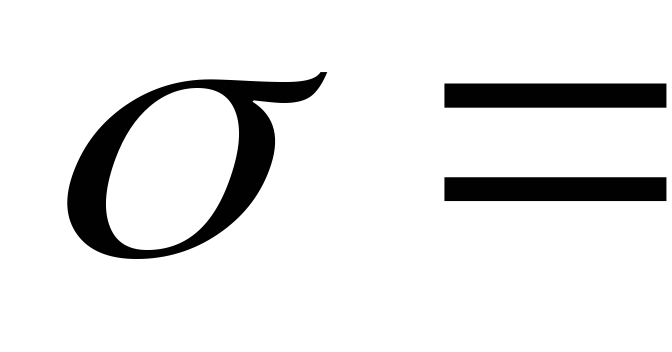
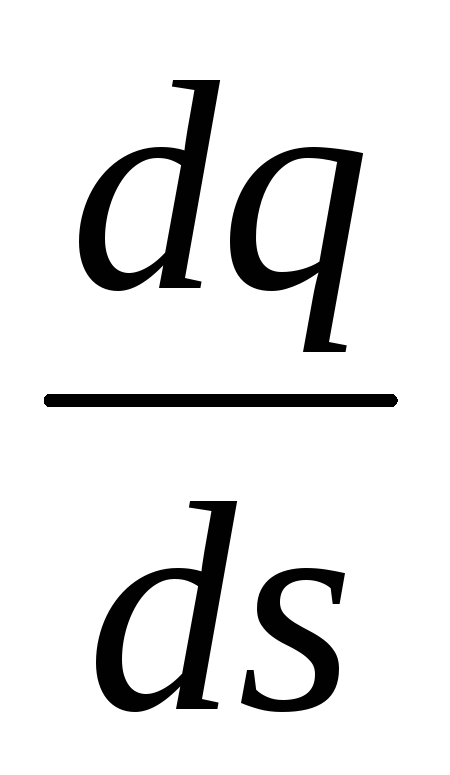
Напряженность поля, создаваемого двумя параллельными бесконечными равномерно и разноименно заряженными плоскостями, с одинаковой по абсолютной величине поверхностной плотностью заряда

(поле плоского конденсатора)

E=,

Приведенная формула справедлива для вычисления напряженности поля между пластинами плоского конденсатора только в том случае, если расстояние между пластинами много меньше линейных размеров пластин конденсатора.

Напряженность поля создаваемого равномерно заряженной сферической поверхностью

, ()

()

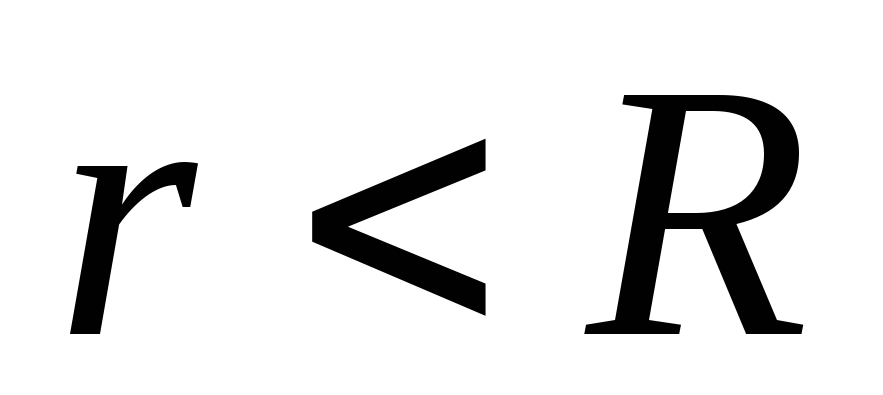Существуют среды, для которых индукция 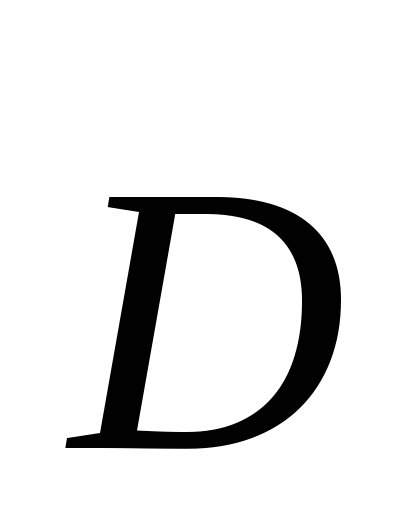электрического поля связана с напряженностью электрического поля соотношением

10. Поток вектора электрической индукции выражается аналогично потоку вектора

электрической напряженности:

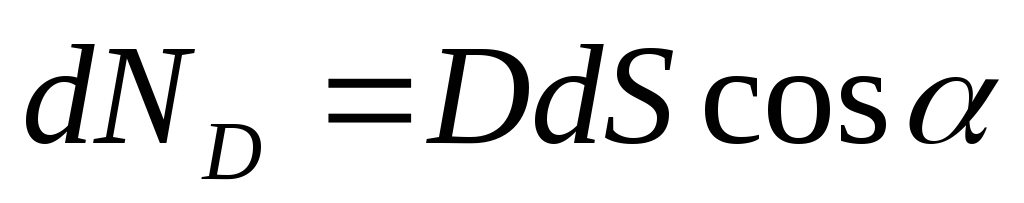
N_D=

где D_n— проекция вектора на направление нормали к элементу поверхности, площадь которой равнаdS.

11. Теорема Остроградского — Гаусса для вектора индукции. Поток N_D вектора

индукции через любую замкнутую поверхность, охватывающую заряды q₁,q₂,…,q_n:

где n — число зарядов (со своим знаком), заключенных внутри замкнутой поверхности.

12. Циркуляция вектора напряженности электрического поля от одной точки до

другой точки этого поля есть физическая величина, численно равная работе по перемещению единичного точечного положительного заряда вдоль некоторой линии соединяющий эти точки:

=,

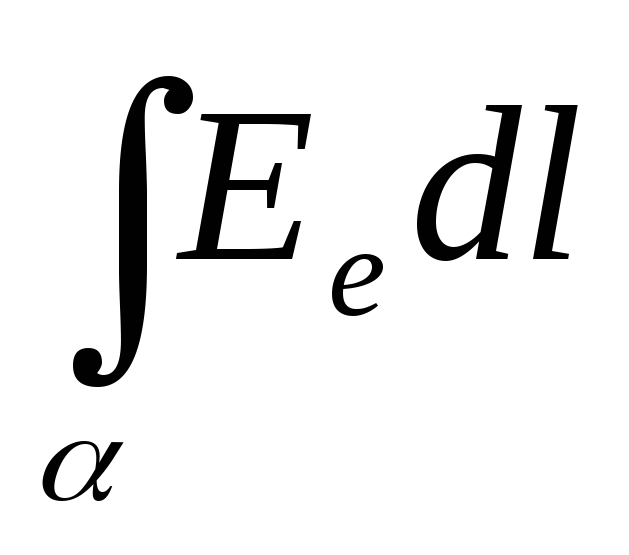где E_l — проекция вектора напряженности на направление касательной к линии.

Электростатическое поле потенциально. Для таких полей циркуляция вектора поля не зависит от пути интегрирования, а циркуляция вектора напряжённости по замкнутому контуру равна нулю:

13. Связь между поляризованностью и напряженностью электрического поля

, ,

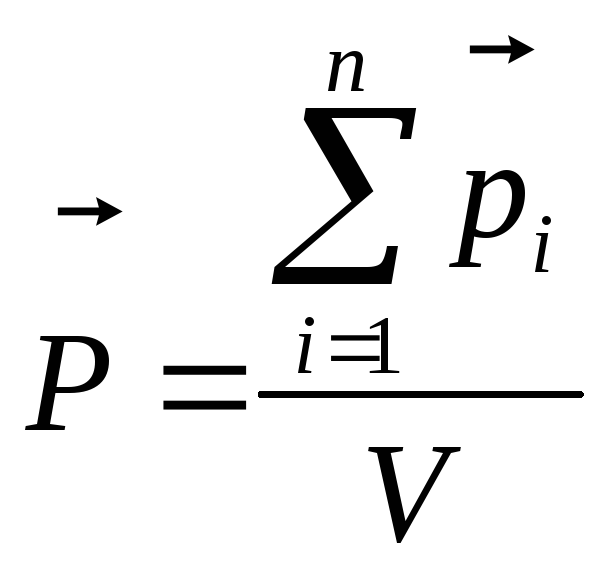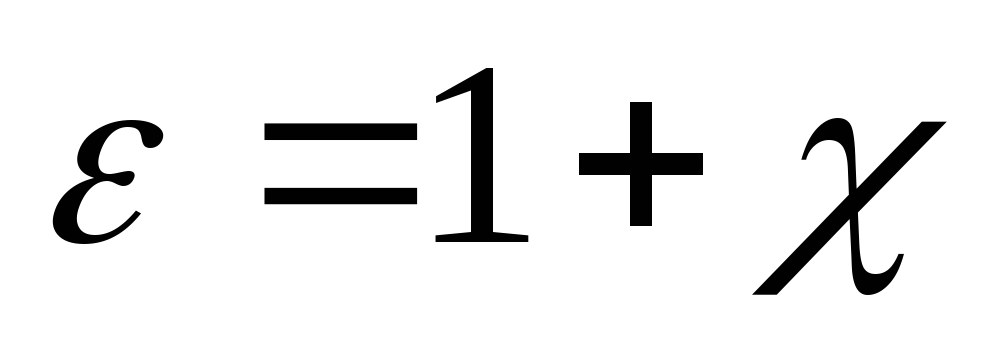
Униполярная индукция — Википедия

Материал из Википедии — свободной энциклопедии

Униполя́рная инду́кция (от уни… и полюс) — возникновение ЭДС в намагниченном теле, движущемся непараллельно оси намагничивания. При этом ЭДС направлена перпендикулярно плоскости, в которой расположены векторы магнитной индукции В и скорости u магнита.

Если намагниченное тело — проводник, то униполярная индукция может быть объяснена в рамках классической электродинамики: под действием силы Лоренца свободные электроны перемещаются внутри тела перпендикулярно направлениям u и B до тех пор, пока в теле не возникнет электрическое поле, препятствующее этому перемещению.

Последовательное объяснение явления униполярной индукции даётся теорией относительности. В системе отсчёта, связанной с магнитом (собственной системе отсчёта), электрическое поле Е отсутствует. Если в лабораторной системе отсчёта магнит движется поступательно, равномерно и прямолинейно со скоростью u, то, согласно релятивистским формулам преобразования напряжённостей полей, в этой системе электрическое поле E с точностью до множителя (1−u2/c2)−1/2,{\displaystyle \left(1-u^{2}/c^{2}\right)^{-1/2},} при малых u практически не отличающегося от единицы, будет равно: E=−{\displaystyle \mathbf {E} =-}[uc×B]{\displaystyle \left[{\frac {\mathbf {u} }{c}}\times \mathbf {B} \right]}, где c — скорость света; эта формула применима к областям как внутри, так и вне намагниченного тела, независимо от того, является ли оно проводящим или непроводящим. Таким образом, униполярная индукция — релятивистский эффект, в котором ясно проявляется относительный характер деления электромагнитного поля на электрическое и магнитное.

Наличие электрического поля приводит к появлению постоянной разности потенциалов, что используется для генерирования постоянного тока в униполярных машинах. Термин «униполярная индукция» неудачен, он возник вследствие того, что в униполярной машине контур, в котором наводится ЭДС, расположен со стороны одного полюса магнита.

• Тамм И. Е. Основы теории электричества. — 8-е изд. — М., 1966.
• Физическая энциклопедия, т.5, стр.224, стр.225, статья «Униполярная индукция», авторы Г. В. Пермитин, Ю. В. Чугунов.

Электростатическая индукция, теория и примеры

Основные принципы электростатической индукция

Любая материя состоит из заряженных частиц: электронов и ядер атомов. Электрические свойства вещества определяет реакция заряженных частиц на внешнее электрическое поле. Под воздействием электрического поля заряженные частицы начинают перемещаться. Характер и механизмы движения частиц при этом различны. Но по результату все виды движения заряженных частиц под воздействием внешнего поля, делят на две группы.

При ограниченном смещении зарядов, такие заряды называют связанными, а процесс перемещения связанных зарядов носит название диэлектрической поляризации. Вещества, у которых преобладает поляризация во внешнем поле, называют диэлектриками. Основной макроскопической характеристикой в этом случае служит диэлектрическая проницаемость вещества ().

Другая группа веществ состоит из сред, в которых происходит неограниченное смещение зарядов в объемах тел. Такие заряды называют свободными. Направленное движение свободных зарядов называют электрическим током. Свойство материи проводить электрический ток называют электропроводностью. При этом характеристикой электропроводности является удельная проводимость () или величина ей обратная – удельное сопротивление (). Вещества, обладающие высокой удельной проводимостью называют проводниками. К типичным проводникам относят металлы.

Если проводник внести в электростатическое поле, то свободные и связанные заряды начинают перемещение. При этом свободные заряды накапливаются на противоположных концах проводника. Они порождают в объеме проводника электростатическое поле, которое имеет направление против внешнего поля. В результате действия этого поля постепенно движение зарядов прекращается, и система приходит в равновесие. В равновесии электрическое поле в проводнике становится равным нулю, диэлектрическая поляризация и электрический ток становятся равны нулю. При этом концентрация свободных зарядов, которые накопились на противоположных поверхностях проводника, является максимальной. Данные заряды локализованы в тонком поверхностном слое проводника. Их характеризуют при помощи поверхностной плотности заряда (). Заряды, которые возникли на противоположных концах проводника, помещенного в электростатическое поле называют индуцированными.

Явление возникновения индуцированных зарядов называют электростатической индукцией. Самой существенной особенностью индуцированных зарядов является то, что их можно разделить механически. При диэлектрической поляризации такое не представляется возможным.

И так, электрические заряды в проводниках способны перемещаться. Если к незаряженному проводнику поднести электрический заряд, то заряды противоположного знака переместятся к этому заряду, а такого же знака отодвинутся от него. При этом наш проводник в целом буде иметь нулевой заряд. В соответствии с законом Кулона сила взаимодействия между зарядами обратно пропорциональная расстоянию между ними. Получится, что незаряженный проводник будет притягиваться к поднесенному к нему заряду.

Если индуцирующий заряд убрать, то проводник вернется в нейтральное состояние. Если индуцирующий заряд оставить на месте, при этом отделить ближнюю и дальние части проводника, изолировав их, то каждая из частей будет нести заряд, имеющий равный по модулю и противоположный по знаку. Электростатические машины устроены в по такому принципу. Они повторяют операции накопления и разделения зарядов.

Определение электростатической индукции

Данное явление вызвано перераспределением зарядов внутри проводников и поляризацией диэлектриков. При этом внешнее электростатическое поле может искажаться индуцированным полем.

Примеры решения задач

Электростатическая индукция — это… Что такое Электростатическая индукция?

Эксперимент с электроскопом показывающий возникновение индуцированного заряда.

Электростатическая индукция — явление наведения собственного электростатического поля, при действии на тело внешнего электрического поля. Явление обусловлено перераспределением зарядов внутри проводящих тел, а также поляризацией внутренних микроструктур^[1] у непроводящих тел. Внешнее электрическое поле может значительно исказиться вблизи тела с индуцированным электрическим полем.

Электростатическая индукция в проводниках

Перераспределение зарядов в хорошо проводящих металлах при действии внешнего электрического поля происходит до тех пор, пока заряды внутри тела практически полностью не скомпенсируют внешнее электрическое поле. При этом на противоположных сторонах^[2] проводящего тела появятся противоположные наведённые (индуцированные) заряды.

Электростатическая индукция в диэлектриках

Диэлектрики в электростатическом поле поляризуются.

Применение

Наиболее массовое применение находит основанная на данном явлении электростатическая защита приборов и соединительных цепей.

Данный эффект используется в ряде приборов, например в генераторе Ван де Граафа.

Ссылки

Примечания

1. ↑ атомов, молекул, кристаллических решёток и т.п.
2. ↑ относительно внешнего электрического поля

электростатической индукции — Electrostatic induction

Электростатическая индукция , также известная как «электростатическое влияние» или просто «влияние» в Европе и Латинской Америке, является перераспределением электрического заряда в объекте, вызванное влиянием соседних зарядов. В присутствии заряженного тела, изолированный проводник развивает положительный заряд на одном конце и отрицательный заряд на другом конце. Индукционная был обнаружен британский ученый Джон Кантон в 1753 году и шведский профессор Йохан Карл Вильке в 1762 электростатических генераторов , таких как машины Wimshurst , в генераторе Ван — де — Граафа и электрофорной , использовать этот принцип. Из — за индукции,электростатический потенциал ( напряжение ) постоянен в любой точке по всему проводнику. Электростатическая индукция также отвечает за привлечение легких непроводящих объектов, такие , как воздушные шары, бумажные или пенополистирол, обрезки в статические электрические заряды. Электростатической индукции законы применяются в динамических ситуациях, насколько квазистатическое приближение справедливо. Электростатической индукции не следует путать с электромагнитной индукции .

объяснение

Демонстрация индукции, в 1870 — х годах. Положительный вывод из электростатической машины (справа) находится рядом с незаряженным латунным цилиндром (слева) , в результате чего левый конца приобретает положительный заряд и право приобретать отрицательный заряд. Небольшой пробковый шарик электроскопам висит от дна показывает , что заряд сосредоточен на концах.

Нормальный незаряженных кусок материи имеет одинаковое количество положительных и отрицательных электрических зарядов в каждой его части, расположенных близко друг к другу, так что ни одна часть его не имеет чистый электрический заряд. Положительные заряды являются атомы » ядра , которые связаны в структуру материи и не могут свободно перемещаться. Отрицательные заряды атомов электроны . В электрически проводящих объектов , таких как металлы, некоторые электроны могут свободно перемещаться в объекте.

Когда заряженный объект приближен незаряженный, электропроводящий объект, например, кусок металла, сила соседнего заряда из — за закон Кулона вызывает разделение этих внутренних сборов. Например, если положительный заряд вносятся около объекта (см картины цилиндрического электрода вблизи электростатической машины), то электроны в металле будут притягиваться к нему и перейти на сторону объекта перед ней. Когда электроны движутся из области, они оставляют несбалансированный положительный заряд из — ядер. Это приводит к области отрицательного заряда на объекте возле внешнего заряда, а область положительного заряда на части от него. Это так называемые индуцированные заряды . Если внешний заряд отрицателен, полярность заряженных областей будет отменена.

Так как этот процесс является лишь перераспределением зарядов , которые уже были в объекте, это не меняет общий заряд на объекте; она по- прежнему не имеет чистый заряд. Этот эффект индукции является обратимым; если рядом заряд удаляется, притяжение между положительными и отрицательными внутренними сборами заставляет их снова перемешиваются.

Зарядка объекта по индукции

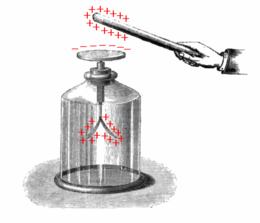Золото-лист электроскоп, показывающий индукцию, перед заземлен. Использование электроскоп, чтобы показать электростатической индукции. Устройство имеет листьев / иглу, которые заряжаются при введении заряженного стержня к нему. Листы согнуть отпуска / иглу, и тем сильнее статические введены, происходит более гибко.

Однако, индукционный эффект также может быть использован , чтобы положить чистый заряд на объекте. Если, в то время как она близка к положительному заряду, вышеупомянутый объект кратковременно соединен через провод щего путь к электрическому заземлению , которая представляет собой большой резервуар как положительные , так и отрицательных заряды, некоторые из отрицательных зарядов в земле будут течь в объект при привлечении близлежащего положительного заряда. Когда контакт с землей сломана, объект остается с чистым отрицательным зарядом.

Этот метод может быть продемонстрирован с использованием золота листьев электроскоп , который является инструментом для обнаружения электрического заряда. Электроскоп сначала выгружают, а заряженный объект затем подносится близко к началу терминала инструмента. Индукция вызывает разделение зарядов внутри электроскоп металлического стержня «с, так что терминал получает суммарный заряд противоположной полярности к этому объекту, в то время как золотые листы получить заряд той же полярность. Так как листья имеют одинаковый заряд, они отталкиваются друг от друга и разведены. Электроскоп не приобрел чистый заряд: заряд в ней была лишь перераспределены, так что если заряженный объект должны были быть перемещены от электроскопа листья соберутся снова.

Но если электрический контакт кратко между электроскопом терминалом и землей , например, прикоснувшись к терминалу с пальцем, это вызывает заряд течь от земли к терминалу, привлеченный заряд на объекте близко к терминалу. Этот заряд нейтрализуется заряд золотых листьев, поэтому листья приходят снова вместе. Электроскоп теперь содержит чистый заряд , противоположный по полярности , что заряженный объект. Когда электрический контакт с землей нарушаются, например, подняв палец, дополнительный заряд , который только что протекал в электроскоп не может бежать, и прибор сохраняет чистый заряд. Заряд удерживается в верхней части электроскопа терминала по привлечению индуцирующего заряда. Но когда индуцирования заряд отодвигается, заряд высвобождается и распространяется по всему электроскопу терминала к листам, так что золотые листы раздвигаются снова.

Знак оставшегося заряда на электроскоп после заземления всегда противоположен по знаку внешнего индуцирующего заряду. Два правила индукции:

• Если объект не заземлен, близлежащий заряд будет индуцировать равные и противоположные заряды в объекте.
• Если какая — либо часть объекта моментально заземлена , а индуцирования заряд близок, заряд противоположная полярности к индуцирующему заряду будет привлечены от земли в объект, и он останется с зарядом противоположных к индуцирующему заряду.

Электростатическое поле внутри проводящего объекта равна нулю

Поверхностные заряды , индуцированные в металлических объектах с помощью соседнего заряда. Электростатическое поле (линии со стрелками) соседнего положительного заряда (+) приводит к тому , мобильные заряды в металлических предметов , чтобы отделить. Отрицательные заряды (синий) привлекают и перейти к поверхности объекта , обращенному к внешней зарядке. Положительные заряды (красный) отталкиваются и двигаться к поверхности , обращенной в сторону. Эти индуцированные поверхностные заряды создают противодействующее электрическое поле , которое точно отменяет поле внешнего заряда всюду внутри металла. Поэтому электростатической индукции гарантирует , что электрическое поле всюду внутри проводящего объекта равна нулю.

Оставшаяся вопрос состоит в том , как большие индуцированные заряды. Движение зарядов обусловлено силой , действующей на них с помощью электрического поля внешнего заряженного объекта, по закону Кулона . Поскольку заряды в металлическом объекте продолжают расходиться, полученные положительные и отрицательные регионы создают свое собственное электрическое поле, которое противодействует поле внешнего заряда. Этот процесс продолжается до тех пор очень быстро ( в течение доли секунды) равновесие будет достигнуто , в котором наведенные заряды точно правильный размер , чтобы отменить внешнее электрическое поле по всей внутренней части металлического предмета. Не Тогда остальные мобильные заряды (электроны) в глубь металла больше не чувствуют силу и чистое движение зарядов прекращается.

Индуцированные заряд находится на поверхности

Так как подвижные заряды в интерьере металлического предмета могут свободно перемещаться в любом направлении, никогда не может быть статической концентрацией заряда внутри металла; если есть, было бы привлечь противоположный заряд полярности, чтобы нейтрализовать его. Поэтому в индукции, подвижные заряды движутся под действием внешнего заряда, пока они не достигают поверхности металла и собирать там, где они сдерживаются от перемещения по границе.

Это устанавливает важный принцип, что электростатические заряды на проводящих объектах находятся на поверхности объекта. Внешние электрические поля вызывают поверхностные заряды на металлических предметах, которые точно отменяют поле внутри.

Напряжения в течение проводящего объекта является постоянная

Электростатический потенциал или напряжение между двумя точками определяются как энергия (работа) , необходимой для перемещения небольшого заряда через электрическое поле между двумя точками, деленной на размере заряда. Если есть электрическое поле , направленное от точки к точке , то она будет оказывать усилие на заряде , двигающемся от до . Работы будут должны быть сделаны на заряд силой , чтобы заставить его двигаться в отношении противной силы электрического поля. Таким образом, электростатическая потенциальная энергия заряда будет увеличиваться. Таким образом, потенциал в точке выше , чем в точке . Электрическое поле в любой точке есть градиент (скорость изменения) от электростатического потенциала  : б{\ Displaystyle \ mathbf {Ь}}a{\ Displaystyle \ mathbf {а}}a{\ Displaystyle \ mathbf {а}}б{\ Displaystyle \ mathbf {Ь}}б{\ Displaystyle \ mathbf {Ь}}б{\ Displaystyle \ mathbf {Ь}}a{\ Displaystyle \ mathbf {а}}Е{\ Displaystyle \ mathbf {E}} В{\ Displaystyle V}

∇Взнак равноЕ{\ Displaystyle \ наб V = \ mathbf {E} \,}

Поскольку не может быть никакого электрического поля внутри проводящего объекта прилагать усилие на заряды , внутри проводящего объекта градиент потенциала равен нулю (Езнак равно0){\ Displaystyle (\ mathbf {Е} = 0) \,}

∇Взнак равно0{\ Displaystyle \ наб V = \ mathbf {0} \,}

Еще один способ сказать это то, что в электростатиках, электростатическая индукция гарантирует, что потенциал (напряжение) в течение проводящего объекта является постоянным.

Индукция в диэлектрических объектов

фрагменты бумаги привлекаемых заряженного CD

Аналогичный эффект индукции происходит в непроводящих ( диэлектрических ) объектах, и отвечают за привлечение небольших легких непроводящих объектов, как воздушные шары, обрывки бумаги или пенопласта , в статические электрические заряды (см кошки, выше), а также статические цепляться в одежда.

В непроводниках, то электроны связаны с атомами или молекулами , и не может свободно перемещаться об объекте как в проводниках; однако они могут двигаться немного внутри молекул. Если положительный заряд приближен непроводящий объект, электроны в каждой молекуле притягиваются к нему, и перейти на сторону молекулы , обращенной к заряд, в то время как положительные ядра отталкиваются и слегка двигаться к противоположной стороне молекулы. Так как отрицательные заряды теперь ближе к внешнему заряду , чем положительные заряды, их притяжение больше , чем отталкивания положительных зарядов, что приводит к небольшому чистому притяжению молекулы по отношению к заряду. Это называется поляризацией , и поляризованные молекулы называют диполи . Этот эффект является микроскопическим, но так как есть очень много молекул, она добавляет до достаточно сил , чтобы переместить световой объект как Styrofoam. Это принцип работы с пробковым шаром электроскопа .

Заметки

внешняя ссылка

Электрическая индукция — это… Что такое Электрическая индукция?

Электри́ческая инду́кция (электри́ческое смеще́ние) — векторная величина, равная сумме вектора напряжённости электрического поля и вектора поляризации.

В СИ: .

В СГС: .

Величина электрической индукции в системе СГС измеряется в СГСЭ или СГСМ единицах, а в СИ — в кулонах на м² (L⁻²TI). В рамках СТО векторы и объединяются в единый тензор, аналогичный тензору электромагнитного поля.

Определяющие уравнения

Уравнения для вектора индукции в СГС имеют вид (2ая пара уравнений Максвелла)

Здесь  — плотность свободных зарядов, а  — плотность тока свободных зарядов. Введение вектора , таким образом, позволяет исключить из уравнений Максвелла неизвестные молекулярные токи и поляризационные заряды.

Материальные уравнения

Для полного определения электромагнитного поля уравнения Максвелла необходимо дополнить материальными уравнениями, связывающими векторы и (а также и ) в веществе. В вакууме эти векторы совпадают, а в веществе связь между ними зачастую предполагают линейной:

Величины образуют тензор диэлектрической проницаемости. В принципе, он может зависеть как от точки внутри тела, так и от частоты колебаний электромагнитного поля. В изотропных средах тензор диэлектрической проницаемости сводится к скаляру, называемому также диэлектрической проницаемостью. Материальные уравнения для приобретают простой вид

Возможны среды, для которых зависимость между и является нелинейной (в основном — сегнетоэлектрики).

Граничные условия

На границе двух веществ скачок нормальной компоненты вектора определяется поверхностной плотностью свободных зарядов:

(в СГС)

(в СИ)

Здесь  — нормальная производная,  — точка на поверхности раздела,  — вектор нормали к этой поверхности в данной точке,  — поверхностная плотность свободных зарядов. Уравнение не зависит от выбора нормали (внешней или внутренней). В частности, для диэлектриков уравнение означает, что нормальная компонента вектора непрерывна на границе сред. Простого уравнения для касательной составляющей записать нельзя, она должна определяться из граничных условий для и материальных уравнений.

Литература

См. также

Закон электромагнитной индукции. Вихревое электрическое поле. Вихревые токи

Закон электромагнитной индукции. Вихревое электрическое поле. Вихревые токи

Электрический ток в цепи возможен, если на свободные заряды проводника действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура называется ЭДС. При изменении магнитного потока через поверхность, ограниченную контуром, в контуре появляются сторонние силы, действие которых характеризуется ЭДС индукции.

Учитывая направление индукционного тока, согласно правилу Ленца:

ЭДС индукции в замкнутом контуре равна скорости изменения магнитного потока через поверхность, ограниченную контуром, взятой с противоположным знаком.

Почему? — т.к. индукционный ток противодействует изменению магнитного потока, ЭДС индукции и скорость изменения магнитного потока имеют разные знаки.

Если рассматривать не единичный контур, а катушку, где N- число витков в катушке:

Величину индукционного тока можно рассчитать по закону Ома для замкнутой цепи

где R — сопротивление проводника.

ВИХРЕВОЕ ЭЛЕКТРИЧЕСКОЕ ПОЛЕ

Причина возникновения электрического тока в неподвижном проводнике — электрическое поле.
Всякое изменение магнитного поля порождает индукционное электрическое поле независимо от наличия или отсутствия замкнутого контура, при этом если проводник разомкнут, то на его концах возникает разность потенциалов; если проводник замкнут, то в нем наблюдается индукционный ток.

Индукционное электрическое поле является вихревым.
Направление силовых линий вихревого электрического поля совпадает с направлением индукционного тока
Индукционное электрическое поле имеет совершенно другие свойства в отличии от электростатического поля.

Электростатическое поле — создается неподвижными электрическими зарядами, силовые линии поля разомкнуты — -потенциальное поле, источниками поля являются электрические заряды, работа сил поля по перемещению пробного заряда по замкнутому пути равна 0.

Индукционное электрическое поле ( вихревое электр. поле ) — вызывается изменениями магнитного поля, силовые линии замкнуты (вихревое поле), источники поля указать нельзя, работа сил поля по перемещению пробного заряда по замкнутому пути равна ЭДС индукции.

Вихревые токи

Индукционные токи в массивных проводниках называют токами Фуко. Токи Фуко могут достигать очень больших значений, т.к. сопротивление массивных проводников мало. Поэтому сердечники трансформаторов делают из изолированных пластин.
В ферритах — магнитных изоляторах вихревые токи практически не возникают.

Использование вихревых токов

— нагрев и плавка металлов в вакууме, демпферы в электроизмерительных приборах.

Вредное действие вихревых токов

— это потери энергии в сердечниках трансформаторов и генераторов из-за выделения большого количества тепла.

Электромагнитное поле — Класс!ная физика

Взаимодействие токов. Магнитное поле. Вектор магнитной индукции. Сила Ампера — Действие магнитного поля на движущийся заряд.Магнитные свойства вещества — Явление электромагнитной индукции. Магнитный поток. Направление индукционного тока. Правило Ленца — ЭДС электромагнитной индукции. Вихревое электрическое поле — ЭДС индукции в движущихся проводниках
— Самоиндукция. Индуктивность. Энергия магнитного поля. Вопросы к пр/работе

Любознательным

Сальто-мортале жука-щелкуна

Если пощекотать лежащего на спинке жука-щелкуна, он подпрыгивает вверх сантиметров на 25, при этом раздается громкий щелчок. Ерунда, возможно, скажете вы.
Но, действительно, жучок без помощи ног делает толчок с начальным ускорением 400 g, а затем переворачивается в воздухе и приземляется уже на ноги. 400 g — удивительно!
Еще более удивительно то, что мощность, развиваемая при толчке, раз в сто больше мощности, которую может обеспечить какая-либо из мышц жучка. Как удается жучку развить такую огромную мощность?
Часто ли он способен совершать свои изумительные прыжки? Чем ограничена частота их повторения?

Оказывается…
Когда жучок лежит вверх ногами, особый выступ на передней части его тела мешает ему распрямиться, чтобы совершить прыжок. Какое-то время он накапливает мышечное напряжение, затем, резко изогнувшись, подбрасывает себя вверх.
Прежде чем жучок снова сможет подпрыгнуть, он должен снова медленно «напрячь» мышцы.

Источник: «Физический фейерверк» Дж. Уокер