Напряжённость магнитного поля — Википедия

Материал из Википедии — свободной энциклопедии

Напряжённость магни́тного по́ля — векторная физическая величина, равная разности вектора магнитной индукции B и вектора намагниченности M. Обычно обозначается символом Н.

В Международной системе единиц (СИ):

H=1μ0B−M,{\displaystyle \mathbf {H} ={\frac {1}{\mu _{0}}}\mathbf {B} -\mathbf {M} ,}

где μ0{\displaystyle \mu _{0}} — магнитная постоянная.

В системе СГС:

H=B−4πM.{\displaystyle \mathbf {H} =\mathbf {B} -4\pi \mathbf {M} .}

В простейшем случае изотропной (по магнитным свойствам) среды и в приближении достаточно низких частот, намагниченность M зависит линейно от приложенного магнитного поля с индукцией B:

M=αB.{\displaystyle \mathbf {M} =\alpha \mathbf {B} .}

Однако исторически принято эту линейную зависимость описывать не коэффициентом α{\displaystyle \alpha }, а использовать связанные величины — магнитную восприимчивость χ{\displaystyle \chi } или магнитную проницаемость μ{\displaystyle \mu }:

M=χ1+4πχB=μ−14πμB.{\displaystyle \mathbf {M} ={\frac {\chi }{1+4\pi \chi }}\mathbf {B} ={\frac {\mu -1}{4\pi \mu }}\mathbf {B} .}

В системе СГС напряжённость магнитного поля измеряется в эрстедах (Э), в системе СИ — в амперах на метр (А/м). В технике эрстед постепенно вытесняется единицей СИ — ампером на метр.

1 Э = 1000/(4π) А/м ≈ 79,5775 А/м.

1 А/м = 4π/1000 Э ≈ 0,01256637 Э.

В вакууме (или в отсутствие среды, способной к магнитной поляризации, а также в случаях, когда последняя пренебрежима) напряжённость магнитного поля (Н) совпадает с вектором магнитной индукции

(B) с точностью до коэффициента, равного 1 в СГС и μ0{\displaystyle \mu _{0}} в СИ.

В магнетиках (магнитных средах) напряжённость магнитного поля имеет физический смысл «внешнего» поля, то есть совпадает (быть может, в зависимости от принятых единиц измерения, с точностью до постоянного коэффициента, как, например, в системе СИ, что общего смысла не меняет) с таким вектором магнитной индукции, какой «был бы, если магнетика не было».

Например, если поле создаётся катушкой с током, в которую вставлен железный сердечник, то напряжённость магнитного поля H внутри сердечника совпадает (в СГС точно, а в СИ — с точностью до постоянного размерного коэффициента) с вектором магнитной индукции

B₀ поля, которое было бы создано этой катушкой при отсутствии сердечника. B₀ в принципе может быть рассчитан исходя из геометрии катушки и тока в ней, без всякой дополнительной информации о материале сердечника и его магнитных свойствах.

При этом надо иметь в виду, что более фундаментальной характеристикой магнитного поля является вектор магнитной индукции B. Именно он определяет силу действия магнитного поля на движущиеся заряженные частицы и токи, а также может быть непосредственно измерен, в то время как напряжённость магнитного поля H можно рассматривать скорее как вспомогательную величину (хотя рассчитать её, по крайней мере, в статическом случае, проще, в чём состоит её ценность: ведь

H создает так называемые свободные токи, которые сравнительно легко непосредственно измерить, а трудно измеримые связанные токи — то есть токи молекулярные и т. п. — учитывать не надо).

Правда, в обычно используемое выражение для энергии магнитного поля (в среде) B и H входят почти равноправно, но надо иметь в виду, что в эту энергию включена и энергия, затраченная на поляризацию среды, а не только энергия собственно поля^[1]. Энергия магнитного поля как такового выражается только через фундаментальную величину B. Тем не менее видно, что величина

H феноменологическая и тут весьма удобна.

1. ↑ Для иллюстрации раскроем выражение для плотности энергии поля в среде wsubst{\displaystyle w_{subst}} в случае линейной связи намагниченности от напряженности магнитного поля M=χH.{\displaystyle \mathbf {M} =\chi \mathbf {H} .} В системе СИwsubst=12H⋅B=12(1μ0B−M)⋅B=12μ0B2−12M⋅B,{\displaystyle w_{subst}={\frac {1}{2}}\mathbf {H} \cdot \mathbf {B} ={\frac {1}{2}}({\frac {1}{\mu _{0}}}\mathbf {B} -\mathbf {M} )\cdot \mathbf {B} ={\frac {1}{2\mu _{0}}}\mathbf {B} ^{2}-{\frac {1}{2}}\mathbf {M} \cdot \mathbf {B} ,}где первый член — энергия магнитного поля, второй — энергия взаимодействия поля со средой (например, с магнитными диполями парамагнетика).

• Иродов И. Е. Основные законы электромагнетизма. — 2-е, стереотипное. — Москва: Высшая школа, 1991.

Магнитная индукция — это… Что такое Магнитная индукция?

Магни́тная инду́кция  — векторная величина, являющаяся силовой характеристикой магнитного поля (его действия на заряженные частицы) в данной точке пространства. Определяет, с какой силой магнитное поле действует на заряд , движущийся со скоростью .

Более конкретно,  — это такой вектор, что сила Лоренца , действующая со стороны магнитного поля^[1] на заряд , движущийся со скоростью , равна

где косым крестом обозначено векторное произведение, α — угол между векторами скорости и магнитной индукции (направление вектора перпендикулярно им обоим и направлено по правилу буравчика).

Также магнитная индукция может быть определена^[2] как отношение максимального механического момента сил, действующих на рамку с током, помещенную в однородное поле, к произведению силы тока в рамке на её площадь.

Является основной фундаментальной характеристикой магнитного поля, аналогичной вектору напряжённости электрического поля.

В системе СГС магнитная индукция поля измеряется в гауссах (Гс), в системе СИ — в теслах (Тл)

1 Тл = 10⁴ Гс

Магнитометры, применяемые для измерения магнитной индукции, называют тесламетрами.

Основные уравнения

Поскольку вектор магнитной индукции является одной из основных фундаментальных физических величин в теории электромагнетизма, он входит в огромное множество уравнений, иногда непосредственно, иногда через связанную с ним напряженность магнитного поля. По сути, единственная область в классической теории электромагнетизма, где он отсутствует, это пожалуй разве только чистая электростатика.

• (Здесь формулы приведем в системе единиц СИ, в виде для вакуума^[3], где есть варианты для вакуума — для среды; запись в другом виде и подробности — см. по ссылкам).

В магнитостатике

В магнитостатическом пределе^[4] наиболее важными являются:

В общем случае

Основные уравнения (классической) электродинамики общего случая (то есть независимо от ограничений магнитостатики), в которых участвует вектор магнитной индукции :

• Формула силы Лоренца
  • Следствия из нее, такие как
    • Выражение для силы Ампера, действующей со стороны магнитного поля на ток (участок провода с током)

    • выражение для вращающего момента, действующего со стороны магнитного поля на магнитный диполь (виток с током, катушку или постоянный магнит):

    • выражение для потенциальной энергии магнитного диполя в магнитном поле:

    • а также следующих из них выражения для силы, действующей на магнитный диполь в неоднородном магнитном поле и т.д..
    • Выражение для силы, действующей со стороны магнитного поля на точечный магнитный заряд:
      • (это выражение, точно соответствующее обычному закону Кулона, широко используется для формальных вычислений, для которых ценна его простота, несмотря на то, что реальных магнитных зарядов в природе не обнаружено; также может прямо применяться к вычислению силы, действующей со стороны магнитного поля на полюс длинного тонкого магнита или соленоида).

• Выражение для плотности энергии магнитного поля
  • Оно в свою очередь входит (вместе с энергией электрического поля) и в выражение для энергии электромагнитного поля и в лагранжиан электромагнитного поля и в его действие. Последнее же с современной точки зрения является фундаментальной основой электродинамики (как классической, так в принципе и квантовой).

Примечания

1. ↑ Если учитывать и действие электрического поля E, то формула (полной) силы Лоренца принимает вид:
   При отсутствии электрического поля (или если член, описывающий его действие, специально вычесть из полной силы) имеем формулу, приведенную в основном тексте.
2. ↑ Это определение с современной точки зрения менее фундаментально, чем приведенное выше (и является просто его следствием), однако с точки зрения близости к одному из практических способов измерения магнитной индукции может быть полезным; также и с исторической точки зрения.
3. ↑ То есть в наиболее фундаментальном и простом для ознакомления виде.
4. ↑ То есть в частном случае постоянных токов и постоянных электрического и магнитного полей или — приближенно — если изменения настолько медленны, что ими можно пренебречь.
5. ↑ Являющаяся частным магнитостатическим случаем закона Ампера — Максвелла (см. в стаье далее).

См. также

Индукция магнитного поля, теория и примеры

Индукция магнитного поля (магнитная индукция, вектор магнитной индукции) () – это одна из основных физических векторных величины, которые характеризуют магнитное поле. Это силовая характеристика данного поля, отображающая действие поля на заряженную частицу в рассматриваемой точке пространства.

Определения индукции магнитного поля

Индукцию магнитного поля можно определить разными способами: понятие вращающего момента рамки с магнитным моментом, используя закон Ампера, силу Лоренца.

1) Модуль вектора индукции магнитного поля в конкретной точке однородного магнитного поля определен максимальным вращающим моментом (), который действует на рамку, обладающую магнитным моментом (), равным единице,, если нормаль к рамке ориентирована перпендикулярно направлению поля:

   

2) Величина индукции магнитного поля равна пределу отношения силы (dF), с которой действует магнитное поле на элементарный проводник с током, к силе тока (I) умноженной на длину этого проводника (dl), при длине проводника стремящейся к нулю. При этом проводник имеет такое расположение в магнитном поле, что данный предел имеет максимальное значение:

   

направлен перпендикулярно элементу dl, и направлению силы Ампера. Если смотреть из конца , то вращение по кратчайшему расстоянию от направления силы Ампера к направлению силы тока в проводнике должно происходить против часовой стрелки.

3) Исходя из определения силы Лоренца (), величину вектора магнитной индукции найдем как:

   

где q – заряд частицы, движущейся в магнитном поле; v – скорость движения частицы; – угол между направлением скорости частицы и вектором поля. Направления силы Лоренца, векторов скорости и магнитной индукции связаны между собой правилом левой руки. Если левую руку расположить так, что в нее входит , четыре вытянутых пальца направить по то отогнутый на 90

o большой палец укажет направление силы, с которой магнитное поле действует на положительно заряженную частицу.

Для однородного изотропного магнетика, заполняющего пространство, вектор магнитной в веществе () и вектор индукции в вакууме(, при одинаковых условиях, связаны формулой:

   

где – относительная магнитная проницаемость вещества.

Суперпозиция магнитных полей

Для магнитного поля справедлив принцип суперпозиции: если присутствует магнитных, то индукция результирующего поля равна векторной сумме отдельных индукций:

   

Примеры решения задач

Магнитные поля и индукция магнитного поля :: SYL.ru

Магнетизм знаком людям с давних времен. Первые письменные упоминания о нем датируются I веком до н. э., но ученые уверены, что знания об этом явлении появились гораздо раньше. Оно является глобальным и жизнь без него на нашей планете вообще невозможна. Поэтому исследователи во все времена старались изучить эту силу и обуздать ее для прогресса человечества.

Магнитное поле

Живя на Земле, мы, сами того не замечая, постоянно находимся под воздействием разнообразных сил. Магнитное поле исключением из этого правила также не является. Хотя, если быть точными, оно определяется как особенный вид материи, а не сила. Источником его возникновения являются заряженные электрические частицы или магниты. Если же брать пространственную характеристику этой материи, то это совокупность сил, способных воздействовать на тела, которые намагничены. Такая ее способность возникает благодаря движению разрядов между молекулами объекта. Главным условием появления такого поля есть постоянное движение электрических зарядов. Взаимодействие магнитного и электрического полей привело к тому, что существовать порознь они не могут. Это явление называется электромагнитным полем. Все элементы такой материи неразрывно связаны и действуют между собой так, что их свойства меняются.

Свойства магнетизма

Магнитное поле, как и любое другое физическое явление на Земле, имеет свои характеристики:

1. Источник возникновения – движущиеся электрические заряды.
2. Индукция магнитного поля – основная силовая его характеристика, которая существует в каждой отдельной его точке и является направленной.
3. Его влияние ограничивается магнитами, движущимися зарядами и проводниками тока.
4. Оно разделяется учеными на два типа: постоянное и переменное.
5. Человек без специальных приборов не может почувствовать воздействие магнетизма.
6. Это электродинамическое явление, ведь источник его происхождения – движущиеся частицы электрического тока. И только такие же частицы могут быть подвержены влиянию магнитного поля.
7. Траектория движения заряженных частиц может быть лишь перпендикулярной.

Явление индукции в магнетизме

Индукция магнитного поля определена своей направленностью, то есть она векторная и присуща любому полю, которое возникает в таких условиях. Направлена она всегда так же, как и стрелка, которая беспрепятственно вращается в компасе. Такого рода поле полностью характеризуется магнитной индукцией. Каждая точка является носителем направления и модуля этой силы. Если же они одинаковы для всех точек данного поля, то оно называется однородным. Индукция магнитного поля в физике обозначается вектором и большой латинской буквой В.

Формула магнитной индукции

Для того чтобы рассчитать эту силовую характеристику, нужно знать формулу ее расчета:

• B = F : I х l.

  В этой формуле:

  B означает индукцию магнитного поля;
  F – силу, которая воздействует на проводник со стороны поля;
  I – силу, с которой ток проходит по проводнику;
  l – собственно длина самого проводника.

Единицей измерения индукции, согласно Международной системе единиц, является тесла (Тл).

Линии, проходящие в магнитном поле

Магнитная индукция имеет вектор, то есть направленность. Если ее отобразить на бумаге, то она будет выражена линиями. Они совпадают с касательными, которые имеют такую же направленность, как и вектор индукции. Если магнитное поле однородное, то эти линии проходят параллельно друг другу. Когда же оно не однородное, направление этой силы будет разное во всех точках возникающего поля, а касательные к ним будут выглядеть как окружности.

Магнетизм соленоида

Магнитное поле может быть создано различными предметами, например, соленоидом. Соленоид, по своей сути, является электромагнитом, то есть катушкой индуктивности. Чтобы создать соленоид, требуется цилиндрическая поверхность (сердцевина) и изолированный проводник под напряжением (провод), который наматывают на сердцевину. Проходящий по проводу ток и создает этот вид материи вокруг соленоида. В этот момент он превращается в магнит. Если же выключить электричество, все особые свойства соленоида исчезают, а при обратном включении вновь возобновляются. Чем больше повода намотано вокруг сердцевины и чем больше подается тока, тем сильнее будет притягательность соленоида.

Магнитная индукция соленоида

Очень интересным для рассмотрения является соленоид, длина которого намного больше, чем его диаметр. Индукция магнитного поля соленоида в таком случае повсюду имеет одну направленность, которая параллельна сердечнику катушки, что означает параллельность каждой линии поля друг другу. Если проводник намотан равномерно, то одинакова не только направленность, — числовое значение также будет неизменным. Из-за того, что соленоид имеет очень простую структуру, его поле было признано эталоном поля.

Магнитосфера Земли

На нашей планете существуют миллионы магнитов разной величины и происхождения, но самым большим из них, к которому мы постоянно прикасаемся, является сама наша Земля. В первый раз о Земле как о подобном предмете было сказано в 1600 году. Этот год ознаменовался появлением книги английского физика У. Гильберта, в которой он тесно связывает Землю и эту материю. Кроме того, он говорит о том, что ось магнитного поля Земли и ось, по которой планета вращается, не являются идентичными, а наоборот, имеют лишь одну точку соприкосновения. Если сделать графический рисунок этого явления вокруг нашего голубого шара, то сразу становится видно, что оно очень похоже с обычным постоянным магнитом. Первые карты, показывающие нашу планету с такой стороны, были нарисованы Э. Галлеем в 1702 году. Каким же образом Земля регенерирует свои особые свойства? Все довольно просто. Как известно, в глубинах нашей планеты есть ядро. Это огромный шар раскаленного железа, которое является отличным проводником тока, то есть заряженное ядро и дает мощное потоки нчастиц. Благодаря этому явлению Земля окружена магнитосферой, которая защищает ее от отрицательных влияний из глубины космоса, и даже от родного нам Солнца. Индукция магнитного поля Земли равна 0,5 · 10^{— 4} Тл.

Изменения в магнитосфере Земли

После открытия магнитного поля Земли многие ученые-физики решили заняться этой проблемой. В 1635 году Г. Геллибранд выяснил, что этот слой земного шара находится в постоянных изменениях. Эти изменения делятся на два типа: постоянные и недолгосрочные. Постоянные возникают из-за залежей рудных полезных ископаемых, которые дают искажения из-за собственных сильных потоков энергии. Виновником же недолгосрочных изменений является так называемый «солнечный ветер». Это поток электрических частиц, которые извергаются с поверхности Солнца. Взаимодействие этих двух явлений приводит к «магнитным бурям». Если такая буря сильная, она даже может привести к потере радиосвязи или неопределенности стрелки компаса. Одним из красивейших последствий подобных бурь является северное сияние, так как полюса особенно сильно подвержены их влиянию.

Таким образом, магнетизм присутствует в жизни каждого человека. Он влияет на нас, хоть мы этого и не ощущаем. Благодаря этому явлению наша планета не подвергается отрицательным влияниям извне, и у нас есть возможность понаблюдать за разноцветными переливами Авроры.

Магнитная индукция — это… Что такое Магнитная индукция?

Магни́тная инду́кция  — векторная величина, являющаяся силовой характеристикой магнитного поля (его действия на заряженные частицы) в данной точке пространства. Определяет, с какой силой магнитное поле действует на заряд , движущийся со скоростью .

Более конкретно,  — это такой вектор, что сила Лоренца , действующая со стороны магнитного поля^[1] на заряд , движущийся со скоростью , равна

где косым крестом обозначено векторное произведение, α — угол между векторами скорости и магнитной индукции (направление вектора перпендикулярно им обоим и направлено по правилу буравчика).

Также магнитная индукция может быть определена^[2] как отношение максимального механического момента сил, действующих на рамку с током, помещенную в однородное поле, к произведению силы тока в рамке на её площадь.

Является основной фундаментальной характеристикой магнитного поля, аналогичной вектору напряжённости электрического поля.

В системе СГС магнитная индукция поля измеряется в гауссах (Гс), в системе СИ — в теслах (Тл)

1 Тл = 10⁴ Гс

Магнитометры, применяемые для измерения магнитной индукции, называют тесламетрами.

Основные уравнения

Поскольку вектор магнитной индукции является одной из основных фундаментальных физических величин в теории электромагнетизма, он входит в огромное множество уравнений, иногда непосредственно, иногда через связанную с ним напряженность магнитного поля. По сути, единственная область в классической теории электромагнетизма, где он отсутствует, это пожалуй разве только чистая электростатика.

• (Здесь формулы приведем в системе единиц СИ, в виде для вакуума^[3], где есть варианты для вакуума — для среды; запись в другом виде и подробности — см. по ссылкам).

В магнитостатике

В магнитостатическом пределе^[4] наиболее важными являются:

В общем случае

Основные уравнения (классической) электродинамики общего случая (то есть независимо от ограничений магнитостатики), в которых участвует вектор магнитной индукции :

• Формула силы Лоренца
  • Следствия из нее, такие как
    • Выражение для силы Ампера, действующей со стороны магнитного поля на ток (участок провода с током)

    • выражение для вращающего момента, действующего со стороны магнитного поля на магнитный диполь (виток с током, катушку или постоянный магнит):

    • выражение для потенциальной энергии магнитного диполя в магнитном поле:

    • а также следующих из них выражения для силы, действующей на магнитный диполь в неоднородном магнитном поле и т.д..
    • Выражение для силы, действующей со стороны магнитного поля на точечный магнитный заряд:
      • (это выражение, точно соответствующее обычному закону Кулона, широко используется для формальных вычислений, для которых ценна его простота, несмотря на то, что реальных магнитных зарядов в природе не обнаружено; также может прямо применяться к вычислению силы, действующей со стороны магнитного поля на полюс длинного тонкого магнита или соленоида).

• Выражение для плотности энергии магнитного поля
  • Оно в свою очередь входит (вместе с энергией электрического поля) и в выражение для энергии электромагнитного поля и в лагранжиан электромагнитного поля и в его действие. Последнее же с современной точки зрения является фундаментальной основой электродинамики (как классической, так в принципе и квантовой).

Примечания

1. ↑ Если учитывать и действие электрического поля E, то формула (полной) силы Лоренца принимает вид:
   При отсутствии электрического поля (или если член, описывающий его действие, специально вычесть из полной силы) имеем формулу, приведенную в основном тексте.
2. ↑ Это определение с современной точки зрения менее фундаментально, чем приведенное выше (и является просто его следствием), однако с точки зрения близости к одному из практических способов измерения магнитной индукции может быть полезным; также и с исторической точки зрения.
3. ↑ То есть в наиболее фундаментальном и простом для ознакомления виде.
4. ↑ То есть в частном случае постоянных токов и постоянных электрического и магнитного полей или — приближенно — если изменения настолько медленны, что ими можно пренебречь.
5. ↑ Являющаяся частным магнитостатическим случаем закона Ампера — Максвелла (см. в стаье далее).

См. также

Магнитная индукция в вакууме | HomeElectronics

Всем доброго времени суток. В прошлой статье я рассказал о магнитном поле и немного остановился на его параметрах. Данная статья продолжает тему магнитного поля и посвящена такому параметру как магнитная индукция. Для упрощения темы я буду рассказывать о магнитном поле в вакууме, так как различные вещества имеют разные магнитные свойства, и как следствие необходимо учитывать их свойства.

Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.

Закон Био – Савара – Лапласа

В результате исследования магнитных полей создаваемых электрическим током, исследователи пришли к таким выводам:

• магнитная индукция, создаваемая электрическим током пропорциональна силе тока;
• магнитная индукция имеет зависимость от формы и размеров проводника, по которому протекает электрический ток;
• магнитная индукция в любой точке магнитного поля зависит от расположения данной точки по отношению к проводнику с током.

Французские учёные Био и Савар, которые пришли к таким выводам обратились к великому математику П. Лапласу для обобщения и вывода основного закона магнитной индукции. Он высказал гипотезу, что индукция в любой точке магнитного поля, создаваемое проводником с током можно представить в виде суммы магнитных индукций элементарных магнитных полей, которые создаются элементарным участком проводника с током. Данная гипотеза и стала законом магнитной индукции, называемого законом Био – Савара – Лапласа. Для рассмотрения данного закона изобразим проводник с током и создаваемую им магнитную индукцию

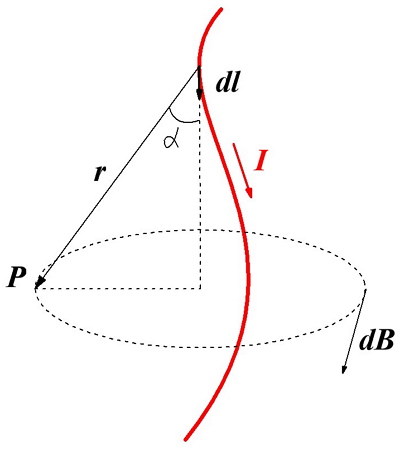
Магнитная индукция dB, создаваемая элементарным участком проводника dl.

Тогда магнитная индукция dB элементарного магнитного поля, которое создается участком проводника dl, с током I в произвольной точке Р будет определяться следующим выражением

где I – сила тока, протекающая по проводнику,

r – радиус-вектор, проведённый от элемента проводника к точке магнитного поля,

dl – минимальный элемент проводника, который создает индукцию dB,

k – коэффициент пропорциональности, зависящий от системы отсчёта, в СИ k = μ₀/(4π)

Так как [dl r] является векторным произведением, тогда итоговое выражение для элементарной магнитной индукции будет выглядеть следующим образом

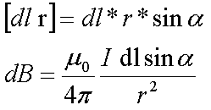
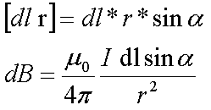
Таким образом, данное выражение позволяет найти магнитную индукцию магнитного поля, которое создается проводником с током произвольной формы и размеров при помощи интегрирования правой части выражения

где символ l обозначает, что интегрирование происходит по всей длине проводника.

Магнитная индукция прямолинейного проводника

Как известно простейшее магнитное поле создает прямолинейный проводник, по которому протекает электрический ток. Как я уже говорил в предыдущей статье, силовые линии данного магнитного поля представляют собой концентрические окружности расположенные вокруг проводника.

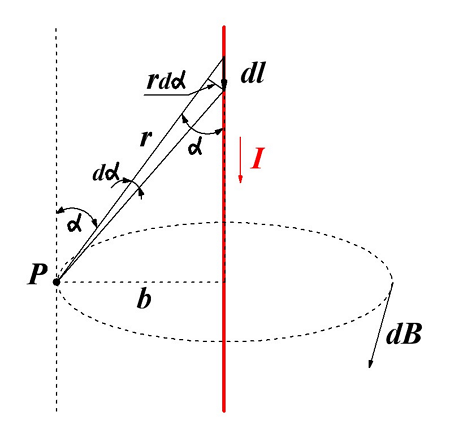
Магнитная индукция магнитного поля создаваемого прямолинейным проводником с током.

Для определения магнитной индукции В прямого провода в точке Р введем некоторые обозначения. Так как точка Р находится на расстоянии b от провода, то расстояние от любой точки провода до точки Р определяется как r = b/sinα. Тогда наименьшую длину проводника dl можно вычислить из следующего выражения

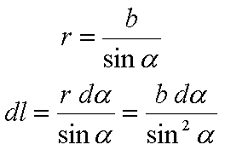
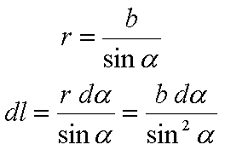
В итоге закон Био – Савара – Лапласа для прямолинейного провода бесконечной длины будет иметь вид

где I – ток, протекающий по проводу,

b – расстояние от центра провода до точки, в которой рассчитывается магнитная индукция.

Теперь просто проинтегрируем получившееся выражение по dα в пределах от 0 до π.

Таким образом, итоговое выражение для магнитной индукции прямолинейного провода бесконечной длины будет иметь вид

где μ₀  – магнитная постоянная, μ₀ = 4π•10^-7 Гн/м,

I – ток, протекающий по проводу,

b – расстояние от центра проводника до точки, в которой измеряется индукция.

Магнитная индукция кольца

Индукция прямого провода имеет небольшое значение и уменьшается при удалении от проводника, поэтому в практических устройствах практически не применяется. Наиболее широко используются магнитные поля созданные проводом, намотанным на какой либо каркас. Поэтому такие поля называются магнитными полями кругового тока. Простейшим таким магнитным поле обладает электрический ток, протекающий по проводнику, который имеет форму окружности радиуса R.

В данном случае практический интерес представляет два случая: магнитное поле в центре окружности и магнитное поле в точке Р, которое лежит на оси окружности. Рассмотрим первый случай.

Магнитная индукция в центре кругового тока.

В данном случае каждый элемент тока dl создаёт в центре окружности элементарную магнитную индукцию dB, которая перпендикулярна к плоскости контура, тогда закон Био-Савара-Лапласа будет иметь вид

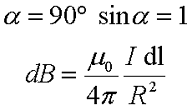
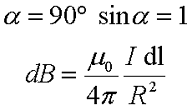
Остается только проинтегрировать полученное выражение по всей длине окружности

где μ₀  – магнитная постоянная, μ₀ = 4π•10^-7 Гн/м,

I – сила тока в проводнике,

R – радиус окружности, в которое свернут проводник.

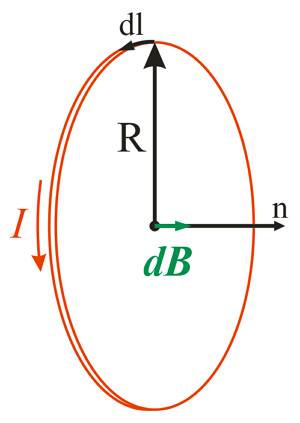
Рассмотрим второй случай, когда точка, в которой вычисляется магнитная индукция, лежит на прямой х, которая перпендикулярна плоскости ограниченной круговым током.

Магнитная индукция в точке, лежащей на оси окружности.

В данном случае индукция в точке Р будет представлять собой сумму элементарных индукций dB_X, которые в свою очередь представляет собой проекцию на ось х элементарной индукции dB

Применив закон Био-Савара-Лапласа вычислим величину магнитной индукции

Теперь проинтегрируем данное выражение по всей длине окружности

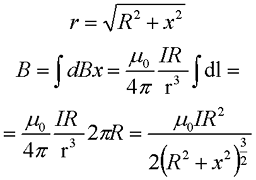
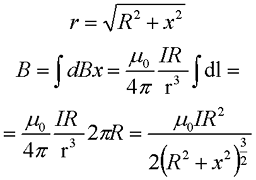
где μ₀ – магнитная постоянная, μ₀ = 4π•10^-7 Гн/м,

I – сила тока в проводнике,

R – радиус окружности, в которое свернут проводник,

х – расстояние от точки, в которой вычисляется магнитная индукция, до центра окружности.

Как видно из формулы при х = 0, получившееся выражение переходит в формулу для магнитной индукции в центре кругового тока.

Циркуляция вектора магнитной индукции

Для расчёта магнитной индукции простых магнитных полей достаточно закона Био-Савара-Лапласа. Однако при более сложных магнитных полях, например, магнитное поле соленоида или тороида, количество расчётов и громоздкость формул значительно увеличится. Для упрощения расчётов вводится понятие циркуляции вектора магнитной индукции.

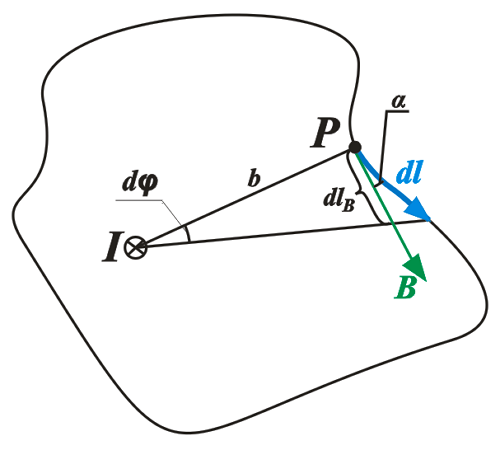
Циркуляция вектора магнитной индукции по произвольному контуру.

Представим некоторый контур l, который перпендикулярный току I. В любой точке Р данного контура, магнитная индукция В направлена по касательной к данному контуру. Тогда произведение векторов dl и В описывается следующим выражением

Так как угол dφ достаточно мал, то векторов dl_В определяется, как длина дуги

Таким образом, зная магнитную индукцию прямолинейного проводника в данной точке, можно вывести выражение для циркуляции вектора магнитной индукции

Теперь остаётся проинтегрировать получившееся выражение по всей длине контура

В нашем случае вектор магнитной индукции циркулирует вокруг одного тока, в случае же нескольких токов выражение циркуляции магнитной индукции переходит в закон полного тока, который гласит:

Циркуляция вектора магнитной индукции по замкнутому контуру пропорциональна алгебраической сумме токов, которые охватывает данный контур.

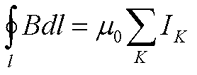
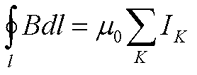
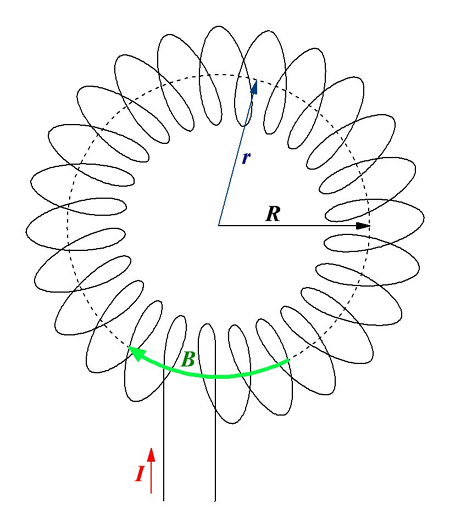
Магнитное поле соленоида и тороида

С помощью закона полного тока и циркуляции вектора магнитной индукции достаточно легко определить магнитную индукцию таких сложных магнитных полей как у соленоида и тороида.

Соленоидом называется цилиндрическая катушка, которая состоит из множества витков проводника, намотанных виток к витку на цилиндрический каркас. Магнитное поле соленоида фактически состоит из множества магнитных полей кругового тока с общей осью, перпендикулярной к плоскости каждого кругового тока.

Магнитная индукция соленоида.

Воспользуемся циркуляцией вектора магнитной индукции и представим циркуляцию по прямоугольному контуру 1-2-3-4. Тогда циркуляция вектора магнитной индукции для данного контура будет иметь вид

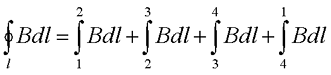
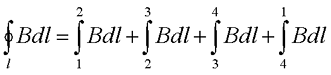
Так как на участках 2-3 и 4-1 вектор магнитной индукции перпендикулярен к контуру, то циркуляция равна нулю. На участке 3-4, который значительно удалён от соленоида, то его так же можно не учитывать. Тогда с учётом закона полного тока магнитная индукция в соленоиде достаточно большой длины будет иметь вид

где n – число витков проводника соленоида, которое приходится на единицу длины,

I – ток, протекающий по соленоиду.

Тороид образуется путём намотки проводника на кольцевой каркас. Данная конструкция эквивалентна системе из множества одинаковых круговых токов, центры которых расположены на окружности.