Импеданс контура — Энциклопедия по машиностроению XXL
Как известно, импеданс контура при питании гар ионическим напряжением с частотой, равной собственной частоте контура /о, чисто активен и равен сопротивлению потерь в контуре / . Если J является функции расстояния от катушки до некоторого поглотителя излучаемой ею энергии и можно записать, что [c.206]Указание Следует определить импеданс контура. [c.627]
Используя формулу (111.68) вместо более общей формулы (111.67) для импеданса контура, содержащего образец с ядерными спинами, мы неявно предположили, что частота Шс = контура равна частоте ш [c.96]
Используя формулу (III.68) вместо более общей формулы (III.67) для импеданса контура, содержащего образец с ядерными спинами, мы неявно предположили, что частота сос = ( С) 2 контура равна частоте (о колебаний, т. е. oq . Если сос oq , то частота колебаний со не будет равна со о, и будет иметь место явление, известное под названием затягивания . Положим в (III.67)
Технологическим ЭИ-процессам свойственен глубоко осциллирующий режим разряда емкостного накопителя в разрядном контуре, содержащем искровой канал в твердом диэлектрике как единственную полезную нагрузку. В такой ситуации разрядный ток ограничивается в основном внутренним импедансом генератора, а электрическое активное сопротивление R(t) искрового канала является базовой величиной для отыскания других электрических характеристик канала энергосодержания, внутренней энергии и в конечном итоге с учетом механизма динамического нагружения среды и разрушения — для построения расчетных схем всего процесса ЭИ-технологии.
Блок-схема типичного ВЧ-С., работающего на фнк-сиров. частоте радиочастотного диапазона 10—400 МГц, приведена на рис. 2. С кольцом С. связана катушка резонансного колебат. контура кС , возбуждаемого генератором тока ВЧ, Резонансный контур согласует низкий импеданс С, с высоким входным сопротивлением усилителя ВЧ. В зависимости от параметра [c.540]
Пример. Функции цепи (импеданс) последовательного резонансного контура, приведенного на рис. 2.12, а, имеют вид [c.86]
Существует два типа корректирующих контуров параллельный и последовательный. В первом типе осуществляется шунтирование импеданса нагрузки цепочкой, состоящей из комбинации индуктивности, емкости и сопротивления. Во втором совершают последовательное подключение корректирующей цепочки.
Параллельный корректирующий контур шунтирует импеданс нагрузки (см. рис. П1.5.2, а). Выходной ток, протекающий через импеданс Zg, до подключения корректирующего контура равен [c.82]
Действие корректирующего параллельного контура на коэффициент передачи определяется Zчастотная характеристика коэффициента передачи параллельным контуром не корректируется. Лишь при условии, когда и Z коэффициент передачи опреде- [c.83]
Вибрации частотой выше 500 гц эффективно подавляются системой амортизации. Так как импеданс фундамента в этом случае велик по сравнению с остальными сопротивлениями цепи, то конечный контур в расчетной схеме рис. 11-4, б можно считать разомкнутым. Расчетная схема приобретает вид, показанный на рис. 11-5, а.
Найдем теперь импеданс Z (ш) С-контура, выразив его через и С. Для случая резонансной частоты = = l/(L импеданс Z (со) дается выражением [c.479]
Если параллельно соединить два контура с одной и той же резонансной частотой, но с разными Q и разными импедансами Z ( oq), то результирующий импеданс запишется в виде
При измерении импеданса по изменению амплитуды датчиком является стержень, совершающий продольные колебания (рис.6.10). Если стержень контактирует с участком жестко склеенных слоев, то вся конструкция колеблется как единое целое. При этом сила реакции Fp будет значительной. Если стержень расположен над дефектной зоной, то этот участок будет колебаться как зажатый по контуру диск, сила реакции F резко уменьшается. Этим методом [c.289]
Таким образом, в безъемкостных контурах импеданс всегда возрастает при наличии . [c.483]
На настроенном в резонанс контуре, содержащем катушку с образцом и питающемся от генератора постоянного тока, будет возникать напряжение, пропорциональное его параллельному импедансу, равному
Дифракция на выпуклом контуре с плавно изменяющимися радиусом кривизны и импедансом, сб. Проблемы матем. физики , вып. 2, Изд-во ЛГУ, 1967. [c.451]
Низкие значения импеданса, т.е. большие емкости, малые индуктивности и небольшие сопротивления определяются при помощи подсоединения неизвестного элемента, например конденсатора Сх, последовательно с переменным конденсатором и катушкой индуктивности (Рис. 14.27а). Сначала неизвестный конденсатор закорачивается и контур настраивается на резонанс, чтобы получить добротность Q. Если величина переменного конденсатора при этом будет равна значению С], а резонансная частота контура — (Оо, то добротность контура можно определить как
Принимая, что воздействующая сила имеет синусоидальный характер, следует разработать схему эквивалентного контура, включая учет нагрузки в виде водной массы и механического силового механизма. Рассчитать и графически представить вещественную и мнимую части общего импеданса в функции частоты. [c.56]
На рис. 77 приведен график этой величины (кривая 3), из которого следует, что характер импеданса чисто реактивный и имеется бесконечная последовательность резонансов и антирезонансов внутреннего объема среды. При малых значениях kr , импеданс имеет упругий характер. Однако этот характер будет сохраняться до тех пор, пока значение диа.метра 2г не станет близким к 0,7Х. При этом цилиндрическая волна, излучаемая каждым элементарным участком трубы, достигает диаметрально противоположного участка трубы, имея уже фазу, отличающуюся иа л от фазы волны, излучаемой в этот момент противоположным участком. В результате суммарное давление на внутренней поверхности г = г становится равным нулю и как следствие становится равным нулю значение Z. Это явление можно интерпретировать как резонанс давлений (или последовательный резонанс). После резонанса величина Z меняет знак и имеет уже характер массы. Он сохраняется до тех пор, пока значение 2г не станет близким к значению X. При этом давление на внутренней поверхности г = г резко повышается, а величина Z -> оо, т. е. наступает антирезонанс (или параллельный резонанс). Далее картина повторяется — резонансы чередуются с антирезонансами. Следует заметить, что этот процесс наглядно иллюстрирует известную теорему Форстера [145], утверждающую, что механический контур любой сложности характеризуется последовательным чередованием резонансных и антирезонансных явлений. При этом, следуя Форстеру, точку kr = О можно трактовать как антирезонанс Z.
Решение. Возможны различные способы внешнего воздействия на колебательную систему. В связи с этим различают последовательный и параллельный механические контуры. В последовательном контуре сила возбуждает массу, а в параллельном сила приложена к пружине. Электрические аналоги и изображение этих систем посредством механических символов приведены на рисунках в и б. Для нахождения полного механического сопротивления этих систем используем электромеханические аналогии. Механический импеданс Z последовательного контура определяется выражением
Однако при (О = (Од в импедансе контура может сохраняться реактивная составляющая за счет импеданса Zp. Для дальнейшей оптимизации режима выбирают частоту о, соответствующую антирезонансу колебаний свободной пьезопластины о = сОа. На этой частоте практически все реактивные импедансы исчезают и импеданс контура генератора Z- = Ra Rp становится чисто активной величиной.
Определим, как зависят от частоты активное, реактивное и полное сопротивления контура. В небольшом диапазоне частот вблизи резонанса полное сопротивление последовательного контура приблизительно равно (рис. 1.1, б), тогда как реактивное сопротивление изменяется линейно, имея емкостный характер ниже резонанса и индуктивный характер выше резонанса, проходярезонансной частоте. При повышении частоты, начиная от резонансной, ток уменьшается и отстает по фазе ог приложенного напряжения, т. е. импеданс контура носит индуктивный характер и. Ч1онотонно возрастает при удалении от резонанса. При понижении частоты от резонансной ток тоже уменьшается, но импеданс контура имеет емкостный характер, возрастая при удалении от резонанса. Так, при токе 0,707 от резонансного фаза его опережает на 45° фазу тока при резонансе. Это явление можно использовать при построении высокочастотных фазовращателей.
Генератор может быть модулирован по любой из обычных схем. Необходимо отметить, что одноламповые генераторы при управлении посредством сетки дают наиболее удовлетворительные результаты. В этом случае на генерацию импульсов, как правило, требуется меньшая мощность, чем в других системах. Кроме того, в таком генераторе импеданс контура, на который подается спусковой сигнал, легче поддерживать на достаточно высоком уровне, предотвращая тем самым искажение формы управляющего напряжения. Импульсы генераторов с малой амплитудой сигналов могут быть легко усилены. Такие схемы отличаются большей устойчивостью работы и большей выходной мощностью, однако они требуют больше деталей и занимают больше места, чем одноламповый генератор.
Рассмотрим работу преобразователя на простом примере включения пьезопластины в электрический контур генератора (рис. 1.38, й). Считая пластину бесконечно протяженной в направлении, перпендикулярном х, тем самым не будем учитывать ее колебаний в поперечном направлении (одномерное приближение). Поверхности пластины нагружены средами с входными акустическими импедансами в направлении объекта контроля и Zft в противоположном направлении (там располагают демпфер). Здесь под входным импедансом понимается выражение, учитывающее активное и реактивное сопротивления границы колебаниям пьезопластины по толщине. Формулы для входного импеданса приведены в подразд. 1.4. Они учитывают наличие промежуточных слоев между пластиной и протяженной средой, удовлетворяющей условию (1.57). Такой средой являются расположенный с одной стороны пьезопластины демпфер, а с другой — изделие или акустическая задержка. [c.63]
Рассмотрим работу пьезопластины, нагруженной на демпфер и протяженную среду в реальных условиях. Пластину подключают к генератору с помощью электрического колебательного контура. На рис. 1.38, г показано подключение с использованием последовательного колебательного контура, в который входит сама пьезопластина. Электрические импедансы = Ra — jfaLa, Zh = l/(—/(o ft), где Сь — емкость соединительного кабеля и монтажа. Для упрощения анализа значением пренебрежем, поэтому оо. Общий импеданс цепи генератора [c.65]
В работе [1] приемная и излучающая катушки рассматривались как независимые устройства. Однако в практике ЭМА возбуждения и приема ультразвука прием часто л елателько производить датчиком с одной и той же высокочастотной катушкой, что и возбуждение, потому что он возбуждает и принимает УЗК волны одной поляризации, что очень важно при работе со сдвиговыми волнами [2]. Кроме того, если для возбуждения ультразвука в качестве индуктивного элемента (или части его) контура ударного возбуждения применяется высО Кочастотная катушка, то контур ударного возбуждения Я)Вляется самонастраиваюш,ейся системой относительно резонансной частоты в зависимости от зазора, так как изменяется вносимый в контур импеданс [3, 4]. Следовательно, частота возбуждения ультразвука при ЭМА способе возбуждения есть функция зазора, что необходимо учитывать при приеме ультразвуковых колебаний, т. е. желательно возбуждение и прием ультразвуковых колебаний осуществлять датчиком с одной катушкой. [c.124]
Принято считать, что реактанс произвольного двухполюсника (мнимая часть его импеданса Z=ii4-iX) имеет индуктивный характер, если он положителен [Х>0, при ехр (1а) )-онисании временной зависимости величин]. Именно этот признак, а не пропорциональность X частоте диапазонах частот. Так, колсбат. контур, составленный из параллельно соединённых катушек самоиндукции (с иидуктивностг ю L) и конденсатора (с ёмкостью С), на частотах ниже резонансной — L ведёт себя как И. с., а нри — как ёмкостное сопроти ле- [c.141]
Это импеданс колебательного СЛ-контура, высоко-добротного при условии LI R > 1. На резонансной (томсоновской) частоте о = (L ) Vs импеданс Z минимален по модулю. Метод комплексных амплитуд порождает метод векторных (круговых) диаграмм, основанный на графич. построении напряжений и токов как векторов на комплексных плоскостях, что придаёт наглядность решениям мн, задач эл.-техники. [c.562]
При Р, в электрич. цепях реактивная часть комплексного импеданса обращается в нуль. При атом в после-доват. цепи падения напряжения на катушке индуктивности и на конденсаторе имеют амплитуду QEg. Однако они складываются в противофазе и взаимно компенсируют друг Друга. В параллельной цепи (рис. 1, б) при Р. происходит взаимная компенсация токов в ёмкостной и индуктивной ветвях. В отличие от последоват. Р., при к-ром вееш. силовое воздействие осуществляется источником напряжения, в параллельном контуре резонансные явления реализуются только в том случае, когда внеш. воздействие задаётся источником тока. Соответственно Р в последоват. контуре называют Р. напряжений, а в параллельном контуре — Р. токов. Если в параллельный контур вместо генератора тока включить генератор напряжения, то на резонансной частоте будут выполняться условия не максимума, а минимума тока, поскольку вследствие компенсации токов в ветвях, содержащих реактивные элементы, проводимость цепи оказывается минимальной (явление антирезонанса). [c.309]
Усиление и регистрация сигнала С. производятся электронными устройствами, находящимися при комнатной темп-ре. Для ослабления влияния НЧ-шумов вида 1// (см. Флуктуации электрические) используется модуляц. метод обработки сигнала С. в отд. катушку модуляции ( да на рис. 1) вводится перем. ток частотой 100—200 кГц, создающий через кольцо С. поток с амплитудой Фо/4. Перем, напряжение на С. усиливается, синхронно детектируется и фильтруется. Согласование низкого импеданса С. с высоким импедансом усилителя осуществляется согласующим устройством типа последоват. контура или резонансного трансформатора. Для измерений в большом диапазоне Д ф,. > ф( используется глубокая отрицаг. обратная связь по магн. потоку. Напряжение через сопротивление обратной связи Я с подаётся в катушку модуляции. В результате измеряемый поток компенсируется, а напряжение на резисторе Лдс служит выходным сигналом прибора, линейно связанным с измеряемым потоком в диапазоне 100—1000 Ф . [c.540]
Из (111.5.2) и (111.5.3) следует, что при последовательном соединении корректирующий импеданс влияет на характеристику коэффициента передачи тем больше, чем больше импеданс к6рректируюш,его контура по сравнению с суммой входного импеданса и импеданса нагрузки. При Zg Zi + Zg характеристика коэффициента передачи по току приближается к характеристике комплексной проводимости корректируюш,его контура. В случае параллельного подсоединения корректируюш.его контура действие последнего на характеристику коэффициента передачи зависит от соотношения между комплексной проводимостью корректируюш его контура и суммой комплексных проводимостей входа и нагрузки. [c.83]
Режекторные фильтры. Если составить цепочки, в которых последовательный импеданс представляет собой L -контур, а шунтирующий состоит из комбинации индуктивности и емкости, то получаем электрический фильтр, способный задерживать некоторую полосу частот. Такие фильтры называют режекторными. На рис. II 1.6.5 представлены схемы режекторных электрических (а) и акустических (б) фильтров, составленных из однородных элементов. На рис. II 1.6.5, в показан общий вид акустического фильтра. В акустическом фильтре Саг И / аг зкустичвские гибкость мембраны и масса трубки, соединенные в узел Са, и Ша, — акустические гибкость объема и масса ответвления, соединенные в цепочку. [c.91]
ПРОХОДНАЯ ЕМКОСТЬ ЭЛЕКТРОННОЙ ЛАМПЫ — электрич. емкость, образованная анодом и управляющей сеткой электронной лампы. Величина П. о. э. л. зависит от типа лампы, ее конструкции, размеров электродов и колеблется в пределах от неск. тысячных долей пф (пентод) до неск. пф (триод). Малая величина П. е. а. л. у пентодов обусловлена наличием экранной сетки. Через П. е. э. л. осуществляется паразитная обратная связь аяоцяож цени с сеточной, характер к-рой зависит от импеданса анодной нагрузки. Так, напр., в резонансном усилителе высокой частоты II. е. э. л. приводит либо к ограничению усиления, либо к самовозбуждению стунени, если резонансный контур в анодной цепи имеет высокую добротность. Для устранения влияния П. о. э л. иногда применяют нейтродинироеание. [c.230]
Ко второму классу относятся безэлектродные методы, в которых удельное сопротивление определяется путем измерения и анализа импеданса на переменном токе катушки индуктивности, обусловленного вихревыми токами в образце, помещенном в поле этой катушки. Метод такого типа может быть использован также для получения информации о коэффициенте Холла и магнитосопротивлении [196]. Однако на практике этим методом обычно определяют только удельное сопротивление путем анализа сдвига фаз. Примерами измерений в стационарном состоянии являются работа Есима и др. [267] и исследования жидкого селена Гобрехта и др. [ПО]. Ли и Лихтер [15] провели детальное обсуждение применений указанного метода для изучения металлических сплавов. Хайсти [116, 117] разработал нестационарный метод измерений, в котором образец падает сквозь катушку резонансного контура генератора радиочастотных колебаний. Этот метод требует получения калибровочной кривой генератора колебаний и специальной геометрии контейнера для образца, но он позволяет производить быстрые измерения и может быть использован для очень широкой области значений удельного сопротивления [118, 119]. Однако точность измерений этим методом ограничена 10—20 % [c.75]
ЛОЖКОЙ участок обшивки будет колебаться, как зажатьп по контуру диск, независимо от всей конструкции. Поскольку жёсткость обшивки меньше жёсткости всей конструкции, импеданс, а следовательно, п сила реакции на стержень резко уменьшаются. По изменению амплитуды (или фазы) силы реакции можно судить о наличии дефекта соединения. Чувствительность импедансного метода позволяет обеспечить обнаружение дефектов соединения диаметром около 5 —10 мм. [c.111]
Таким образом, ход частотной зависимости реактивной составляющей импеданса излучения цилиндра с незамкнутым кольцевым слоем определяется резонансными явлениями, имеющими место в своеобразном механическом контуре, образованном механическими параметрами слоя, присоединенной массой окружающей среды иа внешней поверхности слоя г = г , Фо 1 ф I я и присоединенной массой среды на открытом участке поверхности цилиндра г = Го, j Ф I С Фо- На основании изложенного выше анализа можно также объяснить причину резкого уменьше1шя величины R в области d , 0,5, При этой толщине слоя имеет место антирезонанс (параллельный резонанс) указанного выше механического контура и среднее значение звукового давления у поверхности цилиндра становится минимальным. В результате наблюдается парадоксальное явление — [c.64]
Coil32 — Параллельный колебательный контур
Параллельный колебательный контур в радиотехнике используется как основа частотно-избирательных цепей и встречается намного чаще последовательного. Реальные элементы контура обладают потерями и при анализе цепи используется реалистичная модель из идеальных сосредоточенных элементов в которой потери учитываются с помощью «виртуальных» последовательных активных сопротивлений RL и RC.
Собственная паразитная емкость катушки обычно не учитывается, т. к. она просто суммируется с контурной. Программа Coil32 рассчитывает потери в проводе катушке RL без учета потерь в каркасе, экране, сердечнике и во всех предметах, с которыми взаимодействует окружающая катушку электромагнитная волна. Однако, учитывается скин-эффект и эффект близости. Эти же потери учитывает параметр «конструктивная добротность катушки» — QL. Это не добротность всего контура, а добротность катушки, которая связана с ее сопротивлением потерь следующим соотношением:
 |
[1] |
Потери в контурном конденсаторе на порядок меньше и характеризуются добротностью конденсатора. Поскольку потери конденсатора сосредоточены в основном в диэлектрике, можно считать, что его добротность QC и сопротивление потерь RC связаны с параметром, учитывающем потери в диэлектрике tgδ, следующим образом:
 |
[2] |
При анализе цепи часто ее преобразуют в эквивалентную параллельную RLC-цепь. В этом случае, заменяя сопротивления проводимостями, мы упрощаем анализ и получаем формулы идентичные формулам последовательного контура. Многие радиолюбители полагают, что последовательные RL и RC просто преобразуются в параллельное R. Это не так:
Как видим активные сопротивления и реактивности при таком преобразовании «перепутались», поэтому для наглядности проведем анализ без использования проводимостей, прямо по исходной схеме. Входное сопротивление двухполюсника получается следующим:
Активная и реактивная (мнимая) составляющие:

При резонансе токи в реактивных элементах (IL, IC) в Q раз больше общего тока цепи (I), поэтому для параллельного контура явление носит название резонанса токов.
Резонансная частота параллельного колебательного контура — это частота, при которой реактивная составляющая входного сопротивления равна нулю, входное сопротивление чисто активно, и, соответственно, фазовый сдвиг между током и напряжением на входных зажимах цепи тоже равен нулю. Приравняв Xвх к нулю и проведя соответствующие преобразования получим следующую формулу для резонансной частоты параллельного колебательного контура:
 |
[3] |
Один из важнейших параметров контура — его характеристическое сопротивление:
Формулу резонансной частоты можно представить иначе:
 |
[5] |
ω0 — резонансная частота последовательного колебательного контура.
Как видим резонансная частота параллельного колебательного контура равна резонансной частоте последовательного колебательного контура, составленного из тех же элементов, с добавкой поправочного коэффициента √[(L/C — RL^2)/(L/C — RC^2)]. На практике этот коэффициент всегда близок к единице и равен единице если RL=RC или RL=RC=0.
Пример:
Имеем контур с индуктивностью 3μГн и емкостью 42пФ, сопротивление потерь катушки — RL=2 Ом, конденсатора — RC=0.1 Ом. По формуле Томпсона резонансная частота контура равна 14.178649 МГц, точно вычисляем по формуле [1] — 14.178253 МГц. Как видим, активные сопротивления потерь вносят в идеальный контур дополнительную реактивность и уводят его частоту вниз, в данном случае почти на 400 Гц.
Это совсем небольшое отклонение нужно иметь ввиду, но оно намного меньше отклонений, вносимых неучтенными паразитными емкостями. Поэтому при выполнении условий: RL<< ρ, RC<< ρ, что обычно бывает на практике, можно считать, что условия резонанса токов совпадают с условиями резонанса напряжений в последовательном контуре, составленном из тех же элементов L и C,
ω0 = 1/√LC или ƒ0 = 1/(2π√LC)
На этом «родственная схожесть» последовательного и параллельного контуров не заканчивается.
При выполнении тех же условий: RL<< ρ, RC<< ρ
где Zвх.посл = (RL + RC) + j(ωL — 1 ⁄ ωC) – входное сопротивление последовательного контура, составленного из тех же элементов.
Как видим, можно считать, что сопротивления потерь катушки и конденсатора суммируются, поэтому общую добротность контура Q можно определить следующим выражением:
 |
[6] |
На резонансной частоте ω0:
 |
[7] |
Поскольку реактивные сопротивления взаимно компенсируются, контур на резонансной частоте имеет чисто активное сопротивление равное Rэ (эквивалентное или эффективное сопротивление контура).
Из последней формулы следует, что:
 |
[8] |
Т.е. добротность контура равна отношению его характеристического сопротивления к сопротивлению потерь. Иначе говоря, на данной частоте более добротным будет контур с меньшей емкостью и большей индуктивностью. Как же тогда соотносится добротность контура с конструктивной добротностью катушки? Чтобы понять это, следует иметь ввиду, что характеристическое сопротивление контура численно равно модулю реактивного сопротивления индуктивности или емкости на резонансной частоте. Последние, как известно, в этом случае равны и отличаются лишь знаком. Если мы пренебрежем потерями в конденсаторе, тогда формула [8] сводится к формуле [1]. Ведь на резонансной частоте ρ = |XL|, а в сумме RΣ = RL + RC, последнее слагаемое мы не учитываем. Другими словами, если пренебречь потерями в конденсаторе, то добротность контура равна конструктивной добротности катушки. В итоге мы приходим к выводу, что формулы [1] и [8] в этом случае эквивалентны. Если же нам необходимо учесть потери в конденсаторе, то следует использовать формулу [6].
Необходимо отметить два важных момента:
- Coil32 рассчитывает конструктивную добротность для «голой катушки в вакууме». Наличие экрана увеличивает распределенную емкость и уменьшает индуктивность. Характеристическое сопротивление контура падает, добротность уменьшается. Кроме этого добавляются потери на вихревые токи в экране. Каркас катушки также снижает ее добротность и добротность контура соответственно.
- Добротность катушки растет с ростом частоты только на «низких» частотах, далеких от частоты собственного резонанса катушки. При приближении к собственному резонансу добротность достигает максимума на частотах 60-85% от Fsrf и затем плавно снижается. Это происходит от того, что на этих частотах начинает проявлятся зависимость индуктивности и собственной емкости катушки от частоты.
Амплитудно-частотная характеристика имеет такой же вид, как и резонансная кривая последовательного контура; ФЧХ представляет собой зеркальное отображение ФЧХ последовательного контура.
Важно понятие полоса пропускания контура Это частотный интервал в пределах которого импеданс Zвх не ниже 1 ⁄ √2 (или 0,707) от максимального на резонансной частоте. Справедлива следующая формула, которую можно использовать для измерения добротности:
В практике представляет интерес величина ослабления контуром нежелательных частот:
 |
[10] |
Для расстроек более трех полос пропускания формула упрощается:
где знак не учитывается.
В реальной схеме контур связан с источником колебаний и нагрузкой, которые вносят в него дополнительные потери, снижающие добротность. Эквивалентная добротность Q параллельного колебательного контура:
Q = Q0·Ri ⁄ (Rэ + Ri)
- Q0 — добротность ненагруженного контура
- Ri — входное сопротивление источника
- Rэ — эквивалентное сопротивление ненагруженного котура
Эту формулу можно использовать для учета влияния любых подключенных к контуру сопротивлений (например, нагрузки) на его добротность.
Для уменьшения влияния внешних цепей, а также для трансформации сопротивлений применяют частичное включение нагрузки в контур
Как видно из рисунка это можно сделать различными способами, отводом от катушки, с помощью катушки связи, емкстным делителем. Тогда выходное сопротивление контура:
Rвых = p2Rэ
где p – коэффициент связи. Для емкостного делителя:
p = C1 ⁄ (C1 + C2)
Для индуктивной связи:
p = M ⁄ L
где M — полная взаимоиндуктивность между Lc и L (это относится как к случаю с отводом катушки так и к случаю с катушкой связи). Следует отметить, что коэффициент связи не равен отношению числа витков, как в трансформаторе, поскольку каждый виток катушки Lc пересекается не всеми силовыми линиями катушки контура вследствие рассеяния магнитного поля.
При подключении внешней нагрузки к контуру с помощью частичного включения, результирующая добротность определяется:
Q = Q0·Ru ⁄ (Rэ + Ru)
Ru = p2Ri (Ri – внешняя нагрузка)
Следует отметить, что для максимального коэффициента передачи электромагнитной энергии, выходное сопротивление контура должно быть равно сопротивлению нагрузки. Все вышесказанное справедливо и в случае согласования контура с источником сигнала.
Колебательный контур. LCR, LC — контур. Катушка индуктивности, конденсатор Формула Томсона Энергия
Колебательный контур – электрическая цепь, состоящая из последовательно соединённых конденсатора с ёмкостью
, катушки с индуктивностью и электрического сопротивления .Идеальный колебательный контур — цепь, состоящая только из катушки индуктивности (не имеющей собственного сопротивления) и конденсатора (
-контур). Тогда в такой системе поддерживаются незатухающие электромагнитные колебания силы тока в цепи, напряжения на конденсаторе и заряда конденсатора. Давайте разберём контур и подумаем, откуда возникают колебания. Пусть изначально заряженный конденсатор помещён в описываемую нами цепь.Рис. 1. Колебательный контур
В начальный момент времени весь заряд сосредоточен на конденсаторе, на катушке тока нет (рис. 1.1). Т.к. на обкладках конденсатора внешнего поля тоже нет, то электроны с обкладок начинают «уходить» в цепь (заряд на конденсаторе начинает уменьшаться). При этом (за счёт освобождённых электронов) возрастает ток в цепи. Направление тока, в данном случае, от плюса к минусу (впрочем, как и всегда), и конденсатор представляет собой источник переменного тока для данной системы. Однако при росте тока на катушке, вследствие явления электромагнитной индукции, возникает обратный индукционный ток (
). Направление индукционного тока, согласно правилу Ленца, должно нивелировать (уменьшать) рост основного тока. Когда заряд конденсатора станет равным нулю (весь заряд стечёт), сила индукционного тока в катушке станет максимальной (рис. 1.2).Однако текущий заряд в цепи пропасть не может (закон сохранения заряда), тогда этот заряд, ушедший с одной обкладки через цепь, оказался на другой обкладке. Таким образом, происходит перезарядка конденсатора в обратную сторону (рис. 1.3). Индукционный ток на катушке уменьшается до нуля, т.к. изменение магнитного потока также стремится к нулю.
При полной зарядке конденсатора электроны начинают двигаться в обратную сторону, т.е. происходит разрядка конденсатора в обратную сторону и возникает ток, доходящий до своего максимума при полной разрядке конденсатора (рис. 1.4).
Дальнейшая обратная зарядка конденсатора приводит в систему в положение на рисунке 1.1. Такое поведение системы повторяется сколь угодно долго. Таким образом, мы получаем колебание различных параметров системы: тока в катушке, заряд на конденсаторе, напряжение на конденсаторе. В случае идеальности контура и проводов (отсутствие собственного сопротивления), эти колебания — гармонические.
Для математического описания этих параметров этой системы (в первую очередь, периода электромагнитных колебаний) вводится рассчитанная до нас формула Томсона:
(1)Неидеальным контуром является всё тот же идеальный контур, который мы рассмотрели, с одним небольшим включением: с наличием сопротивления
(-контур). Данное сопротивление может быть как сопротивлением катушки (она не идеальна), так и сопротивлением проводящих проводов. Общая логика возникновения колебаний в неидеальном контуре аналогична той, что и в идеальном. Отличие только в самих колебаниях. В случае наличия сопротивления, часть энергии будет рассеиваться в окружающую среду — сопротивление будет нагреваться, тогда энергия колебательного контура будет уменьшаться и сами колебания станут затухающими.Для работы с контурами в школе используется только общая энергетическая логика. В данном случае, считаем, что полная энергия системы в начале сосредоточена на конденсаторе и/или катушке, и описывается:
(2) (3)
Для идеального контура полная энергия системы остаётся постоянной:
(4)- где
- — полная энергия колебательной системы.
Для неидеального контура часть начальной энергии переходит в тепло, что можно описать законом Джоуля-Ленца. Тогда энергетические превращения в таком контуре можно описать:
(5)Вывод: работа с контурами достаточно сложна. Чаще всего это работа со схемами, в которых присутствуют ключи. Энергетически рассмотреть переход из начального состояния в конечное практически невозможно, тогда стоит работать с начальным и конечным положением системы. Определяем вид контура (идеальный/неидеальный) и рассмотреть энергию системы в обоих случаях. Далее, используя (4) или (5), получаем уравнение, которое можно решать.
Поделиться ссылкой:
Понравилось это:
Нравится Загрузка…
импеданс контура — это… Что такое импеданс контура?
- импеданс контура
Engineering: circuit impedance, loop impedance
Универсальный русско-английский словарь. Академик.ру. 2011.
- импеданс катушки
- импеданс короткого замыкания
Смотреть что такое «импеданс контура» в других словарях:
импеданс разомкнутого контура — pilnutinė atvirosios grandinės varža statusas T sritis radioelektronika atitikmenys: angl. open circuit impedance vok. Leerlaufimpedanz, f rus. импеданс разомкнутого контура, m; полное сопротивление разомкнутой цепи, n pranc. impédance en circuit … Radioelektronikos terminų žodynas
ЭЛЕКТРИЧЕСКИЕ ЦЕПИ — совокупности соединенных определенным образом элементов и устройств, образующих путь для прохождения электрического тока. Теория цепей раздел теоретической электротехники, в котором рассматриваются математические методы вычисления электрических… … Энциклопедия Кольера
электрический — 3.45 электрический [электронный, программируемый электронный]; Е/Е/РЕ (electrical/electronic/ programmable electronic; Е/Е/РЕ) основанный на электрической и/или электронной, и/или программируемой электронной технологии. Источник … Словарь-справочник терминов нормативно-технической документации
Колебательный контур — Колебательный контур осциллятор, представляющий собой электрическую цепь, содержащую соединённые катушку индуктивности и конденсатор. В такой цепи могут возбуждаться колебания тока (и напряжения). Колебательный контур простейшая… … Википедия
Квантовый композитный резонатор Холла — (ККРХ) топологический объект с квантовыми реактивными параметрами ( и ), которые имеют фиксированную резонансную частоту ( ), обусловленную нечетным числом электронов которые двигаются в однородном магнитном поле ( ). ККРХ имеет… … Википедия
Закон электромагнитной индукции Фарадея — Классическая электродинамика … Википедия
ИНДУКТИВНОСТЬ — (от лат. inductio наведение, побуждение), величина, характеризующая магн. св ва электрич. цепи. Ток, текущий в проводящем контуре, создаёт в окружающем пр ве магн. поле, причём магнитный поток Ф, пронизывающий контур (сцепленный с ним), прямо… … Физическая энциклопедия
Электромеханический фильтр — ЭМФ советского производства, предназначенный для выделения нижней боковой полосы в аппаратуре радиосвязи с промежуточной частотой 500 кГц. Ширина полосы пропускания 3,1 кГц. Механическ … Википедия
ГОСТ Р МЭК 60204-1-2007: Безопасность машин. Электрооборудование машин и механизмов. Часть 1. Общие требования — Терминология ГОСТ Р МЭК 60204 1 2007: Безопасность машин. Электрооборудование машин и механизмов. Часть 1. Общие требования оригинал документа: TN систем питания Испытания по методу 1 в соответствии с 18.2.2 могут быть проведены для каждой цепи… … Словарь-справочник терминов нормативно-технической документации
ГОСТ Р МЭК 61557-1-2005: Сети электрические распределительные низковольтные напряжением до 1000 В переменного тока и 1500 В постоянного тока. Электробезопасность. Аппаратура для испытания, измерения или контроля средств защиты. Часть 1. Общие требования — Терминология ГОСТ Р МЭК 61557 1 2005: Сети электрические распределительные низковольтные напряжением до 1000 В переменного тока и 1500 В постоянного тока. Электробезопасность. Аппаратура для испытания, измерения или контроля средств защиты. Часть … Словарь-справочник терминов нормативно-технической документации
Самосогласованные гравитационные константы — полный комплект фундаментальных констант гравидинамики, которые являются самосогласованными и определяют различные физические величины (а также их размерность), и поэтому – результирующую форму Максвеллоподобных гравитационных уравнений).… … Википедия
Тема занятия 5: Колебательный контур.
5.1 Идеальный колебательный контур.
Колебательный контур называется идеальным, если он состоит из катушки и емкости и в нем нет сопротивления потерь.
Р ассмотрим
физические процессы в следующей цепи:
ассмотрим
физические процессы в следующей цепи:
1 Ключ стоит в положении 1. Конденсатор начинает заряжаться, от источника напряжения и в нем накапливается энергия электрического поля,
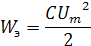
т.е.конденсатор становится источником электрической энергии.
2. Ключ в положении 2. Конденсатор начнет разряжаться. Электрическая энергия, запасенная в конденсаторе переходит в энергию магнитного поля катушки.
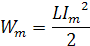
Ток в цепи достигает максимального значения(точка 1). Напряжение на обкладках конденсатора уменьшается до нуля.
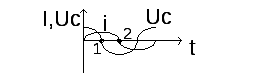
В период от точки 1 до точки 2 ток в контуре уменьшается до нуля, но как только он начинает уменьшатся , то уменьшается магнитное поле катушки и в катушке индуцируется ЭДС самоиндукции, который противодействует уменьшению тока, поэтому он уменьшается до нуля не скачкообразно, а плавно. Так как возникает ЭДС самоиндукции, то катушка становится источником энергии. От этой ЭДС конденсатор начинает заряжаться, но с обратной полярностью (напряжение конденсатора отрицательное) (в точке 2 конденсатор вновь заряжается).
Вывод: в цепи LC происходит непрерывное колебание энергии между электрическим и магнитным полями, поэтому такая цепь называется колебательным контуром.
Получившиеся колебания называются свободнымиилисобственными, поскольку они происходят без помощи постороннего источника электрической энергии, внесенной ранее в контур (в электрическое поле конденсатора). Так как емкость и индуктивность идеальны (нет сопротивления потерь) и энергия из цепи не уходит, амплитуда колебаний с течением времени не меняется и колебания будут незатухающими.
Определим угловую частоту свободных колебаний:
Используем равенство энергий электрического и магнитного полей

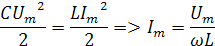


,где ώ угловая частота свободных колебаний.
[ ώ ]=1/с
f0=ώ/2π [Гц].
Период свободных колебаний Т0=1/f.
Частоту свободных колебаний называют частотой собственных колебаний контура.
Из выражения: ώ²LC=1получимώL=1/Cώ, следовательно, при токе в контуре с частотой свободных колебаний индуктивное сопротивление равно емкостному сопротивлению.


Характеристические сопротивления.
Индуктивное или емкостное сопротивление в колебательном контуре при частоте свободных колебаний называется характеристическим сопротивлением.
Характеристическое сопротивление вычисляется по формулам:
5.2 Реальный колебательный контур
Реальный колебательный контур обладает активным сопротивлением, поэтому при воздействии в контуре свободных колебаний энергия предварительно заряженного конденсатора постепенно тратится, преобразуясь в тепловую.
Свободные колебания в контуре являются затухающими, так как в каждый период энергия уменьшается и амплитуда колебаний в каждый период будет уменьшаться.

Рисунок — реальный колебательный контур.
Угловая частота свободных колебаний в реальном колебательном контуре :
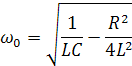
Если R=2… , то угловая частота равна нулю, следовательно свободные колебания в контуре не возникнут.
Таким образом колебательным контуромназывается электрическая цепь состоящая из индуктивности и емкости и обладающая малым активным сопротивлением, меньшим удвоенного характеристического сопротивления, что обеспечивает обмен энергией между индуктивностью и емкостью.
В реальном колебательном контуре свободные колебания затухают тем быстрее, чем больше активное сопротивление.
Для характеристики интенсивности затухания свободных колебаний используется понятие «затухание контура» — отношение активного сопротивления к характеристическому.

На практике используют величину, обратную затуханию – добротность контура.

Для получения незатухающих колебаний в реальном колебательном контуре необходимо в течение каждого периода колебаний пополнять электрическую энергию на активном сопротивлении контура в такт с частотой собственных колебаний. Это осуществляется с помощью генератора.
Если подключить колебательный контур к генератору переменного тока, частота которого отличается от частоты свободных колебаний контура, то в цепи протекает ток с частотой равной частоте напряжения генератора. Эти колебания называют вынужденным.
Если частота генератора отличается от собственной частоты контура, то такой колебательный контур является ненастроенным относительно частоты внешнего воздействия, если же частоты совпадают, то настроенным.
Задача: Определить индуктивность , угловую частоту контура, характеристическое сопротивление, если емкость колебательного контура 100 пФ, частота свободных колебаний 1,59 МГц.
Решение:
Тестовые задания:
Добротность колебательного контура определяется по формуле: |
|
Какие колебания называются свободными |
|
Тема занятия 8: РЕЗОНАНС НАПРЯЖЕНИЙ
Резонанс напряжений – явление возрастания напряжений на реактивных элементах, превышающих напряжение на зажимах цепи при максимальном токе в цепи, которое совпадает по фазе с входным напряжением.
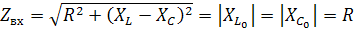
Условия возникновения резонанса:
Последовательное соединение LиCс генератором переменного тока;
Частота генератора должна быть равна частоте собственных колебаний контура , при этом характеристические сопротивления равны;
Сопротивление должно быть меньше, чем 2ρ, так как только в этом случае в цепи возникнут свободные колебания, поддерживаемые внешним источником.
Полное сопротивление цепи:
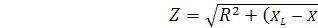 =R,
=R,
так как равны характеристические сопротивления. Следовательно, при резонансе цепь носит чисто активный характер, значит, входное напряжение, и ток в момент резонанса совпадают по фазе. Ток принимает максимальное значение.
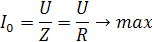
При максимальном значении тока напряжение на участках L и C будут большими и равными между собой.
Напряжение на зажимах цепи:
 .
.
Рассмотрим следующие соотношения:
 ,
следовательно
,
следовательно
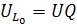
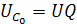 .
.
Q –добротность контура –при резонансе напряжения показывает, во сколько раз напряжение на реактивных элементах больше входного напряжения генератора, питающего цепь. При резонансе коэффициент передачи последовательного колебательного контура

резонанса.

Пример:
Если добротность равна 100, напряжение на зажимах 1В, то
Uc=Ul=QU=100В,
то есть напряжение на зажимах меньше напряжений на емкости и индуктивности. Это явление называется резонансом напряжений
При резонансе, коэффициент передачи равен добротности.
Построим векторную диаграмму напряжения
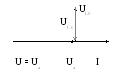
Напряжение на емкости равно напряжению на индуктивности, следовательно напряжение на сопротивлении равно напряжению на зажимах и совпадает по фазе с током.
Рассмотрим энергетический процесс в колебательном контуре:
В цепи имеется обмен энергии между электрическим полем конденсатора и магнитным полем катушки. К генератору энергия катушки не возвращается. От генератора в цепь поступает такое количество энергии, которое тратится на резисторе. Это необходимо для того, чтобы в контуре наблюдались незатухающие колебания. Мощность в цепи только активная.
Докажем это математически:
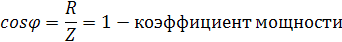
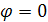
 ,
полная мощность цепи, которая равна
активной мощности.
,
полная мощность цепи, которая равна
активной мощности.
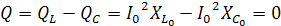 ,
реактивная мощность.
,
реактивная мощность.
8.1 Резонансная частота. Расстройка.
В цепи, содержащей реактивные элементы, произойдет резонанс, если цепь имеет резистивный характер:
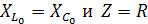
Lώ=l/ώC, следовательно
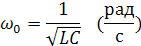
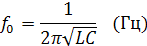 ,
угловая резонансная частота.
,
угловая резонансная частота.
Из формулы видно, что резонанс наступает, если частота питающего генератора равна собственным колебаниям контура.
При работе с колебательным контуром необходимо знать, совпадает ли частота генератора и частота собственных колебаний контура. Если частоты совпадают, то контур остается настроенным в резонанс, если не совпадает – то в контуреприсутствует расстройка.
Настроить колебательный контур в резонанс можно тремя способами:
1 Изменять частоту генератора , при значениях емкости и индуктивности const, то есть изменяя частоту генератора мы подстраиваем эту частоту под частоту колебательного контура
2 Изменять индуктивность катушки, при частоте питания и емкости const;
3 Изменять емкость конденсатора , при частоте питания и индуктивности const.
Во втором и третьем способе изменяя частоту собственных колебаний контура, подстраиваем ее под частоту генератора.
При ненастроенном контуре частота генератора и контура не равны, то есть присутствует расстройка.
Расстройка – отклонение частоты от резонансной частоты.
Существует три вида расстройки:
Абсолютная – разность между данной частотой и резонансной
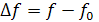

Обобщенная – отношение реактивного сопротивления к активному:
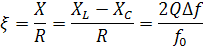
Относительная – отношение абсолютной расстройки к резонансной частоте:

При резонансе все расстройки равны нулю, если частота генератора меньше частоты контура, то расстройка считается отрицательной,
Если больше – положительной.
Таким образом добротность характеризует качество контура, а обобщенная расстройка- удаленность от резонансной частоты.
8.2 Построение зависимостейX, XL, XC отf.

Задачи:
Сопротивление контура 15 Ом, индуктивность 636 мкГн, Емкость 600 пФ, напряжение питающей сети 1,8 В. Найти собственную частоту контура, затухание контура, характеристическое сопротивление, ток, активную мощность, добротность, напряжение на зажимах контура.
Решение:
Напряжение на зажимах генератора 1 В, частота питающей сети 1 МГц, добротность 100, емкость 100 пФ. Найти: затухание, характеристическое сопротивление, активное сопротивление, индуктивность, частоту контура, ток, мощность, напряжения на емкости и индуктивности.
Решение:
Тестовые задания:
Отношение реактивного сопротивления к активному это : | А) Абсолютная расстройка; Б) Обобщенная расстройка; В) Относительная расстройка. |
Тема занятия 9 : Входные и передаточные АЧХ и ФЧХ последовательного колебательного контура.
9.1 Входные АЧХ и ФЧХ.
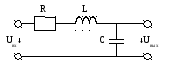
В последовательном колебательном контуре:
 ,
где
,
где
R – активное сопротивление;
X – реактивное сопротивление.
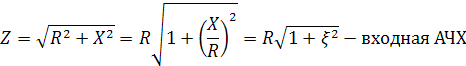
Учитывая, что
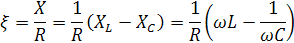 ,то
,то
ώ=0 ζ=-∞ Z=∞
ώ=ώ۪۪ ζ=0
Z=R
ζ=0
Z=R
ώ=∞ ζ=∞ Z=∞, следовательно
график имеет вид: 


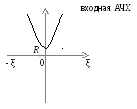





Из графика видно, что контур обладает наименьшим сопротивлением на резонансной частоте, при увеличении расстройки сопротивление увеличивается.
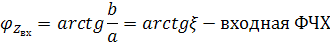

 ζ=0 φ=0 R
ζ=0 φ=0 R
ζ=1 φ=45° RL
ζ=-1 φ=-45° RC
ζ=∞ φ=90° L
ζ=-∞ φ=-90° C.
Построим график:


На участке ζ=[-1;1]
ФЧХ имеет линейный
характер. 
На участке ζ=[-∞;0] — цепь носит активно-емкостной характер;
На участке ζ=[0;∞]- цепь носит frnbdyj-индуктивный характер;
При ζ=0 — цепь носит активный характер;
Передаточные АЧХ и ФЧХ

передаточная характеристика АЧХ
 ζ=-∞
k=0
ζ=-∞
k=0
ζ=0 k=Q
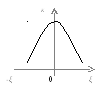 ζ=∞ k=0
ζ=∞ k=0
Построим график зависимости:









Разделим k∕kои получим передаточную
характеристику АЧХ в относительных
единицах, которая имеет вид:
Чтобы построить передаточную ФЧХ необходимо: построить входную ФЧХ, взять её зеркальное ее отображение и сместить на -90°.
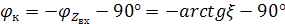

На участке ζ=[-1;1] – передаточная ФЧХ носит линейный характер.
Резонанс токов в параллельном колебательном контуре
Рассмотрим случай параллельного соединения колебательного контура с источником тока (рис. 1) и посмотрим, каково будет сопротивление контура для токов различных частот в этом случае. Если частота тока невелика (ниже резонансной), то почти весь ток пойдет по наиболее легкому для него пути — через индуктивную ветвь; сопротивление контура при низких частотах будет небольшим по величине и индуктивным по своему характеру.
Для токов высоких частот (выше резонансной) более легким путем будет путь через емкостную ветвь, и, следовательно, сопротивление контура будет также небольшим по величине, но емкостным по характеру.
При резонансной частоте, когда емкостное сопротивление равно индуктивному, путь для тока будет одинаково трудным через обе ветви. Мы знаем, что при параллельном соединении двух равных сопротивлений общее сопротивление равняется половине любого из них. Поэтому, казалось бы, что сопротивление контура при резонансе должно равняться половине одного из реактивных сопротивлений. Однако, не следует забывать, что мы имеет дело, с сопротивлениями, хотя и одинаковыми по величине, но имеющими принципиально различный характер. Это различие проявляется в том, что токи в индуктивной и емкостной ветвях контура сдвинуты по фазе друг относительно друга на 180°. Отсюда непосредственно следует, что в неразветвленной части цепи всегда протекает не суммарный, а разностный ток (рис. 1).
Рисунок 1. Токи при параллельном резонансе. В неразвлетвленной части цепи протекает не скммарный, а разностный ток.
Поэтому при резонансе, когда токи в емкостной и индуктивной ветвях равны между собой, ток в неразветвленной части цепи будет равен нулю, какое бы напряжение мы ни прилагали к контуру. При резонансе между точками АВ цепь будет казаться разорванной, т. е. сопротивление ее между этими точками будет бесконечно велико, а отнюдь не будет равным половине одного из реактивных сопротивлений. Практически бесконечно большого сопротивления контура при резонансе не бывает, так как из-за наличия активного сопротивления в контуре (сопротивление провода катушки) сдвиг фаз токов никогда не может быть равным точно 180°.
Однако активное сопротивление катушки обычно бывает много меньше ее индуктивного сопротивления, и поэтому сопротивление колебательного контура при резонансе может достигать очень больших величин.
Сопротивление колебательного контура при параллельном резонансе равно:
где L выражено в гн, С—в ф, RL—в ом.
Полное сопротивление колебательного контура при резонансе является чисто активным в силу того обстоятельства, что индуктивное и емкостное сопротивления взаимно компенсируются.
Кривые изменения полного сопротивления колебательного контура между точками АВ при изменении частоты тока приведены на рис. 2,б.
Рисунок 2. Резонанс токов. а) — схема и обозначения; б) — график полного сопротивления.
При параллельном резонансе токи ,в ветвях контура достигают наибольшей величины; поэтому параллельный резонанс называется резонансом токов.
Явление резонанса имеет огромнейшее значение в радиотехнике. На земном шаре имеется большое количество передающих радиостанций. Передачи всех этих радиостанций распространяются в эфипе и все одновременно принимаются приемной антенной. Нетрудно представить себе, каким получилось бы нагромождение друг на друга передач, если бы мы не могли выделить из этого хаоса только одну нужную нам. Вот тут-то на помощь приходит явление резонанса. Передающие радиостанции излучают в пространство электромагнитную энергию на различных частотах, мы же, настраивая контуры нашего приемника в резонанс с той или иной частотой, тем самым выбираем нужную нам передачу.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
Основные параметры контура
Если предварительно зарядить конденсатор и подключить его к индуктивности (рис. 4.2.7.1), то будет происходить обмен энергией между электрическим полем конденсатора и магнитным полем катушки. В этой цепи будут происходить колебания, поэтому этот контур называется колебательным.
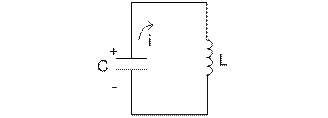
Рис.4.2.7.1.
Так как колебания происходят без воздействия внешнего источника, а за счет заранее занесенной энергии, то они называются свободными.
Колебания происходят с определенной частотой 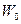 , называемой частотой свободных колебаний.
, называемой частотой свободных колебаний.
Из условия равенства энергий 
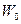 =
=  ;
;  ;
;
Основными параметрами колебательного контура, кроме частоты свободных колебаний, являются:
— период свободных колебаний:
 ;
;
— характеристическое (волновое) сопротивление:
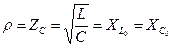
Характеристическим сопротивлением называется индуктивное или емкостное сопротивление в колебательном контуре при частоте свободных колебаний.
Так как в контуре отсутствуют потери, то контур называется идеальным.
В реальном колебательном контуре (рис. 4.2.7.2) имеются потери, поэтому при возникновении в контуре свободных колебаний энергия предварительно заряженного конденсатора тратится безвозвратно, преобразуясь в тепло. В результате затраты энергии постепенно уменьшается её запас и амплитуда контура уменьшается до нуля. Следовательно, колебания в контуре будут затухающими.(рис 4.2.7.3)
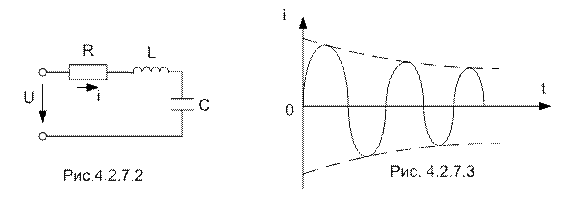
Для характеристики интенсивности затухания свободных колебаний введено понятие «затухание контура». Затуханием называется отношение активного сопротивления контура к его характеристическому сопротивлению.
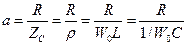
Величина, обратная затуханию, называется добротностью контура.
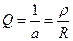
Добротность характеризует качество контура.
Рассмотрим различные варианты последовательного соединения элементов в цепях переменного тока.
4.2.7. Гармонические колебания в цепи при параллельном соединении элементов R,L,C.
К цепи, содержащей параллельное соединение R,L,C
(рис. 4.2.8.1 а) приложено напряжение u=  sin
sin  t. Согласно первому закону Кирхгофа (ЗТК) ток в неразветвленной части равен:
t. Согласно первому закону Кирхгофа (ЗТК) ток в неразветвленной части равен:
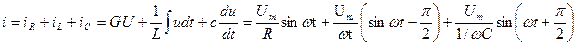 ,
,
где,  =G
=G  ,
,
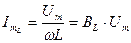 ,
,
 .
.
Полная проводимость цепи будет равна: 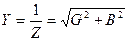
Активная проводимость: 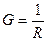
Реактивная проводимость: 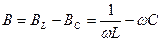
При параллельном соединении элементов строят треугольники токов и проводимостей (рис.4.2.8.1.б,в)
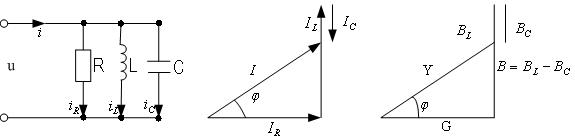
а) б) в)
Рис. 4.2.8.1.
4.2.8. Резонанс в электрических цепях переменного тока.
В радиотехнике и электросвязи большое значение имеет явление резонанса. Такое явление возникает в цепях, содержащих участки, с емкостным и индуктивным характером. Если цепь содержит последовательно соединенные с генератором элементы, то она называется последовательным колебательным контуром.(рис. 4.2.9.1а). Если элементы соединены параллельно с генератором, то цепь носит название – параллельный колебательный контур. (рис. 4.2.9.1б).
Среди многообразия частот имеется частота, на которой в цепи происходит обмен энергией между магнитными и электрическими полями. К генератору энергия не возвращается. От генератора поступает в контур столько энергии, сколько её тратится на активном сопротивлении цепи, тем самым обеспечиваются незатухающие колебания в контуре.
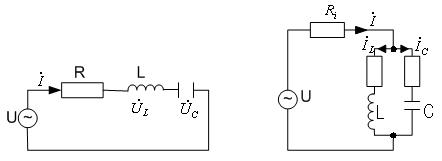
а) б)
рис. 4.2.9.1
· Частоту, на которой наблюдается явление резонанса, называют резонансной и определяют по формуле:
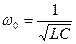 ;
; 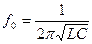
· Характеристическим сопротивлением контура называют реактивные сопротивления на резонансной частоте и определяют как:
 [Ом]
[Ом]
· Резонансные свойства контура характеризуются добротностью контура, которая равна:

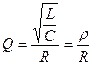
Добротность контура зависит от внутреннего сопротивления генератора  .
.
В последовательном колебательном контуре, (рис.4.2.9.1а) чем больше  , тем больше потери энергии внутри источника, тем меньше добротность, что приводит к ослаблению резонансных свойств контура.
, тем больше потери энергии внутри источника, тем меньше добротность, что приводит к ослаблению резонансных свойств контура.
В параллельном колебательном контуре, (рис. 4.2.9.1б) если  будет мало, то через него будет проходить большая часть разрядного тока конденсатора, что приведет к большим потерям, уменьшит добротность и ухудшит резонансные свойства контура.
будет мало, то через него будет проходить большая часть разрядного тока конденсатора, что приведет к большим потерям, уменьшит добротность и ухудшит резонансные свойства контура.
Различают два типа резонансов. В последовательном колебательном контуре возникает резонанс напряжений, а в параллельном – резонанс токов. Свойства цепей при резонансе рассматриваются в следующей таблице:
Важной характеристикой колебательного контура является полоса пропускания – это полоса частот, в пределах которой величина не меньше 0,707 от своего максимального значения. Полосу пропускания можно определить по формуле:

Где: 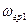 ;
; 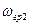 ;
;  ;
; 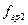 — граничные частоты, на которых величина равна 0,707 от своего максимального значения.
— граничные частоты, на которых величина равна 0,707 от своего максимального значения.
Колебательные контуры и явление резонанса широко используются в радиотехнике и электросвязи. В радиоприемниках и усилителях они являются избирательными цепями, в автогенераторах, электрических фильтрах, в корректорах и других устройствах являются частотно-зависимыми элементами.
Пример:
Электрическая цепь состоит из последовательно соединенных резистора R=15 Ом, катушки индуктивности L=636 мкГн и конденсатора C=600 пФ.
Определить резонансную частоту 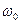 , характеристическое сопротивление
, характеристическое сопротивление  , добротностьQ, затухание d. Чему равны ток
, добротностьQ, затухание d. Чему равны ток  , расходуемая в цепи мощность
, расходуемая в цепи мощность  , напряжения на индуктивности
, напряжения на индуктивности  , и емкости
, и емкости 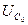 , если контур включен на напряжение U=1,8 B? Какую избирательность обеспечивает данный контур при расстройке на
, если контур включен на напряжение U=1,8 B? Какую избирательность обеспечивает данный контур при расстройке на 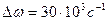 ?
?
Рассчитать и построить зависимости:
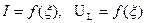
для значений обобщенной расстройки  . Показать на графике полосу пропускания контура.
. Показать на графике полосу пропускания контура.
Решение:
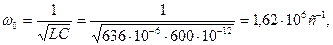
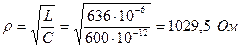 ,
,
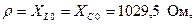

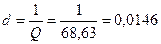 ,
,
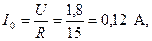
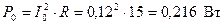 ,
,
 ,
,
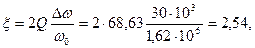
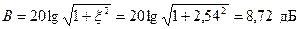 .
.
Рассчитаем и построим заданные зависимости:
1. 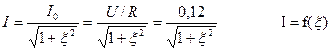
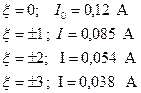

2. 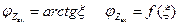
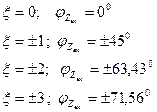

Вопросы для самоконтроля:
1. Что называется колебательным контуром?
2. Какие колебания называются свободными, вынужденными?
3. Что называется «резонансом напряжений»?
4. Что называется «резонансом токов»?
5. Условия возникновения резонансов
6. Что характеризует добротность контура?
7. Как определяется резонансная частота?
4.3. Расчет цепей символическим методом
Символический метод основан на использовании комплексных чисел.
Комплексное число состоит из вещественной А’ и мнимой А» частей. А = А’ + jА».
Комплексное число можно представить вектором на комплексно-числовой плоскости. (рис. 4.3.1.) Проекция вектора на вещественную ось (ось абцисс) соответствует вещественной части комплексного числа А’, проекция вектора на мнимую ось (ось ординат) соответствует коэффициенту при мнимой единице А»,
j-мнимая единица представляет собой поворотный множитель, умножение на который означает поворот вектора на 90° против часовой стрелки.
Комплексным числам А=3+ j4 и В= 5-j2
Соответствуют векторы А и В, изображенные на рис. 4.3.1.
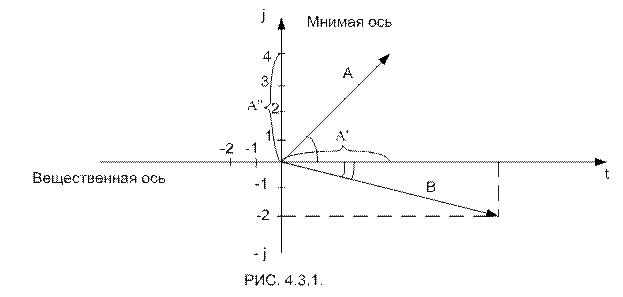
Модуль комплексного числа соответствует длине вектора, изображающего это комплексное число.
Модуль комплексного числа:
|А|=  ;
;
Т.е. |А|= 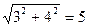 ;
; 
 |В|=
|В|= 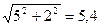
Углы  и
и 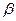 , образованные векторами А и В, называются аргументами комплексного числа
, образованные векторами А и В, называются аргументами комплексного числа
 = arctg
= arctg 
Для приведенных примеров
 = arctg
= arctg  =53°10′
=53°10′
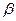 = arctg
= arctg 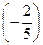 =-21°40′
=-21°40′
Существует 3 формы записи количественного числа:
1. Алгебраическая А = А’ + jА»
2. Тригонометрическая А=|А|cos  +j|А|sin
+j|А|sin  ,
,
Так как А’=|А| cos 
А»=|А| sin 
3. Показательная А=|А|е 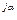 =5е
=5е 
В=|В|е  =5,4е
=5,4е 
Для перевода из показательной формы в алгебраическую пользуются тригонометрической формой записи комплексного числа.
Для перевода из алгебраической в показательную форму определяют модуль и аргумент.
Комплексные числа можно складывать, вычитать, умножать и делить.
Сложение и вычитание комплексных чисел производят в алгебраической форме, а умножение и деление удобнее и проще производить в показательной форме.
При умножении комплексных чисел в показательной форме модули этих чисел перемножаются, а аргументы складываются:
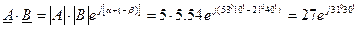
При делении комплексных чисел в показательной форме этих чисел делятся, а аргументы вычитаются

Если ток и напряжение изменяется по синусоидальному закону
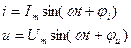
То их можно изобразить векторами и записать комплексными числами
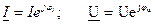
Комплекс полного сопротивления цепи:
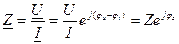
Алгебраическая форма записи комплекса полного сопротивления
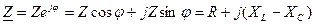
Любую цепь переменного тока можно рассчитывать по закону постоянного тока, если все величины представить в комплексной форме.
Комплекс полной мощности цепи 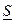 определяется произведением комплекса напряжения
определяется произведением комплекса напряжения  и сопряженного комплекса тока I. У сопряженного комплекса знак перед мнимой единицей j меняется на противоположный
и сопряженного комплекса тока I. У сопряженного комплекса знак перед мнимой единицей j меняется на противоположный

где Р- активная мощность
Q- реактивная мощность
Пример
Определить полное сопротивление цепи (рис.4.3.2) напряжение на зажимах, мощности (активную, реактивную, полную) если

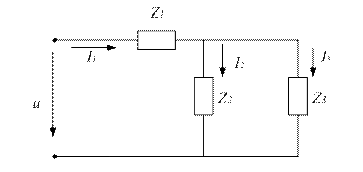
Решение
1. Полное сопротивление цепи
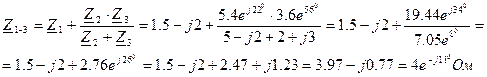
2. Напряжения на зажимах цепи
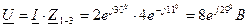
3. Полная мощность цепи

где Р=15.99 = 16 Вт – активная мощность
Q= -0.015 Вт – реактивная мощность
Вопросы для самоконтроля.
1 . Какие формы записи комплексных чисел вы знаете?
2. Сложите два числа
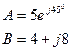
3. Перемножить два числа

4. Выражаем токи через потенциалы, ЭДС и сопротивления.
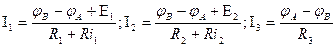 ,
,
5. Примем 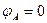
6. Подставляем полученные выражения токов в уравнение 1.


7. Подставим числовые значения и решаем полученное уравнение.

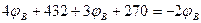
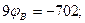
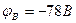
8. Определяем токи в ветвях.
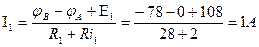
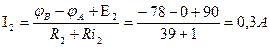

Действительные направления токов совпадают с выбранными.
Тема №3: Трехфазные цепи. [Электротехника Электронное пособие для студентов очной и заочной форм обучения всех технических специальностей]
Основными приемниками электрической энергии являются электрические двигатели, применяемые для приведения в движение рабочих машин. Наиболее простые из них трехфазные асинхронные двигатели. Для производства, распределения и передачи электрической энергии применяют трехфазные генераторы.
Система, состоящая из трех цепей, в которой действуют синусоидальные ЭДС одинаковой частоты, сдвинутые относительно друг друга по фазе и создаваемые одним источником – называется трехфазной.
Система будет симметричной, если будут равны амплитуды фаз и углы сдвига фаз между каждой парой ЭДС.
На рисунке 4.14а, изображены временные диаграммы ЭДС , на рисунке 4.14б, векторная диаграмма, а на 4.14в, иллюстрируется принцип получения трехфазной системы ЭДС . В равномерном магнитном поле с постоянной угловой скоростью  вращаются три одинаковых жёстко скрепленных друг с другом катушки.
вращаются три одинаковых жёстко скрепленных друг с другом катушки.
Плоскости катушек смещены в пространстве относительно друг друга на 120°. В каждой катушке находится синусоидальная ЭДС одинаковой амплитуды. Уравнения ЭДС записывают в следующем виде:
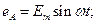



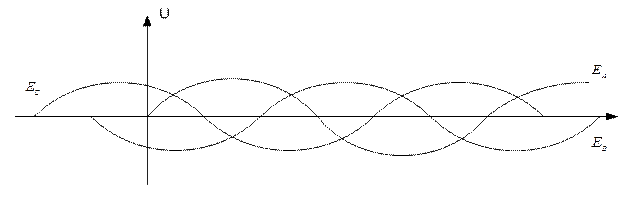 а)
а)
ЕА

ЕС ЕВ
б) в)
Рисунок 5.11
Векторы вращающиеся против часовой стрелки и фазы чередуются А, В, С, что называют прямой последовательностью фаз.
Дата добавления: 2016-11-29; просмотров: 14643;



