В таблице представлена зависимость глубины проникновения электрического тока в металл от частоты сигнала. Более наглядно и точно зависимость толщины скин-слоя от частоты, а также зависимость активного и индуктивного сопротивления от частоты можно оценить на странице Online расчёт комплексного сопротивления. δ=50300√(ρ/µr)f µr — магнитная проницаемость среды ρ — проводимость (Ом·см).
| ||||||
Поверхностный (скин-эффект) в проводнике
Звуковой сигнал изменяет свойства проводников, соединяющих компоненты электронной схемы. Причинами этого могут быть:
- частотные характеристики, вызванные взаимодействием параметров RCLD-кабеля, и неблагоприятные условия входного и выходного импеданса компонентов;
- конструкция кабеля и применяемые материалы.
Важно! Даже при оптимальных параметрах RCLD часто наблюдаются четкие различия в звуке.
Одной из причин, часто связанной с конструкцией кабеля, является поверхностный эффект.
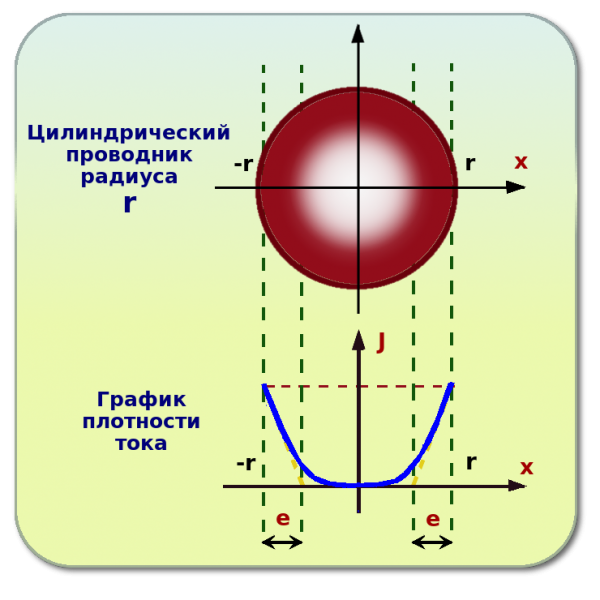
Поверхностный эффект в проводе
Общее объяснение
При постоянном токе его плотность по всему поперечному сечению проводника одинакова. Но переменный ток регулярно меняет свое направление и силу, что генерирует изменяющееся магнитное поле. Изменение потока индуцирует вихревые токи в проводнике, направленные на противодействие току внутри провода. На поверхности их направления совпадают. В результате плотность тока экспоненциально уменьшается по направлению к центру. Ток смещения увеличивается с частотой переменного тока и диаметром проводника.
При высокочастотных сигналах центр проводника практически обесточивается. Сопротивление провода при этом значительно увеличивается за счет смещения тока. Однако это только упрощенная модель.
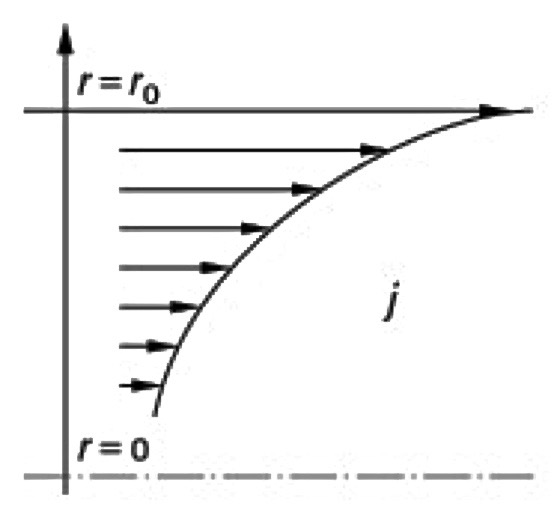
Распределение плотности тока в проводнике
Помимо скин эффекта, существует эффект близости, который создает дополнительную концентрацию плотности тока на стороне поперечного сечения линии, лежащей в области магнитного поля наибольшей силы. Она проявляется, например, на внутренних поверхностях при двухтактном возбуждении или на внешних сторонах в синхронной возбужденной двойной линии.
Глубина проникновения
Расстояние от поверхности проводника, на котором плотность тока упала до коэффициента 1 / e = 0,37, или -8,69 дБ, называется глубиной проникновения и рассчитывается по формуле:
d = √ (ρ / (π × μ × f)), где:
- d – глубина проникновения, мм;
- ρ – удельное сопротивление материала;
- μ – постоянная проницаемости = 4 × p × 10 -7 Генри / м;
- f – частота;
Отсюда можно составить эмпирическое правило для меди:
d = 66 × √ (ρ r / (μ r × f)), где:
- ρ r = ρ / ρ Cu = 1;
- μ r – для немагнитных материалов, таких как медь, равно 1.
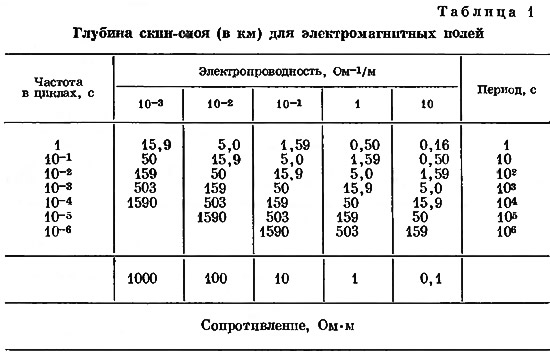
Глубина скин слоя для э/м полей
Из формулы следует, что глубина проникновения для каждой частоты у сверхпроводников равна 0, то есть весь перенос заряда идет по поверхности, а для плохого проводника глубина проникновения очень велика. Глубина проникновения также пропорциональна потерям, возникающим в проводе.
Расчет увеличения сопротивления, возникающего во время скин эффекта, немного сложнее:
- Для круглой сплошной медной проволоки с диаметром 2 мм, что соответствует S = 3,15 мм², полученное сопротивление на частоте 100 кГц, по сравнению с таким же значением для частоты 32 кГц, возрастает в 1,5 раза;
- Для проводника с d = 0, 2 мм удвоение сопротивления происходит только на частоте 10 мГц.
Важно! Для исключения скин эффекта в звуковом диапазоне до 20 кГц проводник может иметь диаметр не более 1 мм. Если диапазон аудиосигнала величин до 50 кГц, диаметр проводника не может превышать 0,6 мм.
Приблизительная формула для определения частоты среза для данного диаметра проводника:
f c = 4 / (π × μ × s Cu × D 2) = 1 / (π 2 × 5,8 × D 2), где:
- f c – частота среза;
- D – диаметр проводника;
- s Cu= удельная проводимость меди = 5,8 × 10 7 (Ω × м) -1;
Несколько значений частоты среза для меди:
- 0,1 мм – 1,75 мГц;
- 0,3 мм – 194 кГц;
- 0,5 мм – 70 кГц;
- 0,8 мм – 27 кГц;
- 1 мм – 17 кГц;
- 2 мм – 4,4 кГц.
Фактический поверхностный эффект не является чистым увеличением сопротивления.
Часть э/м поля, которая не отражается на проводимости из-за неидеальных свойств провода, но проникает в него, можно назвать полем потерь. Компонента электрического поля ориентирована в осевом направлении вдоль длины проводника, а электромагнитная энергия распространяется радиально, начиная с поверхности. Это является причиной скин эффекта.
Таким образом, поле потерь напрямую зависит от проводимости, магнитной проницаемости и частоты сигнала и в конечном итоге преобразуется в тепло.
Способы подавления скин эффекта
Поверхностный эффект можно подавить или значительно уменьшить, используя вместо сплошной проволоки пучок тонких проводов, покрытых специальным изоляционным лаком. В высокочастотной технологии часто используются тонкостенные трубки, поверхность которых покрыта хорошо проводящим слоем, например, серебром.
Акустический кабель
Основные особенности подавления скин эффекта:
- Идеальные проводники для аудиодиапазона – не толще 0,3 мм;
- Структура кабеля должна быть такой, чтобы по всей длине образовывалось однородное магнитное поле между проводниками;
- Провод должен быть максимально чистым и однородным, с поверхностью, абсолютно свободной от оксида меди;
- Следует избегать рядом лежащих неэкранированных шнуров питания из-за генерируемых магнитных полей;
- В качестве диэлектрика лучше использовать материал с возможно меньшей диэлектрической постоянной.
Многожильные провода часто используются и для передачи токов низкой частоты. Сталь или углеродное волокно применяется для передачи мощности на большие расстояния. Широкие дорожки на печатной плате обеспечивают большую площадь поверхности и низкое сопротивление. С учетом этих простых предложений скин-эффекта можно избежать в большинстве случаев применения электроэнергии. Но правильное функционирование конструкций, работающих на сотнях мегагерц и даже гигагерцах, требует тщательного планирования и инженерных решений. Оптоволоконные кабели, в которых для передачи данных используется неметаллическая среда, обычно требуются, чтобы глубина поверхностного слоя стандартных проводников оставалась низкой.
Видео
Оцените статью:Скин-слой Википедия
Поверхностный эффект, скин-эффект — эффект уменьшения амплитуды электромагнитных волн по мере их проникновения вглубь проводящей среды. В результате этого эффекта, например, переменный ток высокой частоты при протекании по проводнику распределяется не равномерно по сечению, а преимущественно в поверхностном слое.
Объяснение поверхностного эффекта[ | ]
Физическая картина возникновения[ | ]
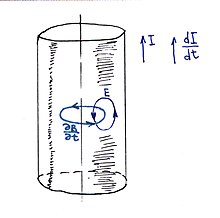Физическая картина возникновения скин-эффекта.Рассмотрим цилиндрический проводник, по которому течёт ток. Вокруг проводника с током имеется магнитное поле, силовые линии которого являются концентрическими окружностями с центром на оси проводника. В результате увеличения силы тока возрастает индукция магнитного поля, а форма силовых линий при этом остаётся прежней. Поэтому в каждой точке внутри проводника производная ∂B∂t{\displaystyle {\frac {\partial \mathbf {B} }{\partial t}}} направлена по касательной к линии индукции магнитного поля и, следовательно, линии ∂B∂t{\displaystyle {\frac {\partial \mathbf {B} }{\partial t}}} также являются окружностями, совпадающими с линиями индукции магнитного поля. Изменяющееся магнитное поле по закону электромагнитной индукции
- rotE=−∂B∂t{\displaystyle \operatorname {rot} \,\mathbf {E} =-{\frac {\partial \mathbf {B} }{\partial t}}}
создаёт электрическое индукционное поле, силовые линии которого представляют замкнутые кривые вокруг линии индукции магнитного поля. Вектор напряжённости индукционного поля в более близких к оси проводника областях направлен противоположно вектору напряжённости электрического поля, создающего ток, а в более дальних — совпадает с ним. В результате плотность тока уменьшается в приосевых областях и увеличивается вблизи поверхности проводника, то есть возникает скин-эффект.
Уравнение, описывающее скин-эффект[ | ]
Исходим из уравнения Максвелла,
Скин-эффект Википедия
Поверхностный эффект, скин-эффект — эффект уменьшения амплитуды электромагнитных волн по мере их проникновения вглубь проводящей среды. В результате этого эффекта, например, переменный ток высокой частоты при протекании по проводнику распределяется не равномерно по сечению, а преимущественно в поверхностном слое.
Объяснение поверхностного эффекта[ | ]
Физическая картина возникновения[ | ]
Физическая картина возникновения скин-эффекта.Рассмотрим цилиндрический проводник, по которому течёт ток. Вокруг проводника с током имеется магнитное поле, силовые линии которого являются концентрическими окружностями с центром на оси проводника. В результате увеличения силы тока возрастает индукция магнитного поля, а форма силовых линий при этом остаётся прежней. Поэтому в каждой точке внутри проводника производная ∂B∂t{\displaystyle {\frac {\partial \mathbf {B} }{\partial t}}} направлена по касательной к линии индукции магнитного поля и, следовательно, линии ∂B∂t{\displaystyle {\frac {\partial \mathbf {B} }{\partial t}}} также являются окружностями, совпадающими с линиями индукции магнитного поля. Изменяющееся магнитное поле по закону электромагнитной индукции
- rotE=−∂B∂t{\displaystyle \operatorname {rot} \,\mathbf {E} =-{\frac {\partial \mathbf {B} }{\partial t}}}
создаёт электрическое индукционное поле, силовые линии которого представляют замкнутые кривые вокруг линии индукции магнитного поля. Вектор напряжённости индукционного поля в более близких к оси проводника областях направлен противоположно вектору напряжённости электрического поля, создающего ток, а в более дальних — совпадает с ним. В результате плотность тока уменьшается в приосевых областях и увеличивается вблизи поверхности проводника, то есть возникает скин-эффект.
Уравнение, описывающее скин-эффект[ | ]
Исходим из уравнения Максвелла,
Cкин-эффект
На высоких частотах ток, протекающий через проводник, распределяется по его сечению неравномерно. Под действием сильных магнитных полей переменного тока происходит «выталкивание» тока от центра проводника к его поверхности (скин-эффект). В результате ток протекает по меньшей площади поперечного сечения, что выглядит как уменьшение диаметра провода. Чем выше частота, тем меньше толщина поверхностного слоя (скин-слоя), по которому течет ток, и тем больше сопротивление проводника протекающему току. Глубина скин-слоя определяется как расстояние ниже поверхности, где плотность тока падает на 1/e от значения на поверхности (e- основание натурального логарифма).
Для минимизации потерь, возникающих из-за скин-эффекта, применяются проводники особой конструкции, которые состоят из большого числа тонких жил, изолированных одна от другой. Жилы переплетены между собой так, что каждая проходит по поверхности и в любом месте поперечного сечения на всём протяжении провода; это усредняет импеданс каждой жилы, в результате чего в них протекают равные токи. В таком проводнике, называемым литцендратом (нем. Litzen — пряди и Draht — провод), ток течет по поверхности каждой жилы, в результате рабочая площадь поперечного сечения проводника значительно увеличивается, а сопротивление токам высокой частоты уменьшается.
Как правило, при проектировании устройств, требующих применения литцендрата, значения рабочей частоты и тока в проводнике известны заранее. Поскольку главное преимущество литцендрата заключается в уменьшении сопротивления переменному току по сравнению с одножильным проводом эквивалентного сечения, основным параметром, который учитывается при выборе конструкции и сечения провода, является рабочая частота. В таблице 1 показана зависимость соотношения между сопротивлениями переменному току и постоянному току (коэффициент H) от коэффициента X для одиночного изолированного проводника круглого сечения:
Таблица 1.
X | 0 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1.0 |
H | 1.0000 | 1.0003 | 1.0007 | 1.0012 | 1.0021 | 1.0034 | 1.005 |
Коэффициент X рассчитывается по формуле:
где: d – диаметр провода, мм, f – частота, МГц.
Из Таблицы 1 и другой эмпирической информации была получена Таблица 2, в которой приведены рекомендуемые диаметры единичной жилы изолированной жилы многожильного провода в зависимости от рабочей частоты.
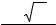
Таблица 2.
| Рекоменду | Диаметр | Активное |
|
Частота | емое | жилы без | Коэффициент | |
сечение | сопротивление | |||
| жилы, | изоляции, | жилы, Ом/м | H |
| мм |
| ||
| AWG |
|
| |
|
|
|
| |
60 Гц…1 кГц | 28 | 0,32 | 0,21775 | 1,0000 |
1…10 кГц | 30 | 0,254 | 0,34718 | 1,0000 |
10…20 кГц | 33 | 0,18 | 0,69455 | 1,0000 |
20…50 кГц | 36 | 0,127 | 1,417 | 1,0000 |
50…100 кГц | 38 | 0,102 | 2,2372 | 1,0000 |
100…200 кГц | 40 | 0,079 | 3,7805 | 1,0000 |
200…350 кГц | 42 | 0,064 | 5,9088 | 1,0000 |
350…850 кГц | 44 | 0,051 | 9,42585 | 1,0003 |
850…1,4 МГц | 46 | 0,04 | 14,9081 | 1,0003 |
1,4…2,8 МГц | 48 | 0,031 | 23,901 | 1,0003 |
После выбора диаметра жилы соотношение между сопротивлениями переменному и постоянному току идеального литцендрата, т.е. такого, в котором каждая жила последовательно «пронизывает» каждую точку площади поперечного сечения, может быть определено по следующей формуле:
RAC |
| Nd1 | 2 |
|
| |
|
|
|
| |||
| = H + K | d |
|
| G , | (2) |
R | 0 | |||||
DC |
|
|
|
|
| |
где: H – коэффициент из Таблиц 1 и 2,
G — коэффициент поправки на вихревые токи, определяемый по формуле:
| d f | 4 | , | (3) |
G = | 1 |
| ||
| 265.176 |
|
|
|
|
|
|
|
N – количество жил в кабеле, d1 – диаметр жилы, мм,
d0 – диаметр жгута, мм, f – частота, Гц,
K – постоянная, зависящая от количества жил в кабеле, определяется по следующей таблице:
Таблица 3.
N | 3 | 9 | 27 | ∞ |
K | 1,55 | 1,84 | 1,92 | 2 |
Сопротивление многожильного кабеля постоянному току зависит от следующих факторов:
1.сечения жилы,
2.количества жил,
3.коэффициента удлинения одиночной жилы по сравнению с единицей длины жгута, возникающего как результат плетения жил. Типичными считаются значения 1,5% для каждого порядка операции плетения жил в жгут и 2,5% для
-2 —
каждого порядка операции скручивания жгутов в кабель.
Следующая формула позволяет определить сопротивление постоянному току литцендрата любой конструкции:
R | = | R (1.015)N B | (1.025)NC |
| |
S |
| , | (4) | ||
|
| ||||
DC | NS |
|
|
| |
|
|
|
|
| |
где: RS – сопротивление единичной жилы, Ом (см. таблицу 2), NB – количество порядков операции плетения в жгут,
NC – количество порядков операции скручивания жгутов в кабель, NS – общее количество жил в кабеле.
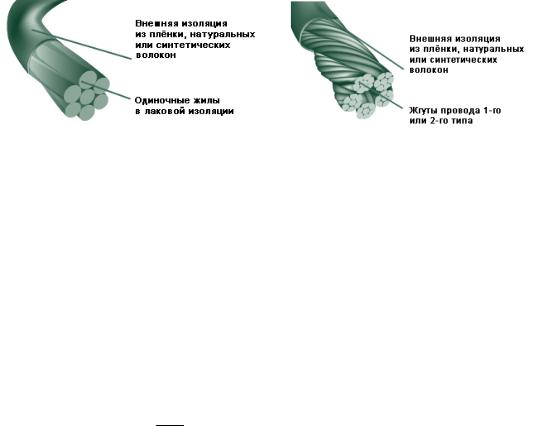
Рис.1. Литцендрат 1-го типа | Рис.2. Литцендрат 2-го типа |
Пример 1. Рассчитаем сопротивления провода типа 2 (см. Рис.2), состоящего из 450 жил диаметром 0,079 мм на частоте 100 кГц. Данный провод производится путём свивания пяти жгутов (скручивание жгутов в кабель первого порядка), каждый их которых, в свою очередь, получен свиванием трёх жгутов (плетение второго порядка), сформированных из
30жил диаметром 0,079 мм (плетение первого порядка).
1.Определим активное сопротивление провода по формуле (4):
R = 3780.5* (1.015)2 (1.025)1 =8.87Ом/ км,
2. Вычисляем отношение RAC при помощи формулы (2):
RDC
R | AC |
| 450*0.079 | 2 | ||
| =1.0000 +2* |
|
| *(7.877 *10−5 )=1.035 , | ||
RDC | 2.388 | |||||
|
|
| ||||
Преимущество литцендрата становится очевидным при сравнении с круглым проводом диаметром 1,67 мм, имеющим эквивалентную площадь сечения. Активное сопротивление одножильного провода составит порядка 7,853 Ом/км, однако на частоте 100 кГц соотношение между сопротивлениями переменному и постоянному току возрастает примерно до 21,4; таким образом, сопротивление переменному току составит
168 Ом/км.
— 3 —
Пример 2. Рассчитаем сопротивления провода типа 2 (см. Рис.2), состоящего из 1260 жил диаметром 0,100 мм на частоте 66 кГц. Этот провод образован из семи жгутов (скручивание жгутов в кабель первого порядка), каждый их которых, в свою очередь, получен свиванием шести жгутов (плетение второго порядка), сформированных из 30 жил диаметром 0,100 мм (плетение первого порядка).
1. Определим активное сопротивление провода по формуле (4):
| R |
| = | 2176.5*(1.015)2 (1.025)1 | =1.824Ом/ км, | |||||
|
|
|
|
|
| |||||
| DC | 1260 |
|
|
|
|
| |||
|
|
|
|
|
|
|
| |||
2. Вычисляем отношение | RAC |
|
| при помощи формулы (2): | ||||||
R |
| |||||||||
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
| DC |
|
| |
| R | AC |
| 1260 *0.1 | 2 | |||||
|
| =1.0000 +2* |
|
|
|
| *(8.81*10−5 )=1.124 , | |||
| RDC |
| 4.75 |
| ||||||
|
|
|
|
| ||||||
Одножильный провод диаметром 3,55 мм имеет такую же площадь поперечного сечения, но очевидно, что при глубине скин-слоя, равного 0,257 мм, такой провод можно рассматривать как тонкостенный цилиндр с толщиной стенки, равной глубине скин-слоя.
По материалам фирмы New England Wire
СКИН-ЭФФЕКТ • Большая российская энциклопедия
СКИН-ЭФФЕ́КТ, затухание электромагнитных волн по мере их проникновения в проводящую среду. Переменное электрич. поле и связанное с ним магнитное поле не проникают в глубь проводника, а сосредоточены в осн. в относительно тонком приповерхностном слое толщиной δ, называемой глубиной скин-слоя. С.-э. обусловлен тем, что при распространении электромагнитной волны в проводящей среде возникают вихревые токи (см. Фуко токи), в результате чего часть электромагнитной энергии преобразуется в теплоту. Это приводит к уменьшению напряжённостей электрич. и магнитного полей и плотности тока, т. е. к затуханию волны. Затухание тем сильнее, чем больше частота ω электромагнитного поля, магнитная проницаемость μ и проводимость σ проводника. С.-э. проявляется в металлах, плазме, ионосфере (на коротких волнах), вырожденных полупроводниках и др. средах с достаточно высокой проводимостью.
Глубина скин-слоя зависит от величин σ и ω, а также от состояния поверхности. На малых частотах δ велика, убывает с ростом частоты и для металлов на частотах оптич. диапазона оказывается сравнимой с длиной волны (порядка 10–7 м). Столь малым проникновением электромагнитного поля и почти полным его отражением объясняется металлич. блеск хороших проводников. На частотах, превышающих плазменную частоту ωp, в проводниках оказывается возможным распространение электромагнитных волн.
При нормальном С.-э., когда δ велика по сравнению с эффективной длиной свободного пробега l электронов, распределение поля в проводнике зависит только от дифференциальной проводимости. В пределе низких частот, когда можно не учитывать частотную дисперсию и пренебречь диэлектрич. проницаемостью ионной решётки, глубина скин-слоя δ=c(2πωσ)–1/2 (c – скорость света). С повышением частоты в ИК-области спектра для металлов δ не зависит от частоты: δ=c/ωp.
При l>δ С.-э. приобретает ряд особенностей, благодаря которым он получил назв. аномального. Такой С.-э. наблюдается в СВЧ-диапазоне в чистых металлах при низких темп-pax. Электроны при аномальном С.-э. становятся неравноценными с точки зрения их вклада в электрич. ток. Существенную роль играют электроны с малыми углами скольжения, для которых отражение близко к зеркальному. На аномальный С.-э. влияет постоянное магнитное поле, параллельное поверхности. Закручиваемые им электроны при зеркальном отражении многократно сталкиваются с поверхностью образца и долгое время движутся в пределах скин-слоя. Это приводит к росту проводимости и уменьшению δ. Др. электроны, не сталкивающиеся с поверхностью, возвращаются в скин-слой после каждого оборота в магнитном поле, вследствие чего в металлах наблюдается циклотронный резонанс.
При достаточно высоких значениях напряжённости переменного электромагнитного поля, когда параметры среды (напр., σ) начинают зависеть от величины поля, С.-э. становится нелинейным, т. е. δ также начинает зависеть от интенсивности электромагнитного поля.
В технике С.-э. часто нежелателен. При сильном С.-э. переменный ток протекает гл. обр. по поверхностному слою провода, при этом его сечение используется не полностью, сопротивление провода и потери мощности в нём возрастают. В ферромагнитных пластинах или лентах магнитопроводов трансформаторов, электрич. машин и др. устройств переменный магнитный поток при сильном С.-э. проходит в осн. по их поверхностному слою, вследствие чего возрастают намагничивающий ток и потери в стали. Вредное влияние С.-э. ослабляют уменьшением толщины пластин или ленты, а при достаточно высоких частотах – применением магнитопроводов из магнитных диэлектриков.
На С.-э. основано действие электромагнитных экранов, взрывомагнитных генераторов, взрывомагнитных генераторов частоты, ВЧ поверхностная закалка стальных изделий и др.
Скин-эффект — Википедия
Поверхностный эффект, скин-эффект — эффект уменьшения амплитуды электромагнитных волн по мере их проникновения вглубь проводящей среды. В результате этого эффекта, например, переменный ток высокой частоты при протекании по проводнику распределяется не равномерно по сечению, а преимущественно в поверхностном слое.
Объяснение поверхностного эффекта
Физическая картина возникновения
Физическая картина возникновения скин-эффекта.Рассмотрим цилиндрический проводник, по которому течёт ток. Вокруг проводника с током имеется магнитное поле, силовые линии которого являются концентрическими окружностями с центром на оси проводника. В результате увеличения силы тока возрастает индукция магнитного поля, а форма силовых линий при этом остаётся прежней. Поэтому в каждой точке внутри проводника производная ∂B∂t{\displaystyle {\frac {\partial \mathbf {B} }{\partial t}}} направлена по касательной к линии индукции магнитного поля и, следовательно, линии ∂B∂t{\displaystyle {\frac {\partial \mathbf {B} }{\partial t}}} также являются окружностями, совпадающими с линиями индукции магнитного поля. Изменяющееся магнитное поле по закону электромагнитной индукции
- rotE=−∂B∂t{\displaystyle \operatorname {rot} \,\mathbf {E} =-{\frac {\partial \mathbf {B} }{\partial t}}}
создаёт электрическое индукционное поле, силовые линии которого представляют замкнутые кривые вокруг линии индукции магнитного поля. Вектор напряжённости индукционного поля в более близких к оси проводника областях направлен противоположно вектору напряжённости электрического поля, создающего ток, а в более дальних — совпадает с ним. В результате плотность тока уменьшается в приосевых областях и увеличивается вблизи поверхности проводника, то есть возникает скин-эффект.
Уравнение, описывающее скин-эффект
Исходим из уравнения Максвелла,
- rotB=μj{\displaystyle \operatorname {rot} \mathbf {B} =\mu \mathbf {j} }
и выражения для j{\displaystyle \mathbf {j} } по закону Ома:
- j=γE{\displaystyle \mathbf {j} =\gamma \mathbf {E} }
Дифференцируя обе части полученного уравнения по времени, находим:
- rot∂B∂t=μγ∂E∂t{\displaystyle \operatorname {rot} {\frac {\partial \mathbf {B} }{\partial t}}=\mu \gamma {\frac {\partial \mathbf {E} }{\partial t}}}
- −rotrotE=μγ∂E∂t{\displaystyle -\operatorname {rot} \operatorname {rot} \mathbf {E} =\mu \gamma {\frac {\partial \mathbf {E} }{\partial t}}}.
Поскольку
- rotrotE=graddivE−∇2E{\displaystyle \operatorname {rot} \operatorname {rot} \mathbf {E} =\operatorname {grad} \operatorname {div} \mathbf {E} -\nabla ^{2}\mathbf {E} } и divE=0{\displaystyle \operatorname {div} \mathbf {E} =0}
окончательно получаем:
- ∇2E=μγ∂E∂t{\displaystyle \nabla ^{2}\mathbf {E} =\mu \gamma {\frac {\partial \mathbf {E} }{\partial t}}}.
Для упрощения решения предположим, что ток течёт по однородному бесконечному проводнику, занимающему полупространство y>0 вдоль оси X. Поверхностью проводника является плоскость Y=0. Таким образом,
- jx=jx(y,t),jy=jz=0{\displaystyle j_{x}=j_{x}(y,t),\qquad j_{y}=j_{z}=0},
- Ex=Ex(y,t),Ey=Ez=0{\displaystyle E_{x}=E_{x}(y,t),\qquad E_{y}=E_{z}=0}.
Тогда
- ∂2Ex∂y2=μγ∂Ex∂t{\displaystyle {\frac {\partial ^{2}E_{x}}{\partial y^{2}}}=\mu \gamma {\frac {\partial E_{x}}{\partial t}}}.
В этом уравнении все величины гармонически зависят от t, и можно положить:
- Ex(y,t)=E0(y)eiωt{\displaystyle E_{x}(y,t)=E_{0}(y)e^{i\omega t}}.
Подставим это в наше уравнение и получим уравнение для E0(y){\displaystyle E_{0}(y)}:
- ∂2E0∂y2=iγμωE0{\displaystyle {\frac {\partial ^{2}E_{0}}{\partial y^{2}}}=i\gamma \mu \omega E_{0}}.
Общее решение этого уравнения таково:
- Ex=A1e−ky+A2eky{\displaystyle E_{x}=A_{1}e^{-ky}+A_{2}e^{ky}}.
Учитывая, что k=iγμω=α(1+i){\displaystyle k={\sqrt {i\gamma \mu \omega }}=\alpha (1+i)}, где α=γμω2{\displaystyle \alpha ={\sqrt {\frac {\gamma \mu \omega }{2}}}}, находим
- E0=A1e−αye−iαy+A2eαyeiαy{\displaystyle E_{0}=A_{1}e^{-\alpha y}e^{-i\alpha y}+A_{2}e^{\alpha y}e^{i\alpha y}}.
При удалении от поверхности проводника (y→∞{\displaystyle y\rightarrow \infty }) второе слагаемое неограниченно возрастает, что является физически недопустимой ситуацией. Следовательно, A2=0{\displaystyle A_{2}=0} и в качестве физически приемлемого решения остаётся только первое слагаемое. Тогда решение задачии имеет вид:
- Ex=A1e−αyei(ωt−αy){\displaystyle E_{x}=A_{1}e^{-\alpha y}e^{i(\omega t-\alpha y)}}.
Взяв действительную часть от этого выражения и перейдя с помощью соотношения j=γE{\displaystyle \mathbf {j} =\gamma \mathbf {E} } к плотности тока, получим
- jx(y,t)=A1e−αycos(ωt−αy){\displaystyle j_{x}(y,t)=A_{1}e^{-\alpha y}\cos {(\omega t-\alpha y)}}.
Принимая во внимание, что jx(0,0)=j0{\displaystyle j_{x}(0,0)=j_{0}} — амплитуда плотности тока на поверхности проводника, приходим к следующему распределению объёмной плотности тока в проводнике:
- jx(y,t)=j0e−αycos(ωt−αy){\displaystyle j_{x}(y,t)=j_{0}e^{-\alpha y}\cos {(\omega t-\alpha y)}}.
Толщина скин-слоя
Объёмная плотность тока максимальна у поверхности проводника. При удалении от поверхности она убывает экспоненциально и на глубине Δ{\displaystyle \Delta } становится меньше в е раз. Эта глубина называется толщиной скин-слоя и на основании полученного выше равна
- Δ=2γμω{\displaystyle \Delta ={\sqrt {\frac {2}{\gamma \mu \omega }}}}.
Очевидно, что при достаточно большой частоте ω{\displaystyle \omega } толщина скин-слоя может быть очень малой. Также из экспоненциального убывания плотности тока следует, что практически весь ток сосредоточен в слое толщиной в несколько Δ{\displaystyle \Delta }, так, уменьшение плотности тока в 100 раз происходит на глубине ≈4,6Δ{\displaystyle \approx 4,6\Delta }, если общая толщина проводника многократно превышает толщину скин-слоя. В качестве примера приведём зависимость глубины скин-слоя от частоты для медного проводника:
| Частота | Δ{\displaystyle \Delta } | Примечания |
|---|---|---|
| 50 Гц | 9,34 мм | 50 Гц — частота электросети в большинстве стран Евразии и Африки |
| 60 Гц | 8,53 мм | 60 Гц — частота электросети в Северной, Центральной и частично Южной Америке |
| 10 кГц | 0,66 мм | |
| 100 кГц | 0,21 мм | |
| 500 кГц | 0,095 мм | |
| 1 МГц | 0,067 мм | |
| 10 МГц | 0,021 мм |
Если проводник имеет ферромагнитные свойства, то толщина скин-слоя будет во много раз меньше. Например, для стали (μ{\displaystyle \mu }=1000) Δ{\displaystyle \Delta }=0.74 мм. Это имеет значение, например, при электрификации железных дорог, поскольку там стальные рельсы используются в качестве обратного провода.
Для расчёта толщины скин-слоя в металле (приближённо) можно использовать следующие эмпирические формулы:
- Δ=c2ε0ωμmρ{\displaystyle \Delta =c{\sqrt {2{\frac {\varepsilon _{0}}{\omega \mu _{m}}}\rho }}}.
Здесь ε0{\displaystyle \varepsilon _{0}} = 8,85419·10−12 Ф/м — электрическая постоянная, ρ{\displaystyle \rho } — удельное сопротивление, c — скорость света, μm{\displaystyle \mu _{m}} — относительная магнитная проницаемость (близка к единице для пара- и диамагнетиков — меди, серебра, и т. п.), ω=2π⋅f{\displaystyle \omega =2\pi \cdot f}. Все величины выражены в системе СИ.
- Δ=503ρμmf{\displaystyle \Delta =503{\sqrt {\frac {\rho }{\mu _{m}f}}}},
ρ{\displaystyle \rho } — удельное сопротивление, μm{\displaystyle \mu _{m}} — относительная магнитная проницаемость, f{\displaystyle f} — частота.
Аномальный скин-эффект
Изложенная теория справедлива лишь при условии, что толщина скин-слоя много больше средней длины свободного пробега электронов, так как мы предполагаем, что при своём движении электрон непрерывно теряет энергию на преодоление омического сопротивления проводника, в результате чего происходит выделение джоулевой теплоты. Такое соотношение справедливо в весьма широких пределах, однако даже при комнатной температуре длина свободного пробега электрона для металлов сопоставима с глубиной скин-слоя — что говорит об аномальном характере эффекта. При очень низкой температуре ситуация только усугубляется[1]: проводимость сильно повышается, а следовательно, увеличивается длина свободного пробега и уменьшается толщина скин-слоя. При этих условиях механизм, приводящий к образованию скин-эффекта, уже не действует. Эффективная толщина слоя, в котором сосредоточен ток, изменяется. Такое явление называется аномальным скин-эффектом.
Применение
На скин-эффекте основано действие взрывомагнитных генераторов (ВМГ), взрывомагнитных генераторов частоты (ВМГЧ) и в частности ударно-волновых излучателей (УВИ).
Благодаря скин-эффекту на высоких частотах теплота выделяется преимущественно в поверхностном слое. Это позволяет раскалить проводник в тонком поверхностном слое без существенного изменения температуры внутренних областей. Данное явление используется в важном, с промышленной точки зрения, методе поверхностной закалки металлов.
Учёт эффекта в технике и борьба с ним
Скин-эффект проявляется всё более явно с увеличением частоты переменного тока, что заставляет учитывать его при конструировании и расчётах электрических схем, работающих с переменным и импульсным током. В связи с тем, что ток высокой частоты течёт по тонкому поверхностному слою проводника, активное сопротивление проводника значительно возрастает, что приводит к быстрому затуханию колебаний высокой частоты. Скин-эффект значительно влияет на характеристики катушек индуктивности и колебательных контуров, такие как добротность, на затухание в линиях передачи, на характеристики фильтров, на расчёты тепловых потерь и КПД, на выбор сечений проводников.
Для уменьшения влияния скин-эффекта применяют проводники различного сечения: плоские (в виде лент), трубчатые (полые внутри), наносят на поверхность проводника слой металла с более низким удельным сопротивлением. Серебро обладает наибольшей удельной проводимостью среди всех металлов, и тонкий его слой, в котором из-за скин-эффекта и протекает бо́льшая часть тока, оказывает заметное влияние (до 10%) на активное сопротивление проводника. Кроме того, слой сульфида, образующийся на поверхности серебра, не проводит ток и не участвует в скин-эффекте, в отличие от слоя окиси-закиси на поверхности меди, обладающего заметной проводимостью, вдобавок ещё и со свойствами полупроводника, и вносящего дополнительные потери на высоких частотах. Также применяется и покрытие золотом, у которого слой окислов отсутствует вовсе. Напротив, покрытие никелем, оловом или оловянно-свинцовым припоем способно значительно, в несколько раз увеличить сопротивление медных проводников на высоких частотах.
Так, в ВЧ аппаратуре используют катушки индуктивности из посеребрённого провода, серебрят печатные и проволочные проводники, поверхности экранов и обкладки конденсаторов, в высоковольтных линиях электропередач применяют провод в медной либо алюминиевой оболочке со стальным сердечником, в высокомощных генераторах переменного тока обмотка изготавливается из трубок, по которым для охлаждения циркулирует водород или дистиллированная вода. Также с целью подавления скин-эффекта используют систему из нескольких переплетённых и изолированных проводов — литцендрат. При передаче больших мощностей на значительные расстояние применяются линии постоянного тока — HVDC, который не подвержен воздействию скин-эффекта.
Покрытие серебром также применяется в сверхвысокочастотном оборудовании, использующем колебательные контуры особой формы: объёмные резонаторы и специфические линии передач — волноводы. Кроме того, на таких частотах особое внимание приходится уделять снижению шероховатости поверхности с целью уменьшения длины пути протекания тока.
Примечания
- ↑ Сивухин Д. В. Общий курс физики. Том 4. Оптика. — 1980. — С. 454.
Литература
- А. Н. Матвеев. Параграф 53 // Электричество и магнетизм. — М.: Высшая школа, 1983. — 463 с.
- A. A. Власов. Глава VI. Параграф 5 // Макроскопическая электродинамика. — 2-е изд.. — М.: Наука, 2005.