Форма сигнала

Изменения тока или напряжения во времени можно представить в виде различных линий, или графиков. Постоянный ток, как неизменяющийся во времени, изображается прямой линией (рис. 3.1(а)), а переменный ток — самыми различными кривыми. Форма кривой переменного тока отражает периодические изменения значения тока от максимального к минимальному, затем опять к максимальному и т. д. (рис. 3.1(б)). Несколько таких кривых показано на рис. 3.2.

Рис. 3.1. График постоянного (а) и переменного (б) токов

Цикл

Повторяющаяся часть сигнала переменного тока называется циклом сигнала. Так, на кривых, изображенных на рис. 3.2, точка А является началом цикла, а точка В — его концом и началом следующего цикла.

 

Частота

Количество циклов сигнала в единицу времени называется частотой сигнала. Единица измерения частоты — герц (Гц). Например, если цикл изменения сигнала повторяется один раз в секунду, то частота сигнала равна 1 Гц, если 10 раз — 10 Гц (рис. 3.3).

 

Рис. 3.2. Типы кривых переменного тока: синусоида (а), меандр (б), прямоугольный (в), треугольный (г), пилообразный (д), импульсы (е).

 

Длительность периода

Время, за которое завершается полный цикл изменения сигнала, называется длительностью его периода Т или просто периодом. Например, если сигнал проходит все изменения за одну секунду, то его период равен 1 если за половину секунды, то период равен 0,5 с.

Рис. 3.3. Сигналы различных частот.                     Рис. 3.4. Коэффициент заполнения меньше 1.

 

Метка и пауза

Один период прямоугольного сигнала можно разделить на метку (Mark) и паузу (Space) (рис. 3.4). Отношение длительности метки к длительности паузы называется коэффициентом заполнения. Если длительность метки t1, а длительность паузы t2, то

Длительность метки       t₁

Коэффициент заполнения = ————————————— = —

              Длительность паузы        t₂

Поскольку сигнал совершает полный цикл изменения за один период, то
Период = t1 + t2.
Если коэффициент заполнения равен 1, то
Длительность метки t1 = Длительность паузы t2.
Это можно записать иначе:
Период = 2 * Длительность паузы = 2 * Длительность метки.

 

Единицы измерения частоты ƒ:

герц, Гц; килогерц, кГц; мегагерц, МГц.

Единицы измерения периода Т:

секунда,с;

миллисекунда, мс = 1/1000 с = 10^-3 с
микросекунда, мкс = 1/1000 мс = 10^-3 мс = 10^-6 с

Рис.3.5.

 

Соотношение между частотой и периодом

Рассмотрим графики сигналов на рис. 3.5. Сигнал В имеет частоту выше, чем сигнал А, но период сигнала В составляет половину периода сигнала А. При увеличении частоты сигнала его период уменьшается, наоборот.

Следующая таблица содержит соотношения единиц измерения частоты и периода. Будет полезно, если вы ее запомните.

Частота  f	1 Гц	1 кГц	1 МГц
Период  Т	1 с	1 мс	1 мкс

 

Звуковые волны

Звуковые волны возникают в воздухе, например, когда кто-нибудь говорит или при работе громкоговорителя или пневматической дрели, при настройке по камертону и т. д. Звуковые волны изменяют давление воздуха, и воздух необходим им для распространения.
Интенсивность звуковых волн характеризуется громкостью, тон характеризует их частоту. При изменении частоты изменяется тон звука.

 

Звуковые частоты

Диапазон звуковых частот, которые воспринимаются ухом человека, называется диапазоном аудиочастот. Он простирается от 20 Гц до 20 кГц. Звуки частотой ниже 20 Гц и выше 20 кГц человек не слышит. На основе этого создан специальный свисток для подзыва собаки. Частота звукового сигнала этого свистка превышает 20 кГц, поэтому собаки, имеющие более широкий частотный диапазон чувствительности уха, слышат его, а человек — нет.

Чистые и инструментальные тоны

Чистым тоном называется простое синусоидальное колебание, содержащее одну частоту (рис. 3.2(а)). Инструментальный тон представляет собой сложное колебание, состоящее из ряда синусоидальных колебаний разной частоты (рис. 3.1(б)). Такие звуковые колебания возникают, когда звучит речь или музыка.

 

Гармоники

При сложении нескольких различных по частоте синусоидальных колебаний возникает сложное колебание. И наоборот, сложный сигнал можно разложить на ряд входящих в него чистых синусоидальных колебаний. Среди этих простых синусоидальных колебаний различают основную, или первую, гармонику и набор гармоник. Таким образом, любой сложный сигнал может быть разложен на следующие компоненты:

1. Первая, или основная, гармоника. Простое синусоидальное колебание, имеющее тот же период, что и исходное сложное колебание.
2. Набор гармоник. Простые синусоидальные колебания, частоты ко¬торых кратны частоте основной гармоники. Например, если частота первой гармоники равна 100 Гц, то

частота 2-й гармоники = 2 * 100 = 200 Гц;
частота 3-й гармоники = 3 * 100 = 300 Гц;
частота 4-й гармоники = 4 * 100 = 400 Гц и т. д.

Чем больше номер гармоники, т. е. чем выше ее частота, тем меньше ее амплитуда. Поэтому высшими гармониками обычно пренебрегают.

 

Высота тона
Высота тона звуковой волны указывает, в какой части диапазона звуковых частот находится ее частота.
Звуки высокой тональности занимают верхнюю половину диапазона аудиочастот, а звуки низкой тональности — нижнюю половину. Женские голоса обычно имеют более высокую тональность, чем мужские. Барабан издает низкие звуки, а флейта — очень высокие, В сложном колебании частота основной гармоники определяет тональность сигнала.

 

Качество звука
Качество звука определяется числом гармоник инструментального сигнала, которые воспроизводятся аппаратурой без искажения.

 

Примеры некоторых сложных сигналов

1. Основная гармоника + 3-я гармоника (рис. 3.6).
2. Основная гармоника + 2-я гармоника (рис. 3.7).

Рис. 3.6. Основная гармоника + 3-я гармоника (аппроксимация прямоугольного сигнала).

Рис. 3.7. Основная гармоника + 2-я гармоника (аппроксимация пилообразного сигнала).

 

Гармонические составляющие прямоугольного сигнала

Прямоугольный сигнал содержит основную гармонику плюс бесконечное множество нечетных гармоник. Например, прямоугольный сигнал частотой 1 кГц состоит из

основной гармоники 1 кГц;
3-й гармоники 3*1 = 3 кГц;
5-й гармоники 5*1 = 5 кГц;
7-й гармоники 7*1 = 7 кГц и т. д.

Заметим, что сложные колебания, содержащие только нечетные гармоники, имеют круто нарастающие фронты и резко спадающие срезы. Чем больше нечетных гармоник содержит сигнал, тем ближе его форма к форме прямоугольного сигнала.

 

Гармонические составляющие пилообразного сигнала
Пилообразный сигнал содержит основную гармонику плюс бесконечное множество четных гармоник. Например, пилообразный сигнал частотой 1 кГц состоит из

основной гармоники 1 кГц;
2-й гармоники 2*1 = 2 кГц;
4-й гармоники 4*1 = 4 кГц;
6-й гармоники 6*1 = 6 кГц и т. д.

 

В этом видео рассказывается о различных видах электрических сигналов:

Добавить комментарий

6. Классификация сигналов в радиоэлектронике. Гармонические сигналы и их описание

Одномерные и многомерные сигналы. Рассмотрим напряжение на зажимах какой-либо цепи. Такой сигнал, описываемый одной функцией времени u(t), принято называть одномерным.

Множество одномерных сигналов образует многомерный сигнал. Например, система напряжений на зажимах многополюсника образует многомерный или векторный сигнал:

u(t) = {u1(t), u2 (t), …, uN (t)} r , целое число N называют размерностью сигнала.

Детерминированные и случайные сигналы. Если математическая модель позволяет точно предсказать мгновенные значения в любой момент времени, то сигнал называется детерминированным. Строго говоря, чисто детерминированных сигналов не существует, так как всегда есть множество неучтённых факторов, вызывающих хаотическое изменение исследуемой физической величины. Однако, если эти факторы вызывают лишь незначительный разброс значений физической величины вблизи предсказанного моделью, то такой сигнал считают детерминированным.

Сигнал, точное предсказание значений которого в любой момент времени невозможно, называют случайным.

Непрерывные и импульсные сигналы. Если сигнал описывается непрерывной функцией времени s(t), то его называют непрерывным.

Очень важный для радиотехники класс сигналов представляют собой импульсы, которые существуют лишь в пределах конечного отрезка времени. Самым замечательным для импульсных сигналов является то, что они позволяют получить колебания значительной интенсивности во время действия импульса при весьма умеренной средней мощности передатчика.

Различают видеоимпульсы (рис. 1.1, а) и радиоимпульсы (рис. 1.1, б). Отношение 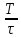называют скважностью импульсов.

а б

A – амплитуда рис 1.1 Ub (t) – огибающая

τ – длительность cos(ω0t + ϕ) – заполнение

tφ – длительность фронта

T – период следования

Аналоговые, дискретные и цифровые сигналы. Чаще всего, физический процесс, порождающий сигнал, развивается во времени таким образом, что значения сигнала можно измерять в любой момент времени. Такой сигнал называют аналоговым. Его реализация во времени даёт некоторую функцию s(t), определённую в любой момент времени t.

В отличие от аналогового, дискретный сигнал задаётся последовательностью его значений s(ti ) в дискретные моменты времени (рис. 1.2).Как правило, шаг дискретизации Δt = ti+1 − ti для такого сигнала постоянен.

Одно из преимуществ дискретных сигналов по сравнению с аналоговыми – отсутствие необходимости воспроизводить сигнал непрерывно во все моменты времени. Это даёт возможность передавать несколько дискретных сигналов по одному и тому же каналу связи за счёт их разделения по времени (временное мультиплексирование сигналов).

При переходе от исходного аналогового сигнала к его дискретному представлению очень важную роль играет правильный выбор шага дискретизации Δt . При слишком малом Δt возрастают, причём неоправданно, объём и сложность обрабатывающей аппаратуры, тогда как при слишком большом Δt возрастает вероятность искажения или потери информации при восстановлении аналогового сигнала по его дискретному изображению.

Существует теорема (теорема Котельникова), которая позволяет для заданного аналогового сигнала найти Δt max такое, что выбор Δt ≤ Δt max гарантирует пренебрежимо малые потери информации при дискретизации и последующем восстановлении рассматриваемого аналогового сигнала.

Особой разновидностью дискретных сигналов являются цифровые сигналы, в которых отсчётные значения s ti представлены в форме чисел. Обычно используется двоичное представление чисел с ограниченным числом разрядов, как правило, не слишком большим. Например, при 8-разрядном кодировании (1-й разряд – знаковый) имеется возможность передавать ±128 градаций исходного аналогового сигнала, что даёт точность лучше одного процента.

рис 1.2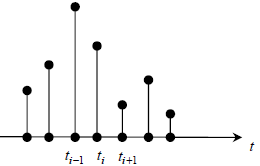

Гармоническое колебание — явление периодического изменения какой-либо величины, при котором зависимость от аргумента имеет характер функции синуса или косинуса. Гармонические колебания можно представить различными способами: функциями времени; вращающимися векторами; комплексными числами; амплитудными и фазовыми спектрами.

Отличительные черты гармонич. колеб.: Простота технической реализации генераторов; Минимальная полоса частот занимаемая гарм. кол.; неизменность формы гарм. кол. При прохождении через линейную цепь с постоянными пораметрами.

Косинусоидальные синусоидальные функции времени 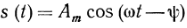где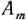-амплитуда,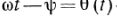-фаза, которую в момет времени (t=0) называют начальной:

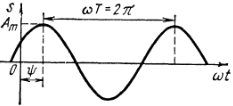Положительный период колебания Т выражают в секундах. Число периодов за секунду называют частотой колебания f= 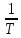и выражают в герцах. Величин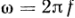у называют угловой частотой и выражают в радианах в секунду.

Векторное представление из выражения 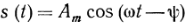видно что гарм. кол. характеризуются амплитудой и фазой (аналогично определяется положение вектора на плоскости). Так как фаза в течении времени меняется, то вектор изоброжающий колебания вращается с постоянной угловой скоростью . При анализе электрической цепи, находящейся под воздействием источников гармонических ЭДС с одинаковыми частотами токи и напряжения в цепи, удобнее изоброжать неподвижными векторами. При этом длина вектора принимается равной амплитуде колебания, а угол поворота — начальной фазе.

Комплексное представление – комплексное число полностью характеризуется модулем Аm и аргументом (альфа), аналогичными амплитуде и фазе гарм. колеб. Комплексное число называют комплексной амплитудй гарм. колеб..

Расчёт эл. Цепей более удобен если воздействие задаётся комплексной амлитудой. Результаты также выдаются в виде комплексных амплитуд. По комплексным амплитудам определяют амплитуды и начальные фазы и записывают гармонич. Функции

Гармонический сигнал — это… Что такое Гармонический сигнал?



Гармонический сигнал

1. Гармонический сигнал

А — амплитуда гармоничного сигнала;

w — круговая частота;

j — начальная фаза

Словарь-справочник терминов нормативно-технической документации. academic.ru. 2015.

• Гармонический корректор аппаратуры системы передачи с ЧРК
• Гармошка

Смотреть что такое «Гармонический сигнал» в других словарях:

• гармонический сигнал — ; А амплитуда гармоничного сигнала; w круговая частота; j начальная фаза Примечание Периодический сигнал может быть образован путем периодического повторения импульсов. Соответствующие термины и определения для такого сигнала вводятся так же, как …   Справочник технического переводчика

• Гармонический сигнал — Гармонический сигнал  это гармонические колебания со временем распространяющиеся в пространстве, которые несут в себе информацию или какие то данные и описываются уравнением: где А  амплитуда сигнала;   фаза гармонического сигнала; …   Википедия

• Контрольный гармонический сигнал — Сигнал, по которому устанавливается оптимальная загрузка радиопередатчика. Его уровень должен быть выше среднего уровня группового сигнала УПС в зависимости от значения пик фактора сигнала Источник: ГОСТ 24695 81: Устройства прео …   Словарь-справочник терминов нормативно-технической документации

• Сигнал (техника) — Сигнал в теории информации и связи называется материальный носитель информации, используемый для передачи сообщений по системе связи. Сигналом может быть любой физический процесс, параметры которого изменяются в соответствии с передаваемым… …   Википедия

• Сигнал — У этого термина существуют и другие значения, см. Сигнал (значения). Эта статья или раздел нуждается в переработке. Пожалуйста, улучшит …   Википедия

• Гармонический анализатор —         вычислительное устройство для нахождения амплитуд гармоник сложных периодических функций (См. Периодическая функция). Применяются при динамических исследованиях кривошипно шатунных механизмов двигателей, для предварительной оценки влияния …   Большая советская энциклопедия

• Электрический сигнал — Сигнал это физический процесс, содержащий в себе некоторую информацию. На практике чаще всего используются электрические сигналы. При этом носителем информации является изменяющиеся во времени ток или напряжение в электрической цепи.… …   Википедия

• модулированный сигнал — Сигнал, мгновенные значения которого пропорциональны произведению мгновенных значений двух или более сигналов, взятых в один и тот же момент времени. Сигнал, являющийся результатом взаимодействия двух или более сигналов, называемого модуляцией.… …   Справочник технического переводчика

• Случайный сигнал — Случайные сигналы сигналы, мгновенные значения которых (в отличие от детерминированных сигналов) не известны, а могут быть лишь предсказаны с некоторой вероятностью, меньшей единицы. Характеристики таких сигналов являются статистическими, то есть …   Википедия

• непрерывный сигнал — 06.01.20 непрерывный сигнал [ continuous wave]: Непрерывный гармонический сигнал заданной частоты, поступающий от устройства считывания/опроса и обеспечивающий электропитание пассивной радиочастотной метки, не подвергнутый амплитудной и/или… …   Словарь-справочник терминов нормативно-технической документации

3. Гармонический сигнал:

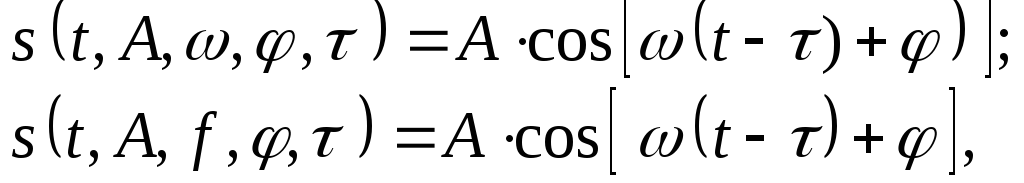
где — значение сигнала,

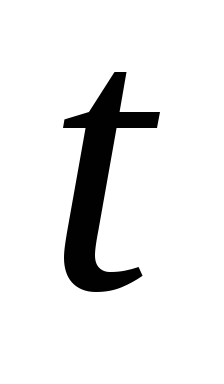— время (с).

Параметрами гармонического сигнала являются:

— его амплитуда,

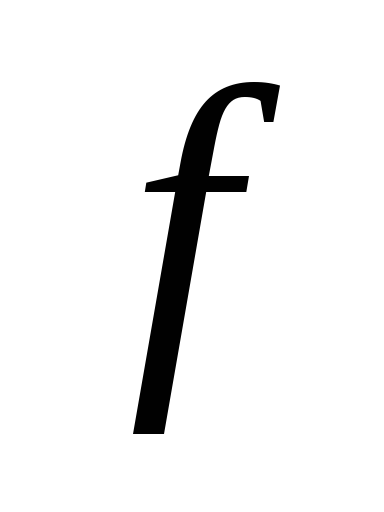— частота изменения сигнала в герцах (Гц),

— круговая частота изменения сигнала (рад/с)

— начальная фаза сигнала,

— задержка сигнала во времени.

Задание 1

Сохраните файл в Mathcad под названием, соответствующем Вашей фамилии.

Введите значения параметров сигнала по Вашему выбору.

Постройте график изменения сигнала и сигналов, получаемых в результате дифференцирования и интегрирования исходного сигнала от нуля до текущего значения.

Изменяя значения параметров сигнала, изучите по изменениям графика влияние параметров на характер изменения сигнала, а также результатов его дифференцирования и интегрирования.

4. Сигнал – функция включения (функция Хэвисайда).

Используя полученные знания по основам программирования в Mathcad, введите функцию единичного скачка в соответствии с ее определением:

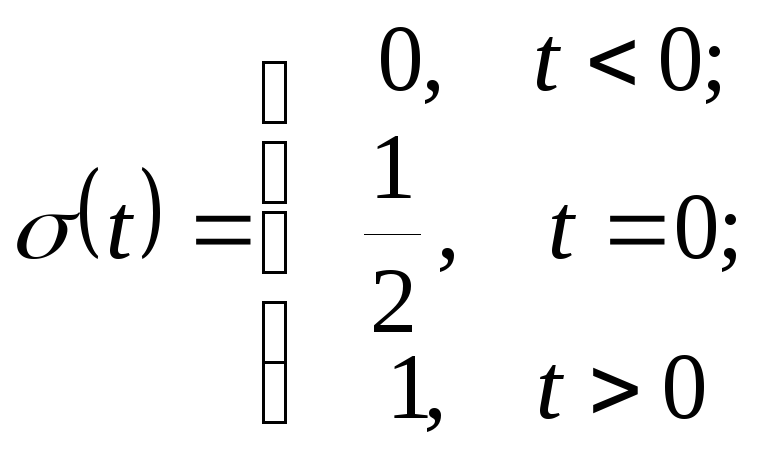
и введением функции Heviside step из окна ввода функций f(x):

Задание 2

Постройте графики изменения сигналов:

Обсудите полученные результаты.

3. Импульс Дирака (δ – импульс, функция Дирака)

Задание 3

Введите выражение для импульса Дирака в соответствии с определением:

,

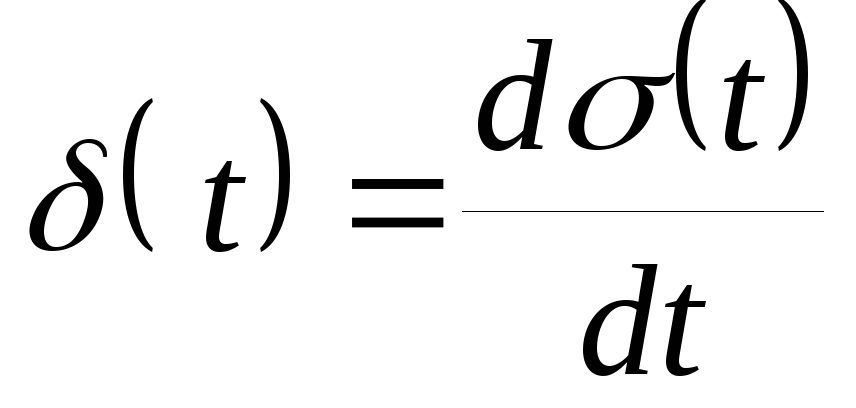Определите значение интеграла:

при ,

не проводя интегрирование, но используя стробоскопическое свойство импульса Дирака.

4. Периодические сигналы

Периодическими называются сигналы, повторяющиеся бесконечно с периодом или частотой, измеряемой в Герцах, или с круговой частотой, измеряемой в.

Периодические сигналы, отвечающие условиям Дирихле, могут быть представлены в виде бесконечной суммы отдельных гармонических сигналов с частотами кратными частотеповторения периодического сигнала, а также с различными амплитудамии начальными фазами. Эта сумма образует ряд Фурье для периодического сигнала.

Наборы амплитуд гармонических составляющих и их начальных фазобразуют амплитудный и фазовый спектры периодического сигнала. Форма спектров, то есть зависимость значений амплитуд и начальных фаз от индексаили частотысоответствующей гармоники, полностью определяется формой периодического сигнала.

Задание 4

Представьте графически:

• меандр с амплитудой в 5 В и частотой 1000 Гц и

• пилообразное напряжение, меняющееся от –5 В до +5 В с частотой 100 Гц.

Эти сигналы пропускаются через усилитель с ограниченным частотным диапазоном.

Изобразите графически, как будет выглядеть сигнал на выходе усилителя с частотным диапазоном 1 кГц, 5 кГц, 10 кГц, 20 кГц.

Лабораторная работа №2: Изучение спектров периодических сигналов

Задан периодический сигнал в виде последовательности импульсов, возникающих в результате заполнения синусоидально изменяющегося напряжения с амплитудойи частотойсинусоидальными колебаниями с частотой 4000 Гц.

Порядок выполнения работы:

— введите аналитическое выражение для импульса s(t) и его параметров,

— изобразите сигнал графически на промежутке времени, немного большем периода его повторения,

— введите индекс k=0..50 в форме ранжированной переменной с вторичной палеты инструментов Matrix, численное значение периода T повторения сигнала и его основной частоты f=1/T и определение мнимой единицы ,

— запишите выражение для элементов комплексного спектра сигнала,

— постройте графически амплитудный спектр сигнала и его фазовый спектр,

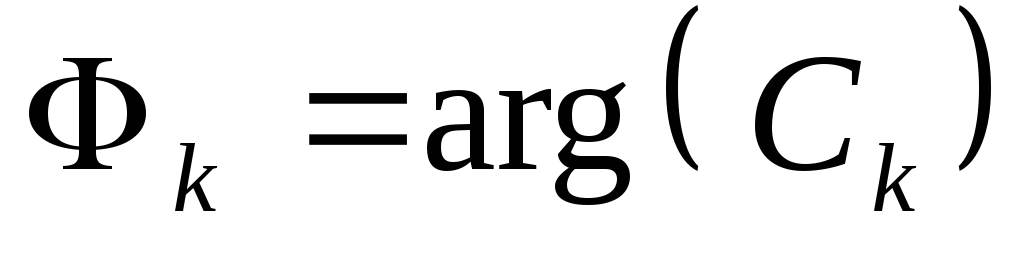— опишите особенности спектра и определите его эффективную ширину,

— запишите аналитическое выражение для сигнала, который получился бы на выходе усилителя с полосой пропускания, равной эффективной ширине спектра сигнала,

— постройте графически в единой системе координат графики исходного сигнала и сигнала на выходе усилителя, опишите характер расхождений сигналов,

— постройте графически погрешность воспроизведения сигнала и вычислите его среднеквадратическое отклонение в %% от наибольшего значения сигнала.

2)Гармонические колебания (рис.2.4.).

S(t) = A_mcos(t — ₀).

Его параметрами являются: A_m – амплитуда ,  — частота, ₀ –начальная фаза. Это пример непрерывного сигнала.

Непериодические сигналы – это сигналы, которые описываются непериодическими функциями времени. Однако их можно рассматривать как периодические, для которых Т .

Примеры непериодических сигналов.

1) Сигнал типа единичная функция (ступенчатый сигнал, функция Хевисайда, рис.2.5.).

2) Одиночный прямоугольный импульс – это сигнал, форма которого прямоугольная (рис.2.6).

3) Сигнал типа (дельта – функция, функция Дирака, рис. 2.7.).

0, t<0

(t)= , t=0

0, t>0

Э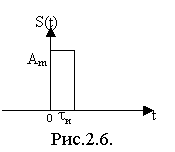та функция обладает свойствами: 1.;

2.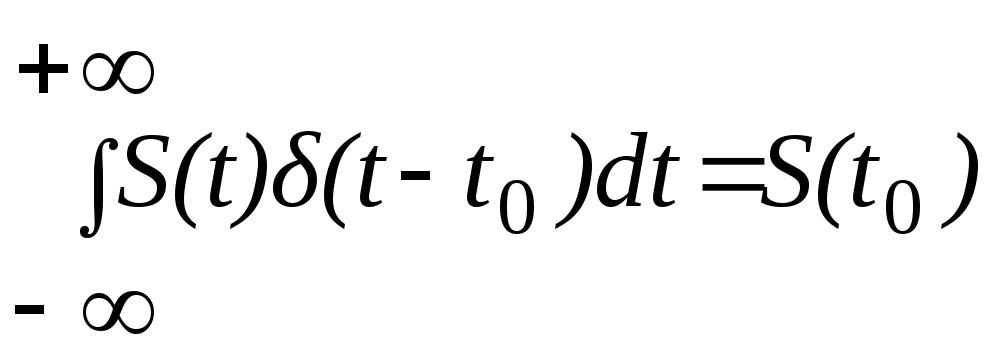-это

соотношение называют, фильтрующее свойство дельта – функции.

Случайные сигналы – это сигналы характер изменения, которых заранее предсказать невозможно. Именно эти сигналы несут информацию о состоянии интересующего нас объекта. С математической точки зрения такие сигналы описываются методами теории вероятности или случайных процессов. Разновидностью случайных сигналов являются помехи – сигналы, которые накладываются на передаваемые сообщения и искажают его характер. По природе происхождения помехи бывают: атмосферные, индустриальные и флуктуационные.

Флуктуационные помехи связаны , с хаотичным движением свободных носителей зарядов в самих элементах электрических цепей.

2.2. Гармоническое колебание и способы его представления

Гармоническим называется колебание, которое описывается гармонической функцией времени: sin(t), cos(t).

Г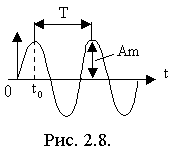армоническое колебание, а также сигнал произвольной формы могут быть представлены в следующих формах:

1) временное представление сигнала;

2) комплексное представление;

3) векторное представление;

4) спектральное;

5) операторное.

1) При временном представлении сигнал записывается в виде аналитической функцией времени: .

Его график – называется временной диаграммой (рис.2.8.). Основными параметрами гармонического сигнала являются:

1. Амплитуда — A_m (наибольшее отклонение от нуля гармонической функции). Размерность амплитуды связана с физической природой сигнала.

2. Период — T (минимальное расстояние между точками находящимися в одной фазе), ω=2π/T — круговая частота, f=1/T – циклическая частота. Их размерность: T  [сек]; f  [Гц]; ω  [рад/сек].

3. ₀=ωt₀ – начальная фаза гармонического колебания гармонического колебания; t₀ – временной сдвиг, если t₀>0, то это означает опережение, если t₀<0, то это означает задержку сигнала, относительно сигнала с t₀=0.

4. Ψ_(t) = (ωt + φ₀) – полная фаза гармонического колебания.

5. ω(t) = dΨ_(t)/dt – мгновенная частота.

2) При комплексном представлении гармоническое колебание, как функция времени, заменяется комплексной амплитудой, т. е. комплексным числом независящим от времени. Это делается для упрощения записи и выполнения операций над гармоническими функциями.

Вспомним комплексные числа. — комплексное число. Его можно записать в одной из трех форм: алгебраической, показательной и тригонометрической:

= ,

где ,

Re[Z] — реальная часть, Im[Z] — мнимая часть

комплексного числа Z.

На рис. 2.9 показано геометрическое представление

комплексного числа на комплексной плоскости. Здесь:

А – mod[Z] – модуль комплексного числа Z, или А=(а²+b²)^1/2 — длины вектор комплексного числа.

φ=arg[Z] – аргумент комплексного числа Z, или φ₀ = arctg(b/a) – начальная фаза.

Выражение А_me^j(ωt+φ) называют комплексом гармонической функции. Тогда учитывая, что Аcosφ = Re{Ae^jφ}, можно записать

Комплексную величину называют комплексной амплитудой гармонического сигнала, а е^jωt – множитель вращения. Комплексная амплитуда содержит информацию о двух важнейших параметрах гармонического сигнала – об амплитуде и о начальной фазе. Комплексная амплитуда и гармоническая функция времени, при известной частоте ω, связаны взаимнооднозначно, т. е.

.

Например: гармоническому колебанию u(t)=256cos(2π100t — 45⁰) соответствует комплексная амплитуда — Ù_m = 256e^—j45 , справедливо и обратное.

3) Векторное представление сигнала – это представление сигнала вектором на комплексной плоскости. Рассмотрим векторное представление следующих сигналов:

а) комплексное гармоническое колебание — гармонический комплекс:

s(t)= А_me^j(ωt-φ)= Å_me^j(ωt) ,

где e^jωt – множитель вращения.

На комплексной плоскости гармонический комплекс представляется вектором А_m c начальной фазой -φ₀, который вращается против часовой стрелки с частотой ω.

б) гармоническое колебание s(t) = A_mcos(ωt- φ₀)= Re{À_me^jωt}.

На комплексной плоскости гармоническое колебание представляется проекцией вращающегося с частотой ω против часовой стрелки вектора гармонического комплекса на реальную ось.

в) Комплексная амплитуда 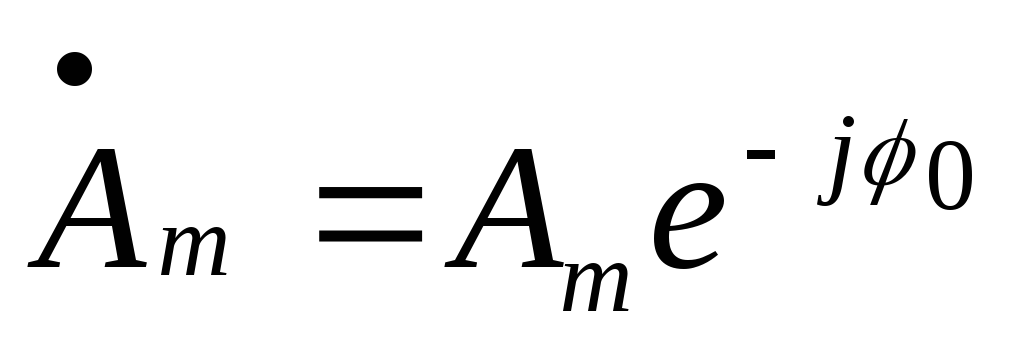. На комплексной плоскости она представляется в виде неподвижного вектора с амплитудой A_m и начальной фазой -₀.

3. Спектральное представление сигнала.

4. Операторное представление сигнала.

Два последних способа описания сигнала рассмотрим подробнее.

Меандр (радиотехника) — Википедия

Материал из Википедии — свободной энциклопедии

Меа́ндр (по названию геометрического орнамента в виде ломаной линии) — периодический сигнал прямоугольной формы, широко используемый в радиотехнике и электронике. Меандр может быть знакопеременным (двухполярным) или однополярным. Во втором случае длительность импульса и длительность паузы между импульсами равны, то есть в этом случае меандр — периодический сигнал прямоугольной формы, имеющий скважность 2 (или коэффициент заполнения 0,5).

Математически меандр можно описать многими разными способами, например, через функцию сигнум:

 x(t)=sgn⁡(sin⁡(t)).{\displaystyle \ x(t)=\operatorname {sgn}(\sin(t)).}

Или через функции Хевисайда h(t){\displaystyle h(t)}:

 x(t)=∑n=−∞+∞(h[t−nT+12]−h[t−nT−12]).{\displaystyle \ x(t)=\sum _{n=-\infty }^{+\infty }\left(h\left[t-nT+{1 \over 2}\right]-h\left[t-nT-{1 \over 2}\right]\right).}

Для того, чтобы скважность равнялась 2 необходимо положить T=2.{\displaystyle T=2.}

И многими другими способами.

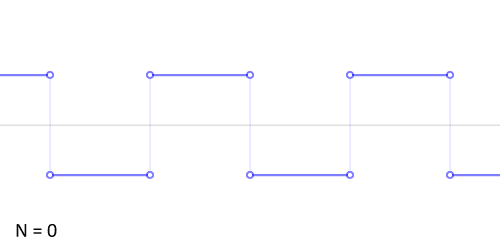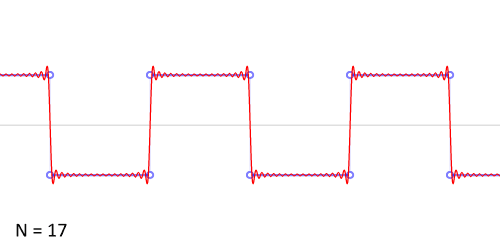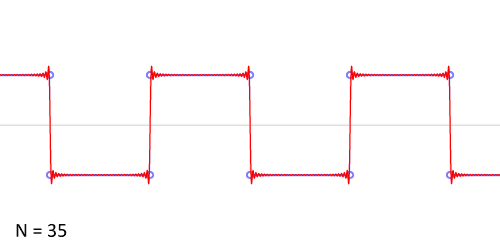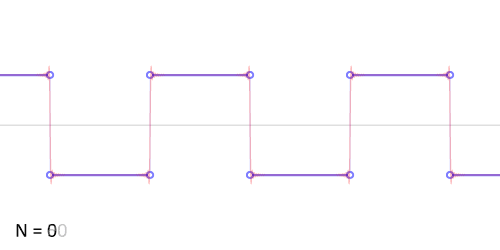Синтез меандра из набора гармоник периодического сигнала. Чем больше число гармоник, тем ближе к идеальной форма сигнала. Выбросы на фронтах обусловлены неравномерной сходимостью ряда Фурье в точках разрыва.

Разложение меандра с нарастающим фронтом при t=0{\displaystyle t=0} в ряд Фурье дает:

xмеандр(t)=4π∑k=1∞sin⁡(2π(2k−1)ft)2k−1==4π(sin⁡(2πft)+13sin⁡(6πft)+15sin⁡(10πft)+…).{\displaystyle {\begin{aligned}x_{\text{меандр}}(t)&={\frac {4}{\pi }}\sum _{k=1}^{\infty }{\frac {\sin \left(2\pi (2k-1)ft\right)}{2k-1}}=\\&={\frac {4}{\pi }}\left(\sin(2\pi ft)+{\frac {1}{3}}\sin(6\pi ft)+{\frac {1}{5}}\sin(10\pi ft)+\dots \right).\end{aligned}}}

Примечательно, что в спектре меандра отсутствуют чётные гармонические составляющие (гармоники). Амплитуда нечетных гармоник обратно пропорциональна их частоте с нулевым сдвигом фазы.

Прямоугольные сигналы в радиотехнике и электронике[править | править код]

Истинный меандр с нулевой длительностью фронтов физически нереализуем.^{[источник не указан 594 дня]} В радиотехнике и электронике меандром обычно называют сигналы со скважностью 2 и длительностями фронтов много меньших периода повторения сигнала.

Сигнал приближённо такого вида (с ненулевой длительностью фронтов и спадов) генерируется различными автогенераторами, например, мультивибраторами, выполненными на транзисторах, логических элементах, операционных усилителях). Также сигналы такого типа обычно присутствуют практически во всех цифровых схемах, например, двоичный триггер со счетным входом, переключаемый периодическими импульсами даёт на выходе меандр.

Гармонический состав — Википедия

Материал из Википедии — свободной энциклопедии

Гармонический состав тока определяет его форму сигнала и содержит в себе основную и побочные, высокочастотные гармоники, которые накладываются друг на друга.

На данный момент развитие тяговых электродвигателей находится на стадии, когда конструктивные изменения уже не возможны или нецелесообразны, и для того чтобы повысить эффективность того или иного двигателя, а так же снизить негативное воздействие на взаимодействующие с системой приборы безопасности и связи, разрабатываются и применяются методы подавления побочного гармонического состава

Методы подавления:[править | править код]

1. Через введения снаббер-конденсатора;
2. Через широтно-импульсную модуляцию; Обобщенная ступенчатая форма сигнала напряжения
3. Выборочное гармоническое устранение;

Рисунок справа показывает, что обобщенная ступень симметричной четверти волны — это форма сигнала напряжения, синтезируется (2м+ 1) — уровневым инвертором, где m это количеством углов переключения. Путем применения анализа ряда Фурье, амплитуда любой нечетной энной гармоники со ступенчатой формой сигнала может быть выражена как hn=4nπ∑k=1m[Vkcos(nak)]{\displaystyle h_{n}={\frac {4}{n\pi }}\sum _{k=1}^{m}[V_{k}cos(na_{k})]}, (1)

где V_k является k-ым уровнем напряжения постоянного тока, n является порядком нечетной гармоники, m количество углов переключения и a_k угол переключения k. Согласно Рис. 16, a₁ до a_m, должен удовлетворить а₁ <а₂ <• • • <а_m <π /2.

Тогда как амплитуды всех четных гармоник будут нулевыми.

Для минимизации гармонического искажения и достижения нужной амплитуды фундаментального компонента, вплоть до m — 1 гармонической составляющей может быть удалена из формы сигнала напряжения. В целом старшие низкочастотные гармоники могут быть выборочно устранены путем надлежащего выбора углов среди разноуровневых инверторов, а высокочастотные гармонические составляющие могут быть  удалены при помощи дополнительных фильтров.Согласно (1), для поддержания количества устраненных гармоник на постоянном уровне все углы переключения должны быть меньше, чем π/2. Однако, если углы переключения не будут удовлетворять этому условию, то схема не будет функционировать.

В результате данная стратегия модуляции в основном обеспечивает узкий диапазон коэффициента модуляции, который является его основным недостатком. Например, в семиуровневой шаговой форме сигнала, ее коэффициент модуляции варьируется от 0,5 до 1,05. Если коэффициент модуляции ниже, чем 0,5 применение схемы все еще возможно, допустимые гармонические составляющие, которые можно устранить, уменьшаться с 2 до 1. Суммарный коэффициент гармонических искажений (THD) увеличится соответственно.