Функция тока — это… Что такое Функция тока?

Функция тока — Функция тока  скалярная функция в гидродинамике, которая задаёт двумерное течение жидкости. Содержание 1 Определение 2 Обобщения 3 Неоднозначность …   Википедия

функция тока — (Ψ) Скалярная функция, являющаяся следствием уравнения неразрывности и сохраняющая постоянное значение вдоль линий или поверхностей тока. Примечание Функция тока используется для описания плоскопараллельного и осесимметричного течений; ее… …   Справочник технического переводчика

функция тока — функция тока — скалярная функция ψ пространственных координат и времени t, сохраняющая неизменным своё значение на линии тока, то есть удовлетворяющая условию Vgradψ = 0, где V — вектор скорости. В аэро и гидродинамике существование… …   Энциклопедия «Авиация»

функция тока — функция тока — скалярная функция ψ пространственных координат и времени t, сохраняющая неизменным своё значение на линии тока, то есть удовлетворяющая условию Vgradψ = 0, где V — вектор скорости.

В аэро и гидродинамике существование… …   Энциклопедия «Авиация»

функция тока — Скалярная функция координат и времени, принимающая в любой момент времени постоянное значение на каждой линии тока и пропорциональная расходу жидкости между поверхностями тока …   Политехнический терминологический толковый словарь

функция стабилизации работы (дифференциальной) защиты по второй гармонике пускового тока — стабилизация работы (дифференциальной) защиты по второй гармонике пускового тока [Интент] Тематики релейная защита Синонимы стабилизация работы (дифференциальной) защиты по второй гармонике пускового тока EN inrush restraint of differential… …   Справочник технического переводчика

функция очередности пуска (компрессоров) — [Перевод Интент] Параллельные тексты EN RU Staggered start feature If there is a power shortage, units will not restart at the same time. To make this feature available, units have to be addressed with a different number between 1 and 12. The… …   Справочник технического переводчика

функция контроля трансформатора тока

— [Интент] Тематики релейная защита EN current transformer supervision function …   Справочник технического переводчика

ДИССИПАТИВНАЯ ФУНКЦИЯ — функция рассеяния, функция, вводимая для учета влияния сил вязкого трения на движение механич. системы. Д. ф. характеризует степень убывания механич. энергии этой системы; вводится также вообще для учета перехода энергии упорядоченного движения в …   Математическая энциклопедия

ГОСТ Р 50345-2010: Аппаратура малогабаритная электрическая. Автоматические выключатели для защиты от сверхтоков бытового и аналогичного назначения. Часть 1. Автоматические выключатели для переменного тока

— Терминология ГОСТ Р 50345 2010: Аппаратура малогабаритная электрическая. Автоматические выключатели для защиты от сверхтоков бытового и аналогичного назначения. Часть 1. Автоматические выключатели для переменного тока оригинал документа: 3. 5.12… …   Словарь-справочник терминов нормативно-технической документации

Функция тока для безвихревого течения

Член, стоящий в правой части уравнения, получается применением формулы (1) = ур Т8 — Н ). Для безвихревого течения правая часть обращается в нуль. В этом случае потенциал скорости удовлетворяет уравнению, мало отличающемуся от уравнения для функции тока   [c.126]

В отличие от потенциала скоростей ф, существующего только для безвихревых течений, функция тока являющаяся решением уравнения неразрывности, существует и для вихревых плоских и пространственных осесимметричных течений.  [c.438]

Определим потенциальную функцию ф(х, у) и функцию тока у) для некоторых простейших случаев безвихревого течения несжимаемой жидкости.  [c.108]

Введенную функцию ч 5(х, у) принято называть функцией тока. Подставляя (4.5) в (4.1), получаем, что и эта функция, так же как и потенциал скорости ф(д , у), удовлетворяет уравнению Лапласа. Если потенциал скорости описывает поле скоростей только безвихревого (потенциального) течения, то функция тока может быть введена всегда, так как условие ее существования следует из уравнения неразрывности, справедливого для любых течений. Однако уравнению Лапласа эта функция будет удовлетворять только для потенциального потока. Поскольку y)=udy—  

[c.80]

Уравнение (4.9.3) имеет чисто кинематическую природу и получено без введения каких-либо динамических предположений. Оно применимо, например, к любому классу течений несжимаемой жидкости, для которых такое течение динамически возможно. Этот вопрос можно всегда решить прямой подстановкой в уравнения движения этой функции тока. В частности, отметим, что выражение (4.9.3) удовлетворяет уравнениям безвихревого дви-  

[c.127]

Чаплыгин исследовал установившееся безвихревое дозвуковое течение нетеплопроводного идеального газа, для которого плотность и давление связаны законом адиабаты. Использование интеграла Бернулли и уравнения неразрывности приводит к нелинейным дифференциальным уравнениям для потенциала скоростей и функции тока в плоскости ху (физическая плоскость). Чаплыгин предложил метод линеаризации выведенных им уравнений, основанный на преобразовании годографа он вводит новые независимые переменные 0 и т = F /2p, где 0 и F — полярные координаты скоро-  

[c.310]

Функции комплексного переменного. Хотя все двухмерные потоки могут быть исследованы методами, изложенными в предыдущих главах, однако более действенным средством их представления является теория комплексных переменных. Функция потенциала и функция тока всякого плоского безвихревого потока могут рассматриваться как действительная и мнимая части функции комплексного переменного, и наоборот. Рассматривая различные функции, можно установить большое число двухмерных потенциальных (безвихревых) течений, представляемых этими функциями. Более того, оказывается теоретически возможным непосредственное определение потенциальной функции, удовлетворяющей заданным граничным условиям, ибо теория показывает, как преобразовать произвольную форму в круг и таким образом отобразить характер течения произвольной формы на круге, решение для которого дано в главе III.

 [c.136]

Так как при выводе интеграла (49) на с1х, йу, йг мы не налагали ограничений, то постоянная в уравнении (50) будет универсальной. Интеграл Лагранжа в форме (50) будет совпадать с интегралом Бернулли (33), полученным для безвихревого стационарного движения идеальной жидкости. Интеграл Бернулли (32), полученный интегрированием уравнений Эйлера вдоль линии тока, отличается от интеграла Лагранжа, так как постоянная в интеграле (32) может быть различной для разных линий тока. Движение жидкости, при котором постоянная в интеграле Бернулли универсальна для всех линий тока, есть потенциальное движение. Пользуясь уравнениями (48), можно доказать очень важную теорему Лагранжа если для движущейся жидкости при действии сил, имеющих потенциальную функцию, в какой-нибудь момент времени существует потенциал скоростей, то течение будет потенциальным во все время движения. В самом деле, уравнения (48) можно записать в следующей форме   [c. 280]

Уравнение импульса показывает тогда, что переменная часть давления Ар О ). При этом граница О В области О в первом приближении должна оставаться прямой. Теория малых возмуш ений, применяемая к сверхзвуковому потоку 1, показывает, что отклонение наклона О В от прямой О (е ). Для получения стационарного решения температура газа То в области О в первом приближении равна температуре стенки Т . Плотность ро тогда в первом приближении постоянна и соответствует значениям р = Ро, Т = То. Подстановка приведенных оценок в уравнения Навье-Стокса и совершение предельного перехода е О показывает, что течение в области О описывается полными уравнениями Эйлера для невязкой несжимаемой жидкости. Движение остается безвихревым, так как все струйки тока начинаются при хд +оо из состояния покоя (втекая затем в зону смешения). Для функции тока можно написать уравнение Лапласа  

[c.39]

При проведении расчетов по определению параметров потока,, обтекающего тела, следует помнить, что для всех значений функции тока, меньших (В), поток будет безвихревым, т. е. в области между телом и линией тока ВВ Р, проходящей через точку В ударной волны, течение потенциальное. Это является следствием того, что начальный участок ударной волны мы приближенно заменили коническим скачком, за которым энтропия всех частиц газа одинакова.  

[c.393]

Простейшим и наиболее глубоко и всесторонне изученным случаем интегрирования уравнений Эйлера для идеальной несжимаемой жидкости является так называемое безвихревое движение или движение с потенциалом скоростей. Понятие потенциала скоростей было введено Эйлером. Существование функции тока в случае плоского движения было установлено Лагранжем. Кинематический смысл этой функции и ее связь с линией тока были разъяснены Рэнкином в 1864 г. Лагранж в 1781 г. первый нашел те динамические условия, при выполнении которых будет существовать безвихревое движение с потенциалом скоростей, Теорема Лагранжа, лежащая в основе всей теории безвихревого течения и оправдывающая практическое применение теориИ( была в 1815 г. строго доказана Коши (1789—1857).  [c.24]

Безвихревое течение идеальной жидкости можно рассмотреть, используя функцию тока 1 з или функцию потенциала скоростей ф. Уравнение для функции тока имеет вид  [c.173]

Наиболее замечате-ньные результаты были получены в XIX в. в области исследования плоских установившихся потенциальных течений несжимаемой жидкости. Еще Ж. Лагранж (1781) ввел функцию тока для плоских течений удовлетворяющую для безвихревых течений, как и потенциал скорости, уравнению Лапласа. Кинематическое истолкование функции тока было дано В. Ренкином Разработка аппарата теории функций комплексного переменного дала возможность широко развить методы исследования плоских задач движения несжимаемой жидкости, которые в самом начале развивались совместно со смежными исследованиями задач электростатики. Первые работы, в которых при помощи теории аналитических функций исследуются простейшие задачи электростатики и гидродинамики, относятся к 60-м годам. Существенное развитие области применения теории функций в гидродинамике связано с изучением открытого Г. Гельмгольцем класса так называемых струйных течений жидкости — течений со свободными ли-78 ниями тока, на которых давление сохраняется постоянным. Интерес к этим течениям возник в связи с попытками получить на основе модели идеальной жидкости реальные картины обтекания тел с образованием силы лобового сопротивления и без бесконечных скоростей.  [c.78]

Классификация задач безвихревого течения. Хронологически первой граничной задачей потенциальной теории была проблема вычисления гармонического потенциала во всей зоне при заданных величинах потенциала на границе. Доказательство существования такого потенциала и выражение его для данных условий известны как проблема Дирихле. Примеры этому общеизвестны в электростатике, где наружное поле отыскивается по потенциалу на поверхности проводника. В потоке жидкости примером является установление потенциала, соответствующего определенным свободным линиям тока. Так как, согласно п. 28, функция тока для двухмерного течения удовлетворяет всем требованиям потенциала, линия тока может рассматриваться для аналитических целей как линия потенциала, и, следовательно, любой двухмерный поток с заданными границами может рассматриваться как проблема Дирихле.  [c.77]

Для плоских установившихся движений газа Л. И. Седов предложил использовать в качестве независимых переменных давление р и функцию тока г , а в качестве искомой функции — угол 0 наклона вектора скорости к оси X. Для функции 0 р, г ) также получается уравнение, линейное относительно ее вторых производных. Л, И. Седов (1950) и М, П. Михайлова (1949) рассмотрели решение задачи Коши для этого уравнения с помощью рядов р1азличного вида и изучили его характеристики, Седов нашел точные решения уравнения для 0, в том числе решение, обобщающее решение Прандтля — Майера на некоторый класс вихревых течений, а также установил свойства монотонности изменения газодинамических параметров вдоль характерных линий в области течения эти свойства обобщают аналогичные предложения для безвихревых течений, установленные А, А. Никольским и Г, И, Тагановым (1946), Седову удалось найти частные примеры точного решения задачи сверхзвукового обтекания тела со смешанным течением за скачком, но для неоднородного набегающего потока.  [c.161]

Течение жидкости может быть вихревым или безвихревым (потенциальным). Исследование безвихревого потока можно свести к нахэждению так называемой потенциальной функции (или потенциала скоростей), знание которой позволяет полностью рассчитать поле скоростей различных течений. Для некоторых видов вихревого потока определение его кинематических характеристик можно свести также к отысканию одной неизвестной функции — функции тока. Следовательно, нахождение потенциала скоростей и функции тока — важнейшая задача аэродинамики. В связи с этим предлагается ряд вопросов н задач, связанных с нахождением потенциальной функции и функции тока, а также построением кинематического характера течения и опре- делением поля скоростей для случаев, когда эти функции известны.  [c.40]

С помощью уравнения (5.1) можно исследовать установившиеся газовые потоки, причем если в этом уравнении е = 0, то оно будет справедливо для двумерного плоского потока, а при е = 1 — для двумерного пространственного (осесимметричного) потока. Кроме того, это уравнение позволяет изучать как вихревые (неизэнтропические), так и безвихревые (изэнтропические) течения газа. В первом случае его можно преобразовать к уравнению для функции тока б  [c.143]

Это и есть искомое уравнение для функции тока. (Этот вывод упрощается в случае изэнтропического течения и становится совсем простым, когда течение является одновременно изэнтропическим и безвихревым.) Член, стоящий в правой части уравнения (42.4), можно связать с уравнением Крокко — Важоньи, которое для плоского течения имеет вид  [c.123]

Круглая струя жидкости с осесимметричными свободными границами представляет собой исторический и уникальный пример безвихревого течения, поле скоростей которого было точно описано с помощью аналитических функций. В других случаях, в том числе и в случае осесимметричных трехмерных течений, не существует формул, аналогичных полученным в двумерной теории. Важный вклад в строгую математическую теорию трехмерных струй и каверн внесли Рябушинский [62], Гилбарг [29], Серрин [72, 73], Гарабедян, Леви и Шеффер [23] и др. Однако практический расчет осесимметричных свободных струйных течений по-прежнему основан на разнообразных приближенных методах. К ним относятся, например, два метода расчета полей течения и сил с помощью замены каверны телом, близким по форме к телу Рэнкина, определяемому методами распределения источников — стоков [59, 89], а также релаксационные [53, 77] и электролитические [67] методы расчета осесимметричных течений. Гарабедян [22] предложил итерационный метод аппроксимации функции тока и использовал его для расчета поля кавитационного течения и сопротивления круглого диска по модели Рябушинского. Сопротивление дисков, конусов и других тел рассчитывалось по известным распределениям давления для аналогичных двумерных профилей [4, 58, 60]. В случае кавитационных течений для трехмерных аналогов двумерных тел получаются другие формы каверн. Однако распределения скоростей (и следовательно, давления) на смоченной части эллипсов и сфероидов подобны. Поэтому для тел с затупленной носовой частью лобовое сопротивление определяется с достаточной точностью. Наоборот, результаты для клина и конуса с одинаковым углом при вершине различны.  [c.226]

Так как движение сообщается неподвижной жидкости, то, когда тело движется через нее, кинетическая энергия всей системы обязательно больше, чем энергия одного тела. Ввиду того, что работа, производящая этот излишек энергии, должна поставляться телом, усилие на тело зависит не только от скорости, но и от ускорения. Таким образом, если временное изменение кинематических соотношений включается в функцию потенциала или тока безвихревого потока, то для определения кинетической энергии жидкости можно использовать форму уравнения Бернулли для неустановившегося двилеения. Кирхгоф упростил эту проблему, доказав, что полное усилие может быть выражено в членах присоединенных масс или приращений действительной массы тела, пропорциональных объему и плотности вовлеченной в дви-леение жидкости коэффициент пропорциональности изменяется с изменением формы тела. Тэйлор увеличил ценность понятия присоединенных масс, выразив их в членах особенностей, порождаемых телом. Наконец, Легалли установил прямое соотношение между силами, действующими на тело, и особенностями. Таким образом, если распределение особенностей задано или установлено одним из методов решения уравнений течения, как это сделано в следующем разделе, тогда силы и моменты могут быть определены непосредственно без нахождения распределения давления.  [c.92]

---

Функция тока плоского течения — Справочник химика 21

    Поскольку для плоского течения существует функция тока у), то система (1.76) может быть приведена к одному уравнению для этой функции [c. 51]

    В общем случае локально безвихревые несжимаемые плоские течения характеризуются существованием комплексных потенциалов W = и + iV. Здесь и — потенциал скоростей, г V функция тока. Комплексный потенциал W есть аналитическая функция комплексной переменной z = х + iy, характеризующей положение точки, а ее производная [c.78]

    В случае, когда движение жидкости происходит так, что конфигурация линий тока в параллельных плоскостях оказывается одинаковой, течение называется плоским. Для всякого плоского движения несжимаемой жидкости существует функция тока 1 (х, у) [при неустановившемся движении г)з(х, у, т)], которая обладает тем свойством, что [c.15]

    Двумерное течение в прямоугольной полости имеет два предельных случая при неограниченном возрастании высоты — это течение в вертикальном слое, ограниченном двумя плоскими поверхностями, а при неограниченном возрастании ширины—это течение в горизонтальном слое. Для двумерных течений уравнения движения (15.2.5) — (15.2.7), записанные через функцию тока, после исключения рщ принимают вид [c.386]

    При потенциальном плоском течении идеальной жидкости rot W = О, функция тока удовлетворяет уравнению Лапласа [c.102]

    Рассмотрим сначала плоское течение. Возьмем минимальную область влияния смешанного до- и сверхзвукового течения в плоскости годографа и граничные условия для функции тока плоского или осесимметричного течения (рис. 3.24). [c.105]

    Двумерным называют такое движение (или течение), поле скорости которого в некоторой системе координат имеет только две ненулевые компоненты [22]. Плоским называют такое двумерное движение жидкости, при котором все ее частицы движутся параллельно некоторой неподвижной плоскости, причем скорости всех частиц, лежаших на одном и том же перпендикуляре к этой плоскости, одинаковы [50]. Функцию тока плоского течения называют функцией тока Лагранжа. Осесимметричным называют течение, при котором линии тока расположены в плоскостях, проходяших через данную ось, и в каждой такой плоскости картина линий тока одинакова [3]. Функцию тока осесимметричного течения называют функцией тока Стокса [46]. [c.101]

    Доказательство. При плоском стационарном ползущем течении уравнения Навье—Стокса (11) сводятся к уравнению 2 = 0. Если У—функция тока, то последнее уравнение эквивалентно уравнению = О, т. е. V — бигармоническая функция. Отсюда следует, что V — аналитическая функция ). Действительно, во всяком круговом кольце функцию V можно разложить в ряд Фурье [c.66]

    В случае плоских и осесимметричных течений (т. е. в случае поперечных колебаний цилиндров и продольных колебаний тел вращения) величину g можно выразить через стоксову функцию тока V. (Так, для плоского течения Это намного уп- [c.228]

    Для учета фронтальных явлений, связанных с фонтанным эффектом, зададим распределение скоростей, используя решение, полученное в работе [256] при изучении изотермического течения ньютоновской жидкости в полубесконечном плоском канале под действием плоского поршня, движущегося со скоростью Ыо- Рассматривая квазистационарное состояние, пренебрегая инерционными членами и вводя в уравнение функцию тока [257], авторы получили решение бигармонического уравнения, перейдя затем к приближенному выражению [c. 177]

    Течение в канале. Рассмотрим в принятой модели простейшую задачу о сверхзвуковом течении в канале с плоскими стенками О функция тока у равна О на нижней и 1 на верхней стенке, так что задача сведется к отображению полосы О получаем соотношения [c.145]

    Вернемся теперь к случаю плоского вихревого течения dpo ф 0. Разобьем область течения линиями тока на подобласти, в каждой из которых полное давление является монотонной функцией ф. Будем называть положительным то направление обхода характеристики, вдоль которого полное давление не возрастает. [c.23]

    Простейшей формой течения, возможной при решетке пластин, будет параллельное течение в направлении плоской пластины, причем пластины в решетке являются отрезками линий тока (фиг. 239). Эта форма течения используется для того, чтобы вывести функцию отображения плоскости решетки (плоскость г) в плоскость единичного круга или плоскость отображения (плоскость С).  [c.339]

    Для этого напомним, что установившееся потенциальное плоско-параллельное течение несжимаемой жидкости определяется заданием характеристической функции течения. Свойства характеристической функции мы здесь перечислять не будем — они излагаются в любом курсе гидродинамики, и мы их вывели, применительно к задачам пластовой гидромеханики, во введении к книге [3]. Покажем только, как можно определить время движения вдоль линии тока, если известна характеристическая функция.  [c.55]

    Метод источников и стоков. Этот метод широко используется в газовой динамике при решении различных линейных задач. Наложение полей течений, соответствующих источникам и стокам различной интенсивности, позволяет получать картину течения при обтекании тел и при течении в каналах. В теории сопла метод источников п стоков может быть применен только в случае течения несжимаемой жидкости, когда в силу линейности уравпений для потенциала и функции тока может быть использован принцип суперпозиции. Подбором системы источников и стоков и их иптеи-сивиостей можно построить течение в канале заданной формы. Однако такая задача весьма сложна. Значительно проще обратная задача, которая позволяет по заданной системе источников и стоков определить формы поверхностей, которые могут быть приняты за стенки сопла. Рассмотрим применение метода для плоского, осесимметричного и пространственного течений. [c.114]

    Итак, функция тока плоского потенциального трансзвукового течения в плоскости годографа иу является решением уравнения Трикоми [c.203]

    Любой аналитической функции W z) соответствует пара действительных функций (pw x,y) и ф х,у), которые можно рассматривать как потенциал скорости и функцию тока некоторого течения. В этом случае кривые, на которых (pw — onst и 0 = onst, оказываются соответственно линиями равного потенциала и линиями тока. Таким образом, кинематическое изучение плоского движения жидкости связывается с теорией функций комплексного переменного [58]. Определив по W(z) поле скоростей течения, можно с помощью интеграла Коши-Лагранжа [c.104]

    Поскольку для всякого плоского течения неснфункция тока 11) (д , у), то в силу (1.12) и (1,13) она связана с потенциалом скорости уравнениями [c.42]

    В основе моделирования лежит математическая тождественность уравнений, описы. вающих стационарное распределение элек-трпческих потенциалов в плоской проводящей области, и уравнений, описывающих распределение потенциалов скорости ф(х, у) и функций тока ч )(л , у) в области течения (см. 1.2). При обтекании тел несжимаемой жидкостью область течения имитируют проводящим листовым материалом постоянной толщины б. Для этой цели обычно используют графитизированную бумагу. [c.403]

    При решении многих практически важных задач гидродинамики точными и численными методами (см., например, [48, 49]) дифференциальные уравнения движения можно упростить, записав их с помошью функции тока. Функцию тока вводят для двумерных плоских и осесимметричных течений, а также для трехмерных, в которых все компоненты вектора скорости не зависят от одной из координат.  [c.101]

    При этом если жидкость сжимаема, то для перечисленных типов течений функцию тока можно ввести лишь для установившегося течения. Уравнению неразрывности (см. 3.3) можно придать двучленную форму, выразив компоненты вектора скорости через производные от функции тока ф (табл. 3.1) так, чтобы уравнение неразрывности удовлетворялось автоматически. Семейство линий уровня функции тока, например при плоском неустановив-шемся течении линий ф х,у,т) = onst (время т играет роль параметра), представляет совокупность линий тока в момент т. [c.101]

    При осесимметричном течении равенства гр = onst представляют поверхности тока. Физический смысл функции тока следу-юший. При плоском движении разность значений функции тока в двух каких-нибудь точках потока равна объемному расходу жидкости через сечение трубки тока, ограниченной линиями, проходя-шими через выбранные точки [1]. При осесимметричном течении аналогичная разность значений функций тока равна объемному расходу, деленному на 2тг. Используя функцию тока, в общем случае можно свести задачу нахождения компонентов вектора скорости Wi, W2, к интегрированию уравнения 4-го порядка для ф и уравнения 2-го порядка для одной компоненты W. Функция тока определяется с точностью до произвольной аддитивной постоянной, значение которой выбирают из соображений удобства. [c.101]

    Для многих практических задач (например, гидродинамики [52] и тепломассопереноса [53] в псевдоожиженном слое, исследования циркуляционных течений [54], полей скоростей в смесителях [55], в гидроциклонах, барботажных слоях [4], волн в жидкостях [57, 46]) хорошее приближение к реальной картине течения можно получить, решая уравнения сохранения в предположении, что жидкость идеальна (/х = 0) и несжимаема [р = onst). В этом случае использование функции тока позволяет представить уравнения гидромеханики в удобной для решения форме. Для вихревых течений идеальной жидкости, когда три компонента поля скоростей зависят от двух координат, запись уравнений с помошью функции тока имеется в [54]. В случае плоского движения, совершаемого в плоскости Оху, компоненты вихря скорости TOtxW = О, rot yW = О, [c.102]

    Поставлена следующая задача. Рассматривается развитие двумерного возмущения с амплитудой e( )течении несжимаемой жидкости типа пограничного слоя с профилем невозмущенной скорости U y). Ура)внение и граничные условия для функции тока возмущения if> (см. 9.1) в системе отсчета, двин ущейся с фазовой скоростью волны с, имеют вид [c.201]

    На границе эжектнрующего и эжектируемого газа примем равенство давлений. Поскольку получение аналитического решения для критических режимов работы звукового эжектора затруднительно, то, исходя из указанных предположений, рассчитаем критические режимы плоского звукового эжектора численным методом. Эжектирующая струя в сеченни тО имеет скорость звука, а дальше по течению является существенно двумерно , поэтому будем рассчитывать ее по законам двумерного сверхзвукового течения газа методом характеристик, воспользовавшись видоизменением метода С. А. Христиановича [4]. В этом случае уравнения, связывающие потенциал скорости и функцию тока, имеют вид  [c.42]

---

Функция тока — Справочник химика 21

    Введем безразмерную функцию тока ф определяемую соотношениями [c.6]

    Здесь ф = (R V ф — размерная функция тока. [c.6]

    Выражая и Ув через функции тока и полагая, что на поверхности сферы ф, = 2 =0(функции тока определены уравнениями (1.7) и (1.8) с точностью до произвольной постоянной), преобразуем граничные [c.7]

    Функции тока (1.34), (1.35) получены Адамаром и Рыбчинским не только для малых значений Re , но и для случая Re, — 1. Выражение для функции тока при Rei -больших значениях Re,, было полу чено Хиллом [18, 19] для случая, когда движение внутри сферической частицы можно считать идеальным. Этот случай реализуется для [c.18]

    Учитывая симметричный характер течения и выражение функции тока вдали от частицы, решение уравнений (1. 32) можно искать в виде  [c.9]

    Таким образом, функция тока Стокса  [c.10]

    Для малых значений Re/ их небольшое увеличение оказывает заметное влияние на вид функции тока. [c.15]

    Подставляя функцию тока в формулы (1.7), (1.8), получаем выражения для нормальной и тангенциальной скоростей потока  [c.16]

    При рещении стационарной внешней задачи в приближении диффузионного пограничного слоя уравнение конвективной диффузии (4.42) преобразовывалось к виду (4.96) и функция тока раскладывалась в ряд Тейлора по степеням V = 1—/ . В качестве граничного условия по в гипотетически предполагалось, что концентрация в лобовой точке в =тг) равна концентрации набегающего потока. В данном приближении удалось получить решение только для д 1 — формулы (4.121) и (4.122). [c.202]

    Подставив выражение для функции тока (1.82) в формулу (1.5), получим  [c.19]

    Величина Ф определяется через компоненты скорости жидкости. Переход к функции тока в (1.106) может быть осуществлен, как обычно, с помощью формул (1.7), (1.8). [c.33]

    Будем считать, что компоненты скорости в уравнении (4.96) известны и заданы через функцию тока формулами (1.7), (1.8). [c.197]

    Отметим, что формулы (4,119) и (4.124) можно применять лишь при не очень больших значениях д. Это обусловлено тем, что использование функции тока в виде (4.99) предполагает постоянство касательной составляющей скорости поперек пограничного слоя, что приближенно верно при малых значениях ц. Ограниченная применимость формул [c.200]

    Тепло- и массообмен для стоксового режима обтекания твердой сферы неньютоновским потоком с зависимостью для функции тока [c.215]

    Если функция тока задана аналитически, то для нахождения критерия Шервуда можно пользоваться формулами (4.122), (4.123),предварительно определив значение вихря на поверхности сферы через линеаризованную функцию тока. Для течения, определяемого функцией тока (4.157) такие вычисления приводят к зависимости  [c.215]

    В работе [403] использовано выражение для функций тока (1,47). 274 [c.274]

    Ф — скоростной потенциал для поля скоростей твердых частиц у г з/ — функция тока для поля скоростей ожижающего агента и [c.119]

    Автомодельное решение предложено Берманом [7] на основе найденного им вида функции тока [c.127]

    Поле скоростей и может быть также охарактеризовано стоксовой функцией тока (вместо скоростного потенциала Ф/)  [c.98]

    Тогда функция тока для скоростного поля ожижающего агента выразится [c.98]

    На рисунках не указан параметр кривых видимо, это безразмерная функция тока г1з/мо ь- Прим. ред. [c.106]     Типичная картина движения твердых частиц показана на рис. 1У-16, а очевидно, что скорость в любой точке можно определить по функции тока. Если пузырь (и соо ветственно твердые частицы) неподвижен, а газ в просветах между частицами (значительно ниже пузыря) движется вверх с постоянной скоростью 7 , то характер газового потока в окрестности сферического пузыря можно описать функцией тока  [c.160]

    Картина потока, характеризуемого функцией представлена на рис. 1У-16, в, г для двух значений а % и /4. Это изображение относится к двухмерному полю но уравнению (IV,16) для трехмерного поля получается примерно такая же картина. По функции тока y fp можно найти локальную скорость газа в любой точке поля и по ней вычислить траектории и трассы, но следует помнить, что функция характеризует идеализированный случай, поэтому можно ожидать некоторых расхождений с экспериментом. Тем не менее, эта упрощенная теория удовлетворительно описывает свойства псевдоожиженного слоя, содержащего пузыри. [c.162]

    Линии тока адамаровского течения изображены на рис. 1.2. Подставляя выражения для функций тока (1.34), (1.35) в формулы (1.7) и (1.8), находим  [c.10]

    Работы Хамипека с соавторами были развиты далее Накано и Тие-ном [13] в части уточнения выражения для внутренней функции тока. Из требования выполнения условий Галеркина для при гаженного решения зфавнения Навье-Стокса для внешней и внутренней задач авторы [13] получили для внешней функции тока формулу (1.47), а для внутренней — выражение [c.15]

    В отличие от работ [10, 11], коэффициенты, входящие в уравнение для функций тока (1.47) и (1.55), зависят не только от fi и Rej, но и от внутреннао» критерия Рейнольдса Re,. [c.15]

    Для нахождения неопределенных коэффициентов в формулах (1.47) и (1.55) авторы [13] получили 12 нелинейных алгебраических уравнений, которые они решали числшным методом в диапазоне параметров 0функций тока, приведеш1ыми в работах [10, И]. Установлено, что внешняя функция тока фг не изменяется в широкой области значений Re, и, следовательно, изменение Rej не оказывает существенного влияния на коэффициент трения и внешний тепломассообмен. Однако изменение Re, заметно влияет на функцию тока фх и, следовательно, на массо- и теплопередачу внутри капли. Функции тока (U5) соответствует меньшая скорость циркуляции внутри капли, чем функции тока (1.46), полученной Хамилеком и Джонсоном [10]. Накано и Тиен отмечают, что при одновременном стремлении Re, и Рег к нулю функции тока (1.47) и (1.55) стремятся к соответствующим выражениям (1.38), (139) Адамара и Рыбчинского, что не вьшолняется для функции тока (1.46), (1.47) Хамилека и Джонсона. [c.15]

    Широдзука и Каваси [55] рассмотрели движение сферы, когда одна или обе фазы являются неньютоновскими жидкостями со степенным реологическим законом. Решение получено при Re > 1 с помощью уравнений минимума диссипации энергии в предположении, что функции тока внутреннего и внешнего течений описываются соотношениями вида  [c.36]

    Применим к уравнению (4.96) преобразование Прандтля — Мизе-са, т. е. перейдем от переменных г, в к ф, в. Учитывая, что в пограничном слое сферы г= +у, где 7функцию тока вблизи сферы в ряд Тейлора [c. 197]

    Массообмен в зоне отрыва можно приближенно рассчитать, вос-пользовавишсь для функции тока в кормовой области сферы разложением типа (4.101). При этом формально считается, что в зоне отрыва образуется диффузионный пограничный слой и что в точке набегания потока со стороны отрывной зоны (точка т = тг) концентрация вещества равна концентрации вдали от сферы. Полный диффузионный поток определяется суммой потоков в пограничных слоях до точки отрыва и в зоне отрьганого течения. Такой приближенный способ учета массообмена в вихревой зоне был применен в работах [281, 286]. Следует однако отметить, что он носит весьма условный характер, так как ввиду наличия циркуляции жидкости в вихревой зоне граничное условие постоянства концентрации вдали от капли для этой области не вьшолняется. На рис. 4.11 кривая/характеризует массообмен твердой сферы. Штриховая часть этой кривой соответствует решению без учета массообмена в зоне отрыва. Заметим, что при фиксированных значениях Ре с изменением Ке от 0,5 до 100 коэффициент массообмена для твердой сферы возрастает примерно в 1,6 раза. На рис. 4.11 приведены также экспериментальные данные Гриффита [287] для капель с отношением вязкостей i =0,38 0,42 и 2,6. Для твердой сферы и капель жидкости в газовом потоке для массо- и теплообмена опытные данные в ряде работ [288-291] обрабатьшались в виде корреляционной зависимости  [c.201]

    Величина К представляет собой поправочный член в формуле Бус-синеска-Хигби (4.16). Для д = О, А» = 1. В работе [299] приведен расчет критерия Шервуда методом диффузионного пограничного слоя для М 10 и 5с=10 с использованием выражений для функций тока (1.47)-(1.49) в диапазоне 10Результаты расчетов сопоставлены с экспериментальными данными Гриффитса [287]. В области 10 расчетные значения оказались в близком соответствии с экспериментальными. При Не = 10 расчетное значение превысило экспериментальные на 10 %. В более поздней работе [300] расчеты были уточнены и при 8 хорошее соответствие расчетньпс и экспериментальных значений критерия Шервуда.  [c.203]

    Уэллек и Хуанг [341] исследовали стационарный массоперенос к сфере при малых значениях Ке, определяя поле скоростей из выражений для функции тока Накано и Тьена [50]. Результаты их расчетов для критерия Шервуда в зависимости от параметров задачи представлены на рис. 4.20. Заметим, что при всех значениях Ре усиление псевдопласти-ческих свойств жидкости приводит к более интенсивному массообмену. Для твердой сферы такой результат находится в противоречии с расчетами по формуле (4.158) и, как отмечено в работе [341], с решением, использующим приближенные значения для функции тока по данным Томита [342]. Это указывает на чувствительность решения к реологическому параметру и на необходимость использования наиболее корректных гидродинамических решений. Данные расчетов [341] показьта-ют, что при Ре>5 10 для решения диффузионной задачи можно воспользоваться формулами (4.119) и (4.122), причем как нетрудно заметить из рис. 4.21, формула (4.119) в этом случае также применима гишь для небольших значений параметра X, характеризующего отноше- [c. 215]

    Ширадзука и Каваси [345] рассчитали массовый потока на сферу при больших 5Ь и Ре в приближении диффузионного пограничного слоя, определяя поле скоростей вокруг сферы из выражений щя функции тока (1.114). На рис. 4.22 приведена зависимость Ум=5Ь/5Ь от и, вычисленная при больших значениях Ре по данным работ [341, 344, 345]. Если в стоксовом режиме обтекания массо- и теплообмен в псевдопластических средах протекает быстрее, а в дилатантных медленнее, чем в ньютоновских жидкостях, то при больших значениях критерия Ке наблюдается обратный эффект. Напомним, что аналогичным образом ведет себя и коэффициент сопротивления (см. раздел 1.4). [c.217]

    Заканчивая рассмотрение метода Дэвидсона, следует отметить, что последний приложим не только к сферическим или круглым пузырям. Скоростные потенциалы твердых частиц и ожижающего агента удовлетворяют также уравнению Лапласа, и в случае двухмерной системы их можно рассматривать как действительнвге части функции комплексного переменного г = х + где х иг/ — координаты точки в прямоугольной системе координат, центр которой совпадает с центром пузыря, а ось х направлена вертикально вверх. Это комплексные потенциалы для полей потоков твердых частиц и ожижающего агента, и их мнимые части дают соответствующие функции тока. В соответствии, с методом Дэвидсона, комплексные потенциалы можно представить как [c.101]

    В перво11 приближении можно считать, что пузырь в псевдоожиженном слое является круглым (сферой или цилиндром), и если это единичный пузырь, удаленный от стенок аппарата, то известны функции тока, характеризующие связанное с ним движение твердых частиц и газа. Поток твердых частиц при обтекании сферы описывается уравнением [c.160]

    Функции тока ожижающего агента (см. рис. У-10, 6) определяются из уравнений (У,24) и (У,25) при использовании соотношений = —д pflдy, и = д flдx для двухмерного потока и / = —(5 ф /Зг/)/г, Пу = (5г )у/йг)/г — для осесимметричного по- [c.186]

---

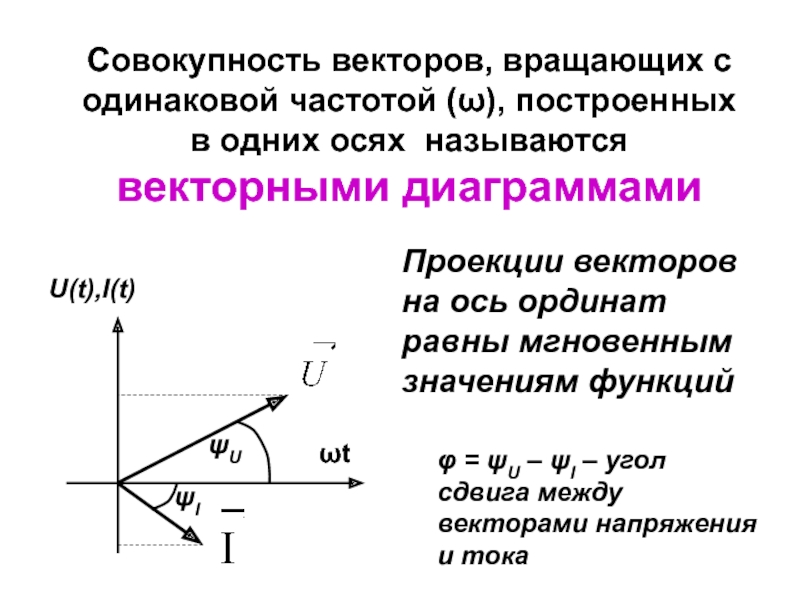
Потенциал скорости и функция тока при плоском безвихревом движении

Содержание:

Потенциал скорости и функция тока при плоском безвихревом движении

Потенциал скорости и функция тока при плоском безвихревом движении. Если при невращательном движении все компоненты вектора rH равны нулю, то простосвязная область, то есть функция таких координат и времени Φ (X, y, r, r) u = Непосредственно подставляя (3.46) вместо (3.59), легко увидеть, что имеет место обратное: если существует функция Φ (x, y, 2, r), которая определяет скорость в соответствии с (3.59), то r1 и= 0. вместо x, y, 2, 1), 3 функций ui и u2 достаточно определить 1 функцию Φ и найти проекцию скорости простым дифференцированием, поэтому исследование поля скоростей значительно упрощается. Движение жидкости, способной вводить потенциал скорости, называется потенциалом.

Поэтому для несжимаемых жидкостей функция потенциала скорости должна удовлетворять уравнению Лапласа (другими словами, она должна быть гармонической функцией). Людмила Фирмаль

• Подставляя уравнение проекции скорости (3.59) в несжимаемое уравнение (3.22), получаем: Если скорость жидкости имеет 2 ненулевые составляющие q =(u, yy) и зависит от 2 переменных x, y, то плоская задача гидродинамики может быть considered. In в этом случае форма уравнения несжимаемости имеет вид Из этого уравнения видно, что всегда существует такая функция Поскольку замена(3.62) на(3.61) делает последнее правильным тождеством.* подставляя (3.62) в уравнение обтекания (3.6), вид плоской задачи имеет вид Мы получаем.

Оттуда вы можете видеть, что на линии потока есть равенство В результате функция y (x, y), определенная уравнением (3.62), называется потоковой функцией. Сравните (3.62) с проекционным представлением скорости через потенциал (p для плоских задач Подставляя (3.66) в несжимаемое уравнение, описанное для условия плоской задачи в виде В этих условиях потенциал скорости p (x, y, r) должен удовлетворять 2-му уравнению Лапласа. Как уже говорилось, если движение скрыто, то вектор вихря скорости будет равен нулю. Об этом свидетельствует подставление выражения для проекции скорости, проходящей через латентное (присвоение p выражению для проекции вектора Лос(3.46).

• Поскольку другие проекции включают производные для u2 или r, ось 2. (x, y) потенциал скорости, а Г2 (x, y) функция потока. Поле скоростей поверхности потока и его общая форма определяются как с помощью уравнения (3.62) или (3.66) для непосредственного вычисления значения прогноза скорости, так и путем построения линии потока на основе уравнения(3.65).

  Приведенные выше свойства потенциала скорости и функции тока привели к эффективному использованию теории функций комплексных переменных при решении плоской задачи о гидродинамике. Людмила Фирмаль

  • Заметим, что при предварительном определении функции Γ () неясно, какой поток описывается функцией 1) и Γ2.Однако линейность оператора Лапласа а дает возможность описывать более сложные потоки, если использовать принцип суперпозиции и суммировать возможности описания простейших потоков, определяемых базовыми функциями.

  Смотрите также:

  Примеры решения задач по гидравлике

  Возможно эти страницы вам будут полезны:

  1. Разложение движения элементарного объема сплошной среды на поступательное, вращательное и деформационное (теорема Гельмгольца).
  2. Субстанциальная производная.
  3. Основы гидродинамики. Предварительные сведения.
  4. Закон сохранения массы.

  Статьи

  Азимутальный вихрь и функция тока в ползущем течении в трубе

  Вестник МГСУ 4/2014
  • Зуйков Андрей Львович - Московский автомобильно-дорожный государственный технический университет (МАДИ; Национальный исследовательский Московский государственный строительный университет (НИУ МГСУ) доктор технических наук, профессор кафедры гидравлики профессор кафедры гидравлики и гидротехнического строительства, Московский автомобильно-дорожный государственный технический университет (МАДИ; Национальный исследовательский Московский государственный строительный университет (НИУ МГСУ), 125319, г. Москва, Ленинградский пр-т, д. 64 129337, г. Москва, Ярославское шоссе, д. 26; Этот e-mail адрес защищен от спам-ботов, для его просмотра у Вас должен быть включен Javascript .

  Страницы 150-159

  Посвящена аналитическому исследованию структуры установившегося неравномерного ползущего течения в цилиндрическом канале. Показано, что структура течения определяется уравнением Лапласа относительно азимутального вихря скорости и уравнением Пуассона относительно функции тока. Распределения азимутального вихря и функции тока получены в виде рядов Фурье — Бесселя.

  DOI: 10.22227/1997-0935.2014.4.150-159

  Библиографический список
  1. Van Dyke M. An Album of Fluid Motion. Stanford. The Parabolic Press. 1982. 184 p.
  2. Giesekesus H. A simple Constitutive Equation for Polymer Fluids Based on the Concept of Deformation Dependent Tensorial Mobility // Journal of Non-Newtonian Fluid Mechanics. 1982. Vol. 11. Pp. 69-109.
  3. Bird R.B., Armstrong R.C., Hassager O. Dynamics of Polymeric Liquids. Vol. 1. Fluid Mechanics. 2nd ed. New York. John Willey and Sons. 1987. 565 p.
  4. Снигерев Б.А., Алиев К.М., Тазюков Ф.Х. Ползущее течение вязкоупругой жидкости со свободной поверхностью в условиях неизотермичности // Известия Саратовского университета. Нов. сер. Сер. Математика. Механика. Информатика. 2011. Т. 11. Вып. 3(1). С. 89-94.
  5. Орехов Г.В., Зуйков А.Л., Волшаник В.В. Контрвихревое ползущее течение // Вестник МГСУ. 2013. № 4. С. 172-180.
  6. Моделирование и расчет контрвихревых течений / В.К. Ахметов, В.В. Волшаник, А.Л. Зуйков, Г.В. Орехов ; под ред. А.Л. Зуйкова. М. : МГСУ, 2012. 252 с.
  7. Зуйков А.Л. Распределение продольных скоростей в циркуляционном течении в трубе // Вестник МГСУ. 2009. № 3. С. 200-204.
  8. Владимиров В.С. Уравнения математической физики. М. : Наука, 1988. 512 с.
  9. Korn G.A., Korn T.M. Mathematical Handbook for Scientists and Engineers: Definitions, Theorems, and Formulas for Reference and Review. New York. General Publishing Company. 2000. 1151 p.
  10. Коренев Б.Г. Введение в теорию бесселевых функций. М. : Наука, 1971. 288 с.

  Скачать статью

  МОДЕЛЬ ТЕЧЕНИЯ ГРОМЕКИ — БЕЛЬТРАМИ

  Вестник МГСУ 4/2013
  • Зуйков Андрей Львович - Московский автомобильно-дорожный государственный технический университет (МАДИ; Национальный исследовательский Московский государственный строительный университет (НИУ МГСУ) доктор технических наук, профессор кафедры гидравлики профессор кафедры гидравлики и гидротехнического строительства, Московский автомобильно-дорожный государственный технический университет (МАДИ; Национальный исследовательский Московский государственный строительный университет (НИУ МГСУ), 125319, г. Москва, Ленинградский пр-т, д. 64 129337, г. Москва, Ярославское шоссе, д. 26; Этот e-mail адрес защищен от спам-ботов, для его просмотра у Вас должен быть включен Javascript .
  • Орехов Генрих Васильевич - Московский государственный строительный университет (ФГБОУ ВПО «МГСУ») кандидат технических наук, доцент, заведующий кафедрой гидроэнергетики и использования водных ресурсов; (8499) 182-99-58, Московский государственный строительный университет (ФГБОУ ВПО «МГСУ»), г. Москва, Ярославское шоссе, д. 26; Этот e-mail адрес защищен от спам-ботов, для его просмотра у Вас должен быть включен Javascript .
  • Волшаник Валерий Валентинович - Московский государственный строительный университет (ФГБОУ ВПО «МГСУ») доктор технических наук, профессор, профессор кафедры гидроэнергетики и использования водных ресурсов; (8499) 182-99-58, Московский государственный строительный университет (ФГБОУ ВПО «МГСУ»), г. Москва, Ярославское шоссе, д. 26; Этот e-mail адрес защищен от спам-ботов, для его просмотра у Вас должен быть включен Javascript .

  Страницы 150-159

  Рассмотрена аналитическая модель винтового течения невязкой несжимаемой жидкости в цилиндрическом канале. Модель основана на решении уравнений Громеки методом разложения Фурье — Бесселя. Получены аналитические функции распределения по длине и радиусу цилиндрического канала аксиальных, азимутальных и радиальных скоростей движения жидкости и функции тока. Выполнен анализ полученного решения.

  DOI: 10.22227/1997-0935.2013.4.150-159

  Библиографический список
  1. Громека И.С. Собрание сочинений. М. : Изд-во АН СССР, 1952. 296 с.
  2. Лойцянский Л.Г. Механика жидкости и газа. 7-е изд., испр. М. : Дрофа, 2003. 840 с.
  3. Бюшгенс С.С. О винтовом потоке // Научные записки МГМИ. 1948. Т. 17. С. 73—90.
  4. Корн Г. , Корн Т. Справочник по математике для научных работников и инженеров. М. : Наука, 1970. 720 с.
  5. Гостинцев Ю.А., Похил П.Ф., Успенский О.А. Поток Громеки — Бельтрами в полубесконечной цилиндрической трубе // Механика жидкости и газа. 1971. № 2. С. 117—120.
  6. Зуйков А.Л. Функция тока и зона рециркуляции в ламинарном течении с закруткой // Вестник МГСУ. 2009. Спецвып. № 2. С. 91—95.

  Скачать статью

  Аксиальные и радиальные скорости в ползущем течении в трубе

  Вестник МГСУ 5/2014
  • Зуйков Андрей Львович - Московский автомобильно-дорожный государственный технический университет (МАДИ; Национальный исследовательский Московский государственный строительный университет (НИУ МГСУ) доктор технических наук, профессор кафедры гидравлики профессор кафедры гидравлики и гидротехнического строительства, Московский автомобильно-дорожный государственный технический университет (МАДИ; Национальный исследовательский Московский государственный строительный университет (НИУ МГСУ), 125319, г. Москва, Ленинградский пр-т, д. 64 129337, г. Москва, Ярославское шоссе, д. 26; Этот e-mail адрес защищен от спам-ботов, для его просмотра у Вас должен быть включен Javascript .

  Страницы 127-134

  Приведено аналитическое исследование полей аксиальных и радиальных скоростей в установившемся неравномерном ползущем течении на начальном участке цилиндрического канала. Показано, что поля скоростей такого течения являются двумерными и определяются функцией тока. Распределения скоростей получены в виде рядов Фурье — Бесселя.

  DOI: 10.22227/1997-0935.2014.5.127-134

  Библиографический список
  1. Орехов Г.В., Зуйков А.Л., Волшаник В.В. Контрвихревое ползущее течение // Вестник МГСУ. 2013. № 4. С. 172-180.
  2. Моделирование и расчет контрвихревых течений / В.К. Ахметов, В.В. Волшаник, А.Л. Зуйков, Г.В. Орехов ; под ред. А.Л. Зуйкова. М. : МГСУ, 2012. 252 с.
  3. Зуйков А. Л. Азимутальный вихрь и функция тока в ползущем течении в трубе // Вестник МГСУ. 2014. № 4. С. 150-159.
  4. Korn G.A., Korn T.M. Mathematical Handbook for Scientists and Engineers: Definitions, Theorems, and Formulas for Reference and Review. New York : General Publishing Company, 2000. 1151 p.

  Скачать статью

  Источник постоянной мощности производства MOONS’ с функцией автоподстройки выходного тока

  Компания MOONS’ анонсировала новую функцию для своей популярной линейки источников тока серии ME применяемых в уличных светильниках: теперь все программируемые источники тока постоянной мощности будут поставляться с новой функцией — с функцией автоподстройки выходного тока (auto-changing output current value function или dynamic constant power function).

  Эта функция создана для поддержания мощности светильника на одном уровне, чтобы компенсировать широкий разброс параметров СИД (даже именитых производителей), а также сильные температурные колебания в течении года в странах, к которым относится и Россия). Это наверняка заинтересует те компании, которые предлагают свои светильники для Энергосервисных контрактов, для их быстрейшего срока окупаемости, а также для тех, кто не хочет вместо блока на 150 Вт (на которую рассчитана нагрузка при 25 °С окружающей среды), ставить более дорогой и мощный 200 Вт.

  Ни для кого не секрет, что характеристики в паспорте на светильник указываются исходя из номинальных условий работы 230 В и Токр = 25 °С. После температурной стабилизации (обычно 1-2 часа работы) температура в точке пайки на СИД достигает на светильниках ~ 70 °С.

  Условия окружающей среды, в виде изменения ее температуры, оказывают влияние на падение напряжения на светодиодах (Vf), что в свою очередь оказывает влияние на потребляемую мощность при поддержании постоянного значения выходного тока источника. Так при снижении температуры окружающей среды светодиоды начинают потреблять больше мощности, что приводит к перегрузке источника питания.

  На примере указанном в таблице ниже мы видим, что в серии могут быть светодиоды с падением напряжения Vfled = 2,85 В (типовое) или 3,1 В (макс) на «горячую» при Tsp = 85 °C (~Токр = 25 °C ). При этом при Токр = -40 °C и температурном коэффициенте -2,5 мВ/C мы имеем Tsp = 25 °C и соответственно Vfled = 3,0 В (типовое) или 3,25 В (макс).

  Для светильника из 200 шт светодиодов на токе 350 мА при 25 °C мощность диодов составит

  200 x 0,35 А x 2,85 В = 199,5 Вт и 200 x 0,35 А x 3,1 В = 217 Вт,

  а при -40 °C мощность диодов составит 200 x 0,35 А x 3,0 В = 210 Вт и 200 x 0,35 А x 3,25 В = 227, 5 Вт.

  С учётом КПД ИП мощность светильника станет ещё выше, а если использовать СИД на больших токах, то разница будет еще более заметной.

  Для решения этой проблемы компания MOONS’ ввела в серийные ИП автоматическую компенсацию и назвала эту функцию «Автоподстройка выходного тока» — уменьшение тока, при достижении верхней границы выходного напряжения, чтобы предотвратить «перезапуск ИП» и обеспечить стабильную работу светильника. Эта функция также работает совместно с функцией «плавного старта», позволяющей избежать резкого включения светильников, при котором возможно повреждение СИД при отрицательных температурах и возникновение аварийных ситуаций на производстве и на улице из-за ослепления рабочих или участников дорожного движения.

  В источниках питания производства MOONS’, с режимом постоянной мощности, заложена функция автоматического регулирования выходного тока, в зависимости от текущего падения напряжения на светодиодах. Если  суммарное падение напряжения на выходе источника будет возрастать с уменьшением температуры окружающей среды, то источник будет уменьшать выходной ток (Iout) и тем самым поддерживать постоянную выходную мощность.

  Зависимость выглядит следующим образом:

  Пример 1:

  Параметры светодиодной линейки: Vf = 150 В постоянного напряжения, I = 1000 мА
  Параметры источника: P = 150 Вт, выходной ток 700-1050 мА, выходное напряжение 142-214 В

  1. Если система работает при низкой температуре, падение напряжения составит 180 В, что при токе 1000 мА составит 180 Вт потребляемой мощности и приведет к перегрузке источника.

  2. Для предотвращения данной ситуации, источник автоматически скорректирует выходной ток до значения 830 мА, опираясь на значения падения напряжения на выходе равном 180 В, что в итоге оставит постоянную мощность на выходе равную 150 Вт.

  С ростом температуры будет иметь место обратный эффект – рост выходного тока в соответствии со снижением падения выходного напряжения в соответствии с постоянной выходной мощностью.

  Пример 2:

  Параметры светодиодной линейки: Vf = 150 В постоянного напряжения, I = 1000 мА
  Параметры источника: P = 150 Вт, выходной ток 700-1050 мА, выходное напряжение 142-214 В

  1. Если система работает при низкой температуре, падение напряжения составит 240 В, что при токе 1000 мА составит 240 Вт потребляемой мощности и приведет к перегрузке источника.

  2. Для предотвращения данной ситуации, источник автоматически скорректирует выходной ток до значения 625 мА, опираясь на значения падения напряжения на выходе равном 214 В (максимальное значение для данного источника), что в итоге оставит постоянную мощность на выходе равную 625 мА х 214 В = 133,75 Вт.

  Следует отметить, что если выходное напряжение больше чем максимальное выходное источника, то источник не сможет поддерживать постоянную мощность на выходе, даже если в нем имеется функция автоподстройки значения выходного тока.

  Функция auto-changing output current value function (dynamic constant power function) уже включена во все источники тока MOONS’ с прошивкой версии более 1.7 (то есть поставка ИП с конца 2017 года). Проверить версию прошивки Вашего ИП можно с помощью программатора MSSL200 и бесплатного ПО с сайта MOONS’ Programmable Driver Configurator_v2.4T как указано на картинке ниже.

  Если у Вас используются ИП с более ранней версией прошивки, например 1.6, то нам требуется баркод, указанный на наклейке Вашего ИП и мы пришлем ПО для его перепрошивки на более свежую версию с поддержкой данной функции и возможно еще новыми интересными для Вас функциями.

  Получить имя текущей функции в Kotlin — Techie Delight

  В этой статье рассматриваются различные способы получения имени текущей функции, выполняемой в Kotlin.

  1. Использование функции

  Class.getEnclosingMethod ()

  Уловка состоит в том, чтобы вызвать Class. getEnclosingMethod () , который возвращает объект java.lang.reflect.Method с почти каждым битом информации о немедленном включении функции базового класса.

  fun main () { val name = object {}.javaClass.enclosingMethod.name println («Текущая функция — $ name») }

  Загрузить Код

  
  Вы также можете определить внутренний класс в функции, чтобы получить ссылку на Class , как показано ниже:

  fun main () { class Main val name: String = Main :: class.java.enclosingMethod.name println («Текущая функция — $ name») }

  Загрузить Код

  2.Использование функции

  Throwable.getStackTrace ()

  Другой подход состоит в том, чтобы получить массив элементов трассировки стека, представляющий трассировку стека, относящуюся к бросаемому объекту, путем вызова getStackTrace () в экземпляре Throwable .

  Первый элемент массива представляет вершину стека, которая является последним вызовом функции в последовательности.

  fun main () { val name = Throwable ().stackTrace [0] .methodName println («Текущая функция — $ name») }

  Загрузить Код

  
  Вы также можете использовать класс Exception , который расширяет Throwable .

  fun main () { val name = Exception (). StackTrace [0] .methodName println («Текущая функция — $ name») }

  Загрузить Код

  3.Использование функции

  Thread.getStackTrace ()

  Другой возможный способ — использовать трассировку стека текущего потока, которая возвращает массив элементов трассировки стека, представляющих дамп стека этого потока.

  Второй элемент возвращаемого массива трассировки стека содержит кадр стека текущей функции.

  fun main () { val name = Thread.currentThread (). StackTrace [1] .methodName println («Текущая функция — $ name») }

  Загрузить Код

  Это все о том, как получить имя текущей функции в Kotlin.

  
  Спасибо за чтение.

  Используйте наш онлайн-компилятор для публикации кода в комментариях с использованием C, C ++, Java, Python, JavaScript, C #, PHP и многих других популярных языков программирования.

  Нам нравится? Направляйте нас к своим друзьям и помогайте нам расти. Счастливое кодирование 🙂

  
  

  Определение имени текущей функции

  Кредит: Алекс Мартелли

  У вас есть сообщения об ошибках, которые включают имя функции, излучающей их.Чтобы скопировать такие сообщения в другие функции, вам придется редактировать их каждый раз, если вы не можете автоматически найти имя текущей функции.

  Эту интроспективную задачу легко выполнить с sys._getframe . Эта функция возвращает объект фрейма, атрибут которого f_code — это объект кода, а co_name атрибут этого объекта является функцией имя:

   импорт систем
  this_function_name = sys._getframe () .f_code.co_name 

  Объекты фрейма и кода также предлагают другую полезную информацию:

   this_line_number = sys._getframe () .f_lineno
  this_filename = sys._getframe () .f_code.co_filename 

  Вызвав sys._getframe (1) , вы можете получить это информация для вызывающего абонента текущей функции. Так что вы можете упакуйте эту функциональность в свои собственные удобные функции:

   def whoami ():
      import sys
      вернуть sys._getframe (1) .f_code.co_name
  
  me = whoami () 

  Это вызывает sys._getframe с аргументом 1, потому что звонок на whoami теперь равен нулю.Сходным образом:

   def callersname ():
      import sys
      вернуть sys._getframe (2) .f_code.co_name
  
  him = callersname () 

  Вы хотите определить имя текущего запущенного функция — например, для создания сообщений об ошибках, которые не нужно менять при копировании на другой функции. Функция _getframe функции sys Модуль делает это и многое другое. Этот рецепт вдохновлен рецептом 10.4 из Perl Cookbook . Python sys._getframe , новое в 2.1, предлагает информацию, эквивалентную (но более богатую) Встроенный в Perl вызывающий абонент , _ _LINE_ _ и _ _FILE_ _ . Если вам понадобится эта функция для более старых версий Python, см. Рецепт 14.9.

  Рецепт 14.9 для версии, которая работает с старые версии Python; документация по _getframe метод sys модуль в библиотеке Ссылка ; Perl Cookbook Рецепт 10.4.

  Получите Python Cookbook прямо сейчас с онлайн-обучением O’Reilly.

  участника O’Reilly проходят онлайн-обучение в режиме реального времени, а также получают книги, видео и цифровой контент от 200+ издателей.

  Искать в текущей функции | Советы по Vim вики

  Vim может искать в ограниченном объеме, например, находя совпадения только в текущей функции или только в текущем блоке, разделенном фигурными скобками ( {...} ). Этот совет предоставляет сценарий, упрощающий поиск в блоке. Процедура работает для любой программы, такой как C или C ++, где блок кода начинается с « {» и заканчивается «} », а функция начинается с « {» на левом поле.

  Использование []

  После создания сценария, показанного ниже, отредактируйте программу, которая использует фигурные скобки ( {...} ) вокруг блоков. Сценарий определяет некоторые сопоставления с помощью клавиши , которая по умолчанию является обратной косой чертой.

  Поместив курсор внутри функции, введите \ [ или \ { или \ / для поиска:

  \ [

  Искать визуально выделенный текст или текущее слово, но только

  в текущей функции ( {...} с открывающей скобкой в ​​первом столбце).

  \ {

  Искать визуально выделенный текст или текущее слово, но только

  в текущем блоке ( {...} ).

  /

  Поиск визуально выделенного текста или любого другого текста, который вы вводите, но только

  в рамках текущей функции.

  Если вы визуально выделите какой-либо текст, введите \ [ или \ { или \ / , поиск обнаружит следующее вхождение выбранного текста, но только в пределах указанной области.

  Если нет выделенного текста:

  • При вводе \ [ или \ { выполняется поиск слова под курсором (аналогично * ).
  • При вводе \ / отображается шаблон поиска, определяющий область действия. Завершите узор, набрав любой желаемый текст, затем нажмите Enter, чтобы завершить поиск.

  После поиска нажмите n или N для поиска следующего или предыдущего вхождения в той же области.

  Скрипт []

  Создать файл ~ /.vim / plugin / scopesearch.vim (Unix) или $ HOME / vimfiles / plugin / scopesearch.vim (Windows), содержащий приведенный ниже сценарий, затем перезапустите Vim.

   "Поиск в области (программный блок {...}).
  "Версия 2010-02-28 из http://vim.wikia.com/wiki/VimTip1530
  
  "Искать в блоке верхнего уровня слово под курсором или выделенный текст.
  nnoremap  [/  =  ScopeSearch ('[[', 1)  
  vnoremap  [ /  =  ScopeSearch ('[[', 2)   gV
  "Искать в текущем блоке слово под курсором или выделенный текст.nnoremap  {/  =  ScopeSearch ('[{', 1)  
  vnoremap  { /  =  ScopeSearch ('[{', 2)   gV
  "Искать введенный пользователем текст в текущем блоке верхнего уровня.
  nnoremap  / /  =  ScopeSearch ('[[', 0) 
  vnoremap  /  /  =  ScopeSearch ('[[', 2)  
  
  "Вернуть шаблон для поиска в указанной области, или
  "вернуть обратную косую черту, чтобы отменить поиск, если область не найдена.~ [')
      вызов setreg ('@', old_reg, old_regtype)
    endif
    пусть saveview = winsaveview ()
    выполнить 'нормально! '. а: навигатор
    пусть первая = строка ('.')
    обычный %
    пусть последняя = строка ('.')
    обычный %
    вызовите winrestview (saveview)
    если первый <последний
      return printf ('\ %%>% dl \ %% <% dl% s', first-1, last + 1, pattern)
    endif
    вернуть "\ b"
  конечная функция
   

  Сценарий использует [[, чтобы перейти к началу текущей функции, или [{, чтобы перейти к началу текущего блока.Это должно поместить курсор на левую скобку. Затем % используется для перехода к соответствующей правой фигурной скобке. Номера строк, содержащих левую и правую фигурные скобки, определяют область действия. Если блок не обнаружен, сценарий возвращает "\ b" (символ возврата), что отменяет поиск, начатый сопоставлением.

  См. Также []

  Список литературы []

  []

  Воспринимаемая несправедливость опосредует взаимосвязь между воспринимаемым пренебрежением в детстве и текущими функциями у пациентов с хронической болью: предварительное пилотное исследование

  Совокупные данные подтверждают связь между кажущимся пренебрежением в детстве и психологическим и физическим здоровьем в зрелом возрасте.На сегодняшний день пути, опосредующие эту связь, остаются в значительной степени неизвестными, хотя другие данные свидетельствуют о том, что негативные модели оценки, включая восприятие несправедливости, связанного с болью, могут быть сформированы предыдущим неблагоприятным социальным опытом. Следовательно, в текущем исследовании изучалась воспринимаемая несправедливость в отношении хронической боли как возможный фактор, связывающий пренебрежение в детстве и последствия, связанные с болью, учитывая его значимость как для адаптации к хронической боли, так и к предыдущему неблагоприятному жизненному опыту. Пациенты (n = 742), посещавшие третичную клинику по лечению боли, прошли опрос, проведенный через совместный реестр информации о результатах в области здравоохранения.Анализ моделирования пути использовался для изучения воспринимаемой несправедливости как посредника в отношениях между пренебрежением в детстве и эмоциональным дистрессом и физическим функционированием после контроля интенсивности боли и катастрофической боли. Пациенты, одобряющие пренебрежение в детстве, сообщали о более высоком уровне воспринимаемой несправедливости и ухудшении эмоционального дистресса и физического состояния. Кроме того, включение воспринимаемой несправедливости в качестве посредника полностью объясняет взаимосвязь между пренебрежением и текущими уровнями физических функций и составляет значительную часть взаимосвязи между пренебрежением и текущими уровнями аффективного дистресса.Эти предварительные результаты предполагают, что воспринимаемая несправедливость, по-видимому, является более непосредственным фактором, благодаря которому предыдущий опыт пренебрежения может отрицательно повлиять на адаптацию к хронической боли. Учитывая единичную оценку пренебрежения заботой о детстве и перекрестный характер текущих результатов, дальнейшие исследования могут быть сосредоточены на воспроизведении этих результатов в лонгитюдных исследованиях с подтвержденными критериями и изучении других неблагоприятных социальных переживаний (например, жестокого обращения, социального неравенства), которые могут способствовать к восприятию несправедливости и плохим исходам, связанным с болью.

  Ключевые слова: Аффективный дистресс; Безнадзорность детства; Хроническая боль; Боль катастрофическая; Воспринимаемая несправедливость; Физическая функция.

  Golang реализует такие операции, как получение текущего имени функции и номера строки файла

  Давайте посмотрим на код напрямую ~

    // Получает имя запущенной функции
  func runFuncName () string {
      pc: = make ([] uintptr, 1)
      время выполнения.Абоненты (2, шт)
      f: = runtime.FuncForPC (pc [0])
      вернуть f.Name ()
  }  

    пакет основной
  Импортировать(
      "fmt"
      "время выполнения"
  )
   
  // Получает имя запущенной функции
  func runFuncName () string {
      pc: = make ([] uintptr, 1)
      runtime.Callers (2, шт)
      f: = runtime.FuncForPC (pc [0])
      вернуть f.Name ()
  }
   
  func test1 () {
      я: = 0
      fmt.Println ("i =", i)
      fmt.Println ("FuncName1 =", runFuncName ())
  }
   
  func test2 () {
      я: = 1
      fmt.Println ("i =", i)
      fmt.Println ("FuncName2 =", runFuncName ())
  }
   
  func main () {
      Fmt.println ("имя функции печати в действии")
      test1 ()
      test2 ()
  }  

  Библиотека времени выполнения golang предоставляет вызывающую функцию, которая может возвращать имя файла и номер строки, выполняемой во время выполнения:

   
  func Caller (пропустить int) (pc uintptr, строка файла, строка int, ok bool) { 

  Вызывающий сообщает файл и информацию о номере строки о вызовах функций в стеке вызывающей горутины. Пропуск аргумента - это количество кадров стека для подъема, где 0 идентифицирует вызывающего абонента.(По историческим причинам значение пропуска для вызывающего и вызывающего абонентов различается.) Возвращаемые значения сообщают счетчик программы, имя файла и номер строки в файле соответствующего вызова. Логическое значение ok является ложным, если не удалось восстановить информацию.

  Метод вызова следующий. Возвращенный файл - это абсолютный путь, а строка - это номер строки. При этом вы можете добавить эту запись в свой журнал и другие функции.

   
  _, файл, строка, ок: = время выполнения.Звонок (1)  

  Дополнение: место работы функции позиционирования go (имя файла, имя функции, строка)

  Время выполнения. Caller () возвращает количество программ PC, имя выполненного файла и количество строк, в которых выполняется функция

  Время выполнения. Funcforpc () передается на ПК, чтобы указатель функции запускался

  .

  файловая структура

   
  - время выполнения
  - -file1.go
  - -file2.go
  - -main.go  

  Файл Main.go

   
  основной пакет
  Импортировать (
  "fmt"
  "дорожка"
  "время выполнения"
  )
  func main () {
  имя, имя_функции, строка: = f2 (0)
  fmt.Printf ("файл:% v; функция:% v; строка:% d", имя, имя_функции, строка)
  }
  func getLocation (skip int) (fileName, funcName string, line int) {
  pc, файл, строка, ok: = runtime.Caller (пропустить)
  if! ok {
  fmt.Println ("получить информацию не удалось")
  возвращение
  }
  fmt.Println (ПК, файл)
  fileName = path.Base (файл)
  funcName = время выполнения.FuncForPC (pc) .Name ()
  возвращение
  }
    

  Файл 1.go

   
  основной пакет
  func f1 (skip int) (fileName, funcName string, line int) {
   fileName, funcName, line = getLocation (пропустить)
   возвращение
  }
    

  Файл2.go файл

   
  основной пакет
  func f2 (skip int) (fileName, funcName string, line int) {
   вернуть f1 (пропустить)
  }
    

  При вызове F2 в файле main.go

   
  func main () {
   имя, имя_функции, строка: = f2 (3)
   fmt.Printf ("файл:% v; функция:% v; строка:% d", имя, имя_функции, строка)
   //output:file:main.go;function:main.main;line:10
  }  

  F2 вызов F1, вызов F1 получение местоположения; F2 -> F1 -> getlocation претерпела трехуровневые вызовы, поэтому, когда в F2 передается 3, будет возвращено текущее местоположение выполнения, имя функции и имя файла функции

  Когда передается 2, возвращается значение (файл: File2.Идти; функция: main.f2; Строка: 8) Имя функции F2, расположение файла и имя файла

  Когда передается 1, он возвращает (file: file1. Go; function: main.f1; Line: 4) имя функции, расположение файла и имя файла функции F1

  Когда передается 0, он возвращает (file: main. Go; function: main.getLocation; Line: 16) имя функции, расположение файла и имя файла функции getlocation

  Это мой личный опыт. Я надеюсь, что смогу дать вам ссылку, и я надеюсь, что вы сможете поддержать разработчика.Если у вас есть ошибки или вы не учитываете их полностью, не стесняйтесь комментировать.

  текущая функция | Документы Microsoft

  • 21.02.2011
  • 2 минуты на чтение

  В этой статье

  Возвращает набор узлов, единственным членом которого является текущий узел.

    текущий набор узлов ()
    

  Замечания

  Функция возвращает набор узлов, единственным членом которого является текущий узел.Для самого внешнего выражения, выражения, не встречающегося в другом выражении, текущий узел всегда совпадает с узлом контекста. Таким образом,

  совпадает с

  Однако текущий узел в квадратных скобках обычно отличается от узла контекста. Например,

  обрабатывает все элементы , которые имеют родительский элемент и атрибут name со значением, равным значению атрибута ref текущего узла.Это отличается от

  , что означает то же, что и

  .

  и поэтому будет обрабатывать все элементы , которые имеют родительский элемент и имеют атрибут name и атрибут ref с тем же значением.

  Пример

  XML-файл (текущий.xml)

    
  
  <узлы>
      первый 
     <узел> 1 
     <узел>
         класс 
     
  
    

  XSLT-файл (current.xsl)

  Выход

  Ниже приводится форматированный вывод, отображаемый в браузере.

  первая

  1

  класс

  Ниже приведены выходные данные процессора XSLT. Чтобы получить этот результат, щелкните правой кнопкой мыши в браузере и выберите пункт меню View XSL Output .

    
  <цитата>
     
   первый 
     
   1 
     <цитата>
        
   класс 
     
  
    

  См. Также

  Номер ссылки

  Справочник по типам данных XML

  получить текущее имя функции в Python · GitHub

  получить текущее имя функции в Python · GitHub

  Мгновенно делитесь кодом, заметками и фрагментами.

  получить текущее имя функции в Python

  .

  	#! / Usr / bin / env python
  	# - * - кодировка: utf-8 - * -
  	#
  	# Примечание. Это может работать только в CPython. Для получения дополнительной информации см. Документ Python о sys._getframe
  	импорт sys
  	# Это также покажет, что имя функции (co_name) в python привязано к коду функции (f_code).
  	# т.е. назначение функции не изменит атрибут "co_name", имя функции
  	def get_current_func_name ():
  	«» Получить текущее имя функции.”“ ”
  	печать sys._getframe.f_code.co_name
  	# print "get_current_func_name"
  	get_current_func_name ()
  	another_func = get_current_func_name ()
  	# print "get_current_func_name"
  	another_func ()
  	##################### Осмотреть ========================
  	# Примечание. Это может работать только в CPython.Для получения дополнительной информации см. Документ python о inspect.currentframe
  	импортная инспекция
  	def get_current_func_name ():
  	«» Получить текущее имя функции. »« »
  	cur_frame = inspect.currentfram ()
  	попытка:
  	печать cur_frame.f_code.co_name
  	наконец:
  	del рама
  	# не используйте приведенный ниже код для получения текущего кадра. Он вернет все кадры, а затем выберет
  	# текущий.
  	# frames = inspect.stack ()
  	# try ：
  	# рамки печати [0] [3]
  	# наконец:
  	# del frames

  Вы не можете выполнить это действие в настоящее время.Вы вошли в систему с другой вкладкой или окном. Перезагрузите, чтобы обновить сеанс. Вы вышли из системы на другой вкладке или в другом окне. Перезагрузите, чтобы обновить сеанс. .