Функция тока — Википедия
Материал из Википедии — свободной энциклопедии
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 28 июля 2015; проверки требуют 2 правки. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 28 июля 2015; проверки требуют 2 правки.Функция тока в гидродинамике — скалярная функция, которая определяет двумерное течение жидкости или газа.
Обычно, функция тока ψ{\displaystyle \psi } определяется из соотношения
- rot(ψz→)=v→,{\displaystyle \operatorname {rot} \,(\psi {\vec {z}})={\vec {v}},}
где v→{\displaystyle {\vec {v}}} — вектор скорости потока, rot{\displaystyle \operatorname {rot} } — ротор.
Для прямоугольной декартовой системы координат это даёт:
- vx=∂ψ∂y;vy=−∂ψ∂x.{\displaystyle v_{x}={\frac {\partial \psi }{\partial y}};\;v_{y}=-{\frac {\partial \psi }{\partial x}}.}
Так как для несжимаемой жидкости поле скорости соленоидально, то у него существует векторный потенциал Ψ→{\displaystyle {\vec {\Psi }}}, определяемый соотношением
- rotΨ→=v→.{\displaystyle \operatorname {rot} \,{\vec {\Psi }}={\vec {v}}.}
Как любой потенциал, функция тока определена с точностью до аддитивной постоянной. Когда в задаче есть твёрдые стенки (на которых скорость равна нулю), то значение функции тока на них обычно принимается равной нулю. Если же стенок нет (заполнено всё пространство), то можно задать значение функции тока на бесконечности, если поле скорости там постоянно.
- Изолинии функции тока совпадают с линиями тока жидкости. Для стационарного (не зависящего от времени) течения они также являются траекториями частиц.
- При некоторых условиях максимум функции тока равен расходу жидкости.
Функция тока плоского течения
В практических задачах гидромеханики двумерных потоков широчайшее применение находит понятие о функции тока. Рассмотрим двумерный поток и ограничимся несжимаемой жидкостью.
Как было показано, для плоского течения дифференциальное уравнение линии тока имеет вид

 . (10.10)
. (10.10)
Плоское
течение или в общем случае двумерное
течение жидкости обладает той особенностью,
что для него можно ввести функцию тока  :
:
 , (10.11)
, (10.11)
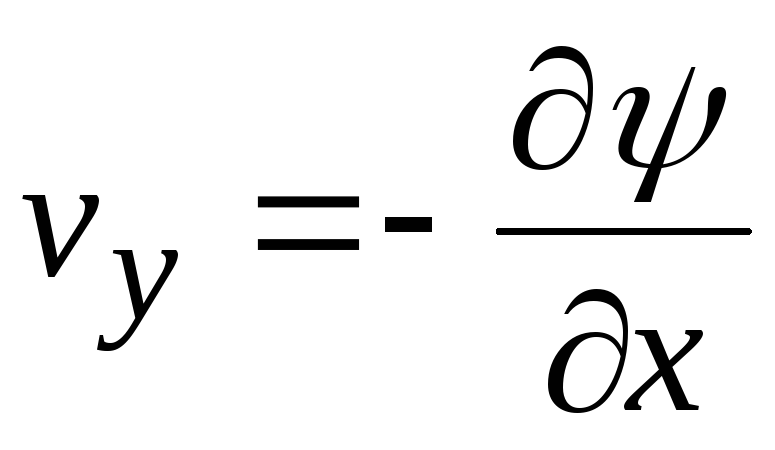 . (10.12)
. (10.12)
Подставляя (10.11) и (10.12) в (10.10), получим
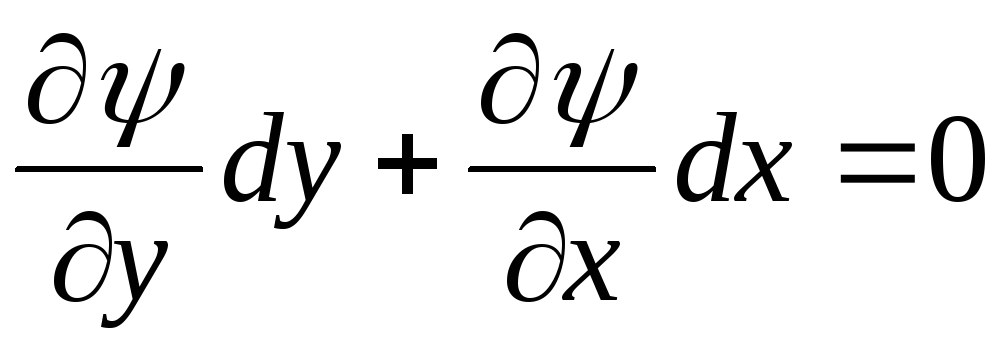 . (10.13)
. (10.13)
Так как по условию (10.3) смешанные производные равны
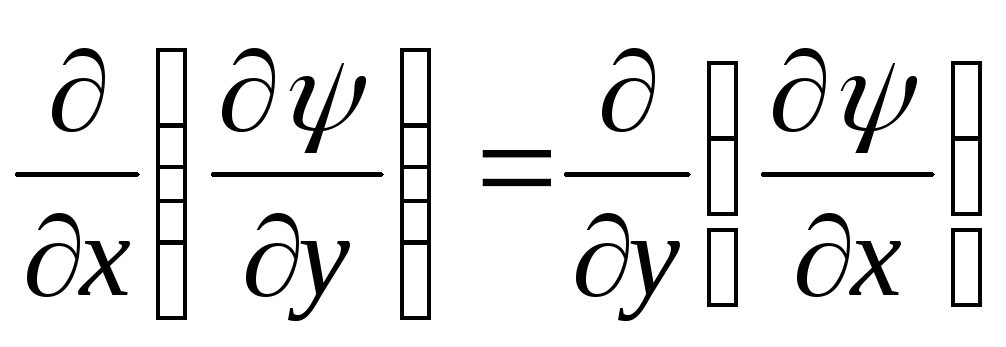 ,
,
то (10.13) является полным дифференциалом и для линии тока можно записать
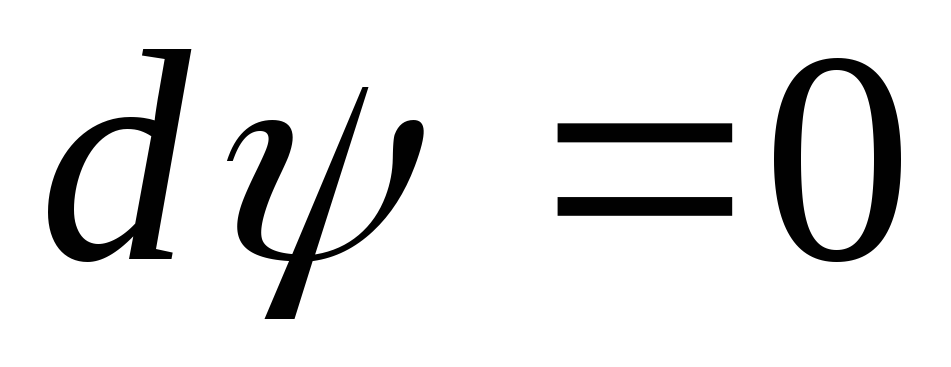
или
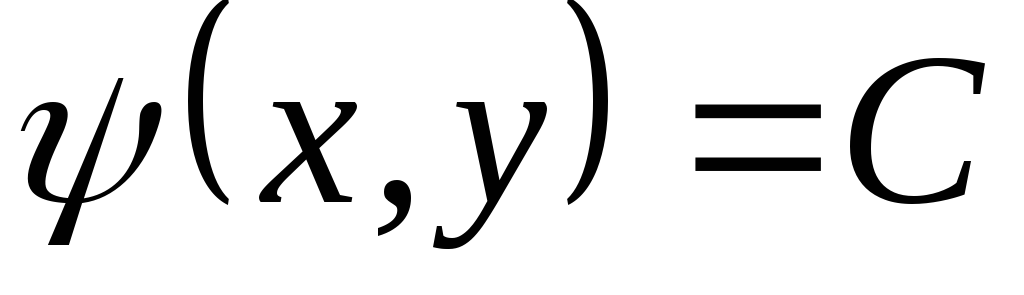
где С – произвольная постоянная.
Уравнение (10.14) является семейством линий тока. Каждому конкретному значению С соответствует своя линия тока. Изменяя значение С, будем получать различные линии тока.
Для
плоского потенциального течения  ,
т.е.
,
т.е.
 ,
,
откуда получаем уравнение Лапласа
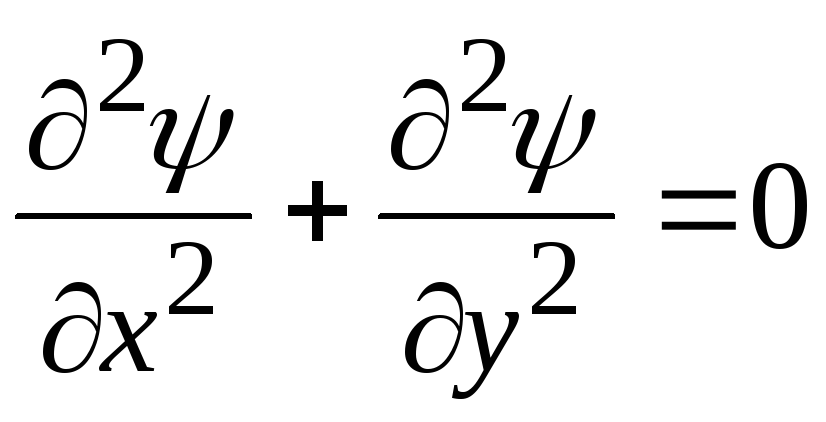
Следует отметить, что потенциал скорости существует только в потенциальном потоке, т.е. в потоке без вихрей. Функция тока существует также и в вихревом потоке, но определена только для двумерного потока.
Если потенциалу скорости задать некоторое фиксированное значение С, то получим семейство линий
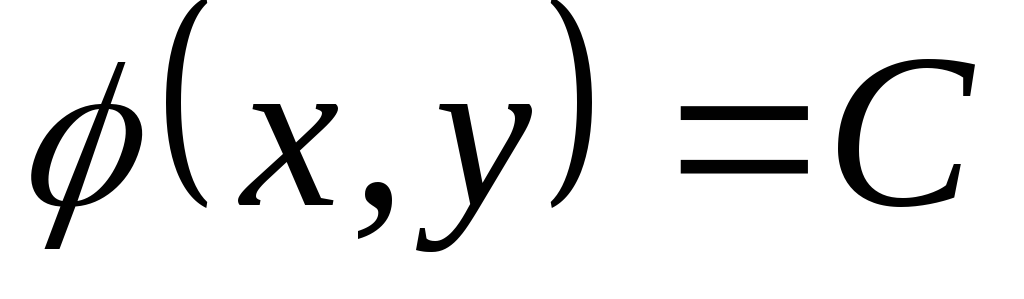 , (10.16)
, (10.16)
обладающих
тем свойством, что вдоль каждой линии
потенциал скорости остается постоянным.
Такие линии называются эквипотенциальными.
В потенциальном потоке скорость жидкости 
Линии
постоянного значения функции тока
совпадают с линиями тока, вдоль которых
направлена скорость потока. По этой
причине в потенциальном плоском
установившемся потоке семейство линий
тока и семейство эквипотенциальных
линий взаимно перпендикулярны или
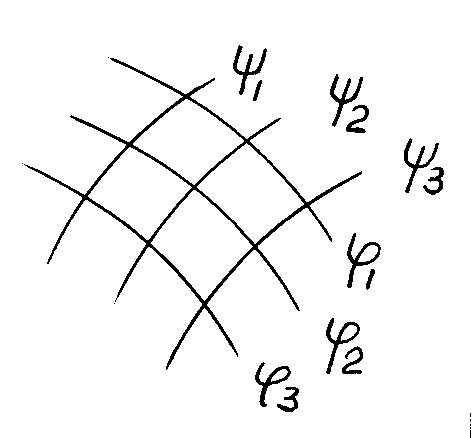
ортогональны. Сетка кривых  и
и 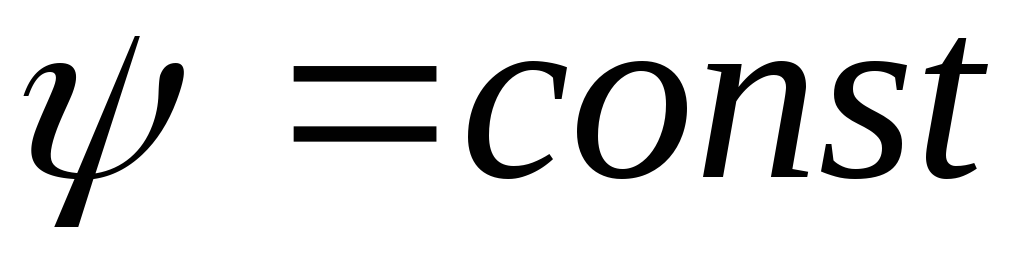 называется гидродинамической сеткой.
Вид ее показан на рис. 10.1.
называется гидродинамической сеткой.
Вид ее показан на рис. 10.1.
Так как в потенциальном поле
 ,
,
то
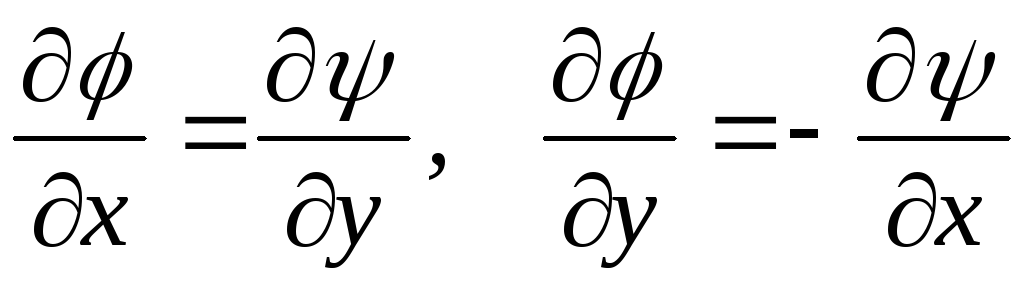 . (10.17)
. (10.17)
Выражения (10.17) называются соотношениями Коши-Римана.
Рассмотрим гидромеханический смысл функции тока, для чего проведем две достаточно близко расположенные линии тока, как показано на рис.6.2.

Возьмем на линиях тока точки А и В. Разложим скорость потока по координатным осям и вычислим расход жидкости между точками в направлениях осей:
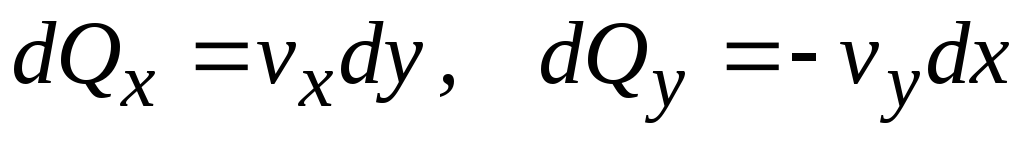 .
.
Общий расход составит
 . (10.18)
. (10.18)
Отсюда следует, что объемный расход между двумя линиями тока равен разности значений функций тока на этих линиях. Если контур замкнут, т.е. точки
 .
.Лекция 11. Методы расчета потенциальных потоков
Для нахождения потенциала скорости и функции тока необходимо проинтегрировать уравнения Лапласа при заданных граничных условиях, что является достаточно сложной задачей. Существует метод, позволяющий определить значения потенциала и функции тока без интегрирования уравнений Лапласа. Общая идея метода сводится к следующему: сначала задаются некоторой функцией, которая удовлетворяет уравнению Лапласа, а затем выясняют, чему соответствует гидромеханическая сетка движения.
Пример 1. Пусть выражение для потенциала скорости имеет вид
 ,
,
где a и b – некоторые действительные числа.
Найдем проекции скорости на координатные оси:
 .
.
Проверим, удовлетворяет ли выражение для потенциала уравнению Лапласа.
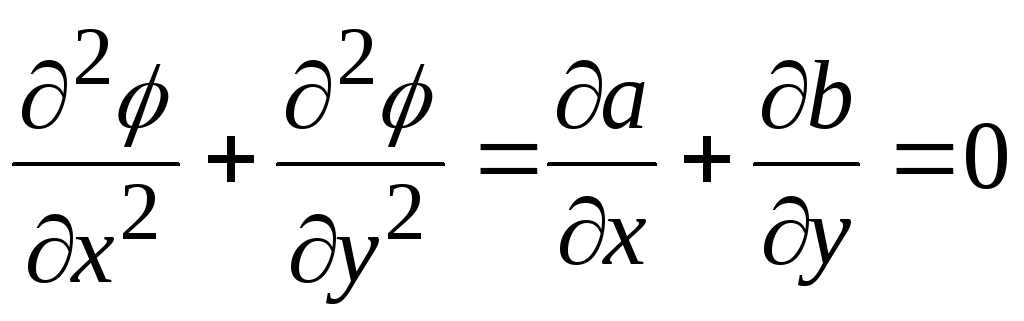 .
.
Выражение
для потенциала скорости соответствует
уравнению Лапласа. Скорости потока в
направлении координатных осей 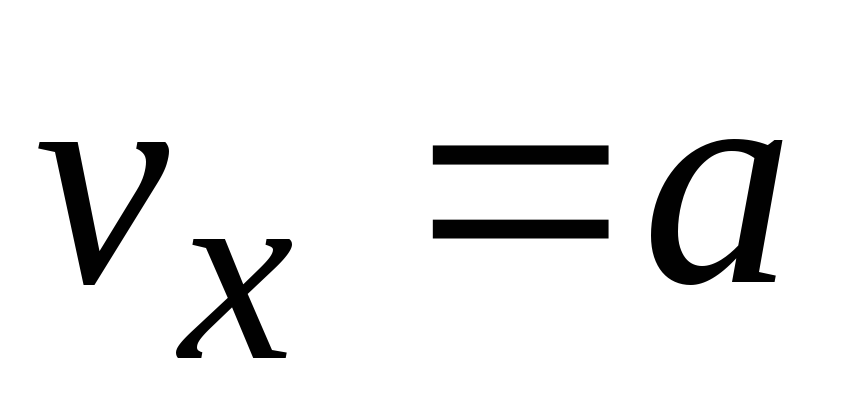 и
и  постоянны, поток двигается с постоянной
скоростью. Полная скорость потока
постоянны, поток двигается с постоянной
скоростью. Полная скорость потока
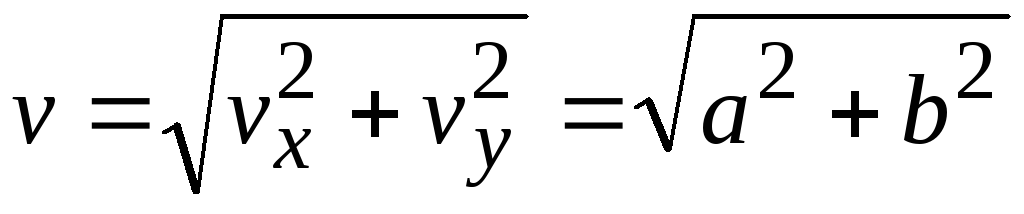 .
.
Выясним, что представляют собой линии тока. Так как
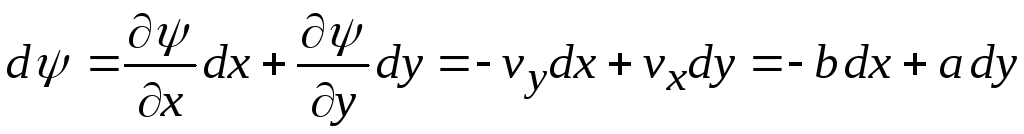 ,
,
то после интегрирования имеем
 .
(11.1)
.
(11.1)
Для
линии тока справедливо соотношение 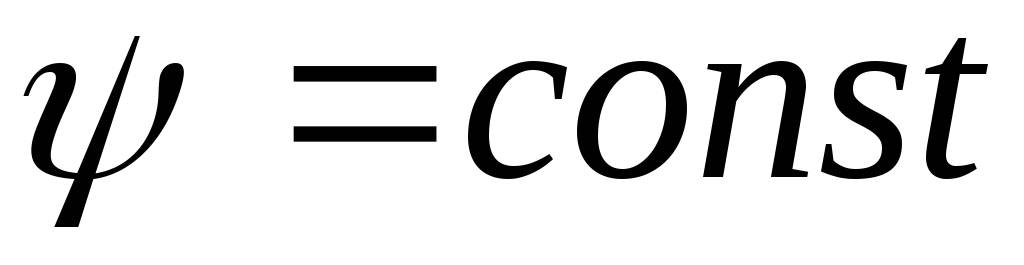 .
Приравнивая (11.1) некоторой постоянной,
получим
.
Приравнивая (11.1) некоторой постоянной,
получим
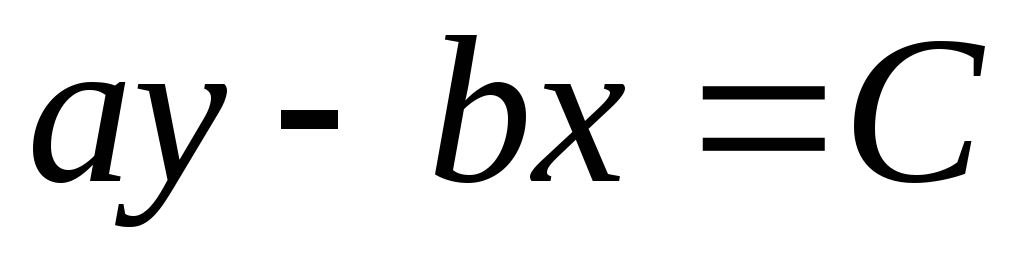 или
или 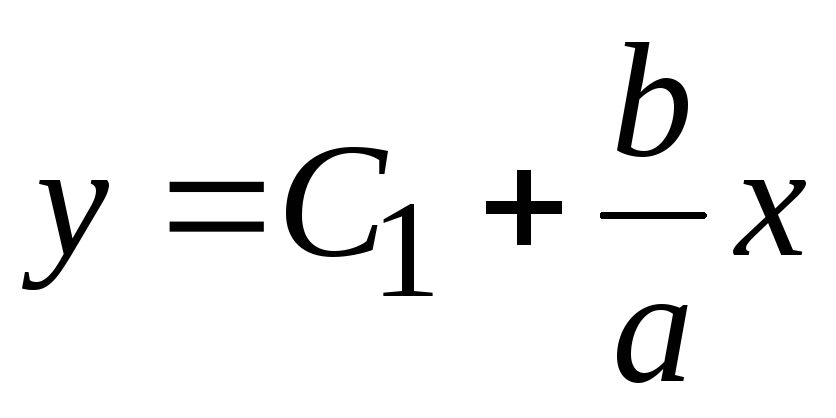 .
.
Это
уравнение семейства параллельных
прямых, наклоненных под углом 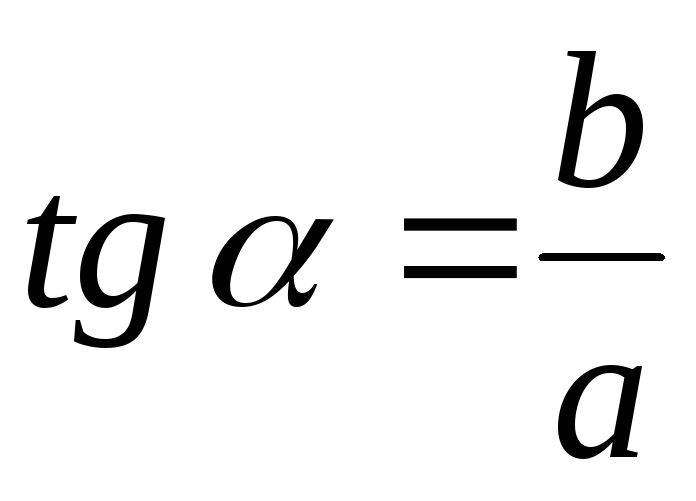 к оси х.
Вид гидродинамической сетки показан
на рис. 11.1.
к оси х.
Вид гидродинамической сетки показан
на рис. 11.1.
Пример 2. Пусть потенциал скорости задан выражением
 ,
,
где а – некоторое действительное число, при этом а >0.
Определяем проекции скорости
 .
.
Проверяем, удовлетворяет ли выражение для потенциала уравнению Лапласа
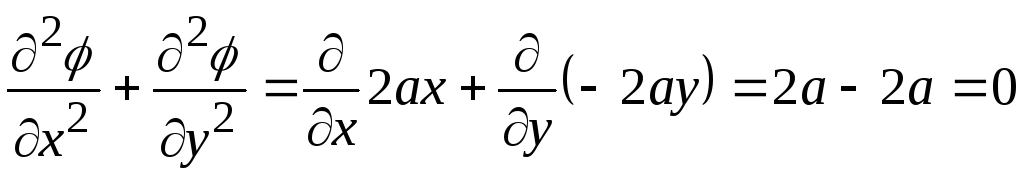 .
.
Выражение соответствует уравнению Лапласа.
Определяем вид функций тока
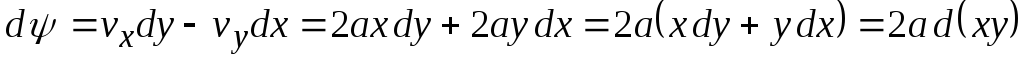 .
.
После интегрирования имеем
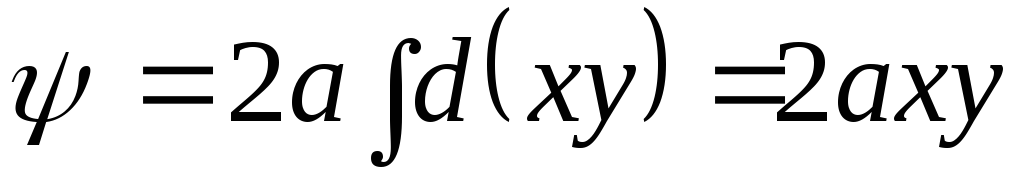 . (11.2)
. (11.2)
Произвольная постоянная в данном случае нас не интересует. Приравнивая (11.2) некоторой постоянной, получим
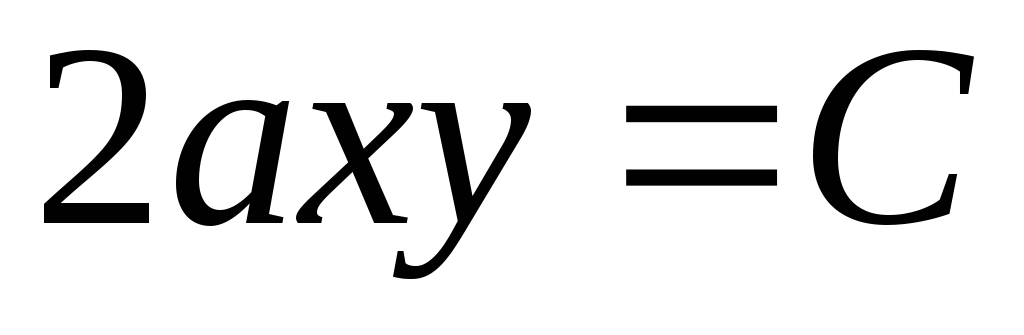 или
или 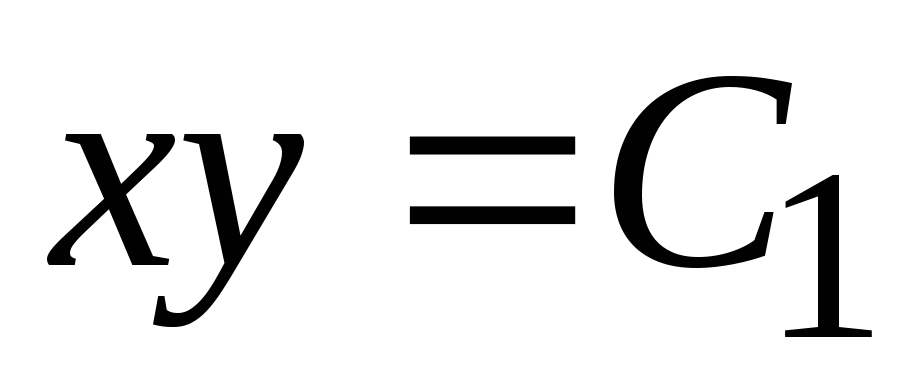 .
.
Получили семейство кривых, описываемых уравнением
 .
.
Отсюда следует, что линии тока представляют собой семейство гипербол с асимптотами, являющимися осями координат. При С1>0 или x>0, y>0, или x<0, y<0 ветви гипербол располагаются в первой и третьей четвертях, в другом случае – во второй и четвертой четвертях. Если C1=0, то линиями тока являются оси координат х=0, у=0.
В
любом случае в начале координат 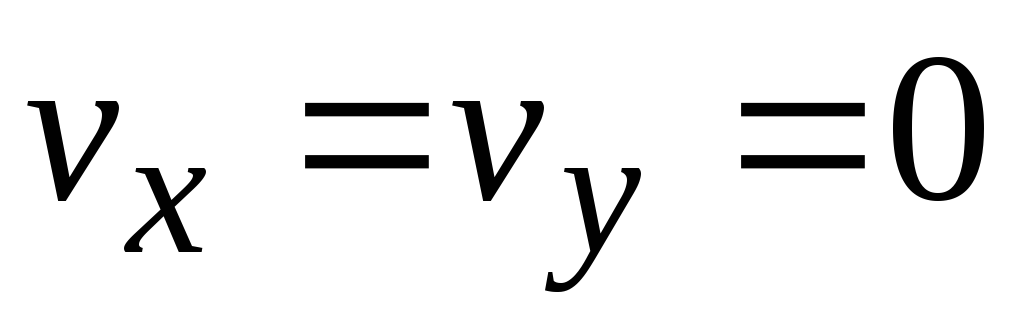 .
Точка потока, в которой скорость равна
нулю, называется критической точкой.
.
Точка потока, в которой скорость равна
нулю, называется критической точкой.
Если потенциал скорости приравнять некоторой постоянной величине, то получим семейство эквипотенциальных линий
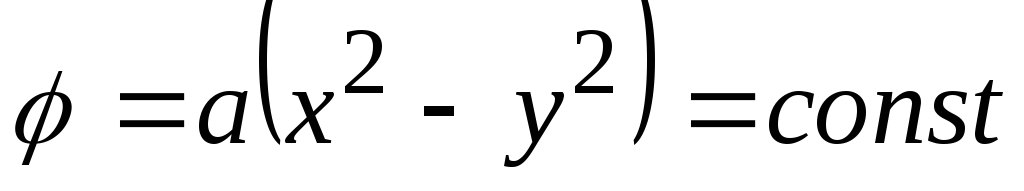 .
.
Это
уравнение описывает семейство гипербол
с асимптотами, являющимися биссектрисами
координатных углов и ортогональных к
гиперболам  .
.
Если положительные части осей х и у принять за твердые стенки, то получим картину обтекания потоком прямого угла. Гидромеханическая сетка потока показана на рис.11.2.
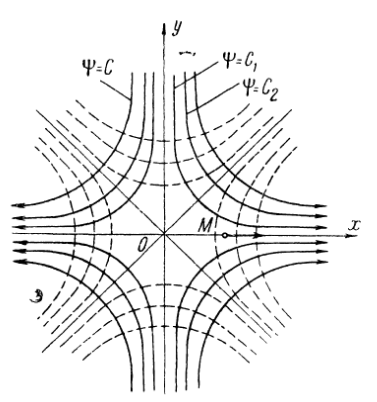

Пример 3. Источник и сток на плоскости. Под источником и стоком на плоскости понимают точку, из которой происходит истечение или втекание жидкости.
Пусть потенциал скорости задан в виде
 ,
,
где а – некоторое действительное число. При а >0 движение жидкости происходит из начала координат к периферии, в центре координат располагается источник жидкости. При a <0 поток движется из периферии к центру координат, в центре координат происходит сток жидкости.
Для
осесимметричного течения более удобными
являются цилиндрические координаты с
осями , , z.
Для двумерного потока координата z исчезает.
Так как 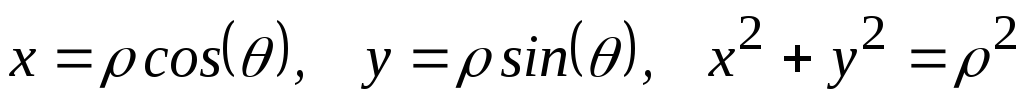 ,
то в полярных координатах выражение
для потенциала скорости принимает вид
,
то в полярных координатах выражение
для потенциала скорости принимает вид
 .
.
Определяем проекции скорости на координатные оси:
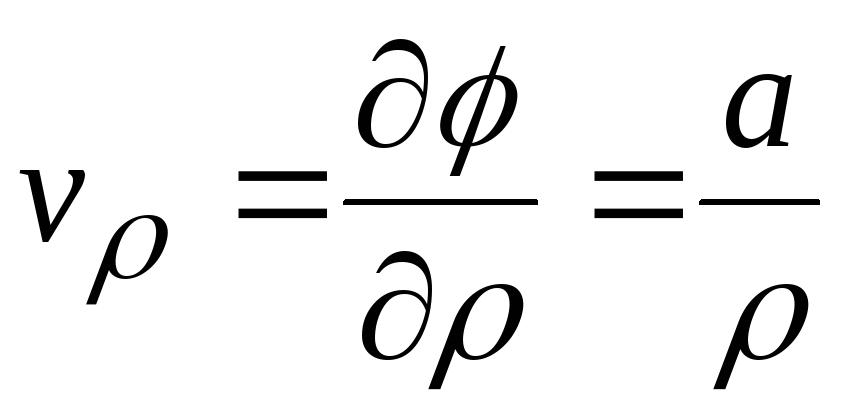 ,
,
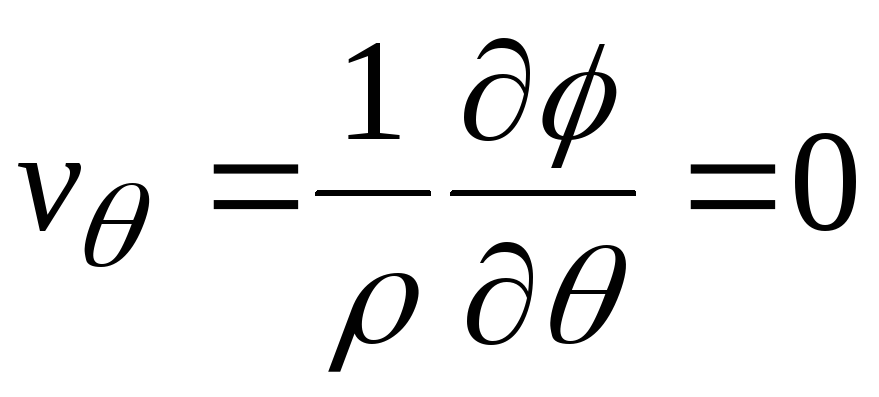 .
.
Отсюда следует, что скорость жидкости и линии тока направлены по радиусам от центра при источнике и к центру при стоке.
Уравнение Лапласа в цилиндрических координатах имеет вид
 .
.
Для плоского течения в полярных координатах ,
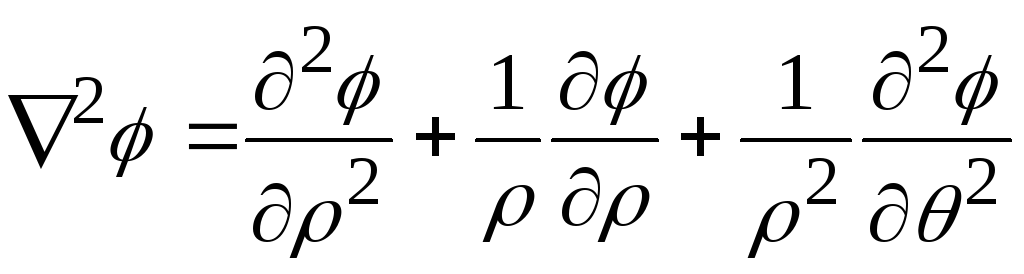 .
.
Проверяем, удовлетворяет ли выражение для потенциала уравнению Лапласа
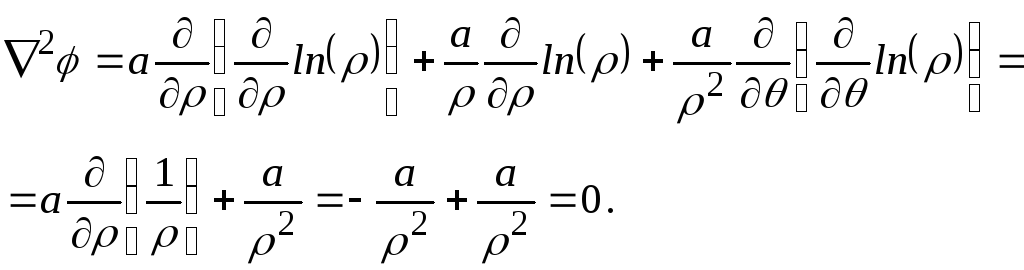
Выражение соответствует уравнению Лапласа.
Уравнение прямой линии в полярных координатах, проходящей через центр координат
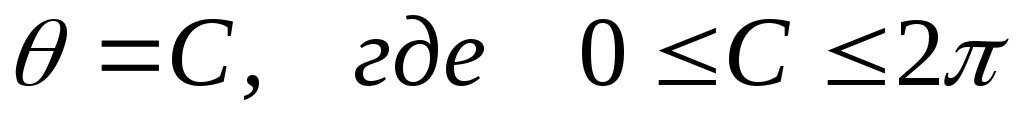 .
.
Выражение для функции тока, постоянной на линии тока

где С – некоторая величина.
Определим
значения параметров в выражениях для
потенциала скорости и функции тока.
Эквипотенциальные линии 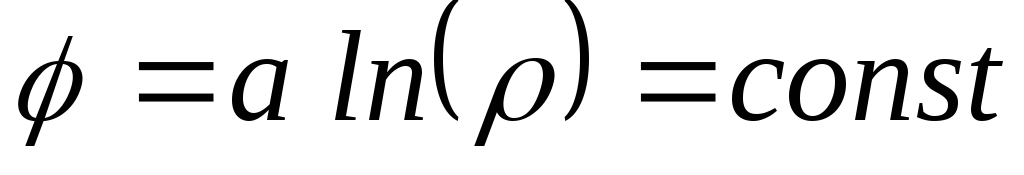 соответствуют выражению
соответствуют выражению 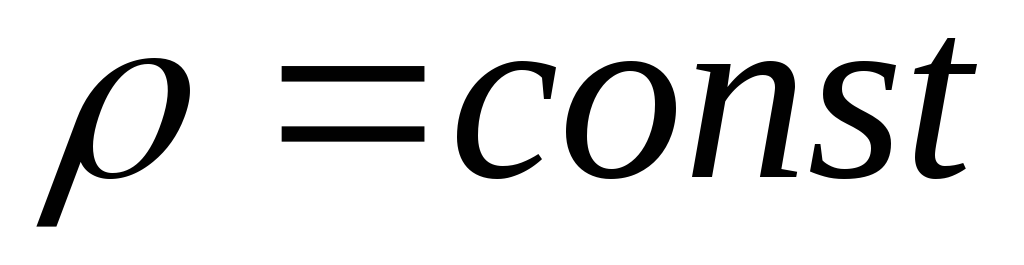 ,
т.е. представляют собой концентрические
окружности. Примем, что толщина слоя
жидкости по оси z равна 1. Тогда на радиусе площадь сечения для прохода жидкости
будет равна
,
т.е. представляют собой концентрические
окружности. Примем, что толщина слоя
жидкости по оси z равна 1. Тогда на радиусе площадь сечения для прохода жидкости
будет равна
 .
.
При объемном расходе жидкости Q на радиусе будет равна
 .
.
Отсюда видно, что скорость потока обратно пропорциональна радиусу, т.е. расстоянию от центра источника или стока. В начале координат скорость обращается в бесконечность, что реально недостижимо.
Так
как  ,
то
,
то 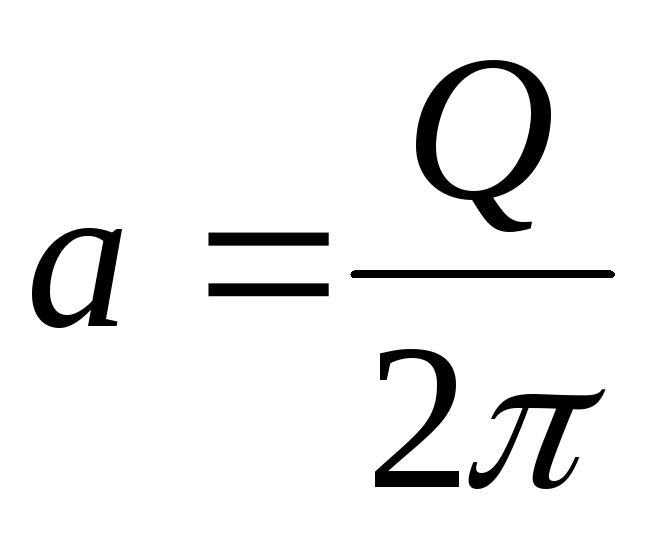 и
и  .
.
На любом радиусе расход жидкости через эквипотенциальную линию, т.е. окружность равен Q, при этом через сектор с углом d расход будет равен
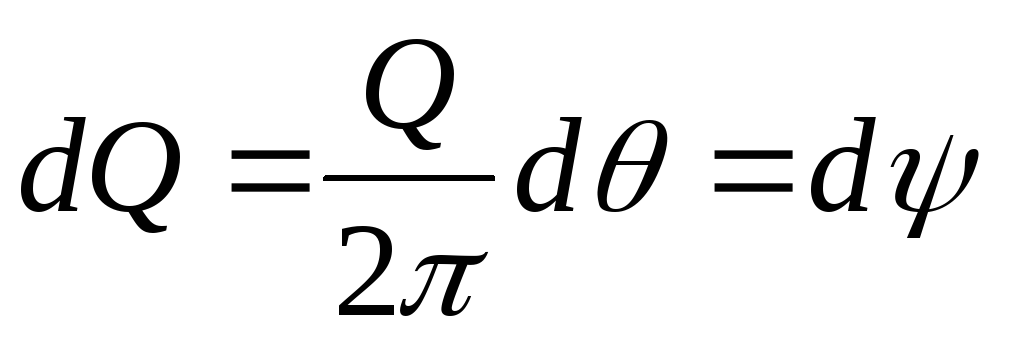 .
.
О тсюда
тсюда 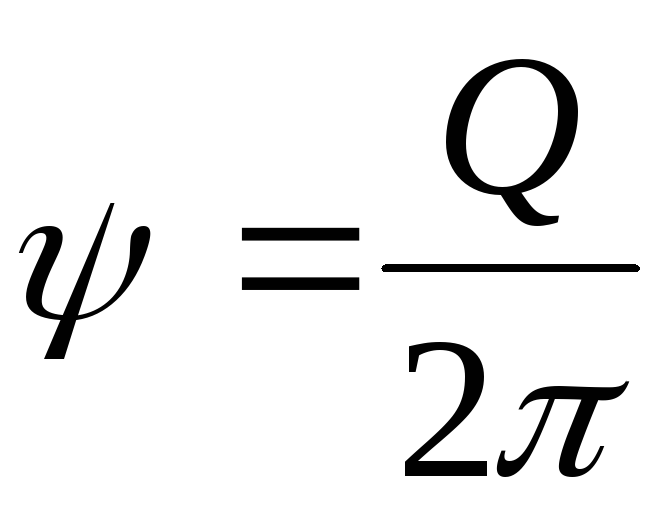 .
.
Гидромеханическая сетка для источника показана на рис.11.3.
Функция тока — Википедия. Что такое Функция тока
Материал из Википедии — свободной энциклопедииФункция тока в гидродинамике — скалярная функция, которая определяет двумерное течение жидкости или газа.
Определение
Обычно, функция тока ψ{\displaystyle \psi } определяется из соотношения
- rot(ψz→)=v→,{\displaystyle \operatorname {rot} \,(\psi {\vec {z}})={\vec {v}},}
где v→{\displaystyle {\vec {v}}} — вектор скорости потока, rot{\displaystyle \operatorname {rot} } — ротор.
Для прямоугольной декартовой системы координат это даёт:
- vx=∂ψ∂y;vy=−∂ψ∂x.{\displaystyle v_{x}={\frac {\partial \psi }{\partial y}};\;v_{y}=-{\frac {\partial \psi }{\partial x}}.}
Обобщения
Так как для несжимаемой жидкости поле скорости соленоидально, то у него существует векторный потенциал Ψ→{\displaystyle {\vec {\Psi }}}, определяемый соотношением
- rotΨ→=v→.{\displaystyle \operatorname {rot} \,{\vec {\Psi }}={\vec {v}}.}
Неоднозначность
Как любой потенциал, функция тока определена с точностью до аддитивной постоянной. Когда в задаче есть твёрдые стенки (на которых скорость равна нулю), то значение функции тока на них обычно принимается равной нулю. Если же стенок нет (заполнено всё пространство), то можно задать значение функции тока на бесконечности, если поле скорости там постоянно.
Свойства
- Изолинии функции тока совпадают с линиями тока жидкости. Для стационарного (не зависящего от времени) течения они также являются траекториями частиц.
- При некоторых условиях максимум функции тока равен расходу жидкости.
Физический смысл функции тока
П
ψn+Δψ
одсчитаем расход несжимаемой жидкости в плоском канале единичной ширины между линиями тока и
и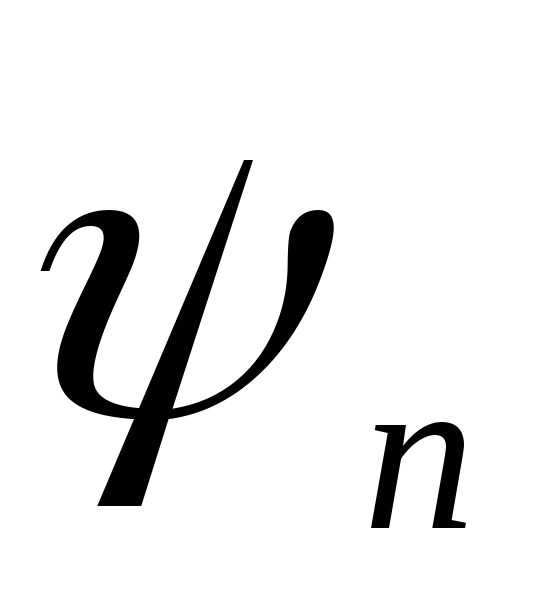 на плоскостиXOY.
В данном случае сечение S будет криволинейным; выберем на нём
элемент dS и заменим его составным,
состоящим из двух прямолинейных отрезков AO=dy и OB=-dx – проекций dS на оси XOY.
Очевидно, что расход через dS и расход через составное сечения равны
одной и той же величине (рис. Д.2.2)
на плоскостиXOY.
В данном случае сечение S будет криволинейным; выберем на нём
элемент dS и заменим его составным,
состоящим из двух прямолинейных отрезков AO=dy и OB=-dx – проекций dS на оси XOY.
Очевидно, что расход через dS и расход через составное сечения равны
одной и той же величине (рис. Д.2.2)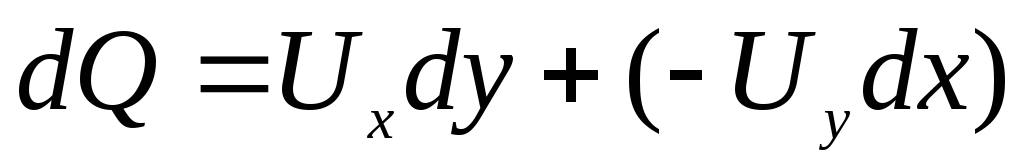 .
.

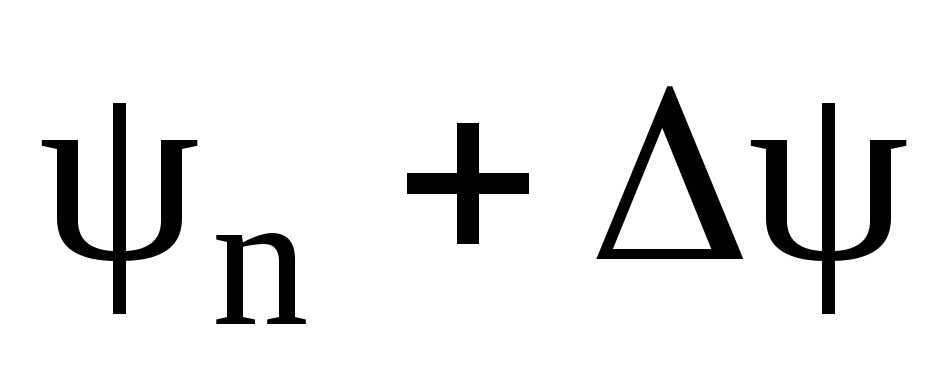
ψn
Рис. Д.2.2
Если учесть, что
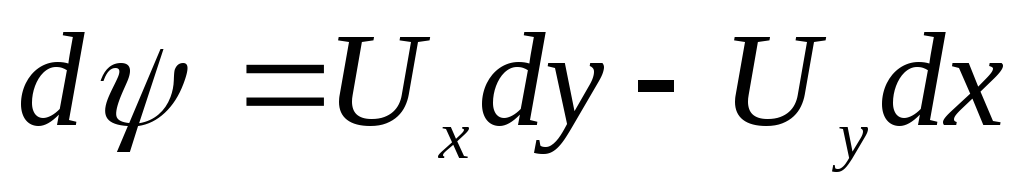
и что
 ,
,
то получим окончательно
 .
.
Итак,
разность  есть объемный
расход жидкости через площадку единичной
высоты, расположенную между линиями
тока
есть объемный
расход жидкости через площадку единичной
высоты, расположенную между линиями
тока  и
и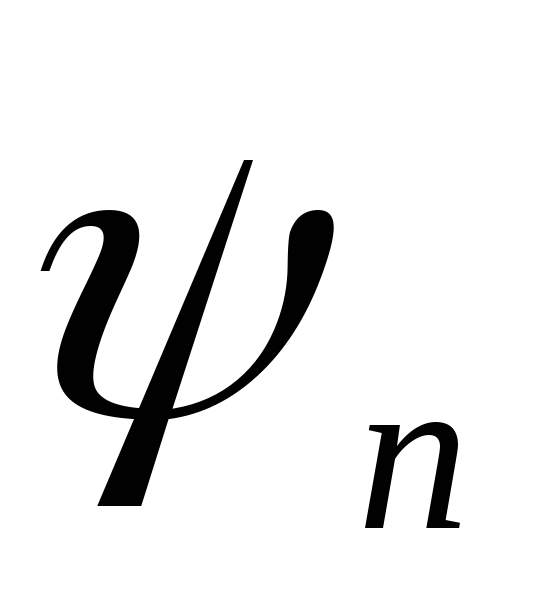 .
.
Примеры плоских сечений
Пример Д.2.1. Рассмотрим плоское прямолинейное и равномерное установившееся течение несжимаемой невязкой жидкости с одинаковой во всём потоке (в любой точке) скоростью, направленной вдоль оси Оy. В этом случае
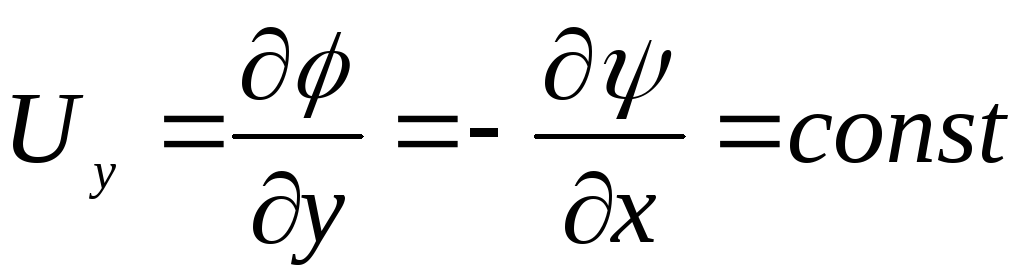 ,
, 
Тогда уравнение неразрывности удовлетворяется, и течение является потенциальным.
Тогда

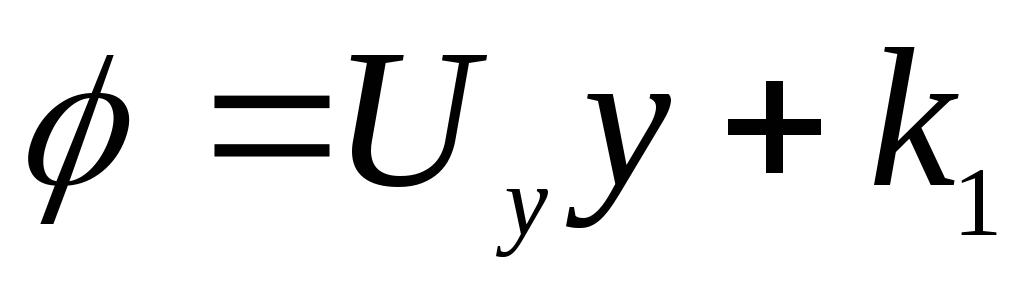

 –
–
линии
равных потенциалов 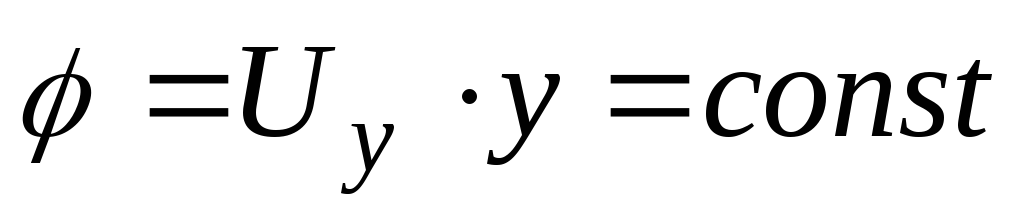 представляют собой прямые, параллельные
оси абсцисс, рис. Д.2.3. Ось Оy
(x=0)
также является одной из эквипотенциальных
линий; обозначим её через
представляют собой прямые, параллельные
оси абсцисс, рис. Д.2.3. Ось Оy
(x=0)
также является одной из эквипотенциальных
линий; обозначим её через 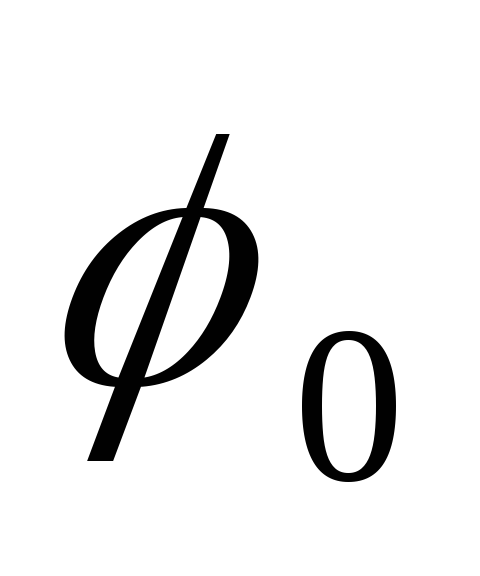 .
.
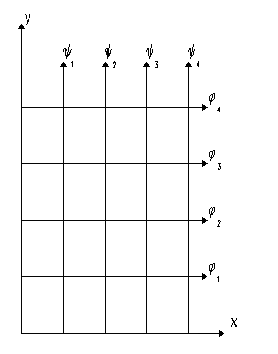
Рис. Д.2.3
М
Рис Д.2.2
ожно допустить, что ,
следовательно
,
следовательно 
Рис. Д.2.2
.Для функции тока найдём аналогично
 .
.
Линии тока представляют прямые, параллельные оси Оy.
Задача Д.2.2. Найти
потенциал и функцию тока
и функцию тока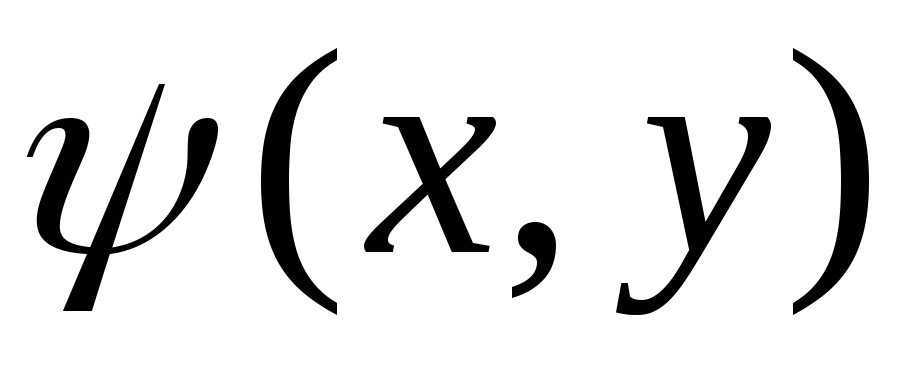 плоского поступательного потока,
направленного под углом к оси абсцисс.
плоского поступательного потока,
направленного под углом к оси абсцисс.
Решение. Такой поток может быть образован в результате наложения плоского однородного поступательного потока, параллельного оси абсцисс на плоский однородный поступательный поток вдоль оси ординат.
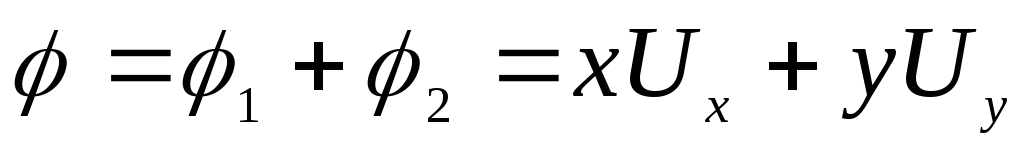 ,
, 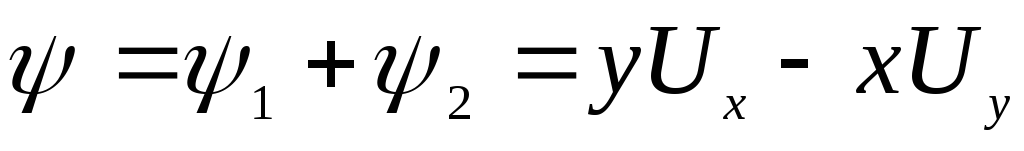 .
.
П ример
Д.2.2. Предположим, что невязкая несжимаемая
жидкость непрерывно подводится к
некоторой точке плоскости и растекается
по ней с одинаковой интенсивностью по
всем направлениям, рис. Д.2.4; такое течение
называется плоским
источником.
ример
Д.2.2. Предположим, что невязкая несжимаемая
жидкость непрерывно подводится к
некоторой точке плоскости и растекается
по ней с одинаковой интенсивностью по
всем направлениям, рис. Д.2.4; такое течение
называется плоским
источником.
Проведём
из центра источника несколько
концентрических окружностей различного
радиуса. Уравнение постоянства расхода
через цилиндрическую поверхность,
построенную на любой окружности и
имеющую высоту, равную единице, будет
иметь вид (при  =const)
=const)
 .
.
С
Рис. Д.2.4
корость, как следует из последнего равенства, выразится так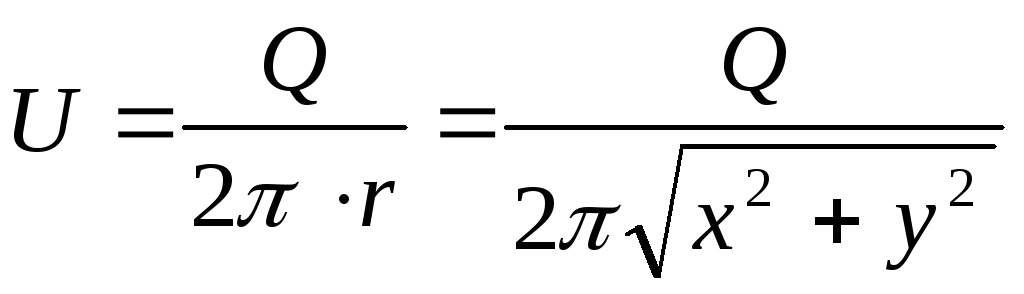 ,
,
где 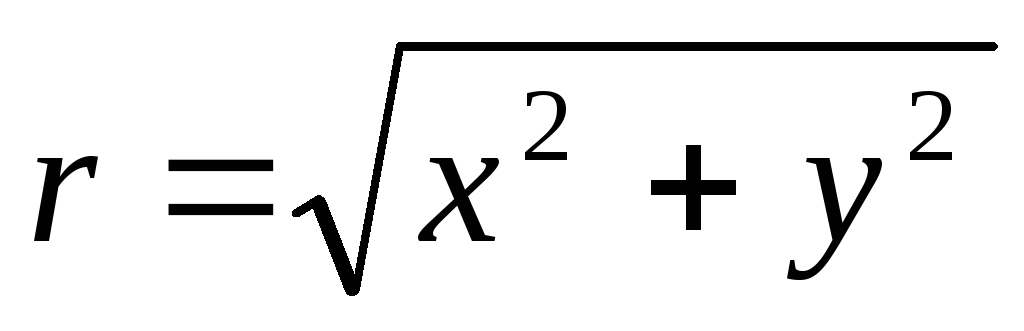 .
.
Поэтому
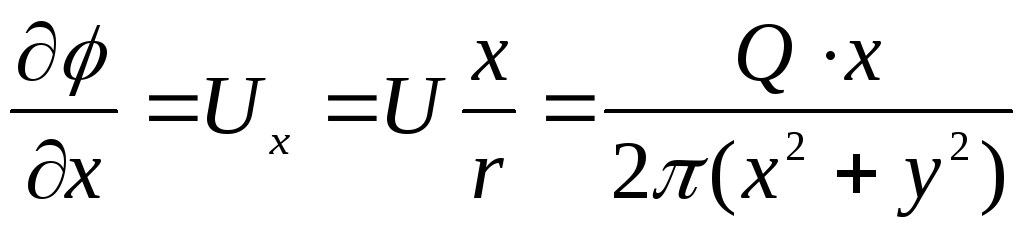 .
.
Аналогично
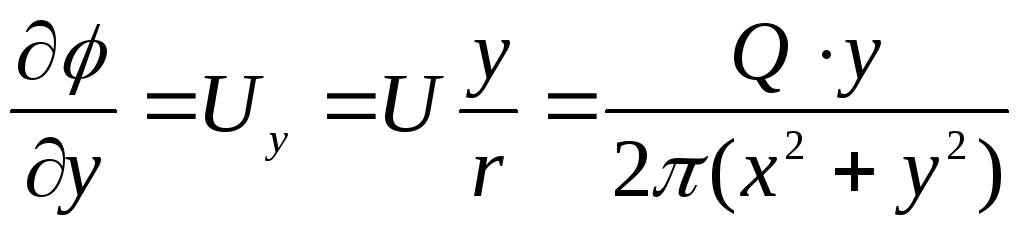 ;
;
окончательно полный дифференциал потенциала скорости
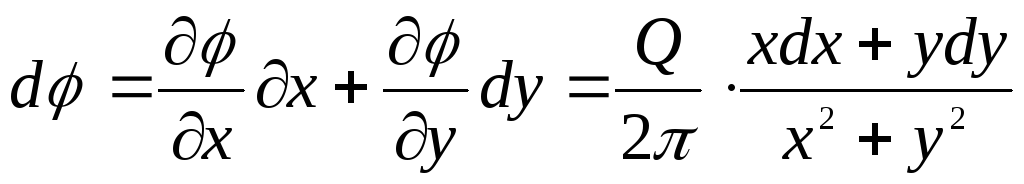 .
.
Интегрируя это выражение, найдём потенциал скорости для источника
 ,
,
где
С – константа интегрирования, которую
можно принять равной нулю, если положить,
что при круге r=1
функция 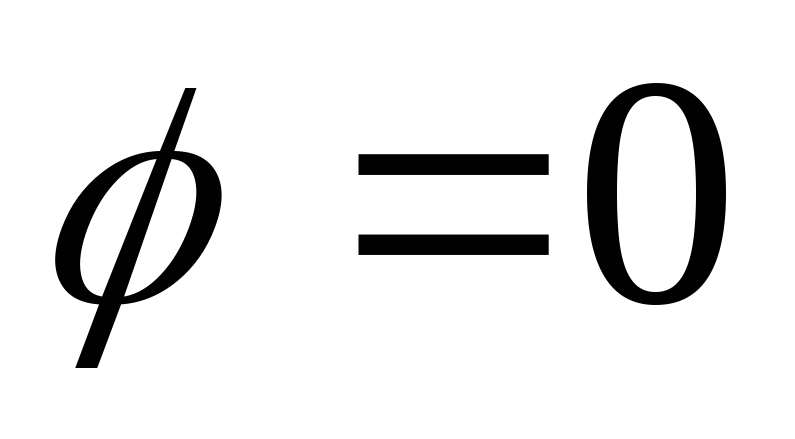 и тогда
и тогда
 ,
(Д.2.10)
,
(Д.2.10)
Для определения функции тока учтём, что
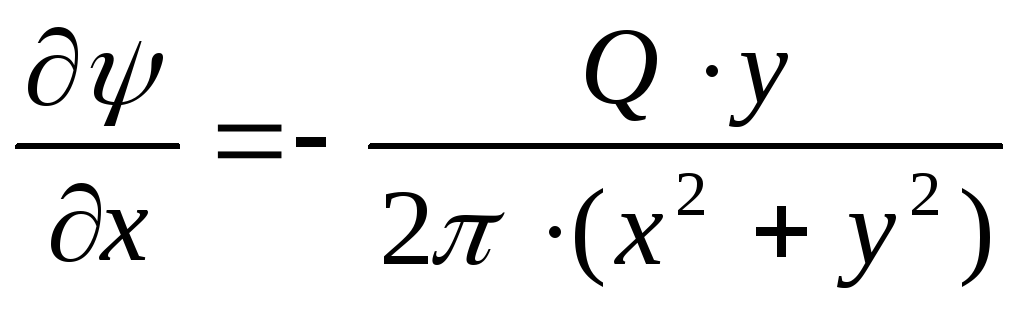 ,
,  ,
,
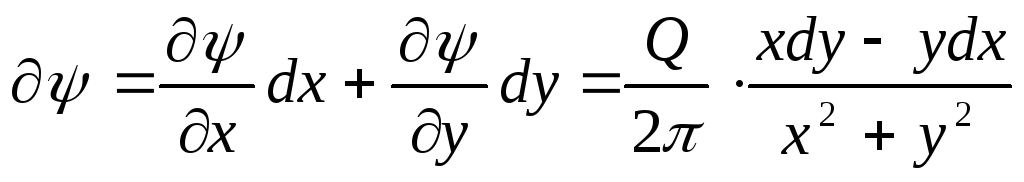 .
.
После интегрирования
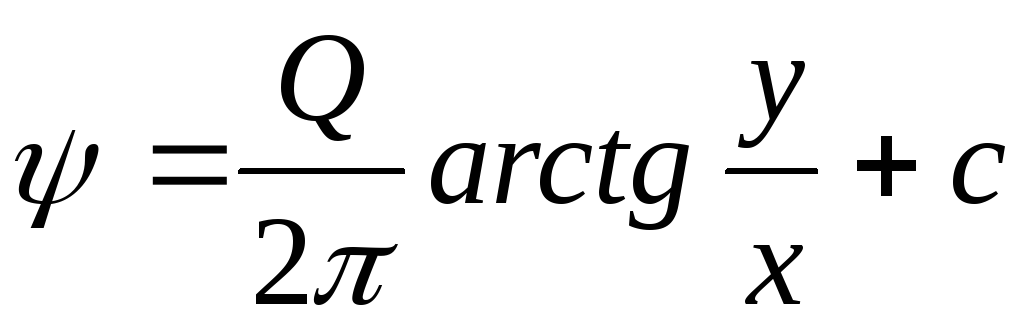 .
.
Из
рис. Д.2.4 видно, что 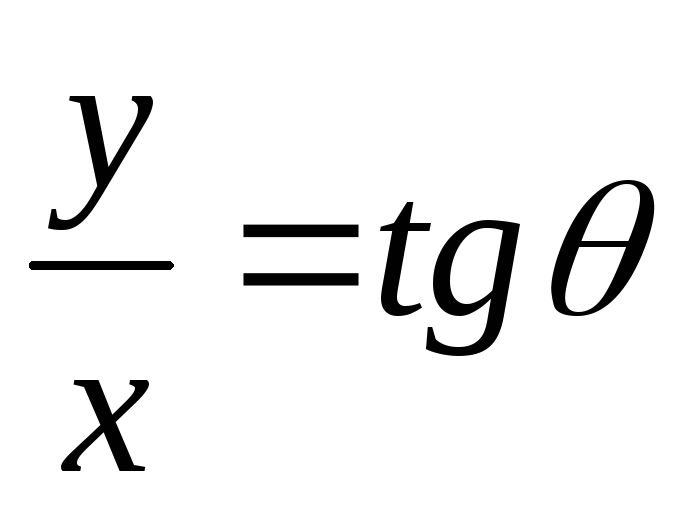 ,
где
,
где – угол, образованный одной из линий
тока. Принимая
– угол, образованный одной из линий
тока. Принимая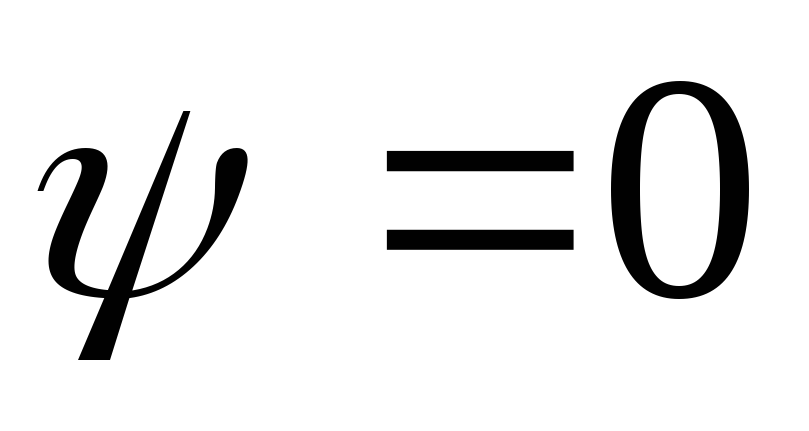 ,
приy=0
получаем c=0
и, следовательно, для функций тока можно
записать
,
приy=0
получаем c=0
и, следовательно, для функций тока можно
записать
 .
(Д.2.11)
.
(Д.2.11)
Эта
зависимость выражает функцию тока
источника. Из выражений (Д.2.10) и (Д.2.11)
следует, что потенциал скорости источника 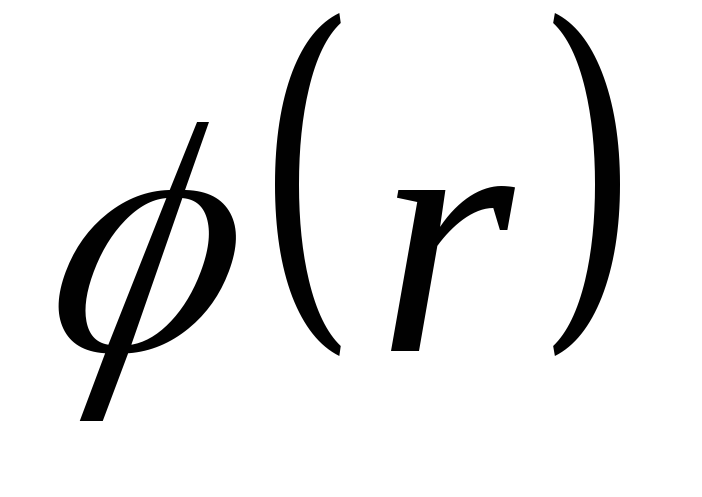 может быть представлен семейством
концентрических окружностей различного
радиуса, а функция тока
может быть представлен семейством
концентрических окружностей различного
радиуса, а функция тока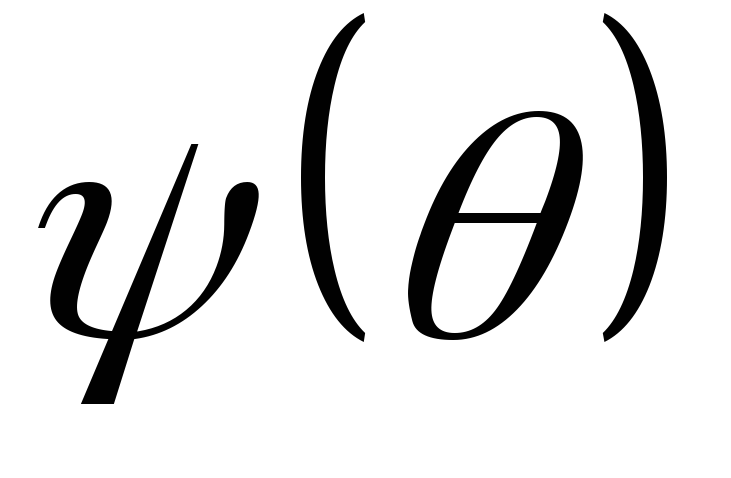 представляется пучком прямых, исходящих
из центра.
представляется пучком прямых, исходящих
из центра.
Потенциал скорости и функция тока для стока будут иметь вид, аналогичный (Д.2.10) и (Д.2.11), но с обратным знаком, т.е.
 ,
, 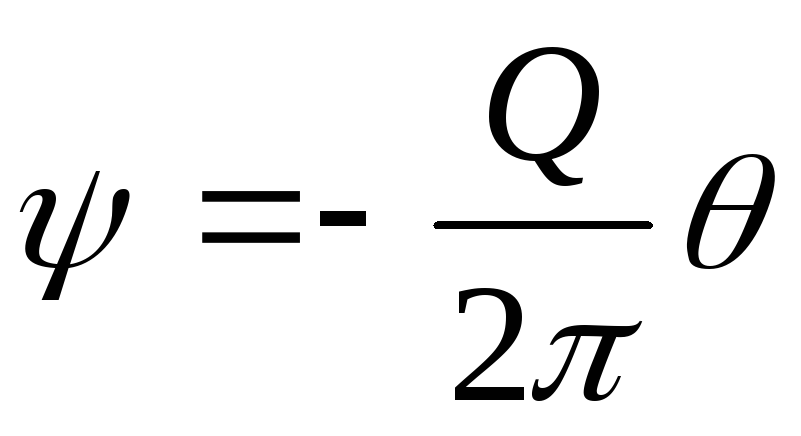 .
.
П
Рис. Д.2.5
ример Д.2.3. Рассмотрим течение, которое получается при одновременном существовании (наложении) на некотором расстоянии друг от друга источника и стока равной интенсивности (равного радиуса). Начало координат поместим в точку, делящую расстояние между центрами источника и стока пополам. Допустим, что источник располагается в точке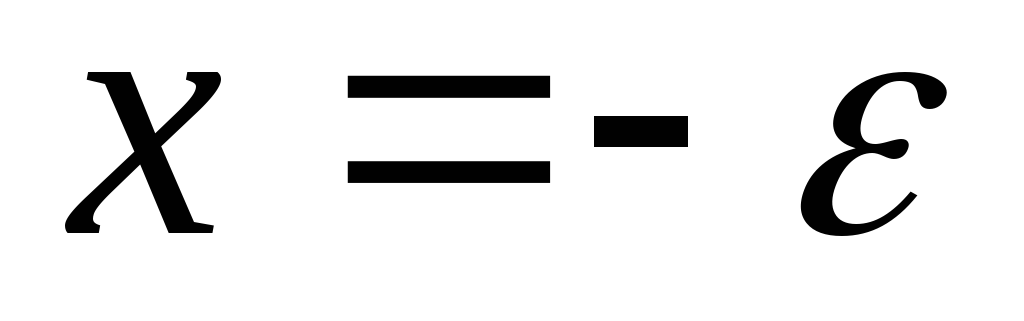 ,
а сток в точке
,
а сток в точке ,
рис. Д.2.5. В этом случае потенциалы
скорости и функции тока для источника
и стока определяются следующими
зависимостями
,
рис. Д.2.5. В этом случае потенциалы
скорости и функции тока для источника
и стока определяются следующими
зависимостями 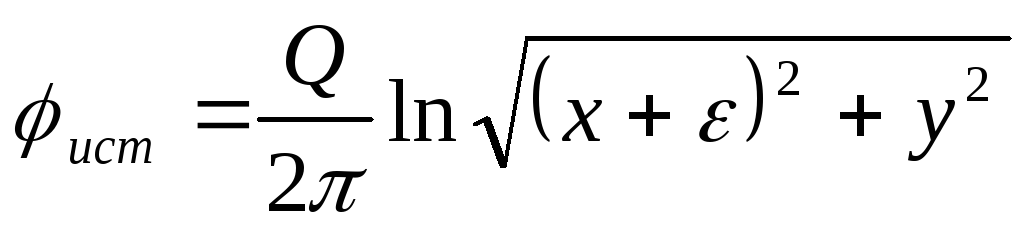 ,
, 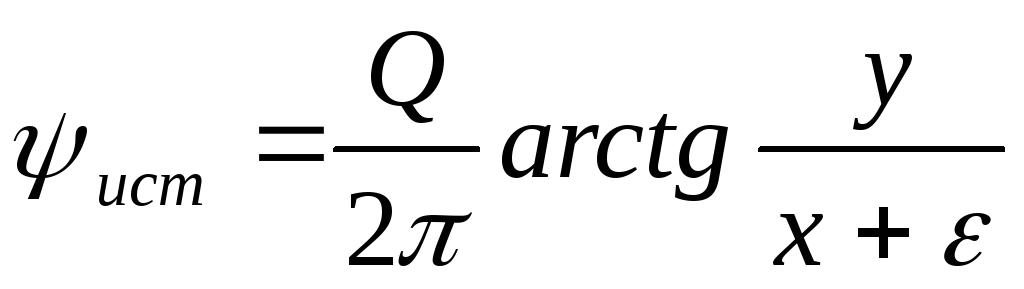 ;
(Д.2.12)
;
(Д.2.12)
 ,
, 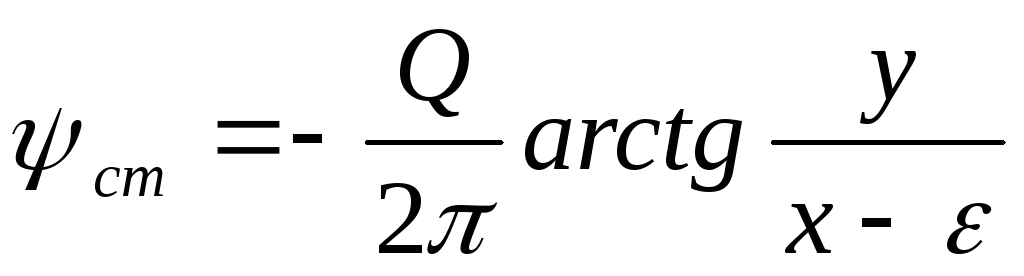 .
(Д.2.13)
.
(Д.2.13)
Будем
теперь сближать источник и сток, т.е.
величина 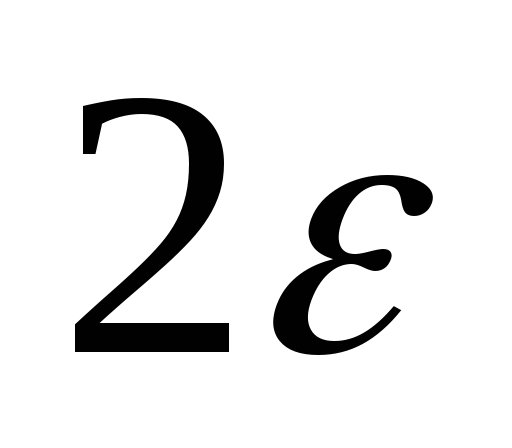 стремится к нулю
стремится к нулю .
В пределе при
.
В пределе при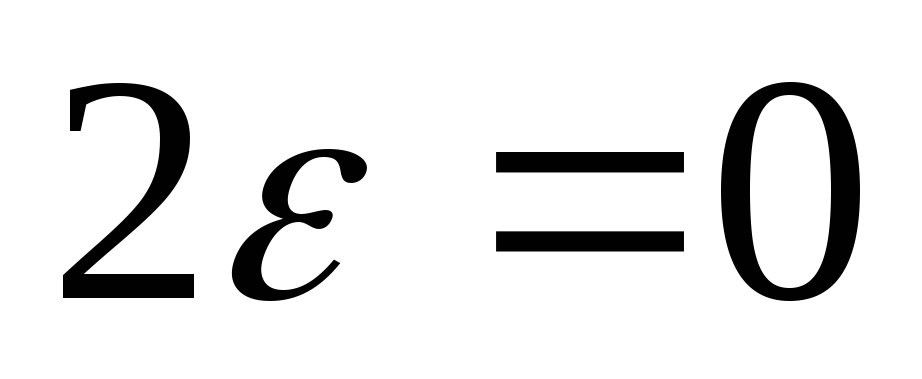 сток поглотит источник и всякое движение
будет отсутствовать. Если одновременно
со сближением центров источника и стока
будем увеличивать их расход так, чтобы
сток поглотит источник и всякое движение
будет отсутствовать. Если одновременно
со сближением центров источника и стока
будем увеличивать их расход так, чтобы
 ,
,
то получим в процессе течение, которое называется диполем. Постоянная М, характеризующая этот поток, называется моментом диполя, а ось Оx – осью диполя. На основании зависимостей (Д.2.12) и (Д.2.13) определяем потенциал скорости и функцию тока рассматриваемого течения (диполя) так, как будет показано ниже.
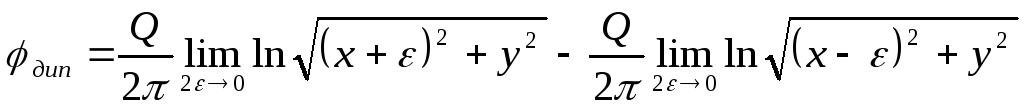 =
=
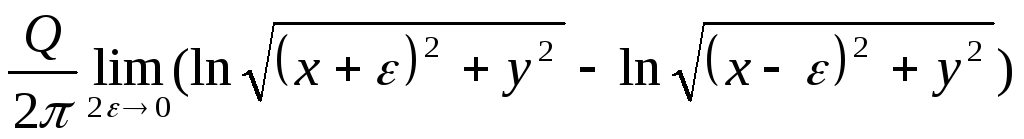 .
.
Умножим
числитель и знаменатель последнего
равенства на 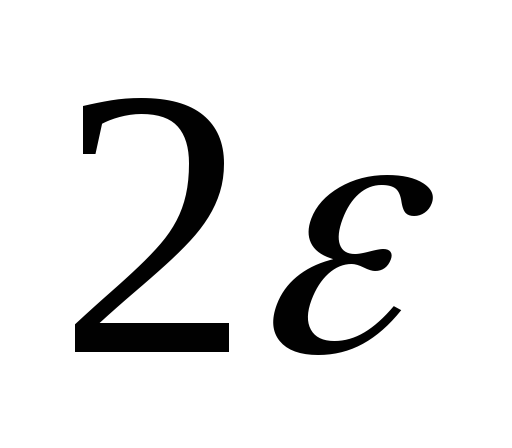 ;
в числителе получим
;
в числителе получим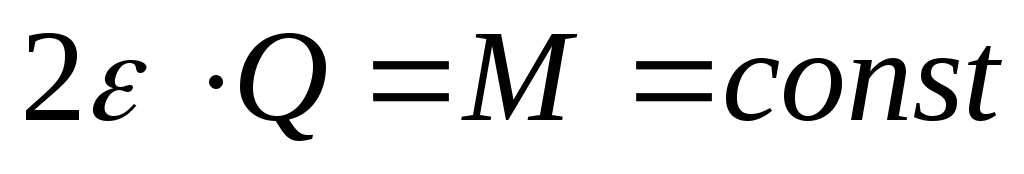 ,
т.е.
,
т.е.

 .
.
В
последнем выражении – предел отношения
приращения функции к приращению аргумента
по координате х, что является частной
производной по х; поэтому выражение для  может быть записано так
может быть записано так
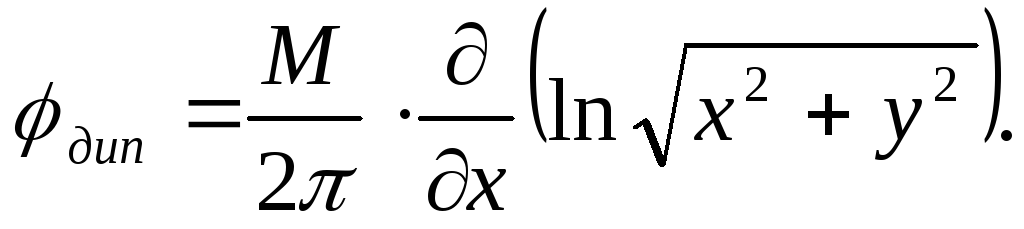 .
.
Аналогично для функции тока диполя получается выражение
 .
.
В ыполняя
операции дифференцирования, приходим
к окончательным выражениям
ыполняя
операции дифференцирования, приходим
к окончательным выражениям
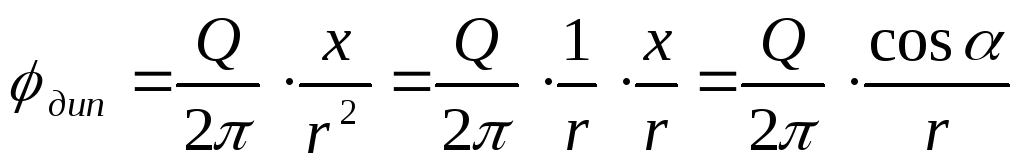 ,
,
 .
.
А
Рис. Д.2.6
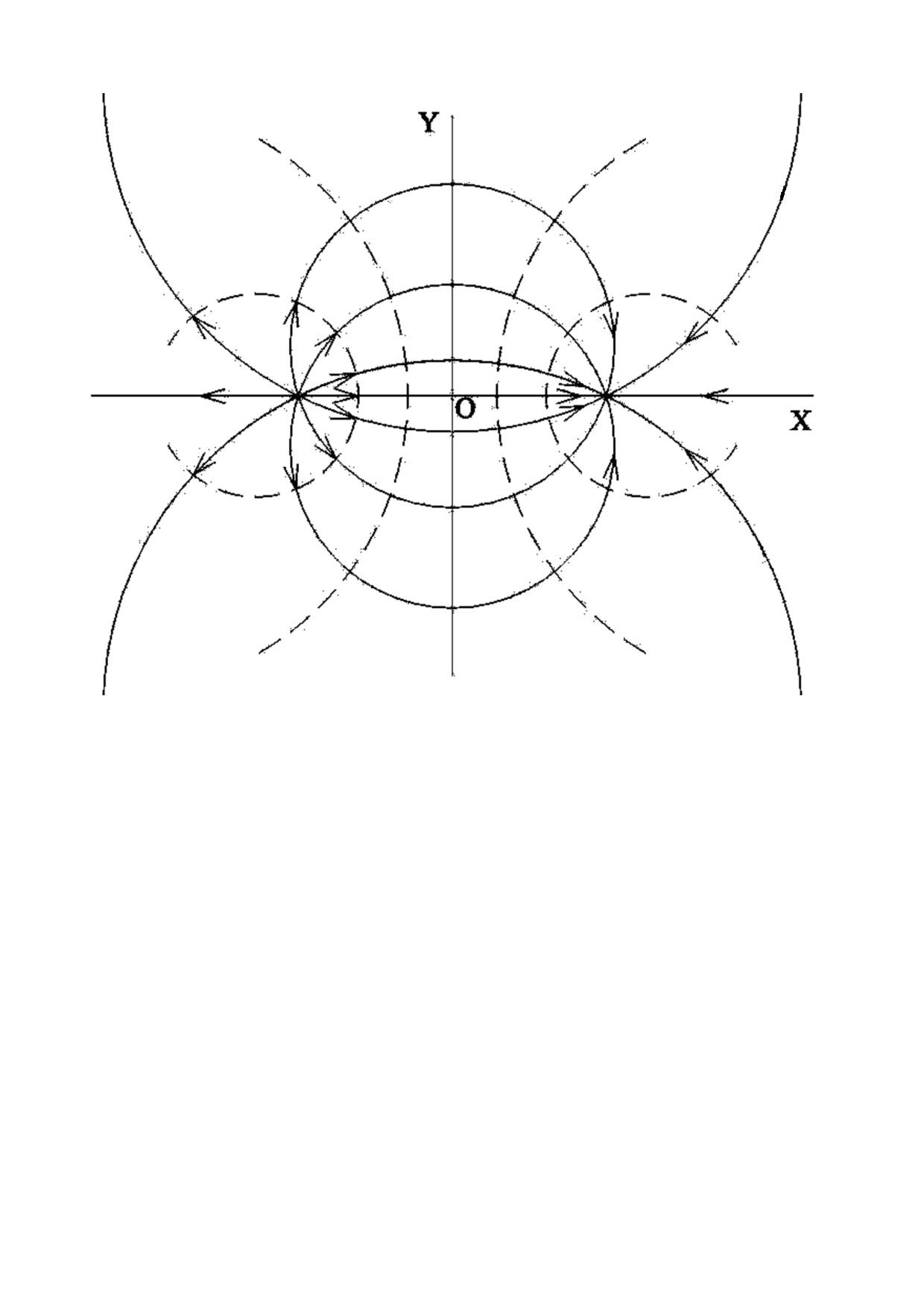
нализ последних уравнений показывает следующее: линии тока диполя есть окружности, проходящие через начало координат и имеющие центры на оси Оу, рис. Д.2.6; эквипотенциальные линии также представляют собой окружности, проходящие через начало координат, но с центрами, расположенными на оси ОХ. Жидкость движется из начала координат в сторону отрицательного направления оси Ох и, описав окружность, снова попадает в начало координат. Течение жидкости в диполе – идеализированное, не встречающееся на практике, но изучение его позволяет построить схемы течений некоторых реальных потоков.Пример Д.2.4. Бесциркуляционное обтекание круглого цилиндра плоским прямолинейным потоком.
Рассмотрим
цилиндр бесконечной длины, который
обтекается безграничным прямолинейным
плоским потоком идеальной жидкости
перпендикулярно его оси и так, что
скорость набегающего потока  направлена вдоль оси Ох; начало координат
поместим на оси цилиндра. Произведём
сложение двух течений: одного – диполя,
помещённого в начале координат, а второго
– прямолинейного со скоростью
направлена вдоль оси Ох; начало координат
поместим на оси цилиндра. Произведём
сложение двух течений: одного – диполя,
помещённого в начале координат, а второго
– прямолинейного со скоростью ,
параллельной оси ОХ. Произведём
суммирование функций тока
,
параллельной оси ОХ. Произведём
суммирование функций тока
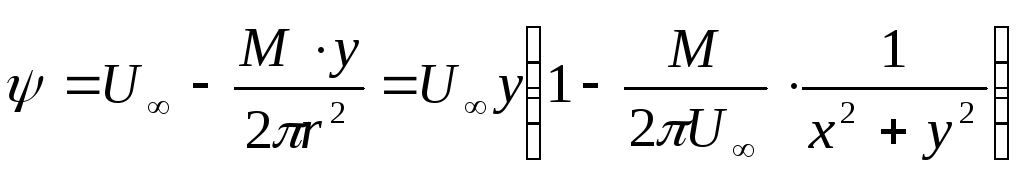 .
(Д.2.14)
.
(Д.2.14)
Из
этого равенства следует, что при у=0, а
также на окружности радиуса  ,
определяемого условием
,
определяемого условием
 ,
(Д.2.15)
,
(Д.2.15)
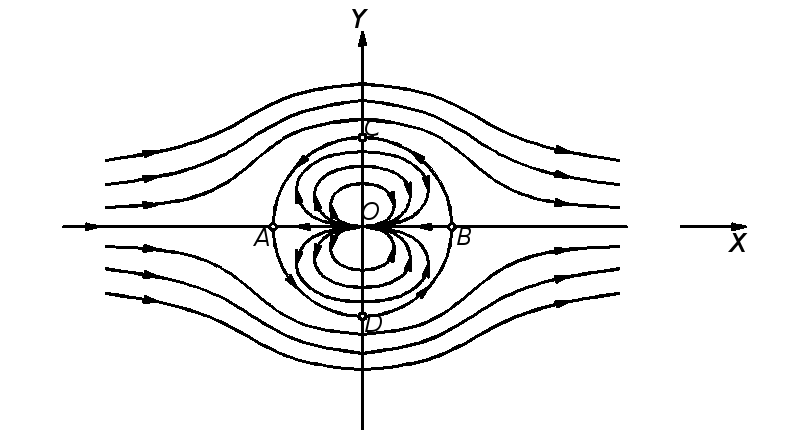
функция тока равна нулю, т.е. постоянна и, следовательно, названные линии являются линиями тока. Картина линий тока приведена на рис. Д.2.7.
Ψ=0
Ψ=0
Ψ=0
Ψ=0
Рис. Д.2.7
Ψ=0
Ψ=0
Так
называемая «нулевая» линия тока  состоит из отрезка отрицательной оси
абсцисс от бесконечности до точки А, из
окружности радиуса
состоит из отрезка отрицательной оси
абсцисс от бесконечности до точки А, из
окружности радиуса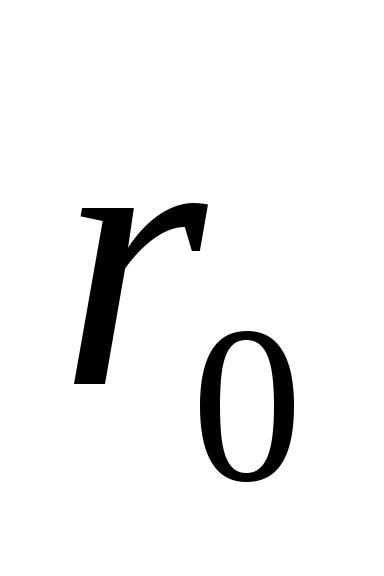 (ACBD)
и из отрезка положительной оси абсцисс
от точки В до бесконечности. Эта «нулевая»
линия тока разграничивает две области
течения жидкости: «внешний поток» (вне
окружности радиуса
(ACBD)
и из отрезка положительной оси абсцисс
от точки В до бесконечности. Эта «нулевая»
линия тока разграничивает две области
течения жидкости: «внешний поток» (вне
окружности радиуса  )
и «внутренний поток», замыкающийся
внутри окружности радиуса
)
и «внутренний поток», замыкающийся
внутри окружности радиуса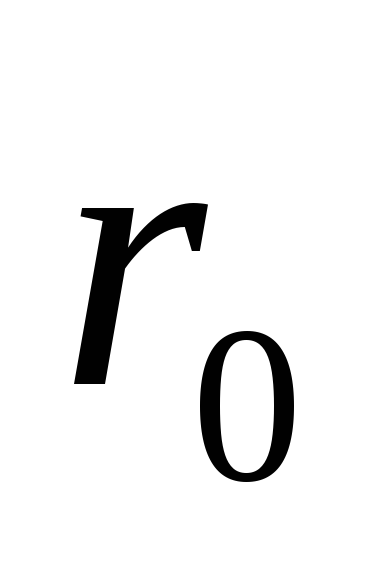 .
Этот «внутренний поток» не влияет на
поведение внешнего потока и ,следовательно,
картина обтекания не изменится, если
предположить, что потоком обтекается
жесткий цилиндр радиуса
.
Этот «внутренний поток» не влияет на
поведение внешнего потока и ,следовательно,
картина обтекания не изменится, если
предположить, что потоком обтекается
жесткий цилиндр радиуса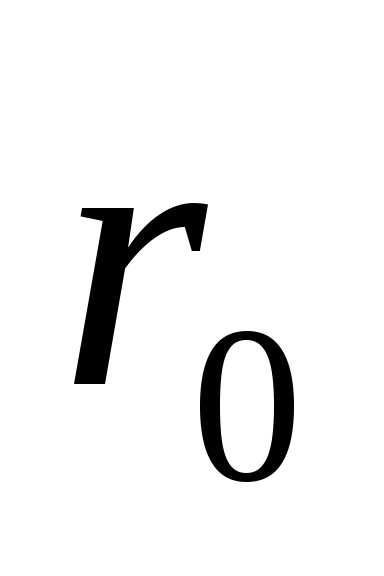 .
Такое течение носит название
бесциркуляционного обтекания цилиндра.
Исключая с помощью (Д.2.15) момент диполя
из (Д.2.14), найдём выражение для функции
тока (при
.
Такое течение носит название
бесциркуляционного обтекания цилиндра.
Исключая с помощью (Д.2.15) момент диполя
из (Д.2.14), найдём выражение для функции
тока (при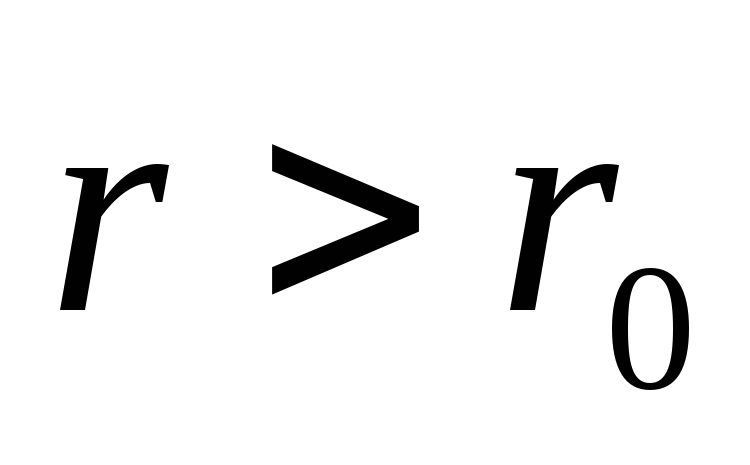 )
)
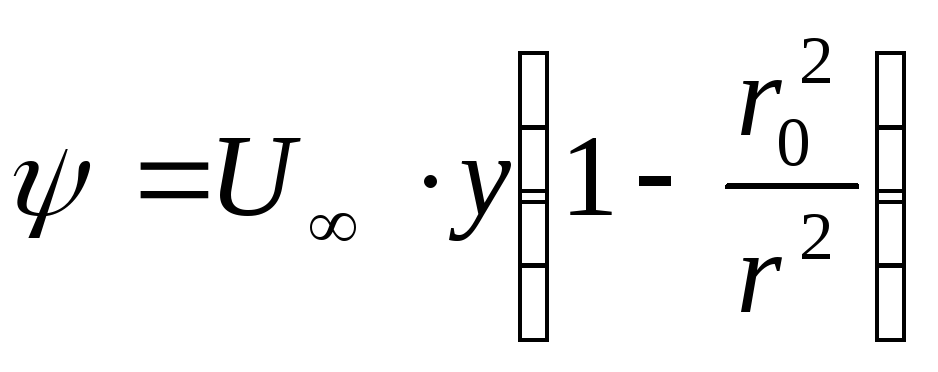 .
.
Потенциал скорости такого течения будет иметь вид
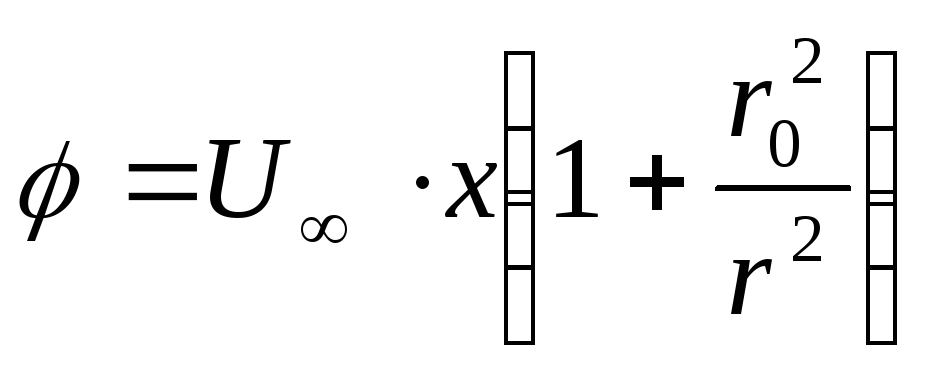 .
.
Формулы
перехода от прямоугольных координат
(х,у) к полярным 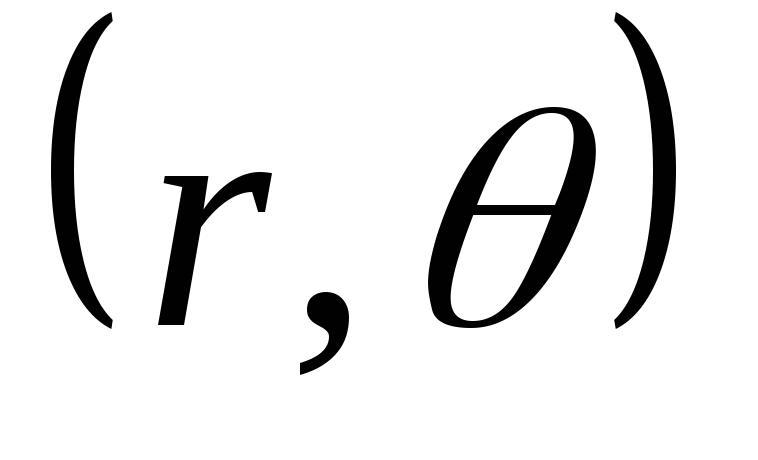 имеют вид
имеют вид
 ,
,
и,
следовательно, функции  и
и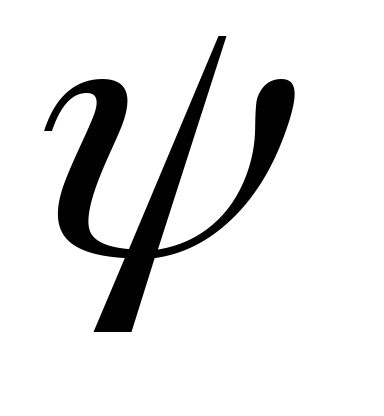 могут быть представлены в полярных
координатах
могут быть представлены в полярных
координатах
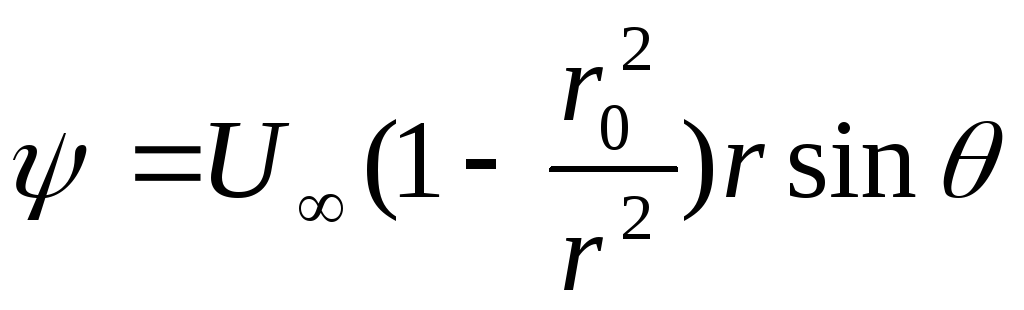 ,
(Д.2.16)
,
(Д.2.16)
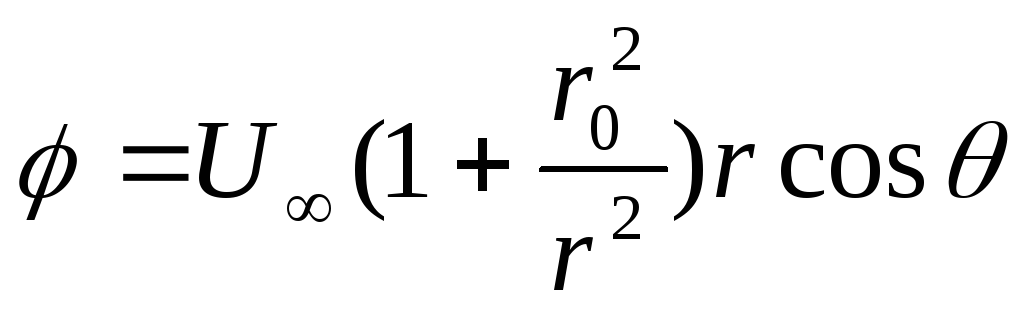 .
(Д.2.17)
.
(Д.2.17)
Найдём
распределение скоростей по контуру
цилиндра. Для этого достаточно найти
тангенциальную составляющую 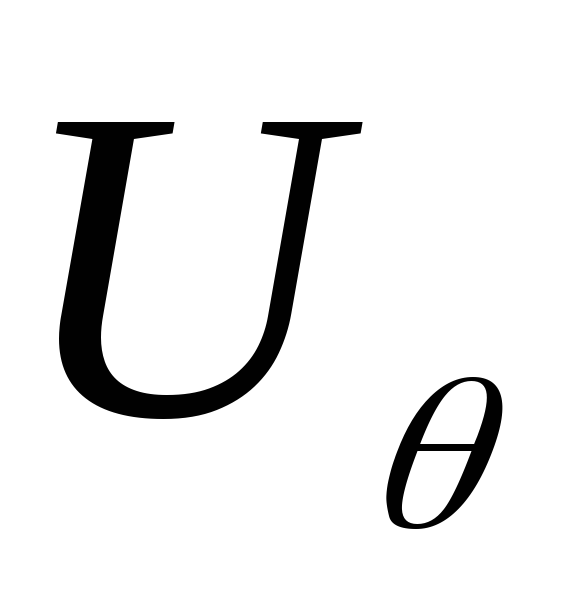 ,
так как скорость направлена по касательной
к линии тока, а радиальная составляющая
скорости на контуре цилиндра равна
нулю. Поэтому
,
так как скорость направлена по касательной
к линии тока, а радиальная составляющая
скорости на контуре цилиндра равна
нулю. Поэтому
 .
.
Знак
«минус» указывает, что скорость направлена
в сторону, противоположную направлению
отсчёта углов  .
Распределение скоростей по развёртке
полуокружности (верхней и нижней) имеет
вид отрезка синусоиды. Скорости в точках
А и В – так называемых точках разветвления
(критических точках) – при
.
Распределение скоростей по развёртке
полуокружности (верхней и нижней) имеет
вид отрезка синусоиды. Скорости в точках
А и В – так называемых точках разветвления
(критических точках) – при и
и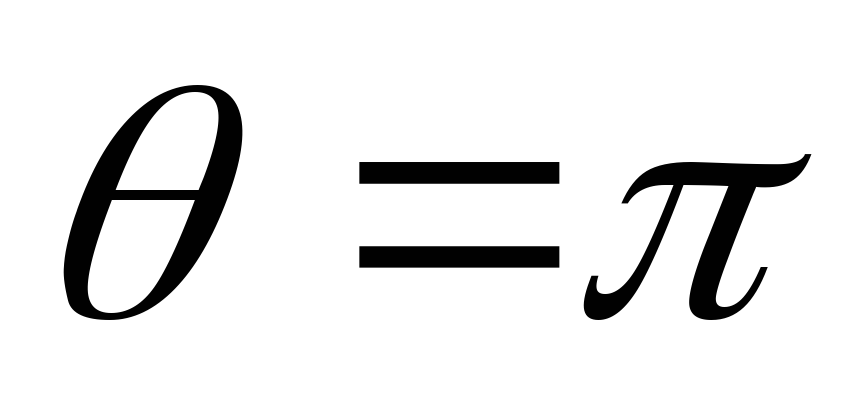 равны нулю. Максимум скорости достигается
на пересечении поверхности цилиндра с
осью ординат
равны нулю. Максимум скорости достигается
на пересечении поверхности цилиндра с
осью ординат
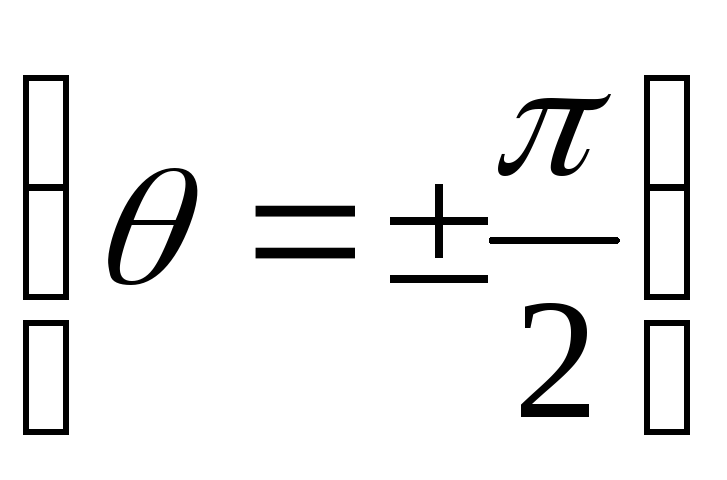 ,
,
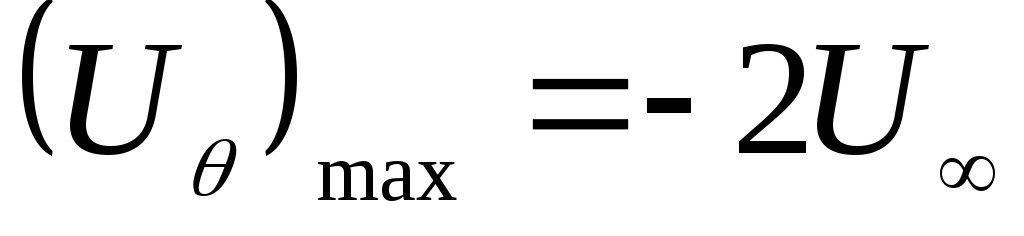 .
(Д.2.18)
.
(Д.2.18)
Задача
Д.2.3. применяя
зависимость (Д.2.16), построить линии тока
для случая обтекания цилиндра при
следующих данных: r=3
см,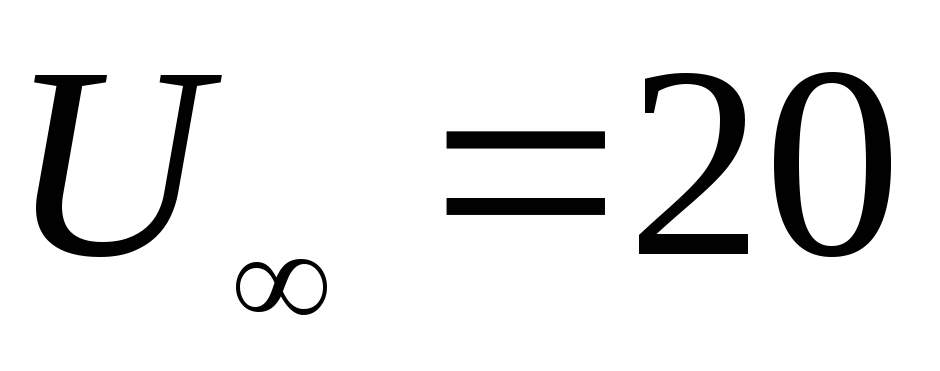 см/с. Построить кривую распределения
скорости
см/с. Построить кривую распределения
скорости на осевом сечении цилиндра от его
поверхности (по вертикали от точкиС,
рис. Д.2.6).
на осевом сечении цилиндра от его
поверхности (по вертикали от точкиС,
рис. Д.2.6).
Функция тока — Википедия
Материал из Википедии — свободной энциклопедии
Функция тока в гидродинамике — скалярная функция, которая определяет двумерное течение жидкости или газа.
Определение
Обычно, функция тока ψ{\displaystyle \psi } определяется из соотношения
- rot(ψz→)=v→,{\displaystyle \operatorname {rot} \,(\psi {\vec {z}})={\vec {v}},}
где v→{\displaystyle {\vec {v}}} — вектор скорости потока, rot{\displaystyle \operatorname {rot} } — ротор.
Для прямоугольной декартовой системы координат это даёт:
- vx=∂ψ∂y;vy=−∂ψ∂x.{\displaystyle v_{x}={\frac {\partial \psi }{\partial y}};\;v_{y}=-{\frac {\partial \psi }{\partial x}}.}
Обобщения
Так как для несжимаемой жидкости поле скорости соленоидально, то у него существует векторный потенциал Ψ→{\displaystyle {\vec {\Psi }}}, определяемый соотношением
- rotΨ→=v→.{\displaystyle \operatorname {rot} \,{\vec {\Psi }}={\vec {v}}.}
Неоднозначность
Как любой потенциал, функция тока определена с точностью до аддитивной постоянной. Когда в задаче есть твёрдые стенки (на которых скорость равна нулю), то значение функции тока на них обычно принимается равной нулю. Если же стенок нет (заполнено всё пространство), то можно задать значение функции тока на бесконечности, если поле скорости там постоянно.
Свойства
- Изолинии функции тока совпадают с линиями тока жидкости. Для стационарного (не зависящего от времени) течения они также являются траекториями частиц.
- При некоторых условиях максимум функции тока равен расходу жидкости.
функция тока — это… Что такое функция тока?
фу́нкция то́ка скалярная функция ψ пространственных координат и времени t, сохраняющая неизменным своё значение на линии тока, то есть удовлетворяющая условию Vgradψ = 0, где V вектор скорости. В аэро- и гидродинамике существование Ф. т. является следствием неразрывности уравнения. Для плоскопараллельного течения в декартовой системе координат x, y Ф. т. связана с проекциями u, υ вектора скорости на эти оси и плотностью ρ соотношениями
.
Уравнение ψ(x, y) = const определяет семейство линий тока исследуемого течения, а разность значений Ф. т. расход жидкости или газа между двумя линиями тока. Для осесимметричного течения в цилиндрической системе координат x, r Ф. т. связана с компонентами ux, ur вектора скорости соотношениями
,
и её часто называют Ф. т. Стокса. Уравнение ψ(х, r) = const определяет семейство поверхностей тока, полученных вращением линий тока вокруг оси симметрии, а разность значений Ф. т. характеризует расход жидкости или газа между двумя рассматриваемыми поверхностями тока. Для трёхмерного течения приходится вводить две функции тока.
Ф. т. используются при изучении движения как идеальной жидкости, так и вязкой жидкости, поэтому уравнения и граничные условия, определяющие их поведение, зависят от исследуемой задачи. В общем случае для определения Ф. т. служат количества движения уравнения, в которых компоненты вектора скорости заменены их выражениями через производные Ф. т. В частном случае плоскопараллельного безвихревого течения идеальной жидкости Ф. т. является решением уравнения Лапласа ∆ψ = 0.
Литература:
См. при статье Аэродинамика, Гидродинамика.
Энциклопедия «Авиация». — М.: Большая Российская Энциклопедия. Свищёв Г. Г.. 1998.
6.5. Гидромеханический смысл функции тока.
Рис. 6.2

 на две составляющие
на две составляющие  и
и  ,
что позволит представить расход как
сумму
,
что позволит представить расход как
сумму 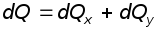 ,
при этом
,
при этом 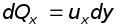 и
и  (рис. 6.2).
(рис. 6.2). 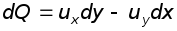
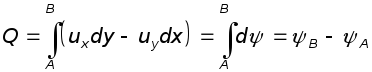 (6.15)
(6.15)
т.е. разность значений функций тока на двух смежных линиях тока равна объемному расходу между ними.
6.6. Связь потенциала скорости и функции тока.
Связь между этими параметрами может быть легко установлена, если записать полученные выше выражения для проекций скоростей
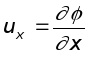 ;
; 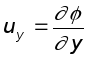 ;
;
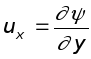 ;
; 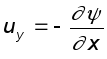 ,
,
откуда
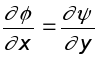 ;
; 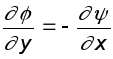 (6.16)
(6.16)
Эти соотношения играют чрезвычайно важную роль в механике жидкости и носят название соотношений Коши-Римана. Более подробно они будут рассмотрены ниже. Пока же ограничимся тем, что перемножим их. Это дает
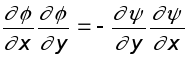 (6.17)
(6.17)Рис. 6.3
Из математики известно, что выражения типа (6.17) свидетельствуют о взаимной ортогональности кривых. Следовательно, линии тока и эквипотенциальные линии образуют сетку взаимно ортогональных кривых, которая носит название гидродинамической сетки движения. Примерный ее вид показан на рис. 6.3.6.7. Методы расчета потенциальных потоков.
Как уже отмечалось, для нахождения потенциала скорости необходимо проинтегрировать уравнение Лапласа при заданных граничных условиях. Задача эта достаточно сложна. Поэтому в теории потенциальных течений особый интерес представляют случаи, которые дают точные значения функций тока и потенциала скорости без интегрирования уравнения Лапласа. Общая идея такого подхода сводится к следующему: задаются какой-то функцией, которая заведомо удовлетворяет уравнению Лапласа и выясняют, что представляет собой гидродинамическая сетка движения. Эту методику рассмотрим на ряде простейших примеров.
Пример 6.1. Пусть выражение для потенциала скорости
имеет вид 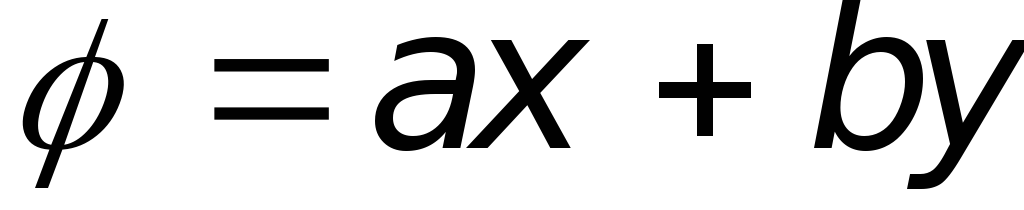 ,
где a и b — действительные числа.
,
где a и b — действительные числа.
Найдем компоненты скорости. Имеем
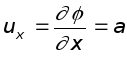 и
и  .
.
Вторые производные равны
нулю, т.е. уравнение Лапласа удовлетворяется.
Так как  и
и 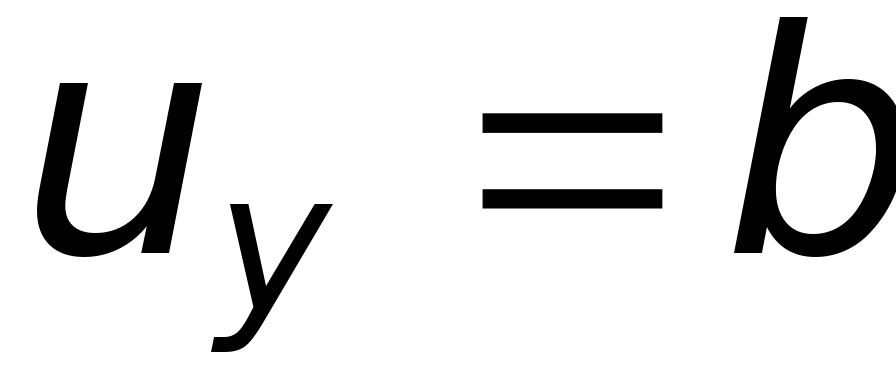 ,
то из этого следует, что поток движется
с постоянной скоростью
,
то из этого следует, что поток движется
с постоянной скоростью
Выясним, что представляют собой линии тока. Дифференциальное уравнение линий тока
 .
.
И после интегрирования
 (6.18)
(6.18)

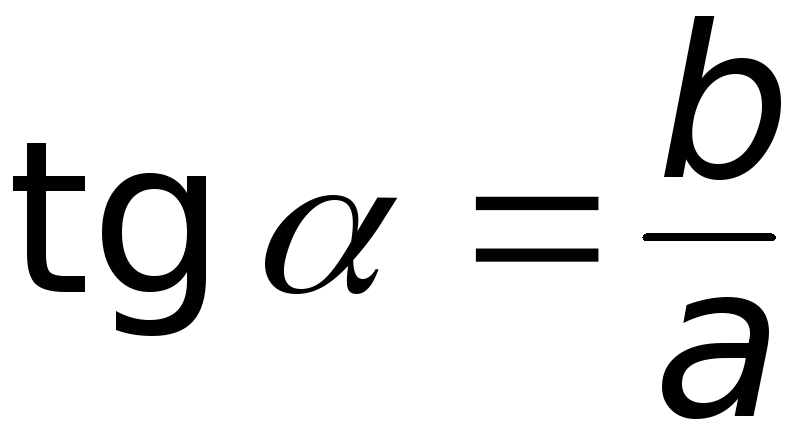 (см. рис. 6.4). Действительно, для линии
тока можем записать:
(см. рис. 6.4). Действительно, для линии
тока можем записать: 

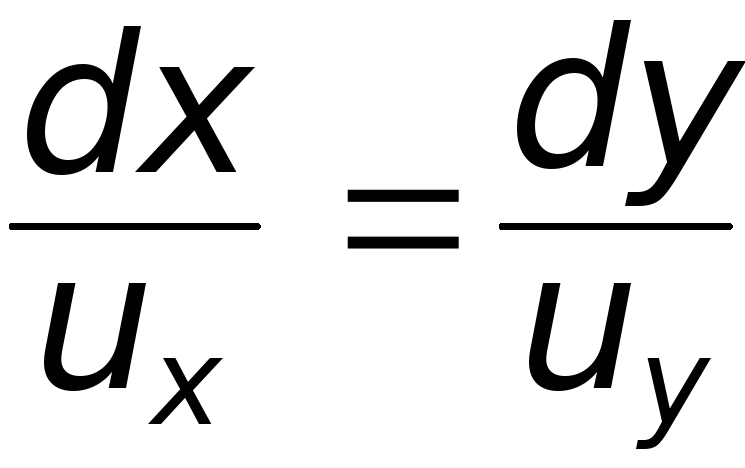 ;
; 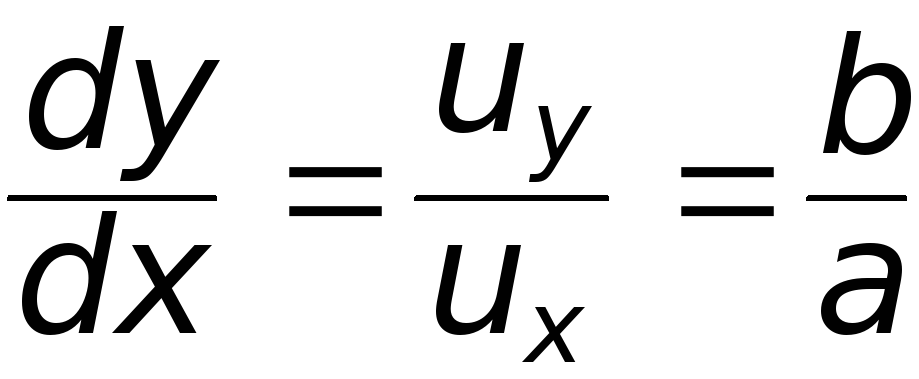 .
.
Пример 6.2.Потенциал скорости задан выражнием
Рис. 6.4

где a — действительное число. Необходимо найти линии тока этого течения.
Прежде всего проверим,
удовлетворяет ли j уравнению Лапласа. Имеем 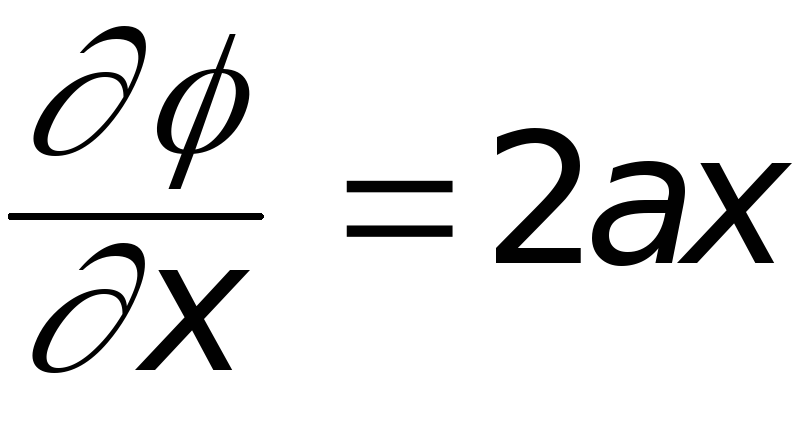 ;
; 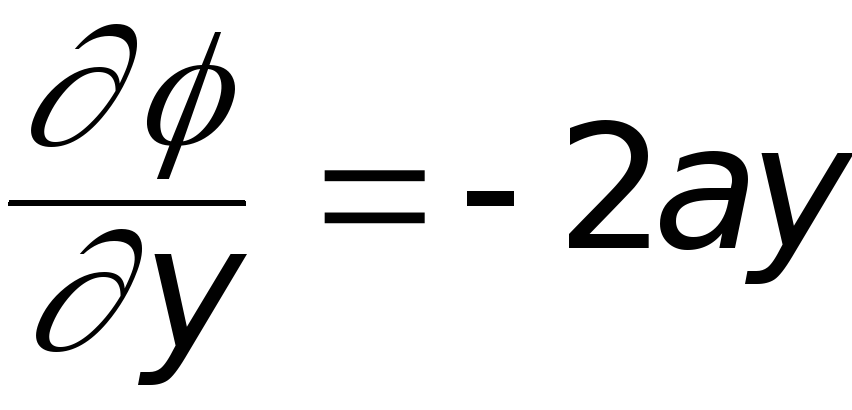 ;
; 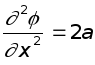 ;
; 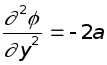 ;
;
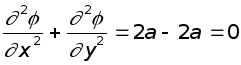 ,
,
т.е. уравнение Лапласа удовлетворяется. Выясним, какое же движение описывается этой функцией, для чего установим вид функции тока.

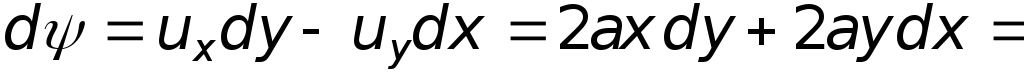
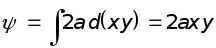 (произвольная постоянная в данном случае
нас не интересует).
(произвольная постоянная в данном случае
нас не интересует).Рис. 6.5
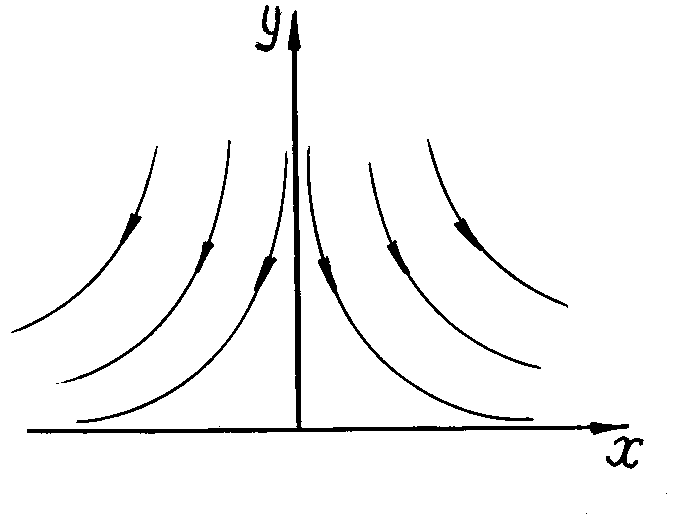
Для нахождения линии тока приравняем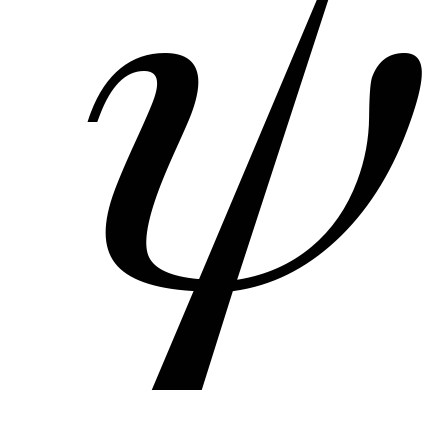 какой-то постоянной величине
какой-то постоянной величине 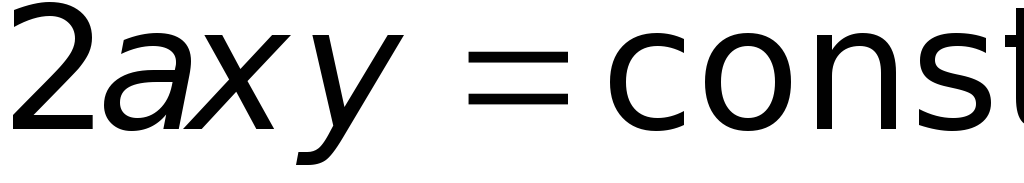 либо
либо 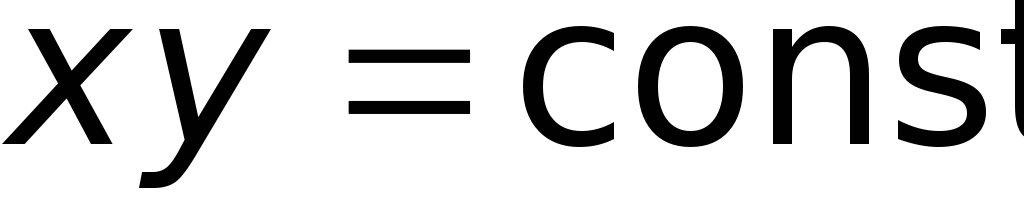 .
Следовательно, линии тока — гиперболы,
для которых оси x и y — асимптоты. На рис.
6.5 показаны линии тока для верхней
половины. Если считать, что оси координат
являются твердыми стенками, то получим
картину обтекания потоком прямого угла.
.
Следовательно, линии тока — гиперболы,
для которых оси x и y — асимптоты. На рис.
6.5 показаны линии тока для верхней
половины. Если считать, что оси координат
являются твердыми стенками, то получим
картину обтекания потоком прямого угла.Существует ряд простейших течений, для которых потенциалы скорости могут быть получены аналитическим путем. Эти течения играют заметную роль в гидромеханике, и поэтому их рассмотрение представляет несомненный интерес.
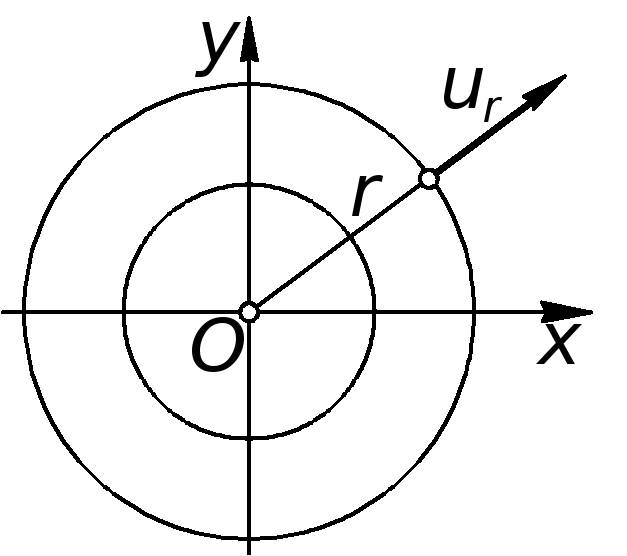
Рис. 6.6
Под источником (стоком) на плоскости понимают точку, из которой происходит истечение (либо втекание) жидкости. Пусть точка O на рис. 6.6 представляет плоский источник, из которого, как из центра, проведем несколько концентрических окружностей. Запишем уравнение неразрывности для цилиндрической поверхности единичной высоты: 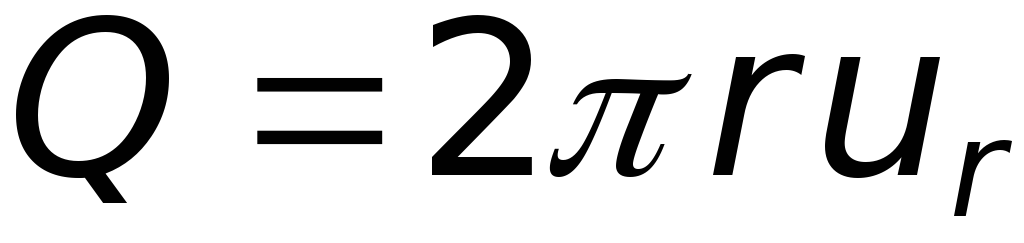
откуда
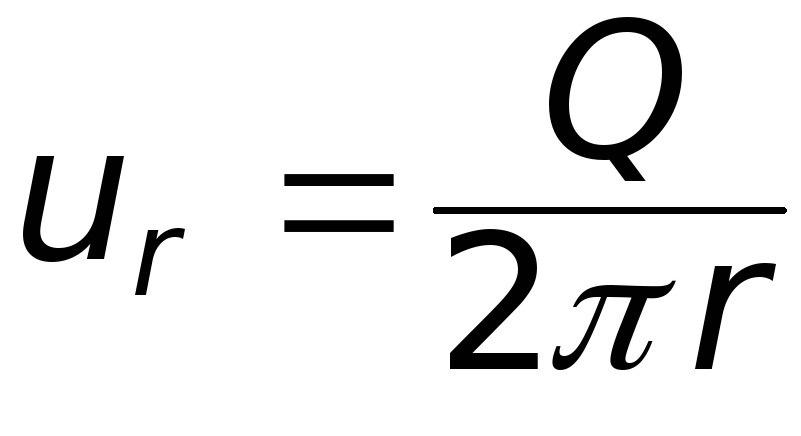 (6.19)
(6.19)
В декартовой системе координат
 (6.20)
(6.20)
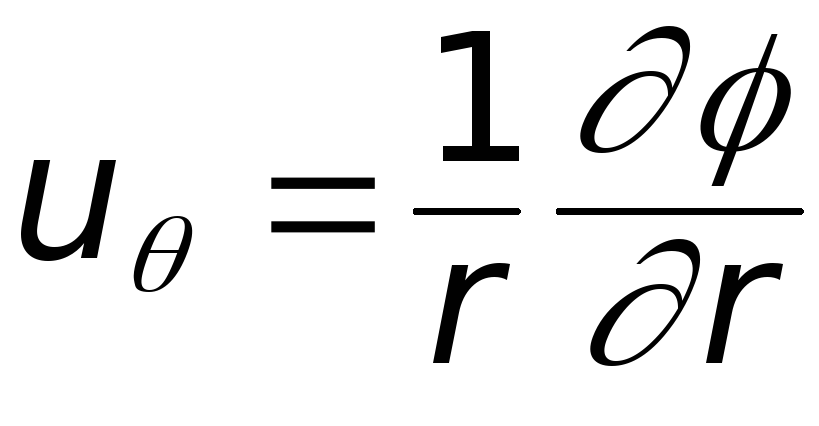 ;
; 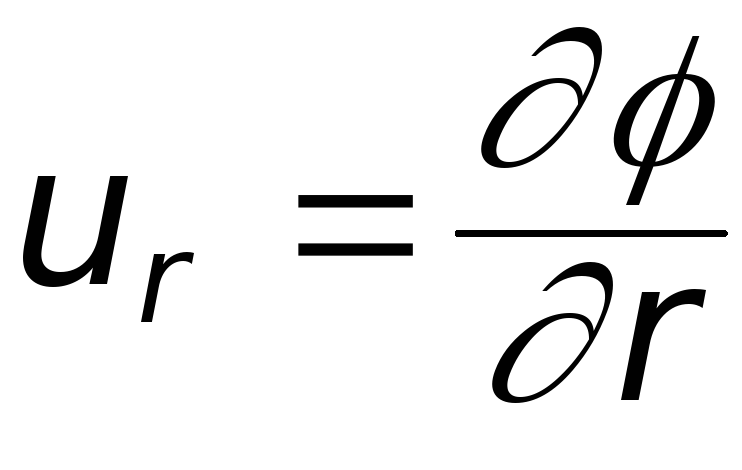 (6.21)
(6.21)
Рис. 6.7
Вывод этих соотношений можно найти в книге: Аржаников Н.С., Мальцев В.Н. Аэродинамика. — М.: Оборонгиз, 1956. — 483 с. Из (6.21) следует, что не зависит от полярного угла, поэтому
можно записать
не зависит от полярного угла, поэтому
можно записать  .
Приравнивая это выражение (6.19), получим
.
Приравнивая это выражение (6.19), получим 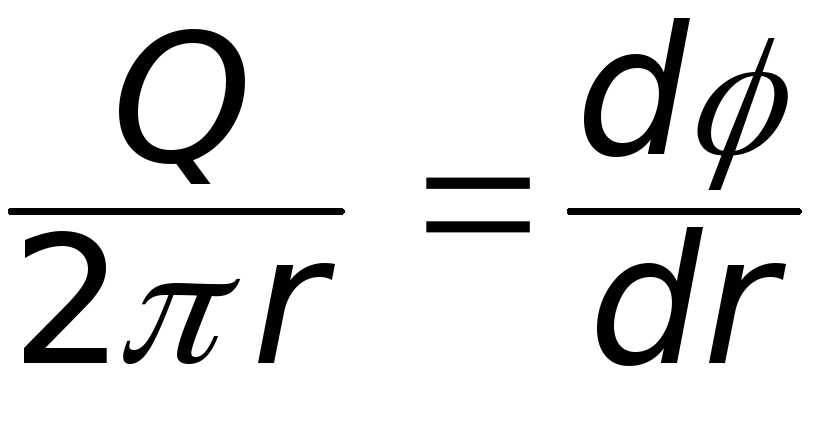 ,
откуда
,
откуда 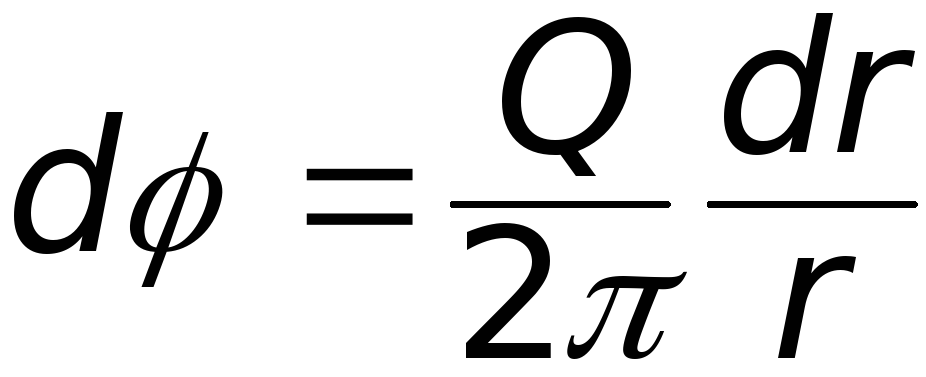 .
.И после интегрирования
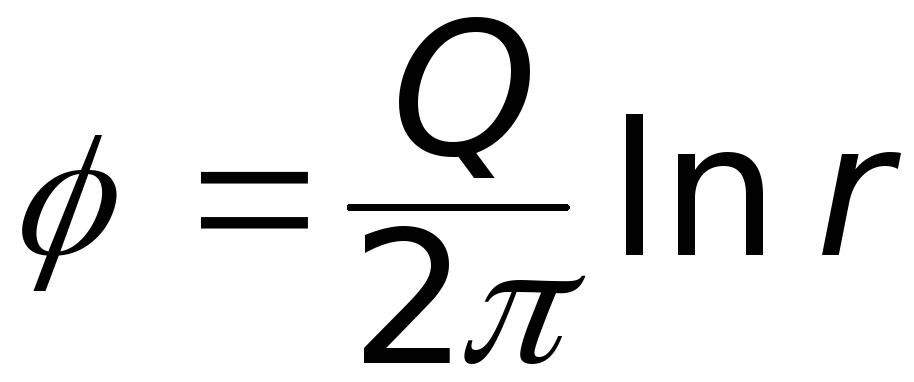 . (6.22)
. (6.22)
Из (6.22) следует, что эквипотенциальные линии источника представляют собой окружности. Формулу (6.22) можно записать и в следующей форме
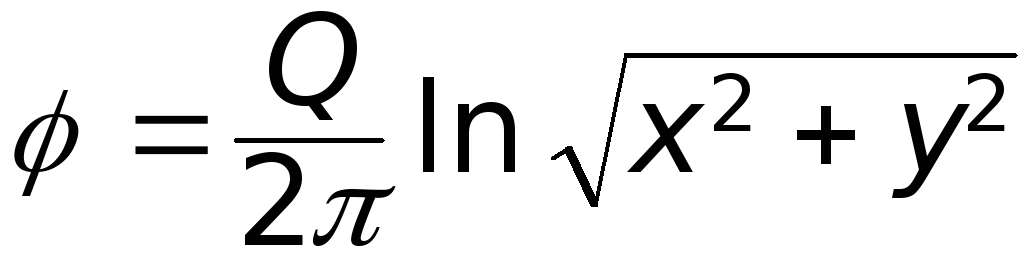 (6.23)
(6.23)
Для нахождения функции тока удобней использовать декартову систему координат. При этом (6.19) принимает вид:
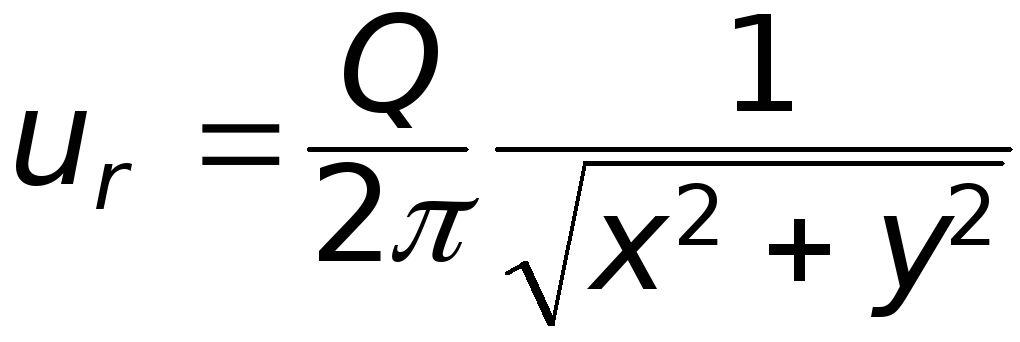 (6.24)
(6.24)
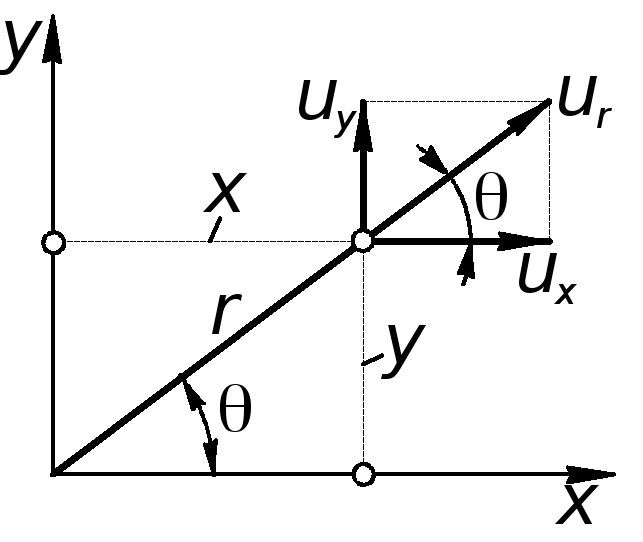
С другой стороны, из рис. 6.7 следует:
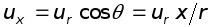
Таким образом

Аналогично
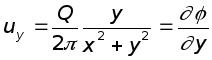
Дифференциальное уравнение функции тока
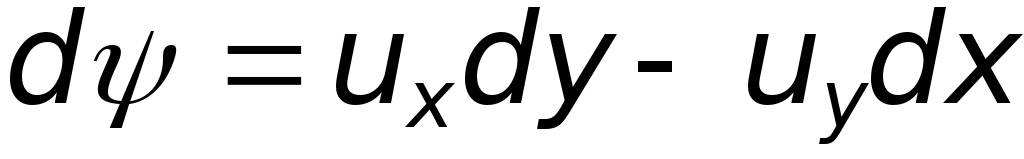 (6.25)
(6.25)
Подстановка значений  и
и  в (6.25) дает
в (6.25) дает
 (6.26)
(6.26)
Выполним некоторые
преобразования. Дифференциал от частного
имеет вид 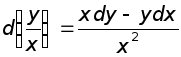 ,
т.е.
,
т.е. 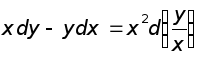 .
.
Из знаменателя (6.26) выносим
за скобки 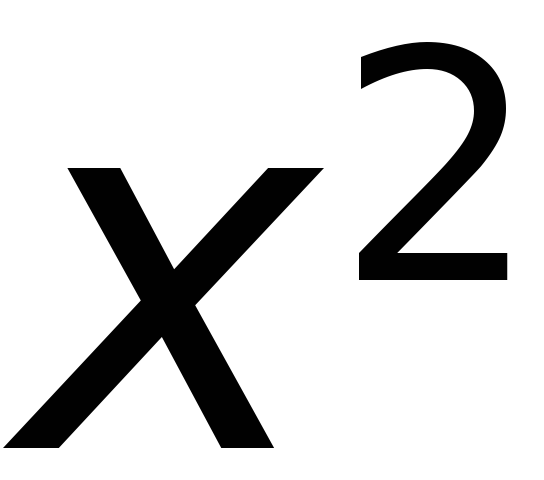 ,
при этом
,
при этом

Таким образом, (6.26) принимает вид

и 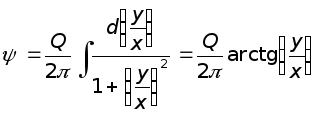 .
.
Но с другой стороны  ,
т.е.
,
т.е. 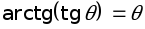 ,
и
,
и
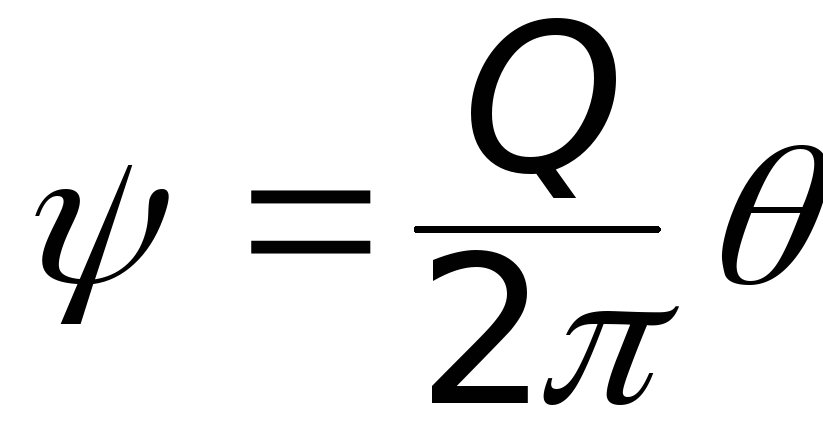 (6.27)
(6.27)
В полярной системе координат (6.27) представляет собой семейство прямых, проходящих через начало координат. Для стока потенциал скорости и функция тока имеют те же выражения, но с противоположными знаками, т.е.
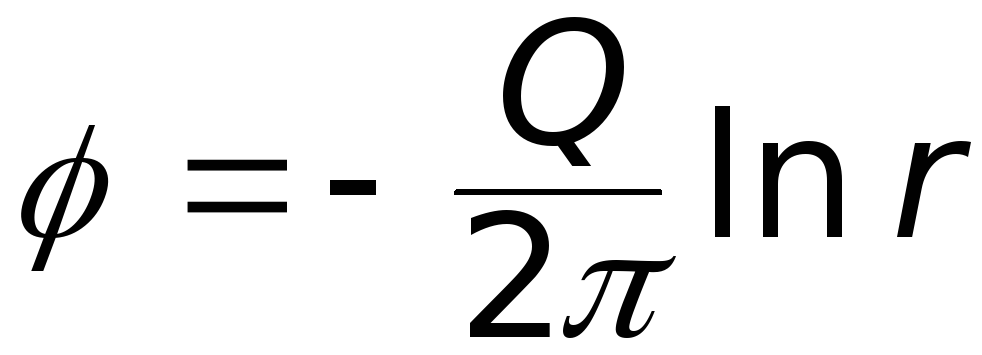 и
и 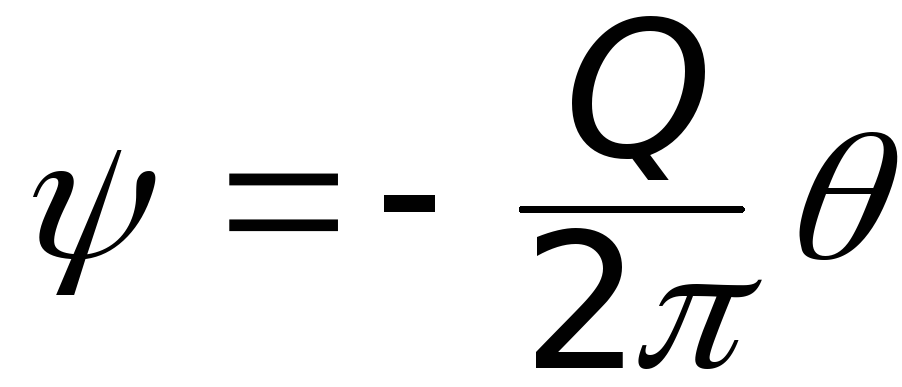 (6.28)
(6.28)
Иногда Q называют мощностью (обильностью) источника.



