Магнитное поле. Формулы ЕГЭ — Репетитор по физике (Краснодар)

Все формулы взяты в строгом соответствии с Федеральным институтом педагогических измерений (ФИПИ)

3.3 МАГНИТНОЕ ПОЛЕ

3.3.1 Механическое взаимодействие магнитов

Около электрического заряда образуется своеобразная форма материи — электрическое поле. Вокруг магнита существует подобная форма материи, но имеет другую природу происхождения (ведь руда электрически нейтральна), ее называют магнитным полем. Для изучения магнитного поля используют прямой или подковообразный магниты. Определенные места магнита обладают наибольшим притягивающим действием, их называют полюсами (северный и южный). Разноименные магнитные полюса притягиваются, а одноименные — отталкиваются.

Магнитное поле. Вектор магнитной индукции

Для силовой характеристики магнитного поля используют вектор индукции магнитного поля B. Магнитное поле графически изображают при помощи силовых линий (линии магнитной индукции). Линии являются замкнутыми, не имеют ни начала, ни конца. Место, из которого выходят магнитные линии — северный полюс (North), входят магнитные линии в южный полюс (South).

Магнитная индукция B  [Тл] — векторная физическая величина, являющаяся силовой характеристикой магнитного поля.

Принцип суперпозиции магнитных полей — если магнитное поле в данной точке пространства создается несколькими источниками поля, то магнитная индукция — векторная сумма индукций каждого из полей в отдельности

:

Линии магнитного поля. Картина линий поля полосового и подковообразного постоянных магнитов

3.3.2 Опыт Эрстеда. Магнитное поле проводника с током. Картина линий поля длинного прямого проводника и замкнутого кольцевого проводника, катушки с током

Магнитное поле существует не только вокруг магнита, но и любого проводника с током. Опыт Эрстеда демонстрирует действие электрического тока на магнит. Если прямой проводник, по которому идёт ток, пропустить через отверстие в листе картона, на котором рассыпаны мелкие железные или стальные опилки, то они образуют концентрические окружности, центр которых располагается на оси проводника. Эти окружности представляют собой силовые линии магнитного поля проводника с током.

3.3.3 Сила Ампера, её направление и величина:

Сила Ампера

— сила, действующая на проводник с током в магнитном поле. Направление силы Ампера определяется по правилу левой руки: если левую руку расположить так, чтобы перпендикулярная составляющая вектора магнитной индукции В входила в ладонь, а четыре вытянутых пальца были направлены по направлению тока, то отогнутый на 90 градусов большой палец покажет направление силы, действующей на отрезок проводника с током, то есть силы Ампера. 

где  I — сила тока в проводнике;

B — модуль вектора индукции магнитного поля;

L — длина проводника, находящегося в магнитном поле;

α — угол между вектором магнитного поля и направлением тока в проводнике.

3.3.4 Сила Лоренца, её направление и величина:

Так как электрический ток представляет собой упорядоченное движение зарядов, то действие магнитного поля на проводник с током есть результат его действия на отдельные движущиеся заряды. Силу, действующую со стороны магнитного поля на движущиеся в нем заряды, называют силой Лоренца. Сила Лоренца определяется соотношением:

где q — величина движущегося заряда;

V — модуль его скорости;

B — модуль вектора индукции магнитного поля;

α — угол между вектором скорости заряда и вектором магнитной индукции.

Обратите внимание, что сила Лоренца перпендикулярна скорости и поэтому она не совершает работы, не изменяет модуль скорости заряда и его кинетической энергии. Но направление скорости изменяется непрерывно.

Сила Лоренца перпендикулярна векторам В и v , и её направление определяется с помощью того же правила левой руки, что и направление силы Ампера:

если левую руку расположить так, чтобы составляющая магнитной индукции В, перпендикулярная скорости заряда, входила в ладонь, а четыре пальца были направлены по движению положительного заряда (против движения отрицательного, например электрона), то отогнутый на 90 градусов большой палец покажет направление действующей на заряд силы Лоренца Fл.

Движение заряженной частицы в однородном магнитном поле

При движении заряженной частицы в магнитном поле сила Лоренца работы не совершает. Поэтому модуль вектора скорости при движении частицы не изменяется. Если заряженная частица движется в однородном магнитном поле под действием силы Лоренца, а ее скорость  лежит в плоскости, перпендикулярной вектору  то частица будет двигаться по окружности радиуса R:

R=mv/qB

Физика 11 класс. Все формулы и определения

Физика 11 класс. Все формулы и определения

«Физика 11 класс. Все формулы и определения» — это Справочник по физике для учащихся 11 класса, доступный для просмотра в Интернете с компьютера, планшета и смартфона. Автор справочных таблиц: Е.А. Марон (кандидат пед. наук, учитель физики). Смотрите также справочные материалы по физике за другие классы:

Формулы 7 класс  Формулы 8 класс  Формулы 9 класс  Формулы 10 класс

---

В пособии «Физика 11 класс. Все формулы и определения» представлено 30 тем за 11 класс.

1 Магнитное поле и его свойства

Магнитное поле и его свойства. Опыт Ампера. Магнитное поле. Вектор магнитной индукции. Модуль вектора магнитной индукции

---

2 Сила Ампера. Сила Лоренца

Сила Ампера. Сила Лоренца. Движение q в однородном магнитном поле.

---

3 Явление электромагнитной индукции

Явление электромагнитной индукции (ЭМИ). Магнитный поток. Правило Ленца. Закон ЭМИ.

---

4 Самоиндукция

Самоиндукция. Проявление самоиндукции. Индуктивность. Энергия МП тока. Теория Максвелла

---

5 Механические колебания

 

Механические колебания. Условия возникновения свободных колебаний. Характеристики механических колебаний. Математический маятник. Гармонические колебания.

---

6 Фаза колебаний. Затухающие и вынужденные колебания

Фаза колебаний. Сдвиг фаз колебаний. Затухающие и вынужденные колебания

---

7 Механические волны

Механические волны. Причины возникновения. Продольные волны. Распространение волн в упругих средах

8 Колебательный контур

Колебательный контур. Электромагнитные колебания. Аналогия. Формула Томсона

---

9 Переменный ток

Переменный ток. Активное сопротивление. Средняя мощность. Резонанс

---

10 Генерирование электроэнергии

Генерирование электроэнергии. Индукционный генератор переменного тока. Передача электроэнергии

---

11 Трансформаторы

Трансформаторы. Устройство трансформатора. Работа нагруженного трансформатора и на холостом ходу

---

12 Электромагнитные волны

Электромагнитные волны. Опыты Герца.

---

13 Принципы радиосвязи

Принципы радиосвязи. Амплитудная модуляция. Детектирование. Распространение радиоволн. Радиолокация

---

14 Световые волны.

Световые волны.

---

15 Законы отражения и преломления света

Закон отражения света. Закон преломления света

---

16 Линза

Линза. Виды линз. Оптическая сила линз. Формула тонкой линзы. Построение изображения в линзах.

---

17 Свойства световых волн

Свойства световых волн. Опыты Ньютона. Интерференция света. Дифракция. Естественный свет

---

18 Элементы теории относительности

Элементы теории относительности. Принцип относительности. Постулаты теории. Основные следствия из теории относительности

---

19 Излучение и спектры

Излучение и спектры. Виды излучений. Виды спектров. Спектральный анализ

---

20 Виды электромагнитных излучений

Виды электромагнитных излучений. Инфракрасное и ультрафиолетовое излучения. Рентгеновские лучи.

---

21 Световые кванты. Фотоэффект

Световые кванты. Фотоэффект. Законы фотоэффекта.

---

22 Теория фотоэффекта

Теория фотоэффекта. Формула Планка. Уравнение Эйнштейна. Фотоны. Корпускулярно-волновой дуализм света.

---

23 Строение атома

Строение атома. Опыт Резерфорда. Планетарная модель атома и ее противоречия. Постулаты Бора.

---

24 Лазеры

Лазеры. Индуцированное излучение. Свойства лазерного излучения. Принцип действия лазера

---

25 Методы наблюдения и регистрации элементарных частиц

Методы наблюдения и регистрации элементарных частиц. Счетчик Гейгера. Камера Вильсона. Пузырьковая камера. Метод толстослойных фотоэмульсий

---

26 Явление радиоактивности

Явление радиоактивности. Опыт Резерфорда. Свойства излучений. Закон радиоактивного распада. Изотопы.

---

27 Строение атомного ядра

Строение атомного ядра. Открытие нейтрона. Модель ядра. Энергия связи атомных ядер. Ядерные реакции

---

28 Деление ядер урана

Деление ядер урана. Механизм деления урана. Цепные ядерные реакции. Образование плутония

---

29 Ядерный реактор. Термоядерные реакции

Ядерный реактор. Термоядерные реакции

---

30 Биологическое действие радиоактивных излучений

Биологическое действие радиоактивных излучений. Поглощенная доза излучений. Экспозиционная доза. Эквивалентная доза поглощенного излучения. Радиационные эффекты

---

Справочник «Физика 11 класс. Все формулы и темы». Смотрите также другие Справочники по физике:

Формулы 7 класс  Формулы 8 класс  Формулы 9 класс  Формулы 10 класс

Характеристики электрического и магнитного полей | Формулы и расчеты онлайн

В нижеследующей таблице дана сводка величин, уравнений и единиц, описывающих электрические и магнитные поля.

Электрические величины		Магнитные величины
Уравнение	Единица	Уравнение	Единица
Сила тока		Напряжение индукции
$ I = \frac{dQ}{dt} $	Ампер	$ U = -N \frac{dΦ}{dt} $	Вольт
Заряд		Магнитный поток
$ Q = It $	Кулон = Ампер · Секунда	$ Φ = BS $	Вебер = Вольт · Секунда
Напряжение (электродвижущая сила)		Магнитодвижущая сила
$ U = Ed $	Вольт	$ F = Hl $	Ампер
Напряженность электрического поля		Напряженность магнитного поля
$ E = \frac{U}{d} $	Вольт/метр	$ H = \frac{IN}{l} $	Ампер/метр
Поверхностная плотность заряда или Электрическое смещение		Магнитная индукция
$ D = \frac{Q}{S} $	Кулон/метр2	$ B = \frac{Φ}{S} $	Тесла = (Вольт · Секунда)/метр2
$ \vect{D} = ε_{0} \vect{E} $	Кулон/метр2	$ \vect{B} = μ_{0} \vect{H} $	Тесла = (Вольт · Секунда)/метр2
Электрическая постоянная		Магнитная постоянная
$ ε_0 = \frac{1}{μ_0 c^2} $	Фарад/метр	$ μ_0 = \frac{1}{ε_0 c^2} $	Генри/метр
Относительная диэлектрическая проницаемость		Относительная магнитная проницаемость
$ ε $		$ μ $
Абсолютная диэлектрическая проницаемость		Абсолютная магнитная проницаемость
$ ε_{а} = ε_{0} ε $	Фарад/метр	$ μ_{а} = μ_{0} μ $	Генри/метр
Емкость		Индуктивность
$ С = \frac{Q}{U} $	Фарад	$ L = \frac{ΦN}{I} $	Генри
Емкость плоского конденсатора		Индуктивность цилиндрической катушки
$ С = ε_{а} \frac{S}{d} $	Фарад	$ L = μ_{а} \frac{SN^2}{l} $	Генри
Энергия электрического поля		Энергия магнитного поля
$ W = \frac{CU^2}{2} $	Джоуль	$ W = \frac{LI^2}{2} $	Джоуль
Энергия плоского конденсатора		Энергия цилиндрической катушки
$ W = ε_{а} \frac{E^2 V}{2} $	Джоуль	$ W = μ_{а} \frac{H^2 V}{2} $	Джоуль
Плотность электрической энергии		Плотность магнитной энергии
$ ω = ε_{а} \frac{E^2}{2} = \frac{DE}{2} $	Джоуль/метр3	$ ω = μ_{а} \frac{H^2}{2} = \frac{BH}{2} $	Джоуль/метр3

Формулы для решения задач по физике

№ п/п	Наименование параметра	Формула	Обозначения
4.1	Закон Био-Савара-Лапласа Модуль вектора Модуль вектора		― магнитная индукция поля, создаваемого элементом проводника с током; μ ― магнитная проницаемость среды, μ0 = 4π∙10−7 Гн/м ― магнитная постоянная, ― вектор, равный по модулю длине dl проводника и совпадающий по направлению с током; I ― сила тока в проводнике, ― расстояние до проводника α ― угол между векторами и ― напряженность магнитного поля, создаваемого элементом проводника с током
4.2	Индукция магнитного поля, создаваемого бесконечно длинным прямым проводником с током Напряженность магнитного поля	вывод формул	μ ― магнитная проницаемость среды, μ0 = 4π∙10−7 Гн/м ― магнитная постоянная, I ― сила тока в проводнике, a ― расстояние до проводника
4.3	Индукция магнитного поля в центре кругового проводника с током Напряженность магнитного поля		μ ― магнитная проницаемость среды, μ0 = 4π∙10−7 Гн/м ― магнитная постоянная, I ― сила тока в проводнике, R ― радиус проводника
4.4	Индукция магнитного поля на оси кругового проводника с током Напряженность магнитного поля	вывод формул	μ ― магнитная проницаемость среды, μ0 = 4π∙10−7 Гн/м ― магнитная постоянная, I ― сила тока в проводнике, R ― радиус проводника, a ― расстояние до плоскости проводника
4.5	Индукция магнитного поля внутри длинного соленоида		μ ― магнитная проницаемость среды, μ0 = 4π∙10−7 Гн/м ― магнитная постоянная, I ― сила тока в проводнике, N ― количество витков, l ― длина соленоида
4.6	Магнитная индукция поля, создаваемая отрезком проводника	вывод формулы	μ ― магнитная проницаемость среды, μ0 = 4π∙10−7 Гн/м ― магнитная постоянная, a ― расстояние до оси проводника, α1 и α2 ― углы между направлением тока и направлением на точку, в которой создано магнитное поле, вершинами которых являются соответственно начало и конец прямого участка проводника
4.7	Связь между напряженностью H и индукцией B магнитного поля		μ ― магнитная проницаемость среды, μ0 = 4π∙10−7 Гн/м ― магнитная постоянная
4.8	Связь между электрической и магнитной напряженностями волны		Е0 ― амплитуда электрической напряженности, H0 ― амплитуда магнитной напряженности
4.9	Фазовая скорость волны v равна		с ― скорость света в вакууме; ε ― диэлектрическая проницаемость; μ ― магнитная проницаемость
4.10	Индуктивность катушки равна		μ0 = 4π∙10−7 Гн/м ― магнитная постоянная; N ― количество витков; N = l/d, d ― диаметр проводника катушки; l ― длина катушки; V ― объем катушки; S ― площадь витка катушки
4.11	Средняя объемная плотность энергии		μ0 = 4π∙10−7 Гн/м ― магнитная постоянная; μ ― магнитная проницаемость среды; для вакуума μ = 1; Н ― действующее значение напряженности магнитного поля
4.12	Средняя объемная плотность энергии		ε0 = 8,85∙10−12 Ф/м ― электрическая постоянная, ε ― диэлектрическая проницаемость среды, E ― действующее значение напряженности электрического поля
4.13	Сила , действующая на заряд Q, движущийся со скоростью в магнитном поле с индукцией (сила Лоренца)	или	α ― угол, образованный вектором скорости движения частицы и вектором индукции магнитного поля
4.14	Cила Ампера (сила, действующая на проводник с током в магнитном поле)		I ― сила тока, l ― длина проводника, В ― индукция магнитного поля, α ― угол между векторами
4.15	Количество заряда, протекающее в контуре	вывод формулы	ΔΨ ― изменение потокосцепления контура; R ― сопротивление контура; N ― количество витков в контуре; ΔФ ― изменение магнитного потока, пронизывающего контур; S ― площадь витка; ΔB ― изменение магнитной индукции
4.16	Циклическая частота колебаний в контуре		L ― индуктивность контура; C ― емкость контура
4.17	Мгновенное значение I силы тока в цепи, обладающей активным сопротивлением R и индуктивностью L, после размыкания цепи		I0 ― значение силы тока в цепи при t = 0; t ― время, прошедшее с момента размыкания цепи
4.18	Мгновенное значение I силы тока в цепи, обладающей активным сопротивлением R и индуктивностью L, после замыкания цепи		ε ― э.д.с. источника тока; t ― время, прошедшее с момента замыкания цепи
4.19	Основной закон электромагнитной индукции		εi ― электродвижущая сила индукции; N ― число витков контура; Ψ ― потокосцепление
4.20	Величина ЭДС самоиндукции пропорциональна скорости изменения силы тока I:		L ― индуктивность контура или катушки
4.21	Работа по перемещению проводника или по повороту контура в магнитном поле		I ― сила тока в проводнике, контуре; dФ ― пересекаемый проводником магнитный поток либо изменение магнитного потока через замкнутый контур
4.22	Вращающий момент, действующий на контур с током, помещенный в магнитное поле Значение вращающего момента	При α=π/2 имеем При α=0 или α=π имеем	― индукция магнитного поля; m ― магнитный момент контура, m = IS, где I ― ток, протекающий по контуру, S ― площадь контура; α ― угол между векторами m и

Все формулы по физике 11 класса

Формула расчета силы Ампера	FA = B I L sinα	Закон Ампера: сила действия однородного магнитного поля на проводник с током прямо пропорциональна силе тока, длине проводника, модулю вектора индукции магнитного поля, синусу угла между вектором индукции магнитного поля и проводником.	FA – сила Ампера, [Н] В – магнитная индукция, [Тл] I – сила тока, [А] L – длина проводника, [м]
Формула расчета силы Лоренца	Fл= q B υ sinα	Сила Лоренца – сила, действующая на точечную заряженную частицу, движущуюся в магнитном поле. Она равна произведению заряда, модуля скорости частицы, модуля вектора индукции магнитного поля и синуса угла между вектором магнитного поля и скоростью движения частицы.	Fл – сила Лоренца, [Н] q – заряд, [Кл] В – магнитная индукция, [Тл] υ – скорость движения заряда, [м/с]
Формула радиуса движения частицы в магнитном поле	r= mυ/qB		r – радиус окружности, по которой движется частица в магнитном поле, [м] m – масса частицы, [кг] q – заряд, [Кл] В – магнитная индукция, [Тл] υ – скорость движения заряда, [м/с]
Формула для вычисления магнитного потока	Ф = B S cosα		Ф – магнитный поток, [Вб] В – магнитная индукция, [Тл] S – площадь контура, [м2]
Формула для вычисления величины заряда	q = It	Заряд – это есть произведение силы тока на время, в течение которого этот заряд протекает по проводнику.	q – заряд, [Кл] I – сила тока, [А] t – время, [c]
Закон Ома для участка цепи	I = U/R	Закон Ома — сила тока в участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна его сопротивлению.	I – сила тока, [А] U – напряжение, [В] R – сопротивление, [Ом]
Формула для вычисления удельного сопротивления проводника	R = ρ L/S ρ = R S/L	Удельное сопротивление – величина, характеризующая электрические свойства вещества, из которого изготовлен проводник.	ρ – удельное сопротивление вещества, [Ом·мм2/м] R – сопротивление, [Ом] S – площадь поперечного сечения проводника, [ммБ2] L – длина проводника, [м]
Законы последовательного соединения проводников	I = I1 = I2 U = U1 + U2 Rобщ = R1 + R2	Последовательным соединением называется соединение, когда элементы идут друг за другом.	I – сила тока, [А] U – напряжение, [В] R – сопротивление, [Ом]
Законы параллельного соединения проводников	U = U1 = U2 I = I1 + I2 1/Rобщ =1/R1 +1/R2	Параллельным соединением проводников называется такое соединение, при котором начала и концы проводников соединяются вместе.	I – сила тока, [А] U – напряжение, [В] R – сопротивление, [Ом]
Формула для вычисления величины заряда.	q = It	Заряд – это есть произведение силы тока на время, в течение которого этот заряд протекает по проводнику.	q – заряд, [Кл] I – сила тока, [А] t – время, [c]
Формула для нахождения работы электрического тока.	A = Uq A = UIt	Работа – это величина, которая характеризует превращение энергии из одного вида в другой, т.е. показывает, как энергия электрического тока, будет превращаться в другие виды энергии – механическую, тепловую и т. д. Работа электрического поля – это произведение электрического напряжения на заряд, протекающий по проводнику. Работа, совершаемая для перемещения электрического заряда в электрическом поле.	A – работа электрического тока, [Дж] U – напряжение на концах участка, [В] q – заряд, [Кл] I – сила тока, [А] t – время, [c]
Формула электрической мощности	P = A/t P = UI P = U2/R	Мощность – работа, выполненная в единицу времени.	P – электрическая мощность, [Вт] A – работа электрического тока, [Дж] t – время, [c] U – напряжение на концах участка, [В] I – сила тока, [А] R – сопротивление, [Ом]
Формула закона Джоуля-Ленца	Q=I2Rt	Закон Джоуля-Ленца при прохождении электрического тока по проводнику количество теплоты, выделяемое в проводнике, прямо пропорционально квадрату тока, сопротивлению проводника и времени, в течение которого электрический ток протекал по проводнику.	Q – количество теплоты, [Дж] I – сила тока, [А]; t – время, [с]. R – сопротивление, [Ом].
ЭЛЕКТРОМАГНИТНОЕ ИЗЛУЧЕНИЕ
Закон отражения света		Луч падающий, луч отраженный и перпендикуляр, восставленный в точку падения луча, лежат в одной плоскости, при этом угол падения луча равен углу отражения луча.
Закон преломления	sinα/sinγ = n2/n1	При увеличении угла падения увеличивается и угол преломления, то есть при угле падения, близком к 90°, преломлённый луч практически исчезает, а вся энергия падающего луча переходит в энергию отражённого.	n – показатель преломления одного вещества относительно другого
Формула вычисления абсолютного показателя преломления вещества	n = c/v	Абсолютный показатель преломления вещества – величина, равная отношению скорости света в вакууме к скорости света в данной среде.	n – абсолютный показатель преломления вещества c – скорость света в вакууме, [м/с] v – скорость света в данной среде, [м/с]
Закон Снеллиуса	sinα/sinγ = v1/v2=n	Закон Снеллиуса (закон преломления света): отношение синуса угла падения к синусу угла преломления есть величина постоянная.
Показатель преломления среды	sinα/sinγ = n	Отношение синуса угла падения к синусу угла преломления есть величина постоянная.	n – показатель преломления среды
Преломляющий угол призмы	δ = α(n – 1)		δ – угол отклонения α – угол падения n – показатель преломления среды
Линейное увеличение оптической системы	Г = H/h		Г – линейное увеличение оптической системы H – размер изображения, [м] h – размер предмета, [м]
Формула оптической силы линзы	D = 1/F	Оптическая сила линзы – способность линзы преломлять лучи.	D – оптическая сила линзы, [дптр] F – фокусное расстояние линзы, [м]
Формула тонкой линзы	1/F = 1/d+1/f		F – фокусное расстояние линзы, [м] d – расстояние от предмета до линзы, [м] f – расстояние от линзы до изображения, [м]
Максимальная результирующая интенсивность	Δt = mT		Δt – максимальная результирующая интенсивность Т – период колебании, [с]
Минимальная результирующая интенсивность	Δt = (2m + 1)T/2		Δt – минимальная результирующая интенсивность Т – период колебании, [с]
Геометрическая разность хода интерферирующих волн	Δ = mλ		Δ – геометрическая разность хода интерферирующих волн λ – длина волны, [м]
Условие интерференционного минимума	Δ = (2m + 1)λ/2		λ – длина волны, [м]
Условие дифракционного минимума на щели	Asinα = m λ		A – ширина щели, [м] λ – длина волны, [м]
Условие главных максимумов при дифракции	dsinα = m λ		d – период решетки λ – длина волны, [м]
Энергия кванта излучения	E = hϑ		Е – энергия кванта излучения, [Дж] ϑ – частота излучения h – постоянная Планка
Закон смещения Вина	λT = b		b – постоянная Вина λ – длина волны, [м] Т – температура черного тела
Закон Стефана-Больцмана	R = ϭT4		ϭ – постоянная Стефана-Больцмана Т – абсолютная температура черного тела R – интегральная светимость абсолютно черного тела
Уравнение Эйнштейна для фотоэффекта			А – работа выхода, [Дж] m – масса тела, [кг] v – скорость движения тела, [м/с] ϑ – частота излучения h – постоянная Планка
ФИЗИКА ВЫСОКИХ ЭНЕРГИИ
Массовое число	M = Z + N		M – массовое число Z – число протонов (электронов), зарядовое число N – число нейтронов
Формула массы ядра	МЯ = МА – Z me		MЯ – масса ядра, [кг] МА – масса изотопа , [кг] me – масса электрона, [кг]
Формула дефекта масс	∆m = Zmp+ Nmn – MЯ	Дефект масс – разность между суммой масс покоя нуклонов, составляющих ядро данного нуклида, и массой покоя атомного ядра этого нуклида.	∆m – дефект масс, [кг] mp – масса протона, [кг] mn – масса нейтрона, [кг]
Формула энергии связи	Есвязи = ∆m c2	Энергия связи ядра – минимальная энергия, необходимая для того, чтобы разделить ядро на составляющие его нуклоны (протоны и нейтроны).	Есвязи – энергия связи, [Дж] m – масса, [кг] с = 3·108м/с – скорость света
Закон радиоактивного распада	N = N02 –t/T1/2		N0 – первоначальное количество ядер N – конечное количество ядер T – период полураспада, [c] t – время, [c]
Доза поглощенного излучения	D = E/m		D – доза поглощенного излучения, [Гр] E – энергия излучения, [Дж] m – масса тела, [кг]
Эквивалентная доза поглощенного излучения	H = Dk		H – эквивалентная доза поглощенного излучения, [Зв] D – доза поглощенного излучения, [Гр] k – коэффициент качества

Магнитное поле — Физика

О магнитном поле

Магнитное поле (МП) это то, что существует в области пространства, в которой на электрически нейтральный проводник с током действует сила, называемая магнитной. ИСТОЧНИКОМ МП является движущаяся электрически заряженная частица (заряд), которая создает также и электрическое поле.

Если вблизи одной движущейсяп заряженной частицы (заряда №1) будет находиться вторая движущаяся с такой же скоростью V заряженная частица (заряд №2), то на второй заряд будут действовать 2 силы: электрическая (кулоновская) 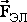и магнитная сила 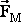, которая будет меньше электрической в 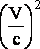раз, где с – скорость света.

Для практически любых ПРОВОДОВ с током выполняется ПРИНЦИП КВАЗИНЕЙТРАЛЬНОСТИ: несмотря на наличие и движение заряженных частиц внутри проводника, любой (не слишком малый) его отрезок имеет нулевой суммарный электрический заряд. Поэтому между обычными проводами с током наблюдается только магнитное взаимодействие.

МАГНИТНАЯ ИНДУКЦИЯ — характеристика силового действия МП на проводник с током, векторная величина, обозначаемая символом .

ЛИНИИ МАГНИТНОЙ ИНДУКЦИИ — линии, в любой точке которых вектор индукции МП направлен по касательной.

Анализ взаимодействия движущихся зарядов с учетом эффектов теории относительности (релятивизма) дает выражение для индукции 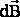МП, создаваемого элементарным отрезком c током I , расположенным в начале координат (закон Био-Савара-Лапласа или Б-С-Л):

,

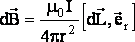где 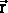— радиус-вектор точки наблюдения, 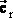— единичный радиус-вектор, направленный в точку наблюдения, m₀ — магнитная постоянная.

МП подчиняется ПРИНЦИПУ СУПЕРПОЗИЦИИ: индукция МП нескольких источников является суммой индукций полей, создаваемых независимо каждым источником .

ЦИРКУЛЯЦИЕЙ МП называется интеграл по замкнутому контуру от скалярного произведения индукции МП на элемент контура: .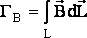

ЗАКОН ЦИРКУЛЯЦИИ МП: циркуляция МП по замкнутому контуру L₀ пропорциональна суммарному току, пронизывающему поверхность S(L₀), ограниченную этим контуром L₀ . .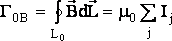

Закон Б-С-Л и принцип суперпозиции МП позволяют получить многие другие закономерности, в частности, индукцию магнитного поля прямого бесконечно длинного проводника с током: .

Линии магнитной индукции поля прямого проводника с током представляют собой концентрические окружности, лежащие в плоскостях, перпендикулярных проводнику, с центрами, расположенными на его оси.

Индукция МП на оси кругового контура (витка) радиуса R с током I на расстоянии r от центра: ,

где — МАГНИТНЫЙ МОМЕНТ витка площадью S, — единичный вектор нормали к поверхности витка.

СОЛЕНОИДОМ называется длинная прямая катушка с током. Величина индукции МП вблизи центра соленоида меняется очень мало. Такое поле можно считать практически однородным.

Из закона циркуляции МП можно получить формулу для индукции МП в центре соленоида B = m₀In , где n – число витков, приходящихся на единицу длины соленоида.

МЕТОДИКА и ПОРЯДОК ИЗМЕРЕНИЙ

Закройте окно теории. Рассмотрите внимательно рисунок, изображающий компьютерную модель. Найдите на нем все основные регуляторы и поле эксперимента. Зарисуйте необходимое в конспект.

ТАБЛИЦА 1. РЕЗУЛЬТАТЫ ИЗМЕРЕНИЙ							ТАБЛИЦА 2. Значения величины тока (не перерисовывать)
	r (см) =	2	3	…	10			Вариант	I1	I2	I3	I4
	1/r, м-1							1 и 5	5	10	15	20
	B1, Тл							2 и 6	-5	-10	-15	-20
	B2, Тл							3 и 7	-15	-10	5	10
	B3, Тл							4 и 8	-20	-15	-10	5
	B4, Тл

Подготовьте таблицу 1, используя образец. Подготовьте также таблицы 3 и 4, аналогичные табл.1, за исключением второй строчки, содержание которой см. в следующем разделе.

ИЗМЕРЕНИЯ

ЭКСПЕРИМЕНТ 1.

1. Закройте окно эксперимента 3, нажав кнопку в правом верхнем углу внутреннего окна. Запустите, дважды щелкнув мышью, следующий эксперимент «Магнитное поле прямого тока». Наблюдайте линии индукции МП прямого провода.
2. Зацепив мышью, перемещайте движок регулятора тока. Зафиксируйте величину тока, указанную в таблице 2 для вашего варианта.
3. Перемещая мышью «руку» вблизи провода, нажимайте левую кнопку мыши на расстояниях r до оси провода, указанных в таблице 1. Значения r и B_{занесите в табл.1. Повторите измерения для трех других значений тока из табл.2.}

ЭКСПЕРИМЕНТ 2.

1. Закройте окно эксперимента 1, нажав кнопку в правом верхнем углу внутреннего окна. Запустите, дважды щелкнув мышью, следующий эксперимент «Магнитное поле кругового витка с током». Наблюдайте линии индукции МП кругового витка (контура).
2. Зацепив мышью, перемещайте движок регулятора тока. Зафиксируйте величину тока, указанную в таблице 2 для вашего варианта.
3. Перемещая мышью «руку» по оси витка, нажимайте левую кнопку мыши на расстояниях r до оси витка, указанных в таблице 1. Значения r и B_{занесите в табл.3, аналогичную табл.1 (кроме второй строки, в которой здесь надо записать 1/(R²+r²)^3/2 (м^-3)). Повторите измерения для трех других значений тока из табл.2.}

ЭКСПЕРИМЕНТ 3.

1. Закройте окно эксперимента 2, нажав кнопку в правом верхнем углу внутреннего окна. Запустите, дважды щелкнув мышью, следующий эксперимент «Магнитное поле соленоида». Наблюдайте линии индукции МП соленоида.
2. Зацепив мышью, перемещайте движок регулятора тока. Зафиксируйте величину тока, указанную в таблице 2 для вашего варианта.
3. Перемещая мышью «руку» по оси соленоида, нажимайте левую кнопку мыши на расстояниях r до оси соленоида, указанных в таблице 1. Значения r и B_{занесите в табл.4, аналогичную табл.1 (кроме второй строки, в которой здесь не надо записывать ничего). Повторите измерения для трех других значений тока из табл.2.}

ОБРАБОТКА РЕЗУЛЬТАТОВ И ОФОРМЛЕНИЕ ОТЧЕТА

1. Вычислите и запишите в таблицы 1, 3 и 4 значения для второй строки.
2. Постройте на одном листе графики зависимости индукции МП (B) прямого провода с током от обратного расстояния (1/r).
3. Постройте на втором листе графики зависимости индукции МП (B) на оси витка с током от куба обратного расстояния 1/(R²+r²)^3/2.
4. На третьем листе постройте графики зависимости индукции МП на оси соленоида от расстояния до его центра.
5. По тангенсу угла наклона графиков на первых двух листах определите постоянную, используя формулы для первого чертежа и для второго (площадь витка S = pR²).
6. Вычислите среднее значение магнитной постоянной.
7. Для магнитного поля соленоида при каждом токе определите протяженность Dr области однородности, в которой индукция меняется не более, чем на 10% от максимальной. Вычислите среднее значение области однородности.
8. Запишите ответы и проанализируйте ответ и график.

Вопросы и задания для самоконтроля

Вопросы и задания для самоконтроля

1. Что такое магнитное поле (МП)?
2. Назовите источники МП.
3. Какие силы действуют между движущимися зарядами?
4. Во сколько раз магнитная сила меньше электрической для двух движущихся точечных электрических зарядов?
5. Сформулируйте определение квазинейтральности проводов с током.
6. Какие силы и почему действуют между проводами с током?
7. Дайте определение линии индукции МП. Зачем их рисуют?
8. Запишите закон Био-Савара-Лапласа. В чем он похож на закон Кулона?
9. Сформулируйте принцип суперпозиции для МП.
10. Дайте определение циркуляции МП.
11. Сформулируйте и запишите формулу закона циркуляции МП.
12. Сформулируйте и запишите формулу для МП прямого провода с током.
13. Как выглядят линии индукции МП прямого провода с током?
14. Сформулируйте и запишите формулу для МП на оси кругового витка (контура) с током.
15. Что такое магнитный момент витка с током?
16. Какую форму имеет линия индукции, проходящая через центр витка с током?
17. Что такое соленоид и для чего он используется?
18. Чему равно магнитное поле в центре соленоида?
19. Является ли МП внутри соленоида точно однородным?
20. Как определить протяженность области однородности МП внутри соленоида, если задана точность?