Период математического маятника | Все Формулы

   

Период колебания математического маятника зависит от длины нити: с уменьшением длины нити период колебания уменьшается.

   

Для математического маятника выполняются некоторые законы:

1 закон. Если, сохраняя одну и ту же длину маятника, подвешивать разные грузы (например 5кг и 100 кг), то период колебаний получится один и тот же, хотя массы грузов сильно различаются. Период математического маятника не зависит от массы груза.

2 закон. Если маятник отклонять на разные, но маленькие углы, то он будет колебаться с одним и тем же периодом, хотя и с разными амплитудами. Пока амплитуда маятника будут малы, колебания и по своей форме будут похожи на гармонические, и тогда период математического маятника не зависит от амплитуды колебаний. Это свойство приняло название изохронизмом..

Давайте выведем формулу периода математического маятника.

На груз m математического маятника действуют сила тяжести mg и сила упругости нити Fynp. Ось 0Х направим вдоль касательной к траектории движения вверх. Запишем второй закон Ньютона для данного случая:

   

С проецируем все на ось ОХ:

   

При малых углах sin\theta\]

   

Сделав замены и маленькие преобразования у нас получается, что уравнение имеет вид:

   

Сравнивая полученное выражение с уравнением гармонических колебаний у нас получается:

   

Из уравнения видно, что циклическая частота пружинного маятника будет иметь вид:

   

Тогда период математического маятника будет равен:

   

Период математического маятника зависит только от ускорения свободного падения g и от длины маятника l. Из полученной формулы следует, что период маятника не зависит от его массы и от амплитуды (при условии, что она достаточно мала). Так же мы установили количественную зависимость между периодом маятника, его длиной и ускорением свободного падения. Период математического маятника пропорционален корню квадратному из отношения длины маятника к ускорению свободного падения. Коэффициент пропорциональности равен 2p

Так же есть:

Период пружинного маятника

   

Период физического маятника

   

Период крутильного маятника

   

В Формуле мы использовали :

T — Период математического маятника

L — Длина подвеса

g=9.8 — Ускорение свободного падения

   

— Циклическая частота пружинного маятника

F — Сила упругости

x — Длина дуги АВ

Законы Кеплера — Википедия

Материал из Википедии — свободной энциклопедии

Зако́ны Ке́плера — три эмпирических соотношения, интуитивно подобранных Иоганном Кеплером на основе анализа астрономических наблюдений Тихо Браге. Описывают идеализированную гелиоцентрическую орбиту планеты. В рамках классической механики выводятся из решения задачи двух тел в случае пренебрежимо малой массы планеты, то есть предельным переходом mp/ms→0{\displaystyle m_{p}/m_{s}\rightarrow 0}, где mp{\displaystyle m_{p}}, ms{\displaystyle m_{s}} — массы планеты и звезды соответственно.

Первый закон Кеплера (закон эллипсов)[править | править код]

Первый закон Кеплера

Каждая планета Солнечной системы обращается по эллипсу, в одном из фокусов которого находится Солнце. Форма эллипса и степень его сходства с окружностью характеризуется отношением e=ca{\displaystyle e={\frac {c}{a}}}, где c{\displaystyle c} — расстояние от центра эллипса до его фокуса (фокальное расстояние), a{\displaystyle {a}} — большая полуось. Величина e{\displaystyle e} называется эксцентриситетом эллипса. При c=0{\displaystyle c=0}, и, следовательно, e=0{\displaystyle e=0} эллипс превращается в окружность.

Доказательство первого закона Кеплера

Закон всемирного тяготения Ньютона гласит, что «каждый объект во Вселенной притягивает каждый другой объект по линии, соединяющей центры масс объектов, пропорционально массе каждого объекта, и обратно пропорционально квадрату расстояния между объектами». Это предполагает, что ускорение a{\displaystyle a} имеет форму

a=d2rdt2=f(r)r^.{\displaystyle \mathbf {a} ={\frac {d^{2}\mathbf {r} }{dt^{2}}}=f(r){\hat {\mathbf {r} }}.}

Вспомним, что в полярных координатах

drdt=r˙r^+rθ˙θ^,{\displaystyle {\frac {d\mathbf {r} }{dt}}={\dot {r}}{\hat {\mathbf {r} }}+r{\dot {\theta }}{\hat {\boldsymbol {\theta }}},}

d2rdt2=(r¨−rθ˙2)r^+(rθ¨+2r˙θ˙)θ^.{\displaystyle {\frac {d^{2}\mathbf {r} }{dt^{2}}}=({\ddot {r}}-r{\dot {\theta }}^{2}){\hat {\mathbf {r} }}+(r{\ddot {\theta }}+2{\dot {r}}{\dot {\theta }}){\hat {\boldsymbol {\theta }}}.}

В координатной форме запишем

r¨−rθ˙2=f(r),{\displaystyle {\ddot {r}}-r{\dot {\theta }}^{2}=f(r),}

rθ¨+2r˙θ˙=0.{\displaystyle r{\ddot {\theta }}+2{\dot {r}}{\dot {\theta }}=0.}

Подставляя θ¨{\displaystyle {\ddot {\theta }}} и r˙{\displaystyle {\dot {r}}} во второе уравнение, получим

rdθ˙dt+2drdtθ˙=0,{\displaystyle r{d{\dot {\theta }} \over dt}+2{dr \over dt}{\dot {\theta }}=0,}

которое упрощается

dθ˙θ˙=−2drr.{\displaystyle {\frac {d{\dot {\theta }}}{\dot {\theta }}}=-2{\frac {dr}{r}}.}

После интегрирования запишем выражение

ln⁡θ˙=−2ln⁡r+ln⁡ℓ,{\displaystyle \ln {\dot {\theta }}=-2\ln r+\ln \ell ,}

ln⁡ℓ=ln⁡r2+ln⁡θ˙,{\displaystyle \ln \ell =\ln r^{2}+\ln {\dot {\theta }},}

ℓ=r2θ˙,{\displaystyle \ell =r^{2}{\dot {\theta }},}

для некоторой константы ℓ{\displaystyle \ell }, которая является удельным угловым моментом (ℓ=r×v{\displaystyle \ell =\mathbf {r} \times \mathbf {v} }).

Пусть

r=1u,{\displaystyle r={\frac {1}{u}},}

r˙=−1u2u˙=−1u2dθdtdudθ=−ℓdudθ,{\displaystyle {\dot {r}}=-{\frac {1}{u^{2}}}{\dot {u}}=-{\frac {1}{u^{2}}}{\frac {d\theta }{dt}}{\frac {du}{d\theta }}=-\ell {\frac {du}{d\theta }},}

r¨=−ℓddtdudθ=−ℓθ˙d2udθ2=−ℓ2u2d2udθ2.{\displaystyle {\ddot {r}}=-\ell {\frac {d}{dt}}{\frac {du}{d\theta }}=-\ell {\dot {\theta }}{\frac {d^{2}u}{d\theta ^{2}}}=-\ell ^{2}u^{2}{\frac {d^{2}u}{d\theta ^{2}}}.}

Уравнение движения в направлении r^{\displaystyle {\hat {\mathbf {r} }}} становится равным

d2udθ2+u=−1ℓ2u2f(1u).{\displaystyle {\frac {d^{2}u}{d\theta ^{2}}}+u=-{\frac {1}{\ell ^{2}u^{2}}}f\left({\frac {1}{u}}\right).}

Закон всемирного тяготения Ньютона связывает силу на единицу массы с расстоянием как

f(1u)=f(r)=−GMr2=−GMu2{\displaystyle f\left({1 \over u}\right)=f(r)=-\,{GM \over r^{2}}=-GMu^{2}}

где G{\displaystyle G} — универсальная гравитационная константа и M{\displaystyle M} — масса звезды.

В результате

d2udθ2+u=GMℓ2.{\displaystyle {\frac {d^{2}u}{d\theta ^{2}}}+u={\frac {GM}{\ell ^{2}}}.}

Это дифференциальное уравнение имеет общее решение:

u=GMℓ2[1+ecos⁡(θ−θ0)].{\displaystyle u={\frac {GM}{\ell ^{2}}}\left[1+e\cos(\theta -\theta _{0})\right].}

для произвольных констант интегрирования e{\displaystyle e} и θ0{\displaystyle \theta _{0}}.

Заменяя u{\displaystyle u} на 1/r{\displaystyle r} и полагая θ0=0{\displaystyle \theta _{0}=0}, получим:

r=1u=ℓ2/GM1+ecos⁡θ.{\displaystyle r={1 \over u}={\frac {\ell ^{2}/GM}{1+e\cos \theta }}.}

Мы получили уравнение конического сечения с эксцентриситетом e{\displaystyle e} и началом системы координат в одном из фокусов. Таким образом, первый закон Кеплера прямо следует из закона всемирного тяготения Ньютона и второго закона Ньютона.

Второй закон Кеплера (закон площадей)[править | править код]

Второй закон Кеплера

Каждая планета движется в плоскости, проходящей через центр Солнца, причём за равные промежутки времени радиус-вектор, соединяющий Солнце и планету, заметает собой равные площади.

Применительно к нашей Солнечной системе, с этим законом связаны два понятия: перигелий — ближайшая к Солнцу точка орбиты, и афелий — наиболее удалённая точка орбиты. Таким образом, из второго закона Кеплера следует, что планета движется вокруг Солнца неравномерно, имея в перигелии большую линейную скорость, чем в афелии.

Каждый год в начале января Земля, проходя через перигелий, движется быстрее, поэтому видимое перемещение Солнца по эклиптике к востоку также происходит быстрее, чем в среднем за год. В начале июля Земля, проходя афелий, движется медленнее, поэтому и перемещение Солнца по эклиптике замедляется. Закон площадей указывает, что сила, управляющая орбитальным движением планет, направлена к Солнцу.

Доказательство второго закона Кеплера

Третий закон Кеплера (гармонический закон)[править | править код]

Квадраты периодов обращения планет вокруг Солнца относятся, как кубы больших полуосей орбит планет.

T12T22=a13a23{\displaystyle {\frac {T_{1}^{2}}{T_{2}^{2}}}={\frac {a_{1}^{3}}{a_{2}^{3}}}},

Третий закон Кеплера

где T1{\displaystyle T_{1}} и T2{\displaystyle T_{2}} — периоды обращения двух планет вокруг Солнца, а a1{\displaystyle a_{1}} и a2{\displaystyle a_{2}} — длины больших полуосей их орбит. Утверждение справедливо также для спутников.

Ньютон установил, что гравитационное притяжение планеты определённой массы зависит только от расстояния до неё, а не от других свойств, таких, как состав или температура. Он показал также, что третий закон Кеплера не совсем точен — в действительности в него входит и масса планеты:

T12(M+m1)T22(M+m2)=a13a23{\displaystyle {\frac {T_{1}^{2}(M+m_{1})}{T_{2}^{2}(M+m_{2})}}={\frac {a_{1}^{3}}{a_{2}^{3}}}},

где M{\displaystyle M} — масса Солнца, а m1{\displaystyle m_{1}} и m2{\displaystyle m_{2}} — массы планет.

Поскольку движение и масса оказались связаны, эту комбинацию гармонического закона Кеплера и закона тяготения Ньютона используют для определения массы планет и спутников, если известны их орбиты и орбитальные периоды.

Доказательство третьего закона Кеплера

Второй закон Кеплера утверждает, что радиус-вектор обращающегося тела заметает равные площади за равные промежутки времени. Если теперь мы возьмём очень малые промежутки времени в момент, когда планета находится в точках P{\displaystyle P} (перигелий) и A{\displaystyle A} (афелий), то мы сможем аппроксимировать площадь треугольниками с высотами, равными расстоянию от планеты до Солнца, и основанием, равным произведению скорости планеты на время.

12⋅(1−ε)a⋅VAdt=12⋅(1+ε)a⋅VBdt{\displaystyle {\begin{matrix}{\frac {1}{2}}\end{matrix}}\cdot (1-\varepsilon )a\cdot V_{A}\,dt={\begin{matrix}{\frac {1}{2}}\end{matrix}}\cdot (1+\varepsilon )a\cdot V_{B}\,dt}

(1−ε)⋅VA=(1+ε)⋅VB{\displaystyle (1-\varepsilon )\cdot V_{A}=(1+\varepsilon )\cdot V_{B}}

VA=VB⋅1+ε1−ε{\displaystyle V_{A}=V_{B}\cdot {\frac {1+\varepsilon }{1-\varepsilon }}}

Используя закон сохранения энергии для полной энергии планеты в точках A{\displaystyle A} и B{\displaystyle B}, запишем

mVA22−GmM(1−ε)a=mVB22−GmM(1+ε)a{\displaystyle {\frac {mV_{A}^{2}}{2}}-{\frac {GmM}{(1-\varepsilon )a}}={\frac {mV_{B}^{2}}{2}}-{\frac {GmM}{(1+\varepsilon )a}}}

VA22−VB22=GM(1−ε)a−GM(1+ε)a{\displaystyle {\frac {V_{A}^{2}}{2}}-{\frac {V_{B}^{2}}{2}}={\frac {GM}{(1-\varepsilon )a}}-{\frac {GM}{(1+\varepsilon )a}}}

VA2−VB22=GMa⋅(1(1−ε)−1(1+ε)){\displaystyle {\frac {V_{A}^{2}-V_{B}^{2}}{2}}={\frac {GM}{a}}\cdot \left({\frac {1}{(1-\varepsilon )}}-{\frac {1}{(1+\varepsilon )}}\right)}

(VB⋅1+ε1−ε)2−VB22=GMa⋅(1+ε−1+ε(1−ε)(1+ε)){\displaystyle {\frac {\left(V_{B}\cdot {\frac {1+\varepsilon }{1-\varepsilon }}\right)^{2}-V_{B}^{2}}{2}}={\frac {GM}{a}}\cdot \left({\frac {1+\varepsilon -1+\varepsilon }{(1-\varepsilon )(1+\varepsilon )}}\right)}

VB2⋅(1+ε1−ε)2−VB2=2GMa⋅(2ε(1−ε)(1+ε)){\displaystyle V_{B}^{2}\cdot \left({\frac {1+\varepsilon }{1-\varepsilon }}\right)^{2}-V_{B}^{2}={\frac {2GM}{a}}\cdot \left({\frac {2\varepsilon }{(1-\varepsilon )(1+\varepsilon )}}\right)}

VB2⋅((1+ε)2−(1−ε)2(1−ε)2)=4GMεa⋅(1−ε)(1+ε){\displaystyle V_{B}^{2}\cdot \left({\frac {(1+\varepsilon )^{2}-(1-\varepsilon )^{2}}{(1-\varepsilon )^{2}}}\right)={\frac {4GM\varepsilon }{a\cdot (1-\varepsilon )(1+\varepsilon )}}}

VB2⋅(1+2ε+ε2−1+2ε−ε2(1−ε)2)=4GMεa⋅(1−ε)(1+ε){\displaystyle V_{B}^{2}\cdot \left({\frac {1+2\varepsilon +\varepsilon ^{2}-1+2\varepsilon -\varepsilon ^{2}}{(1-\varepsilon )^{2}}}\right)={\frac {4GM\varepsilon }{a\cdot (1-\varepsilon )(1+\varepsilon )}}}

VB2⋅4ε=4GMε⋅(1−ε)2a⋅(1−ε)(1+ε){\displaystyle V_{B}^{2}\cdot 4\varepsilon ={\frac {4GM\varepsilon \cdot (1-\varepsilon )^{2}}{a\cdot (1-\varepsilon )(1+\varepsilon )}}}

VB=GM⋅(1−ε)a⋅(1+ε).{\displaystyle V_{B}={\sqrt {\frac {GM\cdot (1-\varepsilon )}{a\cdot (1+\varepsilon )}}}.}

Теперь, когда нашли VB{\displaystyle V_{B}}, мы можем найти секториальную скорость. Так как она постоянна, то можем выбрать любую точку эллипса: например, для точки B получим

dAdt=12⋅(1+ϵ)a⋅VBdtdt=12⋅(1+ϵ)a⋅VB{\displaystyle {\frac {dA}{dt}}={\frac {{\frac {1}{2}}\cdot (1+\epsilon )a\cdot V_{B}\,dt}{dt}}={\begin{matrix}{\frac {1}{2}}\end{matrix}}\cdot (1+\epsilon )a\cdot V_{B}}

=12⋅(1+ε)a⋅GM⋅(1−ε)a⋅(1+ε)=12⋅GMa⋅(1−ε)(1+ε){\displaystyle ={\begin{matrix}{\frac {1}{2}}\end{matrix}}\cdot (1+\varepsilon )a\cdot {\sqrt {\frac {GM\cdot (1-\varepsilon )}{a\cdot (1+\varepsilon )}}}={\begin{matrix}{\frac {1}{2}}\end{matrix}}\cdot {\sqrt {GMa\cdot (1-\varepsilon )(1+\varepsilon )}}}

Однако полная площадь эллипса равна πa(1−ε2)a{\displaystyle \pi a{\sqrt {(1-\varepsilon ^{2})}}a} (что равно πab{\displaystyle \pi ab}, поскольку b=(1−ε2)a{\displaystyle b={\sqrt {(1-\varepsilon ^{2})}}a}). Время полного оборота, таким образом, равно

Урок 08. Практическая работа № 2 «Законы Кеплера. Определение масс небесных тел»

Тема: Законы Кеплера. Определение масс  небесных  тел

Цель занятия: Освоить методику решения задач, используя законы движения планет.

                                                      Теоретические сведения

При решении задач неизвестное движение сравнивается с уже известным путём применения законов Кеплера и формул синодического периода обращения.

Первый закон Кеплера. Все планеты движутся по эллипсам, в одном из фокусов которого находится Солнце.

Второй закон Кеплера. Радиус-вектор планеты описывает в равные времена равные площади.

Третий закон Кеплера. Квадраты времен обращения планет относятся как кубы больших полуосей их орбит:

Для определения масс небесных тел применяют обобщённый третий закон Кеплера с учётом сил всемирного тяготения:

,

где М₁ и М₂ -массы каких-либо небесных тел, а m₁ и m₂ — соответственно массы их спутников.

Обобщённый третий закон  Кеплера применим и к другим системам, например, к движению планеты вокруг Солнца и спутника вокруг планеты. Для этого сравнивают движение Луны вокруг Земли с движением спутника вокруг той планеты, массу которой определяют, и при этом массами спутников в сравнении с массой центрального тела пренебрегают. При этом в исходной формуле индекс надо отнести к движению Луны вокруг Земли массой , а индекс 2 –к движению любого спутника вокруг планеты массой . Тогда масса планеты вычисляется по формуле:

,

где Т_л и α_л— период и большая полуось орбиты спутника планеты , М⊕ -масса Земли.

Формулы, определяющие соотношение между сидерическим (звёздным) Т и синодическим периодами S планеты и периодом обращения Земли , выраженными в годах или сутках,

а) для внешней планеты формула имеет вид:

б) для внутренней планеты:

Выполнение работы

Задание 1. За какое время Марс, находящийся от Солнца примерно в полтора раза, чем Земля, совершает полный оборот вокруг Солнца?

Задание 2. Вычислить массу Юпитера, зная, что его спутник Ио совершает оборот вокруг планеты за 1,77 суток, а большая полуось его орбиты – 422 тыс. км

Задание 3. Противостояния некоторой планеты повторяются через 2 года. Чему равна большая полуось её орбиты?

Задание 4. Определите массу планеты Уран (в массах Земли), если известно, что спутник Урана Титания обращается вокруг него с периодом 8,7 сут. на среднем расстоянии 438 тыс. км. для луны эти величины равны соответственно 27,3 сут. и 384 тыс. км.

Задание 5. Марс дальше от Солнца, чем Земля, в 1.5 раза. Какова продолжительность года на Марсе? Орбиты планет считать круговыми.

Задание 6. Синодический период планеты 500 суток. Определите большую полуось её орбиты и звёздный (сидерический) период обращения.

Задание 7.  Определить период обращения астероида Белоруссия если большая полуось его орбиты    а=2,4 а.е.

Задание 8. Звёздный период обращения Юпитера вокруг Солнца Т=12 лет. Каково среднее расстояние от Юпитера до Солнца?

Примеры решения задач 1-4

Задание 1. За какое время Марс, находящийся от Солнца примерно в полтора раза, чем Земля, совершает полный оборот вокруг Солнца?

Задание 2. Вычислить массу Юпитера, зная, что его спутник Ио совершает оборот вокруг планеты за 1,77 суток, а большая полуось его орбиты – 422 тыс. км

Задание 3. Противостояния некоторой планеты повторяются через 2 года. Чему равна большая полуось её орбиты?

Задание 4. Определите массу планеты Уран (в массах Земли), если известно, что спутник Урана Титания обращается вокруг него с периодом 8,7 сут. на среднем расстоянии 438 тыс. км. для луны эти величины равны соответственно 27,3 сут. и 384 тыс. км.

Сидерический и синодический периоды обращения объектов по своим орбитам

«Небесная механика», как было принято называть науку о звездах во времена Исаака Ньютона, подчиняется классическим законам движения тел. Одними из важных характеристик этого движения являются различные периоды обращения космических объектов по своим орбитам. В статье пойдет речь о сидерическом и синодическом периодах обращения звезд, планет и их естественных спутников.

Понятие о синодическом и сидерическом временных периодах

Практически каждый из нас знает, что планеты движутся по эллиптическим орбитам вокруг своих звезд. Звезды, в свою очередь, совершают орбитальные движения вокруг друг друга или вокруг центра Галактики. Иными словами, все массивные объекты космоса имеют определенные траектории движения, включая кометы и астероиды.

Важной характеристикой для всякого космического объекта является время, которое он затрачивает, чтобы совершить один полный оборот по своей траектории. Это время принято называть периодом. Чаще всего в астрономии при изучении Солнечной системы пользуются двумя периодами: синодическим и сидерическим.

Сидерический временной период — это время, которое требуется объекту, чтобы он совершил полный оборот по своей орбите вокруг своей звезды, при этом за точку отчета берется другая удаленная звезда. Этот период также называют реальным, поскольку именно такое значение времени обращения по орбите получит неподвижный наблюдатель, который будет следить за процессом вращения объекта вокруг его звезды.

Синодический период — это время, через которое объект появится в одной и той же точке на небосводе, если смотреть на него с какой-либо планеты. Например, если взять Луну, Землю и Солнце и задаться вопросом о том, через какое время Луна будет находиться в точке на небе, в которой она находится в данный момент, ответом на него будет значение синодического периода Луны. Этот период также называют кажущимся, поскольку от реального орбитального периода он отличается.

Главное отличие между сидерическим и синодическим периодами

Как уже было сказано, сидерический — это реальный период обращения, а синодический — это кажущийся, однако в чем же главная разница между этими понятиями?

Вся разница заключается в количестве объектов, относительно которых измеряется временная характеристика. Понятие «сидерический период» принимает во внимание всего один относительный объект, например, Марс вращается вокруг Солнца, то есть движение рассматривается только относительно одной звезды. Синодический же временной период — это характеристика, которая учитывает относительное положение двух и более объектов, например, два одинаковых положения Юпитера относительно земного наблюдателя. То есть здесь необходимо учитывать положение Юпитера не только относительно Солнца, но и относительно Земли, которая также вращается вокруг Солнца.

Формула расчета сидерического периода

Для определения реального периода обращения планеты вокруг своей звезды или естественного спутника вокруг своей планеты, необходимо воспользоваться третьим законом Кеплера, который устанавливает взаимосвязь между реальным орбитальным периодом объекта и полудлиной его большой оси. В общем случае форма орбиты любого космического тела представляет собой эллипс.

Формула для определения сидерического периода имеет вид: T = 2*pi*√(a3/(G*M)), где pi = 3,14 — число пи, a — полудлина большой оси эллипса, G = 6,674*10-11 м3/(кг*с2) — универсальная гравитационная постоянная, M — масса объекта, вокруг которого осуществляется вращение.

Таким образом, зная параметры орбиты любого объекта, а также массу звезды, можно легко вычислить значение реального периода обращения этого объекта по своей орбите.

Расчет синодического временного периода

Как вычислить? Синодический период планеты или ее естественного спутника можно рассчитать, если знать значение реального ее периода обращения вокруг рассматриваемого объекта и реального периода обращения этого объекта вокруг своей звезды.

Формула, которая позволяет провести подобный расчет, имеет вид: 1/P = 1/T ± 1/S, здесь P — реальный период обращения рассматриваемого объекта, T — реальный период обращения объекта, относительно которого рассматривается движение, вокруг своей звезды, S — неизвестный синодический временной период.

Знаком «±» в формуле следует пользоваться так: если T > S, тогда формула используется со знаком «+», если же T < S, тогда нужно подставить знак «-«.

Использование формулы на примере Луны

Чтобы показать, как правильно пользоваться приведенным выражением, возьмем для примера вращение Луны вокруг Земли и синодический период обращения Луны рассчитаем.

Известно, что наша планета имеет реальный период обращения по орбите вокруг Солнца, равный T = 365,256363 дней. В свою очередь, из наблюдений можно установить, что на небосводе Луна появляется в рассматриваемой точке через каждые S = 29,530556 дня, то есть это ее синодический период. Поскольку S < T, то формулу, связывающую разные периоды, следует брать со знаком «+», получаем: 1/P = 1/365,256363 + 1/29,530556 = 0,0366, откуда P = 27,3216 дней. Как можно видеть, Луна на 2 дня быстрее совершает свой оборот вокруг Земли, чем земной наблюдатель снова может ее увидеть в отмеченном месте на небосводе.

Большая полуось — Википедия

Большая полуось — один из основных геометрических параметров объектов, образованных посредством конического сечения.

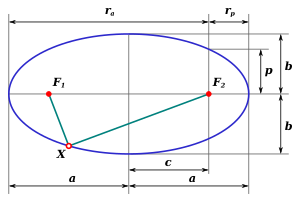Основные параметры эллипса

Большой осью эллипса называется его наибольший диаметр — отрезок проходящий через центр и два фокуса. Большая полуось составляет половину этого расстояния и идёт от центра эллипса через фокус к его краю.

Под углом в 90° к большой полуоси располагается малая полуось — минимальное расстояние от центра эллипса до его края. У частного случая эллипса — круга — большая и малая полуоси равны и являются радиусами. Таким образом, можно рассматривать большую и малую полуоси как некоего рода радиусы эллипса.

Длина большой полуоси a{\displaystyle a} связана с длиной малой полуоси b{\displaystyle b} через эксцентриситет e{\displaystyle e}, фокальный параметр p{\displaystyle p} и фокальное расстояние (полурасстояние между фокусами) c{\displaystyle {\boldsymbol {c}}} следующим образом:

b=a1−e2,{\displaystyle b=a{\sqrt {1-e^{2}}},}

p=a(1−e2),{\displaystyle p=a(1-e^{2}),}

ap=b2.{\displaystyle ap=b^{2}.}

a2=b2+c2{\displaystyle a^{2}=b^{2}+c^{2}}

Большая полуось представляет собой среднее арифметическое между расстояниями от любой точки эллипса до его фокусов.

Рассмотрев уравнение в полярных координатах, с точкой в начале координат (полюс) и лучом, начинающейся из этой точки (полярная ось):

r(1−ecos⁡θ)=p{\displaystyle r(1-e\cos \theta )=p}

Получим средние значения r=p1+e{\displaystyle r={p \over {1+e}}} и r=p1−e{\displaystyle r={p \over {1-e}}} и большую полуось a=p1−e2.{\displaystyle a={p \over 1-e^{2}}.}

График построения параболы простейшей функции y = x²

Параболу можно получить как предел последовательности эллипсов, где один фокус остаётся постоянным, а другой отодвигается в бесконечность, сохраняя p{\displaystyle p} постоянным. Таким образом a{\displaystyle a} и b{\displaystyle b} стремятся к бесконечности, причём a{\displaystyle a} быстрее, чем b{\displaystyle b}.

Большая полуось гиперболы составляет половину минимального расстояния между двумя ветвями гиперболы, на положительной и отрицательной сторонах оси x{\displaystyle x} (слева и справа относительно начала координат). Для ветви расположенной на положительной стороне, полуось будет равна:

(x−h)2a2−(y−k)2b2=1.{\displaystyle {\frac {\left(x-h\right)^{2}}{a^{2}}}-{\frac {\left(y-k\right)^{2}}{b^{2}}}=1.}

Если выразить её через коническое сечение и эксцентриситет, тогда выражение примет вид:

a=pe2−1{\displaystyle a={p \over e^{2}-1}}.

Прямая, содержащая большую ось гиперболы, называется поперечной осью гиперболы.^[1]

Орбитальный период[править | править код]

В небесной механике орбитальный период T{\displaystyle T} обращения малых тел по эллиптической или круговой орбите вокруг более крупного центрального тела рассчитывается по формуле:

T=2πa3μ{\displaystyle T=2\pi {\sqrt {a^{3} \over \mu }}}

где:

a{\displaystyle a} — это размер большой полуоси орбиты

μ{\displaystyle \mu } — это стандартный гравитационный параметр

Следует обратить внимание, что в данной формуле для всех эллипсов период обращения определяется значением большой полуоси, независимо от эксцентриситета.

В астрономии большая полуось, наряду с орбитальным периодом, является одним из самых важных орбитальных элементов орбиты космического тела.

Для объектов Солнечной системы большая полуось связана с орбитальным периодом по третьему закону Кеплера.

T12T22=a13a23{\displaystyle {\frac {T_{1}^{2}}{T_{2}^{2}}}={\frac {a_{1}^{3}}{a_{2}^{3}}}}

где:

T{\displaystyle T} — орбитальный период в годах;

a{\displaystyle a} — большая полуось в астрономических единицах.

Это выражение является частным случаем общего решения задачи двух тел Исаака Ньютона:

T2=4π2G(M+m)a3{\displaystyle T^{2}={\frac {4\pi ^{2}}{G(M+m)}}a^{3}}

где:

G{\displaystyle G} — гравитационная постоянная

M{\displaystyle M} — масса центрального тела

m{\displaystyle m} — масса обращающегося вокруг него спутника. Как правило, масса спутника настолько мала по сравнению с массой центрального тела, что ею можно пренебречь. Поэтому, сделав соответствующие упрощения в этой формуле, получим данную формулу в упрощённом виде, который приведён выше.

Орбита движения спутника вокруг общего с центральным телом центра масс (барицентра), представляет собой эллипс. Большая полуось используется в астрономии всегда применительно к среднему расстоянию между планетой и звездой, в результате орбиты планет Солнечной системы приведены к гелиоцентрической системе, а не к системе движения вокруг центра масс. Эту разницу удобнее всего проиллюстрировать на примере системы Земля—Луна. Отношение масс в этом случае составляет 81,30059. Большая полуось геоцентрической орбиты Луны составляет 384 400 км, в то время как расстояние до Луны относительно центра масс системы Земля—Луна составляет 379 730 км — из-за влияния массы Луны центр масс находится не в центре Земли, а на расстоянии 4670 км от него. В итоге средняя орбитальная скорость Луны относительно центра масс составляет 1,010 км/с, а средняя скорость Земли — 0,012 км/с. Сумма этих скоростей даёт орбитальную скорость Луны 1,022 км/с; то же самое значение можно получить, рассматривая движение Луны относительно центра Земли, а не центра масс.

Среднее расстояние[править | править код]

Часто говорят, что большая полуось является средним расстоянием между центральным и орбитальным телом. Это не совсем верно, так как под средним расстоянием можно понимать разные значения — в зависимости от величины, по которой производят усреднение:

• усреднение по эксцентрической аномалии. В таком случае среднее расстояние будет точно равно большой полуоси орбиты.
• усреднение по истинной аномалии, тогда среднее расстояние будет точно равно малой полуоси орбиты.
• усреднение по средней аномалии даст значение среднего расстояния, усреднённое по времени:

a(1+e22).{\displaystyle a\left(1+{\frac {e^{2}}{2}}\right).}

• усреднение по радиусу, которое получают из следующего соотношения:

ab=a1−e24.{\displaystyle {\sqrt {ab}}=a{\sqrt[{4}]{1-e^{2}}}.}

Энергия; расчёт большой полуоси методом векторов состояния[править | править код]

В небесной механике большая полуось a{\displaystyle a} может быть рассчитана методом векторов орбитального состояния:

a=−μ2ε{\displaystyle a={-\mu \over {2\varepsilon }}}

для эллиптических орбит

a=μ2ε{\displaystyle a={\mu \over {2\varepsilon }}}

для гиперболической траектории

и

ε=v22−μ|r|{\displaystyle \varepsilon ={v^{2} \over {2}}-{\mu \over \left|\mathbf {r} \right|}}

(удельная орбитальная энергия^[en])

и

μ=G(M+m){\displaystyle \mu =G(M+m)}

(стандартный гравитационный параметр), где:

v{\displaystyle v} — орбитальная скорость спутника, на основе вектора скорости,

r{\displaystyle r} — вектор положения спутника в координатах системы отсчёта, относительно которой должны быть вычислены элементы орбиты (например, геоцентрический в плоскости экватора — на орбите вокруг Земли, или гелиоцентрический в плоскости эклиптики — на орбите вокруг Солнца),

G{\displaystyle G} — гравитационная постоянная,

M{\displaystyle M} и m{\displaystyle m} — массы тел.

Большая полуось рассчитывается на основе общей массы и удельной энергии, независимо от значения эксцентриситета орбиты.