Updating… ć 1 Параллельное соединение.pptОльга Федотова, 5 янв. 2016 г., 08:39 1 формулы параллельного соединения.jpg(32k) Ольга Федотова, 5 янв. 2016 г., 08:39 1_1 параллельное соединение.swf(115k) Ольга Федотова, 5 янв. 2016 г., 08:39 1_2 конспект.gif(29k) Ольга Федотова, 5 янв. 2016 г., 08:39 2 практика.swf(13k) Ольга Федотова, 5 янв. 2016 г., 08:39 Ольга Федотова, 5 янв. 2016 г., 08:39 2 сила тока при параллельном соединении.swf(241k) Ольга Федотова, 5 янв. 2016 г., 08:39 2 формулы.jpg(51k) Ольга Федотова, 5 янв. 2016 г., 09:32 Ольга Федотова, 5 янв. (8k) Ольга Федотова, 5 янв. 2016 г., 08:40 3 формула 2 сопротивления.png(3k) Ольга Федотова, 5 янв. 2016 г., 08:40 3 формула 3 сопротивления.jpg(15k) Ольга Федотова, 5 янв. 2016 г., 08:41 3 формула сопротивление.png(1k) Ольга Федотова, 5 янв. 2016 г., 08:41 ć 5 Тест к уроку Параллельное соединение проводников.ppt(101k) Ольга Федотова, 5 янв. 2016 г., 08:41 |
параллельное соединение формула — Школьные Знания.com
Какое количество теплоты необходимо для превращения воды массой 3,5 кг при температуре 100 градусах Цельсия. Удельная теплота парообразования воды рав … на 23 МДж/кг
1 2 3 4 5 6 7 8 9 10
««Основы кинематики»
а5-а8. Единица измерения перемещения.
66-610. Величина, измеряемая в секундах.
в1-в7. …. отсчета.
r2-r10.
… Быстрота изменения скорости.
д4-д8. Тело, размерами которого можно пренебречь.
e5-e8.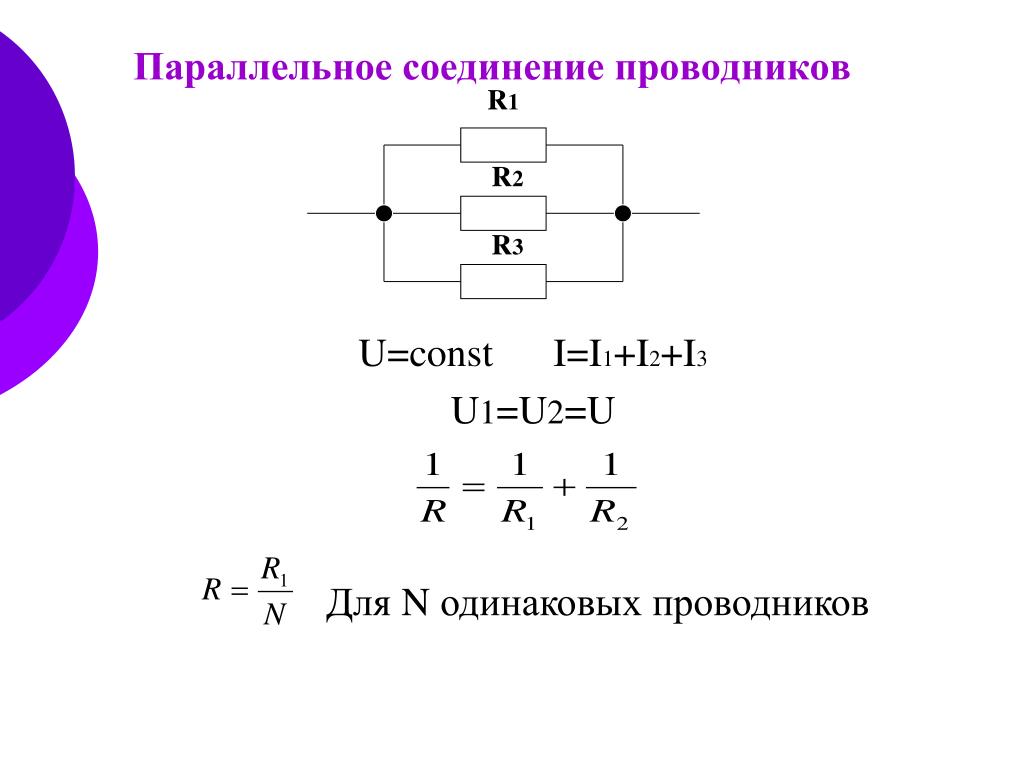 Длина траектории.
ж3-ж10. Быстрота движения.
33-310. Автор гелиоцентрической модели.
и4-и10. Итальянский ученый, изучавший равноускоренное движение
и оспоривший многие утверждения Аристотеля.
кі-к7. Явление прямолинейного, равномерного, свободного
движения.
Ключевое слово в столбце а7-к7 — линия, по которой движется тело.
A
Б
B
т
д
E
ж
3
H
K
Длина траектории.
ж3-ж10. Быстрота движения.
33-310. Автор гелиоцентрической модели.
и4-и10. Итальянский ученый, изучавший равноускоренное движение
и оспоривший многие утверждения Аристотеля.
кі-к7. Явление прямолинейного, равномерного, свободного
движения.
Ключевое слово в столбце а7-к7 — линия, по которой движется тело.
A
Б
B
т
д
E
ж
3
H
K
Помогите Брусок маса якого дорівнює 100г, рухається вгору по вертикальній стіні з прискоренням 1м/с2, що направлене теж угору. Коефіцієнт тертя між б … руском і стіною становить 0,2. Визначите силу, що діє на брусок під кутом 45 градусов до вертикалі
Визначте масу тіла, якщо на поверхні Марса (g=3,76 м/с2) на це тіло діє сила тяжіння 7,52 Н. Обчисліть силу тяжіння, що діятиме на це тло на поверхні … Землі.
до кінців стержня здовжини 105см підвищені тягарці масі яких 250г і 600г.Визначте у якій точці треба підвісити стержень,щоб він перебувае у рівновазі … в горезонтальному положени
риант-2 молярную массу газа? 1.
Тело свободно падает с высотой 0,2 км (надо перевести в м)на земле Если пренебречь сопротивления воздуха через какое время тело упадет на землю? ускор … ение свободного падения 10 м/с²пожалуйста помогите срочно
ДАЮ 100 БАЛЛОВ!Задача на фото
мяч бросили вертикально вверх со скоростью 10м\с Найти его скорость через 1 секунду
Решите задачи 50 балов
Формула расчета параллельного соединения конденсаторов. Последовательное соединение конденсаторов: формула
Содержание:
Схемы в электротехнике состоят из электрических элементов, в которых способы соединения конденсаторов могут быть разными.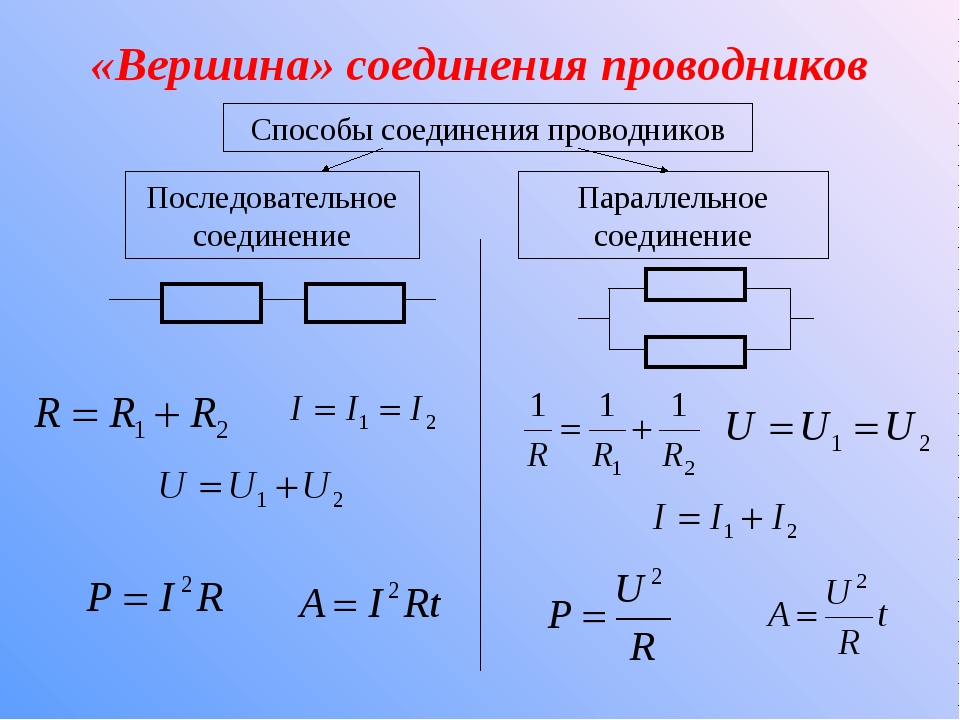 Надо понимать, как правильно подключить конденсатор. Отдельные участки цепи с подключенными конденсаторами можно заменить одним эквивалентным элементом. Он заменит ряд конденсаторов, но должно выполняться обязательное условие: когда напряжение, подводимое к обкладкам эквивалентного конденсатора, равняется напряжению на входе и выходе группы заменяющихся конденсаторов, тогда заряд емкости будет такой же, как и на группе емкостей. Для понимания вопроса, как подключить конденсатор в любой схеме, рассмотрим виды его включения.
Надо понимать, как правильно подключить конденсатор. Отдельные участки цепи с подключенными конденсаторами можно заменить одним эквивалентным элементом. Он заменит ряд конденсаторов, но должно выполняться обязательное условие: когда напряжение, подводимое к обкладкам эквивалентного конденсатора, равняется напряжению на входе и выходе группы заменяющихся конденсаторов, тогда заряд емкости будет такой же, как и на группе емкостей. Для понимания вопроса, как подключить конденсатор в любой схеме, рассмотрим виды его включения.
Параллельное включение конденсаторов в цепь
Параллельное соединение конденсаторов — это когда все пластины подключаются к точкам включения цепи, образовывая батарею емкостей.
Разность потенциалов на пластинах накопителей емкости будет одинаковая, так как они все заряжаются от одного источника тока. В этом случае каждый заряжающийся конденсатор имеет собственный заряд при одинаковой величине, подводимой к ним энергии.
Параллельные конденсаторы, общий параметр количества заряда полученной батареи накопителей, рассчитывается, как сумма всех зарядов, помещающихся на каждой емкости, потому что каждый заряд емкости не зависит от заряда другой емкости, входящей в группу конденсаторов, параллельно включенных в схему.
При параллельном соединении конденсаторов емкость равняется:
Из представленной формулы можно сделать вывод, что всю группу накопителей можно рассматривать как один равноценный им конденсатор.
Конденсаторы, соединенные параллельно, имеют напряжение:
Последовательное включение конденсаторов в цепь
Когда в схеме выполнено последовательное соединение конденсаторов, оно выглядит как цепочка емкостных накопителей, где пластина первого и последнего накопителя емкости (конденсатора) подключены к источнику тока.
Последовательное соединение конденсатора:
При последовательном соединении конденсаторов все устройства этого участка берут одинаковое количество электроэнергии, потому что в процессе участвует первая и последняя пластинка накопителей, а пластины 2, 3 и другие до N проходят зарядку посредством влияния. По этой причине заряд пластины 2 накопителя емкости равняется по значению заряду 1 пластины, но имеет обратный знак. Заряд пластины накопителя 3 равняется значению заряда пластины 2, но так же с обратным знаком, все последующие накопители имеет аналогичную систему заряда.
Заряд пластины накопителя 3 равняется значению заряда пластины 2, но так же с обратным знаком, все последующие накопители имеет аналогичную систему заряда.
Формула нахождения заряда на конденсаторе, схема подключения конденсатора:
Когда выполняется последовательное соединение конденсаторов, напряжение на каждом накопители емкости будет различное, так как в зарядке одинаковым количеством электрической энергии участвуют разные емкости. Зависимость емкости от напряжения такова: чем она меньше, тем большее напряжение необходимо подать на пластины накопителя для его зарядки. И обратная величина: чем выше емкость накопителя, тем меньше требуется напряжения для его зарядки. Можно сделать вывод, что емкость последовательно соединенных накопителей имеет значение для величины напряжения на пластинах — чем она меньше, тем больше напряжения требуется, а также накопители большой емкости требуют меньшего напряжения.
Основное отличие схемы последовательного соединения накопителей емкости в том, что электроэнергия протекает только в одном направлении, а это означает, что в каждом накопителе емкости составленной батареи ток будет одинаковым. В этом виде соединений конденсаторов обеспечивается равномерное накопление энергии независимо от емкости накопителей.
В этом виде соединений конденсаторов обеспечивается равномерное накопление энергии независимо от емкости накопителей.
Группу накопителей емкости можно также на схеме рассматривать как эквивалентный накопитель, на пластины которого подается напряжение, определяемое формулой:
Заряд общего (эквивалентного) накопителя группы емкостных накопителей последовательного соединения равен:
Общему значению емкости последовательно соединенных конденсаторов соответствует выражение:
Смешанное включение емкостных накопителей в схему
Параллельное и последовательное соединение конденсаторов на одном из участков цепи схемы называется специалистами смешанным соединением.
Участок цепи подсоединенных смешанным включением накопителей емкости:
Смешанное соединение конденсаторов в схеме рассчитывается в определенном порядке, который можно представить следующим образом:
- разбивается схема на простые для вычисления участки, это последовательное и параллельное соединение конденсаторов;
- вычисляем эквивалентную емкость для группы конденсаторов, последовательно включенных на участке параллельного соединения;
- проводим нахождение эквивалентной емкости на параллельном участке;
- когда эквивалентные емкости накопителей определены, схему рекомендуется перерисовать;
- рассчитывается емкость получившейся после последовательного включения эквивалентных накопителей электрической энергии.

Накопители емкостей (двухполюсники) включены разными способами в цепь, это дает несколько преимуществ в решении электротехнических задач по сравнению с традиционными способами включения конденсаторов:
- Использование для подключения электрических двигателей и другого оборудования в цехах, в радиотехнических устройствах.
- Упрощение вычисления величин электросхемы. Монтаж выполняется отдельными участками.
- Технические свойства всех элементов не меняются, когда изменяется сила тока и магнитное поле, это применяется для включения разных накопителей. Характеризуется постоянной величиной емкости и напряжения, а заряд пропорционален потенциалу.
Вывод
Разного вида включения конденсаторов в цепь применяются для решения электротехнических задач, в частности, для получения полярных накопителей из нескольких неполярных двухполюсников. В этом случае решением будет соединение группы однополюсных накопителей емкости по встречно-параллельному способу (треугольником). В этой схеме минус соединяется с минусом, а плюс — с плюсом. Происходит увеличение емкости накопителя, и меняется работа двухполюсника.
В этой схеме минус соединяется с минусом, а плюс — с плюсом. Происходит увеличение емкости накопителя, и меняется работа двухполюсника.
Не отображаются имеющиеся вхождения: последовательное параллельное и смешанное соединение конденсаторов, последовательное и параллельное соединение конденсаторов, при параллельном соединении конденсаторов емкость.
Для получения большего спектра емкостей конденсаторы часто соединяют между собой, получают, так называемые батареи конденсаторов. Соединение при этом может быть параллельным, последовательным или комбинированным (смешанным). Рассмотрим случай с двумя конденсаторами.
Последовательное соединение конденсаторов показано на рис. 1
Здесь (рис.1) обкладка одного конденсатора, имеющая отрицательный заряд соединяется с положительной обкладкой следующего конденсатора. При последовательном соединении средние пластины конденсаторов электризуются через влияние, следовательно, их заряды по величине равны и противоположны по знаку. Заряды на этих конденсаторах одинаковы. При этом соединении разности потенциалов складываются:
Заряды на этих конденсаторах одинаковы. При этом соединении разности потенциалов складываются:
При этом имеем:
Получаем, что при последовательном соединении конденсаторов емкость соединения находят как:
Обобщив формулу (3) для N конденсаторов, получаем:
где — электрическая емкость i-го конденсатора.
Последовательное соединение конденсаторов используют тогда, когда для избегания пробоя конденсатора необходимо разность потенциалов распределить между несколькими конденсаторами.
Последовательное соединение конденсаторов показано на рис. 2
При параллельном соединении разности потенциалов между обкладками конденсаторов одинаковы. Суммарный заряд системы равен сумме зарядов на каждом из конденсаторов:
Из сказанного выше получим:
Для батареи из N параллельно соединенных конденсаторов имеем:
Параллельное соединение конденсаторов используют тогда, когда необходимо увеличить емкость конденсатора.
Примеры решения задач
ПРИМЕР 1
| Задание | Получите формулу для расчета емкости слоистого конденсатора. |
| Решение | Конденсатор, который называют слоистым, состоит из двух параллельных металлических обкладок, разделенных несколькими плоскими слоями разных диэлектриков (рис.3). Обозначим диэлектрические проницаемости слоев диэлектриков как . Будем считать, что соответствующая толщина слоя диэлектрика при этом: . Допустим, что между слоями диэлектриков вставлены очень тонкие листы из проводника. От такой процедуры заряды на обкладках конденсатора и напряженности полей в солях диэлектриков останутся неизменными. Останутся без изменений разности потенциалов между обкладками, следовательно, не изменится емкость конденсатора. Но, наличие тонких листов проводника превратит слоистый конденсатор в последовательное соединение конденсаторов. Применим формулы емкости плоского конденсатора: и расчета емкости батареи последовательно соединенных конденсаторов: получаем: |
| Ответ |
ПРИМЕР 2
| Задание | Какой будет емкость соединения конденсаторов (рис.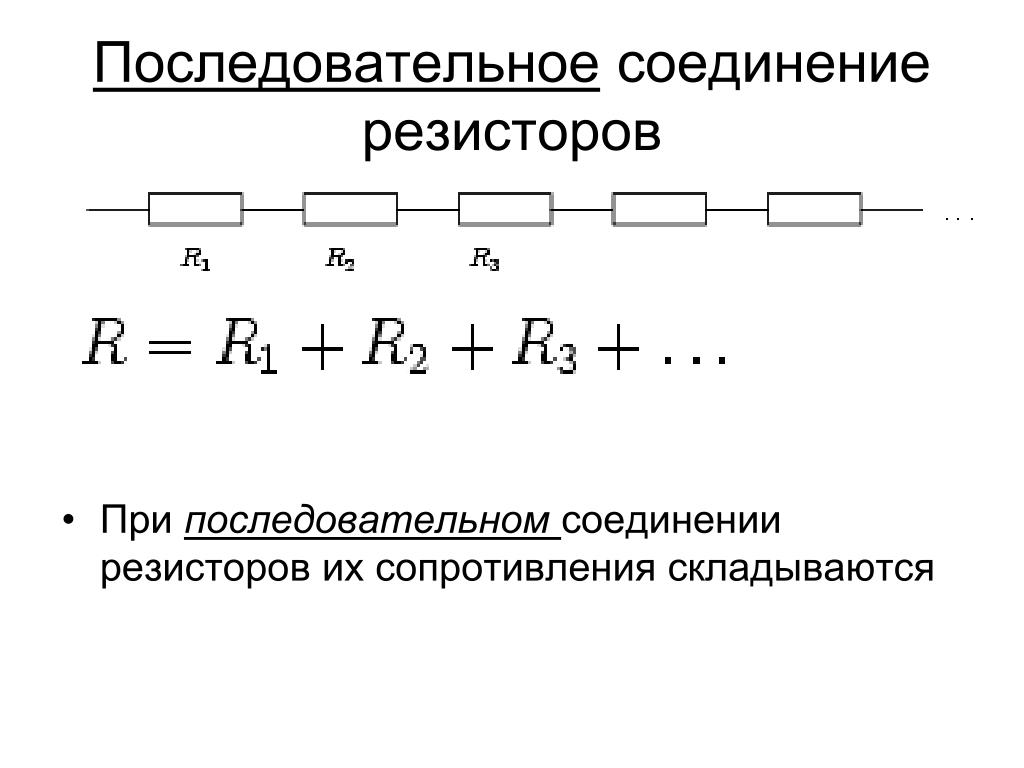 4), если батарея составлена из одинаковых конденсаторов, емкость каждого из них равна Ф. 4), если батарея составлена из одинаковых конденсаторов, емкость каждого из них равна Ф. |
| Решение | Емкость параллельного соединения конденсаторов обозначим как Она равна: |
В этой статье мы попытаемся раскрыть тему соединения конденсаторов разными способам. Из статьи про соединения резисторов мы знаем,что существует последовательное, параллельное и смешанное соединение, это же правило справедливо и для этой статьи. Конденсатор (от лат. слова «condensare» — «уплотнять», «сгущать»)– это очень широко распространённый электрический прибор.
Это два проводника (обкладки), между которыми находится изоляционный материал. Если на него подать напряжение (U), то на его проводниках накопится электрический заряд(Q). Основная его характеристика – ёмкость (C). Свойства конденсатора описываются уравнением Q = UC , заряд на обкладках и напряжение прямо пропорциональны друг другу.
Условное обозначение конденсатора на схемеПусть на конденсатор подается переменное напряжение.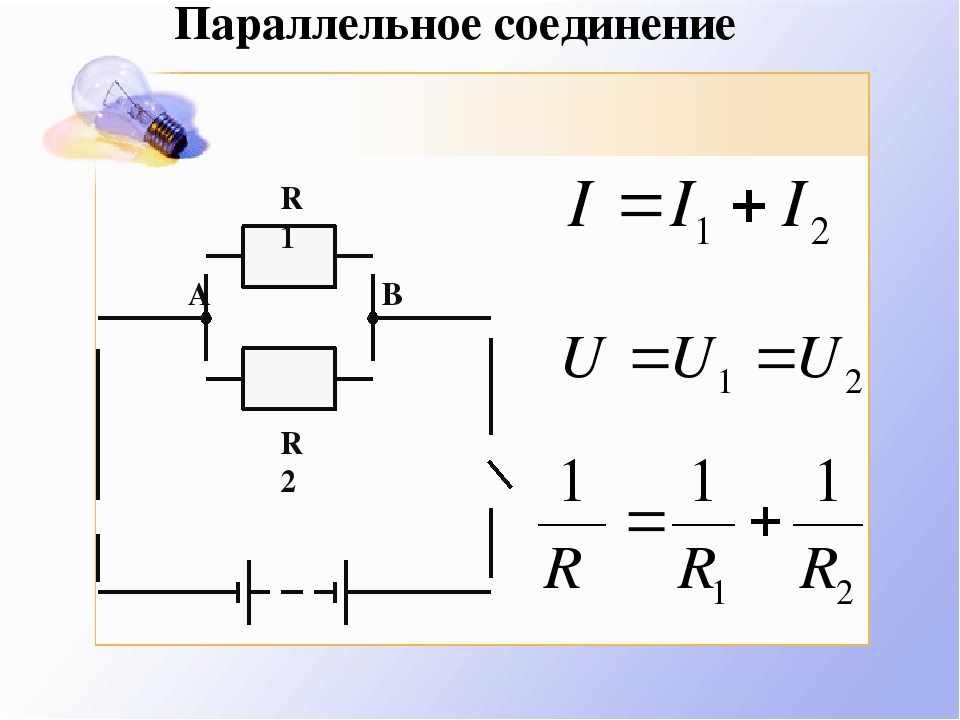 Он заряжается по мере роста напряжения, электрический заряд на обкладках увеличивается. Если напряжение уменьшается, то уменьшается и заряд на его обкладках и он разряжается.
Он заряжается по мере роста напряжения, электрический заряд на обкладках увеличивается. Если напряжение уменьшается, то уменьшается и заряд на его обкладках и он разряжается.
Отсюда следует, что по проводам, соединяющим конденсатор с остальной цепью, электрический ток протекает тогда, когда напряжение на конденсаторе изменяется. При этом не важно, что происходит в диэлектрике между проводниками. Сила тока равна общему заряду, протекшему в единицу времени по подключенному к конденсатору проводу. Она зависит от его емкости и скорости изменения питающего напряжения.
Ёмкость зависит от характеристик изоляции, а также размеров и формы проводника. Единица измерения ёмкости кондёра — фарада (Ф), 1 Ф=1 Кл/В. Однако на практике емкость измеряется чаще в микро- (10-6) или пико- (10-12) фарадах.
В основном используются конденсаторы для построения цепей с частотной зависимостью, для получения мощного короткого электрического импульса, там, где необходимо накапливать энергию. За счёт изменения свойств пространства между обкладками можно использовать их для измерения уровня жидкости.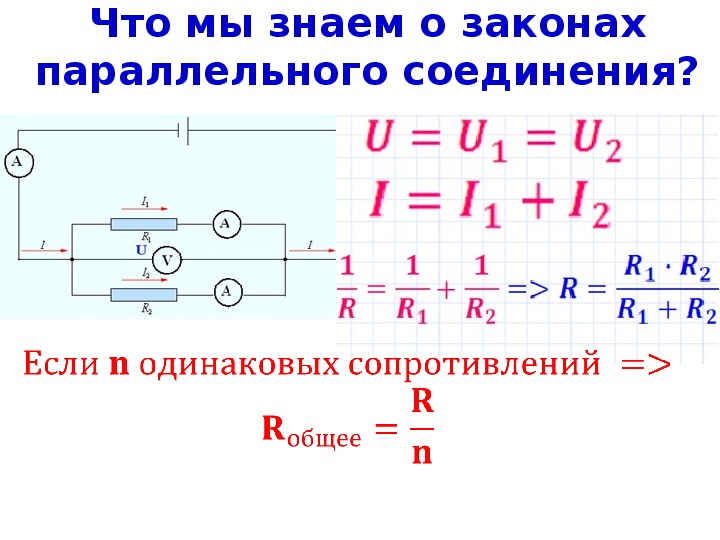
Параллельное соединение
Параллельное соединение – это соединение, при котором выводы всех конденсаторов имеют две общие точки – назовём их входом и выходом схемы. Так все входы объединены в одной точке, а все выходы – в другой, напряжения на всех конденсаторах равны:
Параллельное соединение предполагает распределение полученного от источника заряда на обкладках нескольких конденсаторов, что можно записать так:
Так как напряжение на всех конденсаторах одинаковое, заряды на их обкладках зависят только от ёмкости:
Суммарная емкость параллельной группы конденсаторов:
Суммарная ёмкость такой группы конденсаторов равна сумме емкостей включенных в схему.
Блоки конденсаторов широко используются для повышения мощности и устойчивости работы энергосистем в линиях электропередач. При этом затраты на более мощные элементы линий можно снизить. Повышается стабильность работы ЛЭП, устойчивость ЛЭП к сбоям и перегрузкам.
Последовательное соединение
Последовательное соединение конденсаторов – это их подключение непосредственно друг за другом без разветвлений проводника. От источника напряжения заряды поступают на обкладки первого и последнего в цепи конденсаторов.
В силу электростатической индукции на внутренних обкладках смежных конденсаторов происходит выравнивание заряда на электрически соединённых обкладках смежных конденсаторов, поэтому на них появляются равные по величине и обратные по знаку электрические заряды.
При таком соединении электрические заряды на обкладках отдельных кондёров по величине равны:
Общее напряжение для всей цепи:
Очевидно, что напряжение между проводниками для каждого конденсатора зависит от накопленного заряда и ёмкости, т.е.:
Поэтому эквивалентная ёмкость последовательной цепи равна:
Отсюда следует, что величина, обратная общей емкости, равна сумме величин, обратных емкостям отдельных конденсаторов:
Смешанное соединение
Смешанным соединение конденсаторов называют такое соединение, при котором присутствует соединение последовательное и параллельное одновременно. Чтобы более подробно разобраться, давайте рассмотрим это соединение на примере:
На рисунке видно,что соединены два конденсатора последовательно вверху и внизу и два параллельно. Можно вывести формулу из выше описанных соединении:
Основой любой радиотехники является конденсатор, он используется в самых разнообразных схемах-это и источники питания и применение для аналоговых сигналов хранения данных, а также в телекоммуникационных связи для регулирования частоты.
Конденсаторы, как и резисторы, можно соединять последовательно и параллельно. Рассмотрим соединение конденсаторов: для чего применяются каждая из схем, и их итоговые характеристики.
Эта схема – самая распространенная. В ней обкладки конденсаторов соединяются между собой, образуя эквивалентную емкость, равную сумме соединяемых емкостей.
При параллельном соединении электролитических конденсаторов необходимо, чтобы между собой соединялись выводы одной полярности.
Особенность такого соединения – одинаковое напряжение на всех соединяемых конденсаторах . Номинальное напряжение группы параллельно соединенных конденсаторов равно рабочему напряжению конденсатора группы, у которого оно минимально.
Токи через конденсаторы группы протекают разные: через конденсатор с большей емкостью потечет больший ток.
На практике параллельное соединение применяется для получения емкости нужной величины, когда она выходит за границы диапазона, выпускаемого промышленностью, или не укладываются в стандартный ряд емкостей. В системах регулирования коэффициента мощности (cos ϕ) изменение емкости происходит за счет автоматического подключения или отключения конденсаторов в параллель.
При последовательном соединении обкладки конденсатором соединяются друг к другу, образуя цепочку. Крайние обкладки подключаются к источнику, а ток по всем конденсаторам группы потечет одинаковый.
Эквивалентная емкость последовательно соединенных конденсаторов ограничена самой маленькой емкостью в группе. Объясняется это тем, что как только она полностью зарядится, ток прекратится. Подсчитать общую емкость двух последовательно соединенных конденсаторов можно по формуле
Но применение последовательного соединения для получения нестандартных номиналов емкостей не так распространено, как параллельного.
При последовательном соединении напряжение источника питания распределяется между конденсаторами группы. Это позволяет получить батарею конденсаторов, рассчитанную на большее напряжение , чем номинальное напряжение входящих в нее компонентов. Так из дешевых и небольших по размерам конденсаторов изготавливаются блоки, выдерживающие высокие напряжения.
Еще одна область применения последовательного соединения конденсаторов связана с перераспределением напряжений между ними. Если емкости одинаковы, напряжение делится пополам, если нет – на конденсаторе большей емкости напряжение получается большим. Устройство, работающее на этом принципе, называют емкостным делителем напряжения .
Смешанное соединение конденсаторов
Такие схемы существуют, но в устройствах специального назначения, требующие высокой точности получения величины емкости, а также для их точной настройки.
В электротехнике существуют различные варианты подключения электрических элементов. В частности, существует последовательное, параллельное или смешанное соединение конденсаторов, в зависимости от потребностей схемы. Рассмотрим их.
Параллельное соединение
Параллельное соединение характеризуется тем, что все пластины электрических конденсаторов присоединяются к точкам включения и образовывают собой батареи. В таком случае, во время заряда конденсаторов каждый из них будет иметь различное число электрических зарядов при одинаковом количестве подводимой энергии
Схема параллельного крепленияЕмкость при параллельной установке рассчитывается исходя из емкостей всех конденсаторов в схеме. При этом, количество электрической энергии, поступающей на все отдельные двухполюсные элементы цепи, можно будет рассчитать, суммировав сумму энергии, помещающейся в каждый конденсатор. Вся схема, подключенная таким образом, рассчитывается как один двухполюсник.
C общ = C 1 + C 2 + C 3
Схема – напряжение на накопителях
В отличие от соединения звездой, на обкладки всех конденсаторов попадает одинаковое напряжение. Например, на схеме выше мы видим, что:
V AB = V C1 = V C2 = V C3 = 20 Вольт
Последовательное соединение
Здесь к точкам включения присоединяются контакты только первого и последнего конденсатора.
Схема – схема последовательного соединения
Главной особенностью работы схемы является то, что электрическая энергия будет проходить только по одному направлению, значит, что в каждом из конденсаторов ток будет одинаковым. В такой цепи для каждого накопителя, независимо от его емкости, будет обеспечиваться равное накопление проходящей энергии. Нужно понимать, что каждый из них последовательно соприкасается со следующим и предыдущим, а значит, емкость при последовательном типе может воспроизводиться энергией соседнего накопителя.
Формула, которая отражает зависимость тока от соединения конденсаторов, имеет такой вид:
i = i c 1 = i c 2 = i c 3 = i c 4 , то есть токи проходящие через каждый конденсатор равны между собой.
Следовательно, одинаковой будет не только сила тока, но и электрический заряд. По формуле это определяется как:
Q общ = Q 1 = Q 2 = Q 3
А так определяется общая суммарная емкость конденсаторов при последовательном соединении:
1/C общ = 1/C 1 + 1/C 2 + 1/C 3
Видео: как соединять конденсаторы параллельным и последовательным методом
Смешанное подключение
Но, стоит учитывать, что для соединения различных конденсаторов необходимо учитывать напряжение сети. Для каждого полупроводника этот показатель будет отличаться в зависимости от емкости элемента. Отсюда следует, что отдельные группы полупроводниковых двухполюсников малой емкости будут при зарядке становиться больше, и наоборот, электроемкость большого размера будет нуждаться в меньшем заряде.
Схема: смешанное соединение конденсаторов
Существует также смешанное соединение двух и более конденсаторов. Здесь электрическая энергия распределяется одновременно при помощи параллельного и последовательного подключения электролитических элементов в цепь. Эта схема имеет несколько участков с различным подключением конденсирующих двухполюсников. Иными словами, на одном цепь параллельно включена, на другом – последовательно. Такая электрическая схема имеет ряд достоинств сравнительно с традиционными:
- Можно использовать для любых целей: подключения электродвигателя, станочного оборудования, радиотехнических приборов;
- Простой расчет. Для монтажа вся схема разбивается на отдельные участки цепи, которые рассчитываются по отдельности;
- Свойства компонентов не изменяются независимо от изменений электромагнитного поля, силы тока. Это очень важно при работе с разноименными двухполюсниками. Ёмкость постоянна при постоянном напряжении, но, при этом, потенциал пропорционален заряду;
- Если требуется собрать несколько неполярных полупроводниковых двухполюсников из полярных, то нужно взять несколько однополюсных двухполюсника и соединить их встречно-параллельным способом (в треугольник). Минус к минусу, а плюс к плюсу. Таким образом, за счет увеличения емкости изменяется принцип работы двухполюсного полупроводника.
Напряжение при параллельном соединении резисторов. Сопротивление при параллельном соединении: формула расчета
При решении задач принято преобразовывать схему, так, чтобы она была как можно проще. Для этого применяют эквивалентные преобразования. Эквивалентными называют такие преобразования части схемы электрической цепи, при которых токи и напряжения в не преобразованной её части остаются неизменными.
Существует четыре основных вида соединения проводников: последовательное, параллельное, смешанное и мостовое.
Последовательное соединение
Последовательное соединение – это такое соединение, при котором сила тока на всем участке цепи одинакова. Ярким примером последовательного соединения является старая елочная гирлянда. Там лампочки подключены последовательно, друг за другом. Теперь представьте, одна лампочка перегорает, цепь нарушена и остальные лампочки гаснут. Выход из строя одного элемента, ведет за собой отключение всех остальных, это является существенным недостатком последовательного соединения.
При последовательном соединении сопротивления элементов суммируются.
Параллельное соединение
Параллельное соединение – это соединение, при котором напряжение на концах участка цепи одинаково. Параллельное соединение наиболее распространено, в основном потому, что все элементы находятся под одним напряжением, сила тока распределена по-разному и при выходе одного из элементов все остальные продолжают свою работу.
При параллельном соединении эквивалентное сопротивление находится как:
В случае двух параллельно соединенных резисторов
В случае трех параллельно подключенных резисторов:
Смешанное соединение
Смешанное соединение – соединение, которое является совокупностью последовательных и параллельных соединений. Для нахождения эквивалентного сопротивления нужно, “свернуть” схему поочередным преобразованием параллельных и последовательных участков цепи.
Сначала найдем эквивалентное сопротивление для параллельного участка цепи, а затем прибавим к нему оставшееся сопротивление R 3 . Следует понимать, что после преобразования эквивалентное сопротивление R 1 R 2 и резистор R 3 , соединены последовательно.
Итак, остается самое интересное и самое сложное соединение проводников.
Мостовая схема
Мостовая схема соединения представлена на рисунке ниже.
Для того чтобы свернуть мостовую схему, один из треугольников моста, заменяют эквивалентной звездой.
И находят сопротивления R 1 , R 2 и R 3 .
Последовательное соединение – это соединение двух или более резисторов в форме цепи, в которой каждый отдельный резистор соединяется с другим отдельным резистором только в одной точке.
Параллельное соединение – это соединение, при котором резисторы соединяются между собой обоими контактами. В результате к одной точке (электрическому узлу) может быть присоединено несколько резисторов.
2) Общее сопротивление R общ
При таком соединении, через все резисторы проходит один и тот же электрический ток. Чем больше элементов на данном участке электрической цепи, тем «труднее» току протекать через него. Следовательно, при последовательном соединении резисторов их общее сопротивление увеличивается, и оно равно сумме всех сопротивлений.
Общее сопротивление R общ
При таком соединении, через каждый резистор потечет отдельный ток. Сила данного тока будет обратно пропорциональна сопротивлению резистора. В результате общая проводимость такого участка электрической цепи увеличивается, а общее сопротивление в свою очередь уменьшается.
Таким образом, при параллельном подсоединении резисторов с разным сопротивлением, общее сопротивление будет всегда меньше значения самого маленького отдельного резистора.
Формула эквивалентного общего сопротивления при параллельном соединении резисторов:
Для двух одинаковых резисторов общее сопротивление будет равно половине одного отдельного резистора:
Соответственно, для n одинаковых резисторов общее сопротивление будет равно значению одного резистора, разделенного на n.
3)Электропроводность, электрическая проводимость, проводимость, способность тела пропускать электрический ток под воздействием электрического поля, а также физическая величина, количественно характеризующая эту способность. Тела, проводящие электрический ток, называются проводниками, в отличие от изоляторов.. .
Основная единица измерения сопротивления — Ом. Удельная проводимость — величина обратная сопротивлению, она измеряется в Сименсах, ранее назывшихся mho. Применительно к сыпучим веществам удобнее говорить об особой проводимости, обычно называемой удельной проводимостью.
Удельная проводимость — это проводимость, измеренная между противоположными сторонами куба вещества со стороной 1 см. Единицей данного типа измерений является Сименс/см. При измерении проводимости воды чаще используются более точные мкС/см (микросименс) и мС/см (миллисименс) .
Соответствующие единицы измерения сопротивления (или удельного сопротивления) — Ом/см, МегаОм/см и килоОм/см. При измерении сверхчистой воды чаще используют МегаОм/см, так как это дает более точные результаты. Сопротивление менее чистой воды, как например, водопроводной, измеряют в килоОм/см.
4) Общее сопротивление при последовательном соединении равно сумме сопротивлений Rсумм=R1+R2+R3…
Ток через все сопротивления протекает один (I). Поэтому ток вычисляешь как Отношение напряжения источника U к Rсумм.
Мощность
P=U*I или P=I*I*R (так как U=I*R).
P1=I*I*R1
P2=I*I*R2
P3=I*I*R3
5) мощность электрического тока в цепи, состоящей из параллельно соединенных участков,
равна сумме мощностей на отдельных участках:
При параллельном соединении каждая лампа подсоединяется на своё номинальное напряжение 220 В. при этом в каждой лампе появляется свой номинальный ток, обеспечивающий заданное свечение в соответствии с номинальной мощностью. мощность зависит от сопротивления нити накаливания. чем больше сопротивление нити, тем меньше ток и соответственно меньше номинальная мощность.
при последовательном соединении ток идёт один и тот же в каждой лампе. а напряжение распределяется в зависимости от доли сопротивления каждой лампы по отношению к сопротивлению всей цепи.
для цепи из двух ламп общее напряжение делится.
напряжение на лампе 40 Вт будет 220Х60:(40+60)=132; В.
напряжение на лампе 60 Вт будет 220Х40:(40+60)=80; В.
Параллельным соединением сопротивлений называется такое соединение, когда начала сопротивлений соединены в одну общую точку, а концы — в другую.
Для параллельного соединения сопротивлений характерны следующие свойства:
Напряжения на зажимах всех сопротивлений одинаковы:
U 1 = U 2 = U 3 = U;
— проводимость всех параллельно соединённых сопротивлений равна сумме проводимостей отдельных сопротивлений:
1/R = 1/R 1 + 1/R 2 + 1/R 3 = R 1 R 2 + R 1 R 3 + R 2 R 3 /R 1 R 2 R 3 ,
где R — эквивалентное (равнодействующее) сопротивление трёх сопротивлений (в данном случае R 1 , R 2 и R 3).
Чтобы получить сопротивление такой цепи, надо перевернуть дробь, определяющую величину её проводимости. Следовательно, сопротивление параллельного разветвления из трёх резисторов:
R = R 1 R 2 R 3 /R 1 R 2 + R 2 R 3 + R 1 R 3 .
Эквивалентным сопротивлением называется такое сопротивление, которым можно заменить несколько сопротивлений (включенных параллельно или последовательно), не изменяя величины тока в цепи.
Чтобы найти эквивалентное сопротивление при параллельном соединении, необходимо сложить проводимости всех отдельных участков, т.е. найти общую проводимость. Величина, обратная общей проводимости, и является общим сопротивлением.
При параллельном соединении эквивалентная проводимость равна сумме проводимостей отдельных ветвей, следовательно, эквивалентное сопротивление в этом случае всегда меньше наименьшего из параллельно включенных сопротивлений.
На практике могут быть случаи, когда цепь состоит из более, чем трёх параллельных ветвей. Все полученные соотношения остаются справедливыми и для цепей, состоящих из любого числа параллельно соединённых резисторов.
Найдём эквивалентное сопротивление двух параллельно включенных сопротивлений R 1 и R 2 (см. рис.). Проводимость первой ветви равна 1/R 1 , проводимость второй ветви — 1/R 2 . Общая проводимость:
1/R = 1/R 1 + 1/R 2 .
Приведём к общему знаменателю:
1/R = R 2 + R 1 /R 1 R 2 ,
отсюда эквивалентное сопротивление
R = R 1 R 2 /R 1 + R 2 .
Эта формула и служит для расчётов общего сопротивления цепи, состоящей из двух параллельно включенных сопротивлений.
Таким образом, эквивалентное сопротивление двух параллельно включенных сопротивлений равно произведению этих сопротивлений, делённому на их сумму.
При параллельном соединении n равных сопротивлений R1 эквивалентное сопротивление их будет в n раз меньше, т.е.
R = R 1 /n.
На схеме, изображённой на последнем рисунке, включено пять сопротивлений R 1 по 30 Ом каждое. Следовательно, общее сопротивление R будет
R = R 1 /5 = 30/5 = 6 Ом.
Можно сказать, что сумма токов, подходящих к узловой точке А (на первом рисунке), равна сумме токов, от неё отходящих:
I = I 1 + I 2 + I 3 .
Рассмотрим, как происходит разветвление тока в цепях с сопротивлениями R 1 и R 2 (второй рисунок). Так как напряжение на зажимах этих сопротивлений одинаково, то
U = I 1 R 1 и U = I 2 R 2 .
Левые части этих равенств одинаковы, следовательно, равны и правые части:
I 1 R 1 = I 2 R 2 ,
или
I 1 /I 2 = R 2 /R 1 ,
т.е. ток при параллельном соединении сопротивлений разветвляется обратно пропорционально сопротивлениям ветвей (или прямо пропорционально их проводимостям). Чем больше сопротивление ветви, тем меньше ток в ней, и наоборот.
Таким образом, из нескольких одинаковых резисторов можно получить общий резистор с бОльшей мощностью рассеивания.
При параллельном соединении неодинаковых резисторов в наиболее высокоомном резисторе выделяется наибольшая мощность.
Пример 1. Имеются два сопротивления, включенных параллельно. Сопротивление R 1 = 25 Ом, а R 2 = 50 Ом. Определить общее сопротивление цепи R общ.
Решение. Rобщ = R 1 R 2 /R 1 + R 2 = 25 x 50 / 25 + 50 ≈ 16, 6 Ом.
Пример 2. В ламповом усилителе имеются три лампы, нити накала которых включены параллельно. Ток накала первой лампы I 1 = 1 ампер, второй I 2 = 1, 5 ампера и третьей I 3 = 2, 5 ампера. Определить общий ток цепи накала ламп усилителя I общ.
Решение. I общ = I 1 + I 2 + I 3 = 1 + 1, 5 + 2, 5 = 5 ампер.
Параллельное соединение резисторов часто встречается в радиотехнической аппаратуре. Два или более резисторов включается параллельно в тех случаях, когда ток в цепи слишком большой и может вызвать чрезмерный нагрев резистора.
Примером параллельного соединения потребителей электрической энергии может служить включение электрических ламп обычной осветительной сети, которые соединяются параллельно. Достоинство параллельного соединения потребителей заключается в том, что выключение одного из них не влияет на работу других.
Параллельное соединение резисторов. При параллельном соединении резисторов нескольких приемников они включаются между двумя точками электрической цепи, образуя параллельные ветви (рис. 26, а). Заменяя
лампы резисторами с сопротивлениями R1, R2, R3, получим схему, показанную на рис. 26, б.
При параллельном соединении ко всем резисторам приложено одинаковое напряжение U. Поэтому согласно закону Ома:
I 1 =U/R 1 ; I 2 =U/R 2 ; I 3 =U/R 3 .
Ток в неразветвленной части цепи согласно первому закону Кирхгофа I = I 1 +I 2 +I 3 , или
I = U / R 1 + U / R 2 + U / R 3 = U (1/R 1 + 1/R 2 + 1/R 3) = U / R эк (23)
Следовательно, эквивалентное сопротивление рассматриваемой цепи при параллельном соединении трех резисторов определяется формулой
1/R эк = 1/R 1 + 1/R 2 + 1/R 3 (24)
Вводя в формулу (24) вместо значений 1/R эк, 1/R 1 , 1/R 2 и 1/R 3 соответствующие проводимости G эк, G 1 , G 2 и G 3 , получим: эквивалентная проводимость параллельной цепи равна сумме проводимостей параллельно соединенных резисторов :
G эк = G 1 + G 2 +G 3 (25)
Таким образом, при увеличении числа параллельно включаемых резисторов результирующая проводимость электрической цепи увеличивается, а результирующее сопротивление уменьшается.
Из приведенных формул следует, что токи распределяются между параллельными ветвями обратно пропорционально их электрическим сопротивлениям или прямо пропорционально их проводимостям. Например, при трех ветвях
I 1: I 2: I 3 = 1/R 1: 1/R 2: 1/R 3 = G 1 + G 2 + G 3 (26)
В этом отношении имеет место полная аналогия между распределением токов по отдельным ветвям и распределением потоков воды по трубам.
Приведенные формулы дают возможность определить эквивалентное сопротивление цепи для различных конкретных случаев. Например, при двух параллельно включенных резисторах результирующее сопротивление цепи
R эк =R 1 R 2 /(R 1 +R 2)
при трех параллельно включенных резисторах
R эк =R 1 R 2 R 3 /(R 1 R 2 +R 2 R 3 +R 1 R 3)
При параллельном соединении нескольких, например n, резисторов с одинаковым сопротивлением R1 результирующее сопротивление цепи Rэк будет в n раз меньше сопротивления R1, т.е.
R эк = R1 / n (27)
Проходящий по каждой ветви ток I1, в этом случае будет в п раз меньше общего тока:
I1 = I / n (28)
При параллельном соединении приемников, все они находятся под одним и тем же напряжением, и режим работы каждого из них не зависит от остальных. Это означает, что ток, проходящий по какому-либо из приемников, не будет оказывать существенного влияния на другие приемники. При всяком выключении или выходе из строя любого приемника остальные приемники остаются включенными. Поэтому параллельное соединение имеет существенные преимущества перед последовательным, вследствие чего оно получило наиболее широкое распространение. В частности, электрические лампы и двигатели, предназначенные для работы при определенном (номинальном) напряжении, всегда включают параллельно.
На электровозах постоянного тока и некоторых тепловозах тяговые двигатели в процессе регулирования скорости движения нужно включать под различные напряжения, поэтому они в процессе разгона переключаются с последовательного соединения на параллельное.
Соединение разными способами позволяет получить необходимую величину сопротивления и одного эквивалентного резистора. Всего существует три способы соединения резисторов – последовательное, параллельное и смешанное.
Последовательное соединение резисторовПоследовательное соединение резисторов предполагает использование двух и более радиоэлектронных элемента. Конец предыдущего элемента соединяется с началом последующего и так далее. При последовательном соединении сопротивления и мощности рассеивания всех резисторов складываются.
Рассмотрим следующий пример. Соединим последовательно четыре резистора, каждый имеет R = 1 кОм и мощность рассеивания P = 0,25 Вт .
Rобщ = R1 + R2 + R3 + R4 = 1кОм + 1кОм + 1кОм + 1кОм = 4 кОм.
Pобщ = P1 + P2 + P3 + P4 = 0,25 Вт + 0,25 Вт + 0,25 Вт + 0,25 Вт = 1 Вт.
Таким образом, получается один эквивалентный или общий резистор, имеющий следующие параметры:
Rобщ = 4 кОм; Pобщи = 1 Вт .
В последовательной цепи электрической ток протекает одной и той же величины, поэтому электроны на протяжении всего пути неизбежно наталкиваются на все препятствия в виде сопротивлений. С каждым препятствием уменьшается число свободных зарядов, что приводит к снижению силы электрического тока.
При параллельном соединении резисторов увеличивается количество путей для перемещения свободных зарядов, то есть электронов, из одного участка пути к другому. Поэтому при параллельном соединении резисторов их суммарное (общее, эквивалентное) сопротивление всегда ниже наименьшего сопротивления из всех резисторов.
Величина, обратная сопротивлению называется проводимостью. Проводимость измеряется в сименсах [См] и обозначается большей латинской буквой G .
G = 1/R = 1/Ом = См
Поэтому при выполнении различных подсчетов в электрических цепях, имеющих параллельное соединение, пользуются проводимостью.
Если сопротивления всех параллельно соединенных резисторов равны, то для определения общего Rобщ достаточно R одного из них разделить на их общее количество:
Если R1 = R2 = R3 = R4 = R , то
Rобщ = R/4.
Например, каждый из четырех резисторов имеет R = 10 кОм , тогда
Rобщ = 10 кОм/4 = 2,5 кОм .
Мощности рассеивания суммируются также, как и при последовательном соединении.
Смешанное соединение резисторовСмешанное соединение резисторов представляет собой комбинации последовательных и параллельных соединений. В принципе любую даже самую сложную электрическую цепь, состоящую из источников питания, диодов, и других радиоэлектронных элементов в конкретный момент времени можно заменить резисторами и источниками напряжения, параметры которых изменяются с каждым последующим моментом времени. Для примера изобразим схему, имеющую несколько соединений.
Серияи параллельные резисторы
- Изучив этот раздел, вы сможете:
- Рассчитайте значения общего сопротивления в цепях с последовательным сопротивлением.
- Используйте соответствующие формулы для расчета сопротивления в цепях с параллельным сопротивлением.
- • Вычисление суммы обратных величин.
- • Произведение над суммой.
- Рассчитайте значения общего сопротивления в последовательных / параллельных сетях.
Расчеты в последовательных и параллельных резисторных цепях
Компоненты, включая резисторы в цепи, могут быть соединены вместе двумя способами:
ПОСЛЕДОВАТЕЛЬНО, так что один и тот же ток течет через все компоненты, но на каждом из них может существовать разная разность потенциалов (напряжение).
ПАРАЛЛЕЛЬНО, так что одинаковая разность потенциалов (напряжение) существует на всех компонентах, но каждый компонент может проводить разный ток.
Рис. 4.2.1 Резисторы серии
Рис. 4.2.2 Параллельные резисторы
В любом случае (для резисторов) общее сопротивление той части цепи, которая содержит резисторы, может быть рассчитано с использованием методов, описанных ниже.
Возможность рассчитать суммарное (общее) значение резисторов таким способом позволяет легко вычислить неизвестные значения сопротивления, тока и напряжения для довольно сложных цепей, используя относительно простые методы.Это очень полезно при поиске неисправностей.
ПЕРЕД ДАЛЬНЕЙШЕЙ ДАЛЬНОСТЬЮ ПОПРОБУЙТЕ ИСПОЛЬЗОВАНИЕ ФОРМУЛ ДЛЯ РАСЧЕТА ОБЩИХ ЗНАЧЕНИЙ СЕРИИ И ПАРАЛЛЕЛЬНЫХ РЕЗИСТОРОВ.
Для резисторов в серии:
Общее сопротивление двух или более резисторов, подключенных последовательно , определяется простым сложением индивидуальных значений резисторов, чтобы найти общую сумму (R TOT ):
Для резисторов, включенных параллельно:
Для расчета общего сопротивления цепи, в которой используются параллельные резисторы, можно использовать следующую формулу.
Обратите внимание, однако, что эта формула НЕ дает вам общего сопротивления R TOT . Это дает вам ВЗАИМОДЕЙСТВИЕ R TOT или:
Это совсем другое значение — и НЕ является полным сопротивлением. Он делится на 1, деленный на TOT . Чтобы получить правильное значение для R TOT (которое будет обратным 1 / R TOT , т. Е. TOT /1, просто нажмите соответствующую кнопку на вашем калькуляторе (отмеченную 1 / x или x-1) .
Другой способ расчета параллельных цепей.
Суммарное сопротивление двух резисторов, включенных параллельно , которое не включает обратные, определяется по формуле:
Эту формулу часто называют «произведение над суммой».
Он рассчитывает только ДВА резистора параллельно? Ну да, но это не большая проблема. Если имеется более двух параллельных резисторов, просто выберите два из них и определите общее сопротивление для этих двух — затем используйте это общее сопротивление, как если бы это был один резистор, и составьте еще одну пару с третьим резистором.Определите новую сумму и так далее, пока вы не включите все параллельные резисторы в этой конкретной сети.
О, еще одна вещь, которую следует помнить о произведении над суммой, видите скобки вокруг суммы (нижняя часть) формулы? Это означает, что вы должны решить это, прежде чем использовать его для разделения продукта (верхняя часть) на. Если вы этого не сделаете, ваш ответ будет неправильным.
Звучит сложно? Не совсем, это просто вопрос повторения, и на практике вы не часто встречаетесь с множеством параллельных сетей с гораздо более чем двумя резисторами.Тем не менее, какую формулу вы выберете, зависит от вас, взаимная или сумма продукта.
подсказки
Использование обратного метода
Если вы используете МЕТОД ВЗАИМОДЕЙСТВИЯ для параллельных цепей, НЕ ЗАБУДЬТЕ, когда вы добавили обратные величины отдельных резисторов — вы должны снова найти обратную величину 1 / R1 + 1 / R2 + 1 / R3 = 1 / R TOT , и чтобы найти R TOT , вы должны найти обратное 1 / R TOT .
Упрощающие схемы
Для комбинированных последовательных и параллельных цепей сначала определите участок цепи (последовательный или параллельный).Затем перерисуйте схему, заменив участок, сопротивление которого вы нашли, одним резистором. Теперь у вас есть упрощенная схема, по которой можно найти R TOT .
Вы можете использовать формулу «произведение на сумму»:
Для цепей с более чем двумя параллельными резисторами просто вычислите два параллельных резистора одновременно, используя формулу произведения на сумму, а затем перерисуйте схему, заменив два резистора одним резистором, значение которого является объединенным сопротивлением двух .
Теперь вы можете использовать ваше первое комбинированное значение в качестве единственного резистора со следующим параллельным резистором и так далее. Таким образом, можно выработать большое количество параллельных резисторов с использованием произведения на сумму.
Когда все параллельные резисторы одинакового номинала.
Если несколько одинаковых параллельных резисторов подключены, общее сопротивление будет равно величине резистора, умноженной на обратную величину количества резисторов.
, т. Е. Два параллельных резистора 12 кОм имеют общее сопротивление
12K x 1/2 = 6K
Три параллельно включенных резистора 12 кОм имеют общее сопротивление
12K x 1/3 = 4K и т. Д.
Проверяю ответ
Суммарное значение любого количества параллельных резисторов всегда будет МЕНЬШЕ, чем значение наименьшего отдельного резистора в сети. Используйте этот факт, чтобы проверить свои ответы.
Серияи параллельная комбинация
Попробуйте выполнить несколько расчетов для последовательной и параллельной цепей резисторов. Для этого вам просто нужно использовать информацию на этой странице и на странице «Советы по расчету резисторов». Вас просят вычислить общее сопротивление для каждой цепи.Вы можете выбрать, какую формулу использовать
Вы также можете получить помощь по математике, загрузив нашу бесплатную брошюру «Советы по математике».
Перед тем, как начать, подумайте над этими несколькими советами. Они упростят задачу, если вы будете внимательно им следовать.
1. Разработайте ответы с помощью карандаша и бумаги; перерисуйте схему, над которой работаете.
2. Конечно, ответ — это не просто число, это будет определенное количество Ом, не забудьте указать правильную единицу (например.грамм. Ω, KΩ или MΩ) или ваш ответ не имеет смысла.
3. Когда вы вводите значения в калькулятор, преобразуйте все значения KΩ или MΩ в Ом с помощью клавиши EXP. Если вы здесь ошибетесь, то получите действительно глупые ответы, в тысячи раз слишком большие или слишком маленькие.
Итак, вы прочитали эти инструкции и готовы приступить к работе. Вот способ решить типичную проблему на бумаге, чтобы (с практикой) вы не запутались.
Пример последовательной и параллельной цепи.
Хорошо, есть что вспомнить, так почему бы не попробовать несколько практических вопросов в модуле резисторов 4.5 по определению общего сопротивления некоторых цепей резисторов?
Сопротивление в параллельной цепи
Сопротивление в параллельной цепи
На примерной схеме, рис. 3-44, два резистора подключены параллельно через 5-вольтовую батарею.Каждый имеет значение сопротивления 10 Ом. Формируется полная цепь, состоящая из двух параллельных путей, и ток течет, как показано.
Рисунок 3-44. — Два равных резистора, включенных параллельно.
Вычисление отдельных токов показывает, что через каждое сопротивление проходит половина ампера. Полный ток, протекающий от батареи к переходу резисторов и возвращающийся от резисторов к батарее, равен 1 амперам.
Общее сопротивление цепи можно рассчитать, используя
значений полного напряжения (E T ) и полного тока (I T ).
ПРИМЕЧАНИЕ: С этого момента в примерах задач будут использоваться сокращения и символы для электрических величин.
Дано:
Решение:
Это вычисление показывает, что полное сопротивление составляет 5 Ом; половина номинала любого из двух резисторов.
Поскольку полное сопротивление параллельной цепи меньше, чем у любого из отдельных резисторов, общее сопротивление параллельной цепи не является суммой значений отдельных резисторов, как это было в случае последовательной цепи.Общее сопротивление параллельно включенных резисторов также называется ЭКВИВАЛЕНТНЫМ СОПРОТИВЛЕНИЕМ. ( рэндов эквивалент ). Термины полное сопротивление и эквивалентное сопротивление используются как синонимы.
Существует несколько методов определения эквивалентного сопротивления параллельных цепей. Лучший метод для данной схемы зависит от количества и номинала резисторов. Для схемы, описанной выше, где все резисторы имеют одинаковое значение, используется следующее простое уравнение:
Это уравнение действительно для любого количества параллельных резисторов РАВНОГО ЗНАЧЕНИЯ.
Пример. Параллельно подключены четыре резистора на 40 Ом. Какое у них эквивалентное сопротивление?
Дано:
Решение:
На рис. 3-45 показаны два резистора разного номинала, включенные параллельно. Поскольку показан полный ток, можно рассчитать эквивалентное сопротивление.
Рисунок 3-45. — Пример схемы с неравнопараллельными резисторами.
Дано:
Решение:
Эквивалентное сопротивление цепи, показанной на рисунке 3-45, меньше, чем у любого из двух резисторов (R 1 , R 2 ).Важно помнить, что эквивалентное сопротивление параллельной цепи всегда меньше, чем сопротивление любой ветви.
Эквивалентное сопротивление можно найти, зная отдельные значения сопротивления и напряжение источника. Вычисляя ток каждой ветви, складывая токи ветви для вычисления общего тока и разделив напряжение источника на общий ток, можно найти общий ток. Этот метод хоть и эффективен, но довольно длительный. Более быстрый способ найти эквивалентное сопротивление — использовать общую формулу для параллельных резисторов:
Если вы примените общую формулу к схеме, показанной на рисунке 3-45, вы получите то же значение для эквивалентного сопротивления (2 Ом), что и было полученный в предыдущем расчете, в котором использовались напряжение источника и полный ток.
Дано:
Решение:
Преобразуйте дроби к общему знаменателю.
Поскольку обе стороны являются взаимными (разделенными на одну), игнорируйте взаимную функцию.
Формула, которую вы дали для одинаковых резисторов, включенных параллельно
, является упрощением общей формулы для параллельных резисторов
Существуют и другие упрощения общей формулы для параллельных резисторов, которые можно использовать для расчета общей суммы. или эквивалентное сопротивление в параллельной цепи.
ВЗАИМНЫЙ МЕТОД. — Этот метод основан на взятии обратной величины для каждой стороны уравнения. Это представляет собой общую формулу для резисторов, включенных параллельно:
Эта формула используется для определения эквивалентного сопротивления ряда неравных параллельных резисторов. При решении этих задач вы должны найти наименьший общий знаменатель. Если вы не знаете, как найти наименьший общий знаменатель, освежите его в математике, том 1, NAVEDTRA 10069 (серия).
Пример: три резистора подключены параллельно, как показано на рисунке 3-46. Значения резистора: R 1 = 20 Ом, R 2 = 30 Ом, R 3 = 40 Ом. Какое эквивалентное сопротивление? (Используйте обратный метод.)
Рисунок 3-46. — Пример параллельной схемы с разными резисторами ответвления.
Дано:
Решение:
ПРОДУКТ ПРЕВЫШАЕТ СУММУ. — Удобный способ найти эквивалентное или общее сопротивление двух параллельных резисторов — использовать следующую формулу.
Это уравнение, называемое формулой произведения на сумму, используется так часто, что его следует сохранить в памяти.
Пример. Какое эквивалентное сопротивление резисторов 20 Ом и 30 Ом, подключенных параллельно, как показано на рисунке 3-47?
Рисунок 3-47. — Параллельная схема с двумя неравными резисторами.
Дано:
Решение:
Четыре равных резистора подключены параллельно, каждый резистор имеет омическое значение 100 Ом, каково эквивалентное сопротивление?
Три параллельно соединенных резистора имеют номиналы 12 кОм, 20 кОм и 30 кОм.Какое эквивалентное сопротивление?
Два резистора, соединенных параллельно, имеют номиналы 10 кОм и 30 кОм. Какое эквивалентное сопротивление?
19.3 Параллельные схемы — Физика
Цели обучения раздела
К концу этого раздела вы сможете делать следующее:
- Расшифровка принципиальных схем с параллельными резисторами
- Расчет эквивалентного сопротивления комбинаций резисторов, содержащих последовательные и параллельные резисторы
Поддержка учителей
Поддержка учителей
Цели обучения в этом разделе помогут вашим ученикам овладеть следующими стандартами:
- (5) Научные концепции.Студент знает природу сил в физическом мире. Ожидается, что студент:
- (ж) дизайн. построить и рассчитать в терминах сквозного тока, разности потенциалов, сопротивления и мощности, используемой элементами электрической цепи, соединенными как в последовательной, так и в параллельной комбинациях.
Кроме того, лабораторное руководство по физике в средней школе рассматривает содержание этого раздела лаборатории под названием «Схемы», а также следующие стандарты:
- (5) Учащийся знает природу сил в физическом мире.Ожидается, что студент:
- (F) проектировать, конструировать и рассчитывать в терминах сквозного тока, разности потенциалов, сопротивления и мощности, используемой элементами электрической цепи, соединенными как в последовательной, так и в параллельной комбинациях.
Раздел Основные термины
Параллельные резисторы
В предыдущем разделе мы узнали, что последовательно включенные резисторы — это резисторы, которые подключаются друг за другом. Если вместо этого мы объединим резисторы, подключив их рядом друг с другом, как показано на рисунке 19.16, то говорят, что резисторы подключены параллельно . Резисторы включены параллельно, когда оба конца каждого резистора соединены непосредственно вместе.
Обратите внимание, что верхние части резисторов подключены к одному и тому же проводу, поэтому напряжение на верхушках каждого резистора одинаково. Точно так же все нижние части резисторов подключены к одному и тому же проводу, поэтому напряжение на нижней стороне каждого резистора одинаково. Это означает, что падение напряжения на каждом резисторе одинаковое.В этом случае падение напряжения соответствует номинальному напряжению батареи В, , потому что верхний и нижний провода подключаются к положительной и отрицательной клеммам батареи соответственно.
Хотя падение напряжения на каждом резисторе одинаково, мы не можем сказать то же самое для тока, протекающего через каждый резистор. Таким образом, I1, I2 и I3I1, I2 и I3 не обязательно одинаковы, потому что резисторы R1, R2 и R3R1, R2 и R3 не обязательно имеют одинаковое сопротивление.
Обратите внимание, что три резистора на рисунке 19.16 обеспечивают три разных пути, по которым может течь ток. Это означает, что эквивалентное сопротивление для этих трех резисторов должно быть меньше наименьшего из трех резисторов. Чтобы понять это, представьте, что наименьший резистор — это единственный путь, по которому может течь ток. Теперь добавьте альтернативные пути, подключив другие резисторы параллельно. Поскольку у тока больше путей, общее сопротивление (т. Е. Эквивалентное сопротивление) будет уменьшаться. Следовательно, эквивалентное сопротивление должно быть меньше наименьшего сопротивления параллельных резисторов.
Рисунок 19.16 На левой принципиальной схеме показаны три резистора, включенных параллельно. Напряжение В батареи приложено ко всем трем резисторам. Токи, протекающие через каждую ветвь, не обязательно равны. На правой принципиальной схеме показано эквивалентное сопротивление, которое заменяет три параллельных резистора.
Поддержка учителя
Поддержка учителя
Подчеркните, что напряжение на каждом параллельном резисторе одинаковое, а ток может отличаться; то же самое будет, если пара резисторов будет иметь одинаковое сопротивление.
Чтобы найти эквивалентное сопротивление RequivRequiv трех резисторов R1, R2 и R3R1, R2 и R3, мы применим закон Ома к каждому резистору. Поскольку падение напряжения на каждом резисторе составляет В , мы получаем
V = I1R1, V = I2R2, V = I3R3V = I1R1, V = I2R2, V = I3R319,21
или
I1 = VR1, I2 = VR2, I3 = VR3. I1 = VR1, I2 = VR2, I3 = VR3.19,22
Из сохранения заряда мы также знаем, что три тока I1, I2 и I3I1, I2 и I3 должны складываться, чтобы получить ток I , который проходит через батарею.Если бы это было не так, ток должен был бы таинственным образом создаваться или разрушаться где-то в цепи, что физически невозможно. Таким образом, имеем
Я = I1 + I2 + I3. I = I1 + I2 + I3.19,23
Вставка выражений для I1, I2 и I3I1, I2 и I3 в это уравнение дает
I = VR1 + VR2 + VR3 = V (1R1 + 1R2 + 1R3) I = VR1 + VR2 + VR3 = V (1R1 + 1R2 + 1R3)19,24
или
V = I (11 / R1 + 1 / R2 + 1 / R3). V = I (11 / R1 + 1 / R2 + 1 / R3).19,25
Эта формула представляет собой закон Ома, где множитель в скобках является эквивалентным сопротивлением.
V = I (11 / R1 + 1 / R2 + 1 / R3) = IRэкв. V = I (11 / R1 + 1 / R2 + 1 / R3) = IRequiv.19,26
Таким образом, эквивалентное сопротивление для трех параллельно включенных резисторов составляет
Требование = 11 / R1 + 1 / R2 + 1 / R3. Требование = 11 / R1 + 1 / R2 + 1 / R3.19,27
Та же самая логика работает для любого количества резисторов, включенных параллельно, поэтому общая форма уравнения, которая дает эквивалентное сопротивление резисторов N , подключенных параллельно, составляет
Требование = 11 / R1 + 1 / R2 + ⋯ + 1 / RN. Требование = 11 / R1 + 1 / R2 + ⋯ + 1 / RN.19,28
Рабочий пример
Найдите ток через параллельные резисторы
Три схемы ниже эквивалентны.Если номинальное напряжение батареи Vbattery = 3VVbattery = 3V, каково эквивалентное сопротивление цепи и какой ток проходит через цепь?
Стратегия
Три резистора подключены параллельно, и падение напряжения на них составляет В АКБ . Таким образом, мы можем применить уравнение для эквивалентного сопротивления резисторов, включенных параллельно, которое принимает вид
Требование = 11 / R1 + 1 / R2 + 1 / R3. Требование = 11 / R1 + 1 / R2 + 1 / R3.19,29
Схема с эквивалентным сопротивлением показана ниже.Как только мы узнаем эквивалентное сопротивление, мы можем использовать закон Ома, чтобы найти ток в цепи.
Решение
Вставка заданных значений сопротивления в уравнение эквивалентного сопротивления дает
Требуемое = 11 / R1 + 1 / R2 + 1 / R3 = 11/10 Ом + 1/25 Ом + 1/15 Ом = 4,84 Ом Требуемое = 11 / R1 + 1 / R2 + 1 / R3 = 11/10 Ом + 1/25 Ом + 1/15 Ом = 4,84 Ом.19,30
Таким образом, ток в цепи равен
V = IRI = VR = 3 В 4,84 Ом = 0,62 А. V = IRI = VR = 3 В 4,84 Ом = 0,62 А.19,31
Обсуждение
Хотя 0.62 А протекает через всю цепь, обратите внимание, что этот ток не проходит через каждый резистор. Однако, поскольку электрический заряд должен сохраняться в цепи, сумма токов, проходящих через каждую ветвь цепи, должна составлять ток, проходящий через батарею. Другими словами, мы не можем волшебным образом создать заряд где-нибудь в цепи и добавить этот новый заряд к току. Давайте проверим это рассуждение, используя закон Ома, чтобы найти ток через каждый резистор.
I1 = VR1 = 3 В 10 Ом = 0.30AI2 = VR2 = 3V25Ω = 0.12AI3 = VR3 = 3V15Ω = 0.20AI1 = VR1 = 3V10Ω = 0.30AI2 = VR2 = 3V25Ω = 0.12AI3 = VR3 = 3V15Ω = 0.20A19,32
Как и ожидалось, эти токи в сумме дают 0,62 A, который представляет собой обнаруженный полный ток, проходящий через эквивалентный резистор. Также обратите внимание, что самый маленький резистор имеет наибольший ток, протекающий через него, и наоборот.
Рабочий пример
Рассуждения с параллельными резисторами
Без каких-либо расчетов, каково эквивалентное сопротивление трех одинаковых резисторов R , включенных параллельно?
Стратегия
Три идентичных резистора R , включенных параллельно, образуют три идентичных пути, по которым может течь ток.Таким образом, току протекать через эти резисторы в три раза легче, чем через один из них.
Решение
Если протекать через три одинаковых резистора R в три раза легче, чем через один из них, эквивалентное сопротивление должно быть втрое меньше: R /3.
Обсуждение
Давайте проверим наши рассуждения, вычислив эквивалентное сопротивление трех одинаковых резисторов R , включенных параллельно.Уравнение эквивалентного сопротивления параллельно включенных резисторов дает
Требуется = 11 / R + 1 / R + 1 / R = 13 / R = R3. Требуется = 11 / R + 1 / R + 1 / R = 13 / R = R3.19,33
Таким образом, наши рассуждения были правильными. В общем, когда доступно больше путей, по которым может течь ток, эквивалентное сопротивление уменьшается. Например, если у нас есть идентичные резисторы R , подключенные параллельно, эквивалентное сопротивление будет R /10.
Практические задачи
10.Три резистора 10, 20 и 30 Ом подключены параллельно.Какое эквивалентное сопротивление?
- Эквивалентное сопротивление 5,5 Ом
- Эквивалентное сопротивление 60 Ом
- Эквивалентное сопротивление 6 × 103 Ом
- Эквивалентное сопротивление 6 × 104 Ом
Если падение напряжения на 5 \ text {-V} происходит на R_1, а R_1 подключен параллельно к R_2, каково падение напряжения на R_2?
- Падение напряжения на 0 \, \ text {V}.
- Падение напряжения на 2,5 \, \ text {V}.
- Падение напряжения на нем 5 \, \ text {V}.
- Падение напряжения на нем 10 \, \ text {V}.
Резисторы параллельно и последовательно
Более сложные соединения резисторов иногда представляют собой просто комбинации последовательного и параллельного. Комбинации последовательных и параллельных резисторов могут быть уменьшены до одного эквивалентного сопротивления с помощью техники, показанной на рисунке 19.17. Различные части идентифицируются как последовательные или параллельные, сокращаются до их эквивалентов и далее уменьшаются до тех пор, пока не останется единственное сопротивление. Процесс занимает больше времени, чем труден.
Рисунок 19.17 Эта комбинация из семи резисторов имеет как последовательные, так и параллельные части. Каждое из них идентифицируется и приводится к эквивалентному сопротивлению, а затем уменьшается до тех пор, пока не будет достигнуто единичное эквивалентное сопротивление.
Поддержка учителей
Поддержка учителей
Предупреждение о неправильном представлении
У студентов может возникнуть соблазн немедленно сложить R1R1 и R7R7 вместе, потому что они кажутся последовательными.Обратите внимание, что R1R1 включен последовательно с параллельной комбинацией R7R7 и всех резисторов справа от R7R7. Таким образом, перед добавлением к R1R1 необходимо найти эквивалентное сопротивление этой параллельной комбинации.
Поддержка учителей
Поддержка учителей
Рассмотрите этот пример вместе с учащимися, чтобы убедиться, что они понимают сокращение, которое происходит на каждом этапе.
Давайте проработаем четыре шага на рисунке 19.17, чтобы уменьшить семь резисторов до одного эквивалентного резистора.Чтобы не отвлекать внимание от алгебры, предположим, что каждый резистор имеет сопротивление 10 Ом. На шаге 1 мы уменьшаем два набора параллельных резисторов, обведенных синей пунктирной петлей. Верхний набор имеет три резистора, включенных параллельно, и будет уменьшен до одного эквивалентного резистора RP1RP1. Нижний набор имеет два резистора, включенных параллельно, и будет уменьшен до одного эквивалентного резистора RP2RP2. Используя уравнение эквивалентного сопротивления параллельно включенных резисторов, получаем
RP1 = 11 / R2 + 1 / R3 + 1 / R4 = 11 / 10Ω + 1 / 10Ω + 1 / 10Ω = 103Ω RP2 = 11 / R5 + 1 / R6 = 11 / 10Ω + 1 / 10Ω = 5Ω.RP1 = 11 / R2 + 1 / R3 + 1 / R4 = 11 / 10Ω + 1 / 10Ω + 1 / 10Ω = 103Ω RP2 = 11 / R5 + 1 / R6 = 11 / 10Ω + 1 / 10Ω = 5Ω.19,34
Эти два эквивалентных сопротивления обведены красной пунктирной петлей после шага 1. Они включены последовательно, поэтому мы можем использовать уравнение для эквивалентного сопротивления последовательно включенных резисторов, чтобы уменьшить их до одного эквивалентного сопротивления RS1RS1. Это делается на шаге 2, в результате получается
RS1 = RP1 + RP2 = 103 Ом + 5 Ом = 253 Ом. RS1 = RP1 + RP2 = 103 Ом + 5 Ом = 253 Ом.19,35
Эквивалентный резистор RS1RS1 появляется в зеленой пунктирной петле после шага 2.Этот резистор включен параллельно резистору R7R7, поэтому пара может быть заменена эквивалентным резистором RP3RP3, который равен
. RP3 = 11 / RS1 + 1 / R7 = 13 / 25Ω + 1 / 10Ω = 5011Ω. RP3 = 11 / RS1 + 1 / R7 = 13 / 25Ω + 1 / 10Ω = 5011Ω.19,36
Это делается на шаге 3. Резистор RP3RP3 включен последовательно с резистором R1R1, как показано в фиолетовой пунктирной петле после шага 3. Эти два резистора объединяются на последнем шаге, чтобы сформировать окончательный эквивалент резистора RequivRequiv, что составляет
Requiv = R1 + RP3 = 10 Ом + 5011 Ом = 16011 Ом.Requiv = R1 + RP3 = 10 Ом + 5011 Ом = 16011 Ом.19,37
Таким образом, вся комбинация из семи резисторов может быть заменена одним резистором с сопротивлением около 14,5 Ом.
Это была большая работа, и вы можете спросить, зачем мы ее делаем. Для нас важно знать эквивалентное сопротивление всей цепи, чтобы мы могли рассчитать ток, протекающий по цепи. Закон Ома говорит нам, что ток, протекающий по цепи, зависит от сопротивления цепи и напряжения в цепи.Но чтобы узнать силу тока, мы должны сначала узнать эквивалентное сопротивление.
Вот общий подход к поиску эквивалентного резистора для любой произвольной комбинации резисторов:
- Определите группу резисторов, которые включены только параллельно или только последовательно.
- Для резисторов, включенных последовательно, используйте уравнение для эквивалентного сопротивления резисторов, подключенных последовательно, чтобы уменьшить их до одного эквивалентного сопротивления. Для резисторов, подключенных параллельно, используйте уравнение для эквивалентного сопротивления резисторов, подключенных параллельно, чтобы уменьшить их до одного эквивалентного сопротивления.
- Нарисуйте новую принципиальную схему с резисторами из шага 1, замененными их эквивалентными резисторами.
- Если в цепи осталось более одного резистора, вернитесь к шагу 1 и повторите. В противном случае все готово.
Развлечение в физике
Робот
Роботы захватывают наше коллективное воображение уже более века. Теперь мечта о создании умных машин для выполнения нашей грязной работы, а иногда и просто для того, чтобы составить нам компанию, становится реальностью. Робототехника стала огромной областью исследований и разработок, причем некоторые технологии уже коммерциализированы.Подумайте, например, о небольших автономных пылесосах.
На рис. 19.18 показаны лишь некоторые из множества различных форм, которые могут принимать роботы. Самые продвинутые роботы-гуманоиды могут ходить, наливать напитки и даже танцевать (хотя и не очень изящно). Другие роботы вдохновлены биологией, например, собачий робот , показанный на средней фотографии рис. 19.18. Этот робот может нести сотни фунтов груза по пересеченной местности. Фотография справа на рис. 19.18 показывает внутреннюю работу блока M, , разработанного Массачусетским технологическим институтом.Эти простые на вид блоки содержат инерционные колеса и электромагниты, которые позволяют им вращаться, переворачиваться в воздух и соединяться друг с другом в самых разных формах. Обмениваясь беспроводной связью между собой, они самостоятельно собираются в различные формы, такие как столы, стулья и, возможно, когда-нибудь даже здания.
Все роботы включают в себя огромное количество физики и инженерии. Простое наливание напитка было освоено роботами совсем недавно, после более 30 лет исследований и разработок! Баланс и выбор времени, которые мы, люди, считаем само собой разумеющимися, на самом деле являются очень сложной задачей, требующей отличного баланса, ловкости и обратной связи.Чтобы справиться с этим, требуются датчики для обнаружения баланса, вычислительная мощность для анализа данных и передачи соответствующих компенсирующих действий, а также соединения и приводы для выполнения требуемых действий.
Помимо определения силы тяжести или ускорения, роботы могут содержать несколько различных датчиков для обнаружения света, звука, температуры, запаха, вкуса и т. Д. Все эти устройства основаны на физических принципах, которые вы изучаете в этом тексте. Например, оптика, используемая для машинного зрения, аналогична оптике, используемой в ваших цифровых камерах: пиксельные полупроводниковые детекторы, в которых свет преобразуется в электрические сигналы.Для определения температуры можно использовать простые термисторы, которые представляют собой резисторы, сопротивление которых изменяется в зависимости от температуры.
Сегодня построить робота гораздо проще, чем несколько лет назад. Многие компании сейчас предлагают комплекты для сборки роботов. Они варьируются по сложности, от чего-то подходящего для младших школьников до чего-то, что бросает вызов лучшим профессиональным инженерам. Если интересно, вы можете легко найти их в Интернете и начать создавать своего собственного робота уже сегодня.
Рис. 19.18 Роботы бывают разных форм и размеров, от классического гуманоида типа до собачьих роботов и небольших кубиков, которые самостоятельно собираются для выполнения различных задач.
Watch Physics
Параллельные резисторы
В этом видео лектор обсуждает простую схему с батареей и парой резисторов, подключенных параллельно. Он подчеркивает, что электроны текут в направлении, противоположном положительному току, а также использует тот факт, что напряжение одинаково во всех точках идеального провода.Вывод очень похож на то, что делается в этом тексте, но лектор хорошо его проходит, объясняя каждый шаг.
Проверка захвата
Верно или неверно. На принципиальной схеме мы можем предположить, что напряжение одинаково в каждой точке данного провода.
- ложь
- правда
Watch Physics
Последовательные и параллельные резисторы
В этом видео показано, как рассчитать эквивалентное сопротивление цепи, содержащей резисторы, включенные параллельно и последовательно.Лектор использует тот же подход, что и описанный выше, для поиска эквивалентного сопротивления.
Проверка захвата
Представьте, что N одинаковых резистора соединены параллельно. Каждый резистор имеет сопротивление R . Какое эквивалентное сопротивление для этой группы параллельных резисторов?
- Эквивалентное сопротивление ( R ) N .
- Эквивалентное сопротивление — NR.
- Эквивалентное сопротивление RN.РН.
- Эквивалентное сопротивление — NR.NR.
Рабочий пример
Найдите ток через цепь сложного резистора
Батарея в схеме ниже имеет номинальное напряжение 10 В. Какой ток течет по цепи и в каком направлении?
Стратегия
Примените стратегию поиска эквивалентного сопротивления, чтобы заменить все резисторы одним эквивалентным сопротивлением, затем используйте закон Ома, чтобы найти ток через эквивалентный резистор.
Решение
Комбинацию резисторов R4R4 и R5R5 можно уменьшить до эквивалентного сопротивления
RP1 = 11 / R4 + 1 / R5 = 11/45 Ом + 1/60 Ом = 25,71 Ом R. RP1 = 11 / R4 + 1 / R5 = 11/45 Ом + 1/60 Ом = 25,71 Ом R.19,38
Замена R4R4 и R5R5 с этим эквивалентным сопротивлением дает схему ниже.
Теперь мы заменим два верхних резистора R2R2 и R3R3 эквивалентным резистором RS1RS1 и два нижних резистора RP1RP1 и R6R6 их эквивалентным резистором RS2RS2.Эти резисторы включены последовательно, поэтому мы складываем их вместе, чтобы найти эквивалентное сопротивление.
RS1 = R2 + R3 = 50 Ом + 30 Ом = 80 Ом RS2 = RP1 + R6 = 25,71 Ом + 20 Ом = 45,71 Ом RS1 = R2 + R3 = 50 Ом + 30 Ом = 80 Ом RS2 = RP1 + R6 = 25,71 Ом + 20 Ом = 45,71 Ом19,39
Замена соответствующих резисторов на их эквивалентные резисторы дает схему, приведенную ниже.
Теперь замените два резистора RS1 и RS2RS1 и RS2, которые включены параллельно, на их эквивалентные резисторы RP2RP2. Сопротивление RP2RP2 —
RP2 = 11 / RS1 + 1 / RS2 = 11/80 Ом + 1/45.71 Ом = 29,09 Ом. RP2 = 11 / RS1 + 1 / RS2 = 11/80 Ом + 1 / 45,71 Ом = 29,09 Ом.19,40
Обновление принципиальной схемы путем замены RS1 и RS2 RS1 и RS2 с этим эквивалентным сопротивлением дает схему ниже.
Наконец, мы объединяем резисторы R1 и RP2R1 и RP2, которые включены последовательно. Эквивалентное сопротивление: RS3 = R1 + RP2 = 75 Ом + 29,09 Ом = 104,09 Ом. RS3 = R1 + RP2 = 75 Ом + 29,09 Ом = 104,09 Ом. Окончательная схема показана ниже.
Теперь мы используем закон Ома, чтобы найти ток в цепи.
V = IRS3I = VRS3 = 10V104.09Ω = 0,096AV = IRS3I = VRS3 = 10V 104.09Ω = 0,096A19,41
Ток идет от положительной клеммы батареи к отрицательной клемме батареи, поэтому в этой цепи он течет по часовой стрелке.
Обсуждение
Этот расчет может показаться довольно длинным, но, немного попрактиковавшись, вы сможете объединить несколько этапов. Также обратите внимание, что при вычислении учитывались лишние значащие цифры. Только в конце окончательный результат был округлен до двух значащих цифр.
Рабочий пример
Странные электрические схемы
Иногда вы можете встретить принципиальные схемы, которые нарисованы не очень аккуратно, например, схему, показанную ниже.Эта принципиальная схема больше похожа на то, как настоящая схема может появиться на лабораторном столе. Каково эквивалентное сопротивление резисторов на этой диаграмме, если каждый резистор имеет сопротивление 10 Ом и номинальное напряжение батареи 12 В.
Стратегия
Давайте перерисуем эту принципиальную схему, чтобы было понятнее. Затем мы применим описанную выше стратегию для расчета эквивалентного сопротивления.
Решение
Чтобы перерисовать диаграмму, рассмотрите рисунок ниже.В верхней схеме синие резисторы образуют путь от положительной клеммы батареи к отрицательной. Параллельно с этой цепью расположены красные резисторы, которые составляют еще один путь от положительной к отрицательной клемме батареи. Синий и красный пути показаны более четко на нижней принципиальной схеме. Обратите внимание, что как на верхней, так и на нижней схемах синий и красный пути соединяют положительную клемму аккумулятора с отрицательной клеммой аккумулятора.
Теперь легче увидеть, что R1 и R2R1 и R2 подключены параллельно, а параллельная комбинация находится последовательно с R4R4. Эта комбинация, в свою очередь, параллельна последовательной комбинации R3 и R5R3 и R5. Сначала мы вычисляем синюю ветвь, которая содержит R1, R2 и R4R1, R2 и R4. Эквивалентное сопротивление
Rblue = 11 / R1 + 1 / R2 + R4 = 11 / 10Ω + 1 / 10Ω + 10Ω = 15Ω. Rblue = 11 / R1 + 1 / R2 + R4 = 11 / 10Ω + 1 / 10Ω + 10Ω = 15Ω.19,42
где мы показываем вклад от параллельной комбинации резисторов и от последовательной комбинации резисторов.Теперь рассчитаем эквивалентное сопротивление красной ветви, которое составляет
. Rred = R3 + R5 = 10 Ом + 10 Ом = 20 Ом. Rred = R3 + R5 = 10 Ом + 10 Ом = 20 Ом.19,43
Вставка этих эквивалентных резисторов в схему дает схему ниже.
Эти два резистора включены параллельно, поэтому их можно заменить одним эквивалентным резистором с сопротивлением
Requiv = 11 / Rblue + 1 / Rred = 11 / 15Ω + 1 / 20Ω = 8,6Ω. Requiv = 11 / Rblue + 1 / Rred = 11 / 15Ω + 1 / 20Ω = 8.6Ω.19,44
Окончательная эквивалентная схема показана ниже.
Обсуждение
Найти эквивалентное сопротивление было проще благодаря понятной принципиальной схеме. Вот почему мы стараемся делать четкие принципиальные схемы, на которых резисторы, включенные параллельно, выстроены параллельно друг другу и в одном и том же горизонтальном положении на схеме.
Теперь мы можем использовать закон Ома, чтобы найти ток, проходящий через каждую ветвь этой цепи. Рассмотрим принципиальную схему с RblueRblue и RredRred. Напряжение на каждой из этих ветвей составляет 12 В (т.е.е. номинальное напряжение аккумулятора). Ток в синей ветке —
Iblue = VRblue = 12В15Ω = 0,80A Синий = VRblue = 12V15Ω = 0,80A.19,45
Ток через красную ветвь
Ired = VRred = 12 В20 Ом = 0,60 А. Ired = VRred = 12 В 20 Ом = 0,60 А.19,46
Ток, протекающий через батарею, должен быть суммой этих двух токов (вы понимаете, почему?), Или 1,4 А.
Практические задачи
12.Какова формула эквивалентного сопротивления двух параллельных резисторов с сопротивлением R 1 и R 2 ?
- Эквивалентное сопротивление двух параллельных резисторов Reqv = R1 + R2 Reqv = R1 + R2
- Эквивалентное сопротивление двух параллельных резисторов Reqv = R1 × R2Reqv = R1 × R2
- Эквивалентное сопротивление двух параллельных резисторов Reqv = R1-R2Reqv = R1-R2
- Эквивалентное сопротивление двух параллельных резисторов Reqv = 11 / R1 + 1 / R2Reqv = 11 / R1 + 1 / R2
Рисунок 19.19
Какое эквивалентное сопротивление для двух показанных резисторов?
- Эквивалентное сопротивление 20 Ом
- Эквивалентное сопротивление 21 Ом
- Эквивалентное сопротивление 90 Ом
- Эквивалентное сопротивление 1,925 Ом
Проверьте свое понимание
14.Падение напряжения на параллельных резисторах ________.
- то же для всех резисторов
- больше для больших резисторов На
- меньше для резисторов большего размера
- больше для меньших резисторов
Рассмотрим схему из параллельных резисторов. Наименьший резистор — 25 Ом. Каков верхний предел эквивалентного сопротивления?
- Верхний предел эквивалентного сопротивления составляет 2,5 Ом.
- Верхний предел эквивалентного сопротивления составляет 25 Ом.
- Верхний предел эквивалентного сопротивления составляет 100 Ом.
- Нет верхнего предела.
— обзор
Метка из задачи (3) должна быть установлена на днище металлического кузова автомобиля с помощью прокладки из пенопласта толщиной 5 мм.Рядом с металлической поверхностью серийная модель антенны становится 1,5 пФ и 10 нГн последовательно с 1 Ом. Напряжение холостого хода уменьшается от его значения в разомкнутом состоянии на 2 sin (2π (0,5 / 8,2)) = 0,19. Не обращайте внимания на любые изменения в соответствующих катушках индуктивности и рассчитайте значение напряжения, подаваемого на ИС, предполагая, что 1 В присутствует для того же освещения антенны с открытой меткой.
В (IC) = ______________ В
Что такое коэффициент передачи мощности?
τ = ______________
Если тегу нужно 0.5 В для включения, как повлияет на дальность чтения?
Вывод последовательного параллельного преобразования: представьте, что у нас есть нагрузка (например, наша интегральная схема), подключенная через тройник, который мы моделируем как шунтирующий импеданс Z sh , за которым следует последовательное сопротивление Z ser . Можем ли мы найти значения Z shtr и Z sertr и, возможно, преобразованную нагрузку Z ldtr , такие, что если смотреть слева, серия — шунт и шунт –Серийные схемы имеют одинаковый импеданс, независимо от нагрузки?
Если это можно сделать, то он должен работать для двух ограничивающих нагрузок: разомкнутой цепи и короткого замыкания ( Z L = 0 и ∞).Используя формулы для последовательного и параллельного импедансов (Приложение 3), мы можем получить выражения для входного импеданса для нагрузок короткого замыкания и холостого хода, как показано на следующем рисунке
Теперь мы требуем, чтобы преобразованные версии были равны непреобразованные версии в обоих случаях:
Zsertr = ZserZshZser + Zsh; Zsh = Zsertr + Zshtr
Покажите, что преобразованный импеданс шунта равен:
Zshtr = (Zsh) 2Zser + Zsh
Обратите внимание, что оба они могут быть записаны аналогично:
Zshtr = βZsh; Zsertr = βZser; β≡ZshZser + Zsh
Используя этот факт, мы можем написать утверждение, что полное сопротивление одинаково для ЛЮБОЙ нагрузки как:
Zsh (Zser + ZL ) Zsh (Zser + ZL) = Zsertr + ZshtrZLtrZshtrZLtrZsh (Zser + ZL) Zsh (Zser + ZL) = βZser + βZshZLtrβZshZLtr
Теперь самое сложное: ПОКАЗАТЬ, что это уравнение всегда верно, если:
ZLtr
ZLtr Может быть очень полезно отметить, что:
βZL + Zsh = β (ZL + Zser + Zsh)
Калькулятор и формулы для параллельного расчета резистора и индуктора
Расчет резистора и катушки индуктивности, включенных параллельно
Компьютер рассчитывает напряжения, мощность, ток, импеданс и реактивное сопротивление. для резистора и катушки индуктивности, включенных параллельно.
|
\ (\ Displaystyle I \) Общий ток \ (\ Displaystyle I_R \) Ток через резистор \ (\ Displaystyle I_L \) Ток через катушку \ (\ Displaystyle Y \) Допуск [1 / Z] \ (\ Displaystyle X_L \) Индуктивное реактивное сопротивление \ (\ Displaystyle R \) Эффективное сопротивление \ (\ Displaystyle Z \) Импеданс \ (\ Displaystyle G \) Поведение [1 / R] \ (\ Displaystyle B_L \) Подвеска [1 / X L ] \ (\ Displaystyle Р \) Реальная власть \ (\ Displaystyle S \) Полная мощность \ (\ Displaystyle Q_L \) Индуктивная реактивная мощность \ (\ Displaystyle φ \) Фазовый сдвиг в °
Формулы и описание параллельного RL
Полное сопротивление параллельной цепи RL в переменном токе называется сопротивление Z.Закон Ома применим ко всей цепи.
Ток и напряжение синфазны на омическом сопротивлении. Индуктивное сопротивление конденсатора отстает текущее напряжение на −90 °.
Полный ток I — это сумма геометрически сложенных парциальных токов. Для этого оба парциальных потока образуют катеты прямоугольного треугольника. Его гипотенуза соответствует полному току I.2} \)
Треугольник проводимости
При параллельном подключении парциальные токи ведут себя как значения проводимости сопротивлений.2} \)
Треугольник сопротивления
\ (\ Displaystyle Z = \ гидроразрыва {R · X_L} {\ sqrt {R ^ 2 + {X_L} ^ 2}} \) \ (\ Displaystyle = \ гидроразрыва {1} {Y} \) \ (\ Displaystyle R = \ гидроразрыва {Z · X_L} {\ sqrt {Z ^ 2- {X_L} ^ 2}} \) \ (\ Displaystyle = \ гидроразрыва {1} {G} \) \ (\ Displaystyle X_L = \ гидроразрыва {Z · R} {\ sqrt {Z ^ 2-R ^ 2}} \) \ (\ Displaystyle = \ гидроразрыва {1} {B_L} \)
Треугольник питания
\ (\ Displaystyle S = \ sqrt {P ^ 2 + {Q_L} ^ 2} \) \ (\ Displaystyle = U · I \) \ (\ Displaystyle Р = \ sqrt {S ^ 2- {Q_L} ^ 2} \) \ (\ Displaystyle = U_R · I_R \) \ (\ Displaystyle Q_L = \ sqrt {S ^ 2-P ^ 2} \) \ (\ Displaystyle = U_L · I_L \)
Коэффициент мощности
\ (\ Displaystyle соз (φ) = \ гидроразрыва {P} {S} = \ гидроразрыва {I_R} {I} \)
|
Цепи — ток, разность потенциалов, сопротивление и элементы в последовательной и параллельной цепях, сохранение заряда
Ячейки последовательно и параллельно
Ячейки в серии
Когда элементы соединены последовательно друг с другом, и все они подключены в одном направлении, общая разность потенциалов, подаваемая в цепь, представляет собой суммированные индивидуальные разности потенциалов.
V итого = V 1 + V 2 + V 3
Идентичные ячейки параллельно друг другу
Когда идентичные элементы параллельны друг другу, общая разность потенциалов, подаваемая в цепь, равна разности потенциалов только одной из ячеек.
V итого = V 1 = V 2 = V 3
Итак, если три ячейки 2 В соединены параллельно друг с другом, разность потенциалов, подаваемая в цепь, составляет 2 В.
Резисторы последовательно и параллельно
Резисторы серии
Когда резисторы соединены последовательно друг с другом, общее сопротивление складывается из отдельных сопротивлений.
Резисторы параллельно
Когда резисторы соединены параллельно друг с другом, общее сопротивление определяется с помощью следующего уравнения.
Ток в последовательной и параллельной цепях
Сохранение заряда — «общий заряд, текущий в соединение проводов, должен быть равен полному заряду, вытекающему из соединения».
Первый закон Кирхгофа — «сумма токов, протекающих в месте соединения проводов, должна равняться сумме токов, исходящих от места соединения проводов».
Ток в последовательных цепях .
Когда вы подключаете амперметр к последовательной цепи, ток остается неизменным, куда бы вы ни вставили амперметр.
Ток в параллельных цепях .
Общий ток, протекающий от ячейки к ветвям в цепи, всегда должен быть равен току, протекающему через каждый компонент в ветвях цепи, когда они складываются.
Если компоненты имеют разное сопротивление, тогда ток через каждый компонент может быть разным, но когда вы складываете их вместе, они должны составлять общую сумму тока, выходящего из ячейки.
Разница потенциалов в последовательной и параллельной цепях
Второй закон Кирхгофа — «сумма ЭДС в любом замкнутом контуре в цепи должна быть равна сумме разностей потенциалов в замкнутом контуре в цепи».
Разность потенциалов в последовательной цепи .
Полная разность потенциалов, подаваемая ячейкой, делится между компонентами. Если все компоненты имеют одинаковое сопротивление, между ними будет равная разность потенциалов.
Если сопротивления не равны, они могут иметь разную величину разности потенциалов на них, но при суммировании они всегда должны равняться p.d. поставляется ячейкой.
Разность потенциалов в параллельных цепях .
Разность потенциалов, подаваемая элементом, равна разности потенциалов на каждом компоненте параллельной цепи.
Параллельно подключенных резисторов — Ток, разность потенциалов, мощность и сопротивление — Higher Physics Revision
Ток
При параллельном подключении резисторов ток питания равен сумме токов, протекающих через каждый резистор. Другими словами, токи в ветвях параллельной цепи складываются с током питания.
\ [I_ {S} = I_ {1} + I_ {2} + I_ {3} \]
Это соотношение выражает закон сохранения заряда. Все электроны, вышедшие из источника, должны вернуться в источник, и каждый электрон может пройти только через одну параллельную ветвь.
Разность потенциалов
Когда резисторы соединены параллельно, они имеют одинаковую разность потенциалов на них. Другими словами, любые параллельные компоненты имеют одинаковую разность потенциалов.
Итак, в схеме выше \ (V_ {S} = V_ {1} = V_ {2} = V_ {3} \)
Сопротивление
Для схемы выше формула для определения общего сопротивления резисторов в параллельный — \ (\ frac {1} {{{R_P}}} = \ frac {1} {{{R_1}}}} + \ frac {1} {{{R_2}}} + \ frac {1} {{ {R_3}}} \)
- Вопрос
Устанавливается следующая сеть резисторов.
Рассчитайте полное сопротивление сети.
- Показать ответ
\ [R_ {1} = 12 \ Omega \]
\ [R_ {2} = 18 \ Omega \]
\ [R_ {3} = 6 \ Omega \]




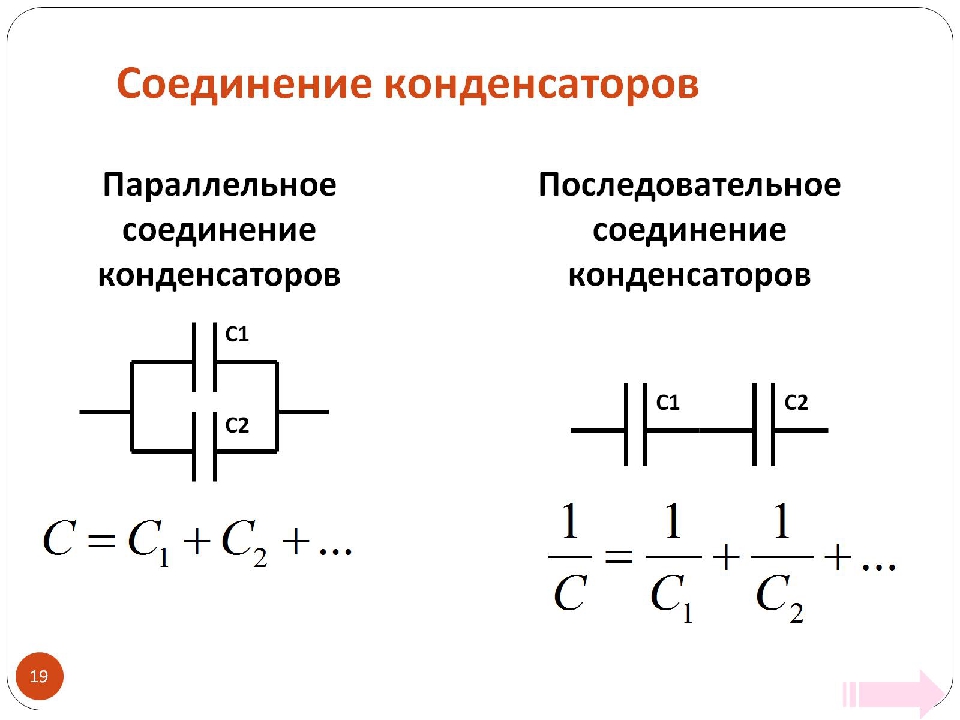
 Такое подключение позволяет включать
Такое подключение позволяет включать
