Формула напряженности магнитного поля в физике
Определение и формула напряженности магнитного поля
ОпределениеНапряженностью магнитного поля называют векторную физическую величину, направленную по касательной к силовым линиям поля, являющуюся характеристикой магнитного поля, равную:
где – вектор магнитной индукции, Гн/м(Н/А2)- магнитная постоянная, – вектор намагниченности среды в исследуемой точке поля.
Для магнитного поля в вакууме напряженность магнитного поля определяется выражением:
В изотропной среде формула (1) преобразуется к виду:
где – скалярная величина, называемая относительной магнитной проницаемостью среды (или просто магнитной проницаемостью). В изотропной среде векторы напряженности магнитного поля и магнитной индукции совпадают по направлению.
Иногда напряженность магнитного поля определяют как векторную величину, направленную по касательной к силовой линии поля, по модулю равной отношению силы (dF), с которой поле воздействует на единичный элемент тока (dl), который расположен перпендикулярно полю в вакууме, к магнитной постоянной:
Закон Био-Савара-Лапласа
Это важнейший в электромагнетизме закон. Он определяет вектор напряженности в произвольной точке магнитного поля, которое создает в вакууме элементарный проводник длинны dl с постоянным током I:
где – вектор элемента проводника, который по модулю равен длине проводника, направление совпадает с направлением тока; – радиус–вектор, который проводят от рассматриваемого элементарного проводника к точке рассмотрения поля; .
Вектор – перпендикулярен плоскости, в которой находятся векторы и , и направлен так, что из его конца вращение вектора по кратчайшему пути до совмещения с вектором происходило по часовой стрелке. Для нахождения направлен
| Напряженность поля точечного заряда. | |
Обозначим: q — заряд, создающий поле, q0 — заряд, помещенный в поле (внешний заряд). Закон Кулона: Тогда напряженность поля точечного заряда: |
|
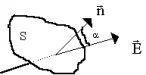
Теорема Гаусса. Потоком вектора напряженности наз. величина Ф, равная произведению модуля вектора напряженности на площадь контура S, ограничивающую некоторую площадь, и на косинус угла между вектором напряженности и нормалью (перпендикуляром) к площадке. |
|
Если считать, что напряженность пропорциональна числу силовых линий, приходящихся на единицу площади поверхности (т.е. густоте), то поток напряженности пропорционален полному числу силовых линий, пересекающих данный контур. |
|
Поток линий напряженности электростатического поля через произвольную замкнутую поверхность прямо пропорционален величине заряда, находящегося в области пространства, ограниченного данной поверхностью. |
|
Применения теоремы Гаусса. |
|
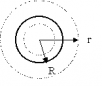
1. Напряженность поля заряженной проводящей сферы радиуса R. Сфера заряжена по поверхности. А) Внутри сферы заряда нет . Е=0 |
|
Б) Снаружи сферы. |
|
На поверхности сферы: | |
2. Напряженность поля шара заряженного по объему. |
|
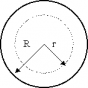
Введем понятие объемной плотности заряда: Объемная плотность заряда показывает, какой заряд содержится в единице объема заряженного по всему объему тела. Объем шара произвольного радиуса Обозначим q — заряд шара, q0 — заряд, находящийся внутри объема произвольного радиуса. |
|
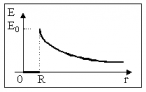
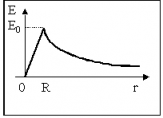
Тогда заряд сферы радиуса r , будет: Следовательно: – напряженность поля внутри шара, равномерно заряженного по объему. Снаружи — см. 1. |
|
3. Напряженность поля бесконечной заряженной плоскости. |
|
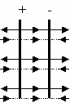
Введем понятие поверхностной плотности заряда: Тогда Коэффициент 2 появляется, т.к. плоскость окружена двумя поверхностями площадью S. Поле бесконечной заряженной плоскости не зависит от расстояния от плоскости! Можно пользоваться, когда расстояние много меньше размеров плоскости. 4. Напряженность поля плоского воздушного конденсатора. Из рисунка видим, что снаружи конденсатора поля пластин взаимно скомпенсированы, и общее поле равно нулю. Внутри конденсатора поля складываются. Используя вывод п.3 получаем: Формула справедлива при условии, что расстояние между пластинами много меньше размеров самих пластин и вдали от краев пластин. |
|
| |
описание, определение единицы измерения, стандартная формула
 В природе существует много интересных явлений, которые обычные люди до сих пор полностью не понимают. К этой категории можно отнести напряжённость электрического поля. Несмотря на то что характеристики этого явления определяются довольно просто, воспользоваться им можно далеко не всегда. Это направление больше носит теоретический характер, из-за чего учёные делают основной упор на получение выгоды в краткосрочной перспективе.
В природе существует много интересных явлений, которые обычные люди до сих пор полностью не понимают. К этой категории можно отнести напряжённость электрического поля. Несмотря на то что характеристики этого явления определяются довольно просто, воспользоваться им можно далеко не всегда. Это направление больше носит теоретический характер, из-за чего учёные делают основной упор на получение выгоды в краткосрочной перспективе.
Краткое описание
Увидеть невооружённым взглядом электрическое поле (ЭП) невозможно: его можно обнаружить в процессе воздействия на заряженные тела. Удивительно, но прямого касания может и не быть, так как должна присутствовать силовая природа. Ведь всем известно, что наэлектризованные волосы будут притягиваться к другим предметам. Многочисленные исследования смогли доказать, что аналогичный принцип действия имеют гравитационные поля. Этот феномен был впервые описан в законе Кулона.
Стандартная формула электрического поля выглядит так: F = d₁ d₂ / 4 π q q₀ r ².
Расшифровка:
 d₁ и d₂ — параметры разрядов в кулонах.
d₁ и d₂ — параметры разрядов в кулонах.- q ₀ — этим символом может обозначаться только электрическая постоянная.
- q — показатель диэлектрической проницаемости.
- F — сила взаимодействия разных зарядов (может измеряться в ньютонах).
- r — расстояние между двумя рассматриваемыми объектами в метрах.
Благодаря формуле напряжённости электростатического поля можно определить тот факт, что чем дальше находиться от центра, тем меньше будет ощущаться его воздействие. Графически его можно изобразить в виде силовых линий. Итоговое их расположение напрямую зависит от геометрических параметров носителя.
На сегодняшний день специалисты научились выделять несколько разновидностей полей:
- Специфические неоднородное. Рассматривается поле вокруг шарообразного или же точечного заряда. Все силовые линии расходятся только в том случае, если этот параметр имеет положительное значение.
- Однородное поле. Все силовые линии располагаются исключительно параллельно друг другу. Эксперты утверждают, что идеальным является тот вариант, когда заряженные пластины бесконечны.
Индуцированные электрическим зарядом силовые линии относятся к замкнутому типу. Иная ситуация наблюдается только у вихревого поля, сформированного вокруг меняющегося магнитного потока.
Ключевые особенности
 ЭП представлено особым видом материи, которая встречается вокруг заряженных элементарных частиц (протоны и электроны). Специалисты не один десяток лет занимаются изучением такого интересного явления. Им удалось доказать, что именно через ЭП передаётся влияние одного неподвижного заряда к другому. Итоговое воздействие происходит в строгом соответствии с известным во всём мире законом Кулона.
ЭП представлено особым видом материи, которая встречается вокруг заряженных элементарных частиц (протоны и электроны). Специалисты не один десяток лет занимаются изучением такого интересного явления. Им удалось доказать, что именно через ЭП передаётся влияние одного неподвижного заряда к другому. Итоговое воздействие происходит в строгом соответствии с известным во всём мире законом Кулона.
Так как в промежутке этого расстояния нет плотных тел, можно утверждать о существовании определённого невидимого поля. А так как оно связано со специфическими явлениями, то его начали называть электрическим. Такие поля существуют вокруг всех предметов, только из-за их невидимости и скомпенсированности взаимодействия друг на друга создаётся впечатление, что они проявляются.
Базовые параметры
Изобразить формулу напряжённости можно при помощи как математических закономерностей, так и графических приёмов. Последние характеристики относятся к векторной категории, имеющей определённое направление. Все эти нюансы крайне важны, так как во время решения практических задач часто приходится оперировать не стандартным модулем величины, а специфической проекцией вектора на заранее выбранную ось.
К основным свойствам ЭП можно отнести следующие факты:
- Оно может как притягивать, так и отталкивать.
 Невидимость для невооружённого глаза (итоговое определение осуществляется через поведение пробного электрического заряда).
Невидимость для невооружённого глаза (итоговое определение осуществляется через поведение пробного электрического заряда).- Всегда присутствует вокруг заряженных частиц, чего нельзя сказать о магнитном поле.
- Имеет векторное направление.
- Взаимодействует исключительно с ЭП.
- Отличается свойствами неоднородности и концентрации (напряжённость).
Электрическое поле можно определить при помощи обычного точного заряда. Если он будет направлен в интересующую точку пространства, то можно выяснить — присутствует ли в этом месте ЭП. Такой метод определения считается наиболее простым и понятным. Интенсивность излучаемого ЭП используется как обозначение напряжённости.
Влияющие на один и тот же заряд силы будут отличаться друг от друга по направлению и размеру в разных измеряемых точках.
Стоит отметить, что закон Кулона не адаптирован под современные требования. Для одной точки поля сила F будет прямо пропорциональна величине точечного заряда. На фоне этого эксперты провели множество исследований. Теперь принято считать силовой характеристикой единицы измерения напряжённости «Е». Этот параметр является векторной величиной. Найти напряжённость электрического поля можно в Ньютонах на Кулон.
Отдельно стоит учесть, что если ЭП образуется сразу несколькими зарядами, то общая напряжённость в определённой точке находится как общая геометрическая сумма.
Изучение потенциала

Именно этот параметр считается распространённой характеристикой ЭП. Потенциал выступает в роли накопленной ценной энергии, используемой для перемещения различных зарядов. В итоге потенциал может весь израсходоваться, из-за чего его показатель будет равен нулю.
Процесс накопления происходит в обратном порядке. В качестве яркого примера можно использовать всё тот же заряд, но находящийся вне ЭП. Только когда определённая сила перемещает его внутрь и постепенно двигает там, появляется необходимый потенциал.
Если человек только столкнулся с этой отраслью и хочет в ней разобраться, то ему лучше представить обычную пружину. В спокойном состоянии у неё отсутствует какой-либо потенциал, из-за чего она может расцениваться только как небольшой металлический предмет. Но как только человек начнёт её постепенно сдавливать, будет образовываться потенциал. Если быстро отпустить пружину, то она мгновенно выпрямится и при этом сдвинет со своего пути все посторонние предметы.
Этот пример ярко демонстрирует то, что уровень потенциала всегда будет соответствовать приложенным усилиям на перемещение заряда. В современной науке этот показатель можно измерить в вольтах.
Сферы применения
Стандартные характеристики ЭП обязательно включают в себя два свойства, которые активно применяются человечеством. Они могут образовывать универсальные ионы, а погруженные в определённую жидкость электроды позволяют без каких-либо усилий разделять их по функциям. Эксперты доказали, что универсальной и доступность электрических полей активно используется в различных отраслях:
- Очистка. В этой отрасли активно используется система качественного разделения разных жидкостей. Эта функция высоко ценится в очистных сооружениях. Ведь та вода, в которой содержится большое количество различного мусора, очень вредна для человека. При этом с такой жидкостью очень сложно что-то сделать, так как далеко не все фильтры могут справиться с проблемой. Именно в такой ситуации на помощь приходят ЭП. Они разделяют воду, за счёт чего отделяются загрязнения. Благодаря этому можно пользоваться быстрым и доступным способом очистки.
 Медицина. Квалифицированные доктора практически ежедневно используют систему воздействия на поражённые ткани пациента направленными ионами. За счёт этого улучшается регенерация органа, убиваются микробы и очищается рана. К тому же уникальные характеристики и свойства ЭП позволяют им работать с большей частотой. Такой эффект широко востребован в медицине, так как за короткий промежуток времени можно повысить температуру некоторых отдельных частей тела, за счет чего восстанавливается кровоток, а также улучшается общее самочувствие пациента.
Медицина. Квалифицированные доктора практически ежедневно используют систему воздействия на поражённые ткани пациента направленными ионами. За счёт этого улучшается регенерация органа, убиваются микробы и очищается рана. К тому же уникальные характеристики и свойства ЭП позволяют им работать с большей частотой. Такой эффект широко востребован в медицине, так как за короткий промежуток времени можно повысить температуру некоторых отдельных частей тела, за счет чего восстанавливается кровоток, а также улучшается общее самочувствие пациента.- Химия. Без электрических полей просто невозможна нормальная работа некоторых отраслей промышленности, где нужно разделять разные жидкости. Такая наука активно используется в стандартных лабораторных условиях, но чаще всего её можно встретить в сфере массовой добычи нефти. Большой спрос спровоцирован тем, что природный материал часто содержит загрязняющие частицы, избавиться от которых традиционным способом весьма проблематично. Более экономичным является применение ЭП. Они позволяют быстро разделить нефть, убрав весь ненужный мусор, облегчив дальнейшую обработку.
Конечно, существует множество других вариантов применения формулы напряжённости электрического поля.
К примеру: эксперты могут применять такое явление в качестве беспроводной системы передачи тока к разным приборам. Но в большинстве случае все такие разработки носят экспериментальный и теоретический характер.
Закон Кулона
 В этом случае силовая характеристика электрического поля работает для точечного заряда, находящегося на расстоянии определённого радиуса от него. Если же взять этот показатель по стандартному модулю, то в итоге получится кулоновское поле.
В этом случае силовая характеристика электрического поля работает для точечного заряда, находящегося на расстоянии определённого радиуса от него. Если же взять этот показатель по стандартному модулю, то в итоге получится кулоновское поле.
Направление вектора напрямую зависит от имеющегося знака заряда. Если он плюсовой, то ЭП будет «передвигаться» по радиусу. В противном случае сам вектор будет направлен в сторону заряда.
Чтобы разобраться в ключевых особенностях закона, можно изучить основные рисунки и диаграммы, где изображены силовые линии. В учебниках основные характеристики ЭП объясняются довольно сложно. Если же для изучения этой темы использовать специализированную литературу, тогда нужно учесть, что при построении рисунков силовых линий их итоговая густота является пропорциональной модулю вектора напряжённости. Это своего рода подсказка от экспертов, которая может помочь во время экзамена или просто для контроля знаний.
Принцип воздействия
Свойства ЭП чаще всего постоянны и однообразны. Для планеты свойственен свой защитный фон, который на живые организмы практически никак не влияет. Незначительные проявления становятся заметными для человека только во время сильной грозы. В такой ситуации может даже казаться, что воздух дрожит от напряжения. Но для большинства людей это не представляет никакой угрозы.
 Индустрия технологий не стоит на месте, благодаря чему специалисты изготавливают всё больше различных агрегатов, каждый из которых способен генерировать собственное ЭП. Показатель существенно превышает естественный фон, который составляет 0.5 кВ/м. Конечно, такая особенность не осталась незамеченной со стороны экспертов. В результате многочисленных проб они вывели максимально допустимое напряжение, которое не создаёт ограничений для человека. Его размер составляет 27 кВ/м.
Индустрия технологий не стоит на месте, благодаря чему специалисты изготавливают всё больше различных агрегатов, каждый из которых способен генерировать собственное ЭП. Показатель существенно превышает естественный фон, который составляет 0.5 кВ/м. Конечно, такая особенность не осталась незамеченной со стороны экспертов. В результате многочисленных проб они вывели максимально допустимое напряжение, которое не создаёт ограничений для человека. Его размер составляет 27 кВ/м.
Даже если включить сразу все бытовые устройства, максимальный показатель не будет превышен. Взрослый человек может получить небольшой процент негативного воздействия только при длительном нахождении возле высоковольтных проводов. В такой среде напряжение очень большое, из-за чего долго стоять или же работать на таком участке категорически запрещено. Специалисты, которые вынуждены по служебным обстоятельствам находиться в окружении таких ЭП, должны успевать выполнить все работы максимум за полтора часа.
Внедрение в технику
Современные масштабы ЭП нашли весьма интересное применение в современном мире. Специалистами был разработан способ беспроводной передачи сигнала от основного источника до потребителя, хотя ещё до недавнего времени всё носило экспериментальный и теоретический характер.
На сегодняшний день уже имеется эффективная реализация технологии зарядки смартфонов без использования гибкого кабеля. Конечно, этот вариант пока не позволяет передавать энергию на дальние расстояния, но все функции находятся в стадии совершенствования.
Стоит отметить, что изучением электрического поля занималось уже много людей. Огромный след в истории оставил известный во всём мире сербский изобретатель Николай Тесла. Благодаря приложенным усилиям ему удалось достичь больших успехов, но не в плане энергетической эффективности.
Формула напряжённости электрического поля
Здесь – напряжённость электрического поля, – сила, действующая на заряд, – величина заряда.
Единица измерения напряжённости электрического поля – В/м (вольт на метр) или Н/Кл (ньютон на кулон).
Напряжённость – векторная величина, характеризующая интенсивность воздействия электрического поля на заряжённую частицу в конкретной точке. Напряжённость поля в различных точках вообще говоря различна, то есть электрическое поле – это векторное поле, направление векторов которого зависит от того, как было создано это поле. По указанной формуле можно рассчитать не только силу воздействия электрического поля на точечный заряд, но и силу воздействия этого поля на заряжённое тело, если распределение заряда в нём известно.
Примеры решения задач по теме «Напряжённость электрического поля»
| Понравился сайт? Расскажи друзьям! | |||
Электростатическое поле, напряженность и электростатический диполь
Электрическое поле, которое окружает заряд, это реальность, независящая от нашего желания что-либо изменить и как-то повлиять на это. Отсюда можно сделать вывод, что электрическое поле является одной из форм существования материи, так же как и вещество.
Электрическое поле зарядов, находящихся в состоянии покоя, называют электростатическим. Чтобы обнаружить электростатическое поле определенного заряда нужно внести в его поле другой заряд, на который будет действовать определенная сила в соответствии с законом Кулона. Однако без наличия второго заряда электростатическое поле первого заряда существует, но никак себя не проявляет.
Напряженностью Е характеризуют электростатическое поле. Напряженность в некоторой точке электрического поля – физическая величина, которая равна силе, действующей на помещенный в определенную точку поля единичный положительный покоящийся заряд, и направленная в сторону действия силы.
Если в электрическое поле, создаваемое зарядом q, внести «пробный» положительный точечный заряд qпр, то по закону Кулона на него будет действовать сила:

Если в одну точку поля помещать различные пробные заряды q/пр, q//пр и так далее, то на каждый из них будут действовать различные силы, пропорциональные величине заряда. Отношение F/qпр для всех зарядов, вносимых в поле, будет идентичным, а также будет зависеть лишь от q и r, определяющих электрическое поле в данной точке. Данную величину можно выразить формулой:

Если предположить, что qпр = 1, то E = F. Отсюда делаем вывод, что напряженность электрического поля является его силовой характеристикой. Из формулы (2) с учетом выражения кулоновской силы (1) следует:

Из формулы (2) видно, что за единицу напряженности принимается напряженность в определенной точке поля, где на единицу заряда будет действовать единица силы. Поэтому в системе СГС единицей напряженности является дин/СГСq, а в системе СИ будет Н/Кл. Соотношение между приведенными единицами называют абсолютной электростатической единицей напряженности (СГСЕ):

Вектор напряженности направлен от заряда вдоль радиуса при образующем поле положительном заряде q+, а при отрицательном – q – по направлению к заряду вдоль радиуса.
Если электрическое поле образовано несколькими зарядами, то силы, которые будут действовать на пробный заряд, складываются по правилу сложения векторов. Поэтому напряженность системы, состоящей из нескольких зарядов, в данной точке поля будет равна векторной сумме напряженностей каждого заряда в отдельности:

Данное явление носит название принцип суперпозиции (наложения) электрических полей.
Напряженность в любой точке электрического поля двух точечных зарядов – q2 и +q1 можно найти использовав принцип суперпозиции:

По правилу параллелограмма будет происходить сложение векторов Е1 и Е2. Направление результирующего вектора Е определяется построением, а его абсолютная величина может быть вычислена с использованием формулы ниже:

Где α – угол между векторами Е1 и Е2.
Давайте рассмотрим электрическое поле, которое создает диполь. Электрический диполь – это система равных по величине (q = q1 = q2), но противоположных по знаку зарядов, расстояние между которыми очень мало, если сравнивать с расстоянием до рассматриваемых точек электрического поля.
Электрический дипольный момент p, являющийся основной характеристикой диполя и определяемый как вектор, направленный от отрицательного заряда к положительному, и равный произведению плеча диполя l на заряд q:

Также вектором является плечо диполя l, направленным от отрицательного заряда к положительному, и определяет расстояние между зарядами. Линия, которая проходит через оба заряда, носит название – ось диполя.
Давайте определим напряженность электрического поля в точке, которая лежит на оси диполя по середине (рисунок ниже а)):

В точке В напряженность Е будет равна векторной сумме напряженностей Е/ и Е//, которые создаются положительными и отрицательными зарядами но отдельности. Между зарядами –q и +q векторы напряженностей Е/ и Е// направлены в одну сторону, поэтому по абсолютной величине результирующая напряженность Е будет равна их сумме.
Если же нам необходимо найти Е в точке A, лежащей на продолжении оси диполя, то в разные стороны будут направлены вектора Е/ и Е//, соответственно по абсолютной величине результирующая напряженность будет равна их разности:

Где r – расстояние между точкой, которая лежит на оси диполя и в которой происходит определение напряженности, и средней точкой диполя.
В случае r>>l, величиной (l/2) в знаменателе можно пренебречь, тогда получим следующее соотношение:

Где p – момент электрический диполя.
Данная формула в системе СГС примет вид:

Теперь нужно вычислить напряженность электрического поля в точке С (рисунок выше б)), лежащей на перпендикуляре, восстановленном из средней точки диполя.
Так как r1 = r2, то будет иметь место равенство:

В точке С вектор результирующей напряженности по абсолютной величине будет равен:

Так как r>>l, то можно считать r1 ≈ r, тогда представленную выше формулу можно записать в другом виде:

Напряженность диполя в произвольной точке можно определить по формуле:

Где α – угол между плечом диполя l и радиус-вектором r, r – расстояние от точки, в которой определяется напряженность поля, до центра диполя, р – электрический момент диполя.
Пример
На расстоянии R = 0,06 м друг от друга находятся два одинаковых точечных заряда q1 = q2 = 10-6 Кл (рисунок ниже):

Необходимо определить напряженность электрического поля в точке А, которая расположена на перпендикуляре, восстановленном в центре отрезка, который соединяет заряды, на расстоянии h = 4 см от этого отрезка. Также нужно определить напряженность и в точке В, находящейся на середине отрезка, который соединяет заряды.
Решение
По принципу суперпозиции (наложением полей) определяется напряженность поля Е. Таким образом, векторной (геометрической) суммой определяется Е, создаваемых каждым зарядом в отдельности: Е = Е1 + Е2.
Напряженность электрического поля первого точечного заряда равна:

Где q1 и q2 – заряды, образующие электрическое поле; r – расстояние от точки, в которой вычисляется напряженность, до заряда; ε0 – электрическая постоянная; ε – относительная диэлектрическая проницаемость среды.
Для определения напряженности в точке В сначала нужно построить векторы напряженности электрических полей от каждого заряда. Поскольку заряды положительны, то векторы Е/ и Е// будут направлены от точки В в разные стороны. По условию q1 = q2:

Это значит, что в средине отрезка напряженность поля равна нулю.
В точке А необходимо произвести геометрическое сложение векторов Е1 и Е2. В точке А напряженность будет равна:

Напряжённость электрического поля — это… Что такое Напряжённость электрического поля?
Напряжённость электри́ческого по́ля — векторная физическая величина, характеризующая электрическое поле в данной точке и численно равная отношению силы действующей на неподвижный[1]пробный заряд, помещенный в данную точку поля, к величине этого заряда :
- .
Из этого определения видно, почему напряженность электрического поля иногда называется силовой характеристикой электрического поля (действительно, всё отличие от вектора силы, действующей на заряженную частицу, только в постоянном[2] множителе).
В каждой точке пространства в данный момент времени существует свое значение вектора (вообще говоря — разное[3] в разных точках пространства), таким образом, — это векторное поле. Формально это выражается в записи
представляющей напряженность электрического поля как функцию пространственных координат (и времени, т.к. может меняться со временем). Это поле вместе с полем вектора магнитной индукции представляет собой электромагнитное поле[4], и законы, которым оно подчиняется, есть предмет электродинамики.
Напряжённость электрического поля в СИ измеряется в вольтах на метр [В/м] или в ньютонах на кулон.
Напряжённость электрического поля в классической электродинамике
Из сказанного выше ясно, что напряженность электрического поля — одна из основных фундаментальных величин классической электродинамики. В этой области физики можно назвать сопоставимыми с ней по значению только вектор магнитной индукции (вместе с вектором напряженности электрического поля образующий тензор электромагнитного поля) и электрический заряд. С некоторой точки зрения столь же важными представляются потенциалы электромагнитного поля (образующие вместе единый электромагнитный потенциал).
Приведем краткий обзор основных контекстов классической электродинамики в отношении напряженности электрического поля.
Сила, с которой действует электромагнитное поле на заряженные частицы
Полная сила, с которой электромагнитное поле (включающее вообще говоря электрическую и магнитную составляющие) действует на заряженную частицу, выражается формулой силы Лоренца:
где q — электрический заряд частицы, — ее скорость, — вектор магнитной индукции (основная характеристика магнитного поля), косым крестом обозначено векторное произведение. Формула приведена в единицах СИ.
Как видим, эта формула полностью согласуется с определением напряженности электрического поля, данном в начале статьи, но является более общей, т.к. включает в себя также действие на заряженную частицу (если та движется) со стороны магнитного поля.
В этой формуле частица предполагается точечной. Однако эта формула позволяет рассчитать и силы, действующие со стороны электромагнитного поля на тела любой формы с любым распределением зарядов и токов — надо только воспользоваться обычным для физики приемом разбиения сложного тела на маленькие (математически — бесконечно маленькие) части, каждая из которых может считаться точечной и таким образом входящей в область применимости формулы.
Остальные формулы, применяемые для расчета электромагнитных сил (такие, как, например, формула силы Ампера) можно считать следствиями[5] фундаментальной формулы силы Лоренца, частными случаями ее применения итп.
Однако для того, чтобы эта формула была применена (даже в самых простых случаях, таких, как расчет силы взаимодействия двух точечных зарядов), необходимо знать (уметь рассчитывать) и чему посвящены следующие параграфы.
Уравнения Максвелла
Достаточным вместе с формулой силы Лоренца теоретическим фундаментом классической электродинамики являются уравнения электромагнитного поля, называемые уравнениями Максвелла. Их стандартная традиционная форма представляет собой четыре уравнения, в три из которых входит вектор напряженности электрического поля:
Здесь — плотность заряда, — плотность тока, — универсальные константы (уравнения здесь записаны в единицах СИ).
Здесь приведена наиболее фундаментальная и простая форма уравнений Максвелла — так называемые «уравнения для вакуума» (хотя, вопреки названию, они вполне применимы и для описания поведения электромагнитного поля в среде). Подробно о других формах записи уравнений Максвелла — см. основную статью.
Этих четырех уравнений вместе с пятым — уравнением силы Лоренца — в принципе достаточно, чтобы полностью описать классическую (то есть не квантовую) электродинамику, то есть они представляют ее полные законы. Для решения конкретных реальных задач с их помощью необходимы еще уравнения движения «материальных частиц» (в классической механике это законы Ньютона), а также зачастую дополнительная информация о конкретных свойствах физических тел и сред, участвующих в рассмотрении (их упругости, электропроводности, поляризуемости итд итп), а также о других силах, участвующих в задаче (например, о гравитации), однако вся эта информация уже не входит в рамки электродинамики как таковой, хотя и оказывается зачастую необходимой для построения замкнутой системы уравнений, позволяющих решить ту или иную конкретную задачу в целом.
«Материальные уравнения»
Такими дополнительными формулами или уравнениями (обычно не точными, а приближенными, зачастую всего лишь эмпирическими), которые не входят непосредственно в область электродинамики, но поневоле используются в ней ради решения конкретных практических задач, называемыми «материальными уравнениями», являются, в частности:
- Закон Ома,
- Закон поляризации
- в разных случаях многие другие формулы и соотношения.
Связь с потенциалами
Связь напряженности электрического поля с потенциалами в общем случае такова:
где — скалярный и векторный потенциалы. Приведем здесь для полноты картины и соответствующее выражение для вектора магнитной индукции:
В частном случае стационарных (не меняющихся со временем) полей, первое уравнение упрощается до:
Это выражение для связи электростатического поля с электростатическим потенциалом.
Электростатика
Важным с практической и с теоретической точек зрения частным случаем в электродинамике является тот случай, когда заряженные тела неподвижны (например, если исследуется состояние равновесия) или скорость их движения достаточно мала чтобы можно было приближенно воспользоваться теми способами расчета, которые справедливы для неподвижных тел. Этим частным случаем занимается раздел электродинамики, называемый электростатикой.
Как мы уже заметили выше, напряженность электрического поля в этом случае выражается через скалярный потенциал как
или
то есть электростатическое поле оказывается потенциальным полем. ( в этом случае — случае электростатики — принято называть электростатическим потенциалом).
- Также и обратно
Уравнения поля (уравнения Максвелла) при этом также сильно упрощаются (уравнения с магнитным полем можно исключить, а в уравнение с дивергенцией можно подставить ) и сводятся к уравнению Пуассона:
а в областях, свободных от заряженных частиц — к уравнению Лапласа:
Учитывая линейность этих уравнений, а следовательно применимость к ним принципа суперпозиции, достаточно найти поле одного точечного единичного заряда, чтобы потом найти потенциал или напряженность поля, создаваемого любым распределением зарядов (суммируя решения для точечного заряда).
Теорема Гаусса
Очень полезной в электростатике оказывается теорема Гаусса, содержание которой сводится к интегральной форме единственного нетривиального для электростатики уравнения Максвелла:
где интегрирование производится по любой замкнутой поверхности S (вычисляя поток через эту поверхность), Q — полный (суммарный) заряд внутри этой поверхности.
Эта теорема дает крайне простой и удобный способ расчета напряженности электрического поля в случае, когда источники имеют достаточно высокую симметрию, а именно сферическую, цилиндрическую или зеркальную+трансляционную. В частности, таким способом легко находится поле точечного заряда, сферы, цилиндра, плоскости.
Напряжённость электрического поля точечного заряда
В единицах СИ
Для точечного заряда в электростатике верен закона Кулона
или
- .
- .
Исторически закон Кулона был открыт первым, хотя с теоретической точки зрения уравнения Максвелла более фундаментальны. С этой точки зрения он является их следствием. Получить этот результат проще всего исходя из теоремы Гаусса, учитывая сферическую симметрию задачи: выбрать поверхность S в виде сферы с центром в точечном заряде, учесть, что направление будет очевидно радиальным, а модуль этого вектора одинаков везде на выбранной сфере (так что E можно вынести за знак интеграла), и тогда, учитывая формулу для площади сферы радиуса r: , имеем:
откуда сразу получаем ответ для E.
Ответ для получается тогда интегрированием E:
Для системы СГС
Формулы и их вывод аналогичны, отличие от СИ лишь в константах.
Напряженность электрического поля произвольного распределения зарядов
По принципу суперпозиции для напряженности поля совокупности дискретных источников имеем:
где каждое
Подставив, получаем:
Для непрерывного распределения аналогично:
где V — область пространства, где расположены заряды (ненулевая плотность заряда), или всё пространство, — радиус-вектор точки, для которой считаем , — радиус-вектор источника, пробегающий все точки области V при интегрировании, dV — элемент объема. Можно подставить x,y,z вместо , вместо , вместо dV.
Системы единиц
В системе СГС напряжённость электрического поля измеряется в СГСЭ единицах, в системе СИ — в ньютонах на кулон или в вольтах на метр (русское В/м, международное V/m).
Литература
Примечания
- ↑ На движущийся заряд действует также магнитное поле, если, конечно, оно имеется (не равно нулю), поэтому в определение напряженности электрического поля вносится условие неподвижности пробного заряда; при условии гарантированного отсутствия магнитного поля неподвижность пробного заряда перестает быть обязательной, однако требование отсутствия магнитного поля в общем случае невозможно (а возможно только в частных классах задач).
- ↑ Для любой частицы ее электрический заряд постоянен. Измениться он может только если от частицы что-то заряженное отделится или если к ней что-то заряженное присоединится.
- ↑ Хотя иногда его значения могут оказываться и одинаковыми в разных точках пространства; если одинаков всюду в пространстве (или какой-то области пространства), говорят об однородном электрическом поле — это всего лишь частный случай электрического поля, хотя и наиболее простой; притом что в реальности электрическое поле может быть однородным лишь приближенно, то есть различия в разных точках пространства есть, но иногда они небольшие и ими можно пренебречь в рамках некоторого приближения.
- ↑ Электромагнитное поле может быть выражено и по-другому, например через электромагнитный потенциал или в несколько иной математической записи (прячущей вектор напряженности электрического поля вместе с вектором магнитной индукции внутрь тензора электромагнитного поля), однако все эти способы записи тесно связаны между собой, таким образом, утверждение о том, что поле — одна из основных составляющих электромагнитного поля не утрачивает смысла.
- ↑ Хотя исторически многие из них были открыты раньше.
См. также
Напряжённость электрического поля — это… Что такое Напряжённость электрического поля?
Напряжённость электри́ческого по́ля — векторная физическая величина, характеризующая электрическое поле в данной точке и численно равная отношению силы действующей на неподвижный[1]пробный заряд, помещенный в данную точку поля, к величине этого заряда :
- .
Из этого определения видно, почему напряженность электрического поля иногда называется силовой характеристикой электрического поля (действительно, всё отличие от вектора силы, действующей на заряженную частицу, только в постоянном[2] множителе).
В каждой точке пространства в данный момент времени существует свое значение вектора (вообще говоря — разное[3] в разных точках пространства), таким образом, — это векторное поле. Формально это выражается в записи
представляющей напряженность электрического поля как функцию пространственных координат (и времени, т.к. может меняться со временем). Это поле вместе с полем вектора магнитной индукции представляет собой электромагнитное поле[4], и законы, которым оно подчиняется, есть предмет электродинамики.
Напряжённость электрического поля в СИ измеряется в вольтах на метр [В/м] или в ньютонах на кулон.
Напряжённость электрического поля в классической электродинамике
Из сказанного выше ясно, что напряженность электрического поля — одна из основных фундаментальных величин классической электродинамики. В этой области физики можно назвать сопоставимыми с ней по значению только вектор магнитной индукции (вместе с вектором напряженности электрического поля образующий тензор электромагнитного поля) и электрический заряд. С некоторой точки зрения столь же важными представляются потенциалы электромагнитного поля (образующие вместе единый электромагнитный потенциал).
Приведем краткий обзор основных контекстов классической электродинамики в отношении напряженности электрического поля.
Сила, с которой действует электромагнитное поле на заряженные частицы
Полная сила, с которой электромагнитное поле (включающее вообще говоря электрическую и магнитную составляющие) действует на заряженную частицу, выражается формулой силы Лоренца:
где q — электрический заряд частицы, — ее скорость, — вектор магнитной индукции (основная характеристика магнитного поля), косым крестом обозначено векторное произведение. Формула приведена в единицах СИ.
Как видим, эта формула полностью согласуется с определением напряженности электрического поля, данном в начале статьи, но является более общей, т.к. включает в себя также действие на заряженную частицу (если та движется) со стороны магнитного поля.
В этой формуле частица предполагается точечной. Однако эта формула позволяет рассчитать и силы, действующие со стороны электромагнитного поля на тела любой формы с любым распределением зарядов и токов — надо только воспользоваться обычным для физики приемом разбиения сложного тела на маленькие (математически — бесконечно маленькие) части, каждая из которых может считаться точечной и таким образом входящей в область применимости формулы.
Остальные формулы, применяемые для расчета электромагнитных сил (такие, как, например, формула силы Ампера) можно считать следствиями[5] фундаментальной формулы силы Лоренца, частными случаями ее применения итп.
Однако для того, чтобы эта формула была применена (даже в самых простых случаях, таких, как расчет силы взаимодействия двух точечных зарядов), необходимо знать (уметь рассчитывать) и чему посвящены следующие параграфы.
Уравнения Максвелла
Достаточным вместе с формулой силы Лоренца теоретическим фундаментом классической электродинамики являются уравнения электромагнитного поля, называемые уравнениями Максвелла. Их стандартная традиционная форма представляет собой четыре уравнения, в три из которых входит вектор напряженности электрического поля:
Здесь — плотность заряда, — плотность тока, — универсальные константы (уравнения здесь записаны в единицах СИ).
Здесь приведена наиболее фундаментальная и простая форма уравнений Максвелла — так называемые «уравнения для вакуума» (хотя, вопреки названию, они вполне применимы и для описания поведения электромагнитного поля в среде). Подробно о других формах записи уравнений Максвелла — см. основную статью.
Этих четырех уравнений вместе с пятым — уравнением силы Лоренца — в принципе достаточно, чтобы полностью описать классическую (то есть не квантовую) электродинамику, то есть они представляют ее полные законы. Для решения конкретных реальных задач с их помощью необходимы еще уравнения движения «материальных частиц» (в классической механике это законы Ньютона), а также зачастую дополнительная информация о конкретных свойствах физических тел и сред, участвующих в рассмотрении (их упругости, электропроводности, поляризуемости итд итп), а также о других силах, участвующих в задаче (например, о гравитации), однако вся эта информация уже не входит в рамки электродинамики как таковой, хотя и оказывается зачастую необходимой для построения замкнутой системы уравнений, позволяющих решить ту или иную конкретную задачу в целом.
«Материальные уравнения»
Такими дополнительными формулами или уравнениями (обычно не точными, а приближенными, зачастую всего лишь эмпирическими), которые не входят непосредственно в область электродинамики, но поневоле используются в ней ради решения конкретных практических задач, называемыми «материальными уравнениями», являются, в частности:
- Закон Ома,
- Закон поляризации
- в разных случаях многие другие формулы и соотношения.
Связь с потенциалами
Связь напряженности электрического поля с потенциалами в общем случае такова:
где — скалярный и векторный потенциалы. Приведем здесь для полноты картины и соответствующее выражение для вектора магнитной индукции:
В частном случае стационарных (не меняющихся со временем) полей, первое уравнение упрощается до:
Это выражение для связи электростатического поля с электростатическим потенциалом.
Электростатика
Важным с практической и с теоретической точек зрения частным случаем в электродинамике является тот случай, когда заряженные тела неподвижны (например, если исследуется состояние равновесия) или скорость их движения достаточно мала чтобы можно было приближенно воспользоваться теми способами расчета, которые справедливы для неподвижных тел. Этим частным случаем занимается раздел электродинамики, называемый электростатикой.
Как мы уже заметили выше, напряженность электрического поля в этом случае выражается через скалярный потенциал как
или
то есть электростатическое поле оказывается потенциальным полем. ( в этом случае — случае электростатики — принято называть электростатическим потенциалом).
- Также и обратно
Уравнения поля (уравнения Максвелла) при этом также сильно упрощаются (уравнения с магнитным полем можно исключить, а в уравнение с дивергенцией можно подставить ) и сводятся к уравнению Пуассона:
а в областях, свободных от заряженных частиц — к уравнению Лапласа:
Учитывая линейность этих уравнений, а следовательно применимость к ним принципа суперпозиции, достаточно найти поле одного точечного единичного заряда, чтобы потом найти потенциал или напряженность поля, создаваемого любым распределением зарядов (суммируя решения для точечного заряда).
Теорема Гаусса
Очень полезной в электростатике оказывается теорема Гаусса, содержание которой сводится к интегральной форме единственного нетривиального для электростатики уравнения Максвелла:
где интегрирование производится по любой замкнутой поверхности S (вычисляя поток через эту поверхность), Q — полный (суммарный) заряд внутри этой поверхности.
Эта теорема дает крайне простой и удобный способ расчета напряженности электрического поля в случае, когда источники имеют достаточно высокую симметрию, а именно сферическую, цилиндрическую или зеркальную+трансляционную. В частности, таким способом легко находится поле точечного заряда, сферы, цилиндра, плоскости.
Напряжённость электрического поля точечного заряда
В единицах СИ
Для точечного заряда в электростатике верен закона Кулона
или
- .
- .
Исторически закон Кулона был открыт первым, хотя с теоретической точки зрения уравнения Максвелла более фундаментальны. С этой точки зрения он является их следствием. Получить этот результат проще всего исходя из теоремы Гаусса, учитывая сферическую симметрию задачи: выбрать поверхность S в виде сферы с центром в точечном заряде, учесть, что направление будет очевидно радиальным, а модуль этого вектора одинаков везде на выбранной сфере (так что E можно вынести за знак интеграла), и тогда, учитывая формулу для площади сферы радиуса r: , имеем:
откуда сразу получаем ответ для E.
Ответ для получается тогда интегрированием E:
Для системы СГС
Формулы и их вывод аналогичны, отличие от СИ лишь в константах.
Напряженность электрического поля произвольного распределения зарядов
По принципу суперпозиции для напряженности поля совокупности дискретных источников имеем:
где каждое
Подставив, получаем:
Для непрерывного распределения аналогично:
где V — область пространства, где расположены заряды (ненулевая плотность заряда), или всё пространство, — радиус-вектор точки, для которой считаем , — радиус-вектор источника, пробегающий все точки области V при интегрировании, dV — элемент объема. Можно подставить x,y,z вместо , вместо , вместо dV.
Системы единиц
В системе СГС напряжённость электрического поля измеряется в СГСЭ единицах, в системе СИ — в ньютонах на кулон или в вольтах на метр (русское В/м, международное V/m).
Литература
Примечания
- ↑ На движущийся заряд действует также магнитное поле, если, конечно, оно имеется (не равно нулю), поэтому в определение напряженности электрического поля вносится условие неподвижности пробного заряда; при условии гарантированного отсутствия магнитного поля неподвижность пробного заряда перестает быть обязательной, однако требование отсутствия магнитного поля в общем случае невозможно (а возможно только в частных классах задач).
- ↑ Для любой частицы ее электрический заряд постоянен. Измениться он может только если от частицы что-то заряженное отделится или если к ней что-то заряженное присоединится.
- ↑ Хотя иногда его значения могут оказываться и одинаковыми в разных точках пространства; если одинаков всюду в пространстве (или какой-то области пространства), говорят об однородном электрическом поле — это всего лишь частный случай электрического поля, хотя и наиболее простой; притом что в реальности электрическое поле может быть однородным лишь приближенно, то есть различия в разных точках пространства есть, но иногда они небольшие и ими можно пренебречь в рамках некоторого приближения.
- ↑ Электромагнитное поле может быть выражено и по-другому, например через электромагнитный потенциал или в несколько иной математической записи (прячущей вектор напряженности электрического поля вместе с вектором магнитной индукции внутрь тензора электромагнитного поля), однако все эти способы записи тесно связаны между собой, таким образом, утверждение о том, что поле — одна из основных составляющих электромагнитного поля не утрачивает смысла.
- ↑ Хотя исторически многие из них были открыты раньше.




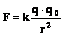 . Напряженность поля:
. Напряженность поля: 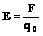 .
.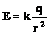
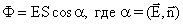
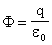
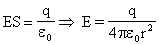
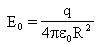
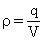
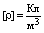
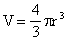 .
.

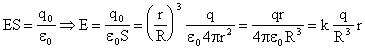 .
. 
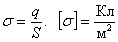
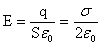 .
.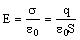 .
.
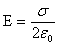
 d₁ и d₂ — параметры разрядов в кулонах.
d₁ и d₂ — параметры разрядов в кулонах. Невидимость для невооружённого глаза (итоговое определение осуществляется через поведение пробного электрического заряда).
Невидимость для невооружённого глаза (итоговое определение осуществляется через поведение пробного электрического заряда). Медицина. Квалифицированные доктора практически ежедневно используют систему воздействия на поражённые ткани пациента направленными ионами. За счёт этого улучшается регенерация органа, убиваются микробы и очищается рана. К тому же уникальные характеристики и свойства ЭП позволяют им работать с большей частотой. Такой эффект широко востребован в медицине, так как за короткий промежуток времени можно повысить температуру некоторых отдельных частей тела, за счет чего восстанавливается кровоток, а также улучшается общее самочувствие пациента.
Медицина. Квалифицированные доктора практически ежедневно используют систему воздействия на поражённые ткани пациента направленными ионами. За счёт этого улучшается регенерация органа, убиваются микробы и очищается рана. К тому же уникальные характеристики и свойства ЭП позволяют им работать с большей частотой. Такой эффект широко востребован в медицине, так как за короткий промежуток времени можно повысить температуру некоторых отдельных частей тела, за счет чего восстанавливается кровоток, а также улучшается общее самочувствие пациента.