Как найти время, скорость и расстояние
Расстояние
Мы постоянно ходим пешком и ездим на транспорте из одной точки в другую. Давайте узнаем, как можно посчитать это пройденное расстояние.
Расстояние — это длина от одного пункта до другого.
- Например: расстояние от дома до школы 3 км, от Москвы до Петербурга 705 км.
Расстояние обозначается латинской буквой s.
Единицы расстояния чаще всего выражаются в метрах (м), километрах (км).
Формула пути Чтобы найти расстояние, нужно умножить скорость на время движения: s = v × t |
Скорость
Двигаться со скоростью черепахи — значит медленно, а со скоростью света — значит очень быстро. Сейчас узнаем, как пишется скорость в математике и как ее найти по формуле.
Скорость определяет путь, который преодолеет объект за единицу времени.
Проще говоря, скоростью называют расстояние, пройденное телом за единицу времени.
Впервые формулу скорости проходят на математике в 5 классе. Сейчас мы ее сформулируем и покажем, как ее использовать.
Формула скорости Чтобы найти скорость, нужно разделить путь на время: v = s : t |
Показатели скорости чаще всего выражаются в м/сек или км/час.
Скорость сближения — это расстояние, которое прошли два объекта навстречу друг другу за единицу времени. Чтобы найти скорость сближения, нужно сложить скорости объектов.
Скорость удаления — это расстояние, которое увеличивается за единицу времени между двумя объектами, которые движутся в противоположных направлениях.
Чтобы найти скорость удаления, нужно сложить скорости объектов.
Чтобы найти скорость удаления при движении в одном направлении, нужно из большей скорости вычесть меньшую скорость.
Онлайн-курсы по математике для детей — отличный способ разобраться в сложных темах под руководством внимательного преподавателя.
Время
Время — самое дорогое, что у нас есть. Но кроме философии, у времени есть важная роль и в математике.
Время — это продолжительность каких-то действий, событий.
- Например: от метро до дома — 10 минут, от дома до дачи — 2 часа.
Время движения обозначается латинской буквой t.
Чаще всего вам будут встречаться такие единицы времени, как секунды, минуты и часы.
Формула времени Чтобы найти время, нужно разделить расстояние на скорость: t = s : v |
Эта формула пригодится, если нужно узнать, за какое время тело преодолеет то или иное расстояние.
Взаимосвязь скорости, времени, расстояния
Скорость, время и расстояние связаны между собой очень крепко. Одно без другого даже сложно представить.
Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время: s = v × t.
Задачка 1. Мы вышли из дома и направились в гости в соседний двор. Мы дошли до соседнего двора за 15 минут. Фитнес-браслет показал, что наша скорость была 50 метров в минуту. Какое расстояние мы прошли?
Если за одну минуту мы прошли 50 метров, то сколько таких пятьдесят метров мы пройдем за 10 минут? Умножив 50 метров на 15, мы определим расстояние от дома до магазина:
v = 50 м/мин
t = 15 мин
s = v × t = 50 × 15 = 750 м
Ответ: мы прошли 750 метров.
Если известно время и расстояние, то можно найти скорость: v = s : t.
Задачка 2. Двое школьников решили проверить, кто быстрее добежит от двора до спортплощадки. Расстояние между двором и площадкой — 100 метров. Первый школьник добежал за 25 секунд, второй за 50 секунд. Кто добежал быстрее?
Расстояние между двором и площадкой — 100 метров. Первый школьник добежал за 25 секунд, второй за 50 секунд. Кто добежал быстрее?
Как рассуждаем:
Быстрее добежал тот, кто за 1 секунду пробежал большее расстояние. Говорят, что у него скорость движения больше. В этой задаче скорость школьников — это расстояние, которое они пробегают за 1 секунду.
Чтобы найти скорость, нужно расстояние разделить на время движения. Найдем скорость первого школьника: для этого разделим 100 метров на время движения первого школьника, то есть на 25 секунд:
100 : 25 = 4
Если расстояние дано в метрах, а время движения в секундах, то скорость измеряется в метрах в секунду (м/с). Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч).
В нашей задаче расстояние дано в метрах, а время в секундах. Значит, будем измерять скорость в метрах в секунду (м/с).
100 м : 25 с = 4 м/с
Так мы узнали, что скорость движения первого школьника 4 метра в секунду.
Теперь найдем скорость движения второго школьника. Для этого разделим расстояние на время движения второго школьника, то есть на 50 секунд:
100 : 50 = 2
Значит, скорость движения второго школьника составляет 2 метра в секунду.
Сейчас можно сравнить скорости движения каждого школьника и узнать, кто добежал быстрее.
4 (м/с) > 2 (м/с)
Скорость первого школьника больше. Значит, он добежал до спортивной площадки быстрее.
Ответ: первый школьник добежал быстрее.
Если известны скорость и расстояние, то можно найти время: t = s : v.
Задачка 3. От школы до стадиона 500 метров. Мы должны дойти до него пешком. Наша скорость будет 100 метров в минуту. За какое время мы дойдем до стадиона из школы?
Как рассуждаем:
Если за одну минуту мы будем проходить 100 метров, то сколько таких минут со ста метрами будет в 500 метрах?
Чтобы ответить на этот вопрос, нужно 500 метров разделить на расстояние, которое мы будем проходить за одну минуту, то есть на 100. Тогда мы получим время, за которое дойдем до стадиона:
Тогда мы получим время, за которое дойдем до стадиона:
s = 500 м
v = 100 м/мин
t = s : v = 500 : 100 = 5 м
Ответ: от школы до стадиона мы дойдем за 5 минут.
Специально для уроков математики можно распечатать или нарисовать самостоятельно такую таблицу, чтобы быстрее запомнить и применять формулы скорости, времени, расстояния.
Расстояние, скорость, время
В этом уроке мы рассмотрим три физические величины, а именно расстояние, скорость и время.
Расстояние
Расстояние мы уже изучали в уроке единицы измерения. Говоря простым языком, расстояние это длина от одного пункта до другого. (Пример: расстояние от дома до школы 2 километра).
Имея дело с большими расстояниями, в основном они будут измеряться в метрах и километрах. Расстояние обозначается латинской буквой
Скорость
Скоростью называют расстояние, пройденное телом за единицу времени. Под единицей времени подразумевается 1 час, 1 минута или 1 секунда.
Под единицей времени подразумевается 1 час, 1 минута или 1 секунда.
Предположим, что двое школьников решили проверить, кто быстрее добежит от двора до спортплощадки. Расстояние от двора до спортплощадки 100 метров. Первый школьник добежал за 25 секунд. Второй за 50 секунд. Кто добежал быстрее?
Быстрее добежал тот, кто за 1 секунду пробежал бóльшее расстояние. Говорят, что у него скорость движения больше. В данном случае скорость школьников это расстояние, которое они пробегают за 1 секунду.
Чтобы найти скорость, нужно расстояние разделить на время движения. Давайте найдём скорость первого школьника. Для этого разделим 100 метров на время движения первого школьника, то есть на 25 секунд:
100 м : 25 с = 4
Если расстояние дано в метрах, а время движения в секундах, то скорость измеряется в метрах в секунду (м/с). Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч).
У нас расстояние дано в метрах, а время в секундах. Значит скорость измеряется в метрах в секунду (м/с)
Значит скорость измеряется в метрах в секунду (м/с)
100м : 25с = 4 (м/с)
Итак, скорость движения первого школьника составляет 4 метра в секунду (м/с).
Теперь найдем скорость движения второго школьника. Для этого разделим расстояние на время движения второго школьника, то есть на 50 секунд:
100 м : 50 c = 2 (м/с)
Значит скорость движения второго школьника составляет 2 метра в секунду (м/с).
Скорость движения первого школьника — 4 (м/с)
Скорость движения второго школьника — 2 (м/с)
4 (м/с) > 2 (м/с)
Скорость первого школьника больше. Значит он добежал до спортплощадки быстрее. Скорость обозначается латинской буквой v.
Время
Иногда возникает ситуация, когда требуется узнать за какое время тело преодолеет то или иное расстояние.
Например, от дома до спортивной секции 1000 метров. Мы должны доехать туда на велосипеде. Наша скорость будет 500 метров в минуту (500м/мин). За какое время мы доедем до спортивной секции?
Если за одну минуту мы будем проезжать 500 метров, то сколько таких минут с пятью ста метрами будет в 1000 метрах?
Очевидно, что надо разделить 1000 метров на то расстояние, которое мы будем проезжать за одну минуту, то есть на 500 метров. Тогда мы получим время, за которое доедем до спортивной секции:
Тогда мы получим время, за которое доедем до спортивной секции:
1000 : 500 = 2 (мин)
Время движения обозначается маленькой латинской буквой t.
Взаимосвязь скорости, времени, расстояния
Скорость принято обозначать маленькой латинской буквой v, время движения – маленькой буквой t, пройденное расстояние – маленькой буквой s. Скорость, время и расстояние связаны между собой.
Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время:
s = v × t
Например, мы вышли из дома и направились в магазин. Мы дошли до магазина за 10 минут. Наша скорость была 50 метров в минуту. Зная свою скорость и время, мы можем найти расстояние.
Если за одну минуту мы прошли 50 метров, то сколько таких пятьдесят метров мы пройдем за 10 минут? Очевидно, что умножив 50 метров на 10, мы определим расстояние от дома до магазина:
v = 50 (м/мин)
t = 10 минут
s = v × t = 50 × 10 = 500 (метров до магазина)
Если известно время и расстояние, то можно найти скорость:
v = s : t
Например, расстояние от дома до школы 900 метров. Школьник дошел до этой школы за 10 минут. Какова была его скорость?
Школьник дошел до этой школы за 10 минут. Какова была его скорость?
Скорость движения школьника это расстояние, которое он проходит за одну минуту. Если за 10 минут он преодолел 900 метров, то какое расстояние он преодолевал за одну минуту?
Чтобы ответить на этот, нужно разделить расстояние на время движения школьника:
s = 900 метров
t = 10 минут
v = s : t = 900 : 10 = 90 (м/мин)
Если известна скорость и расстояние, то можно найти время:
t = s : v
Например, от дома до спортивной секции 500 метров. Мы должны дойти до неё пешком. Наша скорость будет 100 метров в минуту (100 м/мин). За какое время мы дойдем до спортивной секции?
Если за одну минуту мы будем проходить 100 метров, то сколько таких минут со ста метрами будет в 500 метрах?
Чтобы ответить на этот вопрос нужно 500 метров разделить на расстояние, которое мы будем проходить за одну минуту, то есть на 100. Тогда мы получим время, за которое мы дойдем до спортивной секции:
Тогда мы получим время, за которое мы дойдем до спортивной секции:
s = 500 метров
v = 100 (м/мин)
t = s : v = 500 : 100 = 5 (минут до спортивной секции)
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
Урок 35. задачи на движение — Математика — 5 класс
Математика
5 класс
Урок № 35
Задачи на движение
Перечень вопросов, рассматриваемых в теме:
- Понятия скорости, времени, расстояния.
- Формулы нахождения скорости, времени, расстояния.
- Понятия скорости сближения, скорости удаления.
Глоссарий по теме
Расстояние – это длина от одного пункта до другого.
Большие расстояния, в основном, измеряются в метрах и километрах.
Расстояние обозначается латинской буквой S.
Чтобы найти расстояние, надо скорость умножить на время движения:
S = v ∙ t
Скорость – это расстояние, пройденное телом за единицу времени. Под единицей времени подразумевается 1 час, 1 минута или 1 секунда.
Скорость обозначается латинской буквой v.
Чтобы найти скорость, нужно расстояние разделить на время движения:
v = S : t
Время – это продолжительность каких-то действий, событий.
Время движения обозначается маленькой латинской буквой t.
Чтобы найти время, нужно расстояние разделить на скорость движения:
t = S : v
Скорость сближения – это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.
Чтобы найти скорость сближения, нужно сложить скорости объектов.
Скорость удаления – это расстояние, которое увеличивается за единицу времени между двумя объектами, двигающимися в противоположных направлениях.
Чтобы найти скорость удаления, нужно сложить скорости объектов.
Чтобы найти скорость удаления при движении в одном направлении, нужно из большей скорости вычесть меньшую скорость.
Основная литература
1. Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К., Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 258 с.
2. Потапов М. К., Шевкин А. В. Математика. Книга для учителя. 5 – 6 классы — М.: Просвещение, 2010
Дополнительная литература
1. Чесноков А. С., Нешков К. И. Дидактические материалы по математике 5 кл. – М.: Академика учебник, 2014
2. Бурмистрова Т. А. Математика. Сборник рабочих программ. 5–6 классы // Составитель Бурмистрова Т. А.
3. Потапов М. К. Математика: дидактические материалы. 6 кл. // Потапов М. К., Шевкин А. В. — М.: Просвещение, 2010
6 кл. // Потапов М. К., Шевкин А. В. — М.: Просвещение, 2010
Теоретический материал для самостоятельного изучения
Очень часто нам встречаются задачи на нахождение скорости, времени и расстояния. Что же всё это такое? Сейчас нам предстоит в этом разобраться.
Расстояние – это длина от одного пункта до другого. (Например, расстояние от дома до школы 2 километра). В основном большие расстояния измеряются в метрах и километрах. Общепринятое обозначение расстояния – заглавная латинская буква S.
Скоростью называют расстояние, пройденное телом за единицу времени. Под единицей времени подразумевается 1 час, 1 минута или 1 секунда. Скорость обозначается маленькой латинской буквой v.
Рассмотрим задачу:
Двое школьников решили проверить, кто быстрее добежит от двора до спортплощадки. Расстояние от двора до спортплощадки 200 метров. Первый школьник добежал за 50 секунд. Второй за 100 секунд. Кто из ребят бежал быстрее?
Решение:
Быстрее бежал тот, кто за 1 секунду пробежал большее расстояние. Говорят, что у него скорость движения больше. Чтобы найти скорость, нужно расстояние разделить на время движения.
Говорят, что у него скорость движения больше. Чтобы найти скорость, нужно расстояние разделить на время движения.
Давайте найдём скорость первого школьника. Для этого разделим 200 метров на время движения первого школьника, то есть на 50 секунд:
200 м : 50 с = 4
Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч).
У нас расстояние дано в метрах, а время в секундах. Значит, скорость измеряется в метрах в секунду:
200 м : 50 с = 4 (м/с)
Скорость движения первого школьника составляет 4 метра в секунду.
Теперь найдём скорость движения второго школьника. Для этого разделим расстояние на время движения второго школьника:
200 м : 100 c = 2 (м/с)
Скорость движения первого школьника – 4 (м/с).
Скорость движения второго школьника – 2 (м/с).
4 (м/с) > 2 (м/с)
Скорость первого школьника больше. Значит, он бежал до спортплощадки быстрее.
Иногда возникает ситуация, когда требуется узнать, за какое время тело преодолеет то или иное расстояние. Время движения обозначается маленькой латинской буквой t.
Время движения обозначается маленькой латинской буквой t.
Рассмотрим задачу:
От дома до спортивной секции 1200 метров. Мы должны доехать туда на велосипеде. Наша скорость будет 600 метров в минуту. За какое время мы доедем до спортивной секции?
Решение:
Если за одну минуту мы будем проезжать 600 метров, то сколько таких минут нам понадобится для преодоления тысячи двухсот метров? Очевидно, что надо разделить 1200 метров на то расстояние, которое мы будем проезжать за одну минуту, то есть на 600 метров. Тогда мы получим время, за которое мы доедем до спортивной секции:
1200 : 600 = 2 (мин)
Ответ: мы доедем до спортивной секции за 2 минуты.
Скорость, время и расстояние связаны между собой.
Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время:
S = v ∙ t
Рассмотрим задачу:
Мы вышли из дома и направились в магазин. Мы дошли до магазина за 15 минут. Наша скорость была 60 метров в минуту. Какое расстояние мы прошли?
Наша скорость была 60 метров в минуту. Какое расстояние мы прошли?
Решение:
Если за одну минуту мы прошли 60 метров, то сколько таких отрезков по шестьдесят метров мы пройдём за 15 минут? Очевидно, что умножив 60 метров на 15 минут, мы определим расстояние от дома до магазина:
v = 60 (м/мин)
t = 15 (минут)
S = v ∙ t = 60 ∙ 15 = 900 (метров)
Ответ: мы прошли 900 метров.
Если известно время и расстояние, то можно найти скорость:
v = S : t
Рассмотрим задачу:
Расстояние от дома до школы 800 метров. Школьник дошёл до этой школы за 8 минут. Какова была его скорость?
Скорость движения школьника – это расстояние, которое он проходит за одну минуту. Если за 10 минут он преодолел 800 метров, то какое расстояние он преодолевал за одну минуту?
Чтобы ответить на этот вопрос, нужно разделить расстояние на время движения школьника:
S = 800 метров
t = 8 минут
v = S : t = 800 : 8 = 100 (м/мин)
Ответ: скорость школьника была 100 м/мин.
Если известна скорость и расстояние, то можно найти время:
t = S : v
Рассмотрим задачу:
От дома до спортивной секции 600 метров. Мы должны дойти до неё пешком. Наша скорость будет 120 метров в минуту (120 м/мин). За какое время мы дойдём до спортивной секции?
Если за одну минуту мы будем проходить 120 метров, то сколько таких минут со ста двадцатью метрами будет в шестистах метрах?
Чтобы ответить на этот вопрос, нужно 600 метров разделить на расстояние, которое мы будем проходить за одну минуту, то есть на 120. Тогда мы получим время, за которое мы дойдём до спортивной секции:
S = 600 метров
v = 120 (м/мин)
t = S : v = 600 : 120 = 5 (минут).
Ответ: мы дойдём до спортивной секции за 5 минут.
Итак, все рассмотренные нами формулы мы можем представить в виде треугольника для лучшего запоминания:
Теперь рассмотрим типы задач на движение.
Задачи на сближение.
Скорость сближения – это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.
Например, если из двух пунктов навстречу друг другу отправятся два пешехода, причём скорость первого будет 100 метров в минуту, а второго – 105 метров в минуту, то скорость сближения будет составлять 100 плюс 105, то есть 205 метров в минуту. Значит, каждую минуту расстояние между пешеходами будет уменьшаться на 205 метров.
Чтобы найти скорость сближения, нужно сложить скорости объектов.
Задача.
Из двух пунктов навстречу друг другу выехали одновременно два велосипедиста. Скорость первого велосипедиста 13 км/ч, а скорость второго – 15 км/ч. Через 3 часа они встретились. Определите расстояние между населёнными пунктами.
Решение:
- Найдём скорость сближения велосипедистов:
13 км/ч + 15 км/ч = 28 км/ч
- Определим расстояние между населёнными пунктами. Для этого скорость сближения умножим на время движения:
28 ∙ 3 = 84 км
Ответ: расстояние между населёнными пунктами 84 км.
Задачи на скорость удаления.
Скорость удаления – это расстояние, которое увеличивается за единицу времени между двумя объектами, двигающимися в противоположных направлениях.
Например, если два пешехода отправятся из одного и того же пункта в противоположных направлениях, причём скорость первого будет 4 км/ч, а скорость второго 6 км/ч, то скорость удаления будет составлять 4 плюс 6, то есть 10 км/ч. Каждый час расстояние между двумя пешеходами будет увеличиваться на 10 километров.
Чтобы найти скорость удаления, нужно сложить скорости объектов.
Рассмотрим задачу:
С причала одновременно в противоположных направлениях отправились теплоход и катер. Скорость теплохода составляла 60 км/ч, скорость катера 130 км/ч. Какое расстояние будет между ними через 2 часа?
Решение:
- Определим скорость удаления. Для этого сложим их скорости:
60 + 130 = 190 км/ч.
Получили скорость удаления равную 190 км/ч. Данная скорость показывает, что за час расстояние между теплоходом и катером будет увеличиваться на 190 километров.
- Чтобы узнать какое расстояние будет между ними через два часа, нужно 190 умножить на 2:
190 ∙ 2 = 380 км.
Ответ: через 2 часа расстояние между теплоходом и катером будет составлять 380 километров.
Задачи на движение объектов в одном направлении.
В предыдущих пунктах мы рассматривали задачи, в которых объекты (люди, машины, лодки) двигались либо навстречу друг другу, либо в противоположных направлениях. В первом случае мы находили скорость сближения – в ситуации, когда два объекта двигались навстречу друг другу. Во втором случае мы находили скорость удаления – в ситуации, когда два объекта двигались в противоположных направлениях. Но объекты также могут двигаться в одном направлении, причём с различной скоростью.
Чтобы найти скорость удаления при движении в одном направлении, нужно из большей скорости вычесть меньшую скорость.
Рассмотрим задачу:
Из города в одном и том же направлении выехали легковой автомобиль и автобус. Скорость автомобиля 130 км/ч, а скорость автобуса 90 км/ч. Какое расстояние будет между ними через 1 час? Через 3 часа?
Скорость автомобиля 130 км/ч, а скорость автобуса 90 км/ч. Какое расстояние будет между ними через 1 час? Через 3 часа?
Решение:
- Найдём скорость удаления. Для этого из большей скорости вычтем меньшую:
130 км/ч − 90 км/ч = 40 км/ч
- Каждый час легковой автомобиль отдаляется от автобуса на 40 километров. За один час расстояние между автомобилем и автобусом будет 40 км. За 3 часа в три раза больше:
40 ∙ 3 = 120 км
Ответ: через один час расстояние между автомобилем и автобусом будет 40 км, через три часа – 120 км.
Рассмотрим ситуацию, в которой объекты начали своё движение из разных пунктов, но в одном направлении.
Задача.
Пусть на одной улице имеется дом, школа и аттракцион. Дом находится на одном конце улицы, аттракцион на другом, школа между ними. От дома до школы 900 метров. Два пешехода отправились в аттракцион в одно и то же время. Причём первый пешеход отправился в аттракцион от дома со скоростью 90 метров в минуту, а второй пешеход отправился в аттракцион от школы со скоростью 85 метров в минуту. Какое расстояние будет между пешеходами через 3 минуты? Через сколько минут после начала движения первый пешеход догонит второго?
Какое расстояние будет между пешеходами через 3 минуты? Через сколько минут после начала движения первый пешеход догонит второго?
Решение:
- Определим расстояние, пройденное первым пешеходом за 3 минуты. Он двигался со скоростью 90 метров в минуту. За три минуты он пройдёт в три раза больше, то есть 270 метров:
90 ∙ 3 = 270 метров
- Определим расстояние, пройденное вторым пешеходом за 3 минуты. Он двигался со скоростью 85 метров в минуту. За три минуты он пройдёт в три раза больше, то есть 255 метров:
85 ∙ 3 = 255 метров
- Теперь найдём расстояние между пешеходами. Чтобы найти расстояние между пешеходами, можно к расстоянию от дома до школы (900м) прибавить расстояние, пройденное вторым пешеходом (255м), и из полученного результата вычесть расстояние, пройденное первым пешеходом (270м):
900 + 255 = 1155 м
1155 – 270 = 885 м
Либо из расстояния от дома до школы (900 м) вычесть расстояние, пройденное первым пешеходом (270 м), и к полученному результату прибавить расстояние, пройденное вторым пешеходом (255 м):
900 – 270 = 630 м
630 + 255 = 885 м
Таким образом, через три минуты расстояние между пешеходами будет составлять 885 метров.
- Теперь давайте ответим на вопрос: через сколько минут после начала движения первый пешеход догонит второго?
В самом начале пути между пешеходами было расстояние 900 м. Через минуту после начала движения расстояние между ними будет составлять 895 метров, поскольку первый пешеход двигается на 5 метров в минуту быстрее второго:
90 ∙ 1 = 90 м
85 ∙ 1 = 85 м
900 + 85 – 90 = 985 – 90 = 895 м
Через три минуты после начала движения расстояние уменьшится на 15 метров и будет составлять 885 метров. Это был наш ответ на первый вопрос задачи:
90 ∙ 3 = 270 м
85 ∙ 3 = 255 м
900 + 255 – 270 = 1155 – 270 = 885 м
Можно сделать вывод, что каждую минуту расстояние между пешеходами будет уменьшаться на 5 метров.
А раз изначальные 900 метров с каждой минутой уменьшаются на одинаковые 5 метров, то мы можем узнать сколько раз 900 метров содержат по 5 метров, тем самым определяя через сколько минут первый пешеход догонит второго:
900 : 5 = 180 минут.
Ответ: через три минуты расстояние между пешеходами будет составлять 885 метров, первый пешеход догонит второго через 180 минут = 3 часа.
Разбор решения заданий тренировочного модуля
№1. Тип задания: ввод с клавиатуры пропущенных элементов в тексте
Заполните таблицу:
S | v | t | |
1. | 135 км | 9 км/ч | ____ ч |
2. | ____ м | 12 м/с | 4 с |
3. | 132 м | ____ м/мин | 11 мин |
Для заполнения пропусков воспользуемся формулами нахождения скорости, времени, расстояния:
- Надо найти время: t = S : v
135 : 9 = 15 часов.
- Надо найти расстояние: S = v ∙ t
12 ∙ 4 = 48 м.
- Надо найти скорость: v = S : t
132 : 11 = 12 м/мин.
Верный ответ:
S | v | t | |
1. | 135 км | 9 км/ч | 15 часов |
2. | 48 м | 12 м/с | 4 с |
3. | 132 м | 12 м/мин | 11 мин |
№2. Тип задания: единичный / множественный выбор
Выберите верный ответ к задаче:
Из пунктов А и В, расстояние между которыми 300 км, отправились одновременно навстречу друг другу мотоциклист и автомобилист. Скорость автомобиля 60 км/ч, а мотоцикла 30 км/ч. Какое расстояние будет между ними через 3 часа?
Варианты ответов:
- 70
- 30
- 270
- 240
Эта задача относится к типу задач на сближение, т.е. нам надо:
- сложить скорости мотоциклиста и автомобилиста:
60 + 30 = 90 км/ч – скорость сближения;
- узнать, сколько километров они пройдут за 3 часа вместе.
 Для этого:
Для этого:
90 ∙ 3 = 270 км;
- из общего расстояния нам осталось вычесть пройденное:
300 – 270 = 30 км
Верный ответ: 2. 30 км.
Формулы скорость время расстояние таблица. Как найти скорость время и расстояние
Давайте школьный урок физики превратим в увлекательную игру! В этой статье нашей героиней станет формула «Скорость, время, расстояние». Разберем отдельно каждый параметр, приведем интересные примеры.
Скорость
Что же такое «скорость»? Можно наблюдать, как одна машина едет быстрее, другая -медленее; один человек идет быстрым шагом, другой — не торопится. Велосипедисты тоже едут с разной скоростью. Да! Именно скоростью. Что же под ней подразумевается? Конечно же, расстояние, которое прошел человек. проехала машина за какое-то Допустим, что 5 км/ч. То есть за 1 час он прошел 5 километров.
Формула пути (расстояния) — произведение скорости и времени. Конечно же, самый удобный и доступный параметр — это время.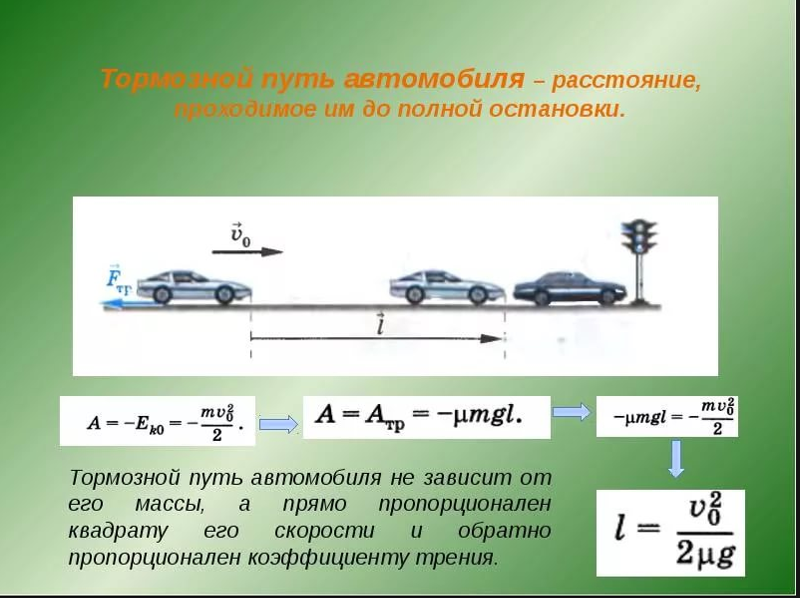 Часы есть у всех. Скорость пешехода не строго 5 км/ч, а приблизительно. Поэтому здесь может быть погрешность. В таком случае, вам лучше взять карту местности. Обратите внимание, какой масштаб. Должно быть указано, сколько километров или метров в 1 см. Приложите линейку и замерьте длину. Например, от дома до музыкальной школы прямая дорога. Отрезок получился 5 см. А в масштабе указано 1 см = 200 м. Значит, реальное расстояние — 200*5=1000 м=1 км. За сколько вы проходите это расстояние? За полчаса? Выражаясь техническим языком, 30 мин=0,5 ч=(1/2) ч. Если мы решим задачу, то получится, что идете со скоростью 2 км/ч. Всегда вам поможет решить задачу формула «скорость, время, расстояние».
Часы есть у всех. Скорость пешехода не строго 5 км/ч, а приблизительно. Поэтому здесь может быть погрешность. В таком случае, вам лучше взять карту местности. Обратите внимание, какой масштаб. Должно быть указано, сколько километров или метров в 1 см. Приложите линейку и замерьте длину. Например, от дома до музыкальной школы прямая дорога. Отрезок получился 5 см. А в масштабе указано 1 см = 200 м. Значит, реальное расстояние — 200*5=1000 м=1 км. За сколько вы проходите это расстояние? За полчаса? Выражаясь техническим языком, 30 мин=0,5 ч=(1/2) ч. Если мы решим задачу, то получится, что идете со скоростью 2 км/ч. Всегда вам поможет решить задачу формула «скорость, время, расстояние».
Не упустите!
Советую вам не упускать очень важные моменты. Когда вам дается задача, смотрите внимательно, в каких единицах измерения даны параметры. Автор задачи может схитрить. Напишет в дано:
Человек проехал по тротуару на велосипеде 2 километра за 15 минут. Не спешите сразу решать задачу по формуле, иначе у вас получится ерунда, а учитель ее вам не засчитает. Помните, что ни в коем случае нельзя делать так: 2 км/15 мин. У вас единица измерения получится км/мин, а не км/ч. Вам нужно добиться последнего. Переведите минуты в часы. Как это сделать? 15 минут — это 1/4 часа или 0,25 ч. Теперь можете смело 2км/0,25ч=8 км/ч. Теперь задача решена верно.
Помните, что ни в коем случае нельзя делать так: 2 км/15 мин. У вас единица измерения получится км/мин, а не км/ч. Вам нужно добиться последнего. Переведите минуты в часы. Как это сделать? 15 минут — это 1/4 часа или 0,25 ч. Теперь можете смело 2км/0,25ч=8 км/ч. Теперь задача решена верно.
Вот так легко запоминается формула «скорость, время, расстояние». Только соблюдайте все правила математики, обращайте внимание на единицы измерения в задаче. Если есть нюансы, как в рассмотренном чуть выше примере, сразу же переводите в систему единиц СИ, как положено.
В этом уроке мы рассмотрим три физические величины, а именно расстояние, скорость и время.
Содержание урокаРасстояние
Расстояние мы уже изучали в уроке . Говоря простым языком, расстояние это длина от одного пункта до другого. (Пример: расстояние от дома до школы 2 километра). Имея дело с большими расстояниями, в основном они будут измеряться в метрах и километрах. Расстояние обозначается латинской буквой S . В принципе, можно обозначить и другой буквой, но буква S общепринята.
В принципе, можно обозначить и другой буквой, но буква S общепринята.
Скорость
Скоростью называют расстояние, пройденное телом за единицу времени. Под единицей времени подразумевается 1 час, 1 минута или 1 секунда.
Предположим, что двое школьников решили проверить, кто быстрее добежит от двора до спортплощадки. Расстояние от двора до спортплощадки 100 метров. Первый школьник добежал за 25 секунд. Второй за 50 секунд. Кто добежал быстрее?
Быстрее добежал тот, кто за 1 секунду пробежал большее расстояние. Говорят, что у него скорость движения больше. В данном случае скорость школьников это расстояние, которое они пробегают за 1 секунду.
Чтобы найти скорость, нужно расстояние разделить на время движения. Давайте найдём скорость первого школьника. Для этого разделим 100 метров на время движения первого школьника, то есть на 25 секунд:
100 м: 25 с = 4
Если расстояние дано в метрах, а время движения в секундах, то скорость измеряется в метрах в секунду (м/с). Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч).
Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч).
У нас расстояние дано в метрах, а время в секундах. Значит скорость измеряется в метрах в секунду (м/с)
100м: 25с = 4 (м/с)
Итак, скорость движения первого школьника составляет 4 метра в секунду (м/с).
Теперь найдем скорость движения второго школьника. Для этого разделим расстояние на время движения второго школьника, то есть на 50 секунд:
100 м: 50 c = 2 (м/с)
Значит скорость движения второго школьника составляет 2 метра в секунду (м/с).
Скорость движения первого школьника — 4 (м/с)
Скорость движения второго школьника — 2 (м/с)
4 (м/с) > 2 (м/с)
Скорость первого школьника больше. Значит он добежал до спортплощадки быстрее. Скорость обозначается латинской буквой v.
Время
Иногда возникает ситуация, когда требуется узнать за какое время тело преодолеет то или иное расстояние.
Например, от дома до спортивной секции 1000 метров. Мы должны доехать туда на велосипеде. Наша скорость будет 500 метров в минуту (500м/мин). За какое время мы доедем до спортивной секции?
Если за одну минуту мы будем проезжать 500 метров, то сколько таких минут с пятью ста метрами будет в 1000 метрах? Очевидно, что надо разделить 1000 метров на то расстояние, которое мы будем проезжать за одну минуту, то есть на 500 метров. Тогда мы получим время, за которое мы доедем до спортивной секции:
1000: 500 = 2 (мин)
Время движения обозначается маленькой латинской буквой t .
Взаимосвязь скорости, времени, расстоянияСкорость принято обозначать маленькой латинской буквой v, время движения – маленькой буквой t , пройденное расстояние – маленькой буквой s. Скорость, время и расстояние связаны между собой.
Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время:
s = v × t
Например, мы вышли из дома и направились в магазин. Мы дошли до магазина за 10 минут. Наша скорость была 50 метров в минуту. Зная свою скорость и время, мы можем найти расстояние.
Мы дошли до магазина за 10 минут. Наша скорость была 50 метров в минуту. Зная свою скорость и время, мы можем найти расстояние.
Если за одну минуту мы прошли 50 метров, то сколько таких пятьдесят метров мы пройдем за 10 минут? Очевидно, что умножив 50 метров на 10, мы определим расстояние от дома до магазина.
v = 50 (м/мин)
t = 10 минут
s = v × t = 50 × 10 = 500 (метров до магазина)
Если известно время и расстояние, то можно найти скорость:
v = s: t
Например, расстояние от дома до школы 900 метров. Школьник дошел до этой школы за 10 минут. Какова была его скорость?
Скорость движения школьника это расстояние, которое он проходит за одну минуту. Если за 10 минут он преодолел 900 метров, то какое расстояние он преодолевал за одну минуту?
Чтобы ответить на этот, нужно разделить расстояние на время движения школьника:
s = 900 метров
t = 10 минут
v = s: t = 900: 10 = 90 (м/мин)
Если известна скорость и расстояние, то можно найти время:
t = s: v
Например, от дома до спортивной секции 500 метров. Мы должны дойти до неё пешком. Наша скорость будет 100 метров в минуту (100 м/мин). За какое время мы дойдем до спортивной секции?
Мы должны дойти до неё пешком. Наша скорость будет 100 метров в минуту (100 м/мин). За какое время мы дойдем до спортивной секции?
Если за одну минуту мы будем проходить 100 метров, то сколько таких минут со ста метрами будет в 500 метрах?
Чтобы ответить на этот вопрос нужно 500 метров разделить на расстояние, которое мы будем проходить за одну минуту, то есть на 100. Тогда мы получим время, за которое мы дойдем до спортивной секции:
s = 500 метров
v = 100 (м/мин)
t = s: v = 500: 100 = 5 (минут до спортивной секции)
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Как решать задачи на движение? Формула зависимости между скоростью, временем и расстоянием. Задачи и решения.
Формула зависимости времени, скорости и расстояния за 4 класс: как обозначается скорость, время, расстояние?
Люди, животные или машины могут двигаться с определенной скоростью. За определенное время они могут пройти определенный путь. Например: сегодня вы можете дойти до своей школы за полчаса. Вы идете с определенной скоростью и преодолеваете 1000 метров за 30 минут. Путь, который преодолевается, в математике обозначают буквой S . Скорость обозначается буквой v . А время, за которое пройден путь, обозначается буквой t .
За определенное время они могут пройти определенный путь. Например: сегодня вы можете дойти до своей школы за полчаса. Вы идете с определенной скоростью и преодолеваете 1000 метров за 30 минут. Путь, который преодолевается, в математике обозначают буквой S . Скорость обозначается буквой v . А время, за которое пройден путь, обозначается буквой t .
- Путь — S
- Скорость — v
- Время — t
Если вы опаздываете в школу, вы можете этот же путь пройти за 20 минут, увеличив свою скорость. А значит, один и тот же путь может быть пройден за разное время и с различной скоростью.
Как зависит время прохождения пути от скорости?
Чем больше скорость, тем быстрее будет пройдено расстояние. И чем меньше скорость, тем больше времени понадобится для прохождения пути.
Как найти время, зная скорость и расстояние?
Для того, чтобы найти время, понадобившееся для прохождения пути, нужно знать расстояние и скорость. Если расстояние разделить на скорость — вы узнаете время. Пример такой задачи:
Если расстояние разделить на скорость — вы узнаете время. Пример такой задачи:
Задача про Зайца. Заяц убегал от Волка со скоростью 1 километр за минуту. Он пробежал до своей норы 3 километра. За какое время Заяц добежал до норы?
Как легко решать задачи на движение, где нужно найти расстояние, время или скорость?
- Внимательно прочитайте задачу и определите, что известно из условия задачи.
- Напишите на черновике эти данные.
- Также напишите, что неизвестно и что нужно найти
- Воспользуйтесь формулой для задач про расстояние, время и скорость
- Введите в формулу известные данные и решите задачу
Решение для задачи про Зайца и Волка.
- Из условия задачи определяем, что нам известно скорость и расстояние.
- Также из условия задачи определяем, что нам нужно найти время, которое нужно было зайцу, чтобы добежать до норы.
Пишем в черновик эти данные например так:
Время — неизвестно
Теперь запишем то же самое математическими знаками:
S — 3 километра
V — 1 км/мин
t — ?
Вспоминаем и записываем в тетрадь формулу для нахождения времени:
t = S: v
t = 3: 1 = 3 минуты
Как найти скорость, если известно время и расстояние?
Для то, чтобы найти скорость, если известно время и расстояние, нужно расстояние разделить на время. Пример такой задачи:
Пример такой задачи:
Заяц убегал от Волка и пробежал до своей норы 3 километра. Он преодолел это расстояние за 3 минуты. С какой скоростью бежал Заяц?
Решение задачи на движение:
- В черновик записываем, что нам известно расстояние и время.
- Из условия задачи определяем, что нужно найти скорость
- Вспоминаем формулу для нахождения скорости.
Формулы для решения таких задач показаны на картинке ниже.
Формулы для решения задач про расстояние, время и скорость
Подставляем известные данные и решаем задачу:
Расстояние до норы — 3 километра
Время, за которое Заяц добежал до норы — 3 минуты
Скорость — неизвестна
Запишем эти известные данные математическими знаками
S — 3 километра
t — 3 минуты
v — ?
Записываем формулу для нахождения скорости
v = S: t
Теперь запишем решение задачи цифрами:
v = 3: 3 = 1 км/мин
Как найти расстояние, если известно время и скорость?
Чтобы найти расстояние, если известно время и скорость нужно время умножить на скорость. Пример такой задачи:
Пример такой задачи:
Заяц убегал от Волка со скоростью 1 километр за 1 минуту. Чтобы добежать до норы ему понадобилось три минуты. Какое расстояние пробежал Заяц?
Решение задачи: Записываем в черновик, что нам известно из условия задачи:
Скорость Зайца — 1 километр за 1 минуту
Время, которое Заяц бежал до норы — 3 минуты
Расстояние — неизвестно
Теперь, то же самое запишем математическими знаками:
v — 1 км/мин
t — 3 минуты
S — ?
Вспоминаем формулу для нахождения расстояния:
S = v ⋅ t
Теперь запишем решение задачи цифрами:
S = 3 ⋅ 1 = 3 км
Как научиться решать более сложные задачи?
Чтобы научиться решать более сложные задачи нужно понять как решаются простые, запомнить какими знаками обозначаются расстояние, скорость и время. Если не получается запомнить математические формулы их нужно выписать на лист бумаги и всегда держать под рукой во время решения задач. Решайте с ребенком несложные задачи, которые можно придумать на ходу, например во время прогулки.
Решайте с ребенком несложные задачи, которые можно придумать на ходу, например во время прогулки.
Ребенок, который умеет решать задачи, может гордиться собой
Когда решают задачи про скорость, время и расстояние, очень часто делают ошибку, из-за того, что забыли перевести единицы измерения.
ВАЖНО: Единицы измерения могут быть любыми, но, если в одной задаче есть разные единицы измерения, переведите их одинаковые. Например, если скорость измерена в километрах за минуту, то расстояние обязательно должно быть представлено в километрах, а время в минутах.
Для любознательных : Общепринятая сейчас система мер называется метрической, но так было не всегда, и в старину на Руси использовали другие единицы измерения.
Задача про удава : Слоненок и мартышка мерили длину удава шагами. Они двигались навстречу друг другу. Скорость мартышка была 60 см за одну секунду, а скорость слоненка 20 см за одну секунду. На измерение они потратили 5 секунд. Какова длина удава? (решение под картинкой)
Какова длина удава? (решение под картинкой)
Решение:
Из условия задачи определяем, что нам известно скорость мартышки и слоненка и время, которое им понадобилось для измерения длины удава.
Запишем эти данные:
Скорость мартышки — 60 см/сек
Скорость слоненка — 20 см/сек
Время — 5 секунд
Расстояние неизвестно
Запишем эти данные математическими знаками:
v1 — 60 см/сек
v2 — 20 см/сек
t — 5 секунд
S — ?
Запишем формулу для расстояние, если известна скорость и время:
S = v ⋅ t
Посчитаем, какое расстояние прошла мартышка:
S1 = 60 ⋅ 5 = 300 см
Теперь посчитаем, сколько прошел слоненок:
S2 = 20 ⋅ 5 = 100 см
Суммируем расстояние, которое прошла мартышка и расстояние, которое прошел слоненок:
S = S1 + S2 = 300 + 100 = 400 см
График зависимости скорости тела от времени: фото
Расстояние, преодолеваемое с разной скорость преодолевается за разное время. Чем больше скорость — тем меньше потребуется времени для передвижения.
Чем больше скорость — тем меньше потребуется времени для передвижения.
Таблица 4 класс: скорость, время, расстояние
В таблице ниже приведены данные для которых нужно придумать задачи, а потом их решить.
| № | Скорость (км/час) | Время (час) | Расстояние (км) |
| 1 | 5 | 2 | ? |
| 2 | 12 | ? | 12 |
| 3 | 60 | 4 | ? |
| 4 | ? | 3 | 300 |
| 5 | 220 | ? | 440 |
Вы можете пофантазировать и придумать задачи к таблице сами. Ниже наши варианты условия задач:
- Мама отправила Красную Шапочку к бабушке. Девочка постоянно отвлекалась и шла по лесу медленно, со скоростью 5 км/час. На путь она потратила 2 часа. Какое расстояние за это время прошла Красная Шапочка?
- Почтальон Печкин вез на велосипеде посылку со скоростью 12 км/час.
 Он знает, что расстояние между его домом и домом Дяди Федора 12 км. Помогите Печкину рассчитать, сколько времени понадобится на дорогу?
Он знает, что расстояние между его домом и домом Дяди Федора 12 км. Помогите Печкину рассчитать, сколько времени понадобится на дорогу? - Папа Ксюши купил автомобиль и решил отвезти семью на море. Машина ехала со скоростью 60 км/час и на дорогу было потрачено 4 часа. Какое расстояние между домом Ксюши и морским побережьем?
- Утки собрались в клин и полетели в теплые края. Птицы махали крыльями без устали 3 часа и преодолели за это время 300 км. Какой была скорость птиц?
- Самолет АН-2 летит со скоростью 220 км/час. Он вылетел из Москвы и летит в Нижний Новгород, расстояние между этими двумя городами 440 км. Сколько времени самолет будет в пути?
Ответы на приведенные задачи можно найти в таблице ниже:
| № | Скорость (км/час) | Время (час) | Расстояние (км) |
| 1 | 5 | 2 | 10 |
| 2 | 12 | 1 | 12 |
| 3 | 60 | 4 | 240 |
| 4 | 100 | 3 | 300 |
| 5 | 220 | 2 | 440 |
Примеры решения задач на скорость, время, расстояние за 4 класс
Если в одной задаче есть несколько объектов движения, нужно научить ребенка рассматривать движение этих объектов отдельно и только потом вместе. Пример такой задачи:
Пример такой задачи:
Двое друзей Вадик и Тема решили прогуляться и вышли из своих домов навстречу друг другу. Вадик ехал на велосипеде, а Тема шел пешком. Вадик ехал со скоростью 10 км/час, а Тема шел со скоростью 5 км в час. Через час они встретились. Какое расстояние между домами Вадика и Темы?
Эту задачу можно решить используя формулу зависимости расстояния от скорости и времени.
S = v ⋅ t
Расстояние, которое проехал Вадик на велосипеде будет равно его скорости умноженной на время в пути.
S = 10 ⋅ 1 = 10 километров
Расстояние, которое прошел Тема считают аналогично:
S = v ⋅ t
Подставляем в формулу цифровые значения его скорости и времени
S = 5 ⋅ 1 = 5 километров
Расстояние, которое проехал Вадик нужно прибавить к расстоянию, которое прошел Тема.
10 + 5 = 15 километров
Как научиться решать сложные задачи, для решения которых требуется логически мыслить?
Развивать логическое мышление ребенка, нужно решая с ним простые, а затем и сложные логические задачи. Эти задачи могут состоять из нескольких этапов. Перейти с одного этапа на другой можно только в том случае, если решен предыдущий. Пример такой задачи:
Эти задачи могут состоять из нескольких этапов. Перейти с одного этапа на другой можно только в том случае, если решен предыдущий. Пример такой задачи:
Антон ехал на велосипеде со скоростью 12 км/час, а Лиза ехала на самокате со скоростью в 2 раза меньше, чем у Антона, а Денис шел пешком со скоростью в 2 раза меньше, чем у Лизы. Какова скорость Дениса?
Чтобы решить эту задачу нужно сначала узнать скорость Лизы и только после этого скорость Дениса.
Кто едет быстрее? Задача про друзей
Иногда в учебниках для 4 класса попадаются непростые задачи. Пример такой задачи:
Два велосипедиста выехали из разных городов навстречу друг другу. Один из них спешил и мчался со скоростью 12 км/час, а второй ехал не спеша со скоростью 8 км/час. Расстояние между городами из которых выехали велосипедисты 60 км. Какое расстояние проедет каждый велосипедист, перед тем как они встретятся? (решение под фото)
Решение:
- 12+8 = 20 (км/час) — это общая скорость двух велосипедистов, или скорость с которой они приближались друг к другу
- 60 : 20 = 3 (часа) — это время через которое велосипедисты встретились
- 3 ⋅ 8 = 24 (км) — это расстояние, которое проехал первый велосипедист
- 12 ⋅ 3 = 36 (км) — это расстояние, которое проехал второй велосипедист
- Проверка: 36+24=60 (км) — это расстояние, которое проехали два велосипедиста.

- Ответ: 24 км, 36 км.
Предлагайте детям в форме игры решать такие задачи. Возможно, они сами захотят составить свою задачу про друзей, животных или птиц.
ВИДЕО: Задачи на движение
Чтобы вычислить среднюю скорость, воспользуйтесь простой формулой: Скорость = Пройденный путь Время {\displaystyle {\text{Скорость}}={\frac {\text{Пройденный путь}}{\text{Время}}}} . Но в некоторых задачах даются два значения скорости — на разных участках пройденного пути или в различные промежутки времени. В этих случаях нужно пользоваться другими формулами для вычисления средней скорости. Навыки решения подобных задач могут пригодиться в реальной жизни, а сами задачи могут встретиться на экзаменах, поэтому запомните формулы и уясните принципы решения задач.
Шаги
По одному значению пути и одному значению времени
- длина пути, пройденного телом;
- время, за которое тело прошло этот путь.
- Например: автомобиль проехал 150 км за 3 ч.
 Найдите среднюю скорость автомобиля.
Найдите среднюю скорость автомобиля.
Формула: , где v {\displaystyle v} — средняя скорость, s {\displaystyle s} — пройденный путь, t {\displaystyle t} — время, за которое пройден путь.
В формулу подставьте пройденный путь. Значение пути подставьте вместо s {\displaystyle s} .
- В нашем примере автомобиль проехал 150 км. Формула запишется так: v = 150 t {\displaystyle v={\frac {150}{t}}} .
В формулу подставьте время. Значение времени подставьте вместо t {\displaystyle t} .
- В нашем примере автомобиль ехал в течение 3 ч. Формула запишется так: .
Разделите путь на время. Вы найдете среднюю скорость (как правило, она измеряется в километрах в час).
- В нашем примере:
v = 150 3 {\displaystyle v={\frac {150}{3}}}Таким образом, если автомобиль проехал 150 км за 3 ч, то он двигался со средней скоростью 50 км/ч.
Вычислите общий пройденный путь. Для этого сложите значения пройденных участков пути. В формулу подставьте общий пройденный путь (вместо s {\displaystyle s} ).
Для этого сложите значения пройденных участков пути. В формулу подставьте общий пройденный путь (вместо s {\displaystyle s} ).
- В нашем примере автомобиль проехал 150 км, 120 км и 70 км. Общий пройденный путь: .
T {\displaystyle t} ).
- . Таким образом, формула запишется так: .
- В нашем примере:
v = 340 6 {\displaystyle v={\frac {340}{6}}}Таким образом, если автомобиль проехал 150 км за 3 ч, 120 км за 2 ч, 70 км за 1 ч, то он двигался со средней скоростью 57 км/ч (округленно).
По нескольким значениям скоростей и нескольким значениям времени
Посмотрите на данные величины. Воспользуйтесь этим методом, если даны следующие величины:
Запишите формулу для вычисления средней скорости. Формула: v = s t {\displaystyle v={\frac {s}{t}}} , где v {\displaystyle v} — средняя скорость, s {\displaystyle s} — общий пройденный путь, t {\displaystyle t} — общее время, за которое пройден путь.

Вычислите общий путь. Для этого умножьте каждую скорость на соответствующее время. Так вы найдете длину каждого участка пути. Чтобы вычислить общий путь, сложите значения пройденных участков пути. В формулу подставьте общий пройденный путь (вместо s {\displaystyle s} ).
- Например:
50 км/ч в течение 3 ч = 50 × 3 = 150 {\displaystyle 50\times 3=150} км
60 км/ч в течение 2 ч = 60 × 2 = 120 {\displaystyle 60\times 2=120} км
70 км/ч в течение 1 ч = 70 × 1 = 70 {\displaystyle 70\times 1=70} км
Общий пройденный путь: 150 + 120 + 70 = 340 {\displaystyle 150+120+70=340} км. Таким образом, формула запишется так: v = 340 t {\displaystyle v={\frac {340}{t}}} .
- Например:
Вычислите общее время в пути. Для этого сложите значения времени, за которые был пройден каждый участок пути. В формулу подставьте общее время (вместо t {\displaystyle t} ).
- В нашем примере автомобиль ехал в течение 3 ч, 2 ч и 1 ч.
 Общее время в пути: 3 + 2 + 1 = 6 {\displaystyle 3+2+1=6}
. Таким образом, формула запишется так: v = 340 6 {\displaystyle v={\frac {340}{6}}}
.
Общее время в пути: 3 + 2 + 1 = 6 {\displaystyle 3+2+1=6}
. Таким образом, формула запишется так: v = 340 6 {\displaystyle v={\frac {340}{6}}}
.
- В нашем примере автомобиль ехал в течение 3 ч, 2 ч и 1 ч.
Разделите общий путь на общее время. Вы найдете среднюю скорость.
- В нашем примере:
v = 340 6 {\displaystyle v={\frac {340}{6}}}
v = 56 , 67 {\displaystyle v=56,67}
Таким образом, если автомобиль двигался со скоростью 50 км/ч в течение 3 ч, со скоростью 60 км/ч в течение 2 ч, со скоростью 70 км/ч в течение 1 ч, то он двигался со средней скоростью 57 км/ч (округленно).
- В нашем примере:
По двум значениям скоростей и двум одинаковым значениям времени
Посмотрите на данные величины. Воспользуйтесь этим методом, если даны следующие величины и условия:
- два или несколько значений скоростей, с которыми двигалось тело;
- тело двигалось с определенными скоростями в течение равных промежутков времени.
- Например: автомобиль двигался со скоростью 40 км/ч в течение 2 ч и со скоростью 60 км/ч в течение других 2 ч.
 Найдите среднюю скорость автомобиля на всем протяжении пути.
Найдите среднюю скорость автомобиля на всем протяжении пути.
Запишите формулу для вычисления средней скорости, если даны две скорости, с которыми тело движется в течение равных промежутков времени. Формула: v = a + b 2 {\displaystyle v={\frac {a+b}{2}}} , где v {\displaystyle v} — средняя скорость, a {\displaystyle a} — скорость тела в течение первого промежутка времени, b {\displaystyle b} — скорость тела в течение второго (такого же, как первый) промежутка времени.
- В таких задачах значения промежутков времени не важны — главное, чтобы они были равны.
- Если дано несколько значений скоростей и равные промежутки времени, перепишите формулу так: v = a + b + c 3 {\displaystyle v={\frac {a+b+c}{3}}} или v = a + b + c + d 4 {\displaystyle v={\frac {a+b+c+d}{4}}} . Если промежутки времени равны, сложите все значения скоростей и разделите их на количество таких значений.
В формулу подставьте значения скоростей.
 Неважно, какое значение подставить вместо a {\displaystyle a} , а какое — вместо b {\displaystyle b} .
Неважно, какое значение подставить вместо a {\displaystyle a} , а какое — вместо b {\displaystyle b} .- Например, если первая скорость равна 40 км/ч, а вторая скорость равна 60 км/ч, формула запишется так: .
Сложите значения двух скоростей. Затем сумму разделите на два. Вы найдете среднюю скорость на всем протяжении пути.
- Например:
v = 40 + 60 2 {\displaystyle v={\frac {40+60}{2}}}
v = 100 2 {\displaystyle v={\frac {100}{2}}}
v = 50 {\displaystyle v=50}
Таким образом, если автомобиль двигался со скоростью 40 км/ч в течение 2 ч и со скоростью 60 км/ч в течение других 2 ч, средняя скорость автомобиля на всем протяжении пути составила 50 км/ч.
- Например:
t = S: V
15: 3 = 5 (с)
Составим выражение: 5 3: 3 = 5 (с) Ответ: 5 с потребуется слепню.
Реши задачу.
1. Катер, двигаясь со скоростью 32 км/ч, прошёл путь между пристанями за 2 ч. Сколько потребуется времени, чтобы пройти этот же путь на лодке, если она движется со скоростью 8 км/ч?
2. Велосипедист, двигаясь со скоростью 10 км/ч, проехал путь между деревнями за 4 ч. Сколько
Велосипедист, двигаясь со скоростью 10 км/ч, проехал путь между деревнями за 4 ч. Сколько
потребуется времени пешеходу, чтобы пройти этот же путь, если он движется со скоростью 15 км/ч?
Составные задачи на время. II тип.
Образец:
Многоножка сначала бежала 3 мин со скоростью 2 дм/м, а потом она побежала со скоростью 3 дм/м. За какое время многоножка пробежала оставшийся путь, если всего она пробежала 15 дм? Рассуждаем так. Это задача на движение в одном направлении. Составим таблицу. Слова «скорость», «время», «расстояние» запишем в таблице зелёной ручкой.
Скорость (V) Время (t) Расстояние (S)
С. — 2 дм/мин З мин?дм
П.-3 дм/мин? ? мин?дм 15дм
Составим план решения этой задачи. Чтобы узнать, время многоножки потом, надо узнать какое расстояние она пробежала потом, а для этого надо знать, какое расстояние она пробежала сначала.
t п S п S с
S с = V с · t
2 3 = 6 (м) — расстояние, которое пробежала многоножка сначала.
S п = S — S с
15 — 6 = 9 (м) — расстояние, которое пробежала многоножка потом.
Чтобы найти время, надо расстояние разделить на скорость.
9: 3 = 3(мин)
Ответ: за 3 мин многоножка пробежала оставшийся путь.
Реши задачу.
1. Волк бежал по лесу 3 ч со скоростью 8 км/ч. По полю он бежал со скоростью 10 км/ч. Сколько времени волк бежал по полю, если он пробежал 44 км?
2. Рак до коряги полз 3 мин со скоростью 18 м/мин. Остальной путь он полз со скоростью 16 м/мин. Сколько времени потребовалось раку на остальной путь, если он прополз 118м?
3. Гена добежал до футбольной площадки за 48 с со скоростью 6 м/с, а потом он побежал к школе со скоростью 7 м/с. Через какое время Гена добежит до школы, если он пробежал 477 м?
4. Пешеход шёл до остановки 3 ч со скоростью 5 км/ч, после остановки он пошёл со скоростью 4 км/ч. Сколько времени пешеход был в пути после остановки, если он прошёл 23 км?
5. Уж плыл до коряги 10с со скоростью 8 дм/с, а потом он поплыл до берега со скоростью 6 дм/с. За какое время доплыл уж до берега, если он проплыл 122дм?
Уж плыл до коряги 10с со скоростью 8 дм/с, а потом он поплыл до берега со скоростью 6 дм/с. За какое время доплыл уж до берега, если он проплыл 122дм?
Составные задачи на скорость. I тип
Образец:
Из норки побежали два ёжика. Один бежал 6 с со скоростью 2 м/с. С какой скоростью должен бежать другой ёжик, чтобы преодолеть это расстояние за 3 с? Рассуждаем так. Это задача на движение в одном направлении. Составим таблицу. Слова «скорость», «время», «расстояние» запишем в таблице зелёной ручкой.
Скорость (V) Время (1) Расстояние (8)
I — 2 м/с 6 с одинаковое
II — ?м/с 3 с
Составим план решения этой задачи. Чтобы найти скорость второго ёжика, надо найти расстояние, которое пробежал первый ёжик.
Чтобы найти расстояние, надо скорость умножить на время.
S = V I · t I
2 · 6 = 12 (м) – расстояние, которое пробежал первый ежик.
Чтобы найти скорость, надо расстояние разделить на время.
V II = S: t II
12:3 = 4(м/с)
Составим выражение: 2 6:3 = 4 (м/с)
Ответ; 4м/с скорость второго ёжика.
Реши задачу.
1. Один кальмар плыл 4 с со скоростью 10 м/с. С какой скоростью должен плыть другой кальмар, чтобы преодолеть это расстояние за 5 с?
2. Трактор, двигаясь со скоростью 9 км/ч, прошёл путь между деревнями за 2 ч. С какой скоростью должен идти пешеход, чтобы преодолеть это расстояние за 3 ч?
3. Автобус, двигаясь со скоростью 64 км/ч, прошёл путь между городами за 2 ч. С какой скоростью должен ехать велосипедист, чтобы преодолеть это расстояние за 8 ч?
4. Чёрный стриж летел 4 мин со скоростью 3 км/мин. С какой скоростью должна лететь утка кряква, чтобы преодолеть это расстояние за 6 мин?
Составные задачи на скорость. II тип
Лыжник до горки ехал 2 ч со скоростью 15 км/ч, а потом по лесу он ехал ещё 3 ч. С какой скоростью лыжник будет ехать по лесу, если всего он проехал 66км?
Калькулятор скорости, времени и расстояния при свободном падении • Механика • Онлайн-конвертеры единиц измерения
Внутри спускаемого аппарата Союз ТМА-19М в экспозиции Музея науки в Лондоне
Определения и формулы
В классической механике состояние объекта, который свободно движется в гравитационном поле, называется свободным падением. Если объект падает в атмосфере, на него действует дополнительная сила сопротивления и его движение зависит не только от гравитационного ускорения, но и от его массы, поперечного сечения и других факторов. Однако на тело, падающее в вакууме, действует только одна сила, а именно сила тяжести.
Если объект падает в атмосфере, на него действует дополнительная сила сопротивления и его движение зависит не только от гравитационного ускорения, но и от его массы, поперечного сечения и других факторов. Однако на тело, падающее в вакууме, действует только одна сила, а именно сила тяжести.
Примерами свободного падения являются космические корабли и спутники на околоземной орбите, потому что на них действует единственная сила — земное притяжение. Планеты, вращающиеся вокруг Солнца, также находятся в свободном падении. Предметы, падающие на землю с небольшой скоростью, также могут считаться свободно падающими, так как в этом случае сопротивление воздуха незначительно и им можно пренебречь. Если единственной силой, действующей на предметы, является сила тяжести, а сопротивление воздуха отсутствует, ускорение одинаково для всех предметов и равно ускорению свободного падения на поверхности Земли 9,8 метров в секунду за секунду second (м/с²) или 32,2 фута в секунду за секунду (фут/ с²). На поверхности других астрономических тел ускорение свободного падения будет другим.
На поверхности других астрономических тел ускорение свободного падения будет другим.
Командный модуль Аполлона-14 в Космическом центре им. Кеннеди, Флорида
Парашютисты, конечно, говорят, что перед раскрытием парашюта они в свободном падении, но на самом деле в свободном падении парашютист не может быть никогда, даже если парашют еще не раскрыт. Да, на парашютиста в «свободном падении» действует сила притяжения, но на него также действует противоположная сила — сопротивление воздуха, причем сила сопротивления воздуха лишь слегка меньше силы земного притяжения.
Если бы не было сопротивления воздуха, скорость тела, находящегося в свободном падении, каждую секунду увеличивалась бы на 9,8 м/с.
Скорость и расстояние свободно падающего тела вычисляется так:
где
v₀ — начальная скорость (м/с).
v — конечная вертикальная скорость (м/с).
h₀ — начальная высота (м).
h — высота падения (м).
t — время падения (с).
g — ускорение свободного падения (9,81 м/с² у поверхности Земли).
Если v₀=0 и h₀=0, имеем:
если известно время свободного падения:
если известно расстояние свободного падения:
если известна конечная скорость свободного падения:
Эти формулы и используются в данном калькуляторе свободного падения.
В свободном падении, когда нет силы для поддержания тела, возникает невесомость. Невесомость — это отсутствие внешних сил, действующих на тело со стороны пола, стула, стола и других окружающих предметов. Иными словами — сил реакции опоры. Обычно эти силы действуют в направлении, перпендикулярном поверхности соприкосновения с опорой, и чаще всего вертикально вверх. Невесомость можно сравнить с плаванием в воде, но так, что кожа воду не ощущает. Все знают это ощущение собственного веса, кода выходишь на берег после долгого купания в море. Именно поэтому для имитации невесомости при тренировках космонавтов и астронавтов используются бассейны с водой.
Само по себе гравитационное поле не может создать давление на ваше тело. Поэтому если вы находитесь в состоянии свободного падения в большом объекте (например, в самолете), который также находится в этом состоянии, на ваше тело не действуют никакие внешние силы взаимодействия тела с опорой и возникает ощущение невесомости, почти такое же, как и в воде.
Самолет для тренировок в условиях невесомости предназначен для создания кратковременной невесомости с целью тренировки космонавтов и астронавтов, а также для выполнения различных экспериментов. Такие самолеты использовались и в настоящее время эксплуатируются в нескольких странах. В течение коротких периодов времени, которые длятся около 25 секунд в течение каждой минуты полета самолет находится в состоянии невесомости, то есть для находящихся в нем людей отсутствует реакция опоры.
Для имитации невесомости использовались различные самолеты: в СССР и в Росси для этого с 1961 года использовались модифицированные серийные самолеты Ту-104АК, Ту-134ЛК, Ту-154МЛК и Ил-76МДК. В США астронавты тренировались с 1959 г. на модифицированных AJ-2, C-131, KC-135 и Boeing 727-200. В Европе Национальным центром космических исследований (CNES, Франция) для тренировок в невесомости используют самолет Airbus A310. Модификация заключается в доработке топливной, гидравлической и некоторых других систем с целью обеспечения их нормальной работы в условиях кратковременной невесомости, а также усиления крыльев для того чтобы самолет мог выдерживать повышенные ускорения (до 2G).
В США астронавты тренировались с 1959 г. на модифицированных AJ-2, C-131, KC-135 и Boeing 727-200. В Европе Национальным центром космических исследований (CNES, Франция) для тренировок в невесомости используют самолет Airbus A310. Модификация заключается в доработке топливной, гидравлической и некоторых других систем с целью обеспечения их нормальной работы в условиях кратковременной невесомости, а также усиления крыльев для того чтобы самолет мог выдерживать повышенные ускорения (до 2G).
Несмотря на то, что иногда при описании условий свободного падения во время космического полета на орбите вокруг Земли говорят об отсутствии гравитации, конечно сила тяжести присутствует в любом космическом аппарате. Что отсутствует, так это вес, то есть сила реакции опоры на объекты, находящиеся в космическом корабле, которые движутся в пространстве с одинаковым ускорением свободного падения, которое только немного меньше, чем на Земле. Например, на околоземной орбите высотой 350 км, на которой Международная космическая станция (МКС) летает вокруг Земли, гравитационное ускорение составляет 8,8 м/с², что всего на 10% меньше, чем на поверхности Земли.
Для описания реального ускорения объекта (обычно летательного аппарата) относительно ускорения свободного падения на поверхности Земли обычно используют особый термин — перегрузка. Если вы лежите, сидите или стоите на земле, на ваше тело действует перегрузка в 1 g (то есть ее нет). Если же вы находитесь в самолете на взлете, вы испытываете перегрузку примерно в 1,5 g. Если тот же самолет выполняет координированный поворот с малым радиусом, то пассажиры, возможно, испытают перегрузку до 2 g, означающую, что их вес удвоился.
Манекен в костюме военного пилота и кислородной маске в Канадском музее авиации и космоса
Люди привыкли жить в условиях отсутствия перегрузок (1 g), поэтому любая перегрузка сильно влияет на человеческий организм. Как и в самолетах-лабораториях для создания невесомости, в которых все системы, работающие с жидкостями, должны быть модифицированы для того, чтобы они правильно работали в условиях нулевой (невесомость) и даже отрицательной перегрузки, люди также нуждаются в помощи и аналогичной «модификации», чтобы выжить в таких условиях. Нетренированный человек может потерять сознание при перегрузке 3–5 g (в зависимости от направления действия перегрузки), так как такая перегрузка достаточна для того, чтоб лишить мозг кислорода, потому что сердце не может подать в него достаточно крови. В связи с этим военные пилоты и космонавты тренируются на центрифугах в условиях высоких перегрузок, чтобы предотвратить потерю сознания при них. Для предотвращения кратковременной потери зрения и сознания, которые, по условиям работы, могут оказаться фатальными, пилоты, космонавты и астронавты надевают высотно-компенсирующие костюмы, который ограничивает отток крови от мозга во время перегрузок путем обеспечения равномерного давления на всю поверхность тела человека.
Нетренированный человек может потерять сознание при перегрузке 3–5 g (в зависимости от направления действия перегрузки), так как такая перегрузка достаточна для того, чтоб лишить мозг кислорода, потому что сердце не может подать в него достаточно крови. В связи с этим военные пилоты и космонавты тренируются на центрифугах в условиях высоких перегрузок, чтобы предотвратить потерю сознания при них. Для предотвращения кратковременной потери зрения и сознания, которые, по условиям работы, могут оказаться фатальными, пилоты, космонавты и астронавты надевают высотно-компенсирующие костюмы, который ограничивает отток крови от мозга во время перегрузок путем обеспечения равномерного давления на всю поверхность тела человека.
Автор статьи: Анатолий Золотков
Формула скорость время расстояние треугольник. Формула нахождения значений скорости, времени и расстояния
Для
всех ступеней коробки передач и
дополнительной коробки рассчитываются
значения
скорости движения автомобиля в зависимости
от частоты вращения коленчатого вала
двигателя (по согласованию с руководителем
расчёт может производиться только
для высшей ступени дополнительной
коробки).
Расчёт ведётся по формуле
где v — скорость автомобиля, км/ч;
n — частота вращения коленчатого вала двигателя, об/мин;
r К — радиус качения, м;
и 0 — передаточное число главной передачи;
и к — передаточное число рассчитываемой ступени коробки передач;
и д — передаточное число рассчитываемой ступени дополнительной (раздаточной) коробки.
Значения частоты вращения коленчатого вала берутся теми же, что и при построении внешней скоростной характеристики.
Рассчитанные значения v t заносятся в столбец 4 табл. 2.1. Графики зависимости скорости движения автомобиля от частоты вращения коленчатого вала двигателя представляют собой серию лучей, выходящих под разными углами из начала координат рисунок 2.2.
Рис.
2.2 Зависимости скорости движения
автомобиля от частоты вращения коленчатого
вала по передачам.
2.6. Тяговая характеристика и тяговый баланс автомобиля
Тяговая характеристика представляет собой зависимость силы тяги автомобиля от скорости движения по передачам. Значения силы тяги Р Т рассчитываются в отдельных точках по формуле
где М К — крутящий момент двигателя, Нм;
η Т — КПД трансмиссии.
Результаты расчёта Р Т заносятся в столбец 7 табл. 2.1, и по ним строятся графики зависимости Р Т = f (V ) по передачам.
Тяговый баланс автомобиля описывается уравнением тягового или силового баланса
Р Т = Р д + Р в + Р и , (2.27)
где Р Т — сила тяги автомобиля, Н;
Р д — суммарная сила сопротивления дороги, Н;
Р в — сила сопротивления воздушной среды, Н;
Р и —
сила инерции автомобиля, Н.
Величина Р д определяется по выражению
Р д = G a ψ , (2.28)
где G a — полный вес автомобиля, Н; ψ — суммарный коэффициент сопротивления дороги.
Суммарный коэффициент сопротивления дороги является величиной, зависящей от скорости автомобиля. Однако учёт этой зависимости сильно осложняет выполнение тягового расчёта и в то же время не даёт важного для практики уточнения. Поэтому при выполнении тягового расчёта рекомендуется принять значение ψ постоянным, равным тому значению, которое было рассчитано для максимальной скорости движения автомобиля при определении мощности двигателя, необходимой для движения на режиме максимальной скорости, т.е. принять везде ψ=ψ v .
При
каком-то одном выбранном значении ψ величина Р д остаётся
постоянной для всех расчётных точек
на всех передачах. Поэтому значение Р д подсчитывается
один раз и в таблицу не заносится. На
графике тяговой характеристики
зависимость P Т = f (v ) представляется
в виде прямой, параллельной оси абсцисс.
На
графике тяговой характеристики
зависимость P Т = f (v ) представляется
в виде прямой, параллельной оси абсцисс.
Рис. 2.3 Тяговая характеристика автомобиля.
Сила сопротивления воздушной среды Р в составляет величину
где с х — коэффициент продольной аэродинамической силы;
р в — плотность воздуха, кг/м 3 ;
к в — коэффициент обтекаемости, кг/м 3 ;
F — лобовая площадь автомобиля, м;
v в — скорость воздушного потока относительно автомобиля, км/ч.
При расчёте можно задать ρ в =1,225 кг/м. Скорость воздушного потока обычно принимается равной скорости движения автомобиля.
Значения Р в рассчитываются
для всех точек и заносятся в столбец 5
табл. 2.1. График зависимости Р в от
скорости представляет собой параболу,
проходящую через начало координат.
Для удобства дальнейшего анализа этот график смещают вверх на величину, равную Р д (в принятом для сил масштабе). Фактически при таком построении этот график выражает зависимость ( P в + P d )= f ( v ).
Сила инерции автомобиля Р и после расчёта Р д и Р в может быть определена как замыкающее слагаемое силового баланса
(2.30)
На
графике значение Р и определяется
отрезком прямой, проведённой для нужного
значения скорости параллельно оси
ординат, между точками пересечения этой
прямой графиков P Т = f [ v ) и ( P д + P в )= f ( v ). Если
заданная скорость может быть обеспечена
на нескольких передачах, то каждой из
этих передач будет соответствовать
своё значение силы инерции. Рассчитанные
значения Р и следует
занести в столбец 6 табл. 2.1.
Если
заданная скорость может быть обеспечена
на нескольких передачах, то каждой из
этих передач будет соответствовать
своё значение силы инерции. Рассчитанные
значения Р и следует
занести в столбец 6 табл. 2.1.
Значение Р Т заносится в столбец 7 табл. 2.1. Тяговая характеристика автомобиля представлена на рис. 2.3.
В данной статье рассказано о том, как найти среднюю скорость. Дано определение этого понятия, а также рассмотрено два важных частных случая нахождения средней скорости. Представлен подробный разбор задач на нахождение средней скорости тела от репетитора по математике и физике.
Определение средней скорости
Средней скоростью движения тела называется отношение пути , пройденного телом, ко времени , в течение которого двигалось тело:
Научимся ее находить на примере следующей задачи:
Обратите внимание, что в данном случае это значение не совпало со средним арифметическим скоростей и , которое равно:
м/с.
Частные случаи нахождения средней скорости
1. Два одинаковых участка пути. Пусть первую половину пути тело двигалось со скоростью , а вторую половину пути — со скоростью . Требуется найти среднюю скорость движения тела.
2. Два одинаковых интервала движения. Пусть тело двигалось со скоростью в течение некоторого промежутка времени, а затем стало двигаться со скоростью в течение такого же промежутка времени. Требуется найти среднюю скорость движения тела.
Здесь мы получили единственный случай, когда средняя скорость движения совпала со средним арифметическим скоростей и на двух участках пути.
Решим напоследок задачу из Всероссийской олимпиады школьников по физике, прошедшей в прошлом году, которая связана с темой нашего сегодняшнего занятия.
Тело двигалось с, и средняя скорость движения составила 4 м/с. Известно, что за последние с движения средняя скорость этого же тела составила 10 м/с. Определите среднюю скорость тела за первые с движения.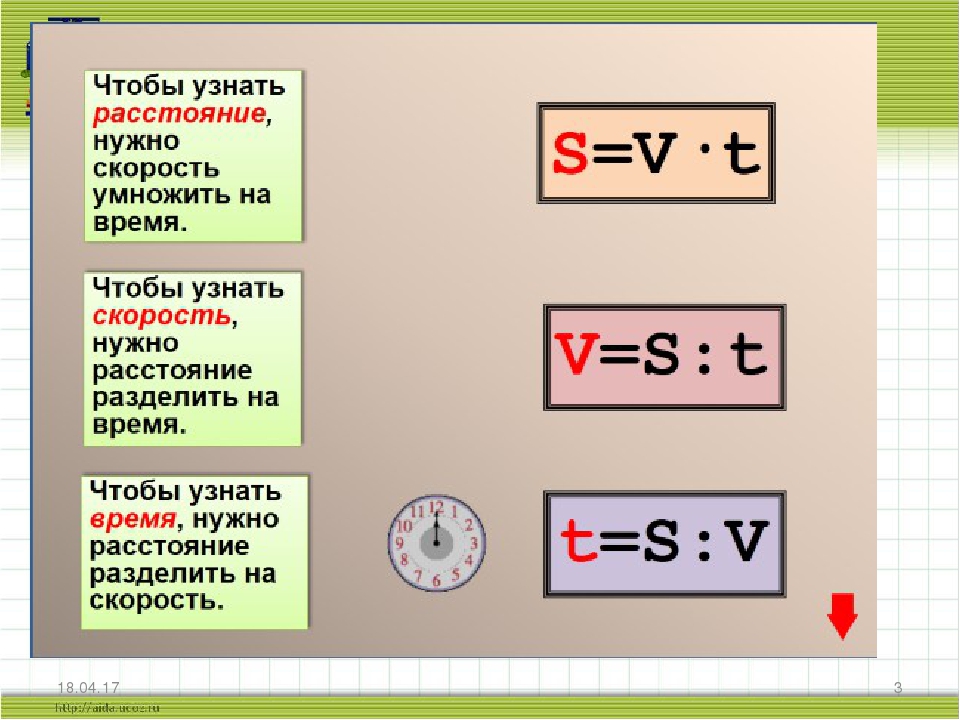 |
Пройденный телом путь составляет: м. Можно найти также путь, который прошло тело за последние с своего движения: м. Тогда за первые с своего движения тело преодолело путь в м. Следовательно, средняя скорость на этом участке пути составила:
м/с.
Задачи на нахождение средней скорости движения очень любят предлагать на ЕГЭ и ОГЭ по физике, вступительных экзаменах, а также олимпиадах. Научиться решать эти задачи должен каждый школьник, если он планирует продолжить свое обучение в вузе. Помочь справиться с этой задачей может знающий товарищ, школьный учитель или репетитор по математике и физике. Удачи вам в изучении физики!
Сергей Валерьевич
Скоростью является тем, насколько быстро движется точка или же тело. Это векторная величина и для того, чтобы задать скорость, необходимо предварительно задать величину скорости, а также непосредственно направление, в сторону которого она измеряется. Рассмотрит то, как рассчитать скорость.
Обычно, скорость рассматривают вдоль траектории движения тела. Тогда, величина будет определяться как путь, который был пройден в единицу времени. Другими словами говоря, для нахождения скорости тела, путь необходимо разделить на время, за которое он был пройден. И в таком случае, формула скорости движения будет выглядеть так: V=S/t.
Тогда, величина будет определяться как путь, который был пройден в единицу времени. Другими словами говоря, для нахождения скорости тела, путь необходимо разделить на время, за которое он был пройден. И в таком случае, формула скорости движения будет выглядеть так: V=S/t.
Как рассчитать среднюю скорость?
В кинематике это понятие является ничем иным, как усредненной характеристикой скорости частиц за время их движения. Есть два основных способа вычисления средней скорости. Средняя скорость пути — это скорость, в которой длина пути, пройденная телом, соотносится со временем, за которое он был пройден. Такая скорость, в отличие от мгновенной скорости, векторной величиной не является. Если тело одинаковые промежутки времени двигалось с одинаковыми скоростями, средняя скорость будет равняться среднему арифметическому от скоростей. Но, если половина пути была с одной скоростью, а вторая половина – с другой, средняя скорость будет равняться среднему гармоническому от всех взятых отдельно скоростей, которые будут равны между собой на разных участках дороги. Формула вычисления следующая:
Формула вычисления следующая:
Как вычислить среднюю скорость по перемещению?
Среднюю скорость можно вывести и по перемещению, она будет векторной, то есть равной по отношению к времени, за которое его совершили. В таком случае, средняя скорость будет равняться нулю в том случае, если тело реально двигалось. Если же перемещение имело место быть по прямой, то средняя путевая скорость будет равна модулю средней скорости по перемещению. Формула выглядит так:
Как рассчитать скорость по тормозному пути?
Тормозным путем является расстояние, которое транспортное средство проходит с момента влияния на тормозную систему транспорта и до полной остановки. Протяженность тормозного пути зависит и от массы, и от скорости, а также состояния проезжей части, погодных условий, шин и так далее. Кроме того, она зависит и от технологических особенностей транспортного средства. В зависимости от того, какие у транспортного средства тормозные колодки, какая логика работы электронных устройств, и других параметров скорость тормозного пути будет разной. 2/2. Из нее следует, что если на торможение дается одинаковое усилие, то тормозной путь будет прямо пропорционален массе тела и квадратно – скорости.
2/2. Из нее следует, что если на торможение дается одинаковое усилие, то тормозной путь будет прямо пропорционален массе тела и квадратно – скорости.
Единицы измерения, естественно, очень важны для всякого рода расчетов, что касается расчетов скорости движения, то тут единицами измерения будут единицы измерения скорости. Но, важно не только знать их, нужно уметь переводить значения в разные величины. Например, скорость измеряется в метрах на секунду (м/с), как перевести такое значение, например, в километры на секунду? Все просто! В одном метре на секунду содержится шесть тысяч сантиметров в минуту и, соответственно, сто сантиметров в секунду. Кроме того, один метр на секунду это три тысячи шестьсот метров в час и шестьдесят метров в минуту. А три и шесть километра в час — это один метр в секунду. Надеемся, что теперь у прочитавших эту статью не будет возникать вопросов о том, как рассчитать скорость движения.
Равномерное движение, это вдвижение спостоянной скоростью. То есть другимим словами, тело за одинаковые промежутки времени должно проходить одинаковое расстояние. Например, если машина будет за каждый час своего пути проезжать расстояние в 50 километров, то такое движение будет являться равномерным.
Например, если машина будет за каждый час своего пути проезжать расстояние в 50 километров, то такое движение будет являться равномерным.
Обычно равномерное движение очень редко можно встретить в реальной жизни. За примеры равномерного движения в природе, можно считать вращение Земли вокруг Солнца. Или например, конец секундной стрелки часов, тоже будет двигаться равномерно.
Расчет скорости при равномерном движении
Скорость тела при равномерном движении будет вычисляться по следующей формуле.
- Скорость = путь / время.
Если обозначить скорость движения буквой V, время движения буквой t, а путь пройденный телом буквой S, то получим следующую формулу.
Единица измерения скорости 1 м/с. То есть тело проходит расстояние в один метр, за время равное одной секунде.
Движения с переменной скоростью называется неравномерным движением. Чаще всего, все тела в природе двигаются именно неравномерно. Например, человек, когда куда-либо идет, двигается неравномерно, то есть его скорость в течении всего пути будет изменяться.
Расчет скорости при неравномерном движении
При неравномерном движении, скорость все время изменяется, и в этом случае говорят о средней скорости движения.
Средняя скорость неравномерного движения вычисляется по формуле
Из формулы для определения скорости, мы можем получить и другие формулы, например, для расчета пройденного пути или времени, которое двигалось тело.
Расчет пути при равномерном движении
Чтобы определить путь, который прошло тело при равномерном движении, необходимо скорость движения тела умножить на время которое это тело двигалось.
То есть, зная скорость и время движения, мы всегда сможем найти путь.
Теперь, получим формулу для расчета времени движения, при известных: скорости движения и пройденном пути.
Расчет времени при равномерном движении
Для того чтобы определить время равномерного движения, необходимо путь пройденный телом, поделить на скорость, с которой это тело двигалось.
Полученные выше формулы будут справедливы, если тело совершало равномерное движение.
При расчете средней скорости неравномерного движения, полагают, что движение было равномерным. Исходя из этого, для вычисления по средней скорости неравномерного движения, пути или времени движения используют те же самые формулы, что и при равномерном движении.
Расчет пути при неравномерном движении
Получаем, что путь пройденный телом при неравномерном движении, равен произведению средней скорости на время которое тело двигалось.
Расчет времени при неравномерном движении
Время необходимое для прохождения некоторого пути при неравномерном движении, равняется частному от деления пути на среднюю скорость неравномерного движения.
Графиком равномерного движения, в координатах S(t) будет являться прямая линия.
Определение
Мгновенной скоростью (или чаще просто скоростью) материальной точки называется физическая величина равная первой производной от радиус–вектора
точки по времени (t). Обозначают скорость обычно буквой v.
Это векторная величина. Математически определение вектора мгновенной скорости записывается как:
Математически определение вектора мгновенной скорости записывается как:
Скорость имеет направление указывающее направление движения материальной точки и лежит на касательной к траектории ее движения. Модуль скорости можно определить как первую производную от длины пути (s) по времени:
Скорость характеризует быстроту перемещения в направлении движения точки по отношениюк рассматриваемой системе координат.
Скорость в разных системах координат
Проекции скорости на оси декартовой системы координат запишутся как:
Следовательно, вектор скоростив декартовых координатах можно представить:
где единичные орты. При этом модуль вектора скорости находят при помощи формулы:
В цилиндрических координатах модуль скорости вычисляют при помощи формулы:
в сферической системе координат:
Частные случаи формул для вычисления скорости
Если модуль скорости не изменяется во времени, то такое движение называют равномерным (v=const). При равномерном движении скорость можно вычислить, применяя формулу:
При равномерном движении скорость можно вычислить, применяя формулу:
где s– длина пути, t – время, за которое материальная точка преодолела путь s.
При ускоренном движении скорость можно найти как:
где – ускорение точки, – отрезок времени, в течение которого рассматривается скорость.
Если движение является равнопеременным, то применяется следующая формула для вычисления скорости:
где – начальная скорость движения, .
Единицы измерения скорости
Основной единицей измерения скорости в системе СИ является: [v]=м/с 2
В СГС: [v]=см/с 2
Примеры решения задач
Пример
Задание. Движение материальной точки А задано уравнением: . Точка начала свое движение при t 0 =0 c.Как будет двигаться рассматриваемая точка по отношению к оси X в момент времени t=0,5 с.
Решение. Найдем уравнение, которое будет задавать скорость рассматриваемой материальной точки, для этого от функции x=x(t), которая задана в условиях задачи, возьмем первую производную по времени, получим:
Для определения направления движения подставим в полученную нами функцию для скорости v=v(t) в (1. 1) указанный в условии момент
времении сравним результат с нулем:
1) указанный в условии момент
времении сравним результат с нулем:
Так как мы получили, что скорость в указанный момент времени отрицательна, следовательно, материальная точка движется против оси X.
Ответ. Против оси X.
Пример
Задание. Скорость материальной точки является функцией от времени вида:
где скорость в м/с, время в c. Какова координата точки в момент времени равный 10 с, в какой момент времени точка будет на расстоянии 10 м от начала координат? Считайте, что при t=0 c точка началадвижение из начала координат по оси X.
Решение. Точка движется по оси X, cвязь координаты x и скорости движения определена формулой.
Примеры использования функции ВРЕМЯ для расчетов в Excel
Функция ВРЕМЯ возвращает десятичное число, выражающее определенное значение во времени. Возвращаемое значение зависит от формата ячейки. Если ячейка имеет формат «Общий», функция ВРЕМЯ вернет результат, отформатированный в виде даты. Числовой результат работы данной функции – десятичное число из интервала от 0 до 0,99988426, которое представляет собой значение в единицах измерения времени от 0:00:00 до 23:59:59.
Числовой результат работы данной функции – десятичное число из интервала от 0 до 0,99988426, которое представляет собой значение в единицах измерения времени от 0:00:00 до 23:59:59.
Особенности работы функции ВРЕМЯ в Excel
Функция ВРЕМЯ в Excel из категории «Дата и время» предназначена для использования специалистами, выполняющими временные расчеты, например, экономистам-нормировщикам.
Функция имеет следующий синтаксис:
=ВРЕМЯ(часы; минуты; секунды)
Рассмотрим параметры, принимаемые на вход данной функцией:
- Часы – обязательный параметр, принимающий значения в интервале от 0 до 32767, задающие часы. При вводе чисел со значениями свыше 23 выполняется вычитание наибольшего ближайшего меньшего значения, кратного 24, результат которого принимается в качестве входного параметра. Например, результат выполнения функции ВРЕМЯ(31;0;0) эквивалентен результату выполнения функции (7;0;0) и равен 07:00.
- Минуты – обязательный параметр, принимающий числа в интервале от 0 до 32767, определяющие минуты.
 При вводе значений, превышающих 59, производится перерасчет в часы и минуты. Например, результат выполнения функции (0;134;0) эквивалентен результату выполнения функции ВРЕМЯ(2;14;0) и равен 02:14.
При вводе значений, превышающих 59, производится перерасчет в часы и минуты. Например, результат выполнения функции (0;134;0) эквивалентен результату выполнения функции ВРЕМЯ(2;14;0) и равен 02:14. - Секунды – обязательный параметр, принимающий значения от 0 до 32767, определяющий секунды. При вводе чисел свыше 59 производится автоматический перерасчет в часы, минуты и секунды. Например, ВРЕМЯ(0;0;190) эквивалентно значению (0;03;10) и равно 00:03:10.
Перечисленные параметры – обязательные. Если один или несколько из них имеют значение 0 (нуль), это должно быть указано явно.
Примеры использования функции ВРЕМЯ в Excel
Пример 1. Длина маршрута общественного транспорта составляет 34 минуты. Время отправки из депо – 8:25 утра. Необходимо узнать, во сколько транспорт прибудет в депо пройдя полный маршрут, пренебрегая возможными задержками на пути.
Заполним таблицу исходных данных. Укажем часы, минуты и секунды отправки транспортного средства из депо, а также длину маршрута:
Для решения задачи необходимо в ячейке E3 ввести следующую формулу:
Значения аргументов функций:
- A3 – часы отправки из депо;
- B3 – минуты выезда;
- C3 – секунды выезда;
- D3 – протяженность маршрута, выраженная в минутах.

То есть, транспортное средство вернется в депо в 8:59 AM.
Как рассчитать прибытие автомобиля к пункту назначения?
Пример 2. Автомобиль движется из одного города в другой со средней скоростью 80 км/ч. Известно, что он выехал в 12:10, а расстояние между городами составляет 420 км. Необходимо определить время прибытия в пункт назначения.
Внесем в таблицу исходных данных часы, минуты и секунды отправки автомобиля:
Определим длительность нахождения автомобиля в пути, зная, что время равно частному от деления расстояния на скорость:
В ячейке F будет использована следующая формула:
Где:
- E3 – расстояние между городами, км;
- D3 – средняя скорость движения авто, км/ч;
- 60 – коэффициент для перевода десятичной дроби в минуты.
Введем в ячейке G2 следующую формулу:
Значения аргументов функций:
- A3 – часы отправки из депо;
- B3 – минуты выезда;
- C3 – секунды выезда;
- F3 – вычисленное ранее время нахождения в пути, выраженное в минутах.

То есть, автомобиль приедет во второй город в 5:25 PM.
Как посчитать длительность производственного процесса на оборудовании в Excel?
Пример 3. Длительность производственного процесса составляет 739 секунд. Необходимо выразить эту длительность в минутах и секундах.
Укажем исходное значение минут в ячейке A2:
Воспользуемся рассматриваемой формулой для вычисления времени:
Результатом выполнения формулы является значение 12:12 AM, что не соответствует условию задачи. Воспользуемся функцией МИНУТЫ, чтобы выделить искомую часть времени:
B2 – ячейка с полученным промежуточным результатом вычислений.
То есть длительность производственного процесса для изготовления единицы продукции составляет 12 минут на одной единице оборудования цеха.
Скорость, дистанция, время, калькулятор
Использование калькулятора
Рассчитайте скорость, расстояние или время по формуле d = st, расстояние равно скорости, умноженной на время. Калькулятор скорости, дистанции и времени может решить неизвестные sdt значение с двумя известными значениями.
Калькулятор скорости, дистанции и времени может решить неизвестные sdt значение с двумя известными значениями.
Время можно ввести или рассчитать в секундах (с), минутах (мин), часах (час) или часах и минутах и секундах (чч: мм: сс).Видеть ярлыки для форматов времени ниже.
Чтобы найти расстояние, используйте формулу для расстояния d = st, или расстояние равно скорости, умноженной на время.
расстояние = скорость x время
Скорость и скорость аналогичны, поскольку они оба представляют собой некоторое расстояние в единицу времени, например мили в час или километры в час. Если ставка r то же, что и скорость с , r = s = d / t.Вы можете использовать эквивалентную формулу d = rt, что означает, что расстояние равно скорости, умноженной на время.
расстояние = скорость x время
Чтобы найти скорость или коэффициент, используйте формулу для скорости s = d / t, что означает, что скорость равна расстоянию, разделенному на время.
скорость = расстояние / время
Чтобы найти время, используйте формулу для времени, t = d / s, что означает, что время равно расстоянию, разделенному на скорость.
время = расстояние / скорость
Форматы ввода времени чч: мм: сс
В качестве разделителей можно использовать тире (-), точку (.) Или двоеточие (:), при этом всегда необходимо использовать 2 разделителя. Например, 15-06-22, 15.06.22 и 15:06:22 интерпретируются как 15 часов 6 минут 22 секунды или 15:06:22.
Разрешенные ограничения на вход:
- часы 0 до 999
- минут 0 до 59
- секунд от 0 до 59
Ярлыки формата времени
Х. .
.
5 ..
5 часов: 0 минут: 0 секунд
05:00:00
X.Y.
5.22.
5 часов: 22 минут: 0 секунд
05:22:00
X.Y.Z
5.22.10
5.01.15
5.3.6
5 часов: 22 минут: 10 секунд
5 часов: 1 минута: 15 секунд
5 часов: 3 минут: 6 секунд
05:22:10
05:01:15
05:03:06
. Ю.
Ю.
,22.
22 минуты
00:22:00
.Y.Z
. 22,15
22 минуты: 15 секунд
00:22:15
..Z
..5
5 секунд
00:00:05
X..Z
5..05
5 часов: 0 минут: 5 секунд
05:00:05
Сопутствующие калькуляторы
Для физических расчетов со скоростью, смещением и скоростью используйте наш
Калькулятор смещения для решения смещения с , средняя скорость v или время t .
— Какова формула времени? Примеры
Формула времени помогает вычислить время, необходимое объекту для прохождения определенного расстояния с заданной скоростью. Единица времени в системе СИ — с. Изучим формулу времени на некоторых решенных примерах.
Что такое формула времени?
Формула времени может быть определена как отношение расстояния, пройденного объектом к единице скорости.Время относится к развитию событий. Это движение происходит таким образом, что оно идет от прошлого к настоящему и, наконец, в будущее.
Формула времени
Формула времени данного тела может быть выражена как
Время = Расстояние ÷ Скорость
Как пользоваться формулой времени?
Формула времени может использоваться для определения времени, затрачиваемого объектом, с учетом расстояния и скорости. Давайте быстро рассмотрим пример, показывающий, как использовать формулу для определения времени.
Пример: Сколько будет общего времени, чтобы преодолеть 3600 м со скоростью 2 метра в секунду?
Решение: Использование формулы для времени,
Время = Расстояние ÷ Скорость
Время = 3600 ÷ (2) = 1800 секунд.
Ответ: Общее время преодоления дистанции 3600 м составляет 1800 секунд.
Хотите находить сложные математические решения за секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором для решения сложных вопросов.С Cuemath находите решения простым и легким способом.
Забронируйте бесплатную пробную версию Класс
Примеры использования формулы времени
Решим несколько интересных задач по формуле времени.
Пример 1: Поезд преодолел расстояние 120 км со скоростью 60 км / ч. Используя формулу времени, рассчитайте время, затраченное поездом на преодоление дистанции.
Раствор:
Чтобы узнать время, затраченное на поезд.
Дано:
Расстояние, пройденное поездом = 120км
Скорость поезда = 60 км / час
Используя Формула времени,
Время = Расстояние / Скорость
= 120/60
= 2 часа
Ответ: Время, за которое поезд преодолевает 120 км со скоростью 60 км / ч, составляет 2 часа.
Пример 2: Велосипедист преодолевает 20 км со скоростью 5 км / ч. Воспользуйтесь формулой времени и найдите время, затраченное велосипедистом на преодоление дистанции.
Раствор:
Чтобы узнать время, затраченное велосипедистом.
Расстояние, пройденное велосипедистом = 20 км
Скорость велосипедиста = 5 км / час.
Используя формулу времени,
Время = Расстояние / Скорость
= 20/5
= 4 часа
Ответ: Время, затрачиваемое велосипедистом на преодоление 20 км со скоростью 5 км / ч, составляет 4 часа.
Пример 3: Используя формулу времени, рассчитать время, затрачиваемое человеком на преодоление расстояния 400 километров со скоростью 20 километров в час?
Раствор:
Формула времени: [Время = Расстояние ÷ Скорость]
Расстояние = 400 километров
Скорость = 20 км / час
Время = (400 ÷ 20) часов
= 20 часов
Ответ: Таким образом, человек преодолел расстояние 400 километров за 20 часов.
Часто задаваемые вопросы о Формуле времени
Как рассчитать расстояние по формуле времени?
Формула для времени задается как [Время = Расстояние ÷ Скорость]. Для расчета расстояния формулу времени можно представить в виде [Расстояние = Скорость × Время].
Как рассчитать скорость по формуле времени?
Формула для времени задается как [Время = Расстояние ÷ Скорость]. Для расчета скорости формула времени будет иметь вид [Скорость = Пройденное расстояние ÷ Время].
Как использовать формулу для времени?
Формула времени может использоваться в нашей повседневной жизни, чтобы определить, сколько времени требуется для выполнения любой задачи.Чтобы понять, как использовать формулу для времени, давайте рассмотрим пример.
Пример: за сколько времени вы сможете проехать 4000 м со скоростью 20 м / с?
Решение: Используя формулу для времени,
Время = Расстояние ÷ Скорость
Время = 4000 ÷ (20) = 200 секунд
Время, необходимое для прохождения дистанции 4000 м со скоростью 20 м / с, составляет 200 секунд.
Какой будет общая формула времени для любой задачи?
Общая формула времени для любой задачи задается как [Время = Расстояние ÷ Скорость].Единица времени в системе СИ — секунды.
Зависимость скорости от скорости
Так же, как расстояние и смещение имеют совершенно разные значения (несмотря на их сходство), то же самое делают и скорость и скорость. Скорость — это скалярная величина, которая указывает, «насколько быстро движется объект». Скорость можно представить как скорость, с которой объект преодолевает расстояние. Быстро движущийся объект имеет высокую скорость и преодолевает относительно большое расстояние за короткое время. Сравните это с медленно движущимся объектом с низкой скоростью; он преодолевает относительно небольшое расстояние за то же время.Объект, который вообще не движется, имеет нулевую скорость.
Скорость как векторная величина Скорость — это векторная величина, которая относится к «скорости, с которой объект меняет свое положение». Представьте себе человека, который быстро движется — шаг вперед и шаг назад — всегда возвращается в исходное положение. Хотя это может привести к безумной активности, это приведет к нулевой скорости. Поскольку человек всегда возвращается в исходное положение, движение никогда не приведет к изменению положения.Поскольку скорость определяется как скорость изменения положения, это движение приводит к нулевой скорости. Если движущийся человек желает максимизировать свою скорость, он должен приложить все усилия, чтобы максимизировать величину, на которую он смещается от своего исходного положения. Каждый шаг должен продвигать этого человека дальше от того места, где он начал. Наверняка человек никогда не должен менять направление и начинать возвращаться в исходное положение.
Представьте себе человека, который быстро движется — шаг вперед и шаг назад — всегда возвращается в исходное положение. Хотя это может привести к безумной активности, это приведет к нулевой скорости. Поскольку человек всегда возвращается в исходное положение, движение никогда не приведет к изменению положения.Поскольку скорость определяется как скорость изменения положения, это движение приводит к нулевой скорости. Если движущийся человек желает максимизировать свою скорость, он должен приложить все усилия, чтобы максимизировать величину, на которую он смещается от своего исходного положения. Каждый шаг должен продвигать этого человека дальше от того места, где он начал. Наверняка человек никогда не должен менять направление и начинать возвращаться в исходное положение.
Скорость — это векторная величина.Таким образом, скорость с учетом направления . Оценивая скорость объекта, нужно следить за его направлением. Недостаточно сказать, что объект имеет скорость 55 миль / час. Необходимо включить информацию о направлении, чтобы полностью описать скорость объекта. Например, вы должны описать скорость объекта как 55 миль / ч, к востоку, . Это одно из существенных различий между скоростью и скоростью. Скорость является скалярной величиной и не отслеживает направление ; скорость — это векторная величина, учитывающая направление .
Необходимо включить информацию о направлении, чтобы полностью описать скорость объекта. Например, вы должны описать скорость объекта как 55 миль / ч, к востоку, . Это одно из существенных различий между скоростью и скоростью. Скорость является скалярной величиной и не отслеживает направление ; скорость — это векторная величина, учитывающая направление .
Определение направления вектора скорости
Задача описания направления вектора скорости проста. Направление вектора скорости совпадает с направлением движения объекта. Неважно, ускоряется объект или замедляется. Если объект движется вправо, его скорость описывается как правая. Если объект движется вниз, его скорость описывается как нисходящая.Таким образом, самолет, движущийся на запад со скоростью 300 миль / час, имеет скорость 300 миль / час на западе. Обратите внимание, что скорость не имеет направления (это скаляр), а скорость в любой момент — это просто значение скорости с направлением.
Расчет средней скорости и средней скорости
Когда объект движется, его скорость часто меняется. Например, во время обычной поездки в школу происходит много изменений скорости.Вместо того, чтобы показания спидометра оставались стабильными, стрелка постоянно перемещается вверх и вниз, отражая остановку и запуск, а также ускорение и замедление. В один момент автомобиль может двигаться со скоростью 50 миль / час, а в другой момент он может быть остановлен (т. Е. 0 миль / час). Тем не менее, во время поездки в школу человек может в среднем 32 мили / час. Среднюю скорость во время всего движения можно рассматривать как среднее значение всех показаний спидометра. Если бы показания спидометра можно было собирать с интервалом в 1 секунду (или 0.1-секундные интервалы или …), а затем усредненные вместе, можно было определить среднюю скорость. Теперь это будет много работы. И, к счастью, есть ярлык. Читать дальше. Средняя скорость движения часто вычисляется по следующей формуле:Напротив, средняя скорость часто вычисляется по этой формуле
Давайте начнем реализацию нашего понимания этих формул со следующей задачи:
Вопрос: Во время отпуска Лиза Карр преодолела расстояние в 440 миль. Поездка заняла 8 часов. Какая у нее была средняя скорость?
Поездка заняла 8 часов. Какая у нее была средняя скорость?
Чтобы вычислить ее среднюю скорость, мы просто разделим пройденное расстояние на время поездки.
Это было легко! Лиза Карр развила в среднем 55 миль в час. Возможно, она не двигалась с постоянной скоростью 55 миль / час. Она, несомненно, была остановлена в какой-то момент времени (возможно, на перерыв в ванной или на обед), и, вероятно, в другие моменты времени она, вероятно, ехала со скоростью 65 миль в час.Тем не менее, она развивала в среднем 55 миль в час. Приведенная выше формула представляет собой сокращенный метод определения средней скорости объекта.
Средняя скорость в сравнении с мгновенной скоростью
Поскольку движущийся объект часто меняет свою скорость во время движения, принято различать среднюю скорость и мгновенную скорость. Различие заключается в следующем.
- Мгновенная скорость — скорость в любой момент времени.

- Средняя скорость — среднее значение всех мгновенных скоростей; можно найти просто по соотношению расстояние / время.
Вы можете думать о мгновенной скорости как о скорости, которую показывает спидометр в любой момент времени, а о средней скорости как о среднем значении всех показаний спидометра в течение поездки. Поскольку задача усреднения показаний спидометра была бы довольно сложной (и, возможно, даже опасной), средняя скорость обычно рассчитывается как отношение расстояния / времени.
Движущиеся объекты не всегда перемещаются с неустойчивой и меняющейся скоростью. Иногда объект будет двигаться с постоянной скоростью с постоянной скоростью. То есть объект будет преодолевать одно и то же расстояние каждый равный промежуток времени. Например, бегун может бежать с постоянной скоростью 6 м / с по прямой в течение нескольких минут. Если ее скорость постоянна, то расстояние, которое проходит каждую секунду, будет таким же. Бегун преодолевал расстояние в 6 метров каждую секунду.Если бы мы могли измерять ее положение (расстояние от произвольной начальной точки) каждую секунду, то мы бы заметили, что положение менялось бы на 6 метров каждую секунду. Это будет разительно контрастировать с объектом, который меняет свою скорость. Объект с изменяющейся скоростью будет перемещаться на разные расстояния каждую секунду. В приведенных ниже таблицах данных показаны объекты с постоянной и изменяющейся скоростью.
А теперь давайте снова рассмотрим движение того учителя физики. Учитель физики идет 4 метра на восток, 2 метра на юг, 4 метра на запад и, наконец, 2 метра на север.Все движение длилось 24 секунды. Определите среднюю скорость и среднюю скорость.
Учитель физики прошел дистанцию 12 метров за 24 секунды; таким образом, ее средняя скорость составляла 0,50 м / с. Однако, поскольку ее смещение составляет 0 метров, ее средняя скорость составляет 0 м / с. Помните, что смещение относится к изменению положения, а скорость основывается на этом изменении положения. В этом случае движения учителя изменяется положение на 0 метров и, следовательно, средняя скорость составляет 0 м / с.
Вот еще один пример, аналогичный тому, что мы видели ранее при обсуждении расстояния и смещения. На схеме ниже показано положение лыжника в разное время. В каждый из указанных моментов лыжник разворачивается и меняет направление движения. Другими словами, лыжник перемещается из пункта А в пункт В, затем из пункта В в пункт D.
Используйте диаграмму, чтобы определить среднюю скорость и среднюю скорость лыжника в течение этих трех минут.По завершении нажмите кнопку, чтобы просмотреть ответ.
В качестве последнего примера рассмотрим футбольного тренера, который ходит взад и вперед по боковой линии. На диаграмме ниже показаны несколько позиций тренера в разное время. В каждой отмеченной позиции тренер делает «разворот» и движется в противоположном направлении. Другими словами, тренер переходит из позиции A в позицию B, затем из позиции C в позицию D.
Какова средняя и средняя скорость тренера? По завершении нажмите кнопку, чтобы просмотреть ответ.
В заключение, скорость и скорость — это кинематические величины, которые имеют совершенно разные определения. Скорость, будучи скалярной величиной, представляет собой скорость, с которой объект преодолевает расстояние. Средняя скорость — это отношение расстояния (скалярной величины) к временному интервалу. Скорость без учета направления . С другой стороны, скорость — это векторная величина; это с учетом направления . Скорость — это скорость изменения положения. Средняя скорость — это отношение смещения или изменения положения (векторная величина) за время.
Мы хотели бы предложить … Иногда просто прочитать об этом недостаточно. Вы должны с ним взаимодействовать! И это именно то, что вы делаете, когда используете одно из интерактивных материалов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего Name That Motion Interactive. Он находится в разделе «Интерактивная физика» и позволяет учащемуся применять концепции скорости, скорости и ускорения.Посетите Назовите это движение.
Калькулятор скорости, расстояния и времени
Используйте этот калькулятор скорости, чтобы легко рассчитать среднюю скорость, пройденное расстояние и продолжительность поездки транспортного средства: автомобиля, автобуса, поезда, велосипеда, мотоцикла, самолета и т. Д. Работает с милями, футами, километрами , метров и т.д ..
Быстрая навигация:
- Расчет скорости, расстояния и времени
- Формула средней скорости
- Формула расстояния
- Формула продолжительности (времени)
- Как рассчитать среднюю скорость автомобиля?
Для того, чтобы использовать вышеуказанный калькулятор скорости, расстояния и времени или выполнить такие вычисления самостоятельно, вам необходимо знать два из трех показателей: скорость, расстояние, время.Вам нужно будет преобразовать метрики в те же единицы времени и расстояния, например мили, километры, метры, ярды, футы и часы, минуты или секунды. Например, если у вас скорость в милях в час (милях в час), время также должно быть в часах. Если у вас расстояние в километрах, скорость также должна быть в км / ч (километрах в час).
Единица результата будет зависеть от введенных вами единиц, но наш калькулятор скорости будет удобно отображать дополнительные единицы там, где это необходимо.
Формула средней скоростиФормула для средней скорости, также называемой средней скоростью в физике и технике:
v = д / т
, где v — скорость, d — расстояние, а t — время, поэтому вы можете прочитать это как Скорость = Расстояние / Время .Как отмечалось выше, сначала убедитесь, что вы правильно конвертируете единицы измерения, или воспользуйтесь нашим калькулятором скорости, который делает это автоматически. Результирующая единица измерения будет зависеть от единиц измерения времени и расстояния, поэтому, если вы вводили в милях и часах, скорость будет в милях в час. Если это было в метрах и секундах, это будет в м / с (метры в секунду).
Пример: Если вы взяли самолет из Нью-Йорка в Лос-Анджелес, и полет длился 5 часов эфирного времени, какова была скорость самолета, учитывая, что траектория полета составляла 2450 миль? Ответ: 2450/5 = средняя скорость 490 миль в час (миль в час).Если вы хотите получить результат в км / ч, вы можете преобразовать мили в км, чтобы получить 788,58 км / ч.
Формула расстоянияФормула для расстояния, если вы знаете время (продолжительность) и среднюю скорость, будет:
d = v x t
, где v — скорость (средняя скорость), t — время, а d — расстояние, поэтому вы можете прочитать это как Distance = Speed x Time . Результат будет зависеть от единицы измерения скорости, например, если скорость указана в милях в час, результат будет в милях, если в км / ч, результат будет в километрах.Как обычно, убедитесь, что единица измерения скорости совпадает с единицей измерения продолжительности поездки. Для вашего удобства наш калькулятор расстояния иногда выводит расстояние в нескольких единицах.
Пример: Если грузовик двигался со средней скоростью 80 км в час в течение 4 часов, сколько миль он преодолел за это время? Сначала вычислите 80 * 4 = 320 км, затем преобразуйте км в мили, разделив на 1,6093 или используя наш конвертер км в мили, чтобы получить ответ: 198.84 миль.
Формула продолжительности (времени)
Время, а точнее продолжительность поездки, можно рассчитать, зная расстояние и среднюю скорость, по формуле:
т = д / в
, где d — пройденное расстояние, v — скорость (скорость), а t — время, поэтому вы можете прочитать это как Время = Расстояние / Скорость . Убедитесь, что вы конвертируете единицы таким образом, чтобы их компоненты расстояния и времени совпадали, или воспользуйтесь нашим калькулятором продолжительности поездки, приведенным выше, который выполнит преобразование автоматически.Например, если у вас есть расстояние в милях и скорость в км / ч, вам нужно будет преобразовать скорость в мили в час или расстояние в километры. Единица времени результата будет соответствовать единице измерения скорости, поэтому, если она измеряется в часах, результат будет в часах. Если он измеряется в некоторых единицах в секунду, результат будет в секундах.
Пример: Если поезд может проехать 500 миль со средней скоростью 50 миль в час, сколько времени потребуется, чтобы проехать 500 миль по маршруту? Ответ: 500/50 = 10 часов.
Как рассчитать среднюю скорость автомобиля?Допустим, вы проехали определенное расстояние на автомобиле или другом транспортном средстве и хотите вычислить его среднюю скорость. Самый простой способ сделать это — использовать калькулятор, приведенный выше, но при желании вы также можете вычислить самостоятельно. В любом случае вам необходимо знать расстояние с удовлетворительным приближением, для чего вы можете использовать карту (например, Google Maps), чтобы измерить расстояние от точки до точки.Убедитесь, что вы измеряете близко к выбранному вами пути, а не по прямой, если вы не путешествуете по воздуху, и в этом случае это было бы хорошим приближением. Конечно, более точным было бы считывание расстояния с помощью GPS. Тогда вам нужно знать время в пути. Убедитесь, что вы вычли из общей продолжительности поездки любые сделанные вами паузы или остановки.
Если общее пройденное расстояние составило 500 миль, а время, которое вам потребовалось, составило 5 часов, тогда ваша средняя скорость будет 500/5 = 100 миль в час (миль в час).Если расстояние составляло 300 километров, и вам потребовалось 5 часов, чтобы преодолеть его, ваша скорость была 300/5 = 60 км / ч (километров в час).
Скорость и скорость: концепции и формулы — стенограмма видео и урока
Определения скорости и скорости
Прежде чем обсуждать формулы для расчета скорости и скорости, нам необходимо рассмотреть более подробные определения каждого термина. Скорость определяется как скорость изменения расстояния во времени. Скорость определяется как скорость изменения смещения во времени.Обратите внимание, что слова расстояние и смещение являются единственной разницей между двумя определениями.
Итак, в чем разница между расстоянием и смещением? Расстояние относится к общему количеству земли, покрытой движущимся объектом, тогда как смещение относится к чистому изменению положения движущегося объекта. Расстояние — это то, что мы называем скалярной величиной , потому что расстояние полностью описывается только величиной без привязки к направлению.Поскольку скорость является функцией расстояния, скорость также является скалярной величиной. Смещение — это векторная величина , потому что смещение полностью описывается как величиной, так и направлением. Поскольку скорость является функцией смещения, скорость является векторной величиной. Если мы объединим определения скорости и скорости, можно сказать, что скорость — это скорость с направлением, и это будет точно.
Формула скорости
Теперь, когда мы понимаем концепции скорости и скорости, мы можем изучить формулы для вычисления этих показателей.Давайте сначала посмотрим на скорость. Как обсуждалось, скорость — это скорость изменения расстояния за период времени. Другими словами, скорость зависит как от расстояния, так и от времени. Таким образом, формула для расчета скорости включает как расстояние, так и время, где скорость прямо пропорциональна изменению расстояния и обратно пропорциональна изменению во времени.
Давайте посмотрим на формулу для скорости: Скорость = расстояние ÷ время
Давайте воспользуемся примером, чтобы попрактиковаться в вычислении скорости.Представьте себе человека, идущего зигзагообразно. Если человек преодолевает зигзагом всего 20 метров, то изменение расстояния равно 20 метрам. Теперь предположим, что ему требуется 60 секунд, чтобы покрыть этот 20-метровый зигзагообразный узор. Следовательно, изменение времени составляет 60 секунд. Мы можем сложить эти значения в нашей формуле и рассчитать скорость.
Давайте сначала вспомним формулу для скорости: Скорость = расстояние ÷ время
Теперь подставим наблюдаемые значения: Скорость = 20 метров ÷ 60 секунд
20 разделенное на 60 равно 0.33. Следовательно, мужчина движется со скоростью 0,33 метра в секунду. Это может быть выражено как Скорость = 0,33 м / сек , где m = метры, а sec = секунды. Возможно, вы более знакомы со скоростью, выраженной в милях в час, или просто миль в час .
Формула для скорости
Давайте посмотрим на формулу для скорости. Как мы уже обсуждали, скорость является мерой изменения смещения во времени, а не только расстояния. Другими словами, скорость — это мера того, сколько времени требуется объекту, чтобы достичь пункта назначения с указанием направления.Скорость прямо пропорциональна перемещению и обратно пропорциональна пройденному времени.
Давайте посмотрим на формулу скорости: Скорость = смещение ÷ время
Давайте еще раз рассмотрим, что человек движется зигзагообразно. Мы определили его скорость 0,33 метра в секунду. Мы знаем его скорость, но как насчет его скорости? Чтобы вычислить скорость, мы должны сначала определить смещение. Чтобы определить смещение, измерьте расстояние по прямой от начальной точки человека до его пункта назначения.Теперь предположим, что мы измеряем это смещение на 5 метров вправо. Теперь мы можем рассчитать скорость.
Давайте сначала вспомним формулу для скорости: Скорость = смещение ÷ время
Подставьте измеренные значения смещения и времени, и мы получим скорость = 5 метров вправо ÷ 60 секунд.
Итак, 5 разделенное на 60 дает 0,08. Следовательно, скорость человека составляет 0,08 метра в секунду вправо. Еще раз, скорость — это векторная величина, выражающая как величину, так и направление.Здесь величина 0,08, направление — вправо.
Краткое содержание урока
Подводя итог, скорость и скорость похожи, но отличаются. Скорость — это мера расстояния, пройденного с течением времени, где расстояние означает, сколько земли покрывает движущийся объект. Скорость — это мера смещения во времени, а смещение относится к чистому изменению положения движущегося объекта. Расстояние и скорость — скалярные величины , поскольку они полностью описываются величиной без привязки к направлению.С другой стороны, смещение и скорость являются векторными величинами , поскольку они полностью описываются как величиной, так и направлением. Скорость можно представить как скорость с направлением. Формула скорости — это изменение расстояния, деленное на изменение во времени. Формула для скорости — это изменение смещения, деленное на изменение во времени.
Результаты обучения
После этого видеоурока вы сможете:
- Различать скорость и скорость
- Напишите уравнения для скорости и скорости
2.2 Скорость и скорость — физика
Задачи обучения разделу
К концу этого раздела вы сможете делать следующее:
- Рассчитать среднюю скорость объекта
- Соотношение смещения и средней скорости
Поддержка учителей
Поддержка учителей
Цели обучения в этом разделе помогут вашим ученикам овладеть следующими стандартами:
- (4) Научные концепции. Учащийся знает и применяет законы движения в самых разных ситуациях.Ожидается, что студент:
- (B) описывают и анализируют движение в одном измерении, используя уравнения с понятиями расстояния, смещения, скорости, средней скорости, мгновенной скорости и ускорения.
Кроме того, руководство лаборатории физики средней школы рассматривает содержание этого раздела лаборатории под названием «Положение и скорость объекта», а также следующие стандарты:
- (4) Научные концепции. Учащийся знает и применяет законы движения в самых разных ситуациях.Ожидается, что студент:
- (В) описывать и анализировать движение в одном измерении, используя уравнения с понятиями расстояния, смещения, скорости, средней скорости, мгновенной скорости и ускорения.
Раздел Основные термины
| средняя скорость | средняя скорость | мгновенная скорость |
| мгновенная скорость | скорость | скорость |
Поддержка учителя
Поддержка учителя
В этом разделе учащиеся применяют то, что они узнали о расстоянии и смещении, к понятиям скорости и скорости.
[BL] [OL] Перед тем, как студенты прочитают раздел, попросите их привести примеры того, как они слышали слово «скорость». Затем спросите их, слышали ли они слово «скорость». Объясните, что эти слова часто используются как синонимы в повседневной жизни, но их научные определения различаются. Скажите студентам, что они узнают об этих различиях по мере чтения раздела.
[AL] Объясните учащимся, что скорость, как и смещение, является векторной величиной. Попросите их поразмышлять о том, чем скорость отличается от скорости.После того, как они поделятся своими идеями, задайте вопросы, которые углубят их мыслительный процесс, например: Почему вы так думаете? Какой пример? Как можно применить эти термины к движению, которое вы видите каждый день?
Скорость
Движение — это нечто большее, чем расстояние и перемещение. Такие вопросы, как: «Сколько времени занимает пешая гонка?» и «Какая была скорость бегуна?» невозможно ответить без понимания других концепций. В этом разделе мы рассмотрим время, скорость и скорость, чтобы расширить наше понимание движения.
Описание того, насколько быстро или медленно движется объект, — это его скорость. Скорость — это скорость, с которой объект меняет свое местоположение. Как и расстояние, скорость — это скаляр, потому что у нее есть величина, но не направление. Поскольку скорость — это показатель, она зависит от временного интервала движения. Вы можете рассчитать прошедшее время или изменение времени ΔtΔt движения как разницу между временем окончания и временем начала
Единицей времени в системе СИ является секунда (с), а единицей скорости в системе СИ являются метры в секунду (м / с), но иногда километры в час (км / ч), мили в час (миль / ч) или другие единицы измерения. скорость используются.
Когда вы описываете скорость объекта, вы часто описываете среднее значение за определенный период времени. Средняя скорость, v avg , представляет собой пройденное расстояние, разделенное на время, в течение которого происходит движение.
vavg = distancetimevavg = distancetimeВы, конечно, можете изменить уравнение, чтобы найти расстояние или время
время = distancevavg.time = distancevavg. distance = vavg × timedistance = vavg × timeПредположим, например, что автомобиль проезжает 150 километров за 3 секунды.2 часа. Его средняя скорость за поездку —
. vavg = расстояние-время = 150 км3,2 ч = 47 км / ч. vavg = расстояние-время = 150 км3,2 ч = 47 км / ч.Скорость автомобиля, вероятно, увеличится и уменьшится во много раз за 3,2 часа поездки. Однако его скорость в определенный момент времени — это его мгновенная скорость. Спидометр автомобиля показывает его мгновенную скорость.
Поддержка учителей
Поддержка учителей
[OL] [AL] Предупредите учащихся, что средняя скорость не всегда равна средней начальной и конечной скорости объекта.Например, предположим, что автомобиль проезжает 100 км. Первые 50 км он движется со скоростью 30 км / ч, а вторые 50 км — со скоростью 60 км / ч. Его средняя скорость будет составлять расстояние / (временной интервал) = (100 км) / [(50 км) / (30 км / ч) + (50 км) / (60 км / ч)] = 40 км / ч. Если бы автомобиль на этих скоростях проехал равное время на 30 и 60 км, а не на равные расстояния, его средняя скорость составила бы 45 км / ч.
[BL] [OL] Предупредите учащихся, что термины «скорость», «средняя скорость» и «мгновенная скорость» на повседневном языке часто называют просто скоростью.Подчеркните важность использования правильной терминологии в науке, чтобы избежать путаницы и правильно передавать идеи.
Рисунок 2.8 За 30 минут до магазина туда и обратно общее расстояние составляет 6 км. Средняя скорость 12 км / ч. Смещение для обхода туда и обратно равно нулю, потому что не было чистого изменения положения.
Рабочий пример
Расчет средней скорости
Мрамор катится 5,2 м за 1,8 с. Какая была средняя скорость мрамора?
Стратегия
Мы знаем расстояние, которое проходит мрамор, 5.2 м, интервал времени 1,8 с. Мы можем использовать эти значения в уравнении средней скорости.
Решение
vavg = расстояние время = 5,2 м 1,8 с = 2,9 м / с vavg = расстояние время = 5,2 м 1,8 с = 2,9 м / сОбсуждение
Средняя скорость — это скаляр, поэтому мы не включаем направление в ответ. Мы можем проверить разумность ответа, оценив: 5 метров разделить на 2 секунды — это 2,5 м / с. Поскольку 2,5 м / с близко к 2,9 м / с, ответ разумный. Речь идет о скорости быстрой ходьбы, так что это тоже имеет смысл.
Практические задачи
8.Питчер перебрасывает бейсбольный мяч от насыпи питчера к своей тарелке за 0,46 с. Дистанция 18,4 м. Какая была средняя скорость бейсбольного мяча?
- 40 м / с
- -40 м / с
- 0,03 м / с
- 8,5 м / с
Кэсси шла к дому своей подруги со средней скоростью 1,40 м / с. Расстояние между домами 205 м. Как долго она продолжала путешествие?
- 146 с
- 0.01 с
- 2,50 мин
- 287 с
Скорость
Векторная версия скорости — это скорость. Скорость описывает скорость и направление объекта. Как и в случае со скоростью, полезно описывать либо среднюю скорость за период времени, либо скорость в конкретный момент. Средняя скорость — это смещение, деленное на время, в течение которого смещение происходит.
vavg = время смещения = ΔdΔt = df − d0tf − t0vavg = время смещения = ΔdΔt = df − d0tf − t0Скорость, как и скорость, выражается в единицах СИ в метрах в секунду (м / с), но поскольку это вектор, вы также должны включить направление.Кроме того, переменная v для скорости выделена жирным шрифтом, потому что это вектор, в отличие от переменной v для скорости, которая выделена курсивом, потому что это скалярная величина.
Советы для успеха
Важно помнить, что средняя скорость — это не то же самое, что средняя скорость без направления. Как мы видели в предыдущем разделе со смещением и расстоянием, изменение направления во временном интервале больше влияет на скорость и скорость.
Предположим, что пассажир двигался к задней части самолета со средней скоростью –4 м / с. По средней скорости мы не можем сказать, остановился ли пассажир на мгновение или отступил перед тем, как добраться до задней части самолета. Чтобы получить более подробную информацию, мы должны рассмотреть меньшие сегменты поездки за меньшие промежутки времени, такие как те, что показаны на рисунке 2.9. Если вы рассматриваете бесконечно малые интервалы, вы можете определить мгновенную скорость, которая является скоростью в определенный момент времени.Мгновенная скорость и средняя скорость одинаковы, если скорость постоянна.
Рис. 2.9. На диаграмме представлена более подробная запись пассажира самолета, направлявшегося к задней части самолета, на меньших участках его пути.
Ранее вы читали, что пройденное расстояние может отличаться от величины смещения. Точно так же скорость может отличаться от величины скорости. Например, вы едете в магазин и через полчаса возвращаетесь домой.Если одометр вашего автомобиля показывает, что общее пройденное расстояние составило 6 км, то ваша средняя скорость составила 12 км / ч. Однако ваша средняя скорость была равна нулю, потому что ваше смещение в оба конца равно нулю.
Watch Physics
Расчет средней скорости или скорости
В этом видео рассматриваются векторы и скаляры и описывается, как рассчитать среднюю скорость и среднюю скорость, когда вы знаете смещение и изменение во времени. В видео также рассказывается, как преобразовать км / ч в м / с.
Проверка захвата
Что из следующего полностью описывает вектор и скалярную величину и правильно дает пример каждого из них?
- Скалярная величина полностью описывается своей величиной, в то время как вектор нуждается как в величине, так и в направлении, чтобы полностью описать его.Смещение — это пример скалярной величины, а время — пример векторной величины.
- Скалярная величина полностью описывается своей величиной, в то время как вектор нуждается как в величине, так и в направлении, чтобы полностью описать его. Время — это пример скалярной величины, а смещение — пример векторной величины.
- Скалярная величина полностью описывается своей величиной и направлением, тогда как вектору нужна только величина, чтобы полностью описать его.Смещение — это пример скалярной величины, а время — пример векторной величины.
- Скалярная величина полностью описывается своей величиной и направлением, тогда как вектору нужна только величина, чтобы полностью описать его. Время — это пример скалярной величины, а смещение — пример векторной величины.
Поддержка учителей
Поддержка учителей
Это видео хорошо подчеркивает разницу между векторами и скалярами.Студент знакомится с идеей использования «s» для обозначения смещения, которое вы можете поощрять, а можете и не поощрять. Перед тем, как ученики посмотрят видео, укажите, что инструктор использует s → s → для смещения вместо d, как в этом тексте. Объясните, что использование маленьких стрелок над переменными — распространенный способ обозначения векторов в курсах физики более высокого уровня. Предупредите учащихся, что в этом видео не используются общепринятые сокращения для часа и секунды. Напомните учащимся, что в своей работе они должны использовать сокращения h для часа и s для секунд.
Рабочий пример
Расчет средней скорости
Студент перемещается на 304 м к северу за 180 с. Какая была средняя скорость ученика?
Стратегия
Мы знаем, что смещение составляет 304 м к северу, а время — 180 с. Мы можем использовать формулу для средней скорости, чтобы решить задачу.
Решение
vavg = ΔdΔt = 304 м180 с = 1,7 м / с на север vavg = ΔdΔt = 304 м180 с = 1,7 м / с на север2,1
Обсуждение
Так как средняя скорость является векторной величиной, вы должны включить в ответ направление и величину.Обратите внимание, однако, что направление можно не указывать до конца, чтобы не загромождать проблему. Обратите внимание на значащие цифры в задаче. Расстояние 304 м состоит из трех значащих цифр, а временной интервал 180 с — только из двух, поэтому частное должно состоять только из двух значащих цифр.
Советы для успеха
Обратите внимание на способ представления скаляров и векторов. В этой книге d обозначает расстояние и перемещение. Точно так же v обозначает скорость, а v обозначает скорость.Переменная, не выделенная жирным шрифтом, указывает на скалярную величину, а переменная, выделенная жирным шрифтом, указывает на векторную величину. Иногда векторы представлены маленькими стрелками над переменной.
Поддержка учителей
Поддержка учителей
Используйте эту задачу, чтобы подчеркнуть важность использования правильного количества значащих цифр в вычислениях. Некоторые студенты имеют тенденцию включать много цифр в свои окончательные расчеты. Они ошибочно полагают, что повышают точность своего ответа, записывая многие цифры, указанные на калькуляторе.Обратите внимание на то, что это приведет к ошибкам в расчетах. В более сложных расчетах эти ошибки могут распространяться и приводить к неправильному окончательному ответу. Вместо этого напомните учащимся всегда носить с собой одну или две дополнительные цифры в промежуточных вычислениях и округлять окончательный ответ до правильного количества значащих цифр.
Рабочий пример
Решение для смещения, когда известны средняя скорость и время
Лейла бегает трусцой со средней скоростью 2.4 м / с на восток. Каково ее смещение через 46 секунд?
Стратегия
Мы знаем, что средняя скорость Лейлы составляет 2,4 м / с на восток, а временной интервал составляет 46 секунд. Мы можем изменить формулу средней скорости, чтобы найти смещение.
Решение
vavg = ΔdΔtΔd = vavgΔt = (2,4 м / с) (46 с) = 1,1 × 102 м на восток vavg = ΔdΔtΔd = vavgΔt = (2,4 м / с) (46 с) = 1,1 × 102 м на восток2,2
Обсуждение
Ответ: примерно в 110 м к востоку, что является разумным смещением для чуть менее минуты бега трусцой.Калькулятор показывает ответ как 110,4 м. Мы решили написать ответ, используя научную нотацию, потому что мы хотели прояснить, что мы использовали только две значащие цифры.
Советы для успеха
Размерный анализ — хороший способ определить, правильно ли вы решили проблему. Запишите расчет, используя только единицы, чтобы убедиться, что они совпадают на противоположных сторонах отметки равенства. В рассмотренном примере у вас
м = (м / с) (с). Поскольку секунды находятся в знаменателе средней скорости и в числителе времени, единица вычитает, оставляя только m и, конечно же, m = m.
Рабочий пример
Решение для времени, когда известны смещение и средняя скорость
Филипп идет по прямой дорожке от своего дома до школы. Сколько времени ему потребуется, чтобы добраться до школы, если он пройдет 428 м на запад со средней скоростью 1,7 м / с на запад?
Стратегия
Мы знаем, что смещение Филиппа составляет 428 м к западу, а его средняя скорость составляет 1,7 м / с к западу. Мы можем рассчитать время, необходимое для поездки, переписав уравнение средней скорости.
Решение
vavg = ΔdΔtΔt = Δdvavg = 428 м 1,7 м / с = 2,5 × 102 svavg = ΔdΔtΔt = Δdvavg = 428 м 1,7 м / с = 2,5 × 102 с2,3
Обсуждение
Здесь мы снова должны были использовать научную запись, потому что ответ мог состоять только из двух значащих цифр. Поскольку время является скаляром, ответ включает только величину, а не направление.
Практические задачи
10.Дальнобойщик проезжает 0,25 ч по прямой трассе с перемещением 16 км к югу.Какова средняя скорость дальнобойщика?
- 4 км / ч север
- 4 км / ч юг
- 64 км / ч север
- 64 км / ч юг
Птица летит со средней скоростью 7,5 м / с на восток от ветки к ветке за 2,4 с. Затем он делает паузу перед полетом со средней скоростью 6,8 м / с на восток в течение 3,5 с к другому ответвлению. Каково полное смещение птицы от начальной точки?
- 42 м запад
- 6 м запад
- 6 м восток
- 42 м на восток
Virtual Physics
The Walking Man
В этом симуляторе вы наведете курсор на человека и переместите его сначала в одном направлении, а затем в противоположном.Не отключайте вкладку Introduction . Вы можете использовать вкладку Charts после того, как узнаете о графике движения позже в этой главе. Внимательно следите за знаком чисел в полях положения и скорости. Пока не обращайте внимания на поле ускорения. Посмотрите, сможете ли вы сделать положение человека положительным, а скорость — отрицательным. Затем посмотрите, сможете ли вы сделать обратное.
Проверка захвата
Какая ситуация правильно описывает, когда положение движущегося человека было отрицательным, но его скорость была положительной?
- Человек движется к 0 слева от 0
- Человек движется к 0 справа от 0
- Человек движется от 0 слева от 0
- Человек движется от 0 справа от 0
Поддержка учителей
Поддержка учителей
Это мощная интерактивная анимация, которую можно использовать для многих уроков.На этом этапе его можно использовать, чтобы показать, что смещение может быть как положительным, так и отрицательным. Он также может показать, что при отрицательном смещении скорость может быть как положительной, так и отрицательной. Позже с его помощью можно будет показать, что скорость и ускорение могут иметь разные знаки. Настоятельно рекомендуется оставить учащихся на вкладке Introduction . Вкладку Charts можно использовать после того, как студенты узнают о графическом движении позже в этой главе.
Проверьте свое понимание
12.Два бегуна, идущие по одной прямой, начинают и заканчивают свой бег одновременно. На полпути у них разные мгновенные скорости. Возможно ли, чтобы их средние скорости на протяжении всей поездки были одинаковыми?
- Да, потому что средняя скорость зависит от чистого или полного смещения.
- Да, потому что средняя скорость зависит от общего пройденного расстояния.
- Нет, потому что скорости обоих бегунов должны оставаться одинаковыми на протяжении всего пути.
- Нет, потому что мгновенные скорости бегунов должны оставаться такими же в средней точке, но могут изменяться в других точках.
Если вы разделите общее расстояние, пройденное за поездку на автомобиле (определенное одометром), на время поездки, вычисляете ли вы среднюю скорость или величину средней скорости, и при каких обстоятельствах эти две величины одинаковы? ?
- Средняя скорость. Оба они одинаковы, когда автомобиль движется с постоянной скоростью и меняет направление.
- Средняя скорость. Оба они одинаковы, когда скорость постоянна и автомобиль не меняет своего направления.
- Величина средней скорости. И то, и другое одинаково, когда автомобиль движется с постоянной скоростью.
- Величина средней скорости. И то, и другое одинаково, когда машина не меняет своего направления.
Может ли средняя скорость быть отрицательной?
- Да, если чистое смещение отрицательное.
- Да, если направление объекта меняется во время движения.
- Нет, потому что средняя скорость описывает только величину, а не направление движения.
- Нет, потому что средняя скорость описывает только величину в положительном направлении движения.
Поддержка учителей
Поддержка учителей
Используйте вопросы «Проверьте свое понимание », чтобы оценить достижение учащимися учебных целей по разделам. Если учащиеся не справляются с какой-либо конкретной целью, Check Your Understanding поможет определить, кто из них и направит их к нужному контенту.Пункты оценивания в TUTOR позволят вам переоценить.
Использование графиков «скорость-время» для нахождения уравнения
Разгон
Силы и движение
Использование графиков скорости и времени для нахождения уравнения
Учебное пособие для 14–16
Представьте себе график, построенный со СКОРОСТЬЮ на вертикальной оси против ВРЕМЕНИ на горизонтальной оси.
Постоянная скорость
Для объекта, движущегося с постоянной скоростью v , график представляет собой просто горизонтальную линию на высоте v над осью. Вы уже знаете, что s , пройденное расстояние, — это скорость, умноженная на время, vt ; но на вашем графике v x t — это ОБЛАСТЬ затененного блока высотой v и длиной t .
Постоянное ускорение
Нарисуйте график для объекта, начиная с состояния покоя и двигаясь все быстрее и быстрее с постоянным ускорением.Линия должна наклоняться вверх по мере увеличения v . И если ускорение постоянное, линия должна быть прямой наклонной линией
.
Возьмите небольшой промежуток времени от T до T ‘ на оси времени, когда скорость была, скажем, v 1 . Посмотрите на столб, который сидит на нем и поднимается до наклонной линии графика (График III). Площадь этого столба равна его высоте v 1 , умноженной на короткое время TT ‘.Эта область — это расстояние, пройденное за это короткое время.
Насколько велико расстояние, пройденное за за весь период
, t , от отдыха до финала v ? Это площадь всех опор от начала до конца. Это площадь треугольника (на Графике IV) с конечной высотой v и основанием t , общим временем.
Площадь любого треугольника равна ½ (высота) x (основание).
Таким образом, расстояние s составляет ½ (высота, v ) x (основание, t ) s = ½ v t .
Предположим, что объект не запускается из состояния покоя , когда часы начинаются с 0, но уже движется со скоростью и . Разгоняется до скорости v , за время t . Тогда график похож на график V ниже; а пройденное расстояние показано заштрихованной областью. Он состоит из двух участков, прямоугольника и треугольника (График VI).
Площадь прямоугольника — u t , треугольника — ½ ( v — u ) t .
Тогда s = u t + ½ ( v — u ) t
- = u t + ½ v t -½ u t
- = ½ v t + ½ u t
- = ( v + u 2) t
В качестве альтернативы, поскольку v — u = a t
- s = u t + ½ ( v — u ) t может быть выражено как
- = u t + ½ ( a t ) t
- = u t + ½ a t 2
Эти формулы верны только для постоянного ускорения.




 Для этого:
Для этого: Он знает, что расстояние между его домом и домом Дяди Федора 12 км. Помогите Печкину рассчитать, сколько времени понадобится на дорогу?
Он знает, что расстояние между его домом и домом Дяди Федора 12 км. Помогите Печкину рассчитать, сколько времени понадобится на дорогу?
 Найдите среднюю скорость автомобиля.
Найдите среднюю скорость автомобиля.
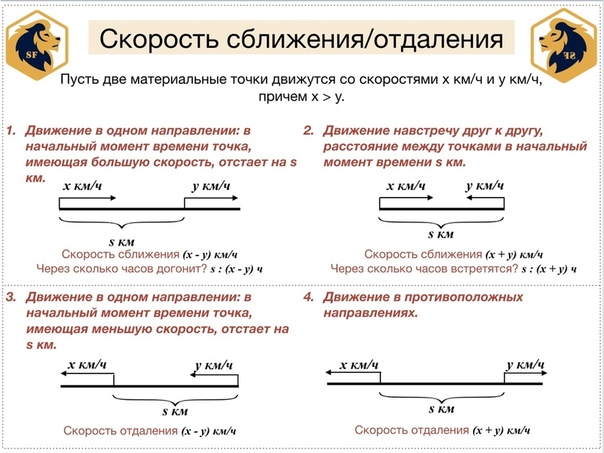 Общее время в пути: 3 + 2 + 1 = 6 {\displaystyle 3+2+1=6}
. Таким образом, формула запишется так: v = 340 6 {\displaystyle v={\frac {340}{6}}}
.
Общее время в пути: 3 + 2 + 1 = 6 {\displaystyle 3+2+1=6}
. Таким образом, формула запишется так: v = 340 6 {\displaystyle v={\frac {340}{6}}}
. Найдите среднюю скорость автомобиля на всем протяжении пути.
Найдите среднюю скорость автомобиля на всем протяжении пути. Неважно, какое значение подставить вместо a {\displaystyle a} , а какое — вместо b {\displaystyle b} .
Неважно, какое значение подставить вместо a {\displaystyle a} , а какое — вместо b {\displaystyle b} . При вводе значений, превышающих 59, производится перерасчет в часы и минуты. Например, результат выполнения функции (0;134;0) эквивалентен результату выполнения функции ВРЕМЯ(2;14;0) и равен 02:14.
При вводе значений, превышающих 59, производится перерасчет в часы и минуты. Например, результат выполнения функции (0;134;0) эквивалентен результату выполнения функции ВРЕМЯ(2;14;0) и равен 02:14.

