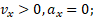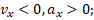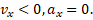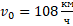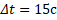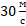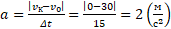Формула времени, t

Скорость, время и расстояние — физические величины, взаимосвязаны процессом движения. Различают равномерное и равноускоренное (равнозамедленное движение) тела. При равномерном движении скорость тела постоянна и не меняется со временем. При равноускоренном движении скорость тела изменяется со временем. Разберемся, как найти время, зная величины скорости и расстояния.

Формулы для определения времени, если известны скорость и расстояние имеют вид:

1. При неравномерном движении — путь пройденный телом равен произведению средней скорости на время на протяжении, которого тело двигалось:

   

где — начальная скорость, — расстояние, — время.

Единица измерения времени – с (секунды).

2. При равномерном движении — время необходимое для прохождения некоторого пути равняется частному от деления пути на среднюю скорость неравномерного движения:

   

где — расстояние, — скорость, — время.

На графиках показаны зависимости скорости от времени для: а – равномерное движение, б – неравномерное движение.

Примеры решения задач по теме «Время»

Понравился сайт? Расскажи друзьям!

Как найти скорость, время и расстояние по формуле вычисления скорости?

С древних времен людей беспокоит мысль о достижении сверх скоростей, так же как не дают покоя раздумья о высотах, летательных аппаратах. На самом деле это два очень сильно связанных между собой понятия. То, насколько быстро можно добраться из одного пункта в другой на летательном аппарате в наше время, зависит полностью от скорости. Рассмотрим же способы и формулы расчета этого показателя, а также времени и расстояния.

Как же рассчитать скорость?

На самом деле, рассчитать ее можно несколькими способами:

• через формулу нахождения мощности;
• через дифференциальные исчисления;
• по угловым параметрам и так далее.

В этой статье рассматривается самый простой способ с самой простой формулой — нахождение значения этого параметра через расстояние и время. Кстати, в формулах дифференциального расчета также присутствуют эти показатели.

Формула выглядит следующим образом:

v=S/t, где

• v — скорость объекта,
• S — расстояние, которое пройдено или должно быть пройдено объектом,
• t — время, за которое пройдено или должно быть пройдено расстояние.

Как видите, в формуле первого класса средней школы нет ничего сложного. Подставив соответствующие значения вместо буквенных обозначений, можно рассчитать быстроту передвижения объекта. Например, найдем значение скорости передвижения автомобиля, если он проехал 100 км за 1 час 30 минут. Сначала требуется перевести 1 час 30 минут в часы, так как в большинстве случаев единицей измерения рассматриваемого параметра считается километр в час (км/ч). Итак, 1 час 30 минут равно 1,5 часа, потому что 30 минут есть половина или 1/2 или 0,5 часа. Сложив вместе 1 час и 0,5 часа получим 1,5 часа.

Теперь нужно подставить имеющиеся значения вместо буквенных символов:

v=100 км/1,5 ч=66,66 км/ч

Здесь v=66,66 км/ч, и это значение очень приблизительное (незнающим людям об этом лучше прочитать в специальной литературе), S=100 км, t=1,5 ч.

Таким нехитрым способом можно найти скорость через время и расстояние.

А что делать, если нужно найти среднее значение? В принципе, вычисления, показанные выше, и дают в итоге результат среднего значение искомого нами параметра. Однако можно вывести и более точное значение, если известно, что на некоторых участках по сравнению с другими скорость объекта была непостоянной. Тогда пользуются таким видом формулы:

vср=(v1+v2+v3+…+vn)/n, где v1, v2, v3, vn — значения скоростей объекта на отдельных участках пути S, n — количество этих участков, vср — средняя скорость объекта на всем протяжении всего пути.

Эту же формулу можно записать иначе, используя путь и время, за которое объект прошел этот путь:

• vср=(S1+S2+…+Sn)/t, где vср — средняя скорость объекта на всем протяжении пути,
• S1, S2, Sn — отдельные неравномерные участки всего пути,
• t — общее время, за которое объект прошел все участки.

Можно записать использовать и такой вид вычислений:

• vср=S/(t1+t2+…+tn), где S — общее пройденное расстояние,
• t1, t2, tn — время прохождения отдельных участков расстояния S.

Но можно записать эту же формулу и в более точном варианте:

vср=S1/t1+S2/t2+…+Sn/tn, где S1/t1, S2/t2, Sn/tn — формулы вычисления скорости на каждом отдельном участке всего пути S.

Таким образом, очень легко найти искомый параметр, используя данные выше формулы. Они очень просты, и как уже было указано, используются в начальных классах. Более сложные формулы базируются на этих же формулах и на тех же принципах построения и вычисления, но имеют другой, более сложный вид, больше переменных и разных коэффициентов.

Это нужно для получения наиболее точного значения показателей.

Другие способы вычисления

Существую и другие способы и методы, которые помогают вычислить значения рассматриваемого параметра. В пример можно привести формулу вычисления мощности:

N=F*v*cos α , где N — механическая мощность,

F — сила,

v — скорость,

cos α — косинус угла между векторами силы и скорости.

Способы вычисления расстояния и времени

Можно и наоборот, зная скорость, найти значение расстояния или времени. Например:

S=v*t, где v — понятно что такое,

S — расстояние, которое требуется найти,

t — время, за которое объект прошел это расстояние.

Таким образом вычисляется значение расстояния.

Или вычисляем значение времени, за которое пройдено расстояние:

t=S/v, где v — все та же скорость,

S — расстояние, пройденный путь,

t — время, значение которого в данном случае нужно найти.

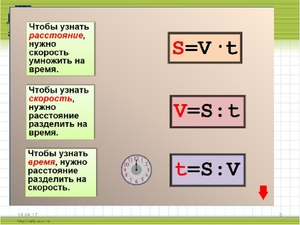
Для нахождения средних значений этих параметров существует довольно много представлений как данной формулы, так и всех остальных. Главное, знать основные правила перестановок и вычислений. А еще главнее знать сами формулы и лучше наизусть. Если же запомнить не получается, тогда лучше записывать. Это поможет, не сомневайтесь.

Пользуясь такими перестановками можно с легкостью найти время, расстояние и другие параметры, используя нужные, правильные способы их вычисления.

И это еще не предел!

Видео

В нашем видео вы найдете интересные примеры решения задач на нахождение скорости, времени и расстояния.

Физика. Формула времени. Решение задач

«Формула времени. Решение задач»

Скорость, время и расстояние — физические величины, взаимосвязаны процессом движения. Виды движений: 1) равномерное (прямолинейное, криволинейное и по окружности), 2) равноускоренное (с постоянным ускорением), 3) гармоническое. Для каждого вида движения своя формула времени.

Время обозначается как t. Единица измерения времени – с (секунды).

Самая простая формула при равномерном прямолинейном движении. Время, необходимое для прохождения пути равняется частному от деления пути на скорость равномерного прямолинейного движения: t = S / v.

При равноускоренном движении время равняется частному от деления разницы конечной и начальной скорости на ускорение:

t = (v — v₀) / a  или частному от деления пути на разность конечной и начальной скорости: t = S / (v — v₀).

Решение задач через формулу времени

Задача № 1.

Конькобежец может развивать скорость до 13 м/с. За какое время он пробежит дистанцию длиной 2,6 км?

 Ответ: 200 с.

---

Задача № 2.

Двигаясь с ускорением 5 м/с² скорость космической ракеты увеличилась на 100 м/с. За какое время произошло такое изменение скорости?

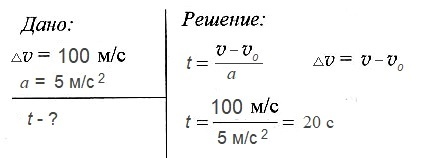 Ответ: 20 с.

---

Задача № 3.

Пункты А и В находятся на берегу реки на некотором расстоянии друг от друга. Моторная лодка проходит расстояние АВ вниз по течению реки за время t₁ = 3 ч, а плот то же расстояние – за время t₀ =12 ч. Какое время t₂ затратит моторная лодка на обратный путь?

Решение. Обозначим расстояние между пунктами А и В через L, скорость моторной лодки относительно воды через v_л , а скорость течения через 

v_т. Тогда t₀ = L / v_т ,  t₁ = L / (v_л +  v_т) ,  t₂ = L / (v_л —  v_т) . Исключая из записанной системы уравнений L, v_л и  v_т
находим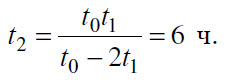 

Ответ: 6 ч.

---

Конспект урока «Формула времени. Решение задач».

Следующая тема: «».

 

Ускорение. Равноускоренное движение. Зависимость скорости от времени при равноускоренном движении

Для того чтобы ответить на вопрос, что же такое равноускоренное движение, обратимся к следующему эксперименту. Возьмем движение автомобиля по наклонной плоскости. Автомобиль начинает движение из состояния покоя. Рассмотрим положение автомобиля через одинаковые промежутки времени 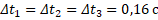 (рис. 1). За равные промежутки времени автомобиль проезжал все большие расстояния 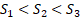, совершал все большие и большие перемещения.

Рис. 1. Положение автомобиля через равные промежутки времени

Повторим этот эксперимент, увеличив угол наклона плоскости к поверхности стола (рис. 2). Опять-таки, рассмотрим положение автомобиля через равные промежутки времени.

Рис. 2. Эксперимент с увеличенным углом наклона плоскости к поверхности стола

Обратите внимание, что расстояние, которое проходит автомобиль за равные промежутки времени 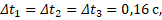 увеличивается быстрее, чем в предыдущий раз. Таким образом, и скорость автомобиля растет быстрее 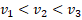. В физике говорят, что во втором случае было большее ускорение.

Ускорение – это физическая величина, равная отношению изменения скорости тела ко времени, за которое это изменение произошло (рис. 3).

Рис. 3. Иллюстрация определения ускорения

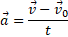
где 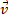 – текущая или конечная скорость;  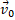– начальная скорость;  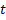– промежуток времени, за который произошло изменение скорости.

Ускорение обозначается буквой 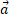, так как этот термин произошел от латинского слова acceleration – «ускоряться, увеличивать скорость». В физике очень много величин обозначаются от первой буквы их латинского наименования или английского аналога (рис. 4).

Рис. 4. Некоторые физические величины

Записав векторное определение ускорения, перейдем к его скалярному определению – проекции ускорения, ведь чаще всего в курсе 10 класса мы будем работать с прямолинейным движением, где нам достаточно одной оси, как правило, оси х.

Определение ускорения в проекции на ось х:

где 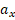 – проекция ускорения на ось х,  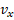– проекция текущей скорости на ось х,  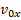– проекция начальной скорости на ось х,  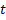или 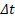 – промежуток времени, за который произошло изменение проекции скорости.

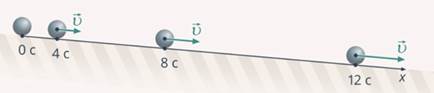
Рис. 5. Иллюстрация определения проекции ускорения

Формулу ускорения можно записать в виде: – изменения скорости за промежуток времени. Мы приходим еще к одному определению ускорения. Ускорение – это скорость изменения скорости. То есть насколько быстро меняется скорость тела.

Мы ввели новую физическую величину, а значит, необходимо указать, в каких единицах она измеряется, в частности в системе СИ. Изменение скорости 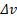 измеряется в , а время 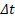 – в секундах. Тогда:

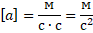
Если мы говорим, что модуль ускорения равен, например, 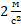 – это значит, что за каждую секунду скорость тела изменялась (либо увеличивалась, либо уменьшалась) на  (рис. 6).

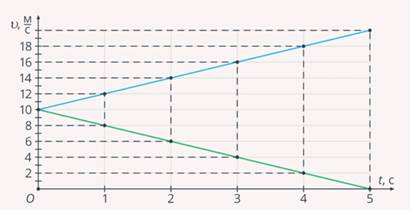
Рис. 6. Физический смысл ускорения

Обратите внимание, что мы говорили о модуле ускорения, не сказав ни слова о его направлении.

Естественно, вектор ускорения направлен в ту же сторону, что и вектор изменения скорости . Обратите внимание, что именно вектор изменения скорости, а не просто вектор скорости, ведь она непрерывно меняется. Скорость может менять не только свою величину, но и направление, как, например, в случае криволинейного движения (рис. 7).

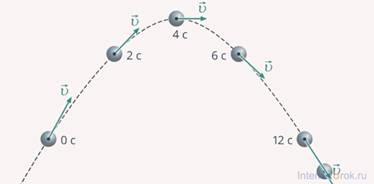
Рис. 7. Тело, брошенное под углом к горизонту

Ускорение направлено в сторону вектора изменения скорости: .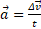

Разберем несколько примеров, которые помогут разобраться в том, куда и как направлено ускорение по отношению к скорости.

Задача. Пусть тело двигалось прямолинейно по следующим этапам:

1. 
2. 
3. 
4. 

Какой из этих этапов не может следовать сразу за предыдущим?

Решение. Разобьем прямолинейную траекторию тела на 4 этапа.

На первом этапе проекция ускорения равна нулю, тело двигалось равномерно с одной и той же скоростью .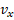

На втором этапе 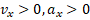, то есть тело начало разгоняться и к концу второго этапа увеличило свою скорость.

На третьем этапе проекция скорости меньше нуля, это значит, что тело меняет направление своего движения. То есть, если бы третий этап начался так, как написано в условии, скорость должна была бы быть направлена влево (рис. 8). Но мы знаем, что к концу этапа скорость тела была направлена вправо. Это значит, что переход между вторым и третьим этапом невозможен. Сначала тело должно остановиться, а только потом начать разгоняться в другую сторону.

Рис. 8. Иллюстрация решения задачи

Рассмотрим отдельно переход между третьим и четвертым этапами. На третьем этапе проекция скорости отрицательна, а проекция ускорения положительна. Это значит, что ускорение тела направлено вправо. На четвертом этапе скорость будет направлена, как и на третьем этапе, влево, а ускорение будет отсутствовать, что вполне возможно. На третьем этапе тело тормозило, а на четвертом оно перестанет менять свою скорость (рис. 9).

Рис. 9. Переход между третьим и четвертым этапом

Ответ. Ошибка допущена в переходе между вторым и третьим этапами.

Если тело движется неравномерно, то оно обладает ускорением. Это ускорение может изменяться в очень широком диапазоне даже за небольшой промежуток времени. Самый простой вид неравномерного движения – движение с неизменным ускорением. Такое движение называется равноускоренным.

Равноускоренным называют такое движение, при котором скорость тела за любые равные промежутки времени изменяется на одинаковую величину (рис. 10).

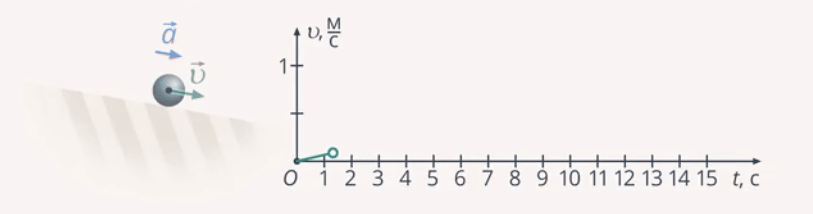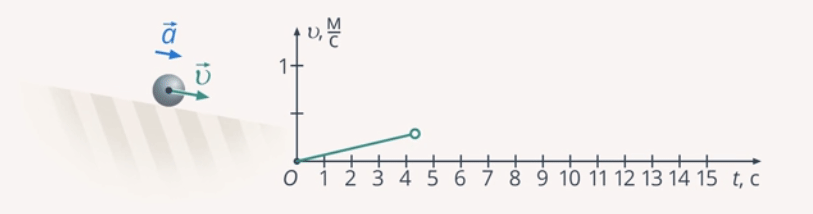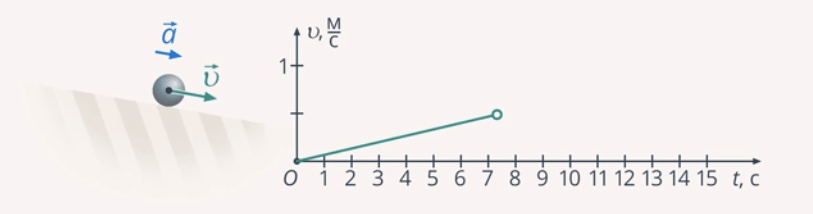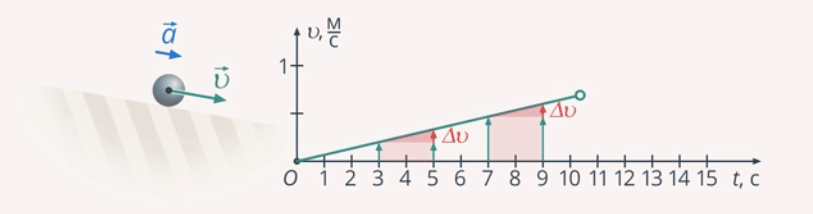
Рис. 10. Иллюстрация равноускоренного движения

Обратите внимание на слово «любые» в определении, как и в случае равномерного движения. Таким образом, еще раз подчеркнем, что равноускоренное движение – это движение с постоянным ускорением.

Примеры равноускоренного движения: движение автомобиля из начала урока (рис. 11), свободное падение (рис. 12) – движение тела в поле силы тяжести, скольжение на льду зимой (рис. 13) и т. д.

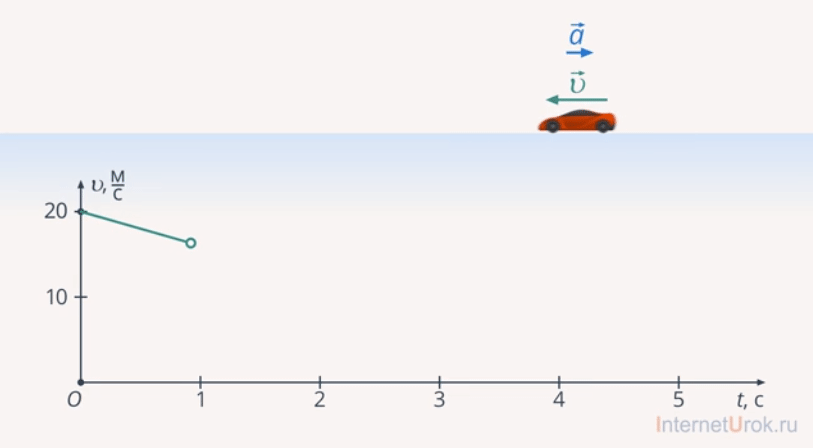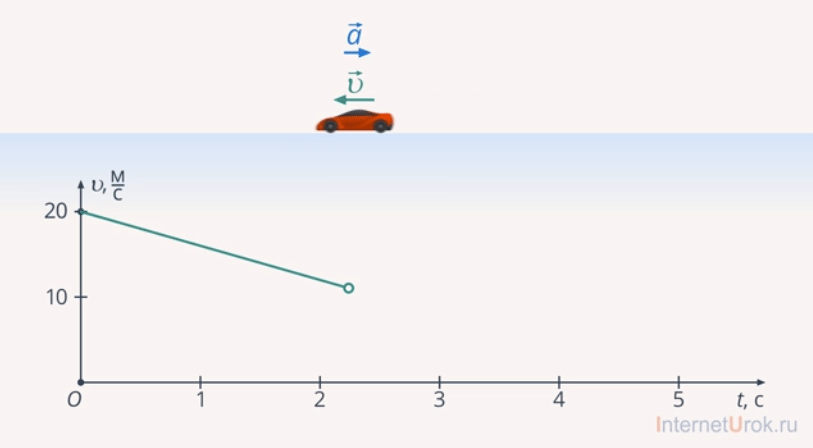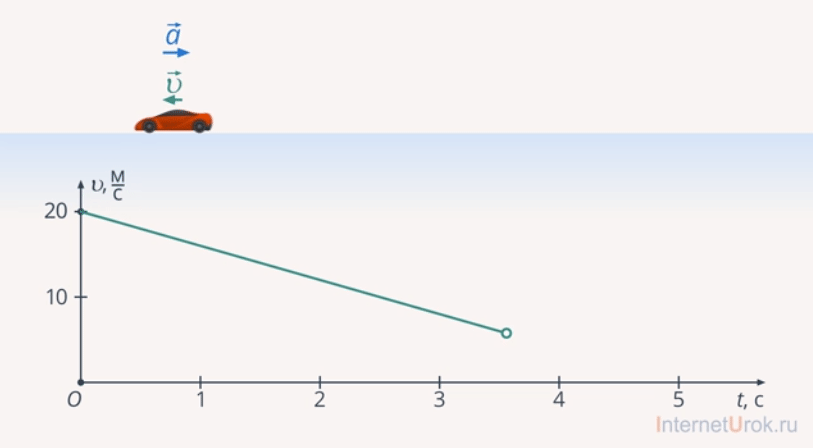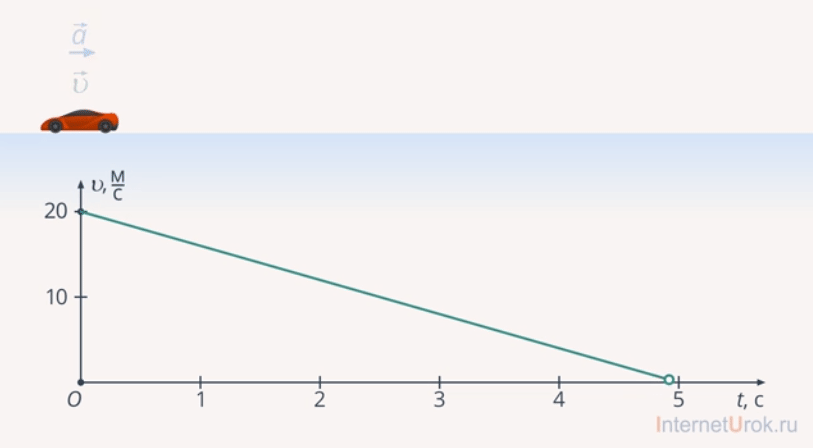
Рис. 11. Пример равноускоренного движения

Рис. 12. Пример равноускоренного движения

Рис. 13. Пример равноускоренного движения

На графике (рис. 14) представлены зависимости проекции ускорения от времени для трех тел. У первого тела проекция ускорения положительна и не изменяется. Можно сказать, что тело движется равноускорено и разгоняется. У второго тела проекция ускорения отрицательна, в этом случае тело может не только тормозить, но и разгоняться в сторону, противоположную выбранной оси. Ускорение третьего тела равно нулю. Это совершенно не значит, что тело покоится. Это значит, что оно движется равномерно прямолинейно.

Рис. 14. График зависимости проекции ускорения при равноускоренном движении от времени

Такой анализ графика позволяет привести еще одно определение для уже изученного ранее движения. Равномерное движение – это равноускоренное движение, если ускорение равно нулю.

Для второго тела проекция ускорения меньше нуля. Мы предположили, что оно могло бы тормозить. Почему же такое движение называется равноускоренным, ведь тело замедляется? Можно услышать такой термин, как равнозамедленное движение, но в физике принято пользоваться одним термином – равноускоренное, понимая, что для второго тела проекция ускорения отрицательна.

С решением главной задачи механики мы разберемся на следующем уроке. А оставшуюся часть этого урока мы посвятим закону нахождения зависимости скорости от времени для равноускоренного движения. Он поможет определить не только закон зависимости координаты от времени, но и анализировать и изучать равноускоренное движение.

Для того чтобы найти закон зависимости 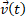, вспомним определение ускорения:

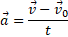
где 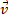 – текущая или конечная скорость;  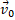– начальная скорость;  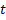– промежуток времени.

Найдем выражение для 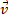 из приведенной выше формулы:

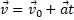 – векторное представление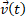

В проекции на ось х, закон будет иметь следующий вид:

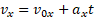
Задача. Чему равен модуль ускорения автомобиля при равноускоренном торможении, если при начальной скорости 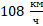 время торможения составило ?

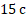Дано:	CИ:	Решение:
	Ответ: .

 

Решение. Так как в задаче речь идет о торможении автомобиля, 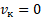. Первым пунктом решения является перевод  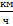в СИ.

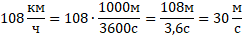
Модуль ускорения может быть найден как отношение изменения скорости ко времени, за которое это изменение произошло: .

Изменение скорости 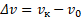. Так как в задаче спрашивают о модуле ускорения:

Подставив известные значения, получим:

Ответ: 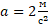. Таким образом, за каждую секунду скорость тела уменьшалась на .

Графики зависимости проекции скорости равноускоренного движения от времени позволяют анализировать и описывать равноускоренное движение. В первую очередь вспомним формулу:

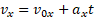
С точки зрения математики такая зависимость называется линейной, а ее график представляет прямую.

На рис. 15 представлены зависимости скорости от времени для трех разных тел. Первое тело начинает движение из состояния покоя (начальная скорость равна нулю). Проекция его ускорения положительна, это значит, что тело разгоняется. Второе тело имеет начальную скорость 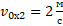, проекция ускорения равна нулю. Таким образом, скорость тела не меняется, тело движется равномерно прямолинейно. Третье тело имеет также начальную скорость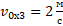, проекция ускорения отрицательна, но это совсем не значит, что тело движется в сторону, противоположную движению первого тела. Это значит, что до определенного момента времени (точка на оси) тело тормозит (модуль его скорости падает). После этого момента времени модуль скорости начинает расти, а знак проекции скорости меняется. Данная точка называется точкой поворота.

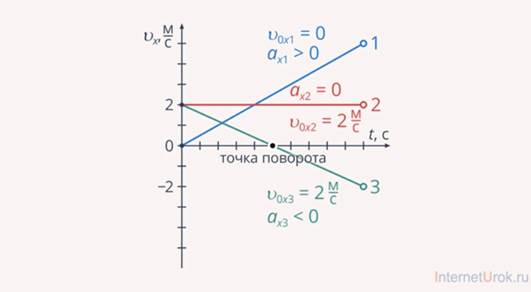
Рис. 15. Графики зависимости проекции скорости равноускоренного движения от времени

Рассмотрим, как движется первое, второе и третье тело, на примере с машинками.

Первое тело начало свое движение из состояния покоя и постепенно увеличивало свою скорость (автомобиль разгоняется) (рис. 16).

Рис. 16. Моделирование движения первого тела

Смоделировать движение второго тела абсолютно точно не получится, ведь оно двигалось равномерно с постоянной скоростью .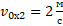

Рис. 17. Моделирование движения второго тела

Сначала модуль скорости движения третьего тела уменьшался, т. е. оно тормозило. После чего в какой-то момент времени модуль скорости начал расти, а знак проекции поменялся. Это значит, что тело начало разгоняться в противоположном направлении.

Рис. 18. Моделирование движения третьего тела

Движение тела, брошенного вертикально вверх, – это еще один вариант моделирования движения третьего тела. Например, подбросим ручку. По мере подъема скорость ручки будет уменьшаться, в верхней точке она будет нулевой. После ручка начнет ускоренно падать, то есть изменит свое направление и будет увеличивать скорость движения.

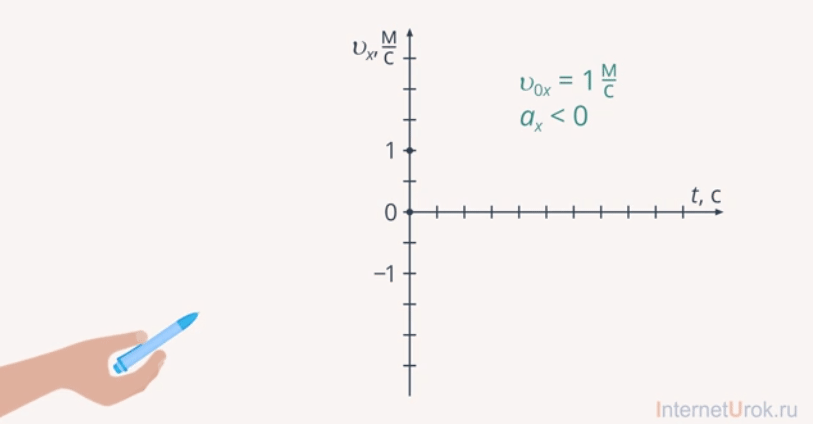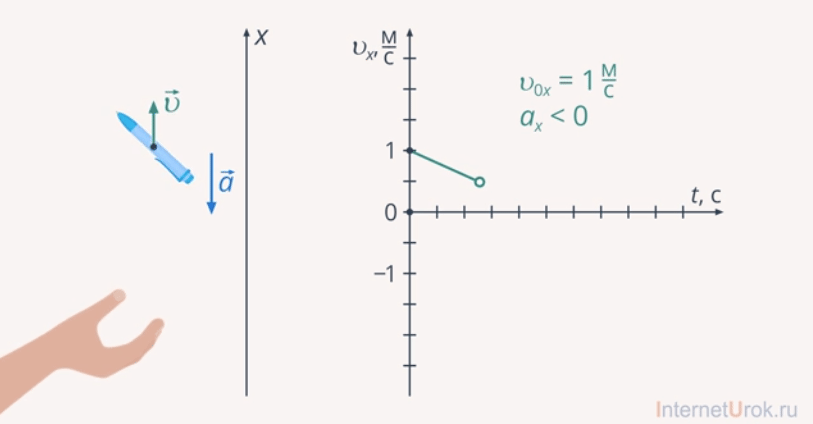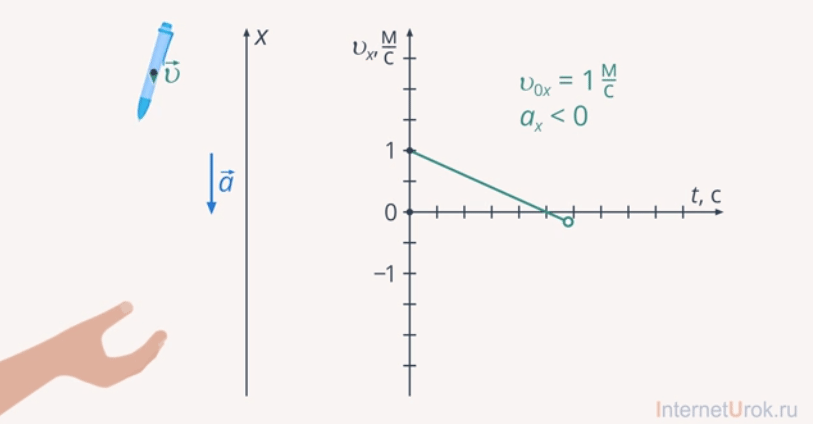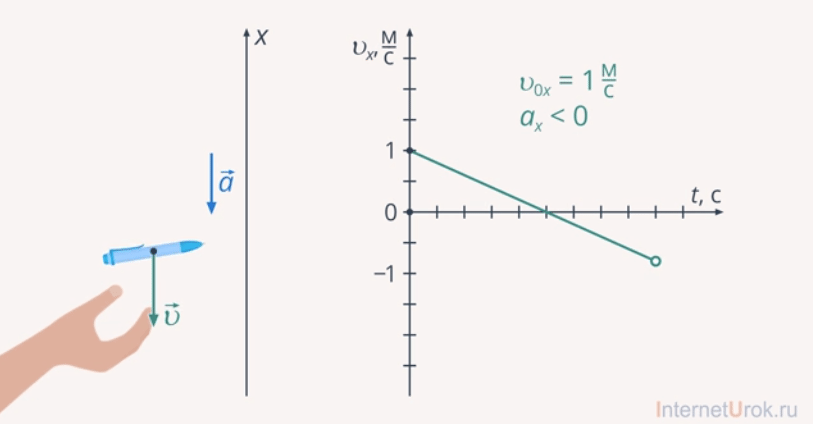
Рис. 19. Моделирование движения третьего тела. Движение тела, брошенного вертикально вверх

Задача. По представленному графику зависимости проекции скорости от времени записать уравнение данной зависимости.

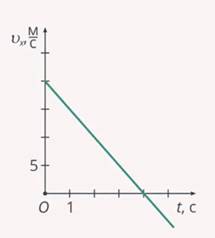
Рис. 20. Задача № 3

Решение. Для начала вспомним формулу:

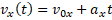
Таким образом, нам необходимо найти значения 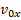 и .

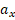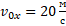 – проекция скорости в начальный момент времени.

Выбираем удобный для решения промежуток времени, тогда:

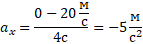
Проекция ускорения отрицательна, а значит, ускорение направлено в противоположную сторону выбранной оси.

Искомое уравнение будет иметь вид:

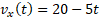
Ответ: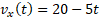

На сегодняшнем уроке мы ввели понятия ускорения и равноускоренного движения.

Формулы равномерного и равноускоренного движения

Равномерное движение

Формула скорости движения при равномерном движении: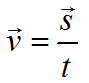

v=const
a=0
v — скорость, м/с
s — перемещение, м
t — время, с
Формула перемещения при равномерном движении: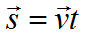

Координата вычисляются через кинематическое уравнение равномерного прямолинейного движения по  формуле: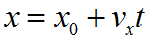

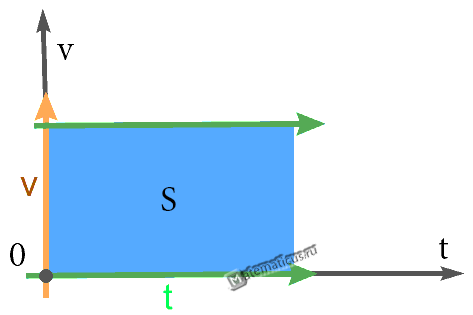
График — Равномерного прямолинейного движения

Равноускоренное движение

Формула скорости при равноускоренном движении: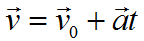

a=const
v₀ — начальная скорость, м/с
a — ускорение, м/с²
Формула для нахождения перемещения при равноускоренном движении: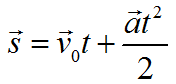

или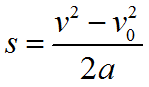

Уравнение равноускоренного движения в проекции на оси координат: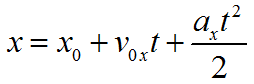

Формула для определения ускорения при равноускоренном прямолинейном движении:

v₀ — начальная скорость, м/с
v — мгновенная скорость, м/с
Формула для определения средней скорости движения: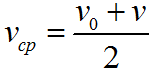

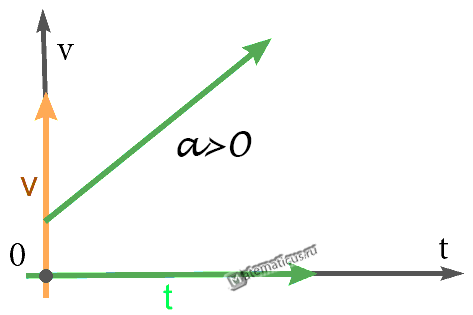
График — Равноускоренное движение при a>0

Равнозамедленное движение

Формула скорости при равнозамедленном движении: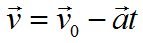

Формула перемещения при равнозамедленном движении: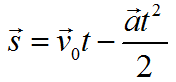

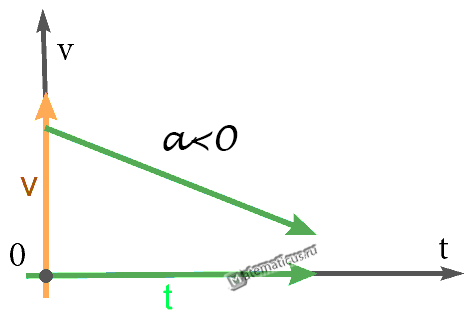
График — Равнозамедленное движение при a<0

Свободное падение

Постоянная величина скорости свободного падения тела равна g=9,8 м/с²
Формула для вычисления скорости при свободном падении тела: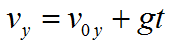

Формула для вычисления перемещения при свободном падении тела: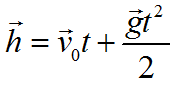


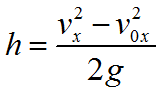
Формула координаты при свободном падении тела: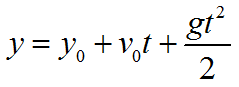

Формула высоты с которой тело свободно падает: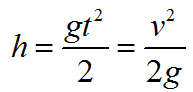

Формула для определения скорости тела в конце свободного падения: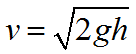

Время свободного падения тела равно: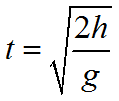

Равноускоренное движение: формулы, примеры

Равноускоренное движение

Равноускоренное движение — это движение, при котором вектор ускорения не меняется по модулю и направлению. Примеры такого движения: велосипед, который катится с горки; камень брошенный под углом к горизонту. Равномерное движение — частный случай равноускоренного движения с ускорением, равным нулю.

Рассмотрим случай свободного падения (тело брошено под уголом к горизонту) более подробно. Такое движение можно представить в виде суммы движений относительно вертикальной и горизонтальной осей.

В любой точке траектории на тело действует ускорение свободного падения g→, которое не меняется по величине и всегда направлено в одну сторону. 

Вдоль оси X движение равномерное и прямолинейное, а вдоль оси Y — равноускоренное и прямолинейное. Будем рассматривать проекции векторов скорости и ускорения на оси.

Формулы для равноускоренного движения

Формула для скорости при равноускоренном движении:

v=v0+at.

Здесь v0 — начальная скорость тела, a=const — ускорение.

Покажем на графике, что при равноускоренном движении зависимость v(t) имеет вид прямой линии.

​​​​​​​

Ускорение можно определить по углу наклона графика скорости. На рисунке выше модуль ускорения равен отношению сторон треугольника ABC.

a=v-v0t=BCAC

Чем больше угол β, тем больше наклон (крутизна) графика по отношению к оси времени. Соответственно, тем больше ускорение тела.

Для первого графика: v0=-2 мс; a=0,5 мс2.

Для второго графика: v0=3 мс; a=-13 мс2.

По данному графику можно также вычислить перемещение тела за время t. Как это сделать?

Выделим на графике малый отрезок времени ∆t. Будем считать, что он настолько мал, что движение за время ∆t можно считать

Графики равномерного, равноускоренного движения, сравнение. Линейная, квадратная зависимость. Правила определения параметров

Тестирование онлайн

Механическое движение представляют графическим способом. Зависимость физических величин выражают при помощи функций. Обозначают

Графики равномерного движения

Зависимость ускорения от времени. Так как при равномерном движении ускорение равно нулю, то зависимость a(t) — прямая линия, которая лежит на оси времени.

Зависимость скорости от времени. Скорость со временем не изменяется, график v(t) — прямая линия, параллельная оси времени.

Правило определения пути по графику v(t): Численное значение перемещения (пути) — это площадь прямоугольника под графиком скорости.

Зависимость пути от времени. График s(t) — наклонная линия.

Правило определения скорости по графику s(t): Тангенс угла наклона графика к оси времени равен скорости движения.

Графики равноускоренного движения

Зависимость ускорения от времени. Ускорение со временем не изменяется, имеет постоянное значение, график a(t) — прямая линия, параллельная оси времени.

Зависимость скорости от времени. При равномерном движении путь изменяется, согласно линейной зависимости . В координатах . Графиком является наклонная линия.

Правило определения пути по графику v(t): Путь тела — это площадь треугольника (или трапеции) под графиком скорости.

Правило определения ускорения по графику v(t): Ускорение тела — это тангенс угла наклона графика к оси времени. Если тело замедляет движение, ускорение отрицательное, угол графика тупой, поэтому находим тангенс смежного угла.

Зависимость пути от времени. При равноускоренном движении путь изменяется, согласно квадратной зависимости . В координатах зависимость имеет вид . Графиком является ветка параболы.

График движения при . График движения при

График движения при . График движения при

Сравнительная таблица графиков