Угловая частота — Википедия
Материал из Википедии — свободной энциклопедии
Углова́я частота́ (синонимы: радиальная частота, циклическая частота, круговая частота, частота вращения) — скалярная физическая величина, мера частоты вращательного или колебательного движения. В случае вращательного движения угловая частота равна модулю вектора угловой скорости. В Международной системе единиц (СИ) и системе СГС угловая частота выражается в радианах в секунду, её размерность обратна размерности времени (радианы безразмерны).
Угловая частота является производной по времени от фазы колебания:
- ω=∂φ/∂t.{\displaystyle \omega =\partial \varphi /\partial t.}
Другое распространённое обозначение ω=φ˙.{\displaystyle \omega ={\dot {\varphi }}.}
Угловая частота связана с частотой ν соотношением[1]
- ω=2πν.{\displaystyle \omega ={2\pi \nu }.}
В случае использования в качестве единицы угловой частоты градусов в секунду связь с обычной частотой будет следующей:
- ω=360∘ν.{\displaystyle \omega ={360^{\circ }\nu }.}
В случае вращательного движения угловая частота численно равна углу, на который повернется вращающееся тело за единицу времени (то есть равна модулю вектора угловой скорости), в случае колебательного движения — приращению полной фазы колебания за единицу времени. Численно угловая (циклическая) частота равна числу циклов (колебаний, оборотов) за 2π единиц времени.
Введение циклической частоты (в её основной размерности — радианах в секунду) позволяет упростить многие формулы в теоретической физике и электронике. Так, резонансная циклическая частота колебательного LC-контура равна ωLC=1/LC,{\displaystyle \omega _{LC}=1/{\sqrt {LC}},} тогда как обычная резонансная частота νLC=1/(2πLC).{\displaystyle \nu _{LC}=1/(2\pi {\sqrt {LC}}).}
В то же время ряд других формул усложняется. Решающим соображением в пользу циклической частоты стало то, что переводные множители 2π и 1/(2π), появляющиеся во многих формулах при использовании радианов для измерения углов и фаз, исчезают при введении циклической частоты.
См. также
Примечания
- ↑ Угловая частота. Большой энциклопедический политехнический словарь. Проверено 27 октября 2016.
Угловая частота — Angular frequency
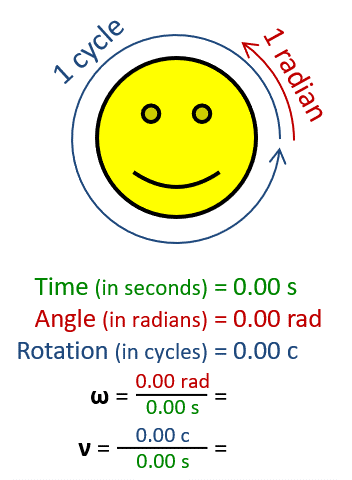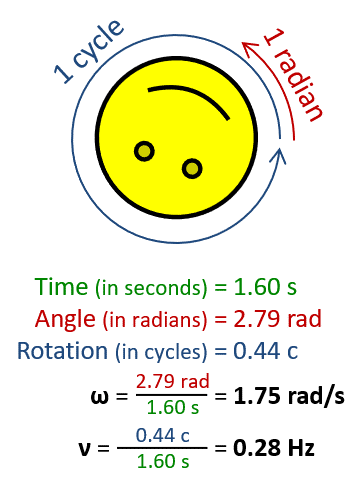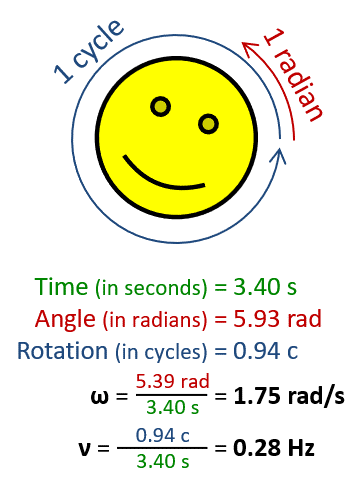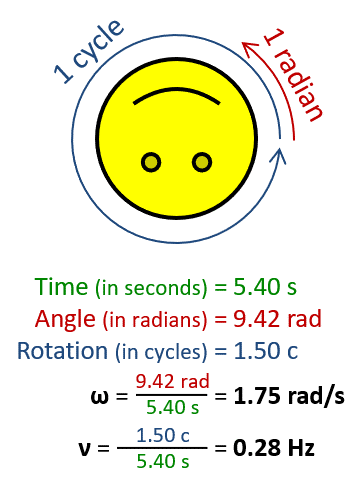 Угловая частота ω (в радианах в секунду), больше , чем частоты v , (в циклах в секунду, также называемых Гц ), с коэффициентом 2 П . Эта цифра используется символ v , вместо е для обозначения частоты.
Угловая частота ω (в радианах в секунду), больше , чем частоты v , (в циклах в секунду, также называемых Гц ), с коэффициентом 2 П . Эта цифра используется символ v , вместо е для обозначения частоты.  Сфера вращается вокруг оси. Очки дальше от оси двигаться быстрее, удовлетворяющими & omega = V / г .
Сфера вращается вокруг оси. Очки дальше от оси двигаться быстрее, удовлетворяющими & omega = V / г .В физике , угловая частота ω (также упоминаемые условиями угловой скорости , радиальная частота , круговая частота , орбитальная частота ,
Угловая частота (или угловая скорость) является величиной вектора величины угловой скорости . Термин вектор угловой частоты иногда используется как синоним векторной величины угловой скорости. ω→{\ Displaystyle {\ VEC {\ Omega}}}
Одна революция равна 2я радиан , следовательно ,
- ωзнак равно2πTзнак равно2πе,{\ Displaystyle \ омега = {{2 \ пи} \ над Т} = {2 \ пи е},}
где:
- ω угловая частота или угловая скорость (измеряется в радианах в секунду ),
- Т представляет собой период (измеряется в секундах ),
- е представляет собой обычную частоту (измеряется в герцах ) (иногда символизируется с v , ).
Единицы
В СИ единицах , угловая частота , как правило , представлена в радианах в секунду , даже когда он не выражает значение вращения. С точки зрения анализа размерностей , блок герц (Гц) тоже верно, но на практике это не используется только для обычной частоты е , и почти никогда не для со . Это соглашение помогает избежать путаницы.
Круговое движение
Во вращающемся или орбитальном объекте, существует зависимость между расстоянием от оси, тангенциальной скорости и угловой частоты вращения:
- ωзнак равноv/р,{\ Displaystyle \ омега = V / R.}
Колебания пружины
Объект прикреплен к пружине может колебаться . Если пружина считается идеальным и безмассов без какого — либо затухания, то движение простое и гармонический с угловой частотой , заданной
- ωзнак равноКм,{\ Displaystyle \ Omega = {\ SQRT {\ гидроразрыва {к} {м}}}}
где
- K представляет собой коэффициент жесткости пружины ,
- м масса объекта.
ω называется собственной частотой (который иногда может быть обозначено как со 0 ).
Как осциллирует объект, его ускорение может быть вычислено путем
- aзнак равно-ω2Икс,{\ Displaystyle а = — \ Omega ^ {2} х,}
где х представляет смещение от положения равновесия.
Использование «обычные» обороты в секунду частоты, те это уравнение будет
- aзнак равно-4π2е2Икс,{\ Displaystyle а = -4 \ пи ^ {2} е ^ {2} х.}
LC схемы
Резонансная угловая частота в серии цепи LC равно корень квадратный из обратной продукта из емкости ( C , измеренной в фарадах ) и индуктивность цепи ( L , с SI единицы генри ):
- ωзнак равно1LС,{\ Displaystyle \ Omega = {\ SQRT {\ гидроразрыва {1} {LC}}}.}
Добавление последовательного сопротивления (например, из-за сопротивление проволоки в катушке) не приводит к изменению частоты резонирует схему серии LC. Для параллельного резонансного контура, приведенное выше уравнение часто является полезным приближение, но частота резонирует действительно зависит от потерь параллельных элементов.
Смотрите также
Ссылки и примечания
Похожие чтения:
внешняя ссылка
<img src=»https://en.wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>угловая частота — это… Что такое угловая частота?
- угловая частота
- углова́я частота́
(круговая частота), число колебаний, совершаемых за 2π единиц времени. Угловая частота ω = 2πn = 2π/T, где ν — число колебаний в единицу времени, Т — период колебаний. Обычно используемая единица времени — секунда; тогда угловая частота измеряется в рад/с.
* * *
УГЛОВАЯ ЧАСТОТАУГЛОВА́Я ЧАСТОТА́ (круговая частота), число колебаний, совершаемых за 2p секунд. Угловой частоты , где n — число колебаний в секунду, Т — период колебаний.
Энциклопедический словарь. 2009.
- угловая скорость
- угловое ускорение
Смотреть что такое «угловая частота» в других словарях:
Угловая частота — Размерность T −1 Единицы измерения … Википедия
угловая частота — периодических колебаний; угловая частота; отрасл. круговая частота Число периодов колебаний в 2π единиц времени. угловая частота синусоидального электрического тока; угловая частота Частота синусоидального электрического тока, умноженная на 2π … Политехнический терминологический толковый словарь
угловая частота — Скорость изменения фазы синусоидального электрического тока, равная частоте синусоидального электрического тока, умноженной на 2π. Примечание — Аналогично определяют угловые частоты синусоидальных электрического напряжения,… … Справочник технического переводчика
УГЛОВАЯ ЧАСТОТА — (круговая частота), число колебаний, совершаемое за 2p секунд. Угловая частота w=2pn=2p/T, где n число колебаний в 1 с., T период колебаний. Угловая частота при вращательном движении число оборотов, совершаемое вращающимся твердым телом за 1 с.,… … Современная энциклопедия
Угловая частота — (круговая частота), число колебаний, совершаемое за 2p секунд. Угловая частота w=2pn=2p/T, где n число колебаний в 1 с., T период колебаний. Угловая частота при вращательном движении число оборотов, совершаемое вращающимся твердым телом за 1 с.,… … Иллюстрированный энциклопедический словарь
УГЛОВАЯ ЧАСТОТА — (круговая частота) число колебаний, совершаемых за 2? секунд. Угловой частоты , где ? число колебаний в секунду, Т период колебаний … Большой Энциклопедический словарь
угловая частота — 3.1.2 угловая частота w (angular frequency), рад/с: Циклическая частота, умноженная на 2π. Источник … Словарь-справочник терминов нормативно-технической документации
угловая частота — kampinis dažnis statusas T sritis fizika atitikmenys: angl. angular frequency; cyclic frequency; radian frequency vok. Kreisfrequenz, f; Winkelfrequenz, f rus. круговая частота, f; угловая частота, f; циклическая частота, f pranc. fréquence… … Fizikos terminų žodynas
угловая частота — kampinis dažnis statusas T sritis automatika atitikmenys: angl. angular frequency; circular frequency vok. Kreisfrequenz, f; Winkelfrequenz, f rus. круговая частота, f; угловая частота, f pranc. fréquence angulaire, f; fréquence circulaire, f … Automatikos terminų žodynas
угловая частота — kampinis dažnis statusas T sritis Standartizacija ir metrologija apibrėžtis Virpesio fazės kitimo sparta, išreiškiama formule: ω = 2πf; čia f – dažnis. Kampinio dažnio ω matavimo vienetas yra rad/s (radianas per sekundę), o dažnio f – Hz (hercas) … Penkiakalbis aiškinamasis metrologijos terminų žodynas
чем угловая частота отличается от частоты колебаний?
хрн знает, я знаю только частоту колебаний и угловую скорость, — по другому: число оборотов за едцу времени. вот между последними зависимость и составляет 2pi,ежли не ошибаюсь
Численно циклическая частота равна числу циклов (колебаний, оборотов) за 2π секунд. Введение циклической частоты (в её основной размерности — радианах в секунду) позволяет упростить многие формулы в теоретической физике и электронике. Так, резонансная циклическая частота колебательного LC-контура равна <img src=»//content.foto.my.mail.ru/mail/badlak/_answers/i-153.jpg» > тогда как обычная резонансная частота <img src=»//content.foto.my.mail.ru/mail/badlak/_answers/i-154.jpg» > В то же время ряд других формул усложняется. Решающим соображением в пользу циклической частоты стало то, что множители 2π и 1/(2π), появляющиеся во многих формулах при использовании радианов для измерения углов и фаз, исчезают при введении циклической частоты. Так что ответ: Она введена для упрощения расчетов. Это тоже самое, но в другой размерности. Как… килограмм и фунт.
Угловое расстояние — Википедия
Материал из Википедии — свободной энциклопедии
В математике (в частности, в геометрии и тригонометрии) и во всех естественных науках (например, в астрономии и геофизике)
Угловое расстояние является фундаментальной величиной в астрономии, определяющей положение любого объекта на небесной сфере по его небесным координатам: либо в угловых единицах, либо во времени. Азимут, высота, склонение или прямое восхождение объекта на небе, среди прочего, являются небесными координатами. Любое из них — это угловое расстояние до точки или плоскости отсчета: горизонта, небесного экватора, меридиана и т. д.
Термин угловое расстояние технически синонимичен самому углу, но предназначен для обозначения линейного расстояния (часто огромного и неизвестного) между этими объектами (например, звездами, наблюдаемыми с Земли).
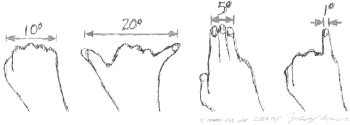
Для визуальных наблюдений без претензий на точность можно вычислить угловое расстояние, конечно, с приближениями порядка степени, и, конечно, очень грубо.
Отдельные вариации — длина руки, толщина пальцев и т. д. — меняют значения в первых приближениях, но не так важны для определения местоположения звезды или планеты, видимой невооруженным глазом или для связи созвездия с соседями.
Поскольку угловое расстояние концептуально совпадает с углом, оно измеряется в тех же единицах, например, градусах или радианах и с использованием таких приборов, как гониометры или оптические приборы, специально предназначенные для поворота в четко определенных направлениях и записи соответствующих углов (такие как телескопы).
Чтобы рассчитать угловое расстояние θ в угловых секундах для двойной звёздные системы, экзопланеты, объекта Солнечной системы и других астрономических объектов, используется размер большой полуоси, выраженной в астрономических единицах (а.е.), деленное на расстояние D, выраженное в парсеках, согласно формуле для малых углов — tan(aD){\displaystyle \tan({\frac {a}{D}})}:
- θ≈aD{\displaystyle \theta \approx {\dfrac {a}{D}}}
Учитывая два угловых положения, каждое из которых определяется прямым восхождением (RA), α∈[0,2π]{\displaystyle \alpha \in [0,2\pi ]} и склонением (dec), δ∈[−π/2,π/2]{\displaystyle \delta \in [-\pi /2,\pi /2]} угловое расстояние между двумя точками можно рассчитать, используя следующую формулу:
- θ=cos−1[sin(δ1)sin(δ2)+cos(δ1)cos(δ2)cos(α1−α2)]{\displaystyle \theta =\cos ^{-1}\left[\sin(\delta _{1})\sin(\delta _{2})+\cos(\delta _{1})\cos(\delta _{2})\cos(\alpha _{1}-\alpha _{2})\right]}



