формула формула мощности электрического тока
Электрический ток является физическим процессом. Если говорить упрощенно, то это упорядоченное движение заряженных частиц. Его протекание можно измерить и соответственно выразить в символьном и цифровом виде. Формула электрического тока, представляет собой выражение качественных и количественных параметров через сопротивление проводника, напряжение или разность потенциалов, а также через его силу. Так как любое перемещение чего-либо, подразумевает под собой совершение работы, то дополнительно можно вести разговор об электричестве используя формулу мощности электрического тока.
Основные понятия и формулы характеризующие электрический ток
Количественным параметром электрического тока является его сила, представляющая собой скалярную величину и выражающуюся в отношении заряда (принято обозначать буквой q) к периоду времени (t), за которое он пересекает сечение проводника.
Формула выражения силы электрического тока через сопротивление и напряжение
В отличие от фундаментальных исследований, в основе которых лежат теоретические выкладки данная зависимость была выведена практическим путем. Автором открытия является физик Ом, в честь которого закон и получил свое имя. По результатам своих опытов и экспериментов Ом пришел к выводу что сила тока (I) напрямую зависит от величины напряжения (U)и имеет обратную зависимость от сопротивления (R) элементов и деталей, включенных в электрическую цепь. Эту связь можно представить в виде –
Автором открытия является физик Ом, в честь которого закон и получил свое имя. По результатам своих опытов и экспериментов Ом пришел к выводу что сила тока (I) напрямую зависит от величины напряжения (U)и имеет обратную зависимость от сопротивления (R) элементов и деталей, включенных в электрическую цепь. Эту связь можно представить в виде –
Формула силы электрического тока
Сопротивление электрического тока: формула
Формула напряжения электрического тока
Работа и мощность электрического тока
Формула мощности (Р) электрического тока напрямую зависит от его работы (А). Под работой тока подразумевается преобразование электрической энергии в механический, тепловой, световой или иной ее вид.
Работа электрического тока формула
Формула мощности электрического тока
Поэтому, если необходимо вычислить, какую работу производит ток, протекая по цепи в течение определенного времени, необходимо умножить мощность на временной промежуток, выраженный в секундах. Рассмотрим применение формул расчета работы и мощности электрического тока на примере электрического двигателя, подключенного к сети 220 В, а сила тока, измеренная амперметром для этого участка, составила 10А.
Р (мощность двигателя) = 10А (сила тока) х 220В (напряжение в сети) = 2200 Вт = 2,2 кВт.
Зная данный показатель, а также реальное или предполагаемое время функционирования электродвигателя можно определить какую работу он совершит за этот отрезок времени или другим словами сколько будет потрачено электроэнергии. Если двигатель был включен, например, 1 час, то можно найти искомое значение.
А (работа, совершенная двигателем) = 2,2 кВт (мощность) х 1 (время работы в часах) = 2,2 кВт ч. Именно этот показатель будет отражен на приборе учета расхода электроэнергии.
Исходя из того, что электрический ток является физическим процессом, то какой-либо его неизвестный параметр можно определить, зная его остальные характеристики. Приведем наиболее распространенные формулы для определения характеристик электрической цепи применяемые в электротехнике.
Напряжение или разность потенциалов
- U = RxI
- U = P/I
Сила электрического тока
Сопротивление
- R = U / I
- R = U2/ P
- R = P / I2
Мощность
В заключение отметим, что приведенная информация справедлива для цепей с постоянным электрическим током. Формулы, применяемые для расчета характеристик переменного тока, будут отличаться за счет введения дополнительных переменных и характеристик свойственных данному типу электричества.
Формулы, применяемые для расчета характеристик переменного тока, будут отличаться за счет введения дополнительных переменных и характеристик свойственных данному типу электричества.
сопротивления через силу тока и напряжение
Электротехника как область науки, занимающаяся использованием электроэнергии, в том числе ее получением, распределением и учетом, оперирует значениями тока, напряжения, мощности и сопротивления. Это основные величины. Кроме этого, имеется множество других характеристик и понятий, но в рамках данной статьи будут рассматриваться именно эти основополагающие понятия.
Многообразие устройств электротехники
Электрический ток
Согласно определению, ток представляет собой упорядоченное движение заряженных частиц в среде.
Электрическое напряжение
Электрическое напряжение – это разность потенциалов на противоположных участках цепи. Точное определение понятия подразумевает работу по переносу электрического заряда между участками цепи.
Сопротивление
Любой проводник в цепи препятствует прохождению через себя тока. Данная характеристика определяет такую физическую величину, как сопротивление. Исходя из величины сопротивления, все вещества относят к проводникам или изоляторам. Точная граница весьма расплывчата, поэтому при некоторых условиях некоторые вещества можно отнести как к изоляторам, так и к проводникам. Участок электросхемы может иметь элемент с определенным значением величины, который именуется резистор.
Резисторы различных типов
Мощность
Скорость преобразования, передачи и потребления электрической энергии определяется мощностью.
Взаимосвязь параметров электрической цепи
Все параметры любой электрической цепи строго взаимосвязаны, поэтому в любой момент времени можно точно определить величину любого из них, зная остальные.
К сведению. Основополагающий закон, по которому производится большинство расчетов, – закон Ома, согласно которому сила тока обратно пропорциональна его сопротивлению и прямо пропорциональна приложенной разности потенциалов.
Закон Ома и его основатель
Формула напряжения тока закона Ома выглядит следующим образом:
I=U/R.
Так, цепь с большим напряжением пропускает больший ток, а при одинаковом напряжении ампераж будет больше там, где меньше сопротивление.
Принятые обозначения в формуле расчета напряжения и тока понятны во всем мире:
- I – сила тока;
- U – напряжение;
- R – сопротивление.
Путем простейшего математического преобразования находится формула расчета сопротивления через силу тока и напряжение.
Кроме закона Ома, используется формула расчета мощности:
P=U∙I.
Символом P здесь обозначена мощность тока.
Любая схема может содержать участки, где имеется последовательное соединение, или есть элемент, подключенный параллельно. Расчеты при этом усложняются, но базовые формулы остаются одинаковыми.
Единицы измерения в формуле
Невозможно выполнять расчеты или измерения, не зная, какими величинами оперировать. Общепринятые обозначения, согласно международной системе измерения СИ:
- Напряжение – Вольт. Обозначается символом В или V в англоязычной литературе;
- Сила тока – Ампер. Обозначается символом А;
- Электрическое сопротивление – Ом. Используется обозначение Ом или Ohm;
- Электрическая мощность – Ватт. Обозначается как Вт или W.
Как работает закон в реальной жизни
Используя совместно формулу расчета мощности и закон Ома, можно производить вычисления, не зная одной из величин. Самый простой пример – для лампы накаливания известны только ее мощность и напряжение. Применяя приведенные выше формулы, можно легко определить параметры нити накаливания и ток через нее.
Самый простой пример – для лампы накаливания известны только ее мощность и напряжение. Применяя приведенные выше формулы, можно легко определить параметры нити накаливания и ток через нее.
Лампа накаливания
Сила тока формула через мощность:
I=P/U;
Сопротивление:
R=U/I.
Такой же результат можно найти из мощности, не прибегая к промежуточным расчетам:
R=U2/P.
Аналогично можно вычислить любую величину, зная только две из них. Для упрощения преобразований имеется мнемоническое отображение формул, позволяющее находить любые величины.
Правило для запоминания расчетов
Внимательно посмотрев на формулы, можно заметить, что, если уменьшить напряжение на лампе в два раза, ожидаемая мощность не снизится аналогично в два раза, а в четыре, согласно формуле:
P=U2/R.
Это довольно распространенная ошибка среди далеких от электротехники людей, которые неправильно соотносят мощность и напряжение, а также их действие на остальные параметры.
Кстати. Сила тока, найденная через сопротивление и напряжение, справедлива как для постоянного, так и для переменного тока, если в ней не используются такие элементы, как конденсатор или индуктивность.
Облегчить расчеты можно, используя онлайн калькулятор.
Пример с обычной водой
Существуют вещества, которые можно отнести одновременно к проводникам и изоляторам. Самый простой пример – обыкновенная вода. Дистиллированная вода является хорошим изолятором, но наличие в ней практически любых примесей делает ее проводником. Особенно это относится к солям различных металлов. При растворении в воде соли диссоциируются на ионы, их наличие – прямой повод для возникновения тока. Чем больше концентрация солей, тем меньшим сопротивлением будет обладать вода.
Зависимость сопротивления воды от содержания солей
Для наглядности можно взять дистиллированную воду для приготовления электролита для автомобильных аккумуляторных батарей. Опустив щупы омметра в воду, можно увидеть, что его показания велики. Добавление всего нескольких кристаллов поваренной соли через некоторое время вызывает резкое уменьшение сопротивления, которое будет тем меньше, чем больше соли перейдет в раствор.
Добавление всего нескольких кристаллов поваренной соли через некоторое время вызывает резкое уменьшение сопротивления, которое будет тем меньше, чем больше соли перейдет в раствор.
По какой формуле определяется напряжение
Использование той или иной формулы напряжения электрического тока для вычисления зависит от того, какие величины известны:
- Ток и сопротивление – U=I∙R;
- Ток и мощность – U=P/I;
- Мощность и сопротивление – U=√P∙R
Различные используемые величины
Кроме основных величин: вольт, ампер, ом, ватт, используют кратные, большие или меньшие. Для обозначений применяют соответствующие приставки:
- Кило – 1000;
- Мега – 1000000;
- Гига – 1000000000;
- Милли – 0.001.
Таким образом, получается:
- Киловольт (кВ) – тысяча вольт;
- Мегаватт (Мвт) – миллион ватт;
- Миллиом (мОм) – одна тысячная Ом;
- Гигаватт (ГВт) – тысяча мегаватт или миллиард ватт.

Как найти напряжение
Формула нахождения напряжения как разности потенциалов в электрическом поле:
U=ϕA-ϕB, где ϕAи ϕB – потенциалы в точках А и В, соответственно.
Также можно записать напряжение как работу по переносу единицы заряда из точки А в точку В в электрическом поле:
U=A/q, где q – величина заряда.
Работа тем больше, чем выше напряженность электрического поля Е, то есть сила, действующая на неподвижный заряд.
Потенциальную энергию заряда в электростатическом поле называют электростатический потенциал.
Гидравлическая аналогия
Чтобы легче усвоить законы электрических цепей, можно представить себе аналогию с гидравлической системой, в которой соединение насоса и трубопроводов образует замкнутую систему. Для этого нужны следующие соответствия:
- Источник питания – насос;
- Проводники – трубы;
- Электроток – движение воды.
Без особых усилий становится понятнее, что чем меньше диаметр труб, тем медленнее по ним движется вода. Чем мощнее насос, тем большее количество воды он способен перекачать. При одинаковой мощности насоса уменьшение диаметра труб приведет к снижению потока воды.
Чем мощнее насос, тем большее количество воды он способен перекачать. При одинаковой мощности насоса уменьшение диаметра труб приведет к снижению потока воды.
Гидравлическая аналогия
Измерительные приборы
Для измерения параметров электрических цепей служат измерительные приборы:
- Вольтметр;
- Амперметр;
- Омметр.
Наиболее часто используется класс комбинированных устройств, в которых переключателем выбирается измеряемая величина – ампервольтомметры или авометры.
Один из самых распространенных авометров
Типичные напряжения
Для стандартизации и возможности использования различного оборудования в быту и технике применяются электрические сети со стандартными значениями:
- Бытовая сеть –220В;
- Бортовая сеть автомобиля – 12 или 24В;
- Батареи и аккумуляторы – 1.5, 3 или 9В.
Потенциал Гальвани
В электрохимии используется понятие потенциала Гальвани, который означает разность потенциала между различными фазами вещества, например, между электродом и электролитом, между электродами из разнородных металлов.
Видео
формулы расчета мощности в проводнике
Прохождение электрического тока через любую проводящую среду объясняется наличием в ней некоторого количества носителей заряда: электронов – для металлов, ионов – в жидкостях и газах. Как найти её величину, определяет физика силы тока.
Электрический ток в проводнике
В спокойном состоянии носители движутся хаотично, но при воздействии на них электрического поля движение становится упорядоченным, определяемым ориентацией этого поля – возникает сила тока в проводнике. Количество носителей, участвующих в переносе заряда, определяется физической величиной – силой тока.
От концентрации и заряда частиц-носителей, или количества электричества, напрямую зависит сила тока, проходящего через проводник. Если принять во внимание время, в течение которого это происходит, тогда узнать, что такое сила тока, и как она зависит от заряда, можно, используя соотношение:
Если принять во внимание время, в течение которого это происходит, тогда узнать, что такое сила тока, и как она зависит от заряда, можно, используя соотношение:
Зависимость силы тока от электрического заряда
Входящие в формулу величины:
- I – сила электрического тока, единицей измерения является ампер, входит в семь основных единиц системы Си. Понятие «электрический ток» ввёл Андре Ампер, единица названа в честь этого французского физика. В настоящее время определяется как ток, вызывающий силу взаимодействия 2×10-7 ньютона между двумя параллельными проводниками, при расстоянии 1 метр между ними;
- Величина электрического заряда, применённая здесь для характеристики силы тока, является производной единицей, измеряется в кулонах. Один кулон – это заряд, проходящий через проводник за 1 секунду при токе 1 ампер;
- Время в секундах.
Сила тока через заряд может вычисляться с применением данных о скорости и концентрации частиц, угла их движения, площади проводника:
I = (qnv)cosαS.
Также используется интегрирование по площади поверхности и сечению проводника.
Определение силы тока с использованием величины заряда применяется в специальных областях физических исследований, в обычной практике не используется.
Связь между электрическими величинами устанавливается законом Ома, который указывает на соответствие силы тока напряжению и сопротивлению:
Сила тока участка цепи и цепи с источником тока
Сила электрического тока здесь как отношение напряжения в электрической цепи к её сопротивлению, эти формулы используются во всех областях электротехники и электроники. Они верны для постоянного тока с резистивной нагрузкой.
В случае косвенного расчета для переменного тока следует учитывать, что измеряется и указывается среднеквадратичное (действующее) значение переменного напряжения, которое меньше амплитудного в 1,41 раза, следовательно, максимальная сила тока в цепи будет больше во столько же раз.
При индуктивном или емкостном характере нагрузки вычисляется комплексное сопротивление для определённых частот – найти силу тока для такого рода нагрузок, используя значение активного сопротивления постоянному току, невозможно.
Так, сопротивление конденсатора постоянному току практически бесконечно, а для переменного:
RC = 1/ FC.
Здесь RC – сопротивление того же конденсатора ёмкостью С, на частоте F, которое во многом зависит от его свойств, сопротивления разных типов ёмкостей для одной частоты значительно различаются. В таких цепях сила тока по формуле, как правило, не определяется – используются различные измерительные приборы.
Для нахождения значения силы тока при известных значениях мощности и напряжения, применяются элементарные преобразования закона Ома:
Тут сила тока – в амперах, сопротивление – в омах, мощность – в вольт-амперах.
Электрический ток имеет свойство разделяться по разным участкам цепи. Если их сопротивления различны, то и сила тока будет разной на любом из них, так находим общий ток цепи.
Если их сопротивления различны, то и сила тока будет разной на любом из них, так находим общий ток цепи.
I = I1 + I2 + I3
Общий ток цепи равен сумме токов на её участках – при полном проходе через электрическую замкнутую цепь ток разветвляется, затем принимает исходное значение.
Видео
Оцените статью:Как найти общую силу тока в проводнике формулой
Электрическим током в электротехнике называется движение заряженных частиц по какому-либо проводнику. Эта величина не характеризуется лишь количеством энергии электричества, проходящей через проводник, так как за один и тот же проводник можно пропустить ток как разной, так и равной силы за разные промежутки времени. Именно поэтому не все так просто, как кажется. Рекомендуется ознакомиться с более развернутыми определениями электротока, чему он равен и как вычисляется. В этой статье будет объяснено, как найти силу тока в проводнике, будет дана формула этого уравнения.
В этой статье будет объяснено, как найти силу тока в проводнике, будет дана формула этого уравнения.
Сила тока – что это
Рассматривая количество электроэнергии, которое протекает через определенный проводник за различные временные интервалы, станет ясно, что за малый промежуток ток протечет более интенсивно, поэтому нужно ввести еще одно определение. Оно означает силу тока, протекающую в проводнике за секунду времени.
Основные величины, характеризующие поток электроновЕсли сформулировать определение на основе всего вышеперечисленного, то сила электротока – это количество электроэнергии, проходящее через поперечное сечение проводника за секунду. Маркируется величина латинской буквой «I».
Гальванометр для измерения небольшой силы токаВажно! Специалисты определяют силу электротока, равную одному амперу, когда через поперечное сечение проводника проходит один кулон электричества за одну секунду.
Часто в электротехнике можно увидеть другие единицы измерения силы электротока: миллиамперы, микроамперы и так далее. Связано это с тем, что для питания современных схем таких величин будет вполне достаточно. 1 ампер – это очень большое значение, так как человека может убить ток в 100 миллиампер, и потому электророзетка для человека ничуть не менее опасна, чем, к примеру, несущийся на скорости автомобиль.
Связано это с тем, что для питания современных схем таких величин будет вполне достаточно. 1 ампер – это очень большое значение, так как человека может убить ток в 100 миллиампер, и потому электророзетка для человека ничуть не менее опасна, чем, к примеру, несущийся на скорости автомобиль.
Если известно количество электроэнергии, которое прошло через проводник за конкретный промежуток времени, то силу (не мощность) можно вычислить по формуле, изображенной на картинке.
Когда электросеть замкнута и не имеет никаких ответвлений, через каждое поперечное сечение за секунду протекает одно и то же количество электричества. Теоретически это обосновывается так: заряд не может накапливаться в определенном месте, и сила электротока везде одинакова.
Виды токовИсточники тока
Источником электротока называется такой электротехнический прибор, который конвертирует определенный вид энергии в электрическую. Такие устройства делятся на физические и химические.
Принцип действия химических источников основан на преобразовании химической энергии в электрическую. Это преобразование происходит самостоятельно и не требует участия извне. В зависимости от возобновляемости элементов и типа реакций, они делятся на:
- Первичные (батарейки) Первичные источники нельзя использовать второй раз, если они разрядились, так как химические реакции, протекающие в них, необратимы. Они делятся на топливные и полутопливные элементы. Топливные аналогичны батарейкам, но химические вещества в них заправляются отдельно, как продукты химической реакции они выходят наружу. Это помогает им работать долгое время. Полутопливные включают в себя один из химических элементов, а второй постепенно поступает на протяжении всего использования. Их срок службы определяется запасом невозобновляемого вещества. Если для такого элемента возможна регенерация через зарядку, то он возобновляет свои возможности как аккумулятор.
- Вторичные (аккумуляторы) перед использованием проходят цикл зарядки.
 Заряд, который они получают в процессе, можно транспортировать вместе с устройствами. После расходования заряда возможна его регенерация за счет зарядки и обратимости химической реакции. Также к вторичным относятся возобновляемые элементы, которые механическим или химическим путем заряжаются и восстанавливают способность питать приборы. Они разработаны таким образом, что после определенного срока требуют замены определенных частей для продолжения реакции.
Заряд, который они получают в процессе, можно транспортировать вместе с устройствами. После расходования заряда возможна его регенерация за счет зарядки и обратимости химической реакции. Также к вторичным относятся возобновляемые элементы, которые механическим или химическим путем заряжаются и восстанавливают способность питать приборы. Они разработаны таким образом, что после определенного срока требуют замены определенных частей для продолжения реакции.
Важно! Следует понимать, что разделение на батарейки и аккумуляторы условно. Свойства аккумулятора могут проявляться, например, у щелочных батарей, которые можно реанимировать при определенной степени заряда.
Также по типу реагентов химические источники делятся на:
- Кислотные.
- Солевые.
- Щелочные.
Физические же источники электротока основаны на преобразовании механической, а также ядерной, тепловой или световой энергии в электрическую.
Сила тока – чему равна, в каких единицах она измеряется, как найти силу тока по формуле
Как уже стало понятно, сила электротока – это физическая величина, показывающая заряд, который проходит через проводник за единицу времени. Основная формула для ее вычисления выглядит так: I = q/t, где q – это заряд, который идет по проводнику в кулонах, а t – это временной интервал в секундах.
Рассчитать силу электротока можно и с помощью закона Ома. Он гласит, что эта величина равна напряжению сети в вольтах, деленному на ее сопротивление в омах. В связи с этим имеет место формула такого рода — I = U/R. Этот закон применим для расчета значений постоянного тока.
Чтобы вычислить переменные параметры электричества, нужно разделить найденные величины на квадратный корень из двух.
К сведению! Это более практичный метод измерения, и им приходится пользоваться часто, так как все приборы в доме или в офисе работают от розеток, которые подают переменный ток. Делается это из-за того, что с ним легче работать, его удобнее трансформировать.
Делается это из-за того, что с ним легче работать, его удобнее трансформировать.
Закон Ома в таблице
Важно! Наглядный пример работы переменного электротока можно наблюдать при включении люминесцентных ламп. Пока они полностью не загорятся, они будут моргать, потому что ток двигается в них то туда, то сюда.
Единицей измерения силы тока является ампер. Он определяется как сила неизменяющегося тока, который проходит по бесконечным параллельным проводникам с наименьшим круговым сечением (с минимальной площадью кругового сечения), отдаленным друг от друга на 1 метр и расположенным в безвоздушном вакуумном пространстве. Это взаимодействие на одном метре длины этих проводников, равное 2 × 10 в минус 7-й степени Ньютона. Если в проводнике за одну секунду времени проходит один кулон заряда, то сила тока в нем равна одному амперу.
Аккумуляторы являются вторичными источниками, но неразрывно связаны с батарейкамиЗачем нужно измерять силу тока
Силу тока в проводнике или на участке электрической цепи измеряют для того, чтобы иметь понятие о характеристиках данного проводника или цепи. Так как сила тока – один из основных параметров электричества, он неразрывно связан с другими значениями по типу напряжения и сопротивления. Более того, как уже стало понятно, три этих величины могут пропорционально определять друг друга.
Так как сила тока – один из основных параметров электричества, он неразрывно связан с другими значениями по типу напряжения и сопротивления. Более того, как уже стало понятно, три этих величины могут пропорционально определять друг друга.
Расчеты силы электротока делаются в разных случаях:
- При прокладке электрических сетей.
- При создании приборов.
- В образовательных целях.
- При выборе подходящих деталей для совершения тех или иных действий.
Электроприбор для измерения силы тока
Для измерения силы электротока используют специальный прибор под названием амперметр. Если требуется измерить токи самых разных сил, то прибегают к использованию миллиамперметров и макроамперметров. Чтобы измерить им требуемую величину, его подключают в цепь последовательно. Ток, который проходит через устройство, будет изменяться им, и данные будут выведены на цифровой дисплей или аналоговые шкалы.
Важно! Стоит помнить, что включать амперметр можно на любом участке сети, поскольку сила тока в простой замкнутой цепи без ответвлений одинакова во всех точках.
Современные тестеры и мультиметры содержат функцию измерения силы электротока, поэтому нет необходимости прибегать к габаритным приборам, предназначенным для промышленного использования
Силу тока в домашних условиях можно измерить с помощью мультиметраТаким образом, сила электротока – это основополагающая характеристика движущихся частиц. Она не только дает понять, какое в сети напряжение и сопротивление, но и определяет другие важные величины по типу ЭДС и т. д.
1.2.1 Формула John G. Simmons
Пользуясь моделью Зоммерфельда (см. пункт 1.1.3) выведем, формулу туннельного тока, протекающего в системе металл-диэлектрик-металл (М-Д-М), в приближении ВКБ теории (см. пункт 1.1.2) при T = 0, в случае потенциального барьера произвольной формы, считая, что масса электронов изотропна во всём пространстве.
пункт 1.1.2) при T = 0, в случае потенциального барьера произвольной формы, считая, что масса электронов изотропна во всём пространстве.
Рис. 1. Модель потенциального барьера М-Д-М для случая, когда система находится в термодинамическом равновесии;
j1 и j2 – работы выхода левого и правого металла соответственно.
Рис. 2. Модель потенциального барьера произвольной формы в системе М-Д-М. Положительный потенциал приложен к правому металлу.
Рассмотрим два металлических электрода, между которыми находится диэлектрическая плёнка толщиной L. Если электроды находятся под одним потенциалом, то система пребывает в термодинамическом равновесии (см. пункт 1.1.3) и уровни Ферми электродов совпадают (рис. 1). Однако, если электроды находятся под разными потенциалами, то между ними возможно протекание электрического тока. На рис. 2 показана энергетическая диаграмма электродов, между которыми приложена разность потенциалов eV. Ширина потенциального барьера, для электронов находящихся на уровне Ферми обозначена как dz = z2 – z1. Будем считать, что весь протекающий ток обусловлен туннельным эффектом.
На рис. 2 показана энергетическая диаграмма электродов, между которыми приложена разность потенциалов eV. Ширина потенциального барьера, для электронов находящихся на уровне Ферми обозначена как dz = z2 – z1. Будем считать, что весь протекающий ток обусловлен туннельным эффектом.
Вероятность D(Ez) того, что электрон может проникнуть через потенциальный барьер высотой U(z) определяется выражением (4) пункта 1.1.2. Количество электронов N1 туннелирующих через барьер из электрода 1 в электрод 2 можно записать как [1, 2]
(1)
где
(2)
и Em – максимальная энергия туннелирующих электронов.
Интегрирование выражения (2) можно выполнить в полярных координатах. Так как в рассматриваемой модели , и полная энергия , то, сделав замену переменных , , получим, что
(3)
Подставляя (3) в (1) имеем
(4)
Количество электронов N2 туннелирующих из электрода 2 в электрод 1, вычисляется аналогичным образом. В соответствии с выражением (4) пункта 1.1.2, прозрачность потенциального барьера в данном случае будет такая же, как если бы к электроду 1 был подан положительный потенциал V, относительно электрода 2. В этом случае
В соответствии с выражением (4) пункта 1.1.2, прозрачность потенциального барьера в данном случае будет такая же, как если бы к электроду 1 был подан положительный потенциал V, относительно электрода 2. В этом случае
(5)
Очевидно, что общий поток электронов N через потенциальный барьер есть N = N1 – N2. Обозначим
(6)
Тогда плотность туннельного тока J запишется как
(7)
Запишем U(z) в виде (см. рис. 2). Тогда производя интегрирование (4) пункта 1.1.2 и используя выражение (П5) из приложения, получим
(8)
где – среднее значение потенциального барьера, отсчитанное от уровня Ферми отрицательно заряженного электрода; ; , b – безразмерный коэффициент, определенный в приложении (П6).
При T = 0 K
(9)
Подставляя (8) и (9) в (7) находим, что
(10)
Выполняя интегрирование (10), получим
(11)
где
.
Таким образом, выражение (11) является приближённым выражением для туннельного тока в системе М-Д-М в случае потенциального барьера произвольной формы.
Выводы.
- Получено общее выражение, для вычисления туннельного тока, протекающего в системе М-Д-М (7).
- Аналитически вычислено приближённое решение туннельного тока в системе М-Д-М (11).
Литература.
- Э. Бурштейн, С. Лундквист. Туннельные явления в твёрдых телах // М.: Мир, 1973.
- John G. Simmons. J. Appl. Phys. — 1963. — V. 34 1793.
- John G. Simmons. J. Appl. Phys. — 1963. — V. 34 238.
3. Делители тока | 5. Схемы делителей и законы Кирхгофа | Часть1
3. Делители тока
Делители тока
Давайте проанализируем простую параллельную цепь и определим силу тока на каждом из ее резисторов:
Как вы уже знаете, напряжение на всех компонентах параллельной цепи одинаково. Исходя из этого можно заполнить верхнюю строчку рассмотренной ранее таблицы:
Исходя из этого можно заполнить верхнюю строчку рассмотренной ранее таблицы:
Теперь, используя закон Ома (I = U/R), мы можем рассчитать силу тока на каждом резисторе (в каждой ветви):
Один из принципов параллельных цепей гласит, что общая сила тока в таких цепях равна сумме отдельных токов. Поэтому, суммируя 6 мА, 2мА и 3мА, мы можем заполнить ячейку общей силы тока в нашей таблице:
И наконец, вычислим общее сопротивление нашей цепи. Сделать это можно при помощи закона Ома (R = U/I), или при помощи формулы параллельного соединения резисторов. В обоих случаях мы получим одинаковый ответ:
Из данной таблицы видно, что сила тока через каждый резистор связана с его сопротивлением (учитывая равенство напряжений на всех резисторах).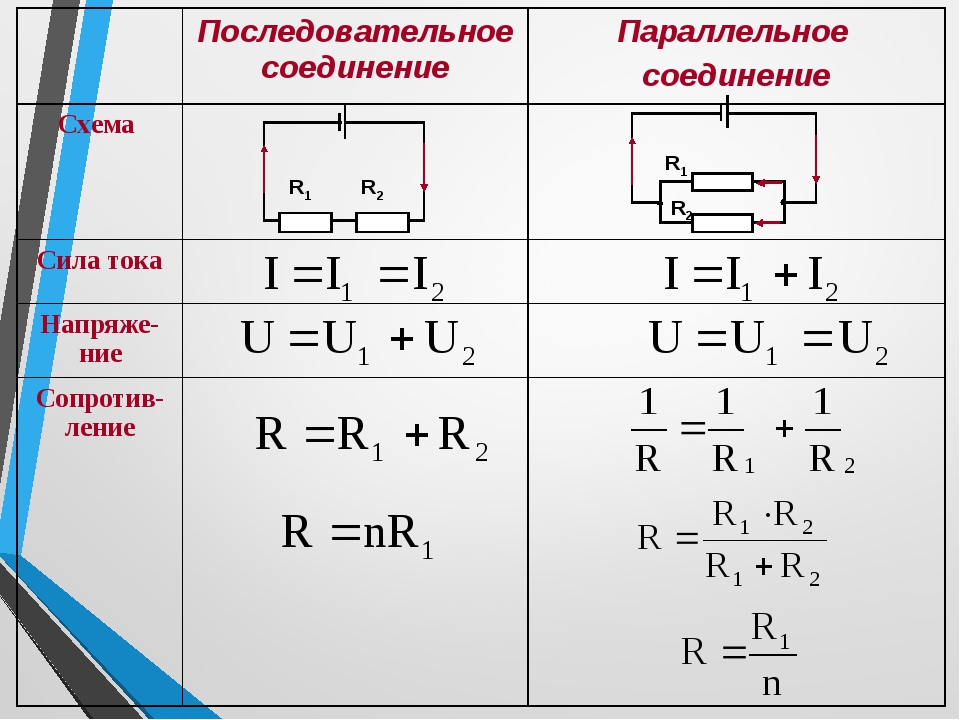 Причем взаимосвязь эта обратнопропорциональна. К примеру, сила тока через резистор R1 вдвое больше, чем через резистор R3, хотя сопротивление последнего в два раза превышает сопротивление первого.
Причем взаимосвязь эта обратнопропорциональна. К примеру, сила тока через резистор R1 вдвое больше, чем через резистор R3, хотя сопротивление последнего в два раза превышает сопротивление первого.
Если мы изменим напряжение питания этой схемы, то обнаружим, что пропорциональность соотношений не изменится:
Несмотря на то, что напряжение источника питания изменилось, ток через резистор R1 по-прежнему в два раза превышает ток через резистор R3. Таким образом, пропорциональность между токами различных ветвей цепи является исключительно функцией сопротивления.
Кроме того, токи отдельных ветвей цепи составляют фиксированные пропорции от ее общей силы тока. Несмотря на четырехкратное увеличение напряжения источника питания, соотношение между током любой ветви и общим током осталось неизменным:
Благодаря способности делить общий ток на пропорциональные части, параллельные цепи часто называют делителями тока. Поэкспериментировав немного с математикой, мы можем вывести формулу для расчета отдельных токов цепи, имея данные о сопротивлениях резисторов, общем сопротивлении цепи и общей силе тока:
Поэкспериментировав немного с математикой, мы можем вывести формулу для расчета отдельных токов цепи, имея данные о сопротивлениях резисторов, общем сопротивлении цепи и общей силе тока:
Отношение общего сопротивления к отдельным сопротивлениям имеет ту же пропорцию, что и отношение отдельных токов к общей силе тока цепи. Полученная выше формула называется формулой делителя тока, с ее помощью легче определять токи отдельных ветвей параллельной цепи, если известна общая сила тока.
Давайте повторно рассчитаем токи каждой из ветвей нашей параллельной цепи, используя только что полученную формулу делителя тока (будем считать, что общая сила тока и общее сопротивление нам известны):
Если сравнить формулы делителя напряжения и делителя тока, то можно увидеть, что они удивительно похожи друг на друга. Однако, в формуле делителя напряжения Rn (отдельное сопротивление) делится на Rобщ., а в формуле делителя тока — наоборот, Rобщ. делится на Rn:
Однако, в формуле делителя напряжения Rn (отдельное сопротивление) делится на Rобщ., а в формуле делителя тока — наоборот, Rобщ. делится на Rn:
Именно из-за отношения сопротивлений очень легко перепутать эти формулы. В целях избежания путаницы вы должны знать, что отношение сопротивлений в обоих уравнениях должно быть меньше единицы (в конце концов это уравнения делителей, а не умножителей!). Если отношение будет больше единицы, значит вы перепутали уравнения. Зная, что общее сопротивление последовательной цепи (делитель напряжения) всегда больше любого из ее отдельных сопротивлений, Rобщ. мы должны поставить в знаменатель отношения, а Rn — в числитель (только в этом случае отношение будет меньше единицы). И наоборот, зная что общее сопротивление параллельной цепи (делитель тока) всегда меньше любого из ее отдельных сопротивлений, Rобщ. мы должны поставить в числитель отношения, а Rn — в знаменатель.
Схемы делителей токов, как и делителей напряжений, нашли применение в электрических цепях измерительных приборов, где часть измеряемого тока необходимо пропустить через чувствительный прибор:
Формула электрического сопротивления через силу тока. Сопротивление тока: формула
Электрическое сопротивление — физическая величина, которая показывает, какое препятствие создается току при его прохождении по проводнику . Единицами измерения служат Омы, в честь Георга Ома. В своем законе он вывел формулу для нахождения сопротивления, которая приведена ниже.
Рассмотрим сопротивление проводников на примере металлов. Металлы имеют внутреннее строение в виде кристаллической решетки. Эта решетка имеет строгую упорядоченность, а её узлами являются положительно заряженные ионы. Носителями заряда в металле выступают “свободные” электроны, которые не принадлежат определенному атому, а хаотично перемещаются между узлами решетки. Из квантовой физики известно, что движение электронов в металле это распространение электромагнитной волны в твердом теле. То есть электрон в проводнике движется со скоростью света (практически), и доказано, что он проявляет свойства не только как частица, но еще и как волна. А сопротивление металла возникает в результате рассеяния электромагнитных волн (то есть электронов) на тепловых колебаниях решетки и её дефектах. При столкновении электронов с узлами кристаллической решетки часть энергии передается узлам, вследствие чего выделяется энергия. Эту энергию можно вычислить при постоянном токе , благодаря закону Джоуля-Ленца – Q=I 2 Rt. Как видите чем больше сопротивление, тем больше энергии выделяется.
Из квантовой физики известно, что движение электронов в металле это распространение электромагнитной волны в твердом теле. То есть электрон в проводнике движется со скоростью света (практически), и доказано, что он проявляет свойства не только как частица, но еще и как волна. А сопротивление металла возникает в результате рассеяния электромагнитных волн (то есть электронов) на тепловых колебаниях решетки и её дефектах. При столкновении электронов с узлами кристаллической решетки часть энергии передается узлам, вследствие чего выделяется энергия. Эту энергию можно вычислить при постоянном токе , благодаря закону Джоуля-Ленца – Q=I 2 Rt. Как видите чем больше сопротивление, тем больше энергии выделяется.
Удельное сопротивление
Существует такое важное понятие как удельное сопротивление, это тоже самое сопротивление, только в единице длины. У каждого металла оно свое, например у меди оно равно 0,0175 Ом*мм2/м, у алюминия 0,0271 Ом*мм2/м. Это значит, брусок из меди длиной 1 м и площадью поперечного сечения 1 мм2 будет иметь сопротивление 0,0175 Ом, а такой же брусок, но из алюминия будет иметь сопротивление 0,0271 Ом. Выходит что электропроводность меди выше чем у алюминия. У каждого металла удельное сопротивление свое, а рассчитать сопротивление всего проводника можно по формуле
Выходит что электропроводность меди выше чем у алюминия. У каждого металла удельное сопротивление свое, а рассчитать сопротивление всего проводника можно по формуле
где p – удельное сопротивление металла, l – длина проводника, s – площадь поперечного сечения.
Значения удельных сопротивлений приведены в таблице удельных сопротивлений металлов (20°C)
Вещество | p , Ом*мм 2 /2 | α,10 -3 1/K |
Алюминий | 0.0271 | |
Вольфрам | 0.055 | |
Железо | 0.098 | |
Золото | 0. | |
Латунь | 0.025-0.06 | |
Манганин | 0.42-0.48 | 0,002-0,05 |
Медь | 0.0175 | |
Никель | ||
Константан | 0.44-0.52 | 0.02 |
Нихром | 0.15 | |
Серебро | 0.016 | |
Цинк | 0.059 |
Кроме удельного сопротивления в таблице есть значения ТКС, об этом коэффициенте чуть позже.
Зависимость удельного сопротивления от деформаций
При холодной обработке металлов давлением, металл испытывает пластическую деформацию. При пластической деформации кристаллическая решетка искажается, количество дефектов становится больше. С увеличением дефектов кристаллической решетки, сопротивление течению электронов по проводнику растет, следовательно, удельное сопротивление металла увеличивается. К примеру, проволоку изготавливают методом протяжки, это значит, что металл испытывает пластическую деформацию, в результате чего, удельное сопротивление растет. На практике для уменьшения сопротивления применяют рекристаллизационный отжиг, это сложный технологический процесс, после которого кристаллическая решетка как бы, “расправляется” и количество дефектов уменьшается, следовательно, и сопротивление металла тоже.
При растяжении или сжатии, металл испытывает упругую деформацию. При упругой деформации вызванной растяжением, амплитуды тепловых колебаний узлов кристаллической решетки увеличиваются, следовательно, электроны испытывают большие затруднения, и в связи с этим, увеличивается удельное сопротивление. При упругой деформации вызванной сжатием, амплитуды тепловых колебаний узлов уменьшаются, следовательно, электронам проще двигаться, и удельное сопротивление уменьшается.
При упругой деформации вызванной сжатием, амплитуды тепловых колебаний узлов уменьшаются, следовательно, электронам проще двигаться, и удельное сопротивление уменьшается.
Влияние температуры на удельное сопротивление
Как мы уже выяснили выше, причиной сопротивления в металле являются узлы кристаллической решетки и их колебания. Так вот, при увеличении температуры, тепловые колебания узлов увеличиваются, а значит, удельное сопротивление также увеличивается. Существует такая величина как температурный коэффициент сопротивления (ТКС), который показывает насколько увеличивается, или уменьшается удельное сопротивление металла при нагреве или охлаждении. Например, температурный коэффициент меди при 20 градусах по цельсию равен 4.1 · 10 − 3 1/градус. Это означает что при нагреве, к примеру, медной проволоки на 1 градус цельсия, её удельное сопротивление увеличится на 4.1 · 10 − 3 Ом. Удельное сопротивление при изменении температуры можно вычислить по формуле
где r это удельное сопротивление после нагрева, r 0 – удельное сопротивление до нагрева, a – температурный коэффициент сопротивления, t 2 – температура до нагрева, t 1 — температура после нагрева.
Подставив наши значения, мы получим: r=0,0175*(1+0.0041*(154-20))=0,0271 Ом*мм 2 /м. Как видите наш брусок из меди длиной 1 м и площадью поперечного сечения 1 мм 2 , после нагрева до 154 градусов, имел бы сопротивление, как у такого же бруска, только из алюминия и при температуре равной 20 градусов цельсия.
Свойство изменения сопротивления при изменении температуры, используется в термометрах сопротивления. Эти приборы могут измерять температуру основываясь на показаниях сопротивления. У термометров сопротивления высокая точность измерений, но малые диапазоны температур.
На практике, свойства проводников препятствовать прохождению
тока используются очень широко. Примером может служить лампа накаливания, где нить из вольфрама, нагревается за счет высокого сопротивления металла, большой длины и узкого сечения. Или любой нагревательный прибор, где спираль разогревается благодаря высокому сопротивлению. В электротехнике, элемент главным свойством которого является сопротивление, называется – резистор . Резистор применяется практически в любой электрической схеме.
Резистор применяется практически в любой электрической схеме.
Каждый человек знает, что по проводам течет электрический ток, за счет чего горит свет или работает прибор, потребляющий электрическую энергию. Это настолько прочно вошло в обычную жизнь, что никто не задумывается о физической составляющей данного явления. Человек, чья профессиональная деятельность не связана с физикой, слышал про электрическое сопротивление, силу тока или мощность последний раз в разрезе школьного курса физики.
Физика очень сложная наука, которая базируется не только на формулах и вычислениях, но в большей степени на понятиях. Особенно ярко это проявляется в разделе «электричество», которое само по себе не является материальной субстанцией, его не возможно «пощупать» или увидеть, но при этом оно занимает важную нишу в человеческой жизни.
Что есть сила сопротивления? Что такое электрическая цепь? Почему ток обладает силой? Для человека, который давно окончил школу, вопросов больше, чем ответов и немногие обладают хотя бы общим представлением, что на самом деле происходит под изоляцией электрического провода.
Какие процессы протекают в проводниках при прохождении через них тока?
Если некое тело, обладающее способностью проводить электрический ток, поместить таким образом, что с одной стороны будет находиться положительный полюс, а с другой отрицательный, то по нему начинает проходить электрический ток. Ток представляет собой в очень упрощенном виде движение отрицательных электронов, имеющее направленность. При этом частицы, имеющие отрицательный заряд, притягиваются к положительному полюсу. Именно за счет этого принято различать полярность электрической цепи, что легко заметить при подключении элементов питания, которые устанавливаются с учетом плюса и минуса.
При движении электроны встречают на своем пути атомы вещества, которым передается часть энергии в результате столкновения, что приводит к нагреву тела, пропускающее ток. При этом при столкновении происходит подтормаживание электронов. Появляющееся электрическое поле имеет способность заново ускорять замедленные электроны, которые снова начинают свое движение к положительному полюсу. Весь этот процесс будет бесконечным, пока тело подключено к источнику электрического поля. Именно движущиеся электроны испытывают на себе сопротивление поля, при этом существует прямая связь между количеством препятствий на пути заряженных частиц и значением данной величины. Сопротивление тока в цепи увеличивается при увеличении количества столкновении электронов.
Весь этот процесс будет бесконечным, пока тело подключено к источнику электрического поля. Именно движущиеся электроны испытывают на себе сопротивление поля, при этом существует прямая связь между количеством препятствий на пути заряженных частиц и значением данной величины. Сопротивление тока в цепи увеличивается при увеличении количества столкновении электронов.
Сопротивление цепи — что это?
Существует два вида определения сопротивления. Первое базируется на законе Ома. Согласно данному определению сопротивление цепи есть численная величина, определяемая как результат деления значения напряжения, создаваемого в проводнике на силу тока, который протекает через него. Формула сопротивления в данном случае будет иметь вид:
R — сопротивление;
U — напряжение;
I — сила тока.
Второе определение формулы сопротивления базируется на физических особенностях токопроводящего материала. Сопротивление источника есть также числовая величина, указывающая на способность тела превращать электрическую энергию в тепловую. Формула сопротивления в Омах для второго случая выглядит следующим образом:
Формула сопротивления в Омах для второго случая выглядит следующим образом:
R=(p*l)/S, где
R — сопротивление;
p — удельное сопротивление;
l — длина проводника;
S — площадь сечения.
При этом оба определения являются правильными и имеют право быть, но преимущественно в школьном курсе изучают лишь первый постулат. Единицы, определяющие сопротивление — Ом, названы так по имени ученого, который открыл сам факт существования данного явления и описал его природу.
Закон Ома или что есть сила в Омах
Одним очень важным открытием для понимания физической сущности электричества является открытый Омом закон, который выводит зависимость силы тока от напряжения. В основе закона лежит простой эксперимент. Представим, что существует простейшая цепь, которая состоит из обычной лампочки и амперметра. При добавлении в цепь большого гальванического элемента можно наблюдать, что нить накаливания лампы не нагревается и в сети практически отсутствует ток. Но если имеющийся гальванический элемент заменить свежим аккумулятором или элементом питания, то лампочка моментально загорается и ток в сети увеличивается. Замерив ток на обоих концах сети можно заметить, что при включении в сеть элемента питания напряжение значительно возрастает.
Но если имеющийся гальванический элемент заменить свежим аккумулятором или элементом питания, то лампочка моментально загорается и ток в сети увеличивается. Замерив ток на обоих концах сети можно заметить, что при включении в сеть элемента питания напряжение значительно возрастает.
Закон Ома для участка цепи
Из проведенного опыта вытекает сформулированный Омом закон, который гласит, что сила тока в проводящем электрический ток теле увеличивается при увеличении напряжения, подаваемого к концам цепи или проводника. При этом сила тока находится в прямо пропорциональной зависимости от напряжения и обратно пропорциональной связи с сопротивлением. Закон Ома — это зависимая связь, в которой принимают участие сила тока, сопротивление и напряжение.
Виды сопротивлений
Физика выделяет несколько видов электрического сопротивления:
- Удельное. Под удельным сопротивлением понимается способность металла или иного тела противостоять прохождению электрического тела. Высокая величина удельного сопротивления будет означать, что данный материал является плохим проводником;
- Сопротивление провода. В данном случае формула сопротивления в Омах будет включать в себя диаметр сечения провода, удельное сопротивление конкретного металла и длину провода;
- Поверхностное сопротивление. Этот вид применяется для расчета удельного сопротивления тонких материалов, в частности пленок. В случае поверхностного сопротивления диаметр сечения в формуле представлен в виде габаритных размеров (толщина, длина, ширина).
Электрическое сопротивление является важным понятием, сделавшее возможным создание резистора, главная задача которого является осуществление контроля и ограничения действия электрического тока. Применение резисторов сводится к препятствованию возрастанию напряжения, поскольку эта деталь способна рассеивать тепло. Также резистор, который является неотъемлемой частью любой современной платы и схемы, применяется для разделения напряжения, понижая данную характеристику.
Инструкция
Найдите силу сопротивления движению, которая действует на равномерно прямолинейно движущееся тело. Для этого при помощи динамометра или другим способом измерьте силу, которую необходимо приложить к телу, чтобы оно двигалось равномерно и прямолинейно. По третьему закону Ньютона она будет численно равна силе сопротивления движения тела.
Определите силу сопротивления движению тела, которое перемещается по горизонтальной поверхности. В этом случае сила трения прямо пропорциональна силе реакции опоры, которая, в свою очередь равна силе тяжести, действующей на тело. Поэтому сила сопротивления движению в этом случае или сила трения Fтр равна произведению массы тела m, которая измеряется весами в килограммах, на ускорение свободного падения g≈9,8 м/с² и коэффициент пропорциональности μ, Fтр=μ∙m∙g. Число μ называется коэффициентом трения и зависит от поверхностей, входящих в контакт при движении. Например, для трения стали по дереву этот коэффициент равен 0,5.
Рассчитайте силу сопротивления движению тела, движущегося по . Кроме коэффициента трения μ, массы тела m и ускорения свободного падения g, она зависит от угла наклона плоскости к горизонту α. Чтобы найти силу сопротивления движению в этом случае, нужно найти произведения коэффициента трения, массы тела, ускорения свободного падения и косинуса угла, под которым плоскость к горизонту Fтр=μ∙m∙g∙сos(α).
При движении тела в воздухе на невысоких скоростях сила сопротивления движению Fс прямо пропорциональна скорости движения тела v, Fc=α∙v. Коэффициент α зависит от свойств тела и вязкости среды и рассчитывается отдельно. При движении на высоких скоростях, например, при падении тела со значительной высоты или движении автомобиля, сила сопротивления прямо пропорциональна квадрату скорости Fc=β∙v². Коэффициент β дополнительно рассчитывается для высоких скоростей.
Источники:
- 1 Общая формула для силы сопротивления воздуха На рисунке
Для определения силы сопротивления воздуха создайте условия, при которых тело начнет под действием силы тяжести двигаться равномерно и прямолинейно. Рассчитайте значение силы тяжести, оно будет равно силе сопротивления воздуха. Если тело движется в воздухе, набирая скорость, сила его сопротивления находится при помощи законов Ньютона, также силу сопротивления воздуха можно найти из закона сохранения механической энергии и специальных аэродинамических формул.
Вам понадобится
- дальномер, весы, спидометр или радар, линейка, секундомер.
Инструкция
Перед измерением сопротивления б/у резистора обязательно выпаяйте его из старой платы или блока. Иначе он может быть шунтирован другими деталями схемы, и вы получите неправильные показания его сопротивления .
Видео по теме
Чтобы найти электрическое сопротивление проводника, воспользуйтесь соответствующими формулами. Сопротивление участка цепи находится по закону Ома. Если же известен материал и геометрические размеры проводника, его сопротивление можно рассчитать при помощи специальной формулы.
Вам понадобится
- — тестер;
- — штангенциркуль;
- — линейка.
Инструкция
Вспомните, что подразумевает собой понятие резистора. В данном случае под резистором надо понимать любой проводник или элемент электрической цепи, имеющий активное резистивное сопротивление. Теперь важно задаться вопросом о том, как действует изменение значения сопротивления на значение силы тока и от чего оно зависит. Суть явления сопротивления заключается в том, что резистора формируют своего рода барьер для прохождения электрических зарядов. Чем выше сопротивление вещества, тем более плотно расположены атомы в решетке резистивного вещества. Данную закономерность и объясняет закон Ома для участка цепи. Как известно, закон Ома для участка цепи звучит следующим образом: сила тока на участке цепи прямо пропорциональна напряжению на участке и обратно пропорциональна сопротивлению самого участка цепи.
Изобразите на листе бумаги график зависимости силы тока от напряжения на резисторе, а также от его сопротивления, исходя из закона Ома. Вы получите график гиперболы в первом случае и график прямой во втором случае. Таким образом, сила тока будет тем больше, чем больше напряжение на резисторе и чем меньше сопротивление. Причем зависимость от сопротивления здесь более яркая, ибо она имеет вид гиперболы.
Обратите внимание, что сопротивление резистора также изменяется при изменении его температуры. Если нагревать резистивный элемент и наблюдать при этом за изменением силы тока, то можно заметить, как при увеличении температуры уменьшается сила тока. Данная закономерность объясняется тем, что при увеличении температуры увеличиваются колебания атомов в узлах кристаллической решетки резистора, уменьшая таким образом свободное пространство для прохождения заряженных частиц. Другой причиной, уменьшающей силу тока в данном случае, является тот факт, что при увеличении температуры вещества увеличивается хаотичное движение частиц, в том числе заряженных. Таким образом, движение свободных частиц в резисторе становится в большей степени хаотичным, чем направленным, что и сказывается на уменьшении силы тока.
Видео по теме
Электричество само по себе невидимо, хотя от этого его опасность ничуть не меньше. Даже наоборот: как раз потому и опаснее. Ведь если бы мы его видели, как видим, например, воду, льющуюся из крана, то наверняка бы избежали множества неприятностей.
Вода. Вот она, водопроводная труба, и вот закрытый кран. Ничего не течет, не капает. Но мы точно знаем: внутри вода. И если система исправно работает, то вода эта там находится под давлением. 2, 3 атмосферы, или сколько там? Неважно. Но давление там есть, иначе система бы не работала. Где-то гудят насосы, гонят воду в систему, создают это самое давление.
А вот наш провод электрический. Где-то далеко, на другом конце тоже гудят генераторы, вырабатывают электричество. И в проводе от этого тоже давление… Нет-нет, не давление, конечно, тут в этом проводе напряжение . Оно тоже измеряется, но в своих единицах: в вольтах.
Давит в трубах на стенки вода, никуда не двигаясь, ждет, когда найдется выход, чтобы ринуться туда мощным потоком. И в проводе молча ждет напряжение, когда замкнется выключатель, чтобы потоки электронов двинулись выполнять свое предназначение.
И вот открылся кран, потекла струя воды. По всей трубе течет, двигаясь от насоса к расходному крану. А как только замкнулись контакты выключателя, в проводах потекли электроны. Что это за движение? Это ток . Электроны текут . И это движение, этот ток тоже имеет свою единицу измерения: ампер.
И еще есть сопротивление . Для воды это, образно говоря, размер отверстия в выпускном кране. Чем больше отверстие, тем меньше сопротивление движению воды. В проводах почти также: чем больше сопротивление провода, тем меньше ток.
Вот, как-то так, если образно представлять себе основные характеристики электричества. А с точки зрения науки все строго: существует так называемый закон Ома. Гласит он следующим образом: I = U/R .
I — сила тока. Измеряется в амперах.
U — напряжение. Измеряется в вольтах.
R — сопротивление. Измеряется в омах.
Есть еще одно понятие — мощность, W. С ним тоже просто: W = U*I . Измеряется в ваттах.
Собственно, это вся необходимая и достаточная для нас теория. Из этих четырех единиц измерения в соответствии с вышеприведенными двумя формулами можно вывести некоторое множество других:
| № | Задача | Формула | Пример |
| 1 | Узнать силу тока, если известны напряжение и сопротивление. | I = U/R | I = 220 в / 500 ом = 0.44 а. |
| 2 | Узнать мощность, если известны ток и напряжение. | W = U*I | W = 220 в * 0.44 а = 96.8 вт. |
| 3 | Узнать сопротивление, если известны напряжение и ток. | R = U/I | R = 220 в / 0.44 а = 500 ом. |
| 4 | Узнать напряжение, если известны ток и сопротивление. | U = I*R | U = 0.44 а * 500 ом = 220 в. |
| 5 | Узнать мощность, если известны ток и сопротивление. | W = I 2 *R | W = 0.44 а * 0.44 а * 500 ом = 96.8 вт. |
| 6 | Узнать мощность, если известны напряжение и сопротивление. | W = U 2 /R | W = 220 в * 220 в / 500 ом = 96.8 вт. |
| 7 | Узнать силу тока, если известны мощность и напряжение. | I = W/U | I = 96.8 вт / 220 в = 0,44 а. |
| 8 | Узнать напряжение, если известны мощность и ток. | U = W/I | U = 96.8 вт / 0.44 а = 220 в. |
| 9 | Узнать сопротивление, если известны мощность и напряжение. | R = U 2 /W | R = 220 в * 220 в / 96.8 вт = 500 ом. |
| 10 | Узнать сопротивление, если известны мощность и ток. | R = W/I 2 | R = 96.8 вт / (0,44 а * 0,44 а) = 500 ом. |
Ты скажешь: — Зачем мне это все надо? Формулы, цифры… Я ж не собираюсь заниматься расчетами.
А я так отвечу: — Перечитай предыдущую статью . Как можно быть уверенным, не зная простейших истин и расчетов? Хотя, собственно, в бытовом практическом плане наиболее интересна только формула 7, где определяется сила тока при известных напряжении и мощности. Как правило, эти 2 величины известны, а результат (сила тока) безусловно необходим для определения допустимого сечения провода и для выбора защиты .
Есть еще одно обстоятельство, о котором следует упомянуть в контексте этой статьи. В электроэнергетике используется так называемый «переменный» ток. То есть, те самые электроны движутся в проводах не всегда в одном направлении, они постоянно меняют его: вперед-назад-вперед-назад… И эта смена направления движения — 100 раз в секунду.
Погоди, но ведь везде говорится, что частота 50 герц! Да, именно так и есть. Частота измеряется в количестве периодов за секунду, но в каждом периоде ток меняет свое направление дважды. Иначе сказать, в одном периоде две вершины, которые характеризуют максимальное значение тока (положительное и отрицательное), и именно в этих вершинах происходит смена направления.
Не будем вдаваться в подробности более глубоко, но все же: почему именно переменный, а не постоянный ток?
Вся проблема в передаче электроэнергии на большие расстояния. Тут как раз вступает в силу неумолимый закон Ома. При больших нагрузках, если напряжение 220 вольт, сила тока может быть очень большой. Для передачи электроэнергии с таким током потребуются провода очень большого сечения.
Выход здесь только один: поднять напряжение. Седьмая формула говорит: I = W/U . Совершенно очевидно, что если мы будем подавать напряжение не 220 вольт, а 220 тысяч вольт, то сила тока уменьшится в тысячу раз. А это значит, что сечение проводов можно взять намного меньше.
Поиск по сайту.
Вы можете изменить поисковую фразу.
В природе существует два основных вида материалов, проводящие ток и не проводящие (диэлектрики). Отличаются эти материалы наличием условий для перемещения в них электрического тока (электронов).
Из токопроводящих материалов (медь, алюминий, графит, и многие другие), делают электрические проводники, в них электроны не связаны и могут свободно перемещаться.
В диэлектриках электроны привязаны к атомам намертво, поэтому ток в них течь не может. Из них делают изоляцию для проводов, детали электроприборов.
Для того чтобы электроны начали перемещаться в проводнике (по участку цепи пошел ток), им нужно создать условия. Для этого в начале участка цепи должен быть избыток электронов, а в конце – недостаток. Для создания таких условий используют источники напряжения – аккумуляторы, батарейки, электростанции.
В 1827 году Георг Симон Ом открыл закон силы электрического тока. Его именем назвали Закон и единицу измерения величины сопротивления. Смысл закона в следующем.
Чем толще труба и больше давление воды в водопроводе (с увеличением диаметра трубы уменьшается сопротивление воде) – тем больше потечет воды. Если представить, что вода это электроны (электрический ток), то, чем толще провод и больше напряжение (с увеличением сечения провода уменьшается сопротивление току) – тем больший ток будет протекать по участку цепи.
Сила тока, протекающая по электрической цепи, прямо пропорциональна приложенному напряжению и обратно пропорциональна величине сопротивления цепи.
Где I – сила тока, измеряется в амперах и обозначается буквой А ; U В ; R – сопротивление, измеряется в омах и обозначается Oм .
Если известны напряжение питания U и сопротивление электроприбора R , то с помощью выше приведенной формулы, воспользовавшись онлайн калькулятором, легко определить силу протекающего по цепи тока I .
С помощью закона Ома рассчитываются электрические параметры электропроводки, нагревательных элементов, всех радиоэлементов современной электронной аппаратуры, будь то компьютер, телевизор или сотовый телефон.
Применение закона Ома на практике
На практике часто приходится определять не силу тока I , а величину сопротивления R . Преобразовав формулу Закона Ома, можно рассчитать величину сопротивления R , зная протекающий ток I и величину напряжения U .
Величину сопротивления может понадобится рассчитать, например, при изготовлении блока нагрузок для проверки блока питания компьютера. На корпусе блока питания компьютера обычно есть табличка, в которой приведен максимальный ток нагрузки по каждому напряжению. Достаточно в поля калькулятора ввести данные величины напряжения и максимальный ток нагрузки и в результате вычисления получим величину сопротивления нагрузки для данного напряжения. Например, для напряжения +5 В при максимальной величине тока 20 А, сопротивление нагрузки составит 0,25 Ом.
Формула Закона Джоуля-Ленца
Величину резистора для изготовления блока нагрузки для блока питания компьютера мы рассчитали, но нужно еще определить какой резистор должен быть мощности? Тут поможет другой закон физики, который, независимо друг от друга открыли одновременно два ученых физика. В 1841 году Джеймс Джоуль, а в 1842 году Эмиль Ленц. Этот закон и назвали в их честь – Закон Джоуля-Ленца .
Потребляемая нагрузкой мощность прямо пропорциональна приложенной величине напряжения и протекающей силе тока. Другими словами, при изменении величины напряжения и тока будет пропорционально будет изменяться и потребляемая мощность.
где P – мощность, измеряется в ваттах и обозначается Вт ; U – напряжение, измеряется в вольтах и обозначается буквой В ; I – сила ток, измеряется в амперах и обозначается буквой А .Зная напряжения питания и силу тока, потребляемую электроприбором, можно по формуле определить, какую он потребляет мощность. Достаточно ввести данные в окошки ниже приведенного онлайн калькулятора.
Закон Джоуля-Ленца позволяет также узнать силу тока, потребляемую электроприбором зная его мощность и напряжение питания. Величина потребляемого тока необходима, например, для выбора сечения провода при прокладке электропроводки или для расчета номинала .
Например, рассчитаем потребляемый ток стиральной машины. По паспорту потребляемая мощность составляет 2200 Вт, напряжение в бытовой электросети составляет 220 В. Подставляем данные в окошки калькулятора, получаем, что стиральная машина потребляет ток величиной 10 А.
Еще один пример, Вы решили в автомобиле установить дополнительную фару или усилитель звука. Зная потребляемую мощность устанавливаемого электроприбора легко рассчитать потребляемый ток и правильно подобрать сечение провода для подключения к электропроводке автомобиля. Допустим, дополнительная фара потребляет мощность 100 Вт (мощность установленной в фару лампочки), бортовое напряжение сети автомобиля 12 В. Подставляем значения мощности и напряжения в окошки калькулятора, получаем, что величина потребляемого тока составит 8,33 А.
Разобравшись всего в двух простейших формулах, Вы легко сможете рассчитать текущие по проводам токи, потребляемую мощность любых электроприборов – практически начнете разбираться в основах электротехники.
Преобразованные формулы Закона Ома и Джоуля-Ленца
Встретил в Интернете картинку в виде круглой таблички, в которой удачно размещены формулы Закона Ома и Джоуля-Ленца и варианты математического преобразования формул. Табличка представляет собой несвязанные между собой четыре сектора и очень удобна для практического применения
По таблице легко выбрать формулу для расчета требуемого параметра электрической цепи по двум другим известным. Например, нужно определить ток потребления изделием по известной мощности и напряжению питающей сети. По таблице в секторе тока видим, что для расчета подойдет формула I=P/U.
А если понадобится определить напряжение питающей сети U по величине потребляемой мощности P и величине тока I, то можно воспользоваться формулой левого нижнего сектора, подойдет формула U=P/I.
Подставляемые в формулы величины должны быть выражены в амперах, вольтах, ваттах или Омах.
Текущая формула — Что такое текущая формула? Примеры
Текущая формула получена из закона Ома. Ток определяется как поток электронов в электрической цепи. Поток электронов происходит за счет разности потенциалов. Сила тока также известна как скорость изменения заряда во времени. Сила тока обозначается буквой I, а единица измерения тока в системе СИ — Ампер. Давайте изучим применение текущей формулы в разделе ниже.
Какова текущая формула?
Согласно закону Ома, ток — это отношение разности потенциалов и сопротивления.Таким образом, текущая формула имеет вид: I = V / R
где
- Представляю ток в амперах,
- В — разность потенциалов в вольтах
- R — сопротивление в Ом (Ом).
Давайте посмотрим на применение текущей формулы в следующем разделе решенных примеров.
Хотите найти сложные математические решения за секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором для решения сложных вопросов.С Cuemath находите решения простым и легким способом.
Забронируйте бесплатную пробную версию Класс
Примеры использования текущей формулы
Пример 1: В электрической цепи разность потенциалов и сопротивление задаются как 20 В и 4 Ом соответственно. Используя формулу тока, найдите ток, протекающий в цепи.
Решение:
Чтобы найти: Ток (I), протекающий в цепи.
Дано:
V = 20 В, R = 4 Ом
Используя текущую формулу
I = V / R
I = 20/4
I = 5
Ответ: В цепи протекает ток 5 ампер.
Пример 2: Полный ток, протекающий в электрической цепи, составляет 50 Ампер, а сопротивление проводов — 14 Ом. Используя текущую формулу, найдите разность потенциалов.
Решение:
Чтобы найти разность потенциалов:
Дано:
I = 50 А, R = 14 Ом
Используя текущую формулу
I = V / R
50 = V / 14
V = 50 × 14
V = 700
Ответ: Разность потенциалов 700 В.
Пример 3: В электрической цепи разность потенциалов составляет 20 В, а значение тока составляет 5 А соответственно. Используя формулу тока, найдите сопротивление цепи.
Решение:
Чтобы найти сопротивление (R) цепи:
Дано:
V = 20 В, I = 5 А
Используя текущую формулу
R = V / I
R = 20/5
R = 4 Ом
Ответ: Сопротивление цепи 4Ω.
Часто задаваемые вопросы по текущей формуле
Как рассчитать ток по текущей формуле?
Если заданы напряжение (В) и сопротивление (R) любой цепи, мы можем использовать формулу тока для вычисления тока, то есть I = V / R (амперы).
Как рассчитать напряжение по формуле тока?
Если заданы ток (I) и сопротивление (R) любой цепи, мы можем составить формулу тока для вычисления напряжения, то есть V = IR (Вольт).
Как рассчитать сопротивление по текущей формуле?
Если заданы ток (I) и разность потенциалов (V) любой цепи, мы можем составить формулу тока для расчета сопротивления, т.е.е., R = V / I (Ом Ом).
Что такое определение текущей формулы? Напишите его единицу СИ.
Ток — это отношение разности потенциалов и сопротивления. Он представлен как (I). Текущая формула представлена как I = V / R. Единица измерения тока в системе СИ — Ампер (Ампер).
Электрический ток — Веб-формулы
Электрический ток определяется по формуле:I = В / R
Соответствующие единицы:
ампер (А) = вольт (В) / Ом (Ом)
Эта формула получена из закона Ома .Где у нас:
В: напряжение
I: ток
R: сопротивление
Если электрическая мощность и полное сопротивление известны, то ток можно определить по следующей формуле:
I = √ ( P / R )
Соответствующие единицы:
Ампер (А) = √ (Ватт (Вт) / Ом (Ом))
Где P — электрическая мощность.
Электрический ток
Скорость прохождения заряда через поперечное сечение некоторой области металлического провода (или электролита) называется током через эту область.
Если скорость потока заряда непостоянна, тогда ток в любой момент задается дифференциальным пределом: I = dQ / dt.
Если заряд Q течет по цепи в течение времени t, то
I = Q / t.
Единица измерения тока S.I называется ампер (А) (кулон в секунду).
1 ампер = 6,25 × 10 8 электронов / сек
В металлических проводниках ток возникает из-за движения электронов, тогда как в электролитах и ионизированных газах как электроны, так и положительные ионы движутся в противоположном направлении.Направление тока принимается за направление движения положительных зарядов.
В проводимости, хотя ток возникает только за счет электронов, ранее предполагалось, что ток возникает из-за положительных зарядов, протекающих от положительного полюса батареи к отрицательному. Поэтому направление тока считается противоположным потоку электронов.
Если ток постоянный: Δq = I.Δt
функция времени:
Заряд = Площадь под графиком = ½ × t 0 × I 0
До Найти ток в электрической цепи
Для простой цепи или одиночного провода мы имеем:
Для сложной цепи с более чем одним проводом мы можем определить ток с помощью двух законов Кирхгофа
Первый закон: Этот закон основан на принципе сохранения заряда и утверждает, что в электрической цепи (или сети проводов) алгебраическая сумма токов, встречающихся в точке, равна нулю.
Стрелка, отмеченная на схеме, представляет направление обычного тока, то есть направление потока положительного заряда, тогда как направление потока электронов дает направление электронного тока, которое противоположно направлению обычного тока.
I 1 + I 4 + I 5 = I 3 + I 2 + I 6
Второй закон: Алгебраическая сумма произведения тока и сопротивление в любом замкнутом контуре цепи равно алгебраической сумме электродвижущих сил, действующих в этом контуре.
Математически.
Электродвижущие силы — ЭДС () источника определяется как работа, совершаемая на единицу заряда при прохождении положительного заряда через гнездо ЭДС от конца с низким потенциалом к концу с высоким потенциалом. Таким образом,
𝜖 = w / Q
Когда ток не течет, ЭДС источника в точности равна разности потенциалов между его концами. Единица ЭДС такая же, как и у потенциала, то есть вольт.
Средний поток электронов в проводнике, не подключенном к батарее, равен нулю, т.е. количество свободных электронов, пересекающих любой участок проводника слева направо, равно количеству электронов, пересекающих участок проводника справа налево. Таким образом, ток не течет по проводнику, пока он не будет подключен к батарее.
Скорость дрейфа свободных электронов в металлическом проводнике
В отсутствие электрического поля свободные электроны в металле беспорядочно вращаются во всех направлениях, поэтому их средняя скорость равна нулю.При приложении электрического поля они ускоряются в направлении, противоположном направлению поля, и поэтому имеют общий дрейф в этом направлении. Однако из-за частых столкновений с атомами их средняя скорость очень мала. Эта средняя скорость, с которой электроны движутся в проводнике под действием разности потенциалов, называется дрейфовой скоростью .
Если E — приложенное поле, e — заряд электрона, m — масса электрона и τ — временной интервал между последовательными столкновениями (время релаксации), то ускорение электрона равна
Поскольку средняя скорость сразу после столкновения равна нулю, а непосредственно перед следующим столкновением это τ, скорость дрейфа должна быть:
Если I — ток через проводник и n — это количество свободных электронов на единицу объема, тогда можно показать, что:
Подвижность µ носителя заряда определяется как скорость дрейфа на единицу электрического поля:
Плотность тока (J)
(i)
(ii) S.I Единица J = Am -2 .
(iii) Плотность тока — это векторная величина, ее направление — это направление потока положительного заряда в данной точке внутри проводника.
(iv) Размеры плотности тока = [M 0 L -2 T o A 1 ]
Носители тока: заряженные частицы, поток которых в определенном направлении составляет электрический ток, являются носителями тока. . Носители тока могут иметь положительный или отрицательный заряд.Ток переносится электронами в проводниках, ионами в электролитах, электронами и дырками в полупроводниках.
Пример 1: Частица с зарядом q кулонов описывает круговую орбиту. Если радиус орбиты равен R, а частота орбитального движения частиц равна f, то найти ток на орбите.
Решение: Через любой участок орбиты заряд проходит f раз за одну секунду. Следовательно, через этот участок общий заряд, проходящий за одну секунду, равен fq.По определению i = fq.
Пример 2: Ток в проводе изменяется со временем в соответствии с уравнением I = 4 + 2t, где I — в амперах, а t — в секундах. Вычислите количество заряда, прошедшего через поперечное сечение провода за время от t = 2 с до t = 6 с.
Решение: Пусть dq будет изменением, которое произошло за небольшой интервал времени dt.
Тогда dq = I dt = (4 + 2t) dt
Следовательно, общий заряд, прошедший за интервал t = 2 секунды и t = 6, равен
q = ∫ 6 2 (4 + 2t) dt = 48 кулонов
Пример 3: Дан токоведущий провод неоднородного сечения.Что из следующего является постоянным по всей сети?
(a) Только ток
(b) Ток и скорость дрейфа
(c) Только скорость дрейфа
(d) Ток, скорость дрейфа
Решение : (a)
Пример4 : Когда разность потенциалов на данном медном проводе увеличивается, скорость дрейфа составляет
носители заряда:
(а) Уменьшается
(б) Увеличивается
(в) Остается прежним
(г) Уменьшается до нуля
Решение : (б)
6 .3: Цепи делителя тока и формула делителя тока
Параллельную цепь часто называют делителем тока из-за ее способности пропорционально или делить общий ток на дробные части
Чтобы понять, что это означает, давайте сначала проанализируем простую параллельную схему, определив токи ответвления через отдельные резисторы:
Зная, что напряжения на всех компонентах в параллельной цепи одинаковы, мы можем заполнить нашу таблицу напряжение / ток / сопротивление шестью вольтами в верхней строке:
Используя закон Ома (I = E / R), мы можем рассчитать ток каждой ветви:
Зная, что токи ответвлений в параллельных цепях складываются, чтобы равняться общему току, мы можем получить общий ток, суммируя 6 мА, 2 мА и 3 мА:
Последним шагом, конечно же, является определение общего сопротивления.Это можно сделать с помощью закона Ома (R = E / I) в столбце «общее» или с помощью формулы параллельного сопротивления для отдельных сопротивлений. В любом случае мы получим один и тот же ответ:
Еще раз, должно быть очевидно, что ток через каждый резистор связан с его сопротивлением, учитывая, что напряжение на всех резисторах одинаково. Здесь соотношение не прямо пропорционально, а наоборот. Например, ток через R 1 в два раза больше, чем ток через R 3 , сопротивление которого в два раза больше, чем R 1 .
Если бы мы изменили напряжение питания этой цепи, мы обнаружили, что (сюрприз!) Эти пропорции не меняются:
Ток через R 1 по-прежнему ровно вдвое больше, чем у R 3 , несмотря на то, что напряжение источника изменилось. Пропорциональность между разными токами ответвления строго зависит от сопротивления.
Также делители напряжения напоминают тот факт, что токи ответвления представляют собой фиксированные пропорции общего тока.Несмотря на четырехкратное увеличение напряжения питания, соотношение между током любой ветви и полным током остается неизменным:
Теперь мы можем сами убедиться в том, что мы сделали в начале этой страницы: параллельную цепь часто называют делителем тока из-за ее способности пропорционально или делить общий ток на дробные части.
Формула текущего делителя
Приложив немного алгебры, мы можем вывести формулу для определения тока параллельного резистора, учитывая не что иное, как общий ток, отдельное сопротивление и общее сопротивление:
Отношение полного сопротивления к индивидуальному сопротивлению такое же, как отношение индивидуального (ответвления) тока к общему току.Это известно как формула делителя тока и представляет собой сокращенный метод определения токов ответвления в параллельной цепи, когда известен полный ток.
Пример формулы делителя тока
Используя исходную параллельную схему в качестве примера, мы можем пересчитать токи ответвления по этой формуле, если мы начнем с знания общего тока и общего сопротивления:
Если вы потратите время на сравнение двух формул делителя, вы увидите, что они очень похожи.Обратите внимание, однако, что отношение в формуле делителя напряжения составляет R n (отдельное сопротивление), деленное на R Total , а соотношение в формуле делителя тока равно R Total , деленное на R n :
Формула делителя тока и формула делителя напряжения
Эти два уравнения довольно легко спутать, получив обратные соотношения сопротивлений. Один из способов помочь запомнить правильную форму — это помнить, что оба отношения в уравнениях делителя напряжения и тока должны быть меньше единицы.Ведь это делитель уравнений, а не умножитель уравнений! Если дробь перевернута, то соотношение будет больше единицы, что неверно.
Зная, что полное сопротивление в последовательной цепи (делитель напряжения) всегда больше, чем любое из отдельных сопротивлений, мы знаем, что доля для этой формулы должна быть R n по сравнению с R Всего . И наоборот, зная, что полное сопротивление в параллельной цепи (делитель тока) всегда меньше, чем любое из отдельных сопротивлений, мы знаем, что доля для этой формулы должна быть R Всего по R n .
Пример схемы делителя токаПрименение: Схема электрического счетчика
Цепи делителя токанаходят применение в схемах электрических счетчиков, где требуется, чтобы часть измеренного тока проходила через чувствительное устройство обнаружения. Используя формулу делителя тока, подходящий шунтирующий резистор может быть подобран таким образом, чтобы пропорционально пропорции правильного количества тока для устройства в любом конкретном случае:
Обзор схемы делителя тока:
- Пропорции параллельных цепей, или «деление» общего тока цепи между токами отдельных ветвей, пропорции строго зависят от сопротивлений: I n = I Total (R Total / R n )
Уравнения Максвелла: плотность электрического тока
Плотность электрического тока
Плотность электрического тока обозначается векторным символом ( J ).2], поскольку ток течет в одном направлении, и площадь измеряется перпендикулярно / перпендикулярно / перпендикулярно этому. Это показано на рисунке 1:
Рисунок 1. Электрический ток I (вверху) — это общий расход заряда в секунду. Плотность тока J (внизу) ток в указанном поперечном сечении.
Полный электрический ток ( I ) может быть связан с плотностью тока ( Дж ) суммируя (или интегрируя) плотность тока по области, где течет заряд:
| [Уравнение 1] |
|---|
| [Уравнение 2] |
|---|
Обратите внимание, что плотность тока часто непостоянна, поэтому взвешенное суммирование (уравнение [1]) необходим.
Наконец, предположим, что среда (материал) имеет электрическую проводимость, заданную на (который измеряется в Сименс / метр, которое является противоположным (обратным) сопротивлением на длину). Тогда плотность электрического тока можно связать с Электрическое поле по уравнению [3]:
| [Уравнение 3] |
|---|
Вы можете не узнать уравнение [3], но на самом деле оно известно — это закон Ома.Вы, вероятно, знаете из электрических цепей, что V = IR, который связывает напряжение, ток и сопротивление. В уравнении [3] E-поле аналогично напряжению, плотность тока аналогична току, а проводимость — это величина, обратная сопротивлению. Вот где закон Ома для цепей происходит от.
Уравнение [3] утверждает, что в материале с ненулевой проводимостью E-поле будет производить электрический ток.
Уравнения Максвелла
Эта страница о плотности электрического тока (J) защищена авторским правом.Авторские права принадлежат Maxwells-Equations.com, 2012.
Калькулятор пускового тока трансформаторас формулой
Калькулятор пускового тока:
Введите входное напряжение в вольтах, сопротивление обмотки постоянному току, затем нажмите кнопку расчета, чтобы получить пусковой ток в амперах.
Что такое пусковой ток:
Пусковой ток — это не что иное, как максимальный ток, протекающий в момент запуска электрооборудования. Ток протекает всего несколько секунд.Пусковой ток вызывает быстрое нагревание оборудования, повреждение катушек, повреждение изоляции и, в худшем случае, выход оборудования из строя.
Пусковой ток вращающегося оборудования будет выше, чем у статического оборудования. Пример. Для одинаковой мощности двигателя требуется более высокий ток, чем у трансформаторов.
Расчет пускового тока:
Приблизительно пусковой ток I (пик) равен отношению двукратного корня максимального приложенного напряжения к сопротивлению обмотки постоянного тока.Этот расчет дает вам приблизительное значение пускового тока для понимания.
I (пик) = 1,414 В м / R (Ом) А
Чтобы получить точное значение пускового тока, используйте приведенную ниже формулу:
В м — максимальное приложенное напряжение в вольтах; L — индуктивность воздушного сердечника трансформатора по Хендри; R — полное сопротивление трансформатора постоянному току в Ом; B N — нормальная номинальная магнитная индукция сердечника трансформатора в Веберах на квадратный метр; B R — остаточная магнитная индукция сердечника трансформатора в Веберах на квадратный метр; B S — плотность потока насыщения материала сердечника в Веберах на квадратный метр.
Пример:
Трансформатор 100 кВА, 440 В имеет сопротивление обмотки постоянного тока 0,45 Ом. Рассчитайте пусковой ток трансформатора.
Примените нашу формулу,
I (пик) = 1,414 x 440 / 0,45
Пусковой ток в амперах = 1382 ампера
При этом ток полной нагрузки трансформатора
I (A) = кВА * 1000 / Напряжение
Ток полной нагрузки в амперах = 1000 * 100/440 = 227 ампер
Следовательно, пусковой ток в 6 раз больше тока полной нагрузки.
Артикул:
Чистая приведенная стоимость (NPV) Определение
Что такое чистая приведенная стоимость (ЧПС)?
Чистая приведенная стоимость (NPV) — это разница между текущей стоимостью денежных поступлений и текущей стоимостью оттока денежных средств за период времени. NPV используется при составлении бюджета капиталовложений и инвестиционном планировании для анализа прибыльности планируемых инвестиций или проектов. NPV — это результат вычислений, используемых для определения сегодняшней стоимости будущего потока платежей.
Ключевые выводы
- Чистая приведенная стоимость, или NPV, используется для расчета текущей общей стоимости будущего потока платежей.
- Если NPV проекта или инвестиции положительна, это означает, что дисконтированная приведенная стоимость всех будущих денежных потоков, связанных с этим проектом или инвестицией, будет положительной и, следовательно, привлекательной.
- Для расчета NPV необходимо оценить будущие денежные потоки для каждого периода и определить правильную ставку дисконтирования.t} \\ & \ textbf {где:} \\ & R_t = \ text {Чистый приток-отток денежных средств за один период} t \\ & i = \ text {Ставка дисконтирования или доход, который можно было бы заработать в} \\ & \ text {альтернативные инвестиции} \\ & t = \ text {Количество периодов таймера} \\ \ end {выровнено}
NPV = t = 1∑n (1 + i) tRt, где: Rt = чистый приток-отток денежных средств в течение одного периода ti = ставка дисконтирования или доход, который может быть получен за счет альтернативных инвестиций st = количество периодов таймера
Если вы не знакомы с обозначением суммирования, вот более простой способ запомнить концепцию NPV:
ЧПС знак равно TVECF — TVIC куда: TVECF знак равно Сегодняшняя стоимость ожидаемых денежных потоков TVIC знак равно Сегодняшняя стоимость вложенных денежных средств \ begin {align} & \ textit {NPV} = \ text {TVECF} — \ text {TVIC} \\ & \ textbf {где:} \\ & \ text {TVECF} = \ text {Сегодняшняя сумма ожидаемых денежных средств потоки} \\ & \ text {TVIC} = \ text {Сегодняшняя стоимость вложенных денежных средств} \\ \ end {выровнено} NPV = TVECF − TVIC, где: TVECF = сегодняшняя стоимость ожидаемых денежных потоков TVIC = сегодняшняя стоимость инвестированных денежных средств.
О чем может вам рассказать чистая приведенная стоимость
NPV учитывает временную стоимость денег и может использоваться для сравнения аналогичных инвестиционных альтернатив.NPV основывается на ставке дисконтирования, которая может быть получена из стоимости капитала, необходимого для инвестирования, и следует избегать любых проектов или инвестиций с отрицательной NPV. Одним из важных недостатков анализа NPV является то, что он делает предположения о будущих событиях, которые могут быть ненадежными.
NPV рассчитывает оценить прибыльность данной инвестиции, исходя из того, что доллар в будущем не будет стоить столько же, сколько доллар сегодня. Деньги теряют ценность со временем из-за инфляции. Однако доллар сегодня можно инвестировать и получить прибыль, в результате чего его будущая стоимость, возможно, будет выше, чем доллар, полученный в тот же момент в будущем.
NPV направлена на определение приведенной стоимости будущих денежных потоков инвестиции, превышающей первоначальную стоимость инвестиции. Элемент ставки дисконтирования формулы NPV дисконтирует будущие денежные потоки до текущей стоимости. Если вычитание первоначальной стоимости инвестиций из суммы денежных потоков на сегодняшний день положительно, тогда вложение оправдано.
Например, инвестор может получить 100 долларов сегодня или через год. Большинство инвесторов не захотели бы откладывать получение 100 долларов сегодня.Однако что, если бы инвестор мог выбрать получение 100 долларов сегодня или 105 долларов через год? Ставка доходности 5% для ожидания в течение одного года может быть выгодной для инвестора, если только другие инвестиции не могут принести доход более 5% за тот же период.
Если бы инвестор знал, что он может заработать 8% от относительно безопасных инвестиций в течение следующего года, он бы предпочел получить 100 долларов сегодня, а не 105 долларов в год, с 5% -ной нормой прибыли. В этом случае ставкой дисконтирования будет 8%.
Положительный и отрицательный NPV
Положительное значение NPV указывает на то, что прогнозируемая прибыль, полученная от проекта или инвестиций — в текущих долларах — превышает ожидаемые затраты, также в текущих долларах. Предполагается, что инвестиции с положительной NPV будут прибыльными.
Инвестиция с отрицательной NPV приведет к чистому убытку. Эта концепция является основой правила чистой приведенной стоимости, согласно которому следует рассматривать только инвестиции с положительными значениями NPV.
Расчет чистой приведенной стоимости
Деньги в настоящем стоят больше, чем такая же сумма в будущем, из-за инфляции и возможных доходов от альтернативных инвестиций, которые можно было бы сделать в промежуточный период. Другими словами, доллар, заработанный в будущем, не будет стоить столько же, сколько доллар, заработанный в настоящем. Элемент ставки дисконтирования формулы NPV позволяет учесть это.
Например, предположим, что инвестор может выбрать платеж в размере 100 долларов сегодня или через год.Рациональный инвестор не захочет откладывать платеж. Однако что, если бы инвестор мог выбрать получение 100 долларов сегодня или 105 долларов в год? Если плательщик был надежным, то эти дополнительные 5%, возможно, стоили ожидания, но только в том случае, если не было ничего другого, что инвесторы могли бы сделать со 100 долларами, которые принесут более 5%.
Инвестор может подождать год, чтобы заработать дополнительные 5%, но это может быть приемлемо не для всех инвесторов. В этом случае 5% — это ставка дисконтирования, которая будет варьироваться в зависимости от инвестора.Если бы инвестор знал, что он может заработать 8% от относительно безопасного вложения в течение следующего года, он не захотел бы откладывать выплату 5%. В этом случае ставка дисконтирования инвестора составляет 8%.
Компания может определить ставку дисконтирования, используя ожидаемую доходность других проектов с аналогичным уровнем риска или стоимость заимствования денег, необходимых для финансирования проекта. Например, компания может избежать проекта, который, как ожидается, будет приносить 10% в год, если финансирование проекта стоит 12%, или альтернативный проект, как ожидается, будет приносить 14% в год.
Представьте, что компания может инвестировать в оборудование, которое будет стоить 1 000 000 долларов и, как ожидается, будет приносить 25 000 долларов дохода в месяц в течение пяти лет. Компания имеет доступный капитал для приобретения оборудования и может в качестве альтернативы инвестировать его в фондовый рынок с ожидаемой доходностью 8% в год. Менеджеры считают, что покупка оборудования или инвестирование в фондовый рынок — аналогичные риски.
NPV можно рассчитать с помощью таблиц, электронных таблиц (например, Excel) или финансовых калькуляторов.
шагов к чистой приведенной стоимости
Для расчета NPV есть два основных шага:
.Шаг 1: ЧПС первоначальной инвестиции
Поскольку оборудование оплачивается авансом, это первый денежный поток, включенный в расчет. Нет необходимости учитывать затраченное время, поэтому не нужно сбрасывать со счетов сегодняшний отток в размере 1 000 000 долларов.
- Определите количество периодов (t): Предполагается, что оборудование будет генерировать ежемесячный денежный поток и прослужит пять лет, что означает, что в расчет будет включено 60 денежных потоков и 60 периодов.{\ frac {1} {12}}) — 1 = 0,64 \%
Периодическая ставка = ((1 + 0,08) 121) -1 = 0,64%
Шаг 2: NPV будущих денежных потоков
Предположим, что ежемесячные денежные потоки зарабатываются в конце месяца, а первый платеж поступает ровно через месяц после покупки оборудования. Это будущий платеж, поэтому его необходимо скорректировать с учетом временной стоимости денег. Инвестор может легко выполнить этот расчет с помощью электронной таблицы или калькулятора. Чтобы проиллюстрировать концепцию, первые пять платежей показаны в таблице ниже.
Изображение Сабрины Цзян © Investopedia 2020Полный расчет приведенной стоимости равен приведенной стоимости всех 60 будущих денежных потоков за вычетом инвестиций в размере 1 000 000 долларов США. Расчет мог бы быть более сложным, если бы предполагалось, что оборудование будет иметь какое-либо значение, оставшееся в конце его срока службы, но в этом примере предполагается, что оно бесполезно.
N п V знак равно — $ 1 , 000 , 000 + ∑ т знак равно 1 60 25 , 00 0 60 ( 1 + 0,0064 ) 60 ЧПС = — \ 1 000 000 долл. {60} \ frac {25 000_ {60}} {(1 + 0.{60}} NPV = — 1 000 000 долларов США + ∑t = 160 (1 + 0,0064) 6025 00060
Эту формулу можно упростить до следующего расчета:
N п V знак равно — $ 1 , 000 , 000 + $ 1 , 242 , 322,82 знак равно $ 242 , 322,82 NPV = — \ 1 000 000 + \ 1 242 322,82 долл. США = \ 242 322,82 долл. США NPV = — 1 000 000 долларов США + 1 242 322,82 доллара США = 242 322,82 доллара США
В этом случае ЧПС положительна; оборудование следует покупать. Если приведенная стоимость этих денежных потоков была отрицательной, потому что ставка дисконтирования была больше, или чистые денежные потоки были меньше, инвестиций следовало бы избежать.
Ограничения чистой приведенной стоимости
Оценка прибыльности инвестиций с помощью NPV в значительной степени зависит от предположений и оценок, поэтому может быть существенное место для ошибок. Предполагаемые факторы включают инвестиционные затраты, ставку дисконтирования и прогнозируемую доходность. Для реализации проекта часто могут потребоваться непредвиденные расходы или могут потребоваться дополнительные расходы в конце проекта.
Чистая приведенная стоимость к сроку окупаемости
Срок окупаемости или «метод окупаемости» — более простая альтернатива NPV.Метод окупаемости рассчитывает, сколько времени потребуется для возврата первоначальных инвестиций. Недостатком является то, что этот метод не учитывает временную стоимость денег. По этой причине сроки окупаемости, рассчитанные для более длительных вложений, имеют больший потенциал неточности.
Более того, срок окупаемости строго ограничен временем, необходимым для возврата первоначальных инвестиционных затрат. Не исключено, что рентабельность инвестиций может резко измениться.Сравнение с использованием сроков окупаемости не учитывает долгосрочную прибыльность альтернативных инвестиций.
NPV и внутренняя норма доходности (IRR)
Внутренняя норма доходности (IRR) очень похожа на NPV, за исключением того, что ставка дисконтирования — это ставка, которая снижает NPV инвестиции до нуля. Этот метод используется для сравнения проектов с разной продолжительностью жизни или размером необходимого капитала.
Например, IRR можно использовать для сравнения ожидаемой прибыльности трехлетнего проекта, требующего инвестиций в размере 50 000 долларов США, с доходностью 10-летнего проекта, требующего инвестиций в размере 200 000 долларов США.Несмотря на то, что IRR полезен, обычно считается, что он уступает NPV, поскольку делает слишком много предположений о риске реинвестирования и распределении капитала.
Что означает чистая приведенная стоимость?
Чистая приведенная стоимость (NPV) — это финансовая метрика, которая направлена на определение общей стоимости потенциальной инвестиционной возможности. Идея NPV состоит в том, чтобы спрогнозировать все будущие поступления и оттоки денежных средств, связанных с инвестициями, дисконтировать все эти будущие потоки денежных средств к настоящему времени, а затем сложить их вместе.Полученное число после сложения всех положительных и отрицательных денежных потоков представляет собой чистую приведенную стоимость инвестиции. Положительное значение NPV означает, что после учета временной стоимости денег вы заработаете деньги, если продолжите инвестирование.
В чем разница между NPV и IRR?
NPV и IRR — это тесно связанные концепции, поскольку IRR инвестиции — это ставка дисконтирования, при которой NPV этой инвестиции будет равна нулю. Другой способ думать об этом заключается в том, что NPV и IRR пытаются ответить на два отдельных, но связанных вопроса.Для NPV возникает вопрос: «Какую общую сумму я заработаю, если продолжу эти инвестиции, с учетом временной стоимости денег?» Что касается IRR, вопрос заключается в следующем: «Если я продолжу эти инвестиции, какова будет эквивалентная годовая норма прибыли, которую я получу?»
Что такое хороший NPV?
Теоретически чистая приведенная стоимость считается «хорошей», если она больше нуля. В конце концов, расчет NPV уже принимает во внимание такие факторы, как стоимость капитала инвестора, альтернативные издержки и толерантность к риску через ставку дисконтирования.Также учитываются будущие денежные потоки проекта, а также временная стоимость денег. Следовательно, даже чистая приведенная стоимость в 1 доллар теоретически должна считаться «хорошей». На практике, однако, многие инвесторы будут настаивать на определенных порогах NPV, таких как 10 000 долларов и выше, чтобы обеспечить себе дополнительный запас прочности.
Почему будущие денежные потоки дисконтируются?
NPV использует дисконтированные денежные потоки, обусловленные временной стоимостью денег (TMV). Временная стоимость денег — это концепция, согласно которой деньги, которые у вас есть сейчас, стоят больше, чем такая же сумма в будущем, из-за их потенциальной доходности за счет инвестиций и других факторов, таких как инфляционные ожидания.Ставка, используемая для учета времени, или ставка дисконтирования, будет зависеть от типа проведенного анализа. Отдельные лица должны использовать альтернативные издержки использования своих денег в другом месте в качестве подходящей ставки дисконтирования — проще говоря, это норма прибыли, которую инвестор может получить на рынке на вложения сопоставимого размера и риска.
Electric Current — Summary — Physics Hypertextbook
Electric Current — Summary — The Physics Hypertextbook.Сводка
- Электрический ток — это скорость, с которой заряд протекает через поверхность.
- Электрический ток часто называют просто током .
- Как скаляр, ток имеет только величину.
- Обозначение тока — I (курсив) из силы тока.
- В форме уравнения ток можно записать как…
Где…средний ток мгновенный ток I = ∆ д = дк ∆ т дт I = электрический ток [A] ∆ q , dq = заряд проходит через некоторую область [C] ∆ t , dt = интервал, момент времени [с] - Единица измерения тока в системе СИ — ампер [А].
- Ампер — это кулон в секунду.
- Ампер — одна из семи основных единиц Международной системы единиц.
- Написание без ударения ампер также допускается в письменной форме на английском языке.
- Укороченная форма amp часто приемлема или даже предпочтительна.
- Единица заряда в системе СИ — кулон [C]
- Кулон — производная единица.
- Один кулон — это количество заряда, переносимого одним ампером тока за одну секунду времени [C = A s].
- Плотность тока — это величина, связанная с электрическим током.
- Обозначение плотности тока: Дж (жирный шрифт).
- Как вектор, плотность тока имеет величину и направление.
- По определению, плотность тока является произведением плотности заряда (ρ) и скорости ( v ).
- Величина плотности тока также эквивалентна отношению тока ( I ) к площади ( A ).
- В форме уравнения плотность тока можно записать как…
Где…векторное определение звездной величины J = ρ v Дж , Дж = плотность тока [А / м 2 ] как вектор или ее скалярная величина I = электрический ток [A] ρ = плотность заряда [Кл / м 3 ] v = Скорость дрейфа [м / с] А = площадь [м 2 ] - Единица измерения плотности тока в системе СИ — ампер на квадратный метр [А / м 2 ].
- Микроскопическое описание тока
- Макроскопическое явление электрического тока можно описать чистым движением микроскопических заряженных частиц.
- В форме уравнения можно записать микроскопическое описание тока и плотности тока…
Где…микроскопический ток микроскопический плотность тока I = nqAv J = nq v I = электрический ток [A] Дж = плотность тока [А / м 2 ] n = плотность частиц [частиц / м 3 ] q = заряд на частицу [Кл] v , v = Скорость дрейфа [м / с] А = площадь [м 2 ]
Нет постоянных условий.
- Механика
- Кинематика
- Движение
- Расстояние и перемещение
- Скорость и скорость
- Разгон
- Уравнения движения
- Свободное падение
- Графики движения
- Кинематика и расчет
- Кинематика в двух измерениях
- Снаряды
- Параметрические уравнения
- Dynamics I: Force
- Силы
- Сила и масса
- Действие-реакция
- Масса
- Динамика
- Статика
- Трение
- Силы в двух измерениях
- Центростремительная сила
- Кодовые рамки
- Энергия
- Работа
- Энергия
- Кинетическая энергия
- Потенциальная энергия
- Сохранение энергии
- Мощность
- Простые станки
- Dynamics II: Импульс
- Импульс и импульс
- Сохранение импульса
- Импульс и энергия
- Импульс в двух измерениях
- Вращательное движение
- Кинематика вращения
- Инерция вращения
- Вращательная динамика
- Вращательная статика
- Угловой момент
- Энергия вращения
- Прокат
- Вращение в двух измерениях
- Сила Кориолиса
- Планетарное движение
- Геоцентризм
- Гелиоцентризм
- Вселенская гравитация
- Орбитальная механика I
- Гравитационная потенциальная энергия
- Орбитальная механика II
- Плотность вытянутых тел
- Периодическое движение
- Пружины
- Генератор простых гармоник
- Маятники
- Резонанс
- Эластичность
- Жидкости
- Плотность
- Давление
- Плавучесть
- Расход жидкости
- Вязкость
- Аэродинамическое сопротивление
- Режимы потока
- Кинематика
- Теплофизика
- Тепло и температура
- Температура
- Тепловое расширение
- Атомная природа материи
- Закон о газе
- Кинетико-молекулярная теория
- Фазы
- Калориметрия
- Явное тепло
- Скрытое тепло
- Химическая потенциальная энергия
- Теплопередача
- Проводимость
- Конвекция
- Радиация
- Термодинамика
- Тепло и работа
- Диаграммы давление-объем
- Двигатели
- Холодильники
- Энергия и энтропия
- Абсолютный ноль
- Тепло и температура
- Волны и оптика
- Волновые явления
- Природа волн
- Периодические волны
- Интерференция и суперпозиция
- Интерфейсы и барьеры
- Звук
- Природа звука
- Интенсивность
- Эффект Доплера (звук)
- Ударные волны
- Дифракция и интерференция (звук)
- Стоячие волны
- ударов
- Музыка и шум
- Физическая оптика
- Природа света
- Поляризация
- Эффект Доплера (светлый)
- Черенковское излучение
- Дифракция и интерференция (свет)
- Тонкопленочная интерференция
- Цвет
- Геометрическая оптика
- Отражение
- Преломление
- Зеркала сферические
- Сферические линзы
- Аберрация
- Волновые явления
- Электричество и магнетизм
- Электростатика
- Электрический заряд
- Закон Кулона
- Электрическое поле
- Электрический потенциал
- Закон Гаусса
- Проводники
- Электростатические приложения
- Конденсаторы
- Диэлектрики
- Аккумуляторы
- Электрический ток
- Электрический ток
- Электрическое сопротивление
- Электроэнергия
- Цепи постоянного тока
- Резисторы в цепях
- Батареи в цепях
- Конденсаторы в цепях
- Правила Кирхгофа
- Магнитостатика
- Магнетизм
- Электромагнетизм
- Закон Ампера
- Электромагнитная сила
- Магнитодинамика
- Электромагнитная индукция
- Закон Фарадея
- Закон Ленца
- Индуктивность
- Цепи переменного тока
- Переменный ток
- RC-цепи
- Цепи RL
- Цепи LC
- Электромагнитные волны
- Уравнения Максвелла
- Электромагнитные волны
- Электромагнитный спектр
- Электростатика
- Современная физика
- Теория относительности
- Пространство-время
- Масса-энергия
- Общая теория относительности
- Quanta
- Излучение черного тела
- Фотоэффект
- Рентгеновские снимки
- Антиматерия
- Волновая механика
- Волны материи
- Атомарные модели
- Полупроводники
- Конденсированное вещество
- Ядерная физика
- Изотопы
- Радиоактивный распад
- Период полураспада
- Энергия связи
- Деление
- Fusion
- Нуклеосинтез
- Ядерное оружие
- Радиобиология
- Физика элементарных частиц
- Квантовая электродинамика
- Квантовая хромодинамика
- Квантовая динамика аромата
- Стандартная модель
- Помимо стандартной модели
- Теория относительности
- Фундаменты
- шт.
- Международная система единиц
- Гауссова система единиц
- Англо-американская система единиц
- Единицы разного назначения
- Время
- Преобразование единиц
- Измерение
- Значащие цифры
- По порядку величины
- Графики
- Графическое представление данных
- Линейная регрессия
- Подгонка по кривой
- Исчисление
- Векторы
- Тригонометрия
- Сложение и вычитание векторов
- Векторное разрешение и компоненты
- Умножение вектора
- ссылку
- Специальные символы
- Часто используемые уравнения
- Физические константы
- Астрономические данные
- Периодическая таблица элементов
- Люди в физике
- шт.
- Назад дело
- Предисловие
- Об этой книге
- Связаться с автором
- гленнелерт.
- Предисловие
- Электрический ток — это скорость, с которой заряд протекает через поверхность.
- Определите количество периодов (t): Предполагается, что оборудование будет генерировать ежемесячный денежный поток и прослужит пять лет, что означает, что в расчет будет включено 60 денежных потоков и 60 периодов.{\ frac {1} {12}}) — 1 = 0,64 \%
Периодическая ставка = ((1 + 0,08) 121) -1 = 0,64%





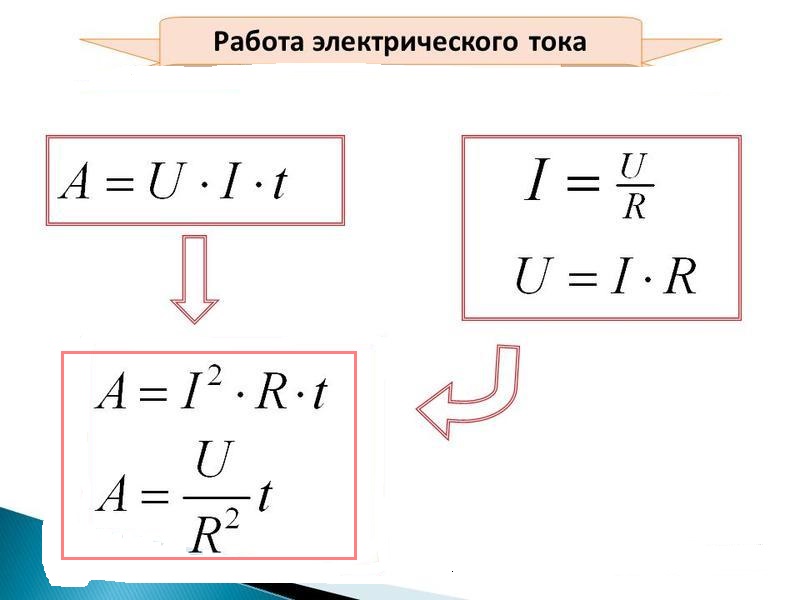 Заряд, который они получают в процессе, можно транспортировать вместе с устройствами. После расходования заряда возможна его регенерация за счет зарядки и обратимости химической реакции. Также к вторичным относятся возобновляемые элементы, которые механическим или химическим путем заряжаются и восстанавливают способность питать приборы. Они разработаны таким образом, что после определенного срока требуют замены определенных частей для продолжения реакции.
Заряд, который они получают в процессе, можно транспортировать вместе с устройствами. После расходования заряда возможна его регенерация за счет зарядки и обратимости химической реакции. Также к вторичным относятся возобновляемые элементы, которые механическим или химическим путем заряжаются и восстанавливают способность питать приборы. Они разработаны таким образом, что после определенного срока требуют замены определенных частей для продолжения реакции. 023
023