Угловая скорость — это… Что такое Угловая скорость?

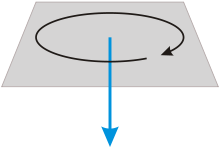Угловая скорость (синяя стрелка) в полторы единицы по часовой стрелке 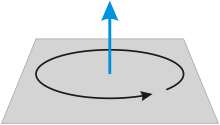Угловая скорость (синяя стрелка) в одну единицу против часовой стрелки

Углова́я ско́рость — векторная физическая величина, характеризующая скорость вращения тела. Вектор угловой скорости по величине равен углу поворота тела в единицу времени:

,

а направлен по оси вращения согласно правилу буравчика, то есть, в ту сторону, в которую ввинчивался бы буравчик с правой резьбой, если бы вращался в ту же сторону.

Единица измерения угловой скорости, принятая в системах СИ и СГС — радианы в секунду. (Примечание: радиан, как и любые единицы измерения угла, — физически безразмерен, поэтому физическая размерность угловой скорости — просто [1/секунда]). В технике также используются обороты в секунду, намного реже — градусы в секунду, грады в секунду. Пожалуй, чаще всего в технике используют обороты в минуту — это идёт с тех времён, когда частоту вращения тихоходных паровых машин определяли просто «вручную», подсчитывая число оборотов за единицу времени.

Вектор (мгновенной) скорости любой точки (абсолютно) твердого тела, вращающегося с угловой скоростью , определяется формулой:

где  — радиус-вектор к данной точке из начала координат, расположенного на оси вращения тела, а квадратными скобками обозначено векторное произведение. Линейную скорость (совпадающую с модулем вектора скорости) точки на определенном расстоянии (радиусе) от оси вращения можно считать так:

Если вместо радианов применять другие единицы углов, то в двух последних формулах появится множитель, не равный единице.

• В случае плоского вращения, то есть когда все векторы скоростей точек тела лежат (всегда) в одной плоскости («плоскости вращения»), угловая скорость тела всегда перпендикулярна этой плоскости, и по сути — если плоскость вращения заведомо известна — может быть заменена скаляром — проекцией на ось, ортогональную плоскости вращения. В этом случае кинематика вращения сильно упрощается, однако в общем случае угловая скорость может менять со временем направление в трехмерном пространстве, и такая упрощенная картина не работает.
• Производная угловой скорости по времени есть угловое ускорение.
• Движение с постоянным вектором угловой скорости называется равномерным вращательным движением (в этом случае угловое ускорение равно нулю).
• Угловая скорость (рассматриваемая как свободный вектор) одинакова во всех инерциальных системах отсчета, однако в разных инерциальных системах отсчета может различаться ось или центр вращения одного и того же конкретного тела в один и тот же момент времени (то есть будет различной «точка приложения» угловой скорости).
• В случае движения одной единственной точки в трехмерном пространстве можно написать выражение для угловой скорости этой точки относительно выбранного начала координат:

, где  — радиус-вектор точки (из начала координат),  — скорость этой точки.  — векторное произведение,  — скалярное произведение векторов. Однако эта формула не определяет угловую скорость однозначно (в случае единственной точки можно подобрать и другие векторы , подходящие по определению, по другому — произвольно — выбрав направление оси вращения), а для общего случая (когда тело включает более одной материальной точки) — эта формула не верна для угловой скорости всего тела (так как дает разные для каждой точки, а при вращении абсолютно твёрдого тела по определению угловая скорость его вращения — единственный вектор). При всём при этом, в двумерном случае (случае плоского вращения) эта формула вполне достаточна, однозначна и корректна, так как в этом частном случае направление оси вращения заведомо однозначно определено.

• При измерении угловой скорости в оборотах в секунду (об/с), модуль угловой скорости равномерного вращательного движения совпадает с частотой вращения f, измеренной в герцах (Гц), то есть в таких единицах . В случае использования обычной физической единицы угловой скорости — радианов в секунду — модуль угловой скорости связан с частотой вращения так: . Наконец, при использовании градусов в секунду связь с частотой вращения будет: .

Связь с конечным поворотом в пространстве

• Пусть поворот, изменяющийся во времени, задан величиной угла и ортом оси конечного поворота в пространстве . Тогда угловая скорость, соответствующая этому повороту, равна

.

.

• Если для описания поворота используется кватернион, выражаемый через угол и орт оси поворота как , то угловая скорость находится из выражения .

.

См. также

Литература

• Лурье А. И. Аналитическая механика\\ А. И. Лурье. — М.: ГИФМЛ, 1961. — С. 100-136

Центробежная сила — Википедия

Центробе́жная си́ла^[1] — составляющая фиктивных сил инерции, которую вводят при переходе из инерциальной системы отсчёта в соответствующим образом вращающуюся неинерциальную. Это позволяет в полученной неинерциальной системе отсчёта продолжать применять законы Ньютона для расчёта ускорения тел через баланс сил.

Зачастую это бывает удобно. Например, когда вращается целиком вся лаборатория, может быть более удобным рассматривать все движения относительно неё, введя лишь дополнительно силы инерции, в том числе центробежную, действующие на все материальные точки, чем учитывать постоянное изменение положения каждой точки относительно инерциальной системы отсчета.

Часто, особенно в технической литературе, во вращающуюся с телом неинерциальную систему отсчёта переходят неявно, и говорят о проявлениях закона инерции как о центробежной силе, действующей со стороны движущегося по круговой траектории

тела на вызывающие это вращение связи, и считают её по определению равной по модулю центростремительной силе и всегда направленной в противоположную ей сторону.

Однако в общем случае, когда мгновенный центр поворота тела по дуге окружности, которой аппроксимируется траектория в каждой её точке, может не совпадать с началом вектора силы, вызывающей движение, неверно называть действующую на связь силу силой центробежной. Ведь есть ещё составляющая силы связи, направленная по касательной к траектории, и эта составляющая будет изменять скорость движения тела по ней. Поэтому некоторые физики вообще избегают использовать термин «центробежная сила», как ненужный^[2]

.

Обычно понятие центробежной силы используется в рамках классической (Ньютоновской) механики, которой касается основная часть данной статьи (хотя обобщение этого понятия и может быть в некоторых случаях достаточно легко получено для релятивистской механики).

По определению, центробежной силой называется сила инерции (то есть в общем случае — часть полной силы инерции) в неинерциальной системе отсчета, не зависящая от скорости движения материальной точки в этой системе отсчета, а также не зависящая от ускорений (линейных или угловых) самой этой системы отсчета относительно инерциальной системы отсчета.

Для материальной точки центробежная сила выражается формулой:

F→=−m[ω→×[ω→×R→]]=m(ω2R→−(ω→⋅R→)ω→),{\displaystyle {\vec {F}}=-m\left[{\vec {\omega }}\times \left[{\vec {\omega }}\times {\vec {R}}\right]\right]=m\left(\omega ^{2}{\vec {R}}-\left({\vec {\omega }}\cdot {\vec {R}}\right){\vec {\omega }}\right),}

где:

F→{\displaystyle {\vec {F}}} — центробежная сила приложенная к телу,

 m{\displaystyle \ m} — масса тела,

ω→{\displaystyle {\vec {\omega }}} — угловая скорость вращения неинерциальной системы отсчёта относительно инерциальной (направление вектора угловой скорости определяется по правилу буравчика),

R→{\displaystyle {\vec {R}}} — радиус-вектор тела во вращающейся системе координат.

Эквивалентное выражение для центробежной силы можно записать как

F→=mω2R0→{\displaystyle {\vec {F}}=m\omega ^{2}{\vec {R_{0}}}}

если использовать обозначение R0→{\displaystyle {\vec {R_{0}}}} для вектора, перпендикулярного оси вращения и проведенного от неё к данной материальной точке.

Центробежная сила для тел конечных размеров может быть рассчитана (как это обычно делается и для любых других сил) суммированием центробежных сил, действующих на материальные точки, являющиеся элементами, на которые мы мысленно разбиваем конечное тело.

Вывод[править | править код]

Пусть тело совершает сложное движение: движется относительно неинерциальной системы отсчёта со скоростью v→n,{\displaystyle {\vec {v}}_{n},} а сама система движется поступательно с линейной скоростью v→0{\displaystyle {\vec {v}}_{0}} в инерциальной системе координат и одновременно вращается с угловой скоростью ω→.{\displaystyle {\vec {\omega }}.}

Тогда линейная скорость тела в инерциальной системе координат равна:

v→=v→0+[ω→×R→]+v→n,{\displaystyle {\vec {v}}={\vec {v}}_{0}+\left[{\vec {\omega }}\times {\vec {R}}\right]+{\vec {v}}_{n},}

где R→{\displaystyle {\vec {R}}} — радиус-вектор центра масс тела относительно неинерциальной системы отсчета. Продифференцируем данное уравнение:

ddtv→=ddtv→0+ddt[ω→×R→]+ddtv→n.{\displaystyle {\frac {d}{dt}}{\vec {v}}={\frac {d}{dt}}{\vec {v}}_{0}+{\frac {d}{dt}}\left[{\vec {\omega }}\times {\vec {R}}\right]+{\frac {d}{dt}}{\vec {v}}_{n}.}

Найдём значение каждого слагаемого в инерциальной системе координат:

ddtv→0=a→0,{\displaystyle {\frac {d}{dt}}{\vec {v}}_{0}={\vec {a}}_{0},}

ddtv→n=a→n+[ω→×v→n],{\displaystyle {\frac {d}{dt}}{\vec {v}}_{n}={\vec {a}}_{n}+\left[{\vec {\omega }}\times {\vec {v}}_{n}\right],}

ddt[ω→×R→]=[ε→×R→]+[ω→×ddtR→]=[ε→×R→]+[ω→×v→n]+[ω→×[ω→×R→]],{\displaystyle {\frac {d}{dt}}\left[{\vec {\omega }}\times {\vec {R}}\right]=\left[{\vec {\varepsilon }}\times {\vec {R}}\right]+\left[{\vec {\omega }}\times {\frac {d}{dt}}{\vec {R}}\right]=\left[{\vec {\varepsilon }}\times {\vec {R}}\right]+\left[{\vec {\omega }}\times {\vec {v}}_{n}\right]+\left[{\vec {\omega }}\times \left[{\vec {\omega }}\times {\vec {R}}\right]\right],} где a→n{\displaystyle {\vec {a}}_{n}} — линейное ускорение относительно системы, ε→{\displaystyle {\vec {\varepsilon }}} — угловое ускорение.

Таким образом, получаем:

ddtv→=a→=a→0+a→n+[ε→×R→]+2[ω→×v→n]+[ω→×[ω→×R→]].{\displaystyle {\frac {d}{dt}}{\vec {v}}={\vec {a}}={\vec {a}}_{0}+{\vec {a}}_{n}+\left[{\vec {\varepsilon }}\times {\vec {R}}\right]+2\left[{\vec {\omega }}\times {\vec {v}}_{n}\right]+\left[{\vec {\omega }}\times \left[{\vec {\omega }}\times {\vec {R}}\right]\right].}

Последнее слагаемое и будет центростремительным ускорением.

Раскрыв двойное векторное произведение и положив R→{\displaystyle {\vec {R}}} перпендикулярным оси вращения, получим:

a→c=ω→(ω→R→)−R→ω→2=−R→ω→2.{\displaystyle {\vec {a}}_{c}={\vec {\omega }}({\vec {\omega }}{\vec {R}})-{\vec {R}}{\vec {\omega }}^{2}=-{\vec {R}}{\vec {\omega }}^{2}.}

Элементарное рассмотрение и мотивировка[править | править код]

Вращение с точки зрения инерциальной системы отсчета[править | править код]

Рассмотрим спицу, вращающуюся вокруг перпендикулярной к ней вертикальной оси с угловой скоростью ω{\displaystyle \omega }. Вместе со спицей вращается надетый на неё шарик, соединённый с осью пружиной.

Согласно второму закону Ньютона шарик займёт положение равновесия на таком расстоянии R{\displaystyle R} от центра диска, на котором сила натяжения пружины Fpr{\displaystyle F_{\mathrm {pr} }} оказывается равной произведению массы шарика m{\displaystyle m} на его ускорение^[3]an=ω2R{\displaystyle a_{n}=\omega ^{2}R}:

Fpr=−mω2R=−mv2R{\displaystyle F_{\mathrm {pr} }=-m\omega ^{2}R=-m{\frac {v^{2}}{R}}}.^[4]

Связанная со спицей система отсчёта вращается по отношению к инерциальной системе. Относительно системы отсчёта, связанной со спицей, шарик покоится, хотя на него действует сила упругости пружины. Это не противоречит второму закону Ньютона, так как вращающаяся система отсчёта не является инерциальной и соотношение F→=ma→{\displaystyle {\vec {F}}=m{\vec {a}}} в ней не выполняется.

Вращение с точки зрения неинерциальной системы отсчёта. Сила инерции[править | править код]

Для практических целей, однако, удобнее считать, что второй закон Ньютона выполняется и с точки зрения вращающейся системы отсчёта, введя для этого формально силу инерции Fcf=−Fpr=mω2R{\displaystyle F_{\mathrm {cf} }=-F_{\mathrm {pr} }=m\omega ^{2}R}^[4], действующую на шарик вдоль радиуса от центра диска наряду с реальной силой Fpr{\displaystyle F_{\mathrm {pr} }}.

Силу инерции Fcf{\displaystyle F_{\mathrm {cf} }}, вводимую во вращающейся системе отсчёта, называют центробежной силой. Эта сила действует на тело во вращающейся системе отсчёта, независимо от того, покоится тело в этой системе или движется относительно неё со скоростью v{\displaystyle v}’.

Следует иметь в виду, что для правильного описания движения тел во вращающихся системах отсчёта, кроме центробежной силы следует также вводить силу Кориолиса.

В литературе встречается и совсем другое понимание термина «центробежная сила». Так иногда называют реальную силу, приложенную не к совершающему вращательное движение телу, а действующую со стороны тела на ограничивающие его движение связи. В рассмотренном выше примере так называли бы силу, действующую со стороны шарика на пружину. (См., например, ниже ссылку на БСЭ.)

Центростремительная и центробежная силы при движении тел по круговым траекториям с общей осью вращения

Применяемый не к связям, а, наоборот, к поворачиваемому телу, как объекту своего воздействия, термин «центробежная сила» (букв. сила, приложенная к поворачивающемуся или вращающемуся материальному телу, заставляющая его бежать от мгновенного центра поворота), есть эвфемизм, основанный на ложном толковании первого закона (принципа Ньютона)^[5] в форме:

Всякое тело сопротивляется изменению своего состояния покоя или равномерного прямолинейного движения под действием внешней силы

Или ещё^[6]:

Всякое тело стремится сохранять состояние покоя или равномерного прямолинейного движения до тех пор, пока не подействует внешняя сила.

Отголоском этой традиции и является представление о некоей силе, как о материальном факторе, реализующем это сопротивление или стремление. О существовании такой силы уместно было бы говорить, если бы, например, вопреки действующим силам, движущееся тело сохраняло бы свою скорость, но это не так^[7].

Первый закон Ньютона, нередко называемый принципом и потому допускающим различия в словесной форме его выражения, сводится к утверждению, что природа вещей такова, что скорость движения материальной точки, как по величине, так и по направлению в некоторой системе отсчёта (сам Ньютон связывал её с эфиром, заполняющим всё пространство)^[5], остаётся постоянной, но начинает изменяться тотчас, как возникает на то причина, называемая силой.

Рассматриваемое тело с массой (точнее — инертной массой) m{\displaystyle m} приобретает отличающееся от нуля ускорение a{\displaystyle a} в тот же момент t=0{\displaystyle t=0}, когда начинает действовать на него сила F{\displaystyle F} (Второй закон Ньютона:F→=ma→{\displaystyle {\vec {F}}=m{\vec {a}}}). Однако для достижения отличающейся от нуля скорости v{\displaystyle v} требуется некоторое время t{\displaystyle t} в соответствии с определением импульса силы: t=mv/F{\displaystyle t=mv/F}. Или, иначе, скорость тела не изменяется сама по себе, без причины, но она начинает изменяться тотчас, как на него начинает действовать сила^[8].

Использование термина «центробежная сила» правомочно тогда, когда точкой её приложения является не испытывающее поворот тело, а ограничивающее его движение связи. В этом смысле центробежная сила представляет собой один из членов в формулировке третьего закона Ньютона, антагониста центростремительной силе, вызывающей поворот рассматриваемого тела и к нему приложенной. Обе эти силы равны по величине и противоположны по направлению, но приложены к разным телам и потому не компенсируют друг друга, а вызывают реально ощутимый эффект — изменение направления движения тела (материальной точки).

Оставаясь в инерциальной системе отсчёта, рассмотрим два небесных тела, например, компонента двойной звезды с массами одного порядка величины M1{\displaystyle {M_{1}}} и M2{\displaystyle {M_{2}}}, находящихся на расстоянии R{\displaystyle R} друг от друга. В принятой модели эти звёзды рассматриваются как материальные точки и R{\displaystyle R} есть расстояние между их центрами масс. В роли связи между этими телами выступает сила Всемирного тяготения FG:GM1M2/R2{\displaystyle {F_{G}}:{GM_{1}M_{2}/R^{2}}}, где G{\displaystyle G}- гравитационная постоянная. Это — единственная здесь действующая сила, она вызывает ускоренное движение тел навстречу друг другу.

Однако, в том случае, если каждое из этих тел совершает вращение вокруг общего центра масс с линейными скоростями v1{\displaystyle {v_{1}}} = ω1{\displaystyle {\omega }_{1}} R1{\displaystyle {R_{1}}} и v2{\displaystyle {v_{2}}} = ω2{\displaystyle {\omega _{2}}} R2{\displaystyle {R_{2}}}, то подобная динамическая система будет неограниченное время сохранять свою конфигурацию, если угловые скорости вращения этих тел будут равны: ω1{\displaystyle {\omega _{1}}} = ω2{\displaystyle {\omega _{2}}} = ω{\displaystyle \omega }, а расстояния от центра вращения (центра масс) будут соотноситься, как: M1/M2{\displaystyle {M_{1}/M_{2}}} = R2/R1{\displaystyle {R_{2}/R_{1}}}, причём R2+R1=R{\displaystyle {R_{2}}+{R_{1}}=R}, что непосредственно следует из равенства действующих сил: F1=M1a1{\displaystyle {F_{1}}={M_{1}}{a_{1}}} и F2=M2a2{\displaystyle {F_{2}}={M_{2}}{a_{2}}}, где ускорения равняются соответственно: a1{\displaystyle {a_{1}}}= ω2R1{\displaystyle {\omega ^{2}}{R_{1}}} и a2=ω2R2{\displaystyle {a_{2}}={\omega ^{2}}{R_{2}}}^[9].

Центростремительные силы, вызывающие движение тел по круговым траекториям равны (по модулю): F1{\displaystyle {F_{1}}} =F2{\displaystyle {F_{2}}} =FG{\displaystyle ={F_{G}}}. При этом первая из них является центростремительной, а вторая — центробежной и наоборот: каждая из сил в соответствии с Третьим законом является и той, и другой.

Поэтому, строго говоря, использование каждого из обсуждаемых терминов излишне, поскольку они не обозначают никаких новых сил, являясь синонимами единственной силы — силы тяготения. То же самое справедливо и в отношении действия любой из упомянутых выше связей.

Однако, по мере изменения соотношения между рассматриваемыми массами, то есть всё более значительного расхождения в движении обладающих этими массами тел, разница в результатах действия каждой из рассматриваемых тел для наблюдателя становится всё более значительной.

В ряде случаев наблюдатель отождествляет себя с одним из принимающих участие тел, и потому оно становится для него неподвижным. В этом случае при столь большом нарушении симметрии в отношении к наблюдаемой картине, одна из этих сил оказывается неинтересной, поскольку практически не вызывает движения.

1. ↑ Вне контекста физики/механики/математики, например, в философии, публицистике или художественной литературе, а также иногда и в разговорной речи, слова центробежная сила могут нередко употребляться просто как обозначение некоего влияния, направленного прочь от некоторого «центра»; в таком употреблении это может быть никак не связано не только с каким-либо вращением, но и с понятием силы, как оно употребляется в физике.
2. ↑ С. Э. Хайкин. Силы инерции и невесомость. М.,1967 г. Издательство «Наука». Главная редакция физико-математической литературы.
3. ↑ Воспользуемся формулой центростремительного ускорения.
4. ↑ ^{1 2} Физическая энциклопедия, т.4 — М.:Большая Российская Энциклопедия стр.494 и стр.495
5. ↑ ^{1 2} Ньютон И. Математические начала натуральной философии. Пер. и прим. А. Н. Крылова. М.: Наука, 1989
6. ↑ Ключевым в этой формулировке является утверждение о наличии у предметов материального мира неких волевых качеств, что было в начале формирования научных представлений об окружающем мире весьма распространённым способом обобщения результатов наблюдения за явлениями природы и выяснения свойственных ей общих закономерностей . Примером такого анималистического представления о природе являлся бытовавший в натурфилософии принцип: «Природа боится пустоты», от которого пришлось отказаться после эксперимента Торричелли (Торричеллиева пустота)
7. ↑ В связи с этим Максвелл заметил, что, с таким же успехом можно было бы сказать, что кофе сопротивляется тому, чтобы стать сладким, апеллируя к тому, что он становится сладким не сам по себе, а лишь после того, что в него положен сахар.
8. ↑ С. Э. Хайкин. Силы инерции и невесомость. М.: «Наука», 1967 г.
9. ↑ При этом в каждый малый момент времени каждое из тел будет приближаться к центру на такое расстояние, какое равно разности расстояний между его траекторией и касательной в точке наблюдения. Иными словами, тела падают друг на друга, но всегда промахиваются.

Равноускоренное движение — Википедия

Равноускоренное движение в поле тяжести Земли. На рисунке видно, что перемещение складывается из прямолинейного равномерного движения и свободного падения

Равноуско́ренное движе́ние — движение тела, при котором его ускорение a→{\displaystyle {\vec {a}}} постоянно по модулю и направлению^[1].

Скорость при этом определяется формулой

v→(t)=v→0+a→t{\displaystyle {\vec {v}}(t)={\vec {v}}_{0}+{\vec {a}}t},

где v→0{\displaystyle {\vec {v}}_{0}} — начальная скорость тела, t{\displaystyle t} — время. Траектория имеет вид участка параболы или прямой.

Примером такого движения является полёт камня, брошенного под углом α{\displaystyle \alpha } к горизонту в однородном поле силы тяжести: камень летит с постоянным ускорением a→=g→{\displaystyle {\vec {a}}={\vec {g}}}, направленным вертикально вниз.

Частным случаем равноускоренного движения является равнозамедленное, когда векторы v→{\displaystyle {\vec {v}}} и a→{\displaystyle {\vec {a}}} противонаправлены, а модуль скорости равномерно уменьшается со временем (в примере с камнем реализуется для α=900{\displaystyle \alpha =90^{0}} при подъёме).

Равноускоренное движение происходит в плоскости, содержащей векторы ускорения a→{\displaystyle {\vec {a}}} и начальной скорости v→0{\displaystyle {\vec {v}}_{0}}. С учётом того, что v→=dr→/dt{\displaystyle {\vec {v}}={\rm {d}}{\vec {r}}/{\rm {d}}t} (здесь r→{\displaystyle {\vec {r}}} — радиус-вектор), траектория описывается выражением

r→(t)=r→0+v→0t+a→t22{\displaystyle {\vec {r}}(t)={\vec {r}}_{0}+{\vec {v}}_{0}t+{\frac {{\vec {a}}t^{2}}{2}}}.

На заданном интервале времени она представляет собой участок параболы, который при параллельности (то есть со- или противо- направленности) векторов a→{\displaystyle {\vec {a}}} и v→0{\displaystyle {\vec {v}}_{0}} превращается в отрезок прямой.

Для каждой из координат, скажем y{\displaystyle y}, могут быть записаны аналогичные по структуре выражения:

y(t)=y0+v0yt+ayt22{\displaystyle y(t)=y_{0}+v_{0y}t+{\frac {a_{y}t^{2}}{2}}},

где ay{\displaystyle a_{y}} — составляющая ускорения вдоль оси y{\displaystyle y}, а r→0=x0i→+y0j→+z0k→{\displaystyle {\vec {r}}_{0}=x_{0}{\vec {i}}+y_{0}{\vec {j}}+z_{0}{\vec {k}}} — радиус-вектор материальной точки в момент t=0{\displaystyle t=0} (i→{\displaystyle {\vec {i}}}, j→{\displaystyle {\vec {j}}}, k→{\displaystyle {\vec {k}}} — орты).

В примере с камнем x0=y0=z0=0{\displaystyle x_{0}=y_{0}=z_{0}=0}, компоненты ускорения ax=az=0{\displaystyle a_{x}=a_{z}=0}, ay=−g{\displaystyle a_{y}=-g}, начальной скорости vx0=v0cos⁡α{\displaystyle v_{x0}=v_{0}\cos \alpha }, vy0=v0sin⁡α{\displaystyle v_{y0}=v_{0}\sin \alpha }, vz0=0{\displaystyle v_{z0}=0}, при этом x(t)=v0xt{\displaystyle x(t)=v_{0x}t}, а значит, y=tg⁡α⋅x−g/2v02cos2⁡α⋅x2{\displaystyle y=\operatorname {tg} \alpha \cdot x-g/2v_{0}^{2}\cos ^{2}\alpha \cdot x^{2}}.

В случае равноускоренного движения любая из компонент скорости, например vx{\displaystyle v_{x}}, зависит от времени линейно:

vx=v0x+axt{\displaystyle v_{x}=v_{0x}+a_{x}t}.

При этом имеет место следующая связь между перемещением (Δx=x−x0{\displaystyle \Delta x=x-x_{0}}) вдоль координаты x{\displaystyle x} и скоростью вдоль той же координаты:

Δx=vx2−v0x22ax{\displaystyle \Delta x={\frac {v_{x}^{2}-v_{0x}^{2}}{2a_{x}}}}.

Отсюда можно получить выражение для x{\displaystyle x}-составляющей конечной скорости тела при известных x{\displaystyle x}-составляющих начальной скорости и ускорения:

vx=±v0x2+2axΔx{\displaystyle v_{x}=\pm {\sqrt {v_{0x}^{2}+2a_{x}\Delta x}}}.

Если ax=0{\displaystyle a_{x}=0}, то vx=vox{\displaystyle v_{x}=v_{ox}}, а Δx=v0xt{\displaystyle \Delta x=v_{0x}t}.

Выражения для смещений Δy{\displaystyle \Delta y}, Δz{\displaystyle \Delta z} и компонент скорости вдоль координат y{\displaystyle y} и z{\displaystyle z} принимают точно такой же вид, как для Δx{\displaystyle \Delta x} и vx{\displaystyle v_{x}}, но символ x{\displaystyle x} всюду заменяется на y{\displaystyle y} или z{\displaystyle z}.

Суммарно, по теореме Пифагора, перемещение составит

|Δr→|=(Δx)2+(Δy)2+(Δz)2{\displaystyle |\Delta {\vec {r}}|={\sqrt {(\Delta x)^{2}+(\Delta y)^{2}+(\Delta z)^{2}}}},

а модуль конечной скорости находится как

|v→|=vx2+vy2+vz2{\displaystyle |{\vec {v}}|={\sqrt {v_{x}^{2}+v_{y}^{2}+v_{z}^{2}}}}.

Равноускоренное движение не может происходить неограниченно долго: это означало бы, что, начиная с какого-то момента времени t{\displaystyle t}, модуль скорости тела |v→|{\displaystyle |{\vec {v}}|} превысит величину скорости света в вакууме c{\displaystyle c}, что исключается теорией относительности.

Равноускоренное движение реализуется при действии на тело (материальную точку) постоянной силы F→{\displaystyle {\vec {F}}}, обычно в однородном гравитационном или электростатическом поле, если величина скорости тела значительно меньше, чем скорость света c{\displaystyle c}. Тогда, по второму закону Ньютона, ускорение составит

a→=F→m,{\displaystyle {\vec {a}}={\frac {\vec {F}}{m}},}

где через m{\displaystyle m} обозначена масса тела. В примере с камнем роль F→{\displaystyle {\vec {F}}} играет сила тяжести.

Если же скорость тела сопоставима со скоростью света, то закон Ньютона в выписанном виде неприменим. При этом, в случае действия постоянной силы, происходит так называемое релятивистски равноускоренное движение, при котором постоянно только собственное ускорение, а ускорение в фиксированной ИСО приближается к нулю со временем по мере приближения величины скорости к её пределу c{\displaystyle c}.

Теорема о кинетической энергии точки[править | править код]

Формула перемещения при равноускоренном движении используется при доказательстве теоремы о кинетической энергии. Для этого необходимо перенести ускорение в левую часть и домножить обе части на массу тела:

maxΔx=mvx22−mv0x22{\displaystyle ma_{x}\Delta x={\frac {mv_{x}^{2}}{2}}-{\frac {mv_{0x}^{2}}{2}}}.

Записав аналогичные соотношения для координат y{\displaystyle y} и z{\displaystyle z} и просуммировав все три равенства, получим соотношение:

F→⋅Δr→=mv22−mv022{\displaystyle {\vec {F}}\cdot \Delta {\vec {r}}={\frac {mv^{2}}{2}}-{\frac {mv_{0}^{2}}{2}}}.

Слева стоит работа постоянной равнодействующей силы F→{\displaystyle {\vec {F}}}, а справа — разность кинетических энергий в конечный и начальный моменты движения. Полученная формула представляет собой математическое выражение теоремы о кинетической энергии точки для случая равноускоренного движения^[2].

Криволинейное равноускоренное движение[править | править код]

Криволинейным равноускоренным (равнопеременным) называется движение по любой кривой, при котором составляющая ускорения, параллельная скорости, является постоянной. Такое движение не подпадает под определение равноускоренного, но в математическом плане может быть рассмотрено аналогично.

В этом случае вводится обобщённая координата S{\displaystyle S}, часто называемая путём. Эта координата соответствует длине пройденной траектории (длине дуги кривой). Таким образом, формула приобретает вид:

ΔS=v2−v022aτ{\displaystyle \Delta S={\frac {v^{2}-v_{0}^{2}}{2a_{\tau }}}},

где aτ{\displaystyle a_{\tau }} — тангенциальное ускорение, которое «отвечает» за изменение модуля скорости тела. Для скорости получаем:

v=±v02+2aτΔS{\displaystyle v=\pm {\sqrt {v_{0}^{2}+2a_{\tau }\Delta S}}}.

При aτ=0{\displaystyle a_{\tau }=0} имеем движение с постоянной по модулю скоростью.

Равноускоренное движение

Передаточное отношение — Википедия

Передаточное отношение (i{\displaystyle i}) — одна из важных характеристик механической передачи вращательного движения. Передаточное отношение показывает, во сколько раз вырос момент силы на ведомом валу по сравнению с ведущим.

i=i12=d2d1=z2z1=M2M1=ω1ω2=n1n2{\displaystyle i=i_{12}={\frac {d_{2}}{d_{1}}}={\frac {z_{2}}{z_{1}}}={\frac {M_{2}}{M_{1}}}={\frac {\omega _{1}}{\omega _{2}}}={\frac {n_{1}}{n_{2}}}}

где: i12{\displaystyle i_{12}} — передаточное отношение от звена 1 к звену 2 (звено 1 — ведущее, звено 2 — ведомое)

d1,d2{\displaystyle d_{1},d_{2}} — диаметры звеньев

z1,z2{\displaystyle z_{1},z_{2}} — количество зубьев звеньев (если таковые имеются)

M1,M2{\displaystyle M_{1},M_{2}} — крутящие моменты звеньев

ω1,ω2{\displaystyle \omega _{1},\omega _{2}} — угловые скорости звеньев

n1,n2{\displaystyle n_{1},n_{2}} — частоты вращения звеньев

Таким образом, если передаточное отношение больше единицы, то передача увеличивает момент силы на ведомом валу, но понижает угловую скорость и частоту.

Поэтому редуктор с передаточным отношением больше единицы называется понижающим.

Размышляя о моменте силы, становится понятным следующее соотношение для многоступенчатых передач:

i=i14=i12⋅i23⋅i34=M2M1⋅M3M2⋅M4M3=M4M1{\displaystyle i=i_{14}=i_{12}\cdot i_{23}\cdot i_{34}={\frac {M_{2}}{M_{1}}}\cdot {\frac {M_{3}}{M_{2}}}\cdot {\frac {M_{4}}{M_{3}}}={\frac {M_{4}}{M_{1}}}}

Однако следует учесть, что данное выражение истинно только в случае отсутствия потерь в зацеплении и других подвижных частях механизма на трение, упругие деформации и другие факторы, что в принципе является невозможным. Поэтому при конструкторских расчетах силовых и кинематических параметров машин необходимо учитывать коэффициент полезного действия как непосредственно самой передачи, так и пар подшипников, а если они есть, то и соединительных муфт. С учетом этого общая формула для определения момента на выходном валу имеет вид [4, с. 12]:

ii,i+1⋅Mi⋅η=Mi+1,{\displaystyle i_{i,i+1}\cdot M_{i}\cdot \eta =M_{i+1},}

где ii,i+1{\displaystyle i_{i,i+1}} — передаточное отношение механизма;

Mi,Mi+1{\displaystyle M_{i},M_{i+1}} — крутящие моменты на входном и выходном валах механизма соответственно;

η{\displaystyle \eta } — КПД механизма.

Следующий абзац возник из-за некоторого разногласия в рядах студентов по поводу ведущего и ведомого звена.

Из курсового проектирования деталей машин [5, с. 118]: «Как правило ременная и цепная передачи служат для понижения частоты вращения. Специальные передачи, повышающие угловую скорость, здесь не рассматриваются, так как в типовых заданиях на курсовое проектирование они не встречаются.»

В этой же книге [4, с. 7] дана формула i=nnomnp{\displaystyle i={\frac {n_{nom}}{n_{p}}}}. Здесь в качестве номинальной nnom{\displaystyle n_{nom}} частоты принимается частота работы электропривода (то есть ведущего звена), а в качестве расчетной np{\displaystyle n_{p}} — частота ведомого звена. Также даны средние значения для различного рода передач: зубчатых 2-6, червячных 8-80, цепных 3-6, ременных 2-4. То есть скорость ведущего звена в i{\displaystyle i} раз больше чем скорость ведомого звена.

Проверка: редуктор, передаточное число которого больше единицы (2>1), скорость понижается (n2<n1), i=ω1ω2=n1n2=2 m/c1 m/c=2{\displaystyle i={\frac {\omega _{1}}{\omega _{2}}}={\frac {n_{1}}{n_{2}}}={\frac {2~m/c}{1~m/c}}=2}. (Момент силы увеличивается)

В случае зубчатых шестерён передаточное отношение всегда является рациональным числом. Характеристика передаточное отношение применима как к механической передаче с одной ступенью (одной кинематической парой), так и к механическим передачам со множеством ступеней. Во втором случае передаточное отношение всей механической передачи будет равно произведению передаточных отношений всех ступеней.

Формально механизмы с передаточным отношением больше единицы называются редукторами, с передаточным отношением меньше единицы — мультипликаторами. Фактически и тот, и другой механизм в обиходе можно называть редуктором, добавляя лишь определение «понижающий» в случае с (i>1{\displaystyle i>1}) и «повышающий» с (i<1{\displaystyle i<1}).

1. Под ред. Скороходова Е. А. Общетехнический справочник. — М.: Машиностроение, 1982. — С. 416.
2. Гулиа Н. В., Клоков В. Г., Юрков С. А. Детали машин. — М.: Издательский центр «Академия», 2004. — С. 416. — ISBN 5-7695-1384-5.
3. Анурьев В. И. Справочник конструктора-машиностроителя: В 3 т. / Под ред. И. Н. Жестковой. — 8-е изд., перераб. и доп.. — М.: Машиностроение, 2001. — ISBN 5-217-02962-5.
4. Курмаз Л. В. Детали машин. Проектирование// Л. В. Курмаз; А. Т. Скойбеда — 2-е изд., испр. и доп. — Мн.: УП «Технопринт», — 2002. — 296с.,ил.
5. Чернавский С. А., Боков К. Н. Курсовое проектирование деталей машин. — 1988.

Сложное движение — Википедия

В физике, при рассмотрении нескольких систем отсчёта (СО), возникает понятие сложного движения — когда материальная точка движется относительно какой-либо системы отсчёта, а та, в свою очередь, движется относительно другой системы отсчёта. При этом возникает вопрос о связи движений точки в этих двух системах отсчета (далее СО).

Материальная точка в двух СО^[1].

Обычно принимают одну из СО за базовую («абсолютную», «лабораторную», «неподвижную», «СО неподвижного наблюдателя», «первую», «нештрихованную» и т. п.), другую называют «подвижной» («СО подвижного наблюдателя», «штрихованной», «второй» и т. п.) и вводят следующие термины:

Переносная скорость V→e(t){\displaystyle {\vec {V}}_{e}(t)} — это скорость в базовой системе отсчёта произвольной точки, зафиксированной относительно подвижной СО, обусловленная движением этой подвижной СО относительно базовой. Например, это скорость той точки подвижной системы отсчёта, в которой в данный момент времени находится материальная точка. Переносная скорость V→e(t){\displaystyle {\vec {V}}_{e}(t)} равна V→R(t)=dR→dt{\displaystyle {\vec {V}}_{R}(t)={\frac {d{\vec {R}}}{dt}}} только в тех случаях, когда подвижная СО движется поступательно.

Вводятся также понятия соответствующих ускорений a→r(t){\displaystyle {\vec {a}}_{r}(t)}, a→r′(t){\displaystyle {\vec {a}}_{r’}(t)}, a→R(t){\displaystyle {\vec {a}}_{R}(t)}, ε→R(t).{\displaystyle {\vec {\varepsilon }}_{R}(t).} и a→e(t){\displaystyle {\vec {a}}_{e}(t)}.

С точки зрения только чистой кинематики (задачи пересчёта кинематических величин — координат, скоростей, ускорений — от одной системы отсчета к другой) не имеет значения, является ли какая-то из систем отсчета инерциальной или нет; это никак не сказывается на формулах преобразования кинематических величин при переходе от одной системы отсчета к другой (то есть эти формулы можно применять и для перехода от одной произвольной неинерциальной вращающейся системы отсчета к другой).

Однако для динамики инерциальные системы отсчета имеют особое значение: в них механические явления описываются наиболее простым образом и, соответственно, уравнения динамики формулируются изначально именно для инерциальных систем отсчета^[3]. Поэтому особенно важны случаи перехода от инерциальной системы отсчета к другой инерциальной, а также от инерциальной к неинерциальной и обратно.

В дальнейшем изложении по умолчанию базовая СО предполагается инерциальной, а на подвижную никаких ограничений не накладывается.

Классическая механика опирается на представления о Евклидовом пространстве и принцип относительности Галилея, что позволяет использовать преобразования Галилея.

Кинематика сложного движения точки[править | править код]

Траектории одного и того же движения в разных системах отсчёта.
Вверху (в инерциальной системе): дырявое ведро с краской двигают на колосниках по прямой над поворачивающейся театральной сценой. Траектория прямая.
Внизу (в неинерциальной системе): то же самое, но при взгляде с точки зрения наблюдателя, стоящего на вращающейся сцене. Траектория кривая, и соответствует следу от краски на сцене.

Кинематика движения, основанная на анализе траектории движущегося тела, в общем случае не даёт полной информации для классификации этих движений. Так, движение по прямой в неинерциальной системе отсчёта может быть криволинейным (и, следовательно, обусловленным действующими на тело силами) в инерциальной СО. И, наоборот, прямолинейное в инерциальной СО может быть криволинейным в неинерциальной, и, следовательно, провоцировать представление о якобы действующих на тело силах.

Путь[править | править код]

Абсолютное движение и его путь представлены изменением радиуса вектора r→{\displaystyle {\vec {r}}}, рассматриваемого в виде суммы векторов переносного и относительного движений:

r→=R→+r′→.{\displaystyle {\vec {r}}={\vec {R}}+{\vec {r’}}.}

Скорость[править | править код]

Основные задачи кинематики сложного движения заключаются в установлении зависимостей между кинематическими характеристиками абсолютного и относительного движений точки (или тела) и характеристиками движения подвижной системы отсчета, то есть переносного движения. Связь скоростей определяется дифференцированием связи для положений. Для точки эти зависимости являются следующими: абсолютная скорость точки равна геометрической сумме относительной и переносной скоростей, то есть:

V→r=V→r′+V→e.{\displaystyle {\vec {V}}_{r}={\vec {V}}_{r’}+{\vec {V}}_{e}.}

Данное равенство представляет собой содержание теоремы о сложении скоростей^[4].

Следует отметить, что вместе с приведённым равенством всегда справедливо и соотношение

dr→dt=d(R→+r′→)dt=dR→dt+dr′→dt.{\displaystyle {\frac {d{\vec {r}}}{dt}}={\frac {d({\vec {R}}+{\vec {r’}})}{dt}}={\frac {d{\vec {R}}}{dt}}+{\frac {d{\vec {r’}}}{dt}}.}

Однако в общем случае в этом соотношении dR→dt{\displaystyle {\frac {d{\vec {R}}}{dt}}} не является переносной скоростью, а dr′→dt{\displaystyle {\frac {d{\vec {r’}}}{dt}}} не относительная скорость. Таковыми они становятся только в тех случаях, когда подвижная СО движется поступательно, то есть, не вращаясь^[5].

Ускорение[править | править код]

Связь ускорений можно найти путём дифференцирования связи для скоростей, не забывая, что относительное перемещение также может зависеть от времени.

Абсолютное ускорение a→r(t){\displaystyle {\vec {a}}_{r}(t)} будет равно сумме:

a→r  =  d2r→dt2  =  d2R→dt2  +  dω→dt×r′→  +  ω→×[ω→×r′→]  +  2 ω→×V→r′  +  a→r′.{\displaystyle {\vec {a}}_{r}\ \ =\ \ {\frac {d^{2}{\vec {r}}}{dt^{2}}}\ \ =\ \ {\frac {d^{2}{\vec {R}}}{dt^{2}}}\ \ +\ \ {\frac {d{\vec {\omega }}}{dt}}\times {\vec {r’}}\ \ +\ \ {\vec {\omega }}\times \left[{\vec {\omega }}\times {\vec {r’}}\right]\ \ +\ \ {2\ {\vec {\omega }}\times {\vec {V}}_{r’}}\ \ +\ \ {\vec {a}}_{r’}.}

Здесь:

• сумма первых трех членов называется переносным ускорением a→e{\displaystyle {\vec {a}}_{e}}.

• первый член — переносное поступательное ускорение второй системы относительно первой,

• второй член — переносное вращательное ускорение второй системы, возникающее из-за неравномерности её вращения.

• третий член представляет собой вектор, противоположно направленный осестремительной составляющей r′→n{\displaystyle {\vec {r’}}_{n}} вектора r→{\displaystyle {\vec {r}}}, перпендикулярной ω→{\displaystyle {\vec {\omega }}} (что можно получить, рассматривая это двойное векторное произведение — оно равно −r′→nω2{\displaystyle -{\vec {r’}}_{n}\omega ^{2}}) и потому представляет собой осестремительное ускорение. Оно совпадает с нормальным переносным ускорением той точки вращающейся системы, с которой в данный момент совпадает движущаяся точка (не путать с нормальным ускорением движущейся точки, направленным по нормали к её траектории).

• четвертый член есть Кориолисово ускорение, порождаемое взаимным влиянием переносного вращательного движения второй системы отсчета и относительного поступательного движения точки относительно её.
• последний член a→r′=dV→r′dt{\displaystyle {\vec {a}}_{r’}={\frac {d{\vec {V}}_{r’}}{dt}}} — ускорение точки относительно подвижной системы отсчета.

Кинематика сложного движения тела[править | править код]

Согласно Первому закону Ньютона, все виды движений при их рассмотрении в инерциальной системе координат могут быть отнесены к одной из двух категорий. А именно — к категории прямолинейных и равномерных (то есть имеющих постоянную скорость) движений, возможных исключительно при отсутствии нескомпенсированных сил, действующих на тело. Нередко встречающееся, даже в справочной литературе^[6] , отнесение этого вида движений к категории поступательных движений противоречит определению понятия «Поступательное движение», поскольку движение, имеющее классификационный признак поступательного, в инерциальной системе может происходить по любой траектории, но не обязательно исключительно по прямой.

К другой категории относятся все остальные виды движений.

Для твёрдого тела, когда все составные (то есть относительные и переносные) движения являются поступательными, абсолютное движение также является поступательным со скоростью, равной геометрической сумме скоростей составных движений. Если составные движения тела являются вращательными вокруг осей, пересекающихся в одной точке (как, например, у гироскопа), то результирующее движение также является вращательным вокруг этой точки с мгновенной угловой скоростью, равной геометрической сумме угловых скоростей составных движений. В общем случае движение будет слагаться из серии мгновенных винтовых движений.

Рассчитать взаимосвязь скоростей разных точек твёрдого тела в разных системах отсчёта можно с помощью комбинирования формулы сложения скоростей и формулы Эйлера для связи скоростей точек твёрдого тела. Связь ускорений находится простым дифференцированием полученного векторного равенства по времени.

Динамика сложного движения точки[править | править код]

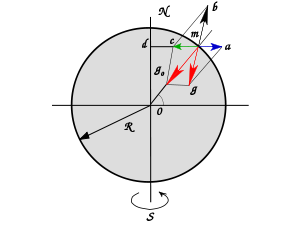Силы, действующие на тело, находящееся на поверхности Земли. Чертёж относится к рассмотрению сил, действующих на тело, в двух различных системах отсчёта. Первая — инерциальная система отсчёта, вторая — неинерциальная система отсчёта, связанная с вращающейся Землёй. В первом случае на тело действуют сила гравитационного притяжения и реакция опоры. Их сумма (зелёный вектор) играет роль центростремительной силы и заставляет тело вращаться вместе с Землёй. Во втором случае действует дополнительная сила — переносная сила инерции (синий вектор), в результате действие всех сил уравновешивается, и тело в этой системе отсчёта ускорения не испытывает.

Концепция Ньютона о пропорциональности получаемого телом ускорения под действием любой силы в инерциальных системах отсчёта выполняется всегда. Под силой при этом понимается мера механического действия на данное материальное тело других тел^[7], обязательно являющаяся результатом взаимодействия тел^[8]. Альтернатив этой концепции в классическом разделе материалистической физики нет.

Однако при рассмотрении движений в неинерциальной системе отсчёта, наряду с силами, происхождение которых можно проследить, как результат взаимодействия с другими телами и полями, возможно ввести в рассмотрение и физические величины другой природы — силы инерции. Их введение и использование позволяет придать уравнению движения тел в неинерциальных системах отсчёта форму, совпадающую с формой уравнения второго закона Ньютона в инерциальных системах отсчёта.

Для того, чтобы различать силы двух упомянутых видов, термин силы инерции часто сопровождают дополнительным определением, таким, как, например фиктивные^[9] или кажущиеся^[10].

Привлечение представлений о силах инерции для описания движения тел в неинерциальных системах отсчёта может быть полезным и эффективным. Например, действием силы инерции в системе отсчёта, связанной с вращающейся вокруг своей оси Землёй, может быть объяснён эффект замедления хода маятниковых часов, наблюдающийся по мере их приближения к экватору. Другой пример — действие силы Кориолиса на воду в реках, текущих в меридиональном направлении. Следствием такого действия является неодинаковость размыва правых и левых (по направлению течения) берегов рек. Ещё более значительным является действие силы Кориолиса на морские течения и воздушные потоки в атмосфере^[9].

Релятивистская механика опирается на неевклидово пространство Минковского и принцип относительности Эйнштейна, что вынуждает прибегать к более сложному преобразованию Лоренца. При скоростях, существенно меньших скорости света, релятивистская механика может быть сведена к классической.

Скорость[править | править код]

При скоростях, близких к скорости света, преобразования Галилея не являются точно инвариантными и классическая формула сложения скоростей перестаёт выполняться. Вместо этого, инвариантными являются преобразования Лоренца, а связь скоростей в двух инерциальных СО получается следующей:

vx′=vx−u1−(vxu)/c2,vy′=vy1−u2c21−(vxu)/c2,vz′=vz1−u2c21−(vxu)/c2,{\displaystyle v_{x}’={\frac {v_{x}-u}{1-(v_{x}u)/c^{2}}},v_{y}’={\frac {v_{y}{\sqrt {1-{\frac {u^{2}}{c^{2}}}}}}{1-(v_{x}u)/c^{2}}},v_{z}’={\frac {v_{z}{\sqrt {1-{\frac {u^{2}}{c^{2}}}}}}{1-(v_{x}u)/c^{2}}},}

в предположении, что скорость u→{\displaystyle {\vec {u}}} направлена вдоль оси х системы S. Легко убедиться, что в пределе нерелятивистских скоростей преобразования Лоренца сводятся к преобразованиям Галилея.

Однако вводится величина — быстрота — которая аддитивна при переходе от одной СО к другой.

Неинерциальные СО[править | править код]

Связь скоростей и ускорений в системах отсчёта, движущихся друг относительно друга ускоренно, является значительно более сложной и определяется локальными свойствами пространства в рассматриваемых точках (зависит от производной тензора Римана).

• Четаев Н. Г. Теоретическая механика. М.: Наука.— 1987.— 368 с.
• Гернет М. М. Курс теоретической механики. М.: Высшая школа.— 1973.— 464 с.
• Тарг С. М. Относительное движение // Физическая энциклопедия / Прохоров А. М. (гл. ред.). — М.: Большая Российская энциклопедия, 1992. — Т. 3. — С. 493. — 672 с. — ISBN 5-85270-019-3.
• Тарг С. М. Относительное движение // Физический энциклопедический словарь / Введенский Б. А. (гл. ред.). — М.: Советская энциклопедия, 1963. — Т. 3. — С. 553. — 624 с.

1. ↑ Бронштейн И. Н., Семендяев К. А.. Справочник по математике. М.: Издательство «Наука». Редакция справочной физико-математической литературы, 1964 г., 608 стр. с ил., С.216 и далее.
2. ↑ То есть точек, неподвижных относительно движущейся системы.
3. ↑ Ландау Л. Д., Лифшиц Е. М. Механика. — М.: Наука, 1988. — Т. «Теоретическая физика», том I. — С. 13-15. — 215 с. — ISBN 5-02-013850-9.
4. ↑ Тарг С. М. Краткий курс теоретической механики. — М.: Высшая школа, 1995. — С. 156. — 416 с. — ISBN 5-06-003117-9.
5. ↑ Голубев Ю. Ф. Основы теоретической механики. — М.: МГУ, 2000. — С. 119. — 720 с. — ISBN 5-211-04244-1.
6. ↑ Физический энциклопедический словарь/ Гл. ред. А. М. Прохоров. Ред.кол. Д. М. Алексеев, А. М. Бонч-Бруевич,А. С. Боровик-Романов и др. -М.: Сов.энциклопедия, 1983.-323 с.,ил, 2 л.цв.ил. страница 282
7. ↑ Тарг С. М. Сила // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1994. — Т. 4. Пойнтинга—Робертсона эффект — Стримеры. — С. 494. — 704 с. — 40 000 экз. — ISBN 5-85270-087-8.
8. ↑ Kleppner D., Kolenkow R. J. An Introduction to Mechanics. — McGraw-Hill, 1973. — P. 59-60. — 546 p. — ISBN 0-07-035048-5.
9. ↑ ^{1 2} Зоммерфельд А. Механика. — Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001. — 368 с. — ISBN 5-93972-051-X.
10. ↑ Борн М. Эйнштейновская теория относительности. — М.: «Мир», 1972. — С. 81. — 368 с.

Кинематика твёрдого тела — Википедия

Материал из Википедии — свободной энциклопедии

Кинема́тика твёрдого тела (от др.-греч. κίνημα — движение) — раздел кинематики, изучающий движение абсолютно твёрдого тела, не вдаваясь в вызывающие его причины.

Аддитивность угловой скорости[править | править код]

Если тело вращается с угловой скоростью ω0→{\displaystyle {\vec {\omega _{0}}}} в системе отсчёта O′{\displaystyle O’}, а эта система отсчёта, в свою очередь, вращается относительно системы отсчёта O{\displaystyle O} с угловой скоростью ωO′→{\displaystyle {\vec {\omega _{O’}}}}, то это тело вращается относительно O{\displaystyle O} с угловой скоростью

ω→=ωO′→+ω0→{\displaystyle {\vec {\omega }}={\vec {\omega _{O’}}}+{\vec {\omega _{0}}}}

Дифференцирование по времени[править | править код]

Вращающееся тело — неинерциальная система отсчёта. Поэтому оператор дифференцирования по времени для векторов, определённых в покоящейся системе координат O{\displaystyle O}, связан с оператором дифференцирования по времени для векторов, определённых в системе координат на вращающемся теле O′{\displaystyle O’}, соотношением:

ddtO=ddtO′+ω→O′×{\displaystyle {\frac {d}{dt_{O}}}={\frac {d}{dt_{O’}}}+{\vec {\omega }}_{O’}\times },

где «×{\displaystyle \times }» — векторное произведение.

Формула Эйлера[править | править код]

Формула Эйлера связывает скорости двух точек твёрдого тела:

v→B=v→A+ω→×AB→,{\displaystyle {\vec {v}}_{B}={\vec {v}}_{A}+{\vec {\omega }}\times {\vec {AB}},}

где ω→{\displaystyle {\vec {\omega }}} — вектор угловой скорости тела.

Выводится эта формула путём дифференцирования формулы r→B=r→A+AB→{\displaystyle {\vec {r}}_{B}={\vec {r}}_{A}+{\vec {AB}}} по времени с учётом замены оператора для неинерциальной системы отсчёта (см. выше). Путём повторного дифференцирования можно получить связь ускорений двух точек:

a→B=a→A+ω→×(ω→×AB→)+ε→×AB→,{\displaystyle {\vec {a}}_{B}={\vec {a}}_{A}+{\vec {\omega }}\times ({\vec {\omega }}\times {\vec {AB}})+{\vec {\varepsilon }}\times {\vec {AB}},}

где ω→{\displaystyle {\vec {\omega }}} — вектор угловой скорости тела, а ε→{\displaystyle {\vec {\varepsilon }}} — вектор углового ускорения тела.

Второе слагаемое называется центростремительным ускорением.

Ускорение Кориолиса[править | править код]

Ускорение точки B (в покоящейся системе координат), движущейся по поверхности вращающегося тела равно

a→=a→B+[ε→×r→B]+[ω→×[ω→×r→B]]+2[ω→×v→B],{\displaystyle {\vec {a}}={\vec {a}}_{B}+\left[{\vec {\varepsilon }}\times {\vec {r}}_{B}\right]+\left[{\vec {\omega }}\times \left[{\vec {\omega }}\times {\vec {r}}_{B}\right]\right]+2\left[{\vec {\omega }}\times {\vec {v}}_{B}\right],}

где r→B=r→B(t){\displaystyle {\vec {r}}_{B}={\vec {r}}_{B}(t)} — радиус-вектор точки В в системе координат на вращающемся теле. Последнее слагаемое и будет кориолисовым ускорением.

основана на формуле сложения скоростей:

v→a=v→r+v→e{\displaystyle {\vec {v}}^{\,a}={\vec {v}}^{\,r}+{\vec {v}}^{\,e}}.