Законы силы, формулы

Существует ряд законов, которые характеризуют физические процессы при механических движениях тел.

Выделяют следующие основные законы сил в физике:

• закон силы тяжести;
• закон всемирного тяготения;
• законы силы трения;
• закон силы упругости;
• законы Ньютона.

Закон силы тяжести

Замечание 1

Сила тяжести является одним из случаев проявления действия гравитационных сил.

Силу тяжести представляют в виде такой силы, которая действует на тело со стороны планеты и придает ему ускорение свободного падения.

Свободное падение можно рассмотреть в виде $mg = G\frac{mM}{r^2}$, откуда получаем формулу ускорения свободного падения:

$g = G\frac{M}{r^2}$.

Формула определения силы тяжести будет выглядеть следующим образом:

${\overline{F}}_g = m\overline{g}$

Сила тяжести имеет определенный вектор распространения. Он всегда направлен вертикально вниз, то есть по направлению к центру планеты. На тело действует силы тяжести постоянно и это означает, что оно совершает свободное падение.

Траектория движения при действии силы тяжести зависит от:

• модуля начальной скорости объекта;
• направления скорости движения тела.

С этим физическим явлением человек сталкивается ежедневно.

Силу тяжести можно также представить в виде формулы $P = mg$. При ускорении свободного падения учитываются также дополнительные величины.

Если рассматривать закон всемирного тяготения, который сформулировал Исаак Ньютон, все тела обладают определенной массой. Они притягиваются друг к другу с силой. Ее назовут гравитационной силой.

$F = G\frac{m_1m_2}{r^2}$

Эта сила прямо пропорциональна произведению масс двух тел и обратно пропорциональна квадрату расстояния между ними.

$G = 6,7\cdot {10}^{-11}\ {H\cdot m^2}/{{kg}^2\ }$, где $G$ — это гравитационная постоянная и она имеет по международной системе измерений СИ постоянное значение.

Определение 1

Весом называют силу, с которой тело действует на поверхность планеты после возникновения силы тяжести.

В случаях, когда тело находится в состоянии покоя или равномерно движется по горизонтальной поверхности, тогда вес будет равен силе реакции опоры и совпадать по значению с величиной силы тяжести:

$Р = тg$

При равноускоренном движении вертикально вес будет отличаться от силы тяжести, исходя из вектора ускорения. При направлении вектора ускорения в противоположную сторону возникает состояние перегрузки. В случаях, когда тело вместе с опорой двигаются с ускорением $а = g$, тогда вес будет равен нулю. Состояние с нулевым весом называют невесомостью.

Напряженность поля тяготения высчитывается следующим образом:

$g = \frac{F}{m}$

Величина $F$ — сила тяготения, которая действует на материальную точку массой $m$.

Тело помещается в определенную точку поля.

Потенциальная энергия гравитационного взаимодействия двух материальных точек, имеющих массы $m_1$ и $m_2$, должны находиться на расстоянии $r$ друг от друга.

Потенциал поля тяготения можно найти по формуле:

$\varphi = \Pi / m$

Здесь $П$ — потенциальная энергия материальной точки с массой $m$. Она помещена в определенную точку поля.

Законы силы трения

Замечание 2

Сила трения возникает при движении и направлена против скольжения тела.

Статическая сила трения будет пропорциональна нормальной реакции. Статическая сила трения не лежит в зависимости от формы и размеров трущихся поверхностей. От материала тел, которые соприкасаются и порождают силу трения, зависит статический коэффициент трения. Однако законы трения нельзя назвать стабильными и точными, поскольку часто наблюдаются в результатах исследований различные отклонения.

Традиционное написание силы трения предполагает использование коэффициента трения ($\eta$), $N$ – сила нормального давления.

$F=\eta N$

Также выделяют внешнее трение, силу трения качения, силу трения скольжения, вязкую силу трения и другие виды трения.

Закон силы упругости

Сила упругости равна жёсткости тела, которую помножили на величину деформации:

$F = k \cdot \Delta l$

В нашей классической формуле силы по поиску силы упругости главное место занимают величины жесткости тела ($k$) и деформации тела ($\Delta l$). Единицей измерения силы является ньютон (Н).

Подобная формула может описать самый простой случай деформации. Его принято называть законом Гука. Он гласит, что при попытке любым доступным способом деформировать тело, сила упругости будет стремиться вернуть форму объекта в первоначальный вид.

Для понимания и точного процесса описания физического явления вводят дополнительные понятия. Коэффициент упругости показывает зависимость от:

• свойств материала;
• размеров стержня.

В частности, выделяют зависимость от размеров стержня или площади поперечного сечения и длины. Тогда коэффициент упругости тела записывают в виде:

$k = \frac{ES}{L}$

В такой формуле величина $E$ является модулем упругости первого рода. Также ее называют модулем Юнга. Она отражает механические характеристики определенного материала.

При проведении расчётов прямых стержней применяется запись закона Гука в относительной форме:

$\Delta l = \frac{FL}{ES}$

Отмечается, что применение закона Гука будет носить эффективный характер только при относительно небольших деформациях. Если идет превышение уровня предела пропорциональности, то связь между деформациями и напряжениями становится нелинейной. Для некоторых сред закон Гука нельзя применять даже при небольших деформациях.

Сила нормальной реакции — Википедия

Материал из Википедии — свободной энциклопедии

Си́ла норма́льной реа́кции (иногда нормальная реакция опоры) — сила, действующая на тело со стороны опоры и направленная перпендикулярно («по нормали», «нормально») к поверхности соприкосновения. Распределена по площади зоны соприкосновения. Подлежит учёту при анализе динамики движения тела. Фигурирует в законе Амонтона — Кулона.

Одним из часто обсуждаемых примеров для иллюстрации силы нормальной реакции является случай нахождения небольшого тела на наклонной плоскости. При этом для простоты считается, что сила реакции приложена в одной точке соприкосновения.

Для расчёта в этом случае используется формула

N — сила нормальной реакции, f — сила трения покоя

|N→|=mgcos⁡θ{\displaystyle |{\vec {N}}|=mg\cos \theta },

где |N→|{\displaystyle |{\vec {N}}|} — модуль вектора силы нормальной реакции, m{\displaystyle m} — масса тела, g{\displaystyle g} — ускорение свободного падения, θ{\displaystyle \theta } — угол между плоскостью опоры и горизонтальной плоскостью.

Выписанной формулой отражается тот факт, что вдоль направления, перпендикулярного наклонной плоскости, движения нет. Это значит, что величина силы нормальной реакции равна проекции силы тяжести mg{\displaystyle mg} на указанное направление.

Из закона Амонтона — Кулона следует, что для модуля вектора силы нормальной реакции справедливо соотношение:

|N→|=|F→|μ,{\displaystyle |{\vec {N}}|={\frac {|{\vec {F}}|}{\mu }},}

где F→{\displaystyle {\vec {F}}} — сила трения скольжения, а μ{\displaystyle \mu } — коэффициент трения.

Поскольку сила трения покоя вычисляется по формуле

|f→|=mgsin⁡θ,{\displaystyle |{\vec {f}}|=mg\sin \theta ,}

можно экспериментальным путём найти такое значение угла θ{\displaystyle \theta }, при котором сила трения покоя будет равна силе трения скольжения:

mgsin⁡θ=μmgcos⁡θ.{\displaystyle mg\sin \theta =\mu mg\cos \theta .}

Отсюда выражается коэффициент трения:

μ=tg θ.{\displaystyle \mu =\mathrm {tg} \ \theta .}

Формула силы трения в физике

Определение и формула силы трения

Определение

Силой трения называют силу, которая возникает при относительном перемещении (или попытке перемещения) тел и является результатом сопротивления движению окружающей среды или других тел.

Силы трения возникают тогда, когда соприкасающиеся тела (или их части) перемещаются относительно друг друга. При этом трение, которое появляется при относительном перемещении соприкасающихся тел, называют внешним. Трение, возникающее между частями одного сплошного тела (газ, жидкость) названо внутренним.

Сила трения – это вектор, который имеет направление вдоль касательной к трущимся поверхностям (слоям). При этом эта сила направлена в сторону противодействия относительному смещению этих поверхностей (слоев). Так, если два слоя жидкости перемещаются друг по другу, при этом движутся с различными скоростями, то сила, которая приложена к слою, перемещающемуся с большей скоростью, имеет направление в сторону, которая противоположна движению. Сила же, которая воздействует на слой, который движется с меньшей скоростью, направлена по движению.

Виды трения

Трение, которое возникает между поверхностями твердых тел, называют сухим. Оно возникает не только при скольжении поверхностей, но и при попытке вызвать перемещение поверхностей. При этом возникает сила трения покоя. Внешнее трение, которое появляется между движущимися телами, называют кинематическим.

Законы сухого трения говорят о том, что максимальная сила трения покоя и сила трения скольжения не зависят от площади поверхностей соприкосновения соприкасающихся тел, подверженных трению. Эти силы пропорциональны модулю силы нормального давления (N), которая прижимает трущиеся поверхности:

где – безразмерный коэффициент трения (покоя или скольжения). Данный коэффициент зависит от природы и состояния поверхностей трущихся тел, например от наличия шероховатостей. Если трение возникает как результат скольжения, то коэффициент трения является функцией скорости. Довольно часто вместо коэффициента трения применяют угол трения, который равен:

Угол равен минимальному углу наклона плоскости к горизонту, при котором тело, лежащее на этой плоскости, начинает скользить, под воздействие силы тяжести.

Более точным считают закон трения, который принимает во внимание силы притяжения между молекулами тел, которые подвергаются трению:

где S – общая площадь контакта

Подъёмная сила — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 31 марта 2018; проверки требуют 13 правок. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 31 марта 2018; проверки требуют 13 правок.

Силы, действующие на крыло самолёта в полёте Обтекание профиля крыла

Подъёмная сила — составляющая полной аэродинамической силы, перпендикулярная вектору скорости движения тела в потоке жидкости или газа, возникающая в результате несимметричности обтекания тела потоком. Полная аэродинамическая сила — это интеграл от давления вокруг контура профиля крыла.

Y+P=∮∂Ω⁡pnd∂Ω{\displaystyle \mathbf {Y} +\mathbf {P} =\oint \limits _{\partial \Omega }p\mathbf {n} \;d\partial \Omega }

где:

• Y — подъёмная сила,
• P — тяга,
• ∂Ω{\displaystyle \partial \Omega } — граница профиля,
• p — величина давления,
• n — нормаль к профилю

Согласно теореме Жуковского, величина подъёмной силы пропорциональна плотности среды, скорости потока и циркуляции скорости потока.

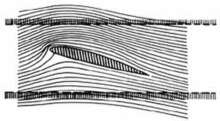
Приближённо возникновение подъёмной силы можно объяснить тем, что ввиду наличия инерции и вязкости у обтекающего крыло газа при ненулевом угле атаки с одной стороны крыла образуется разрежение, а с другой сжатие. Газу со стороны положительного угла атаки необходимо ускориться, преодолев инерцию, чтобы догнать «убегающую» поверхность крыла, а с другой стороны сжаться под воздействием набегающей поверхности. (Более подробно о связи полей скоростей, давления с инерцией и вязкостью среды можно прочитать в описании уравнений Бернулли и уравнения Навье — Стокса). Разность давлений и обусловливает появление силы, направленной в сторону положительного угла атаки.

Если скорость потока воздуха над крылом v1{\displaystyle v_{1}} больше скорости потока воздуха v2{\displaystyle v_{2}} под крылом, то согласно уравнению Бернулли возникает перепад давлений Δp=p2−p1{\displaystyle \Delta p=p_{2}-p_{1}}. Подъемную силу можно рассчитать по формуле Fp=(p2−p1)S=ρ2(v12−v22)S{\displaystyle F_{p}=(p_{2}-p_{1})S={\frac {\rho }{2}}(v_{1}^{2}-v_{2}^{2})S}, где ρ{\displaystyle \rho } — плотность воздуха, S{\displaystyle S} — площадь крыла. Обозначив скорость потока воздуха относительно крыла через u{\displaystyle u}, а скорость циркуляционного потока через v{\displaystyle v}, получим v1=u+v{\displaystyle v_{1}=u+v}, v2=u−v{\displaystyle v_{2}=u-v}, Fp=ρ2(v12−v22)S=ρ2(v1+v2)(v1−v2)S=ρ22u2vS=2ρSvu{\displaystyle F_{p}={\frac {\rho }{2}}(v_{1}^{2}-v_{2}^{2})S={\frac {\rho }{2}}(v_{1}+v_{2})(v_{1}-v_{2})S={\frac {\rho }{2}}2u2vS=2{\rho }Svu} — формула Жуковского^[1].

Коэффициент подъёмной силы — безразмерная величина, характеризующая подъёмную силу крыла определённого профиля при известном угле атаки. Коэффициент определяется экспериментальным путём в аэродинамической трубе, либо по теореме Жуковского.

Джон Смитон уже в XVIII веке рассчитал поправочный коэффициент подъёмной силы (далее Коэффициент Смитона, в формуле не указан) для формулы расчёта подъёмной силы. Формула имеет вид^[2]:

Y=CyρV22S{\displaystyle Y=C_{y}{\frac {\rho V^{2}}{2}}S}

где:

Y{\displaystyle Y} — подъёмная сила (Н)

Cy{\displaystyle C_{y}} — коэффициент подъёмной силы, зависящий от угла атаки (получается опытным путём для разных профилей крыла)

ρ{\displaystyle \rho } — плотность воздуха на высоте полёта (кг/м³)

V{\displaystyle V} — скорость набегающего потока (м/с)

S{\displaystyle S} — характерная площадь (м²)

Формула для расчета лобового сопротивления сходна с вышеприведенной, за исключением того, что используется коэффициент лобового сопротивления Cx{\displaystyle C_{x}} вместо коэффициента подъёмной силы Cy{\displaystyle C_{y}}.

Поправочный коэффициент, значение которого по расчётам Смитона составляло 1.005, использовался более 100 лет, и только опыты Братьев Райт, в ходе которых они обнаружили, что подъёмная сила, действующая на планёры, была слабее расчётной, позволили уточнить «коэффициент Смитона» до значения 1.0033.

При расчётах по этой формуле важно не путать весовую и массовую плотность воздуха. Весовая плотность при стандартных атмосферных условиях (на уровне земли при температуре +15 °С) равна ρ{\displaystyle \rho }=1.225 кг/м³. Но в аэродинамических расчётах часто используют массовую плотность воздуха, которая равна 0.125 кГ*с²/м⁴. В этом случае подъёмная сила Y получается не в ньютонах (Н), а в килограммах (кг). В книгах по аэродинамике^{[источник не указан 813 дней]} не всегда имеются уточнения, о какой плотности и размерности подъёмной силы идёт речь, поэтому в спорных ситуациях нужно проверять формулы, сокращая единицы измерения.

1. ↑ Кабардин О.Ф., Орлов В.А., Пономарева А.В. Факультативный курс физики. 8 класс. — М.: Просвещение, 1985. — Тираж 143 500 экз. — С. 151 — 152
2. ↑ Clancy, L.J., Aerodynamics, Section 4.15

Формула силы упругости

   

Здесь – сила упругости, – жёсткость тела, – деформация тела.

Единица измерения силы – Н (ньютон).

Указанная формула описывает простейший случай деформации и называется законом Гука. Сила упругости возникает при попытке деформировать (сжать, скрутить, растянуть и т.д.) тело и стремиться вернуть тело в первоначальное состояние. Деформацию, после которой тело не изменилось, называют упругой. Жёсткость тела зависит от материала, из которого состоит тело, от его формы и размера. На практике закон Гука применяют для расчётов при малых деформациях, при увеличении силы, вызывающей деформацию, он перестаёт действовать.

Примеры решения задач по теме «Сила упругости»

Понравился сайт? Расскажи друзьям!

Формула силы инерции

Для того чтобы второй закон Ньютона выполнялся в неинерциальных системах отсчета в дополнение к силам, которые действуют на тела вводят силы инерции.

Определение и формула силы инерции

Возникновение сил инерции не связано с действием каких-либо тел. Напомним, что неинерциальными системами отсчета являются любые системы, движущейся с ускорением относительно инерциальных систем.

Третий закон Ньютона для сил инерции не выполняется.

Пусть ускорение тела относительно инерциальной системы отсчета равно . Обычно такое ускорение называют абсолютным, при этом ускорение тела относительно неинерциальной системы отсчета носит название относительного (). Второй закон Ньютона для инерциальной системы отсчета запишем как:

   

где – равнодействующая сила, приложенная к телу массы m. В неинерциальной системе отсчета:

   

поскольку:

   

Добавим к правой части выражения (2) силы инерции, так чтобы выполнялся второй закон Ньютона в неинерциальной системе отсчета:

   

В таком случае получим, что сила инерции равна:

   

Формула (5) для силы инерции дает верное описание движения в неинерциальной системе отсчета. При этом нахождение разности относительного и абсолютного ускорений является кинематической задачей. Ее можно решить, если известен характер движения неинерциальной системы отсчета относительно инерциальной.

Системы отсчета, движущиеся прямолинейно с постоянным ускорением

Система отсчета, которая перемещается прямолинейно с постоянным ускорением – это простейший случай неинерциальной системы. Рассмотрим неинерциальную систему отсчета, которая движется прямолинейно с постоянным ускорением (переносное ускорение) относительно инерциальной системы отсчета. Тогда:

   

Согласно формуле (5) сила инерции равна:

   

Вращающаяся система отсчета

Рассмотрим систему отсчета, вращающуюся относительно неподвижной оси с постоянной скоростью . Для тела находящегося в состоянии покоя в такой системе отсчета формулу для силы инерции можно записать как:

   

где – радиус-вектор, по величине равный расстоянию от оси вращения до рассматриваемого тела, направленный от центра к телу. Сила инерции (8) называется центробежной силой инерции.

Все тела на поверхности Земли испытывают действие центробежной силы инерции.

Отметим, что всякую задачу можно решить в инерциальной системе отсчета. Применение неинерциальных систем продиктовано соображениями удобства применения неинерциальных систем.

Примеры решения задач по теме «Сила инерции»

Формула силы тяги в физике

В том случае, если тело при перемещении имеет ускорение, то на него кроме всех прочих обязательно действует некоторая сила, которая является силой тяги в рассматриваемый момент времени. В действительности, если тело движется прямолинейно и с постоянной скоростью, то сила тяги также действует, так как тело должно преодолевать силы сопротивления. Обычно силу тяги находят, рассматривая силы, действующие на тело, находя равнодействующую и применяя второй закон Ньютона. Жестко определенной формулы для силы тяги не существует.

Не следует считать, что сила тяги, например, транспортного средства действует со стороны двигателя, так как внутренние силы не могут менять скорость системы как единого целого, что входило бы в противоречие с законом сохранения импульса. Однако следует отметить, что для получения у силы трения покоя необходимого направления, мотор вращает колеса, колеса «цепляются за дорогу» и порождается сила тяги. Теоретически было бы возможно не использовать понятие «сила тяги», а говорить о силе трения покоя или силе реакции воздуха. Но удобнее внешние силы, которые действуют на транспорт делить на две части, при этом одни силы называть силами тяги , а другие — силами сопротивления . Это делается для того, чтобы уравнения движения не потеряли свой универсальный вид и полезная механическая мощность (P) имела простое выражение:

Определение и формула силы тяги

Определение

Исходя из формулы (1) силу тяги можно определить через полезную мощность, и скорость транспортного средства (v):

Для автомобиля, поднимающегося в горку, которая имеет уклон , масса автомобиля m сила тяги (F_T) войдет в уравнение:

где a – ускорение, с которым движется автомобиль.

Единицы измерения силы тяги

Основной единицей измерения силы в системе СИ является: [F_T]=Н

В СГС: [F_T]=дин

Примеры решения задач

Пример

Задание. На автомобиль имеющий массу 1 т при его движении по горизонтальной поверхности, действует сила трения, которая равна =0,1 от силы тяжести. Какой будет сила тяги, если автомобиль движется с ускорением 2 м/с?

Решение. Сделаем рисунок.

В качестве основы для решения задачи используем второй закон Ньютона:

Спроектируем уравнение (1.1) на