особенности величины, как найти её для круга
 В инженерной и строительной практике нередко встречаются задачи по расчёту площади поперечного сечения. Если фигуру разрезать по линии, которая перпендикулярна продольной оси предмета, то полученный торец и будет поперечным сечением. Круг — один из наиболее часто встречающихся видов подобного рассечения. Такой срез присущ цилиндру, шару, конусу, тору, эллипсоиду.
В инженерной и строительной практике нередко встречаются задачи по расчёту площади поперечного сечения. Если фигуру разрезать по линии, которая перпендикулярна продольной оси предмета, то полученный торец и будет поперечным сечением. Круг — один из наиболее часто встречающихся видов подобного рассечения. Такой срез присущ цилиндру, шару, конусу, тору, эллипсоиду.
Определение величины
Площадь — это величина, характеризующая размер геометрической фигуры. Её определение — одна из древнейших практических задач. Древние греки умели находить площадь многоугольников: так, каменщикам, чтобы узнать размер стены, приходилось умножать её длину на высоту.

По прошествии долгих лет трудом многих мыслителей был выработан математический аппарат для расчета этой величины практически для любой фигуры.
На Руси существовали особые единицы измерения: копна, соха, короб, верёвка, десятина, четь и другие, так или иначе связанные с пахотой. Две последних получили наибольшее распространение. Однако от древнерусских землемеров нам досталось только само слово — «площадь».
С развитием науки и техники появилось не только множество формул для расчёта площадей любых геометрических фигур, но и приборы, которые делают это за человека. Такие приборы называют планиметрами.
Область применения
Круг — одна из фундаментальных фигур, которые окружают человека повсюду. Трубы, колеса, лампы, конфорки у плиты — всё это имеет форму круга или поперечное сечение в виде круга.
- Определение объемов емкостей.
- Решение задач по сопротивлению материалов и электротехнике.
- Расчет количества материалов при проектировании, строительстве и ремонте.
- Ведение поливного земледелия.
Стоит обратить внимание на разницу между кругом и окружностью. Окружность — это замкнутая кривая, все точки которой равно удалены от центра, в то время как круг — это часть плоскости (геометрическая фигура), ограниченная окружностью.
Круг имеет ряд характеристик:
- радиус (r/R) — отрезок, соединяющий центр фигуры с его границей;
- диаметр (d/D) — отрезок, который соединяет две точки границы круга и проходит через его центр;
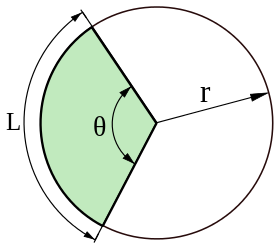
- длина окружности (C/c/L/l).

Теорема гласит: площадь круга (S) равна произведению половины длины окружности и его радиуса. Длина окружности С находится в прямой зависимости от радиуса R с коэффициентом π («пи» = 3,14).
Способы расчета
Чтобы получить круглое поперечное сечение, необходимо разрезать объёмную фигуру перпендикулярно оси вращения. В случае с цилиндром площади всех поперечных сечений будут равны между собой — как, например, кружки колбасы, нарезанные поперек батона, одинаковы.
Шар, по сути, представляет собой напластование блинчиков-кругов различного диаметра от точечного до заданного и обратно до точки. Чтобы найти S какого-либо из блинчиков, необходимо определить его радиус. Принцип его расчёта сводится к решению теоремы Пифагора, где гипотенузой выступает радиус шара, а искомый радиус становится одним из катетов.
При расчёте площади сечений конуса необходимо найти радиус или диаметр каждого из кругов, учитывая, что в продольном разрезе конус — это равнобедренный треугольник.
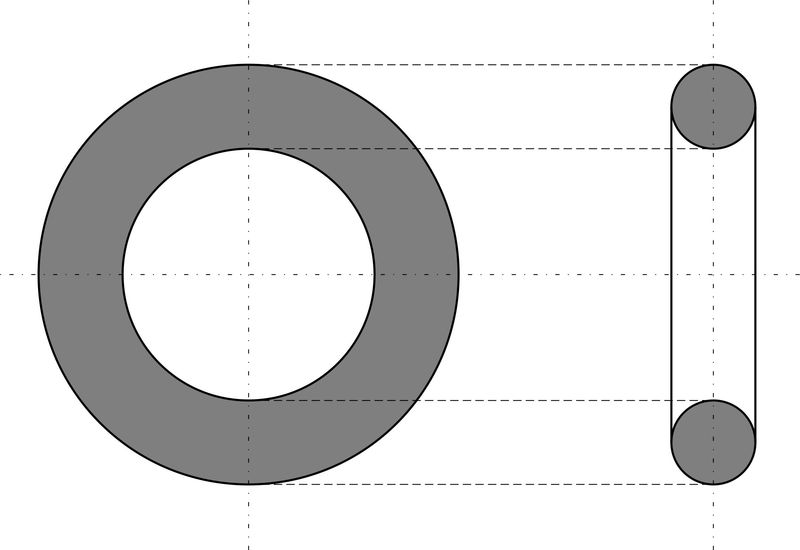
Цилиндр, конус и шар — базовые объемные фигуры. Однако существуют более сложные фигуры, например, тор. Тор, или тороид, при первом приближении являет собой не что иное, как бублик или баранку. Разломив его пополам, на торцах можно увидеть два одинаковых круга. Площадь такого поперечного сечения можно получить, удвоив имеющуюся (на рисунке серая область справа). Если взять нож и рассечь баранку вдоль, на срезе получится кольцо. В случае с такой фигурой необходимо найти площадь круга по внешней окружности и вычесть из нее «дырку от бублика» (показано серым на рисунке слева).
Площадь круглого поперечного сечения рассчитывается исходя из имеющихся характеристик. Она сводится к трем основным формулам. Их можно представить таким образом:

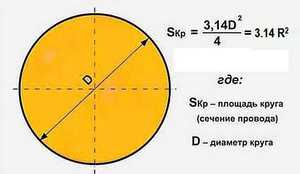
- Самая популярная, легкая в применении и часто используемая формула. Чтобы узнать площадь фигуры, если известен её радиус, нужно возвести это значение в квадрат и умножить на число π. Для бытовых расчетов достаточно двух знаков после запятой, то есть π = 3,14.
- Иногда оперируют диаметром, а не радиусом круга. В этом случае к вычислениям добавляется одна операция: диаметр умножают сам на себя, затем на число π, а произведение делят на 4.
- Если известна длина окружности С и ее радиус R и нужно выяснить площадь круга, ограниченного этой окружностью, не понадобится даже π. Используют следующую формулу: значение С делят пополам и умножают на R. Полученное чисто и будет искомой величиной.
Способов определения того, чему равна площадь круга, достаточно много. Чаще всего, если возникает подобная задача, на ум приходит знакомая еще со школьной скамьи формула «эс равно пи эр квадрат».
Формула площади круга через диаметр или радиус или длину окружности.
Круг это плоская фигура, все точки которой, расположены на любом расстоянии от определенной точки (центр круга) но не больше заданной длины (радиус).
Радиус круга — отрезок, соединяющий центр окружности и любую, максимально удаленную от центра точку круга.
Диаметр круга — отрезок, соединяющий две любые точки максимально удаленные от центра круга и проходящий через этот центр. Диаметр, в два раза больше радиуса
Зная диаметр
или радиус круга или длину окружности, можно найти его площадь.

r — радиус круга
D — диаметр круга
π ≈ 3.14
Формула площади круга, (S):

Решения задач
на тему: Площадь круга
Калькулятор для расчета площади круга через радиус
Калькулятор для расчета площади круга через диаметр

L — длина окружности
О — центр круга
π ≈ 3.14
Формула площади круга если известна длина окружности, (S):

Решения задач
на тему: Площадь круга
Калькулятор для расчета площади круга через длину
- Подробности
- Автор: Сергей Кондратов

Окружность, круг, сегмент, сектор. Формулы и свойства
Определение. Единичная окружность — окружность, радиус которой равна единице.
Определение. Круг — часть плоскости, ограничена окружностью.
Определение. Радиус окружности R — расстояние от центра окружности О до любой точки окружности.
Определение. Диаметр окружности D — отрезок, который соединяет две точки окружности и проходит через ее центр.
Основные свойства окружности
1. Диаметр окружности равен двум радиусам.2. Кратчайшее расстояние от центра окружности к секущей (хорде) всегда меньше радиуса.
3. Через три точки, которые не лежат на одной прямым, можно провести только одну окружность.
4. Среди всех замкнутых кривых с одинаковой длиной, окружность имеет наибольшую площадь.
5. Если две окружности соприкасаются в одной точке, то эта точка лежит на прямой, что проходит через центры этих окружностей.
Формулы длины окружности и площади круга
Формулы длины окружности
1. Формула длины окружности через диаметр:L = πD
2. Формула длины окружности через радиус:L = 2πr
Формулы площади круга
1. Формула площади круга через радиус:S = πr2
2. Формула площади круга через диаметр:S = πD24
Уравнение окружности
1. Уравнение окружности с радиусом r и центром в начале декартовой системы координат:r2 = x2 + y2
2. Уравнение окружности с радиусом r и центром в точке с координатами (a, b) в декартовой системе координат:r2 = (x — a)2 + (y — b)2
3. Параметрическое уравнение окружности с радиусом r и центром в точке с координатами (a, b) в декартовой системе координат:| { | x = a + r cos t |
| y = b + r sin t |
Касательная окружности и ее свойства
Определение. Касательная окружности — прямая, которая касается окружности только в одной точке.
Основные свойства касательных к окружности
1. Касательная всегда перпендикулярна к радиусу окружности, проведенного в точке соприкосновения.
2. Кратчайшее расстояние от центра окружности к касательной равна радиусу окружности.
 3. Если две касательные, с точками соприкосновения B и C, на одной окружности не параллельны, то они пересекаются в точке A, а отрезок между точкой соприкосновения и точкой пересечения одной касательной равен таком же отрезке на другой касательной:
3. Если две касательные, с точками соприкосновения B и C, на одной окружности не параллельны, то они пересекаются в точке A, а отрезок между точкой соприкосновения и точкой пересечения одной касательной равен таком же отрезке на другой касательной:AB = AC
Также, если провести прямую через центр окружности О и точку пересечения A этих касательных, то углы образованный между этой прямой и касательными будут равны:∠ОAС = ∠OAB
Секущая окружности и ее свойства
Определение. Секущая окружности — прямая, которая проходит через две точки окружности.
Основные свойства секущих
 1. Если с точки вне окружности (Q) выходят две секущие, которые пересекают окружность в двух точках A и B для одной секущей и C и D для другой секущей, то произведения отрезков двух секущих равны между собою:
1. Если с точки вне окружности (Q) выходят две секущие, которые пересекают окружность в двух точках A и B для одной секущей и C и D для другой секущей, то произведения отрезков двух секущих равны между собою:AQ ∙ BQ = CQ ∙ DQ
 2. Если из точки Q вне окружности выходит секущая прямая, что пересекает окружность в двух точках A и B, и касательная с точкой соприкосновения C, то произведение отрезков секущей равна квадрату длины отрезка касательной:
2. Если из точки Q вне окружности выходит секущая прямая, что пересекает окружность в двух точках A и B, и касательная с точкой соприкосновения C, то произведение отрезков секущей равна квадрату длины отрезка касательной:AQ ∙ BQ = CQ2
Хорда окружности ее длина и свойства
Определение. Хорда окружности — отрезок, который соединяет две точки окружности.
Длина хорды
 1. Длина хорды через центральный угол и радиус:
1. Длина хорды через центральный угол и радиус:AB = 2r sin α2
 2. Длина хорды через вписанный угол и радиус:
2. Длина хорды через вписанный угол и радиус:AB = 2r sin α
Основные свойства хорд
 1. Две одинаковые хорды стягивают две одинаковые дуги:
1. Две одинаковые хорды стягивают две одинаковые дуги:если хорды AB = CD, то
дуги ◡ AB = ◡ CD
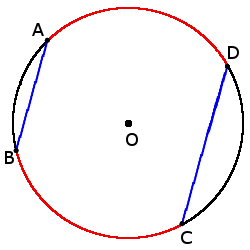 2. Если хорды параллельные, то дуги между ними будут одинаковые:
2. Если хорды параллельные, то дуги между ними будут одинаковые:если хорды AB ∣∣ CD, то
◡ AD = ◡ BC
 3. Если радиус окружности перпендикулярен к хорде, то он разделяет хорду пополам в точке их пересечения:
3. Если радиус окружности перпендикулярен к хорде, то он разделяет хорду пополам в точке их пересечения:если OD ┴ AB, то
AC = BC
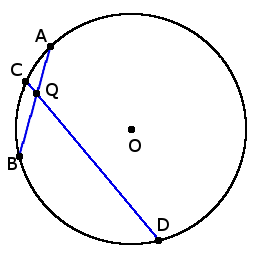 4. Если две хорды AB и CD пересекаются в точке Q, то произведение отрезков, что образовались при пересечении, одной хорды равны произведению отрезков другой хорды:
4. Если две хорды AB и CD пересекаются в точке Q, то произведение отрезков, что образовались при пересечении, одной хорды равны произведению отрезков другой хорды:AQ ∙ BQ = DQ ∙ QC
 5. Хорды с одинаковой длиной находятся на одинаковом расстоянии от центра окружности.
5. Хорды с одинаковой длиной находятся на одинаковом расстоянии от центра окружности.если хорды AB = CD, то
ON = OK
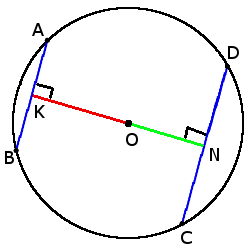 6. Чем больше хорда тем ближе она к центру.
6. Чем больше хорда тем ближе она к центру.если CD > AB, то
ON < OK
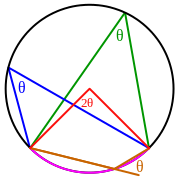
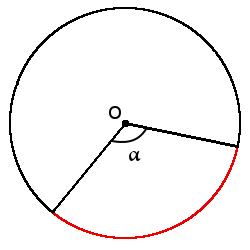
Центральный угол, вписанный угол и их свойства
Определение. Центральный угол окружности — угол, вершиной которого есть центр окружности.
Определение. Угол вписанный в окружность — угол, вершина которого лежит на окружности, а стороны угла пересекают окружность.
Основные свойства углов
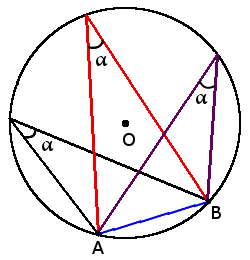 1. Все вписанные углы, которые опираются на одну дугу — равны.
1. Все вписанные углы, которые опираются на одну дугу — равны.  2. Вписанний угол, который опирается на диаметр будет прямым (90°).
2. Вписанний угол, который опирается на диаметр будет прямым (90°).  3. Вписанный угол равен половине центрального угла, что опирается на ту же дугу
3. Вписанный угол равен половине центрального угла, что опирается на ту же дугуβ = α2
 4. Если два вписанных угла опираются на одну хорду и находятся по различные стороны от нее, то сумма этих углов равна 180°.
4. Если два вписанных угла опираются на одну хорду и находятся по различные стороны от нее, то сумма этих углов равна 180°.α + β = 180°
Определение. Дуга окружности (◡) — часть окружности, которая соединяет две точки на окружности.
Определение. Градусная мера дуги — угол между двумя радиусами, которые ограничивают эту дугу. Градусная мера дуги всегда равна градусной мере центрального угла, который ограничивает эту дугу своими сторонами.
 Формула длины дуги через центральный угол (в градусах):
Формула длины дуги через центральный угол (в градусах):l = πr180°∙ α
Определение. Полуокружность — дуга в которой концы соединены диаметром окружности.
Определение. Полукруг (◓) — часть круга, которая ограничена полуокружностью и диаметром.
Определение. Сектор (◔) — часть круга, которая ограничена двумя радиусами и дугой между этими радиусами.
 Формула. Формула площади сектор через центральный угол (в градусах)
Формула. Формула площади сектор через центральный угол (в градусах)S = πr2360°∙ α
Определение. Сегмент — часть круга, которая ограничена дугой и хордой, что соединяет ее концы.
Определение. Концентрические окружности — окружности с различными радиусами, которые имеют общий центр.
Определение. Кольцо — часть плоскости ограниченная двумя концентрическими окружностями.
Площадь круга — Википедия
Площадь круга с радиусом r равна πr2{\displaystyle \pi r^{2}}. Здесь символ π{\displaystyle \pi } (греческая буква «пи») обозначает отношение длины окружности к её диаметру: π≈3,14159265.{\displaystyle \pi \approx 3{,}14159265.}
-

Сектор круга (закрашен зелёным)
-

Сегмент круга (закрашен жёлтым)
Площадь сектора круга равна S=θr22{\displaystyle S={\frac {\theta r^{2}}{2}}}, где θ{\displaystyle \theta } — угловая величина дуги сектора в радианах[1].
Площадь сегмента круга равна S=12r2(θ−sinθ){\displaystyle S={\frac {1}{2}}r^{2}(\theta -\sin \theta )}, где θ{\displaystyle \textstyle \theta } — угол в радианах[1]
Современные математики могут получить площадь круга с помощью методов интегрирования или вещественного анализа. Однако площадь круга изучалась ещё в Древней Греции. Гиппократ Хиосский в своих попытках квадрирования гиппократовых луночек) первым сформулировал утверждение: площадь круга пропорциональна квадрату его диаметра. Евдокс Книдский в IV веке до н. э. строго доказал это утверждение[2][3]. Однако они не установили значения коэффициента пропорциональности.
Античные математики также безуспешно пытались решить задачу «квадратуры круга», то есть построения с помощью циркуля и линейки квадрата, равновеликого по площади заданному кругу. Проблемой занимались крупнейшие античные учёные — Анаксагор, Антифон, Брисон Гераклейский, Архимед и другие; неразрешимость этой задачи следует из неалгебраичности (трансцендентности) числа π{\displaystyle \pi }, которая была доказана в 1882 году Линдеманом[4].
Архимед в III веке до н. э. использовал методы евклидовой геометрии, чтобы показать в своей книге «Измерение круга[en]», что площадь круга равна площади прямоугольного треугольника, основание которого равно длине окружности, а высота равна радиусу окружности. В современных обозначениях, длина окружности равна 2πr{\displaystyle 2\pi r}, а площадь треугольника равна половине произведения основания на высоту, что даёт πr2.{\displaystyle \pi r^{2}.} Архимед уточнил значение числа π{\displaystyle \pi }:
- 31071<π<317{\displaystyle 3{\frac {10}{71}}<\pi <3{\frac {1}{7}}}
Для доказательства Архимед построил для круга вписанный и описанный 96-угольники и вычислил длины их сторон (см. ниже).
 Круг, развёрнутый в треугольник
Круг, развёрнутый в треугольникСредневековые европейские математики использовали для обоснования формулы площади круга метод неделимых. Представим себе разворачивание концентричных кругов бесконечно малой толщины в отрезки, получим прямоугольный треугольник с высотой r и основанием 2πr{\displaystyle 2\pi r} (основание получается из внешней окружности круга). Вычисление площади треугольника даст площадь круга:
- Площадь = 12⋅{\displaystyle {1 \over 2}\cdot } основание ⋅{\displaystyle \cdot } высота = 12⋅2πr⋅r<=πr2{\displaystyle {1 \over 2}\cdot 2\pi r\cdot r<=\pi r^{2}}.
Предельный переход[править | править код]
Площадь правильного многоугольника равна половине периметра, умноженного на апофему (высоту). При увеличении числа сторон многоугольник стремится к кругу, а апофема стремится к радиусу. Это даёт основание считать, что площадь круга равна произведению половины длины окружности на радиус[5], то есть π⋅r⋅r=πr2{\displaystyle \pi \cdot r\cdot r=\pi r^{2}}.
Доказательство Архимеда[править | править код]
Следуя Архимеду, сравним площадь круга с площадью прямоугольного треугольника, основание которого равно длине окружности, а высота равна радиусу. Если площадь круга не равна площади треугольника, она должна быть меньше или больше. Исключим оба варианта, что оставит только одну возможность — площади равны. Для доказательства будем использовать правильные многоугольники.
Не больше[править | править код]
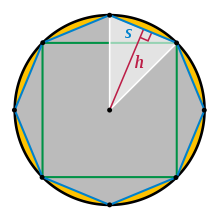 Круг с вписанными квадратом и восьмиугольником. Показан зазор
Круг с вписанными квадратом и восьмиугольником. Показан зазорПредположим, что площадь круга C больше площади треугольника T = 1⁄2cr. Пусть E означает превышение площади. Впишем[en] квадрат в окружность, чтобы все его четыре угла лежали на окружности. Между квадратом и окружностью четыре сегмента. Если общая их площадь G4 больше E, делим каждую дугу пополам, что превращает вписанный квадрат в восьмиугольник и образует восемь сегментов с меньшим общим зазором, G8. Продолжаем деление, пока общий зазор Gn не станет меньше E. Теперь площадь вписанного многоугольника Pn = C − Gn должна быть больше площади треугольника.
- E=C−T>GnPn=C−Gn>C−EPn>T{\displaystyle {\begin{aligned}E&{}=C-T\\&{}>G_{n}\\P_{n}&{}=C-G_{n}\\&{}>C-E\\P_{n}&{}>T\end{aligned}}}
Но это ведёт к противоречию. Для доказательства проведём высоту из центра окружности на середину стороны многоугольника, её длина h меньше радиуса окружности. Пусть каждая сторона многоугольника имеет длину s, сумма всех сторон составит ns, и эта величина меньше длины окружности. Площадь многоугольника состоит из n равных треугольников высоты h с основанием s, что даёт 1⁄2nhs. Но h < r и ns < c, так что площадь многоугольника должна быть меньше площади треугольника 1⁄2cr, получили противоречие.
Не меньше[править | править код]
 Окружность с описанным квадратом и восьмиугольником. Показан зазор
Окружность с описанным квадратом и восьмиугольником. Показан зазорПредположим, что площадь круга меньше площади треугольника. Пусть D означает разницу площадей. Описываем квадрат вокруг окружности, так что середины сторон лежат на ней. Если суммарный зазор между квадратом и окружностью G4 больше D, срезаем углы касательными, превращая квадрат в восьмиугольник и продолжаем такие отсечения пока площадь зазора не станет меньше D. Площадь многоугольника Pn должна быть меньше T.
- D=T−C>GnPn=C+Gn<C+DPn<T{\displaystyle {\begin{aligned}D&{}=T-C\\&{}>G_{n}\\P_{n}&{}=C+G_{n}\\&{}<C+D\\P_{n}&{}<T\end{aligned}}}
Это тоже приводит к противоречию. Каждый перпендикуляр, проведённый от центра круга к середине стороны, является радиусом, т.е. имеет длину r. А поскольку сумма сторон больше длины окружности, многоугольник из n одинаковых треугольников даст площадь, большую T. Снова получили противоречие.
Таким образом, площадь круга в точности равна площади треугольника.
Доказательство перегруппировкой[править | править код]
 Площадь круга после перегруппировки
Площадь круга после перегруппировки  Анимация перегруппировки
Анимация перегруппировкиСледуя Сато Мошуну [6] и Леонардо да Винчи [7], мы можем использовать вписанные правильные многоугольники другим способом. Положим, мы вписали шестиугольник. Разрежем шестиугольник на шесть треугольников, делая сечения через центр. Два противоположных треугольника содержат общие диаметры. Сдвинем теперь треугольники, чтобы радиальные стороны стали смежными. Теперь пара треугольников образует параллелограмм, в котором стороны шестиугольника образуют две противоположные стороны длиной s. Две радиальные стороны становятся боковыми сторонами, а высота параллелограмма равна h (как в доказательстве Архимеда). Фактически, мы можем собрать все треугольники в один большой параллелограмм, располагая в ряд полученные параллелограммы (из двух треугольников). То же самое будет верно, если мы будем увеличивать число сторон. Для многоугольника с 2n сторонами параллелограмм будет иметь основание ns и высоту h. С ростом числа сторон длина основания параллелограмма увеличивается, стремясь к половине окружности, а высота стремится к радиусу. В пределе параллелограмм становится прямоугольником с шириной πr и высотой r.
Приближения площади круга единичного радиуса перегруппировкой треугольников. многоугольник параллелограмм n сторона основание высота площадь 4 1,4142136 2,8284271 0,7071068 2,0000000 6 1,0000000 3,0000000 0,8660254 2,5980762 8 0,7653669 3,0614675 0,9238795 2,8284271 10 0,6180340 3,0901699 0,9510565 2,9389263 12 0,5176381 3,1058285 0,9659258 3,0000000 14 0,4450419 3,1152931 0,9749279 3,0371862 16 0,3901806 3,1214452 0,9807853 3,0614675 96 0,0654382 3,1410320 0,9994646 3,1393502 ∞ 1/∞ π 1 π
Интегрирование[править | править код]
 Площадь круга путём интегрирования
Площадь круга путём интегрированияИспользуя интегралы, мы можем просуммировать площадь круга, разделив его на концентрические окружности подобно луковице. Площадь бесконечно тонкого «слоя» радиуса t будет равна 2πt dt, то есть произведению длины окружности на толщину слоя. В результате получим элементарный интеграл для круга радиуса r.
- Area(r)=∫0r2πtdt=[(2π)t22]t=0r=πr2.{\displaystyle {\begin{aligned}\mathrm {Area} (r)&{}=\int _{0}^{r}2\pi t\,dt\\&{}=\left[(2\pi ){\frac {t^{2}}{2}}\right]_{t=0}^{r}\\&{}=\pi r^{2}.\end{aligned}}}
Можно разбивать круг не на кольца, а на треугольники с бесконечно малым основанием. Площадь каждого такого треугольника равна 1/2 * r * dt. Суммируя (интегрируя) все площади этих треугольников, получим формулу круга:
- Area(r)=∫02πr12rdt=[12rt]t=02πr=πr2.{\displaystyle {\begin{aligned}\mathrm {Area} (r)&{}=\int _{0}^{2\pi r}{\frac {1}{2}}r\,dt\\&{}=\left[{\frac {1}{2}}rt\right]_{t=0}^{2\pi r}\\&{}=\pi r^{2}.\end{aligned}}}
Для применения формулы площади круга необходимо знать с нужной точностью значение числа π{\displaystyle \pi }. Вычисления, проведённые Архимедом, были трудоёмкими, и он остановился на многоугольнике с 96 сторонами. Более быстрый метод использует идеи Снелла (1621), позднее развитые Гюйгенсом (1654) [8].
Метод удвоения Архимеда[править | править код]
Если задан круг, пусть un будет периметром вписанного правильного n-угольника, а Un — периметром описанного правильного n-угольника. Тогда un и Un являются нижней и верхней границей длины окружности, которые становятся точнее с ростом n, а их среднее значение (un + Un)/2 становится особенно хорошей аппроксимацией длины окружности. Чтобы вычислить un и Un для больших n, Архимед вывел следующие формулы:
- u2n=U2nun{\displaystyle u_{2n}={\sqrt {U_{2n}u_{n}}}} (среднее геометрическое)
- U2n=2UnunUn+un{\displaystyle U_{2n}={\frac {2U_{n}u_{n}}{U_{n}+u_{n}}}} (среднее гармоническое).
Начав с шестиугольника, Архимед удваивал n четыре раза, дойдя до 96-угольника, который дал ему хорошую аппроксимацию длины окружности круга.
В современных обозначениях можно воспроизвести эти вычисления (и пойти дальше). Для единичной окружности вписанный шестиугольник имеет периметр u6 = 6, а описанный шестиугольник имеет периметр U6 = 4√3. Удваиваем семь раз, получаем
Удвоения Архимеда семь раз; n = 6×2k. k n un Un (un + Un)/4 0 6 6,0000000 6,9282032 3,2320508 1 12 6,2116571 6,4307806 3,1606094 2 24 6,2652572 6,3193199 3,1461443 3 48 6,2787004 6,2921724 3,1427182 4 96 6,2820639 6,2854292 3,1418733 5 192 6,2829049 6,2837461 3,1416628 6 384 6,2831152 6,2833255 3,1416102 7 768 6,2831678 6,2832204 3,1415970
(здесь (un + Un)/2 аппроксимирует длину единичной окружности, которая равна 2π, так что (un + Un)/4 аппроксимирует π)
Последняя строка таблицы содержит 355⁄113 — лучшее рациональное приближение, то есть не существует приближения лучшего этого со знаменателем до 113. Число 355⁄113 является прекрасным приближением для π, нет рационального числа более близкого к π со знаменателем до 16604.[9]
Улучшение Снелла-Гюйгенса[править | править код]
Снелл предложил (а Гюйгенс доказал) более тесные границы, чем у Архимеда:
- n3sinπn2+cosπn<π<n[2sinπ3n+tanπ3n].{\displaystyle n{\frac {3\sin {\frac {\pi }{n}}}{2+\cos {\frac {\pi }{n}}}}<\pi <n[2\sin {\frac {\pi }{3n}}+\tan {\frac {\pi }{3n}}].}
Для n = 48 формула даёт приближение лучше (около 3,14159292), чем метод Архимеда для n = 768.
Развитие формулы удваивания Архимеда[править | править код]
Круг с подобными треугольниками, описанным, вписанным и дополнительнымПусть одна сторона вписанного правильного n-угольника имеет длину sn и пусть точки A и B — её концы. Пусть A′ — противоположная A точка на окружности, так что A′A является диаметром, а A′AB является вписанным треугольником, опирающимся на этот диаметр. По теореме Фалеса этот треугольник является прямоугольным (угол B прямой). Пусть длина A′B равна cn и эту длину будем называть дополнением sn. Тогда cn2+sn2 = (2r)2. Пусть точка C делит дугу AB пополам, и пусть C′ является противоположной C точкой окружности. Тогда длина CA равна s2n, длина C′A равна c2n, а C′CA снова является прямоугольным треугольником, опирающимся на диаметр C′C. Поскольку C делит дугу AB пополам, диаметр C′C перпендикулярен хорде AB, которую он пересекает, скажем, в точке P. Треугольник C′AP тогда прямоуголен и подобен C′CA, поскольку у них общий угол C′. Получаем, что все три соответствующие стороны находятся в одной и той же пропорции. В частности, мы имеем C′A : C′C = C′P : C′A и AP : C′A = CA : C′C. Центр окружности O делит A′A пополам, так что треугольник OAP подобен A′AB и длина OP равна половине длины A′B. В результате получаем
- c2n2=(r+12cn)2rc2n=sns2n.{\displaystyle {\begin{aligned}c_{2n}^{2}&{}=\left(r+{\frac {1}{2}}c_{n}\right)2r\\c_{2n}&{}={\frac {s_{n}}{s_{2n}}}.\end{aligned}}}
В первом равенстве отрезок C′P равен сумме C′O+OP, что равно r+1⁄2cn, а отрезок C′C является диаметром и его длина равна 2r. Для единичного круга получаем знаменитую формулу удвоения Людольфа Ван Цейлена
- c2n=2+cn.{\displaystyle c_{2n}={\sqrt {2+c_{n}}}.}
Если мы теперь построим правильный описанный n-угольник со стороной ″B″, параллельной AB, то OAB и OA″B″ являются подобными с отношением подобия A″B″ : AB = OC : OP. Обозначим описанную сторону Sn, тогда отношение превращается в Sn : sn = 1 : 1⁄2cn. (Мы снова используем факт, что OP равен половине A′B.) Получаем
- cn=2snSn.{\displaystyle c_{n}=2{\frac {s_{n}}{S_{n}}}.}
Обозначим периметр вписанного многоугольника через un = nsn, а описанного через Un = nSn. Комбинируя равенства, получим
- c2n=sns2n=2s2nS2n,{\displaystyle c_{2n}={\frac {s_{n}}{s_{2n}}}=2{\frac {s_{2n}}{S_{2n}}},}
так что
- u2n2=unU2n.{\displaystyle u_{2n}^{2}=u_{n}U_{2n}.}
Получили среднее геометрическое.
Можно также вывести
- 2s2nS2nsns2n=2+2snSn,{\displaystyle 2{\frac {s_{2n}}{S_{2n}}}{\frac {s_{n}}{s_{2n}}}=2+2{\frac {s_{n}}{S_{n}}},}
или
- 2U2n=1un+1Un.{\displaystyle {\frac {2}{U_{2n}}}={\frac {1}{u_{n}}}+{\frac {1}{U_{n}}}.}
Получили среднее гармоническое.
Аппроксимация случайными бросаниями[править | править код]
 Площадь единичного круга методами Монте-Карло. После 900 бросаний получаем 4×709⁄900 = 3,15111…
Площадь единичного круга методами Монте-Карло. После 900 бросаний получаем 4×709⁄900 = 3,15111…Если более эффективные методы недоступны, можно прибегнуть к «бросанию дротиков». Этот метод Монте-Карло использует факт, что при случайных бросаниях точки равномерно распространяются по площади квадрата, в котором расположен круг, число попаданий в круг приближается к отношению площади круга на площадь квадрата. Следует принимать этот метод как последнюю возможность вычисления площади круга (или фигуры любой формы), поскольку для получения приемлемой точности требует огромного числа испытаний. Для получения точности 10−n необходимо около 100n случайных испытаний [10].
Как мы видели, разбив диск на бесконечное число кусков мы можем из них затем собрать прямоугольник. Интересный факт был открыт относительно недавно Лацковичем [11], что мы можем разбить круг на большое, однако конечное число кусков, а затем перегруппировать их в квадрат той же площади. Сам вопрос о таком конечном разбиении носит название «Квадратура круга Тарского».
Мы можем растянуть круг до формы эллипса. Поскольку это растяжение является линейным преобразованием плокости, оно изменяет площадь, но сохраняет отношения площадей. Этот факт можно использовать для вычисления площади произвольного эллипса, отталкиваясь от площади круга.
Пусть единичный эллипс описан квадратом со стороной 2. Преобразование переводит круг в эллипс путём сжатия или растяжения горизонтального и вертикального диаметров до малой и большой оси эллипса. Квадрат становится прямоугольником, описанным вокруг эллипса. Отношение площади круга к площади квадрата равно π/4, и отношение площади эллипса к площади прямоугольника будет тоже π/4. Если a и b — длины малой и большой осей эллипса. Площадь прямоугольника будет равна ab, а тогда площадь эллипса — πab/4.
Мы можем распространить аналогичные техники и на большие размерности. Например, если мы хотим вычислить объём внутри сферы, и мы знаем формулу для площади сферы, мы можем использовать приём, аналогичный «луковичному» подходу для круга.
- ↑ 1 2 Справочник по элементарной математике, 2006, с. 342.
- ↑ Ван дер Варден. Пробуждающаяся наука. Математика древнего Египта, Вавилона и Греции. — М.: Наука, 1959. — С. 204. — 456 с.
- ↑ История математики. С древнейших времен до начала Нового времени // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. I. — С. 102.
- ↑ Белозеров С. Е. Пять знаменитых задач древности. История и современная теория. — Ростов: изд-во Ростовского университета, 1975. — С. 144—168. — 320 с.
- ↑ Hill, George. Лекции по геометрии для начинающих, страница 124 (1894).
- ↑ Smith, Mikami, 1914.
- ↑ Beckmann, 1976.
- ↑ Gerretsen, Verdenduin, 1983.
- ↑ Не все лучшие рациональные приближения сводятся к непрерывным дробям!
- ↑ Thijsse, 2006.
- ↑ Laczkovich, 1990.
- Выгодский М. Я. Справочник по элементарной математике. — М.: АСТ, 2006. — 509 с. — ISBN 5-17-009554-6.
- Archimedes в переводе Томаса Хита. The Works of Archimedes. — Dover, c. 260 BCE, год публикации 2002. — С. 91–93. — ISBN 978-0-486-42084-4.
- Petr Beckmann. A History of Pi. — St. Martin’s Griffin, 1976. — ISBN 978-0-312-38185-1.
- J. Gerretsen, P. Verdenduin. Fundamentals of Mathematics, Volume II: Geometry. — MIT Press, 1983. — С. 243–250. — ISBN 978-0-262-52094-2.
- Serge Lang. Math! : Encounters with High School Students. — Springer-Verlag, 1985. — ISBN 978-0-387-96129-3.
- Miklós Laczkovich. Equidecomposability and discrepancy: A solution to Tarski’s circle squaring problem // Journal für die reine und angewandte Mathematik. — 1990. — Т. 404. — С. 77–117.
- David Eugene Smith, Yoshio Mikami. A history of Japanese mathematics. — Chicago: Open Court Publishing, 1914. — С. 130–132. — ISBN 978-0-87548-170-8.
- J. M.Thijsse. Computational Physics. — Cambridge University Press, 2006. — С. 273. — ISBN 978-0-521-57588-1.
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия

Основные определения и свойства
| Фигура | Рисунок | Определения и свойства |
| Окружность |  | Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности |
| Дуга |  | Часть окружности, расположенная между двумя точками окружности |
| Круг |  | Конечная часть плоскости, ограниченная окружностью |
| Сектор |  | Часть круга, ограниченная двумя радиусами |
| Сегмент |  | Часть круга, ограниченная хордой |
| Правильный многоугольник |  | Выпуклый многоугольник, у которого все стороны равны и все углы равны |
 | Около любого правильного многоугольника можно описать окружность |
| Окружность |
 Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности |
| Дуга |
 Часть окружности, расположенная между двумя точками окружности |
| Круг |
 Конечная часть плоскости, ограниченная окружностью |
| Сектор |
 Часть круга, ограниченная двумя радиусами |
| Сегмент |
 Часть круга, ограниченная хордой |
| Правильный многоугольник |
 Выпуклый многоугольник, у которого все стороны равны и все углы равны
Около любого правильного многоугольника можно описать окружность |
Определение 1. Площадью круга называют предел, к которому стремятся площади правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.
Определение 2. Длиной окружности называют предел, к которому стремятся периметры правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.
Замечание 1. Доказательство того, что пределы площадей и периметров правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон действительно существуют, выходит за рамки школьной математики и в нашем справочнике не приводится.
Определение 3. Числом π (пи) называют число, равное площади круга радиуса 1.
Замечание 2. Число π является иррациональным числом, т.е. числом, которое выражается бесконечной непериодической десятичной дробью:

Число π является трансцендентным числом, то есть числом, которое не может быть корнем алгебраического уравнения с целочисленными коэффициентами.
Формулы для площади круга и его частей
Формулы для длины окружности и её дуг
Площадь круга
Рассмотрим две окружности с общим центром (концентрические окружности) и радиусами радиусами 1 и R, в каждую из которых вписан правильный n – угольник (рис. 1).
Обозначим через O общий центр этих окружностей. Пусть внутренняя окружность имеет радиус 1.
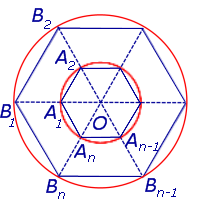
Рис.1
Площадь правильного n – угольника, вписанного в окружность радиуса R, равна


Площадь правильного n – угольника, вписанного в окружность радиуса 1, равна

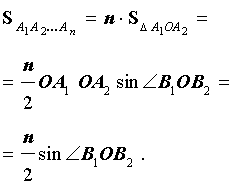
Следовательно,

Поскольку при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса 1, стремится к π, то при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса R, стремится к числу πR2.
Таким образом, площадь круга радиуса R, обозначаемая S, равна
S = πR2.
Длина окружности
Рассмотрим правильный n – угольник B1B2…Bn , вписанный в окружность радиуса радиуса R, и опустим из центраO окружности перпендикуляры на все стороны многоугольника (рис. 2).
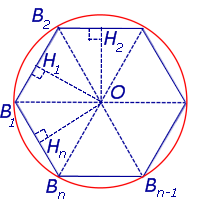
Рис.2
Поскольку площадь n – угольника B1B2…Bn равна


то, обозначая длину окружности радиуса R буквой C, мы, в соответствии с определением 2, при увеличении n получаем равенство:
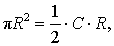
откуда вытекает формула для длины окружности радиуса R:
C = 2πR.
Следствие. Длина окружности радиуса 1 равна 2π.
Длина дуги
Рассмотрим дугу окружности, изображённую на рисунке 3, и обозначим её длину символом L(α), где буквой α обозначена величина соответствующего центрального угла.

Рис.3
В случае, когда величина α выражена в градусах, справедлива пропорция

из которой вытекает равенство:
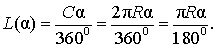
В случае, когда величина α выражена в радианах, справедлива пропорция

из которой вытекает равенство:

Площадь сектора
Рассмотрим круговой сектор, изображённый на рисунке 4, и обозначим его площадь символом S (α) , где буквой α обозначена величина соответствующего центрального угла.
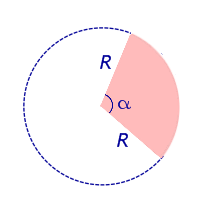
Рис.4
В случае, когда величина α выражена в градусах, справедлива пропорция

из которой вытекает равенство:
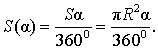
В случае, когда величина α выражена в радианах, справедлива пропорция
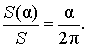
из которой вытекает равенство:

Площадь сегмента
Рассмотрим круговой сегмент, изображённый на рисунке 5, и обозначим его площадь символом S (α), где буквой α обозначена величина соответствующего центрального угла.

Рис.5
Поскольку площадь сегмента равна разности площадей кругового сектора MON и треугольника MON (рис.5), то в случае, когда величина α выражена в градусах, получаем
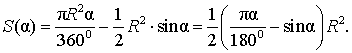
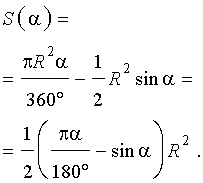
Следовательно,
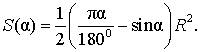
В случае, когда величина α выражена в в радианах, получаем
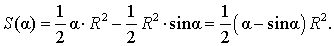
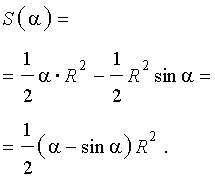
Следовательно,

На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Окружность — Википедия
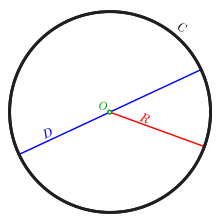 Окружность (C), её центр (O), радиус (R) и диаметр (D)
Окружность (C), её центр (O), радиус (R) и диаметр (D)Окру́жность — замкнутая плоская кривая, которая состоит из всех точек на плоскости, равноудалённых от заданной точки[1]: эта точка называется центром окружности. Отрезок, соединяющий центр с какой-либо точкой окружности, называется радиусом; радиусом называется также и длина этого отрезка. Окружность разбивает плоскость на две части[2] — конечную внутреннюю и бесконечную внешнюю. Внутренность окружности называется кругом; граничные точки (то есть саму окружность) в зависимости от подхода, круг может включать или не включать.
 Построение окружности циркулем
Построение окружности циркулемПрактическое построение окружности возможно с помощью циркуля.
Окружность нулевого радиуса (вырожденная окружность) является точкой, далее этот случай исключается из рассмотрения, если не оговорено иное.
Окружность называется единичной, если её радиус равен единице. Единичная окружность является одним из основных объектов тригонометрии.
Далее всюду буква R{\displaystyle R} обозначает радиус окружности.
Прямая может иметь с окружностью не более двух общих точек.
Прямая, пересекающая окружность в двух различных точках, называется секущей. Отрезок секущей, расположенный внутри окружности, называется хордой. Хорда, проходящая через центр окружности, называется диаметром; тот же термин используется для его длины. Диаметр вдвое больше радиуса: D=2R,{\displaystyle D=2R,} он делит окружность на две равные части и поэтому является её осью симметрии. Диаметр больше любой другой хорды[3].
Хорда разбивает круг на две части, называемые сегментами круга. Два различных радиуса тоже разбивают круг на две части, называемые секторами круга (см. рисунки)[3].
Любые две несовпадающие точки окружности делят её на две части. Каждая из этих частей называется дугой окружности. Дуга называется полуокружностью, если отрезок, соединяющий её концы, является диаметром.
Для заданной окружности имеют место следующие свойства[3].
- Хорды, равноотстоящие от центра, равны. Обратно, если две хорды равны по длине, то они одинаково удалены от центра.
- Равным хордам соответствуют равные дуги, и наоборот.

Прямая, имеющая с окружностью ровно одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности. Касательная к окружности всегда перпендикулярна её радиусу (и диаметру), проведенному в точке касания. То есть радиус является одновременно и нормалью к окружности[4].
Отрезки касательных к окружности, проведённых из одной точки, не лежащей на окружности, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности[5].
-

Вписанный угол θ равен половине величины центрального угла 2θ, опирающегося на ту же самую дугу (розового цвета)
-

К расчёту длины дуги и хорды
Центральный угол — угол с вершиной в центре окружности. Центральный угол может быть принят как угловая мера дуги, на которую он опирается. Центральный угол, образуемый дугой окружности, равной по длине радиусу, в математике принимается в качестве единицы измерения углов, и называется радиан.
Из определения радиана следует, что длина L{\displaystyle L} любой дуги окружности связана с центральным углом θ{\displaystyle \theta }, опирающимся на эту дугу, простым соотношением[6]: L=Rθ.{\displaystyle L=R\theta .} (при этом длина хорды, стягивающей ту же дугу, равна 2Rsinθ2<L{\displaystyle 2R\sin {\theta \over 2}<L}). Поскольку длина окружности равна 2πR{\displaystyle 2\pi R}, с ростом угла значение его радианной меры меняется от 0 до 2π.{\displaystyle 2\pi .}
Вписанный угол — угол, вершина которого лежит на окружности, а стороны пересекают эту окружность.
Внешний угол для вписанного угла — угол, образованный одной стороной и продолжением другой стороны вписанного угла (угол θ коричневого цвета на рис.). Внешний угол для вписанного угла равен вписанному углу, опирающемуся на ту же хорду с другой стороны.
Угол между окружностью и прямой — угол между секущей прямой и одной из двух касательных к окружности в точке пересечения прямой и окружности.
Свойства вписанных углов:
- Вписанный угол либо равен половине центрального угла, опирающегося на его дугу, либо дополняет половину этого угла до 180°. Вписанный угол, опирающийся на дугу длиной в половину окружности, всегда прямой (равен 90°).
- Вписанный угол не меняет своей величины при перемещении его вершины вдоль окружности.
- Два вписанных угла, опирающиеся на одну и ту же дугу, равны.
Другие свойства:
- Угол между двумя секущими, проведёнными из точки, лежащей вне окружности, равен полуразности мер дуг, лежащих между секущими.
- Угол между пересекающимися хордами равен полусумме мер дуги, лежащей в угле, и дуги напротив неё.
- Угол между касательной и хордой, имеющими общую точку, равен половине угловой меры дуги, стягиваемой хордой.
- Изопериметрическое неравенство: Из всех замкнутых кривых данной длины окружность ограничивает область максимальной площади.
- Через три точки, не лежащие на одной прямой, можно провести окружность, и притом только одну.
- Говорят, что две окружности касаются, если они имеют единственную общую точку. Точка касания двух окружностей лежит на прямой, проходящей через их центры.
- Теорема о секущих: Если через произвольную точку E{\displaystyle E} проведена секущая, то произведение расстояний от этой точки до точек пересечения секущей с окружностью не зависит от выбора секущей (и равно абсолютной величине степени точки относительно окружности). Если точка E{\displaystyle E} лежит вне окружности, то из нее к окружности можно провести касательную. Квадрат длины отрезка касательной до точки касания будет равен той же величине.
- Как частный случай предыдущего, при пересечении двух хорд в произвольной точке E{\displaystyle E} получаются отрезки, произведение длин которых у одной хорды равно соответствующему произведению у другой (см. рисунок), т. е. AE⋅EB=CE⋅ED{\displaystyle AE\cdot EB=CE\cdot ED}.
 AE⋅EB=CE⋅ED{\displaystyle AE\cdot EB=CE\cdot ED}
AE⋅EB=CE⋅ED{\displaystyle AE\cdot EB=CE\cdot ED}  Если радиус круга равен 1, то его окружность равна 2π.
Если радиус круга равен 1, то его окружность равна 2π.Длина окружности:
- C=2πR=πD.{\displaystyle C=2\pi R=\pi D.}
Радиус окружности:
- R=C2π=D2.{\displaystyle R={\frac {C}{2\pi }}={\frac {D}{2}}.}
Диаметр окружности:
- D=Cπ=2R.{\displaystyle D={\frac {C}{\pi }}=2R.}
Площадь круга радиуса R:
- S=πR2=πD24.{\displaystyle S=\pi R^{2}={\frac {\pi D^{2}}{4}}.}
Площадь сектора, ограниченного центральным углом α, измеряемым в градусах, радиусом R:
- S=πR2α360∘.{\displaystyle S=\pi R^{2}{\frac {\alpha }{360^{\circ }}}.}
Площадь сегмента, ограниченного дугой окружности, центральным углом α, хордой:
- S=πR2α360∘−R2sinα2.{\displaystyle S=\pi R^{2}{\frac {\alpha }{360^{\circ }}}-{\frac {R^{2}\sin \alpha }{2}}.}
Окружность, наряду с прямой, является самой распространённой кривой практически во всех областях человеческой деятельности. История её исследования и применения уходит в глубокую древность; особенную важность придало этой теме изобретение колеса. Античные учёные рассматривали прямые и окружности как единственный пример «совершенных» кривых, поэтому в геометрии считались допустимыми только построения с помощью циркуля и линейки, а движение планет моделировалось как наложение вращений по окружностям. Теории окружностей посвящена III книга «Начал» Евклида.
Также в древности было открыто, что отношение длины окружности к её диаметру (число π) одно и то же для всех окружностей. Исторически важной темой многовековых исследований было уточнение этого отношения, а также попытки решить проблему «квадратуры круга». В дальнейшем развитие теории окружностей привело к созданию тригонометрии, теории колебаний и многих других практически важных разделов науки и техники.
 Окружность получается как сечение конуса плоскостью, перпендикулярной его оси
Окружность получается как сечение конуса плоскостью, перпендикулярной его осиАналитическая геометрия окружностей[править | править код]
С точки зрения аналитической геометрии, окружность является простой плоской алгебраической кривой второго порядка. Окружность является частным случаем эллипса, у которого полуоси равны, и поэтому окружность относится к коническим сечениям.
Декартовы координаты[править | править код]
 Окружность радиуса r = 1, центр (a, b) = (1.2, −0.5)
Окружность радиуса r = 1, центр (a, b) = (1.2, −0.5)Общее уравнение окружности записывается как:
- x2+y2+Ax+By+C=0,{\displaystyle x^{2}+y^{2}+Ax+By+C=0,}
или
- (x−x0)2+(y−y0)2=R2,{\displaystyle \left(x-x_{0}\right)^{2}+\left(y-y_{0}\right)^{2}=R^{2},}
где
- 2×0=−A,2y0=−B,2R=A2+B2−4C.{\displaystyle 2x_{0}=-A,\;2y_{0}=-B,\;2R={\sqrt {A^{2}+B^{2}-4C}}.}
Точка (x0,y0){\displaystyle \left(x_{0},y_{0}\right)} — центр окружности, R{\displaystyle R} — её радиус.
Уравнение окружности радиуса R{\displaystyle R} с центром в начале координат:
- x2+y2=R2.{\displaystyle x^{2}+y^{2}=R^{2}.}
Уравнение окружности, проходящей через точки (x1,y1),(x2,y2),(x3,y3),{\displaystyle \left(x_{1},y_{1}\right),\left(x_{2},y_{2}\right),\left(x_{3},y_{3}\right),} не лежащие на одной прямой (с помощью определителя):
- |x2+y2xy1x12+y12x1y11x22+y22x2y21x32+y32x3y31|=0.{\displaystyle {\begin{vmatrix}x^{2}+y^{2}&x&y&1\\x_{1}^{2}+y_{1}^{2}&x_{1}&y_{1}&1\\x_{2}^{2}+y_{2}^{2}&x_{2}&y_{2}&1\\x_{3}^{2}+y_{3}^{2}&x_{3}&y_{3}&1\end{vmatrix}}=0.}
Тогда в явном виде координаты центра окружности определяются по формулам:
- x0=−12y1(x22+y22−x32−y32)+y2(x32+y32−x12−y12)+y3(x12+y12−x22−y22)x1(y2−y3)+x2(y3−y1)+x3(y1−y2){\displaystyle x_{0}=-{\frac {1}{2}}{\frac {y_{1}(x_{2}^{2}+y_{2}^{2}-x_{3}^{2}-y_{3}^{2})+y_{2}(x_{3}^{2}+y_{3}^{2}-x_{1}^{2}-y_{1}^{2})+y_{3}(x_{1}^{2}+y_{1}^{2}-x_{2}^{2}-y_{2}^{2})}{x_{1}(y_{2}-y_{3})+x_{2}(y_{3}-y_{1})+x_{3}(y_{1}-y_{2})}}}
- y0=12×1(x22+y22−x32−y32)+x2(x32+y32−x12−y12)+x3(x12+y12−x22−y22)x1(y2−y3)+x2(y3−y1)+x3(y1−y2){\displaystyle y_{0}={\frac {1}{2}}{\frac {x_{1}(x_{2}^{2}+y_{2}^{2}-x_{3}^{2}-y_{3}^{2})+x_{2}(x_{3}^{2}+y_{3}^{2}-x_{1}^{2}-y_{1}^{2})+x_{3}(x_{1}^{2}+y_{1}^{2}-x_{2}^{2}-y_{2}^{2})}{x_{1}(y_{2}-y_{3})+x_{2}(y_{3}-y_{1})+x_{3}(y_{1}-y_{2})}}}
Окружность также можно описать с помощью параметрического уравнения:
- {x=x0+Rcosφy=y0+Rsinφ,0⩽φ<2π.{\displaystyle {\begin{cases}x=x_{0}+R\cos \varphi \\y=y_{0}+R\sin \varphi \end{cases}},\;\;\;0\leqslant \varphi <2\pi .}
В декартовой системе координат окружность не является графиком функции, но она может быть описана как объединение графиков двух следующих функций:
- y=y0±R2−(x−x0)2.{\displaystyle y=y_{0}\pm {\sqrt {R^{2}-(x-x_{0})^{2}}}.}
Если центр окружности совпадает с началом координат, функции принимают вид:
- y=±R2−x2.{\displaystyle y=\pm {\sqrt {R^{2}-x^{2}}}.}
Полярные координаты[править | править код]
Окружность радиуса R{\displaystyle R} с центром в точке (ρ0,ϕ0){\displaystyle \left(\rho _{0},\phi _{0}\right)}:
- ρ2−2ρρ0cos(ϕ−ϕ0)+ρ02=R2.{\displaystyle \rho ^{2}-2\rho \,\rho _{0}\cos \left(\phi -\phi _{0}\right)+\rho _{0}^{2}=R^{2}.}
Если полярные координаты центра окружности ρ0=R,ϕ0=α,{\displaystyle \rho _{0}=R,\;\phi _{0}=\alpha ,} то проходящая через начало координат окружность описывается уравнением:
- ρ(φ)=2Rcos(φ−α),α−π2⩽φ⩽α+π2.{\displaystyle \rho (\varphi )=2R\cos \,(\varphi -\alpha ),\;\;\;\alpha -{\frac {\pi }{2}}\leqslant \varphi \leqslant \alpha +{\frac {\pi }{2}}.}
Если же центр является началом координат, то уравнение будет иметь вид
- ρ=R.{\displaystyle \rho =R.}
Комплексная плоскость[править | править код]
На комплексной плоскости окружность задаётся формулой:
- |z−z0|=R{\displaystyle \left|z-z_{0}\right|=R}
или в параметрическом виде
- z=z0+Reit,t∈R.{\displaystyle z=z_{0}+Re^{it},\,t\in \mathbb {R} .}
Окружности в пространстве[править | править код]
В пространстве окружность радиуса R{\displaystyle R} с центром в точке M0(x0,y0,z0){\displaystyle M_{0}(x_{0},y_{0},z_{0})} можно определить как контур диаметрального сечения сферы
- (x−x0)2+(y−y0)2+(z−z0)2=R2{\displaystyle (x-x_{0})^{2}+(y-y_{0})^{2}+(z-z_{0})^{2}=R^{2}}
плоскостью
- a⋅(x−x0)+b⋅(y−y0)+c⋅(z−z0)=0{\displaystyle a\cdot (x-x_{0})+b\cdot (y-y_{0})+c\cdot (z-z_{0})=0},
где a,b,c{\displaystyle a,b,c} — параметры, не равные одновременно нулю; то есть все точки, лежащие на данной окружности, есть решения системы
- {(x−x0)2+(y−y0)2+(z−z0)2=R2,a⋅(x−x0)+b⋅(y−y0)+c⋅(z−z0)=0.{\displaystyle {\begin{cases}(x-x_{0})^{2}+(y-y_{0})^{2}+(z-z_{0})^{2}=R^{2},\\a{\cdot }(x-x_{0})+b{\cdot }(y-y_{0})+c{\cdot }(z-z_{0})=0.\end{cases}}}
Например, при a=c≠0{\displaystyle a=c\neq 0} решения этой системы можно задать параметрически следующим образом:
- {x=x0+Ra2+c2⋅(c⋅cost−a⋅b⋅sinta2+b2+c2),y=y0+R⋅a2+c2a2+b2+c2⋅sint,z=z0−Ra2+c2⋅(a⋅cost+b⋅c⋅sinta2+b2+c2),t∈[0;2π).{\displaystyle {\begin{cases}x=x_{0}+{\dfrac {R}{\sqrt {a^{2}+c^{2}}}}\cdot \!\left(c\cdot \cos t-{\dfrac {a\cdot b\cdot \sin t}{\sqrt {a^{2}+b^{2}+c^{2}}}}\right)\!,\\[10pt]y=y_{0}+{\dfrac {R\cdot {\sqrt {a^{2}+c^{2}}}}{\sqrt {a^{2}+b^{2}+c^{2}}}}\cdot \sin t,\\[10pt]z=z_{0}-{\dfrac {R}{\sqrt {a^{2}+c^{2}}}}\cdot \!\left(a\cdot \cos t+{\dfrac {b\cdot c\cdot \sin t}{\sqrt {a^{2}+b^{2}+c^{2}}}}\right)\!,\end{cases}}t\in [0;2\pi ).}
Касательные и нормали[править | править код]
Уравнение касательной к окружности в точке (x1,y1
Формула длины окружности через радиус или диаметр
Окружность это замкнутая кривая линия, все точки которой, равноудалены от другой, определенной точки (центр окружности) на заданном расстоянии (радиус).
Радиус окружности — отрезок, соединяющий её центр и любую другую точку расположенную на линии окружности.
Диаметр окружности — отрезок, соединяющий две любые точки расположенные на линии окружности и проходящий через её центр. Диаметр, в два раза больше радиуса

r — радиус окружности
D — диаметр окружности
π ≈ 3.14
Формула длины окружности через радиус или диаметр, (L):

Калькулятор для расчета длины окружности через радиус
Калькулятор для расчета длины окружности через диаметр

S — площадь круга
O — центр круга
π ≈ 3.14
Формула длины окружности через площадь, (L):

Калькулятор для расчета длины окружности через площадь
Формулы для окружности и круга:
- Подробности
- Автор: Сергей Кондратов