Расчет потенциалов простейших электростатических полей
Рассмотрим несколько примеров вычисления разности потенциалов между точками поля, созданного некоторыми заряженными телами.
Разность потенциалов между точками поля, образованного двумя бесконечными заряженными плоскостями
Мы показали, что напряженность связана с потенциалом
тогда
| , | (3.7.1) |
где – напряженность электростатического поля между заряженными плоскостями, найденная в п. 2.5.2 с помощью теоремы Остроградского–Гаусса; σ = q/S– поверхностная плотность заряда.
Теперь, чтобы получить выражение для потенциала между плоскостями, проинтегрируем выражение (3.7.1):
| или . | (3.7.2) |
| При x1 = 0 и x2 = d . | (3.7.3) |
Рис. 3.5
На рисунке 3.5 изображена графическая зависимость напряженности E и потенциала φ от расстояния между плоскостями.
Разность потенциалов между точками поля,образованного бесконечно длинной цилиндрической поверхностью
| (3.7.4) |
Т.к. то , отсюда найдем разность потенциалов в произвольных точках 1 и 2:
.
Рис. 3.6
| (3.7.5) |
На рисунке 3.6 изображена зависимость напряженности E и потенциала от r. (Здесь и далее
Разность потенциалов между обкладками цилиндрического конденсатора
В п. 2.5. мы нашли, что (рис. 3.7)
Отсюда так же, как и в предыдущем случае, разность потенциалов будет равна:
.
Таким образом, внутри меньшего цилиндра имеем , Е = 0, между обкладками потенциал уменьшается по логарифмическому закону, а вторая обкладка (вне цилиндров) экранирует электрическое поле и φ и
Рис. 3.7
| (3.7.6) |
На рисунке 3.7 изображена зависимость напряженности E и потенциала от r.
Разность потенциалов между точками поля, образованного заряженной сферой (пустотелой)
Напряженность поля сферы (рис. 3.8) определяется формулой: .
Рис. 3.8
Т.к. , то
| (3.7.7) |
Разность потенциалов внутри диэлектрического заряженного шара
Имеем диэлектрический шар (рис. 3.9), заряженный с объемной плотностью
В п. 2.5 с помощью теоремы Остроградского–Гаусса мы нашли, что внутри шара .
Рис. 3.9
Теперь найдем разность потенциалов внутри шара:
или
Отсюда находим потенциал шара:
(3.7.9)
Из полученных соотношений можно сделать следующие выводы.
С помощью теоремы Гаусса сравнительно просто можно рассчитать Е и φ от различных заряженных поверхностей.
Напряженность поля в вакууме изменяется скачком при переходе через заряженную поверхность.
Потенциал поля – всегда непрерывная функция координат.
12 Разность потенциалов
Разностью
потенциалов 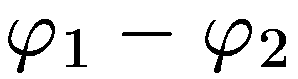 между
точками 1 и 2 называется работа, совершаемая
силами поля при перемещении единичного
положительного заряда по произвольному
пути из точки 1 в точку 2. для потенциальных
полей эта работа не зависит от формы
пути, а определяется только положениями
начальной и конечной точек
между
точками 1 и 2 называется работа, совершаемая
силами поля при перемещении единичного
положительного заряда по произвольному
пути из точки 1 в точку 2. для потенциальных
полей эта работа не зависит от формы
пути, а определяется только положениями
начальной и конечной точек
потенциал определен с точностью до аддитивной постоянной. Работа сил электростатического поля при перемещении заряда q по произвольному пути из начальной точки 1 в конечную точку 2 определяется выражением
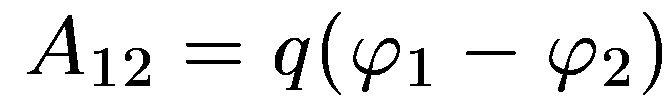
Практической единицей потенциала является вольт. Вольт есть разность потенциалов между такими точками, когда при перемещении одного кулона электричества из одной точки в другую электрическое поле совершает работу в один джоуль.
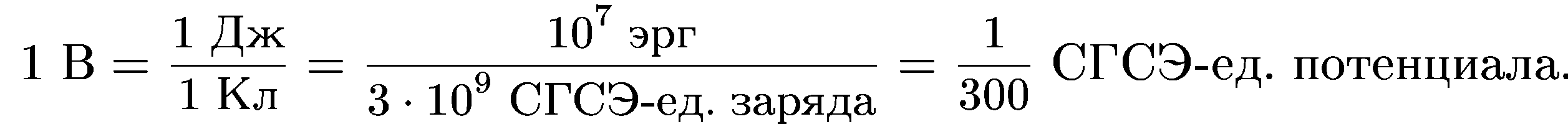
1 и 2 — бесконечно близкие точки, расположенные на оси х, так что Х2 — х1 = dx.
Работа
при перемещении единицы заряда из точки
1 в точку 2 будет Ех dx. Та же работа равна 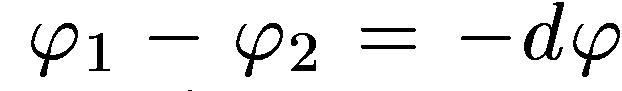 .
Приравнивая оба выражения, получим
.
Приравнивая оба выражения, получим
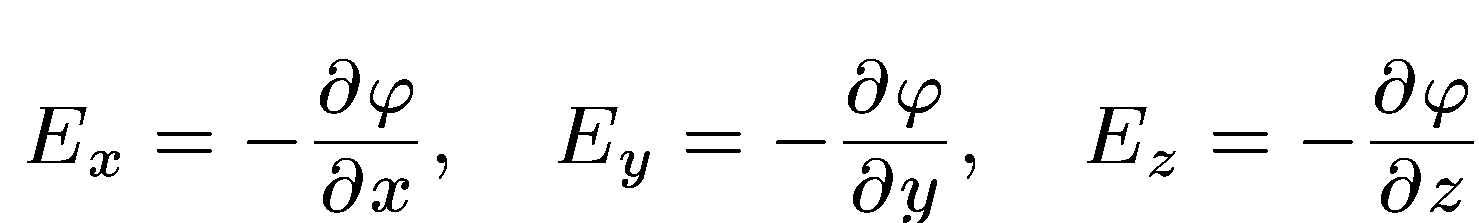
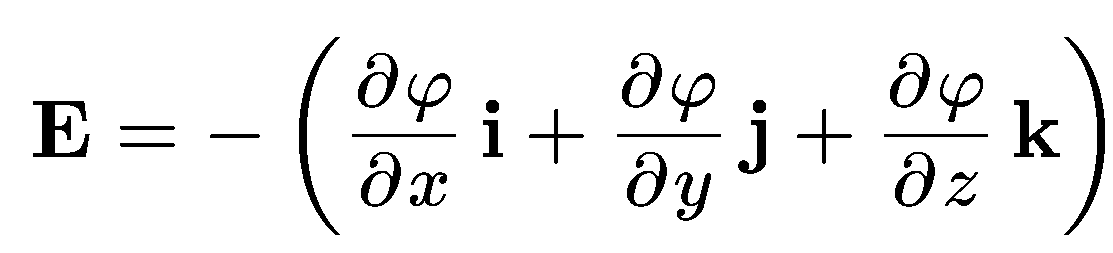 —
градиент скаляра
—
градиент скаляра 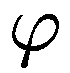
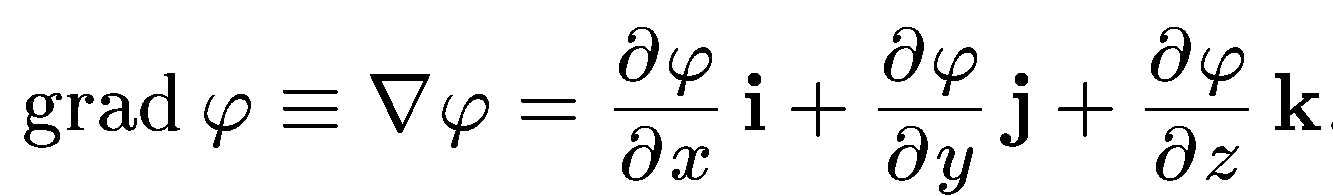
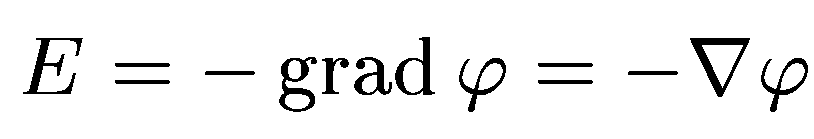
Градиент
функции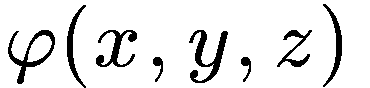 есть вектор, направленный в сторону
максимального возрастания этой функции,
а его длина равна производной функции
есть вектор, направленный в сторону
максимального возрастания этой функции,
а его длина равна производной функции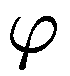 в том же направлении. Геометрический
смысл градиента–
эквипотенциальные поверхности (
поверхности равного потенциала)
поверхность, на которой потенциал
остается постоянным.
в том же направлении. Геометрический
смысл градиента–
эквипотенциальные поверхности (
поверхности равного потенциала)
поверхность, на которой потенциал
остается постоянным.
13 Потенциал зарядов
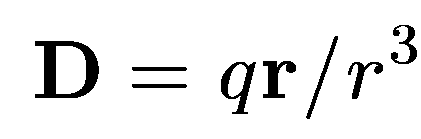 —
электрическое смещение точечного заряда
в однородном диэлектрикеD
–вектор
электрической индукции или электрического
смещения
—
электрическое смещение точечного заряда
в однородном диэлектрикеD
–вектор
электрической индукции или электрического
смещения 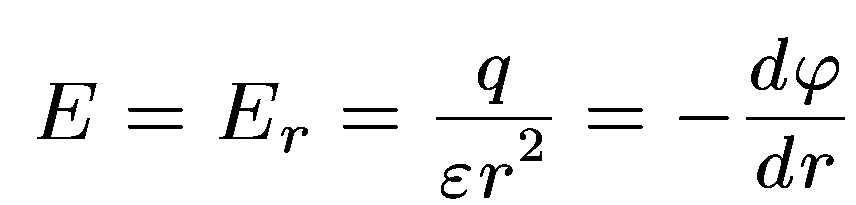
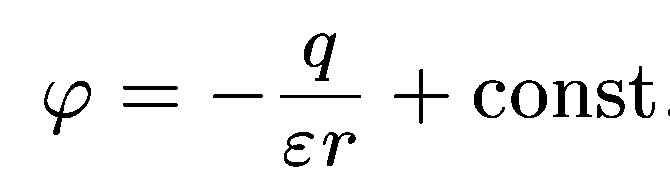 В
качестве постоянной интегрирования
следует взять нуль, чтобы при
В
качестве постоянной интегрирования
следует взять нуль, чтобы при 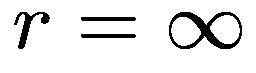 потенциал обратился в ноль, тогда
потенциал обратился в ноль, тогда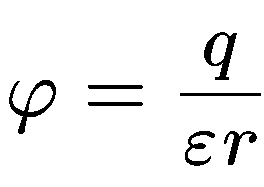
Потенциал поля системы точечных зарядов в однородном диэлектрике.
Используя принцип суперпозии получаем:
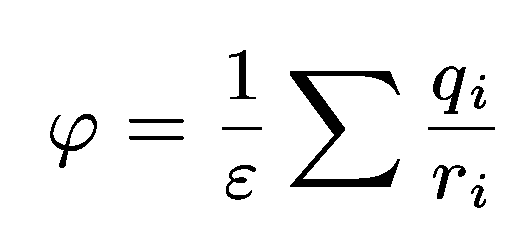
Потенциал непрерывно распределенных электрических зарядов.
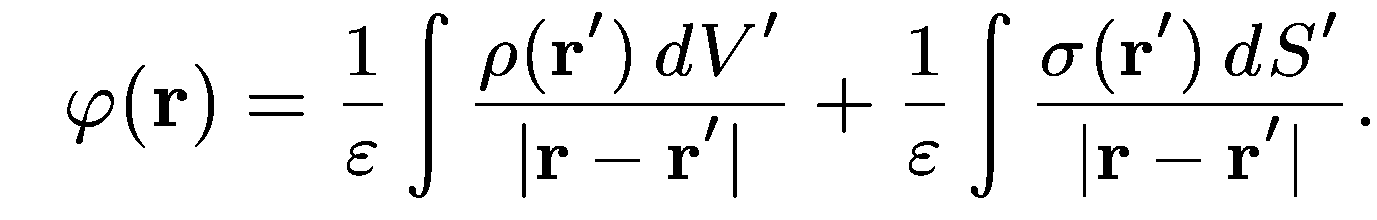
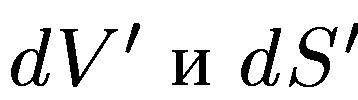 — элементы объема и заряженных поверхностей
с центрами в точке
— элементы объема и заряженных поверхностей
с центрами в точке 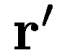
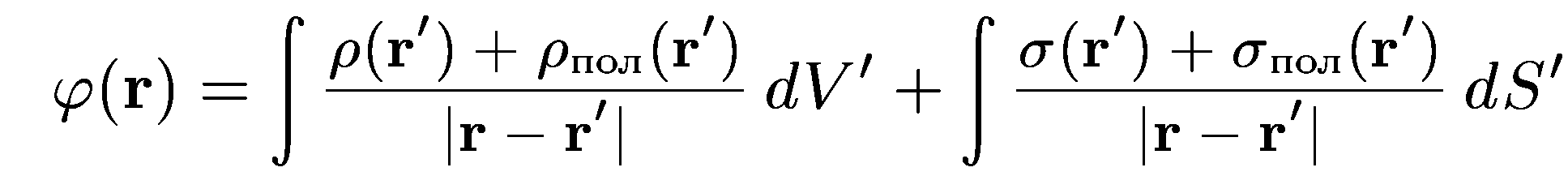 —
в случае если диэлектрик неоднороден,
то интегрирование надо распространить
и на поляризационные заряды. Включение
таких
—
в случае если диэлектрик неоднороден,
то интегрирование надо распространить
и на поляризационные заряды. Включение
таких
зарядов
автоматически учитывает влияние среды,
и величину 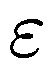 вводить не надо
вводить не надо
14 Электрическое поле в веществе
Электрическое поле в веществе. Вещество, внесенное в электрическое поле, может существенно изменить его. Это связано с тем, что вещество состоит из заряженных частиц. В отсутствие внешнего поля частицы распределяются внутри вещества так, что создаваемое ими электрическое поле в среднем по объемам, включающим большое число атомов или молекул, равно нулю. При наличии внешнего поля происходит перераспределение заряженных частиц, и в веществе возникает собственное электрическое поле. Полное электрическое поле складывается в соответствии с принципом суперпозиции из внешнего поля и внутреннего поля , создаваемого заряженными частицами вещества. Вещество многообразно по своим электрическим свойствам. Наиболее широкие классы вещества составляют проводники и диэлектрики. Проводник — это тело или материал, в котором электрические заряды начинают перемещаться под действием сколь угодно малой силы. Поэтому эти заряды называют свободными. В металлах свободными зарядами являются электроны, в растворах и расплавах солей (кислот и щелочей) — ионы. Диэлектрик — это тело или материал, в котором под действием сколь угодно больших сил заряды смещаются лишь на малое, не превышающее размеров атома расстояние относительно своего положения равновесия. Такие заряды называются связанными. Свободные и связанные заряды. СВОБОДНЫЕ ЗАРЯДЫ 1) избыточные электрич. заряды, сообщённые проводящему или непроводящему телу и вызывающие нарушение его электронейтральности. 2) Электрич. заряды носителей тока. 3) положит. электрич. заряды атомных остатков в металлах. СВЯЗАННЫЕ ЗАРЯДЫ Электрич. заряды частиц, входящих в состав атомов и молекул диэлектрика, а также заряды ионов в кристаллич. диэлектриках с ионной решёткой.
Потенциал электростатического поля. Разность потенциалов
На прошлом уроке мы с вами говорили о том, что на помещённый в электростатическое поле пробный заряд, будет действовать сила, под действием которой заряд способен перемещаться вдоль линии напряжённости поля. Иными словами, электростатическое поле способно совершать работу, значение которой пропорционально величине переносимого заряда и зависит только от того, из какой и в какую точку поля заряд переносится:

При этом на замкнутой траектории работа сил электростатического поля равна нулю.
Напомним, что если работа сил поля не зависит от формы траектории и на замкнутой траектории равна нулю, то такое поле называется потенциальными. Следовательно, точечный заряд, находящийся в любой точке электростатического поля, обладает потенциальной энергией взаимодействия с этим полем, значение которой определяют относительно произвольно выбираемой нулевой точки (чаще всего, это бесконечно удалённая точка поля). В нулевой точке потенциальную энергию заряда в поле принимают равной нулю. Тогда потенциальная энергия взаимодействия точечного заряда с электростатическим полем равна работе, которую совершили бы силы поля при перемещении данного заряда из указанной точки поля в нулевую точку:

Из этого определения следует, что величина потенциальной энергии заряда в электростатическом поле пропорционально значению этого заряда:

Иными словами, если мы будем вносить в одну и туже точку электростатического поля пробные заряды, значения которых будут отличаться в два, три, четыре и так далее раз, то потенциальные энергии этих зарядов будут отличаться во столько же раз.

Однако, отношение потенциальной энергии пробного заряда в поле к значению этого заряда для данной точки поля остаётся неизменным:

Отношение потенциальной энергии пробного заряда, помещённого в данную точку поля, к величине этого заряда, называется потенциалом электростатического поля в данной точке пространства:

Обозначать потенциал мы будем греческой буквой «Фи» (φ).
Вы уже знаете, что силовой характеристикой электрического поля является напряжённость. Потенциал же характеризует энергетическое состояние поля в данной точке пространства.
Поскольку потенциальная энергия заряда в электростатическом поле зависит от выбора нулевой точки, то эта зависимость сохраняется и для потенциала. Если принять, что на бесконечно большом расстоянии от источника поле отсутствует, то потенциал поля в данной точке численно равен работе, совершаемой при перемещении пробного заряда из данной точки поля в бесконечность (то есть в нулевую точку):

Найдём формулу, по которой можно рассчитать потенциал электростатического поля, создаваемого точечным зарядом, на некотором расстоянии от него. Для этого запишем формулу для определения работы электростатического поля:

Здесь r — это расстояние от создающего поле заряда до исследуемой точки поля. А модуль напряжённости поля прямо пропорционален модулю этого заряда и обратно пропорционален квадрату расстояния между зарядом и точкой, в которой определяют значение напряжённости:

Перепишем формулу для потенциала поля с учётом наших рассуждений.

После упрощения, получим формулу, по которой можно рассчитать потенциал электростатического поля точечного заряда на заданном расстоянии от него. Из формулы видно, что знак заряда-источника поля определяет знак потенциала этого поля.
По этой же формуле можно рассчитывать и потенциал поля, создаваемого равномерно заряженной проводящей сферой в точках, находящихся вне сферы. Для точек же, находящихся на поверхности и внутри сферы, в знаменателе формулы «Эр малое» заменяется на радиус сферы:

Если электростатическое поле создаётся системой зарядов, то имеет место принцип суперпозиции: потенциал такого поля в любой точке пространства равен алгебраической сумме потенциалов, создаваемых в этой точке каждым зарядом системы в отдельности:

Зная потенциал поля в данной точке, можно рассчитать потенциальную энергию заряда, помещённого в эту точку:

На прошлом уроке мы с вами отмечали тот факт, что работа сил электростатического поля по перемещению электрического заряда из начальной точки в конечную равна изменению потенциальной энергии, взятому с обратным знаком:


Давайте выразим потенциальную энергию через потенциалы поля в соответствующих точках:

Подставим значения потенциальных энергий в формулу для работы.

Как видно из полученной формулы, работа поля по перемещению заряда из одной его точки в другую пропорциональна значению переносимого заряда и разности потенциалов начальной и конечной точек.
А теперь давайте разделим выражение для работы на величину переносимого заряда q0:

Скалярная физическая величина, численно равная отношению работы сил поля по перемещению заряда между данными точками поля к величине этого заряда, называется разностью потенциалов.
Как и изменение потенциальной энергии, разность потенциалов не зависит от выбора нулевой точки.
Из определения следует, что единицей разности потенциалов в СИ является Дж/Кл. Эта единица называется вольтом, в честь итальянского учёного Алессандро Джузеппе Антонио Анастасио Джероламо Умберто Вольта.
1 В — это разность потенциалов между двумя такими точками электростатического поля, при перемещении между которыми заряда в 1 Кл силами поля совершается работа 1 Дж.
Как вы, наверное, догадались, разность потенциалов очень часто называют напряжением.
То есть напряжение между двумя точками поля определяется работой сил этого поля по перемещению заряда 1 Кл из одной точки в другую. В электростатическом поле напряжение вдоль замкнутого контура всегда равно нулю.
Для закрепления нового материала, решим с вами несколько задач. Задача 1. В центре проводящей сферы с равномерно распределённым положительным зарядом в 45 нКл находится металлический шарик с отрицательным зарядом, модуль которого равен 17 нКл. Определите потенциал электростатического поля в точке, находящейся вне сферы на расстоянии 30 м от её центра.

Задача 2. Электрон влетает в однородное электростатическое поле по направлению силовой линии. Определите потенциал точки поля, в которой электрон поменяет направление движения, если в точке поля с потенциалом 1 В его скорость равнялась 300 км/с.

Связь между напряжённостью электростатического поля и разностью потенциалов. Эквипотенциальные поверхности
Связь между напряжённостью электростатического поля и разностью потенциалов. Эквипотенциальные поверхности
«Физика — 10 класс»
Какие две характеристики электростатического поля вы уже знаете? Как они определяются?
Для чего электрическое поле изображают силовыми линиями?
Каждой точке электрического поля соответствуют определённые значения потенциала и напряжённости. Найдём связь напряжённости электрического поля с разностью потенциалов.
Пусть заряд q перемещается в направлении вектора напряжённости однородного электрического поля Е из точки 1 в точку 2, находящуюся на расстоянии Δd от точки 1 (рис. 14.33). Электрическое поле совершает работу
А = qEΔd.
Эту работу согласно формуле (14.19) можно выразить через разность потенциалов между точками 1 и 2:
А = g(φ1 — φ2) = -qΔφ = qU. (14.20)
Приравнивая выражения для работы, найдём модуль вектора напряжённости поля:
В этой формуле U — разность потенциалов между точками 1 и 2, лежащими на одной силовой линии поля (см. рис. 14.33).
Формула (14.21) показывает: чем меньше меняется потенциал на расстоянии Δd, тем меньше напряжённость электростатического поля. Если потенциал не меняется совсем, то напряжённость поля равна нулю.
Так как при перемещении положительного заряда в направлении вектора напряжённости электростатическое поле совершает положительную работу
А = q(φ1 — φ2) > 0,
то потенциал φ1 больше потенциала φ2.
Напряжённость электрического поля направлена в сторону убывания потенциала.
Любое электростатическое поле в достаточно малой области пространства можно считать однородным.
Формула (14.21) справедлива для произвольного электростатического поля, если только расстояние Δd настолько мало, что изменением напряжённости поля на этом расстоянии можно пренебречь.
Сравним поле силы тяжести и однородное электростатическое поле.
Единица напряжённости электрического поля. Единицу напряжённости электрического поля в СИ устанавливают, используя формулу (14.21).
Напряжённость электрического поля численно равна единице, если разность потенциалов между двумя точками, лежащими на одной силовой линии, на расстоянии 1 м в однородном поле равна 1 В.
Единица напряжённости — вольт на метр (В/м).
Напряжённость, как мы уже знаем, можно также выражать в ньютонах на кулон. Действительно,
Эквипотенциальные поверхности.
При перемещении заряда под углом 90° к силовым линиям электрическое поле не совершает работу, так как электростатическая сила перпендикулярна перемещению. Значит, если провести поверхность, перпендикулярную в каждой её точке силовым линиям, то при перемещении заряда вдоль этой поверхности работа не совершается. А это означает, что все точки поверхности, перпендикулярной силовым линиям, имеют один и тот же потенциал.
Поверхности равного потенциала называют эквипотенциальными.
Эквипотенциальные поверхности однородного поля представляют собой плоскости (рис. 14.34, а), а поля точечного заряда — концентрические сферы (рис. 14.34, б).
Эквипотенциальные поверхности качественно характеризуют распределение поля в пространстве подобно тому, как линии уровня отражают рельеф поверхности на географических картах. Вектор напряжённости перпендикулярен эквипотенциальным поверхностям и направлен в сторону уменьшения потенциала.
Эквипотенциальные поверхности строятся обычно так, что разность потенциалов между двумя соседними поверхностями постоянна. Поэтому согласно формуле (14.21) расстояния между соседними эквипотенциальными поверхностями увеличиваются по мере удаления от точечного заряда, так как напряжённость поля уменьшается.
Эквипотенциальные поверхности однородного поля расположены на равных расстояниях друг от друга.
Эквипотенциальной является поверхность любого проводника в электростатическом поле. Ведь силовые линии перпендикулярны поверхности проводника. Причём не только поверхность, но и все точки внутри проводника имеют один и тот же потенциал. Напряжённость поля внутри проводника равна нулю, значит, равна нулю и разность потенциалов между любыми точками проводника.
Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
Электростатика — Физика, учебник для 10 класса — Класс!ная физика
Что такое электродинамика — Электрический заряд и элементарные частицы. Закон сохранения заряд — Закон Кулона. Единица электрического заряда — Примеры решения задач по теме «Закон Кулона» — Близкодействие и действие на расстоянии — Электрическое поле — Напряжённость электрического поля. Силовые линии — Поле точечного заряда и заряженного шара. Принцип суперпозиции полей — Примеры решения задач по теме «Напряжённость электрического поля. Принцип суперпозиции полей» — Проводники в электростатическом поле — Диэлектрики в электростатическом поле — Потенциальная энергия заряженного тела в однородном электростатическом поле — Потенциал электростатического поля и разность потенциалов — Связь между напряжённостью электростатического поля и разностью потенциалов. Эквипотенциальные поверхности — Примеры решения задач по теме «Потенциальная энергия электростатического поля. Разность потенциалов» — Электроёмкость. Единицы электроёмкости. Конденсатор — Энергия заряженного конденсатора. Применение конденсаторов — Примеры решения задач по теме «Электроёмкость. Энергия заряженного конденсатора»
Разность потенциалов — Большая советская энциклопедия
Ра́зность потенциа́лов
Между двумя точками стационарного электрического или гравитационного поля измеряется работой, совершаемой силами поля при перемещении единичного положительного заряда или, соответственно, единичной массы из одной точки с большим Потенциалом в другую с меньшим потенциалом. Если φ1, φ2— потенциалы начальной и конечной точек траектории перемещаемого заряда (или массы), то Р. п. u = φ1—φ2 ; изменение потенциала Δφ = φ2—φ1= — и.
Работа произвольного электрического поля по перемещению +1 заряда из одной точки в другую называемый электрическим напряжением (См. Электрическое напряжение) между этими точками; в случае стационарного поля напряжение совпадает с Р. п.
Источник: Большая советская энциклопедия на Gufo.me
Значения в других словарях
- РАЗНОСТЬ ПОТЕНЦИАЛОВ — РАЗНОСТЬ ПОТЕНЦИАЛОВ, (электрическое напряжение), разность в НАПРЯЖЕНИИ (ЭЛЕКТРИЧЕСКОМ ПОТЕНЦИАЛЕ) между двумя точками в цепи или в электрическом поле. Обычно выражается в ВОЛЬТАХ. Научно-технический словарь
- РАЗНОСТЬ ПОТЕНЦИАЛОВ — Между двумя точками стационарного электрич. или гравитац. поля измеряется работой, совершаемой силами поля при перемещении единичного положит. заряда или, соответственно, единичной массы из точки с большим потенциалом в точку с меньшим потенциалом. Физический энциклопедический словарь
- РАЗНОСТЬ ПОТЕНЦИАЛОВ — РАЗНОСТЬ ПОТЕНЦИАЛОВ электрическая (электрическое напряжение) между двумя точками — равна работе электрического поля по перемещению единичного положительного заряда из одной точки поля в другую. Большой энциклопедический словарь




