Формула расчета реактивной мощности – Компенсация реактивной мощности: расчет мощности и выбор ступени регулирования конденсаторной батареи — groupnk.ru — Группа НК — комплексные поставки электрооборудования в Москве и регионах

Содержание

Расчет реактивной мощности | Проектирование электроснабжения

Для компенсации реактивной мощности в электрических сетях используют конденсаторные установки. Основным параметром конденсаторной установки является реактивная мощность конденсаторов необходимая компенсации. В этой статье я расскажу, как рассчитывается мощность конденсаторной установки, а также представлю вашему вниманию свою программу для расчета реактивной мощности конденсаторной установки.

После того, как мы подключили все электроприемники, у нас уже есть расчетная мощность, реактивная мощность и коэффициент мощность электроустановки.

Все эти данные необходимы для расчета реактивной мощности конденсаторной установки.

Реактивная мощность конденсаторной установки требуемая для получения нужного коэффициента мощности определяется по формуле:

Qк=Р*К

Qк – реактивная мощность конденсаторной установки, кВАр;

Р – активная мощность, кВт;

К – коэффициент выбираемый из таблицы;

сosf1 – коэффициент мощности по расчету;

сosf2– коэффициент мощности требуемой энергоснабжающей организацией;

Таблица для выбора коэффициента К

Приведу пример.

Пусть P=412кВт, сosf1=0,6, сosf2=0,92.

Из таблицы находим К=0,907 (на пересечении сosf1 и сosf2).

Тогда Qк=412*0,907=373,7кВАр.

Как видим, в таблице присутствуют не все значения. А это значит, что пользоваться этим методом не совсем удобно, приходится интерполировать значения.

На основе этого метода я сделал простую программу для расчета требуемой реактивной мощности конденсаторной установки.

Расчет реактивной мощности конденсаторной установки

Указываем расчетную мощность, реактивную мощность и требуемый коэффициент мощности и программа сразу выдаст вам результат.

Условия получения программы для расчета реактивной мощности конденсаторной установки на странице МОИ ПРОГРАММЫ.

Перечень нормативных документов по компенсации реактивной мощности.

ТКП 45-4.04-149-2009. Системы электрооборудования жилых и общественных зданий. Правила проектирования (гл.8.3).
СП 31-110-2003. Свод правил по проектированию и строительству. «Проектирование и монтаж электроустановок жилых и общественных зданий»(п.6.33-6.34).

Советую почитать:

Расчет установки компенсации реактивной мощности 0.4 кв

Для того чтобы произвести расчет установки компенсации реактивной мощности 0.4 кв, заполните пожалуйста поля, приведенные ниже и нажмите кнопку «Рассчитать».

Формула расчета реактивной мощности КРМ

Q = P_a_{· ( tgφ₁-tgφ₂)} — реактивная мощность установки КРМ (кВАр)

Q = P_a · K, где

P_a -активная мощность (кВт), K- коэффициент из таблицы

P_a_{= S· cosφ}, где

S -полная мощность(кВА)

cos φ — коэффициент мощности

tg(φ₁+φ₂) согласуются со значениями cos φ в таблице.

Таблица определения установки компенсации реактивной мощности, cos(φ):

Текущий (действующий)		Требуемый (достижимый) cos (φ)
tan (φ)	cos (φ)	0.80	0.82	0.85	0.88	0.90	0.92	0.94	0.96	0.98	1.00
tan (φ)	cos (φ)	Коэффициент K
3.18	0.30	2.43	2.48	2.56	2.64	2.70	2.75	2.82	2.89	2.98	3.18
2.96	0.32	2.21	2.26	2.34	2.42	2.48	2.53	2.60	2.67	2.76	2.96
2.77	0.34	2.02	2.07	2.15	2.23	2.28	2.34	2.41	2.48	2.56	2.77
2.59	0.36	1.84	1.89	1.97	2.05	2.10	2.17	2.23	2.30	2.39	2.59
2.43	0.38	1.68	1.73	1.81	1.89	1.95	2.01	2.07	2.14	2.23	2.43
2.29	0.40	1.54	1.59	1.67	1.75	1.81	1.87	1.93	2.00	2.09	2.29
2.16	0.42	1.41	1.46	1.54	1.62	1.68	1.73	1.80	1.87	1.96	2.16
2.04	0.44	1.29	1.34	1.42	1.50	1.56	1.61	1.68	1.75	1.84	2.04
1.93	0.46	1.18	1.23	1.31	1.39	1.45	1.50	1.57	1.64	1.73	1.93
1.83	0.48	1.08	1.13	1.21	1.29	1.34	1.40	1.47	1.54	1.62	1.83
1.73	0.50	0.98	1.03	1.11	1.19	1.25	1.31	1.37	1.45	1.63	1.73
1.64	0.52	0.89	0.94	1.02	1.10	1.16	1.22	1.28	1.35	1.44	1.64
1.56	0.54	0.81	0.86	0.94	1.02	1.07	1.13	1.20	1.27	1.36	1.56
1.48	0.56	0.73	0.78	0.86	0.94	1.00	1.05	1.12	1.19	1.28	1.48
1.40	0.58	0.65	0.70	0.78	0.86	0.92	0.98	1.04	1.11	1.20	1.40
1.33	0.60	0.58	0.63	0.71	0.79	0.85	0.91	0.97	1.04	1.13	1.33
1.30	0.61	0.55	0.60	0.68	0.76	0.81	0.87	0.94	1.01	1.10	1.30
1.27	0.62	0.52	0.57	0.65	0.73	0.78	0.84	0.91	0.99	1.06	1.27
1.23	0.63	0.48	0.53	0.61	0.69	0.75	0.81	0.87	0.94	1.03	1.23
1.20	0.64	0.45	0.50	0.58	0.66	0.72	0.77	0.84	0.91	1.00	1.20
1.17	0.65	0.42	0.47	0.55	0.63	0.68	0.74	0.81	0.88	0.97	1.17
1.14	0.66	0.39	0.44	0.52	0.60	0.65	0.71	0.78	0.85	0.94	1.14
1.11	0.67	0.36	0.41	0.49	0.57	0.63	0.68	0.75	0.82	0.90	1.11
1.08	0.68	0.33	0.38	0.46	0.54	0.59	0.65	0.72	0.79	0.88	1.08
1.05	0.69	0.30	0.35	0.43	0.51	0.56	0.62	0.69	0.76	0.85	1.05
1.02	0.70	0.27	0.32	0.40	0.48	0.54	0.59	0.66	0.73	0.82	1.02
0.99	0.71	0.24	0.29	0.37	0.45	0.51	0.57	0.63	0.70	0.79	0.99
0.96	0.72	0.21	0.26	0.34	0.42	0.48	0.54	0.60	0.67	0.76	0.96
0.94	0.73	0.19	0.24	0.32	0.40	0.45	0.51	0.58	0.65	0.73	0.94
0.91	0.74	0.16	0.21	0.29	0.37	0.42	0.48	0.55	0.62	0.71	0.91
0.88	0.75	0.13	0.18	0.26	0.34	0.40	0.46	0.52	0.59	0.68	0.88
0.86	0.76	0.11	0.16	0.24	0.32	0.37	0.43	0.50	0.57	0.65	0.86
0.83	0.77	0.08	0.13	0.21	0.29	0.34	0.40	0.47	0.54	0.63	0.83
0.80	0.78	0.05	0.10	0.18	0.26	0.32	0.38	0.44	0.51	0.60	0.80
0.78	0.79	0.03	0.08	0.16	0.24	0.29	0.35	0.42	0.49	0.57	0.78
0.75	0.80		0.05	0.13	0.21	0.27	0.32	0.39	0.46	0.55	0.75
0.72	0.81			0.10	0.18	0.24	0.30	0.36	0.43	0.52	0.72
0.70	0.82			0.08	0.16	0.21	0.27	0.34	0.41	0.49	0.70
0.67	0.83			0.05	0.13	0.19	0.25	0.31	0.38	0.47	0.67
0.65	0.84			0.03	0.11	0.16	0.22	0.29	0.36	0.44	0.65
0.62	0.85				0.08	0.14	0.19	0.26	0.33	0.42	0.62
0.59	0.86				0.05	0.11	0.17	0.23	0.30	0.39	0.59
0.57	0.87					0.08	0.14	0.21	0.28	0.36	0.57
0.54	0.88					0.06	0.11	0.18	0.25	0.34	0.54
0.51	0.89					0.03	0.09	0.15	0.22	0.31	0.51
0.48	0.90						0.06	0.12	0.19	0.28	0.48
0.46	0.91						0.03	0.10	0.17	0.25	0.46
0.43	0.92							0.07	0.14	0.22	0.43
0.40	0.93							0.04	0.11	0.19	0.40
0.36	0.94								0.07	0.16	0.36
0.33	0.95									0.13	0.33

Пример:

• Активная мощность двигателя : P=200 кВт

• Действующий cos φ = 0,61

• Требуемый cos φ = 0,96

• Коэффициент K из таблицы = 1,01

Необходимая реактивная мощность КРМ (кВАр):

Q = 200 х 1,01=202 кВАр

По дополнительным вопросам, потому как правильно произвести расчет установки компенсации реактивной мощности 0.4 кв, обращайться по телефону (бесплатный звонок по России с мобильного и городского): 8(800)500-89-05, по e-mail: [email protected] или по форме обратной связи, наши специалисты проконсультируют Вас в рабочее время.

Расчет реактивной мощности УКМ (расчет компенсации реактивной мощности)

Расчет реактивной мощности необходимой для конденсаторной установки осуществляется по формуле:

Qc = P x (tg(φ1)-tg(φ2))

Где:
Р – потребляемая активная мощность;
S и S’ – полная мощность до и после компенсации;
QC – требуемая емкостная мощность;
QL и QL’ – индуктивная составляющая реактивной мощности до и после компенсации.

Таблица: расчет реактивной мощности конденсаторной установки (кВАр), необходимой для достижения заданного cos(φ).

Для удобства расчета реактивной мощности УКМ, обратитесь в таблицу

Текущий (действующий)		Требуемый (достижимый) cos (φ)
tan (φ)	cos (φ)	0.80	0.82	0.85	0.88	0.90	0.92	0.94	0.96	0.98	1.00
tan (φ)	cos (φ)	Коэффициент K
3.18	0.30	2.43	2.48	2.56	2.64	2.70	2.75	2.82	2.89	2.98	3.18
2.96	0.32	2.21	2.26	2.34	2.42	2.48	2.53	2.60	2.67	2.76	2.96
2.77	0.34	2.02	2.07	2.15	2.23	2.28	2.34	2.41	2.48	2.56	2.77
2.59	0.36	1.84	1.89	1.97	2.05	2.10	2.17	2.23	2.30	2.39	2.59
2.43	0.38	1.68	1.73	1.81	1.89	1.95	2.01	2.07	2.14	2.23	2.43
2.29	0.40	1.54	1.59	1.67	1.75	1.81	1.87	1.93	2.00	2.09	2.29
2.16	0.42	1.41	1.46	1.54	1.62	1.68	1.73	1.80	1.87	1.96	2.16
2.04	0.44	1.29	1.34	1.42	1.50	1.56	1.61	1.68	1.75	1.84	2.04
1.93	0.46	1.18	1.23	1.31	1.39	1.45	1.50	1.57	1.64	1.73	1.93
1.83	0.48	1.08	1.13	1.21	1.29	1.34	1.40	1.47	1.54	1.62	1.83
1.73	0.50	0.98	1.03	1.11	1.19	1.25	1.31	1.37	1.45	1.63	1.73
1.64	0.52	0.89	0.94	1.02	1.10	1.16	1.22	1.28	1.35	1.44	1.64
1.56	0.54	0.81	0.86	0.94	1.02	1.07	1.13	1.20	1.27	1.36	1.56
1.48	0.56	0.73	0.78	0.86	0.94	1.00	1.05	1.12	1.19	1.28	1.48
1.40	0.58	0.65	0.70	0.78	0.86	0.92	0.98	1.04	1.11	1.20	1.40
1.33	0.60	0.58	0.63	0.71	0.79	0.85	0.91	0.97	1.04	1.13	1.33
1.30	0.61	0.55	0.60	0.68	0.76	0.81	0.87	0.94	1.01	1.10	1.30
1.27	0.62	0.52	0.57	0.65	0.73	0.78	0.84	0.91	0.99	1.06	1.27
1.23	0.63	0.48	0.53	0.61	0.69	0.75	0.81	0.87	0.94	1.03	1.23
1.20	0.64	0.45	0.50	0.58	0.66	0.72	0.77	0.84	0.91	1.00	1.20
1.17	0.65	0.42	0.47	0.55	0.63	0.68	0.74	0.81	0.88	0.97	1.17
1.14	0.66	0.39	0.44	0.52	0.60	0.65	0.71	0.78	0.85	0.94	1.14
1.11	0.67	0.36	0.41	0.49	0.57	0.63	0.68	0.75	0.82	0.90	1.11
1.08	0.68	0.33	0.38	0.46	0.54	0.59	0.65	0.72	0.79	0.88	1.08
1.05	0.69	0.30	0.35	0.43	0.51	0.56	0.62	0.69	0.76	0.85	1.05
1.02	0.70	0.27	0.32	0.40	0.48	0.54	0.59	0.66	0.73	0.82	1.02
0.99	0.71	0.24	0.29	0.37	0.45	0.51	0.57	0.63	0.70	0.79	0.99
0.96	0.72	0.21	0.26	0.34	0.42	0.48	0.54	0.60	0.67	0.76	0.96
0.94	0.73	0.19	0.24	0.32	0.40	0.45	0.51	0.58	0.65	0.73	0.94
0.91	0.74	0.16	0.21	0.29	0.37	0.42	0.48	0.55	0.62	0.71	0.91
0.88	0.75	0.13	0.18	0.26	0.34	0.40	0.46	0.52	0.59	0.68	0.88
0.86	0.76	0.11	0.16	0.24	0.32	0.37	0.43	0.50	0.57	0.65	0.86
0.83	0.77	0.08	0.13	0.21	0.29	0.34	0.40	0.47	0.54	0.63	0.83
0.80	0.78	0.05	0.10	0.18	0.26	0.32	0.38	0.44	0.51	0.60	0.80
0.78	0.79	0.03	0.08	0.16	0.24	0.29	0.35	0.42	0.49	0.57	0.78
0.75	0.80		0.05	0.13	0.21	0.27	0.32	0.39	0.46	0.55	0.75
0.72	0.81			0.10	0.18	0.24	0.30	0.36	0.43	0.52	0.72
0.70	0.82			0.08	0.16	0.21	0.27	0.34	0.41	0.49	0.70
0.67	0.83			0.05	0.13	0.19	0.25	0.31	0.38	0.47	0.67
0.65	0.84			0.03	0.11	0.16	0.22	0.29	0.36	0.44	0.65
0.62	0.85				0.08	0.14	0.19	0.26	0.33	0.42	0.62
0.59	0.86				0.05	0.11	0.17	0.23	0.30	0.39	0.59
0.57	0.87					0.08	0.14	0.21	0.28	0.36	0.57
0.54	0.88					0.06	0.11	0.18	0.25	0.34	0.54
0.51	0.89					0.03	0.09	0.15	0.22	0.31	0.51
0.48	0.90						0.06	0.12	0.19	0.28	0.48
0.46	0.91						0.03	0.10	0.17	0.25	0.46
0.43	0.92							0.07	0.14	0.22	0.43
0.40	0.93							0.04	0.11	0.19	0.40
0.36	0.94								0.07	0.16	0.36
0.33	0.95									0.13	0.33

Пример расчета мощности конденсаторной установки:

Активная мощность двигателя- 110 кВт
Действующийcos φ– 0,63
Требуемыйcos φ– 0,98
КоэффициентK из таблицы= 1,03

Сам расчет реактивной мощности:
Необходимая реактивная мощности КРМ(кВАр)
Q = 110 • 1,03 = 113,3 кВАр

Навигация по записям

Кто потребляет реактивную мощность? Потребители, расчет, методика

Потребители реактивной мощности

Асинхронные электродвигатели и трансформаторы

Асинхронные электродвигатели и трансформаторы потребляют 60…80 % реактивной энергии в промышленных электросетях. Рассмотрим потребление ими реактивной мощности, основываясь на схемах замещения АД и Тр. Эти схемы идентичны, отличаются только ветвью, имитирующей нагрузку.

Значения сопротивлений ротора АД аналогично вторичной обмотки трансформатора, приводятся с учетом коэффициентов трансформации к параметрам цепей статора АД (первичной обмотки Тр), г0 и х0 — сопротивления ветви намагничивания.

В обоих случаях реактивная составляющая тока нагрузки равна:

Реактивная мощность холостого хода не зависит от нагрузки, а реактивная мощность короткого замыкания зависит от квадратакоэффициента загрузки: в АД — по активной мощности, в Тр — по полной мощности.

При номинальной нагрузке АД значения обеих составляющихреактивной мощности АД примерно равны.

В паспортах АД приводятся значения коэффициента мощности при номинальной нагрузке, что позволяет легко определить Q0 и ЩЩ при любом значении ку В АД значение Q0 составляет около 50 % от номинальной мощности. Этим значением можно пользоваться при приблизительных расчетах.

Значения Q0 составляет 2… 5 % от номинальной мощности Тр. Это объясняется отсутствием воздушного зазора в магнитопроводе Тр, благодаря чему для создания основного магнитного потока требуются меньшие значения намагничавающего тока iор и реактивной мощности.

Несмотря на это суммарное потребление реактивной мощности трансформаторами соизмеримо с потреблением АД, поскольку суммарная номинальная мощность Тр, как правило, во много раз больше, чем АД.

Для уменьшения потребления реактивной мощности:

АД выбирают двигатели с небольшим запасом по активной мощности;
выполняют переключения статорных обмоток с треугольника на звезду при их загрузке ниже 40… 50 %;
исключается режим холостого хода путем установки соответствующих ограничителей;
заменяют асинхронные двигатели синхронными той же мощности, если это возможно по техникоэкономическим условиям.

Для уменьшения потерь реактивной мощности в Тр рекомендуется отключение в резерв Тр, загруженных менее 40 % от номинальной мощности, а также перевод нагрузки на другой трансформатор либо замена на менее мощный Тр.

Дуговые сталеплавильные печи

Дуговые сталеплавильные печи относятся к числу крупных потребителей реактивной мощности. В значительной мере это объясняется необходимостью обеспечения непрерывности горения электрической дуги, что возможно только при наличии индуктивности в цепи ДСП. Достаточный для непрерывного горения дуги угол сдвига по фазе между первыми гармониками тока и напряжения определяется выражением

где Ud — минимальное необходимое напряжение для горения дуги; Um — амплитудное значение напряжения источника питания.

Наличие автоматических регуляторов, позволяющих воздействовать на уровни Ud и Um, позволяет осуществлять работу ДСП с углами ф < 32,5е. Таким образом, минимально возможные соотношения между реактивной и активной мощностями, потребляемыми ДСП без применения регуляторов, позволяющих изменить соотношение Ud и Um, составляет:

На практике в большинстве случаев Qn > 0,637 что объясняется наличием значительных индуктивностей в цепи ДСП.ДСП относятся к резкопеременным несимметричным нагрузкам.

Оценивать значения реактивной мощности, потребляемой ДСП, на основании чисто теоретических предпосылок очень затруднительно изза влияния конструктивных параметров ДСП, материала электродов, состава скрапа, несимметрии и несинусоидальности режима и ряда других параметров. Поэтому на практике используются усредненные данные, полученные в результате многочисленных измерений на действующих ДСП.

Средние значения tgсp за весь период плавки для печей различной емкости составляют:

Тип печи tgcp
ДСП12 и ДСП25 — 0,65
ДСП100 — 0,90
ДСП200 — 0,97

Для печей ДСП100 и ДСП200 приведенные значения tg<p могут использоваться также при оценке 30 минутного максимума реактивной нагрузки. Для ДСП меньшей емкости значение tgq>pсоответствующее 30 минутному максимуму, принимается равным приведенному выше с коэффициентом 0,47.

Максимальное значение реактивной мощности имеет место при так называемом эксплуатационном коротком замыкании:

где Sn.т. — номинальная мощность печного трансформатора; kэкз — кратность эксплуатационного короткого замыкания, соответствующего режиму соприкосновения электродов с плавящимся металлом (среднее значение кэ к 3 для печей ДСП12…ДСП25 — 3,2…3,5; для ДСП100…ДСП200 1,5…2,3).

Вентильные преобразователи

В настоящее время более 50 % электроэнергии, поставляемой промышленными предприятиями, преобразуется с помощью выпрямителей и инверторов; эти устройства называются вентильными преобразователями (ВП).

Они являются крупными потребителями реактивной мощности.

На основе ВП строятся современные регулируемые источники реактивной мощности.

Угол сдвига фаз между первыми гармониками напряжения и тока определяется по формуле

Индукционные печи предназначены для расплавления металлов индуцированными токами, для чего необходимо создание сильных магнитных полей.

Для этой цели необходима значительная реактивая мощность, поэтому коэффициент мощности индукционных (печей очень низкий (от 0,1 до 0,6), в связи с чем в комплект индукционной печи входят регулируемые батареи конденсаторов. Установи дуговой и контактной электросварки являются однофазными резко переменными нагрузками с cos от 0,2 до 0,6.

Особенности расчётов реактивной мощности в несинусоидальных режимах

Библиографическое описание:

Файфер Л. А. Особенности расчётов реактивной мощности в несинусоидальных режимах // Молодой ученый. 2016. №28. С. 203-207. URL https://moluch.ru/archive/132/37063/ (дата обращения: 23.01.2020).

Согласно ГОСТ 13109–2003 основными параметрами являются колебания напряжения, отклонение частоты, несинусоидальность и несимметрия напряжения. Отсюда следует, что активная и реактивная мощность, а также действующие значения токов и напряжений имеют важное значение при исследовании показателей качества электроэнергии. Именно с определением реактивной мощности возникают трудности, так как нет строгого её определения.

Методы определения составляющих мощности и реактивной мощности.

Буденау впервые ввёл понятие «мощность искажение». Встречается обозначение мощности искажения как «D», а также как «T». По Буденау мощность искажения вычисляется по формуле

А. Ф. Крогерис в [1] наглядно изображает составляющие мощности в стандартах США (рисунок 1).

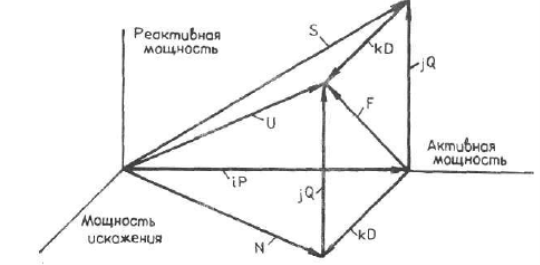
Рис. 1. Составляющие мощности по американским стандартам

Также вопросами составляющих мощности занимались и немецкие учёные. Среди которых выделяет работы Р. Трэгера, который ввёл понятие «мощность взаимного обмена». В немецких нормах при графической интерпретации под S понимают кажущуюся мощность при несинусоидальном режиме, а под S₁— кажущуюся мощность основной гармоники. Соответственно Q и Q₁— это реактивная мощность основной гармоники и при несинусоидальном режиме. Составляющие мощности изображены на рисунке 2.

Рис. 2. Составляющие мощности по немецким стандартам

Можно все существующие методы определения составляющих мощностей разделить на три группы: спектральные, интегральные и энергопотоковые методы. Рассмотрим более подробно каждую группу.

Спектральные методы

Сущность данного метода заключается в том, что составляющие мощности определяются с помощью гармонических составляющих токов и напряжений

Реактивная мощность по Буденау.

Теория Буденаю, состоит в разложении полной мощности на активную, реактивную и мощность искажения. Выражение Буденау представлено формулой

Формулы по Буденау получили широкое признание. Неактивная или реактивная мощность присуща сигналу с n-гармониками:

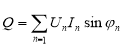Мощность по В. Шеферду и П. Закихани.

Мощность, определяемая в [2] основана на частотном анализе. Он делит гармоники тока и напряжения на общие и необщие гармоники. Реактивная мощность выражена формулой

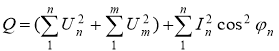Мощность по Шарону.

Определение мощности по Шарону основано также на частотном анализе. Отметим, что у Шарона присутствует термин «кажущийся компонент мощности» которую он определяет в своих трудах. Он развивает исследования формулы и считает, что определении коэффициента мощности в несинусоидальном режиме через функцию косинуса ошибочно. И критикует некоторые моменты теории В. Шеферда и П. Закихани, в частности он считает, что не имеет физического смысла, а лишь математическое понятие. Поэтому он выводит формулу, в которой присутствуют функции гармоник напряжения, тока и функция синуса фазового сдвига.

В [3] реактивную мощность представлена формулой

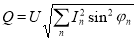
А. Эмануэль в [4] отметил, что мощность искажения широкого признания не получила и говорит, что необходимо уделить внимание оценке угла смещения для основной гармоники.

Реактивная мощность определяется через основные гармоники напряжения и тока выражением

Интегральные методы определения мощности

Реактивная мощность Илиовиси и Маевского [5].

Интегральную формула для расчёта реактивной мощности ввёл М. Илиовиси:

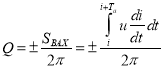Илиовиси и Маевский используют такие понятия, как: мощность сдвига (), мощность искажения (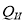) и неактивная мощность ().

Неактивная мощность:

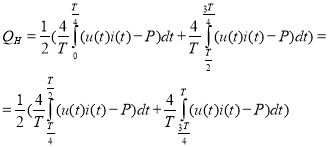Энергопотоковые методы определения мощности

Реактивная мощность Фризе.

Теория Фризе [6] основана на мгновенных значениях токах и напряжениях. Теория состоит в разложении мгновенного тока нагрузки на мгновенный активный ток и мгновенный неактивный (реактивный) ток.

Разделение тока на две составляющие происходит в связи с тем, что ток является активной нагрузкой развивает такую же мощность, что и нагрузка, которая исследуется. В итоге если реактивный ток будет скомпенсирован, то будет видна только активная нагрузка.

Полный ток можно определить через среднеквадратичные значения активного и реактивного тока:

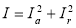Реактивную мощность по Фризе всегда положительна и определяется по формуле

Мощность по Зарнецкому.

Зарнецкий продолжает в свих работах [7] концепции Фризе. Теория предполагает разделение тока на две составляющие: активный и реактивный ток. Отличием теории от выше описанной, является то, что она предполагает разложение токов на большое количество ортогональных компонент. Реактивная мощность по Зарнецкому, определяется выражением

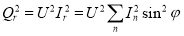pq- теория.

pq- теория или теория мгновенной мощности используется когда активные компенсаторы применяются для компенсации реактивной мощности в случае наличия составляющих высших гармоник [6]. Активная 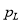и реактивная мощность получаются путём преобразования сигналов из трёхфазной системы координат в двухфазную систему координат:

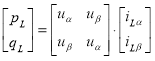Вывод

Сделав обзор существующих методик определения реактивной мощности, отметим, что у каждой методики, теории есть свои преимущества, недостатки. Поэтому вопрос определения мощности является важным и актуальным, и требующим дальнейшего изучения.

Литература:

Крогерис, А. Ф. Мощность переменного тока [Текст]: учеб. / А. Ф. Крогерис. — Рига.:Физ.-энерг.ин-т Латв.АН. — 1993. — 294с.
Shepherd, W. Suggested definition of reactive power for nonsinusoidal systems / W. Shepherd, P. Zakikhani // Proc. IEE. — 1972. — vol. 119, № 9. — P. 1361–1362.
Топорова, Ю. В. Сравнительная характеристика методов определения реактивной мощности [Текст] / Ю. В. Топорова, А. П. Лазуренко // Вісник НТУ «ХПІ». — 2013. — № 17(990). — С. 100–106.
Emanuel, A. E. Suggested definition of reactive power in nonsinusoidal systems and reactive-power definitions and power-factor improvement in nonlinear systems / A. E. Emanuel // Proceedings of the Institution of Electrical Engineers. — 1974. — vol. 121, № 7/ — P. 705–706.
Kusters, N. On the Definition of Reactive Power Factor of the Supply Systems / N. Kusters, W. Moore // IEEE Trans. Power App. Syst. — 1980. — P. 1845–1854.
Чижма, С. Н. совершенствование методов и средств контроля качества электроэнергии и составляющих мощности в электроэнергетических системах с тяговой нагрузкой [Текст]: дис…. доктора тех. наук: 05.14.02 / Сергей Николаевич Чижма; Омский государственный университет путей сообщения. — Омск, 2014. — 367 с.
Czarnecki, L. S. Budeanu and fryze: Two frameworks for interpreting power properties of circuits with nonsinusoidal voltages and currents / L. SCzarnecki // Electrical Engineering. — 1997. — vol. 80, № 9. — P. 359–367.

Основные термины (генерируются автоматически): реактивная мощность, мощность, мощность искажения, составляющая, формула, теория, реактивный ток, основная гармоника, несинусоидальный режим, активная нагрузка.

Формула расчета реактивной мощности – Компенсация реактивной мощности: расчет мощности и выбор ступени регулирования конденсаторной батареи