Расчет потерь напряжения в кабеле

Для того чтобы обеспечить подачу напряжения от распределительного устройства к конечному потребителю используются линии электропередач. Они могут быть воздушными или кабельными и имеют значительную протяженность.

Как и все проводники, они имеют сопротивление, которое зависит от длины и чем они протяжение, тем больше потеря напряжения.

И чем длиннее линия, тем потери напряжения будут больше. Т.е. напряжение на входе и в конце линии будет разное.

Чтобы оборудование работало без сбоев, эти потери нормируются. Они суммарно должны иметь значение, не превышающее 9%.

Максимальное понижение напряжение на вводе составляет пять процентов, а до самого удаленного потребителя не более четырех процентов. В трехфазной сети при трех или четырех проводной сети этот показатель не должен превышать 10%.

Симптомы снижения напряжения у потребителя

Если эти показатели не соблюдаются, конечные потребители не смогут обеспечить номинальные параметры. При снижении напряжения возникают следующие симптомы:

• Осветительные приборы, в которых используются лампы накаливания, начинают работать (светиться) в половину накала;
• При включении электродвигателей уменьшается пусковое усилие на валу. В результате чего двигатель не вращается, и как следствие происходит перегрев обмоток и выход из строя;
• Некоторые электроприборы не включаются. Не хватает напряжения, а другие приборы после включения могу выходить из строя;
• Установки, чувствительные к входному напряжению, работают нестабильно, так же могут не включаться источники света, у которых нет нити накаливания.

Передача электроэнергии производится по воздушным или кабельным сетям. Воздушные изготовлены из алюминия, а кабельные могут быть алюминиевыми или медными.

В кабелях кроме активного сопротивления имеется емкостное сопротивление. Поэтому потеря мощности зависит от длины кабеля.

Причины, приводящие к снижению напряжения

Потери напряжения в линии электропередач возникают по следующим причинам:

• По проводу проходит ток, который нагревает его, в результате увеличивается активное и емкостное сопротивление;
• Трехфазный кабель при симметричной нагрузке имеет одинаковые значения напряжения на жилах, а ток нулевого провода будет стремиться к нулю. Это справедливо если нагрузка постоянная и чисто активная, что в реальных условиях невозможно;
• В сетях, кроме активной нагрузки, имеется реактивная нагрузка в виде обмоток трансформатора, реакторов и т.п. и как следствие в них появляется индуктивная мощность;
• В результате сопротивление будет складываться из активного, емкостного и индуктивного. Оно влияет на потери напряжения в сети.

Потери тока зависят от длины кабеля. Чем он протяжение, тем больше сопротивление, а это значит, что и потери значительнее. Отсюда следует, что потери мощности в кабеле зависят от протяженности или длины линии.

Расчет значения потерь

Для обеспечения работоспособности оборудования необходимо произвести расчет. Он проводится в момент проектирования. Современный уровень развития вычислительной техники позволяет производить вычисления с помощью онлайн калькулятора, который позволяет быстро произвести расчет потерь мощности кабеля.

Для вычисления достаточно ввести необходимые данные. Задают параметры тока – постоянный или переменный. Материал линии электропередач – алюминий или медь. Указывают, по каким параметрам производится расчет потери мощности – по сечению или диаметру провода, току нагрузки или сопротивлению.

Дополнительно указывают напряжение сети и температуру кабеля (зависит от условий эксплуатации и способе прокладки). Эти значения подставляются в таблицу расчета и производят расчет с помощью электронного калькулятора.

Можно произвести расчет на основании математических формул. Чтобы правильно понять и оценить процессы, происходящие при передаче электрической энергии, применяют векторную форму представления характеристик.

А для минимизации расчетов трехфазную сеть представляют как три однофазные сети. Сопротивление сети представлено как последовательное подключение активного и реактивного сопротивления к сопротивлению нагрузки.

При этом формула расчета потери мощности в кабеле существенно упрощается. Для получения необходимых параметров используют формулу.

∆U= I*RL.

Эта формула показывает потерю мощности кабеля в зависимости от тока и сопротивления, распределенного по длине кабеля.

Однако, эта формула справедлива, если знать силу тока и сопротивление. Сопротивление можно вычислить по формуле. Для меди оно будет равно р=0,0175Ом*мм2/м, а для алюминия р=0,028Ом*мм2/м.

Зная значение удельного сопротивления вычисляют сопротивление, которое будет определяться по формуле

R=р*I/S, где р- удельное сопротивление, I-длина линии, S- площадь сечения провода.

Для того чтобы выполнить расчет потерь напряжения по длине кабеля, необходимо полученные значения подставить в формулу и произвести вычисления. Эти расчеты можно производить при монтаже электрических сетей или охранных систем и видеонаблюдения.

Если вычисления потери мощности не производить, то это может привести к снижению питающего напряжения потребителей. В результате произойдет перегрев кабеля, он может сильно нагревается, и как следствие происходит повреждение изоляции.

Что может привести к поражению людей электрическим током или короткому замыканию. Снижение напряжения в линии может привести к выходу их строя электронного оборудования.

Поэтому важно при проектировании электропроводки производить расчет потери напряжения в подводящих проводах и проложенном кабеле.

Методы сокращения потерь

Потери мощности можно сократить следующими методами:

• Увеличить сечение проводников. В результате снизится сопротивление, и потери уменьшатся;
• Снижение потребляемой мощности. Этот параметр не всегда можно изменить;
• Изменение протяженности кабеля.

Уменьшение мощности и изменение длины линии осуществить практически не возможно. Поэтому если увеличивать сечение провода без расчета, то на длинной линии это приведет к неоправданным затратам.

А это значит, что очень важно произвести расчет, который позволит правильно рассчитать потери мощности в кабеле и выбрать оптимальное значение сечения жил.

Потери электроэнергии в изоляции кабельных линий: расчет, формула

Потери в изоляции кабелей за расчетный период Т, ч, определяют по формуле, тыс. кВт·ч:

 

Значения коэффициентов в формуле (2.72) получены автором на основе экспертной оценки исходя из следующих соображений. Для кабелей 6–10 кВ, изготавливавшихся в начале 1960-х гг., tgδ составлял в среднем 0,011. Для современных кабелей tgδ = 0,003. Предполагая линейную зависимость постепенного улучшения качества изоляционных материалов в связи с совершенствованием технологии в течение 40 лет, можно считать, что снижение за этот срок tgδ на 0,008 соответствует тренду 0,0002 ед./год.

Величина в первой скобке формулы (2.72) отражает тот факт, что чем больше срок службы кабеля, тем с худшими характеристиками изоляции он был изготовлен. Кроме того, в течение срока эксплуатации происходит старение изоляции. Происходящее при этом увеличение tgδ отражается второй скобкой. Коэффициент старения, полученный на основе экспертной оценки, aст = 0,05.

Для эксплуатируемых в настоящее время кабелей значения tgδ могут быть приняты равными: 0,008 – для кабелей напряжением 6–10 кВ; 0,006 – 20–35 кВ; 0,003 – 110–220 кВ. Годовые потери, рассчитанные по формуле (2.71) по справочным данным о емкостной проводимости кабелей различных сечений и напряжений, приведены в табл. 2.6.

Таблица 2.6

Потери электроэнергии в изоляции кабелей

Потери мощности и электроэнергии в элементах сети

Лекция № 7

План.

1. Потери мощности в элементах сети.

2. Расчет потерь мощности в линиях электропередач.

3. Расчет потерь мощности в ЛЕП с равномерно распределенной нагрузкой.

4. Расчет потерь мощности в трансформаторах.

5. Приведенные и расчетные нагрузки потребителей.

6. Расчет потерь электроэнергии.

7. Мероприятия по снижению потерь мощности.

Потери мощности в элементах сети

Для количественной характеристики работы элементов электрической сети рассматриваются ее рабочие режимы.

Рабочий режим – это установившееся электрическое состояние, которое характеризуется значениями токов, напряжений, активной, реактивной и полной мощностей.

Основной целью расчета режимов является определение этих параметров, как для проверки допустимости режимов, так и для обеспечения экономичности работы элементов сетей.

Определение значений токов в элементах сети и напряжений в ее узлах начинается с построения картины распределения полной мощности по элементу, т.е. с определения мощностей в начале и конце каждого элемента. Такую картину называют потокораспределением.

Рассчитывая мощности в начале и в конце элемента электрической сети, учитывают потери мощности в сопротивлениях элемента и влияние его проводимостей.

Расчет потерь мощности в линиях электропередач

Потери активной мощности на участке ЛЕП (см. рис. 7.1) обусловлены активным сопротивлением проводов и кабелей, а также несовершенством их изоляции. Мощность, теряемая в активных сопротивлениях трехфазной ЛЕП и расходуемая на ее нагрев, определяется по формуле:

,

где 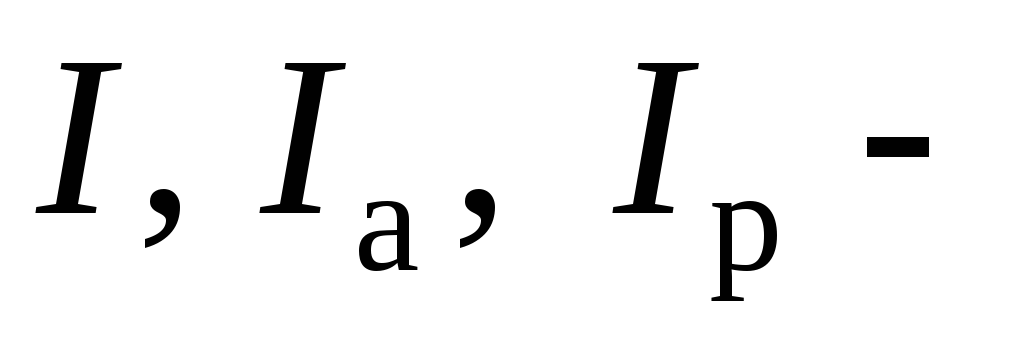полный, активный и реактивный токи в ЛЕП;

P, Q, S – активная, реактивная и полная мощности в начале или конце ЛЕП;

U– линейное напряжение в начале или конце ЛЕП;

R – активное сопротивление одной фазы ЛЕП.

Потери активной мощности в проводимостях ЛЕП обусловлены несовершенством изоляции. В воздушных ЛЕП – появлением короны и, в очень незначительной степени, утечкой тока по изоляторам. В кабельных ЛЕП – появлением тока проводимости а его абсорбции. Рассчитываются потери по формуле:

,

где U– линейное напряжение в начале или конце ЛЕП;

G – активная проводимость ЛЕП.

При проектировании воздушных ЛЕП потери мощности на корону стремятся свести к нулю, выбирая такой диаметр провода, когда возможность возникновения короны практически отсутствует.

Потери реактивной мощности на участке ЛЕП обусловлены индуктивными сопротивлениями проводов и кабелей. Реактивная мощность, теряемая в трехфазной ЛЕП, рассчитывается аналогично мощности, теряемой в активных сопротивлениях:

Генерируемая емкостной проводимостью зарядная мощность ЛЕП рассчитывается по формуле:

,

где U– линейное напряжение в начале или конце ЛЕП;

B – реактивная проводимость ЛЕП.

Зарядная мощность уменьшает реактивную нагрузку сети и тем самым снижает потери мощности в ней.

Расчет потерь мощности в леп с равномерно распределенной нагрузкой

В линиях местных сетей (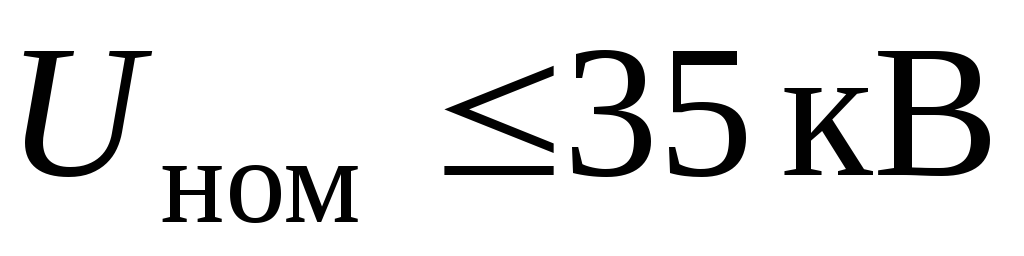) потребители одинаковой мощности могут располагаться на одинаковом расстоянии друг от друга (например, источники света). Такие ЛЕП называются линиями с равномерно распределенной нагрузкой (см. рис. 7.2).

В равномерно нагруженной линии трехфазного переменного тока длиной L с суммарной токовой нагрузкойIплотность тока на единицу длины составитI/L. При погонном активном сопротивленииr₀ потери активной мощности составят:

Если бы нагрузка была сосредоточена в конце, то потери мощности определялись бы как:

.

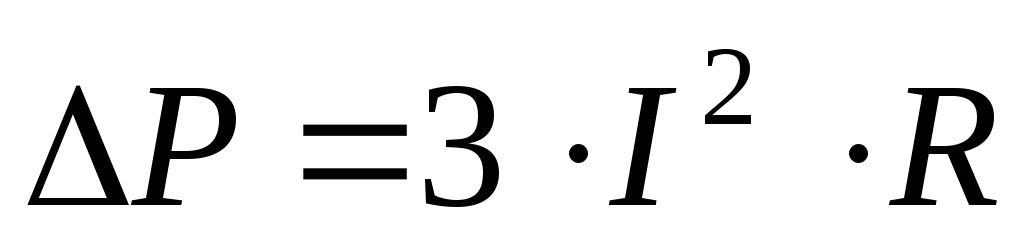Сравнивая приведенные выражения, видим, что потери мощности в линии с равномерно распределенной нагрузкой в 3 раза меньше.

Правила расчёта потерь в кабеле при помощи таблиц Кнорринга | Полезные статьи

Кабельные жилы при пропускании тока будут выделять тепло. Величина тока в совокупности с сопротивлением жил определяют уровень потерь кабеля. Если иметь информацию о сопротивлении жил и о том, насколько велик пропускаемый через них ток, удастся узнать объём потерь в цепи.

 

Расчёт потерь выполняется при помощи формулы: ΔU,%=(Uном-U)∙100/ Uном. Где, Uном – номинальное входное напряжение, U – напряжение нагрузки. Выражаются потери в процентах от номинала, характерного для возникшего напряжения.

Практически намного проще использовать таблицы Кнорринга, востребованные при организации электропроводки. Информация в таблицах синхронизирует «момент нагрузки» и потери. Вычислить момент предлагается в виде произведения нагрузочной мощности (Р), измеряемой в киловаттах, и линейной длины (L), обозначаемой в метрах. Данные в таблицах Кнорринга отображают зависимость понесённых кабелем потерь от «момента нагрузки», применительно к двухпроводным медным линиям. Обязательным условием является наличие напряжения 220В.

Также разработана таблица, определяющая идентичную зависимость, но применительно к трёхфазным четырёхпроводным нулевым линиям при напряжении на уровне 380/220В. Есть схожие сведения и для трёхпроводных линий без нуля при 380В. Однако информация является достоверной исключительно при равенстве нагрузки в фазах, что позволяет определить ток в четырёхпроводных нулевых линиях, а именно в их нулевых жилах, также как нулевой.

Если нагрузка несимметричная применительно к трёхфазным линиям, то неизбежно увеличение потерь. Избежать ошибок в случае существенной нагрузочной асимметрии в нулевых линиях можно, используя таблицы, с данными для двухпроводных медных линий, однако это утверждение верно применительно к самой нагруженной фазе.

Разработана таблица Кнорринга, содержащая информацию, касающуюся зависимости от момента нагрузки кабельных потерь, верная для медных проводников при напряжении на уровне 12В. Рассчитать с помощью этой таблицы можно линейные потери посредством понижающих трансформаторов, питающих светильники с низким вольтажом.

Важно! Таблицы не учитывают линейное индуктивное сопротивление, из-за того, что при задействовании кабелей, оно является крайне малым и не может сравниваться с активным сопротивлением.

Таблицы Кнорринга верны при подключённой в конце линии нагрузке, что позволяет вычислять момент нагрузки по формуле: М=L∙РН. Когда есть несколько схожих по мощности нагрузок, составляющих целостную нагрузку, и распределены они на протяжении всей линии, используется формула: М=L∙ РН ∙n/2.

Если отмечается наличие двух соединённых линий с равномерным распределением нагрузки, можно вычислить потери напряжения, выявив сумму длин линий, при этом сечение кабелей в них допускается различное.