Закон сохранения механической энергии: определение, формулы
Майер предположил, что кровь не меняет цвет, поскольку организму в тропическом климате нет необходимости тратить кислород на поддержание
температуры тела. Вернувшись на родину, перед тем как сформулировать закон сохранения механической энергии, Майер продолжил опыты с открытыми на то время разновидностями энергии:- кинетической,
- потенциальной,
- внутренней,
- механической;
…и смог определить, в чем заключается закон сохранения механической энергии.
Английский физик Джеймс Джоуль, чье имя носит единица измерения энергии, и германский естествоиспытатель Герман Гельмгольц несколькими годами позже также«Тепло, электричество и перемещение представляют собою феномены, которые могут быть сведены к одной силе, измеряются друг другом и переходят друг в друга по определенным законам» — излагал в своей научной работе Майер.

Физика. 8 класс. Учебник.
Учебник соответствует Федеральному государственному образовательному стандарту основного общего образования. Большое количество красочных иллюстраций, разнообразные вопросы и задания, а также дополнительные сведения и любопытные факты способствуют эффективному усвоению учебного материала.
КупитьКинетическая и потенциальная энергия
Энергия тела — физическая величина, определяющая работу наблюдаемого тела или системы тел за бесконечно долгое время.
В изучении механических явлений рассматривают потенциальную и кинетическую энергии.
- Единица энергии в СИ 1 Джоуль (Дж).
Кинетическая энергия — энергия, которой обладает тело в движении (вращении, перемещении в пространстве).
Футбольный мяч, летящий в ворота, летящая в цель стрела, выпущенная метким лучником, едущие с горы сани с сидящим в них хохочущим ребенком — все они во время движения характеризуются кинетической энергией.
Кинетическая энергия напрямую зависит от массы тела и скорости перемещения.
Формула кинетической энергии Ек = mv
Где где m — масса объекта;
v — скорость перемещения объекта в конкретной точке.
Потенциальная энергия. Само по себе тело потенциальной энергией не обладает. Этот вид энергии характеризует взаимосвязь элементов объекта или двух отдельных тел в пространстве.
Стоящие на вершине холма санки, стрела, вложенная лучником в натянутую тетиву, ядро в стволе средневековой пушки — пример объекта, обладающего потенциальной энергией.
Потенциальная энергия бывает положительной или отрицательной относительно определенного условного нулевого уровня, принятого для системы координат:
- сила тяжести,
- сила упругости,
- архимедова сила
Потенциальная энергия объекта зависит от приложенных к нему сил.
Если оценивать расположение объекта в отношении уровня Земли, то потенциальная энергия объекта на поверхности планеты принимается за ноль.
Уравнение Еп = mɡh поможет рассчитать потенциальную энергию на высоте h:где m — масса тела;
ɡ — ускорение свободного падения;
h — высота центров масс объектов относительно поверхности планеты;
ɡ = 9,8 м/с2
Потенциальная энергия упруго деформированного объекта (пружины) рассчитывается согласно уравнению:
где k — коэффициент жёсткости,
∆x — изменение длины объекта вследствие его сжатия или растяжения.
Подробно различные виды потенциальной энергии разбираются на странице 131 учебника «Физика 10 кл. под редакцией Касьянова В. А.»

Физика. 9 класс. Учебник.
Учебник отличаются качественным современным оформлением, в нём приводятся многочисленные слайды и микрофотографии. Выполняя проблемные, поисковые и исследовательские задания, школьники не только активно усваивают материал, но и учатся мыслить, искать и анализировать информацию из разных источников, в том числе из интернета. Особое внимание уделяется практическим заданиям: ученикам предлагается проводить опыты, конструировать модели, разрабатывать проекты.
Суммарное число значений потенциальной и кинетической энергий объекта обозначают как механическая энергия. Для каждого конкретного объекта механическая энергия определяется не выбором системы отсчета, в которой рассчитывают скорость движения исследуемого объекта, а установлением уровня условного нуля для всех видов потенциальных энергий, определенных у данного объекта.
Механическая энергия определяет свойство объекта (системы объектов) совершать работу за счет изменения скорости перемещения объекта или изменения расположения взаимодействующих объектов относительно друг друга.
Что ещё почитать?
Сформулируем закон сохранения механической энергии с помощью математического уравнения:Еk1 + Еп1 = Еk2 + Еп2
Глядя на представленную формулу видно, что энергия не появляется из ниоткуда и не исчезает в неизвестном направлении; лишь происходит преобразование одной разновидности в другую или переход между взаимодействующими объектами.
В изолированной или закрытой системе, т.е. системе, на которую не оказывают влияния силы извне или их возможно игнорировать, энергетический обмен с внешней средой не происходит, и внутренняя энергия объекта не изменяется. В ней могут происходить лишь превращения потенциальной энергии в кинетическую и наоборот. В учебнике «Физика. 10 класс» под редакцией В. А. Касьянова на портале LECTA разобраны примеры задач на закон сохранения энергии.
#ADVERTISING_INSERT#Конспект «Механическая энергия. Закон сохранения энергии»
Механическая энергия.
Закон сохранения энергии
Раздел ОГЭ по физике: 1.18. Механическая энергия. Закон сохранения механической энергии. Формула для закона сохранения механической энергии в отсутствие сил трения. Превращение механической энергии при наличии силы трения.
1. Энергия тела – физическая величина, показывающая работу, которую может совершить рассматриваемое тело (за любое, в том числе неограниченное время наблюдения). Тело, совершающее положительную работу, теряет часть своей энергии. Если же положительная работа совершается над телом, энергия тела увеличивается. Для отрицательной работы – наоборот.
- Энергией называют физическую величину, которая характеризует способность тела или системы взаимодействующих тел совершить работу.
- Единица энергии в СИ 1 Джоуль (Дж).
2. Кинетической энергией называется энеpгия движущихся тел. Под движением тела следует понимать не только перемещение в пространстве, но и вращение тела. Кинетическая энергия тем больше, чем больше масса тела и скорость его движения (перемещения в пространстве и/или вращения). Кинетическая энеpгия зависит от тела, по отношению к которому измеряют скорость рассматриваемого тела.
- Кинетическая энергия Ек тела массой m, движущегося со скоростью v, определяется по формуле
3. Потенциальной энергией называется энергия взаимодействующих тел или частей тела. Различают потенциальную энергию тел, находящихся под действием силы тяжести, силы упругости, архимедовой силы. Любая потенциальная энергия зависит от силы взаимодействия и расстояния между взаимодействующими телами (или частями тела). Потенциальная энергия отсчитывается от условного нулевого уровня.
- Потенциальной энергией обладают, например, груз, поднятый над поверхностью Земли, и сжатая пружина.
- Потенциальная энергия поднятого груза Еп = mgh.
- Кинетическая энергия может превращаться в потенциальную, и обратно.
4. Механической энергией тела называют сумму его кинетической и потенциальной энергий. Поэтому механическая энеpгия любого тела зависит от выбора тела, по отношению к которому измеряют скорость рассматриваемого тела, а также от выбора условных нулевых уровней для всех разновидностей имеющихся у тела потенциальных энергий.
- Механическая энергия характеризует способность тела или системы тел совершить работу вследствие изменения скорости тела или взаимного положения взаимодействующих тел.
5. Внутренней энергией называется такая энергия тела, за счёт которой может совершаться механическая работа, не вызывая убыли механической энергии этого тела. Внутренняя энеpгия не зависит от механической энергии тела и зависит от строения тела и его состояния.
6. Закон сохранения и превращения энергии гласит, что энеpгия ниоткуда не возникает и никуда не исчезает; она лишь переходит из одного вида в другой или от одного тела к другому.
- Закон сохранения механической энергии: если между телами системы действуют только силы тяготения и силы упругости, то сумма кинетической и потенциальной энергии остается неизменной, то есть механическая энергия сохраняется.
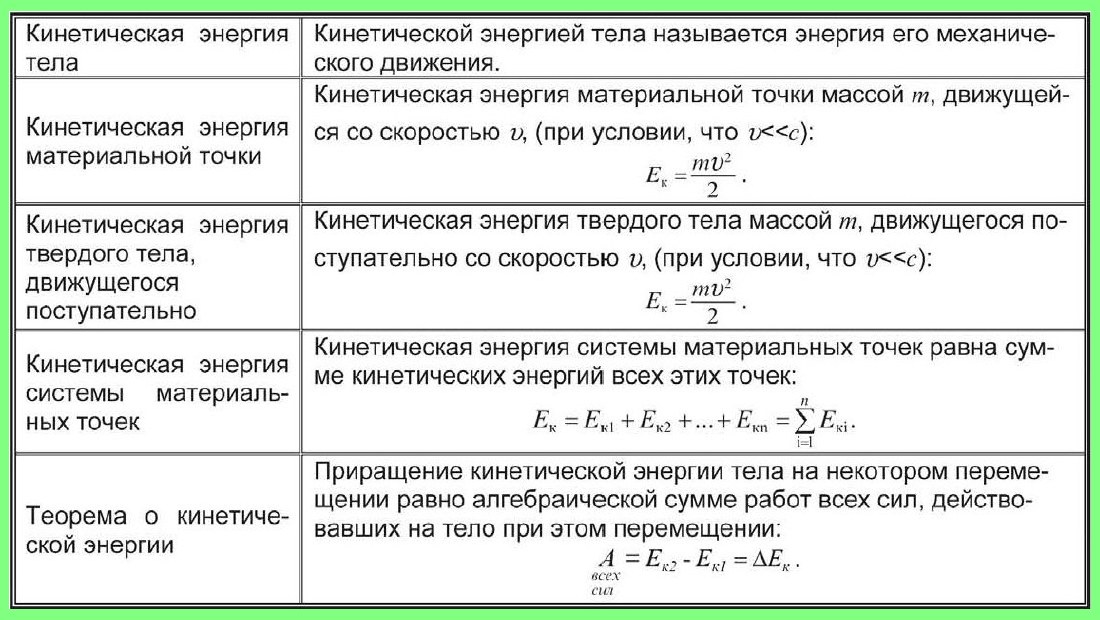
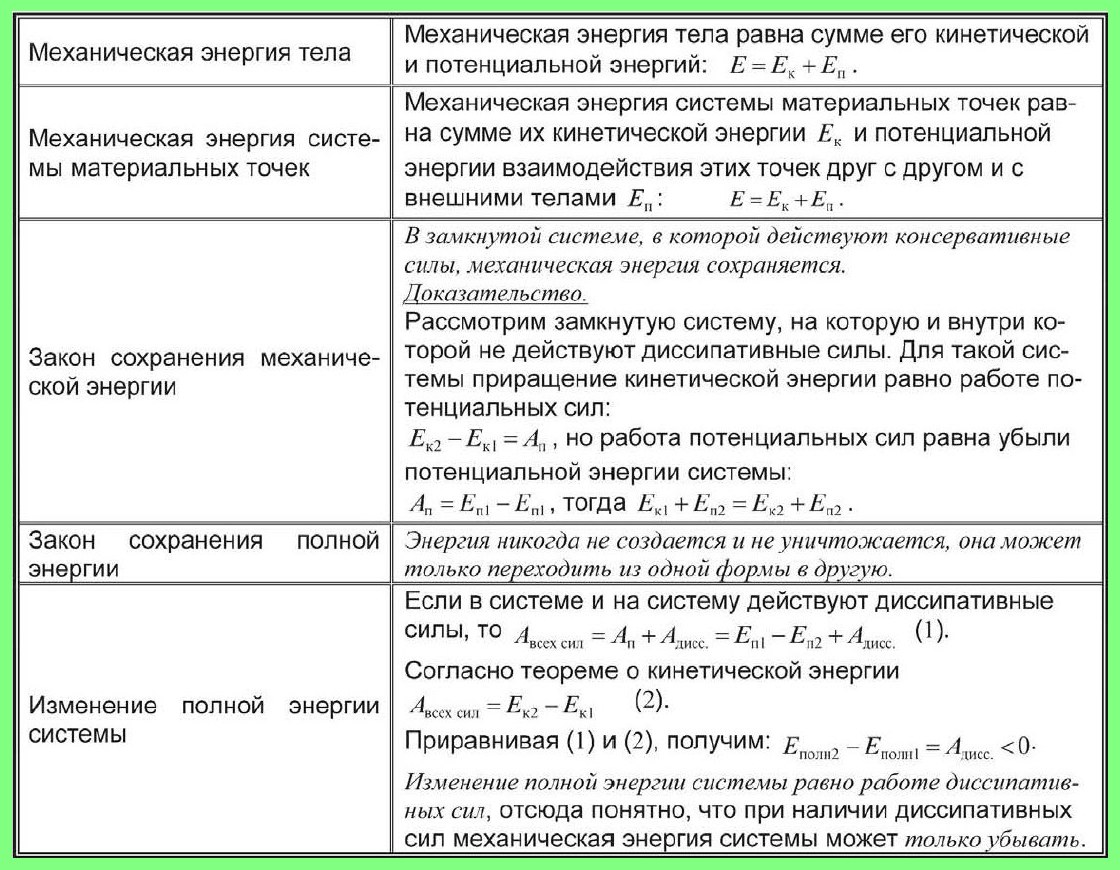
Таблица «Механическая энергия. Закон сохранения энергии».

7. Изменение механической энергии системы тел в общем случае равно сумме работы внешних по отношению к системе тел и работы внутренних сил трения и сопротивления: ΔW = Авнешн + Адиссип
Если система тел замкнута (Авнешн = 0), то ΔW = Адиссип, то есть полная механическая энергия системы тел меняется только за счёт работы внутренних диссипативных сил системы (сил трения).
Если система тел консервативна (то есть отсутствуют силы трения и сопротивления Атр = 0), то ΔW = Авнешн, то есть полная механическая энергия системы тел меняется только за счёт работы внешних по отношению к системе сил.
8. Закон сохранения механической энергии: В замкнутой и консервативной системе тел полная механическая энергия сохраняется: ΔW = 0 или Wп1 + Wк1 = Wп2 + Wк2 . Применим законы сохранения импульса и энергии к основным моделям столкновений тел.
- Абсолютно неупругий удар (удар, при котором тела движутся после столкновения вместе, с одинаковой скоростью). Импульс системы тел сохраняется, а полная механическая энергия не сохраняется:

- Абсолютно упругий удар (удар, при котором сохраняется механическая энергия системы). Сохраняются и импульс системы тел, и полная механическая энергия:
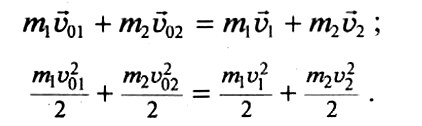
Удар, при котором тела до соударения движутся по прямой, проходящей через их центры масс, называется центральным ударом.
Схема «Механическая энергия.
Закон сохранения энергии. Углубленный уровень«
Конспект урока по физике «Механическая энергия. Закон сохранения энергии». Выберите дальнейшие действия:
Гравитационная энергия — Википедия
Материал из Википедии — свободной энциклопедии
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 8 ноября 2016; проверки требуют 5 правок. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 8 ноября 2016; проверки требуют 5 правок.Гравитационная энергия — потенциальная энергия системы тел (частиц), обусловленная их взаимным гравитационным тяготением.
Гравитационно-связанная система — система, в которой гравитационная энергия больше суммы всех остальных видов энергий (помимо энергии покоя).
Общепринята шкала, согласно которой для любой системы тел, находящихся на конечных расстояниях, гравитационная энергия отрицательна, а для бесконечно удалённых, то есть для гравитационно не взаимодействующих тел, гравитационная энергия равна нулю. Полная энергия системы, равная сумме гравитационной и кинетической энергии, постоянна. Для изолированной системы гравитационная энергия является энергией связи. Системы с положительной полной энергией не могут быть стационарными.
Гравитационная энергия играет очень важную роль на заключительных этапах эволюции звёзд, при их превращении в нейтронные звёзды и сверхновые[1].
Для двух тяготеющих точечных тел с массами M и m гравитационная энергия Ug{\displaystyle U_{g}} равна:
- Ug=−GMmR,{\displaystyle \ U_{g}=-G{Mm \over R},}
где:
- G{\displaystyle \ G} — гравитационная постоянная;
- R{\displaystyle \ R} — расстояние между центрами масс тел.
Этот результат получается из закона тяготения Ньютона, при условии, что для бесконечно удалённых тел гравитационная энергия равна 0. Выражение для гравитационной силы имеет вид
- Fg=GMmR2,{\displaystyle F_{g}=G{Mm \over R^{2}},}
где:
- Fg{\displaystyle F_{g}} — сила гравитационного взаимодействия
С другой стороны согласно определению потенциальной энергии
- Fg=dUgdR.{\displaystyle F_{g}={\frac {dU_{g}}{dR}}.}
Тогда:
- Ug=const−GMmR.{\displaystyle U_{g}=const-G{Mm \over R}.}
Константа в этом выражении может быть выбрана произвольно. Её обычно выбирают равной нулю, чтобы при r, стремящемуся к бесконечности, Ug{\displaystyle U_{g}} стремилось к нулю.
Этот же результат верен для малого тела, находящегося вблизи поверхности большого. В этом случае R можно считать равным h+RM{\displaystyle h+R_{M}}, где RM{\displaystyle R_{M}} — радиус тела массой M, а h — расстояние от центра тяжести тела массой m до поверхности тела массой M.
На поверхности тела M имеем:
- Ug=−GMmRM,{\displaystyle U_{g}=-G{Mm \over R_{M}},}
Если размеры тела M{\displaystyle M} много больше размеров тела m{\displaystyle m}, то формулу гравитационной энергии можно переписать в следующем виде:
- Ug=−GMmRM+h=−mGMRM11+h/RM≈−mGMRM(1−hRM)=mgh−mGMRM,{\displaystyle U_{g}=-G{Mm \over R_{M}+h}=-mG{\frac {M}{R_{M}}}{\frac {1}{1+h/R_{M}}}\approx -mG{\frac {M}{R_{M}}}\left(1-{\frac {h}{R_{M}}}\right)=mgh-m{\frac {GM}{R_{M}}},}
где величину g=GMRM2{\displaystyle g={\frac {GM}{R_{M}^{2}}}} называют ускорением свободного падения. При этом член mGMRM{\displaystyle m{\frac {GM}{R_{M}}}} не зависит от высоты поднятия тела над поверхностью и может быть исключён из выражения путём выбора соответствующей константы. Таким образом для малого тела, находящегося на поверхности большого тела справедлива следующая формула
- Ug=mgh.{\displaystyle U_{g}=mgh.}
В частности, эта формула применяется для вычисления потенциальной энергии тел, находящихся вблизи поверхности Земли.
В общей теории относительности наряду с классическим отрицательным компонентом гравитационной энергии связи появляется положительная компонента, обусловленная гравитационным излучением, то есть полная энергия гравитирующей системы убывает во времени за счёт такого излучения.
Механическая энергия, полная механическая энергия
Понятие энергии для физики является базовым. Нам известно, что закон сохранения энергии – это фундаментальный закон природы. Он служит основанием для пояснения множества явлений механики, термодинамики, электричества и других физических разделов.
Понятие энергии используется при исследовании задач техники, поскольку самая важная техническая проблема – это проблема генерации, передачи и использования энергии.
Механической энергией считают сумму потенциальной и кинетической энергии. Это энергия, которую связывают с перемещением тел, их расположением, возможностью выполнять работу, взаимодействовать.
Полная энергия тела
Самое общее понятие энергии получают из представлений теории относительности Эйнштейна.
Определение 1
Полной энергией тела ($E$) называют физическую величину, равную произведению релятивистской массы тела ($m$) на скорость света ($c$) в квадрате:
$E=mc^2 (1),$
где $m=\frac{m_0}{\sqrt{1-\frac{v^2}{c^2}}}(2)$; $ c=3\cdot 10^8$ м/c.
Определение (1) указывает на то, что полная энергия тела зависит от выбора системы отсчета. Она связана со скоростью перемещения тела относительно избранной системы отсчета, так как со скоростью связана масса $m$ тела (см. выражение (2)).
Минимальную энергию имеет тело в той системе отсчета, по отношению к которой оно покоится.
Определение 2
Энергию тела называют энергией покоя ($E_0$), если относительно рассматриваемо системы отсчета тело находится в покое.
$E_0=m_0c^2 (3).$
Кинетическая энергия
Кинетическую энергию тела можно определить как разность полной энергии и энергии покоя тела:
$E_k=E-E_0 (4).$
Кинетическая энергия зависит от скорости перемещения тела по отношению к избранной системе отсчета.
Принимая во внимание выражение (2), формулу (4) преобразуем к виду:
$E_k=mc^2(1-\sqrt{1-\frac{v^2}{c^2}})(5).$
Умножим и разделим выражение (5) на $1+\sqrt{1-\frac{v^2}{c^2}}$, получаем:
$E_k=\frac{mv^2}{1+\sqrt{1-\frac{v^2}{c^2}}}=\frac{p^2}{m(1+\sqrt{1-\frac{v^2}{c^2}})}(6).$
Кинетическая энергия в классической механике
В классической механике тела перемещаются со скоростями много меньшими, чем скорость света в вакууме, что означает величиной $\frac{v^2}{c^2}$ можно пренебречь в сравнении с единицей, то есть имеем:
$\sqrt{1-\frac{v^2}{c^2}}\approx 1$,
в этом случае для вычисления кинетической энергии мы имеем простую формулу:
$E_k=\frac{mv^2}{2}=\frac{p^2}{2m}(7),$
где $p$ — импульс тела.
Выражение (7) является приближенным, однако, при скоростях с которыми мы имеем дело в обыденной жизни, она дает достаточную точность. Даже, если скорость тела будет несколько сотен метров в секунду, результаты вычисления кинетической энергии при помощи формулы (7) отличны от точных (формула (6)) меньше, чем на десятитысячную часть процента.
Если скорость тела значительно меньше скорости света, кинетическая энергия будет существенно меньше энергии покоя:
$\frac{E_k}{E_0}=\frac{v^2}{2c^2}\ll 1.$
Если тело будет обладать скоростью близкой к скорости света, то почти вся энергия будет равна кинетической энергии тела, то есть энергия покоя станет существенно меньше энергии движения. Например, в синхрофазотронах протоны разгоняют до скоростей примерно равных $v=0,9995c$, в этом случае имеем:
$\frac{E_k}{E_0}=\frac {(m-m_0)c^2}{m_0c^2}\approx 30$.
Кинетическая энергия протонов в синхрофазотроне в 30 раз больше энергии их покоя.
Для ультра релятивистских скоростей можно считать, что:
$E_k\approx E=mc^2 (8).$
Кинетическая энергия – это часть полной энергии тела, которая связана с его движением.
Изменение кинетической энергии будет равно работе ($A$), которую выполняют силы, которые действуют на тело:
$\Delta E_k=A (9).$
Потенциальная энергия
При описании взаимодействия тел при помощи сил в истории использовались две концепции:
- В первой, все взаимодействия считали контактными, реализующимися при непосредственном соприкосновении тел.
- Второй, была концепция дальнодействия (действия на расстоянии). Сторонником этой концепции был Ньютон.
Обе концепции присутствовали в науке достаточно долгое время. Для описания гравитационного взаимодействия с позиций близкодействия было введено понятие поля силы. При помощи понятия силового поля, взаимодействие тел на расстоянии определяется так:
- Одно из тел изменяет свойства пространства вокруг себя, оно создает поле.
- Второе тело «ощущает» данное изменение пространственных свойств, то есть получает со стороны силового поля некоторое воздействие, в месте своего нахождения.
- Силовое поле играет роль переносчика взаимодействия.
- Второе поле воздействует на первое по аналогии.
Все фундаментальные взаимодействия обладают полевой природой. Силовые поля — это векторные поля. Их делят на потенциальные и непотенциальные.
Определение 3
Потенциальным полем называют силовое поле, которое выражается при помощи скалярной потенциальной функции ($U(x,y,z,t)$), зависящей от пространственных координат и времени. Данную функцию называют потенциальной. При этом сила, оказывающая воздействие на частицу и потенциальная функция связаны соотношением:
$\vec F(x,y,z,t)=-(\frac{\partial U(x,y,z,t)}{\partial x}\vec i+\frac{\partial U(x,y,z,t)}{\partial y}\vec j+\frac{\partial U(x,y,z,t)}{\partial y}\vec k)=-grad U (9)$.
Градиент скалярной функции – это вектор, который направлен в сторону наиболее быстрого увеличения данной функции, равный по величине скорости ее увеличения в этом направлении. Знак минус в формуле (9) показывает то, что сила имеет направление в сторону наиболее быстрого уменьшения функции $U$.
Частным случаем потенциальных полей являются поля, которые не зависят в явном виде от времени. Такие поля именуют консервативными. Для консервативных полей $U=U(x,y,z)$.
Иначе говорят, что тело (частица) находится состоянии стационарных внешних условий, например, в постоянном поле гравитации. В этом случае потенциальную функцию $U$ называют потенциальной энергией частицы во внешнем консервативном поле.
Обозначим потенциальную энергию как $E_p$, в таком случае выполняется равенство:
$\vec F=- grad E_p (x,y,z)(10).$
Работа консервативной силы равна изменению потенциальной энергии материальной точки с противоположным знаком, и она не зависит от траектории по которой совершает перемещение частица.
Полная механическая энергия
В общем случае тело обладает и кинетической и потенциальной энергиями одновременно. Сумма данных энергий составляет полную механическую энергию. Полной механической энергией называют физическую величину, равную:
$E_p+E_k=E (11).$
Изменение полной механической энергии материальной точки, которая находится в поле консервативных сил, равно работе, которую выполняют эти силы, оказывающие воздействие на частицу:
$E_2-E_1=A_{12} (12).$
Потенциальная и кинетическая энергия способны переходить друг в друга. Полная механическая энергия системы тел, внутри которой действуют исключительно консервативные силы, складывается из потенциальной энергии системы, как единого целого и суммы кинетических энергий, входящих в нее тел.
Энергия — это… Что такое Энергия?
Эне́ргия (др.-греч. ἐνέργεια — «действие, деятельность, сила, мощь») — скалярная физическая величина, являющаяся единой мерой различных форм движения и взаимодействия материи, мерой перехода движения материи из одних форм в другие. Введение понятия энергии удобно тем, что в случае, если физическая система является замкнутой, то её энергия сохраняется во времени. Это утверждение носит название закона сохранения энергии. Понятие введено Аристотелем в трактате «Физика».
Фундаментальный смысл
С фундаментальной точки зрения энергия представляет собой интеграл движения (то есть сохраняющуюся при движении величину), связанный, согласно теореме Нётер, с однородностью времени. Таким образом, введение понятия энергии как физической величины целесообразно только в том случае, если рассматриваемая физическая система однородна во времени.
Энергия и работа
Энергия является мерой способности физической системы совершить работу, поэтому количественно энергия и работа выражаются в одних единицах.
В специальной теории относительности
Энергия и масса
Согласно специальной теории относительности между массой и энергией существует связь, выражаемая знаменитой формулой Эйнштейна
где E — энергия системы, m — её масса, c — скорость света. Несмотря на то, что исторически предпринимались попытки трактовать это выражение как полную эквивалентность понятия энергии и массы, что, в частности, привело к появлению такого понятия как релятивистская масса, в современной физике принято сужать смысл этого уравнения, понимая под массой массу тела в состоянии покоя (так называемая масса покоя), а под энергией — только внутреннюю энергию, заключённую в системе.
Энергия тела, согласно законам классической механики, зависит от системы отсчета, то есть неодинакова для разных наблюдателей. Если тело движется со скоростью v относительно некоего наблюдателя, то для другого наблюдателя, движущегося с той же скоростью, оно будет казаться неподвижным. Соответственно, для первого наблюдателя кинетическая энергия тела будет равна, , где m — масса тела, а для другого наблюдателя — нулю.
Эта зависимость энергии от системы отсчета сохраняется также в теории относительности. Для определения преобразований, происходящих с энергией при переходе от одной инерциальной системы отсчета к другой используется сложная математическая конструкция — тензор энергии-импульса.
Зависимость энергии тела от скорости рассматривается уже не так, как в ньютоновской физике, а согласно вышеназванной формуле Эйнштейна:
- ,
где — инвариантная масса. В системе отсчета, связанной с телом, его скорость равна нулю, а энергия, которую называют энергией покоя, выражается формулой:
- .
Это минимальная энергия, которую может иметь массивное тело. Значение формулы Эйнштейна также в том, что до неё энергия определялась с точностью до произвольной постоянной, а формула Эйнштейна находит абсолютное значение этой постоянной.
Энергия и импульс
Специальная теория относительности рассматривает энергию как компоненту 4-импульса (4-вектора энергии-импульса), в который наравне с энергией входят три пространственные компоненты импульса. Таким образом энергия и импульс оказываются связанными и оказывают взаимное влияние друг на друга при переходе из одной системы отсчёта в другую.
В квантовой механике
 | В этом разделе не хватает ссылок на источники информации. Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена. Вы можете отредактировать эту статью, добавив ссылки на авторитетные источники. Эта отметка установлена 12 мая 2011. |
В квантовой механике величина энергии пропорциональна частоте и двойственна времени. В частности, в силу фундаментальных причин принципиально невозможно измерить абсолютно точно энергию системы в каком-либо процессе, время протекания которого конечно. При проведении серии измерения одного и того же процесса значения измеренной энергии будут флуктуировать, однако среднее значение всегда определяется законом сохранения энергии. Это приводит к тому, что иногда говорят, что в квантовой механике сохраняется средняя энергия.
В общей теории относительности
В общей теории относительности время не является однородным, поэтому возникают определённые проблемы при попытке введения понятия энергии. В частности, оказывается невозможным определить энергию гравитационного поля как тензор относительно общих преобразований координат.
Энергия и энтропия
Внутреняя энергия (или энергия хаотического движения молекул) является самым «деградированным» видом энергии — она не может превращаться в другие виды энергии без потерь (см.: энтропия).
Физическая размерность
Энергия E имеет размерность, равную:
В системе величин LMT энергия имеет размерность .
| Единица | Эквивалент | |||
|---|---|---|---|---|
| в Дж | в эрг | в межд. кал | в эВ | |
| 1 Дж | 1 | 107 | 0,238846 | 0,624146·1019 |
| 1 эрг | 10−7 | 1 | 2,38846·10−8 | 0,624146·1012 |
| 1 межд. Дж[1] | 1,00020 | 1,00020·107 | 0,238891 | 0,624332·1019 |
| 1 кгс·м | 9,80665 | 9,80665·107 | 2,34227 | 6,12078·1019 |
| 1 кВт·ч | 3,60000·106 | 3,60000·1013 | 8,5985·105 | 2,24693·1025 |
| 1 л·атм | 101,3278 | 1,013278·109 | 24,2017 | 63,24333·1019 |
| 1 межд. кал (calIT) | 4,1868 | 4,1868·107 | 1 | 2,58287·1019 |
| 1 термохим. кал (калТХ) | 4,18400 | 4,18400·107 | 0,99933 | 2,58143·1019 |
| 1 электронвольт (эВ) | 1,60219·10−19 | 1,60219·10−12 | 3,92677·10−20 | 1 |
Виды энергии
Механика различает потенциальную энергию (или, в более общем случае, энергию взаимодействия тел или их частей между собой или с внешними полями) и кинетическую энергию (энергия движения). Их сумма называется полной механической энергией.
Энергией обладают все виды полей. По этому признаку различают: электромагнитную (разделяемую иногда на электрическую и магнитную энергии), гравитационную и ядерную энергии (также может быть разделена на энергию слабого и сильного взаимодействий).
Термодинамика рассматривает внутреннюю энергию и иные термодинамические потенциалы.
В химии рассматриваются такие величины, как энергия связи и энтальпия, имеющие размерность энергии, отнесённой к количеству вещества. См. также: химический потенциал.
Энергия взрыва иногда измеряется в тротиловом эквиваленте.
Кинетическая
Кинетическая энергия — энергия механической системы, зависящая от скоростей движения её точек. Часто выделяют кинетическую энергию поступательного и вращательного движения. Единица измерения в системе СИ — Джоуль. Более строго, кинетическая энергия есть разность между полной энергией системы и её энергией покоя; таким образом, кинетическая энергия — часть полной энергии, обусловленная движением.
Потенциальная
Потенциальная энергия — скалярная физическая величина, характеризует запас энергии некоего тела (или материальной точки), находящегося в потенциальном силовом поле, который идет на приобретение (изменение) кинетической энергии тела за счет работы сил поля. Другое определение: потенциальная энергия — это функция координат, являющаяся слагаемым в лагранжиане системы, и описывающая взаимодействие элементов системы.[2]
Термин «потенциальная энергия» был введен в XIX веке шотландским инженером и физиком Уильямом Ренкином. Единицей измерения энергии в СИ является Джоуль. Потенциальная энергия принимается равной нулю для некоторой конфигурации тел в пространстве, выбор которой определяется удобством дальнейших вычислений. Процесс выбора данной конфигурации называется нормировкой потенциальной энергии.
Электромагнитная
Гравитационная
Гравитационная энергия — потенциальная энергия системы тел (частиц), обусловленная их взаимным тяготением. Гравитационно-связанная система — система, в которой гравитационная энергия больше суммы всех остальных видов энергий (помимо энергии покоя). Общепринята шкала, согласно которой для любой системы тел, находящихся на конечных расстояниях, гравитационная энергия отрицательна, а для бесконечно удалённых, то есть для гравитационно не взаимодействующих тел, гравитационную энергия равна нулю. Полная энергия системы, равная сумме гравитационной и кинетической энергии постоянна, для изолированной системы гравитационная энергия является энергией связи. Системы с положительной полной энергией не могут быть стационарными.
Ядерная
Ядерная энергия (атомная энергия) — это энергия, содержащаяся в атомных ядрах и выделяемая при ядерных реакциях.
Энергия связи — энергия, которая требуется, чтобы разделить ядро на отдельные нуклоны, называется энергией связи. Энергия связи, приходящаяся на один нуклон, неодинакова для разных химических элементов и, даже, изотопов одного и того же химического элемента.
Внутренняя
Внутренняя энергия тела (обозначается как E или U) — это сумма энергий молекулярных взаимодействий и тепловых движений молекулы. Внутреннюю энергию тела нельзя измерить напрямую. Внутренняя энергия является однозначной функцией состояния системы. Это означает, что всякий раз, когда система оказывается в данном состоянии, её внутренняя энергия принимает присущее этому состоянию значение, независимо от предыстории системы. Следовательно, изменение внутренней энергии при переходе из одного состояния в другое будет всегда равно разности между её значениями в конечном и начальном состояниях, независимо от пути, по которому совершался переход.
Химический потенциал
Химический потенциал — один из термодинамических параметров системы, а именно энергия добавления одной частицы в систему без совершения работы.
Энергия взрыва
Взрыв — физический или/и химический быстропротекающий процесс с выделением значительной энергии в небольшом объёме за короткий промежуток времени, приводящий к ударным, вибрационным и тепловым воздействиям на окружающую среду и высокоскоростному расширению газов.
При химическом взрыве, кроме газов, могут образовываться и твёрдые высокодисперсные частицы, взвесь которых называют продуктами взрыва. Энергию взрыва иногда измеряют в тротиловом эквиваленте — мере энерговыделения высокоэнергетических событий, выраженной в количестве тринитротолуола (ТНТ), выделяющем при взрыве равное количество энергии.
Проблемы энергопотребления
Существует довольно много форм энергии, большинство[3] из которых так или иначе используются в энергетике и различных современных технологиях.
Темпы энергопотребления растут во всем мире, поэтому на современном этапе развития цивилизации наиболее актуальна проблема энергосбережения.
Условно источники энергии можно поделить на два типа: невозобновляемые и постоянные. К первым относятся газ, нефть, уголь, уран и т. д. Технология получения и преобразования энергии из этих источников отработана, но, как правило, неэкологична, и многие из них истощаются. К постоянным источникам можно отнести энергию солнца, энергию, получаемую на ГЭС и т. д.
История термина
Термин «энергия» происходит от слова energeia, которое впервые появилось в работах Аристотеля.
Томас Юнг первым использовал понятие «энергия» в современном смысле словаМаркиза Эмили дю Шатле в книге «Уроки физики» (фр. Institutions de Physique, 1740), объединила идею Лейбница с практическими наблюдениями Виллема Гравезанда, чтобы показать: энергия движущегося объекта пропорциональна его массе и квадрату его скорости (не скорости самой по себе как полагал Исаак Ньютон).
В 1807 году Томас Юнг первым использовал термин «энергия» в современном смысле этого слова взамен понятия живая сила.[4]Гаспар-Гюстав Кориолис впервые использовал термин «кинетическая энергия» в 1829 году, а в 1853 году Уильям Ренкин впервые ввёл понятие «потенциальная энергия».
Несколько лет велись споры, является ли энергия субстанцией (теплород) или только физической величиной.
Развитие паровых двигателей требовало от инженеров разработать понятия и формулы, которые позволили бы им описать механический и термический КПД своих систем. Инженеры (Сади Карно), физики (Джеймс Джоуль), математики (Эмиль Клапейрон и Герман Гельмгольц[уточнить]) — все развивали идею, что способность совершать определённые действия, называемая работой, была как-то связана с энергией системы. В 1850-х годах, профессор натурфилософии из Глазго Уильям Томсон и инженер Уильям Ренкин начали работу по замене устаревшего языка механики с такими понятиями как «кинетическая и фактическая (actual) энергии».[4] Уильям Томсон соединил знания об энергии в законы термодинамики, что способствовало стремительному развитию химии. Рудольф Клаузиус, Джозайя Гиббс и Вальтер Нернст объяснили многие химические процессы, используя законы термодинамики. Развитие термодинамики было продолжено Клаузиусом, который ввёл и математически сформулировал понятие энтропии, и Джозефом Стефаном, который ввёл закон излучения абсолютно чёрного тела. В 1853 году Уильям Ренкин ввёл понятие «потенциальная энергия».[4] В 1881 году Уильям Томсон заявил перед слушателями:[5]
|
В течение следующих тридцати лет эта новая наука имела несколько названий, например, «динамическая теория тепла» (англ. dynamical theory of heat) и «энергетика» (англ. energetics). В 1920-х годах общепринятым стало название «термодинамика» — наука о преобразовании энергии.
Особенности преобразования тепла и работы были показаны в первых двух законах термодинамики. Наука об энергии разделилась на множество различных областей, таких как биологическая термодинамика и термоэкономика (англ. thermoeconomics). Параллельно развивались связанные понятия, такие как энтропия, мера потери полезной энергии, мощность, поток энергии за единицу времени, и так далее. В последние два века использование слова энергия в ненаучном смысле широко распространилось в популярной литературе.
В 1918 году было доказано, что закон сохранения энергии есть математическое следствие трансляционной симметрии времени, величины сопряжённой энергии. То есть энергия сохраняется, потому что законы физики не отличают разные моменты времени (см. Теорема Нётер, изотропия пространства).
В 1961 году выдающийся преподаватель физики и нобелевский лауреат, Ричард Фейнман в лекциях так выразился о концепции энергии:[6]
Существует факт, или, если угодно, закон, управляющей всеми явлениями природы, всем, что было известно до сих пор. Исключений из этого закона не существует; насколько мы знаем, он абсолютно точен. Название его — сохранение энергии. Он утверждает, что существует определённая величина, называемая энергией, которая не меняется ни при каких превращениях, происходящих в природе. Само это утверждение весьма и весьма отвлечено. Это по существу математический принцип, утверждающий, что существует некоторая численная величина, которая не изменяется ни при каких обстоятельствах. Это отнюдь не описание механизма явления или чего-то конкретного, просто-напросто отмечается то странное обстоятельство, что можно подсчитать какое-то число и затем спокойно следить, как природа будет выкидывать любые свои трюки, а потом опять подсчитать это число — и оно останется прежним.
Оригинальный текст (англ.)
There is a fact, or if you wish, a law, governing natural phenomena that are known to date. There is no known exception to this law—it is exact so far we know. The law is called conservation of energy; it states that there is a certain quantity, which we call energy that does not change in manifold changes which nature undergoes. That is a most abstract idea, because it is a mathematical principle; it says that there is a numerical quantity, which does not change when something happens. It is not a description of a mechanism, or anything concrete; it is just a strange fact that we can calculate some number, and when we finish watching nature go through her tricks and calculate the number again, it is the same.
— Фейнмановские лекции по физике[7]
См. также
Примечания
- ↑ Г. Д. Бурдун. Джоуль(единица энергии и работы) // Большая советская энциклопедия.
- ↑ Ландау, Л. Д., Лифшиц, Е. М. Теоретическая физика. — 5-е изд. — М.: Физматлит, 2004. — Т. I. Механика. — 224 с. — ISBN 5-9221-0055-6
- ↑ http://profbeckman.narod.ru/InformLekc.files/Inf03.pdf
- ↑ 1 2 3 Смит, Кросби. The science of energy: a cultural history of energy physics in Victorian Britain. — The University of Chicago Press, 1998. — ISBN 0-226-76421-4
- ↑ Томсон, Уильям. Об источниках энергии, доступных человеку для совершения механических эффектов = On the sources of energy available to man for the production of mechanical effect. — BAAS Rep, 1881. С. 513
- ↑ Richard Feynman. The Feynman Lectures on Physics. — США: Addison Wesley, 1964. — Vol. 1. — ISBN 0-201-02115-3
- ↑ Фейнман, Ричард. Фейнмановские лекции по физике = The Feynman Lectures on Physics. — Т. 1.
Ссылки
Теорема о кинетической энергии системы — Википедия
Теоре́ма о кинети́ческой эне́ргии систе́мы — одна из общих теорем динамики[1], является следствием законов Ньютона. Связывает кинетическую энергию механической системы с работой сил, действующих на тела, составляющие систему. В качестве системы, о которой идёт речь, может выступать любая механическая система, состоящая из любых тел[2][3].
Кинетической энергией системы называют сумму кинетических энергий всех тел, входящих в систему. Для определённой таким образом величины справедливо утверждение[2][3]:
Изменение кинетической энергии системы равно работе всех внутренних и внешних сил, действующих на тела системы.
Теорема допускает обобщение на случай неинерциальных систем отсчёта. В этом случае к работе всех внешних и внутренних сил необходимо добавить работу переносных сил инерции (кориолисовы силы инерции не могут производить работу)[4].
Рассмотрим систему материальных точек с массами mi{\displaystyle m_{i}}, скоростями v→i{\displaystyle {\vec {v}}_{i}} и кинетическими энергиями Ti=12mivi2{\displaystyle T_{i}={\frac {1}{2}}m_{i}{v_{i}}^{2}}. Для малого изменения кинетической энергии (дифференциала), происходящего в течение некоторого малого промежутка времени dt,{\displaystyle dt,} будет выполняться
- dTi=miv→idv→i=miv→idv→idtdt.{\displaystyle dT_{i}=m_{i}{\vec {v}}_{i}d{\vec {v}}_{i}=m_{i}{\vec {v}}_{i}{\frac {d{\vec {v}}_{i}}{dt}}dt.}
Учитывая, что dv→idt{\displaystyle {\frac {d{\vec {v}}_{i}}{dt}}} представляет собой ускорение i-ой точки a→i{\displaystyle {\vec {a}}_{i}}, а v→idt{\displaystyle {\vec {v}}_{i}dt} — перемещение той же точки ds→i{\displaystyle d{\vec {s}}_{i}} за время dt{\displaystyle dt}, полученное выражение можно записать в виде:
- dTi=mia→ids→i.{\displaystyle dT_{i}=m_{i}{\vec {a}}_{i}d{\vec {s}}_{i}.}
Используя второй закон Ньютона и обозначая равнодействующую всех сил, действующих на точку, как Fi{\displaystyle F_{i}}, получаем
- dTi=F→ids→i,{\displaystyle dT_{i}={\vec {F}}_{i}d{\vec {s}}_{i},}
а затем в соответствии с определением работы dAi{\displaystyle dA_{i}}
- dTi=dAi.{\displaystyle dT_{i}=dA_{i}.}
Суммирование всех уравнений такого вида, записанных для каждой из материальных точек, приводит к формуле для изменения полной кинетической энергии системы:
- dT=∑idAi.{\displaystyle dT=\sum \limits _{i}dA_{i}.}
Данное равенство выражает утверждение теоремы об изменении кинетической энергии системы в дифференциальном виде.
Проинтегрировав обе части полученного равенства по произвольно взятому промежутку времени между некоторыми t1{\displaystyle t_{1}} и t2{\displaystyle t_{2}}, получим выражение теоремы об изменении кинетической энергии в интегральной форме:
- T2−T1=∑iAi,{\displaystyle T_{2}-T_{1}=\sum \limits _{i}A_{i},}
где T1{\displaystyle T_{1}} и T2{\displaystyle T_{2}} — значения кинетической энергии системы в моменты времени t1{\displaystyle t_{1}} и t2{\displaystyle t_{2}} соответственно.
Необходимо подчеркнуть, что здесь, в отличие от случаев теоремы об изменении количества движения системы и теоремы о движении центра масс системы, учитывается действие не только внешних, но внутренних сил.
Закон сохранения механической энергии[править | править код]
Отдельный интерес представляют системы, в которых на тела действуют потенциальные силы[5]. Для таких сил вводится понятие потенциальной энергии, изменение которой в случае одной материальной точки по определению удовлетворяет соотношению:
- W2i−W1i=−Api,{\displaystyle W_{2i}-W_{1i}=-A_{pi},}
где W1i{\displaystyle W_{1i}} и W2i{\displaystyle W_{2i}} — значения потенциальной энергии точки в начальном и конечном состояниях соответственно, а Api{\displaystyle A_{pi}} — работа потенциальной силы, совершаемая при перемещении точки из начального состояния в конечное.
Изменение потенциальной энергии системы получается в результате суммирования изменений энергий всех тел системы:
- W2−W1=−∑iApi.{\displaystyle W_{2}-W_{1}=-\sum \limits _{i}A_{pi}.}
Если все внутренние и внешние силы, действующие на тела системы, потенциальны[6], то
- ∑iAi=∑iApi=−(W2−W1).{\displaystyle \sum \limits _{i}A_{i}=\sum \limits _{i}A_{pi}=-(W_{2}-W_{1}).}
Подставляя полученное выражение в уравнение теоремы о кинетической энергии, получим:
- T2−T1=−(W2−W1){\displaystyle T_{2}-T_{1}=-(W_{2}-W_{1})}
или, что то же самое
- T2+W2=T1+W1.{\displaystyle T_{2}+W_{2}=T_{1}+W_{1}.}
Иначе говоря, получается, что для полной механической энергии системы T+W{\displaystyle T+W} выполняется
- T+W=const.{\displaystyle T+W=const.}
Таким образом, можно сделать вывод:
Если на тела системы действуют только потенциальные силы, то полная механическая энергия системы сохраняется.
Данное утверждение и составляет содержание закона сохранения механической энергии, являющегося следствием теоремы о кинетической энергии и одновременно частным случаем общего физического закона сохранения энергии[2][3].
Случай системы с идеальными стационарными связями[править | править код]
Основной источник: [7]В тех случаях, когда предметом изучения является лишь движение системы, а реакции связей не представляют интереса, пользуются формулировкой теоремы для системы с идеальными стационарными связями, которая выводится с учетом принципа Даламбера-Лагранжа.
Теорема об изменении кинетической энергии системы с идеальными стационарными связями утверждает[7]:
Дифференциал кинетической энергии системы с идеальными стационарными связями равен сумме элементарных работ на действительных перемещениях действующих внешних и внутренних сил
Доказательство[править | править код]
Заменяя в общем уравнении динамики δrk→{\displaystyle \delta {\vec {r_{k}}}} на vk→dt{\displaystyle {\vec {v_{k}}}dt}, получаем:
- (∑mkwk→)vk→dt=∑Fk→vk→dt{\displaystyle (\sum m_{k}{\vec {w_{k}}}){\vec {v_{k}}}dt=\sum {\vec {F_{k}}}{\vec {v_{k}}}dt}
или
- (d∑mkvk→)vk→=∑Fkae→vk→dt+∑Fkai→vk→dt{\displaystyle (d\sum m_{k}{\vec {v_{k}}}){\vec {v_{k}}}=\sum {\vec {F_{k}^{ae}}}{\vec {v_{k}}}dt+\sum {\vec {F_{k}^{ai}}}{\vec {v_{k}}}dt}
Поскольку dvk→vk→=dvk22{\displaystyle d{\vec {v_{k}}}{\vec {v_{k}}}=d{\frac {v_{k}^{2}}{2}}}, получаем окончательно:
- dT=d′Aae+d′Aai{\displaystyle dT=d’A^{ae}+d’A^{ai}}
- ↑ Тарг С. М. Динамика // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1988. — Т. 1: Ааронова — Бома эффект — Длинные линии. — С. 616-617. — 707 с. — 100 000 экз.
- ↑ 1 2 3 Тарг С. М. Краткий курс теоретической механики. — М.: Высшая школа, 1995. — С. 301-323. — 416 с. — ISBN 5-06-003117-9.
- ↑ 1 2 3 Журавлёв В. Ф. Основы теоретической механики. — М.: Физматлит, 2001. — С. 70-71. — 319 с. — ISBN 5-95052-041-3.
- ↑ Жирнов Н. И. Классическая механика. — Серия: учебное пособие для студентов физико-математических факультетов педагогических институтов. — М., Просвещение, 1980. — Тираж 28 000 экз. — с. 262
- ↑ Напомним, что силы называют потенциальными, если работа, совершаемая ими при перемещении материальной точки, определяется только начальным и конечным положениями точки и не зависит от выбора траектории.
- ↑ То есть, диссипативные силы отсутствуют.
- ↑ 1 2 Бугаенко Г. А., Маланин В. В., Яковлев В. И. Основы классической механики. — М.: Высшая школа, 1999. — С. 221-223. — ISBN 5-06-003587-5
Закон сохранения энергии, общая форма. Полная энергия: механическая, кинетическая, потенциальная. Формулировка, формулы
Тестирование онлайн
Закон сохранения энергии
Полная механическая энергия замкнутой системы тел остается неизменной
Закон сохранения энергии можно представить в виде
Если между телами действуют силы трения, то закон сохранения энергии видоизменяется. Изменение полной механической энергии равно работе сил трения
Рассмотрим свободное падение тела с некоторой высоты h2. Тело еще не движется (допустим, мы его держим), скорость равна нулю, кинетическая энергия равна нулю. Потенциальная энергия максимальная, так как сейчас тело находится выше всего от земли, чем в состоянии 2 или 3.
В состоянии 2 тело обладает кинетической энергией (так как уже развило скорость), но при этом потенциальная энергия уменьшилась, так как h3 меньше h2. Часть потенциальной энергии перешло в кинетическую.
Состояние 3 — это состояние перед самой остановкой. Тело как бы только-только дотронулось до земли, при этом скорость максимальная. Тело обладает максимальной кинетической энергией. Потенциальная энергия равна нулю (тело находится на земле).
Полные механические энергии равны между собой , если пренебрегать силой сопротивления воздуха. Например, максимальная потенциальная энергия в состоянии 1 равна максимальной кинетической энергии в состоянии 3.
А куда потом исчезает кинетическая энергия? Исчезает бесследно? Опыт показывает, что механическое движение никогда не исчезает бесследно и никогда оно не возникает само собой. Во время торможения тела произошло нагревание поверхностей. В результате действия сил трения кинетическая энергия не исчезла, а превратилась во внутреннюю энергию теплового движения молекул.
При любых физических взаимодействиях энергия не возникает и не исчезает, а только превращается из одной формы в другую.
Главное запомнить
1) Суть закона сохранения энергии



