общие сведения, зависимость от других величин и формулы расчета

Любое вещество, находясь в разнообразных состояниях, обладает определенным сопротивлением. В некоторых случаях возникает необходимость рассчитать полное сопротивление цепи или конкретного участка. В такой ситуации следует воспользоваться формулами. Кроме того, нужно понимать основной смысл сопротивления и электропроводимости, а также зависимость этих понятий от некоторых величин.

Физический смысл

Все вещества по проводимости электрического тока (ЭТ) делятся на проводники, полупроводники и диэлектрики. Проводниками являются элементы, хорошо проводящие ЭТ. Это обусловлено наличием свободных электронов (СЭ). Полупроводники — особая группа веществ, проводимость которых зависит от внешних факторов, например, от температуры, освещенности и т. д. Диэлектриками являются все вещества, которые не проводят ЭТ из-за отсутствия или недостаточного количества СЭ. Для протекания тока по веществу требуется наличие СЭ, количество которых зависит от электронной конфигурации.

Электронная конфигурация какого-либо элемента берется из таблицы Менделеева. Ток оказывает на проводник тепловое действие, так как происходит взаимодействие СЭ с кристаллической решеткой (КР).Они замедляются, но с течением времени под действием электромагнитного поля снова ускоряются, после чего процесс взаимодействия повторяется много раз.

Процесс взаимодействия свободных заряженных частиц с КР вещества называется электрическим сопротивлением проводника. Обозначается сопротивление или электропроводимость буквой R, единицей измерения этой величины является Ом.

Зависимость электропроводимости

R зависит от внешних факторов окружающей среды, электрических величин, а также характерных особенностей проводника. Эти зависимости используются при расчетах схем и изготовлении радиодеталей. Существует несколько способов нахождения R, а иногда они комбинируются для получения эффективности и точности вычислений.

Электрические величины

К электрическим величинам, от которых зависит величина R, относятся I, U, электродвижущая сила (ЕДС обозначается е) и тип тока. R в электрических цепях рассчитывается по закону Ома для определенного участка цепи: I, протекающая в заданном участке электрической цепи, прямо пропорциональна U на этом участке и обратно пропорциональна R выбранного участка цепи. В виде формулы его можно записать следующим образом:

I = U / R.

Исходя из следствия этого закона, можно получить сопротивление участка цепи: R = U / I. Если требуется произвести расчет R на всем участке цепи, то нужно воспользоваться формулой (следствием из закона Ома для полной цепи) с учетом внутреннего R источника питания: R = (e / I) — R внутреннее. Величина электрической проводимости рассчитывается не только при помощи законов Ома, но и с использованием геометрических параметров проводника и температуры. Кроме того, необходимо учитывать и тип тока (постоянный или переменный).

Геометрические параметры и тип вещества

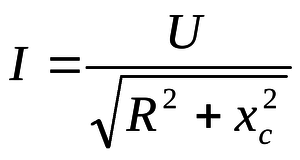Если основными носителями заряда являются СЭ, а свойства проводимости прямо пропорционально зависят от их количества и структуры КР, то тип вещества является одним из факторов, влияющих на R проводника. Вещества и их составляющие элементы, имеющие различные электронные конфигурации, согласно таблице Менделеева обладают разными КР, что и обуславливается различным R.

Зависимость от материала выражается коэффициентом, обозначающимся

p. Он характеризует показатель удельного R проводника. Его значение берется из таблицы (при температуре +20 °C). Величина, обратная p, называется удельной проводимостью и обозначается σ. Взаимосвязь σ и p можно выразить формулой p = 1 / σ.

Кроме того, от площади поперечного сечения (S) также зависит R проводника. Эта зависимость обусловлена тем, что при маленьком сечении плотность потока Э протекает через проводник и взаимодействие с КР становится более частым. Площадь поперечного сечения достаточно просто вычислить. Для этого необходимо воспользоваться некоторым алгоритмом, если проводник (П) представляет собой провод цилиндрической формы:

1. Измерение диаметра проводника при помощи штангенциркуля (ШЦ).
2. Нахождение S при помощи формулы S = 3,1416 * sqr (d) / 4.

П может из себя представлять многожильный провод, поэтому для точного расчета необходимо найти S одной жилы, воспользовавшись алгоритмом нахождения для цилиндрической формы П, а затем результат умножить на количество жил.

Кроме того, бывают провода в форме квадрата и прямоугольника, но они встречаются редко. Для этого нужно выполнить следующие вычисления:

1. Для квадратной формы нужно замерить ШЦ одну из сторон и возвести ее в квадрат: S = sqr(a).
2. Для прямоугольной формы следует измерить две противолежащие стороны при помощи ШЦ, а затем произвести расчет по формуле
   S = a * b.

Из этих алгоритмов нахождения S можно сделать универсальный (абстрактный алгоритм). Он подходит для нахождения или расчетов величин, независимо от формы П при его разрезе, выполненном строго перпендикулярно относительно П. Алгоритм имеет следующий вид:

1. Визуально определить геометрическую фигуру при разрезе П.
2. Найти в справочнике формулу S.
3. Произвести измерения при помощи ШЦ необходимых величин.
4. Подставить в формулу и вычислить S.

Еще одной величиной является длина П, при увеличении которой R увеличивается. На основании этих величин можно вывести следующую формулу зависимости от типа вещества, длины (L) и S проводника: R = p * L / S.

Однако это значение R можно определить при температуре +20 °C. Для получения более точных расчетов нужно рассмотреть зависимость от температуры.

Температура проводника

Научно подтвержденным является факт, что p зависит от температуры. Это утверждение можно доказать практическим путем. Для проведения опыта необходимы следующие элементы, изображенные на схеме: спираль из нихрома (используется в нагревательных элементах), соединительные медные провода, источник питания, амперметр (для измерения I), вольтметр (измеряет U) и реостат.

На схеме нагревательный элемент изображен в виде резистора. При его включении следует внимательно наблюдать за показаниями амперметра. Спираль начинает нагреваться, и показания амперметра уменьшаются по мере нагревания. Согласно закону Ома для участка цепи необходимо сделать вывод, что при росте R ток уменьшается (обратно пропорциональная зависимость). Следовательно, значение R зависит от температуры. При нагревании происходит увеличение ионов в КР нихромовой спирали и Э начинают чаще сталкиваться с ними.

В формуле R = p * L / S можно методом исключения найти показатель, зависящий от температуры. Последняя не оказывает влияния на длину П. По формуле вычисления S зависимость также не прослеживается, поскольку геометрия П не зависит от температуры. Остается p, который зависит от температуры. В физике существует формула зависимости p = p0 * [1 + a * (t — 20)]. Буква а является температурным коэффициентом:

• для металлов а > 0;
• для электролитов a < 0.

Переменная t — температура П, p0 — удельное сопротивление, взятое из справочника для конкретного материала. Кроме того, p зависит еще и от деформации П, поскольку при этом КР меняет свою структуру. Это происходит в процессе обработки металла при низких температурах и давлении. Такая деформация является пластической, при ней искажается КР, и увеличивается R течения Э.

В этом случае происходит увеличение p. Процесс является обратимым, поэтому часть дефектов уменьшается (рекристаллический отжиг). Если на металл действуют силы растяжения или сжатия, то эта деформация является упругой. Величина p уменьшается под действием силы сжатия, при которой происходит резкое уменьшение тепловых колебаний (ТК), а Э легче двигаются. Но под действием силы растяжения происходит прямо пропорциональное увеличение p, при котором амплитуда ТК увеличивается.

Конечную формулу можно записать в виде R = p0 * [1 + a * (t — 20)] * L / S. Однако этот вариант нахождения R был рассмотрен в цепях с постоянным I, а под действием переменного I появляются новые величины, влияющие на расчеты.

Цепь переменного тока

Закон Ома применяется только для цепей постоянного тока. Для переменного U он изменен и, следовательно, существуют другие формулы нахождения R. Сопротивление в цепях с переменным I (ПТ) бывает:

• активным;
• индуктивным;
• емкостным;
• полным.

Активное сопротивление свидетельствует о том, что в цепи присутствует резистор или любая другая неемкостная или неиндуктивная нагрузка. Для его расчета необходимо произвести измерение значений амплитуд Um и Im. При помощи приборов можно получить только действующие значения этих величин. Амплитудные значения рассчитываются по формулам Um = Ud * sqrt(2) и Im = Id * sqrt(2). Для определения активного сопротивления (обозначается R) нужно воспользоваться формулой Iм = Uм / R. Из неё можно получить R = Ud * sqrt(2) / Im = Id * sqrt(2).

Если в цепи переменного I (ЦПТ) присутствуют катушка индуктивности, дроссель, контур и т. д., то появляется индуктивное R, которое обозначается Xl. Для расчета необходимо воспользоваться формулой Xl = w * L, предварительно измеряв частоту ПТ и рассчитав индуктивность.

Величина циклической частоты находится по формуле, для которой нужно измерять частоту ПТ (f): w = 2 * 3,1416 * f. Последняя измеряется при помощи осциллографа или частотомера. Для расчета индуктивности катушки необходимо воспользоваться справочником по физике или онлайн-калькулятором.

При наличии в ЦПТ емкости (конденсатора) возникает емкостное R, которое обозначается Xc. При протекании постоянного U конденсатор не пропускает I, а в ЦПТ он пропускает I и обладает емкостью (C) и Xc. Рассчитывается это значение по формуле Xc = 1 / (w * C), где:

• w — циклическая частота, которая рассчитывается аналогично вычислению Xl;
• C — емкость конденсатора, указанная на корпусе или измеренная соответствующим прибором.

Полное сопротивление цепи обозначается Z и представляет собой сумму всей нагрузки ЦПТ (активного, индуктивного и емкостного сопротивления). Для расчета нужно воспользоваться формулой полного сопротивления: Z = sqrt [sqr(R) + sqr (Xc — Xl)]. В ЦПТ величина Z зависит от:

• геометрии П;
• типа вещества, из которого сделан П;
• температуры;
• деформации различного вида;
• электрических показателей I, U, f, L, C и R.

Закон Ома для участка цепи принимает следующий вид: I = U / Z. Необязательно рассчитывать электропроводимость П, так как для этих целей существуют омметры. Расчет Xl и Xс следует производить самостоятельно.

Измерение сопротивления

На расчет R необходимо потратить определенное время. Эту задачу упрощает прибор, который называется омметром. Он состоит из цифрового или стрелочного индикатора. Практически все современные комбинированные приборы (мультиметры) оснащены функцией измерения R. Однако есть и специализированные устройства, применяющиеся для определенных целей, например, для измерения R изоляции жил кабеля. Этот тип прибора называется мегаомметром. Омметр применяется не только для измерения величины R, но и для прозвонки радиокомпонентов, кабелей, отдельных шлейфов и других элементов на исправность и обрыв цепи.

Для измерения R необходимо обесточить участок или радиокомпонент и проследить за разрядкой цепей, где присутствуют конденсаторы. Перед проведением измерений нужно выставить необходимый режим на приборе и закоротить щупы для проверки прибора на исправность. Некоторые модели снабжены функцией звукового сигнала. После теста прибора следует приступить к измерениям.

Для нахождения точной величины Z проводника необходимо учитывать все величины, от которых оно зависит. Вычисление Z позволяет точно рассчитать электрическую схему какого-либо устройства для избегания трудоемких измерений. Измерить омметром можно только величину активного сопротивления, а Xl и Xc следует рассчитывать самостоятельно. Однако при помощи онлайн-калькуляторов сделать это не составит особого труда.

Закон Ома для цепи переменного тока

Введённый нами переменный ток, в любом случае, является током, таким образом, для переменного тока существует закон Ома. Для введения закона воспользуемся классической схемой колебательного LCR-контура (рис. 1). На концах контура извне подаётся переменное ЭДС:

(1)

Рис. 1. Колебательный LCR-контур

В данном случае, его официальное название — закон Ома для последовательной цепи переменного тока.

Формульно:

(2)

Параметр полного сопротивления цепи переменного тока включает в себя сопротивление как пассивных элементов (реостат, лампа, провод и т.д.), так и активных (катушка индуктивности, конденсатор). В общем случае:

(3)

Введённые обозначения:

• индуктивное сопротивление

(4)

• ёмкосное сопротивление

(5)

Вывод: для переменного тока связь между силой тока и ЭДС задаётся соотношением (2). Поиск составляющих — соотношения (3)-(5). В целом, больше в курсе школьной физики задач придумать нельзя.

Поделиться ссылкой:

Понравилось это:

Нравится Загрузка…

§ 17.3 Полное сопротивление в цепи переменного тока. Резонанс напряжений

Переменный ток – любой ток, изменяющийся со временем. Переменный ток можно рассматривать как вынужденные электромагнитные колебания. Наибольшее распространение в промышленности получил гармонический переменный ток. Этот ток получают с помощью установленных на электростанциях генераторов переменного тока. В нашей стране стандартная техническая частота вырабатываемого ими тока составляет 50 Гц.

Сопротивление, которое оказывается электрическая цепь переменному току, отличается от того, которое имеет место при наличии постоянного тока. В цепи с переменным током принято различать активное R и реактивное Х сопротивление. Активным обладают те элементы цепи, в которых электрическая энергия необратимо преобразуется во внутреннюю, а реактивным — те элементы (конденсаторы и катушки индуктивности), в которых подобного преобразования не происходит. Сопротивление конденсатора при этом называют ёмкостным Х_C, а катушки индуктивным Х_L. Реактивным сопротивлением обладают те элементы электрической цепи, на которых разность фаз колебаний силы тока и напряжения составляет π/2. В элементах с чисто активным сопротивлением колебания силы тока и напряжения совпадают по фазе.

Рассмотрим цепь, в которой последовательно соединены резистор, катушка индуктивности и конденсатор.

Сила тока в цепи и напряжение изменяются не в одной фазе, поэтому

I=I_m sin(ωt- φ), (17.26)

где – разность фаз напряжения и силы тока.

Сумма напряжений на отдельных участках равна внешнему напряжению:

U=U_R +U_L+ U_C= U_m sinωt (17.27)

где U_R = U_mR sin(ωt- φ) — в фазе с током; (17.28)

U_L = U_mL sin(ωt- φ + π/2) – опережает силу тока по фазе; (17.29)

U_С = U_mС sin(ωt- φ — π/2) – отстаёт от силы тока по фазе. (17.30)

Подставим в (17.27) можно получить выражение для полного сопротивления.

U= U_mR sin(ωt- φ) + U_mL sin(ωt- φ + π/2)+ U_mС sin(ωt- φ — π/2)= U_m sinωt (17.31)

Однако более просто и наглядно удаётся это сделать с помощью векторных диаграмм (рис.17.7).

На рис.17.7 по оси токов направлен вектор амплитуды силы тока I_m. так как во всей цепи амплитуда силы тока одинакова, то амплитуда напряжений на участках отложим относительно этого вектора: вектор U_mR – в одной фазе с силой тока; вектор U_mL – с опережением силы тока по фазе на π/2, вектор U_mС – с отставанием от силы тока по фазе на π/2.

Суммируя три вектора, находим графически значения и U. Используя теорему Пифагора, имеем

U² _m= U² _mR + (U_mL — U_mС) ² (17.32)

Подставляя выражения этих амплитуд и учитывая закон Ома, находим

I² _mZ² = I² _m R²+ (I_m ωL — I_m/Cω) ² (17.33)

где Z– полное сопротивление цепи переменного тока, называемое импедансом. Получаем

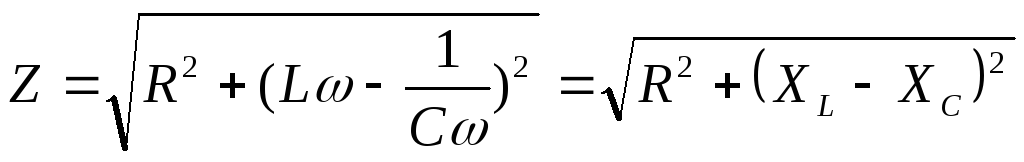(17.34)

где R-активное сопротивление, оно обуславливает выделение количества теплоты в цепи в соответствии с законом Джоуля-Ленца; Х_L-Х_С реактивное сопротивление, оно не вызывает нагревания элементов электрической цепи.

Если индуктивное и ёмкостное сопротивление цепи при их последовательном соединении будут одинаковы Х_L= Х_С, то Z=R. Это означает, что сила тока и приложенное напряжение изменяются в одной фазе так, как будто в цепи имеется только омическое сопротивление; напряжения на катушке индуктивности и конденсаторе одинаковы по амплитуде, но противоположны по фазе. Такой случай вынужденных электрических колебаний называют резонансом напряжений.

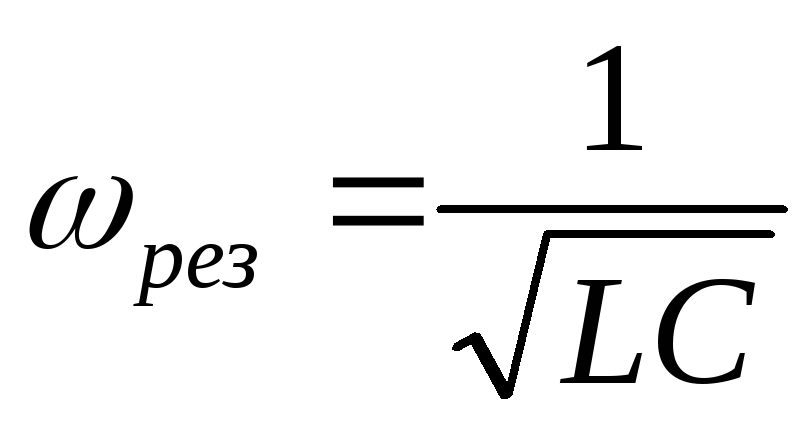(17.35)

Аналогичным образом с помощью векторной диаграммы можно исследовать явление резонанса при параллельном соединении элементов R, L и C (так называемый резонанс токов).

Явление возрастания амплитуды колебаний тока при совпадении частоты ω колебаний внешнего источника с собственной частотой ω₀ электрической цепи называется электрическим резонансом.

Рис. 17.8 иллюстрирует явление резонанса в последовательном электрическом контуре. На рисунке графически изображена зависимость отношения амплитуды U_C напряжения на конденсаторе к амплитуде U_m напряжения источника от его частоты ω для различных значений добротности Q. Кривые на рис. 17.8 называются резонансными кривыми.

Можно показать, что максимум резонансных кривых для контуров с низкой добротностью несколько сдвинуты в область низких частот.

Полное сопротивление в цепи переменного тока. Резонанс напряжений — МегаЛекции

Переменный ток – любой ток, изменяющийся со временем. Переменный ток можно рассматривать как вынужденные электромагнитные колебания. Наибольшее распространение в промышленности получил гармонический переменный ток. Этот ток получают с помощью установленных на электростанциях генераторов переменного тока. В нашей стране стандартная техническая частота вырабатываемого ими тока составляет 50 Гц.

Сопротивление, которое оказывается электрическая цепь переменному току, отличается от того, которое имеет место при наличии постоянного тока. В цепи с переменным током принято различать активное R и реактивное Х сопротивление. Активным обладают те элементы цепи, в которых электрическая энергия необратимо преобразуется во внутреннюю, а реактивным — те элементы (конденсаторы и катушки индуктивности), в которых подобного преобразования не происходит. Сопротивление конденсатора при этом называют ёмкостным Х_C, а катушки индуктивным Х_L. Реактивным сопротивлением обладают те элементы электрической цепи, на которых разность фаз колебаний силы тока и напряжения составляет π/2. В элементах с чисто активным сопротивлением колебания силы тока и напряжения совпадают по фазе.

Рассмотрим цепь, в которой последовательно соединены резистор, катушка индуктивности и конденсатор.

Сила тока в цепи и напряжение изменяются не в одной фазе, поэтому

I=I_m sin(ωt- φ), (17.26)

где – разность фаз напряжения и силы тока.

Сумма напряжений на отдельных участках равна внешнему напряжению:

U=U_R +U_L+ U_C= U_m sinωt (17.27)

где U_R = U_mR sin(ωt- φ) — в фазе с током; (17.28)

U_L = U_mL sin(ωt- φ + π/2) – опережает силу тока по фазе; (17.29)

U_С = U_mС sin(ωt- φ — π/2) – отстаёт от силы тока по фазе. (17.30)

Подставим в (17.27) можно получить выражение для полного сопротивления.

U= U_mR sin(ωt- φ) + U_mL sin(ωt- φ + π/2)+ U_mС sin(ωt- φ — π/2)= U_m sinωt (17.31)

Однако более просто и наглядно удаётся это сделать с помощью векторных диаграмм (рис.17.7).

На рис.17.7 по оси токов направлен вектор амплитуды силы тока I_m. так как во всей цепи амплитуда силы тока одинакова, то амплитуда напряжений на участках отложим относительно этого вектора: вектор U_mR – в одной фазе с силой тока; вектор U_mL – с опережением силы тока по фазе на π/2, вектор U_mС – с отставанием от силы тока по фазе на π/2.

Суммируя три вектора, находим графически значения и U. Используя теорему Пифагора, имеем

U² _m= U² _mR + (U_mL — U_mС) ² (17.32)

Подставляя выражения этих амплитуд и учитывая закон Ома, находим

I² _mZ² = I² _m R²+ (I_m ωL — I_m/Cω) ² (17.33)

где Z– полное сопротивление цепи переменного тока, называемое импедансом. Получаем

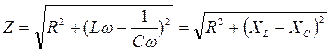(17.34)

где R-активное сопротивление, оно обуславливает выделение количества теплоты в цепи в соответствии с законом Джоуля-Ленца; Х_L-Х_Среактивное сопротивление, оно не вызывает нагревания элементов электрической цепи.

Если индуктивное и ёмкостное сопротивление цепи при их последовательном соединении будут одинаковы Х_L= Х_С, то Z=R. Это означает, что сила тока и приложенное напряжение изменяются в одной фазе так, как будто в цепи имеется только омическое сопротивление; напряжения на катушке индуктивности и конденсаторе одинаковы по амплитуде, но противоположны по фазе. Такой случай вынужденных электрических колебаний называют резонансом напряжений.

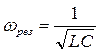(17.35)

Аналогичным образом с помощью векторной диаграммы можно исследовать явление резонанса при параллельном соединении элементов R, L и C (так называемый резонанс токов).

Явление возрастания амплитуды колебаний тока при совпадении частоты ω колебаний внешнего источника с собственной частотой ω₀ электрической цепи называется электрическим резонансом.

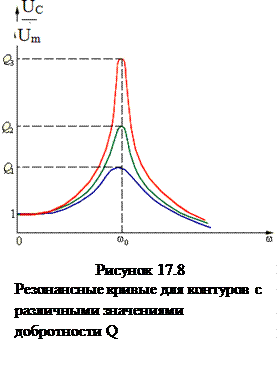Рис. 17.8 иллюстрирует явление резонанса в последовательном электрическом контуре. На рисунке графически изображена зависимость отношения амплитуды U_C напряжения на конденсаторе к амплитуде U_m напряжения источника от его частоты ω для различных значений добротности Q. Кривые на рис. 17.8 называются резонансными кривыми.

Можно показать, что максимум резонансных кривых для контуров с низкой добротностью несколько сдвинуты в область низких частот.

 

Мощность переменного тока

При протекании переменного тока по участку цепи электромагнитное поле совершает работу, и в цепи выделяется джоулево тепло. Мгновенная мощность в цепи переменного тока равна произведению мгновенных значений тока и напряжения: P= IU. Практический интерес представляет среднее за период переменного тока значение мощности

P=P_cp=I_mU_mcosωt·cos(ωt+φ) (17.36)

Здесь I_m и U_m – амплитудные значения тока и напряжения на данном участке цепи, φ – фазовый сдвиг между током и напряжением. Если участок цепи содержит только резистор с сопротивлением R, то фазовый сдвиг φ = 0:

(17.37)

Для того, чтобы это выражение по виду совпадало с формулой для мощности постоянного тока, вводятся понятия действующих или эффективных значений силы тока и напряжения:

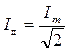и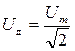(17.38)

Средняя мощность переменного тока на участке цепи, содержащем резистор, равна

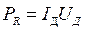(17.39)

Если участок цепи содержит только конденсатор емкости C, то фазовый сдвиг между током и напряжением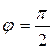. Поэтому

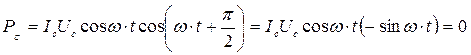(17.40)

Аналогично можно показать, что P_L = 0.

Таким образом, мощность в цепи переменного тока выделяется только на активном сопротивлении. Средняя мощность переменного тока на конденсаторе и катушке индуктивности равна нулю.

 

Примеры решения задач

Пример . Колебательный контур состоит из воздушного плоского конденсатора (расстояние между пластинами d=1мм, площадь поперечного сечения S=2 см² каждая) и соленоида без сердечника (длина ℓ=10см, площадь поперечного сечения S₁=2 см², число витков N=100). Пренебрегая сопротивлением контура, определите частоту ω₀ собственных колебаний контура.

Дано: d=1 мм=1∙10^-3 м; S=100 см²=10^-2 м²; ε=1; ℓ=10см=0,01м; S₁=2 см²=2∙10^-4 м²; N=100; μ=1.

Найти: ω₀.

Решение. Собственная частота колебательного контура

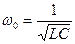, (1)

где индуктивность соленоида

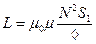(2)

(μ₀=4π∙10^-7 Гн/м – магнитная постоянная; μ- магнитная проницаемость среды; ℓ — длина соленоида; S₁— площадь его поперечного сечения; N — число витков соленоида) и ёмкость плоского конденсатора

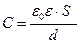(3)

(ε₀ – 8,85∙10^-12 Ф/м – электрическая постоянная; ε- диэлектрическая проницаемость среды; d — расстояние между пластинами конденсатора; S — площадь пластин конденсатора).

Подставив выражения (2) и (3) в формулу (1) и учитывая, что 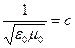(с=3∙10⁸ м/с – скорость распространения света в вакууме), найдём искомую частоту собственных колебаний контура:

.

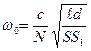Ответ: ω₀=2,12∙10⁷ рад/с.

 

Пример . Колебательный контур содержит конденсатор ёмкостью С=40 нФ и катушку индуктивностью L=1,6 мГн. Определите максимальное напряжение U_m на обкладках конденсатора, если максимальная сила тока I_m в колебательном контуре равна 1A. Сопротивлением контура пренебречь.

Дано: С=40нФ=40∙10^-8 Ф; L=1,6 мГн=1,6∙10^-3 Гн; I_m=1А; R=0.

Найти: U_m.

Решение. Максимальное напряжение на обкладках конденсатора

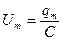, (1)

где q_m – амплитуда колебаний заряда на обкладках конденсатора ёмкостью С.

В случае свободных незатухающих колебаний (R=0) заряд на обкладках конденсатора совершает гармонические колебания по закону

q=q_mcosω₀t,

где собственная частота колебательного контура

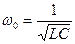(2)

Сила тока в колебательном контуре

,

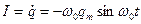где максимальная сила тока

I_m=ω₀q_m,

откуда

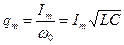(3)

[учли формулу (2)].

Подставив выражение (3) в Формулу (1), найдём искомое максимальное напряжение на обкладках конденсатора

.

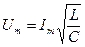Ответ: U_m=200 В.

 

Пример . Частота свободных незатухающих электромагнитных колебании в контуре, содержащем катушку индуктивности L=0,5 Гн, составляет 50 Гц. Запишите для данного контура уравнение изменения заряда на обкладках конденсатора в зависимости от времени, если максимальная энергия магнитного поля Wm в катушке составляет 4 мкДж.

Дано: L=0,5 Гн; ν₀=50 Гц; Wm =4 мкДж=4∙10^-6 Дж.

Найти: q(t).

Решение. В случае свободных незатухающих колебаний (R≈0) заряд на обкладках конденсатора совершает гармонические колебания по закону

q=q_mcosω₀t, (1)

где q_m — амплитуда колебаний заряда на обкладках конденсатора с циклической

частотой

ω₀=2πν₀, (2)

Максимальная энергия магнитного поля в катушке

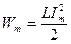(3)

где I_m – амплитуда колебаний силы тока. Из уравнения (3)

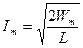. (4)

Продифференцировав уравнение (1) по времени, определим силу тока в колебательном контуре:

,

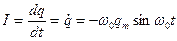где амплитуда силы тока I_m=ω₀q_m. Тогда

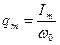(5)

Подставив выражение (4) в формулу (5) и учитывая (2), найдём амплитуду колебаний заряда

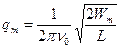
Вычисляя, получаем q_m=1,27∙10^-5 Кл

Подставив в уравнение (1) числовые значения q_m и ω₀, искомое уравнение (с числовыми коэффициентами) изменения заряда на обкладках конденсатора примет вил:

q=1,27∙10^-5cos100πt, Кл.

Ответ: q=1,27∙10^-5cos100πt, Кл.

 

Пример . Колебательный контур состоит из конденсатора ёмкостью С=100 пФ, катушки индуктивности L=0,01 Гн и резистора сопротивлением R=20 Ом. Определите: 1) период затухающих колебаний; 2) через сколько полных колебаний амплитуда тока в контуре уменьшится в е раз..

Дано: C=100пФ =1∙10^-7 Ф; L=0,01 Гн; R=20 Ом.

Найти: 1) Т; 2) N.

Решение. Искомый период электромагнитных колебаний в контуре

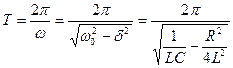
(учли, что собственная частота контура 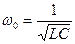и коэффициент затухания ).

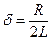Число полных колебаний, совершаемых за время уменьшения амплитуды силы

тока в е раз,

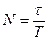, (1)

где время релаксации

.

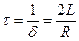Подставив это выражение в формулу (1), найдём искомое число полных колебаний:

.

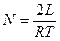Ответ: 1) Т=0,2 мс; 2) N=5.

 

Пример . Определите добротность Q колебательного контура, если собственная частота ω₀ колебательного контура отличается на 5% от частоты ω свободных затухающих колебаний.

Дано: ω₀=1,05 ω.

Найти: Q.

Решение. В реальном колебательном контуре ( т.е. обладающем сопротивлением) частота ω свободных затухающих электромагнитных колебаний меньше собственной частоты ω₀ колебательного контура (при R≈0):

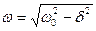, (1)

где δ– коэффициент затухания.

Добротность колебательного контура

,

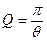где логарифмический декремент затухания Т (Т- период затухающих колебаний ). Учитывая приведённые формулу, найдём коэффициент затухания

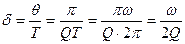. (2)

Подставив выражение (2) в формулу (1), получаем

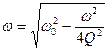или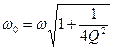

откуда искомая добротность

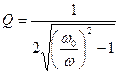
Ответ: Q=1,56

 

 

 

---

Рекомендуемые страницы:

Воспользуйтесь поиском по сайту:

из каких состовляющих состоит полное сопротивление цепи?

Сопротивление цепи плюс внутреннее сопротивление элемента. Вот именно поэтому реальное напряжение между полюсами батарейки меньше, чем между ЭДС этой батарейки.

из сопротивления участка цепи и внутреннего сопотивления источника питания.

Полное сопротивление цепи состоит из активной составляющей, которая не влияет на фазу тока или напряжения, и реактивной составляющей (имеющей емкостной или индуктивный характер) , соответственно сдвигающей фазу тока либо напряжения.

ПОЛНОЕ СОПРОТИВЛЕНИЕ — величина, характеризующая сопротивление электрической цепи току. Полное сопротивление синусоидальному току выражается отношением действующего напряжения U к действующему току I в этой цепи: ,где r и x — активное и реактивное сопротивления. Измеряется в омах. Полное сопротивление цепи переменного тока <img src=»//otvet.imgsmail.ru/download/9442a5f7783c1b2fa15a37f7df607273_i-102.jpg» > <img src=»//otvet.imgsmail.ru/download/9442a5f7783c1b2fa15a37f7df607273_i-101.jpg» > Понятие полного сопротивления играет важную роль при расчетах цепей переменного тока. Для определения полного сопротивления цепи во многих случаях удобно использовать наглядный метод векторных диаграмм. При построении векторной диаграммы следует учесть, что при параллельном соединении напряжение на всех элементах R, C и L одно и то же и равно напряжению внешнего источника. Токи, текущие в разных ветвях цепи, отличаются не только по значениям амплитуд, но и по фазовым сдвигам относительно приложенного напряжения. Поэтому полное сопротивление цепи нельзя вычислить по законам параллельного соединения цепей постоянного тока. Более подробно с примерами и формулами см. по ссылке

Сопротивления в цепях переменного тока — КиберПедия

Цепь переменного тока с активным сопротивлением. Сопротивления в цепях переменного тока бывают активными и реактивными. Активные сопротивления расходуют энергию, реактивные — не расходуют.

Реактивными сопротивлениями, включенными в цепь переменного тока, являются сопротивления ка­тушки индуктивности L и конден­сатора С. Сопротивление катушки называется индуктивным сопротив­лением (Xj), сопротивление кон­денсатора — емкостным (Х_с).

На рис. 1.5 показана цепь пере­менного тока с активным сопротив­лением и векторная диаграмма, из которой видно, что ток и напряже­ние совпадают по фазе. Они изменя­ются по одному и тому же закону, следовательно, можно записать:

i = I_Msin t, (1.12)

u = U _m sin t. (1.13)

Действующее значение силы тока в цепи с активным сопротив­лением равно:

I= (1.14)

где U— действующее значение напряжения на сопротивлении; R — значение активного сопротивления.

Это выражение является выражением закона Ома для цепи с активным сопротивлением. Мощность, расходуемая в цепи на ак­тивном сопротивлении, равна:

P = IU cosy, (1.15)

где ф — угол сдвига фаз между током и напряжением.

Так как ток и напряжение совпадают по фазе, то угол сдвига Ф = 0°, a cos ф = 1. Мощность же в цепи равна произведению дей­ствующих значений тока и напряжения:

Р = IU, Р = I²R. (1,16)

 

Переменный ток в цепи с индуктивным сопротивлени­ем. Если катушку индуктив­ности, активное сопротивле­ние которой равно нулю, i подключить к источнику переменного тока (рис. 1.6), то и катушке потечет синусоидально изменяющийся пере­менный ток.

Согласно правилу Ленца, индуцированная, в катушке ЭДС противодействует изменениям силы тока. Это значит, что при увели­чении силы тока в катушке ЭДС самоиндукции стремится создать ток, направленный навстречу вызывавшему ее току, а при умень­шении силы тока она, наоборот, стремится создать ток, совпада­ющий по направлению с ним.

Из векторной диаграммы видно, что ЭДС самоиндукции отста­ет по фазе от тока на 90°.

Напряжение на катушке ил на источнике тока равно:

U_L = U = 2п fLI = LI. (1.17)

Произведение угловой скорости на индуктивность катушки называется индуктивным сопротивлением Х.

X_L= L. (1.18)

Энергия в катушке индуктивности не расходуется. В первую чет­верть периода она запасается в ее магнитном поле, а во вторую — отдается источнику тока. Произведение напряжения U_L на величи­ну силы тока в цепи называется реактивной мощностью.

В рассмотренной цепи активная мощность равна нулю, так как энергия в ней не расходуется, сдвиг по фазе между векторами тока /и напряжением U равен 90° и cosy = 0.

Переменный ток в цепи с последовательными активным и индук­тивным сопротивлениями. Теперь рассмотрим цепь с реальной ка­тушкой, которую можно представить как цепь с последовательно включенными индуктивностью L и активным сопротивлением R (рис. 1.7). Если в цепи с последовательными активным и индуктив­ным сопротивлениями протекает переменный синусоидальный ток, то напряжение на индуктивности, как было установлено ранее, опережает ток на 90°, а напряжение на активном сопротивлении

Рис. 1.7. Схема цепи с последовательными активным и индуктивным сопротивлениями (а) и векторная диаграмма напряжений (б) совпадает с ним по фазе. Так как напряжения U_L, U_R по фазе не совпа­дают, то напряжение, приложенное ко всей цепи, равно их геомет­рической сумме. Сложив векторы U_Ln U_R, нахо­дим величину вектора U, который сдвинут по фазе относительно вектора тока / на угол φ < 90°,

опережая его. Таким образом, в цепи переменного тока с последовательно соединенным активным сопротивлением и катушкой индуктивно­сти ток отстает по фазе от напряжения.

Построив векторную диаграмму, рассмотрим треугольник со сто­ронами U_L, U_R, U. Этот треугольник называется треугольником напря­жений. Так как он прямоугольный, то

U = √U²_R+U². (1.19)

Из треугольника напряжений можно получить подобный ему треугольник сопротивлений со сторонами R, X_L и Z. Из этого треу­гольника полное сопротивление цепи равно:

Z = √R²+Xl (1.20)

Так как сдвиг по фазе между током и напряжением меньше 90°, то энергия в такой цепи расходуется лишь на активном со­противлении R.

Активная мощность при этом равна:

P = IU coscp. (1.21)

Цепь переменного тока с емкостью. Если к источнику перемен­ного тока подключить конденсатор, то в цепи появится ток. Спо­собность конденсатора пропускать переменный ток объясняется тем, что под действием переменного синусоидального напряже­ния конденсатор периодически заряжается и разряжается, вслед­ствие чего происходит перемещение электрических зарядов в про­водниках, соединяющих конденсатор с источником тока. Соотно­шение фаз тока и напряжения представлено на рис. 1.8. В цепи с емкостью ток опережает по фазе напряжение на 90°. Закон Ома для цепи переменного тока с емкостью определяет действующее зна­чение силы тока:

 

(1.22)

 

Величина Х_с= называется емкостным сопротивлением. Она

обратно пропорциональна частоте тока в цепи и емкости конден­сатора. Измеряется в омах (Ом).

 

Мощность переменного тока

Для цепей переменного тока различают активную, полную и реактивную мощности.

Активная мощность представляет собой действительную мощ­ность переменного тока, аналогичную мощности, развиваемой постоянным током. Она производит полезную работу; может быть преобразована с помощью электродвигателей в механическую мощ­ность, механическую энергию; измеряется в ваттах (Вт) и опреде­ляется по формуле

Р = IU cos ф. (1.23)

Полной мощностью называют максимально возможную величи­ну активной мощности, развиваемую переменным током при за­данных значениях напряжения и силы тока и при наиболее благо­приятных условиях, а именно, когда coscp = 1. Полная мощность обозначается латинской буквой 5¹ и измеряется в вольт-амперах (В-А). Из определения полной мощности следует выражение

S = UI. (1-24)

Сравнивая между собой формулы (1.23) и (1.24), находим со­отношение между активной и полной мощностями:

Р = S coscp, (1.25)

 

(1.26)

Полной мощностью (кВА) принято измерять мощность гене­раторов переменного тока, машин, производящих электроэнер­гию, и трансформаторов, аппаратов, предназначенных для преоб­разования электрической энергии одного напряжения в электри­ческую энергию другого напряжения. Полная мощность этих ма­шин определяется произведением номинальных (нормальных) ве­личин их напряжения и силы тока (т.е. величин этих параметров, на которые рассчитаны машины). А активная их мощность зависит от коэффициента мощности, при котором они работают (Р.= Scoscp). В свою очередь этот коэффициент мощности зависит от соотноше­ния величин активного и реактивного сопротивления, включен­ных в цепь, иными словами, от характера электроприемников, питаемых данным генератором или трансформатором.

Реактивная мощность. Для рассмотрения реактивной мощнос­ти необходимо иметь представление об активной и реактивной со­ставляющих переменного тока. Сравнивая между собой формулы для определения мощности переменного и постоянного тока, мож­но видеть, что на месте полной величины силы тока I в формуле мощности стоит выражение Icosφ, где cosφ — величина, меньше единицы (и только в отдельных случаях равная ей). Отсюда следует, что в цепях переменного тока не весь ток создает полезную, активную мощность, а только некоторая его часть, которая на­зывается активной составляющей тока.

Проекция вектора тока на горизонтальное направление, перпендикулярное вектору напряжения, равная Isincp, называется ре­активной составляющей переменного тока. Реактивная составляющая тока не участвует в создании активной мощности.

Произведение действующего в цепи на­пряжения на реактивную составляющую тока носит название реактивной мощности и обо­значается латинской буквой Q. Реактивная мощность измеряется в единицах, называе­мых «вар». Из приведенного определения ре­активной мощности вытекает соотношение

Q = UI sin φ,

где Q — реактивная мощность, вар; U— напряжение, В; /— сила тока, A; sinφ — числовой коэффициент, зависящий от угла сдвига фаз в данной цепи.

Реактивная мощность, так же как и реактивная составляющая тока, характеризует собой ту энергию, которая идет на создание магнит­ного поля индуктивности или электрического поля конденсатора (если последний включен в данную цепь). Эта энергия в процессе протека­ния переменного тока в цепях со сдвигом фаз совершает непрерыв­ные колебания между источником энергии и ее потребителем.

Активная, реактивная и полная мощности переменного тока связаны между собой соотношением

S²=P²+Q². (1.28)

Это соотношение можно представить как векторную диаграм­му, получаемую на основании диаграммы напряжений или токов, носящую название «треугольника мощностей» (рис. 1.9). Два катета этого треугольника представляют собой в том или ином масштабе активную и реактивную мощности (соответственно в кВт и квар), а гипотенуза — полную мощность (кВ А). Угол φ численно равен углу сдвига фаз тока и напряжения в цепи. Значение косинуса это­го угла называют коэффициентом мощности.