Коэффициент полезного действия
Допустим, мы отдыхаем на даче, и нам нужно принести из колодца воды. Мы опускаем в него ведро, зачерпываем воду и начинаем поднимать. Не забыли, какова наша цель? Правильно: набрать воды. Но взгляните: мы поднимаем не только воду, но и само ведро, а также тяжёлую цепь, на которой оно висит. Это символизирует двухцветная стрелка: вес поднимаемого нами груза складывается из веса воды и веса ведра и цепи.
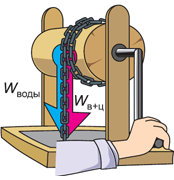 |
Рассматривая ситуацию качественно, мы скажем: наряду с полезной работой по подъёму воды мы совершаем и другую работу – подъём ведра и цепи. Разумеется, без цепи и ведра мы не смогли бы набрать воды, однако, с точки зрения конечной цели, их вес «вредит» нам. Если бы этот вес был бы меньше, то и полная совершённая работа тоже была бы меньше (при той же полезной).
Теперь перейдём к количественному изучению этих работ и введём физическую величину, называемую коэффициентом полезного действия.
Задача. Яблоки, отобранные для переработки, грузчик высыпает из корзин в грузовик. Масса пустой корзины 2 кг, а яблок в ней – 18 кг. Чему равна доля полезной работы грузчика от его полной работы?
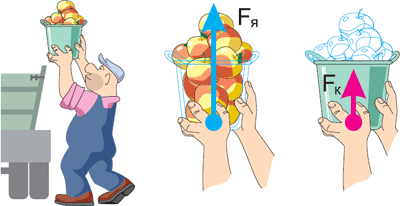 |
Решение. Полной работой является перемещение яблок в корзинах. Эта работа складывается из подъёма яблок и подъёма корзин. Важно: поднятие яблок – полезная работа, а поднятие корзин – «бесполезная», потому что цель работы грузчика – переместить только яблоки.
Введём обозначения: Fя – сила, с которой руки поднимают вверх только яблоки, а Fк – сила, с которой руки поднимают вверх только корзину. Каждая из этих сил равна соответствующей силе тяжести: F=mg.
Пользуясь формулой A = ±( F||· l ) , «распишем» работы этих двух сил:
Aполезн = +Fя · lя = mя g · h и Aбесполезн = +Fк · lк = mк g · h
Полная работа складывается из двух работ, то есть равна их сумме:
Aполн = Aполезн + Aбесполезн = mя g h + mк g h = ( mя + mк ) · g h
В задаче нас просят вычислить долю полезной работы грузчика от его полной работы. Сделаем это, поделив полезную работу на полную:
| Доля = | Aполезн | = | mя · g h | = | 18 кг | = | 18 кг | = 0,9 | ||
| Aполн | ( mя + mк ) · g h | ( 18 + 2 ) кг | 20 кг |
В физике такие доли принято выражать в процентах и обозначать греческой буквой «η» (читается: «эта»). В итоге получим:
η = 0,9 или η = 0,9 ·100% = 90% , что то же самое.
Это число показывает, что из 100% полной работы грузчика доля его полезной работы составляет 90%. Задача решена.
Физическая величина, равная отношению полезной работы к полной совершённой работе, в физике имеет собственное название – КПД – коэффициент полезного действия:
| η = | Aполезн | η – коэффициент полезного действия Aполезн – полезная работа, Дж Aполн – полная работа, Дж | |||
| Aполн |
После вычисления КПД по этой формуле его принято умножать на 100%. И наоборот: для подстановки КПД в эту формулу его значение нужно перевести из процентов в десятичную дробь, поделив на 100%.
КПД плоскости, блока, рычага
В этой статье научимся определять КПД наклонной плоскости, блоков и рычагов.
КПД неподвижного блока равен отношению полезной работы к затраченной, высоту подъема можно сократить:
![Rendered by QuickLaTeX.com \[\eta=\frac{mgh}{Fh}\cdot100\%=\frac{mg}{F}\cdot100\%\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-d77d864407319869ea9b690c58679721_l3.png)
Подвижный блок дает выигрыш в силе в два раза, поэтому для него
![Rendered by QuickLaTeX.com \[\eta=\frac{mg}{2F}\cdot100\%\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-ef3490afd904258e9ba5f37fbf964afa_l3.png)
КПД рычага равен, аналогично, отношению полезной работы к затраченной:
![Rendered by QuickLaTeX.com \[\eta=\frac{Ph_2}{Fh_1}\cdot100\%\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-0fac2697a73be5b0150c73bcf08de921_l3.png)

КПД наклонной плоскости равен:
![Rendered by QuickLaTeX.com \[\eta=\frac{mgh}{FS}\cdot100\%\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-ab3ab6135b8e5b2ba13b52d1a0a07779_l3.png)

И по-прежнему это то же отношение полезной работы к затраченной.
Задача 1. С помощью подвижного блока поднимают груз весом 400 Н на высоту 4 м, действуя на веревку с силой 220 Н. Чему равен КПД блока?
Так как блок по условию подвижный, то дает выигрыш в силе в 2 раза:
![Rendered by QuickLaTeX.com \[\eta=\frac{mg}{2F}\cdot100\%=\frac{400}{440}\cdot100\%=91\%\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-2f20824f584fd24d6192623b1967fb06_l3.png)
Ответ: 91%.
Задача 2. С помощью рычага груз массой 150 кг подняли на высоту 0,2 м. При этом к длинному плечу была приложена сила 600 Н, под действием которой конец этого плеча опустился на 0,6 м. Найдите КПД рычага.
![Rendered by QuickLaTeX.com \[\eta=\frac{Ph_2}{Fh_1}\cdot100\%=\frac{mgh_2}{Fh_1}\cdot100\%=\frac{1500\cdot0,2}{600\cdot0,6}\cdot100\%=83\%\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-17c56a821f34abd74070c157a365e51b_l3.png)
Ответ: 83 %
Задача 3. С помощью рычага, КПД которого 80%, подняли груз массой 120 кг на высоту 40 см. На какое` расстояние опустилось длинное плечо рычага, если к нему была приложена сила 500 Н?
КПД рычага:
![Rendered by QuickLaTeX.com \[\eta=\frac{Ph_2}{Fh_1}\cdot100\%\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-0fac2697a73be5b0150c73bcf08de921_l3.png)
Отсюда
![Rendered by QuickLaTeX.com \[h_1=\frac{Ph_2}{F \eta }\cdot100\%=\frac{120\cdot10\cdot0,4}{500\cdot0,8 }=1,2\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-20771bc49270aa032072a0626ddc386e_l3.png)
Ответ: 1,2 м.
Задача 4. Определить КПД наклонной плоскости при подъеме тела, если учащийся с помощью динамометра и линейки получил такие результаты: вес тела 1,4 Н; высота плоскости 0,2 м; длина плоскости 0,56 м; сила, приложенная к телу, 1 Н.
![Rendered by QuickLaTeX.com \[\eta=\frac{mgh}{FS}\cdot100\%=\frac{1,4\cdot0,2}{1\cdot0,56}\cdot100\%=50\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-2d71251d9d163af6e76e8115426a7074_l3.png)
Ответ: 50%.
Задача 5. Бетонную плиту объемом 0,5 м поднимают из воды с помощью подвижного блока. Какую силу необходимо прикладывать, когда плиту поднимают в воде и над поверхностью воды?
поднимают из воды с помощью подвижного блока. Какую силу необходимо прикладывать, когда плиту поднимают в воде и над поверхностью воды?
Плотность бетона равна  кг/м
кг/м .
.
Найдем массу бетонной плиты:  кг. Вес плиты 11 кН. Поэтому, если блок подвижный, то достаточно развивать силу 5,5 кН, чтобы поднять эту плиту на воздухе с помощью подвижного блока. В воде нам будет помогать сила Архимеда:
кг. Вес плиты 11 кН. Поэтому, если блок подвижный, то достаточно развивать силу 5,5 кН, чтобы поднять эту плиту на воздухе с помощью подвижного блока. В воде нам будет помогать сила Архимеда:
![Rendered by QuickLaTeX.com \[F_A=\rho_0 g V=1000\cdot10\cdot0,5=5000\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-37ddf5b346d753e24b151c979ec8573c_l3.png)
Таким образом, в воде вес плиты станет меньше на 5000 Н и станет равен 6000 Н. Поэтому достаточно 3000 Н для подъема плиты в воде при помощи такого блока.
Ответ: 5,5 кН на воздухе, 3 кН в воде.
Задача 6. По наклонной плоскости длиной 5 м и высотой 1,5 м поднимают равномерно груз массой 180 кг. Какую силу нужно приложить к грузу, если КПД плоскости 60%?
КПД наклонной плоскости равен:
![Rendered by QuickLaTeX.com \[\eta=\frac{mgh}{FS}\cdot100\%\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-ab3ab6135b8e5b2ba13b52d1a0a07779_l3.png)
Откуда
![Rendered by QuickLaTeX.com \[F=\frac{ mgh }{\eta S}\cdot100\%=\frac{ 180\cdot 10\cdot1,5 }{60\cdot 5}\cdot100\%=6000\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-6a9dc765575742ef4e38c8c83a4b92b8_l3.png)
Ответ: 6 кН.
Задача 7. Какую работу необходимо совершить для подъема гранитной плиты объемом 4 м на высоту 2 м с помощью механизма с КПД 60%?
на высоту 2 м с помощью механизма с КПД 60%?
Полезная работа равна
![Rendered by QuickLaTeX.com \[A=mgh=\rho V g h\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-6b8ee7b4016149f070c038233986c4b1_l3.png)
КПД механизма равен:
![Rendered by QuickLaTeX.com \[\eta=\frac{A}{A_p}\cdot100\%\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-f5bf2fc7028da9442ffa421c5583f01f_l3.png)
Полная работа тогда
![Rendered by QuickLaTeX.com \[A_p=\frac{A}{\eta }\cdot100\%=\frac{\rho V g h }{\eta }\cdot100\%=\frac{2600\cdot4\cdot10\cdot2 }{60 }\cdot100\%=3467\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-2fb3b9c100a3945847f969aaa22bc333_l3.png)
Ответ: 3467 Дж.
Задача 8. С помощью подвижного блока поднимают груз массой 75 кг на высоту 10 м. КПД равен 60%. Определить полезную работу и силу, необходимую для подъема груза.
КПД подвижного блока:
![Rendered by QuickLaTeX.com \[\eta=\frac{mg}{2F}\cdot100\%\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-ef3490afd904258e9ba5f37fbf964afa_l3.png)
Отсюда
![Rendered by QuickLaTeX.com \[A=mgh=75\cdot10\cdot10=7500\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-6aea2ca4b92619b22606e40c650e18fe_l3.png)
![Rendered by QuickLaTeX.com \[F=\frac{mg}{2\eta}\cdot100\%=\frac{750}{2\cdot60}\cdot100\%=625\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-1749cc377be5497a04cac68742de4610_l3.png)
Ответ:  Дж,
Дж,  Н.
Н.
05-б. Коэффициент полезного действия
§ 05-б. Коэффициент полезного действия
Допустим, мы отдыхаем на даче, и нам нужно принести из колодца воды. Мы опускаем в него ведро, зачерпываем воду и начинаем поднимать. Не забыли, какова наша цель? Правильно: набрать воды. Но взгляните: мы поднимаем не только воду, но и само ведро, а также тяжёлую цепь, на которой оно висит. Это символизирует двухцветная стрелка: вес поднимаемого нами груза складывается из веса воды и веса ведра и цепи.
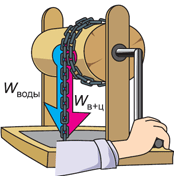
Рассматривая ситуацию качественно, мы скажем: наряду с полезной работой по подъёму воды мы совершаем и другую работу – подъём ведра и цепи. Разумеется, без цепи и ведра мы не смогли бы набрать воды, однако, с точки зрения конечной цели, их вес «вредит» нам. Если бы этот вес был бы меньше, то и полная совершённая работа тоже была бы меньше (при той же полезной).
Теперь перейдём к количественному изучению этих работ и введём физическую величину, называемую коэффициентом полезного действия.
Задача. Яблоки, отобранные для переработки, грузчик высыпает из корзин в грузовик. Масса пустой корзины 2 кг, а яблок в ней – 18 кг. Чему равна доля полезной работы грузчика от его полной работы?
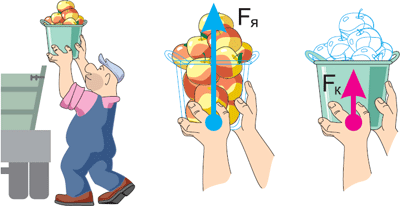
Решение. Полной работой является перемещение яблок в корзинах. Эта работа складывается из подъёма яблок и подъёма корзин. Важно: поднятие яблок – полезная работа, а поднятие корзин – «бесполезная», потому что цель работы грузчика – переместить только яблоки.
Введём обозначения: Fя – сила, с которой руки поднимают вверх только яблоки, а Fк – сила, с которой руки поднимают вверх только корзину. Каждая из этих сил равна соответствующей силе тяжести: F=mg.
Пользуясь формулой A = ±( F||· l ) , «распишем» работы этих двух сил:
Aполезн = +Fя · lя = mяg · h и Aбесполезн = +Fк · lк = mкg · h
Полная работа складывается из двух работ, то есть равна их сумме:
Aполн = Aполезн + Aбесполезн = mяg h + mкg h = ( mя + mк ) · g h
В задаче нас просят вычислить долю полезной работы грузчика от его полной работы. Сделаем это, поделив полезную работу на полную:
| Доля = | Aполезн | = | mя · g h | = | 18 кг | = | 18 кг | = 0,9 | ||
| Aполн | ( mя + mк ) · g h | ( 18 + 2 ) кг | 20 кг |
В физике такие доли принято выражать в процентах и обозначать греческой буквой «η» (читается: «эта»). В итоге получим:
η = 0,9 или η = 0,9 ·100% = 90% , что то же самое.
Это число показывает, что из 100% полной работы грузчика доля его полезной работы составляет 90%. Задача решена.
Физическая величина, равная отношению полезной работы к полной совершённой работе, в физике имеет собственное название – КПД – коэффициент полезного действия
Формула для подсчета коэффициента полезного действия. Формула читается так: «Эта равна отношению Аполезн к Аполн».
| η = | Aполезн | η – коэффициент полезного действия | |||
| Aполн |
После вычисления КПД по этой формуле его принято умножать на 100%. И наоборот: для подстановки КПД в эту формулу его значение нужно перевести из процентов в десятичную дробь, поделив на 100%.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Источник
Не можешь написать работу сам?
Доверь её нашим специалистам
от 100 р.стоимость заказа
2 часамин. срок
Узнать стоимость
Коэффициент полезного действия механизма
Определение и формула коэффициента полезного действия механизма
В жизни человек сталкивается с проблемой и необходимостью превращения разных видов энергии. Устройства, которые предназначены для преобразований энергии, называют энергетическими машинами (механизмами). К энергетическим машинам, например, можно отнести: электрогенератор, двигатель внутреннего сгорания, электрический двигатель, паровую машину и др.
В теории любой вид энергии может полностью превратиться в другой вид энергии. Но на практике помимо преобразований энергии в машинах происходят превращения энергии, которые названы потерями. Совершенство энергетических машин определяет коэффициент полезного действия (КПД).
Коэффициент полезного действия можно определить через работу, как отношение (полезная работа) к A (полная работа):
Кроме того, можно найти как отношение мощностей:
где — мощность, которую подводят механизму; — мощность, которую получает потребитель от механизма. Выражение (3) можно записать иначе:
где — часть мощности, которая теряется в механизме.
Из определений КПД очевидно, что он не может быть более 100% (или не моет быть больше единицы). Интервал в котором находится КПД: .
Коэффициент полезного действия используют не только в оценке уровня совершенства машины, но и определения эффективности любого сложного механизма и всякого рода приспособлений, которые являются потребителями энергии.
Любой механизм стараются сделать так, чтобы бесполезные потери энергии были минимальны (). С этой целью пытаются уменьшить силы трения (разного рода сопротивления).
КПД соединений механизмов
При рассмотрении конструктивно сложного механизма (устройства), вычисляют КПД всей конструкции и коэффициенты полезного действия всех его узлов и механизмов, которые потребляют и преобразуют энергию.
Если мы имеем n механизмов, которые соединены последовательно, то результирующий КПД системы находят как произведение КПД каждой части:
При параллельном соединении механизмов (рис.1) (один двигатель приводит в действие несколько механизмов), полезная работа является суммой полезных работ на выходе из каждой отдельной части системы. Если работу затрачиваемую двигателем обозначить как , то КПД в данном случае найдем как:
Рис. 1
Единицы измерения КПД
В большинстве случаев КПД выражают в процентах
Примеры решения задач
ФИЗИКА: Задачи на простые механизмы — Ответы и решения
Задачи на КПД простых механизмов с решениями
Формулы, используемые на уроках «Задачи на КПД простых механизмов».
Название величины | Обозначение | Единица измерения | Формула |
Сила | F | Н | |
Полезная работа | Ап | Дж | Ап = mgh1 |
Затраченая работа | Аз | Дж | Аз = Fh2 |
КПД | ɳ | % | ɳ = Ап / Аз * 100% |
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.

Задача № 2. Вычислите КПД рычага, с помощью которого груз массой 200 кг равномерно подняли на высоту 0,03 м, при этом к длинному плечу рычага была приложена сила 400 Н, а точка приложения силы опустилась на 0,2 м.

Задача № 3. Груз массой 30 кг поднимают на высоту 12 м с помощью неподвижного блока, действуя на веревку силой 400 Н. Вычислите КПД установки.

Задача № 4. Высота наклонной плоскости 1,2 м, а длина 12 м. Для подъема по ней груза весом 2000 Н потребовалась сила 250 Н. Определите КПД этой наклонной плоскости.

Задача № 5. Груз массой 15 кг равномерно перемещают по наклонной плоскости, прикладывая при этом силу в 40 Н. Чему равно КПД наклонной плоскости, если длина ее 1,8 м, а высота — 30 см?

Краткая теория для решения задачи на КПД простых механизмов.

Конспект урока «Задачи на КПД простых механизмов с решениями».
Следующая тема: «».



