Формула полезной мощности в физике
Определение и формула полезной мощности
ОпределениеМощность — это физическая величина, которую использует как основную характеристику любого устройства, которое применяют для совершения работы. Полезная мощность может быть использована для выполнения поставленной задачи.
Отношение работы ($\Delta A$) к промежутку времени за которое она выполнена ($\Delta t$) называют средней мощностью ($\left\langle P\right\rangle $) за это время:
\[\left\langle P\right\rangle =\frac{\Delta A}{\Delta t}\left(1\right).\]Мгновенной мощностью или чаще просто мощностью называют предел отношения (1) при $\Delta t\to 0$:
\[P={\mathop{\lim }_{\Delta t\to 0} \frac{\Delta A}{\Delta t}\ }=A'(t)\left(2\right).\]Приняв во внимание, что:
\[\Delta A=\overline{F}\cdot \Delta \overline{r\ }\left(3\right),\]где $\Delta \overline{r\ }$ — перемещение тела под действием силы $\overline{F}$, в выражении (2) имеем:
\[P={\mathop{\lim }_{\Delta t\to 0} \left(\frac{\overline{F}\cdot \Delta \overline{r\ }}{\Delta t}\right)\ }=\overline{F}{\mathop{\lim }_{\Delta t\to 0} \left(\frac{\Delta \overline{r\ }}{\Delta t}\right)=\ }\overline{F}\cdot \overline{v}\left(4\right),\]Коэффициент полезного действия
При выполнении необходимой (полезной) работы, например, механической, приходится выполнять работу большую по величине, так как в реальности существуют силы сопротивления и часть энергии подвержена диссипации (рассеиванию). Эффективность совершения работы определяется при помощи коэффициента полезного действия ($\eta $), при этом:
\[\eta =\frac{P_p}{P}\left(5\right),\]где $P_p$ — полезная мощность; $P$ — затраченная мощность. Из выражения (5) следует, что полезная мощность может быть найдена как:
Формула полезной мощности источника тока
Пусть электрическая цепь состоит из источника тока, имеющего сопротивление $r$ и нагрузки (сопротивление $R$). Мощность источника найдем как:
\[P=?I\ \left(7\right),\]где $?$ — ЭДС источника тока; $I$ — сила тока. При этом $P$ — полная мощность цепи.
Обозначим $U$ — напряжение на внешнем участке цепи, тогда формулу (7) представим в виде:
\[P=?I=UI+I^2r=P_p+P_0\left(8\right),\]где $P_p=UI=I^2R=\frac{U^2}{R}(9)$ — полезная мощность; $P_0=I^2r$ — мощность потерь. При этом КПД источника определяют как:
\[\eta =\frac{P_p}{P_p+P_0}\left(9\right).\]Максимальную полезную мощность (мощность на нагрузке) электрический ток дает, если внешнее сопротивление цепи будет равно внутреннему сопротивлению источника тока. При этом условии полезная мощность равна 50\% общей мощности.
При коротком замыкании (когда $R\to 0;;U\to 0$) или в режиме холостого хода $(R\to \infty ;;I\to 0$) полезная мощность равна нулю.
Примеры задач с решением
Пример 1Задание. Коэффициент полезного действия электрического двигателя равен $\eta $ =42%. Какой будет его полезная мощность, если при напряжении $U=$110 В через двига
Формула полезной мощности в физике
Определение и формула полезной мощности
ОпределениеМощность — это физическая величина, которую использует как основную характеристику любого устройства, которое применяют для совершения работы. Полезная мощность может быть использована для выполнения поставленной задачи.
Отношение работы ($\Delta A$) к промежутку времени за которое она выполнена ($\Delta t$) называют средней мощностью ($\left\langle P\right\rangle $) за это время:
\[\left\langle P\right\rangle =\frac{\Delta A}{\Delta t}\left(1\right).\]Мгновенной мощностью или чаще просто мощностью называют предел отношения (1) при $\Delta t\to 0$:
\[P={\mathop{\lim }_{\Delta t\to 0} \frac{\Delta A}{\Delta t}\ }=A'(t)\left(2\right).\]Приняв во внимание, что:
\[\Delta A=\overline{F}\cdot \Delta \overline{r\ }\left(3\right),\]где $\Delta \overline{r\ }$ — перемещение тела под действием силы $\overline{F}$, в выражении (2) имеем:
\[P={\mathop{\lim }_{\Delta t\to 0} \left(\frac{\overline{F}\cdot \Delta \overline{r\ }}{\Delta t}\right)\ }=\overline{F}{\mathop{\lim }_{\Delta t\to 0} \left(\frac{\Delta \overline{r\ }}{\Delta t}\right)=\ }\overline{F}\cdot \overline{v}\left(4\right),\]где $\ \overline{v}-$ мгновенная скорость.
Коэффициент полезного действия
При выполнении необходимой (полезной) работы, например, механической, приходится выполнять работу большую по величине, так как в реальности существуют силы сопротивления и часть энергии подвержена диссипации (рассеиванию). Эффективность совершения работы определяется при помощи коэффициента полезного действия ($\eta $), при этом:
\[\eta =\frac{P_p}{P}\left(5\right),\]где $P_p$ — полезная мощность; $P$ — затраченная мощность. Из выражения (5) следует, что полезная мощность может быть найдена как:
\[P_p=\eta P\ \left(6\right).\]Формула полезной мощности источника тока
Пусть электрическая цепь состоит из источника тока, имеющего сопротивление $r$ и нагрузки (сопротивление $R$). Мощность источника найдем как:
\[P=?I\ \left(7\right),\]где $?$ — ЭДС источника тока; $I$ — сила тока. При этом $P$ — полная мощность цепи.
Обозначим $U$ — напряжение на внешнем участке цепи, тогда формулу (7) представим в виде:
\[P=?I=UI+I^2r=P_p+P_0\left(8\right),\]где $P_p=UI=I^2R=\frac{U^2}{R}(9)$ — полезная мощность; $P_0=I^2r$ — мощность потерь. При этом КПД источника определяют как:
\[\eta =\frac{P_p}{P_p+P_0}\left(9\right).\]Максимальную полезную мощность (мощность на нагрузке) электрический ток дает, если внешнее сопротивление цепи будет равно внутреннему сопротивлению источника тока. При этом условии полезная мощность равна 50\% общей мощности.
При коротком замыкании (когда $R\to 0;;U\to 0$) или в режиме холостого хода $(R\to \infty ;;I\to 0$) полезная мощность равна нулю.
Примеры задач с решением
Пример 1Задание. Коэффициент полезного действия электрического двигателя равен $\eta $ =42%. Какой будет его полезная мощность, если при напряжении $U=$110 В через двига
Формула полезной мощности в физике
Определение и формула полезной мощности
ОпределениеМощность — это физическая величина, которую использует как основную характеристику любого устройства, которое применяют для совершения работы. Полезная мощность может быть использована для выполнения поставленной задачи.
Отношение работы ($\Delta A$) к промежутку времени за которое она выполнена ($\Delta t$) называют средней мощностью ($\left\langle P\right\rangle $) за это время:
\[\left\langle P\right\rangle =\frac{\Delta A}{\Delta t}\left(1\right).\]Мгновенной мощностью или чаще просто мощностью называют предел отношения (1) при $\Delta t\to 0$:
\[P={\mathop{\lim }_{\Delta t\to 0} \frac{\Delta A}{\Delta t}\ }=A'(t)\left(2\right).\]Приняв во внимание, что:
\[\Delta A=\overline{F}\cdot \Delta \overline{r\ }\left(3\right),\]где $\Delta \overline{r\ }$ — перемещение тела под действием силы $\overline{F}$, в выражении (2) имеем:
\[P={\mathop{\lim }_{\Delta t\to 0} \left(\frac{\overline{F}\cdot \Delta \overline{r\ }}{\Delta t}\right)\ }=\overline{F}{\mathop{\lim }_{\Delta t\to 0} \left(\frac{\Delta \overline{r\ }}{\Delta t}\right)=\ }\overline{F}\cdot \overline{v}\left(4\right),\]где $\ \overline{v}-$ мгновенная скорость.
Коэффициент полезного действия
При выполнении необходимой (полезной) работы, например, механической, приходится выполнять работу большую по величине, так как в реальности существуют силы сопротивления и часть энергии подвержена диссипации (рассеиванию). Эффективность совершения работы определяется при помощи коэффициента полезного действия ($\eta $), при этом:
\[\eta =\frac{P_p}{P}\left(5\right),\]где $P_p$ — полезная мощность; $P$ — затраченная мощность. Из выражения (5) следует, что полезная мощность может быть найдена как:
\[P_p=\eta P\ \left(6\right).\]Формула полезной мощности источника тока
Пусть электрическая цепь состоит из источника тока, имеющего сопротивление $r$ и нагрузки (сопротивление $R$). Мощность источника найдем как:
\[P=?I\ \left(7\right),\]где $?$ — ЭДС источника тока; $I$ — сила тока. При этом $P$ — полная мощность цепи.
Обозначим $U$ — напряжение на внешнем участке цепи, тогда формулу (7) представим в виде:
\[P=?I=UI+I^2r=P_p+P_0\left(8\right),\]где $P_p=UI=I^2R=\frac{U^2}{R}(9)$ — полезная мощность; $P_0=I^2r$ — мощность потерь. При этом КПД источника определяют как:
\[\eta =\frac{P_p}{P_p+P_0}\left(9\right).\]Максимальную полезную мощность (мощность на нагрузке) электрический ток дает, если внешнее сопротивление цепи будет равно внутреннему сопротивлению источника тока. При этом условии полезная мощность равна 50\% общей мощности.
При коротком замыкании (когда $R\to 0;;U\to 0$) или в режиме холостого хода $(R\to \infty ;;I\to 0$) полезная мощность равна нулю.
Примеры задач с решением
Пример 1Задание. Коэффициент полезного действия электрического двигателя равен $\eta $ =42%. Какой будет его полезная мощность, если при напряжении $U=$110 В через дви
Полезная мощность — это… Что такое Полезная мощность?
- Полезная мощность
Полезная мощность (Useful capacity) – мощность ( машины, оборудования, энергетического агрегата или иного технического устройства) отдаваемая устройством в определенной форме и для определенной цели; равна полной мощности за вычетом затрат мощности на приведение в действие вспомогательных агрегатов или механизмов, необходимых для его работы.
Экономико-математический словарь: Словарь современной экономической науки. — М.: Дело. Л. И. Лопатников. 2003.
- Покупательная способность денег
- Полезность
Смотреть что такое «Полезная мощность» в других словарях:
полезная мощность — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] полезная мощность Мощность (машины, оборудования, энергетического агрегата или иного технического устройства)… … Справочник технического переводчика
полезная мощность — 3.10 полезная мощность: Эффективная мощность в киловаттах, полученная на испытательном стенде на хвостовике коленчатого вала или измеренная методом по ГОСТ Р 41.85. Источник … Словарь-справочник терминов нормативно-технической документации
полезная мощность — naudingoji galia statusas T sritis Standartizacija ir metrologija apibrėžtis Galia, susijusi su tam tikros sistemos, įrenginio, aparato ar įtaiso atliekamu naudingu darbu. atitikmenys: angl. net power; useful power vok. Abgabeleistung, f;… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
полезная мощность — naudingoji galia statusas T sritis fizika atitikmenys: angl. net power; useful power vok. Abgabeleistung, f; Nutzabgabe, f; Nutzleistung, f rus. полезная мощность, f pranc. puissance utile, f … Fizikos terminų žodynas
Полезная мощность — мощность, которую можно получить на валу двигателя; то же, что Эффективная мощность … Большая советская энциклопедия
Полезная мощность — – мощность, отдаваемая устройством в определенной форме и для определенной цели. СТ МЭК 50(151) 78 … Коммерческая электроэнергетика. Словарь-справочник
Полезная мощность — English: Output power Мощность, отдаваемая устройством в определенной форме и для определенной цели (по СТ МЭК 50(151) 78) Источник: Термины и определения в электроэнергетике. Справочник … Строительный словарь
полезная мощность насоса — Мощность, сообщаемая насосом подаваемой жидкой среде и определяемая зависимостью где Q подача насоса, м3/с; P давление насоса, Па; QM массовая подача насоса, кг/с; LП полезная удельная работа насоса, Дж/кг; NП полезная мощность насоса, Вт. [ГОСТ… … Справочник технического переводчика
полезная мощность (в автотранспортной технике) — полезная мощность Мощность, выраженная в киловаттах, полученная на испытательном стенде на хвостовике коленчатого вала или его эквивалента и измеряемая в соответствии с методом измерения мощности, установленным в ГОСТ Р 41.24. [ГОСТ Р 41.49 2003] … Справочник технического переводчика
полезная мощность в ваттах — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN watts out … Справочник технического переводчика
Полная мощность
 (12.10)
(12.10)
Полезная мощность максимальна
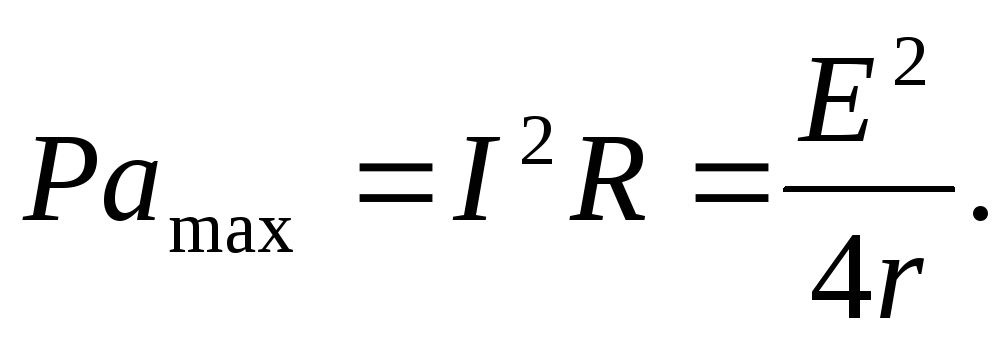 (12.11)
(12.11)
Коротким замыканием называется режим работы цепи, при котором внешнее сопротивление R = 0. При этом
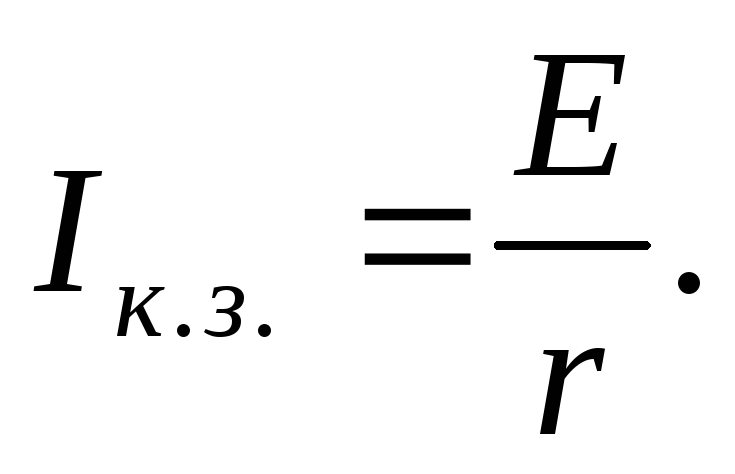 (12.12)
(12.12)
Полезная мощность
Полная мощность
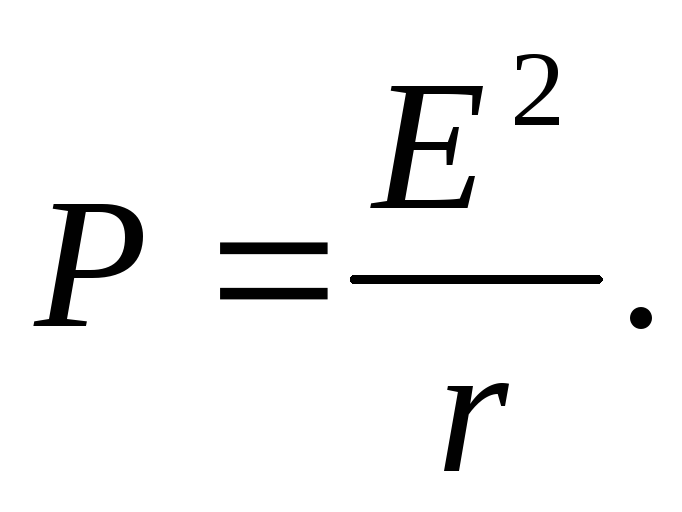 (12.13)
(12.13)
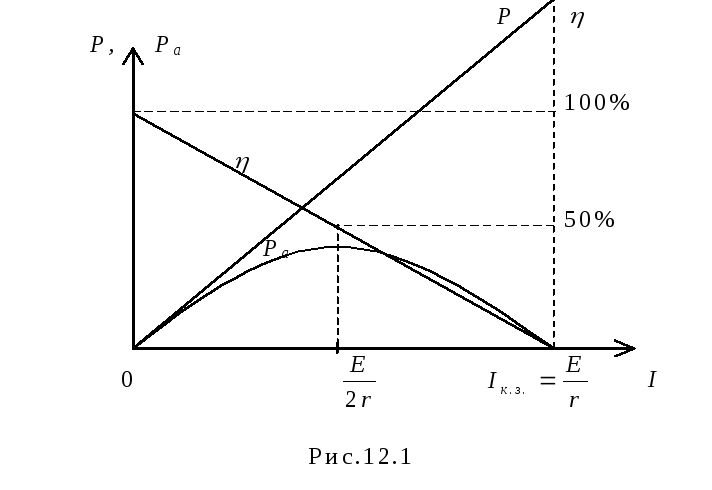
График зависимости Ра(I) – парабола, ветви которой направлены вниз (рис12.1). На этом же рисунке показаны зависимость КПД от силы тока.
Примеры решения задач
Задача 1. Батарея состоит из n = 5 последовательно соединённых элементов с Е = 1,4 В и внутренним сопротивлением r = 0,3 Ом каждый. При каком токе полезная мощность батареи равна 8 Вт? Какова наибольшая полезная мощность батареи?
 Дано: Решение
Дано: Решение
n = 5 При последовательном соединении элементов ток в цепи
Е = 1,4 В 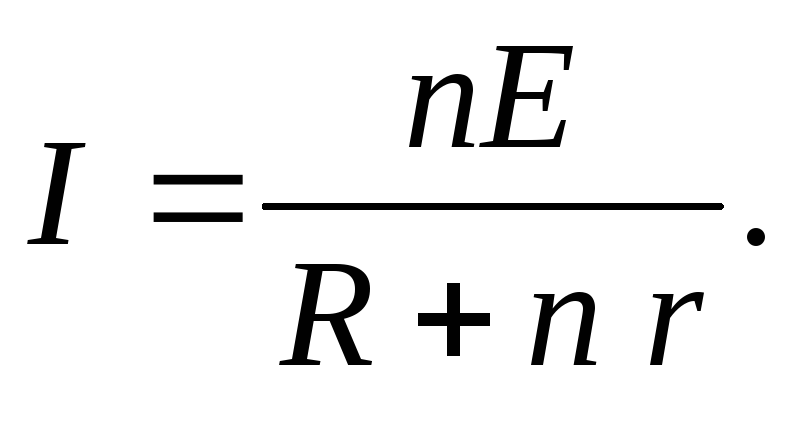 (1)
(1)
Ра = 8 Вт Из формулы полезной
мощности 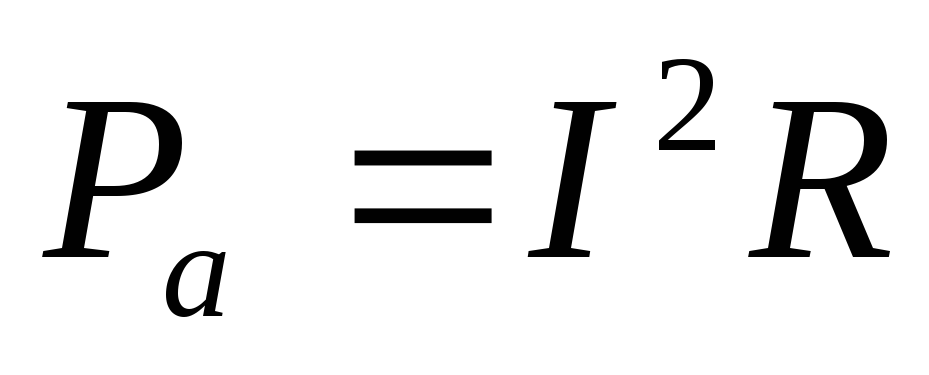
 внешнее сопротивление R и подставим в формулу (1)
внешнее сопротивление R и подставим в формулу (1)
I — ? 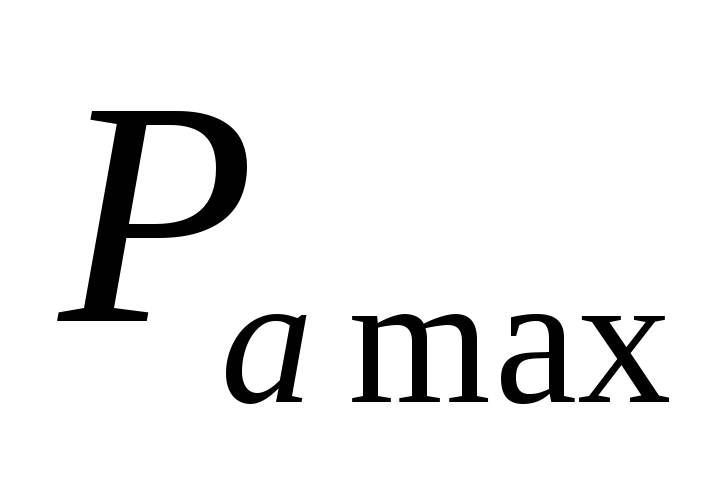 -?
-? 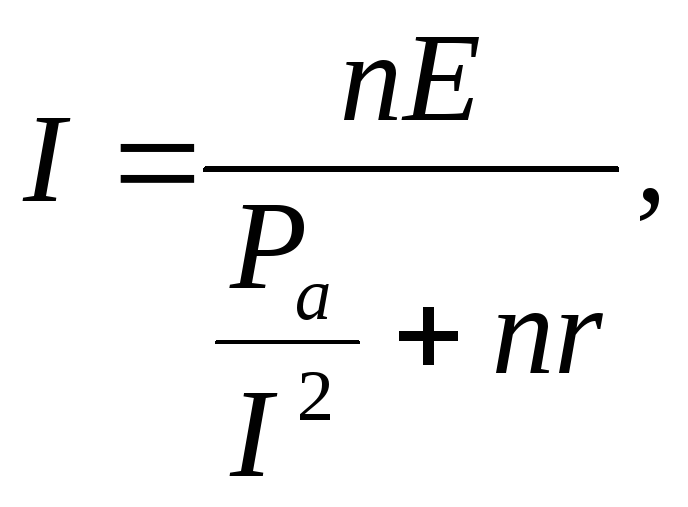
после преобразований получим квадратное уравнение, решая которое, найдём значение токов:
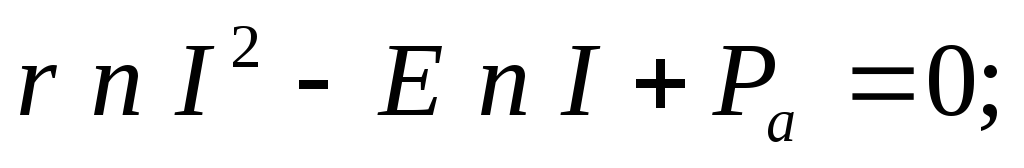
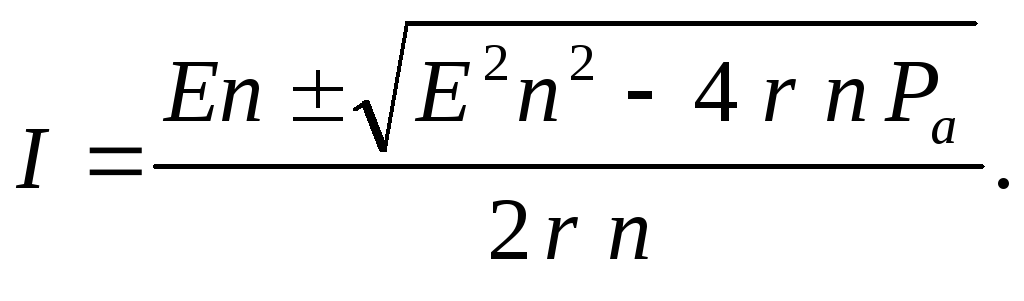

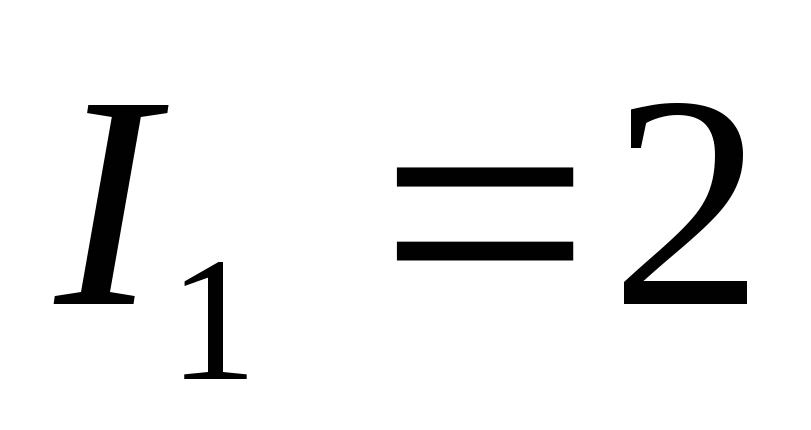 А; I2 =
А; I2 = 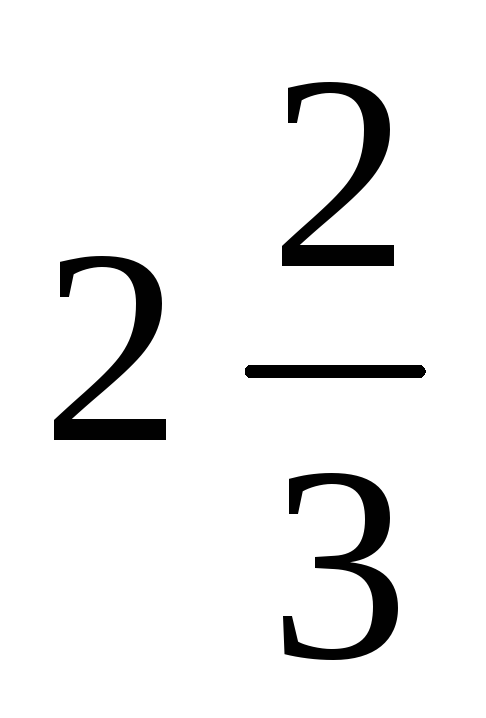 A.
A.
Итак, при токах I1 и I2 полезная мощность одинакова. При анализе графика зависимости полезной мощности от тока видно, что при I1 потери мощности меньше и КПД выше.
Полезная мощность максимальна при R =
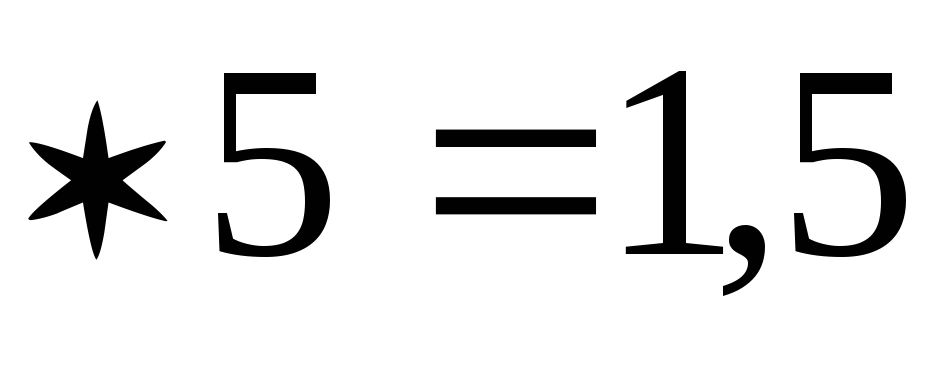 Ом.
Ом. 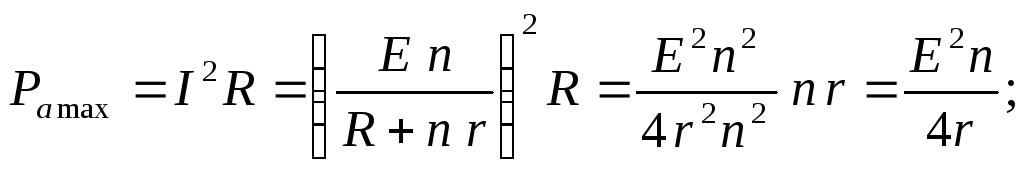
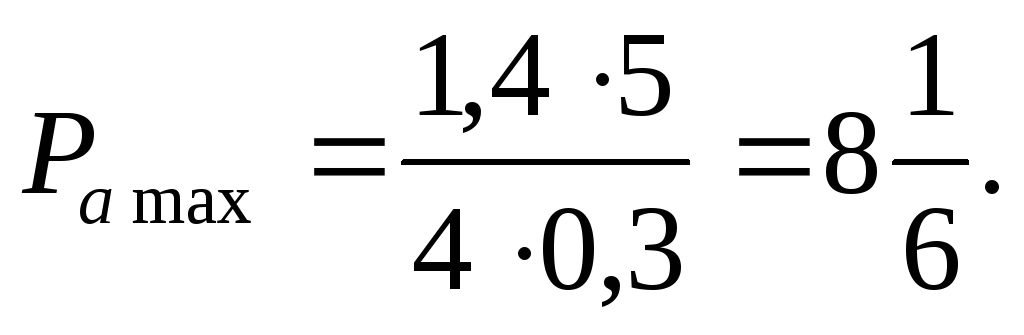
Ответ: I1 = 2 A; I2 =  A;Pamax =
A;Pamax =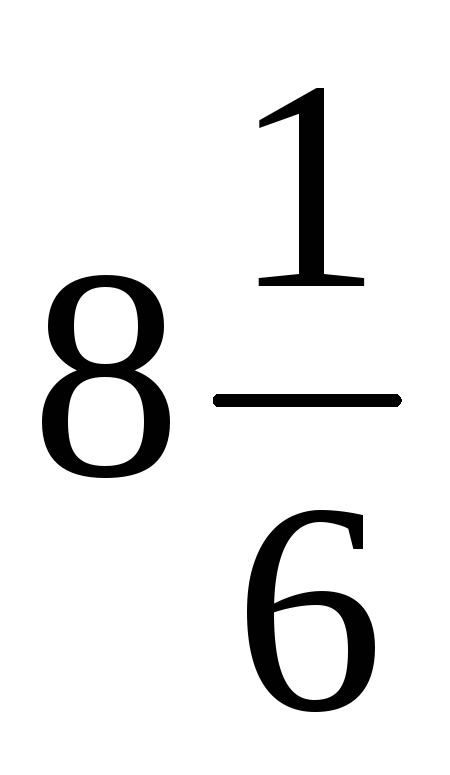 Вт.
Вт.
Задача 2. Полезная мощность, выделяемая во внешней части цепи, достигает наибольшего значения 5 Вт при силе тока 5 А. Найти внутреннее сопротивление и ЭДС источника тока.
 Дано: Решение
Дано: Решение
Pamax = 5 Вт Полезная мощность 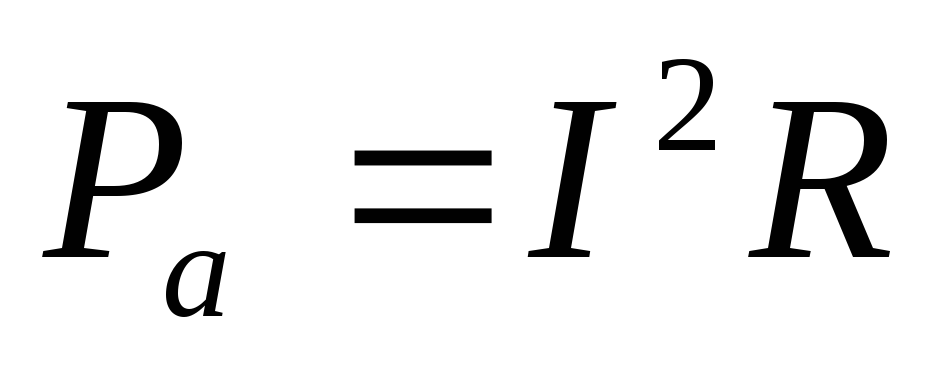 (1)
(1)
I = 5 A
по закону Ома 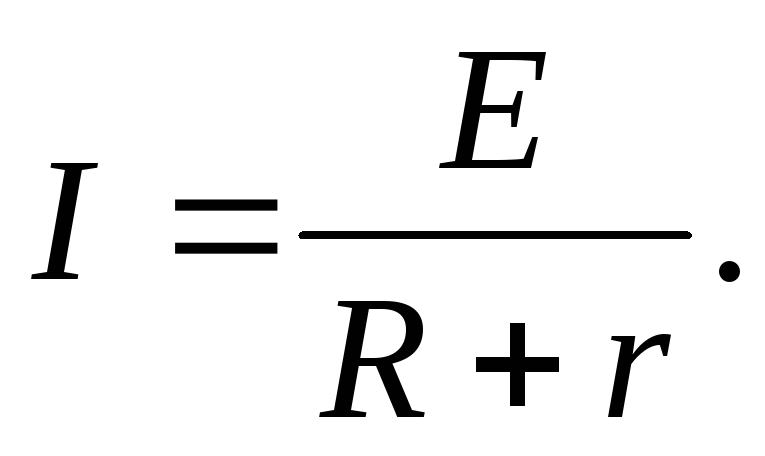 (2)
(2)

r — ? Е — ? формулы (1) 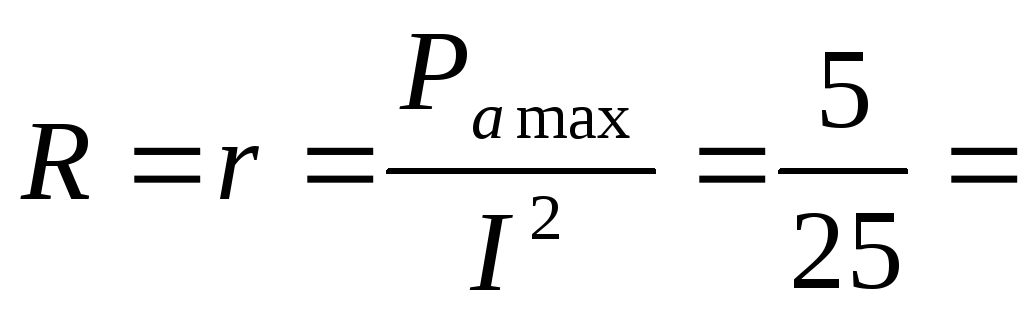 0,2
Ом.
0,2
Ом.
Из
формулы (2) 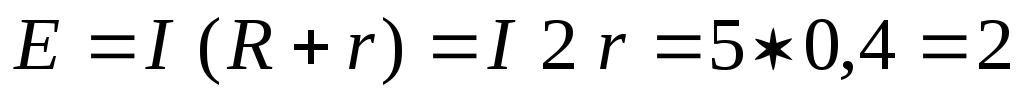 В.
В.
Ответ: r = 0,2 Ом; Е = 2 В.
Задача 3. От генератора, ЭДС которого равна 110В, требуется передать энергию на расстояние 2,5 км по двухпроводной линии. Потребляемая мощность равна 10 кВт. Найти минимальное сечение медных подводящих проводов, если потери мощности в сети не должны превышать 1 %.
Д ано: Решение
ано: Решение
Е
= 110 В
Сопротивление проводов 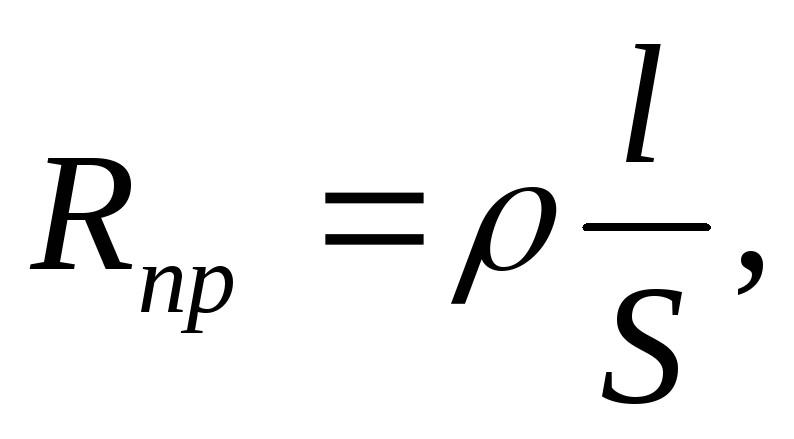
l = 5103 м где — удельное сопротивление меди; l – длина проводов;
Ра = 104 Вт S – сечение.
= 1,710-8 Ом.м Потребляемая мощность Pa = I E, мощность, теряемая
Рпр = 100 Вт в сети Pпр = I 2Rпр, а так как в пороводах и потребителе
 S — ? ток одинаковый,
то
S — ? ток одинаковый,
то
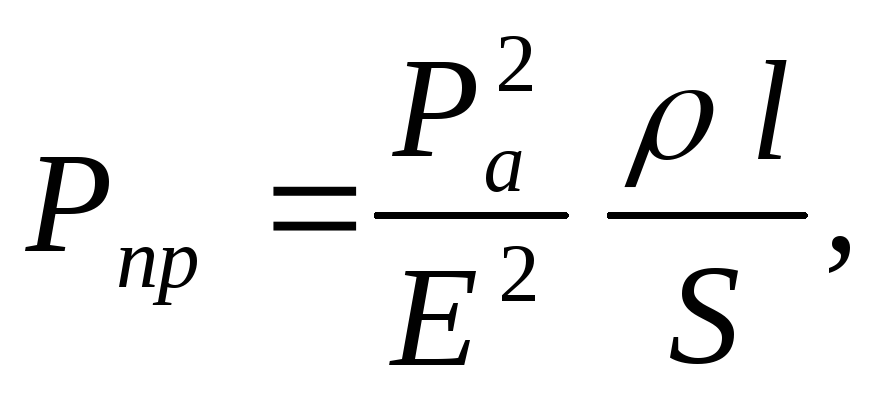
откуда 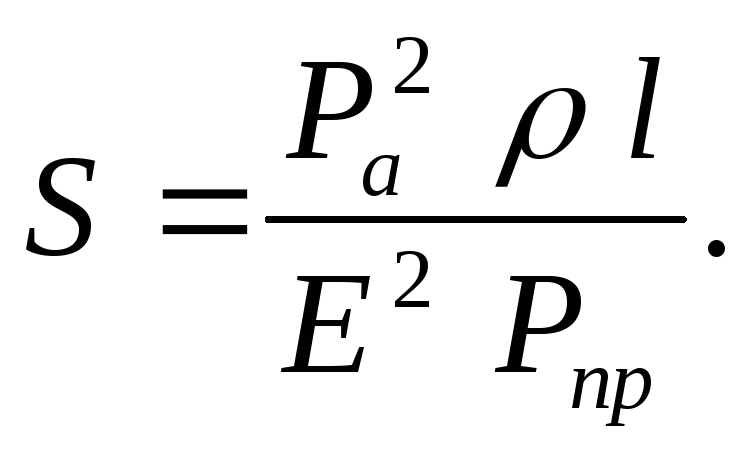
Подставив числовые значения, получим
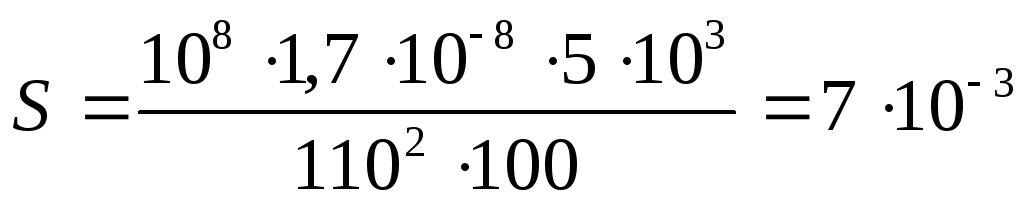 м2.
м2.
Ответ: S = 710-3 м2.
Задача 4. Найти внутреннее сопротивление генератора, если известно, что мощность, выделяемая во внешней цепи, одинакова при двух значениях внешнего сопротивления R1 = 5 Ом и R2 = 0,2 Ом. Найти КПД генератора в каждом из этих случаев.
 Дано: Решение
Дано: Решение
Р1 = Р2 Мощность, выделяемая во внешней цепи, Pa = I 2R. По закону Ома
R1 = 5 Ом для замкнутой цепи 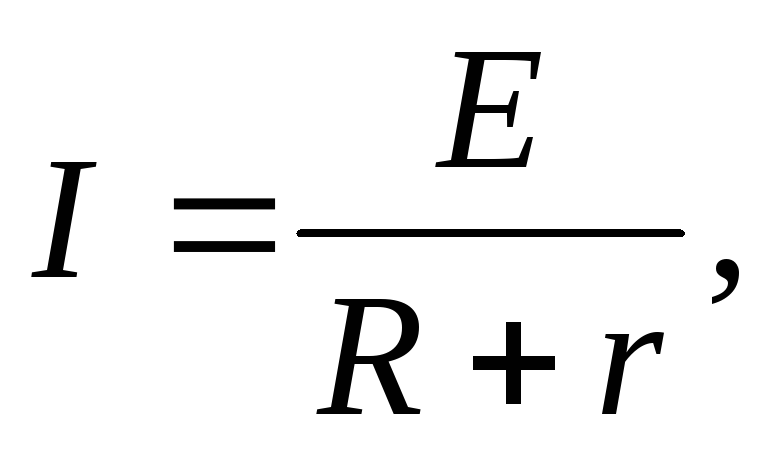 тогда
тогда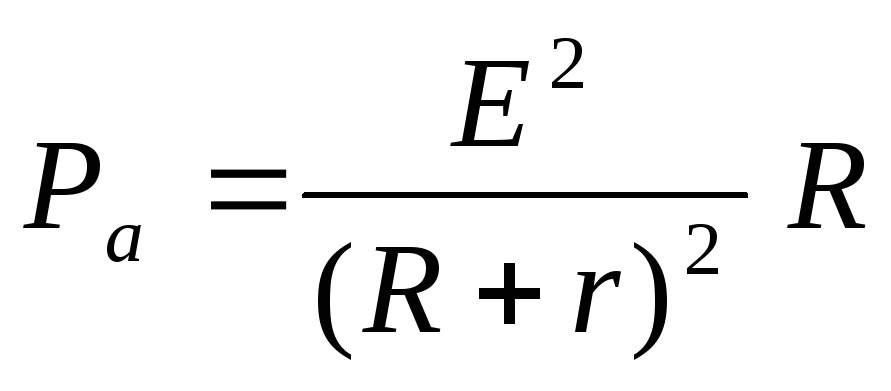 .
.
R2 = 0,2 Ом Используя условие задачи Р1 = Р2, получим
r -?
-? 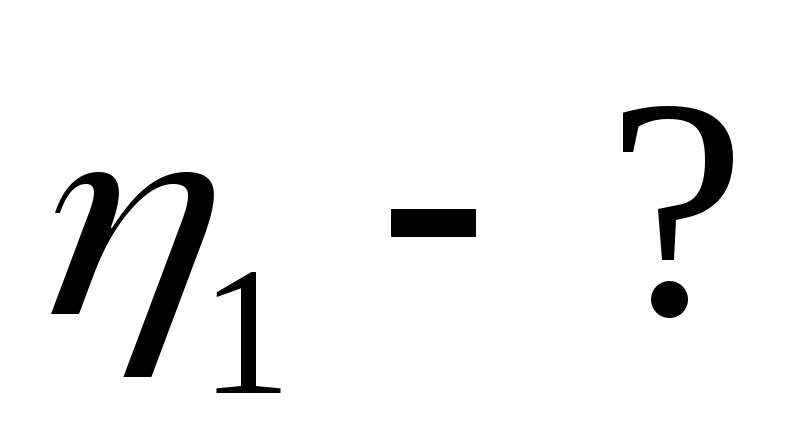
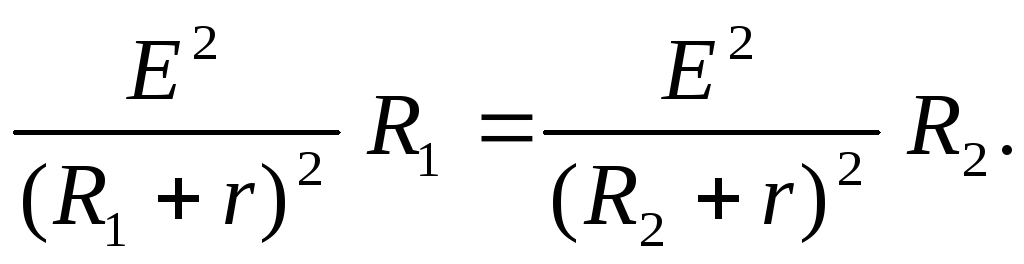
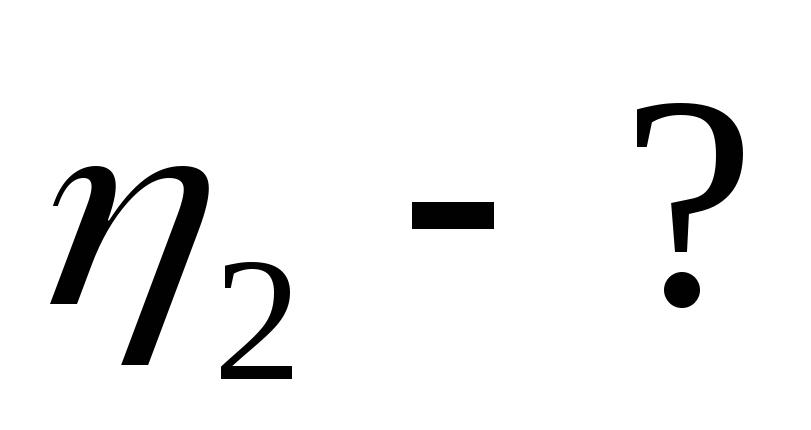
Преобразуя полученное равенство, находим внутреннее сопротивление источника r:
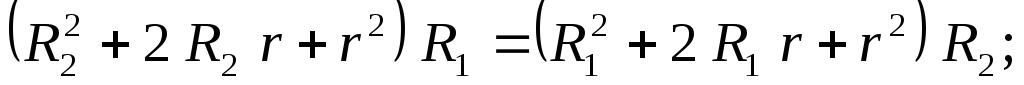
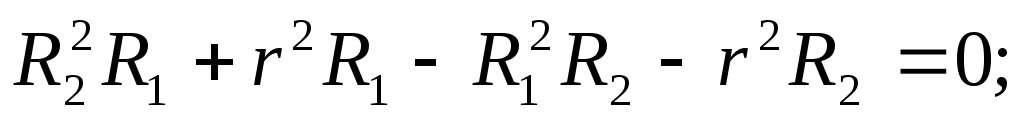
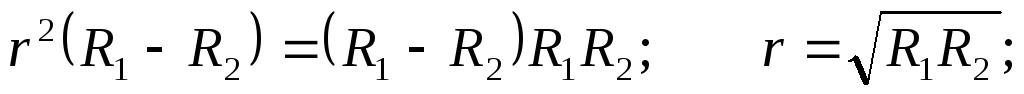
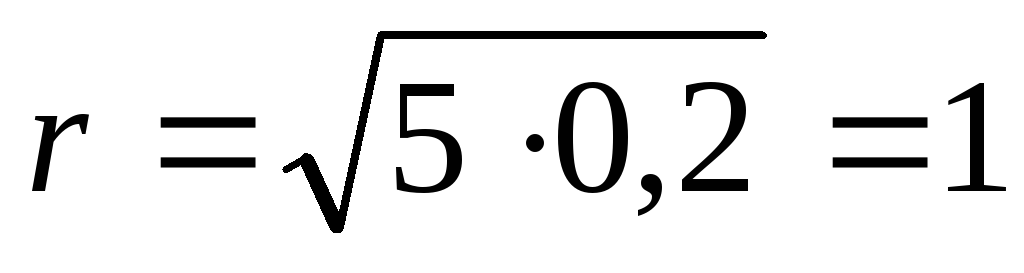 Ом.
Ом.
Коэффициентом полезного действия называется величина
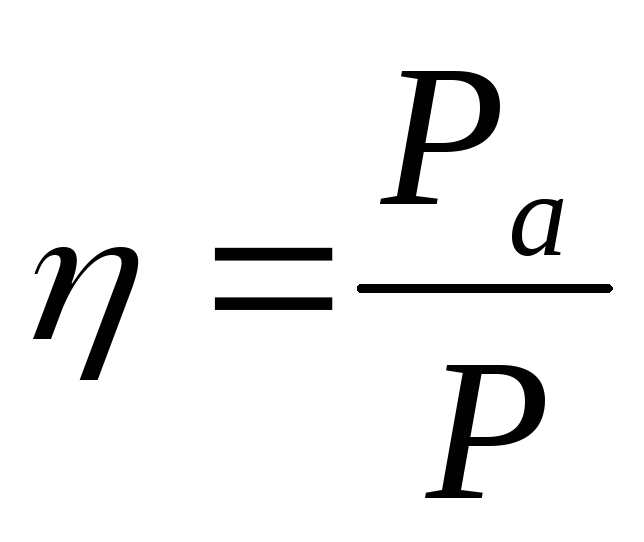 ,
,
где Ра – мощность, выделяемая во внешней цепи; Р – полная мощность.
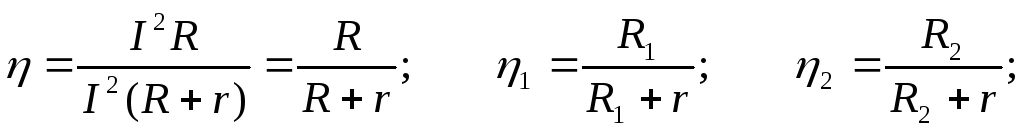

Ответ: r = 1 Ом; 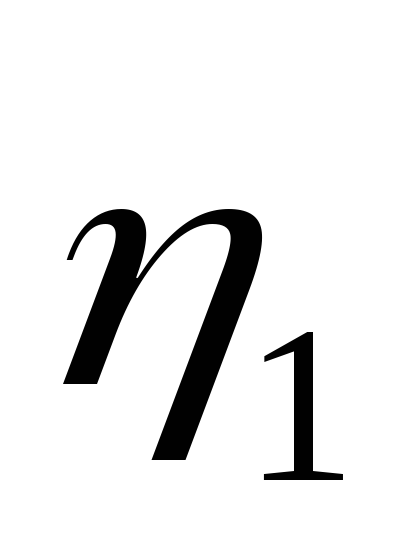 =
83 %;
=
83 %; =
17 %.
=
17 %.
Задача 5. ЭДС батареи Е = 16 В, внутреннее сопротивление r = 3 Ом. Найти сопротивление внешней цепи, если известно, что в ней выделяется мощность Ра = 16 Вт. Определить КПД батареи.
 Дано: Решение
Дано: Решение
Е = 16 В Мощность, выделяемая во внешней части цепи Ра = I 2R.
r = 3 Ом
Силу тока найдём по закону Ома для
замкнутой цепи: 
Ра = 16 Вт тогда 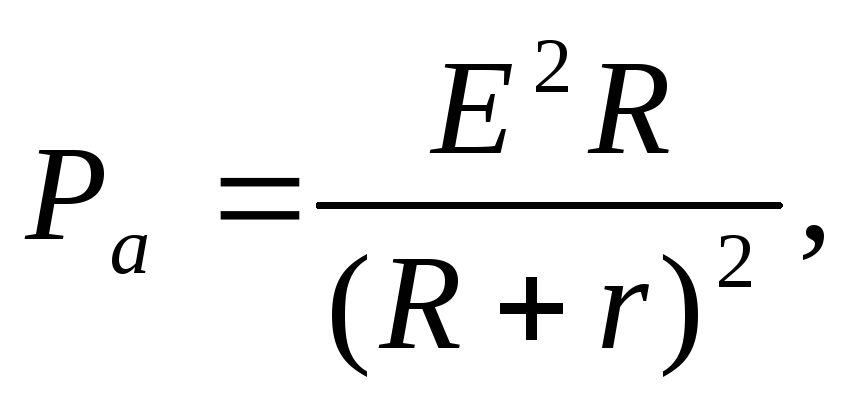 или
или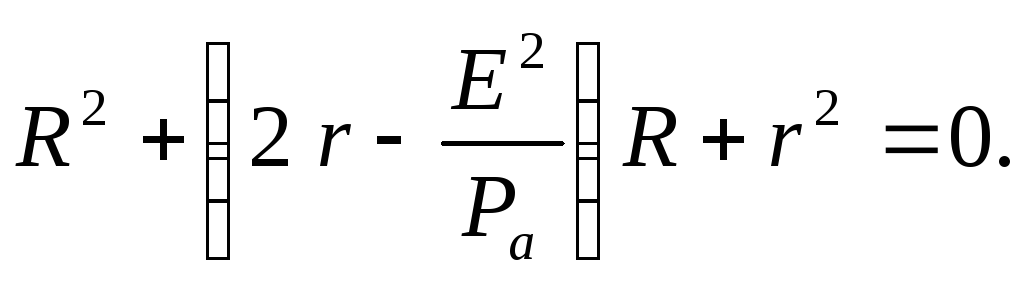
 —
? R — ? Подставляем числовые значения
заданных величин в это квадратное
уравнение и решаем его относительно R:
—
? R — ? Подставляем числовые значения
заданных величин в это квадратное
уравнение и решаем его относительно R:
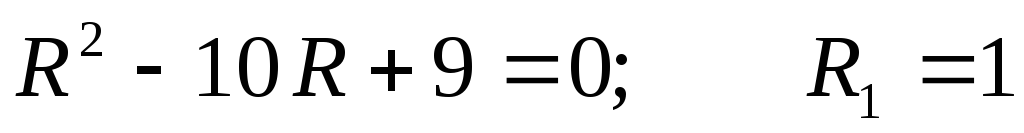 Ом; R2 = 9 Ом.
Ом; R2 = 9 Ом.
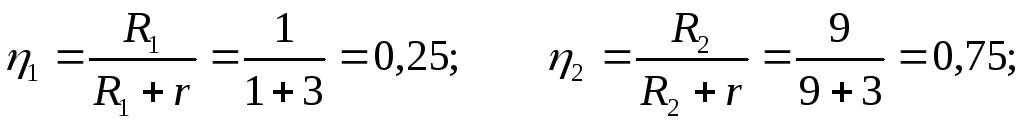

Ответ: R1 = 1 Ом; R2 = 9 Ом; 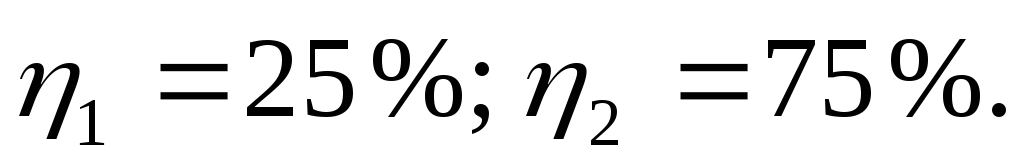
Задача 6. Две электрические лампочки включены в сеть параллельно. Сопротивление первой лампочки 360 Ом, сопротивление второй 240 Ом. Какая из лампочек поглощает большую мощность? Во сколько раз?
 Дано: Решение
Дано: Решение
R1 = 360 Ом Мощность, выделяемая в лампочке,
R2 = 240 Ом P = I 2R (1)
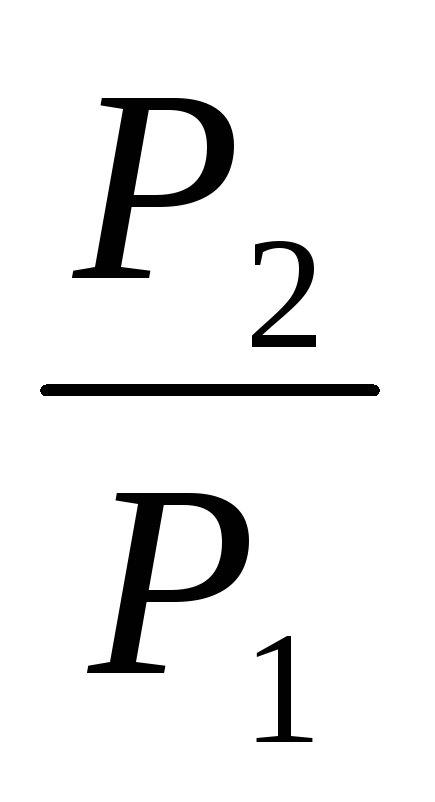
 —
? При параллельном соединении на лампочках
будет одинаковое напряжение, поэтому
сравнивать мощности лучше, преобразовав
формулу (1) используя закон Ома
—
? При параллельном соединении на лампочках
будет одинаковое напряжение, поэтому
сравнивать мощности лучше, преобразовав
формулу (1) используя закон Ома 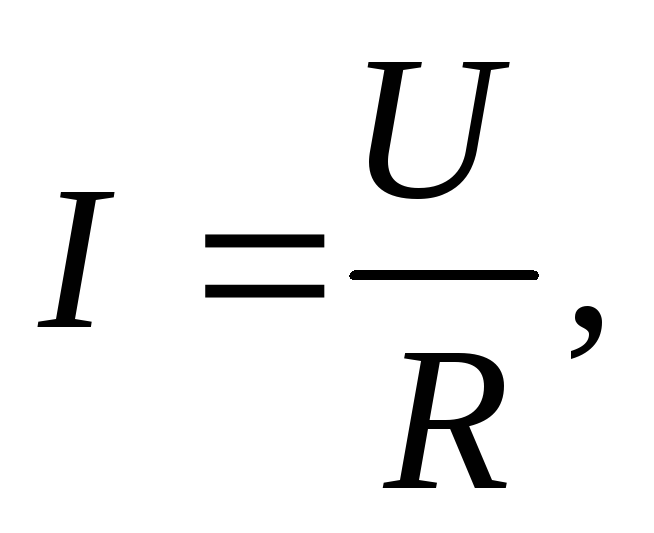 тогда
тогда 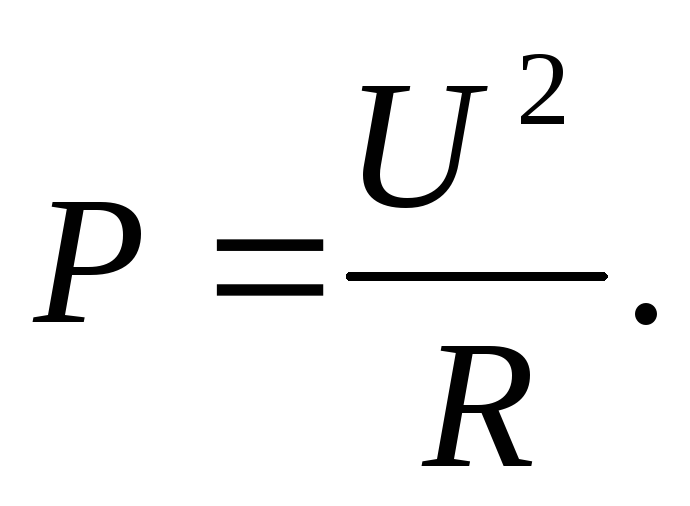
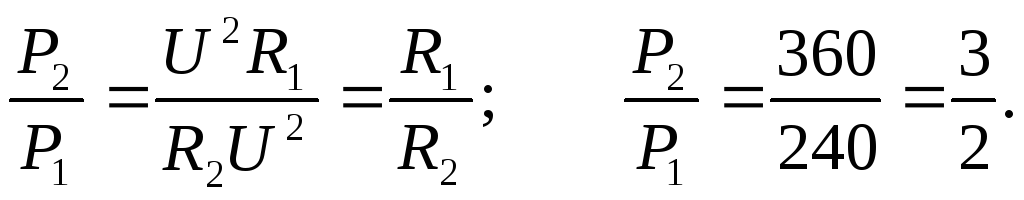
При параллельном соединении лампочек большая мощность выделяется в лампочке с меньшим сопротивлением.
Ответ: 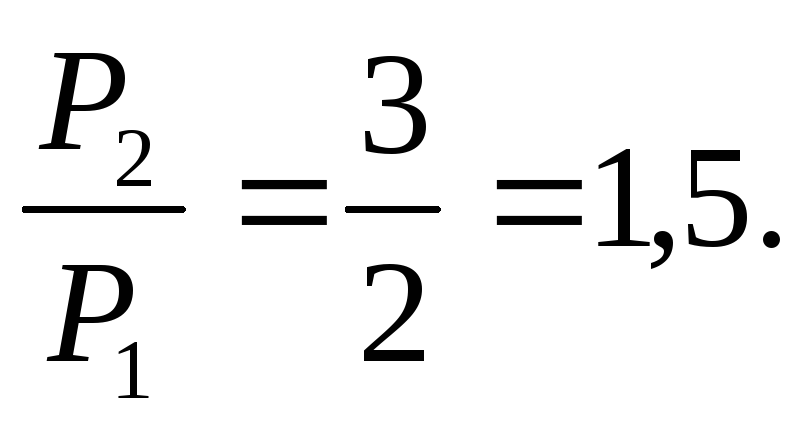
Задача 7. Два потребителя сопротивлениями R1 = 2 Ом и R2 = 4 Ом подключаются к сети постоянного тока первый раз параллельно, а второй – последовательно. В каком случае потребляется большая мощность от сети? Рассмотреть случай, когда R1 = R2.
 Дано: Решение
Дано: Решение
R1 = 2 Ом Потребляемая от сети мощность
R2 = 4 Ом 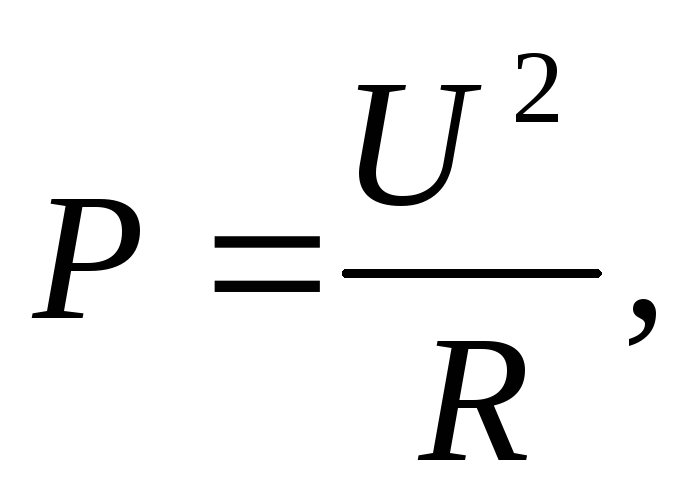 (1)
(1)
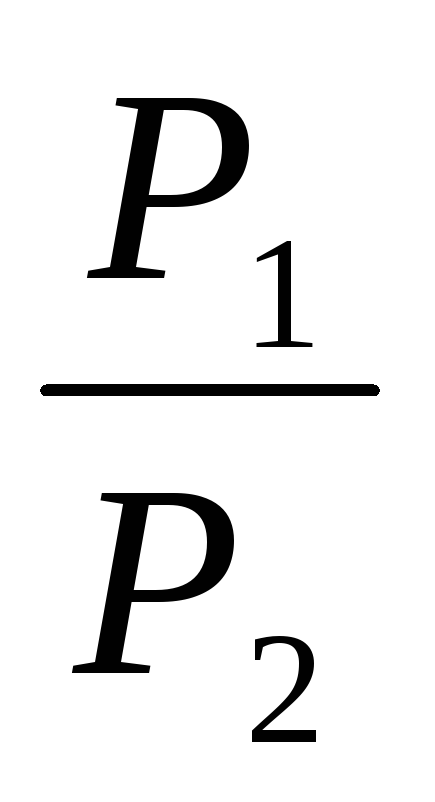
 —
? где R – общее сопротивление потребителей; U – напряжение в сети. При параллельном
соединении потребителей их общее
сопротивление
—
? где R – общее сопротивление потребителей; U – напряжение в сети. При параллельном
соединении потребителей их общее
сопротивление 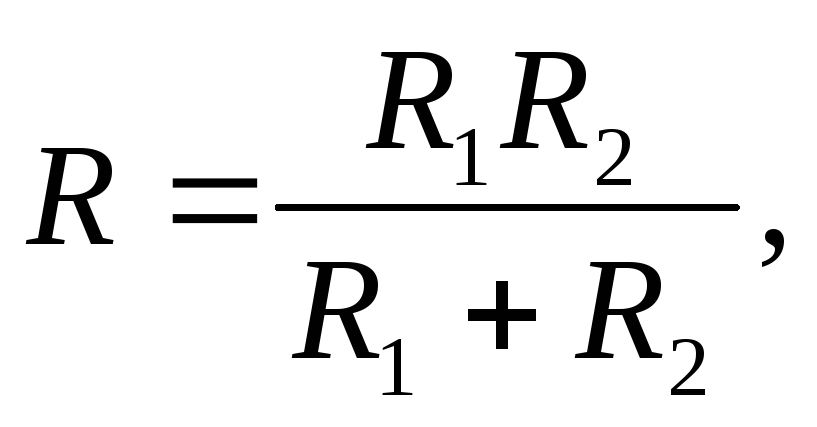 а при последовательномR = R1 + R2.
а при последовательномR = R1 + R2.
В
первом случае, согласно формуле (1),
потребляемая мощность 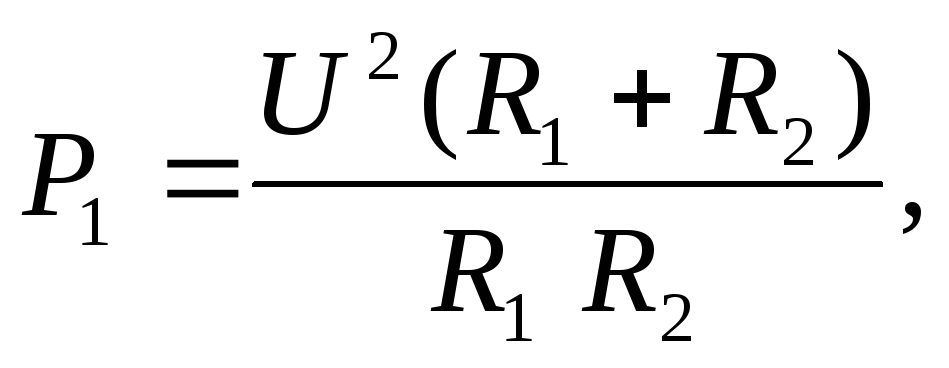 а во втором
а во втором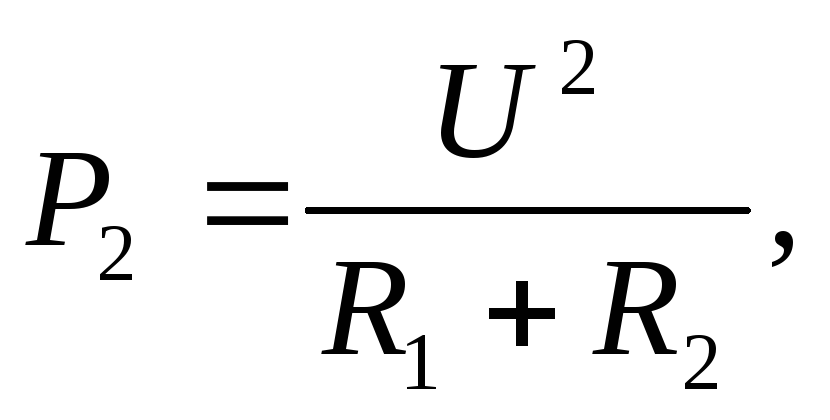 откуда
откуда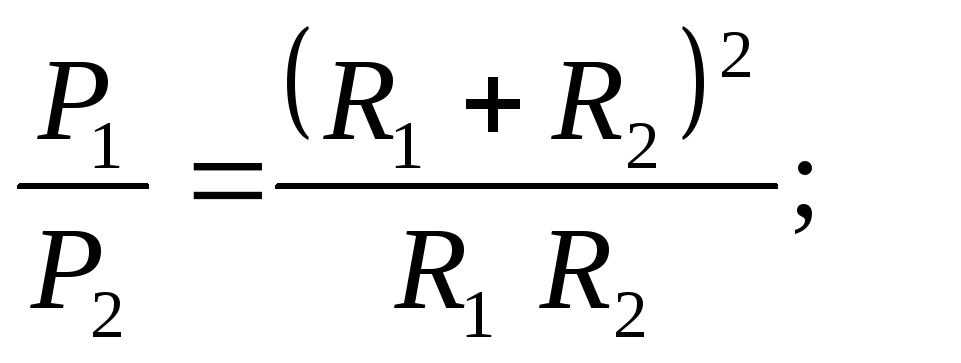
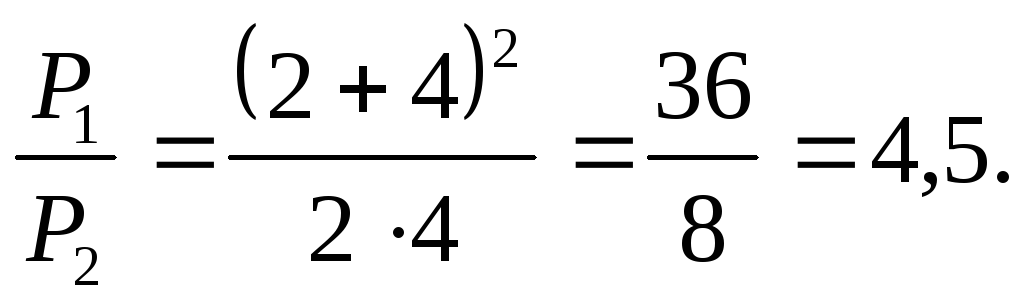
Таким образом, при параллельном подключении нагрузок потребляется большая мощность от сети, чем при последовательном.
При 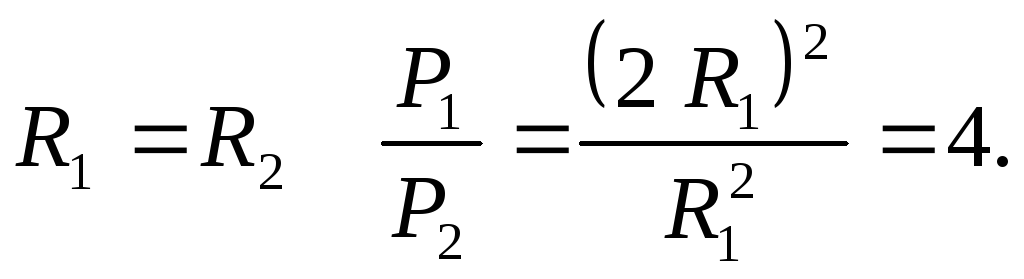
Ответ: 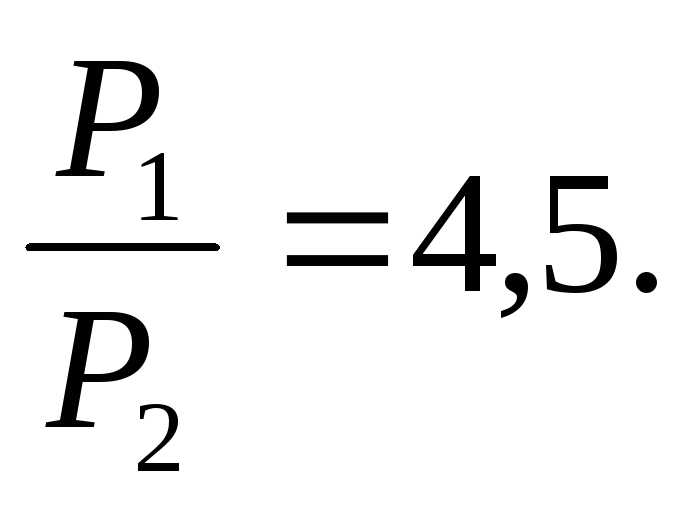
Задача 8.. Нагреватель кипятильника состоит из четырёх секций, сопротивление каждой секции R = 1 Ом. Нагреватель питается от аккумуляторной батареи с Е = 8 В и внутренним сопротивлением r = 1 Ом. Как следует подключить элементы нагревателя, чтобы вода в кипятильнике нагрелась в максимально короткий срок? Каковы при этом полная мощность, расходуемая аккумулятором, и его КПД?

Дано:
R1 = 1 Ом
n = 4
Е = 8 В
r = 1 Ом

Решение
Мак симальную полезную мощность источник даёт в случае, если внешнее сопротивление R равно внутреннему r.
 Следовательно,
чтобы воданагрелась
в максимально короткий срок, нужно
секции включить так,
Следовательно,
чтобы воданагрелась
в максимально короткий срок, нужно
секции включить так,
чтобы R = r. Это условие выполняется при смешанном соединении секций (рис.12.2.а,б).
Мощность,
которую расходует аккумулятор, равна Р = I E.
По закону Ома для замкнутой цепи 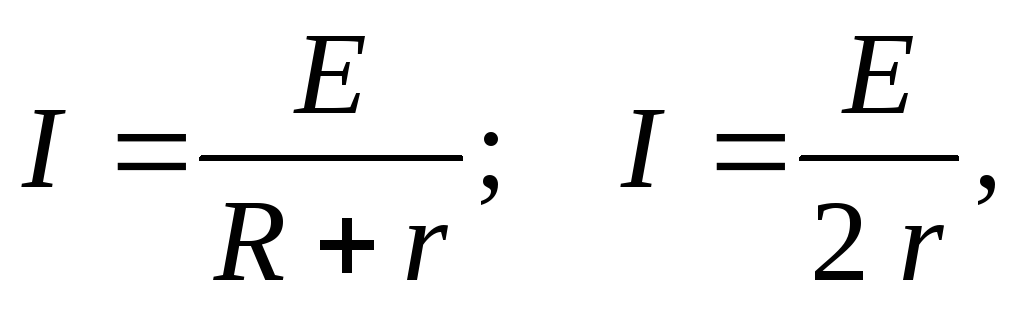 тогда
тогда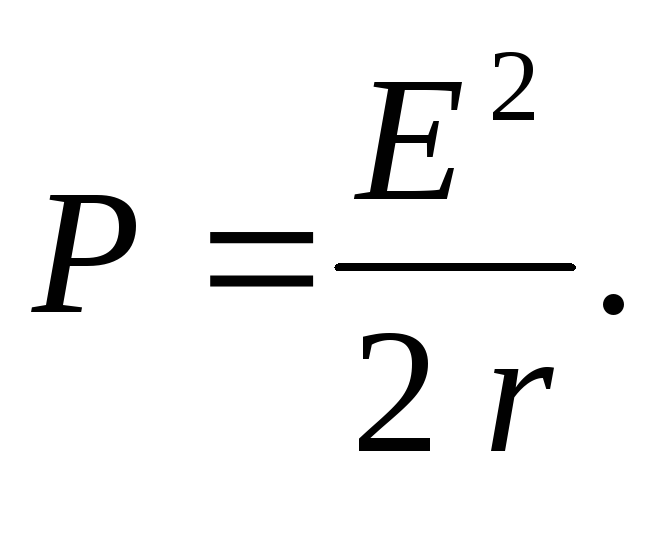
Вычислим 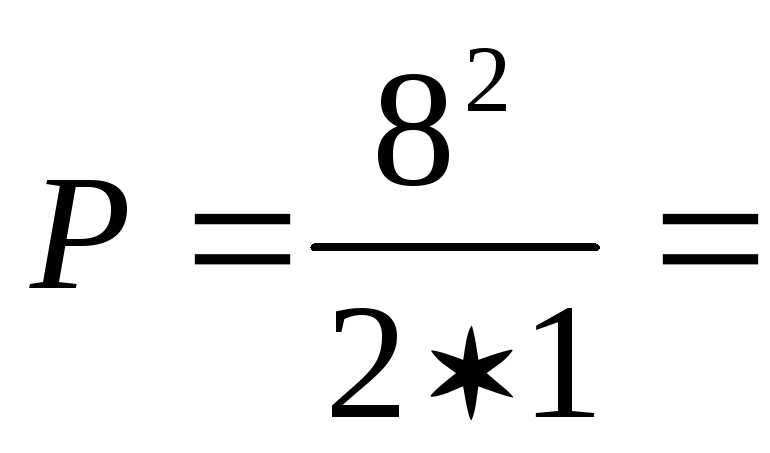 32
Вт;
32
Вт;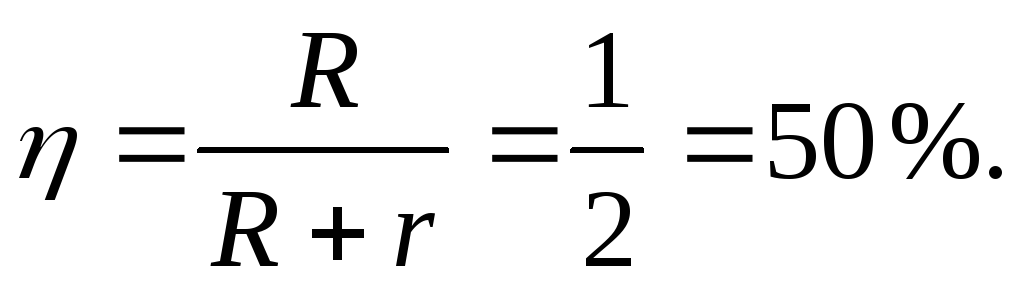
Ответ: Р = 32 Вт; = 50 %.
Задача 9*. Ток в проводнике сопротивлением R = 12 Ом равномерно убывает от I0 = 5 А до нуля в течение времени = 10 с. Какое количество теплоты выделяется в проводнике за это время?
Дано:
R = 12 Ом
I0 = 5 А
I = 0
= 10 с
Q — ?
 Решение
РешениеТак как сила тока в проводнике изменяется, то для подсчёта количества теплоты формулой Q = I 2R t воспользоваться нельзя.
Возьмём
дифференциал dQ = I 2R dt,
тогда  В силу равномерности изменения тока
можно записатьI = k t,
где k – коэффициент пропорциональности.
В силу равномерности изменения тока
можно записатьI = k t,
где k – коэффициент пропорциональности.
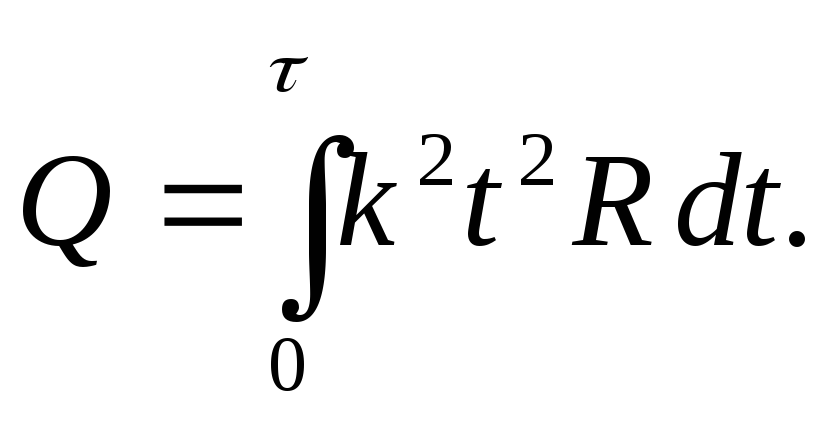
Значение
коэффициента пропорциональности k найдём из условия, что при = 10 с ток I0 = 5 А, I0 = k,
отсюда 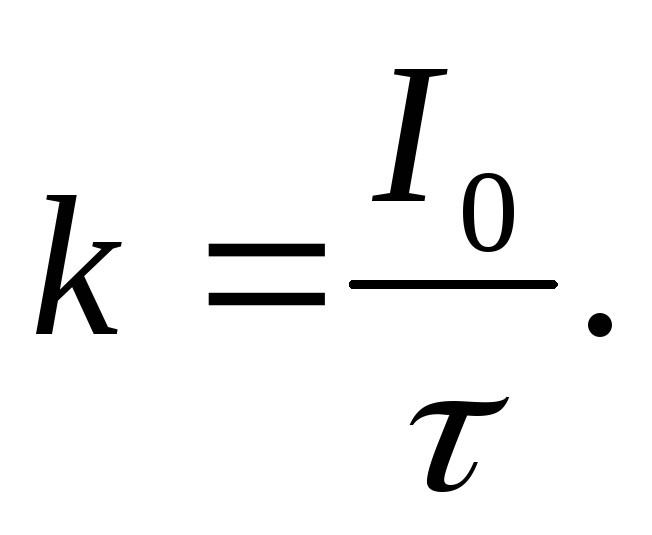
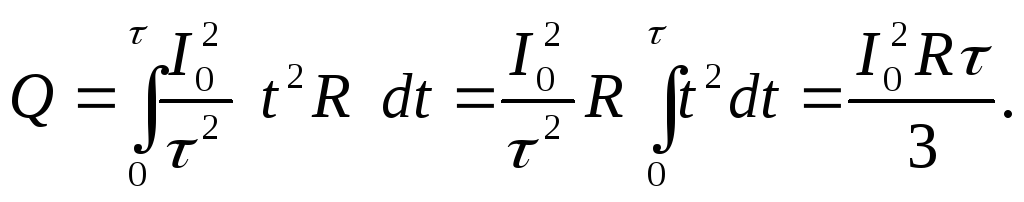
Подставим числовые значения:
Дж.
Ответ: Q = 1000 Дж.
Исследование зависимости мощности и КПД источника тока от внешней нагрузки
ЗАКОН ОМА ДЛЯ ПОЛНОЙ ЦЕПИ:
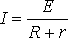 , (1)
, (1)
I- сила тока в цепи; Е- электродвижущая сила источника тока, включённого в цепь; R- сопротивление внешней цепи; r- внутреннее сопротивление источника тока.
МОЩНОСТЬ, ВЫДЕЛЯЕМАЯ ВО ВНЕШНЕЙ ЦЕПИ
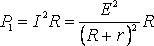 . (2)
. (2)
Из формулы (2) видно, что при коротком замыкании цепи (R®0) и при R®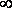 эта мощность равна нулю. При всех других конечных значениях R мощность Р1> 0. Следовательно, функция Р1 имеет максимум. Значение R0, соответствующее максимальной мощности, можно получить, дифференцируя Р1 по R и приравнивая первую производную к нулю:
эта мощность равна нулю. При всех других конечных значениях R мощность Р1> 0. Следовательно, функция Р1 имеет максимум. Значение R0, соответствующее максимальной мощности, можно получить, дифференцируя Р1 по R и приравнивая первую производную к нулю:
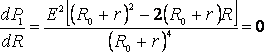 . (3)
. (3)
Из формулы (3), с учётом того, что R и r всегда положительны, а Е ? 0, после несложных алгебраических преобразований получим:
R0 = r. (4)
Следовательно, мощность, выделяемая во внешней цепи, достигает наибольшего значения при сопротивлении внешней цепи равном внутреннему сопротивлению источника тока.
При этом сила тока в цепи 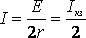 (5)
(5)
равна половине тока короткого замыкания. При этом мощность, выделяемая во внешней цепи, достигает своего максимального значения, равного
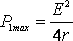 . (6)
. (6)
Когда источник замкнут на внешнее сопротивление, то ток протекает и внутри источника и при этом на внутреннем сопротивлении источника выделяется некоторое количество тепла. Мощность, затрачиваемая на выделение этого тепла равна
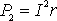 .
.  (7)
(7)
Следовательно, полная мощность, выделяемая во всей цепи , определится формулой
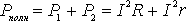 = I2(R+r) = IE (8)
= I2(R+r) = IE (8)
КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ
КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ источника тока равен 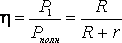 . (9)
. (9)
Из формулы (8) следует, что
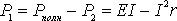 , (10)
, (10)
т.е. Р1 изменяется с изменением силы тока в цепи по параболическому закону и принимает нулевые значения при I = 0 и при 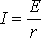 . Первое значение соответствует разомкнутой цепи ( R>> r ), второе – короткому замыканию ( R<< r). Зависимость к.п.д. от силы тока в цепи с учётом формул (8), (9), (10) примет вид
. Первое значение соответствует разомкнутой цепи ( R>> r ), второе – короткому замыканию ( R<< r). Зависимость к.п.д. от силы тока в цепи с учётом формул (8), (9), (10) примет вид
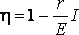 (11)
(11)
Таким образом, к.п.д. достигает наибольшего значения h =1 в случае разомкнутой цепи ( I = 0), а затем уменьшается по линейному закону, обращаясь в нуль при коротком замыкании.
Зависимость мощностей Р1, Рполн = EI и к.п.д. источника тока от силы тока в цепи показаны на рис.1.


Рис.1. I0 E/r
Из графиков видно, что получить одновременно полезную мощность и к.п.д. невозможно. Когда мощность, выделяемая на внешнем участке цепи Р1, достигает наибольшего значения, к.п.д. в этот момент равен 50%.
МЕТОДИКА И ПОРЯДОК ИЗМЕРЕНИЙ

Рис. 2.
Соберите на экране цепь, показанную на рис. 2. Для этого сначала щелкните левой кнопкой мыши над кнопкой  э.д.с. в нижней части экрана. Переместите маркер мыши на рабочую часть экрана, где расположены точки. Щелкните левой кнопкой мыши в рабочей части экрана, где будет расположен источник э.д.с.
э.д.с. в нижней части экрана. Переместите маркер мыши на рабочую часть экрана, где расположены точки. Щелкните левой кнопкой мыши в рабочей части экрана, где будет расположен источник э.д.с.
Разместите далее последовательно с источником резистор, изображающий его внутреннее сопротивление (нажав предварительно кнопку  в нижней части экрана) и амперметр (кнопка
в нижней части экрана) и амперметр (кнопка  там же). Затем расположите аналогичным образом резисторы нагрузки и вольтметр
там же). Затем расположите аналогичным образом резисторы нагрузки и вольтметр  , измеряющий напряжение на нагрузке.
, измеряющий напряжение на нагрузке.
Подключите соединительные провода. Для этого нажмите кнопку провода  внизу экрана, после чего переместите маркер мыши в рабочую зону схемы. Щелкайте левой кнопкой мыши в местах рабочей зоны экрана, где должны находиться соединительные провода.
внизу экрана, после чего переместите маркер мыши в рабочую зону схемы. Щелкайте левой кнопкой мыши в местах рабочей зоны экрана, где должны находиться соединительные провода.
4. Установите значения параметров для каждого элемента. Для этого щелкните левой кнопкой мыши на кнопке со стрелкой  . Затем щелкните на данном элементе. Подведите маркер мыши к движку появившегося регулятора, нажмите на левую кнопку мыши и, удерживая ее в нажатом состоянии, меняйте величину параметра и установите числовое значение, обозначенное в таблице 1 для вашего варианта.
. Затем щелкните на данном элементе. Подведите маркер мыши к движку появившегося регулятора, нажмите на левую кнопку мыши и, удерживая ее в нажатом состоянии, меняйте величину параметра и установите числовое значение, обозначенное в таблице 1 для вашего варианта.
Таблица 1. Исходные параметры электрической цепи
|
Номер варианта |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
Е, В |
10,0 |
9,5 |
9,0 |
8,5 |
8,0 |
8,5 |
9,0 |
9,5 |
|
r, Ом |
4,8 |
5,7 |
6,6 |
7,5 |
6,4 |
7,3 |
8,2 |
9,1 |
5. Установите сопротивление внешней цепи 2 Ом, нажмите кнопку «Счёт» и запишите показания электроизмерительных приборов в соответствующие строки таблицы 2.
6. Последовательно увеличивайте с помощью движка регулятора сопротивление внешней цепи на 0,5 Ом от 2 Ом до 20 Ом и, нажимая кнопку «Счёт», записывайте показания электроизмерительных приборов в таблицу 2.
7. Вычислите по формулам (2), (7), (8), (9) Р1, Р2, Рполн и h для каждой пары показаний вольтметра и амперметра и запишите рассчитанные значения в табл.2.
8. Постройте на одном листе миллиметровой бумаге графики зависимости P1 = f(R), P2 = f(R), Pполн=f(R), h = f (R) и U = f(R).
9. Рассчитайте погрешности измерений и сделайте выводы по результатам проведённых опытов.
Таблица 2. Результаты измерений и расчётов
|
R, Ом |
2,0 |
2,5 |
3,0 |
… |
20 |
||
|
U, В |
|||||||
|
I, А |
|||||||
|
P1, Вт |
|||||||
|
P2, ВТ |
|||||||
|
Pполн, ВТ |
|||||||
|
h |
Вопросы и задания для самоконтроля
- Запишите закон Джоуля-Ленца в интегральной и дифференциальной формах.
- Что такое ток короткого замыкания?
- Что такое полная мощность?
- Как вычисляется к.п.д. источника тока?
- Докажите, что наибольшая полезная мощность выделяется при равенстве внешнего и внутреннего сопротивлений цепи.
- Верно ли утверждение, что мощность, выделяемая во внутренней части цепи, постоянна для данного источника?
- К зажимам батарейки карманного фонаря присоединили вольтметр, который показал 3,5 В.
- Затем вольтметр отсоединили и на его место подключили лампу, на цоколе которой было написано: Р=30 Вт, U=3,5 В. Лампа не горела.
- Объясните явление.
- При поочерёдном замыкании аккумулятора на сопротивления R1 и R2 в них за одно и то же время выделилось равное количество тепла. Определите внутреннее сопротивление аккумулятора.
расчёт(формулы) и от чего зависит
КПД – коэффициент полезного действия, одна из важнейших характеристик, определяющая эффективность работы устройства, относящее к трансформаторам. Рассмотрим особенности определения указанного показателя трансформатора с учётом принципа работы, конструкции данного электрооборудования и факторов, влияющих на эффективность эксплуатации.
Общие сведения о трансформаторах
Трансформатором называют электромагнитное устройство, преобразующим переменный ток с изменением значения напряжения. Принцип работы прибора предполагает использование электромагнитной индукции.
Аппарат состоит из следующих основных элементов:
- первичной и вторичной обмоток;
- сердечника, вокруг которого навиты обмотки.
 Принцип работы трансформатора
Принцип работы трансформатораИзменение характеристик достигается за счёт разного количества витков в обмотках на входе и выходе.
Ток на выходной катушке возбуждается за счёт создания магнитного потока при подаче напряжения на входные контакты.
Что такое КПД трансформатора и от чего зависит
Коэффициентом полезного действия (полная расшифровка данной аббревиатуры) называют отношение полезной электроэнергии к поданной на прибор.
Кроме энергии, показатель КПД может определяться расчётом по мощностным показателям при соотношении полезной величины к общей. Эта характеристика очень важна при выборе аппарата и определяет эффективность его использования.
Величина КПД зависит от потерь энергии, которые допускаются в процессе работы аппарата. Эти потери существуют следующего типа:
- электрического – в проводниках катушек;
- магнитного – в материале сердечника.

Величина указанных потерь при проектировании устройства зависит от следующих факторов:
- габаритных размеров устройства и формы магнитной системы;
- компактности катушек;
- плотности составленных комплектов пластин в сердечнике;
- диаметра провода в катушках.
Снижение потерь в агрегате достигается в процессе проектирования устройства, с применением для изготовления сердечника магнито-мягких ферромагнитных материалов. Электротехническая сталь набирается в тонкие пластины, изолированные друг относительно друга специальным слоем нанесённого лака.
В процессе эксплуатации эффективность аппарата определяется:
- поданной нагрузкой;
- диэлектрической средой – веществом, использованным в качестве диэлектрика;
- равномерностью подачи нагрузки;
- температурой масла в агрегате;
- степенью нагрева катушек и сердечника.
Если в ходе работы агрегат постоянно недогружать или нарушать паспортные условия эксплуатации, помимо опасности выхода из строя это ведёт к снижению эффективности устройства.
Трансформатор, в отличие от электрических машин, практически не допускает механических потерь энергии, поскольку не включает движущихся узлов. Незначительный расход энергии возникает за счёт температурного нагрева устройства.
Методы определения КПД
КПД трансформатора можно подсчитать, с использованием нескольких методов. Данная величина зависит от суммарной мощности устройства, возрастая с увеличением указанного показателя. Значение эффективности колеблется в пределах от 0,8 до 0,92 при значении мощности от 10 до 300 кВт.
Зная величину предельной мощности, можно определить значение КПД, используя специальные таблицы.
Непосредственное измерение
Формула для вычисления данного показателя может быть представлена в нескольких выражениях:
ɳ = (Р2/Р1)х100% = (Р1 – ΔР)/Р1х100% = 1 – ΔР/Р1х100%,
в которой:
- ɳ – значение КПД;
- Р2 и Р1 – соответственно величина полезной и потребляемой сетевой мощности;
- ΔР – величина суммарных мощностных потерь.
Из указанной формулы видно, что значение показателя КПД не может превышать единицу.
После поэтапного преобразования приведённой формулы с учётом использования значений электротока, напряжения и угла между фазами, получается такое соотношение:
ɳ = U2хI2хcosφ2/ U2хI2хcosφ2 + Робм + Рс,
в которой:
- U2 и I2 – соответственно, значение напряжения и тока во вторичной обмотке;
- Робм и Рс – величина потерь в обмотках и сердечнике.
Представленная формула содержится в ГОСТе, описывающем определение данного показателя.
 Расчёты КПД
Расчёты КПДОпределение косвенным методом
Для приборов, обладающих большой эффективностью работы, при величине КПД, превышающем 0,96, точный расчёт не всегда оказывается возможным. Поэтому данное значение определяется при помощи косвенного метода, предполагающего оценку мощностных показателей в первичной катушке, вторичной и допущенных потерь.

Оценивая характеристики трансформатора, следует отметить высокую эффективность использования указанного оборудования, обусловленную его конструктивными особенностями.
Более подробно про КПД трансформатора можете прочитать здесь(откроется в новой вкладе, читать со страницы 14):Открыть файл



