Расчет сечения провода по мощности и по плотности тока: формулы и примеры
Грамотный подбор кабеля для восстановления или прокладки электропроводки гарантирует безупречную работу системы. Приборы будут получать питание в полноценном объеме. Не случится перегрева изоляции с последующими разрушительными последствиями. Разумный расчет сечения провода по мощности избавит и от угроз воспламенения, и от лишних затрат на покупку недешевого провода. Давайте разберемся в алгоритме расчетов.
Упрощенно кабель можно сравнить с трубопроводом, транспортирующим газ или воду. Точно так же по его жиле перемещается поток, параметры которого ограничены размером данного токоведущего канала. Следствием неверного подбора его сечения являются два распространенных ошибочных варианта:
- Слишком узкий токоведущий канал, из-за которого в разы возрастает плотность тока. Рост плотности тока влечет за собой перегрев изоляции, затем ее оплавление. В результате оплавления по минимуму появятся «слабые» места для регулярных утечек, по максимуму пожар.
- Излишне широкая жила, что, в сущности, совсем неплохо. Причем, наличие простора для транспортировки электро-потока весьма положительно отражается на функционале и эксплуатационных сроках проводки. Однако карман владельца облегчится на сумму, примерно вдвое превышающую по факту требующиеся деньги.
Первый из ошибочных вариантов представляет собой откровенную опасность, в лучшем случае повлечет увеличение оплаты за электроэнергию. Второй вариант не опасен, но крайне нежелателен.


«Протоптанные» пути вычислений
Все существующие расчетные способы опираются на выведенный Омом закон, согласно которому сила тока, помноженная на напряжение, равняется мощности. Бытовое напряжение – величина постоянная, равная в однофазной сети стандартным 220 В. Значит, в легендарной формуле остаются лишь две переменные: это ток с мощностью. «Плясать» в расчетах можно и нужно от одной из них. Через расчетные значения тока и предполагаемой нагрузки в таблицах ПУЭ найдем требующийся размер сечения.
Обратите внимание, что сечение кабеля рассчитывают для силовых линий, т.е. для проводов к розеткам. Линии освещения априори прокладывают кабелем с традиционной величиной площади сечения 1,5 мм².


Если в обустраиваемом помещении нет мощного диско-прожектора или люстры, требующей питания в 3,3кВт и больше, то увеличивать площадь сечения жилы осветительного кабеля не имеет смысла. А вот розеточный вопрос – дело сугубо индивидуальное, т.к. подключать к одной линии могут такие неравнозначные тандемы, как фен с водонагревателем или электрочайник с микроволновкой.
Тем, кто планирует нагрузить силовую линию электрической варочной поверхностью, бойлером, стиральной машиной и подобной «прожорливой» техникой, желательно распределить всю нагрузку на несколько розеточных групп.


Если технической возможности разбить нагрузку на группы нет, бывалые электрики рекомендуют без затей прокладывать кабель с медной жилой сечением 4-6 мм². Почему с медной токоведущей сердцевиной? Потому что строгим кодексом ПУЭ прокладка кабеля с алюминиевой «начинкой» в жилье и в активно используемых бытовых помещениях запрещена. Сопротивление у электротехнической меди гораздо меньше, тока она пропускает больше и не греется при этом, как алюминий. Алюминиевые провода используются при устройстве наружных воздушных сетей, кое-где они еще остались в старых домах.
Обратите внимание! Площадь сечения и диаметр жилы кабеля – вещи разные. Первая обозначается в квадратных мм, второй просто в мм. Главное не перепутать!
Для поиска табличных значений мощности и допустимой силы тока можно пользоваться обоими показателями. Если в таблице указан размер площади сечения в мм², а нам известен только диаметр в мм, площадь нужно найти по следующей формуле:


Расчет размера сечения по нагрузке
Простейший способ подбора кабеля с нужным размером — расчет сечения провода по суммарной мощности всех подключаемых к линии агрегатов.
Алгоритм расчетных действий следующий:
- для начала определимся с агрегатами, которые предположительно могут использоваться нами одновременно. Например, в период работы бойлера нам вдруг захочется включить кофемолку, фен и стиралку;
- затем согласно данным техпаспортов или согласно приблизительным сведениям из приведенной ниже таблицы банально суммируем мощность одновременно работающих по нашим планам бытовых агрегатов;
- предположим, что в сумме у нас вышло 9,2 кВт, но конкретно этого значения в таблицах ПУЭ нет. Значит, придется округлить в безопасную большую сторону – т.е. взять ближайшее значение с некоторым превышением мощности. Это будет 10,1 кВт и соответствующее ему значение сечения 6 мм².
Все округления «направляем» в сторону увеличения. В принципе суммировать можно и силу тока, указанную в техпаспортах. Расчеты и округления по току производятся аналогичным образом.




Как рассчитать сечение по току?
Табличные значения не могут учесть индивидуальных особенностей устройства и эксплуатации сети. Специфика у таблиц среднестатистическая. Не приведены в них параметры максимально допустимых для конкретного кабеля токов, а ведь они отличаются у продукции с разными марками. Весьма поверхностно затронут в таблицах тип прокладки. Дотошным мастерам, отвергающим легкий путь поиска по таблицам, лучше воспользоваться способом расчета размера сечения провода по току. Точнее по его плотности.
Допустимая и рабочая плотность тока
Начнем с освоения азов: запомним на практике выведенный интервал 6 — 10. Это значения, полученные электриками многолетним «опытным путем». В указанных пределах варьирует сила тока, протекающего по 1 мм² медной жилы. Т.е. кабель с медной сердцевиной сечением 1 мм² без перегрева и оплавления изоляции предоставляет возможность току от 6 до 10 А спокойно достигать ожидающего его агрегата-потребителя. Разберемся, откуда взялась и что означает обозначенная интервальная вилка.
Согласно кодексу электрических законов ПУЭ 40% отводится кабелю на неопасный для его оболочки перегрев, значит:
- 6 А, распределенные на 1 мм² токоведущей сердцевины, являются нормальной рабочей плотностью тока. В данных условиях проводник работать может бесконечно долго без каких-либо ограничений по времени;
- 10 А, распределенные на 1 мм² медной жилы, протекать по проводнику могут краткосрочно. Например, при включении прибора.
Потоку энергии 12 А в медном миллиметровом канале будет изначально «тесно». От тесноты и толкучки электронов увеличится плотность тока. Следом повысится температура медной составляющей, что неизменно отразиться на состоянии изоляционной оболочки.


Обратите внимание, что для кабеля с алюминиевой токоведущей жилой плотность тока отображает интервал 4 – 6 Ампер, приходящийся на 1 мм² проводника.
Выяснили, что предельная величина плотности тока для проводника из электротехнической меди 10 А на площадь сечения 1 мм², а нормальные 6 А. Следовательно:
- кабель с жилой сечением 2,5 мм² сможет транспортировать ток в 25 А всего лишь несколько десятых секунды во время включения техники;
- он же бесконечно долго сможет передавать ток в 15А.
Приведенные выше значения плотности тока действительны для открытой проводки. Если кабель прокладывается в стене, в металлической гильзе или в пластиковом кабель канале, указанную величину плотности тока нужно помножить на поправочный коэффициент 0,8. Запомните и еще одну тонкость в организации открытого типа проводки. Из соображений механической прочности кабель с сечением меньше 4 мм² в открытых схемах не используют.


Изучение схемы расчета
Суперсложных вычислений снова не будет, расчет провода по предстоящей нагрузке предельно прост.
- Сначала найдем предельно допустимую нагрузку. Для этого суммируем мощность приборов, которые предполагаем одновременно подключать к линии. Сложим, например, мощность стиральной машины 2000 Вт, фена 1000 Вт и произвольно какого-либо обогревателя 1500 Вт. Получили мы 4500 Вт или 4,5 кВт.
- Затем делим наш результат на стандартную величину напряжения бытовой сети 220 В. Мы получили 20,45…А, округляем до целого числа, как положено, в большую сторону.
- Далее вводим поправочный коэффициент, если в нем есть необходимость. Значение с коэффициентом будет равно 16,8, округленно 17 А, без коэффициента 21 А.
- Вспоминаем о том, что рассчитывали рабочие параметры мощности, а нужно еще учесть предельно допустимое значение. Для этого вычисленную нами силу тока умножаем на 1,4, ведь поправка на тепловое воздействие 40%. Получили: 23,8 А и 29,4 А соответственно.
- Значит, в нашем примере для безопасной работы открытой проводки потребуется кабель с сечением более 3 мм², а для скрытого варианта 2,5 мм².
Не забудем о том, что в силу разнообразных обстоятельств порой включаем одновременно больше агрегатов, чем рассчитывали. Что есть еще лампочки и прочие приборы, незначительно потребляющие энергию. Запасемся некоторым резервом сечения на случай увеличения парка бытовой техники и с расчетами отправимся за важной покупкой.
Видео-руководство для точных расчетов
Какой кабель лучше купить?
Следуя жестким рекомендациям ПУЭ, покупать для обустройства личной собственности будем кабельную продукцию с «литерными группами» NYM и ВВГ в маркировке. Именно они не вызывают нареканий и придирок со стороны электриков и пожарников. Вариант NYM – аналог отечественных изделий ВВГ.


Лучше всего, если отечественный кабель будет сопровождать индекс НГ, это означает, что проводка будет пожароустойчивой. Если предполагается прокладывать линию за перегородкой, между лагами или над подвесным потолком, купите изделия с низким дымовыделением. У них будет индекс LS.


Вот таким нехитрым способом рассчитывается сечение токопроводящей жилы кабеля. Сведения о принципах вычислений помогут рационально подобрать данный важный элемент электросети. Необходимый и достаточный размер токоведущей сердцевины обеспечит питанием домашнюю технику и не станет причиной возгорания проводки.
4. Дайте определение плотности тока. В каких единицах измеряется плотность тока? Как направлен вектор плотности тока?
Плотность тока j- векторная физическая величина , модуль которой определяется отношением силы тока I в проводнике и площади S поперечного сечения проводника:
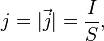
В СИ единицей плотности тока является [A/м2]
Направление вектора плотности тока совпадает с направлением вектора скорости упорядоченного движения положительно заряженных частиц:
I = ∆ q / ∆ t ; (∆ q=q0nS∆l; ∆ t = ∆ l /V)
I
= nvSq0,
где:
n — концентрация;
q0 — единичный заряд ;
v — средняя скорость
упорядоченного движения частиц;
S —
площадь поперечного сечения проводника,
через который течет ток,
То плотность
тока j
= I/ S = nv Sq
5. Запишите закон Ома в дифференциальной форме и поясните все величины.
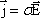 дифференциальная
форма закона Ома.
дифференциальная
форма закона Ома.
где:
 —вектор
плотности
тока,
—вектор
плотности
тока, —удельная
проводимость,
—удельная
проводимость, —вектор
напряжённости
электрического
поля.
—вектор
напряжённости
электрического
поля.

Вычислим
R
через 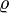 —
удельное сопротивление материала :
—
удельное сопротивление материала :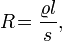
I=U/R=US/l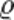 следует
что
U= Il
следует
что
U= Il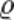 /S
/S
E=U/l=Il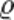 /Sl=(I/S )*
/Sl=(I/S )*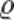 следует
I/S=E/
следует
I/S=E/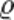
1/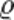 =
=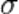 следует что
следует что 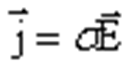
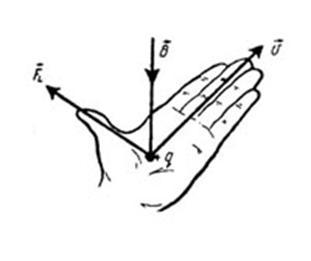
9 вопрос
При движении частицы в магнитном поле сила Лоренца не совершает работу , так как она всегда перпендикулярна скорости . отсюда следует что угол равен 90 градусов и значит cos равен 0
A=FS cos £=0 ( A=qVBsinβ*cos£) (A=F*r- скалярное произведение)
10 вопрос
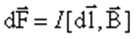
dFA= IdlB sin £
Два прямых противоположно направленных тока будут отталкиваться друг от друга
Предположим , что они оба бесконечной длины
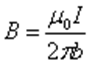
dF21= -I1dl (µ0I2 /2pir)
dF12=I2dl (-µ0I1/ 2 pi r)
dF21=dF12
Сила взаимодействия двух проводников с токами :
F=
µ
µ0— магнитная постоянная; I1I2 – силы токов ; r – расстояние между проводниками
17.
Закон Фарадея [править]
Согласно закону электромагнитной индукции Фарадея (в СИ):
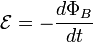
где
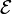 — электродвижущая
сила,
действующая вдоль произвольно выбранного
контура,
— электродвижущая
сила,
действующая вдоль произвольно выбранного
контура,
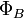
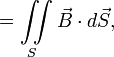 —магнитный
поток через
поверхность, натянутую на этот контур.
—магнитный
поток через
поверхность, натянутую на этот контур.Знак «минус» в формуле отражает правило Ленца, названное так по имени русского физика Э. Х. Ленца:
Индукционный ток, возникающий в замкнутом проводящем контуре, имеет такое направление, что создаваемое им магнитное поле противодействует тому изменению магнитного потока, которым был вызван данный ток.
Для катушки, находящейся в переменном магнитном поле, закон Фарадея можно записать следующим образом:
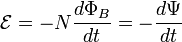
где
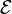
 —
число
витков,
—
число
витков,
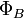 —
магнитный
поток через один виток,
—
магнитный
поток через один виток,
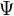 — потокосцепление катушки.
— потокосцепление катушки.
Следует отметить, что закон Фарадея в такой форме, очевидно, описывает лишь ту часть ЭДС, что возникает при изменении магнитного потока через контур за счёт изменения со временем самого поля без изменения (движения) границ контура (об учете последнего см. ниже).
Если
же, скажем, магнитное поле постоянно, а
магнитный поток изменяется вследствие
движения границ контура (например, при
увеличении его площади), то возникающая
ЭДС порождается силами, удерживающими
заряды на контуре (в проводнике) и силой
Лоренца,
порождаемой прямым действием магнитного
поля на движущиеся (с контуром) заряды.
При этом равенство 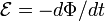 продолжает
соблюдаться, но ЭДС в левой части теперь
не сводится к
продолжает
соблюдаться, но ЭДС в левой части теперь
не сводится к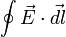 (которое
в данном частном примере вообще равно
нулю). В общем случае (когда и магнитное
поле меняется со временем, и контур
движется или меняет форму) последняя
формула верна так же, но ЭДС в левой
части в таком случае есть сумма обоих
слагаемых, упомянутых выше (то есть
порождается частично вихревым
электрическим полем, а частично силой
Лоренца и силой реакции движущегося
проводника).
(которое
в данном частном примере вообще равно
нулю). В общем случае (когда и магнитное
поле меняется со временем, и контур
движется или меняет форму) последняя
формула верна так же, но ЭДС в левой
части в таком случае есть сумма обоих
слагаемых, упомянутых выше (то есть
порождается частично вихревым
электрическим полем, а частично силой
Лоренца и силой реакции движущегося
проводника).
16.
Индукцио́нный ток — электрический ток, возникающий в замкнутом проводящем контуре при изменении потока магнитной индукции, пронизывающего этот контур. Величина и направление индукционного тока определяются законом электромагнитной индукции и правилом Ленца.
Магни́тный пото́к
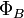 как
интегралвектора магнитной
индукции
как
интегралвектора магнитной
индукции  через
конечнуюповерхность
через
конечнуюповерхность  .
Определяется через интеграл по поверхности
.
Определяется через интеграл по поверхности 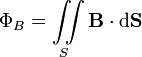
при этом векторный элемент площади поверхности определяется как
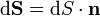
где 
Также магнитный поток можно рассчитать как скалярное произведение вектора магнитной индукции на вектор площади:
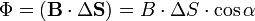
где α — угол между вектором магнитной индукции и нормалью к плоскости площади.
Магнитный поток через контур также можно выразить через циркуляцию векторного потенциала магнитного поля по этому контуру:
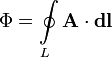
Электрический ток, сила, плотность, условия существования. Источник тока. Курсы по физике
Тестирование онлайн
Электрический ток. Основные понятия
Сила, плотность тока
Условия существования тока
Электрический ток — направленное движение заряженных частиц. Направление, в котором движутся положительно заряженные частицы, считается
В металлах единственными носителями тока являются электроны. Направление тока противоположно направлению движения электронов.
Для существования тока необходимо:
1) наличие свободных заряженных частиц;
2) существование внешнего электрического поля;
3) наличие источника тока — источника сторонних сил.
Характеристики тока
Сила тока — скалярная величина, определяется по формуле
Если ток изменяется, то заряд, прошедший через поперечное сечение проводника, определяется как площадь фигуры, ограниченной зависимостью I(t).
Плотность тока — векторная величина, определяется по формуле
Прибор для измерения силы тока называется амперметром. Включается в сеть последовательно. Собственное сопротивление амперметра должно быть мало, поскольку включение амперметра не должно изменять силу тока в цепи.
В быту «источником тока» часто неточно называют любой источник электрического напряжения (батарею, генератор, розетку), но в строго физическом смысле это не так, более того, обычно используемые в быту источники напряжения по своим характеристикам гораздо ближе к источнику ЭДС, чем к источнику тока.
Примерами источника тока могут являться катушка индуктивности, вторичная обмотка трансформатора. Внутреннее сопротивление источника тока стремится к нулю.
Под действием электрического поля, созданного источником тока, свободные заряды движутся в веществе с некоторой средней скоростью — скорость дрейфа.
Сила и плотность тока. Линии тока
Электрический ток количественно характеризует сила тока (I), которая равна производной от заряда ($q$) по времени для тока, который течет через поверхность S:
По своей сути сила тока — это поток заряда через поверхность S.
Перенос отрицательного заряда в одном направлении эквивалентен переносу такого же положительного заряда в противоположном направлении. В том случае, если ток создается зарядами обоих знаков $(dq^+\ и\ dq^-)$, то можно записать, что сила тока равна:
\[I=\frac{dq^+}{dt}+\frac{dq^-}{dt}\left(2\right).\]Положительным направлением тока считают направление движения положительных зарядов. Ток может быть постоянным и переменным. В том случае, если сила тока и его направление не изменяется во времени, то такой ток называют постоянным и для него выражение для силы тока можно записать в виде:
\[I=\frac{q}{\triangle t}\left(3\right),\]где сила тока определена, как заряд, который проходит через поверхность S в единицу времени. В системе СИ основной единицей измерения силы тока является Ампер (А).
\[1A=\frac{1Кл}{1с}.\]Плотность тока. Связь плотности тока с зарядом и силой тока, напряженностью
Выделим в проводнике, по которому течет ток, малый объем dV произвольной формы. Обозначим через $\left\langle v\right\rangle $— среднюю скорость, с которой движутся носители заряда в проводнике. пусть $n_0\ $— концентрация носителей заряда. Выберем бесконечно малую площадку dS на поверхности проводника, которая перпендикулярно скорости $\left\langle v\right\rangle $ (рис.1).

Рис. 1
Построим на площадке dS очень короткий прямой цилиндр с высотой $\left\langle v\right\rangle dt.$ Все частицы, которые находились внутри этого цилиндра за время dt пройдут через площадку dS и перенесут через нее в направлении скорости $\left\langle v\right\rangle \ $заряд равный:
\[dq=n_0q_e\left\langle v\right\rangle dSdt\left(4\right),\]где $q_e=1,6\cdot {10}^{-19}Кл$ — заряд электрона, то есть отдельной частицы — носителя тока. Разделим выражение (4) на $dSdt$ получим:
\[j=\frac{dq}{dSdt}\left(5\right),\]где $j$ — модуль плотности электрического тока.
\[j=n_0q_e\left\langle v\right\rangle \left(6\right),\]где $j$ — модуль плотности электрического тока в проводнике, где заряд переносят электроны.
Если ток образуется в результате движения нескольких типов зарядов, то плотность тока можно определить как:
\[j=\sum\limits_i{n_iq_i\left\langle v_i\right\rangle \left(7\right)},\]где i — определяет носитель заряда.
Плотность тока — векторная величина. Обратимся вновь к рис.1. Пусть $\overrightarrow{n}$ — единичная нормаль к площадке dS. Если частицы, которые переносят заряд положительные, то переносимый ими заряд в направлении нормали больше нуля. В общем случае элементарный заряд, который переносится в единицу времени, можно записать как:
\[\frac{dq}{dt}=\left(\overrightarrow{j}\overrightarrow{n}\right)dS=j_ndS\ \left(8\right).\]Формула (8) справедлива и в том случае, когда площадка dS неперпендикулярная вектору плотности тока. Так как составляющая вектора $\overrightarrow{j}$, перпендикулярная нормали, через площадку dS электричества не переносит. Таким образом, плотность тока в проводнике окончательно запишем, используя формулу (6) следующим образом:
\[\overrightarrow{j}=-n_0q_e\left\langle \overrightarrow{v}\right\rangle \left(9\right).\]И так, плотность тока равна количеству электричества (заряду), который протекает за одну секунду через единицу сечения проводника. Для однородного цилиндрического проводника можно записать, что:
\[j=\frac{I}{S\triangle t}\left(10\right),\]где S — площадь сечения проводника.
Плотность постоянного тока одинакова по всему сечению проводника. Для двух разных сечений проводника ($S_1{,S}_2$) с постоянным током выполняется равенство:
\[\frac{j_1}{j_2}=\frac{S_2}{S_1}\left(11\right).\]Из закона Ома для плотности токов можно записать:
\[\overrightarrow{j}=\lambda \overrightarrow{E}\left(13\right),\]где $\lambda $ — коэффициент удельной электропроводности.
Зная плотность тока, можно выразить силу тока как:
\[I=\int\limits_S{j_ndS\ \left(14\right),}\]где интегрирование проводят по всей поверхности S любого сечения проводника.
Единица плотности тока $\frac{A}{м^2}$.
Линии тока
Направлениями линий тока являются направления движения положительных зарядов. Нарисовав линии тока, получают наглядное представление о движении электронов и ионов, которые образуют ток. Если внутри проводника выделить трубку с током, у которой боковая поверхность состоит из линий тока, то движущиеся заряженные частицы не будут пересекать боковую поверхность такой трубки. Подобную трубку называют трубкой тока. Например, поверхность металлической проволоки в изоляторе будет являться трубой тока.
Пример 2
Задание: Найдите среднюю скорость движения электронов в проводнике молярная масса вещества, которого равна $\mu $, поперечное сечение проводника S. Сила тока в проводнике I. Считать, что на каждый атом вещества в проводнике приходится два свободных электрона.
Решение:
Силу тока (I) в проводнике можно считать постоянной и соответственно записать, что:
\[I=\frac{q}{\triangle t}=\frac{Nq_e}{\triangle t}\left(2.1\right),\]где заряд q найдем как произведение числа электронов проводимости в проводнике, на заряд одного электрона $q_e$, который является известной величиной. $\triangle t$ — промежуток времени за который через поперечное сечение проводника проходит заряд q.
Найти N можно, если использовать известное соотношение из молекулярной физики:
\[\frac{N’}{N_A\ }=\frac{m}{\mu }=\frac{\rho V}{\mu }\left(2.2\right),\]где $N’$- количество атомов в проводнике объем, которого V, плотность $\rho $, молярная масса $\mu $. $N_A$ — число Авогадро. По условию задачи $N=2N’$.
Найдем из (2.2) число свободных электронов:
\[N=2\frac{\rho V}{\mu }N_A\ \left(2.3\right).\]Подставим (2.3) в (2.1), получим:
\[I=2\frac{\rho V}{\mu }N_A\frac{q_e}{\triangle t}=\frac{2\rho q_eN_ASl}{\mu \triangle t}\left(2.4\right),\]где объем проводника найден как $V=Sl$, где $l$ — длина проводника. Выразим ее.
\[l=\frac{\mu \triangle tI}{2\rho q_eN_AS}\left(2.5\right).\]Среднюю скорость движения электронов можно найти как:
\[\left\langle v\right\rangle =\frac{l}{\triangle t}=\frac{\mu I}{2\rho q_eN_AS}.\]Ответ: $\left\langle v\right\rangle =\frac{\mu I}{2\rho q_eN_AS}.$
Сила тока и плотность тока в проводнике — КиберПедия
В проводниках часть валентных электронов не связана с определенными атомами и может свободно перемещаться по всему его объему. В отсутствие приложенного к проводнику электрического поля такие свободные электроны — электроны проводимости — движутся хаотично, часто сталкиваясь с ионами и атомами, и изменяя при этом энергию и направление своего движения. Через любое сечение проводника в одну сторону проходит столько же электронов, сколько и в противоположную. Поэтому результирующего переноса электронов через такое сечение нет, и электрический ток равен нулю. Если же к концам проводника приложить разность потенциалов, то под действием сил электрического поля свободные заряды в проводнике начнут двигаться из области большего потенциала в область меньшего — возникнет электрический ток. Исторически сложилось так, что за направление тока принимают направление движение положительных зарядов, которое соответствует их переходу от большего потенциала к меньшему.
Электрический ток характеризуется силой тока I (рис. 4.1).
Сила тока есть скалярная величина, численно равная заряду переносимому через поперечное сечение проводника в единицу времени
|
Рис. 4.1. Сила тока в проводнике
Согласно (4.1), сила тока в проводнике равна отношению заряда , прошедшего через поперечное сечение проводника за время к этому времени.
Замечание: В общем случае сила тока через некоторую поверхность равна потоку заряда через эту поверхность.
Если сила тока с течением времени не изменяется, то есть за любые равные промежутки времени через любое сечение проводника проходят одинаковые заряды, то такой ток называется постоянным, и тогда заряд, протекший за время t, может быть найден как (рис. 4.2)
| (4.2) |
Рис. 4.2. Постоянный ток, протекающий через разные сечения проводника
| Величина , численно равная заряду, проходящему через единицу площади поперечного сечения проводника за единицу времени, называется плотностью тока. |
С учетом определения силы тока плотность тока через данное сечение может быть выражена через силу тока , протекающего через это сечение
| (4.3) |
При равномерном распределении потока зарядов по всей площади сечения проводника плотность тока равна
| (4.4) |
| В СИ единицей измерения силы тока является ампер (А). В СИ эта единица измерения является основной. |
Уравнение (4.1) связывает единицы измерения силы тока и заряда
| В СИ единицей измерения плотности тока является ампер на квадратный метр (А/м2): |
Это очень малая величина, поэтому на практике обычно имеют дело с более крупными единицами, например
Плотность тока можно выразить через объемную плотность зарядов и скорость их движения v (рис. 4.3).
Рис. 4.3. К связи плотности тока j с объемной плотностью зарядов и дрейфовой скоростью v носителей заряда. За время dt через площадку S пройдут все заряды из объема dV = vdt S
Полный заряд, проходящий за время dt через некоторую поверхность S, перпендикулярную вектору скорости v, равен
| (4.5) |
Так как dq/(Sdt) есть модуль плотности тока j, можно записать
| (4.6) |
Поскольку скорость v есть векторная величина, то и плотность тока также удобно считать векторной величиной, следовательно
Здесь плотность заряда, скорость направленного движения носителей заряда.
Замечание: Для общности использован индекс , так как носителями заряда, способными участвовать в создании тока проводимости, могут быть не только электроны, но, например, протоны в пучке, полученном из ускорителя или многозарядные ионы в плазме, или так называемые «дырки» в полупроводниках «р» типа, короче, любые заряженные частицы, способные перемещаться под воздействием внешних силовых полей.
Кроме того, удобно выразить плотность заряда через число носителей заряда в единице объема — (концентрацию носителей заряда) . В итоге получаем:
| (4.7) |
Следует подчеркнуть, что плотность тока, в отличие от силы тока — дифференциальная векторная величина. Зная плотность тока, мы знаем распределение течения заряда по проводнику. Силу тока всегда можно вычислить по его плотности. Соотношение (4.4) может быть «обращено»: если взять бесконечно малый элемент площади , то сила тока через него определится как . Соответственно, силу тока через любую поверхность S можно найти интегрированием
| (4.8) |
Что же понимать под скоростью заряда v, если таких зарядов — множество, и они заведомо не движутся все одинаково? В отсутствие внешнего электрического поля, скорости теплового движения носителей тока распределены хаотично, подчиняясь общим закономерностям статистической физики. Среднее статистическое значение ввиду изотропии распределения по направлениям теплового движения. При наложении поля возникает некоторая дрейфовая скорость — средняя скорость направленного движения носителей заряда:
которая будет отлична от нуля. Проведем аналогию. Когда вода вырывается из шланга, и мы интересуемся, какое ее количество поступает в единицу времени на клумбу, нам надо знать скорость струи и поперечное сечение шланга. И нас совершенно не волнуют скорости отдельных молекул, хотя они и очень велики, намного больше скорости струи воды, как мы убедились в предыдущей части курса.
Таким образом, скорость в выражении (4.7) — это дрейфовая скорость носителей тока в присутствии внешнего электрического поля или любого другого силового поля, обуславливающего направленное (упорядоченное) движение носители заряда. Если в веществе возможно движение зарядов разного знака, то полная плотность тока определяется векторной суммой плотностей потоков заряда каждого знака.
Как уже указывалось, в отсутствие электрического поля движение носителей заряда хаотично и не создает результирующего тока. Если, приложив электрическое поле, сообщить носителям заряда даже малую (по сравнению с их тепловой скоростью) скорость дрейфа, то, из-за наличия в проводниках огромного количества свободных электронов, возникнет значительный ток.
Поскольку дрейфовая скорость носителей тока создается электрическим полем, логично предположить пропорциональность
так что и плотность тока будет пропорциональна вектору напряженности (рис. 4.4)
| (4.9) |
Более подробно этот вопрос обсуждается в Дополнении
Входящий в соотношение (4.9)
| Коэффициент пропорциональности называется проводимостьювещества проводника. |
Проводимость связывает напряженность поля в данной точке с установившейся скоростью «течения» носителей заряда. Поэтому она может зависеть от локальных свойств проводника вблизи этой точки (то есть от строения вещества), но не зависит от формы и размеров проводника в целом. Соотношение (4.9) носит название закона Ома для плотности тока в проводнике (его называют также законом Ома в дифференциальной форме).
Рис. 4.4. Силовые линии электрического поля совпадают с линиями тока
Чтобы понять порядки величин, оценим дрейфовую скорость носителей заряда в одном из наиболее распространенных материалов — меди. Возьмем для примера силу тока I = 1 А, и пусть площадь поперечного сечения провода составляет
1 мм2 = 10–6 м2. Тогда плотность тока равна j = 106 А/м2. Теперь воспользуемся соотношением (4.7)
Носителями зарядов в меди являются электроны (е = 1.6·10-19 Кл), и нам осталось оценить их концентрацию . В таблице Менделеева медь помещается в первой группе элементов, у нее один валентный электрон, который может быть отдан в зону проводимости. Поэтому число свободных электронов примерно совпадает с числом атомов. Берем из справочника плотность меди — r Cu=8,9·103 кг/м3. Молярная масса меди указана в таблице Менделеева — MCu = 63,5·10–3 кг/моль. Отношение
— это число молей в 1 м3. Умножая на число Авогадро Na = 6,02·1023 моль–1, получаем число атомов в единице объема, то есть концентрацию электронов
Теперь получаем искомую оценку дрейфовой скорости электронов
Для сравнения: скорости хаотического теплового движения электронов при 20°С в меди по порядку величины составляют 106 м/с, то есть на одиннадцать порядков величины больше.
Возьмем произвольную воображаемую замкнутую поверхность S, которую в разных направлениях пересекают движущиеся заряды. Мы видели, что полный ток через поверхность равен
где dq — заряд, пересекающий поверхность за время dt. Обозначим через q ‘ заряд, находящийся внутри поверхности. Его можно выразить через плотность заряда , проинтегрированную по всему объему, ограниченному поверхностью
Из фундаментального закона природы — закона сохранения заряда — следует, что заряд dq, вышедший через поверхность за время dt, уменьшит заряд q ‘ внутри поверхности точно на эту же величину, то есть dq ‘ = –dq или
Подставляя сюда написанные выше выражения для скоростей изменения заряда внутри поверхности , получаем математическое соотношение, выражающее закон сохранения заряда в интегральной форме
| (4.10) |
Напомним, что интегрирования ведутся по произвольной поверхности S и ограниченному ею объему V.
Предельный ток печатной дорожки / Habr
Шутки в сторону, тема серьёзная, пожароопасная. Поехали. Это третья статья из цикла, в ней рассмотрены модели оценки предельного тока печатной дорожки, который в некоторых ситуациях является определяющим параметром при выборе толщины проводящих слоёв печатной платы.В предыдущей статье говорилось о том, выбор толщины медных слоёв печатной платы определяется, прежде всего, требуемыми минимальным зазором и минимальной шириной проводника, а также максимальным током, протекающим по проводнику. Эти параметры могут противоречить друг другу: чем тоньше проводящий слой, тем меньший топологический рисунок может быть получен, но тем меньший предельный ток выдержит печатная дорожка (при прочих равных условиях – ширина проводника, частота тока, теплоотвод и др.). Тепловая энергия Q выделяющаяся на омическом сопротивлении R печатной дорожки (джоулево тепло Q=I2Rt, где I – сила тока, t — время), вызывает повышение её температуры относительно окружающей среды, приводя к перегреву самого проводника и связанных с ним компонентов или, в крайнем случае, к его перегоранию при предельном токе (англ. fusing current). Соотношение между током через печатную дорожку и приростом температуры зависит от многих параметров и в общем виде трудно представимо, однако существуют формулы, позволяющие сделать предварительные оценки.
Прис, Ондердонк и Брукс
Одна из первых попыток принадлежит У.Г.Прису (англ. W.H.Preece). Свою эмпирическую зависимость он получил в лабораторном эксперименте, в котором он постепенно увеличивал ток через проводник до момента его накала докрасна. Формула Приса связывает ток накала c диаметром проводника d для различных материалов:
где K – табличная константа, примерно равная 80 для меди. Используя соотношение площади круга, можно переписать эту формулу для случая медного проводника с площадью сечения S:
В эксперименте Приса проводник был подвешен в воздухе, в отличие от проводника на печатной плате, условия теплоотвода для которого совсем другие. Более близкими являются условия теплоотвода для случаев одиночного соединительного проводника, а также для некоторых случаев микропроволочной разварки (когда для её защиты не используется компаундирование), где эта формула может давать хорошую оценку для предельного тока.
Допустимым приростом температуры печатной дорожки обычно считается 10-30 ˚С. Это значение может быть и больше в зависимости от параметров проекта, однако во всём диапазоне рабочих температур изделия температура дорожки должна быть меньше температуры стеклования материала печатной платы (англ. glass transition temperature, Tg) и тем более температуры накала меди. Поэтому полезна зависимость прироста температуры ∆T от тока I печатной дорожки шириной w и толщиной фольги h, приведённая Д.Бруксом в [1]:
где C, α, β, γ – константы, значения которых для внешних и внутренних слоёв приведены в таблице 1. Стоит учитывать, что на внешних слоях толщина фольги обычно больше на 20-40 мкм относительно базового значения в связи с дополнительным напылением при создании переходных отверстий. Также влияние финишного покрытия на платах без маски может быть значительным. Это используют в силовых приборах, когда на вскрытую от маски печатную дорожку паяют дополнительный припой.
Ещё одной известной формулой расчёта предельной токонесущей способности проводника является формула Ондердонка (англ. I.M.Onderdonk), которая содержит такой важный параметр, как время. Она связывает время t пропускания тока I через медный проводник сечением S и прирост температуры ∆T относительно начальной температуры T0:
Так как при выводе формулы [2] исключается всякий теплоотвод, то для случая печатной дорожки эта формула применима для короткого импульса тока длительностью до 1-2 секунд. С увеличением времени и влияния теплоотвода точность оценки падает, в разы занижая предельный ток. Графики зависимостей по всем трём приведённым формулам для различных параметров печатной дорожки приведены на рисунках 1 и 2.
Всегда важно учитывать условия эксперимента или аналитические допущения при выводе, чтобы понимать границы применимости той или иной формулы. Ни одна из приведённых формул не даст точное и оптимальное соотношение между предельным током и требуемым сечением проводника для реальных приложений. Это же касается и простых калькуляторов, которые можно найти в сети Интернет (например), потому что они основаны на этих или аналогичных формулах. Влияние соседних проводников и компонентов как источников и приемников тепла, излучения, активного или пассивного охлаждения может быть учтено только при термоэлектрическом моделировании в специализированных САПР (таких как Cadence, ANSYS и других). Однако даже в этом случае результаты моделирования и эксперимента могут значительно отличаться. Дело в том, что печатная дорожка имеет не прямоугольное сечение, а близкое к трапециевидному (рис. 3), а её ширина и значение проводимости медной фольги могут не только отличаются от расчётных по модели, но и имеют некоторый разброс от образца к образцу, партии к партии, изготовителю к изготовителю и т.д. Влияние отклонений ширины усиливается с её уменьшением. Тем не менее, расчётные результаты по формулам и рекомендации стандартов чаще всего будут представлять наихудший случай, обеспечивая тем самым запас прочности системы. Если разработчику требуется оптимизировать соотношение между предельным током и требуемым сечением печатной дорожки, то к этой цели необходимо идти итеративным путём моделирования и эксперимента.
Скин-эффект
Увеличение сечения печатной дорожки пропорционально снижает её омическое сопротивление на единицу длины, что уменьшает тепловые потери при протекании постоянного тока. Ситуация с переменным током не так проста по причине существования скин-эффекта (англ. skin effect), который приводит к тому, что плотность переменного тока неравномерно распределена по сечению проводника, экспоненциально убывая до нуля от поверхности проводника к центру. Для удобства расчётов применяется понятие эффективного сечения проводника с глубиной, определяемой соотношением:
где f – частота тока, σ – проводимость металла, μ – магнитная проницаемость. На глубине равной δ плотность тока становится меньше в e раз относительно плотности тока на поверхности JS. Математически можно показать верность следующего приближённого равенства для плотности тока J(x,y) в проводнике:
То есть для приближённых вычислений можно принять, что ток течёт только в граничном слое проводника периметра l глубиной δ, причём с равномерным распределением (рис. 4).
В рамках этой упрощённой модели, если глубина поверхностного слоя меньше половины толщины печатной дорожки, то импеданс печатной дорожки на данной частоте будет определяться именно этим эффективным сечением, приводя к увеличению омического сопротивления и незначительному снижению индуктивности. На рис. 5 представлена зависимость глубины поверхностного слоя от частоты тока с учётом разброса проводимости осаждённой меди. Из него видно, что для слоёв меди толщиной 18 мкм граничная частота (выше которой скин-эффект играет роль) находится в районе 50-70 МГц, а для слоёв толщиной 35 мкм – в районе 15-20 МГц. Отметим, что на частотах свыше 100 МГц глубина скин-эффекта меняется незначительно, это позволяет пренебрегать его зависимостью от частоты при расчётах для высокочастотных сигналов.
При проектировании печатных плат с постоянно действующими токами величиной в несколько ампер необходимо выполнять тепловые расчёты как для электрических компонентов, так и для проводников. Представленные модели и аналитические соотношения позволяют выполнить оценку предельного тока печатных дорожек и на её основании выбрать необходимую толщину медных слоёв и топологию проводников. Для получения точного решения необходимо использовать специализированные САПР, при этом желательно задавать геометрию с учётом технологических погрешностей изготовления и данные по проводимости меди, полученные от производителя печатных плат. Очень рекомендую ознакомиться со статьями Д.Брукса, посвящёнными подробному анализу методов оценки температуры печатных проводников, где представлены наглядные результаты моделирования температурных полей.
Литература
[1] Brooks D. G., Adam J. «Trace Currents and Temperatures Revisited», UltraCAD, 2015.
[2] Adam J., Brooks D. G. «In Search For Preece and Onderdonk», UltraCAD, 2015.
Статья была впервые опубликована в журнале «Компоненты и технологии» 2018, №1. Публикация на «Geektimes» согласована с редакцией журнала.




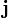 —вектор
плотности
тока,
—вектор
плотности
тока,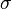 —удельная
проводимость,
—удельная
проводимость,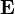 —вектор
напряжённости
электрического
поля.
—вектор
напряжённости
электрического
поля.