Площадь круга | Онлайн калькуляторы, расчеты и формулы на GELEOT.RU

Для того чтобы найти площадь круга, существует единственная формула, которую нужно запомнить – это произведение числа π на квадрат радиуса.
Доказательством этой формулы будет служить следующий расчет. На чертеже внутри и снаружи круга рисуем правильный многоугольник – многоугольник с равными сторонами.

Из центра круга проводим радиусы в указанные вершины многоугольников. Радиусы во вписанном многоугольнике делят его на определенное количество n одинаковых равнобедренных треугольников. Таким образом, площадь вписанного многоугольника – это n площадей треугольников S_в=nS_∆. Тогда как площадь каждого треугольника, исходя из его свойств, равна

. Так как конгруэнтные стороны a этого треугольника являются радиусами, то формула приобретает вид , а формула площади всего многоугольника – , считая сумму всех сторон nc, как периметр многоугольника P. Аналогично получаем площадь описанного многоугольника: . Если считать, что количество nc, как сторон многоугольника стремится к бесконечности, то его форма максимально приближается к кругу, и периметр становится близок по значению к длине окружности, а cosα стремится к 1. В этом случае обе формулы – и для вписанного, и для описанного многоугольника приобретают следующий вид:

---

Поскольку радиус тесно связан отношениями с диаметром и длиной окружности, то путем нехитрых замен можно также вычислить площадь круга через диаметр или длину окружности.
Диаметр – это удвоенный радиус, следовательно, подставляя его в формулу вместо последнего, нужно разделить его обратно на два. Так как в первоначальной формуле S=πr

2 радиус возводится во вторую степень, полученная половина диаметра также должна будет быть в квадрате, и это уже будет выглядеть как .

---

Длина окружности представляет собой удвоенное произведение радиуса и числа π: P=2πr, обратным методом получаем, что радиус равен длине окружности, разделенной на его множитель: . Подставляя это в основную формулу, не забываем возвести выражение во вторую степень, и получаем, что площадь круга через длину окружности равна

.

формула через длину окружности, площадь

В данной публикации мы рассмотрим, как можно вычислить радиус круга (окружности) и разберем примеры решения задач для закрепления материала.

Формулы вычисления радиуса круга

1. Через длину окружности/периметр круга

Радиус круга/окружности рассчитывается по формуле:

C – это длина окружности/периметр круга; равняется удвоенному произведению числа π на его радиус:

C = 2πR

π – число, приближенное значение которого равно 3,14.

2. Через площадь круга

Радиус круга/окружности вычисляется таким образом:

S – это площадь круга; равна числу π, умноженному на квадрат его радиуса:

S = πR²

Примеры задач

Задание 1
Длина окружности равняется 87,92 см. Найдите ее радиус.

Решение:
Используем первую формулу (через периметр):

Задание 2
Найдите радиус круга, если его площадь составляет 254,34 см².

Решение:
Воспользуемся формулой, выраженной через площадь фигуры:

Сопромат.in.ua: Площадь сечения некоторых фигур

Приведены формулы вычисления площади некоторых фигур, которые вы можете вычислить непосредственно на этой странице.

Фигура	Формула вычисления площади	Примечания	Вычислить площадь
Квадрат	$$a^2$$	a длина стороны квадрата.
Равносторонний треугольник	$$\frac{\sqrt{3}}{4}a^2$$	a – длина одной из сторон
Треугольник	$$\sqrt{s(s-a)(s-b)(s-c)}$$	где s = 1/2 (a + b + c), a,b,c – длины сторон треугольника
	$$\frac{1}{2}b\cdot h_b$$	где b – длина стороны треугольника hb – высота, проведённая на сторону b
	$$\frac{1}{2} a b \sin \gamma $$	где a и b – длина сторон треугольника [math]\gamma[/math] – угол между ними в °
Правильный шестиугольник	$$\frac{3\sqrt{3}}{2}s^2$$	s – сторона шестиугольника
Правильный восьмиугольник	$$2\left(1+\sqrt{2}\right)s^2$$	s – сторона восьмиугольника R – радиус описанной окружности $$s={R\over\sqrt{1+{\sqrt{2}/2}}} ≈ {R\over 1.3066}$$
Прямоугольник	$$a\cdot b$$	a и b стороны прямоугольника (длина и ширина)
Параллелограмм	$$b\cdot h$$	b – длина одной из основ параллелограмма h – высота параллелограмма
Трапеция	$$\frac{a+b}{2}\cdot h $$	a и b длины параллельных сторон, а h – высота (расстояние между параллельными сторонами)
Правильный многоугольник (это многоугольник, у которого все углы и все стороны равны между собой)	$$\frac{ns^2} {4 \cdot \tan(\pi/n)} $$	s -длина стороны, а n число сторон.
Круг	$$\pi r^2 \text{   или  } \frac{\pi d^2}{4} $$	r – радиус, а d – диаметр
Эллипс	$$\pi ab $$	a и b – большая и малая полуоси эллипса, соответственно.
Сектор (часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга)	$$\frac{1}{2} r^2 \theta $$	r и [math]\theta[/math] – радиус и угол (в радианах), соответственно
	$$\frac{1}{2} r^2 \frac{\theta \pi}{180} $$	r и [math]\theta[/math] – радиус и угол (в ° ), соответственно

Сфера, шар, сегмент и сектор. Формулы и свойства

Определение.

Сфера (поверхность шара) — это совокупность всех точек в трехмерном пространстве, которые находятся на одинаковом расстоянии от одной точки, называемой центром сферы (О).

Сферу можно описать, как объёмную фигуру, которая образуется вращением окружности вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.

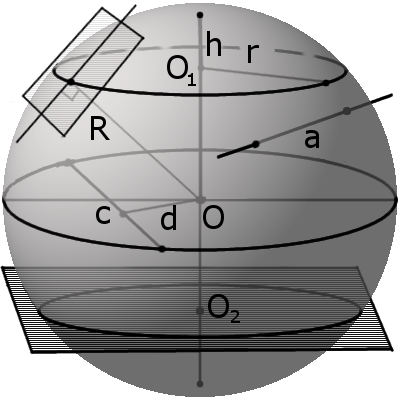
Определение.

Шар — это совокупность всех точек в трехмерном пространстве, расстояние от которых не превышает определенного расстояния до точки, называемой центром шара (О) (совокупность всех точек трехмерного пространства ограниченных сферой).

Шар можно описать как объёмную фигуру, которая образуется вращением круга вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.

Определение. Радиус сферы (шара) (R) — это расстояние от центра сферы (шара) O к любой точке сферы (поверхности шара).

Определение. Диаметр сферы (шара) (D) — это отрезок, соединяющий две точки сферы (поверхности шара) и проходящий через ее центр.

Формула. Объём шара: Формула. Площадь поверхности сферы через радиус или диаметр:

S = 4πR² = πD²

Уравнение сферы

1. Уравнение сферы с радиусом R и центром в начале декартовой системе координат:

x² + y² + z² = R²

2. Уравнение сферы с радиусом R и центром в точке с координатами (x₀, y₀, z₀) в декартовой системе координат:

(x — x₀)² + (y — y₀)² + (z — z₀)² = R²

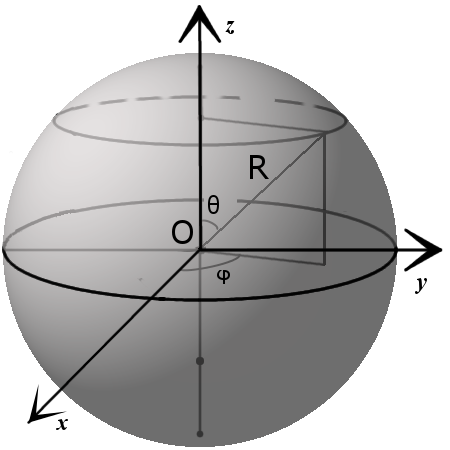3. Параметрическое уравнение сферы с центром в точке (x₀, y₀, z₀):
x = x₀ + R · sin θ · cos φ y = y₀ + R · sin θ · sin φ z = z₀ + R · cos θ
где θ ϵ [0,π], φ ϵ [0,2π].

Определение. Диаметрально противоположными точками называются любые две точки на поверхности шара (сфере), которые соединены диаметром.

Основные свойства сферы и шара

1. Все точки сферы одинаково удалены от центра.

2. Любое сечение сферы плоскостью является окружностью.

3. Любое сечение шара плоскостью есть кругом.

4. Сфера имеет наибольший объём среди всех пространственных фигур с одинаковой площадью поверхности.

5. Через любые две диаметрально противоположные точки можно провести множество больших окружностей для сферы или кругов для шара.

6. Через любые две точки, кроме диаметрально противоположных точек, можно провести только одну большую окружность для сферы или большой круг для шара.

7. Любые два больших круга одного шара пересекаются по прямой, проходящей через центр шара, а окружности пересекаются в двух диаметрально противоположных точках.

8. Если расстояние между центрами любых двух шаров меньше суммы их радиусов и больше модуля разности их радиусов, то такие шары пересекаются, а в плоскости пересечения образуется круг.

Секущая, хорда, секущая плоскость сферы и их свойства

Определение. Секущая сферы — это прямая, которая пересекает сферу в двух точках. Точки пересечения называются точками протыкания поверхности или точками входа и выхода на поверхности.

Определение. Хорда сферы (шара) — это отрезок, соединяющий две точки сферы (поверхности шара).

Определение. Секущая плоскость — это плоскость, которая пересекает сферу.

Определение. Диаметральная плоскость — это секущая плоскость, проходящая через центр сферы или шара, сеченме образует соответственно большую окружность и большой круг. Большая окружность и большой круг имеют центр, который совпадают с центром сферы (шара).

Любая хорда, проходящая через центр сферы (шара) является диаметром.

Хорда является отрезком секущей прямой.

Расстояние d от центра сферы до секущей всегда меньше чем радиус сферы:

d < R

Расстояние m между секущей плоскостью и центром сферы всегда меньше радиуса R:

m < R

Местом сечения секущей плоскости на сфере всегда будет малая окружность, а на шаре местом сечения будет малый круг. Малая окружность и малый круг имеют свои центры, не совпадающих с центром сферы (шара). Радиус r такого круга можно найти по формуле:

r = √R² — m²,

где R — радиус сферы (шара), m — расстояние от центра шара до секущей плоскости.

Определение. Полусфера (полушар) — это половина сферы (шара), которая образуется при ее сечении диаметральной плоскостью.

Касательная, касательная плоскость к сфере и их свойства

Определение.Касательная к сфере — это прямая, которая касается сферы только в одной точке.

Определение.Касательная плоскость к сфере — это плоскость, которая соприкасается со сферой только в одной точке.

Касательная пряма (плоскость) всегда перпендикулярна радиусу сферы проведенному к точке соприкосновения

Расстояние от центра сферы до касательной прямой (плоскости) равно радиусу сферы.

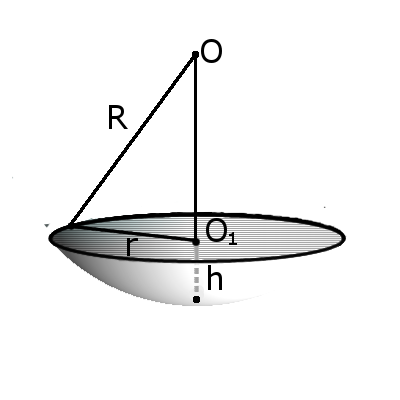Определение. Сегмент шара — это часть шара, которая отсекается от шара секущей плоскостью. Основой сегмента называют круг, который образовался в месте сечения. Высотой сегмента h называют длину перпендикуляра проведенного с середины основы сегмента к поверхности сегмента. Формула. Площадь внешней поверхности сегмента сферы с высотой h через радиус сферы R:

S = 2πRh

Формула. Объём сегмента сферы с высотой h через радиус сферы R: Определение. Срез шара — это часть шара, которая образуется в результате его сечения двумя параллельными плоскостями и находится между ними. 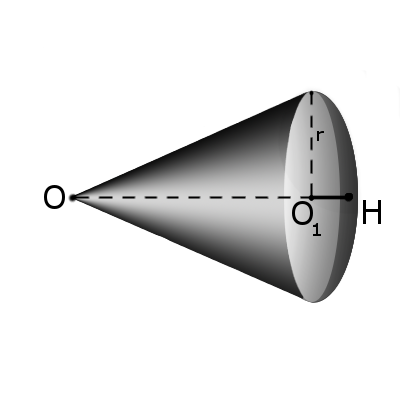Определение. Сектором называется часть шара, ограниченная совокупностью всех лучей, исходящих из центра шара О и образующих круг на его поверхности с радиусом r. Формула. Площадь поверхности сектора S с высотой O₁H (h) через радиус шара OH (R):

S = πR(2h + √2hR — h²)

Формула. Объём сектора V с высотой O₁H (h) через радиус шара OH (R):

Определение. Касательными сферами (шарами) называются любые две сферы (шара), которые имеют одну общую точку соприкосновения. Если расстояние между центрами больше суммы радиусов, то фигуры не касаются и не пересекаются.

Определение. Концентрическими сферами называются любые две сферы, которые имеют общий центр и радиусы различной длины.

Как найти радиус окружности — Лайфхакер

Выбирайте формулу в зависимости от известных величин.

Через площадь круга

1. Разделите площадь круга на число пи.
2. Найдите корень из результата.

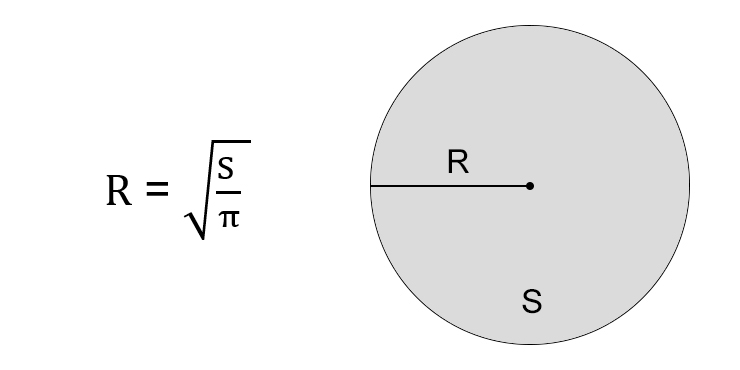Иллюстрация: Лайфхакер

• R — искомый радиус окружности.
• S — площадь круга. Напомним, кругом называют плоскость внутри окружности.
• π (пи) — константа, равная 3,14.

Сейчас читают 🔥

Через длину окружности

1. Умножьте число пи на два.
2. Разделите длину окружности на результат.

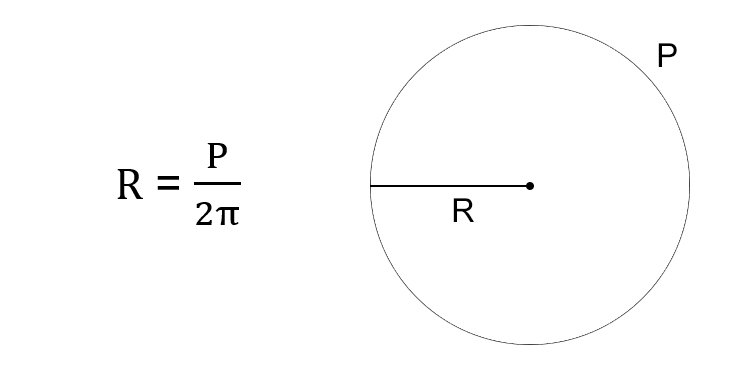Иллюстрация: Лайфхакер

• R — искомый радиус окружности.
• P — длина окружности (периметр круга).
• π (пи) — константа, равная 3,14.

Через диаметр окружности

Если вы вдруг забыли, радиус равняется половине диаметра. Поэтому, если диаметр известен, просто разделите его на два.

Иллюстрация: Лайфхакер

• R — искомый радиус окружности.
• D — диаметр.

Через диагональ вписанного прямоугольника

Диагональ прямоугольника является диаметром окружности, в которую он вписан. А диаметр, как мы уже вспомнили, в два раза больше радиуса. Поэтому достаточно разделить диагональ на два.

Иллюстрация: Лайфхакер

• R — искомый радиус окружности.
• d — диагональ вписанного прямоугольника. Напомним, она делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Поэтому, если диагональ неизвестна, её можно найти через соседние стороны прямоугольника с помощью теоремы Пифагора.
• a, b — стороны вписанного прямоугольника.

Через сторону описанного квадрата

Сторона описанного квадрата равна диаметру окружности. А диаметр — повторимся — равен двум радиусам. Поэтому разделите сторону квадрата на два.

Иллюстрация: Лайфхакер

• r — искомый радиус окружности.
• a — сторона описанного квадрата.

Через стороны и площадь вписанного треугольника

1. Перемножьте три стороны треугольника.
2. Разделите результат на четыре площади треугольника.

Иллюстрация: Лайфхакер

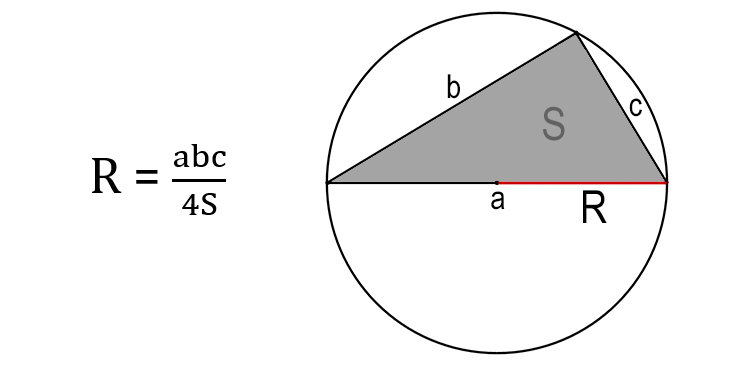
Через площадь и полупериметр описанного треугольника

Разделите площадь описанного треугольника на его полупериметр.

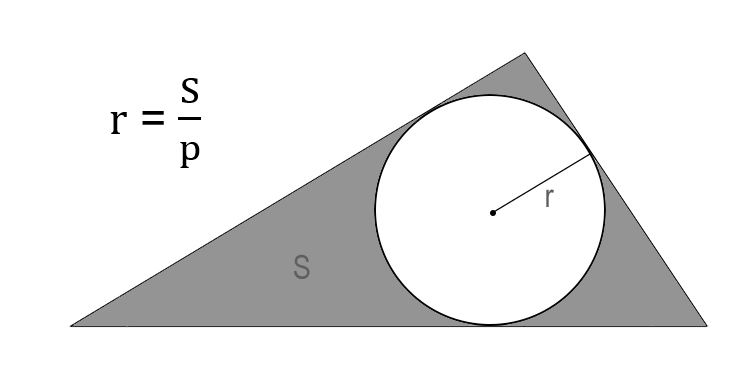Иллюстрация: Лайфхакер

• r — искомый радиус окружности.
• S — площадь треугольника.
• p — полупериметр треугольника (равен половине от суммы всех сторон).

Через площадь сектора и его центральный угол

1. Умножьте площадь сектора на 360 градусов.
2. Разделите результат на произведение пи и центрального угла.
3. Найдите корень из полученного числа.

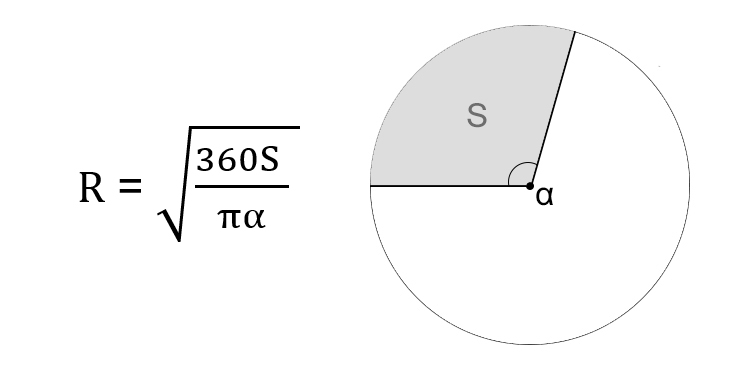Иллюстрация: Лайфхакер

• R — искомый радиус окружности.
• S — площадь сектора круга.
• α — центральный угол.
• π (пи) — константа, равная 3,14.

Через сторону вписанного правильного многоугольника

1. Разделите 180 градусов на количество сторон многоугольника.
2. Найдите синус полученного числа.
3. Умножьте результат на два.
4. Разделите сторону многоугольника на результат всех предыдущих действий.

Иллюстрация: Лайфхакер

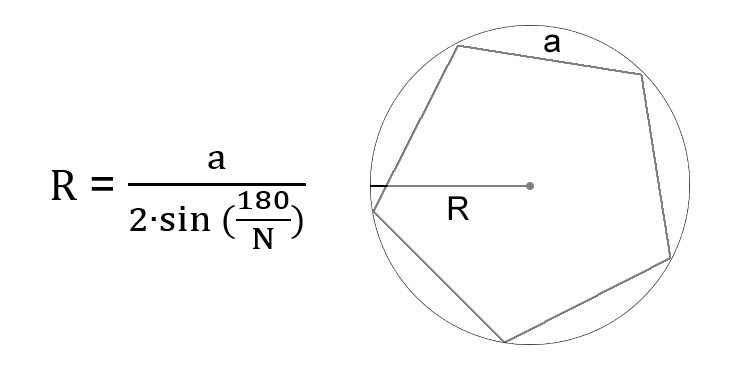
• R — искомый радиус окружности.
• a — сторона правильного многоугольника. Напомним, в правильном многоугольнике все стороны равны.
• N — количество сторон многоугольника. К примеру, если в задаче фигурирует пятиугольник, как на изображении выше, N будет равняться 5.

Читайте также 📐✂️📌

4} {64} 90009 90004 Elastic bending and moment of inertia 90005 90008 The moment of inertia (second moment or area) is used in beam theory to describe the rigidity of a beam against flexure. The bending moment M applied to a cross-section is related with its moment of inertia with the following equation: 90009 90008 M = E \ times I \ times \ kappa 90009 90008 where E is the Young’s modulus, a property of the material, and \ kappa , The curvature of the beam due to the applied load.Therefore, it can be seen from the former equation, that when a certain bending moment M is applied to a beam cross-section, the resulting curvature is reversely proportional to the moment of inertia I. 90009 90004 Polar moment of inertia 90005 90008 The polar moment of inertia, describes the rigidity of a cross-section against torsional moment, likewise the planar moments of inertia described above, are related to flexural bending. The calculation of the polar moment of inertia I_z around an axis z (perpendicular to the section), can be done with the Perpendicular Axes Theorem: 90009 90008 I_z = I_x + I_y 90009 90008 where the I_x and I_y are the moments of inertia around axes x and y, which are mutually perpendicular with z and meet at a common origin.4 . 90009 90006 Elastic modulus 90007 90008 The elastic section modulus S_x of any cross section around axis x (centroidal), describes the response of the section under elastic flexural bending. It is defined as: 90009 90008 S_x = \ frac {I_x} {Y} 90009 90008 where I_x , The moment of inertia of the section around x axis and Y the distance from centroid of a section fiber, parallel to the axis. Typically, the most distant fibers are of particular interest.3} {4} 90009 90004 Elastic stresses 90005 90008 If a bending moment M_x is applied around axis x, the section will respond with normal stresses, varying linearly with the distance from the neutral axis (which under elastic regime coincides to the centroidal x-x axis). Along neutral axis the stresses are zero. Absolute maximum \ sigma will occur at the most distant fiber, with magnitude given by the formula: 90009 90008 \ Sigma = \ frac {M_x} {S_x} 90009 90008 From the last equation, the section modulus can be considered for flexural bending, a property analogous to cross-sectional A, for axial loading.3 . 90009 90006 Plastic modulus 90007 90008 The plastic section modulus is similar to the elastic one, but defined with the assumption of full plastic yielding of the cross section due to flexural bending. In that case the whole section is divided in two parts, one in tension and one in compression, each under uniform stress field. For materials with equal tensile and compressive yield stresses, this leads to the division of the section into two equal areas, A_t , In tension and A_c , In compression, separated by the neutral axis.This is a result of equilibrium of internal forces in the cross-section, under plastic bending conditions. Indeed, the internal compressive force, over the entire compressive area, would be A_cf_y , Assuming full plastification (i.e. the material would have yielded everywhere) and that the compressive yield stress is equal to f_y (Ignoring any plastic hardening in this context). Similarly, the internal tensile force would be A_t f_y , Using the same assumptions.Enforcing equilibrium: 90009 90008 A_cf_y = A_t f_y \ Rightarrow 90009 90008 A_c = A_t 90009 90008 The axis is called 90075 plastic neutral axis 90076, and for non-symmetric sections, is not the same with the elastic neutral axis (which again is the centroidal one). The circular section however, is a symmetrical one and therefore the plastic neutral coincides with the elastic one. In other words, the plastic neutral axes passes through the center of the circle.90009 90008 The plastic modulus, for flexural bending around a given axis, is given by the general formula: 90009 90008 Z = A_c Y_c + A_t Y_t 90009 90008 where Y_c , The distance of the centroid of the compressive area from the plastic neutral axis and Y_t the respective distance of the centroid of the tensile area. 90009 90008 For the case of a circular cross-section, the plastic neutral axis passes through centroid, as already mentioned, dividing the whole area into two equal parts.3} {3} 90009 90006 Radius of gyration 90007 90008 Radius of gyration R_g of any cross-section, relative to an axis, is given by the general formula: 90009 90008 R_g = \ sqrt {\ frac {I} {A}} 90009 90008 where I the moment of inertia of the cross-section around the same axis and A its area. The dimensions of radius of gyration are [Length] . It describes how far from centroid the area is distributed. Small radius indicates a more compact cross-section.For a circular section, substitution to the above expression gives the following radius of gyration, around any axis, through center: 90009 90008 R_g = \ frac {R} {2} 90009 90008 Circle is the shape with minimum radius of gyration, compared to any other section with the same area A. 90009 90006 Circular section formulas 90007 90008 The following table, includes the formulas, one can use to calculate the main mechanical properties of the circular section. 90009 90108 90109 90110 90111 90004 Circular section properties 90005 90114 90115 90110 90117 Quantity 90114 90117 Formula 90114 90115 90122 90123 90110 90125 Area: 90126 90125 A = \ pi R ^ 2 = {\ pi D ^ 2 \ over 4} 90126 90115 90110 90125 Circumference: 90126 90125 P = 2 \ pi R = \ pi D 90126 90115 90110 90125 Moment of inertia: 90126 90125 I = \ frac {\ pi R ^ 4} {4} = \ frac {\ pi D ^ 4} {64} 90126 90115 90110 90125 Elastic modulus: 90126 90125 S = \ frac {\ pi R ^ 3} {4} = \ frac {\ pi D ^ 3} {32} 90126 90115 90110 90125 Plastic modulus: 90126 90125 Z = \ frac {4R ^ 3} {3} = \ frac {D ^ 3} {6} 90126 90115 90110 90125 Radius of gyration: 90126 90125 R_g = {R \ over 2} = {D \ over 4} 90126 90115 90110 90125 Approximations: 90126 90125 90008 P = 6.3 90009 90126 90115 90174 90175 90006 Related pages 90007 90008 Liked this page? Share it with friends! 90009.90000 Calculus — Volumes of Known Cross Sections 90001 This device can not display Java animations. The above is a substitute static image 90002 1. Square on side 90003 90004 The applet initially shows the yellow region bounded by 90005 f 90006 (90005 x 90006) = 90005 x 90006 +1 and 90005 g 90006 (90005 x 90006) = 90005 x 90006 ² from 0 to 1. This is the base of a solid which has square cross sections when sliced ​​perpendicular to the 90005 x 90006 -axis (ie, one side of each square lies in the yellow region).Move the 90005 x 90006 slider to move a representative slice about the region, noticing that the size of the square changes. The two ends are also shown in light gray. 90021 90004 Note that the slice is sticking up from the screen, and the perspective causes it to look like a rectangle. The volume of one of these square slices with thickness 90005 dx 90006 and side length 90005 s 90006 is just the area of ​​the square times 90005 dx 90006, or 90005 s 90006 ² 90005 dx 90006. But 90005 s 90006 is just the distance between the two curves for a given 90005 x 90006, or 90005 s 90006 = 90005 x 90006 +1 — 90005 x 90006 ².So the integral which sums up all these slices is just 90043 We will leave it as an exercise for the reader to show that this is 41/30 or about 1.367. 90021 90002 2. Square on diagonal 90003 90004 Select the second example from the drop down menu, showing the same region. This time the cross sections (when sliced ​​perpendicular to the 90005 x 90006 -axis) are also squares, but the diagonal of the square lies on the region. This means that the square sticks up out of the screen and also down below the screen.Move the 90005 x 90006 slider to move a representative slice about the region, noticing that the size of the square changes. The volume of one of these square slices with thickness 90005 dx 90006 and diagonal length 90005 d 90006 is just the area of ​​the square times 90005 dx 90006, or 90005 d 90006 ² / 2 90005 dx 90006. But 90005 d 90006 is just the distance between the two curves for a given 90005 x 90006, or 90005 d 90006 = 90005 x 90006 +1 — 90005 x 90006 ². So the integral which sums up all these slices is just 90072 We will leave it as an exercise for the reader to show that this is 41/60 or about 0.683. 90021 90002 3. Semicircle 90003 90004 Select the third example from the drop down menu. This time the cross sections (when sliced ​​perpendicular to the 90005 x 90006 -axis) are semicircles with the diameter lying on the yellow region. This means that the slice sticks up out of the screen. Move the 90005 x 90006 slider to move a representative slice about the region, noticing that the size of the slice changes. The volume of one of these slices with thickness 90005 dx 90006 and diameter length 90005 d 90006 is just the area of ​​the semicircle times 90005 dx 90006, or π (90005 d / 2 90006) ² / 2 90005 dx 90006.But 90005 d 90006 is just the distance between the two curves for a given 90005 x 90006, or 90005 d 90006 = 90005 x 90006 +1 — 90005 x 90006 ². So the integral which sums up all these slices is just 90101 We will leave it as an exercise for the reader to show that this is 41π / 240 or about 0.537. 90021 90002 4. Circle 90003 90004 Select the fourth example from the drop down menu. This time the cross sections (when sliced ​​perpendicular to the 90005 x 90006 -axis) are circles with the diameter lying on the yellow region.This means that the slice sticks up out of the screen and down below the screen. Move the 90005 x 90006 slider to move a representative slice about the region, noticing that the size of the slice changes. The volume of one of these slices with thickness 90005 dx 90006 and diameter length 90005 d 90006 is just the area of ​​the circle times 90005 dx 90006, or π (90005 d / 2 90006) ² 90005 dx 90006. But 90005 d 90006 is just the distance between the two curves for a given 90005 x 90006, or 90005 d 90006 = 90005 x 90006 +1 — 90005 x 90006 ².So the integral which sums up all these slices is just 90130 We will leave it as an exercise for the reader to show that this is 41π / 120 or about 1.073. Note that this is a different solid than one generated by revolution about an axis; in this case there is no straight-line axis. 90021 90002 5. Equilateral triangle 90003 90004 Select the fifth example from the drop down menu. This time the cross sections (when sliced ​​perpendicular to the 90005 x 90006 -axis) are equilateral triangles with one side lying on the yellow region.This means that the slice sticks up out of the screen. Move the 90005 x 90006 slider to move a representative slice about the region, noticing that the size of the slice changes. The volume of one of these slices with thickness 90005 dx 90006 and side length 90005 s 90006 is just the area of ​​the triangle times 90005 dx 90006, or 90145 But 90005 s 90006 is just the distance between the two curves for a given 90005 x 90006, or 90005 s 90006 = 90005 x 90006 +1 — 90005 x 90006 ².So the integral which sums up all these slices is just 90156 We will leave it as an exercise for the reader to show that this is 41√3 / 120 or about 0.592. 90021 90002 6. Right isosceles triangle on hypotenuse 90003 90004 Select the sixth example from the drop down menu. This time the cross sections (when sliced ​​perpendicular to the 90005 x 90006 -axis) are right isosceles triangles with the hypotenuse lying on the yellow region. This means that the right angle corner sticks up out of the screen.Move the 90005 x 90006 slider to move a representative slice about the region, noticing that the size of the slice changes. The volume of one of these slices with thickness 90005 dx 90006 and hypotenuse length 90005 h 90006 is just the area of ​​the triangle times 90005 dx 90006, or 90005 h 90006 ² / 4 90005 dx 90006. But 90005 h 90006 is just the distance between the two curves for a given 90005 x 90006, or 90005 h 90006 = 90005 x 90006 +1 — 90005 x 90006 ². So the integral which sums up all these slices is just 90185 We will leave it as an exercise for the reader to show that this is 41/120 or about 0.342. 90021 90002 7. Right isosceles triangle on leg 90003 90004 Select the seventh example from the drop down menu. This time the cross sections (when sliced ​​perpendicular to the 90005 x 90006 -axis) are right isosceles triangles with one leg lying on the yellow region. This means that the other leg and hypotenuse stick up out of the screen. Move the 90005 x 90006 slider to move a representative slice about the region, noticing that the size of the slice changes. The volume of one of these slices with thickness 90005 dx 90006 and leg length 90005 l 90006 is just the area of ​​the triangle times 90005 dx 90006, or 90005 l 90006 ² / 2 90005 dx 90006.But 90005 l 90006 is just the distance between the two curves for a given 90005 x 90006, or 90005 l 90006 = 90005 x 90006 +1 — 90005 x 90006 ². So the integral which sums up all these slices is just 90214 We will leave it as an exercise for the reader to show that this is 41/60 or about 0.683. 90021 90002 8. Square. Slices horizontal 90003 90004 Select the eighth example. Here the functions are functions of 90005 y 90006 instead of 90005 x 90006 and the slices are taken perpendicular to the 90005 y 90006 axis.Initially the cross section is a square. Move the 90005 y 90006 slider to move a representative slice about the region, noticing that the size of the square changes. The integral which sums up all these slices is just 90227 As you would expect (since the region is the same as example 1, just with 90005 x 90006 and 90005 y 90006 flipped), the area is the same as in example 1. You can use the choice box to select other cross section shapes. 90021 90002 Explore 90003 90004 Select the ninth example.This lets you enter your own functions, limits of integration, cross section type, and whether 90005 x 90006 and 90005 y 90006 are swapped (remember to define your functions with 90005 y 90006 if you click the inverse box). 90021 90002 Other ‘Applications of Integration’ topics 90003 90004 (C) 2011 Copyright Math Open Reference. 90246 All rights reserved 90021 .2 \ right) 90009 90008 where D_i = D-2t the inner, hollow area diameter. 90009 90008 Its circumferences, outer and inner, can be found from the respective circumferences of the outer and inner circles of the tubular section. These are: 90009 90008 P_ {out} = 2 \ pi R 90009 90008 P_ {in} = 2 \ pi R_i 90009 90008 The total circumferences (inner and outer combined) is then found with the formula: 90009 90008 P = 2 \ pi (R + R_i) 90009 90006 Moment of Inertia 90007 90008 The moment of inertia (second moment of area) of a circular hollow section, around any axis passing through its centroid, is given by the following expression: 90009 90008 I = \ frac {\ pi} {4} \ left (R ^ 4-R_i ^ 4 \ right) 90009 90008 where, R , Is the outer radius of the section, R_i = R-t , Is the inner radius and t , The wall thickness.4 . 90009 90004 Flexural bending and moment of inertia 90005 90008 The moment of inertia (second moment or area) is used in beam theory to describe the rigidity of a beam against flexure. The bending moment M, applied to a cross-section, is related with its moment of inertia with the following equation: 90009 90008 M = E \ times I \ times \ kappa 90009 90008 where E is the Young’s modulus, a property of the material, and \ kappa the curvature of the beam due to the applied load.Therefore, it can be seen from the former equation, that when a certain bending moment M is applied to a beam cross-section, the resulting curvature is reversely proportional to the moment of inertia I. 90009 90004 Polar moment of inertia 90005 90008 The polar moment of inertia, describes the rigidity of a cross-section against torsional moments, likewise the planar moments of inertia, described above, are related to flexural bending. The calculation of the polar moment of inertia I_z , Around an axis z (perpendicular to the section), can be done with the Perpendicular Axes Theorem: 90009 90008 I_z = I_x + I_y 90009 90008 where the I_x and I_y are the moments of inertia around axes x and y, which are mutually perpendicular to z and meet at a common origin.4 \ right) 90009 90006 Elastic section modulus 90007 90008 The elastic section modulus S_x of any cross section around an axis x, passing through centroid, describes the response of the section under elastic flexural bending. It is defined as: 90009 90008 S_x = \ frac {I_x} {Y} 90009 90008 where, I_x is the moment of inertia of the section around same axis x, and Y is the distance from centroid of a given section fiber, parallel to the axis x.Typically, the most distant fibers are of special interest, because, they provide the ultimate normal stresses of the cross section, as will be explained right after. Taking into consideration that the most distant fibers, of a circular tube, are indeed points of its outer circumference, their distance, from section center is: Y = R . Substitution to the above formula, gives its elastic section modulus, around any centroidal axis, of the circular tube section: 90009 90008 S = \ frac {\ pi} {4 R} \ left (R ^ 4 — R_i ^ 4 \ right) 90009 90008 The dimensions of section modulus are [Length] ^ 3 .90009 90004 Elastic modulus and normal stresses 90005 90008 If a bending moment M_x is applied around centroidal axis x, the section will respond with normal stresses, varying linearly with the distance from the axis, assuming the material is linearly elastic and the beam flexural behavior follows the simple beam theory (known as Euler-Bernoulli beam theory). That axis is called 90087 elastic neutral axis 90088 (or just neutral axis, in short). Over neutral axis, the normal stresses are zero, by definition.90009 90008 As we move away from neutral axis, normal stresses \ sigma increase in magnitude, proportionally with distance, as shown in the previous figure. Specifically, the relationship between applied bending moment and normal stresses is given by the formula: 90009 90008 \ Sigma (y) = — {M_x y \ over I} 90009 90008 When normal stresses are negative, it means they are compressive, while positive normal stresses are tensile. Therefore, by application of the above formula, positive y values ​​result in compressive normal stresses (negative).This is true for the sectional area above the neutral axis, in last figure. The opposite occurs for negative y values, which result in tensile stresses (positive). In other words, the entire area below neutral axis is in tension. Take in mind, that this analysis is valid for sagging moment M_x , As indicated in the figure. For a hogging moment, the stresses are inverted, so that tension appears above the neutral axis. The above formula, in that case, is still valid, if we provide a negative sign to any hogging bending moments.Nevertheless, it is quite easy to verify the direction of normal stresses, by inspection alone, rather than rely on sign conventions. 90009 90008 Absolute maximum \ sigma will occur at the most distant fiber. Taking the (where y = Y ), With magnitude given by the formula: 90009 90008 \ Sigma = — {M_x Y \ over I} = — \ frac {M_x} {S_x} 90009 90008 From the last equation, the section modulus can be considered for flexural bending, a property analogous to cross-sectional A, for axial loading.For the latter, the normal stress is F / A. 90009 90006 Plastic section modulus 90007 90008 The plastic section modulus is similar to the elastic one, but defined with the assumption of full plastic yielding of the cross section due to flexural bending. In that case the whole section is divided in two parts, one in tension and one in compression, each under uniform stress field. For materials with equal tensile and compressive yield stresses, this leads to the division of the section into two equal areas, A_t in tension and A_c in compression, separated by the neutral axis.This is a result of equilibrium of internal forces in the cross-section, under plastic bending. Indeed, the compressive force would be A_cf_y , Assuming the yield stress is equal to f_y , In compression, and that the material over the entire compressive area has yielded (thus the stresses are equal to f_y everywhere). Similarly, the tensile force would be A_t f_y , Using the same assumptions. Enforcing equilibrium: 90009 90008 A_cf_y = A_t f_y \ Rightarrow 90009 90008 A_c = A_t 90009 90008 The axis is called 90087 plastic neutral axis 90088, and for non-symmetric sections, is not the same with the elastic neutral axis (which again is the centroidal one).Circular tube is a symmetric section though, for any possible axis through the center. As a result, the plastic neutral axis, should pass through the center too, when only a bending moment is applied. 90009 90008 In the general case, the plastic section modulus is given by the following formula (assuming bending around x axis): 90009 90008 Z_x = A_c Y_c + A_t Y_t 90009 90008 where Y_c , The distance of the centroid of the compressive area A_c , From the plastic neutral axis, and Y_t , The respective distance of the centroid of the tensile area A_t .These distances, for the case of a circular tube cross-section however, due to symmetry, are equal ( Y_c = Y_t ). By definition also, the tensile and compressive areas are equal too, as have been explained earlier. This can only be true if each of these areas is equal to half the cross section area: A_c = A_t = {A \ over2} . Therefore, the plastic section modulus formula becomes: 90009 90008 Z = {A \ over2} Y_c + {A \ over2} Y_c \ Rightarrow 90009 90008 Z = A Y_c 90009 90008 Finding distance Y_c , Of the compressive area centroid, from the sectional center, is straightforward, given the centroid of a semicircle has a distance, from circle center, equal to: {4R \ over3 \ pi} (Check our centroids table here).3 \ right) 90009 90008 where, D , Is the outer diameter and D_i , Is the inner one, equal to: D_i = D-2t . 90009 90006 Radius of gyration 90007 90008 Radius of gyration R_g of a cross-section is given by the formula: 90009 90008 R_g = \ sqrt {\ frac {I} {A}} 90009 90008 where I the moment of inertia of the cross-section around a given axis and A its area. The dimensions of radius of gyration are [Length] .2}} {2} 90009 90008 Circle is the shape with minimum radius of gyration, compared to any other section with the same area A. Circular tube section though, should have considerably higher radius of gyration, because all of its sectional area is positioned at a distance from the center . 90155 90009 90006 Circular tube section formulas 90007 90008 The following table, includes the formulas, one can use to calculate the main mechanical properties of the circular tube section.2}} {4} 90179 90168 90233 90234 90006 Related pages 90007 90008 Liked this page? Share it with friends! 90009.90000 Cross-sectional area to diameter conversion circle intersection cross section diameter electric cable conductor formula wire diameter and wiring and calculation cross section AGW American Wire Gauge thick area of ​​a solid wire formula conductivity resistivity stranded wire litz length current 90001 Cross-sectional area to diameter conversion circle intersection cross section diameter electric cable conductor formula wire diameter and wiring and calculation cross section AGW American Wire Gauge thick area of ​​a solid wire formula conductivity resistivity stranded wire litz length current — sengpielaudio Sengpiel Berlin 90002 90002 90004 Conversion 90005 90004 and 90005 90004 calculation 90005 90004 — cross section <> diameter 90005 90002 90002 90004 ● 90005 90004 Cable diameter 90005 90004 to circle 90005 90004 cross-sectional area 90005 90004 and vice versa ● 90005 90002 90002 90004 Round 90005 90004 electric cable 90005 90004, 90005 90004 conductor 90005 90004, 90005 90004 wire 90005 90004, 90005 90004 cord 90005 90004, 90005 90004 string 90005 90004, 90005 90004 wiring 90005 90004, and 90005 90004 rope 90005 90002 90002 90056 90057 90058 Cross section is just a two-dimensional view of a slice through an object.90002 An often asked question: How can you convert the diameter of a 90004 round 90005 wire 90062 d 90063 = 2 × 90062 r 90063 to the 90002 circle cross section surface or the cross-section area 90062 A 90063 (slice plane) to the cable diameter 90062 d 90063? 90002 Why is the diameter value greater than the area value? Because that’s not the same. 90002 Resistance varies inversely with the cross-sectional area of ​​a wire. 90002 90002 The required cross-section of an electrical line depends on the following factors: 90002 1) Rated voltage.Net form. (Three-phase (DS) / AC (WS)) 90002 2) Fuse — Upstream backup = Maximum permissible current (Amp) 90002 3) On schedule to be transmitted power (kVA) 90002 4) Cable length in meters (m) 90002 5) Permissible voltage drop (% of the rated voltage) 90002 6) Line material. Copper (Cu) or aluminum (Al) 90081 90082 90083 90084 90057 90086 90004 The used browser does not support JavaScript. 90002 You will see the program but the function will not work. 90005 90081 90082 90083 90093 The «unit» is usually millimeters but it can also be inches, feet, yards, meters (metres), 90002 or centimeters, when you take for the area the square of that measure.90002 90002 90004 Litz wire 90005 (stranded wire) consisting of many thin wires need a 14% larger diameter compared to a solid wire. 90099 90100 90057 90058 90002 90004 Cross sectional area is not diameter. 90005 90002 90002 90081 90082 90083 90002 90112 90057 90058 90002 90004 Cross section is an area. 90002 Diameter is a linear measure. 90002 That can not be the same. 90002 90002 The cable diameter in millimeters 90002 is not the cable cross-section in 90002 square millimeters.90005 90002 90002 90081 90127 90081 90082 90083 90056 90057 90058 The cross section or the cross sectional area is the area of ​​such a cut. 90002 It need not necessarily have to be a circle. 90002 90002 Commercially available wire (cable) size as cross sectional area: 90002 0.75 mm 90138 2 90139, 1.5 mm 90138 2 90139, 2.5 mm 90138 2 90139, 4 mm 90138 2 90139, 6 mm 90138 2 90139, 10 mm 90138 2 90139 , 16 mm 90138 2 90139. 90081 90082 90083 90004 Calculation of the cross section 90062 A 90063, entering the diameter 90062 d = 90063 90004 2 90005 90062 r 90063: 90005 90002 90002 90062 r 90063 = radius of the wire or cable 90002 90062 d 90063 = 2 90062 r 90063 = diameter of the wire or cable 90002 90004 Calculation of the diameter 90062 d = 90063 2 90062 r 90063, entering the cross section 90062 A 90063: 90005 90002 90002 90004 The conductor (electric cable) 90005 90002 90056 90057 90058 There are four factors that affect the resistance of a conductor: 90002 1) the cross sectional area of ​​a conductor 90062 A 90063, calculated from the diameter 90062 d 90063 90002 2) the length of the conductor 90002 3) the temperature in the conductor 90002 4) the material constituting the conductor 90081 90082 90083 90002 90056 90057 90058 There is no exact formula for the 90004 minimum wire size 90005 from the 90004 maximum amperage 90005.90002 It depends on many circumstances, such as for example, if the calculation is for DC, AC or 90002 even for three-phase current, whether the cable is released freely, or is placed under the 90002 ground. Also, it depends on the ambient temperature, the allowable current density, and the 90002 allowable voltage drop, and whether solid or litz wire is present. And there is always the 90002 nice but unsatisfactory advice to use for security reasons a thicker and hence more 90002 expensive cable.Common questions are about the voltage drop on wires. 90081 90082 90083 90093 90004 Voltage drop 90005 90004 90062 Δ V 90063 90005 90099 90056 90057 90058 The voltage drop formula with the specific resistance (resistivity) 90062 ρ 90063 (rho) is: 90002 90002 90234 90057 90058 90002 90062 Δ V 90063 = 90062 I 90063 × 90062 R 90063 = 90062 I 90063 × (2 × 90062 l 90063 × 90062 ρ 90063 90062/90063 90062 A 90063) 90002 90081 90082 90083 90002 90062 I 90063 = Current in ampere 90002 90062 l 90063 = Wire (cable) length in meters (times 2, because there is always a return wire) 90002 90062 ρ 90063 = rho, electrical resistivity (also known as specific electrical resistance or volume 90002 resistivity) of 90004 copper 90005 = 0.01724 ohm × mm 90138 2 90139 / m (also Ω × m) 90002 (Ohms for 90062 l 90063 = 1 m length and 90062 A 90063 = 1 mm 90138 2 90139 cross section area of ​​the wire) 90062 ρ = 90063 1/90062 σ 90063 90002 90062 A 90063 = Cross section area in mm 90138 2 90139 90002 90062 σ 90063 = sigma, electrical conductivity (electrical conductance) of copper = 58 S 90004 · 90005 m / mm 90138 2 90139 90081 90082 90083 90002 90299 90057 90058 90302 90057 90127 90004 Quantity of resistance 90005 90081 90058 90081 90082 90057 90127 90081 90058 90081 90082 90057 90058 90062 R 90063 = resistance 90081 90058 Ω 90081 90082 90057 90058 90062 ρ 90063 = specific resistance 90081 90058 Ω × m 90081 90082 90057 90058 90062 l 90063 = double length of the cable 90081 90058 m 90081 90082 90057 90058 90062 A 90063 = cross section 90081 90058 mm 90138 2 90139 90081 90082 90083 90081 90082 90083 90093 The derived SI unit of electrical resistivity 90062 ρ 90063 is Ω × 90004 90005 m, shortened from the clear Ω × 90004 90005 mm / m.90002 The reciprocal of electrical resistivity is electrical conductivity. 90099 90004 Electrical conductivity and electrical resistivity 90062 κ 90063 or 90062 σ 90063 = 1/90062 ρ 90063 90002 Electrical conductance and electrical resistance 90005 90004 90062 ρ 90063 90005 90004 = 1/90005 90004 90062 κ 90063 90005 90004 = 1/90005 90004 90062 σ 90063 90005 90093 90004 Difference between electrical resistivity and electrical conductivity 90005 90099 90056 90057 90058 The conductance in siemens is the reciprocal of the resistance in ohms.90081 90082 90083 90002 90056 90057 90058 To use the calculator, simply enter a value. 90002 The calculator works in both directions of the 90004 ↔ 90005 sign. 90081 90082 90083 90002 90056 90057 90058 The value of the electrical conductivity (conductance) and the specific electrical resistance 90002 (resistivity) is a temperature dependent material constant. Mostly it is given at 20 or 25 ° C. 90081 90082 90083 90093 90004 Resistance = resistivity x length / area 90005 90099 90421 90057 90058 90004 The specific resistivity of conductors changes with temperature.90005 90002 In a limited temperature range it is approximately linear: 90002 90002 where 90062 α 90063 is the temperature coefficient, 90062 T 90063 is the temperature and 90062 T 90063 90435 0 90436 is any temperature, 90002 such as 90062 T 90063 90435 0 90436 = 293.15 K = 20C at which the electrical resistivity 90062 ρ 90063 (90062 T 90063 90435 0 90436) is known. 90081 90082 90083 90093 90004 Convert resistance to electrical conductance 90005 90002 90004 Conversion of reciprocal siemens to ohms 90005 90002 90004 1 ohm [Ω] = 1 / siemens [1 / S] 90005 90002 90004 1 siemens [S] = 1 / ohm [1 / Ω] 90005 90099 90056 90057 90058 To use the calculator, simply enter a value.90002 The calculator works in both directions of the 90004 ↔ 90005 sign. 90081 90082 90083 90093 1 millisiemens = 0.001 mho = 1000 ohms 90099 90056 90057 90058 Mathematically, conductance is the reciprocal, or inverse, of resistance: 90093 90099 The symbol for conductance is the capital letter «G» and the unit is the 90002 mho, which is «ohm» spelled backwards. Later, the unit mho was 90002 replaced by the unit Siemens — abbreviated with the letter «S». 90081 90082 90083 90093 90004 Calculator: Ohm’s law 90005 90099 90093 90004 Table of typical loudspeaker cables 90005 90099 90112 90057 90058 Cable diameter 90062 d 90063 90081 90058 0.798 mm 90081 90058 0.977 mm 90081 90058 1.128 mm 90081 90058 1.382 mm 90081 90058 1.784 mm 90081 90058 2.257 mm 90081 90058 2.764 mm 90081 90058 3.568 mm 90081 90082 90057 90058 Cable nominal cross section 90062 A 90063 90081 90058 0.5 mm 90138 2 90139 90081 90058 0.75 mm 90138 2 90139 90081 90058 1.0 mm 90138 2 90139 90081 90058 1.5 mm 90138 2 90139 90081 90058 2.5 mm 90138 2 90139 90081 90058 4.0 mm 90138 2 90139 90081 90058 6.0 mm 90138 2 90139 90081 90058 10.0 mm 90138 2 90139 90081 90082 90057 90058 90004 Maximum electrical current 90005 90081 90058 3 A 90081 90058 7.6 A 90081 90058 10.4 A 90081 90058 13.5 A 90081 90058 18.3 A 90081 90058 25 A 90081 90058 32 A 90081 90058 — 90081 90082 90083 90093 Always consider, the cross section must be made larger with higher power and higher length of 90002 the cable, but also with lesser impedance. Here is a table to tell the possible power loss. 90099 90112 90057 90582 Cable length 90002 in m 90081 90582 Section 90002 in mm 90138 2 90139 90081 90582 Resistance 90002 in ohm 90081 90593 Power loss at 90081 90593 Damping factor at 90081 90082 90057 90127 Impedance 90002 8 ohm 90081 90127 Impedance 90002 4 ohm 90081 90127 Impedance 90002 8 ohm 90081 90127 Impedance 90002 4 ohm 90081 90082 90057 90613 1 90081 90127 0.75 90081 90127 0.042 90081 90127 0.53% 90081 90127 1.05% 90081 90127 98 90081 90127 49 90081 90082 90057 90127 1.50 90081 90127 0.021 90081 90127 0.31% 90081 90127 0.63% 90081 90127 123 90081 90127 62 90081 90082 90057 90127 2.50 90081 90127 0.013 90081 90127 0.16% 90081 90127 0.33% 90081 90127 151 90081 90127 75 90081 90082 90057 90127 4.00 90081 90127 0.008 90081 90127 0.10% 90081 90127 0.20% 90081 90127 167 90081 90127 83 90081 90082 90057 90613 2 90081 90127 0.75 90081 90127 0.084 90081 90127 1.06% 90081 90127 2.10% 90081 90127 65 90081 90127 33 90081 90082 90057 90127 1.50 90081 90127 0.042 90081 90127 0.62% 90081 90127 1.26% 90081 90127 85 90081 90127 43 90081 90082 90057 90127 2.50 90081 90127 0.026 90081 90127 0.32% 90081 90127 0.66% 90081 90127 113 90081 90127 56 90081 90082 90057 90127 4.00 90081 90127 0.016 90081 90127 0.20% 90081 90127 0.40% 90081 90127 133 90081 90127 66 90081 90082 90057 90613 5 90081 90127 0.75 90081 90127 0.210 90081 90127 2.63% 90081 90127 5.25% 90081 90127 32 90081 90127 16 90081 90082 90057 90127 1.50 90081 90127 0.125 90081 90127 1.56% 90081 90127 3.13% 90081 90127 48 90081 90127 24 90081 90082 90057 90127 2.50 90081 90127 0.065 90081 90127 0.81% 90081 90127 1.63% 90081 90127 76 90081 90127 38 90081 90082 90057 90127 4.00 90081 90127 0.040 90081 90127 0.50% 90081 90127 1.00% 90081 90127 100 90081 90127 50 90081 90082 90057 90613 10 90081 90127 0.75 90081 90127 0.420 90081 90127 5.25% 90081 90127 10.50% 90081 90127 17 90081 90127 9 90081 90082 90057 90127 1.50 90081 90127 0.250 90081 90127 3.13% 90081 90127 6.25% 90081 90127 28 90081 90127 14 90081 90082 90057 90127 2.50 90081 90127 0.130 90081 90127 1.63% 90081 90127 3.25% 90081 90127 47 90081 90127 24 90081 90082 90057 90127 4.00 90081 90127 0.080 90081 90127 1.00% 90081 90127 2.00% 90081 90127 67 90081 90127 33 90081 90082 90057 90613 20 90081 90127 0.75 90081 90127 0.840 90081 90127 10.50% 90081 90127 21.00% 90081 90127 9 90081 90127 5 90081 90082 90057 90127 1.50 90081 90127 0.500 90081 90127 6.25% 90081 90127 12.50% 90081 90127 15 90081 90127 7 90081 90082 90057 90127 2.50 90081 90127 0.260 90081 90127 3.25% 90081 90127 6.50% 90081 90127 27 90081 90127 13 90081 90082 90057 90127 4.00 90081 90127 0.160 90081 90127 2.00% 90081 90127 4.00% 90081 90127 40 90081 90127 20 90081 90082 90083 90093 The damping factor values ​​show, what remains of an accepted damping factor of 200 90002 depending on the cable length, the cross section, and the impedance of the loudspeaker.90002 90004 Conversion and calculation of cable diameter to AWG 90005 90002 90004 and AWG to cable diameter in mm — American Wire Gauge 90005 90099 90056 90057 90058 The gauges we most commonly use are even numbers, such as 18, 16, 14, etc. 90002 If you get an answer that is odd, such as 17, 19, etc., use the next lower even number. 90002 90002 90004 AWG stands for American Wire Gauge 90005 and refers to the strength of wires. 90002 These AWG numbers show the diameter and accordingly the cross section as a code.90002 They are only used in the USA. Sometimes you find AWG numbers also in catalogues 90002 and technical data in Europe. 90081 90082 90083 90093 90004 American Wire Gauge — AWG Chart 90005 90099 90112 90057 90932 AWG 90002 number 90934 90932 46 90934 90932 45 90934 90932 44 90934 90932 43 90934 90932 42 90934 90932 41 90934 90932 40 90934 90932 39 90934 90932 38 90934 90932 37 90934 90932 36 90934 90932 35 90934 90932 34 90934 90082 90057 90963 Diameter 90002 in inch 90934 90058 0.0016 90081 90058 0.0018 90081 90058 0.0020 90081 90058 0.0022 90081 90058 0.0024 90081 90058 0.0027 90081 90058 0.0031 90081 90058 0.0035 90081 90058 0.0040 90081 90058 0.0045 90081 90058 0.0050 90081 90058 0.0056 90081 90058 0.0063 90081 90082 90057 90963 Diameter (Ø) 90002 in mm 90934 90058 0.04 90081 90058 0.05 90081 90058 0.05 90081 90058 0.06 90081 90058 0.06 90081 90058 0.07 90081 90058 0.08 90081 90058 0.09 90081 90058 0.10 90081 90058 0.11 90081 90058 0.13 90081 90058 0.14 90081 90058 0.16 90081 90082 90057 90963 Cross section 90002 in mm 90138 2 90139 90934 90058 0.0013 90081 90058 0.0016 90081 90058 0.0020 90081 90058 0.0025 90081 90058 0.0029 90081 90058 0.0037 90081 90058 0.0049 90081 90058 0.0062 90081 90058 0.0081 90081 90058 0.010 90081 90058 0.013 90081 90058 0.016 90081 90058 0.020 90081 90082 90057 91058 90002 90081 90082 90057 90932 AWG 90002 number 90934 90932 33 90934 90932 32 90934 90932 31 90934 90932 30 90934 90932 29 90934 90932 28 90934 90932 27 90934 90932 26 90934 90932 25 90934 90932 24 90934 90932 23 90934 90932 22 90934 90932 21 90934 90082 90057 90932 Diameter 90002 in inch 90934 90058 0.0071 90081 90058 0.0079 90081 90058 0.0089 90081 90058 0.0100 90081 90058 0.0113 90081 90058 0.0126 90081 90058 0.0142 90081 90058 0.0159 90081 90058 0.0179 90081 90058 0.0201 90081 90058 0.0226 90081 90058 0.0253 90081 90058 0.0285 90081 90082 90057 90932 Diameter (Ø) 90002 in mm 90934 90058 0.18 90081 90058 0.20 90081 90058 0.23 90081 90058 0.25 90081 90058 0.29 90081 90058 0.32 90081 90058 0.36 90081 90058 0.40 90081 90058 0.45 90081 90058 0.51 90081 90058 0.57 90081 90058 0.64 90081 90058 0.72 90081 90082 90057 90932 Cross section 90002 in mm 90138 2 90139 90934 90058 0.026 90081 90058 0.032 90081 90058 0.040 90081 90058 0.051 90081 90058 0.065 90081 90058 0.080 90081 90058 0.10 90081 90058 0.13 90081 90058 0.16 90081 90058 0.20 90081 90058 0.26 90081 90058 0.32 90081 90058 0.41 90081 90082 90057 91058 90002 90081 90082 90057 90932 AWG 90002 number 90934 90932 20 90934 90932 19 90934 90932 18 90934 90932 17 90934 90932 16 90934 90932 15 90934 90932 14 90934 90932 13 90934 90932 12 90934 90932 11 90934 90932 10 90934 90932 9 90934 90932 8 90934 90082 90057 90963 Diameter 90002 in inch 90934 90058 0.0319 90081 90058 0.0359 90081 90058 0.0403 90081 90058 0.0453 90081 90058 0.0508 90081 90058 0.0571 90081 90058 0.0641 90081 90058 0.0719 90081 90058 0.0808 90081 90058 0.0907 90081 90058 0.1019 90081 90058 0.1144 90081 90058 0.1285 90081 90082 90057 90963 Diameter (Ø) 90002 in mm 90934 90058 0.81 90081 90058 0.91 90081 90058 1.02 90081 90058 1.15 90081 90058 1.29 90081 90058 1.45 90081 90058 1.63 90081 90058 1.83 90081 90058 2.05 90081 90058 2.30 90081 90058 2.59 90081 90058 2.91 90081 90058 3.26 90081 90082 90057 90963 Cross section 90002 in mm 90138 2 90139 90934 90058 0.52 90081 90058 0.65 90081 90058 0.82 90081 90058 1.0 90081 90058 1.3 90081 90058 1.7 90081 90058 2.1 90081 90058 2.6 90081 90058 3.3 90081 90058 4.2 90081 90058 5.3 90081 90058 6.6 90081 90058 8.4 90081 90082 90057 91058 90002 90081 90082 90057 90932 AWG 90002 number 90934 90932 7 90934 90932 6 90934 90932 5 90934 90932 4 90934 90932 3 90934 90932 2 90934 90932 1 90934 90932 0 90002 (1/0) 90002 (0) 90934 90932 00 90002 (2/0) 90002 (-1) 90934 90932 000 90002 (3/0) 90002 (-2) 90934 90932 0000 90002 (4/0) 90002 (-3) 90934 90932 00000 90002 (5/0) 90002 (-4) 90934 90932 000000 90002 (6/0) 90002 (-5) 90934 90082 90057 90963 Diameter 90002 in inch 90934 90058 0.1443 90081 90058 0.1620 90081 90058 0.1819 90081 90058 0.2043 90081 90058 0.2294 90081 90058 0.2576 90081 90058 0.2893 90081 90058 0.3249 90081 90058 0.3648 90081 90058 0.4096 90081 90058 0.4600 90081 90058 0.5165 90081 90058 0.5800 90081 90082 90057 90963 Diameter (Ø) 90002 in mm 90934 90058 3.67 90081 90058 4.11 90081 90058 4.62 90081 90058 5.19 90081 90058 5.83 90081 90058 6.54 90081 90058 7.35 90081 90058 8.25 90081 90058 9.27 90081 90058 10.40 90081 90058 11.68 90081 90058 13.13 90081 90058 14.73 90081 90082 90057 90963 Cross section 90002 in mm 90138 2 90139 90934 90058 10.6 90081 90058 13.3 90081 90058 16.8 90081 90058 21.1 90081 90058 26.7 90081 90058 33.6 90081 90058 42.4 90081 90058 53.5 90081 90058 67.4 90081 90058 85.0 90081 90058 107.2 90081 90058 135.2 90081 90058 170.5 90081 90082 90083 90093 90004 How are high frequencies damped by the length of the cable? 90005 90099 .