Конспект «Скорость равномерного движения тела по окружности»
Скорость равномерного движения тела по окружности
Код ОГЭ 1.5. Скорость равномерного движения тела по окружности. Направление скорости. Формула для вычисления скорости через радиус окружности и период обращения. Центростремительное ускорение. Направление центростремительного ускорения. Формула для вычисления ускорения. Формула, связывающая период и частоту обращения.
Равномерное вращение – движение точки с постоянной по модулю скоростью (ʋ = const) по траектории, представляющей собой окружность. Равномерное движение точки по окружности – это движение, при котором точка за любые равные промежутки времени проходит равные пути.
Но так как скорость всегда направлена по касательной к траектории движения, то по направлению она изменяется. Значит, равномерное движение по окружности – это ускоренное движение!
Величины, характеризующие равномерное вращение
- Линейная скорость равномерного вращения

- Период обращения
 . Время одного полного оборота: Т = t / N, где N – число полных оборотов за промежуток времени t.
. Время одного полного оборота: Т = t / N, где N – число полных оборотов за промежуток времени t. - Частота обращения
 . Число оборотов в единицу времени: v = N / t. Связана с периодом обращения соотношением v = 1 / T. Внимание! Полезно установить связь между линейной скоростью с другими параметрами обращения!
. Число оборотов в единицу времени: v = N / t. Связана с периодом обращения соотношением v = 1 / T. Внимание! Полезно установить связь между линейной скоростью с другими параметрами обращения!
За один полный оборот .
.
- Центростремительное ускорение

 , где ʋ – модуль линейной скорости в данной точке окружности.
, где ʋ – модуль линейной скорости в данной точке окружности.
Вектор центростремительного ускорения перпендикулярен вектору скорости и направлен по радиусу к центру окружности. Центростремительное ускорение меняет скорость по направлению, но не меняет по величине. При равномерном вращении центростремительное ускорение постоянно по величине и связано с периодом и частотой вращения соотношениями:
Конспект урока для 9 класса «Скорость равномерного движения тела по окружности».
Следующая тема: «Масса. Плотность вещества» (код ОГЭ 1.5).
Движение тела по криволинейной траектории. Движение по окружности. Характеристики вращательного движения. Центростремительное ускорение
Вам хорошо известно, что в зависимости от формы траектории движение делится на прямолинейное и криволинейное. С прямолинейным движением мы научились работать на предыдущих уроках, а именно решать главную задачу механики для такого вида движения.
Однако ясно, что в реальном мире мы чаще всего имеем дело с криволинейным движением, когда траектория представляет собой кривую линию. Примерами такого движения является траектория тела, брошенного под углом к горизонту, движение Земли вокруг Солнца и даже траектория движения ваших глаз, следящих сейчас за этим конспектом.
Вопросу о том, как решается главная задача механики в случае криволинейного движения, и будет посвящен этот урок.
Для начала определимся, какие принципиальные отличия есть у криволинейного движения (рис. 1) относительно прямолинейного и к чему эти отличия приводят.

Рис. 1. Траектория криволинейного движения
Поговорим о том, как удобно описывать движение тела при криволинейном движении.
Можно разбить движение на отдельные участки, на каждом из которых движение можно считать прямолинейным (рис. 2).
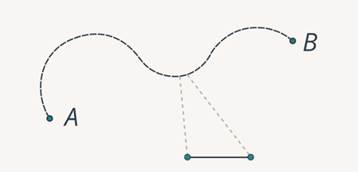
Рис. 2. Разбиение криволинейного движения на участки прямолинейного движения
А дальше на каждом из этих участков мы можем пользоваться законами прямолинейного движения, которые мы уже знаем. В принципе, такой подход возможен.
Однако более удобным является следующий подход. Мы представим это движение как совокупность нескольких движений по дугам окружностей (рис. 3). Обратите внимание, что таких разбиений меньше, чем в предыдущем случае, кроме того, движение по окружности является криволинейным. К тому же примеры движения по окружности в природе встречается очень часто. Из этого можно сделать вывод:
Для того чтобы описывать криволинейное движение, нужно научиться описывать движение по окружности, а потом произвольное движение представлять в виде совокупностей движений по дугам окружностей.
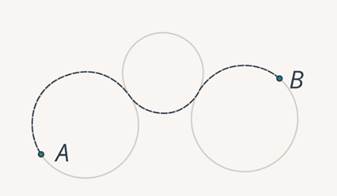
Рис. 3. Разбиение криволинейного движения на движения по дугам окружностей
Итак, начнем изучение криволинейного движения с изучения равномерного движения по окружности. Давайте разберемся, каковы принципиальные отличия криволинейного движения от прямолинейного. Для начала вспомним, что в девятом классе мы изучили тот факт, что скорость тела при движении по окружности направлена по касательной к траектории (рис. 4). Кстати, этот факт вы можете пронаблюдать на опыте, если посмотрите, как движутся искры при использовании точильного камня.
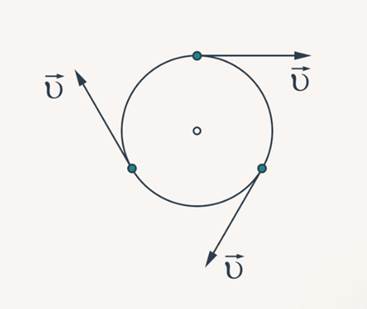
Рис. 4. Направление скорости при движении по окружности
Рассмотрим движение тела по дуге окружности (рис. 5).
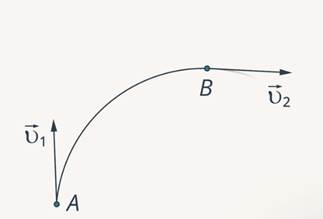
Рис. 5. Скорость тела при движении по окружности
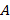 равен модулю скорости тела в точке
равен модулю скорости тела в точке 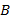 :
: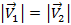
Однако вектор 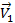 не равен вектору
не равен вектору 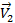
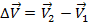
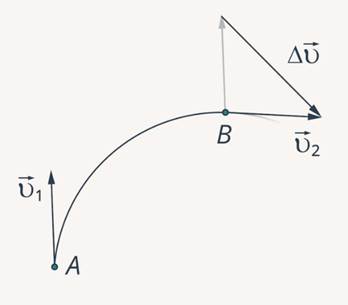
Рис. 6. Вектор разности скоростей
Причем изменение скорости произошло через некоторое время 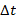 . Таким образом, мы получаем знакомую комбинацию:
. Таким образом, мы получаем знакомую комбинацию:
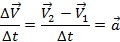
Это не что иное, как изменение скорости за промежуток времени, или ускорение тела. Можно сделать очень важный вывод:
Движение по криволинейной траектории является ускоренным. Природа этого ускорения – непрерывное изменение направление вектора скорости.
Еще раз отметим, что, даже если говорится, что тело равномерно движется по окружности, имеется в виду, что модуль скорости тела не изменяется. Однако такое движение всегда является ускоренным, поскольку изменяется направление скорости.
В девятом классе вы изучали, чему равно такое ускорение и как оно направлено (рис. 7). Центростремительное ускорение 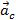
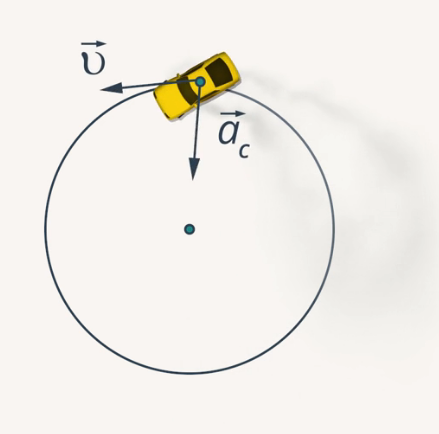
Рис. 7. Центростремительное ускорение
Модуль центростремительного ускорения может быть рассчитан по формуле:
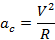
Переходим к описанию равномерного движения тела по окружности. Договоримся, что скорость 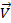
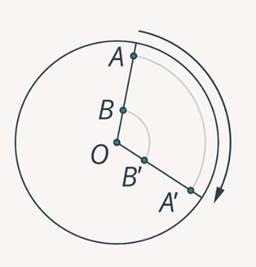
Рис. 8. Движение точек диска
Рассмотрим диск, который для определенности вращается по часовой стрелке. На его радиусе отметим две точки 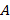 и
и 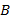 (рис. 8). Рассмотрим их движение. За некоторое время
(рис. 8). Рассмотрим их движение. За некоторое время 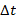 эти точки переместятся по дугам окружности и станут точками
эти точки переместятся по дугам окружности и станут точками 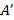 и
и 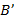 . Очевидно, что точка
. Очевидно, что точка 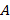 совершила большее перемещение, чем точка
совершила большее перемещение, чем точка 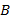 . Из этого можно сделать вывод, что чем дальше от оси вращения находится точка, тем с большей линейной скоростью она движется
. Из этого можно сделать вывод, что чем дальше от оси вращения находится точка, тем с большей линейной скоростью она движется 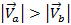
Однако если внимательно посмотреть на точки 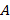 и
и 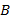 , можно сказать, что неизменным остался угол
, можно сказать, что неизменным остался угол 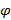 , на который они повернулись относительно оси вращения
, на который они повернулись относительно оси вращения 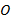 . Именно угловые характеристики мы и будем использовать для описания движения по окружности. Отметим, что для описания движения по окружности можно использовать угловые характеристики.
. Именно угловые характеристики мы и будем использовать для описания движения по окружности. Отметим, что для описания движения по окружности можно использовать угловые характеристики.
Начнем рассмотрение движения по окружности с самого простого случая – равномерного движения по окружности. Напомним, что равномерным поступательным движением называется движение, при котором за любые равные промежутки времени тело совершает одинаковые перемещения. По аналогии можно дать определение равномерного движения по окружности.
Равномерным движением по окружности называется движение, при котором за любые равные промежутки времени тело поворачивается на одинаковые углы.
Аналогично понятию линейной скорости вводится понятие угловой скорости.
Угловой скоростью равномерного движения (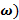 называется физическая величина, равная отношению угла, на который повернулось тело, ко времени, за которое произошел этот поворот.
называется физическая величина, равная отношению угла, на который повернулось тело, ко времени, за которое произошел этот поворот.
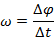
В физике чаще всего используется радианная мера угла. Например, угол в 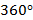 равен
равен 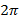 радиан. Измеряется угловая скорость в радианах в секунду:
радиан. Измеряется угловая скорость в радианах в секунду:
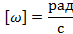
Найдем связь между угловой скоростью вращения точки и линейной скоростью этой точки.
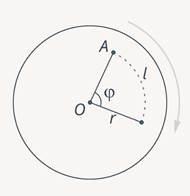
Рис. 9. Связь между угловой и линейной скоростью
Точка 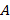 проходит при вращении дугу длиной
проходит при вращении дугу длиной 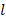 , поворачиваясь при этом на угол
, поворачиваясь при этом на угол 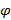 . Из определения радианной меры угла можно записать:
. Из определения радианной меры угла можно записать:
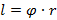
Разделим левую и правую части равенства на промежуток времени 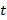 , за который было совершено перемещение, затем воспользуемся определением угловой и линейной скоростей:
, за который было совершено перемещение, затем воспользуемся определением угловой и линейной скоростей:
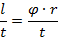
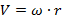
Обратим внимание, что чем дальше точка находится от оси вращения, тем выше ее линейная скорость. А точки, расположенные на самой оси вращения, неподвижны. Примером этого может служить карусель: чем ближе вы находитесь к центру карусели, тем легче вам на ней удержаться.
Такая зависимость линейной и угловой скоростей используется в геостационарных спутниках (спутники, которые всегда находятся над одной и той же точкой земной поверхности). Благодаря таким спутникам мы имеем возможность получать телевизионные сигналы.
Вспомним, что ранее мы вводили понятия периода и частоты вращения.
Период вращения – время одного полного оборота. Период вращения обозначается буквой 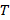 и измеряется в секундах в СИ:
и измеряется в секундах в СИ:
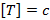
Частота вращения – физическая величина, равная количеству оборотов, которое тело совершает за единицу времени.
Частота обозначается буквой  и измеряется в обратных секунда
и измеряется в обратных секунда
Движение по окружности. Примеры решения задач по физике. 9-10 класс
Движение по окружности. Примеры решения задач по физике. 9-10 класс
Задачи по физике — это просто!
Вспомним
Формулы центростремительного ускорения и центростремительной силы:
Формулы скорости движения тела по окружности и частоты вращения:
Единица измерения частоты вращения — 1/с или оборот/с.
А теперь к задачам!
Элементарные задачи из курса школьной физики на движение по окружности с постоянной по модулю скоростью.
Задача 1
C какой скоростью велосипедист проходит закругление с радиусом 25 метров, если центростремительная скорость его движения равна 4 м/с?
Задача 2
Колесо радиусом 40 см делает один оборот за 0,4 секунды. Найти скорость точек на ободе колеса.
Задача 3
Колесо велосипедиста имеет радиус 40 см. С какой скоростью едет велосипедист, если колесо делает 4 оборота в секунду? Чему равен период вращения колеса?
Задача 4
С какой скоростью велосипедист должен проходить середину выпуклого моста радиусом 22,5 метра, чтобы его центростремительное ускорение было бы равно ускорению свободного падения?
Задача 5
Чему равно центростремительное ускорение тела, движущегося по окружности радиусом 50 см при частоте вращения 5 оборотов в секунду?
Задача 6
Скорость точек экватора Солнца при его вращении вокруг своей оси равно 2 км/с. Найти период вращения Солнца вокруг своей оси и центростремительное ускорение точек его экватора.
Задача 7
Какова скорость движения автомобиля, если его колесо радиусом 30 см делает 500 оборотов в минуту?
Задача 8
Чему равна центростремительная сила и центростремительное ускорение, действующие на пращу массой 800 г, вращающуюся на веревке длиной 60 сантиметров равномерно со скоростью 2 м/с?
Задача 9
Период обращения космического корабля вокруг Земли равен 90 минутам. Высота подъема корабля над поверхностью Земли составляет 300 км, радиус Земли равен 6400 км. Определить скорость корабля.
Неравномерное движение по окружности
В этой статье рассмотрено движение по окружности, причем по условию центр колеса движется с ускорением, неравномерно, вследствие чего у точек колеса кроме нормального ускорения также имеется и “линейное”. Так как оно направлено не по касательной к траектории движения, то оно не может быть названо тангенциальным, но оно содержит в себе тангенциальное ускорение: это одна из его проекций.
Задача. Скорость центра колеса, катящегося без проскальзывания по горизонтальной поверхности, изменяется со временем по закону . Радиус колеса равен м. Найти скорости и ускорения четырех точек: A, B, C и D колеса, лежащих на противоположных концах взаимно перпендикулярных диаметров, один из которых горизонтален, в момент времени с.
Неравномерное движение по кругу.
Если вам доводилось уже решать задачи на движение по окружности, то вы знаете, что прежде всего надо найти мгновенный центр вращения. Здесь таким центром будет являться точка . Относительно этой точки скорость центра колеса будет равна , а, так как точка располагается от центра вращения на расстоянии двух радиусов – вдвое дальше, чем центр колеса, – то и скорость точки будет вдвое больше: . Так происходит, потому что скорость точки складывается из линейной скорости вращения (показана на рисунке рыжим) и скорости поступательного движения (черным), а вектора этих скоростей коллинеарны: направлены в точке параллельно линии движения, и в одну сторону, поэтому мы их складываем. У точек и вектор скорости также будет суммой вектора скорости поступательного движения и линейной скорости вращения. Но в обеих этих точках данные векторы перпендикулярно направлены, хотя и равны по модулю, так что скорости точек будут равными по модулю, а направлены в разные стороны (показаны синими стрелками):
Здесь надо отметить, что угол между векторами скоростей точек и и горизонтом составит – это в дальнейшем пригодится.
Также из рисунка понятно, почему скорость точки равна нулю: линейная скорость вращения направлена против скорости поступательного движения и компенсирует ее.
Теперь скорости точек можно определить численно:
Давайте определим ускорение каждой точки. У точки скорость нулевая, но это не означает, что ее ускорение тоже равно нулю, потому что линейная скорость вращения точки не равна нулю. Поэтому ускорение точки – обычное нормальное ускорение:
У точки ускорение будет складываться из двух составляющих: во-первых, она имеет нормальное ускорение, как и все остальные точки, только потому, что участвует во вращательном движении, во-вторых, точка также имеет и составляющую ускорения, обусловленную тем, что скорость переменна:
Тогда полное ускорение точки может быть определено по теореме Пифагора, ведь векторы линейного и нормального ускорений перпендикулярны друг другу (именно для этой точки):
С точками и все будет немножечко сложнее: нормальное ускорение у них тоже есть, и есть ускорение «линейное» – связанное с изменением скорости, вызывающее это изменение, но вот направлены эти два вектора уже не перпендикулярно друг другу. Ускорение «линейное» совпадает по направлению с вектором мгновенной скорости. А эта скорость, как мы знаем, направлена под углом к горизонту и для точки , и для точки . Поэтому, согласно рисунку, ускорение точки найдем так:
Аналогично можно определить ускорение точки (глядя на рисунок):
Ответ: , м/с, м/с,
м/с, м/с, м/с, м/с.
Задачи. Равномерное движение по окружности — PhysBook
Уровень А
1. Колесо совершает за одну минуту:
а) 30 оборотов;
б) 1500 оборотов.
Определите его период.
Решение
2. Период вращения лопастей ветряной мельницы равен 5 с. Определите число оборотов лопастей за 1 ч.
Решение
3. Определите частоту движения:
а) секундной;
б) минутной, – стрелок механических часов.
Секундная стрелка часов совершает один оборот за 1 мин, минутная стрелка – один оборот за 1 ч.
Решение
4. Частота вращения воздушного винта самолета 25 Гц. За какое время винт совершает 3000 оборотов.
Решение
5. Период вращения Земли вокруг своей оси равен 1 сут. Определите частоту ее вращения.
Решение
6. Колесо совершило 15 полных оборотов. Определите его угловое перемещение.
Решение
7. Колесо радиуса 0,5 м прокатилось 100 м. Определите угловое перемещение колеса.
Решение
8. Определите угловую скорость вращения колеса, если за 60 с колесо поворачивается на 20π.
Решение
9. Угловая скорость барабана сепаратора 900 рад/с. Определите угловое перемещение барабана за 15 с.
Решение
10. Определите угловую скорость вала, вращающегося:
а) с периодом 10 с;
б) с частотой 30 Гц.
Решение
11. Маховик вращается с постоянной угловой скоростью 9 рад/с. Определите:
а) частоту его вращения;
б) период его вращения.
Решение
12. Укажите направление скорости в точках А, В, С, D (рис. 1), если круг вращается:
а) по часовой стрелке;
б) против часовой стрелки.
Рис. 1
Решение
13. Колесо велосипеда имеет радиус 25 см. Определите линейную скорость точек обода колеса, если оно вращается с частотой 4 Гц.
Решение
14. Точильный круг радиусом 10 см делает один оборот за 0,2 с. Найдите скорость точек, наиболее удаленных от оси вращения.
Решение
15. Скорость точек экватора Солнца при его вращении вокруг своей оси равна 2,0 км/с. Найдите период вращения Солнца вокруг своей оси, если радиус Солнца 6,96∙108 м.
Решение
16. Тело движется по окружности радиусом 3 м со скоростью 12π м/с. Чему равна частота обращения?
Решение
17. Тело движется по дуге окружности радиусом 50 м. Определите линейную скорость тела, если известно, что его угловая скорость равна π рад/с.
Решение
18. Спортсмен бежит равномерно по окружности радиусом 100 м со скоростью 10 м/с. Определите его угловую скорость.
Решение
19. Укажите направление ускорения в точках A, B, C, D при движении по окружности (рис. 2).
Рис. 2
Решение
20. Велосипедист движется по закруглению дороги радиусом 50 м со скоростью 36 км/ч. С каким ускорением он проходит закругление?
Решение
21. Каков радиус кривизны закругления дороги, если по ней автомобиль движется с центростремительным ускорением 1 м/с2 при скорости 10 м/с?
Решение
22. С какой скоростью велосипедист проходит закругление велотрека радиусом 50 м, если он имеет центростремительное ускорение 2 м/с2?
Решение
23. Шкив вращается с угловой скоростью 50 рад/с. Определите центростремительное ускорение точек находящихся на расстоянии 20 мм от оси вращения.
Решение
24. Земля вращается вокруг своей оси с центростремительным ускорением 0,034 м/с2. Определите угловую скорость вращения, если радиус Земли 6400 км.
Решение
Уровень B
1. Может ли тело двигаться по окружности без ускорения?
Решение
2. Первая в мире орбитальная космическая станция, образованная в результате стыковки космических кораблей «Союз-4» и «Союз-5» 16 января 1969 г., имела период вращения 88,85 мин и среднюю высоту над поверхностью Земли 230 км (считайте орбиту круговой). Найдите среднюю скорость движения станции. Радиус Земли принять равным 6400 км.
Решение
3. Искусственный спутник Земли (ИСЗ) движется по круговой орбите со скоростью 8,0 км/с с периодом вращения 96 мин. Определите высоту полета спутника над поверхностью Земли. Радиус Земли принять равным 6400 км.
Решение
4. Какова линейная скорость точек Земной поверхности на широте Санкт-Петербурга (60°) при суточном вращении Земли? Радиус Земли принять равным 6400 км.
Решение
5. Допустимо ли насадить точильный круг на вал двигателя, делающего 2850 оборотов в минуту, если на круге имеется штамп завода «35 м/с, Ø 250 мм»?
Решение
6. Скорость поезда 72 км/ч. Сколько оборотов в минуту делают колеса локомотива, радиус которых 1,2 м?
Решение
7. Какова угловая скорость вращения колеса ветродвигателя, если за 2 мин колесо сделало 50 оборотов?
Решение
8. За какое время колесо, имеющее угловую скорость 4π рад/с, сделает 100 оборотов?
Решение
9. Диск диаметром 50 см равномерно перекатывают на расстояние 2 м за 4 с. Какова угловая скорость вращения диска?
Решение
10. Тело движется по дуге окружности радиусом 50 м. Определите линейную скорость движения тела и пройденный им путь, если известно, что его угловое перемещение за 10 с равно 1,57 рад.
Решение
11. Как изменится линейная скорость вращения материальной точки по окружности, если угловую скорость точки увеличить в 2 раза, а расстояние от точки до оси вращения уменьшить в 4 раза?
Решение
12. Рабочее колесо турбины Красноярской ГЭС им. 50-летия СССР имеет диаметр 7,5 м и вращается с частотой 93,8 об/мин. Каково центростремительное ускорение концов лопаток турбины?
Решение
13. Ветряное колесо радиусом 2,0 м делает 40 оборотов в минуту. Найдите центростремительное ускорение концевых точек лопастей колеса.
Решение
14. Период вращения первого пилотируемого корабля-спутника «Восток» вокруг Земли был равен 90 мин. С каким ускорением двигался корабль, если его средняя высота над Землей 320 км? Радиус Земли принять равным 6400 км.
Решение
15. Угловая скорость вращения лопастей колеса ветродвигателя 6 рад/с. Найдите центростремительное ускорение концов лопастей, если линейная скорость концов лопастей 20 м/с.
Решение
16. Две материальные точки движутся по окружностям радиусами R1 = 10 см и R2 = 30 см с одинаковыми скоростями 0,20 м/с. Во сколько раз отличаются их центростремительные ускорения?
Решение
17. Две материальные точки движутся по окружностям радиусами R1 = 0,2 м и R2 = 0,4 м с одинаковыми периодами. Найдите отношение их центростремительных ускорений.
Решение




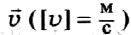
 . Время одного полного оборота: Т = t / N, где N – число полных оборотов за промежуток времени t.
. Время одного полного оборота: Т = t / N, где N – число полных оборотов за промежуток времени t. . Число оборотов в единицу времени: v = N / t. Связана с периодом обращения соотношением v = 1 / T. Внимание! Полезно установить связь между линейной скоростью с другими параметрами обращения!
. Число оборотов в единицу времени: v = N / t. Связана с периодом обращения соотношением v = 1 / T. Внимание! Полезно установить связь между линейной скоростью с другими параметрами обращения! .
.
 , где ʋ – модуль линейной скорости в данной точке окружности.
, где ʋ – модуль линейной скорости в данной точке окружности.