Формулы сокращённого умножения многочленов — Википедия
Формулы сокращённого умножения многочленов — часто встречающиеся случаи умножения многочленов. Многие из них являются частным случаем бинома Ньютона. Изучаются в средней школе в курсе алгебры.
Содержание
- 1 Формулы для квадратов
- 2 Формулы для кубов
- 3 Формулы для четвёртой степени
- 4 Формулы для n-ой степени
- 5 Некоторые свойства формул
- 6 См. также
- 7 Литература
Формулы для квадратов
- (a±b)2=a2±2ab+b2{\displaystyle (a\pm b)^{2}=a^{2}\pm 2ab+b^{2}}
- a2−b2=(a+b)(a−b){\displaystyle a^{2}-b^{2}=(a+b)(a-b)}
- (a+b+c)2=a2+b2+c2+2ab+2ac+2bc{\displaystyle \left(a+b+c\right)^{2}=a^{2}+b^{2}+c^{2}+2ab+2ac+2bc}
Формулы для кубов
- (a±b)3=a3±3a2b+3ab2±b3{\displaystyle (a\pm b)^{3}=a^{3}\pm 3a^{2}b+3ab^{2}\pm b^{3}}
- a3±b3=(a±b)(a2∓ab+b2){\displaystyle a^{3}\pm b^{3}=(a\pm b)(a^{2}\mp ab+b^{2})}
- (a+b+c)3=a3+b3+c3+3a2b+3a2c+3ab2+3ac2+3b2c+3bc2+6abc{\displaystyle \left(a+b+c\right)^{3}=a^{3}+b^{3}+c^{3}+3a^{2}b+3a^{2}c+3ab^{2}+3ac^{2}+3b^{2}c+3bc^{2}+6abc}
Формулы для четвёртой степени
- (a±b)4=a4±4a3b+6a2b2±4ab3+b4{\displaystyle (a\pm b)^{4}=a^{4}\pm 4a^{3}b+6a^{2}b^{2}\pm 4ab^{3}+b^{4}}
- a4−b4=(a−b)(a+b)(a2+b2){\displaystyle a^{4}-b^{4}=(a-b)(a+b)(a^{2}+b^{2})} (выводится из a2−b2{\displaystyle a^{2}-b^{2}})
Формулы для n-ой степени
- an−bn=(a−b)(an−1+an−2b+an−3b2+…+a2bn−3+abn−2+bn−1){\displaystyle a^{n}-b^{n}=(a-b)(a^{n-1}+a^{n-2}b+a^{n-3}b^{2}+…+a^{2}b^{n-3}+ab^{n-2}+b^{n-1})}
- a2n−b2n=(a+b)(a2n−1−a2n−2b+a2n−3b2−…−a2b2n−3+ab2n−2−b2n−1){\displaystyle a^{2n}-b^{2n}=(a+b)(a^{2n-1}-a^{2n-2}b+a^{2n-3}b^{2}-…-a^{2}b^{2n-3}+ab^{2n-2}-b^{2n-1})}, где n∈N{\displaystyle n\in N}
- a2n−b2n=(an+bn)(an−bn){\displaystyle a^{2n}-b^{2n}=(a^{n}+b^{n})(a^{n}-b^{n})}
- a2n+1+b2n+1=(a+b)(a2n−a2n−1b+a2n−2b2−…+a2b2n−2−ab2n−1+b2n){\displaystyle a^{2n+1}+b^{2n+1}=(a+b)(a^{2n}-a^{2n-1}b+a^{2n-2}b^{2}-…+a^{2}b^{2n-2}-ab^{2n-1}+b^{2n})}, где n∈N{\displaystyle n\in N}
Некоторые свойства формул
- (a−b)2n=(b−a)2n{\displaystyle (a-b)^{2n}=(b-a)^{2n}}, где n∈N{\displaystyle n\in N}
- (a−b)2n+1=−(b−a)2n+1{\displaystyle (a-b)^{2n+1}=-(b-a)^{2n+1}}, где n∈N{\displaystyle n\in N}
См. также
- Многочлен
- Бином Ньютона
- Факторизация многочленов
Литература
- М. Я. Выгодский. Справочник по элементарной математике. — Москва, 1958.
Формулы сокращенного умножения: таблица, примеры использования
Формулы сокращенного умножения (ФСУ) применяются для возведения в степень и умножения чисел и выражений. Часто эти формулы позволяют произвести вычисления более компактно и быстро.
В данной статье мы перечислим основные формулы сокращенного умножения, сгруппируем их в таблицу, рассмотрим примеры использования этих формул, а также остановимся на принципах доказательств формул сокращенного умножения.
Формулы сокращенного умножения. Таблица
Впервые тема ФСУ рассматривается в рамках курса «Алгебра» за 7 класс. Приведем ниже 7 основных формул.
Формулы сокращенного умножения- формула квадрата суммы: a+b2=a2+2ab+b2
- формула квадрата разности: a-b2=a2-2ab+b2
- формула куба суммы: a+b3=a3+3a2b+3ab2+b3
- формула куба разности: a-b3=a3-3a2b+3ab2-b3
- формула разности квадратов: a2-b2=a-ba+b
- формула суммы кубов: a3+b3=a+ba2-ab+b2
- формула разности кубов: a3-b3=a-ba2+ab+b2
Буквами a, b, c в данных выражениях могут быть любые числа, переменные или выражения. Для удобства использования лучше выучить семь основных формул наизусть. Сведем их в таблицу и приведем ниже, обведя рамкой.

Первые четыре формулы позволяют вычислять соответственно квадрат или куб суммы или разности двух выражений.
Пятая формула вычисляет разность квадратов выражений путем произведения их суммы и разности.
Шестая и седьмая формулы — соответственно умножение суммы и разности выражений на неполный квадрат разности и неполный квадрат суммы.
Формула сокращенного умножения иногда еще называют тождествами сокращенного умножения. В этом нет ничего удивительного, так как каждое равенство представляет собой тождество.
При решении практических примеров часто используют формулы сокращ
Формулы сокращенного умножения
Формулы сокращенного умножения.
Цели:
— Изучение формул сокращенного умножения: квадрата суммы и квадрата разности двух выражений; разности квадратов двух выражений; куба суммы и куба разности двух выражений; суммы и разности кубов двух выражений.
— Применение формул сокращенного умножения при решении примеров.
Для упрощения выражений, разложения многочленов на множители, приведения многочленов к стандартному виду используются формулы сокращенного умножения. Формулы сокращенного умножения нужно знать наизусть.
Пусть а, b R. Тогда:
1. Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
(a + b)2
2. Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
(a — b)2 = a2 — 2ab + b2
3. Разность квадратов двух выражений равна произведению разности этих выражений и их суммы.a2 — b2 = (a -b) (a+b)
4. Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.
(a + b)3 = a3 + 3a2b + 3ab2 + b3
5. Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.
(a — b)3 = a3 — 3a2b + 3ab2 — b3
6. Сумма кубов двух выражений равна произведению суммы первого и второго выражения на неполный квадрат разности этих выражений.
a3
7. Разность кубов двух выражений равна произведению разности первого и второго выражения на неполный квадрат суммы этих выражений.
a3 — b3 = (a — b) (a2 + ab + b2)
Применение формул сокращенного умножения при решении примеров.
Пример 1.
Вычислить
а) (40+1)2
б) 982
Решение:
а) Используя формулу квадрата суммы двух выражений, имеем
(40+1)2 = 402 + 2 · 40 · 1 + 12 = 1600 + 80 + 1 = 1681
б) Используя формулу квадрата разности двух выражений, получим
982 = (100 – 2)2 = 1002 — 2 · 100 · 2 + 22 = 10000 – 400 + 4 = 9604
Пример 2.
Вычислить
Решение
Используя формулу разности квадратов двух выражений, получим
Пример 3.
Упростить выражение
(х — у)2 + (х + у)2
Решение
Воспользуемся формулами квадрата суммы и квадрата разности двух выражений
(х — у)2 + (х + у)2 = х2 — 2ху + у2 + х2 + 2ху + у
Формулы сокращенного умножения в одной таблице:
(a + b)2 = a2 + 2ab + b2
(a — b)2 = a2 — 2ab + b2
a2 — b2 = (a — b) (a+b)
(a + b)3 = a3 + 3a2b + 3ab2 + b3
(a — b)3 = a3 — 3a2b + 3ab2 — b3
a3 + b3 = (a + b) (a2 — ab + b2)
a3 — b3 = (a — b) (a
Формулы сокращённого умножения. Разность кубов и сумма кубов
При изучении формул сокращенного умножения мы уже изучили:
 – квадрат суммы и разности;
– квадрат суммы и разности;
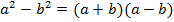 – разность квадратов.
– разность квадратов.
Выведем формулу разности кубов.
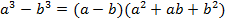 .
.
Наша задача – доказать, что при раскрытии скобок в правой части и приведении подобных слагаемых мы придем в результате к левой части.
Выполняем умножение многочленов:
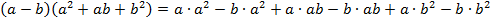
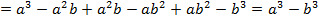 .
.
Что и требовалось доказать.
Выражение 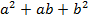 называется неполным квадратом суммы, так как отсутствует двойка перед произведением выражений.
называется неполным квадратом суммы, так как отсутствует двойка перед произведением выражений.
Определение
Разность кубов двух выражений есть произведение разности этих выражений на неполный квадрат их суммы.
Выведем формулу суммы кубов.
 .
.
Выполняем умножение многочленов:

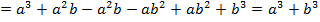 .
.
Что и требовалось доказать.
Выражение 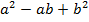
Определение
Сумма кубов двух выражений есть произведение суммы этих выражений на неполный квадрат их разности.
Пример 1 – упростить выражение:
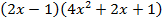 .
.
Пусть 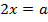 и
и 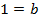
 .
.
Это изучаемая формула – разности кубов:
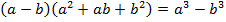
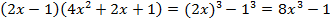 .
.
Пример 2 – упростить выражение:
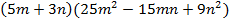 .
.
Пусть 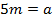 и
и 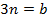 , имеем:
, имеем:
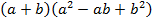 .
.
Это изучаемая формула – суммы кубов:
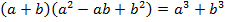
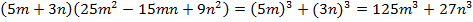 .
.
Пример 3 – разложить на множители:
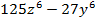 .
.
Несложно заметить формулу разности кубов:
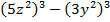 .
.
Применяем изучаемую формулу:
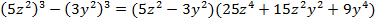 .
.
Пример 4 – разложить на множители:
 .
.
Несложно заметить формулу разности кубов:
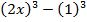 .
.
Применяем изучаемую формулу:
.
Пример 5 – решить уравнение:
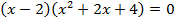 .
.
Пусть 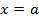 и
и  , имеем:
, имеем:
 .
.
Это изучаемая формула – разности кубов:
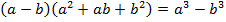
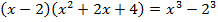
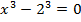
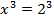
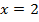 .
.
Пример 6 – решить уравнение:
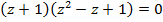 .
.
Пусть  и
и 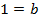 , имеем:
, имеем:
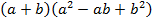 .
.
Это изучаемая формула – суммы кубов:
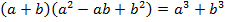
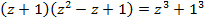
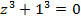
z3 = -13
z = -1
Пример 7 – вычислить при 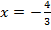 :
:
 .
.
Пусть 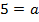 и
и 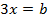 , имеем:
, имеем:
 .
.
Это изучаемая формула – разности кубов:
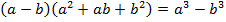
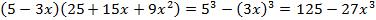
 .
.
Подставим значение переменной:
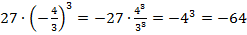 .
.
Пример 8: докажите, что 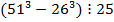 .
.
Доказательство.
Применим формулу разности кубов и разложим заданное выражение на множители:
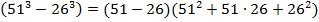 .
.
Вторую скобку оставим без изменений, выполним вычисления в первой скобке:
 .
.
Получили произведение чисел, содержащее множитель 25, очевидно, что данное выражение кратно 25.
Вывод: на данном уроке мы рассмотрели формулы разности и суммы кубов и их применение для различных типов задач.
Список литературы
- Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 7. 6 издание. – М.: Просвещение, 2010.
- Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебра 7. – М.: ВЕНТАНА-ГРАФ.
- Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е. и др. Алгебра 7 – М.: Просвещение, 2006.
Домашнее задание
- Задание 1 – упростить выражения:
а) ; б)
; б)  .
. - Задание 2 – разложить на множители:
a) ; б)
; б)  .
. - Задание 3 – № 882, 883 – Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 7.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Школьный помощник (Источник).
- Инженерный справочник (Источник).
- Интернет-портал Grandars.ru (Источник).
Сумма и разность кубов | umath.ru
Сумма кубов
![\[a^3 + b^3 = (a + b)(a^2 - ab + b^2).\]](/800/600/https/umath.ru/wp-content/ql-cache/quicklatex.com-23581065a51e0a22782aa83f242f56f0_l3.png)
Выражение  отличается от правой части формулы квадрата разности только коэффициентом при
отличается от правой части формулы квадрата разности только коэффициентом при  Поэтому это выражение называют неполным квадратом разности.
Поэтому это выражение называют неполным квадратом разности.
Читают: сумма кубов двух выражений равна произведению суммы этих выражений на неполный квадрат их разности.
Формулу суммы кубов можно получить из формулы куба суммы:
![\[(a + b)^3 = a^3 + 3a^2b + 3ab^2 + b^3.\]](/800/600/https/umath.ru/wp-content/ql-cache/quicklatex.com-7ca09042d21806330c74a4c1c8e2e352_l3.png)
Выразим отсюда 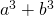 :
:
![\[a^3 + b^3 = (a + b)^3 - 3a^2b - 3ab^2 = (a + b)^3 - 3ab(a + b) = \]](/800/600/https/umath.ru/wp-content/ql-cache/quicklatex.com-8f6696a7e360b39d34628031d9a12db0_l3.png)
![\[ = (a + b)((a + b)^2 - 3ab) = (a + b)(a^2 - ab + b^2).\]](/800/600/https/umath.ru/wp-content/ql-cache/quicklatex.com-13523afe624406c2325529b51f5a16b3_l3.png)
Разность кубов
Заменив в формуле суммы кубов 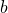 на
на 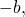 получим формулу разности кубов:
получим формулу разности кубов:
![\[a^3 - b^3 = (a - b)(a^2 + ab + b^2).\]](/800/600/https/umath.ru/wp-content/ql-cache/quicklatex.com-a6c8252d90efe5b887495d03143f3a3e_l3.png)
Выражение 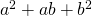 называют неполным квадратом суммы.
называют неполным квадратом суммы.
Читают: разность кубов двух выражений равна произведению разности этих выражений на неполных квадрат их суммы.
Пример 1. Разложить на множители многочлен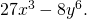
Решение. Заметим, что  а
а 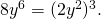 Поэтому по формуле разности кубов получаем
Поэтому по формуле разности кубов получаем
![\[27x^3 - 8y^6 = (3x - 2y^2)(9x^2 + 6xy^2 + 4y^4).\]](/800/600/https/umath.ru/wp-content/ql-cache/quicklatex.com-35806b0f5f713b054f0586c3b50f313c_l3.png)
Все главные формулы по математике — Математика — Теория, тесты, формулы и задачи
Оглавление:
Формулы сокращенного умножения
К оглавлению…
Квадрат суммы:

Квадрат разности:

Разность квадратов:

Разность кубов:

Сумма кубов:

Куб суммы:

Куб разности:

Последние две формулы также часто удобно использовать в виде:


Квадратное уравнение и формула разложения квадратного трехчлена на множители
К оглавлению…
Пусть квадратное уравнение имеет вид:

Тогда дискриминант находят по формуле:

Если D > 0, то квадратное уравнение имеет два корня, которые находят по формуле:

Если D = 0, то квадратное уравнение имеет один корень (его кратность: 2), который ищется по формуле:

Если D < 0, то квадратное уравнение не имеет корней. В случае когда квадратное уравнение имеет два корня, соответствующий квадратный трехчлен может быть разложен на множители по следующей формуле:

Если квадратное уравнение имеет один корень, то разложение соответствующего квадратного трехчлена на множители задается следующей формулой:

Только в случае если квадратное уравнение имеет два корня (т.е. дискриминант строго больше ноля) выполняется Теорема Виета. Согласно Теореме Виета, сумма корней квадратного уравнения равна:

Произведение корней квадратного уравнения может быть вычислено по формуле:

Парабола
График параболы задается квадратичной функцией:

При этом координаты вершины параболы могут быть вычислены по следующим формулам. Икс вершины:

Игрек вершины параболы:

Свойства степеней и корней
К оглавлению…
Основные свойства степеней:






Последнее свойство выполняется только при n > 0. Ноль можно возводить только в положительную степень.

Основные свойства математических корней:





Для арифметических корней:

Последнее справедливо: если n – нечетное, то для любого a; если же n – четное, то только при a больше либо равном нолю. Для корня нечетной степени выполняется также следующее равенство:

Для корня четной степени имеется следующее свойство:

Формулы с логарифмами
К оглавлению…
Определение логарифма:

Определение логарифма можно записать и другим способом:

Свойства логарифмов:
Логарифм произведения:

Логарифм дроби:

Вынесение степени за знак логарифма:



Другие полезные свойства логарифмов:


Арифметическая прогрессия
К оглавлению…
Формулы n-го члена арифметической прогрессии:


Соотношение между тремя соседними членами арифметической прогрессии:

Формула суммы арифметической прогрессии:

Свойство арифметической прогрессии:

Геометрическая прогрессия
К оглавлению…
Формулы n-го члена геометрической прогрессии:


Соотношение между тремя соседними членами геометрической прогрессии:

Формула суммы геометрической прогрессии:

Формула суммы бесконечно убывающей геометрической прогрессии:

Свойство геометрической прогрессии:

Тригонометрия
К оглавлению…
Пусть имеется прямоугольный треугольник:

Тогда, определение синуса:

Определение косинуса:

Определение тангенса:

Определение котангенса:
Основное тригонометрическое тождество:
Простейшие следствия из основного тригонометрического тождества:


Формулы двойного угла
Синус двойного угла:

Косинус двойного угла:

Тангенс двойного угла:

Котангенс двойного угла:

Тригонометрические формулы сложения
Синус суммы:
Синус разности:

Косинус суммы:

Косинус разности:
Тангенс суммы:

Тангенс разности:

Котангенс суммы:

Котангенс разности:

Тригонометрические формулы преобразования суммы в произведение
Сумма синусов:

Разность синусов:
Сумма косинусов:

Разность косинусов:

Сумма тангенсов:

Разность тангенсов:

Сумма котангенсов:

Разность котангенсов:

Тригонометрические формулы преобразования произведения в сумму
Произведение синусов:

Произведение синуса и косинуса:

Произведение косинусов:

Формулы понижения степени
Формула понижения степени для синуса:

Формула понижения степени для косинуса:

Формула понижения степени для тангенса:
Формула понижения степени для котангенса:
Формулы половинного угла
Формула половинного угла для тангенса:

Формула половинного угла для котангенса:

Тригонометрические формулы приведения
Формулы приведения задаются в виде таблицы:

Тригонометрическая окружность
По тригонометрической окружности легко определять табличные значения тригонометрических функций:

Тригонометрические уравнения
К оглавлению…
Формулы решений простейших тригонометрических уравнений. Для синуса существует две равнозначные формы записи решения:


Для остальных тригонометрических функций запись однозначна. Для косинуса:

Для тангенса:

Для котангенса:

Решение тригонометрических уравнений в некоторых частных случаях:








Геометрия на плоскости (планиметрия)
К оглавлению…
Пусть имеется произвольный треугольник:

Тогда, сумма углов треугольника:

Площадь треугольника через две стороны и угол между ними:

Площадь треугольника через сторону и высоту опущенную на неё:

Полупериметр треугольника находится по следующей формуле:

Формула Герона для площади треугольника:

Площадь треугольника через радиус описанной окружности:

Формула медианы:

Свойство биссектрисы:

Формулы биссектрисы:

Основное свойство высот треугольника:
Формула высоты:

Еще одно полезное свойство высот треугольника:

Теорема косинусов:

Теорема синусов:

Радиус окружности, вписанной в правильный треугольник:

Радиус окружности, описанной около правильного треугольника:

Площадь правильного треугольника:

Теорема Пифагора для прямоугольного треугольника (c — гипотенуза, a и b — катеты):

Радиус окружности, вписанной в прямоугольный треугольник:

Радиус окружности, описанной вокруг прямоугольного треугольника:

Площадь прямоугольного треугольника (h — высота опущенная на гипотенузу):
Свойства высоты, опущенной на гипотенузу прямоугольного треугольника:



Длина средней линии трапеции:

Площадь трапеции:

Площадь параллелограмма через сторону и высоту опущенную на неё:

Площадь параллелограмма через две стороны и угол между ними:

Площадь квадрата через длину его стороны:
Площадь квадрата через длину его диагонали:

Площадь ромба (первая формула — через две диагонали, вторая — через длину стороны и угол между сторонами):

Площадь прямоугольника через две смежные стороны:

Площадь произвольного выпуклого четырёхугольника через две диагонали и угол между ними:

Связь площади произвольной фигуры, её полупериметра и радиуса вписанной окружности (очевидно, что формула выполняется только для фигур в которые можно вписать окружность, т.е. в том числе для любых треугольников):

Свойство касательных:
Свойство хорды:

Теорема о пропорциональных отрезках хорд:

Теорема о касательной и секущей:

Теорема о двух секущих:
Теорема о центральном и вписанном углах (величина центрального угла в два раза больше величины вписанного угла, если они опираются на общую дугу):

Свойство вписанных углов (все вписанные углы опирающиеся на общую дугу равны между собой):

Свойство центральных углов и хорд:

Свойство центральных углов и секущих:

Условие, при выполнении которого возможно вписать окружность в четырёхугольник:

Условие, при выполнении которого возможно описать окружность вокруг четырёхугольника:
Сумма углов n-угольника:

Центральный угол правильного n-угольника:

Площадь правильного n-угольника:

Длина окружности:

Длина дуги окружности:

Площадь круга:

Площадь сектора:

Площадь кольца:

Площадь кругового сегмента:

Геометрия в пространстве (стереометрия)
К оглавлению…
Главная диагональ куба:

Объем куба:

Объём прямоугольного параллелепипеда:
Главная диагональ прямоугольного параллелепипеда (эту формулу также можно назвать: «трёхмерная Теорема Пифагора»):

Объём призмы:

Площадь боковой поверхности прямой призмы (P – периметр основания, l – боковое ребро, в данном случае равное высоте h):

Объём кругового цилиндра:

Площадь боковой поверхности прямого кругового цилиндра:

Объём пирамиды:

Площадь боковой поверхности правильной пирамиды (P – периметр основания, l – апофема, т.е. высота боковой грани):
Объем кругового конуса:

Площадь боковой поверхности прямого кругового конуса:

Длина образующей прямого кругового конуса:

Объём шара:

Площадь поверхности шара (или, другими словами, площадь сферы):

Координаты
К оглавлению…
Длина отрезка на координатной оси:

Длина отрезка на координатной плоскости:

Длина отрезка в трёхмерной системе координат:
Координаты середины отрезка (для координатной оси используется только первая формула, для координатной плоскости — первые две формулы, для трехмерной системы координат — все три формулы):

Таблица умножения
К оглавлению…

Таблица квадратов двухзначных чисел
К оглавлению…

Расширенная PDF версия документа «Все главные формулы по школьной математике»:
К оглавлению…
Оформление сертификатов соответствия продукции в Санкт-Петербурге от компании «Формула качества»
Добро пожаловать!
«Формула качества» предоставляет российскому бизнесу качественные услуги юридического, экспертного, лабораторного и организационного характера по сертификации продукции в России, которые призваны обеспечить:
- Правомочность, а, следовательно, легальность
- Гарантийность, а значит, стабильность
- Соответствие качества, а значит, расширение возможностей и рынков
- Надежность, а значит, статусность компании и имени
Очевидно, что ведение бизнеса во всех секторах рынка России становится прозрачнее, законнее и имеет четкие условия существования, например, с обязательной сертификацией продукции в РФ. Так, нормами отечественного законодательства отчетливо прописаны:
- порядок проведения продукции на рынок,
- требования к безопасности и качеству продукта,
- режимы и формы проверок,
- условия ввоза, вывоза и трансграничного перемещения и проч.
Соблюдение всех установленных конвенций и оформление необходимого пакета разрешительных бумаг, сертификатов, деклараций, лицензий, паспортов – это юридические составляющие легального, надежного имиджа любой компании.
Наши эксперты осуществляют
- техническое сопровождение (лабораторные исследования) вашей продукции,
- юридическое обоснование и подтверждение ее соответствия требуемым техническим регламентам,
- а также поддерживают ваши стремления роста, предоставляя услуги тендерного консалтинга.
Сфера сертификации продукции в СПб, в которой работают наши специалисты, охватывает все актуальные позиции, включая оформление разрешений от соответствующих надзорных органов страны и получение госрегистрации продуктов.
Лицензионная область нашей деятельности предусматривает работы по получению необходимых документов, требуемых для ведения бизнеса, связанного с транспортными перевозками товаров по территории ТС.
На самом деле, мы можем много больше и готовы предложить каждому нашему партнеру индивидуальные решения, связанные лишь с его потребностями, интересами и требованиями. Наша компания во всех случаях предоставляет персонального менеджера-специалиста, проводящего полный и грамотный консалтинг по всем необходимым вопросам и курирующего процесс оформления и получения бумаг до его успешного окончания.
Таким образом, мы всегда обеспечиваем продуктивную результативность всех обращений!




 ; б)
; б) 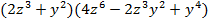 .
.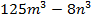 ; б)
; б) 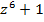 .
.