определение, формулы – простое и доходчивое объяснение

Определение силы трения

Виды силы трения

Как найти силу трения?

Формула силы трения

Рекомендованная литература и полезные ссылки

Сила трения, видео

Сила трения возникает из соприкосновения поверхностей двух физических тел, пребывающих в движении по отношению друг к другу. Теория трения издревле волновала умы человечества, древние инженеры: строители Египетских пирамид, Стоунхенджа в Англии или таинственных каменных истуканов на острове Пасхе, все они (как впрочем, и их современные коллеги) решали насущную проблему, связанную с трением и тем как его максимально уменьшить. Ведь именно сила трения делает трудным перемещение тяжелых грузов по земле (тех же камней для пирамид или Стоунхенджа), и чтобы облегчить эту задачу, нашими далекими предками было придумано такое полезное изобретение как колесо и сделано множество других важных открытий. В нашей статье мы посмотрим на силу трения в физическом аспекте, разберем, как действует она на те или иные тела, какие есть ее виды и формулы расчета.

Определение силы трения

Что такое сила трения? Классическое определение звучит так: сила трения – это сила, появляющаяся при соприкосновении двух тел во время движения и препятствующая этому самому движению. Иными словами, чем больше сила трения между телами, тем труднее их двигать относительно друг друга. Что же касается самой физической природы трения, то оно появляется как результат взаимодействия между атомами и молекулами тел, соприкасающихся между собой.

Также стоит заметить, что при трении двух тел на них действует третий закон Ньютона: сила трения, действующая на первое тело (тело А), равна силе трения, действующей на второе тело (тело Б), только по модулю эти силы имеют противоположное направление.

На этой картинке, сила трения, действующая на холодильник, равна силе трения, действующей на пол, но направлены эти силы в противоположные стороны.

Виды силы трения

В зависимости от характера движения тел различают такие виды сил трения как:

• Покоя. Сила трения покоя возникает при соприкосновении двух тел, которые, однако, не движутся относительно друг друга, и имеет нулевое значение.
• Скольжения. Сила трения скольжения – наиболее классическая иллюстрация действия трения, возникает при скольжении тел относительно друг друга. На ее величину влияет масса тела (чем она больше, тем больше сила трения), характер поверхности (разумеется, при скольжении по льду сила трения будет в разы меньше чем при скольжении по земле).
• Качения. Сила трения качения появляется, когда одно тело катится по поверхности другого, например, при езде на велосипеде или автомобиле. При качении сила трения гораздо меньше, чем при скольжении. Это опытным, эмпирическим путем установили еще те далекие наши предки, которые изобрели колесо – величайшее изобретение в истории науки и техники.
• Верчения. Сила трения верчения проявляется при вращении одного тела по поверхности другого.

Что же касается самого трения то и оно бывает нескольких видов:

• Сухое – проявляется при соприкосновении твердых поверхностей.
• Вязкое, также подобное трение называют жидкостным, появляется при соприкосновении твердого тела c жидкостью либо газом. Например, на корабль, плывущий по воде, как и на поверхность воды, действует вязкое (жидкостное) трение. Сила вязкого трения обычно гораздо меньше силы сухого трения.
• Смешанное, возникает, когда между поверхностями, которые соприкасаются, есть слой смазки.

Интересный факт: при осаде Константинополя в 1453 году турки, чтобы обойти специальную цепь, преграждающую путь турецким кораблям в залив Золотой Рог перетянули их по суше. А для того, чтобы уменьшить силу трения при перемещении больших тяжелых военных кораблей сделали настил из деревянных рельсов, который обильно смазали салом. Таким образом, благодаря смазке и смешанному трению, сила которого гораздо меньше, чем при трении сухом, турки удачно воплотили свой замысел, приведя защитников Константинополя в подлинное смятение.

Султан Мехмед II наблюдает за перевозкой своих судов.

Как видите, знание законов физики и механики не раз и не два находило свое практическое воплощение в реальной жизни.

Но вернемся от истории снова к физике, трение также разделяют на внешнее и внутреннее. Внешнее трение характерно для взаимодействия исключительно твердых тел. Внутреннее трение характеризуется вязкостью и возникает при взаимодействии жидкостей или газов, а такое взаимодействие может происходить внутри условно одного тела. Например, в водах мирового океана есть разные течения, с более холодной или более теплой водой, при взаимодействии этих течений между ними и возникает внутреннее трение.

Как найти силу трения?

Чтобы рассчитать силу трения необходимо знать коэффициент трения k, который зависит от характера поверхности. Коэффициент трения – постоянная величина и его значение можно узнать из специальной таблицы.

Помимо коэффициента трения необходимо знать силу реакцию опоры N, которая, по сути, равна силе тяжести (гравитации) зависящей от массы тела (m) и ускорения свободного падения. Ее формула будет иметь следующий вид:

N = m * g

Где m – масса тела, а g – ускорение свободного падения, это постоянная величина равная 9,8 м/с².

Формула силы трения

Сила трения высчитывается путем произведения реакции опоры N и коэффициента трения k. Формула силы трения будет иметь следующий вид:

F_тр = k * N.

В некоторых формулах коэффициент трения k обозначается символом µ.

Написанные выше расчеты справедливы в самом простом случае, когда тело лежит на строго горизонтальной поверхности.

Если же движение происходит по наклонной плоскости, то расчеты силы трения несколько усложняются. На тело, как и раньше, действует сила гравитации и реакция опоры поверхности, но не в одном направлении.

Таким образом, формула силы трения для тела, которое движется по наклонной поверхности, будет иметь следующий вид:

F_тр = k * m * g * cosα.

Где k – коэффициент трения, m – масса тела, g гравитационная постоянная (помним, что она равна 9,8 м/с²), cosα – отношение катета, прилежащего к углу, к гипотенузе треугольника (косинус).

При определении силы трения на наклонных поверхностях ярко проявляется связь между физикой и геометрией.

Рекомендованная литература и полезные ссылки

• Сила трения. ЗФТШ, МФТИ. Дата обращения 14 февраля 2019.
• Енохович А. С. Справочник по физике. — Просвещение, 1978. — С. 85. — 416 с.
• Зайцев А. К. Основы учения о трении, износе и смазке машин. Часть 1. Трение в машинах. Теория, расчет и конструкция подшипников и подпятников скольжения. Машгиз. М.-Л. — 1947. 256 с.
• Bowden F. P., Tabor D. The Friction and Lubrication of Solids. Oxford University Press, 2001.
  Persson Bo N. J.: Sliding Friction. Physical Principles and Applications. Springer, 2002.
• Popov V. L. Kontaktmechanik und Reibung. Ein Lehr- und Anwendungsbuch von der Nanotribologie bis zur numerischen Simulation, Springer, 2009.
• Rabinowicz E. Friction and Wear of Materials. Wiley-Interscience, 1995.

Сила трения, видео

И в завершении образовательное видео по теме нашей статьи.

Автор: Павел Чайка, главный редактор журнала Познавайка

При написании статьи старался сделать ее максимально интересной, полезной и качественной. Буду благодарен за любую обратную связь и конструктивную критику в виде комментариев к статье. Также Ваше пожелание/вопрос/предложение можете написать на мою почту [email protected] или в Фейсбук, с уважением автор.

Сила трения ℹ️ определение, природа и причины возникновения, виды, основные свойства, формулы, обозначение и единицы измерения, примеры и условия расчетов

Сила трения появляется, когда две поверхности соприкасаются и движутся относительно друг друга. Процесс изучает физика, в частности механика. Она рассматривает основные законы, которым поддаются тела при их движении и взаимодействии, выясняет причины, влияющие на изменение положения предметов.

Определение и природа силы трения

Сила трения F_тр возникает при касании двух тел. Она создает препятствия для их дальнейшего движения. 

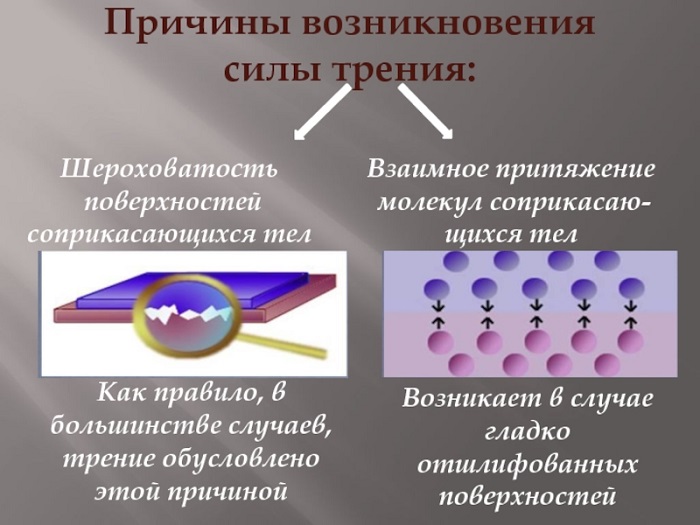
Это происходит при взаимодействии атомов и молекул, из которых состоят предметы. Поэтому природа ее появления – электромагнитные волны. Она действует в двух направлениях, направлена на оба тела. 

При этом ее значение по модулю не изменяется. Если на одно из двух соприкасающихся тел действует сила, то она оказывает влияние и на другое.

На предмет, остающийся без движения, влияет сила трения покоя. Пока ее значение не превысит внешнее вмешательство, пытающееся сместить предмет, он не изменит положение. 

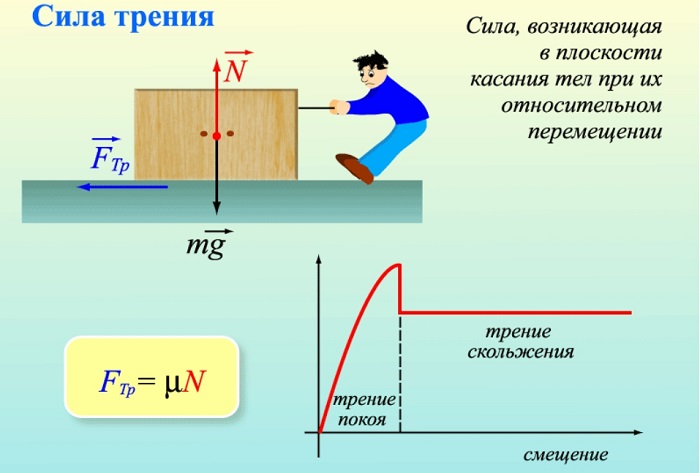
Когда же ее величина возрастет до определенного предела, произойдет перемещение в новое место. Тогда появляется сила трения скольжения, ее направление противоположно смещению предмета.

Благодаря действию трения невозможно перемещаться вечно. Движение закончится через определенное время. Если же внешняя сила вновь превысит значение трения покоя, то перемещение возобновится.

Виды силы трения

Основные виды силы трения:

1. Покоя. Она сопротивляется внешним факторам, пытающимся сдвинуть тело. При их отсутствии ее значение приравнивают к нулю.

2. Скольжения. Она находится в прямой зависимости от коэффициента трения и значения силы, с которой поверхность оказывает давление на тело. Ее направление действия всегда перпендикулярно поверхности. Она обычно ниже, чем максимальная сила трения покоя.

3. Качения. Она возникает, когда одно тело катится по поверхности другого. Например, при соприкосновении колеса едущего велосипеда с дорогой или при работе подшипникового механизма. Она оказывает гораздо меньшее действие, чем трение скольжения, если остальные условия считать неизменными. Ее открытие стало незаменимым для техники. Колеса и круглые детали, вращающиеся и меняющие положение, являются основой многих механизмов и работы транспортных средств.

4. Верчения. Она появляется, когда один предмет начинает вращаться по поверхности другого.

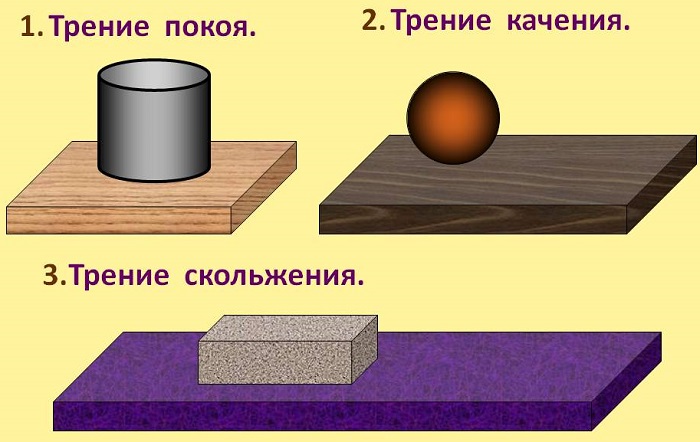
Само трение может быть нескольких видов:

1. Сухим. Проявляется при соприкосновении твердых поверхностей. На них не наблюдаются другие материалы и слои. Такое в природе и жизни встречается крайне редко.

2. Вязким. Его еще называют жидкостным. Возникает при взаимодействии твердого тела с жидкостью или газом. Они могут течь мимо неподвижного предмета. Или он перемещается в жидкой или газообразной субстанции. Например, лодку тянут на канате по реке. Тело заставляет перемещаться верхний слой жидкости или газа. Словно тянет его за собой. Он в свою очередь действует на другой слой, расположенный ниже. Чем дальше от тела, тем ниже скорость движения слоев. Это происходит из-за уменьшения влияния твердого предмета. Между слоями возникает сила трения, так как тела движутся относительно друг друга. Она приводит к их торможению, а значит и действует на твердое тело, останавливая его. Температура определяет степень вязкости веществ. Например, она снижается при нагревании масла. Это наглядно видно на работе автомобильного мотора. Когда машина долго находилась на холоде, двигатель нужно сначала разогреть, чтобы увеличить скорость его вращения. У газов обратная зависимость. Вязкость растет с увеличением температуры.

3. Смешанным. Оно наблюдается, когда между телами, соприкасающимися поверхностями, есть слой смазки.

Также трение разделяют на внутреннее и внешнее. Последнее возникает при взаимодействии твердых тел. Значит к нему можно отнести сухое трение. 

Внутреннее же характеризуется вязкостью. Именно при взаимодействии жидкостей или газа смещение происходит внутри одного тела, когда слои движутся относительно друг друга.

Как найти силу трения

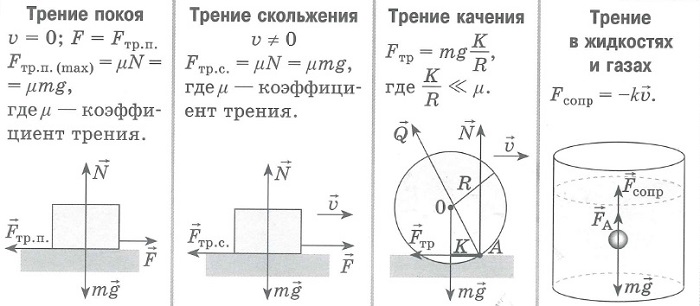
Чтобы найти силу трения, нужно знать коэффициент трения k, зависящий от свойств поверхности. Это постоянная величина, значение которой берется из таблиц. 

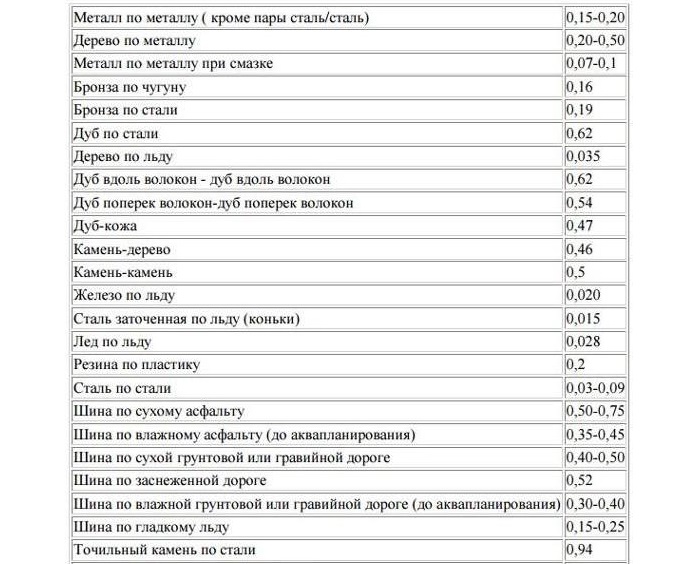
Также понадобится сила реакции опоры N. Нужная величина определяется произведением двух значений:

F_тр = k * N

Буквой k обозначается коэффициент. Также можно встретить символ µ. Обычно он находится в пределах от 0,1 до 1. 

Например, для резины, перемещающейся по сухому асфальту, при движении он колеблется от 0,5 до 0,8. При скольжении металла по дереву – 0,4, железа по чугуну – 0,18.

Сила реакции опоры не отличается от величины силы тяжести, зависящей от веса тела. Поэтому ее значение равно произведению массы тела (m) на ускорение свободного падения (g).

N = m * g

Это постоянная величина, составляющая 9,8 м/с². Это правило действует, когда приходится иметь дело с горизонтальной поверхностью. Сила тяжести и реакция опоры уравновешивают друг друга. Поэтому их считают равными величинами.

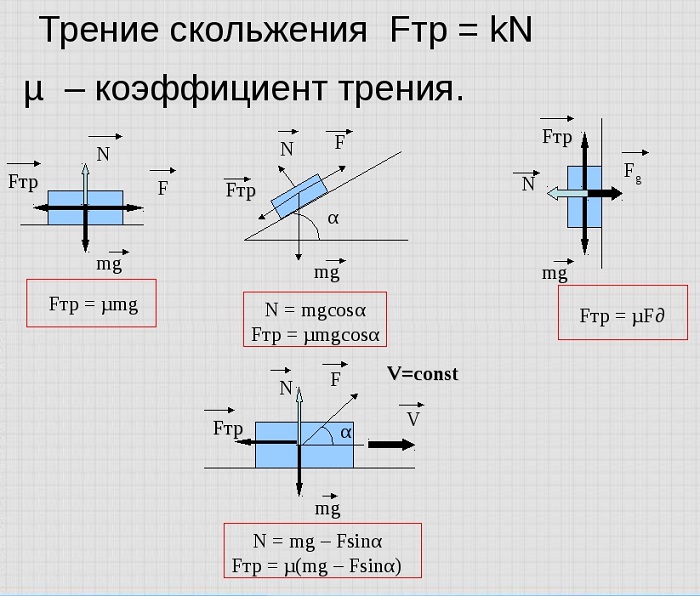
Если же происходит движение по наклонной плоскости, ход рассуждений несколько меняется. На предмет по-прежнему действуют силы тяжести и реакция опоры, но не в одном направлении.

 

При знании угла наклона плоскости к горизонту, формула трансформируется и приобретает следующий вид:

N = k * m *·g *·cosα

Здесь необходимо руководствоваться тем, что косинус это отношение катета, прилежащего к углу, к гипотенузе треугольника. Это один из тех случаев, доказывающих тесную взаимосвязь физики и тригонометрии.

Пример решения задачи

Задача, на применение полученных знаний, связанных с силой трения, поможет закрепить материал.

Условие задачи. На полу стоит коробка весом 7 кг. Коэффициент трения между ней и полом составляет 0,3. К коробке прикладывают силу, равную 14 Н. Сдвинется ли она с места?

Решение.

Коробка находится на горизонтальной плоскости. Она подвержена действию силы тяжести, которую уравнивает реакция опоры. Они направлены перпендикулярно коробке и полу. Значит, для определения силы реакции опоры, нужно умножить массу коробки на ускорение:

N = m * g;

N = 10 кг * 9,8 м/с² = 98 кг * м/с² = 98 Н;

F_тр = k * N;

F_тр = 0,3·* 98Н = 29,4 Н.

Ответ: полученное значение превышает усилия, приложенные к коробке со стороны, так как 29,4 Н > 14 Н. Значит, она останется на первоначальном месте.

Сила трения присутствует в жизни постоянно. Она мешает предметам сдвинуться с места и противится их длительному скольжению и перемещению. Ее значение зависит от поверхностей, с которыми приходится соприкасаться, их свойств и характеристик. 

Площадь соприкосновения не учитывается, зато имеет значение положение тела. Например, сила, возникающая при движении автомобиля по ровной поверхности, отличается от величины при перемещении по горной местности, расположенной под углом к горизонту. А если машине приходится двигаться на мокрой дороге, то значение снова меняется.

Шпаргалка по физике для 7 класса (формулы)

Нахождение скорости тела при равномерном движении:

_________________________

Нахождение плотности вещества:

_________________________

Нахождение модуля силы упругости при растяжении или сжатии (закон Гука), справедлив только для упругой деформации:

_________________________

Сила тяжести:

________________________

Вес тела:

(если тело и опора неподвижны или движутся прямолинейно и равномерно; сила тяжести приложена к телу, а вес к опоре или подвесу).

__________________________

Равнодействующая двух сил (модуль):

Если силы направлены по одной прямой в одну и ту же сторону.

Если силы направлены по одной прямой в противоположные стороны.

__________________________

Давление:

__________________________

Давление жидкости на дно и стенки сосуда:

Давление внутри жидкости на одной и той же глубине одинаково по всем направлениям.

___________________________

Гидравлический пресс:

___________________________

Действие жидкости и газа на погруженное в них тело (выталкивающая сила):

__________________________

Архимедова сила:

__________________________

Механическая работа:

Механическая работа прямо пропорциональна приложенной силе и прямо пропорциональна пройденному пути.

Если направление силы, действующей на тело, перпендикулярно направлению движения, то эта сила работы не совершает, работа равна нулю:

_________________________

Мощность:

Мощность равна отношению работы ко времени, за которое она была совершена.

_________________________

Правило равновесия рычага:

Рычаг находится в равновесии тогда, когда силы, действующие на него, обратно пропорциональны плечам этих сил.

__________________________

Момент силы:

Произведение модуля силы, вращающей тело, на ее плечо называется моментом силы.

____________________________

Равенство работ при использовании простых механизмов («Золотое правило» механики):

Действуя на длинное плечо рычага, мы выигрываем в силе, но при этом во столько же раз проигрываем в пути.

_____________________________

КПД:

____________________________

Потенциальная и кинетическая энергия:

потенциальная энергия – энергия, которая определяется взаимным положением взаимодействующих тел или частей одного и того же тела (энергия взаимодействия)

кинетическая энергия – энергия, которой обладает тело вследствие своего движения (энергия движения)

Как найти силу ампера формула

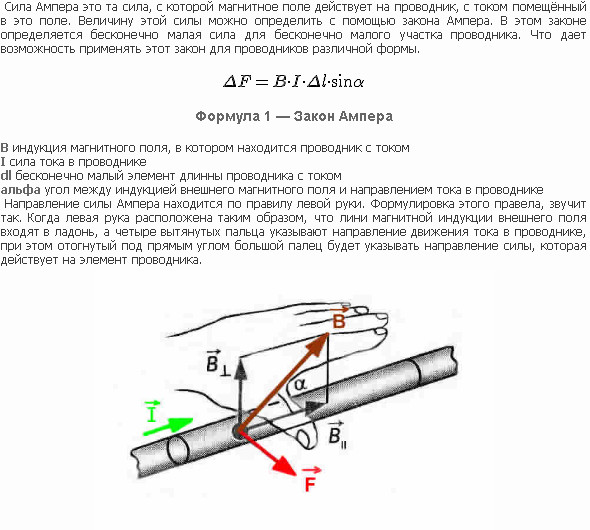
Сила, с которой магнитное поле действует на элемент объёма dV проводника с током плотности, находящегося в магнитном поле с индукцией :
.

Если ток течёт по тонкому проводнику, то, где — «элемент длины» проводника — вектор, по модулю равный dl и совпадающий по направлению с током. Тогда предыдущее равенство можно переписать следующим образом:
Сила, с которой магнитное поле действует на элемент проводника с током, находящегося в магнитном поле, прямо пропорциональна силе тока I в проводнике и векторному произведению элемента длины проводника на магнитную индукцию :
.

Направление силы определяется по правилу вычисления векторного произведения, которое удобно запомнить при помощи правила левой руки.

Модуль силы Ампера можно найти по формуле:
dF = IBdlsinα,

где α — угол между векторами магнитной индукции и тока.

Мы уже ввели логику того, что на движущийся в магнитном поле заряд действует сила. И опять нами была введена эта сила — сила Лоренца. Но сила Лоренца — сила, действующая на единичный заряд (т.е. одинокое тело), а если таких тел много? Например, если в магнитное поле помещён проводник с током. Ток — это упорядоченное движение заряженных частиц, тогда, если поместить проводник с током в магнитное поле, на каждый из зарядов будет действовать сила Лоренца (рис. 1).

Рис. 1. Суммарная сила Лоренца

Если просуммировать все эти силы, мы получим общую силу, действующую на проводник с током. Назовём эту силу — силой Ампера. Ток в проводнике организуется электронами (одинаковыми зарядами), и будем считать, что скорость продольного движения у них всех одинакова. Тогда суммарную силу Лоренца запишем как:

• — суммарная сила Лоренца,
• — количество зарядов в проводнике,
• — заряд носителя,
• — скорость движения носителя,
• — магнитная индукция поля,
• — синус угла между скоростью и вектором магнитной индукции.

Подставим (2) в (1):

Пусть длина проводника — , считая, что электроны движутся равномерно, то , тогда:

• — сила Ампера,
• — сила тока в проводнике,
• — магнитная индукция,
• — длина проводника в поле,
• — синус угла между направлением тока и направлением вектора магнитной индукции.

Сила (4) и является силой Ампера. Для определения направления силы Ампера пользуются правилом левой руки для силы Ампера: ориентируем левую руку так, чтобы линии магнитной индукции входили в ладонь, четыре пальца по току, тогда противопоставленный палец показывает направление силы Ампера.

В ряде задач не лишним будет использование соотношение для момента силы Ампера. Такие задачи чаще всего связаны с контуром (замкнутой кривой), помещённой в магнитное поле. Моментом сил называется произведение силы на плечо силы, тогда:

• — момент силы Ампера,
• — ток в проводнике,
• — магнитная индукция,
• — площадь контура,
• — синус угла между направлением силы тока и вектором магнитной индукции.

Вывод: в задачах сила Ампера вводится в очень ограниченной системе. Проводник с током должен быть помещён в магнитное поле. Только тогда и возникает эта сила (4). Ещё использование сопряжено со втором законом Ньютона и дальнейшими кинематическими характеристиками движения.

Закон Ампера показывает, с какой силой действует магнитное поле на помещенный в него проводник. Эту силу также называют силой Ампера.

Ампер первым установил, что проводники, по которым течет электрический ток, взаимодействуют механически (притягиваются или отталкиваются).

Конкретное направление силы Ампера можно найти с помощью правила левой руки. Левую руку надо расположить так, чтобы линии поля входили в ладонь, четыре пальца были направлены по току, тогда отогнутый на 90 градусов большой палец укажет направление силы Ампера.

Еще Ампер установил, что два параллельных проводника с током притягиваются, если токи имеют одинаковые направления и отталкиваются, если токи текут в противоположные стороны. Это просто объяснить, если представить, что один проводник создает магнитное поле, а другой проводник в него помещен и это поле действует на него. Можно использовать правило левой руки и выяснить, как направлена сила.

Закон Ампера

Сила Ампера – сила, действующая на проводник тока, находящийся в магнитном поле и равная произведению силы тока в проводнике, модуля вектора индукции магнитного поля, длины проводника и синуса угла между вектором магнитного поля и направлением тока в проводнике.

Для прямолинейного проводника сила Ампера имеет вид:

где: ( I ) — сила тока, которая течет в проводнике, ( overrightarrow ) — вектор индукции магнитного поля, в которое проводник помещен, ( overrightarrow ) — длина проводника в поле, направление задано направлением тока, ( alpha ) — угол между векторами ( overrightarrowи overrightarrow ) .

Этой формулой можно пользоваться:

• если длина проводника такая, что индукция во всех точках проводника может считаться одинаковой;
• если магнитное поле однородное (тогда длина проводника может быть любой, но при этом проводник целиком должен находиться в поле).

Если размер проводника произволен, а поле неоднородно, то формула выглядит следующим образом:

Значение закона Ампера

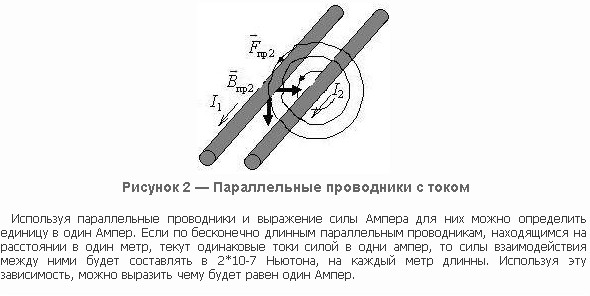
На основании закона Ампера устанавливают единицы силы тока в системах СИ и СГСМ. Так как ампер равен силе постоянного тока, который при течении по двум параллельным бесконечно длинным прямолинейным проводникам бесконечно малого кругового сечения, находящихся на расстоянии 1м друг от друга в вакууме вызывает силу взаимодействия этих проводников равную ( 2cdot <10>^<-7>Н ) на каждый метр длины.

Ток в один ампер – это такой ток, при котором два однородных параллельных проводника, расположенные в вакууме на расстоянии один метр друг от друга взаимодействуют с силой ( 2cdot <10>^ <-7>) Ньютона.

Закон взаимодействия токов – два находящихся в вакууме параллельных проводника, диаметры которых много меньше расстояний между ними, взаимодействуют с силой прямо пропорциональной произведению токов в этих проводниках и обратно пропорциональной расстоянию между ними.

Ответы Mail.ru: как найти силу упругости?

по закону Гука где f — сила упругости; х — удлинение (деформация) тела; k — коэффициент пропорциональности, зависящий от размеров и материала тела, называемый жесткостью. Единица жесткости в СИ — ньютон на метр (Н/м) . f=-kx

сила=коэффициент жесткость пружины*удлинение пружины

Веруська, в учебнике не написано как находить силы!

F упр = k (коэффициент упругости) * дельта X (растяжение пружины, верёвки и т. д.)

F упр = k (коэффициент упругости) * дельта X (растяжение пружины, верёвки и т. д.)

найдите пажалуйста силу упругости с помощью которой пуржина жесткостью 200н. м на метр удленяется на 10см.

Как найти силу трения скольжения 🚩 f трения формула 🚩 Естественные науки

Инструкция

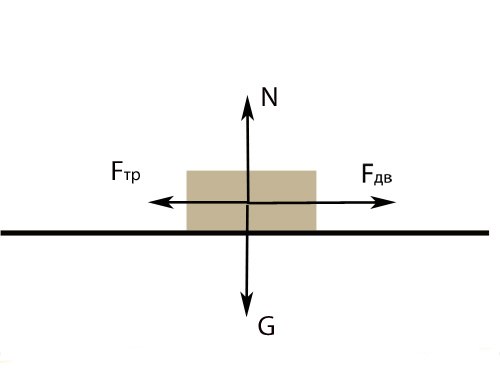
Случай 1. Формула для силы трения скольжения: Fтр = мN, где м – коэффициент трения скольжения, N – сила реакции опоры, Н. Для тела, скользящего по горизонтальной плоскости, N = G = mg, где G — вес тела, Н; m – масса тела, кг; g – ускорение свободного падения, м/с2. Значения безразмерного коэффициента м для данной пары материалов даны в справочной литературе. Зная массу тела и пару материалов. скользящих друг относительно друга, найдите силу трения.

Случай 2. Рассмотрите тело, скользящее по горизонтальной поверхности и двигающееся равноускоренно. На него действуют четыре силы: сила, приводящее тело в движение, сила тяжести, сила реакции опоры, сила трения скольжения. Так как поверхность горизонтальная, сила реакции опоры и сила тяжести направлены вдоль одной прямой и уравновешивают друг друга. Перемещение описывает уравнение: Fдв — Fтр = ma; где Fдв – модуль силы, приводящей тело в движение, Н; Fтр – модуль силы трения, Н; m – масса тела, кг; a – ускорение, м/с2. Зная значения массы, ускорения тела и силы, воздействующей на него, найдите силу трения. Если эти значения не заданы прямо, посмотрите, есть ли в условии данные, из которых можно найти эти величины.

Пример задачи 1: на брусок массой 5 кг, лежащий на поверхности, воздействуют силой 10 Н. В результате брусок двигается равноускоренно и проходит 10 метров за 10 секунд. Найдите силу трения скольжения.

Уравнение для движения бруска:Fдв — Fтр = ma. Путь тела для равноускоренного движения задается равенством: S = 1/2at^2. Отсюда вы можете определить ускорение: a = 2S/t^2. Подставьте данные условия: а = 2*10/10^2 = 0,2 м/с2. Теперь найдите равнодействующую двух сил: ma = 5*0,2 = 1 Н. Вычислите силу трения: Fтр = 10-1 = 9 Н.

Случай 3. Если тело на горизонтальной поверхности находится в состоянии покоя, либо двигается равномерно, по второму закону Ньютона силы находятся в равновесии : Fтр = Fдв.

Пример задачи 2: бруску массой 1 кг, находящемуся на ровной поверхности, сообщили импульс, в результате которого он проехал 10 метров за 5 секунд и остановилось. Определите силу трения скольжения.

Как и в первом примере, на скольжение бруска влияют сила движения и сила трения. В результате этого воздействия тело останавливается, т.е. приходит равновесие. Уравнение движения бруска: Fтр = Fдв. Или: N*м = ma. Брусок скользит равноускоренно. Рассчитайте его ускорение подобно задаче 1: a = 2S/t^2. Подставьте значения величин из условия: а = 2*10/5^2 = 0,8 м/с2. Теперь найдите силу трения: Fтр = ma = 0,8*1 = 0,8 Н.

Случай 4. На тело, самопроизвольно скользящее по наклонной плоскости, действуют три силы: сила тяжести (G), сила реакции опоры (N) и сила трения (Fтр). Сила тяжести может быть записана в таком виде: G = mg, Н, где m – масса тела, кг; g – ускорение свободного падения, м/с2. Поскольку эти силы направлены не вдоль одной прямой, запишите уравнение движения в векторном виде.

Сложив по правилу параллелограмма силы N и mg, вы получите результирующую силу F’. Из рисунка можно сделать выводы: N = mg*cosα; F’ = mg*sinα. Где α – угол наклона плоскости. Силу трения можно записать формулой: Fтр = м*N = м*mg*cosα. Уравнение для движения принимает вид: F’-Fтр = ma. Или: Fтр = mg*sinα-ma.

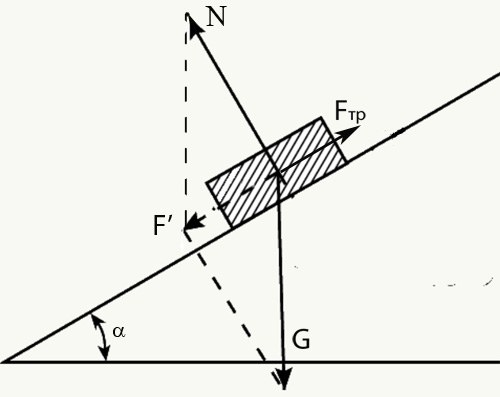
Случай 5. Если же к телу приложена дополнительная сила F, направленная вдоль наклонной плоскости, то сила трения будет выражаться: Fтр = mg*sinα+F-ma, если направление движения и силы F совпадают. Или: Fтр = mg*sinα-F-ma, если сила F противодействует движению.

Пример задачи 3: брусок массой 1 кг соскользнул с вершины наклонной плоскости за 5 секунд, пройдя путь 10 метров. Определите силу трения, если угол наклона плоскости 45о. Рассмотрите также случай, когда на брусок воздействовала дополнительная сила 2 Н, приложенная вдоль угла наклона по направлению движения.

Найдите ускорение тела аналогично примерам 1 и 2: а = 2*10/5^2 = 0,8 м/с2. Вычислите силу трения в первом случае: Fтр = 1*9,8*sin(45о)-1*0,8 = 7,53 Н. Определите силу трения во втором случае: Fтр = 1*9,8*sin(45о)+2-1*0,8= 9,53 Н.

Случай 6. Тело двигается по наклонной поверхности равномерно. Значит, по второму закону Ньютона система находится в равновесии. Если скольжение самопроизвольное, движение тела подчиняется уравнению: mg*sinα = Fтр.

Если же к телу приложена дополнительная сила (F), препятствующая равноускоренному перемещению, выражение для движения имеет вид: mg*sinα–Fтр-F = 0. Отсюда найдите силу трения: Fтр = mg*sinα-F.

По какой формуле найти силу тяги???

2 закон Ньютона. сила тяги + сила трения = масса*ускорение масса*ускорение=0,2*0,7= 0,14Н сила тяги = масса*ускорение — сила трения сила тяги = 0,14 — 0,06 сила тяги = 0,08Н

Формулы такой нет. Это выдержка из объяснения. Сила тяги . Вычислим силу тяги космического корабля, стартующего с Земли вертикально вверх. Движение корабля будем рассматривать в системе координат, связанной с Землёй, причём эту систему принимаем за инерциальную. Пусть m – секундный расход топлива, u – скорость истечения газов из сопла двигателя относительно ракеты (относительно ракеты) , m &gt; 0 и u &gt; 0, (D — приращение, то есть «дельта».) Работающий двигатель как бы “забирает” у ракеты непрерывно, порция за порцией, горючее и, сжигая его в камере сгорания, выбрасывает, образуя реактивную струю. Пусть в некоторый момент времени двигатель “забрал” порцию горючего массой D m. Количество движения этой порции до сгорания направлено вверх и равно v D m, где v – мгновенная скорость ракеты относительно Земли (абсолютная скорость) . За малый промежуток времени D t масса D m сгорает и выбрасывается из сопла двигателя с относительной скоростью u в направлении, противоположном движению ракеты, то есть скоростью v – u относительно Земли. Вначале, при v &lt; u, абсолютная скорость истечения газов отрицательна (направлена к Земле) , а позже, когда v &gt; u, положительна (направлена от Земли) . После сгорания выбрасываемая масса обладает абсолютным количеством движения ( v – u) D m, следовательно, за время приращения её количества движения составит: ( v – u) D m – v D m = –u D m. В единицу времени изменение количества движения массы равно – u D m / D t. Физически эта величина представляет собой силу F ‘ давления на струю, создаваемую работой реактивного двигателя. Учитывая, что D m / D t = m, получаем: F ‘ = –m u. (1) Знак “минус” показывает, что сила F ‘, действующая на образующуюся газовую струю, направлена к Земле. По третьему закону Ньютона при взаимодействии двигателя с выбрасываемой им струёй последняя действует на двигатель ракеты в противоположную сторону с силой F = – F ‘, то есть F = m u (2) Её называют реактивной силой. Таким образом, при стационарном режиме работы реактивного двигателя сила тяги постоянна, направлена вверх (в сторону движения корабля) и равна произведению секундного расхода топлива на относительную скорость выбрасываемых газов. Зная реактивную силу, можно написать уравнение движения ракеты, которое без учёта поля тяготения имеет вид: m D v / D t = m u, (3) где D v / D t – ускорение ракеты. При наличии поля тяготения уравнение движения будет: m D v / D t = m u – m g. (4) Внешнее силовое поле не изменяет величины создаваемой двигателем реактивной силы, так как последняя определяется лишь режимом работы самого двигателя ракеты, оно меняет только закон движения корабля. Интегрируя уравнение (3), К. Э. Циолковский впервые нашёл, что скорость корабля в пространстве вне поля тяготения возрастает по логарифмическому закону: v = u ln (m0 / m), (5) где m0 – начальная масса корабля, m – его масса в произвольный момент.

Нужно не минус 0,06 а плюс 0,06

Ре­ше­ние. По вто­ро­му за­ко­ну Нью­то­на уско­ре­ние прямо про­пор­ци­о­наль­но рав­но­дей­ству­ю­щей сил и об­рат­но про­пор­ци­о­наль­но массе тела. Найдём силу тяги : 0.2 кг *0.7+0.06=0.2

Fтяги. -Fтрен. =ma Fтрен. =цN || ц= коэффицент трения Fтяги=ma+mgц Fтяги=m(a+gц) Находим ц по Fтрен. 0.06=ц0.2*10 ц=0.03 Fтяги=0.2(0.7+0.03*10)=0,2

решение будет таким (если кому-то еще интересно) Дано: m=200 г=0.2 кг а= 0.7 м/с2 Fтр=0.06 Н Найти: F-? Решение: -Fтр + F = ma (2 закон Ньютона) -0.06+F=0.2 * 0.7 F=0.2 * 0.7 + 0.06 F= 0.2

а=(Fтяг+Fтр) /m Fтяг=ma+Fтр Fтяг=0,2*0,7+0,06=0,2

масса*ускорение=силая тяги——————————сила трении. они направлены в разные стороны (сила тяги и трения)!!!! 0,14+0,06=2. почему +? у нас было Х-0,06=0,14(0,7*0,2) Х=0,14+0,06 — мы меняем знак когда с одно стороны на другую переносим. элементарно! Х=2Н