§16. Электромагнитная индукция. Энергия магнитного поля Основные формулы

Магнитный поток Ф через плоский контур площадью S равен:

а) в случае однородного поля

,

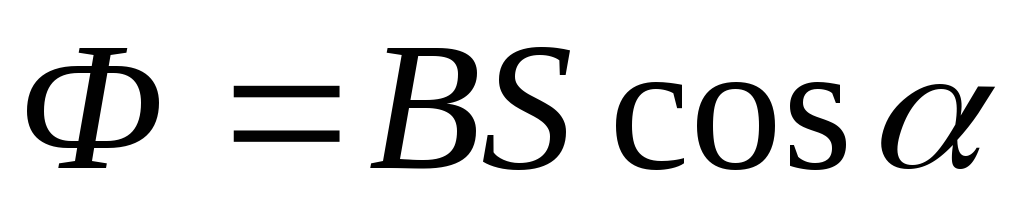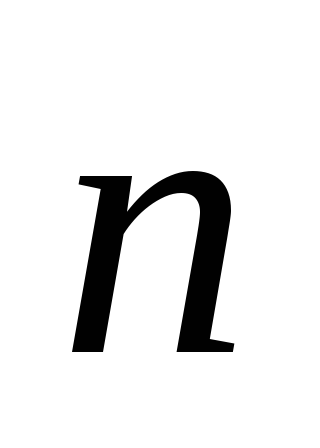где – угол между вектором нормали к плоскости контура и вектором магнитной индукции ;

б) в случае неоднородного поля

,

где интегрирование ведется по всей поверхности

S.

Потокосцепление, то есть полный магнитный поток, сцепленный со всеми витками контура, равно

,

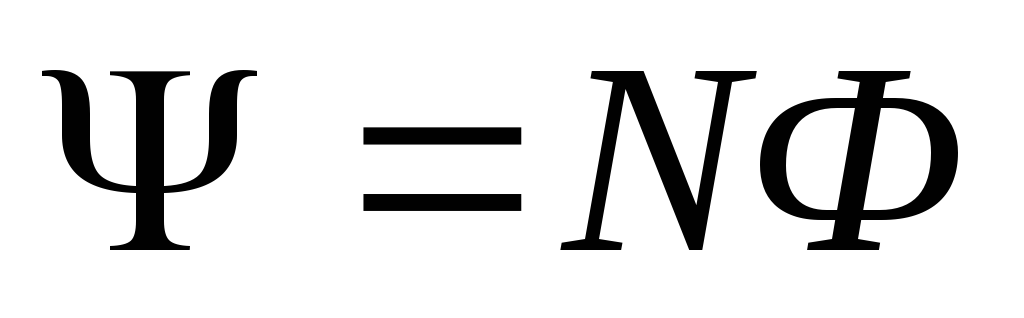где N – число витков контура, Ф – магнитный поток сквозь один виток.

Работа по перемещению замкнутого контура с током в постоянном магнитном поле равна

,

где

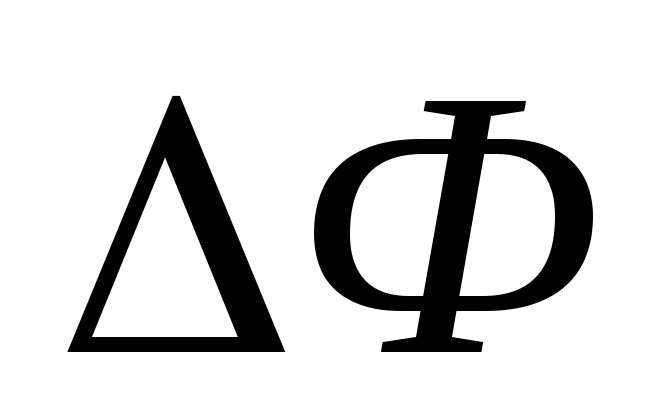I – сила тока в контуре; – изменение магнитного потока, пронизывающего поверхность, ограничивающую контур.

Основной закон электромагнитной индукции имеет вид

.

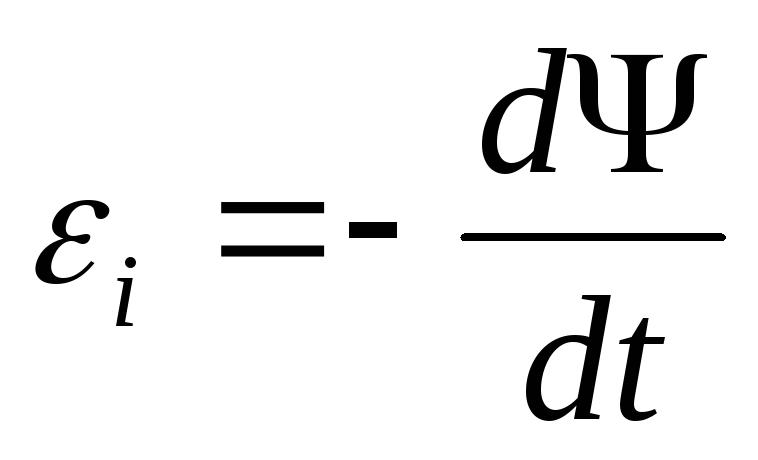Частные случаи применения основного закона электромагнитной индукции:

а) разность потенциалов U на концах проводника длиной l, движущегося со скоростью V в однородном магнитном поле с индукцией

B, равна

,

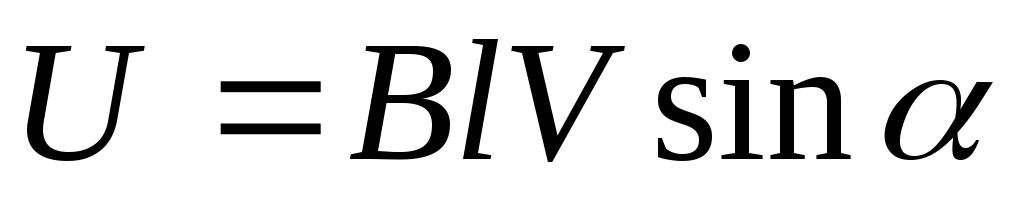где α – угол между направлениями векторов скорости и индукции магнитного поля;

б) электродвижущая сила индукции, возникающая в рамке, равномерно вращающейся в однородном магнитном поле, равна

,

где N – число витков в рамке; В – индукция поля; S – площадь одного витка;

– угловая скорость вращения рамки; t – время.

Заряд, протекающий по замкнутому контуру при изменении потокосцепления , равен

,

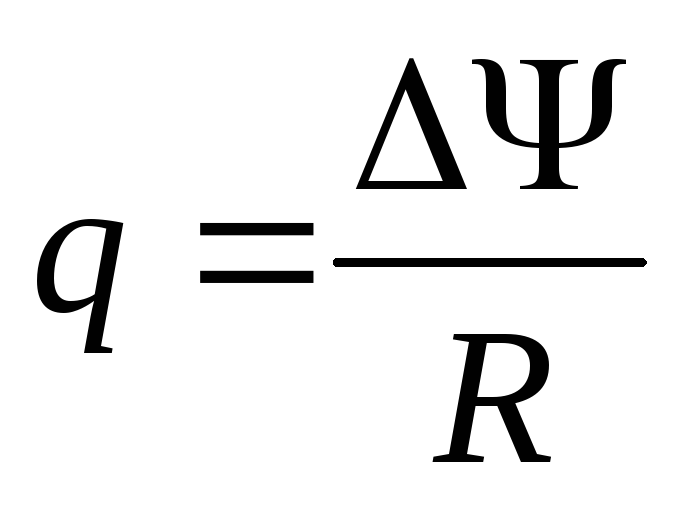где R – сопротивление контура.

Индуктивность контура равна

,

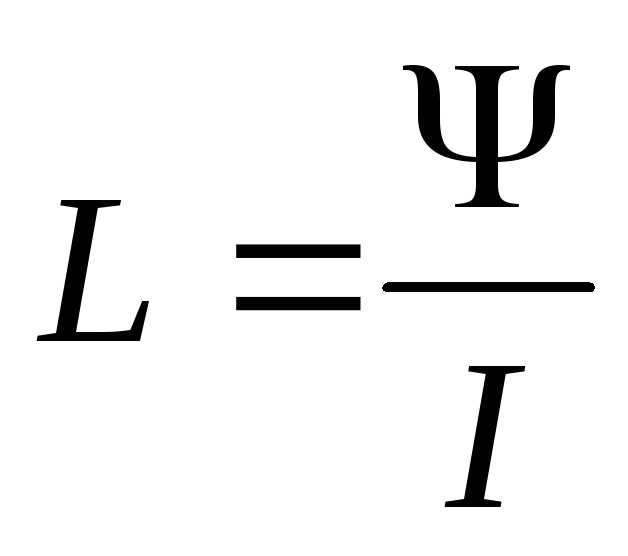
где I – сила тока в контуре ; Ψ– потокосцепление самоиндукции.

Электродвижущая сила самоиндукции, возникающая в замкнутом контуре при изменении силы тока в нем, определяется по формуле

.

Индуктивность соленоида равна

,

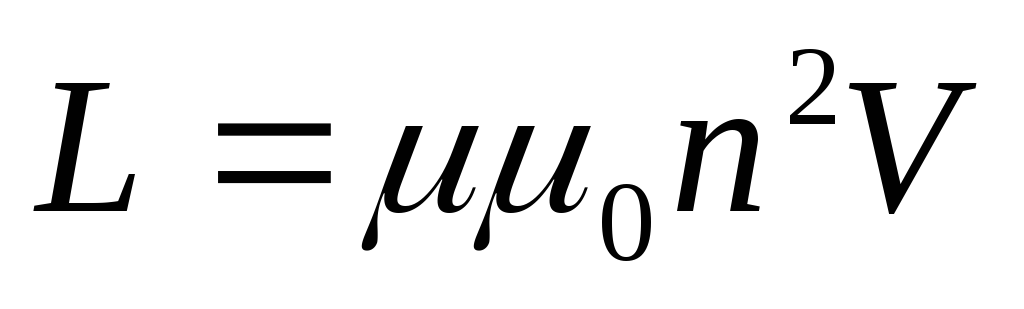где n – число витков соленоида на единице его длины;

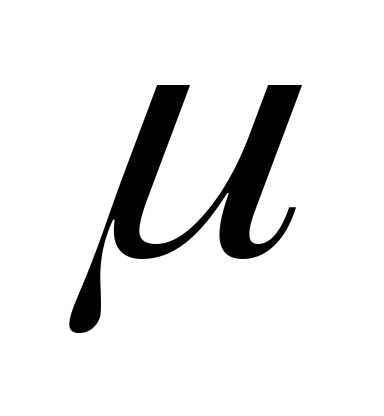V – объём соленоида; – магнитная проницаемость среды внутри соленоида, которую можно определить из соотношения .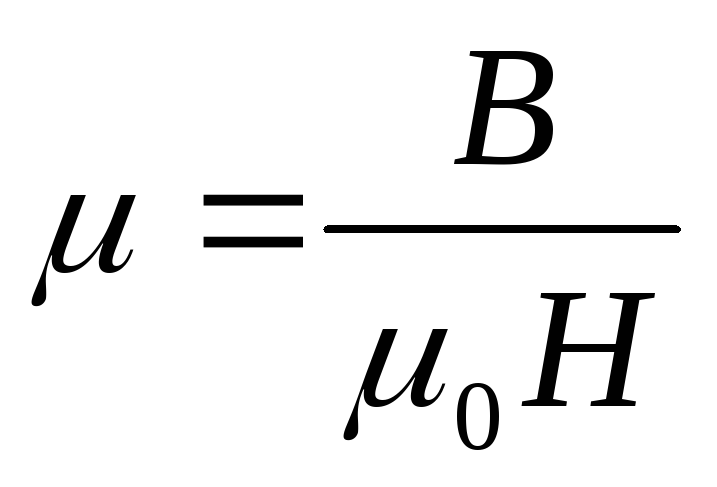

Мгновенное значение силы тока в цепи, обладающей сопротивлением R и индуктивностью L, равно:

а) после замыкания цепи

,

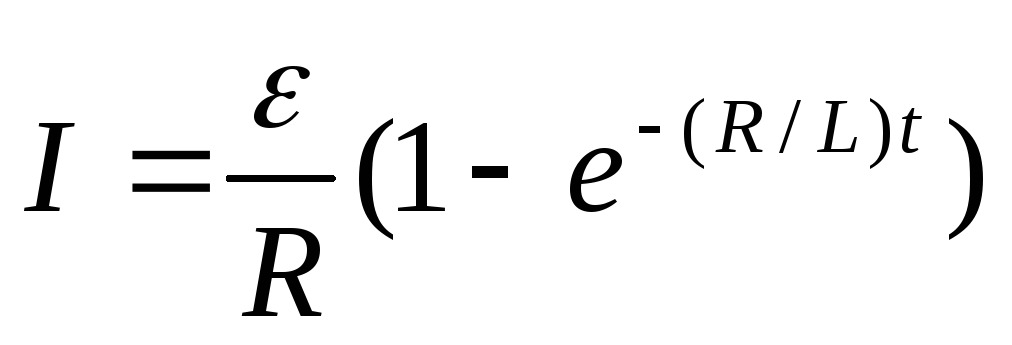где

– электродвижущая сила источника;

б) после размыкания цепи

,

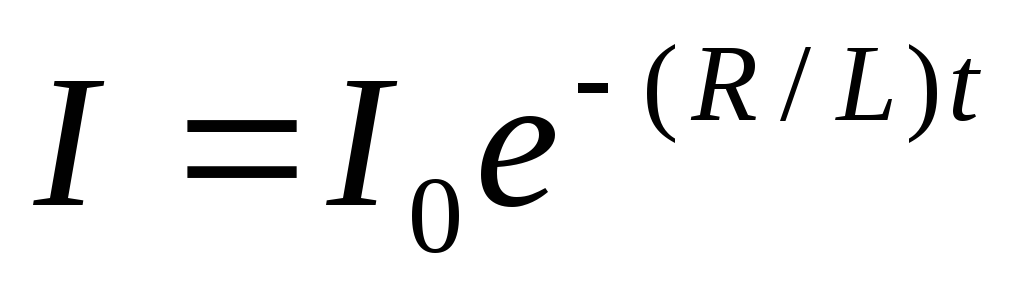где 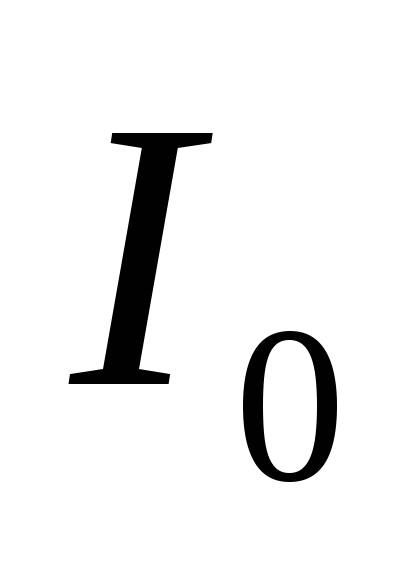– начальное значение силы тока в цепи.

Энергия магнитного поля, создаваемого током I в замкнутом контуре с индуктивностью L , определяется по формуле

.

Объёмная плотность энергии магнитного поля равна

.

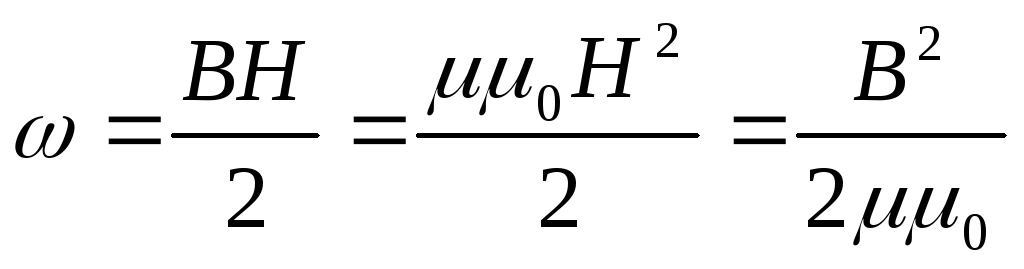Задачи

16.1. Найти магнитный поток Ф, создаваемый соленоидом сече­нием S = 10 см², если он имеет n = 10 витков на каждый сантиметр его длины при силе тока I = 20 А.

16.2. Плоский контур, площадь S которого равна 25 см², находится в однородном магнитном поле с индукцией B = 0,04 Тл. Определить магнитный поток

Ф, пронизывающий контур, если плос­кость его составляет угол β = 30° с линиями индукции.

16.3. Соленоид длиной l = 1 м и сечением S = 16 см² содержит N = 2000 витков. Вычислить потокосцепление Ψ при силе тока I в обмотке 10 А.

16.4. Плоская квадратная рамка со стороной а = 20 см лежит в одной плос­кости с бесконечно длинным прямым проводом, по которому течет ток I = 100 А. Рамка расположена так, что ближайшая к проводу сторона параллельна ему и находится на расстоянии l = 10 см от провода. Определить магнитный поток Ф, пронизывающий рамку.

16.5. В однородном магнитном поле с индукцией B = 0,01 Тл находится прямой провод длиной l = 8 см, расположенный перпендикулярно линиям индукции. По проводу течет ток I = 2 А. Под действием сил поля провод переместился на расстояние S = 5 см. Найти работу А сил поля.

16.6. Плоский контур, площадь S которого равна 300 см², находится в однородном магнитном поле с индукцией В = 0,01 Тл. Плоскость контура перпендикулярна линиям индукции. В контуре поддерживается неизменный ток I = 10 А, Определить работу A внешних сил по перемещению контура с током в область пространст­ва, магнитное поле в которой отсутствует.

16.7. По проводу, согнутому в виде квадрата со стороной дли­ной a = 10 см, течет ток I = 20 А, сила которого поддерживается не­изменной. Плоскость квадрата составляет угол α = 20⁰ с линиями индукции однородного магнитного поля (B = 0,1 Тл). Вычислить работу А, которую необходимо совершить для того, чтобы удалить провод за пределы поля.

16.8. По кольцу, сделанному из тонкого гибкого провода, радиусом R = 10 см, течет ток I = 100 А. Перпендикулярно плоскости кольца возбуждено магнитное поле с индукцией B = 0,1 Тл по направле­нию, совпадающему с индукцией В₁ собственного магнитного поля кольца. Определить работу

А внешних сил, которые, действуя на провод, деформировали его и придали ему форму квадрата. Сила тока при этом поддерживалась неизменной. Работой против упру­гих сил пренебречь.

16.9. Виток, по которому течет ток I = 20 А, свободно установился в однородном магнитном поле с индукцией B = 0,016 Тл. Диа­метр d витка равен 10 см. Определить работу A, которую нужно совершить, чтобы повернуть виток на угол α= π/2 относительно оси, совпадающей с диаметром.

16.10. Квадратная рамка со стороной a = 10 см, по которой течет ток I = 200 А, свободно установилась в однородном магнитном поле (B = 0,2 Тл). Определить работу, которую необходимо совер­шить при повороте рамки вокруг оси, лежащей в плоскости рамки и перпендикулярной линиям магнитной индукции, на угол α = 2π/3.

16.11. Магнитный поток Ф = 40 мВб пронизывает замкнутый контур. Определить среднее значение электродвижущей силы индукции 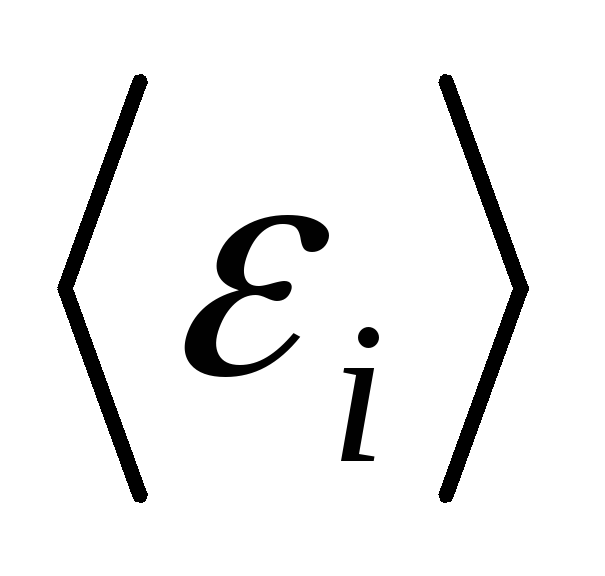, возникающей в контуре, если магнитный поток изменится до нуля за время Δt = 2 мс.

16.12. Прямой провод длиной l = 40 см движется в однородном магнитном поле со скоростью v = 5 м/с перпендикулярно линиям индукции. Разность потенциалов U между концами провода равна 0,6 В. Вычислить индукцию В магнитного поля.

16.13. В однородном магнитном поле с индукцией B = 1 Тл нахо­дится прямой провод длиной l = 20 см, концы которого замкнуты вне поля. Сопротивление R всей цепи равно 0,1 Ом. Найти силу F, которую нужно приложить к проводу, чтобы перемещать его пер­пендикулярно линиям индукции со скоростью V = 2,5 м/с.

16.14. Прямой провод длиной l = 10 см помещен в однородное магнитное поле с индукцией B = 1 Тл. Концы его замкнуты гибким проводом, находящимся вне поля. Сопротивление R всей цепи равно 0,4 Ом. Какая мощность Р потребуется для того, чтобы двигать про­вод перпендикулярно линиям индукции со скоростью v = 20 м/с?

16.15. По П-образному проводнику, расположенному в горизонтальной плоскости, может скользить без трения перемычка 12 (рис. 16.1). Она имеет длину l, массу m и сопротивление R. Вся система находится в вертикальном однородном магнитном поле с индукцией В. В момент t = 0 на пере­мычку стали действовать постоянной гори­зонтальной силой F, и перемычка начала перемещаться вправо. Найти скорость пере­мычки как функцию времени. Магнитное поле индукционного тока и сопротивление П-образного проводника пренебрежимо малы.

16.16. К источнику тока с электродвижущей силой = 0,5 В и ничтожно малым внут­ренним сопротивлением присоединены два металлических стержня, расположенные горизонтально и параллельно друг другу. Расстояние l между стержнями равно 20 см. Стержни находятся в однородном магнитном поле, направленном вертикально. Магнитная индукция B = 1,5 Тл. По стержням под действием сил поля скользит со скоростью V = 1 м/с прямолинейный провод сопротивлением R = 0,02 Ом. Сопротивление стержней пренебрежимо мало. Опреде­лить: 1) электродвижущую силу индукции ε_i; 2) силу F, действующую на провод со стороны поля; 3) силу тока I в цепи; 4) мощность Р₁, расходуемую на движение провода; 5) мощность Р₂, расходуемую на нагревание провода; 6) мощность Р₃, отдаваемую в цепь источника тока.

16.17. В однородном магнитном поле с индукцией B = 0,4 Тл в плоскости, перпендикулярной линиям индукции поля, вращается стержень длиной l = 10 см. Ось вращения проходит через один из концов стержня. Определить разность потенциалов U на концах стержня при частоте вращения n = 16 с^-1.

1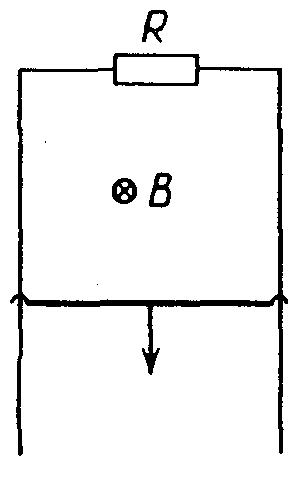6.18. По двум гладким вертикальным проводам, отстоящим друг от друга на расстояние l, скользит под действием силы тяжести проводник-перемычка массы m. Вверху провода замкнуты на сопротивление R (рис. 16.2). Система находится в однородном магнитном поле с индукцией В, перпендикулярном плоскости, в которой перемещается перемычка. Пренебрегая сопротивлением проводов, перемычки и скользящих контактов, а также магнитным полем индукционного тока, найти установившуюся скорость перемычки.

16.19. Система отличается от рассмотренной в предыдущей задаче (см. рис. 16.2) лишь тем, что вместо сопротивления R к концам вертикальных проводов подключен конденсатор емкости С. Найти ускорение перемычки.

16.20. Металлический диск радиуса R = 25 см вращают с постоянной угловой скоростью ω = 130 рад/с вокруг его оси. Найти разность потенциалов между центром и ободом диска, если: а) внешнего магнитного поля нет; б) имеется перпендикулярное диску внешнее однородное магнитное поле с индукцией В = 5,0 мТл.

16.21. Непроводящее тонкое кольцо массы m, имеющее заряд q, может свободно вращаться вокруг своей оси. В момент t = 0 включили однородное магнитное поле, перпендикулярное плоскости кольца. Индукция поля начала нарастать по некоторому закону В(t). Найти угловую скорость ω кольца как функцию В.

16.22. Рамка площадью S = 200 см² равномерно вращается с частотой n = 10 с^-1 относительно оси, лежащей в плоскости рамки и перпендикулярной линиям индукции однородного магнитного поля (B = 0,2 Тл). Каково среднее значение электродвижущей силы индукции 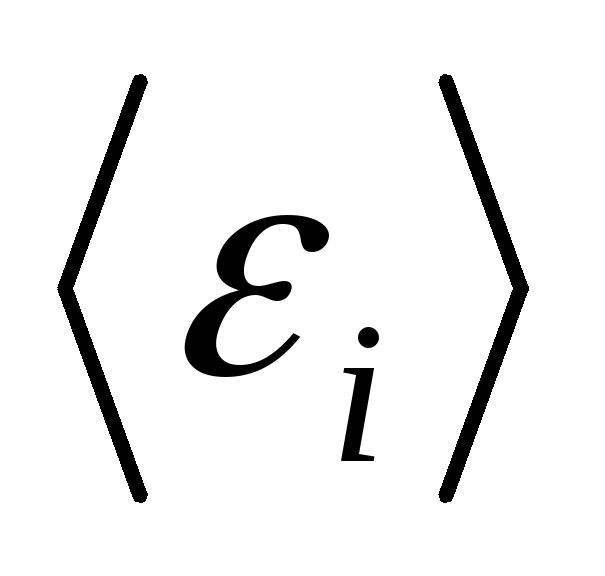за время, в течение которого магнитный поток, пронизывающий рамку, изменится от нуля до максимального значения?

16.23. В однородном магнитном поле с индукцией В = 0,35 Тл равномерно с частотой n = 480 c^-1 вращается рамка, содержащая N = 500 витков площадью S = 50 см². Ось вращения лежит в плоскости рамки и перпендикулярна линиям индукции. Определить максимальную электродвижущую силу индукции 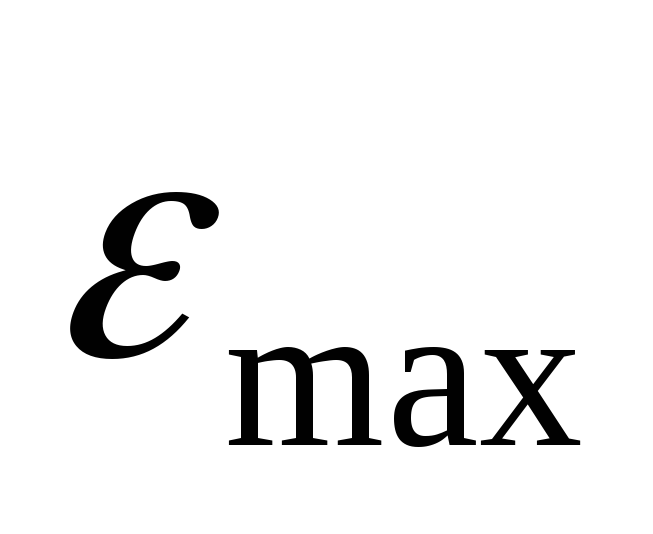, возникающую в рамке.

16.24. Рамка площадью S = 100 см² содержит N = 10³ витков провода сопротивлением R₁ = 12 Ом. К концам обмотки подключено внешнее сопротивление R₂ = 20 Ом. Рамка равномерно вращается в однородном магнитном поле (B = 0,1 Тл) с частотой n = 8 с^-1. Оп­ределить максимальную мощность P_max переменного тока в цепи.

16.25. Магнитная индукция B поля между полюсами двухполюсного генератора равна 0,8 Тл. Ротор имеет N = 100 витков площадью S = 400 см². Определить частоту n вращения якоря, если максималь­ное значение электродвижущей силы индукции 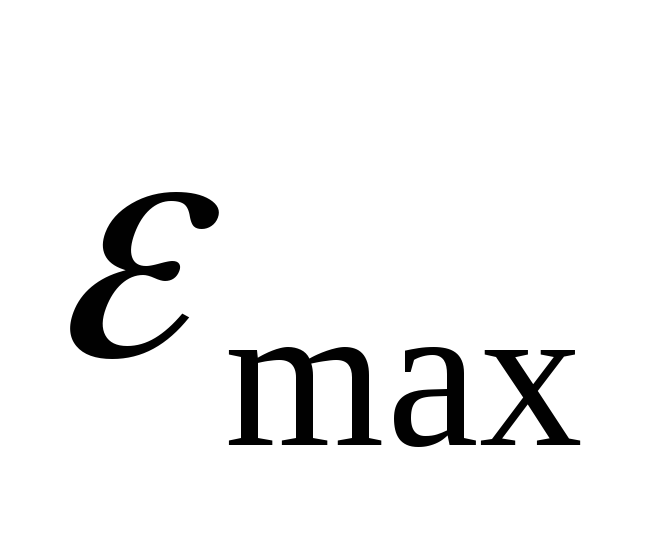= 200 В.

16.26. Проволочный виток радиусом r = 4 см, имеющий сопротивление R = 0,01 Ом, находится в однородном магнитном поле с индукцией B = 0,04 Тл. Плоскость витка составляет угол α = 30⁰ с линиями индукции поля. Какое количество электричества q протечет по витку, если магнитное поле исчезнет?

16.27. Проволочное кольцо радиусом r = 10 см лежит на столе. Какое количество электричества q протечет по кольцу, если его повернуть с одной стороны на другую? Сопротивление R кольца равно 1 Ом. Вертикальная составляющая индукции B магнитного поля Земли равна 50 мкТл.

16.28. В проволочное кольцо, присоединенное к баллистическому гальванометру, вставили прямой магнит. По цепи протекло количество электричества q = 10 мкКл. Определить магнитный поток Ф, пересеченный кольцом, если сопротивление R цепи гальванометра равно 30 Ом.

16.29. Между полюсами электромагнита помещена катушка, сое­диненная с баллистическим гальванометром. Ось катушки параллельна линиям индукции. Катушка сопротивлением R₁ = 4 Ом име­ет N = 15 витков площадью S = 2 см³. Сопротивление R₂ гальвано­метра равно 46 Ом. Когда ток в обмотке электромагнита выключи­ли, по цепи гальванометра протекло количество электричества q = 90 мкКл. Вычислить магнитную индукцию В поля электромагнита.

16.30. Рамка из провода сопротивлением R = 0,01 Ом равномер­но вращается в однородном магнитном поле с индукцией B = 0,05 Тл. Ось вращения лежит в плоскости рамки и перпендикулярна линиям индукции. Площадь S рамки равна 100 см². Найти, какое количест­во электричества q протечет через рамку за время поворота ее на угол α = 30° в следующих трех случаях:1) от 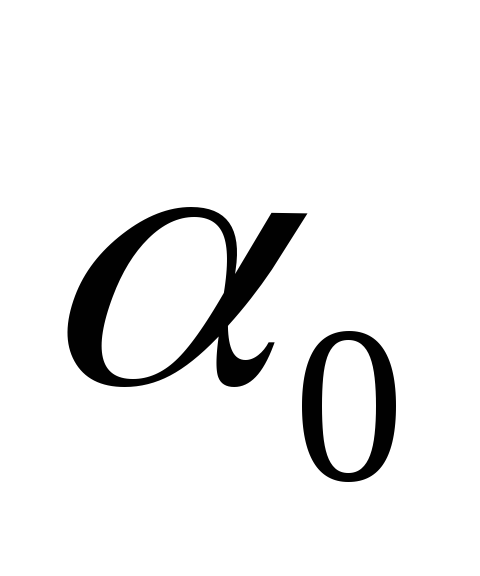= 0 до 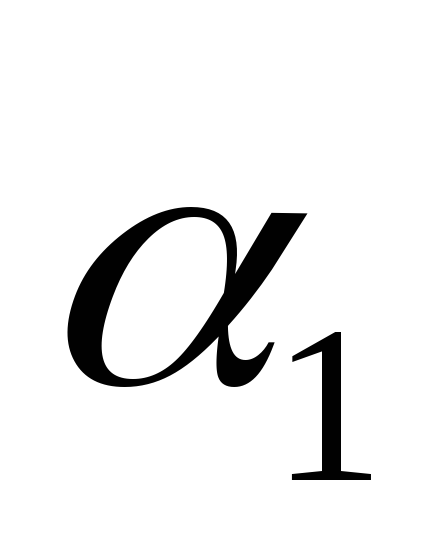= 30°; 2) от 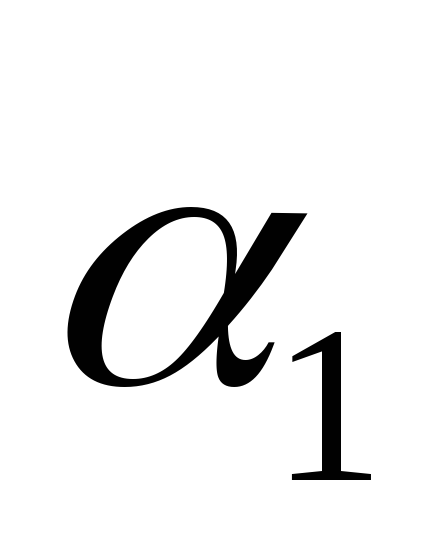до 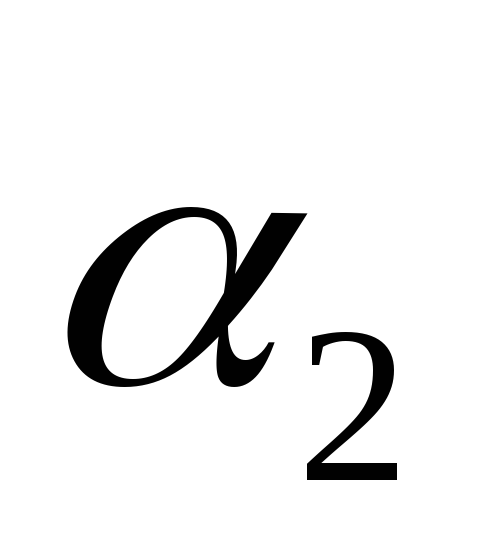= 60°; 3) от = 90°.

16.31. Тонкий медный провод массой m = 1 г согнут в виде квад­рата, и концы его замкнуты. Квадрат помещен в однородное маг­нитное поле (В = 0,1 Тл) так, что плоскость его перпендикулярна линиям индукции поля. Определить количество электричества q, которое протечет по проводнику, если квадрат, потянув за противо­положные вершины, вытянуть в линию.

16.32. По длинному прямому проводу течет ток. Вблизи провода расположена квадратная рамка из тонкого провода сопротивлением R = 0,02 Ом. Провод лежит в плоскости рамки и параллелен двум ее сторонам, расстояния до которых от провода соответствен­но равны a₁ = 10 см, a₂ = 20 см. Найти силу тока I в проводе, если при его включении через рамку протекло количество электричества q = 693 мкКл.

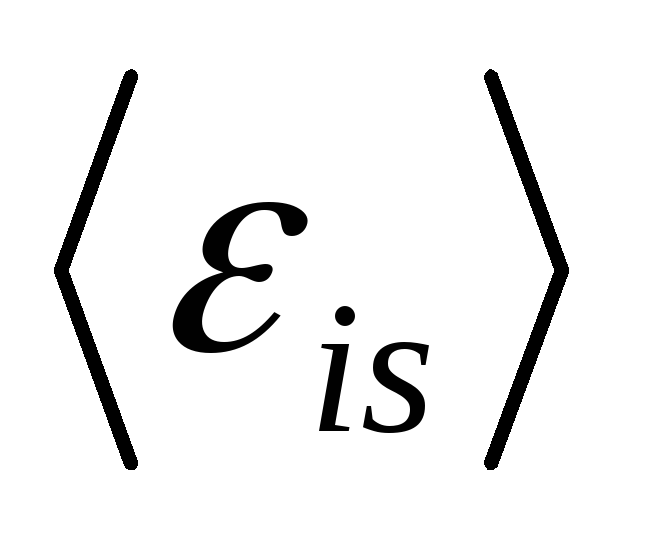16.33. По катушке индуктивностью L = 0,03 мГн течет ток I = 0,6 А. При размыкании цепи сила тока изменяется практически до нуля за время = 120 мкс. Определить среднюю электродвижущую силу самоиндукции , возникающую в контуре.

16.34. С помощью реостата равномерно увеличивают силу тока в катушке на = 0,1 А в 1 с. Индуктивность L катушки равна 0,01 Гн. Найти среднее значение электродвижущей силы самоиндукции .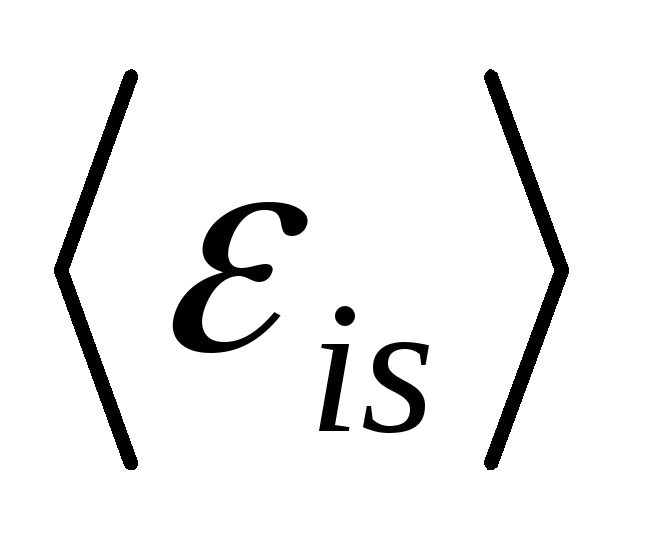

16.35. Индуктивность L катушки равна 2 мГн. Ток частотой ν= 50 Гц, протекающий по катушке, изменяется по синусоидальному закону. Определить среднюю электродвижущую силу самоиндукции 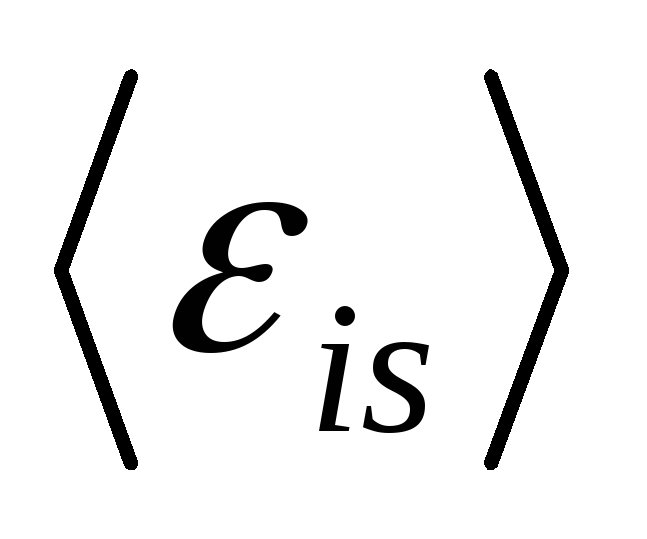, воз­никающую за интервал времени Δt, в течение которого ток в катуш­ке изменяется от минимального до максимального значения. Амплитудное значение силы тока I₀ = 10 А.

16.36. Катушка, намотанная на немагнитный цилиндрический каркас, имеет N₁ = 750 витков и индуктивность L₁ = 25 мГн. Чтобы увеличить индуктивность катушки до L₂ = 36 мГн, обмотку с катушки сняли и заменили обмоткой из более тонкой проволоки с таким расчетом, чтобы длина катушки осталась прежней. Определить чис­ло N₂ витков катушки после перемотки.

16.37. Соленоид индуктивностью L = 4 мГн содержит N = 600 витков. Определить магнитный поток Ф, если сила тока I, протекающего по обмотке, равна 12 А.

16.38. Индуктивность L катушки без сердечника равна 0,02 Гн. Какое потокосцепление Ψ создается, когда по обмотке течет ток I = 5 А?

16.39. Длинный прямой соленоид, намотанный на немагнитный каркас, имеет N = 1000 витков и индуктивность L = 3 мГн. Какой магнитный поток Ф и какое потокосцепление 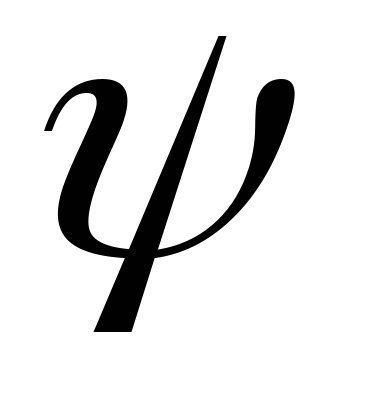создает соленоид при силе тока I = 1 А?

16.40. В цепи шел ток I₀ = 50 А. Источник тока можно отключить от цепи, не разрывая ее. Определить силу тока в этой цепи через t = 0,01 с после отключения ее от источника тока. Сопротивление R цепи равно 20 Ом, ее индуктивность L = 0,1 Гн.

16.41. Источник тока замкнули на катушку с сопротивлением R = 10 Ом и индуктивностью L = 1 Гн. Через сколько времени сила тока в цепи достигнет 0,9 предельного значения?

16.42. В схеме (рис. 2.104) известны ЭДС ε источника, сопротивление R и индуктивности катушек L₂ и L₂. Внутреннее сопротивление источника и сопротив­ления катушек пренебрежимо малы. Най­ти установившиеся токи в катушках после замыкания ключа К.

Энергия магнитного поля

      Рассмотрим случай, о котором мы уже говорили (рис. 5.6).

Рис. 5.6

      Сначала замкнем соленоид L на источник ЭДС , в нем будет протекать ток . Затем в момент времени  переключим ключ в положение 2 – замкнем соленоид на сопротивление R. В цепи будет течь убывающий ток I. При этом будет совершена работа:  ,  или

     

,

(5.5.1)

      Эта работа пойдет на нагревание проводников. Но откуда взялась эта энергия? Поскольку других изменений, кроме исчезновения магнитного поля в окружном пространстве, не произошло, остается заключить, что энергия была локализована в магнитном поле. Значит, проводник с индуктивностью L, по которой течет ток I, обладает энергией

,

(5.5.3)

      Выразим энергию магнитного поля через параметры магнитного поля. Для соленоида:

.

; отсюда

      Подставим эти значения в формулу (5.5.3):

,

(5.5.4)

      Обозначим w – плотность энергии, или энергия в объеме V, тогда

,

(5.5.5)

      но т.к. , то

или

(5.5.6)

      Энергия однородного магнитного поля в длинном соленоиде может быть рассчитана по формуле

,

(5.5.7)

а плотность энергии

,

(5.5.8)

      Плотность энергии магнитного поля в соленоиде с сердечником будет складываться из энергии поля в вакууме и в магнетике сердечника:

,   отсюда     .

      Т.к. в вакууме , имеем

Контрольные вопросы

1.            Какие опыты Фарадея легли в основу открытия явления электромагнитной индукции?

2.            Что является причиной возникновения ЭДС индукции в замкнутом проводящем контуре? От чего и как зависит ЭДС индукции, возникающая в контуре?

3.            В чем заключается явление электромагнитной индукции?

4.            Почему для обнаружения индукционного тока лучше использовать замкнутый проводник в виде катушки, а не в виде одного витка провода?

5.            Сформулируйте правило Ленца, проиллюстрировав его примерами.

6.            Как направлен индукционный ток?

7.            Всегда ли при изменении магнитной индукции в проводящем контуре в нем возникает ЭДС индукции? индукционный ток?

8.            Чему равна ЭДС индукции контура?

9.            Сформулируйте закон Ома для контура.

10.        Как связано направление индукционного тока и направление скорости изменения потока магнитной индукции?

11.        Сформулируйте закон Фарадея для контура с током, состоящего из одного и нескольких витков.

12.        Возникает ли индукционный ток в проводящей рамке, поступательно движущейся в однородном магнитном поле?

13.        Покажите, что закон Фарадея есть следствие закона сохранения энергии.

14.        Какова природа ЭДС электромагнитной индукции?

15.        Выведите выражение для ЭДС индукции в плоской рамке, равномерно вращающейся в однородном магнитном поле. За счет чего ее можно увеличить?

16.        Что такое вихревые токи? Вредны они или полезны?

17.        Почему сердечники трансформаторов не делают сплошными?

18.        Какое явление называется скин-эффектом?

19.        Произведите классификацию ускорителей.

20.        Каковы параметры линейных ускорителей.

21.        Когда заряженная частица движется в магнитном поле по спирали? От чего зависит шаг спирали? Ответы подтвердите выводами формул.

22.        Что такое ускорители заряженных частиц? Какие они бывают и чем характеризуются?

23.        Почему для ускорения электронов не применяются циклотроны?

24.        В чем заключается принцип автофазировки? Где он используется?

25.        Когда ЭДС самоиндукции больше – при замыкании или размыкании цепи постоянного тока?

26.        В чем заключается физический смысл индуктивности контура? взаимной индуктивности двух контуров? От чего они зависят?

27.        В чем заключаются явления самоиндукции и взаимной индукции? Вычислите ЭДС индукции для обоих случаев.

28.        В чем заключается физический смысл времени релаксации ? Докажите, что  имеет размерность времени.

29.        Запишите и проанализируйте выражения для объемной плотности энергии электростатического и магнитного полей. Чему равна объемная плотность энергии электромагнитного поля?

30.        Напряженность магнитного поля возросла в два раза. Как изменилась объемная плотность энергии магнитного поля?

31.        Приведите соотношение между точками в первичной и вторичной обмотках повышающего трансформатора.

      В таблице 5.1 приведены сравнительные характеристики электрического и магнитного полей.

Таблица  5.1

Электрическое  поле	Формулы  и обозначения	Магнитное поле	Формулы и обозначения
Точечный заряд		Ток
Электрическая постоянная		Магнитная постоянная
Диэлектрическая проницаемость		Магнитная проницаемость
Диэлектрическая восприимчивость		Магнитная восприимчивость
Взаимодействие точечных зарядов		Взаимодействие токов
Силовая характеристика электрич. поля		Силовая характеристика магнитного поля
Принцип суперпозиции		Принцип суперпозиции
Поляризованностъ		Намагниченность
Электроемкость проводника		Индуктивность катушки
Энергия заряженного конденсатора		Энергия катушки с током
Объемная плотность энергии		Объемная плотность энергии
Поток; вектора сквозь поверхность S		Поток вектора сквозь поверхность S
Циркуляция вектора		Циркуляция Вектора

---

Энергия магнитного поля. Видеоурок. Физика 11 Класс

На этом уроке мы повторим явление самоиндукции. Ознакомимся с энергией магнитного поля. Также узнаем о том, как вычислить плотность энергии магнитного поля.

Вспомним, в чем состоит явление самоиндукции. При изменении силы тока, протекающего через проводник, в этом же проводнике возникает ЭДС индукции, препятствующая изменению основного тока в проводниках. Это приводит к тому, что сила тока в проводнике достигает своего максимального значения не мгновенно, а в течение некоторого времени. Данное явление наблюдается и при размыкании цепи: сила тока падает до нуля не мгновенно, а постепенно. Явление самоиндукции связано с тем, что проводник с током находится в пространстве собственного магнитного потока и при любом изменении тока в проводнике меняется и магнитный поток, что, в свою очередь, приводит к возникновению ЭДС индукции (рис. 1).

Рис. 1. Самоиндукция

ЭДС индукции определяется как отношение изменения силы тока к изменению времени и умноженное на индуктивность проводника. А индуктивность определяется геометрическими параметрами проводника. Знак «минус» указывает на то, что возникающая ЭДС препятствует изменению тока.

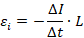
Обратим внимание на то, что при размыкании цепи ток в ней хоть и убывает, но все равно существует – это доказывает процесс переноса заряда, которому необходима энергия. Но откуда она берется? Поскольку никаких других изменений, кроме убывания магнитного поля, вокруг проводника не происходит, можно сделать предположение, что энергия локализована в магнитном поле

Необходимо выяснить, откуда берется энергия и как ее рассчитать.

Рассмотрим опыт. Пусть имеется электрическая цепь, в которой катушка с индуктивностью (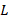) последовательно соединена с лампочкой и через переключатель может быть замкнута либо на источник постоянного тока (), либо на резистор с сопротивлением (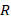) (рис. 2).  

Рис. 2. Схема

Если в цепь включить амперметр, то можно получить график зависимости тока в цепи от времени. Сначала замкнем катушку на источник ЭДС – в цепи будет протекать ток 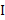 (рис. 3).

Рис. 3. График изменения тока

Затем, в некоторый момент времени  переключим ключ, замыкая катушку на резистор  – в цепи будет протекать убывающий ток. С момента времени  до полного исчезновения тока пройдет определенное время, в течение которого будет происходить перенос заряда в цепи катушки и резистора. Следовательно, будет совершаться работа: убывание тока в катушке вызовет явление самоиндукции, и в ней возникнет ЭДС самоиндукции. Разобьем участок 2 графика изменения тока на бесконечно малые интервалы времени , такие, что на каждом интервале изменения тока можно считать линейными (рис. 4).

 

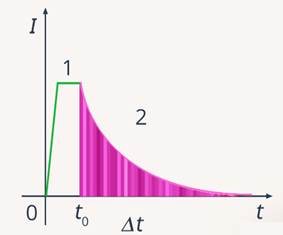
Рис. 4. Разбиение участка 2 на интервалы  

На каждом таком участке будет совершаться работа, численно равная произведению ЭДС индукции на переносимый за этот интервал времени заряд:

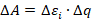
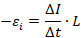
Подставим выражение для ЭДС самоиндукции в выражение для работы на интервале времени :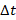

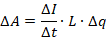
Отношение перенесенного заряда 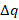 к интервалу времени  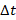является средним значением тока на этом элементарном интервале времени:

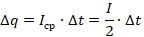
Тогда выражение для работы на элементарном интервале времени примет вид:

Если просуммировать работу по всем элементарным участкам 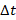 от 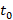 до 0, получим выражение для полной работы за весь интервал времени:

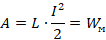
Такая работа пойдет на нагревание проводников внутри катушки, замкнутой на резистор.

Выразим энергию магнитного поля через параметры магнитного поля. Для катушки индуктивность равна:

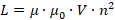
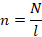
Модуль магнитной индукции катушки определяется соотношением:

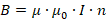
Тогда для энергии магнитного поля получим выражение:

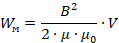
Разделим выражение для энергии магнитного поля катушки на ее объем, считая, что все магнитное поле сосредоточено в объеме катушки:

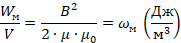
Развивая теорию электромагнетизма, Джеймс Кларк Максвелл показал, что полученное выражение для длинной катушки справедливо для любых магнитных полей, а полученная величина называется плотностью энергии магнитного поля.

При замыкании цепи ток нарастает не мгновенно, а в течение некоторого времени, поскольку источник тока должен совершить работу против ЭДС самоиндукции. Эта работа аккумулируется в магнитном поле, которое окружает проводник с током. Впоследствии энергия магнитного поля преобразуется в работу вихревого электрического поля, которое возникает в проводнике после размыкания цепи и затем некоторое время поддерживает индукционный ток в этом проводнике. Энергия магнитного поля вычисляется по формуле: «половина произведения индуктивности проводника на квадрат силы тока, протекающего через проводник».

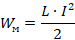
Список литературы

1. Касьянов В.А., Физика 11 кл.: Учебн. для общеобразоват. учреждений. – 4-е изд., стереотип. – М.: Дрофа, 2004. – 416с.: ил., 8 л. цв. вкл.
2. Тихомирова С.А., Яровский Б.М., Физика 11. – М.: Мнемозина.      
3. Генденштейн Л.Э., Дик Ю.И., Физика 11. – М.: Мнемозина.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-портал «Физика» (Источник).
2. Интернет-портал «Terver.ru» (Источник).
3. Интернет-портал «Классная физика» (Источник).

 

Домашнее задание

1. Касьянов В.А., Физика 11 кл.: Учебн. для общеобразоват. учреждений. – 4-е изд., стереотип. – М.: Дрофа, 2004. – 416с.: ил., 8 л. цв. вкл., ст. 101, в. 5, з. 4, 5.
2. Почему при размыкании цепи питания трансформатора или электродвигателя может возникнуть сильная искра?
3. Какова индуктивность контура, если при равномерном изменении силы тока на 5 А за 50 мс в этом контуре создается ЭДС 10 В?
4. ^* Катушку с индуктивностью 50 мГн, по которой шел ток 2 А, с помощью переключателя замкнули накоротко. Какое количество теплоты выделилось в катушке к тому моменту, когда сила тока уменьшилась до 1 А?

7. Энергия магнитного поля Основные формулы

• Энергия Wмагнитного поля, создаваемого током в замкнутом контуре индуктивностьюL,определяется формулой

,

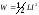где I–сила тока в контуре.

• Объемная (пространственная) плотность энергии однородного магнитного поля (например, поля длинного соленоида)

.

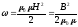• Формула Томсона. Период собственных колебаний в контуре без активного сопротивления

,

где L–индуктивность контура;С–его электроемкость.

• Связь длины электромагнитной волны с периодом Ти частотойυколебаний

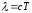или,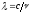

где с — скорость электромагнитных волн в вакууме (с=3*10⁸м/с).

• Скорость электромагнитных волн в среде

где ε –диэлектрическая проницаемость; μ–магнитная проницаемость среды.

Примеры решения задач

Пример 7.1.На стержень из немагнитного материала длинойl=50 см намотан в один слой провод так, что на каждый сантиметр длины стержня приходитсяn= 20 витков. Определить энергиюWмагнитного поля внутри соленоида, если сила токаIв обмотке равна 0,5 А. ПлощадьSсечения стержня равна 2 см².

Решение.Энергия магнитного поля соленоида с индуктивностьюL,по обмотке которого течет ток I,выражается формулой

. (1)

Индуктивность соленоида в случае немагнитного сердечника зависит только от числа витков на единицу длины и от объема Vсердечника:L=μ₀n²V,гдеμ₀–магнитная постоянная. Подставив выражение индуктивностиLв формулу (1), получим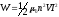. Учтя, чтоV=lS,запишем

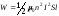. (2)

Сделав вычисления по формуле (2), найдем

W=l26 мкДж.

Пример 7.2.По обмотке метрового соленоида со стальным сердечником течет токI=2А. Определить объемную плотностьωэнергии магнитного поля в сердечнике, если числопвитков на каждом сантиметре длины lсоленоида равно 7 см^-1.

Решение.Объемная плотность энергии магнитного поля определяется по формуле

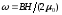. (1)

Напряженность Нмагнитного поля найдем по формулеH=nl. Подставив сюда значенияп, l (п=7 см^-1,l=1 м,nl=700 м^-1) иI, найдем

H=1400 А/м.

Магнитную индукцию Вопределим по графику (см. рис. 5.1) зависимостиВотН.Находим, что напряженностиH=1400 А/м соответствует магнитная индукцияB=1,2 Тл.

Произведя вычисление по формуле (1), найдем объемную плотность энергии:

ω=840 Дж/м³.

Пример 7.3.На железный сердечник длинойl=20 см малого сечения (d<l) намотаноN=200 витков. Определить магнитную проницаемостьμжелеза при силе токаI=0,4 А.

Решение.Магнитная проницаемостьμсвязана с магнитной индукциейВи напряженностьюНмагнитного поля соотношением

B= μ₀μH. (1)

Эта формула не выражает линейной зависимости ВотН,так какμ является функциейН.Поэтому для определения магнитной проницаемости обычно пользуются графиком зависимостиВ(Н)(см. рис. 5.1). Из формулы (1) выразим магнитную проницаемость:

μ=B/( μ₀H). (2)

Напряженность Нмагнитного поля вычислим по формуле (катушку с малым сечением можно принять за соленоид)Н=п1,гдеп —число витков, приходящихся на отрезок катушки длиной 1 м. Выразив в этой формулепчерез числоNвитков катушки и ее длинуl, получим

H=(N/l)I.

Подставив сюда значения N, lиIи произведя вычисления, найдем

H=400 А/м.

По графику Рис. 5.1 находим, что напряженности Н=400 А/м соответствует магнитная индукция B=1,05 Тл. Подставив найденные значенияВ и Н, атакже значениеμ₀в формулу (2), вычислим магнитную проницаемость:

μ=2,09 *10³.

Задача 7.1

Вариант №	l, см	n	Ток I, А	S, см2
1	52	24	2,16	3,12
2	52,4	27	0,72	2,3
3	50,2	20	2,46	2,11
4	54,2	21	0,76	3,47
5	50,3	29	1,79	2,54
6	53,7	23	2,18	3,34
7	54,4	20	1,07	3,51
8	50,4	30	2,45	2,98
9	54	24	2,33	3,2
10	53,3	22	1,65	3,93
11	51	25	0,75	2,51
12	51,6	28	1,48	3,31
13	50,6	22	1,67	2,18
14	55	23	1,01	3,4
15	52	26	0,58	2,34
16	52,5	30	0,54	3,76
17	51,7	22	0,63	2,41
18	50	23	1,19	3,06
19	52,1	27	0,91	2,05
20	51,8	27	0,83	3,72
21	53,8	26	1,25	2,94
22	54,2	21	1,49	3,01
23	51,6	27	1,64	3,42
24	54	22	1,16	2,86
25	54,1	21	2,1	2,47
26	50,9	29	2,39	2,88
27	51	30	1,22	2,66
28	54,6	28	2,09	3,96
29	50,8	27	2,14	3,45
30	53,1	23	2,37	2,65

Задача 7.2

Вариант №	Ток I, А	n, cм-1	l, м
1	1,99	9	0,68
2	1,32	9	0,48
3	1,24	7	1,1
4	1,41	8	0,25
5	1,34	10	1,08
6	1,76	10	1,03
7	1,77	9	0,97
8	1,79	7	1
9	1,84	10	0,69
10	1,41	9	0,42
11	1,91	9	0,62
12	1,76	7	0,98
13	1,18	8	0,48
14	1,03	10	0,73
15	1,92	7	0,78
16	1,73	8	0,74
17	1,45	7	0,52
18	1,59	7	0,41
19	1,57	8	0,22
20	1,41	7	0,63
21	1,21	9	0,68
22	1,27	9	1,12
23	1,21	8	0,25
24	1,69	8	0,22
25	1,92	9	0,31
26	1,66	8	0,32
27	1,33	10	0,96
28	1,61	7	0,41
29	1,8	9	0,77
30	1,68	8	0,96

Задача 7.3

Вариант №	l, см	N	Ток I, А
1	11	178	0,525
2	19	183	0,438
3	18	140	0,534
4	12	144	0,511
5	15	116	0,401
6	10	168	0,506
7	17	136	0,581
8	17	157	0,456
9	19	137	0,444
10	15	116	0,427
11	19	197	0,519
12	19	183	0,409
13	15	143	0,526
14	20	161	0,584
15	17	120	0,496
16	11	144	0,484
17	20	190	0,545
18	15	162	0,423
19	10	191	0,484
20	18	138	0,465
21	17	168	0,462
22	14	158	0,469
23	11	119	0,403
24	11	198	0,437
25	19	143	0,461
26	13	172	0,446
27	15	152	0,408
28	18	150	0,589
29	11	164	0,579
30	11	109	0,475

41

Магнитная энергия контура с током

Электрический ток обладает запасом так называемой магнитной энергии. Если в процессе вычисления данной энергии принимать все провода за идеально проводящие, то это не повлияет на результат, по той причине, что магнитная энергия зависима лишь от величины и распределения токов, а также от магнитных свойств заполняющей пространство среды.

Вывод формулы энергии магнитного поля

Для начала рассмотрим случай с одиночным неподвижным замкнутым контуром (витком проводника).

Пример 1

Пускай изначально сила тока в нем равняется нулю. Не важно каким способом доводим значение тока в витке до I. Вместе с ростом тока в контуре повышается и значение магнитного потока Ф, проходящего через него. Возникает электродвижущая сила (ЭДС) индукции. Элементарная работа, производимая внешним источником против ЭДС индукции, будет эквивалентна следующему выражению: δAвнеш=-εиндIdt.

Применяя закон Фарадея, выводим: δAвнеш=1cIdΦ.

Данное соотношение носит общий характер. Оно является справедливым и для ферромагнитных материалов, ведь в процессе его вывода относительно магнитных свойств среды не вводилось никаких предположений. Однако стоит отметить, что в случае, когда среда не обладает гистерезисом, к примеру, являясь пара- или диамагнетиком, δAвнеш будет применяться исключительно в целях роста значения магнитной энергии Wm, соответственно:

dWm=IcdΦ.

Исходя из условий закона Био-Савара-Лапласа, можно заявить, что индукция магнитного поля тока линейно зависима от силы тока. В условиях переменной силы тока, протекающего по жесткому неподвижному контуру, картина силовых линий не претерпевает изменений, а индукция в каждой точке прогрессирует пропорционально силе тока. Соответственно, поток магнитной индукции Ф, проходящий через неизменную и недвижимую площадь, тоже пропорционален силе тока, по этой причине: Φ=LIc,

где L представляет собой индуктивность контура, постоянный коэффициент пропорциональности, не обладающий зависимостью от силы тока и индукции магнитного поля. Подставим (5) в (4), получим:

Из формулы (6) следует, что:

Определение 1

Индуктивность. Энергия магнитного поля — FizikatTYT

Индуктивность – это коэффициент пропорциональности между электрическим током, протекающим по замкнутому контуру, и магнитным потоком через поверхность, ограниченную контуром.

Математическая формула, соответствующая этому определению:

Ф = L*I

где Ф – магнитный поток,

L – индуктивность,

I – сила тока.

Это классическое определение индуктивности, принятое на начальном этапе изучения электромагнитных явлений. В нем отражено одно из проявлений индуктивности. Познакомившись с ним, можно подумать, что индуктивность – свойство небольшого класса объектов, неких замкнутых контуров, создающих магнитное поле. Это не так; проявления индуктивности многообразны, и мы сталкиваемся с ними в повседневной жизни, зачастую не сознавая этого.

В девятнадцатом веке ученые только начинали изучать электромагнитные явления. Понятие индуктивности, как особого свойства электропроводящего контура, сформулировано в 1886 году, при изучении постоянного тока.

Правило Ленца и индуктивность

Электрический ток создает магнитное поле – это была сенсация в девятнадцатом веке. Электрические и магнитные явления представлялись в прошлом совершенно разными явлениями, и открытие связи между ними вызвало горячий интерес исследователей. Магнитное поле казалось многоликим, присущим совершенно разным объектам – куску магнитной руды, Земному шару и… проводу с током. Сейчас известно, что в каждом из этих объектов магнитное поле порождается движением электрического заряда.

В современной науке установлена общая природа электрического и магнитного полей. При изучении постоянного тока был сделан первый шаг к пониманию этой истины – открыта связь между  током и магнитным полем, между силой тока и силой создаваемого им магнитного поля.

Символ L, которым обозначается индуктивность, выбран в честь физика Эмиля Ленца. Он изучал магнитные явления, возникающие при протекании электрического тока. Сила Ленца – это сила, действующая на проводник с током, помещенный в магнитное поле.

Ленц также наблюдал, как катушки из электрических проводов, по которым пропускался ток, притягивались или отталкивались, подобно постоянным магнитам. Притяжение или отталкивание? Это определялось направлением тока в витках, взаимным расположением катушек. А сила взаимодействия определялась количеством витков и силой тока. При одинаковом токе, катушка с большим числом витков создавала большее магнитное поле.

Контур с током и катушка индуктивности

Контур с током может быть одиночным (одновитковая катушка)

Контур с током может состоять из нескольких контуров (многовитковая катушка)

В электротехнике и радиотехнике применяются многовитковые катушки.

Чем больше витков, тем больше индуктивность катушки. Один и тот же ток, протекающий через одиночный виток и через многовитковую катушку, создаст разное по силе магнитное поле. У многовитковой катушки индуктивность больше, чем у одного витка; она пропорциональна количеству витков.

Когда нужно создать сильное магнитное поле, наматывают сотни и тысячи витков из тонкой медной проволоки. Такие катушки применяются в электромагнитах, трансформаторах, электродвигателях.

Индуктивность,  индукция, самоиндукция

Если обозначение индуктивности L выбрано в честь физика Ленца, то единица измерения индуктивности Генри (Гн) носит имя другого физика – Джозефа Генри.

Ленц исследовал магнитные явления, возникающие при наличии постоянного тока, а Генри занимался переменным током. Точнее, он рассматривал переходные процессы, возникающие при включении и выключении электрического тока.

Что происходит, когда ток в цепи, содержащей катушку индуктивности, включается? Он не возрастает мгновенно, а увеличивается плавно. Чем больше витков в катушке, тем более растянут во времени процесс нарастания тока. Но число витков влияет еще и на силу магнитного поля, создаваемого током в катушке!

Джозеф Генри установил связь этих явлений. Оказывается, чем больше индуктивность, тем более инерционный процесс возрастания тока при включении. Это можно сравнить с массой в механике: чем массивнее тело, тем дольше оно разгоняется при воздействии на него силы.

Почему в катушке тормозится увеличение тока? Мы наблюдаем здесь явление самоиндукции. Ведь ток создает магнитное поле, не так ли?

Но на этом преобразование полей не останавливается. Меняющееся магнитное поле создает электрическое поле! Если в поле находится проводник, в нем наводится электродвижущая сила.  Это явление названо электромагнитной индукцией.

Именно меняющееся, переменное магнитное поле способно создать электрическое поле и навести в проводнике электрический ток.

После того, как щелкнул выключатель, в цепи происходят такие процессы:

1. Появляется и начинает увеличиваться электрический ток;
2. Возрастающий электрический ток создает меняющееся магнитное поле;
3. Переменное магнитное поле в том же самом проводнике наводит электрическое напряжение, противоположное приложенному;
4. Наведенная магнитным полем электродвижущая сила, противоположная напряжению от источника, уменьшает суммарное напряжение, действующее на цепь, а ток соответствует уменьшенному напряжению.

Напряжение, наведенное магнитным полем в проводнике, называется ЭДС самоиндукции. Ток в проводнике является причиной возникновения противоположного напряжения в том же проводнике, то есть причиной торможения тока является сам ток; поэтому процесс назван самоиндукцией.

Величина ЭДС самоиндукции зависит от скорости изменения тока и от индуктивности:

Минус в формуле указывает на то, что в цепи возникает противо ЭДС, направленная так, чтобы тормозить изменение тока.

В соответствии с этой формулой, единицу индуктивности 1 Генри определили следующим образом:

Один Генри – это индуктивность, при которой скорость изменения тока, равная одному амперу в секунду, приводит к наведению ЭДС самоиндукции, равной одному вольту.

1Вольт = — 1 Генри * 1 Ампер/секунда, или

1В = — 1 Гн * 1А/с

Индуктивность как мера самоиндукции проще поддается измерению, чем индуктивность – как коэффициент между током и магнитным потоком. В благодарность за открытие явления самоиндукции физики присвоили имя Джозефа Генри единице измерения индуктивности.

Энергия магнитного поля

Магнитное поле обладает энергией. Магнитные силы совершают механическую работу, притягивая или отталкивая другие магниты или тела из магнитных материалов. Меняющееся магнитное поле индуцирует электрический ток в проводниках.

Магнитную энергию можно выразить через математическую формулу.  В предыдущем разделе упоминалась инерционность индуктивной цепи, ее роль в электромагнитных явлениях сравнивалась с ролью массы в механике. Интересно, что эта аналогия углубляется при рассмотрении энергии.

Формула энергии магнитного поля похожа на формулу кинетической энергии механического тела:

Энергия магнитного поля пропорциональна индуктивности и квадрату величины тока.

Во время переходного процесса, когда при включении ток в цепи замедленно нарастает, происходит накопление магнитной энергии. Эта энергия может использоваться для совершения работы. И эта энергия создает проблемы при выключении тока в цепи с большой индуктивностью.

Если ток уменьшать, возникнет ЭДС, замедляющая уменьшение тока. Но если ток выключить, резко разорвав цепь, скорость изменения тока от конкретного значения до нуля теоретически должна быть бесконечно велика. Это значит, ЭДС самоиндукции при выключении тока тоже должна быть бесконечно велика.

Этот математический парадокс возник из-за упрощенных идеализированных формул.  В реальности ток не прекращается мгновенно, размыкание контактов занимает некоторый короткий промежуток времени, но все равно скорость изменения тока велика, и наводится ЭДС значительной величины. Обычным явлением при выключении цепи является искрение. Если выключать ток в цепи с большой индуктивностью, то попытка резкого прекращения тока может стать причиной вспышки электрической дуги.

Что произойдет, если дуга не вспыхнула, а ток прекратился? Куда девалась энергия магнитного поля? Частично она перешла в тепловую энергию – контакты выключателя нагрелись. Остальная часть энергии магнитного поля, при его резком уменьшении до нуля, перешла в электромагнитную волну. Переменное магнитное поле индуцировало переменное электрическое поле; в свою очередь, переменное электрическое вызвало новую волну магнитного, и так далее.

Выключение тока простым щелчком выключателя – посылает в бесконечное пространство широкий «шумовой» спектр электромагнитных колебаний.

Распрямим провод — индуктивность остается

Первоначально индуктивность считали атрибутом контура или катушки. Причина этого – в способах измерения. Магнитный поток через контур или катушку локализован, его можно измерить (хотя точность измерений долгое время была невысокой). Если катушку раскрутить и провод выпрямить, и пропускать ток по прямому проводу, магнитное поле все равно возникнет. Но померить его поток непросто!

А что произойдет с самоиндукцией? Ток в прямом проводе возрастает быстрее, чем в катушке. Но если провод протянуть на несколько километров (построить линию электропередач), то явление самоиндукции наблюдается.  Возрастание тока, при его подаче в линию передач, происходит не мгновенно. Значит, прямой провод обладает индуктивностью, хотя и меньшей, чем катушка.

На рисунке показан проводник с током и силовые линии магнитного поля, имеющие форму окружностей.

Индуктивность и реактивное сопротивление

Катушка индуктивности может оказывать ничтожно малое сопротивление установившемуся постоянному току, но ее сопротивление переменному току значительно.  Такое сопротивление называется реактивным.

Реактивное сопротивление переводит энергию электрического тока в энергию электромагнитного поля. Если на цепь, обладающую индуктивностью L, подать переменное напряжение с частотой f, то реактивное сопротивление будет равно

Чем выше реактивное сопротивление, тем меньше будет переменный ток.

Реактивное сопротивление зависит от частоты. Элементы с маленькой индуктивностью создают ничтожно малое сопротивление на низких частотах, но при переходе от частоты 50 Герц к частоте 50 МГц (мегагерц) сопротивление возрастает в миллион раз.

При низких частотах не принимаются во внимание индуктивности небольших отрезков провода, но при сотнях мегагерц и при гигагерцах приходится учитывать даже индуктивность проволочных  выводов радиодеталей. В технике сверхвысоких частот применяются безкорпусные элементы, не имеющие проволочных выводов. Вместо них – контактные площадки, которые паяют на печатную плату.

Цепь с индуктивным сопротивлением, при подаче переменного тока, излучает электромагнитные волны. Но возможен и обратный процесс: при воздействии электромагнитного поля в индуктивности наводится переменный ток.

Стиральная машина и индуктивное сопротивление

Пользователи автоматических стиральных машин часто жалуются на то, что ток «пробивает на барабан».  Электрическая изоляция таких машин, как правило, в полном порядке, но все равно есть неприятное ощущение от прикосновения к металлическому барабану, при загрузке и выгрузке вещей.

Причина – в наведенном токе. Машина-автомат имеет блок питания, в котором сетевое напряжение преобразуется в высокочастотное.  Это высокочастотное напряжение наводится на все электропроводящие предметы, в частности на металлический барабан. Индуктивность барабана не нормируется, но наверняка она мала. Тем не менее, ток высокой частоты электронной схемы индуцирует на металлических частях стиральной машины отклик – небольшой ток.

Подобное явление иногда наблюдают пользователи современных водонагревателей с электронным управлением, греющих водопроводную воду.  Если блок питания в устройстве  оказывается близко к трубе с водой, на ней может наводиться переменный высокочастотный ток,  и вода из крана «щиплется». Избежать неприятных ощущений можно, отключив электрическое напряжение от котла.

Индуктивность человеческого тела

Наше тело является электрическим проводником,  а все проводники, в той или иной степени, обладают индуктивностью. Это значит, что мы подвержены воздействию электромагнитного поля, под его воздействием в нашем теле могут индуцироваться переменные токи.

Индуктивность человеческого тела значительно меньше. чем индуктивность антенны или дросселя, и небольшие электромагнитные поля практически не влияют на нас. Но чем выше мощность излучения, а главное – чем выше частота электромагнитного поля, тем воздействие сильнее. Сильное поле СВЧ диапазона представляет смертельную опасность.

Для защиты людей на производствах, связанных с сильными электромагнитными полями, применяют специальную экранирующую одежду, экранированные помещения. Существуют зоны, закрытые для посещения – вокруг мощных антенн, радиолокаторов.

Периодически появляется информация о вреде длительных разговоров по мобильному телефону, когда трубка прижата к голове. Телефон излучает высокочастотный электромагнитный сигнал небольшой мощности, из-за малой мощности его влияние незначительно. Но при длительном воздействии это излучение  может нанести вред здоровью. Использовать скайп, установленный на компьютер, предпочтительнее.

Самоиндукция. Индуктивность. Энергия магнитного поля тока

Самоиндукция. Индуктивность. Энергия магнитного поля тока

Самоиндукция

Каждый проводник, по которому протекает эл.ток, находится в собственном магнитном поле.

При изменении силы тока в проводнике меняется м.поле, т.е. изменяется магнитный поток, создаваемый этим током. Изменение магнитного потока ведет в возникновению вихревого эл.поля и в цепи появляется ЭДС индукции.

Это явление называется самоиндукцией.

Самоиндукция — явление возникновения ЭДС индукции в эл.цепи в результате изменения силы тока.
Возникающая при этом ЭДС называется ЭДС самоиндукции

Проявление явления самоиндукции

Замыкание цепи

При замыкании в эл.цепи нарастает ток, что вызывает в катушке увеличение магнитного потока, возникает вихревое эл.поле, направленное против тока, т.е. в катушке возникает ЭДС самоиндукции, препятствующая нарастанию тока в цепи (вихревое поле тормозит электроны).
В результате Л1 загорается позже, чем Л2.

Размыкание цепи

При размыкании эл.цепи ток убывает, возникает уменьшение м.потока в катушке, возникает вихревое эл.поле, направленное как ток (стремящееся сохранить прежнюю силу тока) , т.е. в катушке возникает ЭДС самоиндукции, поддерживающая ток в цепи.
В результате Л при выключении ярко вспыхивает.

Вывод:

в электротехнике явление самоиндукции проявляется при замыкании цепи (электрический ток нарастает постепенно) и при размыкании цепи (электрический ток пропадает не сразу).

ИНДУКТИВНОСТЬ

От чего зависит ЭДС самоиндукции?

Электрический ток создает собственное магнитное поле. Магнитный поток через контур пропорционален индукции магнитного поля (Ф ~ B), индукция пропорциональна силе тока в проводнике
(B ~ I), следовательно магнитный поток пропорционален силе тока (Ф ~ I).
ЭДС самоиндукции зависит от скорости изменения силы тока в эл.цепи, от свойств проводника (размеров и формы) и от относительной магнитной проницаемости среды, в которой находится проводник.
Физическая величина, показывающая зависимость ЭДС самоиндукции от размеров и формы проводника и от среды, в которой находится проводник, называется коэффициентом самоиндукции или индуктивностью.

Индуктивность — физическая величина, численно равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1Ампер за 1 секунду.
Также индуктивность можно рассчитать по формуле:

где Ф — магнитный поток через контур, I — сила тока в контуре.

Единицы измерения индуктивности в системе СИ:

Индуктивность катушки зависит от:
числа витков, размеров и формы катушки и от относительной магнитной проницаемости среды ( возможен сердечник).

ЭДС САМОИНДУКЦИИ

ЭДС самоиндукции препятствует нарастанию силы тока при включении цепи и убыванию силы тока при размыкании цепи.

ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ ТОКА

Вокруг проводника с током существует магнитное поле, которое обладает энергией.
Откуда она берется? Источник тока, включенный в эл.цепь, обладает запасом энергии.
В момент замыкания эл.цепи источник тока расходует часть своей энергии на преодоление действия возникающей ЭДС самоиндукции. Эта часть энергии, называемая собственной энергией тока, и идет на образование магнитного поля.

Энергия магнитного поля равна собственной энергии тока.
Собственная энергия тока численно равна работе, которую должен совершить источник тока для преодоления ЭДС самоиндукции, чтобы создать ток в цепи.

Энергия магнитного поля, созданного током, прямо пропорциональна квадрату силы тока.
Куда пропадает энергия магнитного поля после прекращения тока? — выделяется ( при размыкании цепи с достаточно большой силой тока возможно возникновение искры или дуги)

ВОПРОСЫ К ПРОВЕРОЧНОЙ РАБОТЕ

по теме «Электромагнитная индукция»

1. Перечислить 6 способов получения индукционного тока.
2. Явление электромагнитной индукции (определение).
3. Правило Ленца.
4. Магнитный поток ( определение, чертеж, формула, входящие величины, их ед. измерения).
5. Закон электромагнитной индукции (определение, формула).
6. Свойства вихревого электрического поля.
7. ЭДС индукции проводника, движущегося в однородном магнитном поле ( причина появления, чертеж, формула, входящие величины, их ед. измерения).
8. Самоиндукция (кратко проявление в электротехнике, определение).
9. ЭДС самоиндукции (ее действие и формула).
10. Индуктивность (определение, формулы, ед. измерения).
11. Энергия магнитного поля тока (формула, откуда появляется энергия м. поля тока, куда пропадает при прекращении тока).

Электромагнитное поле — Класс!ная физика

Взаимодействие токов. Магнитное поле. Вектор магнитной индукции. Сила Ампера — Действие магнитного поля на движущийся заряд.Магнитные свойства вещества — Явление электромагнитной индукции. Магнитный поток. Направление индукционного тока. Правило Ленца — ЭДС электромагнитной индукции. Вихревое электрическое поле — ЭДС индукции в движущихся проводниках
— Самоиндукция. Индуктивность. Энергия магнитного поля. Вопросы к пр/работе