Электрическая емкость

Дата публикации: 12 марта 2015.
Категория: Электротехника.

Сообщение электрического разряда проводнику называется электризацией. Чем больший заряд принял проводник, тем больше его электризация, или, иначе говоря, тем выше его электрический потенциал.

Между количеством электричества и потенциалом данного уединенного проводника существует линейная зависимость: отношение заряда проводника к его потенциалу есть величина постоянная:

Для какого-либо другого проводника отношение заряда к потенциалу есть также величина постоянная, но отличная от этого отношения для первого проводника.

Одной из причин, влияющих на эту разницу, являются размеры самого проводника. Один и тот же заряд, сообщенный различным проводникам, может создать различные потенциалы. Чтобы повысить потенциал какого-либо проводника на одну единицу потенциала, необходим определенный заряд.

Электрическая емкость и ее единица измерения

Свойство проводящих тел накапливать и удерживать электрический заряд, измеряемое отношением заряда уединенного проводника к его потенциалу, называется электрической емкостью, или просто емкостью, и обозначается буквой С.

Приведенная формула электрической емкости позволяет установить единицу электрической емкости.

Практически заряд измеряется в кулонах, потенциал в вольтах, а емкость в фарадах:

Емкостью в 1 фараду обладает проводник, которому сообщают заряд в 1 кулон и при этом потенциал проводника увеличивается на 1 вольт.

Единица измерения электрической емкости – фарада (обозначается ф или F) очень велика. Поэтому чаще пользуются более мелкими единицами – микрофарадой (мкф или μF), составляющей миллионную часть фарады:

1 мкф = 10^-6ф ,

и пикофарадой (пф), составляющей миллионную часть микрофарады:

1 пф = 10^-6мкф = 10^-12ф .

Найдем выражение практической единицы – фарады в абсолютных единицах:

Электрический конденсатор

Устройство, предназначенное для накопления электрических зарядов, называется электрическим конденсатором.

Рисунок 1. Модель простейшего конденсатора

Конденсатор состоит из двух металлических пластин (обкладок), разделенных между собой слоем диэлектрика. Чтобы зарядить конденсатор, нужно его обкладки соединить с полюсами электрической машины. Разноименные заряды, скопившиеся на обкладках конденсатора, связаны между собой электрическим полем. Близко расположенные пластины конденсатора, влияя одна на другую, позволяют получить на обкладках большой электрический заряд при относительно невысокой разности потенциалов между обкладками. Электрическая емкость конденсатора есть отношение заряда конденсатора к разности потенциалов между его обкладками:

Как показывают измерения, емкость конденсатора увеличится, если увеличить поверхность обкладок или приблизить их одну к другой. На емкость конденсатора оказывает влияние также материал диэлектрика. Чем больше электрическая проницаемость диэлектрика, тем больше емкость конденсатора по сравнению с емкостью того же конденсатора, диэлектриком в котором служит пустота (воздух). Выбирая диэлектрик для конденсатора, нужно стремиться к тому, чтобы диэлектрик обладал большой электрической прочностью (хорошими изолирующими качествами). Плохой диэлектрик приводит к пробою его и разряду конденсатора. Несовершенный диэлектрик повлечет за собой утечку тока через него и постепенный разряд конденсатора.

Длинные линии передачи высокого напряжения можно рассматривать как своеобразные обкладки конденсатора. Емкость провода нужно рассматривать не только относительно другого провода, но также относительно земли, стен помещений и окружающих предметов. Значительной емкостью обладают подводные и подземные кабели ввиду близкого расположения токоведущих жил между собой.

Конденсатор постоянной емкости

Конденсаторы, емкость которых изменять нельзя, называются конденсаторами постоянной емкости.

Рисунок 2. Схема устройства конденсатора
постоянной емкости

Наиболее распространенные в настоящее время конденсаторы постоянной емкости состоят из очень тонких металлических (станиолевых) листов с парафинированной бумажной или слюдяной прослойкой между ними.

Для увеличения емкости (увеличения площади пластин конденсатора) чаще всего берут по нескольку станиолевых листов и соединяют их в две группы, входящие одна в другую и разделенные диэлектриком, как схематически показано на рисунке 2. Иногда также берут две длинные станиолевые пластины, прокладывают между ними и снаружи парафинированную бумагу и затем свертывают все в компактный пакет или трубку. Конденсаторы большой емкости во многих случаях помещают в металлическую коробку и заливают парафином.

Рисунок 3. Внешний вид современных конденсаторов постоянной емкости

Определим емкость плоского конденсатора. Возьмем произвольную замкнутую поверхность вокруг одной из пластин конденсатора. Тогда по теореме Гаусса поток вектора напряженности, проходящий через любую замкнутую поверхность, внутри которой находится электрический заряд, равен:

(1)

Предполагая, что поле конденсатора однородно (пренебрегая искажением поля у краев пластин), получаем напряженность электрического поля в конденсаторе:

(2)

где d – расстояние между пластинами или толщина диэлектрика. Подставив значение E из формулы (2) в формулу (1), получим:

откуда

Так как

то выражение емкости плоского конденсатора примет вид:

где S – площадь пластин в м²; d – толщина диэлектрика в м; ε – относительная электрическая проницаемость диэлектрика (диэлектрическая проницаемость).

Таким образом, для увеличения емкости плоского конденсатора нужно увеличить площадь его пластин (обкладок) S, уменьшить расстояние между ними d и в качестве диэлектрика поставить материал с большой относительной электрической проницаемостью (ε).

Видео об устройстве конденсатора постоянной емкости:

Конденсатор переменной емкости

Конденсаторы, емкость которых можно менять, называются конденсаторами переменной емкости.

Наиболее простой конденсатор переменной емкости имеет несколько (реже один) медных или алюминиевых полудисков, соединенных между собой электрически и укрепленных неподвижно. Другой ряд таких же полудисков собран на общей оси. При повороте этой оси каждый из укрепленных на ней полудисков входит меду двумя неподвижными полудисками. Поворачивая ось и меняя таким образом взаимное расположение подвижных и неподвижных полудисков, мы можем менять емкость конденсатора. На рисунке 3 показана схема устройства и на рисунке 4 – общий вид воздушного конденсатора переменной емкости.

Рисунок 3. Схема устройства конденсатора переменной емкости

Рисунок 4. Общий вид конденсатора переменной емкости

Видео об устройстве серийного конденсатора переменной емкости:

Видео о том, как можно сделать самодельный конденсатор переменной емкости своими руками:

Видео о том, как можно сделать самодельный конденсатор переменной емкости своими руками:

Электролитические конденсаторы

В радиотехнике применяются также электролитические конденсаторы. Эти конденсаторы изготовляются двух типов: жидкостные и сухие. В обоих типах конденсаторов употребляется оксидированный алюминий. Путем специальной электрохимической обработки на поверхности алюминия получают тонкий (порядка нескольких десятков микрон) слой оксида алюминия Al₂O₃, представляющий так называемую оксидную изоляцию алюминия. Оксидная изоляция обладает электроизолирующими свойствами, а также является механически прочной, нагревостойкой, но гигроскопичной.

В жидкостных электролитических конденсаторах алюминиевую оксидированную пластину помещают внутрь металлического корпуса, который служит второй пластиной. В корпус заливают электролит, состоящий из раствора борной кислоты с некоторыми примесями.

Сухие электролитические конденсаторы изготовляют путем сворачивания трех лент. Одна лента представляет собой алюминиевую оксидированную фольгу (тонко раскатанный лист металла). Другой пластиной является лента из алюминиевой фольги. Между двумя металлическими лентами помещается бумажная или марлевая лента, пропитанная вязким электролитом. Плотно свернутые ленты помещаются в алюминиевый корпус и заливаются битумом. Тонкий оксидный изолирующий слой с высокой электрической проницаемостью (ε = 9) позволяет получить дешевые конденсаторы с большой удельной емкостью.

Видео об устройстве электролитического конденсатора:

Параллельное соединение конденсаторов

Рисунок 5. Параллельное
соединение конденсаторов

Когда емкость конденсатора мала, то соединяют несколько конденсаторов параллельно (рисунок 5).

При параллельном соединении конденсаторов напряжение на обкладках каждого конденсатора одно и то же. Поэтому можно написать:

U₁ = U₂ = U₃ = U .

Количество электричества (заряд) каждого конденсатора:

q₁ = C₁ × U; q₂ = C₂ × U; q₃ = C₃ × U .

Общий заряд батареи конденсаторов:

q = q₁ + q₂ + q₃ ;

q = C₁ × U + C₂ × U + C₃ × U = U (C₁ + C₂ + C₃) .

Обозначая емкость батареи конденсаторов через C, получаем:

q = C × U ,

тогда

C × U = U × (C₁ + C₂ + C₃)

или окончательно формула емкости при параллельном соединении конденсаторов примет вид:

C = C₁ + C₂ + C₃ .

Следовательно, при параллельном соединении конденсаторов общая емкость равна сумме емкостей отдельных конденсаторов. При параллельном соединении каждый конденсатор окажется включенным на полное напряжение сети.

Последовательное соединение конденсаторов

Рисунок 6. Последовательное
соединение конденсаторов

Рассмотрим последовательное соединение конденсаторов (рисунок 6).

Если левая обкладка первого конденсатора заряжена положительно (+), то вследствие электростатической индукции правая обкладка этого конденсатора получит отрицательный заряд (–), перешедший с левой обкладки второго конденсатора, которая сама зарядится положительно, и так далее. Значит, при последовательном соединении каждый конденсатор независимо от величины его емкости получит один и тот же заряд, то есть

q₁ = q₂ = q₃ = q .

Напряжение, приложенное ко всей батареи конденсаторов, равно сумме напряжений на обкладках каждого конденсатора:

U = U₁ + U₂ + U₃ .

Так как

для всей батареи

теперь можно написать

или, сокращая на q, получим окончательно, что емкость конденсаторов при последовательном соединении равна:

Таким образом, при последовательном соединении конденсаторов обратная величина общей емкости равна сумме обратных величин емкостей отдельных конденсаторов. Каждый из конденсаторов включен на меньшее напряжение, чем напряжение сети.

Конденсаторы широко применяются в радиотехнике, рентгенотехнике, высокочастотной промышленной электротехнике, для увеличения коэффициента мощности электроустановок и так далее.

Источник: Кузнецов М.И., «Основы электротехники» — 9-е издание, исправленное — Москва: Высшая школа, 1964 — 560с.

формула, в чем измеряется и как, от чего зависит емкость

В схемах электронных устройств конденсаторы выполняют большое количество полезных функций. Хотя конструкция этих приспособлений остаётся максимально простой. Но надо внимательно изучить ёмкость конденсатора и сами устройства, чтобы узнать, какого эффекта можно от них добиться.

Что это такое

Конденсатор — устройство, внутри которого сгущается или собирается электрический заряд в определённых количествах. Можно назвать это приспособление своеобразным аккумулятором. Отличие от существующих аналогов — в готовности сразу отдать всё накопленное, буквально в несколько секунд. Ещё одна отличительная черта — отсутствие внутри источника ЭДС. Как найти ёмкость, будет рассказано далее.

Возможные модели

Для чего нужен

Эти устройства отличаются также широкой сферой применения. Вот лишь некоторые допустимые варианты:

1. Хранение аналоговых сигналов.
2. Сохранение цифровых данных.
3. Сфера телекоммуникационной связи. В этом случае главная функция — регулировка частоты, настройка профессионального оборудования.
4. Использование при создании различных источников питания.
5. Сглаживание выпрямленного напряжения на выходе устройств. Другой вопрос — в чём измеряется ёмкость конденсаторов.

Ещё одна возможная функция — генерация высокого напряжения, которое во много раз больше по сравнению с входными параметрами. Конденсаторы могут быть отличным хранилищем для электронов. Даже при отключении цепи от заряда энергия продолжает сохраняться внутри, на протяжении длительного времени.

Разные габариты

Принцип действия

Основные элементы любого конденсатора — это две проводящие обкладки. У каждой из них — свой электрический заряд, знаки у них противоположные. Этот заряд сохраняется благодаря диэлектриком, который разделяет обкладки.

В конденсаторах используется несколько разновидностей материалов в качестве изоляции. Это касается таких решений:

• Полистирол;
• Тантал;
• Слюд;
• Керамика.

Воздух вместе с бумагой и пластиком тоже популярные материалы, с помощью которых создают конденсаторы. Благодаря их применению обкладки внутри не соприкасаются друг с другом.

Электролитические изделия

Характеристики

На корпусе устройства обычно пишут о том, какие параметры для него характерны. Из других важных сведений из маркировки — дата выпуска, наименование фирмы производителя, тип конденсатора.

• Показатель номинальной ёмкости.

Интересно. Один из самых важных. ГОСТ 2.702 — основной документ, регулирующий это направление. На схемах без указания единиц измерения пишут ёмкость, если она находится в пределах от 0 до 9 999 пФ. Если диапазон больше — то о микрофарадах обязательно упоминают. На самом конденсаторе соответствующая маркировка тоже стоит.

• Отклонения от номинального значения.
• Номинальное напряжение. Благодаря ему проще понять, как определить ёмкость конденсатора, формула которой остаётся одинаковой.

Для работы рекомендуется брать конденсаторы, у которых есть некоторый запас относительно данного параметра. С меньшим значением применять приборы не рекомендуют. Иначе диэлектрик пострадает от пробоя, устройство выйдет из строя раньше указанного времени.

• Рабочие температуры, постоянный и переменный ток — характеристики дополнительные, информация о них не всегда выносится на этикетку.
• Конденсаторы бывают однофазными и трёхфазными, для внутренней или наружной установки.

Внутреннее устройство

Величина заряда конденсатора

Как уже говорилось, конденсаторы — это электронные устройства, главное предназначение которых — накопление заряда в определённых количествах. Эта способность зависит от другой главной характеристики, получившей название ёмкости.

Её можно определить по формуле:

C = q/U.

Это как соотношение между количеством электрического заряда и напряжением. Самое простое объяснение, какой может быть ёмкость конденсатора, формула через площадь у которой несколько иная.

Керамические

В чём измеряется

Для этого используются величины, названные фарадами и микрофарадами. В честь учёного, который открыл соответствующее явление.

Разные устройства

Формула ёмкости

Основная формула уже была описана выше. Ёмкость относят к величинам постоянного характера. Её определяют другие параметры, например — размер конденсатора, конструктивные особенности.

За единицу ёмкости принимают ёмкость конденсатора, которому хватает единичного заряда для получения разности потенциалов в 1 Вольт. Определять конечные цифры благодаря этому очень просто.

Горизонтальные

Плоского

Обычно между обкладками внутри плоского конденсатора создаётся так называемое однородное поле. Только около краёв подобное свойство может быть нарушено. Этими эффектами у краёв часто пренебрегают, когда организуют расчёты. Но такой подход допустим, только если расстояние между пластинами достаточно маленькое по сравнению с линейными размерами.

Плоский конденсатор отличается ёмкостью, которую считают по формуле:

C = (Ee0S)/d.

E0 — постоянная электрическая величина.

S — площадь каждой пластины. Часто учитывают детали конструкции с минимальной площадью.

D — обозначение расстояния между пластинами.

Другое дело — когда конструкцию строят на нескольких слоях диэлектрика. Тогда их тоже включают в формулу, обычно добавляют к знаменателю. Без объёма в такой ситуации тоже не обойтись.

Особенности применения

Сферического

Сферический — это конденсатор, обкладки которого выполнены в виде двух сферических проводящих поверхностей. Диэлектрик заполняет пространство между указанными выше деталями. В таком случае формула в знаменателе содержит дополнительные обозначения R — радиус каждой из пластин.

 

Суперконденсаторы

Цилиндрического

В данном случае пластины выглядят как две соосные или коаксиальные цилиндрические поверхности с проводящим эффектом. При этом радиус у каждого элемента разный. И здесь пространство между разными частями заполнено диэлектриком. L — обозначение высоты цилиндра. И к формуле добавляют символ для диаметра. Его измеряют отдельно для обкладки внутри и снаружи.

Назначение

Как с помощью закона Гаусса рассчитать ёмкость конденсатора?

Главное — чтобы изначально присутствовала ёмкость с заданной геометрией у конденсатора. Остаётся вставить в стандартную формулу разность между потенциалами. Благодаря этому уменьшается общий уровень нагрузки, который обозначают как Q.

Соотношения между полями E и V применяют для поиска характеристик, которые остались неизвестными для формулы. Закон Гауса — универсальный инструмент, упрощающий любые вычисления в этой сфере. Измеряться так могут многие показатели.

Разнообразие выбора

Эксплуатационные характеристики

Не идеальные, но реальные конденсаторы обладают рядом дополнительных характеристик помимо тех, о которых сказано выше. Среди них:

1. Зависимость между ёмкостью и температурой.
2. Потери диэлектрического характера.
3. Сопротивление материала, из которого изготовлены обкладки.
4. Ток утечки.
5. Уровень полярности.
6. Номинальное напряжение.

Важно разобраться, какой источник может быть у потерь. Но для этого необходимо разобраться с таким понятием, как графики синусоидного тока, различные направления этого вида энергии. В обкладках ток равен нулю, когда конденсатор набрал максимальный заряд. Напряжение в этом случае у изделия отсутствует. То есть, по фазе напряжение вместе с током сдвигаются на угол в 90 градусов. Идеальная ситуация — когда у конденсатора появляется только реактивная мощность.

Важно. Но реальность такова, что у обкладок появляется собственное сопротивление. Часть энергии нужна, чтобы температура диэлектрика повысилась до определённого уровня. Из-за этого и появляются потери внутри конструкции. Эта характеристика в большинстве случаев остаётся незначительной, но в некоторых ситуациях пренебрегать ей не получится.

Тангенс угла диэлектрических потерь — главная единица измерения, применяемая в этом случае. Это соотношение между активной и реактивной разновидностями мощности. Измерение величины возможно, но только в теоретическом плане. Иначе рассчитать результаты невозможно.

Переменный вид

Каким ещё бывает техническое исполнение конденсаторов?

Постоянные и переменные, подстроечные — группы конденсаторов, которые выделяются в зависимости от возможности регулировать основные рабочие параметры. Форма позволяет выделить плоские и цилиндрические, сферические разновидности. Но тип диэлектрика — главное свойство, по которому чаще всего проводят классификацию.

Импортные и отечественные разработки

Бумажные

Бумага, чаще всего — промасленная — вот главный диэлектрик для таких ситуаций. Конденсаторы данного вида известны крупными габаритами. Без промасливания можно изменить характеристику в меньшую сторону. Обычно служат устройствами со стабилизирующей и накопительной функциями. Но из современной электроники их всё чаще вытесаняют плёночные аналоги, которые считают более современными.

Если промасливание отсутствует, появляется серьёзный недостаток — реакция на влажность воздуха, даже если упаковка остаётся абсолютно герметичной. Энергопотери увеличиваются при наличии промокшей бумаги.

Разные характеристики

Диэлектрики-органические плёнки

Выполняются из органических полимеров, например:

• Фоторопласт.
• Полистирол.
• Полипропилен.
• Полисульфон.
• Поликарбонат.
• Полиамид.
• Полиэтилентерифталат.

Размеры таких конденсаторов более компактные, если сравнить с предыдущим вариантом. При этом диэлектрические потери не становятся больше, даже если влажность увеличивается. Но при перегреве многие устройства часто выходят из строя. А если недостаток отсутствует — приобретение прибора связано с дополнительными расходами.

Твёрдые неорганические материалы

Примеры — стекло и керамика, слюда.

Стабильность, линейность указанных характеристик — главное преимущество. Некоторые устройства реагируют даже на уровень радиации окружающей среды. Но иногда такая зависимость может стать и проблемой. Чем менее выражены недостатки — тем дороже стоит устройство.

Оксидные диэлектрики

Подходят для производства танталовых и твердотельных конденсаторов, моделей из алюминия. Отличаются такой характеристикой, как полярность. При неправильном подключении могут быстро выйти из строя. То же касается ситуации с высоким номиналом напряжения. Но зато это компактные устройства со стабильной работой, достаточными показателями по ёмкости. Могут проработать около 60 тысяч часов, если эксплуатировать устройство правильно.

Маркировка конденсаторов

Ёмкость вместе с номинальным напряжением — характеристики, которые должны быть отражены в маркировке. Ещё применяют циферно-буквенную разновидность обозначений для основных параметров.

Интересно. В российской практике существует четыре буквы для обозначения устройств.

Первая буква К позволяет понять, что перед покупателем — именно конденсатор. Далее идёт цифра для обозначения разновидности применяемого диэлектрика. Следующим указывают назначение, тоже в виде буквы. Последние значки могут иметь разное назначение.

Эксплуатация

Выбор и эксплуатация

Главное — использовать приборы в режимах, не превышающих номинальные значения. Тогда никаких дефектов и проблем появиться не должно.

Обратите внимание. Электрохимические процессы диэлектрика — главная причина старения основных элементов при воздействии постоянного напряжения. Причина — постоянный ноль, увеличение влажности и температуры в окружающей среде. Вид диэлектрика, конструктивное исполнение определяют, как поведёт себя то или иное устройство в этих условиях.

Ионизационные процессы станут причиной старения в случае с переменным напряжением, импульсными режимами.

Защищённые керамические конденсаторы считаются наиболее прочными и надёжными моделями из всех. Либо стоит отдавать предпочтение оксидно-полупроводниковым вариантам. Каждый из них гарантирует максимальный срок службы.

Со временем любой конденсатор теряет ёмкость. Это нормальный процесс, проходящий в оборудовании. Поэтому не рекомендуется размещать устройства с другими предметами, которые подвержены сильному нагреву. Электролиты могут стать слабым местом для любой электроники. Качество детали во многом зависит от того, какого выбрать производителя. Но такая проблема заслуживает отдельного разговора.

Электрическая емкость: определение, формулы, единицы измерения

В электротехнике часто встречается понятие ёмкости. При этом речь идёт не о ведре или другом сосуде, а об электрической ёмкости проводника, аккумулятора и конденсатора. Путать эти понятия нельзя. В этой статье мы разберемся, что такое электрическая ёмкость, от чего она зависит и в каких единицах измеряется.

Определение

Для проводников электрической ёмкостью называется величина, которая характеризует способность тела накапливать электрический заряд. Это и есть её физический смысл. Обозначается латинской буквой C. Она равна отношению заряда к потенциалу, если это записать в виде формулы, то получается следующее:

C=q/Ф

Электроемкость любого предмета зависит от его формы и геометрических размеров. Если рассмотреть проводник в форме шара, в качестве примера, то формула для расчета её величины будет иметь вид:

Эта формула справедлива для уединенного проводника. Если расположить рядом два проводника и разделить их диэлектриком, тогда получится конденсатор. Об этом немного позже, сейчас давайте разберемся, в чем измеряется электроемкость.

Единица измерения электрической ёмкости — фарад. Если разложить её на составляющие согласно формуле то:

1 фарад =1 Кл/1 В

Исторически сложилось так, что размерность этой единицы выбрана не совсем верно. Дело в том, что на практике приходится работать с величинами электроемкости: мили-, микро-, нано- и пикофарад. Что равняется долям фарада, а именно:

1 мФ = 10^(-3) Ф

1 мкФ = 10^(-6) Ф

1 нФ = 10^(-9) Ф

1 пФ = 10^(-12) Ф

Конденсаторы

Конденсатор — это две пластины из проводящего материала, расположенные друг напротив друга, между которым находится слой диэлектрика. В заряженном состоянии обкладки имеют разные потенциалы: одна из них будет положительной, а вторая отрицательной. Электроемкость конденсатора зависит от величины заряда на его обкладках и разности потенциалов, напряжения между ними. Между пластинами возникает электростатическое поле, которое удерживает заряды на обкладках. Формула электрической емкости конденсатора в общем случае:

C=q/U

Если сказать простыми словами, то емкость конденсатора зависит от площади пластин и расстояния между ними, а также относительной диэлектрической проницаемости материала, расположенного между ними. Их различают по используемому диэлектрику:

• керамические;
• плёночные;
• слюдяные;
• металлобумажные;
• электролитические;
• танталовые и пр.

По форме обкладок:

• плоские;
• цилиндрические;
• сферические и пр.

Так как формула площади фигуры зависит от её формы, то и формула ёмкости будет разной для каждого случая.

Для плоского конденсатора:

Для двух концентрических сфер с общим центром:

Для цилиндрического конденсатора:

Как и у других элементов электрической цепи и в этом случае есть два основных способа соединения конденсаторов: параллельное и последовательное.

От этого зависит итоговая электрическая емкость полученной цепи. Расчёты ёмкости нескольких конденсаторов напоминают расчёты сопротивления резисторов в разном включении, только формулы для способов соединения расположены наоборот, то есть:

1. При параллельном соединении общая электроемкость цепи является суммой емкостей каждого из элементов. Каждый следующий подключенный увеличивает итоговую емкость

Cобщ=C1+C2+C3

2. При последовательном подключении электроемкость цепи снижается, подобно снижение сопротивления в цепи параллельно включённых резисторов. То есть:

Cобщ=(1/С1)+ (1/С2)+ (1/С3)

Важно! В параллельной схеме соединения напряжения на обкладках каждого элемента одинаковы. Это используют для получения больших значений электроемкости. В последовательном включении двух элементов напряжения на обкладках каждого из конденсаторов составляют по половине общего напряжения. Для трёх – трети и так далее.

Аккумуляторы и электроемкость

Основными характеристиками аккумуляторных батарей является:

• Номинальное напряжение.
• Емкость.
• Максимальный ток разряда.

В данном случае для определения количественной характеристики времени работы или, говоря простым языком, чтобы рассчитать, на какое время работы прибора хватит аккумулятора, используют величину ёмкости.

В аккумуляторных батареях для описания электрической ёмкости используют следующие размерности:

• А*ч — ампер-часы для больших аккумуляторов, например автомобильных.
• мА*ч — милиампер-часы, для аккумуляторов для носимых устройств, например смартфонов, квадрокопетров и электронных сигарет.
• Вт*часы — ватт-часы.

Эти характеристики позволяют определить, сколько времени работы выдержит аккумулятор при конкретной нагрузке. Для определения электрическую емкость аккумулятора измеряют в кулонах (Кл). В свою очередь кулон равен количеству электричества, переданному аккумулятору при силе тока 1А за 1с. Тогда если перевести в часы, то при токе в 1А за 1 час передается 3600 Кл.

Одним из способов измерения емкости аккумулятора является его разряд заведомо известным током, при этом вы должны замерить время разряда. Допустим, если аккумулятор разрядился до минимального уровня напряжения за 10 часов током в 5А – значит его емкость 50 А*ч

Электроемкость – это важная величина в электронике и электротехнике. На практике конденсаторы применяются практически в каждой схеме электронного устройства. Например, в блоках питания – для сглаживания пульсаций, уменьшения влияния высоковольтных всплесков на силовые ключи. Во времязадающих цепях различных схем, а также в ШИМ-контроллерах для того, чтобы задать рабочую частоту. Аккумуляторы также применяются повсеместно. Вообще задачи накапливания энергии и сдвига фаз встречаются очень часто.

Более подробно изучить вопрос поможет предоставленное видео:

Кратко объяснение изложено в этом видео уроке:

Теперь вы знаете, что такое электрическая емкость, в каких единицах происходит ее измерение и от чего зависит данная величина. Надеемся, предоставленная информация была для вас полезной и понятной!

Материалы по теме:

39. Электроемкость. Емкость шара, емкость плоского конденсатора. Единицы измерения емкости.

Электрической емкостью проводника наз. отношение заряда проводника к его потенциалу:

Емкость определяется геометрической формой, размерами проводника и свойствами среды (от материала проводника не зависит). Чем больше емкость проводника, тем меньше меняется потенциал при изменении заряда.

Емкость шара в СИ:

Ёмкость плоского конденсатора.

, т.о. емкость плоского конденсатора зависит только от его размеров, формы и диэлектрической проницаемости. Для создания конденсатора большой емкости необходимо увеличить площадь пластин и уменьшить толщину слоя диэлектрика.

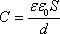
Единицы емкости.

Емкостью 1Ф (фарад) обладает такой проводник, у которого потенциал возрастает на 1 В при сообщении ему заряда в 1 Кл.

Емкостью 1Ф  обладал бы уединенный шар, радиус которого был бы равен 13 радиусам Солнца.

Емкость Земли  700 мкФ

Если проводник не уединенный, то потенциалы складываются по правилу суперпозиции и емкость проводника меняется.

40. Конденсаторы. Электроёмкость конденсатора. Применение конденсаторов

Конденсатор представляет собой систему из двух проводников, разделенных слоем диэлектрика, толщина которого мала по сравнению с размерами проводников.  Проводники наз. обкладками  конденсатора. Если заряды пластин конденсатора одинаковы по модулю и противоположны по знаку, то  под зарядом конденсатора понимают абсолютное значение заряда одной из его обкладок.

Электроемкостью конденсатора называют отношение заряда конденсатора к разности потенциалов между обкладками: .

Назначение конденсаторов

1. Накапливать на короткое время заряд или энергию для быстрого изменения потенциала.

2. Не пропускать постоянный ток.

3. В радиотехнике: колебательный контур, выпрямитель.

41. Магнитное поле, его свойства. Характеристики магнитного поля: магнитная индукция, напряженность.  Магнитное поле— форма существования материи, окружающей движущиеся электрические заряды (проводники с током, постоянные магниты).Основные свойства магнитного поля: порождается движущимися электрическими зарядами, проводниками с током, постоянными магнитами и переменным электрическим полем; действует с силой на движущиеся электрические заряды, проводники с током, намагниченные тела; переменное магнитное поле порождает переменное электрическое поле. Магнитное поле изображается графически с помощью магнитных силовых линий или линий магнитной индукции.Магнитными силовыми линияминазываются линии, вдоль которых в магнитном поле располагаются железные опилки или оси маленьких магнитных стрелок. В каждой точке такой линии вектор  направлен по касательной. Линии магнитной индукции всегда замкнуты, что говорит об отсутствии в природе магнитных зарядов и вихревом характере магнитного поля.МАГНИТНАЯ ИНДУКЦИЯ

— это силовая характеристика магнитного поля.

Вектор магнитной индукции направлен всегда так, как сориентирована свободно вращающаяся магнитная стрелка в магнитном поле.

Единица измерения магнитной индукции в системе СИ:

Напряжённость магни́тного по́ля— векторная физическая величина, равная разности вектора магнитной индукцииBи вектора намагниченностиM.

В Международной системе единиц (СИ): 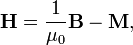где— магнитная постоянная.

Магнитным моментомрамки с током называется вектор равный произведению силы тока, текущего по рамке, на вектор площади.

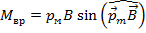
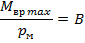
42. Закон Био — Савара- Лапласа. Примеры простейших магнитных полей проводников с током.  Закон Био́—Савара—Лапла́са — физический закон для определения вектора индукции магнитного поля, порождаемого постоянным электрическим током.

а) Магнитное поле прямого тока

 

 ;  ;

б) Магнитное поле в центре кругового проводника с током

α = 90°; sin α = 1.

Электрическая ёмкость связи. Методика расчёта

Электрическая ёмкость связи. Методика расчёта

В этой работе мы познакомим вас с методикой расчёта электрической ёмкости для симметричных тел, найдём отличия классического расчёта и более реалистичного — для некоторых видов конденсаторов, дадим определение для ёмкости связи. Такие расчёты необходимы для решения более сложных задач с использованием электростатического конденсатора. В них принципиально важно разделять различные виды ёмкостей.

Здесь мы будем рассматривать ёмкость с нестандартных позиций, тем не менее, все расчёты останутся в рамках классики. С точки зрения классических представлений она находится, как отношение заряда и потенциала её проводника — для уединённой ёмкости, и отношение заряда и разности потенциалов — для двухобкладочной ёмкости [1]: \[C = {q \over \varphi} \qquad (1)\] Такое определение годится для энергетики происходящих в конденсаторе процессов: затраченной энергии на его заряд и полученной после — от его разряда. Здесь вопросов нет. Дальше мы покажем отличие в некоторых свойствах для определённых типов конденсаторов, а пока подойдём к ёмкости с другой позиции и будем рассматривать её, как отношение потока электрического поля [2], проходящего через проводник обкладки, делённого на её потенциал. Математически, этот поток необходимо ещё умножить на \(\varepsilon_0\) — абсолютную диэлектрическую постоянную [3]: \[C = {\varepsilon_0 \Phi \over \varphi} \qquad (2)\] Казалось бы, это то же самое, просто записано в другим виде, но далее мы покажем принципиальное отличие такой постановки вопроса. Сам же поток полностью называется так: поток вектора напряжённости электрического поля и находится по теореме Гаусса [2]: \[\Phi = \oint \limits _{S} {E\, S} \qquad (3)\] где: \(E\) — напряжённость электрического поля, \(S\) — площадь поверхности, через которую протекает поток \(\Phi\) (рис. 1a). Для симметричных тел с таким же симметричным распределением электрического поля эта формула сильно упрощается и будет использоваться нами далее именно в таком виде: \[\Phi = E\, S \qquad (4)\] Здесь нужно заметить, что линии электрического поля в этом случае считаются перпендикулярными к поверхности пронизываемой ими площади. Мы также знаем, что этот поток, умноженный на диэлектрическую постоянную, даёт нам заряд, который этот поток образует проходя через поверхность: \[q_2 = \varepsilon_0 \Phi = \varepsilon_0 E\, S \qquad (5)\] Но мы также можем найти суммарный поток от начального источника заряда (рис. 1a): \[q_1 = \varepsilon_0 E\, S_g \qquad (6)\] Отсюда мы можем вывести сразу две формулы, которые нам понадобятся в дальнейшем.
1. Мы можем найти неизвестную пока напряжённость поля: \[E = {q_1 \over \varepsilon_0 S_g} \qquad (7)\] 2. Введём коэффициент распостранения заряда, который выводится на основании (5) и (6): \[k_q = {q_2 \over q_1} = {S \over S_g} \qquad (8)\] Он показывает, насколько уменьшается заряд \(q_2\), который мы измеряем на площадке \(S\), находящейся на расстоянии \(d\) от начального зяряда \(q_1\).

Потенциал на площадке \(S\) находится по классической формуле: \[\varphi = \int E\, \Bbb{d} x \qquad (9)\] где: \(x\) — ось отностительно центра симметричного тела. Мы специально пока не ставим пределы интегрирования, т.к. для уединённой ёмкости и двухобкладочной они будут разные. Их мы будем устанавливать в каждом случае отдельно. Подставляя сюда формулу (7) находим: \[\varphi = {q_1 \over \varepsilon_0} \int {\Bbb{d} x \over S_g} \qquad (10)\] Тогда искомая ёмкость будет находиться по следующей простой формуле: \[C = {\varepsilon_0 k_q \over \int {\Bbb{d} x \over S_g}} \qquad (11)\] При всех упрощениях, связанных с её применением, она хорошо отражает, как классические, так неклассические представления о ёмкости. Кроме того, в ней полностью отсутствуют поля и заряды, а остаётся только геометрия конденсатора. Конечно же, как и в классике здесь мы вводим допущение, что окружающие предметы достаточно удалены и никак не влияют на электрические поля конденсатора. Давайте для начала проверим эту формулу на классических примерах.

Рис.1. Схемы для нахождения ёмкости плоского сферического и коаксиального конденсаторов

Сразу же определимся, что в последующих трёх примерах коэффициент распостранения заряда будет равен единице, т.к. весь потоки через первую и вторую обкладки — одинаковые: \(k_q=1\).

Плоский конденсатор

Возьмём два проводящих круга с площадями \(S_1\) и \(S_2\), и расположим их соосно и перпендикулярно друг к другу на расстоянии \(d\) (рис. 1b). Ось \(\ell\), по которой мы будем проводить интегрирование по формуле (11), расположена в центре кругов и перпендикулярна к их плоскости. Подсчитаем ёмкость системы, в которой площади кругов одинаковые: \(S_1=S_2=S\). Поскольку в этом случае поток не претерпевает изменений вдоль оси, то \(S\) выносится за знак интеграла, а пределы интегрирования, очевидно, будут такие: (\(0, d\)): \[C = {\varepsilon_0 \over (d/S)} = {\varepsilon_0 S \over d} \qquad (12)\] Т.е. получаем классическую формулу плоского конденсатора [1].

Сферический конденсатор

Вычисление ёмкости такого конденсатора также не вызывает трудностей (рис. 1c). Достаточно вспомнить, что площадь сферы находится по формуле: \(S = 4\pi x^2\) и подствить её в (11): \[C = {\varepsilon_0 \over \int {\Bbb{d} x \over 4\pi x^2}} \qquad (13)\] Пределы интегрирования здесь будут находиться между двумя радиусами сфер: (\(r_1, r_2\)). Тогда ёмкость сферического конденсатора будет такой: \[C = {4\pi\varepsilon_0 \over 1/r_1 — 1/r_2} \qquad (14)\] что также полностью соответствует классике. К слову, число \(\pi\) в таких формулах показывает, что исследуемая обкладка не только симметрична, но ещё является и телом вращения.

Коаксиальный конденсатор

Для геометрического расчёта конденсатора по приводимой здесь методике, очень важно правильно выбрать ось симметрии \(x\), вдоль которой будет производиться интегрирование. В первых двух случаях она была очевидна, а в случае коаксиального конденсатора на ней нужно остановиться подробнее (рис. 1d). Эта ось должна быть направлена вдоль силовых линий электрического поля и в то же время — быть в их центре. Для цилиндров, из которых состоит коаксиальный конденсатор, такая ось может проходить через центр цилиндров и направлена — перпендикулярно их осей. Тогда площадь обкладки конденсатора (цилиндра) находится так: \(S = 2\pi x \ell\), где: \(\ell\) — длина цилиндра. Подставляем эту площадь в формулу (11): \[C = {\varepsilon_0 \over \int {\Bbb{d} x \over 2\pi x \ell}} \qquad (15)\] Пределы интегрирования здесь будут находиться между двумя радиусами этих цилиндров: (\(r_1, r_2\)). Окончательно находим искомую ёмкость \[C = {2\pi \varepsilon_0 \ell \over \ln (r_2 / r_1)} \qquad (16)\] которая также совпадает с классической [1].

Ёмкость связи

Если найти значение ёмкости между двумя проводящими обкладками, расположенными на некотором расстоянии, то обнаружится, что например, плоский, сферический и коаксиальный конденсаторы рассчитываются без учёта их уединённых ёмкостей, а две сферы — с учётом таковых. Так, ёмкость между двумя проводящими сферами (шарами) классическим образом рассчитывается так [1,4,5]: \[C = 2\pi \varepsilon_0 r \left(1 + \frac{1}{2D} + \frac{1}{4D^2} + … \right) \qquad (17)\] где: \(D=d/(2r)\). Отсюда прямо следует, что при больших значениях \(d\) (рис. 2c) ёмкость перестаёт меняться, фиксируется на значении: \(C = 2\pi \varepsilon_0 r\), и более не зависит от расстояния между сферами. Это является совершенно правильным с точки зрения энергетических соотношений. Действительно, если зарядить сферы противоположными зарядами, то если между ними протянуть провод с включённым последовательно с ним активным сопротивлением, и разрядить таким образом сферы, то на этом сопротивлении выделится как раз энергия, которая тратилась и на их зарядку. Причём, расстояние между сферами не играет никакой роли. Всё верно.

Но смотрите, какая интересная картина получается в случае, если мы захотим на таких сферах устроить радио или энерго -связь (рис 2a). Раз с какого-то момента ёмкость перестаёт меняться от расстояния, то по известной схеме (рис. 2b) мы могли бы передавать информацию и энергию на неограниченные расстояния. Причём, даже между планетами и звёдами! Однако, как мы знаем из практики, с расстоянием мощность приёмного сигнала падает, что вполне логично, иначе с одного передатчика мы могли бы собирать бесконечное количество энегии 🙂 Где здесь ошибка?

Рис.2. Связь между двумя сферами (a,b) и схема для расчёта ёмкости связи между двумя сферами (c,d)

Эта ошибка, а скорее — недопонимание, исчезнет, если выделить при расчёте конденсаторов отдельную категорию, в которой подсчёт параметров будет производиться без учёта их уединённой ёмкости. Ёмкость, рассчитанную таким способом, мы будем называть ёмкостью связи или конденсатором связи.

В подавляющем большинстве случаев конденсатор именно так и рассчитывается. Например, по описываемой здесь методике у конденсатора можно подсчитать исключительно его ёмкость связи. Также, классические ёмкости плоского, сферического и коаксиального конденсаторов — считаются без учёта уединённых ёмкостей их обкладок.

Ёмкость связи между двумя сферами

Давайте теперь рассчитаем ёмкость связи между двумя сферами с радиусом \(r\) и расстоянием между ними — \(d\). Ось интегрирования проведём между центрами сфер (рис. 2c). Из теории электростатики известно, что заряд на сфере можно мысленно поместить в её центр и далее, на этом основании, производить подсчёты. Так мы и сделаем с первой (левой на рисунке) сферой (рис. 2d). Из этой точки будут радиально исходить силовые электрические линии \(\bar E\), часть которых пройдёт и сквозь вторую сферу. Тогда пронизывающий её поток будет охватывать шаровой сектор (изображён зелёным цветом), площадь которого находится из формул тригонометрии: \[S = 2\pi \sqrt{d^2 — r^2} (d — \sqrt{d^2 — r^2}) \qquad (18)\] Напомним, что силовые электрические линии должны быть перпендикулярны пронизываемой ими площади. Также напомним, как находится площадь сферы, охватывающей весь поток: \[S_g = 4\pi d^2 \qquad (19)\] Тогда коэффициент распостранения заряда здесь будет таким: \[k_q = \frac12 \sqrt{1 — \delta^2} (1 — \sqrt{1 — \delta^2}),\, \delta = \frac{r}{d} \qquad (20)\] Заменяя \(d\) на \(x\) и подставляя площадь (19) в формулу (11) получаем искомую ёмкость: \[C = {\varepsilon_0 k_q \over \int {\Bbb{d} x \over 4\pi x^2}} \qquad (21)\] Границы интегрирование здесь такие: (\(r, d-r\)). Решая интеграл и подставляя эти границы, получаем ёмкость связи между двумя сферами: \[C = {4\pi r \varepsilon_0 {1 — \delta \over 1 — 2\delta} k_q }, \quad \delta \lt 1/2 \qquad (22)\] Если взять \(\delta = 1/2 \), т.е. когда сферы будут соприкасаться, то ёмкость будет стремиться к бесконечности, что равносильно замыканию между её выводами. Это согласуется с нашими начальными предположениями (рис. 2b). Если же расстояние между сферами большое, т.е. если \(d \gg r\), то эта формула упрощается, а ёмкость — находится так: \[C \approx {\pi r^3 \varepsilon_0 \over d^2} \qquad (23)\] Теперь всё стало на свои места: с увеличением расстояния, ёмкость связи уменьшается на всём интервале.

Используемые материалы

1. Википедия. Электрическая ёмкость.
2. Википедия. Теорема Гаусса.
3. Википедия. Абсолютная диэлектрическая проницаемость вакуума.
4. Задачи электростатики. Урок 13.
5. Rawlins, A.D. Note on the Capacitance of Two Closely Separated Spheres // IMA Journal of Applied Mathematics. 1985. — Vol. 34, no. 1. — P. 119—120

Конденсаторы и емкость. Формулы конденсатора

Одним из важнейших компонентов электрических цепей является конденсатор. В общем виде, конденсатор представляет из себя две пластины проводящего материала, между которыми заключен диэлектрик. При подключении конденсатора к источнику напряжения, на пластинах конденсатора появляется заряд +Q на верхней и –Q на нижней. Сила тока протекающего через конденсатор во время зарядки описывается формулой:

I= C * (dV/dt)

Решая данное уравнение относительно V, можно вычислить значение напряжения в момент времени t.
V = 1/C ∫ Idt

Как видно из уравнения, сила тока протекающего через конденсатор пропорциональна изменению напряжения во времени. При отключении источника питания от конденсатора, заряд а его пластинах будет равен:

Q=C*V

Где, С – Емкость конденсатора в Фарадах, V — напряжение в Вольтах.

Емкость конденсатора напрямую зависит от его конструктивных параметров. Емкость плоского конденсатора площадь пластин которого S с расстоянием d между ними
описывается формулой:

C=(E0 * E * S)/d

Где, E — Диэлектрическая проницаемость среды между пластинами, E0 — Электрическая постоянная.

На схемах, конденсатор обозначается следующими символами:

Промышленностью выпускаются как полярные так и неполярные конденсаторы. При включении полярных конденсаторов следует соблюдать полярность включения выводов. Зачастую отрицательный вывод конденсатора помечен специальным образом, чаще всего непосредственно на корпусе конденсатора. Внешний вид такого конденсатора представлен на следующем рисунке:

Внешний вид керамического конденсатора (неполярного) представлен на следующем изображении:

На данных конденсаторах, емкость указывается непосредственно на корпусе, в виде цифрового обозначения. Таблица этих обозначений приведена в конце статьи.

Последовательное и параллельное включение

Конденсаторы,как и резисторы, можно объединять между собой последовательным и параллельным соединением.

При последовательном соединении, общая емкость будет равна:
(1/Cобщ) = 1/C1+1/C2+1/C3
При параллельном, формула емкости запишется следующим образом:
Собщ=C1+C2+C3

Энергия запасенная в конденсаторе

Количество энергии запасенной конденсатором можно вычислить согласно следующей формуле:
E = ½ * C*V2

Ёмкость — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 28 ноября 2018; проверки требует 1 правка. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 28 ноября 2018; проверки требует 1 правка.

Ёмкость — многозначное слово, может означать:

• Ёмкость — внутренний объём сосуда, вместимость, то есть максимальный объём помещающегося внутрь него вещества.
• Ёмкость — предмет (сосуд, вместилище), используемый для хранения какого-либо вещества.

Электротехника, радиотехника, электроника, физика[править | править код]

• Электрическая ёмкость — характеристика проводника, показывающая способность проводника накапливать электрический заряд.
• Ёмкость — то же, что идеальный конденсатор или емкостной элемент — идеализированный элемент электрической цепи, обладающий свойством запасать энергию электрического поля, причем запасания энергии магнитного поля или преобразования электрической энергии в другие виды энергии в нем не происходит. Ёмкость — единственный параметр ёмкостного элемента и основной параметр конденсатора.

Аккумуляторы[править | править код]

• Ёмкость зарядная — количество электричества (заряд), сообщаемое аккумулятору во время заряда.
• Ёмкость номинальная — количество электричества (заряд), который должен отдать новый полностью заряженный аккумулятор при разряде до наименьшего допустимого напряжения в нормальных условиях эксплуатации.
• Ёмкость энергетическая — энергия, отдаваемая полностью заряженным аккумулятором при разряде до наименьшего допустимого напряжения.

В математике ёмкостью называются характеристики множества схожие с мерой. Например: