Сила Лоренца | Все формулы

Сообщение от администратора:

Ребята! Кто давно хотел выучить английский?
Переходите по моей ссылке и получите два бесплатных урока в школе английского языка SkyEng! 
Занимаюсь там сам — очень круто. Прогресс налицо.

В приложении можно учить слова, тренировать аудирование и произношение.

Попробуйте. Два урока бесплатно по моей ссылке!
Жмите СЮДА

Сила Лоренца — Сила, с которой, электромагнитное поле действует на точечную заряженную частицу

Направление силы Лоренца определяется по правилу левой руки — Если поставить левую руку так, чтобы перпендикулярная скорости составляющая вектора индукции входила в ладонь, а четыре пальца были бы расположены по направлению скорости движения положительного заряда (или против направления скорости отрицательного заряда), то отогнутый большой палец укажет направление силы Лоренца

Так как

сила Лоренца всегда перпендикулярна скорости заряда, то она не совершает работы.

Рассмотрим 2 вида движения заряженных частиц:

1) Если заряженная частица движется параллельно силовым линиям магнитного поля, то Сила Лоренца равняется нулю Fл = 0 , и заряд в магнитном поле движется равномерно и прямолинейно.

2) Если заряженная частица движется перпендикулярно силовым линиям магнитного поля, то сила Лоренца является центростремительной и равна :

Радиус данной окружности будет равен:

В формуле мы использовали :

— Сила Лоренца

— Заряд электрона

— Скорость заряда

— Магнитная индукция

— Угол между вектором магнитной индукцией и вектором скорости

— Центростремительное ускорение

— Радиус окружности

Сила Лоренца | Все Формулы

   

Сила Лоренца — Сила, с которой, электромагнитное поле действует на точечную заряженную частицу

   

   

Сила Лоренца (Правило левой руки)

Направление силы Лоренца определяется по правилу левой руки — Если поставить левую руку так, чтобы перпендикулярная скорости составляющая вектора индукции входила в ладонь, а четыре пальца были бы расположены по направлению скорости движения положительного заряда (или против направления скорости отрицательного заряда), то отогнутый большой палец укажет направление силы Лоренца

Сила Лоренца

Так как сила Лоренца всегда перпендикулярна скорости заряда, то она не совершает работы.

Рассмотрим 2 вида движения заряженных частиц:

1) Если заряженная частица движется параллельно силовым линиям магнитного поля, то Сила Лоренца равняется нулю Fл = 0 , и заряд в магнитном поле движется равномерно и прямолинейно.

2) Если заряженная частица движется перпендикулярно силовым линиям магнитного поля, то сила Лоренца является центростремительной и равна :

   

Сила Лоренца (движение частицы по окружности)

Радиус данной окружности будет равен:

   

В формуле мы использовали :

   

— Сила Лоренца

q — Заряд электрона

   

— Скорость заряда

B — Магнитная индукция

   

— Угол между вектором магнитной индукцией и вектором скорости

   

— Центростремительное ускорение

R — Радиус окружности

Работа силы Лоренца

Механическая работа А равна скалярному произведению силы на перемещение, которое произошло под действием этой силы:

А = (FS) = FScosα

где α -угол между направлением силы и перемещения.

Если этот угол равен 90⁰, работа силы равна нулю.

Поэтому полная работа силы Лоренца всегда равна нулю

Движение заряженной частицы в магнитном поле

Введение

Виды движения материальной точки:

равномерное прямолинейное, а=0, F=0

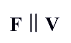
равноускоренное, a=const,

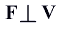
равномерное движение по окружности,

Рассмотрим различные случаи движения заряженной частицы в магнитном поле

1. Частица влетает в магнитное поле перпендикулярно силовым линиям.

Определить направление силы Лоренца и нарисовать траекторию движения частицы.

Сила, действующая на частицу, перпендикулярна скорости, поэтому траектория движения частицы

– окружность.

Определим радиус траектории частицы

По второму закону Ньютона F = ma

равнодействующая сила — сила Лоренца,

угол α равен 90 ⁰F = BqVsinα = BqV

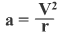
центростремительное ускорение

Подставляя F и а в уравнение 2го закона Ньютона, получаем

откуда для радиуса:

размерность радиуса – метр

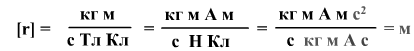
Задача: в камере Вильсона получены треки α-частицы и протона. Радиусы траекторий частиц одинаковы. Сравнить скорости движения частиц.

Пояснение: α- частица – это ядро гелия. В ее состав входит 2 протона и 2 нейтрона. Поэтому заряд α – частицы в 2 раза больше заряда протона, а масса – в 4 раза.

Дано

m_α = 4 m_p

q_α = 2 q_p

R_α = R_p

V_α/V_p — ?

Ответ: V_p=2V_α

Период обращения частицы в магнитном поле

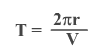
Период обращения частицы по окружности определяется формулой (1)

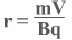
радиус окружности найден (2)

п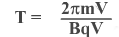одставляя (2) в (1), получаем

откуда

Размерность периода

Вопрос: Как зависит период обращения частицы в магнитном поле от ее скорости?

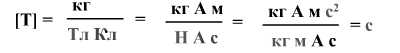
Ответ: Период обращения частицы в магнитном поле не зависит от ее скорости

2. Частица влетает в магнитное поле под углом к силовым линиям

Выберем оси координат как показано на рисунке.

Обозначим на чертеже проекции скорости частицы на направление магнитной индукции и на ось Х

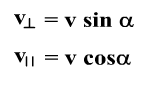
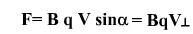
Сила Лоренца

направлена перпендикулярно чертежу, от нас

Траектория движения частицы – спираль

радиус витка спирали

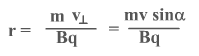
3. Частица влетает в магнитное поле параллельно силовым линиям

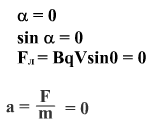
равнодействующая сил, приложенных к частице, равна нулю => движение равномерное прямолинейное, траектория движения частицы – прямая линия.

Вопрос А. Первоначально неподвижный электрон помещен в магнитное поле с индукцией В. Описать движение электрона. Пояснить ответ.

Электрон будет оставаться в покое, потому что магнитное поле на покоющийся заряд не действует

Вопрос В. Частица движется в перекрывающихся магнитном и электрическом полях. Может ли ее движение быть равномерным прямолинейным?

Может, если векторная сумма силы Лоренца и электрической силы равна нулю. Это возможно, если поля перпендикулярны друг другу (см чертеж)

Р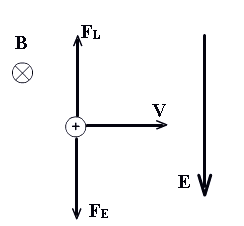ешение

Движение частицы будет равномерным

прямолинейным, если действующие на нее силы

уравновешены. Это может произойти, например,

при таком расположении полей.

Условие равновесия: F_L = F_E; BqV = Eq; V = B/E

5 Сила Лоренца. Формула Лоренца. Движение заряженных частиц в электрическом и магнитных полях.

Сила, действующая на электрический заряд Q, движущийся в магнитном поле со скоростью v, называется силой Лоренца и выражается формулой

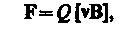(114.1)

где В — индукция магнитного поля, в котором заряд движется.

Направление силы Лоренца определяется с помощью правила левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор В, а четыре вытянутых пальца направить вдоль вектора

v (для Q > 0 направления I и v совпадают, для Q < 0 — противоположны), то отогнутый большой палец покажет направление силы, действующей на положительный заряд. На рис. 169 показана взаимная ориентация векторов v, В (поле направлено к нам, на рисунке показано точками) и F для положительного заряда. На отрицательный заряд сила действует в противоположном направлении. Модуль силы Лоренца (см. (114.1)) равен

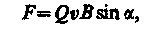
где  — угол между v и В.

Выражение для силы Лоренца (114.1) позволяет найти ряд закономерностей движения заряженных частиц в магнитном поле. Направление силы Лоренца и направление вызываемого ею отклонения заряженной частицы в магнитном поле зависят от знака заряда Q частицы. На этом основано определение знака заряда частиц, движущихся в магнитных полях.

Если заряженная частица движется в магнитном поле со скоростью v, перпендикулярной вектору В, то сила Лоренца F = Q[vB] постоянна по модулю и нормальна к траектории частицы. Согласно второму закону Ньютона, эта сила создает центростремительное ускорение. Отсюда следует, что частица будет двигаться по окружности, радиус r которой определяется из условия QvB = mv²/r, откуда

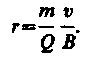(115.1)

Период вращения частицы, т. е. время Т, за которое она совершает один полный оборот,

Подставив сюда выражение (115.1), получим

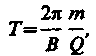(115.2)

т. е. период вращения частицы в однородном магнитном поле определяется только величиной, обратной удельному заряду (Q/m) частицы, и магнитной индукцией поля, но не зависит от ее скорости (при v ≪ c). На этом основано действие циклических ускорителей заряженных частиц (см. § 116).

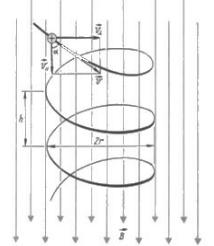
Если скорость v заряженной частицы направлена под углом  к вектору В (рис. 170), то ее движение можно представить в виде суперпозиции: 1) равномерного прямолинейного движения вдоль поля со скоростью v₁ = vcos; 2) равномерного движения со скоростью v_ = vsin по окружности в плоскости, перпендикулярной полю. Радиус окружности определяется формулой (115.1) (в данном случае надо заменить v на v_ = vsin). В результате сложения обоих движений возникает движение по спирали, ось которой параллельна магнитному полю (рис. 170).

Рис. 170

Шаг винтовой линии

Подставив в последнее выражение (115.2), получим

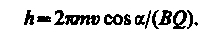
Направление, в котором закручивается спираль, зависит от знака заряда частицы.

Если скорость т заряженной частицы составляет угол а с направлением вектора В неоднородного магнитного поля, индукция которого возрастает в направлении движения частицы, то г и А уменьшаются с ростом В. На этом основана фокусировка заряженных частиц в магнитном поле.

Формула Лоренца — Лоренца — Википедия

Фо́рмула Ло́ренца — Ло́ренца связывает показатель преломления вещества с электронной поляризуемостью частиц (атомов, ионов, молекул), из которых оно состоит. Формулу получили датский физик Людвиг В. Лоренц (дат. Ludvig Valentin Lorenz ) и голландский физик Хендрик А. Лоренц (нидерл. Hendrik Antoon Lorentz) в 1880 году независимо друг от друга^[1][2].

Если вещество состоит из частиц одного сорта, то формула имеет вид^[3]:

n2−1n2+2=4π3Nα,{\displaystyle {\frac {n^{2}-1}{n^{2}+2}}={\frac {4\pi }{3}}N\alpha ,}

где n{\displaystyle n} — показатель преломления, N{\displaystyle N} — количество частиц в единице объёма, а α{\displaystyle \alpha } — их поляризуемость.

Уточним, что под поляризуемостью частицы здесь понимается коэффициент α{\displaystyle \alpha }, связывающий напряжённость электрического поля E{\displaystyle {\boldsymbol {E}}}, действующего на частицу, с дипольным моментом p{\displaystyle {\boldsymbol {p}}}, образующимся у частицы под действием этого поля^[4]:

p=αE.{\displaystyle {\boldsymbol {p}}=\alpha {\boldsymbol {E}}.}

Здесь и далее жирным шрифтом выделяются векторные величины.

Формулу записывают также в виде:

n2−1n2+2⋅Mρ=4π3NAα,{\displaystyle {\frac {n^{2}-1}{n^{2}+2}}\cdot {\frac {M}{\rho }}={\frac {4\pi }{3}}N_{\mathrm {A} }\alpha ,}

где M{\displaystyle M} — молекулярная масса вещества, ρ{\displaystyle \rho } — его плотность, а NA{\displaystyle N_{\mathrm {A} }} — постоянная Авогадро. При этом величину 4π3NAα{\displaystyle {\frac {4\pi }{3}}N_{\mathrm {A} }\alpha } называют молекулярной рефракцией.

Если вещество состоит из частиц нескольких сортов с поляризуемостями αi{\displaystyle \alpha _{i}} и объёмными концентрациями Ni{\displaystyle N_{i}}, то формула принимает вид:

n2−1n2+2=4π3[N1α1+N2α2+⋯+Nnαn].{\displaystyle {\frac {n^{2}-1}{n^{2}+2}}={\frac {4\pi }{3}}\left[N_{1}\alpha _{1}+N_{2}\alpha _{2}+\cdots +N_{n}\alpha _{n}\right].}

Вывод формулы основан на рассмотрении микроскопического поля и его взаимодействия с атомами, молекулами и ионами вещества. При выводе предполагается, что среда является изотропной, а составляющие её частицы собственным дипольным моментом не обладают^[5].

Воздействие внешнего электромагнитного поля с относительно высокими частотами, соответствующими видимому и УФ-диапазону спектра, приводит к смещению только электронных оболочек относительно атомных ядер, в то время как более массивные частицы (атомы и ионы) за период колебаний поля сместиться с занимаемых ими мест не успевают. Соответственно, в поляризацию среды вносит вклад только электронная поляризация, и показатель преломления оказывается связан с электронной поляризуемостью частиц формулой Лоренца — Лоренца.

При более низких частотах колебаний поля атомы и ионы успевают смещаться под действием поля, и поэтому вносят свой вклад в общую поляризацию. В результате становится необходимым, помимо электронной поляризуемости, учитывать атомную и ионную поляризуемости. Аналогом формулы Лоренца — Лоренца для постоянных полей является формула Клаузиуса — Моссотти^[6], описывающая связь диэлектрической проницаемости вещества с поляризуемостями составляющих его частиц:

ε−1ε+2⋅Mρ=4π3NAα.{\displaystyle {\frac {\varepsilon -1}{\varepsilon +2}}\cdot {\frac {M}{\rho }}={\frac {4\pi }{3}}N_{\mathrm {A} }\alpha .}

В полярных диэлектриках частицы среды обладают собственным дипольным моментом, то есть таким, который они имеют и в отсутствие внешнего электрического поля. Непосредственное применение формулы Лоренца — Лоренца в её обычном виде в таких случаях невозможно. Дальнейшим развитием формулы Лоренца — Лоренца, пригодным в том числе и для случая полярных диэлектриков (но для относительно низких частот колебаний поля), стала формула формула Ланжевена — Дебая^[7].

Формула Лоренца — Лоренца лежит в основе структурной рефрактометрии. Она широко используется при изучении и контроле составов различных веществ, для исследования их строения и превращений, происходящих в результате протекания химических реакций^[8][9].

Формула Лоренца — Лоренца является одним из оснований теории дисперсии света в классическом приближении^[5][10]. В этой теории оптические электроны рассматриваются как дипольные осцилляторы, характеризуемые собственной частотой ω0{\displaystyle \omega _{0}}. В случае, когда затуханием колебаний электронов можно пренебречь^[11], уравнение колебаний имеет вид:

r¨+ω02r=emE(t),{\displaystyle {\ddot {\boldsymbol {r}}}+\omega _{0}^{2}{\boldsymbol {r}}={\frac {e}{m}}{\boldsymbol {E}}(t),}

где r{\displaystyle {\boldsymbol {r}}} — смещение электрона из положения равновесия, r¨{\displaystyle {\ddot {\boldsymbol {r}}}} — вторая производная r{\displaystyle {\boldsymbol {r}}} по времени (ускорение электрона), e{\displaystyle e} и m{\displaystyle m} — заряд и масса электрона соответственно, а E(t){\displaystyle {\boldsymbol {E}}(t)} — напряжённость электрического поля.

В результате решения уравнения для монохроматического поля, изменяющегося с частотой ω{\displaystyle \omega }, сначала получается зависимость r(t){\displaystyle {\boldsymbol {r}}(t)}, а затем и поляризуемость α{\displaystyle \alpha }:

α=e2m1ω02−ω2.{\displaystyle \alpha ={\frac {e^{2}}{m}}{\frac {1}{\omega _{0}^{2}-\omega ^{2}}}.}

После подстановки полученного выражения в формулу Лоренца — Лоренца возникает дисперсионная формула вида:

n2−1n2+2=4πNe23m1ω02−ω2.{\displaystyle {\frac {n^{2}-1}{n^{2}+2}}={\frac {4\pi Ne^{2}}{3m}}{\frac {1}{\omega _{0}^{2}-\omega ^{2}}}.}

Обычно свой вклад в формирование показателя преломления вносят несколько линий поглощения с частотами ω0i{\displaystyle \omega _{0i}}. В таком случае дисперсионная формула принимает вид:

n2−1n2+2=4πNe23m∑ifiω0i2−ω2,{\displaystyle {\frac {n^{2}-1}{n^{2}+2}}={\frac {4\pi Ne^{2}}{3m}}\sum _{i}{\frac {f_{i}}{\omega _{0i}^{2}-\omega ^{2}}},}

где fi{\displaystyle f_{i}} — безразмерные коэффициенты (силы осцилляторов), показывающие эффективность участия соответствующих осцилляторов в явлениях дисперсии и удовлетворяющие правилу ∑ifi=1{\displaystyle \sum _{i}f_{i}=1}.

Хендрик А. Лоренц Людвиг В. Лоренц

Статьи Людвига В. Лоренца^[12] и Хендрика А. Лоренца^[13] с сообщениями о получении формулы были опубликованы практически одновременно в 1880 году. М. Борн и Э. Вольф такое одновременное получение результата учёными с почти одинаковыми (в оригинальном написании) фамилиями называют «удивительным совпадением»^[5].

Сам Хендрик Лоренц в своей книге писал так: «…этот результат был найден Лоренцом в Копенгагене за несколько времени до того, как я вывел его из электромагнитной теории света, что, конечно, является любопытным случаем совпадения»^[14].

Хотя Хендрик А. Лоренц не был тем, кто первым вывел формулу, и на эту роль не претендовал, в её наименовании, обычно употребляемом в англоязычной литературе, его имя стоит в начале: «Lorentz — Lorenz equation», «Lorentz — Lorenz formula» или «Lorentz — Lorenz relation».

Ранее, до того, как в русской научно-технической литературе сложилась общепринятая традиция, использовались различные варианты наименования формулы, включая такие, как формула «Лоренц — Лоренца», «Лоренц — Лорентца», «Лорентц — Лоренца» и «Лорентца — Лоренца».

В своё время значение формулы Лоренца — Лоренца не исчерпывалось только тем, что она дала возможность количественного описания формирования значения показателя преломления веществ. Как писали М. Борн и Э. Вольф, «…она служит мостом, связывающим феноменологическую теорию Максвелла с теорией атомного строения вещества»^[5].

Несмотря на солидный «возраст», формулу Лоренца — Лоренца в настоящее время не только достаточно широко применяют, но и продолжают развивать, расширяя возможности её использования^[15].

1. ↑ Лоренца — Лоренца формула // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1990. — Т. 2. — С. 611. — 704 с. — 100 000 экз. — ISBN 5-85270-061-4.
2. ↑ Лоренца — Лоренца формула / Короленко П. В. // Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов. — М. : Большая российская энциклопедия, 2004—2017.
3. ↑ Здесь и далее используется система единиц измерения СГС.
4. ↑ Гусев А. А. Поляризуемость // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1994. — Т. 4. — С. 72-74. — 704 с. — 40 000 экз.
5. ↑ ^{1 2 3 4} Борн М., Вольф Э. Основы оптики. Изд. 2-е. — М.: «Наука», 1973. — 720 с. — 20 000 экз.
6. ↑ Леванюк А. П. Клаузиуса — Мосотти формула // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1990. — Т. 2. Добротность — Магнитооптика. — С. 373-374. — 704 с. — 100 000 экз. — ISBN 5-85270-061-4.
7. ↑ Ланжевена — Дебая формула. Статья в Физическом энциклопедическом словаре.
8. ↑ Бацанов С. С. Структурная рефрактометрия. Изд. 2-е. — М.: «Высшая школа», 1976. — 304 с.
9. ↑ Иоффе Б. В. Рефрактометрические методы химии. — Л.: «Химия», Ленинградское отделение, 1983. — 350 с.
10. ↑ Бутиков Е. И. Оптика. — 2-е изд., перераб. и доп.. — СПб.: Невский Диалект, БХВ-Петербург, 2003. — 480 с. — 3 000 экз. — ISBN 5-94157-380-4.
11. ↑ Затухание мало, если частота света существенно отличается от частот, на которых располагаются линии поглощения вещества.
12. ↑ L. Lorenz. «Über die Refractionsconstante, » Ann. Phys. 1880. V. 11, 70—103.
13. ↑ H. A. Lorentz, Über die Beziehung zwischen der Fortpflanzungsgeschwindigkeit des Lichtes und der Körperdichte. Ann. Phys. 1880. V. 9, 641—665.
14. ↑ Лорентц Г. А. Теория электронов и её применение к явлениям света и теплового излучения. — М.: Государственное издательство технико-теоретической литературы, 1956. — С. 215. — 472 с. — (Классики естествознания). — 5 000 экз.
15. ↑ Mário G. Silveirinha. Generalized Lorentz-Lorenz formulas for microstructured materials. Phys. Rev. B. 2007, Vol.76, Issue 24, 245117, 17 December 2007.

🎓 формула для силы Лоренца ⚗ from english to russian 🧬

ˈfɔ:mjulə сущ.
1) формула, формулировка to devise a formula ≈ формулировать a scientific formula ≈ научная формула At the Yalta Conference verbal formulae were found to disguise growing differences between the Russians and the Anglo-Americans. ≈ На Ялтинской конференции были найдены формулировки, позволяющие замаскировать растущие разногласия между Россией с одной стороны и Англией и Америкой — с другой.
2) доктрина, лозунг, догмат the Mohammedan formula of faith ≈ мусульманский догмат веры Syn: slogan, catchword
3) а) рецепт Syn: recipe, prescription б) молочная смесь (для грудных детей) to make up formula, prepare formula ≈ готовить смесь
4) класс гоночного автомобиля the noise of Formula One racing engines ≈ рев двигателей автомобилей Формулы-1 формула — legal * юридическая формула — «sincerely yours» is a * used in letters «искренне ваш» — обычная формула в конце письма — empirical * эмпирическая формула — they sought a * that would allow settling of the dispute они искали формулировку /основу/ для разрешения спора — * weight( химическое) молекулярная масса по формуле соединения — to follow the * описывается формулой рецепт — a * for a cough mixture рецепт на микстуру от кашля — drinking alcohol and driving is a * for trouble( образное) вести машину в состоянии опьянения — это верный способ заработать неприятность молочная смесь (для грудных детей) ;
детская смесь догмат (религии) шаблон, стереотип — * paintings стандартные, шаблонные картины формула или класс (гоночного автомобиля) approximation ~ приближенная формула assumption ~ исходная формула atomic ~ атомарная формула closed ~ замкнутая формула complicated ~ сложная формула cost ~ формула вычисления затрат costing ~ формула расчета себестоимости design ~ расчетная формула empiric ~ эмпирическая формула empirical ~ эмпирическая формула exact ~ точная формула forecast ~ формула для вычисления прогноза forecasting ~ формула для вычисления прогноза formula аналитическое выражение ~ детская смесь ~ лозунг, доктрина ~ рецепт ~ формула (в точных науках) ~ (pl -as, — ае) формула, формулировка ~ формула interpolation ~ интерполяционная формула optimum allocation ~ формула оптимального распределения osculatory ~ степень родства prediction ~ формула для вычисления прогноза ready-made ~ готовая формула recurrent ~ рекуррентная формула short ~ простая формула smoothing ~ формула сглаживания straight-line ~ формула линейной зависимости summation ~ формула суммирования valid ~ общезначимая формула

Сила Лоренца

«Великая книга природы

написана языком математики».

Галилео Галилей

Данная тема посвящена решению задач на силу Лоренца.

Задача 1. Протон влетает в однородное магнитное поле с начальной скоростью 20 Мм/с под углом 45º к направлению линий магнитной индукции. Найдите модуль вектора магнитной индукции этого поля, если на протон действует сила 4×10^–13 Н.

ДАНО:	СИ	РЕШЕНИЕ Сила Лоренца определяется по формуле Тогда модуль вектора магнитной индукции равен

Ответ: 177 мТл.

Задача 2. Электрон влетает в магнитное поле с индукцией 25 мкТл. Определите радиус кривизны траектории, по которой электрон будет двигаться, если направление его начальной скорости перпендикулярно направлению линий магнитной индукции. Начальная скорость электрона равна 630 км/с.

ДАНО:	СИ	РЕШЕНИЕ Применим правило левой руки: если расположить левую руку так, что линии магнитной индукции входят в ладонь, а четыре пальца указывают направление скорости, то отогнутый большой палец укажет направление силы Лоренца, которая будет действовать на положительный заряд. Электрон имеет отрицательный заряд, поэтому сила Лоренца направлена в противоположную сторону. Сила Лоренца определяется по формуле Согласно второму закону Ньютона Центростремительное ускорение равно отношению квадрата скорости к радиусу кривизны траектории, а синус девяноста градусов равен единице, тогда получаем, что Тогда радиус кривизны траектории равен

Ответ: 14 см.

Задача 3. Частица влетает в однородное магнитное поле и пролетает сквозь него без изменения траектории. В каких случаях это возможно?

РЕШЕНИЕ

Траектория движения частицы не будет изменяться если сила Лоренца будет равна нулю.

Запишем формулу для определения силы Лоренца

Таким образом,

Данное произведение будет равно нулю в том случае, если один из множителей равен нулю. По условию задачи скорость и индукция поля не равны нулю. Следовательно,

При этом

Ответ: либо частица двигается параллельно линиям магнитной индукции, либо она не имеет заряда.

Задача 4. В однородном магнитном поле с индукцией 0,2 мТл по окружности движется частица. Найдите время, за которое направление скорости частицы изменится на противоположное, если заряд частицы равен 60 нКл, а масса – 2×10^–13 кг.

ДАНО:	СИ	РЕШЕНИЕ Запишем формулу, по которой вычисляется сила Лоренца При любом криволинейном движении тело движется с центростремительным ускорением. Запишем второй закон Ньютона С учётом того, что центростремительное ускорение равно отношению квадрата скорости к радиусу кривизны траектории, получим Приравняем выражения для определения радиуса кривизны Т.к время есть отношение пройденного пути к скорости, то

Ответ: 52 мс.

Задача 5. Протон, пройдя ускоряющую разность потенциалов 60 В, влетел в однородное магнитное поле с индукцией 5×10^–2 Тл. Считая, что протон вращается в плоскости, перпендикулярной линиям магнитной индукции, найдите радиус кривизны траектории и частоту вращения.

ДАНО:

РЕШЕНИЕ Запишем формулу для определения силы Лоренца При любом криволинейном движении тело двигается с центростремительным ускорением. Исходя из этого, запишем второй закон Ньютона Любое движущееся тело обладает кинетической энергией Работа электрического поля по переносу заряда определяется как Именно работа электрического поля, в данном случае, переходит в  кинетическую энергию протона. Поэтому получаем Выразим скорость и подставим её в формулул для определения радиуса кривизны траектории Частота вращения определяется по формуле Тогда Проверим размерности

Ответ: радиус кривизны траектории – 2,24 см; частота вращения – 760 кГц.