§ 6. Рівномірний рух тіла по колу. Період і частота обертання. Кутова і лінійна швидкість. Доцентрове прискорення
Кутове переміщення. Кутова швидкість. Період обертання. Частота обертання. Лінійна швидкість тіла, що рухається по колу. Прискорення під час рівномірного руху тіла по колу.
Почнемо розгляд руху матеріальної точки по колу з найпростішого – рівномірного руху по колу. Прикладами руху тіла по колу можуть слугувати рух супутників по колових орбітах, рух планет навколо Сонця, рух Місяця навколо Землі (мал. 1.42, а), рух будь-якої точки на тілі, що обертається (мал. 1.42, б).
К
Мал.1.38,а
Мал.1.38,б
утове переміщення, кутова швидкість. Нехай матеріальна точка рівномірно рухається по колу радіуса R і у момент часу t знаходиться в точці А, а в момент часу t2 зайняла положення В (мал. 1.43). Радіус R, проведений з центра кола до матеріальної точки за часК
Мал.1.38,в
утове переміщення тіла в системі одиниць СI виражають урадіанах. Радіан – це центральний кут між двома радіусами кола, довжина дуги між якими дорівнює радіусу. Його скорочене позначення – 1 рад.Для характеристики руху тіла по колу використовують поняття кутової швидкості.
К
Мал.2.19
утовою швидкістю називається фізична величина, яка вимірюється відношенням кутового переміщення φ до інтервалу часу ∆t, протягом якого це переміщення відбулося: 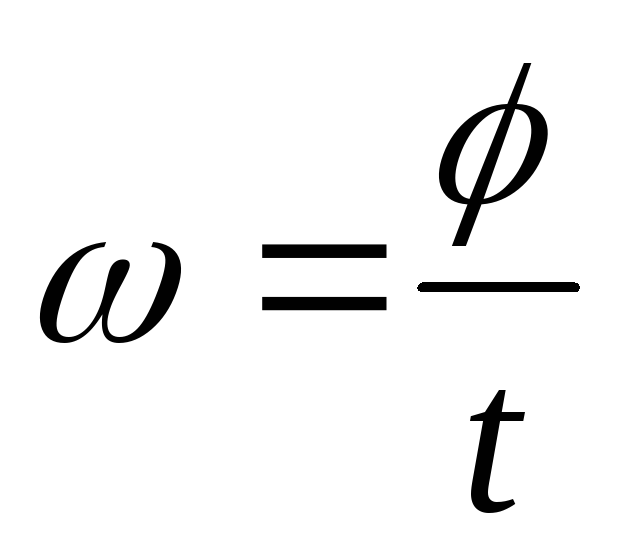 ,
,
(ω – читається – «омега»)
Кутова швидкість вимірюється у радіанах за секунду (рад/с). 1 рад/с дорівнює кутовій швидкості такого рівномірного руху по колу, під час якого за 1 секунду тіло здійснює переміщення в 1 радіан.
Рух, під час якого матеріальна точка рухається по колу з незмінною кутовою швидкістю називають рівномірним рухом по колу.
Період і частота обертання – характеристики руху тіла по колу.
П
Мал.2.19
еріодом обертання називають час, протягом якого тіло здійснює один повний оберт по колу. 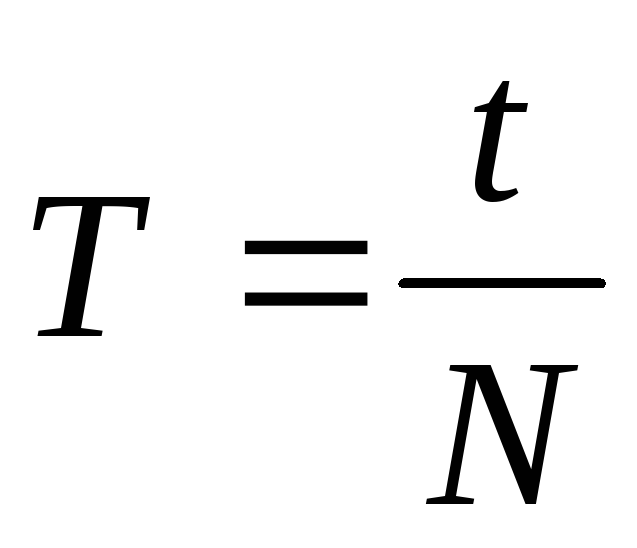 ,
,
де N – число обертів, зроблених за час t.
Ч
Мал.2.19
астотою обертання називають величину, обернену до періоду обертання тіла.Частоту обертання прийнято позначати грецькою літерою υ (читається «ню»):
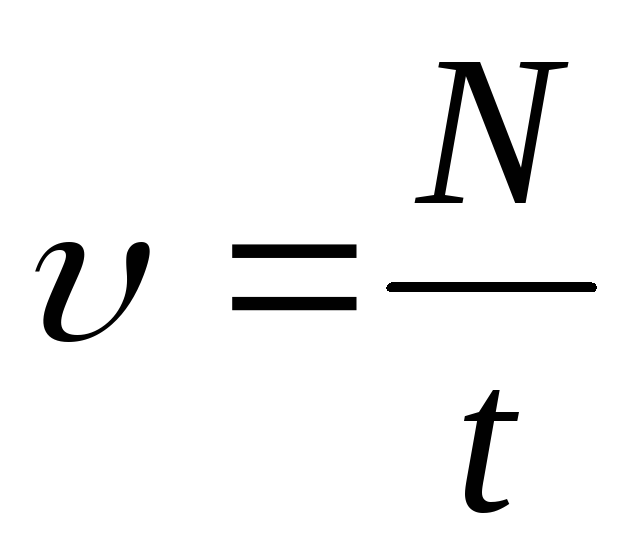 ,
,
За одиницю частоти в системі СI прийнято 1 оберт за секунду: 1 об/с або 1 с-1. Легко помітити, що період і частота – величини взаємно обернені:
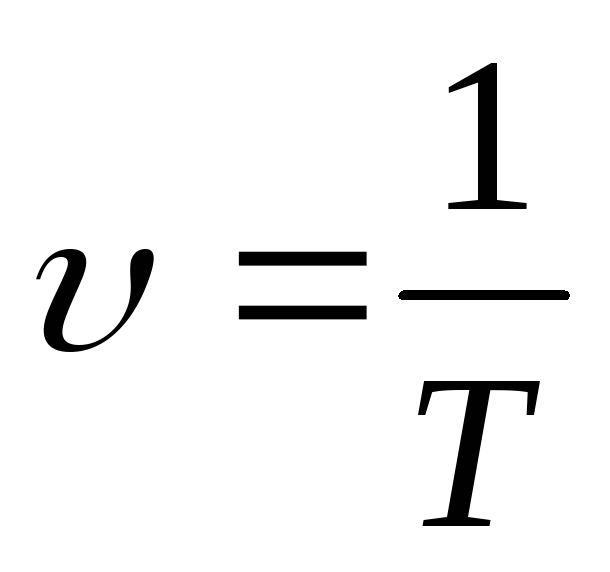 та
та 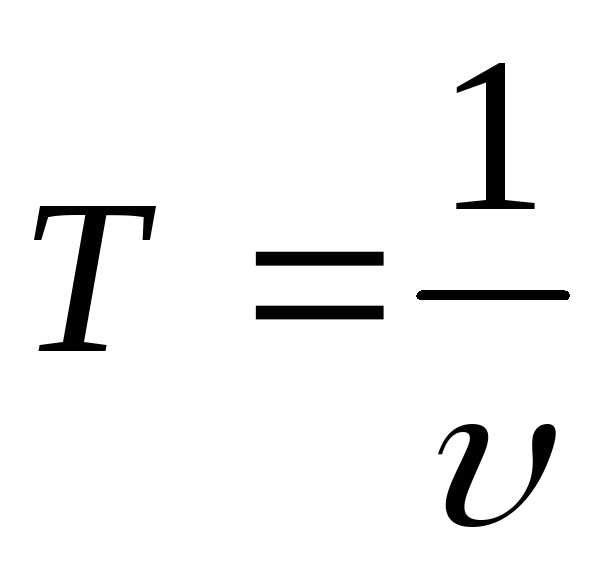 .
.
Кутове переміщення φ тіла за період Т дорівнює 2π. Тому кутова швидкість буде
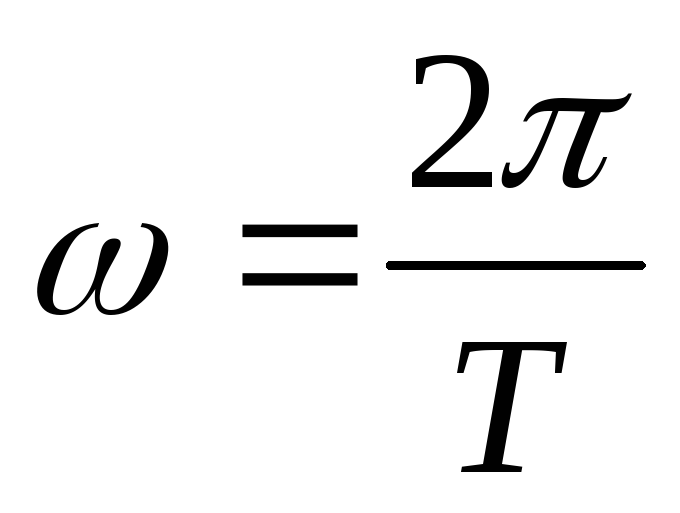 ,
або, врахувавши, що
,
або, врахувавши, що 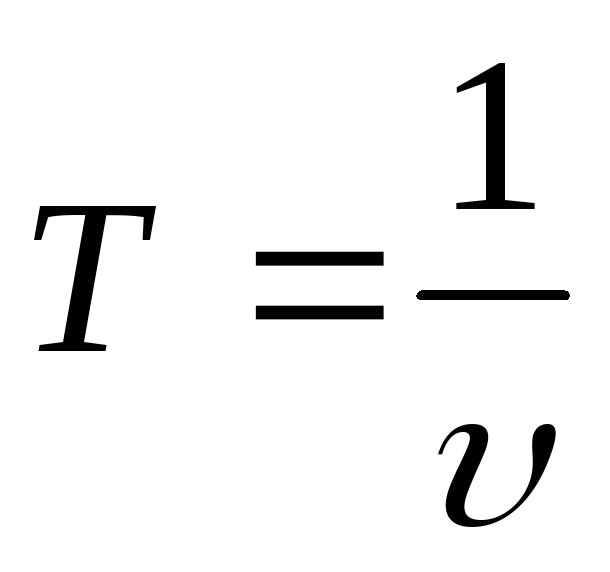 ,
одержимо:ω
= 2πυ.
,
одержимо:ω
= 2πυ.
Лінійна швидкість тіла, що рухається по колу. До руху тіла по колу застосовують і поняття швидкості, яке було введено для характеристики прямолінійного руху. У випадку руху тіла по колу цю швидкість називають
Лінійна
швидкість тіла, що рухається по колу,
залишаючись незмінною (сталою) за
модулем, неперервно змінюється за
напрямом і в будь-якій точці, як ми бачили
раніше, спрямована по дотичній до
траєкторії. Оскільки модуль лінійної
швидкості сталий, то його можна обчислити
за формулою: 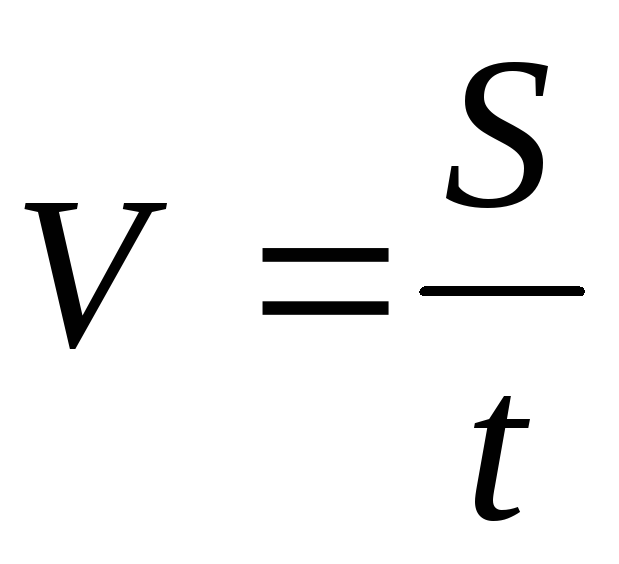 .
За один оберт (тобто колиt
= T) тіло
пройде відстань, яка дорівнює довжині
кола:
.
За один оберт (тобто колиt
= T) тіло
пройде відстань, яка дорівнює довжині
кола:
S = 2πR, де R – радіус кола. Звідси:
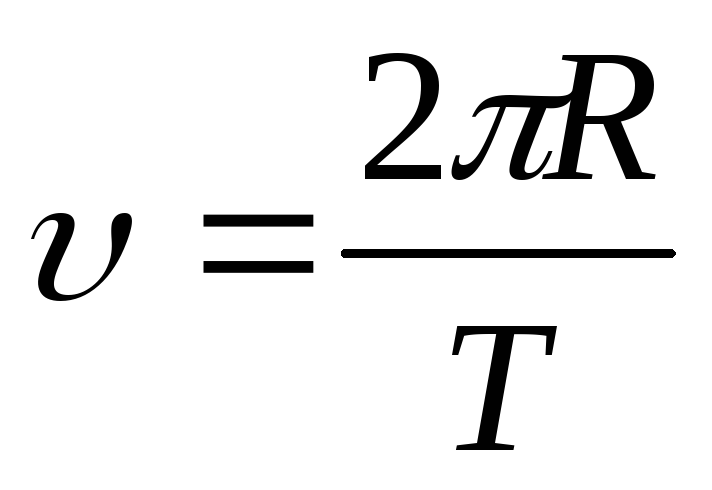 ,
або, враховуючи, що
,
або, враховуючи, що 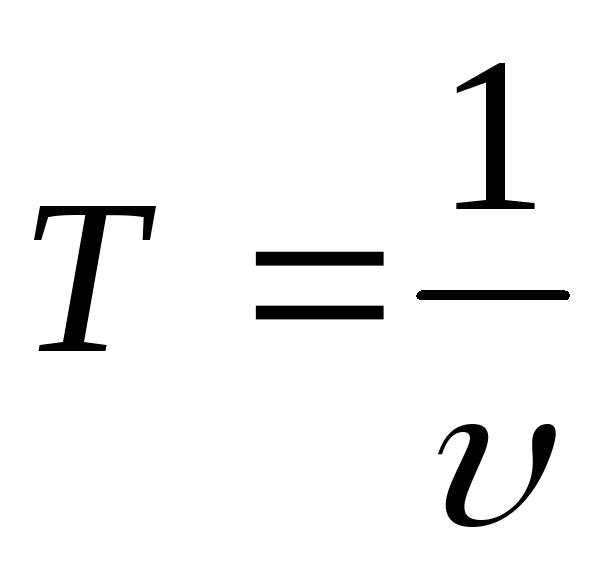
Знайдемо відношення лінійної швидкості V до кутової ω:
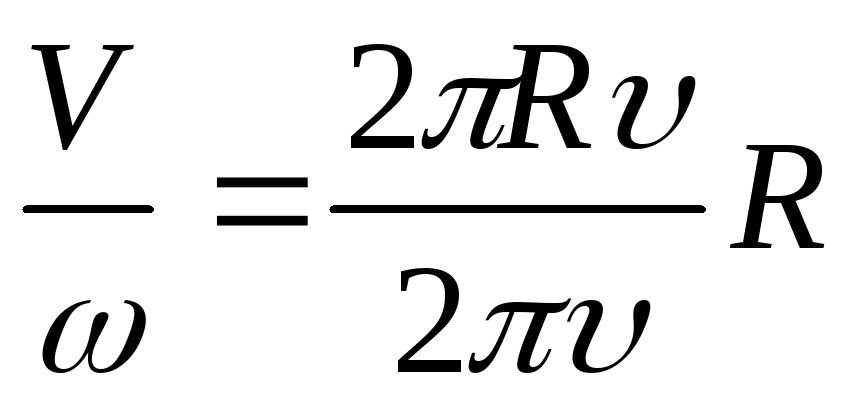 ,
звідки V = ωR та
,
звідки V = ωR та 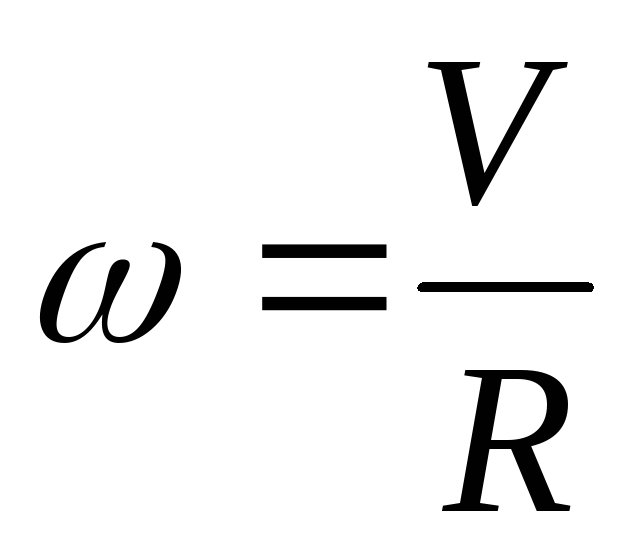 (1).
(1).
Приклад 1. Час одного оберту Землі навколо осі дорівнює 24 год. Обчислити кутову та лінійну швидкості обертання на екваторі. Радіус Землі взяти рівним 6 400 км.
Розв’язування: обертання Землі вважатимемо рівномірним. Тоді v = ωR
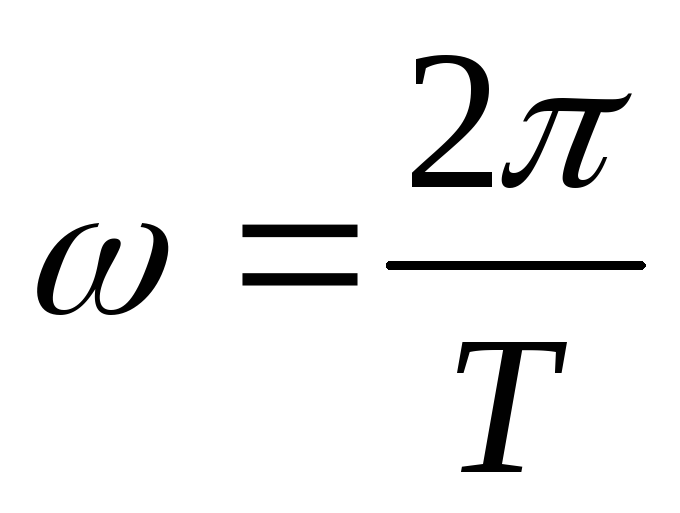 .
Час t виразимо
в секундах: t = 3600 · 24 = 86400 с.
.
Час t виразимо
в секундах: t = 3600 · 24 = 86400 с.R = 64
· 105 м Обчислення:
= 64
· 105 м Обчислення:
T

 = 86400с
= 86400с
ω – ?
V
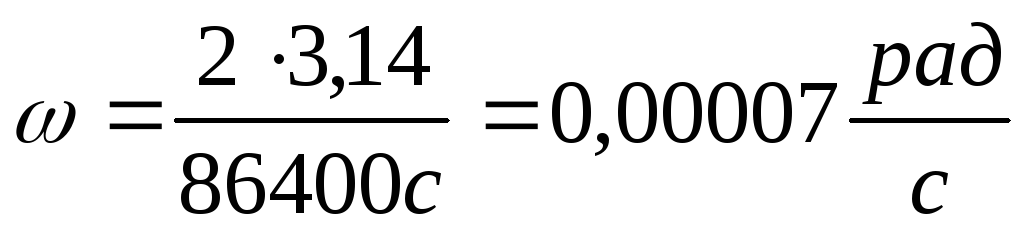 ;
;
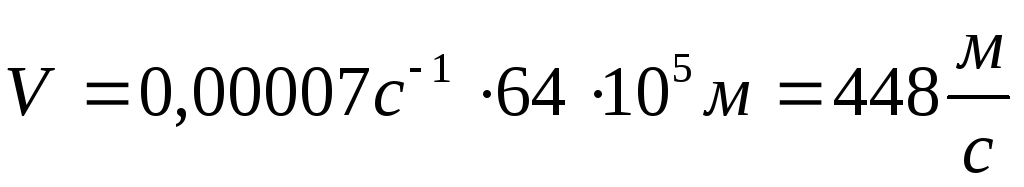 .
.
Відповідь: 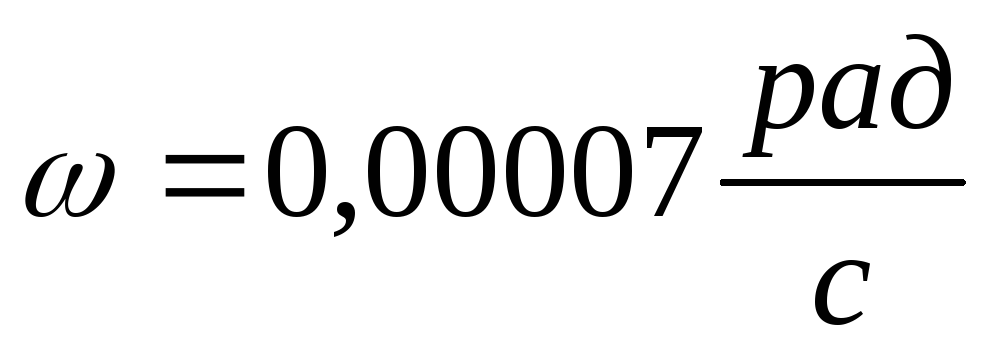 ω
;
ω
; 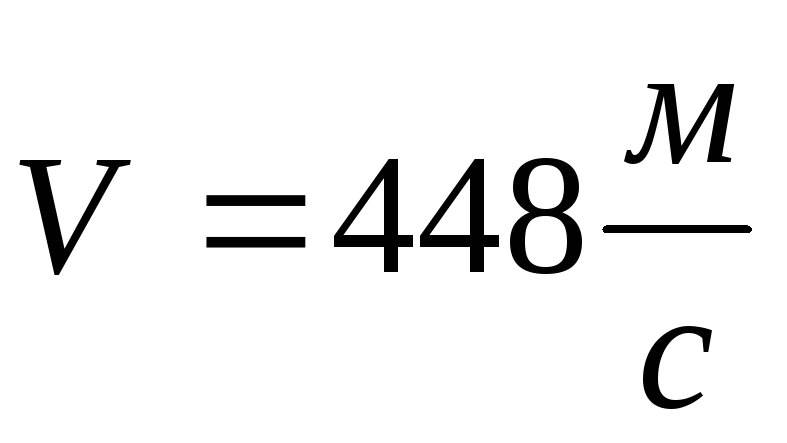 .
.
З формули (1) видно, що чим далі розміщена точка тіла від осі, тим більша її лінійна швидкість.
Прискорення при рівномірному русі тіла по колу. * При рівномірному русі тіла по колу його лінійна швидкість, залишаючись незмінною за модулем, неперервно змінюється за напрямом. Зміна швидкості за напрямом свідчить про те, що і під час рівномірного руху тіла по колу є прискорення, яке й стає причиною зміни напряму швидкості. Це прискорення одержало назву
Скористаємось уже відомим (див. § 3, с. … – …) вам способом визначення прискорення. За означенням, прискорення характеризує стрімкість зміни швидкості і дорівнює відношенню зміни швидкості до проміжку часу, за який ця зміна відбулася:
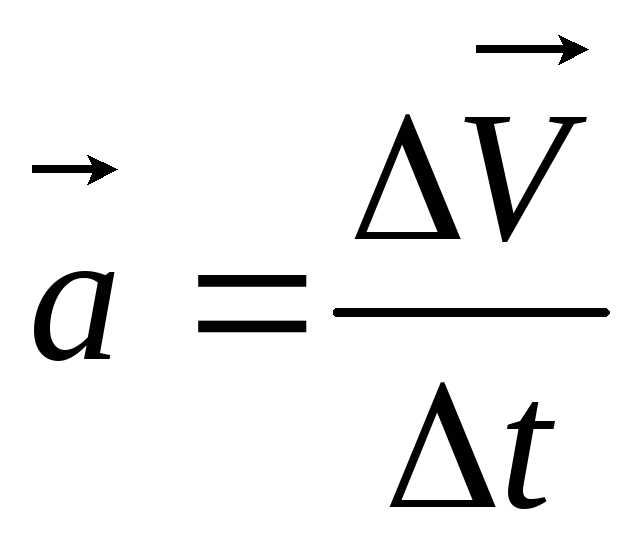 ,
або в скалярній формі
,
або в скалярній формі 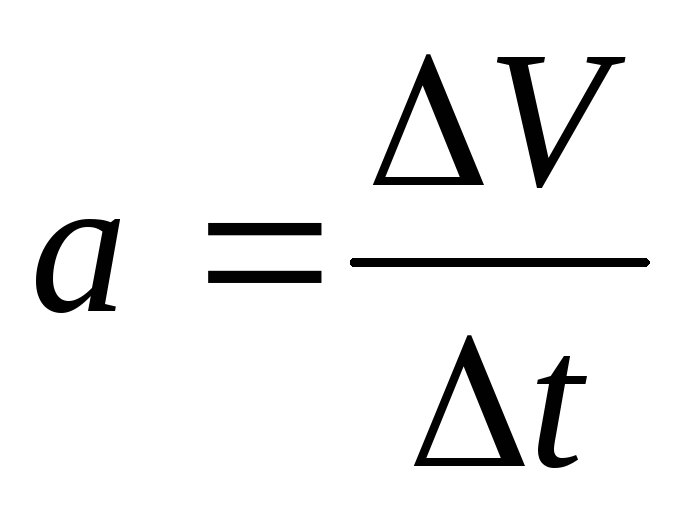
Нехай
тіло, що рівномірно рухається по колу,
в момент часу t знаходилось у точці А (мал.
1.44), а через
дуже малий проміжок часу ∆ t перемістилось у дуже близько розміщену
точку В (на
малюнку віддаль АВ для наочності показано
збільшеною). Швидкість у точці А позначимо VA, а в точці В– VB. Оскільки рух рівномірний, то модулі
швидкості у цих точках рівні. Щоб знайти
зміст швидкості за час ∆ t,
віднімемо (за правилом трикутника) від
вектора 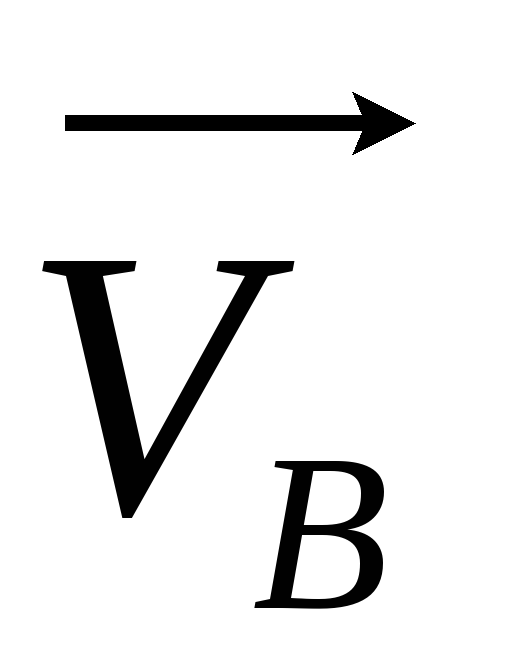 вектор
вектор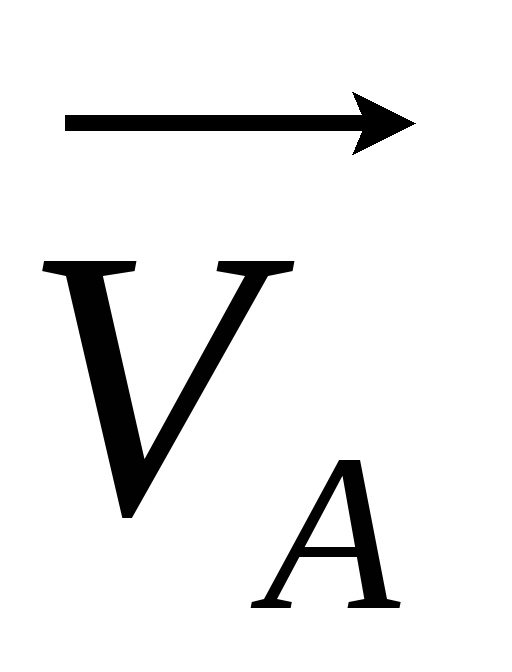
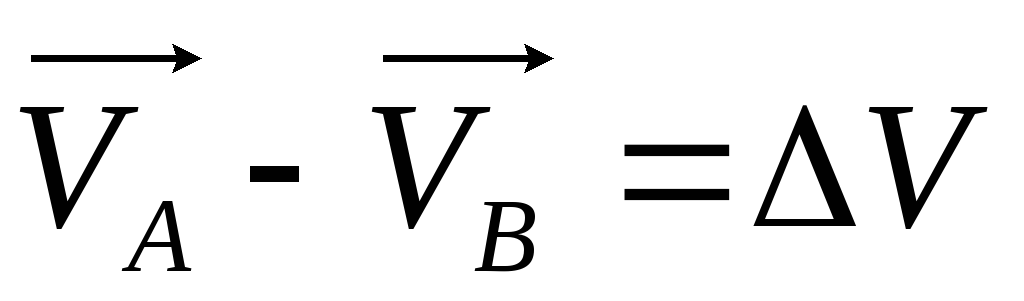
Для
цього перенесемо вектор 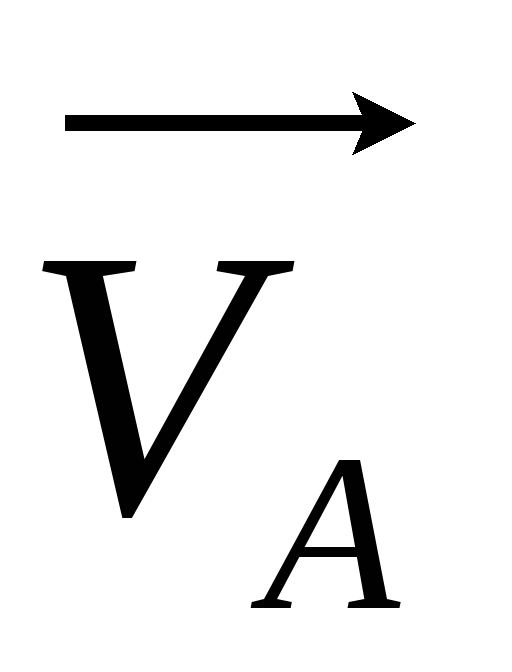 у точку В(мал.
1.44), зберігши
його напрям; вектор
у точку В(мал.
1.44), зберігши
його напрям; вектор 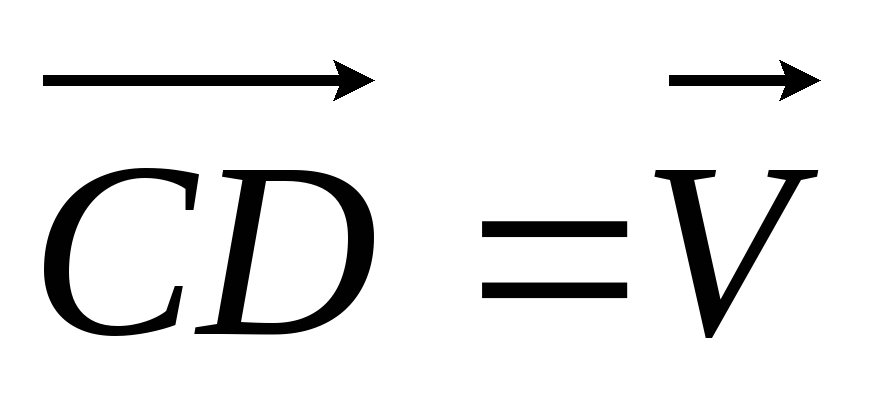 відповідає приросту швидкості ∆V. За
малий інтервал часу ∆t точка А
переміститься на ∆S = АВ рівне дузі АВ. Зауважимо, що при
малих кутах ∆φ дуга АВ співпадає з хордою АВ. Щоб
визначити модуль прискорення а у цій довільно обраній точці А, розглянемо
трикутники АОВ та ВСD. Вони подібні,
оскільки обидва рівнобедрені і
АОВ =
DВС як кути з перпендикулярними сторонами.
З подібності цих трикутників можна
записати:
відповідає приросту швидкості ∆V. За
малий інтервал часу ∆t точка А
переміститься на ∆S = АВ рівне дузі АВ. Зауважимо, що при
малих кутах ∆φ дуга АВ співпадає з хордою АВ. Щоб
визначити модуль прискорення а у цій довільно обраній точці А, розглянемо
трикутники АОВ та ВСD. Вони подібні,
оскільки обидва рівнобедрені і
АОВ =
DВС як кути з перпендикулярними сторонами.
З подібності цих трикутників можна
записати:
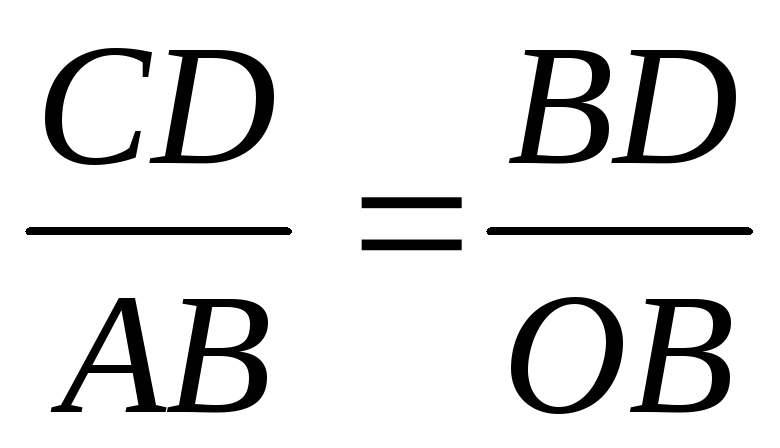 ,
або
,
або 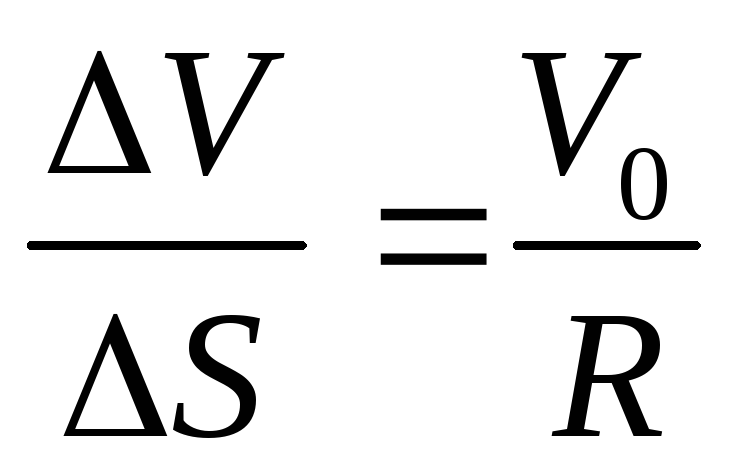 .
.
Але
∆S
V∆t; а VA = VB =V.
Тому 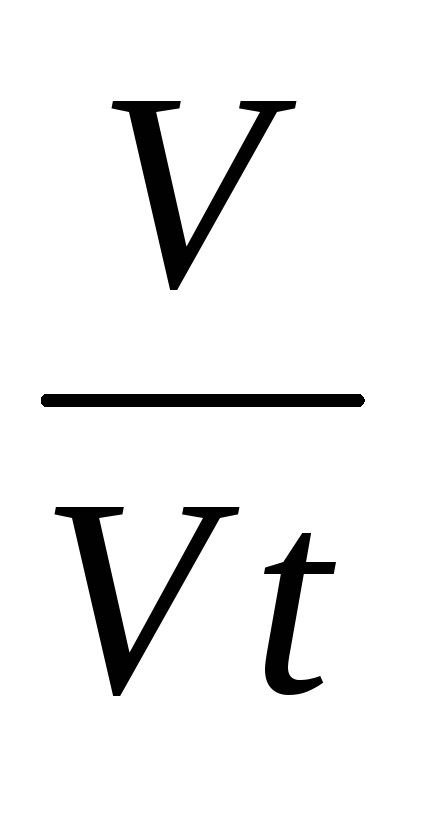 =
=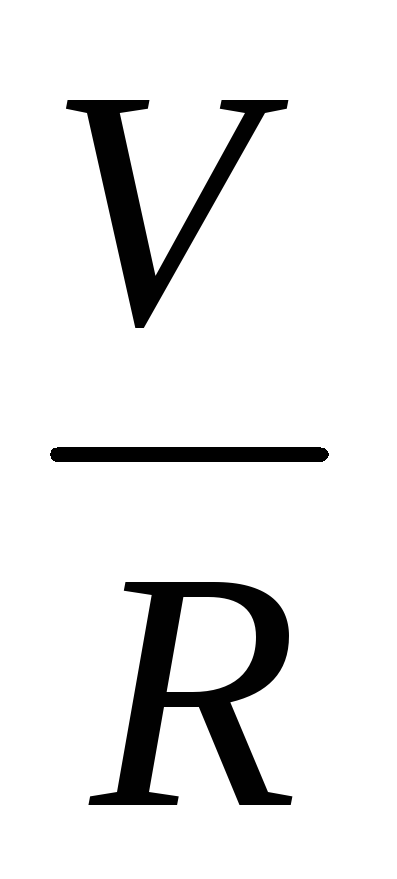 ,
звідки
,
звідки
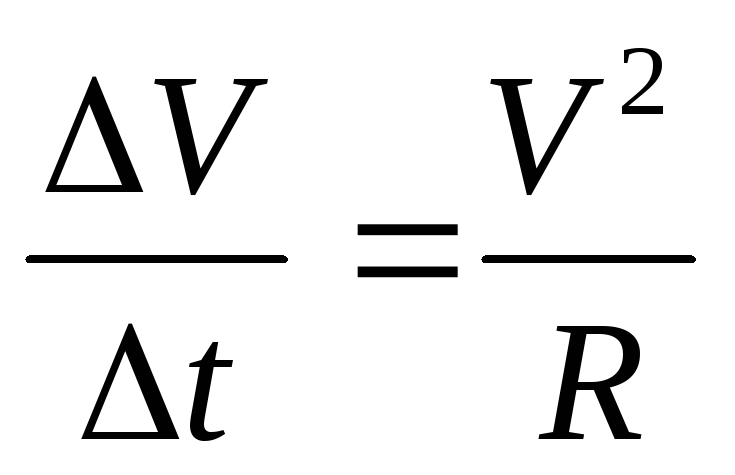 ;
або
;
або 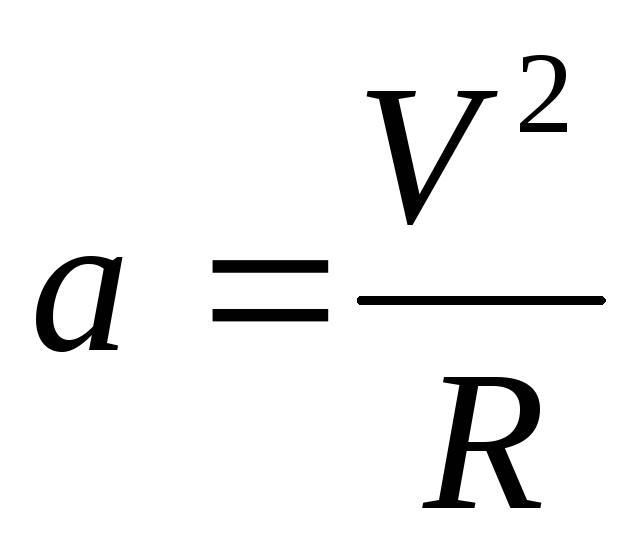
Під час рівномірного руху тіла (матеріальної точки) по колу діє доцентрове прискорення, яке у будь-якій точці траєкторії перпендикулярне до лінійної швидкості і напрямлене до центра кола.
Задача 1. Місяць рухається навколо Землі по колу радіусом 384 000 км з періодом обертання 27 діб 7 годин 45 хвилин. Обчислити лінійну швидкість та доцентрове прискорення Місяця. У скільки разів воно менше від прискорення вільного падіння?
Розв’язання.
Т = (27 · 24 · 3600)с + (7 · 60 · 60)с + (45 · 60)с = 2360700с.
R = 384000 000 м.
Лінійна
швидкість Місяця 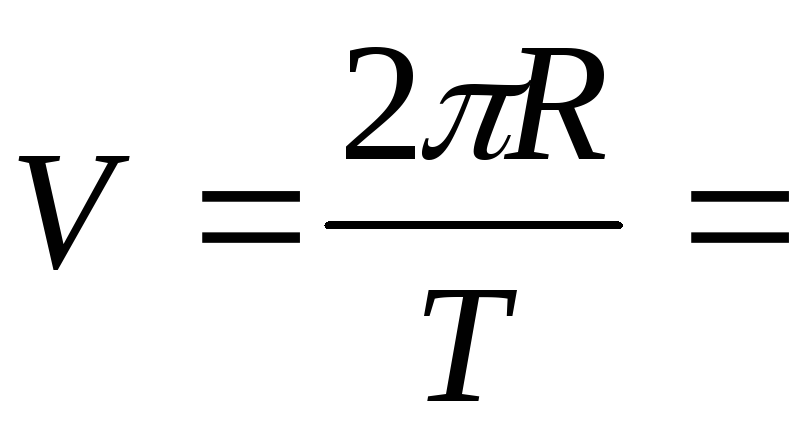
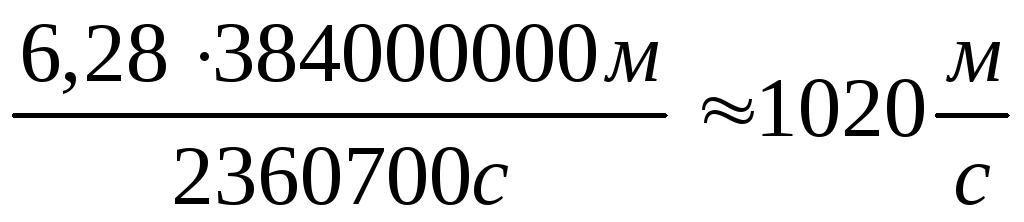 .
.
Доцентрове прискорення Місяця становитиме:
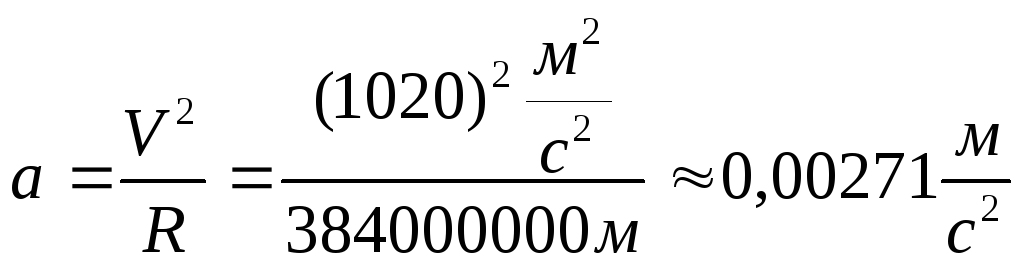 .
.
Як
видно, це маленьке прискорення у
порівнянні з прискоренням вільного
падіння поблизу поверхні Землі – 9,8
м/с2: 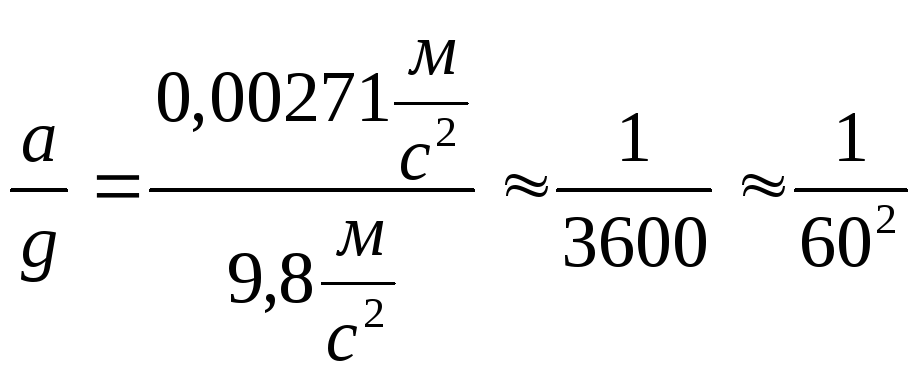 .
.
Зазначимо, що відстань Місяця від Землі більша за радіус земної кулі (RЗ = 6400 км) у 60 разів:
 .
.
Звернемо увагу на цей факт тому, що, як побачимо у наступному розділі (див. § 2.7, с. …), він дав змогу видатному англійському фізику І. Ньютону зробити одне з найважливіших відкриттів – відкрити закон всесвітнього тяжіння.
Задача 2.
Автомобіль рухається по заокругленню радіусом 100 м із швидкістю 36 км/год. Визначити його доцентрове прискорення.
Розв’язання.
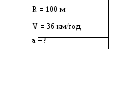
Доцентрове
прискорення визначимо з формули 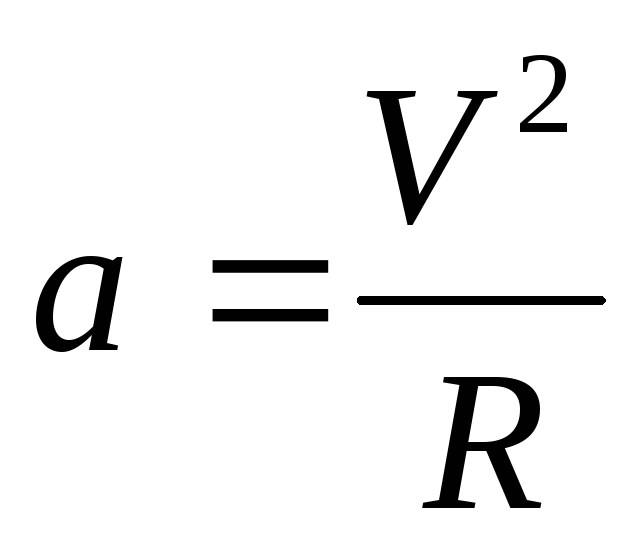 .
.
Обчислимо прискорення:
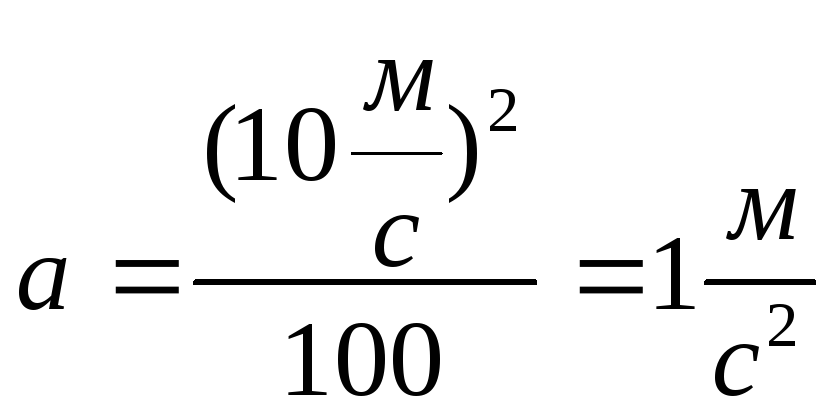
Визначимо
швидкість у метрах за секунду V = 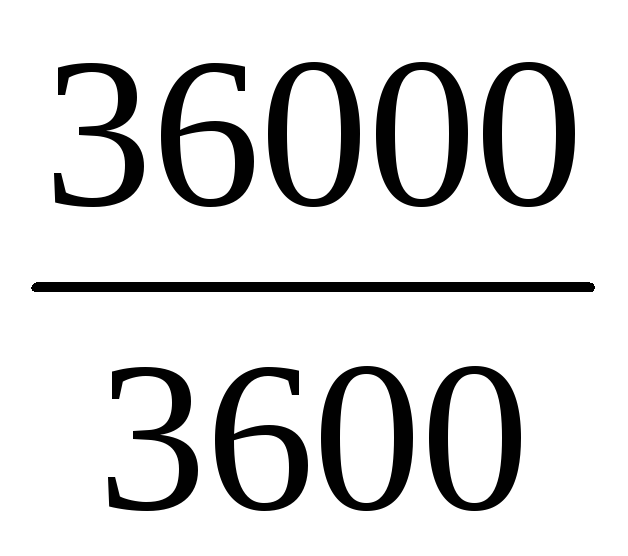 =
10 м/с.
=
10 м/с.
? Запитання для самоперевірки
Що таке кутове переміщення?
Дайте означення періоду і частоти обертання.
Напишіть формулу кутової швидкості та поясніть значення величин, що до неї входять.
Визначте кутову швидкість секундної стрілки годинника.
Період коливань — Вікіпедія
Матеріал з Вікіпедії — вільної енциклопедії.
Перíод колива́нь — проміжок часу між двома послідовними максимальними відхиленнями фізичної системи від положення рівноваги.
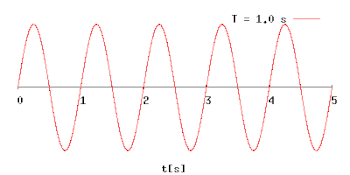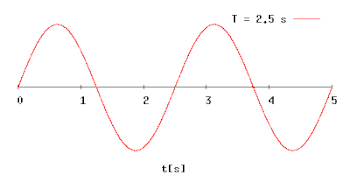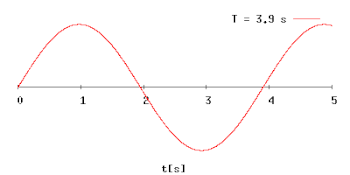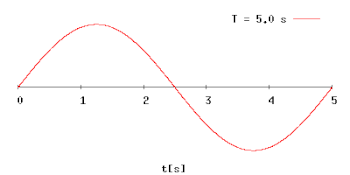 Анімація діаграми гармонічних коливань із зростаючим у часі періодом коливань (T)
Анімація діаграми гармонічних коливань із зростаючим у часі періодом коливань (T)Період коливань позначається зазвичай великою літерою T.
Частота коливань (ν) дорівнює часу поділеному на кількість коливань:
- T=tN.{\displaystyle T={\frac {t}{N}}.}
Частота коливань (ν) є обернено пропорційною до періоду:
- T=1ν, ν=1T.{\displaystyle T={\frac {1}{\nu }},\ \ \ \nu ={\frac {1}{T}}.}
Для хвильових процесів період пов’язаний з довжиною хвилі λ{\displaystyle \lambda }
- v=λν, T=λv,{\displaystyle v=\lambda \nu ,\ \ \ T={\frac {\lambda }{v}},}
де v{\displaystyle v} — швидкість поширення хвилі.
Коливання можуть бути періодичними як у лінійних так і в нелінійних системах. Періодичні коливання в лінійних системах називаються гармонічними. Характерною особливістю гармонічних коливань є те, що в них період не залежить від амплітуди коливань. У загальному випадку періодичних але нелінійних коливань період залежить від амплітуди.
Періоди деяких коливних процесів покладено в основу вимірювання часу.
Періоди коливань найпростіших фізичних систем[ред. | ред. код]
Пружинний маятник[ред. | ред. код]
Період коливань пружинного маятника можна обчислити за формулою:
- T=2πmk{\displaystyle T=2\pi {\sqrt {\frac {m}{k}}}},
де m{\displaystyle m} — маса вантажу, k{\displaystyle k} — жорсткість пружини.
Математичний маятник[ред. | ред. код]
Період малих коливань математичного маятника:
- T=2πlg{\displaystyle T=2\pi {\sqrt {\frac {l}{g}}}},
де l{\displaystyle l} — довжина підвісу, g{\displaystyle g} — прискорення вільного падіння.
Фізичний маятник[ред. | ред. код]
Період малих коливань фізичного маятника:
- T=2πJmgl{\displaystyle T=2\pi {\sqrt {\frac {J}{mgl}}}},
де J{\displaystyle J} — момент інерції маятника відносно осі обертання, m{\displaystyle m} — маса маятника, l{\displaystyle l} — відстань від обертання до центра мас.
Крутильний маятник[ред. | ред. код]
Період коливань крутильного маятника:
- T=2πIK{\displaystyle T=2\pi {\sqrt {\frac {I}{K}}}},
де I{\displaystyle I} — момент інерції маятника відносно осі кручення, а K{\displaystyle K} — крутильний коефіцієнт жорсткості маятника.
Електричний коливальний (LC) контур[ред. | ред. код]
Період коливань електричного коливального контура (формула Томсона):
- T=2πLC{\displaystyle T=2\pi {\sqrt {LC}}},
де L{\displaystyle L} — індуктивність котушки, C{\displaystyle C} — ємність конденсатора.
Цю формулу отримав у 1853 році англійський фізик Вільям Томсон.
- Яворський Б. М., Детлаф А. А., Лебедев А. К. Довідник з фізики для інженерів та студентів вищих навчальних закладів / Переклад з 8-го переробл. і випр. вид. Т.: Навчальна книга — Богдан, 2007. — 1040 с. — ISBN 966-692-818-3
Рівномірний рух по колу. Період і частота обертання. Лінійна і кутова швидкості. Доцентрове прискорення.
⇐ ПредыдущаяСтр 4 из 7Следующая ⇒Найпростішим видом криволінійного поступального руху тіла є його рух по колу, коли всі точки цього тіла рухаються по однакових колах. Такий рух зустрічається досить рідко: так рухаються кабінки оглядових коліс у міських парках. Водночас будь-який складний криволінійний рух тіла на досить малій ділянці його траєкторії можна наближено розглядати як рівномірний рух по колу. Тому вивчати довільний криволінійний рух треба починати від простішого: вивчення рівномірного руху по колу. Прикладами рівномірного руху по колу можна наближено вважати: рух штучних супутників Землі, рух частин, що обертаються в механізмах тощо.
Почнемо вивчення цього руху з важливої кінематичної величини — миттєвої швидкості. Миттєва швидкість у будь-якій точці криволінійної траєкторії руху тіла напрямлена по дотичній до траєкторії в цій точці. У цьому можна переконатися, спостерігаючи за роботою на точилі. Якщо притиснути до обертового точильного каменя кінець стальної дротини, то розжарені частинки, що відриваються від каменя, буде видно у вигляді іскор. Ці частинки летять з тією швидкістю, яку вони мали в момент відривання від каменя. Напрям руху іскор збігається з дотичною до кола в тій точці, де дротина торкається каменя. По дотичній до кола рухаються також бризки від коліс буксуючого автомобіля.
Модуль миттєвої швидкості під час рівномірного руху по колу з плином часу не змінюється. Рівномірним рухом по колу називають рух, під час якого тіло (матеріальна точка) за будь-які рівні проміжки часу проходить однакові відрізки дуг. Прикладами рівномірного руху по колу можна наближено вважати: рух штучних супутників Землі, рух частин, що обертаються в механізмах тощо. Швидкість такого руху матеріальної точки по лінії (колу) за модулем стала і в кожній точці кола напрямлена по дотичній.
Положення точки А, що рухається вздовж кола, визначають радіус-вектором 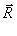 , проведеним з центра кола О до цієї точки (рис.2.1.22). Модуль радіуса-вектора дорівнює радіусу цього кола R.
, проведеним з центра кола О до цієї точки (рис.2.1.22). Модуль радіуса-вектора дорівнює радіусу цього кола R.
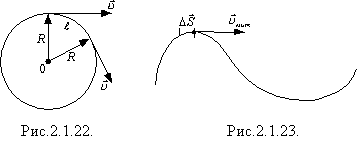
Швидкість руху тіла по колу (лінійну швидкість) за аналогією з рівномірним прямолінійним рухом можна знайти за формулою

де l — довжина дуги кола, пройденої матеріальною точкою за час t. Лінійна швидкість чисельно дорівнює модулю миттєвої швидкості (рис.2.1.23):
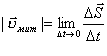 .
.
Нехай тіло здійснить один оберт по колу, тоді формула (2.1.20) набуде вигляду

де Т — це час одного оберту по колу радіусом R, с. Цей час називають періодом обертання. Лінійну швидкість вимірюють в метрах за секунду (м/с).
Набагато частіше в природі й техніці зустрічається обертальний рух тіла, коли нерухомою залишається одна точка або сукупність точок, що лежать на осі обертання. Таким є рух дзиґи, колеса нерухомого велосипеда, стрілок годинника тощо. Під час обертання навколо нерухомої осі О різні точки 1, 2, 3 тіла (рис.2.1.24) матимуть різні лінійні швидкості 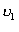 ,
, 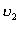 ,
, 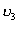 , тому не можна говорити про швидкість тіла. Бажано знайти такі характеристики обертального руху тіла, які були б спільними, однаковими для всіх його точок.
, тому не можна говорити про швидкість тіла. Бажано знайти такі характеристики обертального руху тіла, які були б спільними, однаковими для всіх його точок.
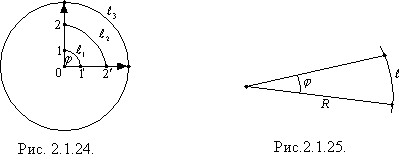
Як видно з рис.2.1.24 кожна з точок цього диска має свою лінійну швидкість, бо за один і той же час вони проходять відповідно відрізки дуг l1>l2>l3. Однаковою для цих точок буде кутова швидкість обертання. Кутова швидкість w точки, що рівномірно рухається по колу, чисельно дорівнює відношенню кута j, на який повертається радіус-вектор, до часу t і залишається сталою:

У фізиці кути вимірюють в радіанах (рад). Радіан — це безрозмірна одиниця вимірювання плоского кута. Один радіан відповідає центральному куту, довжина дуги якого точно дорівнює радіусу кола. У градусах радіан становить 57о30′. Центральний кут для кола становить 2 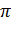 рад, для півкола —
рад, для півкола — 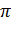 рад тощо. Записуючи центральний кут через j, позначку «рад» часто опускають для скорочення. Щоб знайти значення кута j в радіанах слід провести з його вершини довільну дугу і знайти відношення довжини цієї дуги до радіуса R (рис.2.1.25):
рад тощо. Записуючи центральний кут через j, позначку «рад» часто опускають для скорочення. Щоб знайти значення кута j в радіанах слід провести з його вершини довільну дугу і знайти відношення довжини цієї дуги до радіуса R (рис.2.1.25):
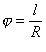
Отже, одиницею вимірювання кутової швидкості є 1 рад/с, що відповідає швидкості точки, яка обертається рівномірно й радіус-вектор якої за 1 с описує кут в 1 рад. А формула (2.1.22) для одного оберту по колу набуде вигляду

де 2p відповідає куту 2p радіан; Т — періоду обертання, с. Величину, обернену до періоду обертання, називають частотою обертання і вимірюють кількістю обертів за одиницю часу ([n] = 1/c):

Для довільної кількості обертів частоту обертання знаходять за формулою:
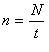
де N — кількість обертів, t — час обертання тіла.
Після підстановки виразу для частоти обертання (2.1.24) формула (2.1.21) набуде вигляду 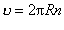 , а формула (2.1.23) —
, а формула (2.1.23) — 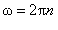 .
.
Знайдемо співвідношення лінійної і кутової швидкостей на підставі формул (2.1.21) (2.1.23):

Оскільки лінійна швидкість змінюється за напрямом, то матеріальна точка, що рухається по колу, набуває прискорення. Прискорення тіла, яке рівномірно рухається по колу, в будь-якій його точці є доцентровим, тобто напрямлене по радіусу кола до його центра. У будь-якій точці вектор прискорення перпендикулярний до вектора швидкості. Цю особливість прискорення рівномірного руху по колу зображено на рис.2.1.26.
Чому дорівнює модуль доцентрового прискорення? Числове значення (модуль) прискорення можна легко знайти з рис.2.1.26.
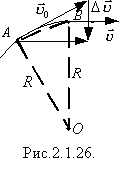
Трикутник, утворений векторами 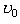 ,
, 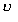 і
і 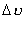 , рівнобедрений, бо
, рівнобедрений, бо 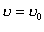 . Трикутник ОАВ на рис.2.1.26 також рівнобедрений, оскільки сторони ОА і ОВ — радіуси кола. Кути при вершинах обох трикутників рівні, бо вони утворені взаємно перпендикулярними сторонами:
. Трикутник ОАВ на рис.2.1.26 також рівнобедрений, оскільки сторони ОА і ОВ — радіуси кола. Кути при вершинах обох трикутників рівні, бо вони утворені взаємно перпендикулярними сторонами: 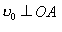 і
і 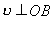 . Тому трикутники подібні як рівнобедрені з рівними кутами при вершинах. З подібності трикутників випливає пропорційність відповідних сторін:
. Тому трикутники подібні як рівнобедрені з рівними кутами при вершинах. З подібності трикутників випливає пропорційність відповідних сторін:
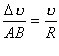 ,
,
де 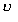 і
і 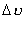 — модулі швидкості й зміни швидкості під час переходу з точки А в точку В, R — радіус кола. Якщо точки А і В дуже близькі одна до одної, то хорду АВ не можна відрізнити від дуги АВ. А довжина дуги АВ — це шлях, пройдений тілом із сталою за модулем швидкістю
— модулі швидкості й зміни швидкості під час переходу з точки А в точку В, R — радіус кола. Якщо точки А і В дуже близькі одна до одної, то хорду АВ не можна відрізнити від дуги АВ. А довжина дуги АВ — це шлях, пройдений тілом із сталою за модулем швидкістю 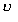 . Він дорівнює
. Він дорівнює 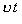 . Тому можна записати:
. Тому можна записати:
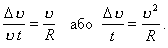
Оскільки розглядуваний інтервал часу t дуже малий, то 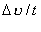 — це модуль прискорення. Отже,
— це модуль прискорення. Отже,

Підставивши у рівняння (2.1.26) вирази (2.1.20), (2.1.23), (2.1.25) для 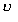 і w, дістанемо інші вирази для доцентрового прискорення:
і w, дістанемо інші вирази для доцентрового прискорення:
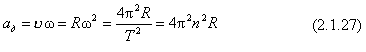
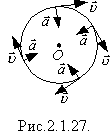
Таким чином, під час рівномірного руху по колу в усіх точках кола доцентрове прискорення за модулем однакове. Проте напрямлене воно завжди по радіусу до центра (рис.2.1.27) так, що напрям прискорення від точки до точки змінюється. Тому рівномірний рух тіла по колу не можна вважати рівноприскореним.
Будь-який рух по криволінійній траєкторії можна подати як рух по дугах кіл різних радіусів. Одну зі складних траєкторій, по якій рухається тіло, і доцентрове прискорення тіла в різних її точках зображено на рис.2.1.28:
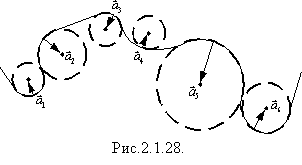
Отже, в будь-якій точці криволінійної траєкторії тіло рухається з прискоренням, напрямленим до центра того кола, частиною якого є ділянка траєкторії поблизу цієї точки. А модуль прискорення залежить від швидкості тіла та від радіуса відповідного кола.
Циклотронна частота — Вікіпедія
Матеріал з Вікіпедії — вільної енциклопедії.
Циклотро́нна частота́ — циклічна частота обертання вільної зарядженої частки в однорідному магнітному полі [1].
Позначається ωH{\displaystyle \omega _{H}}.
- ωH=|q|Bmc{\displaystyle \omega _{H}={\frac {|q|B}{mc}}},
де q — заряд частки, В — магнітна індукція, m — маса частки, c — швидкість світла [2].
На заряджену частку в магнітному полі діє сила Лоренца (в системі СГСГ).
- F=qc[v,B]{\displaystyle F={\frac {q}{c}}[\mathbf {v} ,\mathbf {B} ]},
де v{\displaystyle \mathbf {v} } — швидкість частки.
Магнітне поле не впливає на класичну заряджену частку, яка рухається вздовж поля. Якщо ж класична заряджена частка має складову швидкості перпендикулярну вектору магнітної індукції (v⊥{\displaystyle v_{\perp }}), така частка здійснюватиме обертання із циклічною частотою, яка визначається наведеною формулою й називається циклотронною частотою. Якщо частка має складову швидкості вздовж поля й складову швидкості перпендикулярну полю, то вона рухатиметься по гвинтовій лінії.
Радіус спіралі:
- — в системі СГСГ
- rH=mcv⊥|q|B{\displaystyle r_{H}={\frac {mcv_{\perp }}{|q|B}}}
- — в системі СІ
- rH=mv⊥|q|B{\displaystyle r_{H}={\frac {mv_{\perp }}{|q|B}}}
називають циклотронним або ларморовим радіусом.
Магнітне поле закручує рух частки, й чим воно сильніше, тим менший радіус обертання.
Енергія квантовомеханічної зарядженої частки в магнітному полі задається формулою (див. Рівні Ландау)
- E=(n+12)ℏωH+pz22m{\displaystyle E=\left(n+{\frac {1}{2}}\right)\hbar \omega _{H}+{\frac {p_{z}^{2}}{2m}}},
де n — певне квантове число, яке пробігає значення від 0 до нескінченості, pz{\displaystyle p_{z}} — складова імпульсу частки, направлена вздовж поля [3].
Явище обертання часток в магнітному полі використовується в прискорювачах заряджених часток — циклотронах.
- ↑ Циклотронну частоту іноді називають ларморівською частотою, однак у інших випадках ларморівською частотою називають у два рази меншу величину
- ↑ Формула приведена в системі СГСГ
- ↑ Дана формула не враховує вклад у енергію спіна



