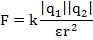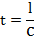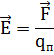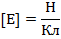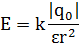Электричество и магнетизм — основные формулы по физике

Физические законы, формулы, переменные	Формулы электричество и магнетизм
Закон Кулона: где q1 и q2 — величины точечных зарядов, ԑ1 — электрическая постоянная; ε — диэлектрическая проницаемость изотропной среды (для вакуума ε = 1), r — расстояние между зарядами.
Напряженность электрического поля: где Ḟ — сила, действующая на заряд q0 , находящийся в данной точке поля.
Напряженность поля на расстоянии r от источника поля: 1) точечного заряда 2) бесконечно длинной заряженной нити с линейной плотностью заряда τ: 3) равномерно заряженной бесконечной плоскости с поверхностной плотностью заряда σ: 4) между двумя разноименно заряженными плоскостями
Потенциал электрического поля: где W — потенциальная энергия заряда q0 .
Потенциал поля точечного заряда на расстоянии r от заряда:
По принципу суперпозиции полей, напряженность:
Потенциал: где Ēi и ϕi — напряженность и потенциал в данной точке поля, создаваемый i-м зарядом.
Работа сил электрического поля по перемещению заряда q из точки с потенциалом ϕ1 в точку с потенциалом ϕ2 :
Связь между напряженностью и потенциалом 1) для неоднородного поля: 2) для однородного поля:	1) 2)
Электроемкость уединенного проводника:
Электроемкость конденсатора: где U = ϕ1 — ϕ2 — напряжение.
Электроемкость плоского конденсатора: где S — площадь пластины (одной) конденсатора, d — расстояние между пластинами.
Энергия заряженного конденсатора:
Сила тока:
Плотность тока: где S — площадь поперечного сечения проводника.
Сопротивление проводника: ρ — удельное сопротивление; l — длина проводника; S — площадь поперечного сечения.
Закон Ома 1) для однородного участка цепи: 2) в дифференциальной форме: 3) для участка цепи, содержащего ЭДС: где ε — ЭДС источника тока, R и r — внешнее и внутреннее сопротивления цепи; 4) для замкнутой цепи:
Закон Джоуля-Ленца 1) для однородного участка цепи постоянного тока: где Q — количество тепла, выделяющееся в проводнике с током, t — время прохождения тока; 2) для участка цепи с изменяющимся со временем током:	1) 2)
Мощность тока:
Связь магнитной индукции и напряженности магнитного поля: где B — вектор магнитной индукции, μ √ магнитная проницаемость изотропной среды, (для вакуума μ = 1), µ0 — магнитная постоянная , H — напряженность магнитного поля.
Магнитная индукция (индукция магнитного поля): 1) в центре кругового тока где R — радиус кругового тока,2) поля бесконечно длинного прямого тока где r — кратчайшее расстояние до оси проводника;3) поля, созданного отрезком проводника с током гдеɑ1 и ɑ2 — углы между отрезком проводника и линией, соединяющей концы отрезка и точкой поля; 4) поля бесконечно длинного соленоида где n — число витков на единицу длины соленоида.
Сила Лоренца: по модулю где F — сила, действующая на заряд, движущийся в магнитном поле, v — скорость заряда q, α — угол между векторами v и B.
Поток вектора магнитной индукции (магнитный поток через площадку S): 1) для однородного магнитного поля , где α — угол между вектором B и нормалью к площадке, 2) для неоднородного поля	1) 2)
Потокосцепление (полный поток): где N — число витков катушки.
Закон Фарадея-Ленца: где ԑi — ЭДС индукции.
ЭДС самоиндукции: где L — индуктивность контура.
Индуктивность соленоида: где n — число витков на единицу длины соленоида, V — объем соленоида.
Энергия магнитного поля:
Заряд, протекающий по замкнутому контуру при изменении магнитного потока через контур: где ∆Ф = Ф2 – Ф1 — изменение магнитного потока, R — сопротивление контура.
Работа по перемещению замкнутого контура с током I в магнитном поле:

Таблица большая основных формул электричества и магнетизма

	Адрес этой страницы (вложенность) в справочнике dpva.ru:  главная страница  / / Техническая информация / / Физический справочник / / Электрические и магнитные величины / / Понятия и формулы для электричества и магнетизма.  / / Таблица большая основных формул электричества и магнетизма Поделиться:    Таблица большая основных формул электричества и магнетизма  Физические законы, формулы, переменные  Формулы электричество и магнетизм Закон Кулона: где q1 и q2 — величины точечных зарядов,  ε1  — электрическая постоянная; ε — диэлектрическая проницаемость изотропной среды (для вакуума ε = 1), r — расстояние между зарядами. Напряженность электрического поля, где:  F — сила, действующая на заряд q0 , находящийся в данной точке поля. Напряженность поля на расстоянии r от источника поля: 1) точечного заряда 2) бесконечно длинной заряженной нити с линейной плотностью заряда τ: 3) плоскости с поверхностной плотностью заряда σ (не зависит от расстояния): 4) между двумя разноименно заряженными плоскостями с поверхностной плотностью заряда σ (во вне такого «суперконденсатора» поле равно нулю по принцину суперпозиции): Потенциал электрического поля: где W — потенциальная энергия заряда q0 . Потенциал поля точечного заряда на расстоянии r от заряда: По принципу суперпозиции полей, Напряженность, принцип суперпозиции:  Εi — напряженность и в данной точке поля, создаваемая

Электрическое поле — Википедия

Материал из Википедии — свободной энциклопедии

Электрическое поле — одна из двух компонент электромагнитного поля, представляющая собой векторное поле^[1], существующее вокруг тел или частиц, обладающих электрическим зарядом, а также возникающее при изменении магнитного поля (например, в электромагнитных волнах). Электрическое поле непосредственно невидимо, но может быть обнаружено благодаря его силовому воздействию на заряженные тела^[2].

Для количественного определения электрического поля вводится силовая характеристика — напряжённость электрического поля — векторная физическая величина, равная отношению силы, с которой поле действует на положительный пробный заряд, помещённый в данную точку пространства, к величине этого заряда. Направление вектора напряженности совпадает в каждой точке пространства с направлением силы, действующей на положительный пробный заряд.

В классической физике, применимой при рассмотрении крупномасштабных (больше размера атома) взаимодействий, электрическое поле рассматривается как одна из составляющих единого электромагнитного поля и проявление электромагнитного взаимодействия. В квантовой электродинамике — это компонент электрослабого взаимодействия.

В классической физике система уравнений Максвелла описывает взаимодействие электрического поля, магнитного поля и воздействие зарядов на эту систему полей.

Основным действием электрического поля является силовое воздействие на неподвижные относительно наблюдателя электрически заряженные тела или частицы. На движущиеся заряды силовое воздействие оказывает и магнитное поле (вторая составляющая силы Лоренца).

Электрическое поле обладает энергией. Плотность этой энергии определяется величиной поля и может быть найдена по формуле

u=12(E→D→),{\displaystyle u={\frac {1}{2}}\left({\vec {E}}{\vec {D}}\right),}

где E — напряжённость электрического поля, D — индукция электрического поля.

Однородное поле[править | править код]

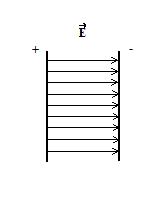Направление линий напряжённости между двумя разнозаряженными пластинами

Однородное поле — это электрическое поле, в котором напряжённость одинакова по модулю и направлению во всех точках пространства. Приблизительно однородным является поле между двумя разноимённо заряженными плоскими металлическими пластинами. В однородном электрическом поле линии напряжённости направлены параллельно друг другу.

Наблюдение электрического поля в быту[править | править код]

Для того, чтобы создать электрическое поле, необходимо создать электрический заряд. Натрите какой-нибудь диэлектрик о шерсть или что-нибудь подобное, например, пластиковую ручку о собственные чистые волосы. На ручке создастся заряд, а вокруг — электрическое поле. Заряженная ручка будет притягивать к себе мелкие обрывки бумаги. Если натирать о шерсть предмет большей ширины, например, резиновую ленту, то в темноте можно будет видеть мелкие искры, возникающие вследствие электрических разрядов.

Электрическое поле часто возникает возле телевизионного экрана (относится к телевизорам с ЭЛТ) при включении или выключении телеприёмника. Это поле можно почувствовать по его действию на волоски на руках или лице.

Электрическое поле внутри проводников с избыточными зарядами[править | править код]

Из опытов, приводимых в электростатике, известно, что избыточные заряды привнесённые в проводник извне, перемещаются к поверхности проводника и остаются у поверхности проводника. Само перемещение избыточных зарядов к поверхности проводника свидетельствует о наличии электрического поля внутри проводника в период перемещения к поверхности проводника.

Электрическое поле внутри проводников с недостатком собственных электронов[править | править код]

При недостатке собственных электронов тело получает положительный заряд «дырочной» природы. Дырки при этом ведут себя подобно электронам и также распределяются по поверхности тела.

Расчёты электрического поля можно проводить аналитическими^[3][4][5] или численными методами^[6]. Аналитические методы удается применить лишь в простейших случаях, на практике в основном используются численные методы. Численные методы включают в себя: метод сеток или метод конечных разностей; вариационные методы; метод конечных элементов; метод интегральных уравнений; метод эквивалентных зарядов^[6].

• Орир, Джей — Популярная физика: [пер. с англ.].: Мир, 1966. — 446 с.
• Учебник «Элементарный учебник физики» под ред. Ландсберга Г. С., Часть 2 (Электричество и магнетизм.)
• Трофимова Т. И. Курс физики: Учеб. пособие для вузов.—2-е изд., перераб. и доп.— М.: Высш. шк., 1990.—478 с.: ил. ISBN 5-06-001540-8

Формулы — Электричество и магнетизм

Электростатическое поле в вакууме

Закон Кулона: ,

где

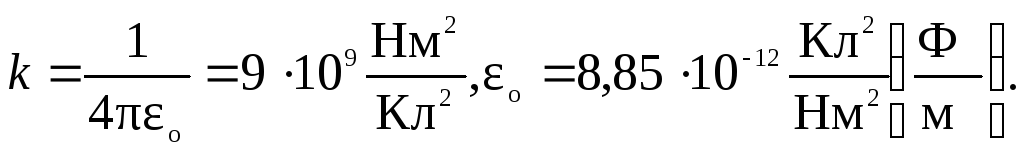
Напряженность электрического поля:

Напряженность поля точечного заряда:

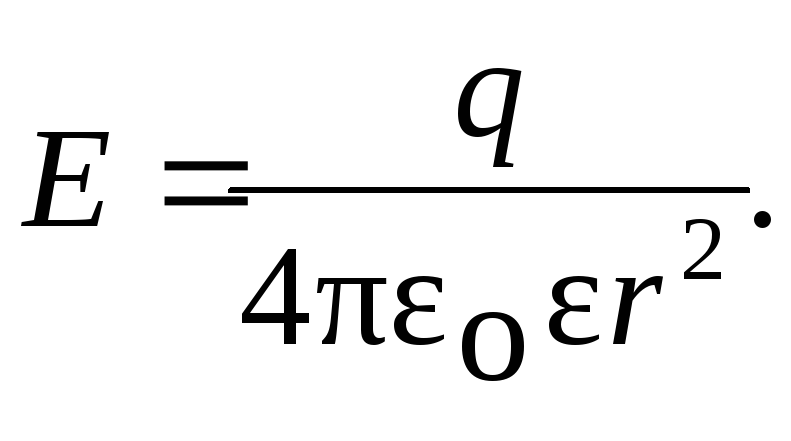
Напряженность поля заряженного шара:

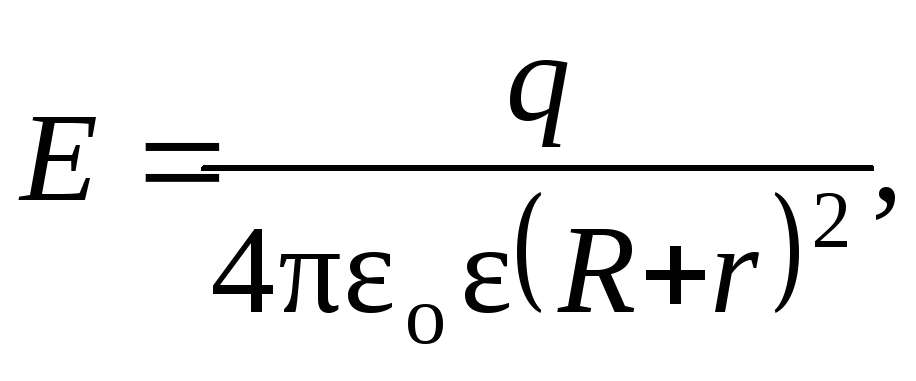
где R — радиус шара.

Принцип суперпозиции электрических полей:

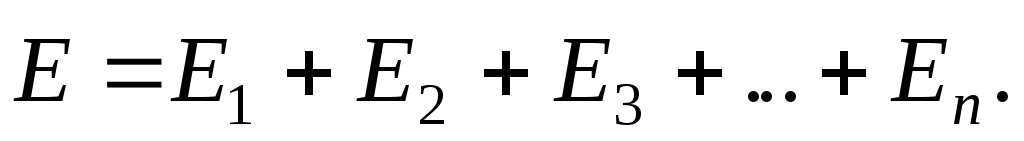
Поток вектора напряженности через поверхность S:

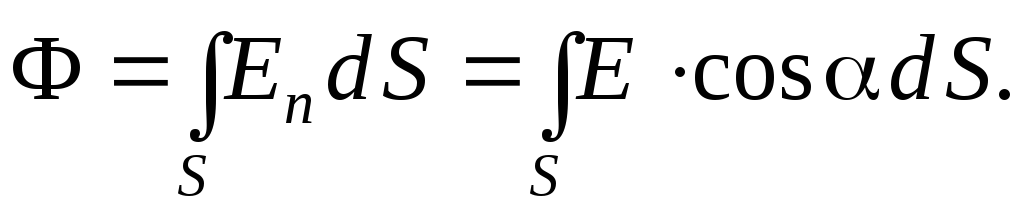
Теорема Гаусса: ,

где Ф_Е – поток вектора напряженности через замкнутую поверхность S, q – заряд, заключенный внутри поверхности S.

Линейная плотность заряда: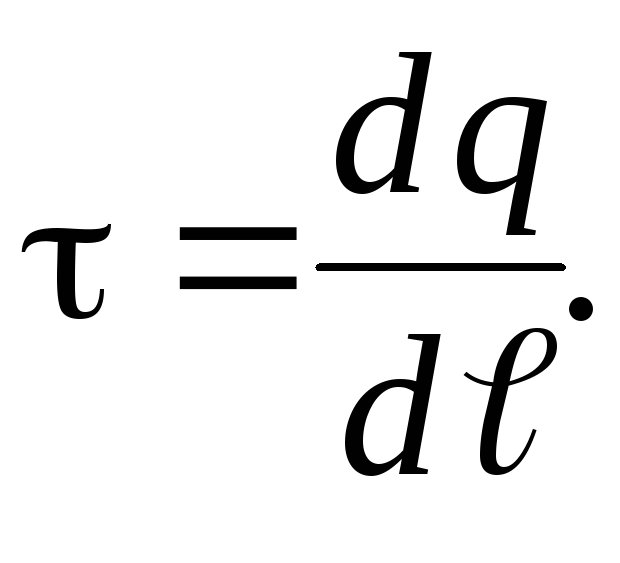

Поверхностная плотность заряда: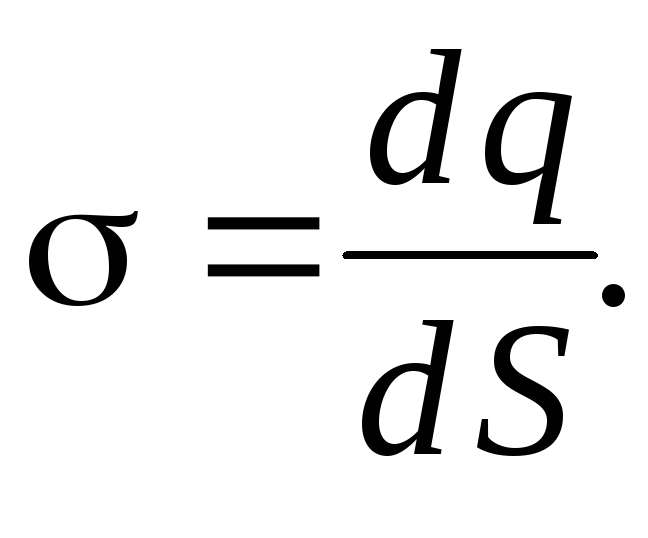

Объемная плотность заряда: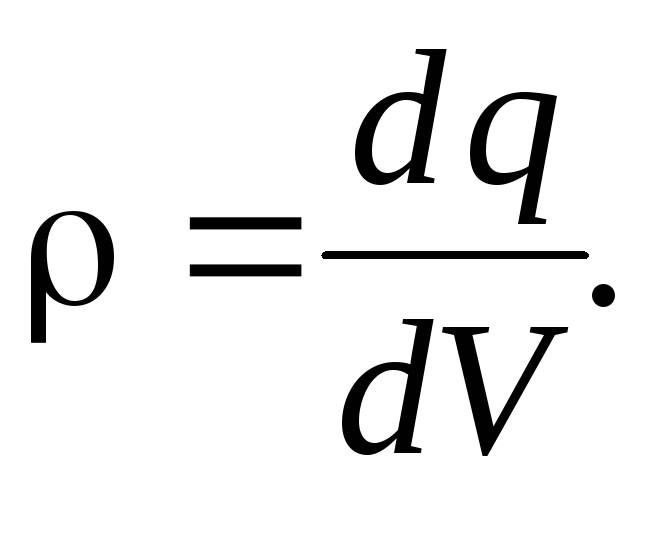

Напряженность поля, создаваемого бесконечной равномерно заряженной плоскостью, нитью:

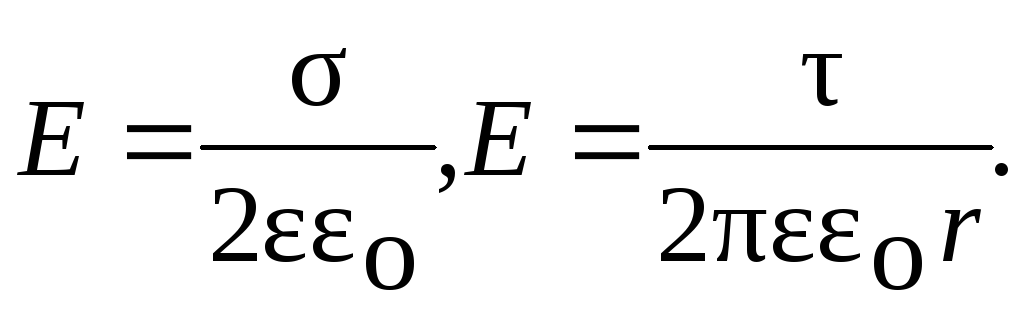
Электрическое смещение:

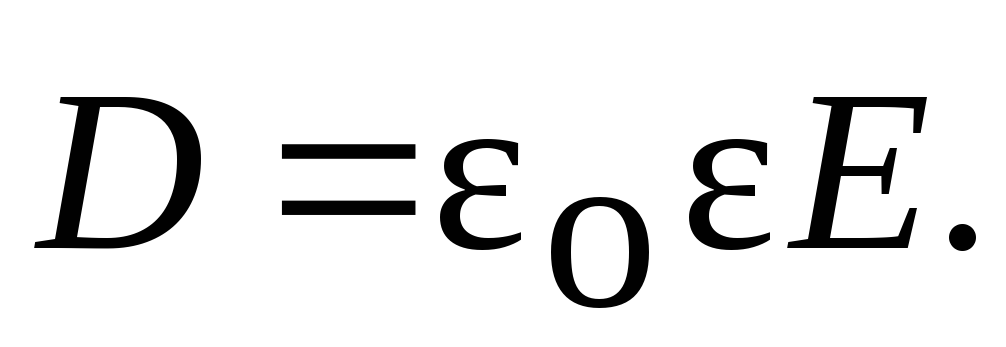
Потенциал электрического поля:

Потенциал поля точечного заряда:

Потенциал поля заряженного шара:

Работа по перемещению заряда в электрическом поле: А = q (__

где (__ — разность потенциалов.

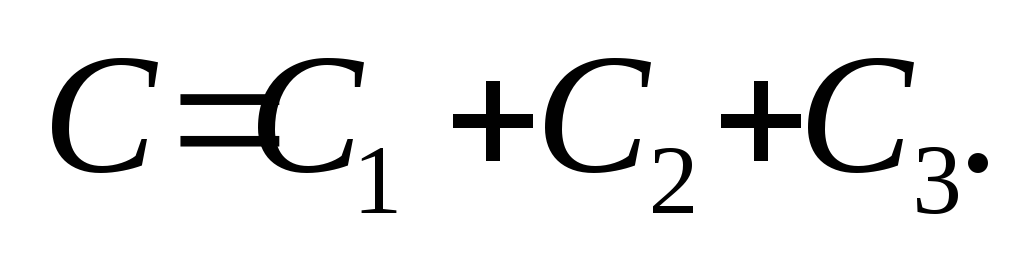
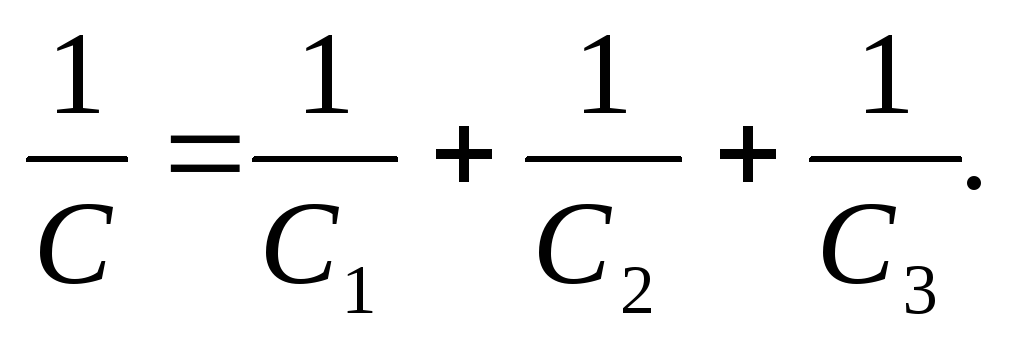
Энергия заряженного конденсатора

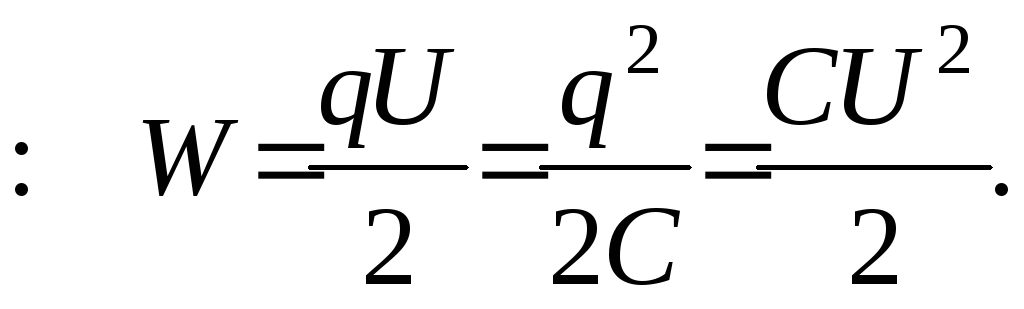
Энергия системы точечных зарядов:

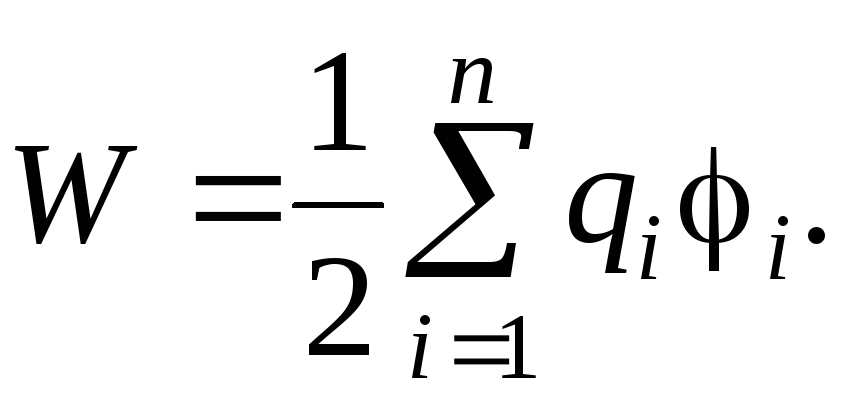
Электрический момент диполя:

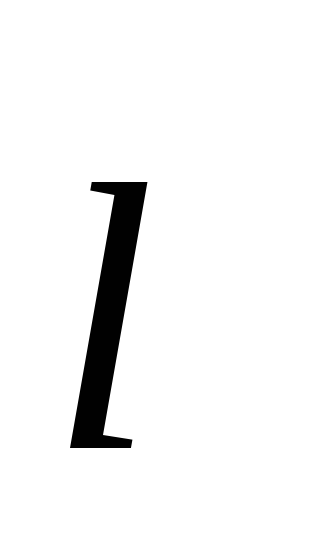
Механический момент, действующий на диполь в электрическом поле:

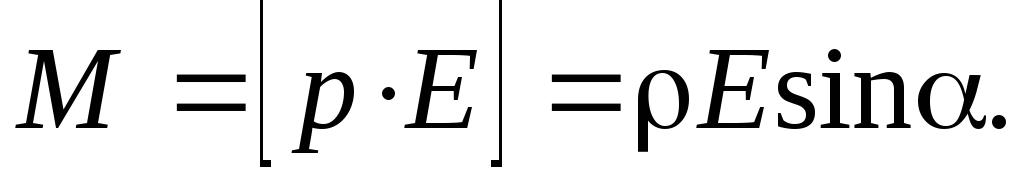
Поляризованность диэлектрика:

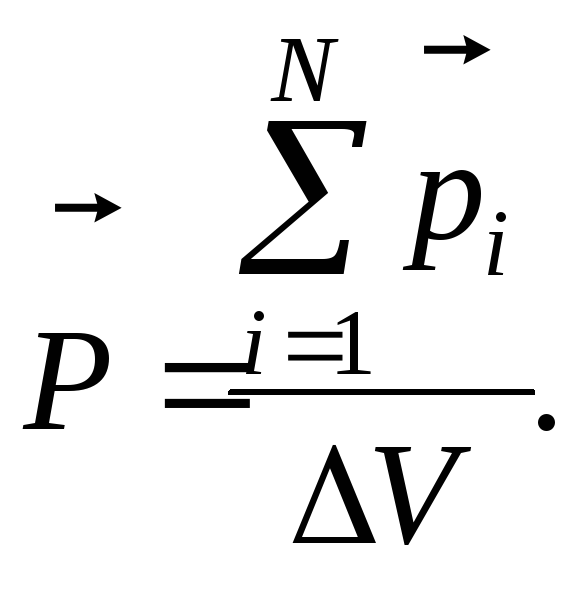
Связь поляризованности и напряженности электрического поля: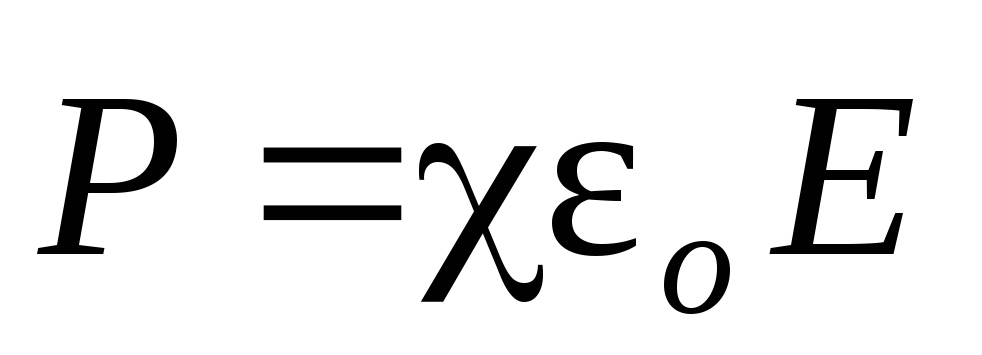, где χ – диэлектрическая восприимчивость.

Постоянный ток

Сила тока: .

Плотность тока: 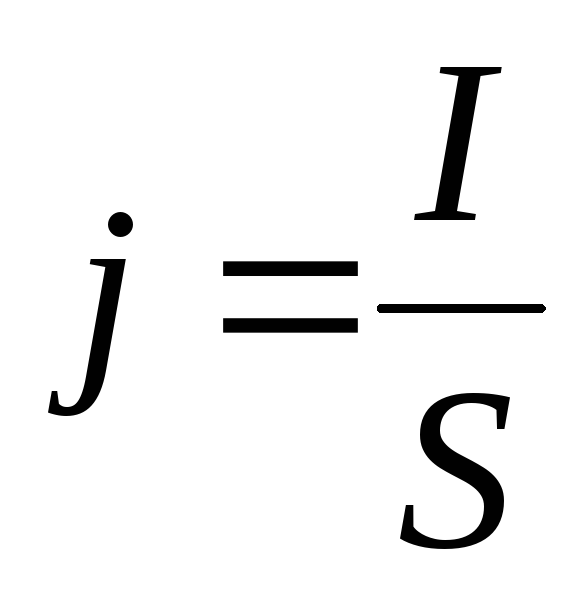, где j=qnV.

Закон Ома для однородного участка цепи:

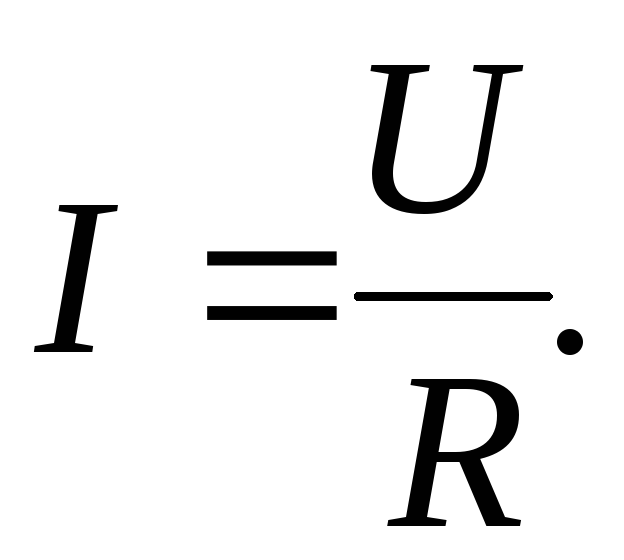
Сопротивление проводника:

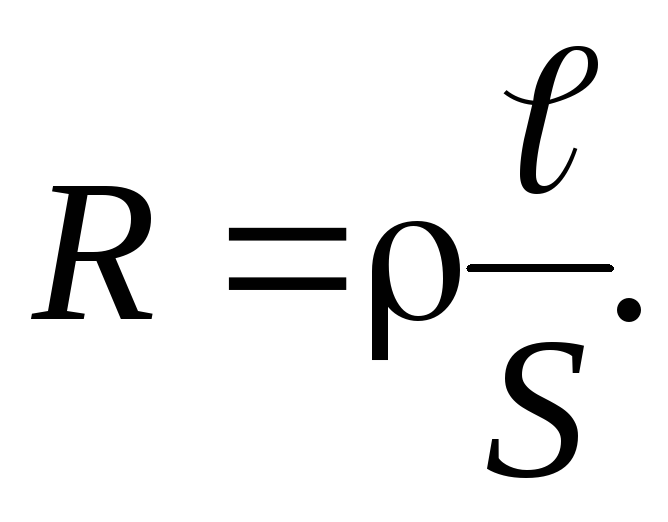
Зависимость удельного сопротивления от температуры:

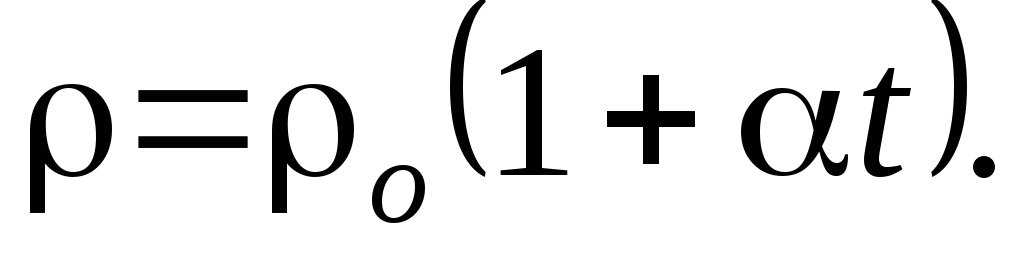
Закон Ома для неоднородного участка цепи:

Сила тока короткого замыкания:

.

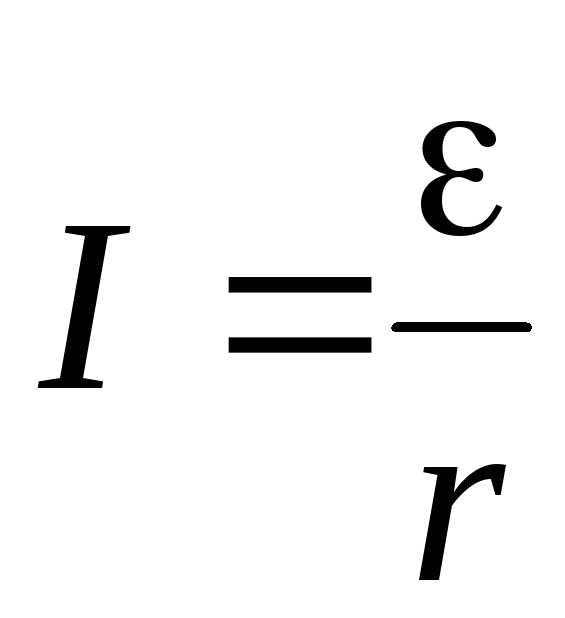Закон Ома для замкнутой цепи: .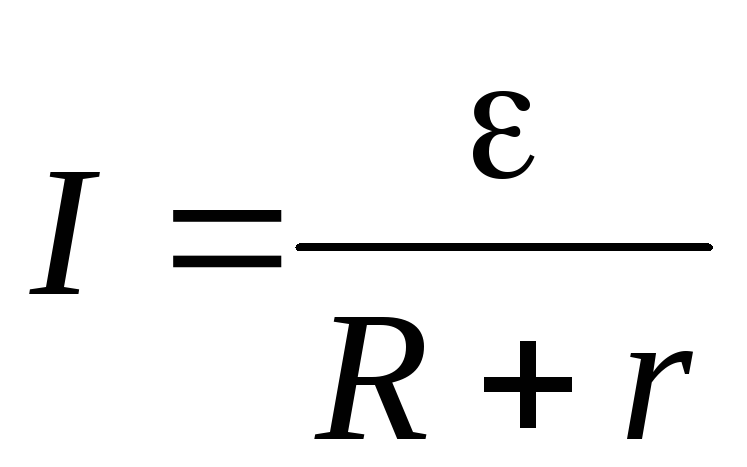

Работа электрического поля на участке цепи:

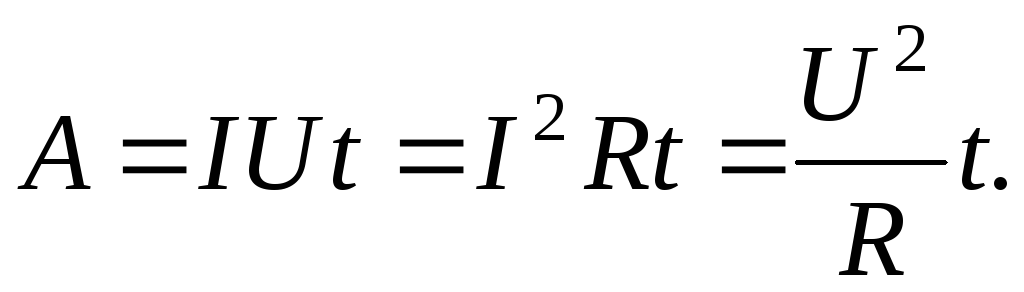
Закон Джоуля-Ленца:

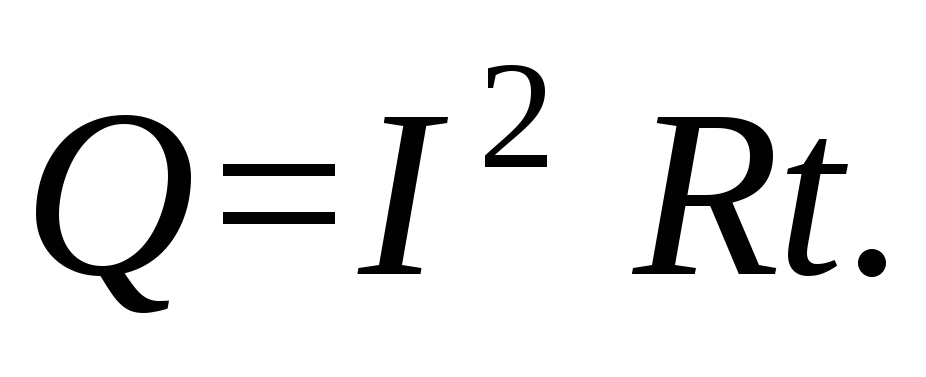
Мощность тока: P=I ^. U .

Полная мощность, выделяемая в цепи: P=I ^.  .

Первый закон Кирхгофа: .

Второй закон Кирхгофа: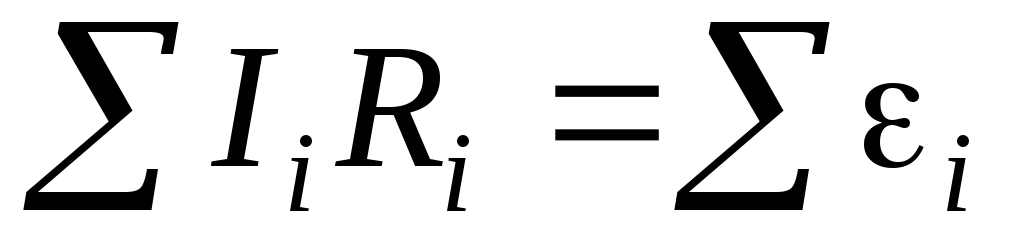

Магнитное поле в вакууме и веществе

Закон Био-Савара-Лапласа:

,

где _о=410^-7Гн/м.

Магнитная индукция в центре кругового тока:

.

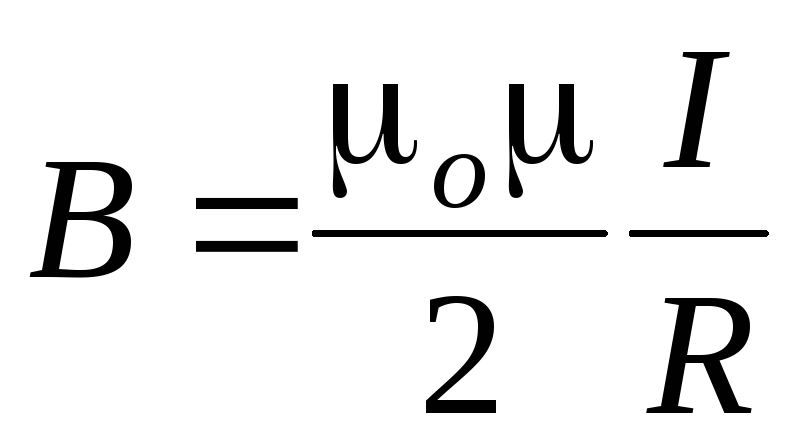Магнитная индукция поля, создаваемого бесконечно длинным прямым проводником с током:

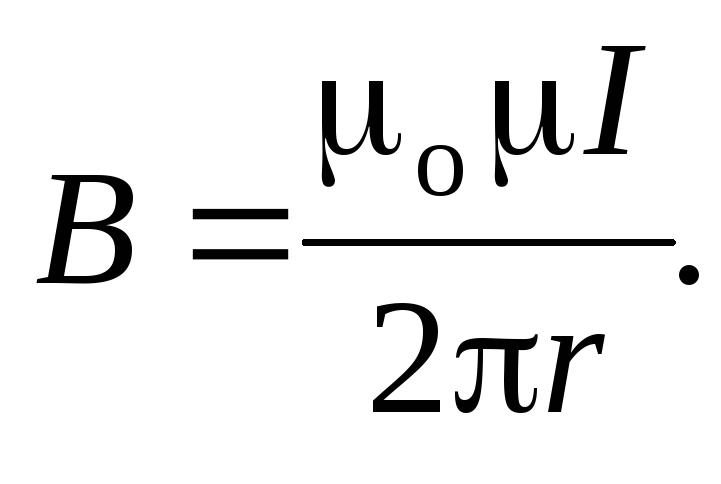
Магнитная индукция поля,

создаваемого отрезком проводника:

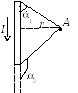
Связь магнитной индукции с напряженностью магнитного поля:

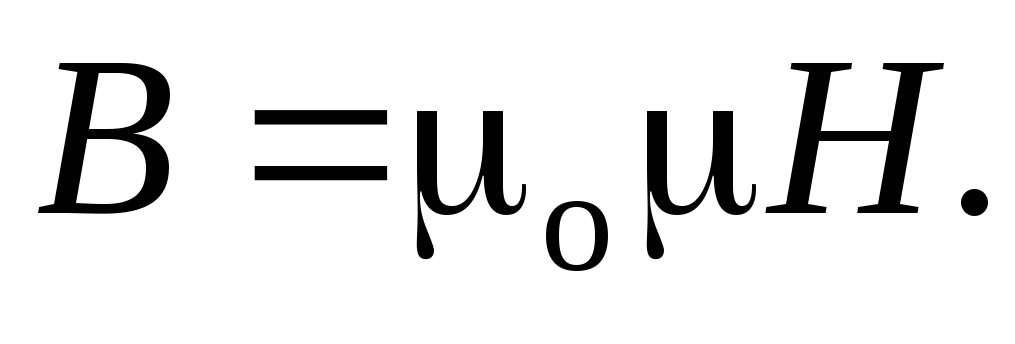
Магнитная индукция поля, создаваемого соленоидом в средней его части (или тороида на его оси):

Принцип суперпозиции магнитных полей:

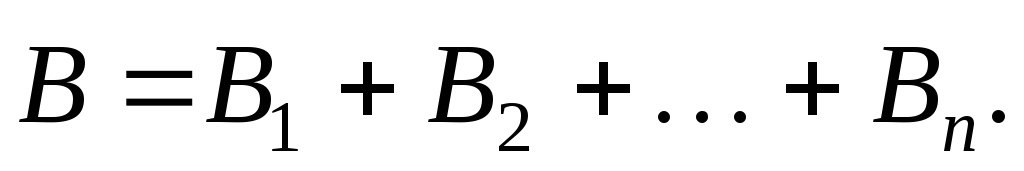
Закон Ампера:

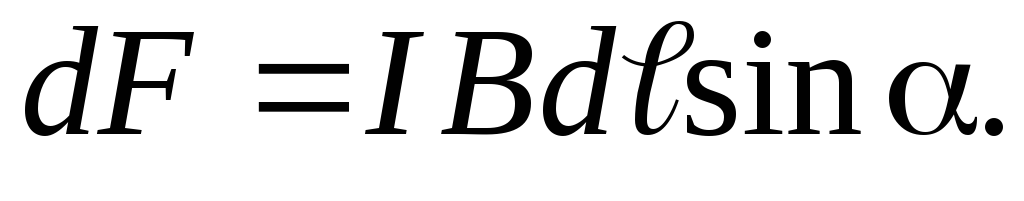
Сила взаимодействия двух прямых бесконечно длинных параллельных проводников с токами:

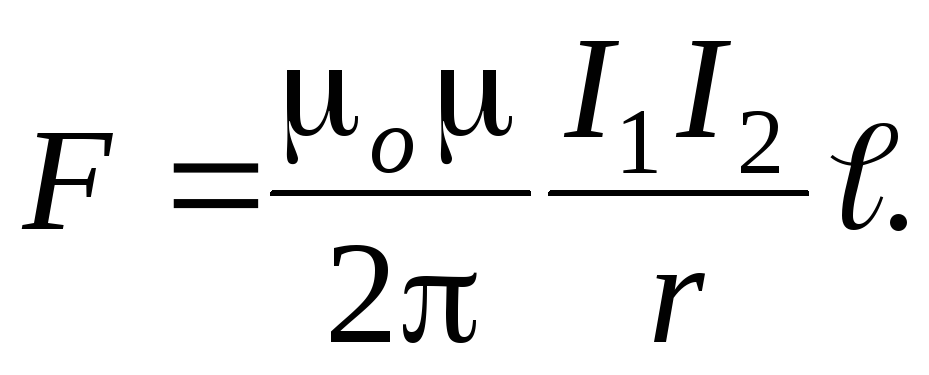
Магнитный момент контура с током:

P_m=I ^. S .

Механический момент, действующий на контур с током, помещенный в однородное магнитное поле:

M = p_m ^. B sin 

Сила, действующая на заряд, движущийся в магнитном поле (сила Лоренца):

F = q V B sin 

Закон полного тока:

Магнитный поток через плоский контур:

Ф = B S cos  .

Потокосцепление, то есть полный магнитный поток, сцепленный со всеми витками соленоида или тороида:

.

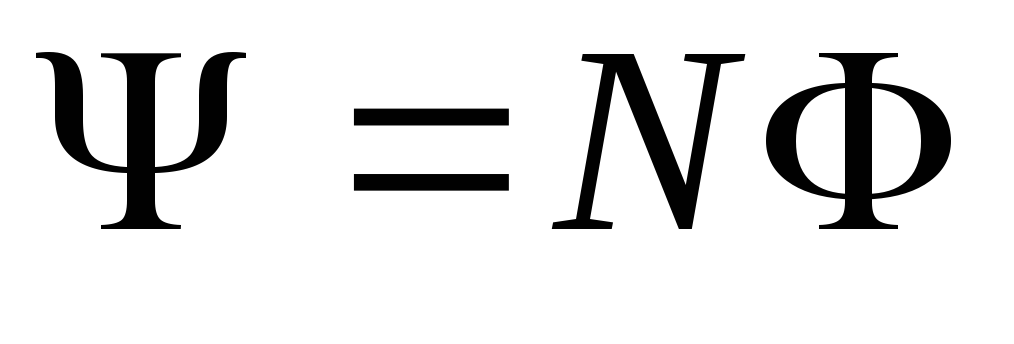М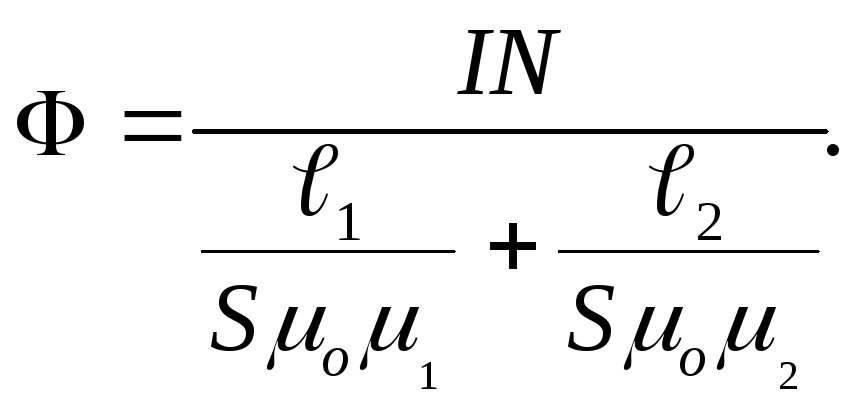агнитный поток сквозь тороид, сердечник которого составлен из двух частей, изготовленных из веществ с различными магнитными проницаемостями:

Made in Russia Made by Miha

Электрическое поле. Формулы ЕГЭ — Репетитор по физике (Краснодар)

Все формулы взяты в строгом соответствии с Федеральным институтом педагогических измерений (ФИПИ)

3.1 ЭЛЕКТРИЧЕСКОЕ ПОЛЕ

3.1.1 Электризация тел и её проявления. Электрический заряд. Два вида заряда. Элементарный электрический заряд. Закон сохранения электрического заряда

1.       Существуют заряды двух видов: положительные (+) и отрицательные (-). Положительный заряд возникает при трении стекла о кожу или шелк, а отрицательный — при трении янтаря (или эбонита) о шерсть.

2.       Заряды (или заряженные тела) взаимодействуют друг с другом. Одноименные заряды отталкиваются, а разноименные заряды притягиваются.

3.       Состояние электризации можно передать от одного тела к другому, что связано с переносом электрического заряда. При этом телу можно передать больший или меньший заряд, т. е. заряд имеет величину. При электризации трением заряд приобретают оба тела, причем одно — положительный, а другое — отрицательный. Следует подчеркнуть, что абсолютные величины зарядов наэлектризованных трением тел равны, что подтверждается многочисленными измерениями зарядов с помощью электрометров.

Объяснить, почему тела электризуются (т. е. заряжаются) при трении, стало возможным после открытия электрона и изучения строения атома. Как известно, все вещества состоят из атомов; атомы, в свою очередь, состоят из элементарных частиц — отрицательно заряженных электронов, положительно заряженных протонов и нейтральных частиц —нейтронов. Электроны и протоны являются носителями элементарных (минимальных) электрических зарядов.

Элементарный электрический заряд (е) — это наименьший электрический заряд, положительный или отрицательный, равный величине заряда электрона:

Закон сохранения электрического заряда — алгебраическая сумма электрических зарядов всех частиц изолированной системы не меняется при происходящих в ней процессах.

3.1.2 Взаимодействие зарядов. Точечные заряды. Закон Кулона:

Электрический заряд (Кл) — это физическая величина, являющаяся источником электрического поля, посредством которого осуществляется взаимодействие частиц, обладающих зарядом.

Закон Кулона — это один из основных законов электростатики. Он определяет величину и направление силы взаимодействия между двумя неподвижными точечными зарядами.

Кулон (Кл) — единица СИ количества электричества (электрического заряда).Она является производной единицей и определяется через единицу силы тока — 1 ампер (А), которая входит в число основных единиц СИ.

За единицу электрического заряда принимают заряд, проходящий через поперечное сечение проводника при силе тока 1 А за 1 с.

[1 Кл = 1 А ·Bс]

Точечный заряд — заряженное тело, размер которого много меньше расстояния его возможного воздействия на другие тела. В таком случае ни форма, ни размеры заряженных тел не влияют практически на взаимодействие между ними.

 

3.1.3 Электрическое поле. Его действие на электрические заряды

Электрическое поле — это особая форма материи, посредством которой осуществляется взаимодействие электрически заряженных частиц.

Главным свойством электрического поля является действие его на электрические заряды с некоторой силой. По этому действию устанавливается факт его существования. Действие поля на единичный заряд — напряженность поля — является одной из его основных характеристик, по которой изучается распределение поля в пространстве.

 

3.1.4 Напряжённость электрического поля (Н/м) — векторная характеристика поля, сила, действующая на единичный покоящийся в данной системе отсчета электрический заряд:

Поле точечного заряда:

Однородное поле:

Картины линий полей

 

3.1.5 Потенциальность электростатического поля

Потенциал (потенциальная функция) (от лат. potentia — сила) является энергетической характеристикой векторных полей, к числу которых относятся гравитационное, электромагнитное и электростатическое поля.

Потенциал электростатического поля в данной точке численно равен работе, которую совершают силы поля при перемещении единичного положительного заряда из данной точки в бесконечность.

Разность потенциалов и напряжение

Работа по перемещению заряда (Дж) в однородном электростатическом поле зависит только от начального и конечного положений движущегося заряда и не зависит от формы траектории. При перемещении заряда по замкнутой траектории работа равна нулю.

Потенциальная энергия заряда в электростатическом поле(Дж):

Потенциал электростатического поля(Дж/Кл):

Связь напряжённости поля и разности потенциалов для однородного электростатического поля: U = Ed 

 

3.1.6 Принцип суперпозиции электрических полей:

 

3.1.7 Проводники в электростатическом поле. Условие равновесия зарядов: внутри проводника

Внутри и на поверхности проводника

 

3.1.8 Диэлектрики в электростатическом поле. Диэлектрическая проницаемость вещества ε.

Диэлектрики (или изоляторы) — вещества, относительно плохо проводящие электрический ток (по сравнению с проводниками).

Полярные диэлектрики состоят из молекул, в которых центры распределения положительных и отрицательных зарядов не совпадают. Такие молекулы можно представить в виде двух одинаковых по модулю разноименных точечных зарядов, находящихся на некотором расстоянии друг от друга, называемых диполем.

Неполярные диэлектрики состоят из атомов и молекул, у которых центры распределения положительных и отрицательных зарядов совпадают.

Относительная диэлектрическая проницаемость среды ε — это физическая величина, показывающая, во сколько раз модуль напряженности электростатического поля Е внутри однородного диэлектрика меньше модуля напряженности поля Е0 в вакууме:

3.1.9 Конденсатор. Электроёмкость конденсатора(Ф):

Электроёмкость плоского конденсатора — величина заряда, которую нужно сообщить конденсатору, чтобы изменить его потенциал на единицу:

 

3.1.10 Параллельное соединение конденсаторов:

Последовательное соединение конденсаторов:

 

3.1.11 Энергия заряженного конденсатора (Дж):

Электрическое поле. Напряженность. Линии напряженности. Видеоурок. Физика 10 Класс

Закон Кулона, изученный на прошлом уроке, был установлен экспериментально и справедлив для покоящихся заряженных тел. Каким же образом происходит взаимодействие заряженных тел на расстоянии? До некоторых пор при изучении электрических взаимодействий бок о бок развивались две принципиально разные теории: теория близкодействия и теория дальнодействия (действия на расстоянии).

Теория близкодействия заключается в том, что заряженные тела взаимодействуют друг с другом посредством промежуточного звена (например, цепь в задаче о поднятии ведра из колодца является промежуточным звеном, посредством которого мы воздействуем на ведро, то есть поднимаем его).

Теория дальнодействия гласит, что заряженные тела взаимодействуют через пустоту. Шарль Кулон придерживался именно этой теории и говорил, что заряженные тела «чувствуют» друг друга. В начале XIX века конец спорам положил Майкл Фарадей (рис. 1). В работах, связанных с электрическим полем, он установил, что между заряженными телами существует некий объект, который и осуществляет действие заряженных тел друг на друга. Работы Майкла Фарадея были подтверждены Джеймсом Максвеллом (рис. 2). Он показал, что действие одного заряженного тела на другое распространяется за конечное время, таким образом, между заряженными телами должно существовать промежуточное звено, через которое осуществляется взаимодействие.

Рис. 1. Майкл Фарадей (Источник)

Рис. 2. Джеймс Клерк Максвелл (Источник)

Определение: Электрическое поле – это особая форма материи, которая создается покоящимися зарядами и определяется действием на другие заряды.

Электрическое поле характеризуется определенными величинами. Одна из них называется напряженностью.

Вспомним, что по закону Кулона, сила взаимодействия двух зарядов:

Максвелл показал, что это взаимодействие осуществляется за конечное время:

где l – расстояние между заряженными частицами, а c – скорость света, скорость распространения электромагнитных волн.

Рассмотрим эксперимент по взаимодействию двух зарядов. Пусть электрическое поле создается положительным зарядом +q₀, и в это поле на некотором расстоянии помещается пробный, точечный положительный заряд +q (рис. 3,а). Согласно закону Кулона, на пробный заряд будет действовать сила электростатического взаимодействия со стороны заряда, создающего электрическое поле. Тогда отношение этой силы к величине пробного заряда будет характеризовать действие электрического поля в данной точке. Если же в эту точку будет помещен вдвое больший пробный заряд, то сила взаимодействия также увеличится вдвое (рис. 3,б). Аналогичным образом отношение силы к величине пробного заряда снова даст значение действия электрического поля в данной точке. Так же действие электрического поля определяется и в том случае, если пробный заряд отрицательный (рис. 3,в).

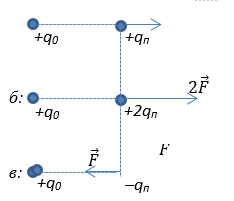
Рис. 3. Сила электростатического взаимодействия двух точечных зарядов

Таким образом, в точке, где находится пробный заряд, поле характеризуется величиной:

Эта величина и называется напряженностью электрического поля. Напряженность поля в данной точке не зависит от величины пробного заряда: во всех трех случаях отношение силы к величине заряда – постоянная величина. Единица измерения напряженности:

Напряженность – векторная величина, является силовой характеристикой электрического поля, направлена в ту же сторону, куда и сила электростатического взаимодействия. Она показывает, с какой силой электрическое поле действует на помещенный в него заряд.

Рассмотрим напряженность электрического поля уединенного точечного заряда либо заряженной сферы.

Из определения напряженности следует, что для случая взаимодействия двух точечных зарядов, зная силу их кулоновского взаимодействия, можем получить величину напряженности электрического поля, которое создается зарядом q₀ в точке на расстоянии r от него до точки, в которой исследуется электрическое поле:

Данная формула показывает, что напряженность поля точечного заряда изменяется обратно пропорционально квадрату расстояния от данного заряда, то есть, например, при увеличении расстояния в два раза, напряженность уменьшается в четыре раза.     

Попытаемся теперь охарактеризовать электростатическое поле нескольких зарядов. В этом случае необходимо воспользоваться сложением векторных величин напряженностей всех зарядов. Внесем пробный заряд и запишем сумму векторов сил, действующих на этот заряд. Результирующее значение напряженности получится при разделении значений этих сил на величину пробного заряда. Данный метод называется принципом суперпозиции.

Напряженность электростатического поля принято изображать графически при помощи силовых линий, которые также называют линиями напряженности. Такое изображение можно получить, построив вектора напряженности поля в как можно большем количестве точек вблизи данного заряда или целой системы заряженных тел.

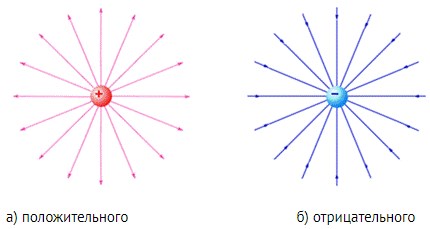
Рис. 4. Линии напряженности электрического поля точечного заряда (Источник)

Рассмотрим несколько примеров изображения силовых линий. Линии напряженности выходят из положительного заряда (рис. 4,а), то есть положительный заряд является источником силовых линий. Заканчиваются линии напряженности на отрицательном заряде (рис. 4,б).

Рассмотрим теперь систему, состоящую из положительного и отрицательного зарядов, находящихся на конечном расстоянии друг от друга (рис. 5). В этом случае линии напряженности направлены от положительного заряда к отрицательному.

Большой интерес представляет электрическое поле между двумя бесконечными плоскостями. Если одна из пластин заряжена положительно, а другая отрицательно, то в зазоре между плоскостями создается однородное электростатическое поле, линии напряженности которого оказываются параллельными друг другу (рис. 6). 

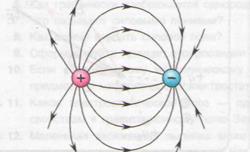
Рис. 5. Линии напряженности системы двух зарядов (Источник)  

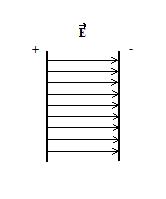
Рис. 6. Линии напряженности поля между заряженными пластинами (Источник)

В случае неоднородного электрического поля величина напряженности определяется густотой силовых линий: там, где силовые линии гуще, величина напряженности поля больше (рис. 7).

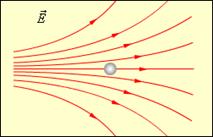
Рис. 7. Неоднородное электрическое поле (Источник)

Определение: Линиями напряженности называют непрерывные линии, касательные к которым в каждой точке совпадают с векторами напряженности в этой точке.

Линии напряженности начинаются на положительных зарядах, заканчиваются на отрицательных и являются непрерывными.

Изображать электрическое поле с помощью силовых линий мы можем так, как сами посчитаем нужным, то есть число силовых линий, их густота ничем не ограничивается. Но при этом необходимо учитывать направление векторов напряженности поля и их абсолютные величины.

Очень важно следующее замечание. Как говорилось ранее, закон Кулона применим только для точечных покоящихся зарядов, а также заряженных шариков, сфер. Напряженность же позволяет характеризовать электрическое поле вне зависимости от формы заряженного тела, которое это поле создает.

 

Список литературы

1. Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика: учеб. для 10 кл. общеобразоват. учреждений: базовый и профил. уровни. – М.: Просвещение, 2008.
2. Касьянов В.А. Физика. 10 кл.: учеб. для общеобразоват. учеб. заведений. — М.: Дрофа, 2000.
3. Рымкевич А.П. Физика. Задачник. 10-11 кл.: пособие для общеобразоват. учреждений. – М.: Дрофа, 2013.
4. Генденштейн Л.Э., Дик Ю.И. Физика. 10 класс. В 2 ч. Ч. 1. Учебник для общеобразовательных учреждений (базовый уровень) – М.: Мнемозина, 2009.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Nauka.guskoff.ru (Источник).
2. Youtube (Источник).
3. Physics.ru (Источник).

 

Домашнее задание

1. Стр. 378: № 1–3. Касьянов В.А. Физика. 10 кл.: учеб. для общеобразоват. учеб. заведений. — М.: Дрофа, 2000. (Источник)
2. С каким ускорением движется электрон в поле напряженностью 10 кВ/м?
3. В вершинах равностороннего треугольника со стороной a находятся заряды +q, +q и –q. Найти напряженность поля Е в центре треугольника.

Электростатика. Теория и формулы для ЕГЭ + шпаргалка

ЭЛЕКТРОСТАТИКА
Теория и формулы (кратко и сжато)

Электростатика – раздел электродинамики, изучающий покоящиеся электрически заряженные тела. Существует два вида электрических зарядов: положительные (стекло о шелк) и отрицательные (эбонит о шерсть).

Элементарный заряд – минимальный заряд (е = 1,6∙10^-19 Кл)

Заряд любого тела кратен целому числу элементарных зарядов:     q = N∙е

Электризация тел – перераспределение заряда между телами. Способы электризации: трение,  касание, влияние.

Закон сохранения электрического заряда – в замкнутой системе алгебраическая сумма зарядов всех частиц остается неизменной.  q_{1 +} q ₂ + q ₃ + …..+ q_n =  const

Пробный заряд – точечный положительный заряд.

Закон Кулона

Закон Кулона (установлен опытным путем в 1785 году) Сила взаимодействия двух неподвижных точечных зарядов в вакууме прямо пропорциональна произведению модулей зарядов и обратно пропорционально квадрату расстояния между ними.

---

Электрическое поле

Электрическое поле – вид материи, осуществляющий взаимодействие между электрическими зарядами, возникает вокруг зарядов, действует только на заряды

---

 

Силовые линии напряженности электрического поля – непрерывные линии, касательные к которым в каждой точке, через которые они проходят, совпадают с вектором напряженности.

Свойства силовых линий: 

• не замкнуты;
• не пересекаются;
• непрерывны;
• направление совпадает с направлением вектора напряжённости;
• начало на + q или в бесконечности, конец на – q или в бесконечности;
• гуще вблизи зарядов (где больше напряжённость).
• перпендикулярны поверхности проводника

Разность потенциалов или напряжение (Δφ или U) — это разность потенциалов в начальной и конечной точках траектории заряда            Δφ = φ₁ – φ₂

Чем меньше меняется потенциал на отрезке пути, тем меньше напряженность поля.
Напряженность электрического поля направлена в сторону уменьшения потенциала.

Электроемкость

Электроемкость С — характеризует способность проводника  накапливать электрический заряд на своей поверхности.

• — не зависит от электрического заряда и напряжения.
• — зависит от геометрических размеров проводников, их формы, взаимного расположения, электрических свойств среды между проводниками.

Проводники и диэлектрики

Конденсаторы

Конденсатор — электротехническое устройство, служащее для быстрого накопления электрического заряда и быстрой отдачи его в цепь (два проводника, разделенных слоем диэлектрика ).

---

Скачать таблицы по теме «Электростатика»

 

---

Конспект уроков по теме «Электростатика. Теория и формулы» + шпаргалка.

Еще конспекты для 10-11 классов: