сколько отдашь, столько и получишь

Ни одна сфера человеческой деятельности не обходится без точных наук. И как бы ни были сложны человеческие взаимоотношения, они тоже сводятся к этим законам.  предлагает вспомнить законы физики, с которыми человек сталкивается и переживает каждый день своей жизни.

Чт 02 марта 2017, 12:43

Фото: forumsmile.ru

Самый простой, но самый важный закон – это

Закон сохранения и преобразования  энергии.

Энергия любой замкнутой системы при всех процессах, происходящих в системе, остается постоянной. А мы с Вами именно в такой замкнутой системе и находимся. Т.е. сколько отдадим, столько и получим. Если мы хотим что-то получить, надо столько же перед этим отдать. И никак иначе!

А нам, конечно же, хочется получать большую зарплату, а на работу при этом не ходить. Иногда создается иллюзия, что «дуракам везет» и многим счастье сваливается на голову.

Вчитайтесь в любую сказку. Героям постоянно надо преодолевать огромные трудности! То искупаться в воде студеной, то в кипятке.

Мужчины обращают на себя внимание женщин ухаживаниями. Женщины в свою очередь заботятся потом об этих мужчинах и о детях. И так далее. Так что, если вы хотите что-то получить, потрудитесь сначала отдать.

Сила действия равна силе противодействия.

Этот закон физики отражает предыдущий, в принципе. Если человек совершил негативный поступок – осознанный или нет – а потом получил ответ, т.е. противодействие. Иногда причина и следствие бывают разнесены во времени, и можно сразу и не понять, откуда ветер дует. Надо, главное, помнить, что ничего просто так не бывает.

Закон рычага. 

Архимед воскликнул: «Дайте мне точку опоры, и я переверну Землю!». Любую тяжесть можно перенести, если подобрать правильный рычаг. Нужно всегда прикинуть какой длины понадобится рычаг, чтобы добиться той или иной цели и сделать для себя вывод, расставить приоритеты: нужно ли тратить столько сил, чтобы создать правильный рычаг и передвинуть эту тяжесть или проще оставить ее в покое и заняться другой деятельностью.

Правило буравчика. 

Правило заключается в том, что указывает на направление магнитного поля. Это правило отвечает на вечный вопрос: кто виноват? И указывает на то, что во всем, что с нами происходит, виноваты мы сами. Как бы обидно не было, как бы сложно не было, как бы, на первый взгляд несправедливо не было, надо всегда отдавать себе отчет в том, что причиной изначально были мы сами.

Закон гвоздя.

Когда человек хочет забить гвоздь, он же не стучит где-то рядом с гвоздем, он стучит именно по шляпке гвоздя. Но ведь гвозди сами не залезают в стены. Нужно всегда подбирать правильный молоток, чтобы не разбить гвоздь кувалдой. И забивая, надо рассчитывать удар, чтобы не погнулась шляпка. Будьте проще, заботьтесь друг о друге. Научитесь думать о ближнем.

И наконец, закон Энтропии.

Под энтропией понимают меру беспорядка системы. Иными словами, чем больше хаоса в системе, тем больше энтропия. Более точная формулировка: при самопроизвольных процессах, протекающих в системах, энтропия всегда возрастает. Как правило, все самопроизвольные процессы необратимы. Они приводят к реальным изменениям в системе, и вернуть ее в первоначальное состояние без затраты энергии невозможно. При этом нельзя в точности повторить (на все 100%) ее исходное состояние.

Чтобы лучше уяснить, о каком порядке и беспорядке идет речь, поставим опыт. Насыплем в стеклянную банку чёрных и белых дробинок. Сначала насыплем чёрных, затем белых. Дробинки будут располагаться в два слоя: снизу чёрный, сверху белый – все упорядочено. Затем несколько раз встряхнем банку. Дробинки равномерно перемешаются. И сколько бы мы затем не трясли эту банку, нам вряд ли удастся добиться, чтобы дробинки снова расположились в два слоя. Вот она, энтропия в действии!

Состояние, когда дробинки были расположены в два слоя, считается упорядоченным.

Состояние, когда дробинки равномерно перемешаны, считается беспорядочным. Чтобы вернуться в упорядоченное состояние, нужно практически чудо! Или повторная кропотливая работа с дробинками. А чтобы навести хаос в банке, почти не требуется усилий.

Автомобильное колесо. Когда оно накачено, в нем избыток свободной энергии. Колесо может ехать, и значит, оно работает. Это порядок. А если проколоть колесо? Давление в нем упадет, свободная энергия «уйдет» в окружающую среду (рассеется), и работать такое колесо уже не сможет. Это хаос. Чтобы вернуть систему в исходное состояние, т.е. навести порядок, нужно провести немалую работу: заклеить камеру, смонтировать колесо, накачать его и т.д., после чего это опять нужная вещь, которая способна приносить пользу.

Тепло передается от горячего тела холодному, а не наоборот. Обратный процесс теоретически возможен, а практически никто не возьмется это делать, поскольку потребуются колоссальные усилия, специальные установки и оборудование.

Также и в обществе. Люди стареют. Дома рушатся. Утесы оседают в море. Галактики разбегаются. К беспорядку самопроизвольно стремится любая окружающая нас действительность.

Однако люди часто говорят о беспорядке как о свободе: «Нет, не хотим мы порядка! Дайте нам такую свободу, чтобы каждый мог делать то, что хочет!» Но когда каждый делает, что хочет, это не свобода – это хаос.  В наше время многие восхваляют беспорядок, пропагандируют анархию — словом, все то, что разрушает и разделяет. Но свобода — не в хаосе, свобода именно в порядке.

Упорядочивая свою жизнь, человек создает себе запас свободной энергии, которую затем реализует на осуществление своих планов: работу, учебу, отдых, творчество, спорт и т.п. – иными словами, противостоит энтропии. Иначе, как бы мы смогли накопить за последние 250 лет столько материальных ценностей?!

Энтропия – это мера беспорядка, мера необратимого рассеивания энергии. Чем больше энтропия, тем больше беспорядка. Дом, в котором никто не живет, ветшает. Железо со временем ржавеет, автомобиль стареет. Отношения, о сохранении которых никто не заботится, разрушаются. Так и все остальное в нашей жизни, совершенно все!

Естественное состояние природы не равновесие, а возрастание энтропии. Этот закон неумолимо работает и в жизни одного человека. Ему ничего не надо делать, чтобы его энтропия возрастала, это происходит самопроизвольно, по закону природы. Для того чтобы снизить энтропию (беспорядок), надо приложить немало усилий. Это своего рода пощечина позитивным до дури людям (под лежачий камень и вода не течет), которых довольно много!

Поддержание успеха требует постоянных усилий. Если мы не развиваемся, то мы деградируем. И чтобы сохранить то, что у нас было раньше, мы должны сегодня сделать больше, чем делали вчера. Вещи можно содержать в порядке и даже улучшить: если краска на доме выцвела, его можно покрасить заново, причем еще красивее, чем раньше.

Люди должны пытаться «усмирить» произвольное деструктивное поведение, которое преобладает в современном мире повсеместно, стараться снизить состояние хаоса, который мы же и разогнали до грандиозных пределов. И это физический закон, а не просто треп о депрессии и негативном мышлении. Всё либо развивается, либо деградирует.

Живой организм рождается, развивается и умирает, и никто никогда не наблюдал, чтобы после смерти он оживал, молодел и возвращался в семя или утробу. Когда говорят, что прошлое никогда не возвращается, то, конечно, имеют в виду, в первую очередь, эти жизненные явления. Развитие организмов задает положительное направление стрелы времени, и смена одного состояния системы другим происходит всегда в одном направлении для всех без исключения процессов.

Валериан Чупин

Источник информации: Чайковские.Новости

Комментарии (3)

Богатство современного общества прирастает, и будет прирастать во все большей мере, прежде всего всеобщим трудом. Промышленный капитал явился первой исторической формой общественного производства, когда интенсивно начал эксплуатироваться всеобщий труд. Причем сначала тот, который достался ему даром. Наука, как заметил Маркс, ничего не стоила капиталу. Действительно, ни один капиталист не заплатил вознаграждение ни Архимеду, ни Кардано, ни Галилею, ни Гюйгенсу, ни Ньютону за практическое использование их идей. Но именно промышленный капитал в массовом масштабе начинает эксплуатировать механическую технику, а тем самым и всеобщий труд, овеществленный в ней. Маркс К, Энгельс Ф. Соч., т. 25, ч. 1, с. 116.

господин В. Чупин оказался опять в иллюзиях. В социуме немного не так как в физике. Об этом говорит «Закон прибавочной стоимости»открытый Марксом. и понятие -эксплуатация.Пусть он для пример посмотрит в свой карман: Пенсии то хватает на жизнь.?А ведь проработал он в школе не один десяток лет…5349

пойду приберусь, может свободы прибавится…

Советской монете — 100 лет

В 2021 году отмечается 100-летие чеканки первых советских монет и 100-летие провозглашения перехода к новой экономической политике – НЭПу.  Эти даты тесно связаны между собой. До 1921 года в Советском государстве монет в обращении не было.

Вс 31 октября 2021, 09:57

Комментариев: 1

Смерть от алкоголя

В Перми от отравления алкоголем скончались пять человек.

Чт 18 ноября 2021, 16:46

Комментариев: 0

Лучший домик для птиц могут смастерить чайковцы

Станция детского, юношеского туризма и экологии приглашает жителей Чайковского всех возрастов принять участие в конкурсе «Лучшая кормушка, домик для птиц».

Вт 02 ноября 2021, 09:52

Комментариев: 0

Коллективный иск по вакцинации от Covid-19 рассмотрит краевой суд

Пермский краевой суд рассмотрит коллективный иск 142 жителей региона к главному санитарному врачу Прикамья Виталию Костраеву об отмене обязательной вакцинации от коронавируса. Судебное заседание состоится 21 декабря 2021 года.

Пт 12 ноября 2021, 10:45

Комментариев: 108

ЛЕНТА НОВОСТЕЙ

В Чайковском построят мусоросортировочный комплекс До 2024 года в Прикамье планируют построить девять объектов для сортировки мусора. Причем в Чайковском мусоросортивочный комплекс, согласно информации регионального Министерства ЖКХ, может быть построен уже в 2022 году. Ср 24 ноября 2021, 11:24 Комментариев: 4
Депутаты проголосовали за QR-код Депутаты Законодательного собрания Пермского края большинством голосов поддержали законопроект о введении QR-кодов. Они посчитали, что это поможет сдержать рост заболеваемости и облегчить нагрузку на систему здравоохранения. Чт 25 ноября 2021, 15:41 Комментариев: 11

Международная Научная школа устойчивого развития

Главная

Устойчивое развитие подразумевает удовлетворение потребностей современного поколения, не угрожая возможности будущих поколений удовлетворять собственные потребности (ООН, 1987 г.).

Практические решения по реализации стратегии устойчивого развития базируются на фундаментальных и прикладных научных исследованиях. Именно наука не только добывает новые знания о мире и его общих законах, но и способна сформулировать так необходимую Человечеству новую стратегию развития и методы ее реализации на основе фундаментальных законов в системе «природа – общество – человек».

И в самом деле: чтобы перейти к устойчивому развитию в системе «природа – общество – человек», нужно досконально изучить, понять и описать все связи между различными областями человеческой деятельности, социальными институтами и природными структурами.

Увидеть и обсудить проблему устойчивого развития во взаимосвязи с другими явлениями и процессами позволяют исследования системного характера. Локальная эффективность отдельных моделей устойчивого развития совершенно недостаточна для утверждения объективного статуса понятия «устойчивое развитие».

Как может быть достигнут этот статус? Адекватный ответ на этот вопрос дает Научная школа устойчивого развития: путем выработки общеобязательного научного метода решения проблемы устойчивого развития на основе общих законов в системе «природа – общество – человек», прежде всего – законов сохранения развития Жизни как космопланетарного явления, за счет чего связываются воедино природные farmacia maschile, общественные и духовные процессы.

Идеология такой модели устойчивого развития принципиально отличается от  других подходов в этой области и требует изменения значительной части наших представлений о мире, ориентируя каждого человека и общество в целом на сохранение развития Жизни в локальном и глобальном масштабах. Для решения именно этой задачи создан Интернет-портал Научной школы устойчивого развития.

Главной целью Научной школы устойчивого развития является такое развитие Человека, которое дает ему возможность выдвигать и воплощать в жизнь Идеи, реализация которых сохраняет рост и развитие жизнеспособности в системе «природа – общество – человек» в долгосрочной перспективе в условиях негативных внешних и внутренних воздействий.

Подробнее о проблеме устойчивого развития:

Условия плавания тел в жидкости — определение, примеры

Сила: что это за величина

Перед тем, как разобраться в процессе плавания тел, нужно понять, что такое сила.

В повседневной жизни мы часто встречаем, как любое тело деформируется (меняет форму или размер), ускоряется или тормозит, падает. В общем, чего только с разными телами в реальной жизни не происходит. Причина любого действия или взаимодействия — ее величество сила.

• Сила — это физическая векторная величина, которая воздействует на данное тело со стороны других тел.

Она измеряется в Ньютонах — единице измерения, которую назвали в честь Исаака Ньютона.

Сила — величина векторная. Это значит, что, помимо модуля, у нее есть направление. От того, куда направлена сила, зависит результат.

Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный. В этом случае результат выражается в направлении движения.

Закон Архимеда

Этот закон известен преимущественно не своей формулировкой, а историей его возникновения.

Легенда гласит, что царь Герон II попросил Архимеда определить, из чистого ли золота сделана его корона, при этом, не причиняя вреда самой короне. 3]

Дальше, согласно легенде, Архимед, озабоченный мыслями о том, как определить объем короны, погрузился в ванну — и вдруг заметил, что уровень воды в ванне поднялся. И тут ученый осознал, что объем его тела вытеснил равный ему объем воды, следовательно, и корона, если ее опустить в заполненный до краев таз, вытеснит из него объем воды, равный ее объему.

Решение задачи было найдено и, согласно самой расхожей версии легенды, ученый закричал «Эврика!» и побежал докладывать о своей победе в царский дворец (по легенде он даже не оделся).

Закон Архимеда

Выталкивающая сила, действующая на тело, погруженное в жидкость, равна по модулю весу вытесненной жидкости и противоположно ему направлена.

На поверхность твердого тела, погруженного в жидкость или газ, действуют силы давления. Эти силы увеличиваются с глубиной погружения, и на нижнюю часть тела будет действовать со стороны жидкости большая сила, чем на верхнюю.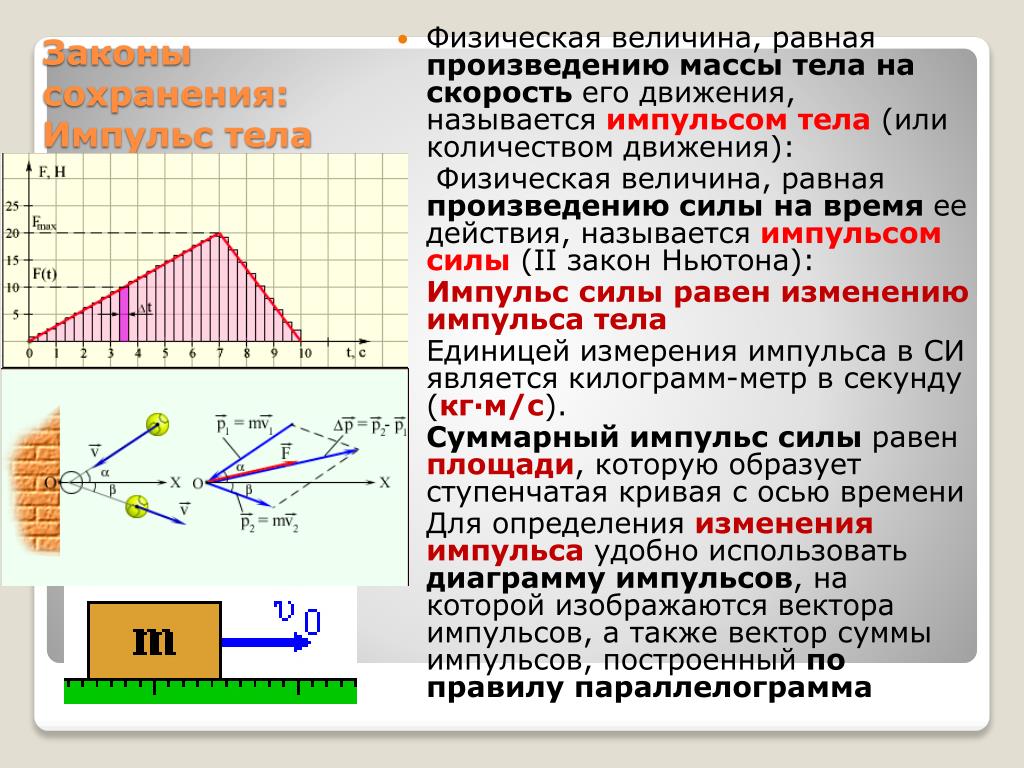 2

А теперь давайте порешаем задачки.

Задача 1

В сосуд погружены три железных шарика равных объемов. Одинаковы ли силы, выталкивающие шарики? (Плотность жидкости вследствие ничтожно малой сжимаемости на любой глубине считать примерно одинаковой).

Решение:

Да, так как объемы одинаковы, а архимедова сила зависит от объема погруженной части тела, а не от глубины.

Задача 2

На поверхности воды плавают бруски из дерева, пробки и льда. Укажите, какой брусок из пробки, а какой изо льда? Какая существует зависимость между плотностью тела и объемом этого тела над водой?

Решение:

Чем меньше плотность тела, тем большая часть его находится над водой. Дерево плотнее пробки, а лед плотнее дерева. Значит изо льда — материал №1, а из пробки — №3.

Задача 3

На графике показана зависимость модуля силы Архимеда FАрх, действующей на медленно погружаемый в жидкость кубик, от глубины погружения x. Длина ребра кубика равна 10 см, его нижнее основание всё время параллельно поверхности жидкости. Определите плотность жидкости. Ускорение свободного падения принять равным 10 м/с2.

Решение:

Сила Архимеда, действующая на кубик равна F_Арх = ρ_ж * g * V_погр

V — объём погруженной части кубика,

ρ — плотность жидкости.

Учитывая, что нижнее основание кубика всё время параллельно поверхности жидкости, можем записать:

F_Арх = ρ_ж * g * V_{погр = ρж * g * a² * x}

а — длина стороны кубика.

Выразим плотность:

ρ = F_Арх / (g * a² * x)

Рассматривая любую точку данного графика, получим:

ρ = F_Арх / (g * a² * x) = 20,25 / (10 * 7,5 * 10^-2) = 2700 кг/м3

Ответ: плотность жидкости равна 2700 кг/м3

Задача 4

В сосуде с водой, не касаясь стенок и дна, плавает деревянный кубик с длиной ребра 20 см. Кубик вынимают из воды, заменяют половину его объёма на материал, плотность которого в 6 раз больше плотности древесины, и помещают получившийся составной кубик обратно в сосуд с водой. На сколько увеличится модуль силы Архимеда, действующей на кубик? (Плотность сосны — 400 кг/м3.)

Решение:

В первом случае кубик плавает в воде, а это значит, что сила тяжести уравновешивается силой Архимеда:

F_Арх1 = mg = ρ_т * g * a³ = 400 * 0,2³ * 10 = 32 Н

После замены части кубика его средняя плотность станет равной

0,5 * 400 + 0,5 * 2400 = 1400 кг/м3

Получившаяся плотность больше плотности воды = 100 кг/м3. Это значит, что во втором случае кубик полностью погрузится в воду. Сила Архимеда в этом случае будет равна:

F_Арх2 = ρ_т * g * V_т = 1000 * 10 * 0,23 = 80 Н

Отсюда получаем, что сила Архимеда увеличится на 48 Н.

Ответ: сила Архимеда увеличится 48 Н

Плавание тел

Из закона Архимеда есть следствия об условиях плавания тел.

Условия плавания тел

Погружение	Плавание внутри жидкости	Плавание на поверхности жидкости
ρж<ρт Если плотность тела больше, чем плотность жидкости или газа, — оно уйдёт на дно	ρж = ρт Если плотности тела и жидкости или газа равны — тело будет находиться в безразличном равновесии в толще жидкости или газа.	ρж>ρт Если плотность тела меньше плотности жидкости или газа — оно будет плавать на поверхности.

Почему корабли не тонут? Корабль сделан из металла, плотность которого больше плотности воды. И, по идее, он должен тонуть. Но дело в том, что корпус корабля заполнен воздухом, поэтому общая плотность судна оказывается меньше плотности воды, и сила Архимеда выталкивает его на поверхность. Если корабль получит пробоину, то пространство внутри заполнится водой — следовательно, общая плотность корабля увеличится. Судно утонет. В подводных лодках есть специальные резервуары, заполняемые водой или сжатым воздухом. Если нужно уйти на глубину — водой, если подняться — сжатым воздухом. Рыбы используют такой же принцип в плавательном пузыре — наполняют его воздухом, чтобы подняться наверх. Человеку, чтобы не утонуть, тоже достаточно набрать в легкие воздух и не двигаться — вода будет выталкивать тело на поверхность. Именно поэтому важно не тратить силы и кислород в легких на панику и борьбу, а расслабиться и позволить физическим законам сделать все за нас.

Physical Law — обзор

1 ЗА ПРЕДЕЛАМИ ЧИСТОГО ФОРМАЛИЗМА: ВАЖНОСТЬ ЭФФЕКТИВНОГО РЕШЕНИЯ МНОГОЭЛЕКТРОННОЙ ЗАДАЧИ (MEP) ДЛЯ НЕСТАБИЛЬНЫХ (ИЛИ НЕСТАЦИОНАРНЫХ, ИЛИ РЕЗОНАНСНЫХ) СОСТОЯНИЙ В БЕЗПОЛЕВЫХ И ПОЛЕВЫХ ЭЛЕКТРОННЫХ СПЕКТРАХ АТОМЫ И МОЛЕКУЛЫ

… Таким образом, основные физические законы, необходимые для математической теории большей части физики и всей химии, полностью известны, и трудность состоит только в том, что точное применение этих законов приводит к слишком сложным уравнениям. быть растворимым.

PAM Dirac, 1929 [1]

Трудность, на которую Дирак [1] ​​ссылается в приведенной выше хорошо известной цитате, интерпретируется здесь следующим образом: Что касается физики атомов и молекул, преимущества теории должны выходить за рамки чисто формализм и феноменология и должны допускать две вещи: во-первых, возможность систематического вычисления, исходя из первых принципов, физически значимых величин с достаточной точностью по сравнению с измерением. Во-вторых, возможность применения общеприменимых концепций и облегчения перехода от более простого в вычислительном отношении к более сложному без ненужных скидок на требуемую квантовую механику (КМ) для полиэлектронных состояний.

Тема этой главы сосредоточена на возможности объединения практическим и экономическим способом существенных концептуальных и формальных элементов описания нестабильных состояний (также называемых здесь нестационарными , распадающимися или резонансных состояний ) в атомах и молекулах, с вычислительными методологиями, которые решают многоэлектронную задачу (MEP) для различных электронных структур, особенно возбужденных атомов.

Эти состояния образуются внутри непрерывных спектров полного гамильтониана и ответственны за такие явления, как резонансы в рассеянии электронов на атомах или молекулах, автоионизация , предиссоциация и т. Д. Кроме того, в этой работе мы также рассматриваем как нестабильные состояния те состояния, которые состояния, которые являются конструкциями независимой от времени теории взаимодействия атома (молекулы) с внешним полем, которое является либо статическим, либо периодическим, и в этом случае эффект взаимодействия получается как среднее значение за цикл. В этих рамках состояние «атом + поле» находится внутри непрерывного (ионизация или диссоциация) спектра, и поэтому некоторые особенности проблемы напоминают особенности нестабильных состояний бесполевого гамильтониана. Вероятность распада этих индуцированных полем нестабильных состояний соответствует либо туннелированию, либо ионизации-диссоциации за счет поглощения одного или нескольких фотонов.

Концептуальная схема рассмотрения индуцированных полем резонансов работы, обсуждаемая в этой статье, следует из той, которая оказалась полезной для решения MEP для бесполевых резонансов .Поэтому в следующих разделах упор делается на бесполевой случай. Соответствующий формализм и вычислительная методология составляют основу теории и расчета индуцированных полем резонансов, которые обсуждаются в разделе 11.

В статье синтезируются новый материал и комментарии с избранными опубликованными теоретическими и численными результатами автора и соавторов. назад в 1972 год [11a]. Поскольку существует центральная тема, которая пронизывает формализмы и приложения этой работы, ее структура получила общее название: подход, ориентированный на состояние, (SSA) [9, 10].Согласно SSA, критически важным для развития формализма, который является как физически полезным, так и вычислительно практичным, является, во-первых, выбор подходящей для каждой задачи формы пробных волновых функций, а во-вторых, возможность использования соответствующих функциональных пространств, которые конкретные и оптимальные по возможности для государства и интересующего имущества. Отличительной особенностью SSA является то, что он делает прозрачным взаимодействие между электронной структурой и динамикой.

Структуры, используемые в SSA в настоящей статье, зависят от энергии или времени и используют методы, которые на практике решают соответствующие уравнения Шредингера непертурбативно.Применялись как эрмитов, так и неэрмитов формализмы с использованием кулоновских или релятивистских гамильтонианов Брейта-Паули. В основе анализа и обсуждаемых методов лежит постоянный учет того факта, что форма каждой резонансной волновой функции равна _r = a ₀ + X _as (уравнение 1). При необходимости расширение на многомерные формы очевидно. В зависимости от формализма коэффициент a и «асимптотическая» часть, X _как , являются функциями либо энергии (действительной или комплексной), либо времени.Многотельный, интегрируемый в квадрате, Ψ ₀ , представляет собой локализованную часть распадающегося (нестабильного) состояния, т. Е. Нестабильный волновой пакет, который предполагается приготовить при t = 0. Его энергия E ₀ , является реальным и встроенным в непрерывный спектр. Это минимум среднего значения соответствующего эффективного гамильтониана, зависящего от состояния, который удерживает все частицы связанными.

Когда принят эрмитов формализм реальной энергии, смешение компонент связанного рассеяния в случае бесполевых резонансов вычисляется с помощью многоканального (в общем) формализма K-матрицы с замороженным ядром, зависимым от члена, нормированные по энергии орбитали хартри-фоковского (HF) рассеяния в качестве базисных наборов для непрерывного спектра. С другой стороны, следуя нашей работе 1970-х и начала 80-х годов, показано, что, начиная с эрмитовского формализма Фано 1961 г. [29], который строго учитывает перемешивание дискретного континуума, когда соответствующие граничные условия формально накладываются на решение задачи Уравнение Шредингера в окрестности двух смежных комплексных собственных значений уравнений Шредингера (CESE) возникают естественным образом, собственные функции которых имеют двухкомпонентную форму , в то время как их собственные значения комплексно сопряжены.Физически приемлемым решением для затухающего состояния ,, является решение с граничным условием уходящей волны, для которого комплексная энергия составляет z _r = E _r — (i / 2) Γ. Методы были разработаны и применены для непертурбативного решения соответствующего состояния CESE как для бесполевого, так и для индуцированного полем случая в рамках неэрмитовых формализмов с оптимизированными суперпозициями действительных и комплексных функций действительных или комплексных координат. .

Наконец, что касается темы необратимого распада, обсуждение вкратце рассматривает аспекты актуальности трех временных областей: 1) Режим экспоненциального распада (ED), exp (- Γt ), который является режимом, определяющим резонансное состояние на энергетической оси с точки зрения его энергии, E _r , и его ширины, Γ. 2) режим предварительного ED, который определяет степень устойчивости a (t) Ψ ₀ при взаимодействии с X _as ( t ), и 3) режим не -ED, который запускается после продолжительности (обычно) многих жизней в режиме ED.

1.1 Необходимость сочетать прозрачную теорию нестабильных состояний с практическими вычислительными методами для решения МЭП в атомах и молекулах

Хорошо известно, что очень простые системы или простые модели полиэлектронных систем очень часто являются основой для разнообразных теоретических подходов, от феноменологии до количественных ответов. Для требований некоторых задач таких приближений может быть достаточно. Однако, независимо от того, насколько приятна визуализация и вычислительные возможности простых моделей, факт в том, что атомы и молекулы не являются, скажем, одномерными системами из учебника, и их свойства не могут быть поняты путем простого изучения только низколежащих состояний, скажем, одно- или двухэлектронные системы.В конце концов, теоретическая работа (и, конечно же, экспериментальная!) Должна иметь дело с реальными системами произвольной структуры и иметь дело с вездесущими MEP. Любой формализм, каким бы строгим и подробным он ни казался, базовая структура которого не облегчает вычислительное решение различных MEP, включающих резонансные состояния, ограничен либо описательной феноменологией (которая, конечно, полезна, когда это необходимо), либо специальной простые случаи, когда расчет становится возможным.

Парадигма такого ограничения — это парадигма, касающаяся строгого применения широко цитируемого формализма Фешбаха, который объясняет образование и эффекты резонансов в ядерных реакциях [2]. Точная реализация этого формализма в отношении использования правильно определенных операторов проекции к резонансным состояниям атомных систем была впервые продемонстрирована в 1965 году О. Малли и Гельтманом [3a], хотя и только для некоторых низколежащих резонансных состояний двух -электронные атомы. В статьях, которые последовали в этом направлении для двухэлектронных систем, исследовались аспекты высокой точности вычислений, например.г., исх. [3b]. Однако, как указывали авторы этих работ в 1960-х и начале 1970-х годов, эта основанная на теории процедура действительна и практична только для двухэлектронных систем, поскольку там состояния мишени точно известны, а свойства проекционных операторов равны строго выполнено, а вычислительный алгоритм соответствует формализму. Чтобы обойти внутренние требования формализма рассеяния Фешбаха в отношении его распространения на системы с более чем двумя электронами, в 1980-х годах были предложены модификации в терминах «квазипроекционных операторов», которые применялись к нижним резонансам из трех -электрон He ^— и Li [4]. Через несколько лет после публикаций Темкина и Бхатиа [4a], Bylicki [5] проник в существенные теоретические аспекты этой проблемы в сочетании с систематическими вычислениями трехэлектронных резонансов He. Например, он обратил внимание на выбор условий орбитальной ортогональности при определении операторов проекции на открытые и закрытые каналы — практическое приближение, берущее начало, как указывал Былицкий, в полиэлектронной теории [5]. [11]. В любом случае, независимо от того, как выбираются «квази» операторы Фешбаха, огромные трудности электронной структуры и МЭП, которые сопровождают методы «проекции Фешбаха и квазипроецирования», остаются [3–5].Следовательно, прямая реализация формализма Фешбаха (P, Q) для высокоуровневых вычислительных целей, которая была продемонстрирована в низколежащих резонансных состояниях двухэлектронных систем, столкнулась с практическими, а также фундаментальными трудностями, когда дело доходит до резонанса. (автоионизирующие) состояния атомов различных типов и энергий и любого количества электронов.

Чтобы под другим углом подчеркнуть аргумент о вычислении, предположим, что рассматривается один из строгих результатов теории рассеяния [6, 7], а именно, что изолированные резонансы в сечениях рассеяния соответствуют простым комплексным полюсам (в общем, многоканальность) S-матрица.Эти сложные полюса определяют комплексные энергии, при которых уравнение Шредингера имеет решения без входящих волн и только с исходящими волнами во всех каналах, результат, который был явным в трактовке Зигертом s-волнового рассеяния с помощью короткодействующего потенциала [8a] .

Что ж, хотя общие формулы теории рассеяния существуют, спустя много десятилетий после установления формализма у человека есть право задавать такие вопросы, как: каково физическое происхождение комплексных полюсов S-матрицы, представляющих резонансные состояния, и как это отражается на построении S-матрицы из первых принципов? диапазон энергий и для различных симметрий? Ответ, данный любым, кто знаком с этой областью, не будет обнадеживающим даже для изолированных состояний, которые являются основным объектом формального обсуждения в этой главе. Например, электронные структуры резонансных состояний, соответствующих сложным полюсам, которые должны быть обнаружены при таком расчете типа рассеяния, могут значительно отличаться от состояния к состоянию. Кроме того, реальная и мнимая части каждого полюса могут отличаться на порядки. К тому же возможное наличие псевдорезонансов усложняет ситуацию.

На самом деле все становится намного сложнее, когда дело доходит до ab initio вычисления соседних резонансов, некоторые из которых могут перекрываться.Например, так обстоит дело со спектрами резонансных состояний H ^— для различных симметрий, что является предметом раздела 7.2.

Неизбежный вывод, который следует из рассмотрения вышеизложенного, состоит в том, что, даже если бы все детали формализма и техники электронной структуры были поняты на практике, надежные вычисления S-матрицы и ее сложных полюсов, представляющих резонансные состояния, были бы быть в вычислительном отношении чрезвычайно требовательным, если не невозможным, даже с современными компьютерами, по крайней мере, если бы к проблемам подходили так же, как до сих пор проводились вычисления процессов рассеяния.

1.2 Формализм и полиэлектронные методы в рамках подхода, ориентированного на состояние. нестабильные состояния в целом и, в частности, состояния, которые обычно представлены многочастичными волновыми функциями, такими как те, которые обнаруживаются в спектрах атомов и малых молекул. С другой стороны, обсуждение направлено на демонстрацию того, почему и как можно решать, из первых принципов и с многоэлектронной точки зрения, большое количество проблем, связанных с бесполевыми и индуцированными полем нестабильными состояниями. состояния, для которых в принципе возможны надежные расчеты электронной структуры.

Обсуждаются только определенные вопросы, которые считаются основными для целей обзора и понимания теории и вычислительной методологии, в рамках, которые включают как энергозависимый, так и зависящий от времени анализ и методы. Конечно, дополнительную информацию по формальному анализу (некоторые из которых не благоприятствуют вычислительным возможностям), о различных теориях и их реализации, о вычислениях и моделях можно найти в многочисленных публикациях, посвященных огромной теме резонансных состояний. Надеемся, что многие из них читатель сможет найти, изучив главы этого тома.

Что касается расчета и необходимости эффективного решения MEP для большого количества случаев, как обсуждаемый здесь формализм, так и соответствующая вычислительная методология были разработаны на основе следующего утверждения: особенно для возбужденных состояний критически важно использовать специфические для состояния формы пробных волновых функций, для анализа происхождения и вклада различных основных частей, для представления их различными функциональными пространствами, которые отражают их различные типы вклада в физику каждой проблемы, и для оптимизации этих функций с помощью подходящих процедур. .По этой причине соответствующие формализмы и методологии были в совокупности названы подходом, специфичным для состояния , например, Refs. [9, 10].

Различные анализы, примеры и приложения SSA, представленные в следующих разделах, показывают, как можно получить надежные волновые функции нестабильных состояний. Они имеют форму, которая является прозрачной и пригодной для использования независимо от того, описывают ли они бесполевые или индуцированные полем системы возбужденных состояний, скажем, из 2, 15 или 30 электронов, и от того, имеется ли один или несколько открытых каналов.Таким образом могут быть (и действительно были) получены дополнительные свойства и хорошее понимание взаимодействия между структурой и динамикой. Обсуждение вместе с соответствующими ссылками объясняет, как SSA сформировал основу для формальной и вычислительной обработки — непертурбативно — множества прототипных проблем, включающих бесполевых , а также индуцированных полем резонансных состояний в атомы и в малых молекулах.

Молекулярные приложения до сих пор включали расчет электронной структуры и поверхностей потенциальной энергии «составных состояний» отрицательных ионов и «диабатических состояний» в непрерывном спектре полиэлектронной диатомики и триатомики, а также энергий и парциальных ширин с межканальным взаимодействием колебательная форма и предиссоциативных резонансов диатомовых водорослей. Те же принципы и методики можно применить ко многим другим подобным случаям.

Несколько слов о случае, индуцированном полем: он касается проблем, в которых гамильтониан включает не зависящее от времени или усредненное по времени (по циклу) взаимодействие атомных или молекулярных основных или возбужденных состояний с сильными статическими и переменными полями, где теории возмущений низкого порядка недостаточно. Следуя структуре распада состояния с комплексным собственным значением , которое использовалось (используется) для бесполевого случая, эти проблемы формулируются как индуцированные полем резонансные состояния, где взаимодействие смешивает бесполевые состояния, представленные функциональными пространствами с действительными координатами, с непрерывным спектром, где свободный электрон (ы) представлен орбиталями комплексных координат (раздел 11).Практическая, неэрмитовская методология комплексной энергии была разработана и применена для непертурбативного вычисления таких величин, как скорости многофотонной ионизации и сверхпороговой ионизации, двойной ионизации с корреляцией электронных пар на пороге, ионизации, индуцированной постоянным полем и гиперполяризуемости, индуцированные полем сдвиги и ширины дважды возбужденных состояний (ДЭС), управление ионизацией ди- или трихроматическими полями. Кроме того, упоминается также тот факт, что проблема взаимодействия атома с сильным полем также решалась в терминах теории возмущений большого порядка с комплексными энергиями , где при вычислении членов используются функциональные пространства, которые могут быть специфический.

Я завершаю это введение двумя комментариями:

(1)

Аспекты содержания этой главы помещены в исторический контекст и дополнены соответствующими ссылками. Такая хронологическая перспектива всегда улучшает понимание важности внедрения новых подходов и методов. Например, до начала 1970-х годов в опубликованных методах типа связанных состояний для аппроксимации волновых функций резонансного состояния использовались отдельные наборы связанных орбиталей (см. Раздел 2 и ссылки на него).В то же время не было известно, правомерно и / или возможно ли непосредственно решать уравнения HF для сложных структур возбужденного состояния с открытыми (подобластями) оболочек, которые находятся в непрерывном спектре. Возможность нахождения таких физически значимых HF-решений была впервые продемонстрирована в [5]. [11], где были вычислены действительные зависящие от состояния ВЧ волновые функции для прототипного трижды возбужденного He ^— «2s ² 2p» ² p ^o и «2s2p ² » ² D резонансных состояний, в соответствии с орбитальными ограничениями ортогональности и асимптотического поведения и удовлетворением теоремы вириала , которая в сочетании с вычислительным опытом обеспечивает надлежащую сходимость вариационных вычислений.Как только такие ВЧ-волновые функции получены (в настоящее время это делается систематически, особенно с точки зрения решения численных многоконфигурационных ВЧ-уравнений (MCHF) для конкретных состояний), вычисление электронной корреляции и многоканального континуума включает в себя реализацию передовых, но практические методы и использование различных функциональных пространств (см. последующие разделы в этой главе).

(2)

Численные результаты и пояснительный характер частей следующих разделов, касающихся понимания и систематического многоэлектронного рассмотрения резонансов, дают читателю возможность оценить преимущества, ограничения и недостатки не только SSA, но и других методов, на которые делается ссылка.Это должно быть полезно в текущих исследованиях по множеству тем, касающихся полиэлектронных атомов и молекул. Например, обсуждение прямого вычисления специфичного для состояния локализованного компонента резонансных состояний, Ψ ₀ , объясняет, как такие волновые функции могут быть сразу же практическими для использования в подходе расширения для конкретных состояний (SSEA), который был введен как общий метод непертурбативного решения нестационарного уравнения Шредингера (TDSE) (см. главу 6).

Физические законы, философские аспекты | Encyclopedia.com

Рассматривая законы физики, эта статья представляет собой исторический обзор понимания человечества природы и существования этих законов, а также критику различных философских позиций, касающихся их.

Представление о том, что природа регулируется физическими законами в своих свойствах и действиях, получило четкую формулировку только в современной науке, но коренится в представлениях, которые постепенно формировались на основе человеческого опыта.Анимистический взгляд на природу, которого придерживались первобытные народы посредством размышлений и наблюдений, уступил место рациональному и философскому понятию физической реальности и природных явлений как регулярного соединения причин и следствий. Этой рационализации концепции природы способствовали астрономические наблюдения за движением звезд и развитие технических искусств, включая создание инструментов и машин, которые воплощают основные приложения математики.В этих достижениях уже можно обнаружить предзнаменование законов физики в современном смысле этого слова.

Исторический обзор. Математическая концепция природы вошла в философию с Пифагором и пифагорейцами, а также с Платоном, который учил, что Бог действует как геометрический в мире. Для Аристотеля существование физических законов имеет более прочную основу в его концепции природы как активного принципа движения и покоя в телах. Более того, Аристотель отличает небесные события от земных: первые регулируются абсолютно необходимыми законами, не допускающими никаких исключений, вторые — хотя и подчиняются определенным законам природы, а не просто случайности — допускают исключения и тем самым оставляют место для случайные события ( Phys. 192b 20–23, 195b 31–198a 13).

После Аристотеля философия — и схоластическая философия в частности — сохранили и развили аристотелевскую концепцию природы, подтверждая ее философский анализ концепцией мира, предложенной в Библии. Священное Писание описывает вселенную как дело мудрости и всемогущества Бога-Создателя, Который все распоряжается «мерой, числом и весом» (Премудрость 11.20). Согласно Св. Томасу Аквинскому, «поскольку все вещи, подчиненные божественной власти, управляются и измеряются … очевидно, что все вещи каким-то образом причастны к вечному закону, а именно, поскольку, будучи наложенным на них, они имеют склонность к их собственные действия и цели…. И это участие вечного закона в разумном существе называется естественным законом…. Однако в иррациональном существе [вечный закон] не разделяется рациональным образом; поэтому его нельзя назвать законом, кроме как посредством подобия »( Summa theologiae 1a2ae, 91.2 и 3). Таким образом, все создания имеют от своего Создателя определенные естественные склонности к своим собственным целям,« которые мы говорим естественными законов »( In Dion de div. nom., 10.1).

Таким образом, уже в античной и средневековой мысли четко сформулирована закономерность физической природы, и основоположники современной науки, особенно Галилей и Исаак Ньютон, были ясно осознавая преемственность своей мысли с предшествующей философской традицией.

Онтологическое значение законов. Следовательно, не только в аристотелевской и схоластической философии, но и для основоположников современной науки физический закон имеет онтологическое значение. Регулярная и постоянная связь в последовательности физических явлений, выраженная математической функцией, связывающей экспериментальные переменные определенным образом, в свою очередь, является выражением онтологической необходимости, основанной на самой природе физических агентов, которая возникает из директивная воля и божественная мудрость Творца.Более того, эта концепция, даже очищенная от ее метафизических и теологических коннотаций, оставалась доминирующей в современной физической науке до XIX века. Классический позитивизм А. Конта однозначно признавал реализм физических законов, которые он считал догматически универсальными фактами, не менее достоверно проверяемыми, чем единичные факты [ Cours de Философия позитивного (Париж 1930) Урок 1]. Подобную реалистическую концепцию отстаивает современный диалектический материализм, который, согласно учению К.Маркс и Ф. Энгельс, считают, что научное знание ассимилируется как пассивное представление и верное зеркало реальности (см. материализм, диалектический и исторический).

Эмпиризм и критика. Этой объективной и рационалистической концепции физических законов противопоставляется эмпиризм, особенно в крайней форме, предложенной Д. Юмом. Согласно Юму, необходимость явлений, выраженных в физическом законе, является чем-то чисто субъективным, просто психологическим ожиданием, возникающим в результате ряда постоянных связей, наблюдаемых в прошлом ( Трактат о человеческой природе, 1.3.6). Желая спасти необходимость физических законов, скомпрометированных скептическим эмпиризмом Юма, И. Кант прибегнул к синтетическим априорным суждениям. Для него закон — это применение ментальной категории к явлениям, уже упорядоченным в репрезентации через субъективные формы пространства и времени. С точки зрения Канта, закон действителен для феноменального мира, но не может быть признан действительным для самой реальности ( Критика чистого разума, Анализ принципов).

Мотивы, вызвавшие критику Юма и Канта, сливаются в конце XIX века в эмпириокритицизме Э.Мах. Это превращает мир восприятия в чистые ощущения и, следовательно, естественные науки в простой анализ ощущений. Для Маха физические законы не обязательно действуют в действительности, поскольку это предполагает неопровержимый постулат регулярности в природе. Это просто ограничение, которое субъект накладывает на себя, предвосхищая будущие ощущения, ради экономии и как средство функциональной адаптации в борьбе за жизнь ( Analyze der Empfindungen, Jena 1900).

Условность. Очень близок к этой концепции конвенционализм Дж. Х. Пуанкаре, для которого общие принципы — как математики, так и физики — являются свободными условностями или замаскированными определениями, принятыми в качестве критериев научного удобства, т. Е. Из-за их простоты и логической последовательности ( La Science et l’hypothèse, , Париж, 1902 г.). Конвенционализм Пуанкаре был вдохновлен не столько философскими предрассудками, сколько эволюцией математики и физики в XIX веке, которая показала, что многие законы и принципы, которые классическая наука и позитивизм считали необходимыми и вечными, должны быть пересмотрены и пересмотрены. заменены другими принципами и законами, более соответствующими экспериментальным фактам.Отсюда легко было заключить, что принципы и физические законы не являются абсолютно навязанными опытом и не выражают объективных отношений или причин явлений, но постулируются ученым как подходящие условности и как приблизительные и предварительные выражения. Следовательно, физические законы становятся просто алгебраическими соотношениями, связывающими числа, полученные в результате экспериментального измерения; такие отношения могут быть аппроксимированы бесконечным числом способов математическими функциями, из которых простейшие отношения выбраны только для удобства и экономии.

Неопозитивизм. Неопозитивизм Винер Крайс, Рудольф Карнап и Отто Нейрат подхватили учение Юма и Маха, устранив его психологические элементы и сведя эмпиризм к простому номинализму. Для логического позитивизма единственными значимыми предложениями являются «протокольные утверждения», которые констатируют экспериментально проверяемый факт; физические законы, провозглашенные универсалиями, не могут быть проверены. Скорее, по своей абстрактности они даже не являются полными предложениями, а только пропозициональными функциями, содержащими неопределенные переменные, в которые можно подставить определенные и конкретные значения.Таким образом, для логических позитивистов универсальный закон трансформируется в протокольное высказывание [J. Йоргенсен, Развитие логического эмпиризма (Чикаго, 1951) 30].

Критический реализм. Субъективистская концепция физических законов широко распространена в современной мысли и принимается даже философами-неохоластами, такими как Дж. Маритен и Ф. Ренуар, которые считают ее законным очищением наук от философских и метафизических элементов. Тем не менее, многие ученые и философы защищают онтологическую ценность физических законов своего рода критическим реализмом, который прокладывает средний путь между противоположными крайностями.Среди них в первую очередь следует упомянуть основоположников современной физики, а именно Макса Планка и Альберта Эйнштейна. Критический реализм придает эмпирику и субъективистским взглядам заслугу борьбы с преувеличенным реализмом платоновского или механистического типа, который доминировал в классической физике. Таким образом, он признает существенную активность разума в формулировании научных законов, которые обязательно содержат субъективные, приблизительные и предварительные элементы. В то же время, однако, он допускает способность человеческого мышления познавать материальную реальность в себе и проникать в ее сущность через наблюдаемые явления и научные рассуждения.

Однородность. Онтологическая ценность физических законов может быть подтверждена критической теорией познания в целом, а затем усилена рассмотрением практической ценности самой науки. Если на самом деле физические законы лишены всякой онтологической ценности, способность предсказывать явления на основе физических законов и практическая ценность науки в технических приложениях будут лишь случайными и случайными совпадениями, как заметил даже Пуанкаре, выступая против экстремистской интерпретации, данной Э.Ле Руа к своему учению [Х. Пуанкаре, La Valeur de la science (Париж 1905 г.) 220]. Следовательно, следует признать, что постоянная и единообразная закономерность, наблюдаемая в опыте и утверждаемая в физических законах, имеет онтологическую основу в природе физических агентов. Эта природа не зависит от человеческого знания и предшествует самому действию. Таким образом, физический закон объективно, in act primo, как причинный предшественник регулируемой им деятельности, еще до того, как был открыт и сформулирован учеными, еще до появления человека на Земле.Таким образом, принципы единообразия в природе или онтологического детерминизма физических агентов предлагают онтологическую основу и рациональное объяснение физических законов.

Детерминизм. Онтологический детерминизм физических агентов, или принцип детерминированной причинности, является необходимой предпосылкой для формулировки физических законов, а также онтологической основой для научной индукции. Как таковое, оно не может быть результатом этого типа индукции, но должно рассматриваться как применение самоочевидного принципа достаточной причины, согласно которому все существующее или происходящее имеет причину для выхода или возникновения.Если бы физический агент, лишенный знания и выбора, по своей природе не был бы определен к одному действию, а не к другому, он был бы безразличен к любому действию и, следовательно, не действовал бы (St. Thomas, C. gen. 3.2) . Однако даже в том, что касается физического детерминизма, современная физика смягчила жесткость, на которую претендовала классическая физика. Этот детерминизм уже не абсолютный, а относительный. Таким образом, с метафизической точки зрения, можно отвергнуть незаконную экстраполяцию детерминизма из физического мира на человеческую волю и, тем более, на божественную волю.С физической точки зрения открытие статистических законов и квантового индетерминизма показало ценность концепции природы, подобной концепции Аристотеля. Увидев детерминизм и необходимость как проистекающие из формы, он признает существование неопределенности и потенциальности, возникающих из материи, и допускает существование случайных событий как исключений из естественного закона.

См. Также: закон; естественное право; индетерминизм; механизм.

Библиография: ф.selvaggi, Filosofia delle scienze (Рим, 1953 г.). f. Renoirte, Космология: элементы критики наук и космологии, tr j. f. Коффи (Нью-Йорк, 1950). м. bunge, Metascaught Queries (Спрингфилд, Иллинойс, 1959). е. simard, La Nature et la portée de la méthode scientifique (Quebec 1956). а. грамм. м. ван Мелсен, Наука и технологии (Питтсбург, 1961 г.). р. б. Линдси и Х. margenau, Основы физики (Нью-Йорк, 1936 г.).j. de vries, «Das Problem der Naturgesetzlichkeit bei Thomas von Aquin», Scholastik 10–24 (1949) 503–517.

[ф. selvaggi]

6 Каковы пределы физического закона? | Связь кварков с космосом: одиннадцать научных вопросов для нового века

энергии, сравнимой с энергией удачного бейсбольного мяча; возможно, ученые видят доказательства существования совершенно новых форм материи. Также могут быть созданы нейтрино очень высоких энергий, некоторые из которых могут быть произведены струями, и эксперименты находятся на пороге возможности их обнаружения.

Наконец, наиболее проницающими сигналами из всех являются гравитационные волны, впервые предсказанные Эйнштейном в 1918 году (см. Вставку 6.4). Ученые знают, что эти волны действительно существуют, потому что энергия, которую они уносят в космос, влияет на орбиты двойных пульсаров способом, который хорошо согласуется с прецизионными измерениями наблюдаемых систем двойных пульсаров. Однако напрямую они пока не обнаружены. Наиболее многообещающие источники гравитационных волн, которые связаны со столкновениями и слияниями больших черных дыр, даже более ярки, чем гамма-всплески.

НОВЫЕ ВЫЗОВЫ В ЭКСТРЕМАЛЬНОЙ АСТРОФИЗИКЕ

Четыре проблемные области, взятые из интерфейса физики и астрономии, готовы к согласованной атаке.

Черные дыры и сильная гравитация

Теория гравитации Исаака Ньютона была заменена общей теорией относительности Альберта Эйнштейна, которая широко считается «истинной» теорией гравитации до тех пор, пока квантово-механические поправки не важны.Тонкие различия между теориями Ньютона и Эйнштейна были проверены в Солнечной системе путем наблюдения за движением Луны, планет и света. Пока общая теория относительности прошла все тесты с количественной точностью, которая в некоторых случаях превышает 1 часть из 1000. За пределами Солнечной системы первый двойной пульсар PSR1913 + 16 стал испытанием в более сильных полях. Контролируя время прихода регулярных радиоимпульсов от этого источника, можно было измерить орбитальный распад, вызванный потерями мощности, когда две вращающиеся нейтронные звезды излучали гравитационное излучение.Теория и наблюдения согласуются в пределах примерно 3 частей на 1000. Проверка общей теории относительности была настолько значимой, что немногие ученые сомневаются в ее применимости в исследуемых режимах.

Однако и в солнечной системе, и в испытаниях пульсаров гравитация все еще относительно слаба в том смысле, что характерные скорости тел меньше примерно одной тысячной скорости света. Поэтому критический предел теории, согласно которой объекты движутся со скоростями, близкими к свету, еще не испытан.Это основной принцип физики: если физический закон действительно понят и был проверен с очень высокой точностью хотя бы в одном месте, он должен быть

.

13,7: Космос и культура: NPR

Сундарбанс, мангровый лес на краю Бенгальского залива, простирается на юго-западе Бангладеш и юго-востоке Индии. НАСА скрыть подпись

переключить подпись НАСА

Мы, люди, непослушная группа.Настолько, что нам нужны законы для поддержания порядка, чтобы мы не сбились с пути. Без наших законов общество быстро погрузилось бы в хаос. Человеческие законы — гаранты порядка, необходимый контроль против присущей нашему виду жадности.

Природа, с другой стороны, показывает упорядоченные узоры во всех масштабах: деревья разветвляются, а также реки, тела и артерии; приливы и орбиты планет периодические, день сменяет ночь, времена года меняются, у Луны есть фазы. Проявление порядка в Природе позволяло проводить методический подсчет и организацию как средство достижения определенного уровня контроля над тем, что в противном случае было бы далеким и недоступным, марширующими моделями мира, движущимися путями, недоступными для человека.

Законы природы, от самых простых до самых сложных, — это попытки обобщить это широко распространенное проявление порядка. Они открываются в результате многократных наблюдений и часто допускают краткое математическое выражение. Иногда законы выводятся из математики, как если бы мы могли разгадывать секретные закономерности Природы. Физики любят говорить, что простейшие законы с наибольшей объяснительной силой являются наиболее элегантными и красивыми. Любимый пример — закон сохранения энергии (или, еще лучше, энергии и количества движения), или электрического заряда: при каждом взаимодействии между телами материи полная энергия одинакова до и после, а общий электрический заряд то же самое до и после.Даже если эти законы являются приближениями (как и любые физические законы), в том смысле, что они являются результатами измерений с конечной точностью, мы еще не видели никаких признаков отклонения.

Законы природы сильно отличаются от законов человека. В то время как законы человека стремятся упорядочить и контролировать индивидуальное и социальное поведение, чтобы сделать совместную жизнь менее рискованной, законы природы выводятся из длительного наблюдения повторяющихся закономерностей и тенденций. В то время как законы человека могут варьироваться от культуры к культуре, поскольку они основаны на моральных ценностях, которым не хватает универсальных стандартов, законы природы нацелены на универсальность, на выявление поведения, которое является истинным — в том смысле, что оно поддается проверке — во времени и пространстве. .Таким образом, хотя некоторые культурные тенденции, принятые в одной группе, могут показаться другим варварскими (например, женское обрезание), звезды во Вселенной горят по одним и тем же правилам с тех пор, как впервые появились примерно через 200 миллионов лет после Большого взрыва. . Точно так же, хотя в некоторых странах смертная казнь отвратительна, а в других она применяется с почти фанатичным энтузиазмом, атомы и молекулы на триллионах планет и лун в этой и других галактиках объединяются и рекомбинируются в химических реакциях, которые следуют образцам порядка, основанным на хорошем -определенные законы сохранения и притяжения и отталкивания.

Разнообразие человеческих законов показывает, что мы мало знаем о себе и о том, что является или должно быть поистине универсальными моральными стандартами. С другой стороны, очевидная уверенность в законах природы, кажется, придает чувство доверия и окончательности законам природы, которые вдохновили многие движения использовать их в качестве основы для всех законов, включая законы человека. Просвещение, конечно, хорошо известный пример. К счастью, квантовая революция начала двадцатого века быстро показала, что самонадеянность детерминизма часового механизма сильно преувеличена; во Вселенной существует неопределенность, и любая надежда превратить физику в оракул обречена на провал.

Учитывая этот несколько новый образ мышления, необходимо рассмотреть вопрос, который задают некоторые люди, такие как физик Ли Смолин и философ из Гарварда Роберто Мангабейра Унгер, — могут ли измениться законы природы. (На его веб-сайте можно найти сокровищницу произведений и размышлений Унгера.) В конце концов, законы человека, безусловно, меняются по мере того, как конституции изменяются, пересматриваются и интерпретируются судами по всей планете. Могли ли в прошлом законы природы быть другими? Могут ли они измениться в будущем?

Мы не знаем ответа на этот вопрос; ради нас самих, мы надеемся, что если они это сделают, то это произойдет только в очень далеком будущем.Нарушение законов природы спровоцирует ужаснейшее разрушение организованных материальных структур, от галактик до людей. К счастью, у нас есть основания чувствовать себя в безопасности.

Мы знаем, что если законы природы действительно меняются, то этого не происходило очень давно. Вселенная развивалась по аналогичным законам, по крайней мере, через несколько секунд после Большого взрыва до сегодняшнего дня, то есть в течение последних 13,7 миллиардов лет (или около того). Возможно, что законы были другими сразу после Большого взрыва или даже до Большого взрыва, в другом цикле существования, но это было тогда.

Размышление о том, могут ли изменяться законы природы, — достойный предмет естественной философии, и я расскажу об этом в другой раз более подробно. Между тем, мы можем продолжать изучать довольно устойчивые законы Природы в том виде, в котором они действуют сейчас, прилагая при этом дополнительные усилия для развития более высоких моральных стандартов для нашего вида.

Вы можете быть в курсе того, о чем думает Марсело, в Facebook и Twitter: @mgleiser

Детерминизм, физическая возможность и законы природы

Предположим теперь, что предположения (1) — (4) верны для теории T с дифференциальным уравнением E , а (5) — нет.Тогда из формулировки (A) полученного представления и из определения (D) следует, что T не является детерминированным. Существует ли учет законов природы, который в сочетании с формулировкой (B) полученного взгляда делает T детерминированным согласно (D)?

Набор физически возможных миров формулировки (A) представляет собой объединение набора решений E , которые являются детерминированными, и набора решений E , которые не являются детерминированными. Для достижения детерминизма набор физически возможных миров формулировки (B) должен быть уже: он может содержать все детерминированные решения, но не может содержать более одного решения из любого из « букетов недетерминизма » (из любого из наборы решений E , согласующиеся в некоторых своих состояниях).Таким образом, мы ищем объяснение закона природы, которое венчает E как представление закона возможных миров, представленных детерминированными решениями, но которое венчает E как представление закона не более чем одного из возможных миры, которые представлены решениями в букете недетерминизма.

Какие свойства могут отличать детерминированные решения от недетерминированных? Ясно следующее различие: для детерминированных решений E максимально информативен в том смысле, что будучи дополненным состоянием, он предоставляет все не-номические факты. E , однако, не является максимально информативным в этом смысле для недетерминированного решения, и на самом деле может довольно плохо сузить набор не-номических фактов, которые могут быть получены. Эта разница в информативности E для детерминированных и недетерминированных решений сигнализирует о том, что некоторый вариант учета законов Лучших Систем может помочь нам.

Учет законов, который использует разницу в информативности E между детерминированными и недетерминированными решениями, может помочь обеспечить детерминизм теории.Предположим, что s является недетерминированным решением E : хотя s удовлетворяет E , E не обязательно является законом мира, представленным s , потому что может быть альтернативное утверждение (не обязательно дифференциальное уравнение) \ (L ‘\), которое наше рассмотрение законов венчает как закон мира, представленный s на том основании, что \ (L’ \) более информативен для s , чем E . Если такая альтернатива \ (L ‘\) существует, то s физически невозможно в соответствии с формулировкой (B) физической возможности, поскольку формулировка (B) требует, чтобы физически возможный мир имел те же законы, что и теория , но E не является законом s .В общем, если бы для любого недетерминированного решения существовало альтернативное предложение, увенчанное законом указанного недетерминированного решения, то детерминизм теории был бы восстановлен. Если учет законов относится к типу «Лучшие системы», тогда альтернативное предложение \ (L ‘\) должно обеспечить лучший баланс информативности и простоты, чем закон, представленный E . Подводя итог, если для любого недетерминированного решения такая альтернатива \ (L ‘\) существовала, то точка зрения Best Systems вместе с предположениями (D), (1) — (4), \ (\ lnot \) (5 ) и формулировка (B) повлечет за собой, что теория T является детерминированной, несмотря на то, что T не является детерминированной при предположениях (D), (1) — (4), \ (\ lnot \) (5) и формулировке ( А).

Эта проблема определяет исследовательский проект, успех которого повлечет за собой безотказность детерминизма. Что касается математико-физической стороны проекта, мы хотели бы узнать, можно ли для каждого недетерминированного решения физически значимого дифференциального уравнения найти другое простое предложение, которое более информативно в отношении этого решения, чем исходное дифференциальное уравнение. С философской стороны проекта мы будем стремиться независимо мотивировать понятия простоты и информативности, которые характеризуют указанное предложение, и на основе этих понятий мы будем искать вариант точки зрения лучших систем, которая венчает это и такие положения как законы соответствующие недетерминированные решения.Теперь посмотрим на вероятность успеха этого исследовательского проекта по спасению детерминизма.

Может ли наш исследовательский проект увенчаться успехом?

Абстрактно перспективы нашего исследовательского проекта спасения детерминизма кажутся мрачными. В качестве простого примера рассмотрим Купол Джона Нортона, проанализированный Нортоном [32, 33] и Маламентом [27]. Представьте себе шар, покоящийся на тщательно спроектированной куполообразной поверхности. Мяч может двигаться без трения, но его движение ограничено по поверхности, и на него влияет только однородное гравитационное поле.Наша физическая теория T — это классическая механика с законами Ньютона, в частности вторым законом: \ (F = ma \). Чтобы определить, как мяч движется, нам нужно решить задачу начального значения, где сила F закона Ньютона определяется формой купола и гравитационным полем, а начальные значения — это начальное положение и импульс мяча. Если бы это была обычная проблема в классической механике, мы бы получили уникальное решение, рассказывающее нам, как движется мяч.Однако форма Купола хитроумно спроектирована так, что наша задача с начальным значением дает множество различных решений: мяч самопроизвольно начинает катиться с вершины Купола, но классическая механика не может сказать нам, когда наступает этот начальный момент. Другими словами, Купол показывает, что при предположениях (1) — (4) свойство (5) не выполняется в классической механике. Учитывая определение (D) и формулировку (A), решения Купола недетерминированы, и, следовательно, мы получаем несколько парадоксальный вывод о том, что детерминизм не работает в классической механике.{(1)} = 0 \). Конкретный выбор \ (\ tau \) дает конкретное решение Купола. {(k)} = 0, \ end {выровнено} $$

(2)

, где k — еще не определенное число.Благотворительный читатель согласится с тем, что, по крайней мере, на первый взгляд, вполне разумно считать, что уравнение (2) «проще», чем уравнение (1). Могут возникнуть проблемы с числом k , которое не является достаточно «простым», но (2) является однородным и относится только к дифференцированию, тогда как (1) неоднородно и включает, помимо дифференцирования, также квадратный корень переменной .

Решения уравнения (2) являются полиномами до k -й степени.Полиномы могут использоваться для аппроксимации конечных траекторий и, таким образом, могут приближенно описывать путь, по которому мяч, катящийся по Куполу, проходит в любом конкретном решении Купола. С математической точки зрения для любого конечного участка решения s уравнения (1) мы можем найти значение для k , так что решение \ (s ‘\) уравнения (2) остается в пределах желаемого уровня приближения к . с . Правильно подобрав количество начальных значений k , мы можем однозначно определить это \ (s ‘\) решение.Таким образом, предполагая, что наша Лучшая система систематизирует только конечную продолжительность жизни Вселенной Купола, уравнение (2) может считаться предложением дедуктивной системы, которая приближается к истине, является информативной и простой.

Поскольку уравнение (2) истинно только приблизительно, в то время как уравнение (1) точно верно для решения Купола, учет законов, венчающих (2) как закон для такого решения, должен позволить приблизительной истине быть достаточной для законность. Лучшая приблизительно истинная система — это такой отчет.Если мы примем, что уравнение (2) проще, чем уравнение (1), возникает вопрос баланса, следует ли (2) или (1) считаться законом в решении Dome в соответствии с BATS. Поскольку потеря истинности из-за приближения может быть сколь угодно малой, если выигрыш в простоте и информативности влияет на баланс информативности, простоты и приближения к истине, тогда общий баланс может быть улучшен подходящим выбором небольших приближение. В случае, если окажется, что уравнение (2) обеспечивает лучший баланс, чем уравнение (1), мы получаем вывод, что в формулировке (B) физической возможности недетерминированное решение Купола физически невозможно в соответствии с классической механикой, поскольку ее законы не те, что у Ньютона.Однако законы детерминированных решений \ (F = ma \) будут по-прежнему законами Ньютона, поскольку для детерминированных решений мы потеряем информативность, перейдя к приближению, подобному (2). Таким образом, детерминированные решения физически возможны согласно классической механике, а недетерминированные решения — нет.

Этот вывод не зависит от предположения, что в мире присутствует только один экземпляр системы Купол-частица. Принимая x за 3 N -мерное векторное уравнение (2), применимо к системе точечных частиц N и, следовательно, оно имеет решения, аппроксимирующие любые конечные продолжительности жизни миров, которые содержат, скажем, N число куполов. -частичных систем, не теряя при этом простоты и информативности.Тем не менее, этот аргумент имеет много недостатков, в частности, предположение, что наша Лучшая Система систематизирует только конечную продолжительность жизни возможного мира. Выигрыш в простоте с помощью уравнения (2) может оказаться слишком маленьким, чтобы отдавать предпочтение одной системе по сравнению с другой, и даже может быть иллюзорным. Расстояние, измеренное между траекториями по супремум-норме, может не иметь физического значения. Еще одним неприятным моментом является то, что уравнение (2) требует k числовых значений для определения решения вместо 3 уравнения (1) (два плюс время, когда мяч начинает самопроизвольно катиться), их единственным преимуществом является то, что все k из них — начальные значения.Это поднимает вопрос о том, должна ли информативность или простота законов зависеть от их способности сочетаться с дополнительными доступными информативными и простыми предложениями, чтобы производить дальнейшие информативные и простые предложения о мире (подробности по этому вопросу см. В [21]). ).

В общем, вместо попытки найти какую-то абстрактную схему для аппроксимации недетерминированных решений произвольных дифференциальных уравнений, кажется целесообразным исследовать взаимосвязь различных конкретных дифференциальных уравнений в физике.Среди дифференциальных уравнений в частных производных типичными источниками нарушения единственности являются так называемые параболические и эллиптические уравнения, такие как классическое уравнение теплопроводности или уравнение Лапласа. В общем смысле такие уравнения могут быть аппроксимированы квазилинейными гиперболическими уравнениями первого порядка, начальные задачи которых имеют единственное решение. Роберт Герох, один из главных авторитетов в области уравнений в частных производных в физике, полагает, что

Можно привести доводы в пользу того, что, по крайней мере на фундаментальном уровне, все «уравнения в частных производных физики» являются гиперболическими, т.е.грамм. эллиптические и параболические системы возникают во всех случаях как простые приближения гиперболических систем. Таким образом, уравнение Пуассона для электрического потенциала — это всего лишь часть гиперболической системы уравнений Максвелла. ([19], стр. 2, 3)

Герох затем переходит к демонстрации того, что общая процедура симметризации доступна для квазилинейных гиперболических систем первого порядка; для симметричных систем известны общие теоремы о существовании и единственности решений.

Если, наоборот, недетерминированное решение s параболического или эллиптического уравнения E физической теории T может быть аппроксимировано детерминированным решением \ (s ‘\) гиперболического уравнения \ (E’ \) другой физической теории \ (Т ‘\), а затем физика, помимо помощи в решении проблемы детерминированности теории T , может также помочь облегчить философскую проблему неопределенности, преследующей ключевые концепции — информативность, простоту и приближение — Лучшая приблизительно истинная система учета законов.Поскольку \ (E ‘\) представляет собой закон другой физической теории, он, вероятно, пройдет как простой, так и информативный. Имея проблемы с уникальными начальными значениями, \ (E ‘\) также, вероятно, будет более информативным, чем E . Более того, поскольку основная мотивация отстаивать простоту и информативность как определяющие характеристики законов состоит в том, что они кажутся верными для фундаментальных уравнений, которые появляются в наших физических теориях, мы можем даже обойти проблему определения того, что мы подразумеваем под информативностью и простота в целом.Смысл, в котором s и \ (s ‘\) приближаются друг к другу, явным образом объясняется математическим утверждением самого аппроксимативного соотношения, и это чувство приближения также может обеспечить соответствующее понятие приближения к истине, требуемое лучшими приближениями. Истинный системный учет законов.

Этот анализ носит поверхностный характер, но он добавляет еще одну причину, по которой следует продолжить тщательное исследование приближенных соотношений различных физических теорий.О перспективах нашего исследовательского проекта по сохранению детерминизма можно будет адекватно судить только после того, как такое подробное исследование будет осуществлено.

Универсальные законы.

Законы природы, выраженные в физике в виде законов и теорий, часто называют универсальными . Это означает, что, насколько нам удалось их протестировать, они применимы везде и всегда, в прошлом, настоящем и будущем.

Конечно, мы еще не тестировали их везде и всегда.Так как же мы можем быть настолько уверены в том, что они действительно универсальны? Может быть, где-то есть исключение из одного из них, которого мы еще не обнаружили? Может ли быть странная форма материи, на которую не распространяются законы?

Давайте рассмотрим эти вопросы, сначала посмотрев на прошлую историю физики.

Исторические примеры.

В предыстории физики были замечены определенные закономерности природы и сформулированы в виде принципов или законов. Были сформулированы законы механики (рычагов и шкивов), которые оказались полезными для создания механических устройств.Но никто не предполагал, что эти законы, применимые к машинам, могут также применяться, скажем, к движениям тел в небесах. Фактически тогда считалось, что законы земной материи (земли, воды, воздуха и огня) существенно отличаются от законов, управляющих небесными явлениями за пределами Земли. Небесное царство якобы было создано не из обычного земного материала, а из чего-то другого, квинтэссенции (пятая сущность). Не ожидалось, что все, что происходит в этом мире, подчиняется тем же законам, что и земное вещество (четыре сущности).

Но движение светящихся тел в небесном царстве было законным, и законы движения Солнца, Луны и планет в небе вскоре были согласованы и развились в сложную математическую систему, геоцентрическую систему Птоэльма (центрированную на Земле). Он оказался весьма успешным, поскольку мог очень точно предсказывать положения небесных тел в прошлом и будущем и даже предсказывать затмения. И у него была философская привлекательность, так как в его основе лежали круги, считающиеся «самой совершенной» геометрической фигурой.

Но по мере того, как данные улучшались, эта система требовала настройки и включала в себя больше кругов и различные уловки для изменения скорости объектов вокруг этих кругов. Он стал громоздким, но работал по своему назначению — предсказывать положение планет в небе.

Однако у него все еще были проблемы. Положение планеты Марс было плохо смоделировано, и система должна была рассматривать планеты Меркурий и Венеру иначе, чем другие планеты.

Эта историческая тема хорошо освещена во многих книгах, поэтому мне нет необходимости писать по ней еще одну книгу. Эти книги говорят нам, что система Птолемея была «свергнута» гелиоцентрической (центрированной по солнцу) системой Коперника. Что мотивировало новую систему и почему ее не сразу приняли?

Критики отмечали, что систему Коперника было не намного проще использовать для планетарных расчетов. Он по-прежнему был основан на кругах, и только на шесть кругов меньше. Он действительно относился к Меркурию и Венере так же, как и к остальным планетам, тем самым устранив один из раздражающих аспектов системы Птолемея.

Иоганн Кеплер смог избавиться от множества кругов, эпициклов и выступов, введя эллиптические планетные орбиты.

Система Коперника во многом отличалась от системы Птоэльма. В центре системы Птолемея была неподвижная и неподвижная Земля. Система Коперника поместила Солнце в центр, а Земля и планеты вращались вокруг Солнца. Эта разница должна привести к наблюдаемому тесту. Если Земля двигалась таким образом, должен быть наблюдаемый «звездный параллакс».Положение каждой звезды на небе должно показывать ежегодное движение, движение по небольшим эллиптическим орбитам из-за изменения положения Земли. Такого движения не наблюдалось. Это наблюдалось только в 19 веке. Движение было очень маленьким, потому что звезды находятся очень далеко, на расстояниях, невообразимо больших, чем предполагали критики системы Коперника.

Суть всего в том, что «коперниканская революция» была чем-то большим, чем философский сдвиг. По эмоциональному призыву это не удалось.Это было вызвано экспериментальными данными и проверено экспериментами. Все успехи в физике основаны на данных. Система Птолемея оказалась весьма успешной в том смысле, что она могла предсказывать положение планет на небе. Однако он не мог предсказать расстояния до объектов от Земли. Фактически, если серьезно отнестись к этим красивым изображениям системы Птолемея, они предсказали бы смехотворно неверные расстояния. Но в то время методы наблюдений вообще не могли хорошо измерить астрономические расстояния. Расстояние до Луны и Солнца было довольно хорошо измерено тригонометрией, но дотелескопические методы не могли измерить расстояния до планет и звезд.

Была ли таким образом показана «неправильная» модель Птолемея? Едва ли. Он работал для своих очень ограниченных целей и все еще работает. Иногда отмечают, что оптико-механические проекторы планетариев работали по модели с центром в Земле, поскольку их единственная цель заключалась в том, чтобы показать положение небесных тел на небе. Современные планетарии работают по-другому и могут показать Вселенную с любой точки обзора, а не только с Земли. Решила ли модель Коперника вопрос о том, движется ли Земля? Не совсем, просто предполагалось, что Земля движется.Улучшила ли модель Коперника точность предсказаний положения планет? Нет, как сразу заметили его критики.

Даже сегодня некоторые люди поддерживают неподвижность Земли, так же как некоторые из них также заявляют, что Земля плоская, а также неподвижная. Есть даже те, кто заявляет, что Земля — ​​это полая оболочка со всей вселенной внутри, и мы ходим внутри этой оболочки. Искажая геометрию в соответствии со своими предрассудками, они разрабатывают сложную систему, которая, как они объявляют, столь же разумна, как и традиционная научная точка зрения.Действительно, могут, хотя немногие из тех, кто верит в эти модели, достаточно разбираются в математике, чтобы разобраться в деталях. Но они игнорируют тот факт, что нужно иметь дело с физикой. Чтобы сохранить свою искривленную геометрию, им пришлось бы пересмотреть все фундаментальные законы физики, законы силы, законы гравитации, законы сохранения и даже отказаться от постоянства скорости света. Они этого не сделали, потому что задача не в их силах.

Так почему же сейчас полностью отказались от геоцентрических моделей? Исаак Ньютон несет ответственность.Геоцентрические модели были только описательными и применялись только к положению объектов, видимых в небе. Ньютон представил более универсальную модель движения, используя концепцию силы, которая включала его три закона движения и закон всемирного тяготения. Эти законы применимы как к земным, так и к небесным явлениям, и они прекрасно прошли проверку эксперимента. Они соответствуют данным, предоставленным как земными лабораториями, так и астрономическими обсерваториями. И спустя столетия, прошедшие со времен Ньютона, они продолжают выдерживать испытание экспериментом и наблюдением.

Ньютону можно приписать демонстрацию того, что природа имеет основные закономерности, которые можно выразить как универсальные законы. Любая модель солнечной системы — это просто следствие этих законов.

Что может принести успехи в будущем?

У науки еще есть над чем поработать. Вопросы без ответа изобилуют космологией, элементарными частицами и квантовой механикой. Приведет ли прогресс в какой-либо из этих областей к отказу от классической механики Ньютона и ее замене? Я подозреваю, что нет.Относительность не аннулировала классическую физику. Квантовая механика тоже этого не сделала.

Те, кто фантазируют и строят гипотезы о чудесных достижениях физики, возлагают свои надежды на поиск исключений из известных законов. Возможные места для поиска:

• Далекие места в космосе, где все может подчиняться другим законам.
• Пока еще не наблюдаемые экзотические явления.
• Пока еще не обнаруженные странные частицы, которые ведут себя иначе, чем обычная материя.

У нас уже есть примеры. Субатомные частицы подчиняются законам, совершенно отличным от законов человеческих объектов. Но их открытие и законы, которым они подчиняются, никоим образом не меняют поведения бильярдных шаров или каких-либо технологических механизмов и естественных процессов нашего повседневного опыта и наших промышленных технологий. Здесь правят законы Ньютона.

Спекуляции о таких экзотических вещах не ведутся, пока кто-нибудь не представит в их пользу экспериментальные доказательства.А пока это философия, а не физика.

Создание гипотез.

Не-ученые часто предполагают, что ученые просто сидят и придумывают гипотезы, чтобы другие могли их проверить. Если какие-то из них успешны, они получают за них кредит. Так не работает. Каждая гипотеза мотивируется проблемой, которую необходимо решить, проблемой, возникающей из природы и экспериментальных данных, — что-то наблюдаемое, что не совсем соответствует известным законам.

Гипотезы мотивированы экспериментальными данными, а также сформированы ими.Гипотеза сформулирована с четким намерением, что ее последствия должны учитывать эти данные. Вы не можете просто выдвинуть гипотезу, не задумываясь о ее последствиях.

Ловушки экстраполяции.

Студенты-физики часто слишком сильно сосредотачиваются на изучении уравнений, представляющих законы природы. Они могут не понимать, что каждый закон физики — это идеализация и приближение. В природе нет идеальных прямых линий или кругов. Каждое измерение имеет экспериментальную погрешность.Исчисление основано на концепции предела. Но если вы возьмете предел любой физической величины, поскольку ее размер стремится к нулю, вы выйдете за пределы того, что можно измерить инструментами, и даже в квантовую сферу, где количества не делятся бесконечно и не имеют гладкого поведения при малых размерах. Поэтому само основание исчисления несовершенно (применительно к природе) — потому что ничто не может быть бесконечно делимым. Ньютон ничего не знал о молекулах и атомах. Тем не менее, результаты расчетных операций по-прежнему очень хороши и полезны в пределах требуемых измерений.Математики и физики хорошо осведомлены об этих проблемах, они знают, при каких условиях эти процессы могут давать несовершенные ответы, и они знают, как обойти проблему. Они понимают, что математика не представляет собой научную истину, а всего лишь инструмент для выражения поведения природы. Даже несовершенный молоток может забить гвоздь при строительстве дома.

Опытные ученые — люди практики. Они знают, что совершенство не только невозможно, но и не обязательно для его целей.Они знают, когда что-то «достаточно хорошо», чтобы делать правильные и подтверждаемые выводы, и не зацикливаются на поиске последнего десятичного знака.

В качестве повседневного примера рассмотрим закон F = kΔx, представляющий приложенную силу для растяжения провода на величину Δx. k — постоянная упругости, зависящая от металла, из которого сделана проволока. Теперь вы можете вставить любое значение силы в уравнение, но если сила достаточно велика, проволока выйдет за пределы своего предела упругости и сломается. Само по себе уравнение не говорит вам об этом.Вы экстраполировали уравнение за пределы его физической применимости.

Кроме того, уравнение представляет собой прямую линию, линейную зависимость. Однако некоторые материалы (например, резина) подчиняются нелинейному закону упругости. Так что имеет значение, о каком материале вы говорите.

Этот пример представляет собой закон, описывающий поведение материалов. Все материалы сложны, и на них влияет множество условий. В этом случае важна даже температура. (Металлическая проволока удлиняется при повышении температуры.Если температура слишком высока, проволока плавится.) Это пример класса законов, которые являются , а не фундаментальными или основными законами физики (например, законами Ньютона).

Почти в каждом уравнении в учебнике физики есть такие «подводные камни», обычно объясняемые в тексте, которые пропускают слишком многие студенты.

— Дональд Э. Симанек, 2004, 2014, 2017.

---

Вернитесь в Музей неработающих устройств.
Вернуться в главное меню.

ОПРЕДЕЛЕНИЕ СИМВОЛОВ, ИСПОЛЬЗУЕМЫХ ДЛЯ ОПИСАНИЯ ФИЗИЧЕСКИХ ЗАКОНОВ СВЕТА

DLE, вероятно, вырабатывается всеми фруктами, овощами и растительным материалом, подвергающимся фотосинтезу.Однако интенсивность и продолжительность излучаемого света широко варьируются в зависимости от многих факторов. Из-за сильной зависимости DLE от содержания хлорофилла можно ожидать вариации DLE для разных разновидностей одного и того же продукта. Следовательно, оценка качества на основе измерений DLE требует тщательного выбора критериев измерения, таких как продолжительность и интенсивность освещения, период темноты и температура. Необходимо получить точные значения DLE для конкретного продукта при заданных условиях; и условия измерения должны быть тщательно проверены, чтобы установить стандартные критерии измерения.В целом оценка качества фруктов и овощей основана на трех основных аспектах: оценка зрелости и / или спелости, анализ состава и обнаружение внутренних и внешних дефектов. Измерения DLE до сих пор были сосредоточены в основном на оценке зрелости из-за определенной взаимосвязи между излучаемым светом и концентрацией хлорофилла, которая изменяется по мере созревания. Следует отметить, что одного хлорофилла недостаточно; это комплекс хлорофилла in situ и родственных соединений в растительном сырье, которые совместно вносят вклад в DLE.Состав фруктов, например содержание сахара, был связан с DLE. В последнее время измерения DLE стали применяться для обнаружения определенных физиологических реакций на стресс и дефектов, таких как переохлаждение. Однако эти области исследований еще не полностью изучены. Дальнейшее исследование, касающееся качества состава, а также внутренних и внешних дефектов фруктов и овощей с помощью измерения DLE, может предложить решения некоторых сложных проблем оценки качества. Продолжительность ДЛЭ после возбуждения составляет не менее нескольких секунд.С механической точки зрения этот продолжительный период излучения света предлагает удобное время для разделения возбуждения и измерения. Однако экспоненциальный спад требует очень точного контроля времени между освещением и измерением. Широкий спектр активации обеспечивает широкий выбор и простую конструкцию источников возбуждения. Однако размер, форма и разновидности растительного материала затрудняют единообразные измерения DLE. Предлагается, чтобы измерительные приборы DLE были сконструированы так, чтобы производить несколько измерений по всей поверхности образца.