Физический смысл магнитной индукции:
⇐ ПредыдущаяСтр 7 из 11Следующая ⇒Индукция магнитного поля численно равна максимальной силе, с которой данное поле действует на проводник длиной 1 метр с силой тока 1 Ампер.

Направление индукции магнитного поля –
от Южного к Северному полюсу свободно установившейся магнитной стрелки.
 Магнитный поток
Магнитный поток
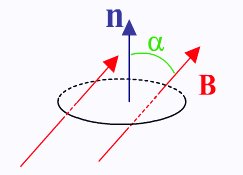
Нарисуем замкнутый контур, n – нормаль к его плоскости.
Поместим контур в магнитное поле с индукцией В.
Магнитный поток- это скалярная физическая величина, равная произведению модуля вектора индукции магнитного поля на площадь контура и на косинус угла между вектором индукции и нормалью к площади контура
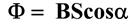
Единица измерения магнитного потока – Вебер
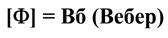
Вб = Тл*м2
Явление электромагнитной индукции
Явление электромагнитной индукции было открыто выдающимся английским физиком М. Фарадеем в 1831 г. Фарадей наблюдал возникновение электрического тока в замкнутом проводящем контуре при изменении во времени магнитного потока
Вопрос Фарадея:: если током можно намагнитить железо, то не может ли магнит вызвать появление тока?
Явление ЭМИ состоит в том, что при любом изменении магнитного потока, пронизывающего замкнутый контур, в контуре возникает ЭДС индукции. Если контур проводящий, то в нем будет протекать ток, который называется индукционным. Если контур из диэлектрика, то он поляризуется.
Сторонние силы действуют внутри источника тока и вызывают разделение зарядов, т. е. движение электронов от + к – источника. Имеют неэлектрическую природу.
ЭДС индукции возникает только в тот интервал времени, когда
Изменение магнитного потока через контур:
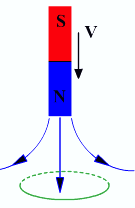
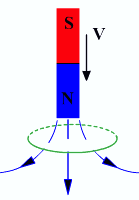 .
.
Закон электромагнитной индукции (закон Фарадея)
ЭДС индукции
По закону ЭМИ изменение магнитного потока приводит к появлению ЭДС, которая называется ЭДС индукции.
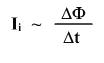
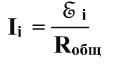 По закону Ома для полной цепи сила тока равна отношению ЭДС к полному сопротивлению цепи
По закону Ома для полной цепи сила тока равна отношению ЭДС к полному сопротивлению цепи
следовательно, ЭДС индукции пропорциональна скорости изменения магнитного потока
 |
Закон электромагнитной индукции (Фарадея):
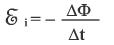 |
Понятие об электромагнитной теории Максвелла. Вихревое электрическое поле. Правило Ленца. Самоиндукция. Индуктивность.
Направление индукционного тока.
Правило Ленца (1883 г)индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток.
 Опыт Ленца
Опыт Ленца
Описание опыта:замкнутое кольцо отталкивается от магнита, если его вдвигают в кольцо, и притягивается, если магнит выдвигают.
Движение кольца обусловлено магнитным полем индукционного тока.
Применение правила Ленца
Пример Магнит движется вправо (вдвигается в контур)
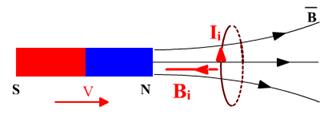 |
1. Определить направление силовых линий внешнего поля B.
2. Определить, увеличивается или уменьшается магнитный поток через
контур.
3. Определить направление индукционного магнитного поля Bi
Если магнитный поток увеличивается, Bi направлено против B, компенсируя это увеличение. Если магнитный поток уменьшается, Bi направлено одинаково с B, компенсируя это уменьшение.
- По правилу буравчика определить направление индукционного тока.
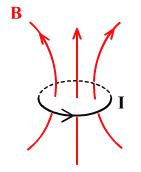
Вихревое электрическое поле
Причина появления ЭДС индукции в замкнутом контуре при изменении магнитного потока заключается в возникновении вихревого электрического поля в любой области пространства, где существует переменное магнитное поле. – гипотеза Максвелла. Силовые линии вихревого поля замкнуты.
Перечислим свойства известных нам полей
1. Электростатическое, возникает везде, где есть эл. заряды. Силовые линии начинаются и заканчиваются на зарядах. Потенциальное, т.е. работа по замкнутому контуру равна нулю. напряженность, потенциал.
2. Поле тока – магнитное, вихревое, работа по замкнутому контуру не равна нулю. Ток течет в сторону убывания потенциала. Поле действует только на движущиеся заряды
3. Вихревое электрическое поле. Действует на любые заряды. Работа по замкнутому контуру равна ЭДС индукции. ЭДС индукции определяется законом Фарадея.
 Самоиндукция. Индуктивность
Самоиндукция. Индуктивность
Самоиндукция является важным частным случаем
электромагнитной индукции, когда изменяющийся
магнитный поток, вызывающий ЭДС индукции,
создается током в самом контуре.
возникает магнитное поле. Силовые линии этого поля
пронизывают все окружающее пространство, в том числе, пересекают площадь самого контура.
Магнитный поток, который вызван током в этом самом контуре, называется собственным магнитным потоком.
Поскольку магнитный поток пропорционален индукции магнитного поля, собственный магнитный поток пропорционален силе тока в контуре
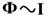 | |||
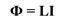 |
Следовательно, можно ввести коэффициент пропорциональности
Коэффициент пропорциональности L между собственным магнитным потоком в контуре и силой тока в нем называется индуктивностью контура.
Индуктивность проводника зависит от размеров, формы проводника, магнитных свойств среды.
Единица измерения индуктивности называется Генри
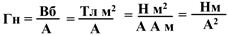 |
Стационарное магнитное поле и его характеристики. Физический смысл и единица измерения магнитной индукции. Магнитный поток
2. Действие магнитного поля на проводник с током. Сила Ампера — это сила, с которой магнитное поле действует на помещенный в него проводник с током. 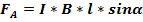
Для определения направления силы Ампера применяют правило левой руки: если ладонь левой руки расположить так, чтобы вектор индукции магнитного поля ( 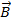 ) входил в ладонь, четыре вытянутых пальца указывали направление тока (I), тогда отогнутый на 90° большой палец укажет направление силы Ампера (
) входил в ладонь, четыре вытянутых пальца указывали направление тока (I), тогда отогнутый на 90° большой палец укажет направление силы Ампера ( 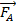
3. Действие магнитного поля на контур с током. Вращабщий момент
4. Действие магнитного поля на движущий электрический заряд.Электрический ток – это совокупность упорядоченно движущихся заряженных частиц. Поэтому действие магнитного поля на проводник с током есть результат действия поля на движущиеся заряженные частицы внутри проводника.
Силу, действующую на движущуюся заряженную частицу со стороны магнитного поля, называют силой Лоренца. Модуль силы Лоренца равен отношению модуля силы Ампера, действующей на участок проводника, к числу заряженных частиц в этом участке проводника: 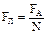
Сила Ампера равна 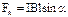 , сила тока равна
, сила тока равна 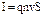 (см. стр. 12). Подставив эти выражения в формулу для силы Лоренца, получим:
(см. стр. 12). Подставив эти выражения в формулу для силы Лоренца, получим:
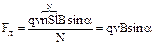 где
где 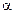 — угол между векторами скорости и магнитной индукции.
— угол между векторами скорости и магнитной индукции.
Направление силы Лоренца определяют для положительного заряда по правилу левой руки. (Для отрицательного заряда сила Лоренца будет направлена в противоположную сторону).
Так как сила Лоренца перпендикулярна скорости частицы, то она не совершает работу. А, согласно теореме о кинетической энергии, это означает, что сила Лоренца не меняет кинетическую энергию частицы и, следовательно модуль ее скорости. Под действием силы Лоренца меняется лишь направление скорости частицы.
5. Закон Фарадея для электромагнитной индукции. Правило Ленца, при изменении магнитного потока, проходящего через него.
Электромагнитная индукция была открыта Майклом Фарадеем 29 августа 1831 года. Он обнаружил, что электродвижущая сила, возникающая в замкнутом проводящем контуре, пропорциональна скорости изменения магнитного потока через поверхность, ограниченную этим контуром. Согласно закону электромагнитной индукции Фарадея (в СИ): 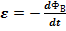 где
где  — электродвижущая сила, действующая вдоль произвольно выбранного контура,
— электродвижущая сила, действующая вдоль произвольно выбранного контура, 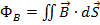 — магнитный поток через поверхность, натянутую на этот контур.
— магнитный поток через поверхность, натянутую на этот контур.
Знак «минус» в формуле отражает правило Ленца, названное так по имени русского физика Э. Х. Ленца: Индукционный ток, возникающий в замкнутом проводящем контуре, имеет такое направление, что создаваемое им магнитное поле противодействует тому изменению магнитного потока, которым был вызван данный ток.
Для катушки, находящейся в переменном магнитном поле, закон Фарадея можно записать следующим образом:  где
где  — электродвижущая сила, N — число витков,
— электродвижущая сила, N — число витков, 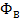 — магнитный поток через один виток,
— магнитный поток через один виток, 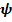 — потокосцепление катушки.
— потокосцепление катушки.
Правило Ленца правило для определения направления индукционного тока: Индукционный ток, возникающий при относительном движении проводящего контура и источника магнитного поля, всегда имеет такое направление, что его собственный магнитный поток компенсирует изменения внешнего магнитного потока, вызвавшего этот ток. Сформулировано в 1833 г. Э. Х. Ленцем. Если ток увеличивается, то и магнитный поток увеличивается.Если 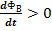 =>
=> 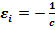 индукционный ток направлен против основного тока. Если
индукционный ток направлен против основного тока. Если 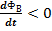 индукционный ток направлен в том же направлении, что и основной ток.
индукционный ток направлен в том же направлении, что и основной ток.
Индукционный ток всегда направлен так, чтобы уменьшить действие причины его вызывающей.
В обобщенной формулировке правило Ленца гласит, что индукционный ток всегда направлен так, чтобы противодействовать вызвавшей его первопричине.
ЭДС (ε) — отношение работы сторонних сил по разделению зарядов к величине этого заряда, иначе, способность данного источника давать необходимое количество зарядов необходимой энергии. 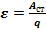 — ЭДС.
— ЭДС.
εi возникает при изменении магнитного потока Ф, пронизывающего контур. 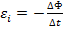 -ЭДС индукции.
-ЭДС индукции. 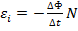 — — ЭДС индукции в контуре, содержащем N витков провода.
— — ЭДС индукции в контуре, содержащем N витков провода.
Физический смысл
В вакууме (или в отсутствие среды, способной к магнитной поляризации, а также в случаях, когда последняя пренебрежима) напряжённость магнитного поля совпадает с вектором магнитной индукции с точностью до коэффициента, равного 1 в СГС и μ0 в СИ. В магнетиках (магнитных средах) напряжённость магнитного поля имеет физический смысл «внешнего» поля, то есть совпадает (быть может, в зависимости от принятых единиц измерения, с точностью до постоянного коэффициента, как например в системе СИ, что общего смысла не меняет) с таким вектором магнитной индукции, какой «был бы, если магнетика не было». Например, если поле создаётся катушкой с током, в которую вставлен железный сердечник, то напряжённость магнитного поля H внутри сердечника совпадает (в СГСточно, а в СИ — с точностью до постоянного размерного коэффициента) с векторомB0, который был бы создан этой катушкой при отсутствии сердечника и который в принципе может быть рассчитан исходя из геометрии катушки и тока в ней, без всякой дополнительной информации о материале сердечника и его магнитных свойствах. При этом надо иметь в виду, что более фундаментальной характеристикой магнитного поля является вектор магнитной индукции B. Именно он определяет силу действия магнитного поля на движущиеся заряженные частицы и токи, а также может быть непосредственно измерен, в то время как напряжённость магнитного поля H можно рассматривать скорее как вспомогательную величину (хотя рассчитать её, по крайней мере, в статическом случае, проще, в чём и состоит её ценность: ведь H создают так называемые свободные токи, которые сравнительно легко непосредственно измерить, а трудно измеримые связанные токи — то есть токи молекулярные и т. п. — учитывать не надо). Правда, в обычно используемое выражение для энергии магнитного поля (в среде) B и H входят почти равноправно, но надо иметь в виду, что в эту энергию включена и энергия, затраченная на поляризацию среды, а не только энергия собственно поля[1]. Энергия магнитного поля как такового выражается только через фундаментальное B. Тем не менее видно, что величина H феноменологически и тут весьма удобна.
74 Виды магнетиков Диамагнетики имеют магнитную проницаемость чуть меньше 1. Отличаются тем, что выталкиваются из области магнитного поля. Парамагнетики имеют магнитную проницаемость чуть более 1. Подавляющее количество материалов являются диа- и пара- магнетиками. Ферромагнетики обладают исключительно большой магнитной проницаемостью, доходящей до миллиона. По мере усиления поля проявляется явление гистерезиса, когда при увеличении напряженности и при последующем уменьшении напряженности значения В(Н) не совпадают друг с другом. В литературе различают несколько определений магнитной проницаемости. Начальная магнитная проницаемость mн — значение магнитной проницаемости при малой напряженности поля. Максимальная магнитная проницаемость mmax — максимальное значение магнитной проницаемости, которое достигается обычно в средних магнитных полях. Из других основных терминов, характеризующих магнитные материалы, отметим следующие. Намагниченность насыщения — максимальная намагниченность, которая достигается в сильных полях, когда все магнитные моменты доменов ориентированы вдоль магнитного поля. Петля гистерезиса — зависимость индукции от напряженности магнитного поля при изменении поля по циклу: подъем до определенного значения — уменьшение, переход через нуль, после достижения того же значения с обратным знаком — рост и т.п. Максимальная петля гистерезиса — достигающая максимальной намагниченности насыщения. Остаточная индукция Bост — индукция магнитного поля на обратном ходе петли гистерезиса при нулевой напряженности магнитного поля. Коэрцитивная сила Нс — напряженность поля на обратном ходе петли гистерезиса при которой достигается нулевая индукция.
75
Магнитные моменты атомов |
Магнитный момент Элементарные
частицы обладают внутренним
квантовомеханическим свойством
известным как спин.
Оно аналогичноугловому
моментуобъекта вращающегося вокруг
собственногоцентра
масс, хотя строго говоря, эти частицы
являются точечными и нельзя говорить
об их вращении. Спин измеряют в единицах
приведённойпланковской
постоянной( Магнитное поле, создаваемоемагнитным моментоматома, определяется этими различными формами углового момента, как и в классической физике вращающиеся заряженные объекты создают магнитное поле. Однако, наиболее значительный вклад происходит от спина. Благодаря свойству электрона, как и всех фермионов, подчинятьсяправилу запрета Паули, по которому два электрона не могут находиться в одном и том жеквантовом состоянии, связанные электроны спариваются друг с другом, и один из электронов находится в состоянии со спином вверх, а другой — с противоположной проекцией спина — состояние со спином вниз. Таким образом магнитные моменты электронов сокращаются, уменьшая полный магнитный дипольный момент системы до нуля в некоторых атомах с чётным числом электронов.[32] В ферромагнитныхэлементах, таких как железо, нечётное число электронов приводит к появлению неспаренного электрона и к ненулевому полному магнитному моменту. Орбитали соседнихатомов перекрываются, и наименьшее энергетическое состояние достигается, когда все спины неспаренных электронов принимают одну ориентацию, процесс известный как обменное взаимодействие. Когдамагнитные моменты ферромагнитных атомов выравниваются, материал может создавать измеримое макроскопическое магнитное поле. Парамагнитные материалысостоят изатомов , магнитные моменты которых разориентированы в отсутствии магнитного поля, но магнитные моменты отдельных атомов выравниваются при приложении магнитного поля.[32][33] Ядро атома тоже может обладать ненулевым полным спином. Обычно при термодинамическом равновесииспины ядер ориентированы случайным образом. Однако, для некоторых элементов (таких какксенон-129) возможно поляризовать значительную часть ядерных спинов для создания состояния с сонаправленными спинами —состояния называемогогиперполяризацией. Это состояние имеет важное прикладное значение вмагнитно-резонансной томографии.[34][35] |
76 Магнитное поле обладает энергией. Подобно тому, как в заряженном конденсаторе имеется запас электрической энергии, в катушке, по виткам которой протекает ток, имеется запас магнитной энергии.
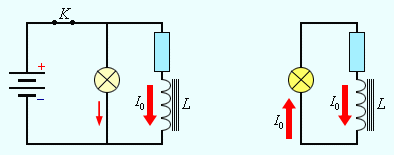
Если включить электрическую лампу параллельно катушке с большой индуктивностью в электрическую цепь постоянного тока, то при размыкании ключа наблюдается кратковременная вспышка лампы. Ток в цепи возникает под действием ЭДС самоиндукции. Источником энергии, выделяющейся при этом в электрической цепи, является магнитное поле катушки. Энергия Wм магнитного поля катушки с индуктивностью L, создаваемого током I, равна Wм = LI2/ 2 Формула очень похожа на формулу для кинетической энергии, роль массы m выполняет индуктивность L, а скорости v соответствуетсила тока I.
77Дивергенция
(расхождение вектора) – это алгебраическая
скалярная величина, характеризующая
источники поля в рассматриваемой точке
поля или указывающая на отсутствие
источников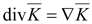 Численно дивергенцию в
данной точке определяют как предел, к
которому стремится отношение потока
вектора через замкнутую поверхность
к объему, ограниченному этой поверхностью,
при стремлении этого объема к нулю
Численно дивергенцию в
данной точке определяют как предел, к
которому стремится отношение потока
вектора через замкнутую поверхность
к объему, ограниченному этой поверхностью,
при стремлении этого объема к нулю .(14.14)
Дивергенция вектора магнитной индукции
.(14.14)
Дивергенция вектора магнитной индукции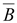 всегда
равна нулю, так как линии вектора
всегда
равна нулю, так как линии вектора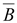 замкнуты
(не имеют начала и конца).
В декартовой системе координат
замкнуты
(не имеют начала и конца).
В декартовой системе координат (14.15).
(14.15).
Теорема о циркуляции магнитного поля займёмся
вычислением циркуляции вектора
магнитной индукции Обратим
внимание на то, что модуль вектора
магнитной индукции в нашем случае
одинаков во всех точках силовой линии
и, следовательно, контура L: Циркуляция положительна, когда направление обхода контура связано с направлением тока правилом буравчика (рис. 9.10.a). В противном случае циркуляция отрицательна |
[Править] Физический смысл
В вакууме (или в отсутствие среды, способной к магнитной поляризации, а также в случаях, когда последняя пренебрежима) напряжённость магнитного поля совпадает с вектором магнитной индукции с точностью до коэффициента, равного 1 в СГС и μ0 в СИ.
В магнетиках (магнитных средах) напряжённость магнитного поля имеет физический смысл «внешнего» поля, то есть совпадает (быть может, в зависимости от принятых единиц измерения, с точностью до постоянного коэффициента, как например в системе СИ, что общего смысла не меняет) с таким вектором магнитной индукции, какой «был бы, если магнетика не было».
Например, если поле создаётся катушкой с током, в которую вставлен железный сердечник, то напряжённость магнитного поля H внутри сердечника совпадает (в СГСточно, а в СИ — с точностью до постоянного размерного коэффициента) с векторомB0, который был бы создан этой катушкой при отсутствии сердечника и который в принципе может быть рассчитан исходя из геометрии катушки и тока в ней, без всякой дополнительной информации о материале сердечника и его магнитных свойствах.
При этом надо иметь в виду, что более фундаментальной характеристикой магнитного поля является вектор магнитной индукции B. Именно он определяет силу действия магнитного поля на движущиеся заряженные частицы и токи, а также может быть непосредственно измерен, в то время как напряжённость магнитного поля H можно рассматривать скорее как вспомогательную величину (хотя рассчитать её, по крайней мере, в статическом случае, проще, в чём и состоит её ценность: ведь H создают так называемые свободные токи, которые сравнительно легко непосредственно измерить, а трудно измеримые связанные токи — то есть токи молекулярные и т. п. — учитывать не надо).
Правда, в обычно используемое выражение для энергии магнитного поля (в среде) B и H входят почти равноправно, но надо иметь в виду, что в эту энергию включена и энергия, затраченная на поляризацию среды, а не только энергия собственно поля[1]. Энергия магнитного поля как такового выражается только через фундаментальное B. Тем не менее видно, что величина H феноменологически и тут весьма удобна.
74Виды магнетиков Диамагнетикиимеют магнитную проницаемость чуть меньше 1. Отличаются тем, что выталкиваются из области магнитного поля.
Парамагнетикиимеют магнитную проницаемость чуть более 1. Подавляющее количество материалов являются диа- и пара- магнетиками.
Ферромагнетикиобладают исключительно большой магнитной проницаемостью, доходящей до миллиона.
По мере усиления поля проявляется явление гистерезиса, когда при увеличении напряженности и при последующем уменьшении напряженности значения В(Н) не совпадают друг с другом. В литературе различают несколько определений магнитной проницаемости.
Начальная магнитная проницаемостьmн— значение магнитной проницаемости при малой напряженности поля.
Максимальная магнитная проницаемость mmax— максимальное значение магнитной проницаемости, которое достигается обычно в средних магнитных полях.
Из других основных терминов, характеризующих магнитные материалы, отметим следующие.
Намагниченность насыщения — максимальная намагниченность, которая достигается в сильных полях, когда все магнитные моменты доменов ориентированы вдоль магнитного поля.
Петля гистерезиса —зависимость индукции от напряженности магнитного поля при изменении поля по циклу: подъем до определенного значения — уменьшение, переход через нуль, после достижения того же значения с обратным знаком — рост и т.п.
Максимальная петля гистерезиса — достигающая максимальной намагниченности насыщения.
Остаточная индукция Bост — индукция магнитного поля на обратном ходе петли гистерезиса при нулевой напряженности магнитного поля.
Коэрцитивная сила Нс— напряженность поля на обратном ходе петли гистерезиса при которой достигается нулевая индукция.
75
Магнитные моменты атомов |
Магнитный момент Элементарные
частицы обладают внутренним
квантовомеханическим свойством
известным как спин.
Оно аналогичноугловому
моментуобъекта вращающегося вокруг
собственногоцентра
масс, хотя строго говоря, эти частицы
являются точечными и нельзя говорить
об их вращении. Спин измеряют в единицах
приведённойпланковской
постоянной( Магнитное поле, создаваемоемагнитным моментоматома, определяется этими различными формами углового момента, как и в классической физике вращающиеся заряженные объекты создают магнитное поле. Однако, наиболее значительный вклад происходит от спина. Благодаря свойству электрона, как и всех фермионов, подчинятьсяправилу запрета Паули, по которому два электрона не могут находиться в одном и том жеквантовом состоянии, связанные электроны спариваются друг с другом, и один из электронов находится в состоянии со спином вверх, а другой — с противоположной проекцией спина — состояние со спином вниз. Таким образом магнитные моменты электронов сокращаются, уменьшая полный магнитный дипольный момент системы до нуля в некоторых атомах с чётным числом электронов.[32] В ферромагнитныхэлементах, таких как железо, нечётное число электронов приводит к появлению неспаренного электрона и к ненулевому полному магнитному моменту. Орбитали соседнихатомов перекрываются, и наименьшее энергетическое состояние достигается, когда все спины неспаренных электронов принимают одну ориентацию, процесс известный как обменное взаимодействие. Когдамагнитные моменты ферромагнитных атомов выравниваются, материал может создавать измеримое макроскопическое магнитное поле. Парамагнитные материалысостоят изатомов , магнитные моменты которых разориентированы в отсутствии магнитного поля, но магнитные моменты отдельных атомов выравниваются при приложении магнитного поля.[32][33] Ядро атома тоже может обладать ненулевым полным спином. Обычно при термодинамическом равновесииспины ядер ориентированы случайным образом. Однако, для некоторых элементов (таких какксенон-129) возможно поляризовать значительную часть ядерных спинов для создания состояния с сонаправленными спинами —состояния называемогогиперполяризацией. Это состояние имеет важное прикладное значение вмагнитно-резонансной томографии.[34][35] |
76 Магнитное поле обладает энергией. Подобно тому, как в заряженном конденсаторе имеется запас электрической энергии, в катушке, по виткам которой протекает ток, имеется запас магнитной энергии.
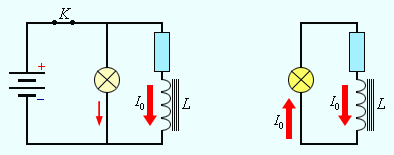
Если включить электрическую лампу параллельно катушке с большой индуктивностью в электрическую цепь постоянного тока, то при размыкании ключа наблюдается кратковременная вспышка лампы. Ток в цепи возникает под действием ЭДС самоиндукции. Источником энергии, выделяющейся при этом в электрической цепи, является магнитное поле катушки.
Энергия Wм магнитного поля катушки с индуктивностью L, создаваемого током I, равна
Wм = LI2/ 2
Формула очень похожа на формулу для кинетической энергии, роль массы m выполняет индуктивность L, а скорости v соответствуетсила тока I.
77Дивергенция (расхождение вектора) – это алгебраическая скалярная величина, характеризующая источники поля в рассматриваемой точке поля или указывающая на отсутствие источников
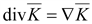 .
.
Численно дивергенцию в данной точке определяют как предел, к которому стремится отношение потока вектора через замкнутую поверхность к объему, ограниченному этой поверхностью, при стремлении этого объема к нулю
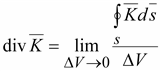 .(14.14)
.(14.14)
Дивергенция
вектора магнитной индукции 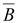 всегда
равна нулю, так как линии вектора
всегда
равна нулю, так как линии вектора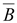 замкнуты
(не имеют начала и конца).
замкнуты
(не имеют начала и конца).
В декартовой системе координат
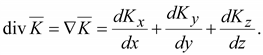 (14.15).
(14.15).
Теорема о циркуляции магнитного поля |
Теперь
займёмся вычислением циркуляции
вектора магнитной индукции
Рис. 9.7. Обратим внимание на то, что модуль вектора магнитной индукции в нашем случае одинаков во всех точках силовой линии и, следовательно, контура L:
Согласно
(9.8),
Вывод. В рассмотренном частном случае циркуляция вектора магнитной индукции по замкнутому контуру пропорциональна току, охватываемому этим контуром. Циркуляция положительна, когда направление обхода контура связано с направлением тока правилом буравчика (рис. 9.10.a). В противном случае циркуляция отрицательна |
в чем заключается физический смысл закона электромагнитной индукции?
При всяком изменении магнитного потока, пронизывющего замкнутый контур, в нём возникает индукционный электрический ток.
Изменение направлений спинов в атомах, изменяет время необходимое для омнена электронами на участке индукции. После этого в результате давления энтропии, свободные электроны и «дырки» начинают искать равновестное состояние с теми участками, которые вне магнитного поля. Возникает ток. Электродвижущая сила, возникающая в замкнутом проводящем контуре, пропорциональна скорости изменения магнитного потока через поверхность, ограниченную этим контуром. Величина электродвижущей силы (ЭДС) не зависит от того, что является причиной изменения потока — изменение самого магнитного поля или движение контура (или его части) в магнитном поле. Электрический ток, вызванный этой ЭДС, называется индукционным током.
При изменении магнитного потока в проводнике наводится ЭДС, а если проводник образует замкнутый контур — под действием этой ЭДС течёт ток.
xyй пиздa cпeрма малафья eбaл я вaши xyeвы законы
Напряжённость магнитного поля — это… Что такое Напряжённость магнитного поля?
Напряжённость магни́тного по́ля (стандартное обозначение Н) — векторная физическая величина, равная разности вектора магнитной индукции B и вектора намагниченности M.
В СИ: где — магнитная постоянная.
В СГС:
- В простейшем случае изотропной (по магнитным свойствам) среды и в приближении достаточно низких частот изменения поля B и H просто пропорциональны друг другу, отличаясь просто числовым множителем (зависящим от среды) B = μ H в системе СГС или B = μ0μ H в системе СИ (см. Магнитная проницаемость, также см. Магнитная восприимчивость).
В системе СГС напряжённость магнитного поля измеряется в эрстедах (Э), в системе СИ — в амперах на метр (А/м). В технике эрстед постепенно вытесняется единицей СИ — ампером на метр.
1 Э = 1000/(4π) А/м ≈ 79,5775 А/м.
1 А/м = 4π/1000 Э ≈ 0,01256637 Э.
Физический смысл
В вакууме (или в отсутствие среды, способной к магнитной поляризации, а также в случаях, когда последняя пренебрежима) напряжённость магнитного поля совпадает с вектором магнитной индукции с точностью до коэффициента, равного 1 в СГС и μ0 в СИ.
В магнетиках (магнитных средах) напряжённость магнитного поля имеет физический смысл «внешнего» поля, то есть совпадает (быть может, в зависимости от принятых единиц измерения, с точностью до постоянного коэффициента, как например в системе СИ, что общего смысла не меняет) с таким вектором магнитной индукции, какой «был бы, если магнетика не было».
Например, если поле создаётся катушкой с током, в которую вставлен железный сердечник, то напряжённость магнитного поля H внутри сердечника совпадает (в СГС точно, а в СИ — с точностью до постоянного размерного коэффициента) с вектором B0, который был бы создан этой катушкой при отсутствии сердечника и который в принципе может быть рассчитан исходя из геометрии катушки и тока в ней, без всякой дополнительной информации о материале сердечника и его магнитных свойствах.
При этом надо иметь в виду, что более фундаментальной характеристикой магнитного поля является вектор магнитной индукции B. Именно он определяет силу действия магнитного поля на движущиеся заряженные частицы и токи, а также может быть непосредственно измерен, в то время как напряжённость магнитного поля H можно рассматривать скорее как вспомогательную величину (хотя рассчитать её, по крайней мере, в статическом случае, проще, в чём и состоит её ценность: ведь H создают так называемые свободные токи, которые сравнительно легко непосредственно измерить, а трудно измеримые связанные токи — то есть токи молекулярные и т. п. — учитывать не надо).
Правда, в обычно используемое выражение для энергии магнитного поля (в среде) B и H входят почти равноправно, но надо иметь в виду, что в эту энергию включена и энергия, затраченная на поляризацию среды, а не только энергия собственно поля[1]. Энергия магнитного поля как такового выражается только через фундаментальное B. Тем не менее видно, что величина H феноменологически и тут весьма удобна.
См. также
Примечания
- ↑ Действительно, для иллюстрации рассмотрим выражение для так называемой плотности энергии поля в среде для сравнительно простого случая линейной связи намагниченности напряженности магнитного поля Тогда (используем здесь СИ) раскрывается как
Магнитная проницаемость — Википедия
Магни́тная проница́емость — физическая величина, коэффициент (зависящий от свойств среды), характеризующий связь между магнитной индукцией B{\displaystyle {B}} и напряжённостью магнитного поля H{\displaystyle {H}} в веществе.
Для разных сред этот коэффициент различен, поэтому говорят о магнитной проницаемости конкретной среды (подразумевая её состав, состояние, температуру и т. д.).
Обычно обозначается греческой буквой μ{\displaystyle \mu }. Может быть как скаляром (у изотропных веществ), так и тензором (у анизотропных).
Впервые этот термин встречается в работе Вернера Сименса «Beiträge zur Theorie des Elektromagnetismus» («Вклад в теорию электромагнетизма») опубликованной в 1881 году[1].
В общем, соотношение между магнитной индукцией и напряженностью магнитного поля через магнитную проницаемость вводится как:
- B→=μH→,{\displaystyle {\vec {B}}=\mu {\vec {H}},}
и μ{\displaystyle \mu } в общем случае здесь следует понимать как тензор, что в компонентной записи имеет вид[2]:
- Bi=μijHj{\displaystyle \ B_{i}=\mu _{ij}H_{j}}
Для изотропных веществ соотношение:
- B→=μH→{\displaystyle {\vec {B}}=\mu {\vec {H}}}
можно понимать в смысле умножение вектора на скаляр (магнитная проницаемость сводится в этом случае к скаляру).
В системе СГС магнитная проницаемость — безразмерная величина, в Международной системе единиц (СИ) вводят как размерную (абсолютную), так и безразмерную (относительную) магнитные проницаемости:
- μr=μμ0{\displaystyle \mu _{r}={\frac {\mu }{\mu _{0}}}},
- где μr{\displaystyle \mu _{r}} — относительная, а μ{\displaystyle \mu } — абсолютная проницаемость, μ0{\displaystyle \mu _{0}} — магнитная постоянная.
Нередко обозначение μ{\displaystyle \mu } используется не для абсолютной, а именно для относительной магнитной проницаемости (при этом μ{\displaystyle \mu } совпадает с таковым в СГС).
Размерность абсолютной магнитной проницаемости в СИ такая же, как размерность магнитной постоянной, то есть Гн/м или Н/А2.
Относительная магнитная проницаемость в СИ связана с магнитной восприимчивостью χ соотношением:
- μr=1+χ,{\displaystyle \mu _{r}=1+\chi ,}
а в Гауссовой системе магнитная проницаемость связана с магнитной восприимчивостью χ соотношением:
- μ=1+4πχ.{\displaystyle \mu =1+4\pi \chi .}
Вообще говоря, магнитная проницаемость зависит как от свойств вещества, так и от величины и направления магнитного поля для анизотропных веществ (и, кроме того, от температуры, давления и т. д.).
Также она зависит от скорости изменения поля со временем, в частности, для синусоидального изменения поля — зависит от частоты этого колебания (в этом случае для описания намагничивания вводят комплексную магнитную проницаемость, чтобы описать влияние вещества на сдвиг фазы B относительно H). При достаточно низких частотах — небольшой быстроте изменения поля, её можно обычно считать в этом смысле независимой от частоты.
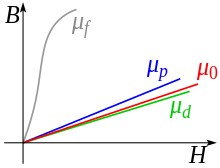 Схематический график зависимости ‘B’ от ‘H’ (кривая намагничивания) для ферромагнетиков, парамагнетиков и диамагнетиков, а также для вакуума, иллюстрирующий различие магнитной проницаемости (представляющей собою наклон графика) для: ферромагнетиков (μf), парамагнетиков (μp), вакуума(μ0) и диамагнетиков (μd)
Схематический график зависимости ‘B’ от ‘H’ (кривая намагничивания) для ферромагнетиков, парамагнетиков и диамагнетиков, а также для вакуума, иллюстрирующий различие магнитной проницаемости (представляющей собою наклон графика) для: ферромагнетиков (μf), парамагнетиков (μp), вакуума(μ0) и диамагнетиков (μd) 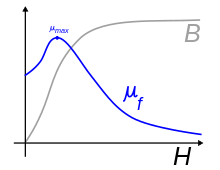
- Магнитная проницаемость сильно зависит от величины поля для нелинейных по магнитной восприимчивости сред (типичный пример — ферромагнетики, для которых характерен магнитный гистерезис). Для таких сред магнитная проницаемость, как независящее от поля число, может указываться приближенно, в линейном приближении.
- Для парамагнетиков и диамагнетиков линейное приближение достаточно хорошо выполняется для широкого диапазона изменения величины поля.
Классификация веществ по значению магнитной проницаемости[править | править код]
Подавляющее большинство веществ относятся либо к классу диамагнетиков (μ⪅1{\displaystyle \mu \lessapprox 1}), либо к классу парамагнетиков (μ⪆1{\displaystyle \mu \gtrapprox 1}). Но существует ряд веществ — (ферромагнетики), например железо, обладают более выраженными магнитными свойствами.
Для ферромагнетиков, вследствие гистерезиса, понятие магнитной проницаемости, строго говоря, неприменимо. Однако, в определённом диапазоне изменения намагничивающего поля (в тех случаях, когда можно было пренебречь остаточной намагниченностью, но до насыщения) можно, в лучшем или худшем приближении, всё же представить эту зависимость как линейную (а для магнитомягких материалов ограничение снизу может быть и не слишком практически существенно), и в этом смысле величина магнитной проницаемости бывает измерена и для них.
Магнитная проницаемость сверхпроводников равна нулю, так как материал выталкивает магнитное поле при переходе в сверхпроводящее состояние, иногда говорят, что сверхпроводники — идеальные диамагнетики.
Абсолютная магнитная проницаемость воздуха приблизительно равна магнитной проницаемости вакуума и в технических расчетах принимается равной[3] магнитной постоянной = 4π × 10−7{\displaystyle 4\pi \ \times \ 10^{-7}} Гн/м
Магнитные проницаемости некоторых веществ и материалов[править | править код]
Относительная магнитная проницаемость некоторых[4] веществ[править | править код]
| Парамагнетики, μ>1{\displaystyle \mu >1} | (μ−1)⋅10−6{\displaystyle (\mu -1)\cdot 10^{-6}} | Диамагнетики, μ<1{\displaystyle \mu <1} | (1−μ)⋅10−6{\displaystyle (1-\mu )\cdot 10^{-6}} |
|---|---|---|---|
| Азот | 0,013 | Водород | 0,063 |
| Воздух | 0,38 | Бензол | 7,5 |
| Кислород | 1,9 | Вода | 9 |
| Эбонит | 14 | Медь | 10,3 |
| Алюминий | 23 | Стекло | 12,6 |
| Вольфрам | 176 | Каменная соль | 12,6 |
| Платина | 360 | Кварц | 15,1 |
| Жидкий кислород | 3400 | Висмут | 176 |
Магнитная восприимчивость и магнитная проницаемость некоторых материалов[править | править код]
| Medium | Восприимчивость χm (объемная, СИ) | Проницаемость μ, Гн/м | Относительная проницаемость μ/μ0 | Магнитное поле | Максимум частоты |
|---|---|---|---|---|---|
| Метглас (англ. Metglas) | 1,25 | 1 000 000[5] | при 0,5 Тл | 100 кГц | |
| Наноперм (англ. Nanoperm) | 10⋅10-2 | 80 000[6] | при 0,5 Тл | 10 кГц | |
| Мю-металл | 2,5⋅10-2 | 20 000[7] | при 0,002 Тл | ||
| Мю-металл | 50 000[8] | ||||
| Пермаллой | 1,0⋅10-2 | 8000[7] | при 0,002 Тл | ||
| Электротехническая сталь | 5,0⋅10-3 | 4000[7][нет в источнике] | при 0,002 Тл | ||
| Никель-цинковый Феррит | 2,0⋅10-5 — 8,0⋅10-4 | 16-640 | от 100 кГц до 1 МГц[источник не указан 2907 дней] | ||
| Марганец-цинковый Феррит | >8,0⋅10-4 | 640 (и более) | от 100 кГц до 1 МГц | ||
| Сталь | 1,26⋅10-4 | 100[7] | при 0,002 Тл | ||
| Никель | 1,25⋅10-4 | 100[7] — 600 | при 0,002 Тл | ||
| Неодимовый магнит | 1,05[9] | до 1,2—1,4 Тл | |||
| Платина | 1,2569701⋅10-6 | 1,000265 | |||
| Алюминий | 2,22⋅10-5[10] | 1,2566650⋅10-6 | 1,000022 | ||
| Дерево | 1,00000043[10] | ||||
| Воздух | 1,00000037[11] | ||||
| Бетон | 1[12] | ||||
| Вакуум | 0 | 1,2566371⋅10-6 (μ0) | 1[13] | ||
| Водород | -2,2⋅10-9[10] | 1,2566371⋅10-6 | 1,0000000 | ||
| Фторопласт | 1,2567⋅10-6[7] | 1,0000 | |||
| Сапфир | -2,1⋅10-7 | 1,2566368⋅10-6 | 0,99999976 | ||
| Медь | -6,4⋅10-6 или -9,2⋅10-6[10] | 1,2566290⋅10-6 | 0,999994 | ||
| Вода | -8,0⋅10-6 | 1,2566270⋅10-6 | 0,999992 | ||
| Висмут | -1,66⋅10-4 | 1 | 0,999834 | ||
| Сверхпроводники | −1 | 0 | 0 |
- ↑ Werner von Siemens, Lebenserinnerungen
- ↑ Подразумевается суммирование по повторяющемуся индексу (j), то есть запись следует понимать так: μijHj≡∑j=13μijHj.{\displaystyle \mu _{ij}H_{j}\equiv \sum \limits _{j=1}^{3}\mu _{ij}H_{j}.} Эта запись, как легко видеть, означает умножение вектора слева на матрицу по правилам матричного умножения.
- ↑ Намагничивание стали. Магнитная проницаемость. (неопр.) (недоступная ссылка). Дата обращения 16 июля 2011. Архивировано 19 марта 2011 года.
- ↑ Магнитная проницаемость. Магнитная проницаемость среды. Относительная магнитная проницаемость. Магнитная проницаемость вещества (неопр.) (недоступная ссылка). Дата обращения 16 июля 2011. Архивировано 12 февраля 2012 года.
- ↑ «Metglas Magnetic Alloy 2714A», »Metglas» (неопр.) (недоступная ссылка). Metglas.com. Дата обращения 8 ноября 2011. Архивировано 3 июня 2012 года.
- ↑ «Typical material properties of NANOPERM», »Magnetec» (неопр.) (PDF). Дата обращения 8 ноября 2011.
- ↑ 1 2 3 4 5 6 «Relative Permeability», »Hyperphysics» (неопр.). Hyperphysics.phy-astr.gsu.edu. Дата обращения 8 ноября 2011. Архивировано 3 июня 2012 года.
- ↑ Nickel Alloys-Stainless Steels, Nickel Copper Alloys, Nickel Chromium Alloys, Low Expansion Alloys (неопр.). Nickel-alloys.net. Дата обращения 8 ноября 2011. Архивировано 3 июня 2012 года.
- ↑ Juha Pyrhönen, Tapani Jokinen, Valéria Hrabovcová. Design of Rotating Electrical Machines (неопр.). — John Wiley and Sons, 2009. — С. 232. — ISBN 0-470-69516-1.
- ↑ 1 2 3 4 Richard A. Clarke. Clarke, R. »Magnetic properties of materials», surrey.ac.uk (неопр.). Ee.surrey.ac.uk. Дата обращения 8 ноября 2011. Архивировано 3 июня 2012 года.
- ↑ B. D. Cullity and C. D. Graham (2008), Introduction to Magnetic Materials, 2nd edition, 568 pp., p.16
- ↑ NDT.net. Determination of dielectric properties of insitu concrete at radar frequencies (неопр.). Ndt.net. Дата обращения 8 ноября 2011. Архивировано 3 июня 2012 года.
- ↑ точно, по определению.




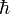 ),
тогда электроны, протоны и нейтроны
имеют спин равный ½
),
тогда электроны, протоны и нейтроны
имеют спин равный ½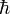 .
В атоме электроны обращаются вокругядраи обладаюторбитальным
угловым моментомпомимо спина, в
то время как ядро само по себе имеет
угловой момент благодаря ядерному
спину.[31]
.
В атоме электроны обращаются вокругядраи обладаюторбитальным
угловым моментомпомимо спина, в
то время как ядро само по себе имеет
угловой момент благодаря ядерному
спину.[31]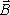 по
замкнутому контуру. Начнём с простого
контура. Пусть для начала контур
совпадает с силовой линией магнитного
поля прямолинейного тока (рис. 9.7.). По
определению, циркуляция вектора по
замкнутому контуру равна следующему
интегралу:
по
замкнутому контуру. Начнём с простого
контура. Пусть для начала контур
совпадает с силовой линией магнитного
поля прямолинейного тока (рис. 9.7.). По
определению, циркуляция вектора по
замкнутому контуру равна следующему
интегралу: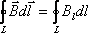
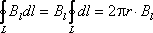 .
(9.15)
Согласно (9.8),
.
(9.15)
Согласно (9.8),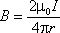 .
Поэтому циркуляцию вектора
.
Поэтому циркуляцию вектора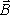 (9.15)
можно записать так:
(9.15)
можно записать так: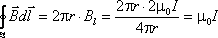 Вывод.
В рассмотренном частном случаециркуляция
вектора магнитной индукции по
замкнутому контуру пропорциональна
току, охватываемому этим контуром.
Вывод.
В рассмотренном частном случаециркуляция
вектора магнитной индукции по
замкнутому контуру пропорциональна
току, охватываемому этим контуром.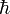 ),
тогда электроны, протоны и нейтроны
имеют спин равный ½
),
тогда электроны, протоны и нейтроны
имеют спин равный ½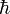 .
В атоме электроны обращаются вокругядраи обладаюторбитальным
угловым моментомпомимо спина, в то
время как ядро само по себе имеет
угловой момент благодаря ядерному
спину.[31]
.
В атоме электроны обращаются вокругядраи обладаюторбитальным
угловым моментомпомимо спина, в то
время как ядро само по себе имеет
угловой момент благодаря ядерному
спину.[31]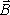 по
замкнутому контуру. Начнём с простого
контура. Пусть для начала контур
совпадает с силовой линией магнитного
поля прямолинейного тока (рис. 9.7.). По
определению, циркуляция вектора по
замкнутому контуру равна следующему
интегралу:
по
замкнутому контуру. Начнём с простого
контура. Пусть для начала контур
совпадает с силовой линией магнитного
поля прямолинейного тока (рис. 9.7.). По
определению, циркуляция вектора по
замкнутому контуру равна следующему
интегралу: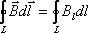 .
.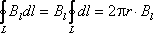 .
(9.15)
.
(9.15)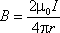 .
Поэтому циркуляцию вектора
.
Поэтому циркуляцию вектора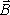 (9.15)
можно записать так:
(9.15)
можно записать так: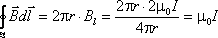 .
.