Работа как физическая величина. Физика, 7 класс: уроки, тесты, задания.

1.	Условия совершения механической работы Сложность: лёгкое	3
2.	Килоджоули Сложность: лёгкое	1
3.	Миллиджоули Сложность: лёгкое	1
4.	Зависимость работы от направления силы Сложность: лёгкое	3
5.	Примеры механической работы Сложность: лёгкое	2
6.	Совершается или не совершается работа? Сложность: лёгкое	1
7.	Работа, совершаемая при подъёме гидравлического молота Сложность: среднее	2
8.	Величина проделанной работы Сложность: среднее	2
9.	Расчёт работы Сложность: среднее	2
10.	Расчёт работы (2) Сложность: среднее	2
11.	Работа. Задача Сложность: среднее	3
12.	Вычисление работы Сложность: сложное	5
13.	Вычисление массы Сложность: сложное	5

Механическая работа — это… Что такое Механическая работа?

Механическая работа

Работа силы

Ключевые статьи

См. также: Портал:Физика

Механическая работа — это физическая величина, являющаяся скалярной количественной мерой действия силы или сил на тело или систему, зависящая от численной величины, направления силы (сил) и от перемещения точки (точек) тела или системы

[1].

Определение

В механике можно ввести понятие работы, исходя из довольно простых представлений^[2]

Работа силы (сил) над одной точкой

• Работа нескольких сил определяется естественным образом как работа их равнодействующей (их векторной суммы). Поэтому дальше будем говорить об одной силе.

При прямолинейном движении одной материальной точки и постоянном значении приложенной к ней силы работа (этой силы) равна произведению величины проекции вектора силы на направление движения и величины совершённого перемещения^[3]:

Здесь точкой обозначено скалярное произведение^[4],  — вектор перемещения; подразумевается, что действующая сила постоянна в течение всего того времени, за которое вычисляется работа.

Если сила не постоянна, то в этом случае она вычисляется как интеграл^[5]:

(подразумевается суммирование по кривой, которая является пределом ломаной, составленной из последовательных перемещений если вначале считать их конечными, а потом устремить длину каждого к нулю).

Если существует зависимость силы от координат^[6], интеграл определяется^[7] следующим образом:

,

где и  — радиус-векторы начального и конечного положения тела соответственно.

• Cледствие: если направление движения тела ортогонально силе, работа (этой силы) равна нулю.

Работа силы (сил) над системой или неточечным телом

Работа сил над системой материальных точек определяется как сумма работ этих сил над каждой точкой (работы, совершённые над каждой точкой системы, суммируются в суммарную работу этих сил над системой).

Даже если изначально тело не является системой дискретных точек, можно разбить его (мысленно) на множество бесконечно малых элементов (кусочков), каждый из которых считать материальной точкой, вычисляя работу в соответствии с определением выше. В этом случае дискретная сумма заменяется на интеграл.

• Эти определения могут быть использованы как для какой-то конкретной силы или класса сил — для вычисления именно их работы отдельно, так и для вычисления полной работы, совершаемой всеми силами, действующими на систему.

Кинетическая энергия

Кинетическая энергия вводится в механике в прямой связи с понятием работы.

Схема рассуждений такова: 1) попробуем записать работу, совершаемую всеми силами, действующими на материальную точку и, пользуясь вторым законом Ньютона (позволяющим выразить силу через ускорение), попытаться выразить ответ только через кинематические величины, 2) убедившись, что это удалось, и что этот ответ зависит только от начального и конечного состояния движения, введём новую физическую величину, через которую эта работа будет просто выражаться (это и будет кинетическая энергия).

Если  — полная работа, совершённая над частицей, определяемая как сумма работ совершенных приложенными к частице силами, то она выражается как:

где называется кинетической энергией. Для материальной точки, кинетическая энергия определяется как работа силы, ускорившей точку от нулевой скорости до величины скорости и выражается как:

Для сложных объектов, состоящих из множества частиц, кинетическая энергия тела равна сумме кинетических энергий частиц.

Потенциальная энергия

Сила называется потенциальной, если существует скалярная функция координат, известная как потенциальная энергия и обозначаемая , такая что

Если все силы, действующие на частицу консервативны, и является полной потенциальной энергией, полученной суммированием потенциальных энергий соответствующих каждой силе, тогда:

.

Этот результат известен как сохранение механической энергии и утверждает, что полная механическая энергия в замкнутой системе, в которой действуют консервативные силы

является постоянной относительно времени. Этот закон широко используется при решении задач классической механики.

Работа в термодинамике

В термодинамике работа, совершенная газом при расширении^[8], рассчитывается как интеграл давления по объёму:

Работа, совершенная над газом, совпадает с этим выражением по абсолютной величине, но противоположна по знаку.

• Естественное обобщение этой формулы применимо не только к процессам, где давление есть однозначная функция объема, но и к любому процессу (изображаемому любой кривой в плоскости PV), в частности, к циклическим процессам.
• В принципе, формула применима не только к газу, но и к чему угодно, способному оказывать давление (надо только чтобы давление в сосуде было всюду одинаковым, что неявно подразумевается в формуле).

Эта формула прямо связана с механической работой. Действительно, попробуем написать механическую работу при расширении сосуда, учитывая, что сила давления газа будет направлена перпендикулярно каждой элементарной площадке, равна произведению давления P на площадь dS площадки, и тогда работа, совершаемая газом для смещения h одной такой элементарной площадки будет

Видно, что это и есть произведение давления на приращение объема вблизи данной элементарной площадкой. А просуммировав по всем dS получим конечный результат, где будет уже полное приращение объема, как и в главной формуле параграфа.

Рассмотрим несколько детальнее, чем это было сделано выше, построение определения энергии как риманова интеграла.

Пусть материальная точка движется по непрерывно дифференцируемой кривой , где s — переменная длина дуги, и на неё действует сила , направленная по касательной к траектории в направлении движения (если сила не направлена по касательной, то будем понимать под проекцию силы на положительную касательную кривой, таким образом сведя и этот случай к рассматриваемому далее). Величина , называется элементарной работой силы на участке и принимается за приближенное значение работы, которую производит сила , воздействующая на материальную точку, когда последняя проходит кривую . Сумма всех элементарных работ является интегральной суммой Римана функции .

В соответствии с определением интеграла Римана, можем дать определение работе:

Предел, к которому стремится сумма всех элементарных работ, когда мелкость разбиения стремится к нулю, называется работой силы вдоль кривой .

Таким образом, если обозначить эту работу буквой , то, в силу данного определения,

,

следовательно,

(1).

Если положение точки на траектории её движения описывается с помощью какого-либо другого параметра (например, времени) и если величина пройденного пути , является непрерывно дифференцируемой функцией, то из формулы (1) получим

Единицей измерения работы в СИ является Джоуль, в СГС — эрг

1 Дж = 1 кг·м²/с² = 1 Н·м

1 эрг = 1 г·см²/с² = 1 дин·см

1 эрг = 10⁻⁷Дж

Ссылки

1. ↑ Концепции современного естествознания
2. ↑ Такие представления можно конкретизировать как систему постулатов, приводящую достаточно однозначно к определению, описанному в основной статье:
   1. работу совершает только компонента силы, совпадающая с направлением перемещения точки, к которой она приложена, или противоположная направлению перемещения точки (в последнем случае работа считается отрицательной),
   2. работа постоянной силы пропорциональна компоненте такой силы, описанной в пункте 1, и длине вектора перемещения,
   3. работа по перемещению точки за несколько последовательных промежутков времени суммируется (работа за всё это время равна сумме работ, совершенных за каждый промежуток),
   4. работа суммы (векторной суммы) сил, приложенных к точке равна сумме работ, совершенных каждой силой в отдельности,
   5. работа, совершенная над системой (телом) равна сумме работ, совершенных над каждой ее частью (в частности — равна сумме работ, совершенных над каждой точкой системы).
3. ↑ Механическая работа. Мощность
4. ↑ Можно считать, что механическая работа может служить в области физики одной из главных иллюстраций для скалярного произведения.
5. ↑ Это делается исходя из того, что можно разбить суммарное конечное перемещение на маленькие последовательные перемещения , на каждом из которых сила будет почти постоянной, а значит можно будет воспользоваться определением для постоянной силы, введенным выше. Затем работы на всех этих перемещениях суммируется, что и дает в результате интеграл.
6. ↑ Как это очень часто бывает. Например, в случае кулоновского поля, растягивающейся пружины, силы тяготения планеты итд итд.
7. ↑ По сути через предыдущий, поскольку здесь ; вектор же малого перемещения совпадает с .
8. ↑ Работа, совершаемая газом при его сжатии, очевидно отрицательна, но вычисляется по той же формуле. Работа, совершаемая газом (или над газом) без его расширения или сжатия (например, в процессе перемешивания мешалкой), в принципе может быть выражена подобной формулой, но всё же не прямо этой, так как она требует обобщения: дело в том, что в формуле давление подразумевается одинаковым по всему объему (что часто выполняется в термодинамике, поскольку речь там часто идет о процессах, близких к равновесным), что и приводит к наиболее простой формуле (в случае же вращающейся мешалки, например, давление будет разным на передней и задней стороне лопасти, что приведет к необходимому усложнению формулы, если мы захотим применить ее к такому случаю; эти соображения относятся и ко всем другим неравновесным случаям, когда давление неодинаково в разных частях системы).

Литература

• Кудрявцев Л. Д. Курс математического анализа. — 5-е, переработанное и дополненное. — М.: Дрофа, 2003. — Т. 1. — С. 640—641. — 703 с.

См. также

Механическая работа (Работа силы)

Еще в древности при применении простых машин (рычаг, блок, ворот и т. д.) была обнаружена замечательная особенность всех этих машин: оказалось, что в простых машинах перемещения вполне определенным образом связаны с силами, развиваемыми машиной. Именно, отношение перемещений двух концов простой машины, к которым приложены силы, всегда обратно отношению сил, приложенных к этим концам.

Например, если для равновесия рычага сила F₁ должна быть в n раз больше по модулю силы F₂ (смотри рисунок), то при вращении рычага путь S₁ , пройденный точкой приложения силы F₁, будет в n раз меньше пути S₂, пройденного точкой приложения силы F₂.

Это обстоятельство было сформулировано еще в древности следующим образом: «то, что мы выигрываем в силе, мы проигрываем в пути». Положение это имеет столь общее и вместе с тем столь важное значение, что оно получило название «золотого правила» механики. Заметим, что «золотое правило» механики практически соблюдается только в тех случаях, когда движение простых машин происходит равномерно или с малыми ускорениями.

Пользуясь введенными обозначениями, можно выразить «золотое правило» формулой

,

или

F₁S₁ = F₂S₂

Итак, мы видим, что в простой машине при равномерном движении всегда существует вполне определенная связь между силами и перемещениями: если направления силы и перемещения совпадают, то произведения силы на перемещение для обеих точек приложения сил оказываются одинаковыми. Таким образом, это произведение играет особую роль: с его помощью можно характеризовать действие простых машин (отметим, что эта характеристика используется для многих иных явлений). Ввиду его важности это произведение рассматривается как самостоятельная физическая величина, получившая название работы силы.

Общее выражение для работы силы выглядит следующим образом:

А = F S cos α

Работа силы при перемещении равна произведению модулей силы и перемещения и косинуса угла между ними.

Сила и перемещение — векторные величины, характеризующиеся как модулем, так и направлением.

Работа — скалярная физическая величина. Знак работы определяется знаком cos :

• Работа силы положительна (А > 0), если угол α острый (0° < α < 90°), cos α > 0.
• Работа силы, отрицательна (А < 0), если угол α тупой (90° < α < 180°), cos α < 0.
• Работа силы перпендикулярной перемещению, равна нулю (α = 90°) cos α = 0.

Т. е. положительной считается работа сил, сонаправленных с перемещением тела, отрицательной — работа сил, направленных противоположно перемещению.

Если на движущееся тело действуют несколько сил, то в выражении для работы используется модуль равнодействующей всех сил. Работа же этой равнодействующей равна сумме работ отдельных сил.

Домашняя работа к уроку «Физические величины. Измерение физических величин»

Предлагаемое домашняя работа состоит из двух частей: практическая часть и творческая.

Практическая часть представляет собой логическую игру, где ученику для анализа будет предложен НЕ научный текст (игра создается учителем на специализированных сайтах по генерированию тестов, кроссвордов, логических игр и др. Ссылку на игру учитель размещает в электронном журнале, своем сайте, если такой есть, и дает учащимся). Задача  учащегося внимательно прочесть текст, проанализировать его и вычленить такие понятия как физическая величина, обозначение физической величины, название и обозначение единиц измерения физических величин и название прибора для измерения физической величины.

Посмотреть пример практической части домашнего задания можно по ссылке: логическая игра

В творческой части ученику предлагается самому придумать и изготовить прибор для измерения физической величины. 

Следует заметить, что первая часть работы обязательна для всех, а творческая часть может быть предложена, только для желающих (на усмотрение учителя).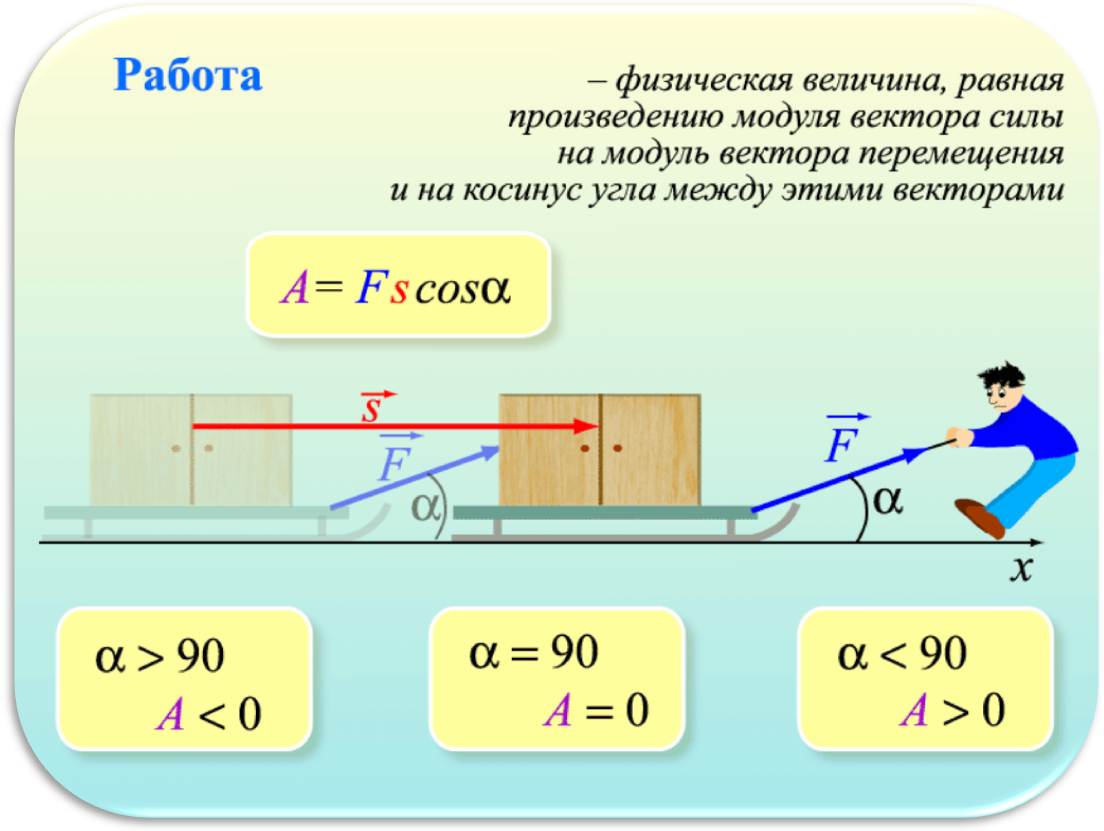  

Необычность данного задания для ученика состоит в том, что:

1. стандартное домашнее задание, к которому привык ребенок, это прочесть параграф и выполнить упражнение. Здесь же ученику предлагают прочесть и проанализировать обычный текст, который он может встретить в жизни; 

 2. первая часть задания выполняется в интернете, а это значит ребенок может его выполнить в любом месте, в любое время, что очень удобно. Отмечу, что такая форма выполнения домашнего задания может быть интересна учащимся;

3. творческая часть задания позволяет включить свое воображение, показать свои знания по данной теме и, конечно, подключить свое умение работать руками.

Удобство для учителя заключается в том, что интернет сайты на которых учитель сделает первую часть  домашней работы очень удобны в использовании, так как за учителя будет проделана вся работа по анализу выполнения детьми задания. Это существенно экономит время учителя, что немало важно. Кроме того, при подготовке к уроку учитель будет знать какие понятия ученики хорошо усвоили, а какие следует отработать. Более того в анализе результатов по прохождению задания можно увидеть время, которое учащиеся потратили на его выполнения и соответственно можно судить а том, было ли это задание сложным для учеников или легким, а может в самый раз  по сложности. Ну а по результатам творческой работы можно устроить выставку или придумать конференцию, или игру про палату мер и весов. Тут все уже ограничивается фантазией и возможностями учителя и детей.

 

Механическая работа. Мощность

В данной теме речь пойдёт о механической работе и мощности.

Механическая работа — это скалярная физическая величина, которая характеризует процесс перемещения тела под действием силы. Под действием постоянной силы тело двигается прямолинейно и совершает перемещение в направлении действия силы, то сила совершает работу, равную произведению модуля этой силы и модуля перемещения.

Из определения следует единица измерения работы в метрической системе единиц

Эта единица названа в честь английского ученого Джеймса Прескотта Джоуля, впервые экспериментально обосновавшего эквивалентность работы и теплоты.

Это самый простой случай, когда перемещение тела и сила, действующая на него, совпадают по направлению.

Теперь рассмотрим, как вычисляется работа, когда направление действия силы не совпадает с направлением перемещения тела. Для этого рассмотрим следующий опыт. Через блок перекинута нить на которой висит брусок некоторой массы. На брусок действуют две силы — сила тяжести и сила натяжения нити.

Если равномерно тянуть за нить, то тело будет равномерно двигаться, и, следовательно, результирующая сила, действующая на тело, будет равна нулю.

Значит, при некотором перемещении тела работа результирующей силы тоже будет равна нулю.

Однако сила натяжения нити совершает работу.

Поскольку при равномерном движении сила натяжения нити по модулю равна силе тяжести тела, то можно предположить, что сила тяжести совершает такую же работу по величине, но отрицательную.

Отсюда можно сделать вывод: работа силы может быть положительной, отрицательной или равной нулю.

Заметим, что сила тяжести по направлению противоположна перемещению тела. Это обстоятельство и другие соображения позволяют предложить общую формулу для работы постоянной силы при равномерном прямолинейном движении. Если вектор силы и перемещения составляют между собой угол a, то работа этой силы равна произведению модуля силы на модуль перемещения и на косинус угла между ними.

Это и есть общее выражение для работы постоянной силы.

Из этой формулы видно, что в случае, когда угол между направлением вектора силы и вектора перемещения острый, то косинус этого угла будет больше нуля и, следовательно, больше нуля будет работа силы.

Если вектор силы и вектор перемещения составляют между собой тупой угол, то значение косинуса этого угла меньше нуля. Значит и работа этой силы будет отрицательна.

И, наконец, если вектор силы перпендикулярен вектору перемещения, то работа не совершается (вернее, работа этой силы равна нулю).

Если к движущемуся телу приложено несколько сил, то каждая из них совершает работу, а общая работа равна алгебраической сумме работ, совершаемых отдельными силами.

Работу, совершенную силой, можно найти и графически. Так, если действие силы на тело не меняется с течением времени и совпадает по направлению с перемещением, то работа этой силы численно равна площади заштрихованного прямоугольника.

Если же сила изменяется в процессе движения, то работа этой силы тоже будет численно равна площади под кривой. В частности, на рисунке представлен график силы, которая линейно уменьшается с пройденным расстоянием до нуля. Очевидно, что работа этой силы на пройденном пути, численно равна площади треугольника.

Ранее говорилось, что основными силами в механике являются гравитационные силы (в частности сила тяжести), силы упругости и силы трения.

Проанализируем более подробно работы, совершаемые каждой из этих сил. Начнем с работы силы тяжести. Будем ее рассматривать считая, что тело находится на небольших расстояниях от поверхности Земли. В этом случае сила тяжести будет постоянной по модулю равной

Пусть тело массой m падает с некоторой высоты h₁ до высоты h₂. Тогда модуль перемещения тела равен разности этих высот

Так как направления перемещения и силы совпадают, то работа силы тяжести положительна и равна произведению модуля силы тяжести и разности высот.

Следует помнить, что высоты, на которых находится тело, можно отсчитывать от любого уровня. Это может быть уровень поверхности Земли, пола или поверхности стола. Высоту выбранного уровня принимают равной нулю. Поэтому этот уровень называют нулевым. Так, если тело падает с высоты h до нулевого уровня, то работа силы тяжести равна

Теперь выясним, какую работу совершает сила тяжести, если тело движется не по вертикали. Для этого рассмотрим движение тела по наклонной плоскости.

Пусть тело некоторой массы m совершило перемещение, равное по модулю длине наклонной плоскости. Работа силы тяжести в этом случае равна

Из рисунка видно, что

Поэтому работа силы тяжести в этом случае также равна

Таким образом, получили для работы силы тяжести такое же выражение, как и в случае движения тела по вертикали. Отсюда следует главный вывод о том, что работа силы тяжести не зависит от того, по какой траектории движется тело и всегда равна произведению модуля силы тяжести на разность высот в начальном и конечном положениях тела.

Тогда очевидно, что если тело движется по замкнутой траектории, где начальное и конечное положения тела совпадают, то работа силы тяжести равна нулю. Напомним, что такие силы, работа которых не зависит от формы траектории, а определяется только начальным и конечным положениями тела в пространстве, называются потенциальными или консервативными. Следовательно, сила тяжести — это консервативная сила.

Теперь проанализируем работу, совершаемую силой упругости. Сила упругости — это сила, возникающая при деформации тела внешними воздействиями.

Рассмотрим систему, состоящую из пружины и тела некоторой массы, лежащего на достаточно гладкой горизонтальной поверхности. Левый конец пружины прикреплен к стене, а правый — к телу. Направим ось икс так, как показано на рисунке.

Если тело сместить на некоторое расстояние от положения равновесия, то пружина будет действовать на него с силой упругости, направленной вправо. Модуль проекции этой силы на ось Ox будет определяться на основании закона Гука.

Теперь отпустим тело. Тогда под действием силы упругости пружины тело будет смещаться вправо.

При этом сила упругости будет совершать работу. Предположим, что тело переместилось так, что расстояние от положения равновесия стало х₂. Очевидно, что тогда модуль перемещения тела равен разности между начальной и конечной координатой тела.

Для нахождения работы, совершенной пружиной по перемещению тела, необходимо учесть, что сила упругости меняется, так как ее величина зависит от удлинения пружины. Воспользуемся графиком зависимости модуля силы упругости от удлинения пружины.

Известно, что работа силы численно равна площади под графиком силы. В рассматриваемом случае это площадь трапеции, основаниями которой являются силы упругости пружины в положении один и два, а высота — это перемещение тела.

Из полученной формулы следует, что работа силы упругости пружины зависит только от координат начального и конечного положений. Из рисунка видно, что х₁ и х₂ — это и удлинение пружины, и координаты ее конца в выбранной системе координат. Следовательно, работа силы упругости не зависит от формы траектории. А если траектория замкнута, то работа равна нулю. Таким образом, сила упругости является потенциальной силой.

И проанализируем работу, совершаемую силой трения. Рассмотрим тело, находящееся на некоторой поверхности (например, брусок на поверхности стола).

Если толкнуть брусок, то он придет в движение, однако, через некоторое время, остановится. В процессе движения бруска на него действуют: сила тяжести, сила нормальной реакции опоры и сила трения скольжения. Под действием этих трех сил и движется брусок. Поскольку сила тяжести компенсируется силой нормальной реакции стола, то равнодействующая сила равна действующей на брусок силе трения. А так как сила трения направлена противоположна перемещению, то работа этой силы будет отрицательной (так как косинус ста восьмидесяти градусов равен минус единице).

Из формулы следует, что работа силы трения зависит от модуля перемещения тела. И даже если тело вернется в исходную точку, то работа силы трения не будет равна нулю. Такие силы, работа которых зависит от формы траектории движения тела и на замкнутой траектории отличны от нуля, называются непотенциальными или диссипативными (от латинского — рассеяние).

Однако не надо думать, что работа сил трения всегда отрицательна. Ведь именно благодаря силе трения покоя человек и различные машины движутся по Земле. Действительно, при ходьбе человек действует на поверхность Земли с некоторой силой F₁ (кроме силы нормальной реакции), а по третьему закону Ньютона Земля действует на ногу человека с силой трения покоя, равной по модулю силе воздействия человека, но противоположно направленной. Благодаря этой силе человек движется. Сила трения покоя направлена также, как и скорость человека, и, следовательно, работа этой силы положительна.

Таки образом, были рассмотрены работы основных трех сил, с которыми чаще всего мы сталкиваемся в механике. Однако, одна и та же работа в разных случаях может быть выполнена за различные промежутки времени, то есть она может совершаться неодинаково быстро. Очевидно, что чем меньшее времени требуется для выполнения данной работы, тем эффективнее работает машина, механизм и прочее.

Величина, характеризующая быстроту совершения работы, и равная отношению работы, совершаемой силой, к промежутку времени, в течение которого она совершается, называется мощностью.

Исходя из определения видим, что единицей измерения мощности является

Эта единица получила название Ватт, в честь английского ученого Джеймса Уатта — изобретателя универсального парового двигателя.

При движении любого тела на него в общем случае действует несколько сил, каждая из которых совершает работу и, следовательно, для каждой силы можно вычислить мощность. Так, если тело движется прямолинейно и на него действует постоянная сила, то она совершает работу, равную

Тогда мощность силы равна отношению работы этой силы к промежутку времени.

Мощность силы также равна произведению модуля силы на модуль скорости и на косинус угла между направлениями вектора силы и вектора скорости.

По записанной формуле можно рассчитывать и среднюю, и мгновенную мощности, подставляя значение средней или мгновенной скорости.

Из полученной формулы следует, что при заданной мощности мотора сила тяги тем меньше, чем больше скорость движения. Вот почему водители автомобилей при подъеме в гору, когда нужна наибольшая сила тяги, переключают двигатель на пониженную передачу.

И так, любой двигатель или механическое устройство предназначены для выполнения определенной механической работы. Эта работа называется полезной работой. Для двигателя автомобиля — это работа по его перемещению, для токарного станка — работа по вытачиванию детали.

Однако в любой машине, в любом двигателе полезная работа всегда меньше той энергии, которая затрачивается для приведения их в действие, потому что всегда существуют силы трения, работа которых приводит к нагреванию каких-либо частей устройства. А нагревание нельзя считать полезным результатом действия машины. Поэтому каждое устройство характеризуется особой величиной, которая показывает, насколько эффективно используется подводимая к нему энергия. Эта величина называется коэффициентом полезного действия и обычно обозначается греческой буквой h.

И так, коэффициентом полезного действия называется отношение полезной работы, совершенной машиной за некоторый промежуток времени, ко всей затраченной работе (или подведенной энергии) за тот же промежуток времени.

Коэффициент полезного действия обычно выражается в процентах. Поскольку и полезную, и затраченную работы можно представить, как произведение мощности на промежуток времени в течение которого работала машина, то

Основные выводы:

Рассмотрели важную физическую величины – работу. Рассмотрели работы наиболее часто встречающихся сил — силы тяжести, упругости и силы трения. Повторили понятие мощности, а также вспомнили, что называют коэффициентом полезного действия механизма.

Обобщающий урок по физике в 7 классе. по теме: «Механическая работа и мощность».

Обобщающий урок по физике в 7 классе.

по теме: «Механическая работа и мощность».

Учителя физики: Вельбой А.Н.

Обобщающий урок по физике в 7 классе.

по теме: «Механическая работа и мощность».

Цель урока:

Образовательные: проверить теоритические знания и практические навыки и умения по теме «Работа и мощность»

Развивающие: развивать умения делать необходимые расчеты; логические рассуждения.

Воспитательные: выработать умения работать в коллективе, активизировать мыслительную деятельность учащихся.

Тип урока: урок повторения и обобщения ранее изученного материала.

Вид урока: урок – соревнование и урок-практикум.

Методы обучения: работа с раздаточным материалом; решение задач.

Оборудование: конверты с заданиями для каждой команды.

Ход урока.

1. Организационный момент.

Учащиеся рассаживаются по местам, заранее разделившись на 2 команды и выбирают капитана команды.

2. Проведения урока –соревнования и практикума

Учитель: Здравствуйте, ребята! Эпиграфом к нашему уроку будут слова «Жизнь учит только тех, кто её изучает».В. Ключевского

Нужно трудиться, лучше изучить окружающий нас мир. Мир, в котором всем нам приходится жить, расти, взрослеть, — огромен, сложен, иногда даже опасен. Согласитесь, что вам придется многое узнать и многому научиться, чтобы найти своё место в этом мире. В моем приветствии прозвучало слово трудиться С какой физической величиной, которую мы уже изучили связано это слово.? Правильно, работа, а еще какая физическая величина не может существовать без работы? Правильно, мощность. Мы сегодня с вами на уроке вспомним эти понятия, формулы по которым они вычисляются и единицы измерения. Урок наш пройдет в виде соревнования двух групп, во второй половине урока мы проделам практическую работу и порешаем задачи.Ф сечас делимся на две команды

Задания для конверта 1. «Найди правильную дорогу».

В данном конверте карточка, где в три столбика выписаны обозначения физических величин, их единицы и их названия. Необходимо стрелками соединить каждую физическую величину со своей единицей измерения и названием:

Обозначение физической величины

Единица измерения

Название физической величины

V

м\с

Плотность

ρ

Дж

Сила

M

М³

Работа

A

Вт

Масса

F

Кг\м³

Объем

υ

Кг

Мощность

N

Н

Скорость

Задания для конверта 2. «Найди лишнего».

В конверт вложены карточки с терминами. Необходимо найти лишнюю карточку.

«Физические величины»: объем, масса, плотность, сила, скорость, механическая работа, газ, вес, длина, время, мощность. (газ)

«Физические явления»: молния, инерция, радуга, падение тел, тяготение, движение, момент силы, нагревание, трение. (мощность)

Задания для конверта 3. «Найди правильные формулы».

В конверте 10 -15 карточек, на которых выписаны формулы. Среди которых только 4 -6 правильных.

Продолжим наш путь дальше .Я предлагаю всем тестовую работу:

Ответьте «да» или «нет» (на слайде вопросы)(+)или (-)

1.Луна, двигаясь вокруг Земли, совершает механическую работу.

2.Гиря, висящая на шнуре, совершает механическую работу.

3.Пассажир, едущий в автобусе, совершает механическую работу.

4.Муха, летающая по комнате, совершает механическую работу.

5.Ученик, думающий над решением задачи, совершает механическую работу.

6.Девочка, играя на скрипке, совершает механическую работу.

7.Ветер, гонящий по небу облака, совершает механическую работу.

8.Ученик, бегущий стометровку, совершает механическую работу.

9.Компьютер, решая задачу, совершает механическую работу.

10.Земля, двигаясь по орбите вокруг Солнца, совершает механическую работу.

Ответы :нет нет нет да нет да да да нет нет.

Итак , ребята на сегодня путь по теме «Механическая работа и мощность» окончен. Как вы считаете , цели поставленные в начале урока достигнуты ? Работа , которую вы сегодня совершили можно назвать положительной? Что нового для себя вы узнали ? Довольны ли собственной работой? И все – таки вы сегодня работали или трудились ?

В завершение я хочу обратиться к вам со следующими стихами:

Путь к цели выбирайте трудный —
Пусть жжет огонь и льет вода,
В ушах уже грохочут трубы…
Запомни — выбор есть всегда!

Домашнее задание:

Подготовить презентацию(5 слайдов) по теме:

— Простые механизмы

— Простые механизмы на кухне

— Простые механизмы в помощь огороднику

Предложите, как определить самого мощного ученика в вашем классе

Презентация к уроку физики в 7 классе «Работа и мощность»

библиотека
материалов

Содержание слайдов

Номер слайда 1

Механическая работа и мощность. Курс дистанционного обучения по физике«Простые механизмы»Урок №1

Номер слайда 2

Что такое механическая работа?Работа. В обыденной жизни под словом «работа» мы называем различные действия человека или устройства. Например, мы говорим:работает пылесосработает компьютер

Номер слайда 3

Не мешай мне работать! Я читаюучебник физики! ЧТО МЫ ПОНИМАЕМ ПОД СЛОВОМ «РАБОТА»?Подумаешь! Я тожеработаю – прыгаю!В физике «механической работой» называют работу какой-нибудь силы (силы тяжести, упругости, трения и т. д.) над телом, в результате действия которой тело перемещается.

Номер слайда 4

Механическая работа не совершается, если тело не сдвинули!Выполняется ли работа?

Номер слайда 5

Пример выполненной работы. Кто совершает работу?- Лошадь!

Номер слайда 6

Пример выполненной работы

Номер слайда 7

Условия для выполнения работы. На тело должна действовать сила FПод действием этой силы тело должно перемещаться

Номер слайда 8

Работа — физическая величина, равная произведению силы, действующей на тело, на путь, совершенный телом под действием силы в направлении этой силы. А = F · s. А — механическая работа,F — сила,S — пройдённый путь.

Номер слайда 9

— физическая величина, которая характеризует результат действия силы. А — механическая работа, F — сила, S — пройденный путь. МЕХАНИЧЕСКАЯ РАБОТА

Номер слайда 10

МЕХАНИЧЕСКАЯ РАБОТАСИ: [A] = [H ∙ м = Дж]1 Дж = 1 Н ∙ 1м

Номер слайда 11

Единицы работы1к. Дж=1000 Дж1 МДж=1000 000 Дж1м. Дж=0,001 Дж. Fт=1 Н1м. За единицу работы принимают работу, совершаемую силой в 1 Н, на пути, равном 1 м. Измеряют в Джоулях. А = 1 Дж=1 Н·1м

Номер слайда 12

Когда механическая работа не совершается?ххstyle.colorfillcolorfill.typefill.onrrrrr

Номер слайда 13

SFFтр. SFт. SИтак, если сила и перемещение сонаправлены, то совершается положительная работа!Если сила и перемещение перпендикулярны друг другу, то работа не совершается!Если сила и перемещение противоположно направлены, то совершается отрицательная работа!rrr

Номер слайда 14

Кто быстрее совершит одинаковую работу?Почему?

Номер слайда 15

Мощность- физическая величина, которая характеризует скорость выполнения работы. Мощность. Работа. Время=N=A / t

Номер слайда 16

Мощность характеризует быстроту совершения работы. Мощность (N) – физическая величина, равная отношению работы A к промежутку времени t, в течение которого совершена эта работа. Мощность показывает, какая работа совершается за единицу времени.

Номер слайда 17

В Международной системе (СИ) единица мощности называется Ватт (Вт) в честь английского изобретателя Джеймса Ватта (Уатта), построившего первую паровую машину.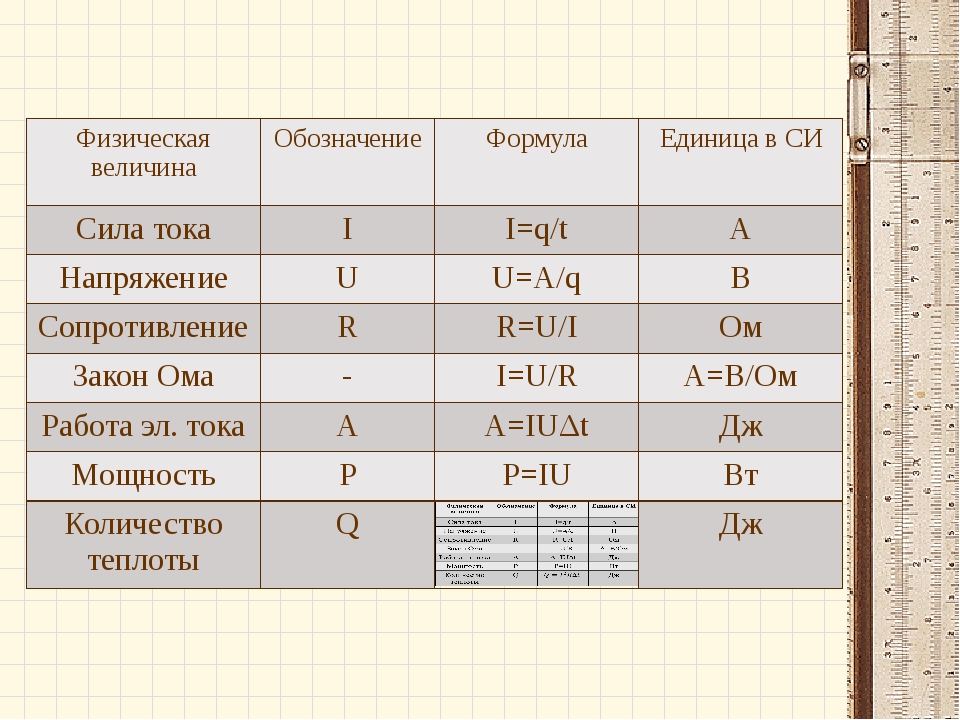 [ N ] = Вт = Дж / c1 Вт = 1 Дж / 1с1 Ватт равен мощности силы, совершающей работу в 1 Дж за 1 секунду

Номер слайда 18

Сам Ватт (1736-1819) пользовался другой единицей мощности — лошадиной силой (1 л.с.), которую он ввёл с целью возможности сравнения работоспособности паровой машины и лошади.1л.с. = 735 Вт«Живые двигатели» кратковременно могут повышать свою мощность в несколько раз. Лошадь может доводить свою мощность при беге и прыжках до десятикратной и более величины.

Номер слайда 19

Единицы мощности1к. Вт=1000 Вт1 МВт=1000 000 Вт1м. Вт=0,001 Вт1 л.с=736 Вт. Fт=1 Н1м. За единицу мощности принимают работу, совершаемую силой в 1 Дж, за 1 секунду. Измеряют в Ваттах. N = 1 Вт=1 Дж/1с1л.с. = 735 Вт

Номер слайда 20

ОКАЗЫВАЕТСЯ, ЧТО … Оказывается, самым мощным источником механической энергии является огнестрельное оружие!С помощью пушки можно бросить ядро массой 900кг со скоростью 500м/с, развивая за 0,01 секунды около 110 000 000 Дж работы. Эта работа равнозначна работе по подъему 75 т груза на вершину пирамиды Хеопса (высота 150м ). Мощность выстрела пушки будет составлять 11 000 000 000 Вт = 15 000 000 л.с.

Номер слайда 21

Домашнее задание§55-56 читать, выучить формулы работы и мощности. Решить задачи в учебнике: упражнение №31 (1,2,3,4) задачник №661 (устно), № 672, 706 (письменно).

Номер слайда 22

Задача Какова мощность крана, который поднимает плиту массой 12 тонн на высоту 30 метра за 2 минуты?Решение: N = A/t A = F * S S = h. F = m * g N= 120000 Дж/120с Дано: m = 12тh = 30мt = 2 мин. Найти: N = ?Ответ: N= 1к. Вт = 12000кг = 120 с= 12000кг * 9,8 Н/кг= 120000 Дж= 1000 Вт. Ответ: N= 1к. Вт

Номер слайда 23

Какую работу совершал Кирилл, поднимая кирпичи для кладки печи, на высоту 0,5 м. Размеры кирпича 20х 10х 5 см3.style.colorfillcolorfill.type

Номер слайда 24

Дано: СИ Решение: а= 20 см b= 10 cм c = 5 cм h = 0,5 м ρ = 1800 кг/ М3 А — ?= 0,2 м= 0,1 м= 0,05 м. А = F ∙S S = h. F = m ∙gm = ρ∙ VV = a ∙b∙c. V= 0,2 м ∙0,1 м∙0,05 м = 0,001 М3m = 1800 кг/ М3 ∙ 0, 001 м3 = 1,8 кг F = 1,8 кг ∙10 =18 Н А = 18 Н ∙ 0,5 м = 9 Дж

Номер слайда 25

Какую мощность развивает Анатолий, поднимая из колодца глубиной 6 м ведро воды за 1, 5 минуты? Объём воды в ведре 8 л, масса пустого ведра 400 г.

Номер слайда 26

Дано: СИ Решение: h= 6 м m1= 400 г V = 8 л t= 1,5 мин.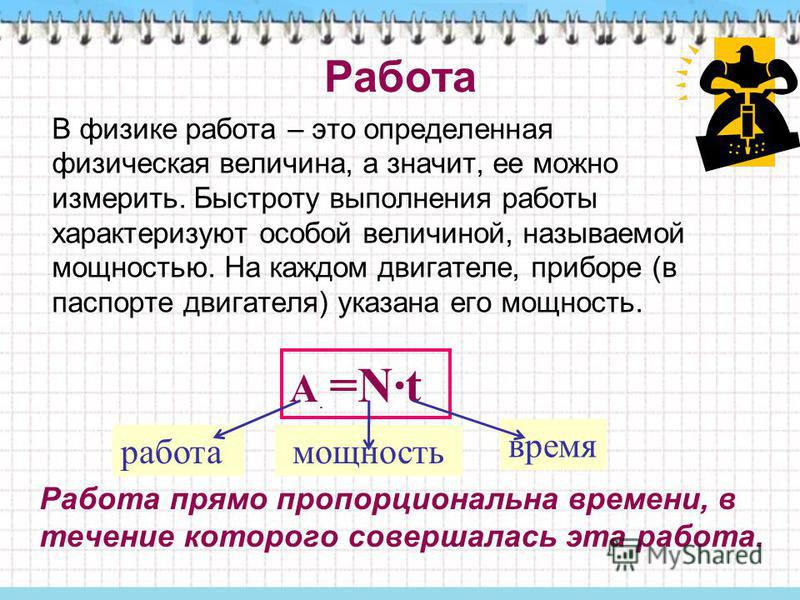 N-? = 0,4 кг= 0,008 М3 = 90 с. N = F = m ∙g A = F ∙s s = hm = m1 + m2 m2 = ρ∙Vm2 = 1000 кг/М3 ∙0, 008 М3 = 8 кг F = ( 8 кг + 0,4 кг)∙9,8 ≈ 84 НА = 84 Н ∙6 м = 504 Дж. N = = 5,6 Вт

Номер слайда 27

Гришка, сколачивая опалубку, развивал мощность 0,1 к. Вт, делая 60 ударов молотком за 1 минуту. Определите работу, производимую им за 1 удар.

Номер слайда 28

Дано: Си Решение: N = 0,1 к. Вт n= 60 t= 1мин А- ?=100 Вт = 60 с. N = A = N ∙ t. A 1 = A = 100 Вт ∙60 с = 600 Дж А 1 = = 100 Дж

1.3 Язык физики: физические величины и единицы

Точность, прецизионность и значащие числа

Наука основана на экспериментах, требующих точных измерений. Достоверность измерения можно описать с точки зрения его точности и прецизионности (см. Рисунок 1.19 и рисунок 1.20). Точность — это насколько измерение близко к правильному значению для этого измерения. Например, предположим, что вы измеряете длину стандартного листа бумаги для принтера.На упаковке, в которой вы приобрели бумагу, указано, что она имеет длину 11 дюймов, и предположим, что указанное значение верное. Вы трижды измеряете длину бумаги и получаете следующие размеры: 11,1 дюйма, 11,2 дюйма и 10,9 дюйма. Эти измерения довольно точны, потому что они очень близки к правильному значению 11,0 дюймов. Напротив, если бы вы получили размер в 12 дюймов, ваше измерение не было бы очень точным. Вот почему измерительные приборы калибруются на основе известного измерения.Если прибор постоянно возвращает правильное значение известного измерения, его можно безопасно использовать для поиска неизвестных значений.

Рис. 1.19. Механические весы с двумя чашами используются для сравнения различных масс. Обычно объект неизвестной массы помещается в одну чашу, а объекты известной массы — в другую. Когда стержень, соединяющий две посуды, расположен горизонтально, массы в обеих посуде равны. Известные массы обычно представляют собой металлические цилиндры стандартной массы, например 1 грамм, 10 грамм и 100 грамм.(Серж Мелки)

Рис. 1.20. В то время как механические весы могут считывать массу объекта только с точностью до десятых долей грамма, некоторые цифровые весы могут измерять массу объекта с точностью до ближайшей тысячной доли грамма. Как и в других измерительных приборах, точность шкалы ограничивается последними измеренными цифрами. Это сотые доли в изображенной здесь шкале. (Splarka, Wikimedia Commons)

«Точность» указывает, насколько хорошо повторные измерения чего-либо дают одинаковые или похожие результаты.Следовательно, точность измерений означает, насколько близки друг к другу измерения, когда вы измеряете одно и то же несколько раз. Один из способов анализа точности измерений — определение диапазона или разницы между самым низким и самым высоким измеренными значениями. В случае размеров бумаги для принтера наименьшее значение составляло 10,9 дюйма, а максимальное значение — 11,2 дюйма. Таким образом, измеренные значения отклонялись друг от друга не более чем на 0,3 дюйма. Эти измерения были достаточно точными, потому что они варьировались всего на долю дюйма.Однако, если бы измеренные значения были 10,9 дюймов, 11,1 дюймов и 11,9 дюймов, тогда измерения не были бы очень точными, потому что есть много отклонений от одного измерения к другому.

Измерения в бумажном примере точны и точны, но в некоторых случаях измерения точны, но неточны, или они точны, но неточны. Давайте рассмотрим систему GPS, которая пытается определить местоположение ресторана в городе. Думайте о расположении ресторана как о самом центре мишени в яблочко.Затем представьте каждую попытку GPS определить местонахождение ресторана как черную точку в яблочко.

На рис. 1.21 вы можете видеть, что измерения GPS разнесены далеко друг от друга, но все они относительно близки к фактическому местоположению ресторана в центре цели. Это указывает на низкую точность измерительной системы с высокой точностью. Однако на рис. 1.22 измерения GPS сосредоточены довольно близко друг к другу, но они находятся далеко от целевого местоположения.Это указывает на высокую точность измерительной системы с низкой точностью. Наконец, на рис. 1.23 GPS является точным и точным, что позволяет определить местонахождение ресторана.

Рис. 1.21. Система GPS пытается определить местонахождение ресторана в центре мишени. Черные точки представляют каждую попытку определить местоположение ресторана. Точки расположены довольно далеко друг от друга, что указывает на низкую точность, но каждая из них находится довольно близко к фактическому местоположению ресторана, что указывает на высокую точность.(Темное зло)

Рис. 1.22 На этом рисунке точки сосредоточены близко друг к другу, что указывает на высокую точность, но они довольно далеко от фактического местоположения ресторана, что указывает на низкую точность. (Темное зло)

Рис. 1.23 На этом рисунке точки сосредоточены близко друг к другу, что указывает на высокую точность, и они находятся недалеко от фактического местоположения ресторана, что указывает на высокую точность. (Темное зло)

Неопределенность

Точность и прецизионность измерительной системы определяют неопределенность ее измерений.Неопределенность — это способ описать, насколько ваше измеренное значение отклоняется от фактического значения, которое имеет объект. Если ваши измерения не очень точны или точны, то неопределенность ваших значений будет очень высокой. В более общем плане неопределенность можно рассматривать как отказ от ответственности за ваши измеренные значения. Например, если кто-то попросил вас указать пробег вашего автомобиля, вы можете сказать, что это 45 000 миль, плюс-минус 500 миль. Сумма плюс или минус — это неопределенность в вашей стоимости.То есть вы указываете, что фактический пробег вашего автомобиля может составлять от 44 500 миль до 45 500 миль или где-то посередине. Все измерения содержат некоторую неопределенность. В нашем примере измерения длины бумаги мы можем сказать, что длина бумаги составляет 11 дюймов плюс-минус 0,2 дюйма или 11,0 ± 0,2 дюйма. Неопределенность измерения, A , часто обозначается как δA («дельта A »),

.

Факторы, способствующие неопределенности измерения, включают следующее:

1. Ограничения измерительного прибора
2. Навык человека, производящего измерение
3. Неровности в измеряемом объекте
4. Любые другие факторы, влияющие на результат (сильно зависят от ситуации)

В примере с бумагой для принтера неточность может быть вызвана: тем фактом, что наименьшее деление на линейке равно 0. 1 дюйм, человек, использующий линейку, имеет плохое зрение или неуверенность, вызванную бумагорезательной машиной (например, одна сторона бумаги немного длиннее другой). Хорошей практикой является тщательное рассмотрение всех возможных источников неопределенности в измерение и уменьшение или устранение их,

Неопределенность в процентах

Один из методов выражения неопределенности — это процент от измеренного значения. Если измерение A выражается с неопределенностью δ A , неопределенность в процентах составляет

1.2% неопределенность = δAA × 100%.% Неопределенность = δAA × 100%.

Рабочий пример

Расчет процента неопределенности: мешок яблок

В продуктовом магазине продаются 5-фунтовые пакеты с яблоками. Вы покупаете четыре пакета в течение месяца и каждый раз взвешиваете яблоки. Вы получите следующие размеры:

• Неделя 1 Вес: 4,8 фунта 4,8 фунта
• Вес 2 недели: 5,3 фунта 5,3 фунта
• Неделя 3 Вес: 4,9 фунта 4,9 фунта
• 4 неделя вес: 5. 4 фунта 5,4 фунта

Вы определили, что вес мешка 5 фунтов имеет погрешность ± 0,4 фунта. Какова погрешность веса мешка в процентах?

Стратегия

Во-первых, обратите внимание, что ожидаемое значение веса мешка, AA, составляет 5 фунтов. Неопределенность этого значения, δAδA, составляет 0,4 фунта. Мы можем использовать следующее уравнение для определения процентной неопределенности веса

% Неопределенности = δAA × 100%.% Неопределенности = δAA × 100%.

Решение

Подставьте известные значения в уравнение

% Неопределенности = 0.4 фунта5 фунтов × 100% = 8%.% Погрешности = 0,4 фунта5 фунтов × 100% = 8%.

Обсуждение

Мы можем сделать вывод, что вес мешка с яблоками составляет 5 фунтов ± 8 процентов. Подумайте, как изменился бы этот процент неопределенности, если бы мешок с яблоками был вдвое тяжелее, но неопределенность в весе осталась бы прежней. Совет для будущих расчетов: при вычислении процентной погрешности всегда помните, что вы должны умножить дробь на 100 процентов. Если вы этого не сделаете, у вас будет десятичное количество, а не процентное значение.

Неопределенность в расчетах

Есть неопределенность в любом вычислении на основе измеренных величин. Например, площадь пола, рассчитанная на основе измерений его длины и ширины, имеет неопределенность, потому что и длина, и ширина имеют неопределенности. Насколько велика неопределенность в том, что вы вычисляете умножением или делением? Если измерения в расчетах имеют небольшие погрешности (несколько процентов или меньше), то можно использовать метод сложения процентов.В этом методе говорится, что процент неопределенности в величине, вычисленной путем умножения или деления, представляет собой сумму процентных погрешностей в элементах, использованных для выполнения расчета. Например, если пол имеет длину 4,00 м и ширину 3,00 м с погрешностью 2 процента и 1 процент соответственно, то площадь пола составляет 12,0 м ² и имеет погрешность 3 процента ( выраженная как площадь, это 0,36 м ( ² ), которую мы округляем до 0,4 м ( ² , так как площадь пола дается с точностью до одной десятой квадратного метра).

Чтобы быстро продемонстрировать точность, прецизионность и неопределенность измерений в зависимости от единиц измерения, попробуйте это моделирование. У вас будет возможность измерить длину и вес стола, используя единицы измерения в миллиметрах и сантиметрах. Как вы думаете, что обеспечит большую точность, точность и неопределенность при измерении стола и блокнота в моделировании? Подумайте, как природа гипотезы или вопроса исследования может повлиять на точность измерительного инструмента, необходимого для сбора данных.

Прецизионность измерительных инструментов и значащих цифр

Важным фактором точности измерений является точность измерительного инструмента. В общем, точный измерительный инструмент — это инструмент, который может измерять значения с очень маленькими приращениями. Например, рассмотрите возможность измерения толщины монеты. Стандартная линейка может измерять толщину с точностью до миллиметра, а микрометр может измерять толщину с точностью до 0,005 миллиметра.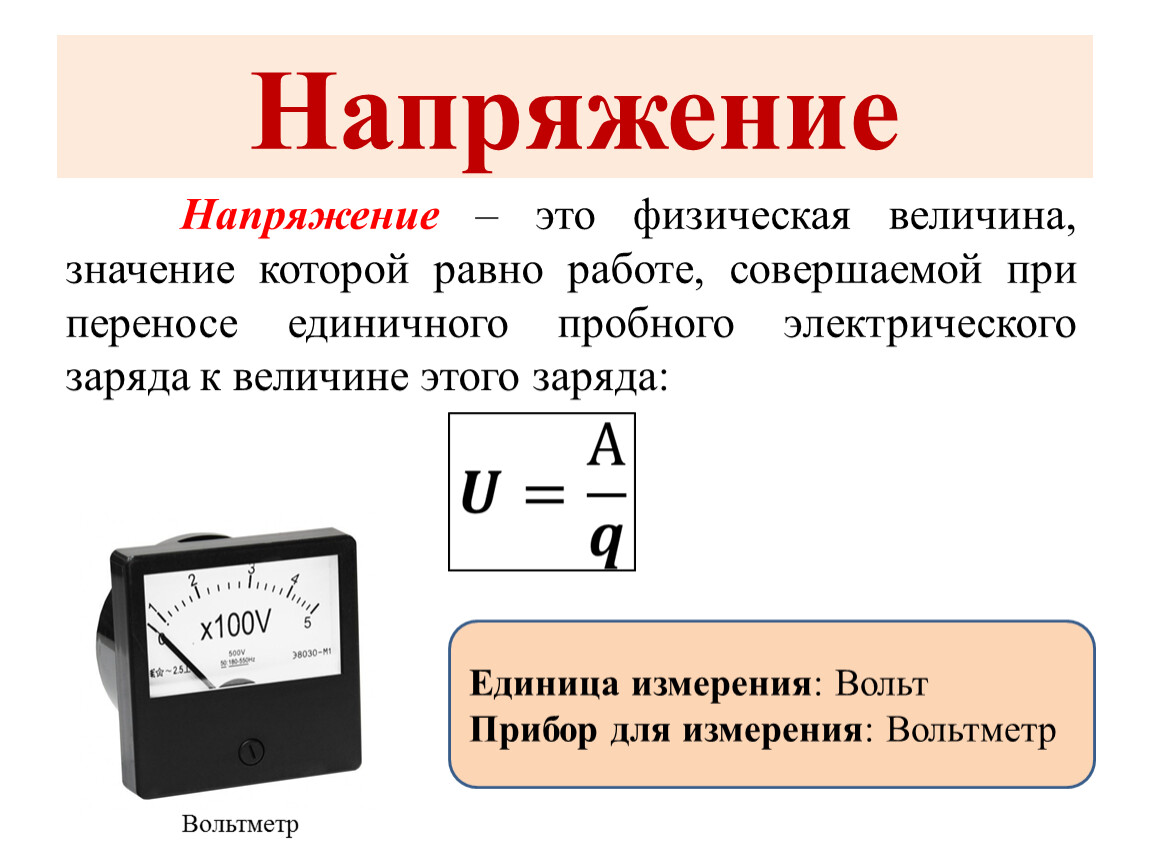 Микрометр — более точный измерительный инструмент, потому что он может измерять очень небольшие различия в толщине.Чем точнее измерительный инструмент, тем точнее и точнее могут быть измерения.

Когда мы выражаем измеренные значения, мы можем перечислить только столько цифр, сколько мы первоначально измерили с помощью нашего измерительного инструмента (например, линейки, показанные на рисунке 1.24). Например, если вы используете стандартную линейку для измерения длины палки, вы можете измерить ее дециметровой линейкой как 3,6 см. Вы не можете выразить это значение как 3,65 см, потому что ваш измерительный инструмент не был достаточно точным, чтобы измерить сотую долю сантиметра.Следует отметить, что последняя цифра в измеренном значении была определена каким-то образом лицом, выполняющим измерение. Например, человек, измеряющий длину палки линейкой, замечает, что длина палки находится где-то между 36 и 37 мм. Он или она должны оценить значение последней цифры. Правило состоит в том, что последняя цифра, записанная в измерении, является первой цифрой с некоторой погрешностью. Например, последнее измеренное значение 36,5 мм состоит из трех цифр или трех значащих цифр.Количество значащих цифр в измерении указывает на точность измерительного инструмента. Чем точнее инструмент измерения, тем большее количество значащих цифр он может сообщить.

Рисунок 1.24 Показаны три метрические линейки. Первая линейка измеряется в дециметрах и может измерять до трех дециметров. Вторая линейка имеет длину в сантиметрах и может измерять три целых шесть десятых сантиметра. Последняя линейка в миллиметрах и может измерять тридцать шесть целых пять десятых миллиметра.

Нули

Особое внимание уделяется нулям при подсчете значащих цифр.Например, нули в 0,053 не имеют значения, потому что они всего лишь заполнители, устанавливающие десятичную точку. В 0,053 есть две значащие цифры — 5 и 3. Однако, если ноль встречается между другими значащими цифрами, нули имеют значение. Например, оба нуля в 10.053 значимы, поскольку эти нули были фактически измерены. Таким образом, заполнитель 10.053 содержит пять значащих цифр. Нули в 1300 могут иметь значение, а могут и не иметь значения, в зависимости от стиля написания чисел.Они могут означать, что число известно до последнего нуля, или нули могут быть заполнителями. Итак, 1300 может иметь две, три или четыре значащих цифры. Чтобы избежать этой двусмысленности, запишите 1300 в экспоненциальном формате как 1,3 × 10 ³ . Только значащие цифры приведены в множителе x для числа в экспоненциальном представлении (в форме x × 10yx × 10y). Следовательно, мы знаем, что 1 и 3 — единственные значащие цифры в этом числе. Таким образом, нули имеют значение, кроме случаев, когда они служат только в качестве заполнителей.В таблице 1.4 приведены примеры количества значащих цифр в различных числах.

657, 4, and there are no zeros and all non-zero numbers are always significant. The second data row contains 0.4578, 4, and the first zero is only a placeholder for the decimal point. The third data row contains 0.000458, 3, and the first four zeros are placeholders needed to report the data to the ten-thousandths place. The fourth data row contains 2000.56, 6, and the three zeros are significant here because they occur between other significant figures. The fifth data row contains 45600, 3, and with no underlines or scientific notation, we assume that the last two zeros are placeholders and are not significant. The sixth data row contains 15895000 (with the third-to-last and second-to-last zeros underlined, 7, and the two underlined zeros are significant, while the last zero is not, as it is not underlined. The seventh data row contains 5.456 times ten to the thirteenth, 4, and in scientific notation, all numbers reported in front of the multiplication sign are significant. The final data row contains 6. 520 times 10 to the negative twenty-third, 4, and in scientific notation, all numbers reported in front of the multiplication sign are significant, including zeros.»>

Таблица 1.4

Номер	Значимые цифры	Обоснование
1,657	4	Нет нулей, и все ненулевые числа всегда значимы.
0,4578	4	Первый ноль — это только место для десятичной запятой.
0,000458	3	Первые четыре нуля — это заполнители, необходимые для представления данных с точностью до десятитысячных.
2000,56	6	Три нуля здесь значимы, потому что они встречаются между другими значащими цифрами.
45 600	3	Без подчеркивания или научного обозначения мы предполагаем, что последние два нуля являются заполнителями и не имеют значения.
15895 00 0	7	Два подчеркнутых нуля значимы, а последний ноль — нет, поскольку он не подчеркнут.
5,457 × 10 13	4	В экспоненциальном представлении все числа перед знаком умножения являются значащими
6.520 × 10 –23	4	В экспоненциальном представлении все числа перед знаком умножения значимы, включая нули.

Значимые цифры в расчетах

При объединении измерений с разной степенью точности и точности количество значащих цифр в окончательном ответе не может быть больше количества значащих цифр в наименее точном измеренном значении. Есть два разных правила: одно для умножения и деления, а другое — для сложения и вычитания, как описано ниже.

1. Для умножения и деления: Ответ должен иметь такое же количество значащих цифр, что и начальное значение с наименьшим количеством значащих цифр. Например, площадь круга можно вычислить по его радиусу, используя A = πr2A = πr2. Посмотрим, сколько значащих цифр будет у площади, если в радиусе всего две значащие цифры, например, r = 2,0 м. Тогда, используя калькулятор, который хранит восемь значащих цифр, вы получите

   A = πr2 = (3,1415927 …) × (2,0 м) 2 = 4,5238934 м2. A = πr2 = (3,1415927 …) × (2,0 м) 2 = 4,5238934 м2.

   Но поскольку радиус состоит только из двух значащих цифр, вычисленная площадь имеет значение только до двух значащих цифр или

   , даже если значение ππ имеет значение не менее восьми цифр.

2. Для сложения и вычитания : ответ должен иметь те же числовые разряды (например, разряд десятков, разрядов единиц, разрядов десятков и т. Д.), Что и наименее точное начальное значение. Предположим, вы купили в продуктовом магазине 7,56 кг картофеля, измеренного по шкале с точностью 0,01 кг. Затем вы кладете в лабораторию 6,052 кг картофеля, измеренного по шкале с точностью до 0,001 кг. Наконец, вы идете домой и добавляете 13,7 кг картофеля, измеренное на весах с точностью до 0.1 кг. Сколько у вас сейчас килограммов картошки и сколько значащих цифр уместно в ответе? Масса находится простым сложением и вычитанием:

   7,56 кг − 6,052 кг + 13,7 кг_ 15,208 кг 7,56 кг − 6,052 кг + 13,7 кг_ 15,208 кг

   Наименьшее измерение — 13,7 кг. Это измерение выражается с точностью до 0,1 десятичного знака, поэтому наш окончательный ответ также должен быть выражен с точностью до 0,1. Таким образом, ответ следует округлить до десятых, получая 15,2 кг. То же верно и для недесятичных чисел.Например,

   6527,23 + 2 = 6528,23 = 6528,6527,23 + 2 = 6528,23 = 6528.

   Мы не можем указать десятичные разряды в ответе, потому что 2 не имеет значимых десятичных знаков. Следовательно, мы можем отчитаться только до одного места.

   Рекомендуется оставлять лишние значащие цифры при вычислении и округлять до правильного числа значащих цифр только в окончательных ответах. Причина в том, что небольшие ошибки из-за округления при вычислении иногда могут привести к значительным ошибкам в окончательном ответе.В качестве примера попробуйте вычислить 5,098– (5.000) × (1010) 5,098– (5.000) × (1010), чтобы получить окончательный ответ только на две значащие цифры. Учет всего значимого во время расчета дает 48. Округление до двух значащих цифр в середине расчета изменяет его до 5,100 — (5.000) × (1000) = 100,5,100 — (5.000) × (1000) = 100, что вполне естественно. выключенный. Точно так же вы бы избегали округления в середине вычислений при подсчете и ведении бухгалтерского учета, когда нужно аккуратно сложить и вычесть много маленьких чисел, чтобы получить, возможно, гораздо большие окончательные числа.

Значимые цифры в этом тексте

В этом учебнике предполагается, что большинство чисел состоит из трех значащих цифр. Кроме того, во всех проработанных примерах используется постоянное количество значащих цифр. Вы заметите, что ответ, полученный из трех цифр, основан на вводе как минимум трех цифр. Если на входе меньше значащих цифр, в ответе также будет меньше значащих цифр. Также уделяется внимание тому, чтобы количество значащих цифр соответствовало создаваемой ситуации.В некоторых темах, таких как оптика, будет использоваться более трех значащих цифр. Наконец, если число является точным, например 2 в формуле, c = 2πrc = 2πr, это не влияет на количество значащих цифр в вычислении.

Рабочий пример

Приблизительные огромные числа: триллион долларов

Федеральный дефицит США в 2008 финансовом году был немногим больше 10 триллионов долларов. Большинство из нас не имеют представления о том, сколько на самом деле стоит даже один триллион.Предположим, вам дали триллион долларов банкнотами по 100 долларов. Если вы составили стопки по 100 купюр, как показано на рис. 1.25, и использовали их для равномерного покрытия футбольного поля (между концевыми зонами), сделайте приблизительное представление о том, насколько высокой станет стопка денег. (Здесь мы будем использовать футы / дюймы, а не метры, потому что футбольные поля измеряются в ярдах.) Один из ваших друзей говорит, что 3 дюйма, а другой говорит, что 10 футов. Как вы думаете?

Рис. 1.25. Банковская стопка содержит сто банкнот по 100 долларов и стоит 10 000 долларов.Сколько банковских стеков составляет триллион долларов? (Эндрю Мэджилл)

Стратегия

Когда вы представляете себе ситуацию, вы, вероятно, представляете себе тысячи маленьких стопок по 100 завернутых банкнот по 100 долларов, которые вы могли бы увидеть в фильмах или в банке. Поскольку это величина, которую легко оценить, давайте начнем с нее. Мы можем найти объем стопки из 100 купюр, узнать, сколько стопок составляют один триллион долларов, а затем установить этот объем равным площади футбольного поля, умноженной на неизвестную высоту.

Решение

1. Рассчитайте объем стопки из 100 купюр. Размеры одной банкноты составляют примерно 3 на 6 дюймов. Пачка из 100 таких банкнот имеет толщину примерно 0,5 дюйма. Таким образом, общий объем стопки из 100 купюр равен объем стопки = длина × ширина × высота, объем стопки = 6 дюймов × 3 дюйма × 0,5 дюйма, объем стопки = 9 дюймов. 3. объем стопки = длина × ширина × высота, объем стопки = 6 дюйма × 3 дюйма × 0,5 дюйма, объем стопки = 9 дюймов 3.

2. Подсчитайте количество стопок.Обратите внимание, что триллион долларов равен 1 × 1012 $ 1 × 1012, а стопка из ста 100-долларовых банкнот равна 10000, 10000 долларов или 1 × 104 доллара 1 × 104. Количество стопок у вас будет

   . 1,3 $ 1 × 1012 (триллион долларов) / 1 × 104 доллара на стек = 1 × 108 стеков. 1 доллар × 1012 (триллион долларов) / 1 × 104 доллара на стек = 1 × 108 стеков.

3. Вычислите площадь футбольного поля в квадратных дюймах. Площадь футбольного поля составляет 100 ярдов × 50 ярдов 100 ярдов × 50 ярдов, что дает 5 000 ярдов 25 000 ярдов2.Поскольку мы работаем в дюймах, нам нужно преобразовать квадратные ярды в квадратные дюймы

   . Площадь = 5000 ярдов2 × 3 фут1 ярд × 3 фут1 ярд × 12 дюймов 1 фут × 12 дюймов 1 фут = 6 480 000 дюймов 2, Площадь ≈6 × 106 дюймов 2 Площадь = 5000 ярдов2 × 3 фут1 ярд × 3 фут1 ярд × 12 дюймов 0,1 фут × 12 дюймов 1 фут = 6 480 000 дюймов 2, Площадь ≈6 × 106 дюймов 2.

   Это преобразование дает нам 6 × 106 дюймов 26 × 106 дюймов 2 для площади поля. (Обратите внимание, что в этих расчетах мы используем только одну значащую цифру.)

4. Рассчитайте общий объем купюр.Объем всех стопок по 100 долларов составляет 9 дюймов 3 / стопка × 108 стопок = 9 × 108 дюймов 39 дюймов / стопка × 108 стопок = 9 × 108 дюймов 3
5. Рассчитайте высоту. Чтобы определить высоту купюр, используйте следующее уравнение объем купюр = площадь поля × высота денег Высота денег = объем купюр площадь поля Высота денег = 9 × 108 дюймов 36 × 106 дюймов 2 = 1,33 × 102 дюймов Высота денег = 1 × 102 дюйма = 100 дюймы объем купюр = площадь поля × высота денег Высота денег = объем купюр площадь поля Высота денег = 9 × 108 дюймов36 × 106 дюймов 2 = 1,33 × 102 дюйма Высота монеты = 1 × 102 дюйма = 100 дюймов

   Высота денег будет около 100 дюймов. Преобразование этого значения в футы дает

   . 100 дюймов × 1 фут 12 дюймов = 8,33 футов ≈ 8 футов 100 дюймов × 1 фут 12 дюймов = 8,33 футов ≈ 8 футов

Обсуждение

Окончательное приблизительное значение намного выше, чем ранняя оценка в 3 дюйма, но другая ранняя оценка в 10 футов (120 дюймов) была примерно правильной. Как это приближение соответствует вашему первому предположению? Что это упражнение может сказать вам с точки зрения приблизительных оценок , и тщательно рассчитанных приближений?

В приведенном выше примере окончательное приблизительное значение намного выше, чем ранняя оценка первого друга в 3 дюйма.Однако ранняя оценка другого друга в 10 футов (120 дюймов) была примерно верной. Как это приближение соответствует вашему первому предположению? Что это упражнение может предложить о значении приблизительных приблизительных оценок по сравнению с тщательно рассчитанными приближениями?

Размеры и единицы

Механическая система, испытывающая одномерные демпфированные колебания, может быть моделируется уравнением

, где \ (m \) — масса системы, \ (b \) — некоторый коэффициент демпфирования, \ (k \) — жесткость пружины, а \ (u (t) \) — смещение система.Это уравнение, выражающее баланс трех физических эффекты: \ (mu » \) (масса, умноженная на ускорение), \ (bu ‘\) (демпфирующая сила) и \ (ку \) (сила пружины). Различные физические величины, такие как \ (m \), \ (u (t) \), \ (b \) и \ (k \), все имеют разные размеры , измеренные в разные единиц , но \ (mu » \), \ (bu ‘\) и \ (ku \) должны иметь одинаковые размерность, иначе добавлять их не было бы смысла.

Основные концепции

Базовые блоки и размеры

Базовые единицы обладают важным свойством, присущим всем остальным единицам. от них.В системе СИ таких базовых единиц семь и соответствующих физические величины: метр (м) на длину, килограмм (кг) для массы, секунды на время, кельвин (K) для температуры, ампер (А) для электрического тока, кандела (кд) для силы света, и моль (моль) для количества вещества.

Нам нужны подходящие математические обозначения для вычислений с такие измерения, как длина, масса, время и т. д. Размер длина записывается как [L], размерность массы как [M], размерность времени как [T], а размерность температуры как \ ([\ Theta] \) ( размеры остальных базовых блоков просто опущены, так как мы не производим много их использую в этом тексте). {- 2}] \)

Префиксы для единиц

Единицы часто имеют префиксы.9 \) Па.

Теорема Букингема Пи

Почти все тексты по масштабированию имеют трактовку знаменитого Бекингема. Теорема Пи, которую можно использовать для вывода физических законов на основе единицы измерения совместимость, а не лежащие в основе физические механизмы. Этот буклет сосредоточен на моделях, в которых физические механизмы уже выражены через дифференциальные уравнения. Тем не менее, Pi Теорема занимает заметное место в литературе по масштабированию, и поскольку мы время от времени будем на него ссылаться, теорема такова: кратко обсуждается ниже.

Сама теорема просто состоит из двух частей. Во-первых, если проблема включает \ (n \) физические параметры, в которых \ (m \) независимые типы единиц (например, длина, масса и т. д.), тогда параметры могут быть в сочетании с ровно \ (n-m \) независимыми безразмерными числами, отнесенными как Пи. Во-вторых, любое безразмерное отношение между исходным \ (n \) параметры могут быть преобразованы в отношение между \ (n-m \) безразмерные числа. Такие отношения могут быть идентичностями или неравенства, указывающие, например, является ли данный эффект незначительный.Более того, преобразование системы уравнений в безразмерная форма соответствует выражающим коэффициентам, а также как свободные и зависимые переменные в единицах числа Пи.

В качестве примера представьте тело, движущееся с постоянной скоростью \ (v \). Какие расстояние \ (s \), пройденное за время \ (t \)? Теорема Пи приводит к одна безразмерная переменная \ (\ pi = vt / s \) и приводит к формуле \ (s = Cvt \), где \ (C \) — неопределенная константа. Результат очень близко к известной формуле \ (s = vt \), возникающей из дифференциала уравнение \ (s ‘= v \) в физике, но с дополнительной константой.

На первый взгляд теорема Пи может показаться граничащей с тривиально. Тем не менее, это может привести к значительному прогрессу для избранных проблемы, такие как турбулентные струи, ядерные взрывы или сходство решения, без детальных знаний математических или физических модели. Следовательно, новичку в масштабировании это может показаться чем-то особенным. очень глубокий, если не волшебный. Во всяком случае, если перейти к более сложным задач со многими параметрами, использование теоремы дает сравнительно меньший выигрыш по мере увеличения числа Пи.Многие Пи также могут быть рекомбинированы разными способами. Итак, хорошо физическое понимание и / или информация, передаваемая через набор уравнений, требуется для выбрать полезные безразмерные числа или соответствующее масштабирование упомянутый набор уравнений. Иногда изучение уравнений также показывает, что некоторые числа Пи, полученные в результате применения теоремы, на самом деле может быть удалено из проблемы. Как следствие, когда моделирование сложной физической задачи, реальная оценка масштабирования и безразмерные числа так или иначе будут включены в анализ основных уравнений вместо того, чтобы быть отдельной проблемой с теоремой Пи.И в учебниках, и в статьях обсуждение масштабирование в контексте уравнений слишком часто отсутствует или представлен в нерешительности. Следовательно, внимание авторов будет об этом процессе, хотя мы не приводим много примеров по теореме Пи. Мы не говорим, что теорема Пи мало ценить. В ряде случаев, например, в экспериментах, он может предоставить ценные и даже важные рекомендации, но в частности В учебнике мы стремимся рассказать дополнительную историю о масштабировании.Кроме того, как будет показано в этом буклете, безразмерные числа в проблема также возникает очень естественным образом из-за масштабирования дифференциальные уравнения. Если есть модель, основанная на дифференциальных уравнений, в классических размерный анализ.

Абсолютные ошибки, относительные ошибки и единицы

Математически не имеет значения, какие единицы мы используем для физического количество. Однако когда мы имеем дело с приближениями и ошибками, единицы важны.{-3} \) независимо от того, измеряется ли длина в км или мм.

Тем не менее, вместо того, чтобы полагаться исключительно на относительные ошибки, лучше масштабировать проблему так, чтобы количества, входящие в вычисления имеют размер единицы (или, по крайней мере, умеренные), а не очень большой или очень маленький. Техника этих заметок показывает, как это может быть сделано.

Агрегаты и ЭВМ

Традиционные числовые вычисления включают только числа и, следовательно, требует безразмерных математических выражений.Обычно неявный используется тривиальное масштабирование. Можно, например, просто масштабировать всю длину величин на 1 м, всех временных величин на 1 с и всех массовых величин на 1 кг, чтобы получить необходимые для расчетов безразмерные числа. Это наиболее распространенный подход, хотя он очень редко используется в явном виде. заявил.

Пакеты символьных вычислений, такие как Mathematica и Maple, позволяют вычисления с величинами, имеющими размерность. Это тоже возможно в популярных компьютерных языках, используемых для численных вычислений (раздел PhysicalQuantity: инструмент для вычислений с помощью единиц предоставляет конкретный пример на Python).{-3} \)). Хотя таблицы преобразования единиц измерения часто встречаются в школе, ошибки при пересчете единиц измерения, вероятно, ранжируют самый высокий среди всех ошибок, совершаемых учеными и инженерами (и когда из-за ошибки преобразования единиц в самолете заканчивается топливо, это серьезно!). Наличие хороших программных инструментов для помощи в подразделении поэтому конверсия имеет первостепенное значение, что мотивирует лечение этого тема в разделах PhysicalQuantity: инструмент для вычислений с единицами измерения и Parampool: пользовательские интерфейсы с автоматическим преобразованием единиц.Читатели, которые в первую очередь заинтересованы в методе математического масштабирования. смело пропустите этот материал и сразу переходите к разделу Задачи экспоненциального распада.

Пример проблем, связанных с системами единиц

Немного проработанный пример масштабирования в реальном научный / инженерный проект может стимулировать читателя мотивация. В полном объеме изучено цунами и пролетов. геофизика, геология, история, гидродинамика, статистика, геодезия, инженерия и гражданская защита.Эта сложность отражается в разнообразие практик использования единиц, весов и концепции. Если сузить рамки до моделирования цунами распространение, аспект масштабирования, по крайней мере, может показаться простым, поскольку мы в основном касается продолжительности и времени. Тем не менее, даже здесь неоднородность физических единиц является препятствием.

Незначительной проблемой является периодическое использование единиц, не относящихся к системе СИ, таких как дюймы или в старых диаграммах, даже саженях. Более важна неоднородность величина различных переменных и различия в присущие, в частности, горизонтальные и вертикальные масштабы.Обычно отметки поверхности указаны в метрах или меньше. Для дальних водоемов распространения, а также небольшие цунами (которые до сих пор остаются научными интереса) отметки поверхности часто указываются в см или даже мм. В глубоком океане характерная глубина порядка величина больше этой, обычно \ (5000 \, \ hbox {m} \). Распространение расстояния, с другой стороны, составляют сотни или тысячи километров. Часто лучше всего описываются местоположения и вычислительные сети. в географических координатах (долгота / широта), которые связаны с Единицы СИ на 1 минуту широты составляют примерно одну морскую милю. (\ (1852 \, \ hbox {m} \)), и 1 минута долготы составляет это количество раз косинус широты.Периоды волн цунами в основном колеблются от от минут до часа, надеюсь, достаточно коротких, чтобы их можно было хорошо разделить из полусуточного периода приливов и отливов. Время распространения обычно часы или, может быть, лучшая часть дня, когда Тихий океан Океан пройден.

Ученые, инженеры и бюрократы в сообществе цунами имеют тенденцию быть конкретными и несоответствующими в отношении форматов и единиц измерения, поскольку а также тип требуемых данных. Чтобы удовлетворить эти требования, Разработчик моделирования цунами должен производить разнообразные данные, которые представлены в единицах измерения. и форматы, которые нельзя использовать внутри ее моделей.На с другой стороны, она также должна быть готова принять входные данные в разнообразные формы. Некоторые наборы данных могут быть большими, что означает ненужное дублирование с другими единицами измерения или масштабированием должно быть избегали. Кроме того, модели цунами часто маркируются по сравнение с экспериментальными данными. Лабораторный масштаб обычно \ (\ hbox {cm} \) или \ (\ hbox {m} \), самое большее, что подразумевает, что измеренные данные представлены в единицах, отличных от используемых в реальных событиях земного масштаба, или даже в вольтах, с информацией о преобразовании, полученной от измерительных приборов.

Все подробности устройства в различных форматах файлов явно мешают и порождают ряд заблуждений и ошибок, которые могут вызвать потеря драгоценного времени или усилий. Чтобы уменьшить такие проблемы, разработчики вычислительных инструментов должны сочетать разумную гибкость относительно единиц ввода и вывода с четким и последовательным соглашение о масштабировании в инструментах. Фактически, это также относится к академические инструменты для внутреннего использования.

Приведенное выше обсуждение указывает на некоторые передовые методы, которые продвигает.Во-первых, всегда выполняйте вычисления с помощью масштабированного дифференциального уравнения. модели. В этом буклете рассказывается, как это сделать. Во-вторых, пользователи программного обеспечения часто хотят указать входные данные с измерением и получить выходные данные с размером. Затем программное обеспечение должно применить такие инструменты, как PhysicalQuantity (раздел PhysicalQuantity: инструмент для вычислений с единицами измерения) или более сложный пакет Parampool (раздел Parampool: пользовательские интерфейсы с автоматическим преобразованием единиц измерения), чтобы разрешить ввод с явными размерами и при необходимости преобразуйте размеры в нужные типы.Эти инструменты тривиально применять, если вычислительное программное обеспечение написан на Python, но это просто, если программное обеспечение написаны на скомпилированных языках, таких как Fortran, C или C ++. В последнем случай, когда вы просто создаете модуль чтения ввода в Python, который захватывает данные из пользовательский интерфейс и передает их в вычислительное программное обеспечение, либо через файлы или вызовы функций (вызываемые соответствующие функции должны быть обернуты в Python с такими инструментами, как f2py, Cython, Ткать SWIG, Мгновенный, или аналогичный, см. [Ref03] (Приложение C) для основных примеры обертывания кода C и Fortran в f2py и Cython).

PhysicalQuantity: инструмент для вычислений с модулями

Эти заметки содержат довольно много компьютерного кода, чтобы проиллюстрировать, как теория подробно отображает работающее программное обеспечение. Python — это язык программирования используется, прежде всего потому, что это легко читаемый, мощный, полноценный язык, позволяющий использовать MATLAB-подобный код а также код на основе классов, обычно используемый в Java, C # и C ++. Экосистема Python для научных вычислений за последние годы выросла. быстро набирает популярность и заменяет более специализированные инструменты как MATLAB, R и IDL.Примеры кодирования в этом буклете требуют только знания основных процедурное программирование на Python.

Читатели без знания переменных Python, функций, тестов if, и при импорте модулей следует обращаться, например, к краткому руководству по научным Python, конспекты научных лекций Python, или полный учебник [Ref04] параллельно с чтением о Код Python в настоящих заметках.

Эти примечания относятся к Python 2.7

Python существует в двух несовместимых версиях, пронумерованных 2 и 3.Различия можно сделать небольшими, и есть инструменты для написания код, работающий под обеими версиями.

Поскольку Python версии 2 все еще доминирует в научных вычислениях мы придерживаемся этой версии, но написать код версии 2.7, максимально приближенный к версии 3.4 и позже. В большинстве наших программ отличается только оператор print . между версиями 2 и 3.

Вычисления с модулями в Python хорошо поддерживаются очень полезный инструмент PhysicalQuantity из пакета ScientificPython от Конрада Хинсен.К сожалению, ScientificPython не поддерживает писать, работать с NumPy версии 1.9 или новее, поэтому мы изолировали PhysicalQuantity объект в модуле PhysicalQuantities и сделал его общедоступным доступно на GitHub. Также существует альтернативный пакет Unum для вычислений с числами с единиц, но здесь мы будем придерживаться предыдущего модуля.

Продемонстрируем использование объекта PhysicalQuantity с помощью вычисление \ (s = vt \), где \ (v \) — скорость, заданная в единицах измерения ярдов на минута , а \ (t \) — время в часах.Сначала нам нужно знать, что единицы называются в PhysicalQuantities . Для этого запустите pydoc Физическое количество или

 Терминал> pydoc Scientific.Physics.PhysicalQuantities
 

, если у вас установлен весь пакет ScientificPython. В итоговая документация показывает имена единицы. Особенно, ярды задаются ярдом , минуты мин , а часы по ч . Теперь мы можем вычислить \ (s = vt \) следующим образом:

 >>> # С ScientificPython:
>>> от Науч.Physics.PhysicalQuantities import \
... PhysicalQuantity как PQ
>>> # С PhysicalQuantities как отдельным / автономным модулем:
>>> из PhysicalQuantities импортировать PhysicalQuantity как PQ
>>>
>>> v = PQ ('120 ярдов / мин') # скорость
>>> t = PQ ('1 h') # время
>>> s = v * t # расстояние
>>> print s # s - строка
120,0 ч * ярд / мин
 

Нечетная единица ч * ярд / мин лучше преобразовать в стандартную единицу СИ, например как метр:

 >>> с.convertToUnit ('м')
>>> print s
6583,68 м
 

Обратите внимание, что s — это объект PhysicalQuantity со значением и Ед. изм. Для математических вычислений нам нужно извлечь значение как объект с плавающей запятой . Мы также можем извлечь единицу в виде строки:

 >>> print s.getValue () # float
6583,68
>>> print s.getUnitName () # строка
м
 

Вот пример того, как преобразовать единицу нечетной скорости ярды на минута на что-то более стандартное:

 >>> v.{-1} \)
где джоуль заменяет калорийность? 

 
 >>> c = PQ ('1 кал / (г * К)')
>>> c.convertToUnit ('Дж / (г * К)')
>>> печать c
4,184 Дж / К / г
 
 Parampool: пользовательский интерфейс с автоматическим преобразованием единиц измерения 
 Пакет Parampool позволяет
создание пользовательских интерфейсов с поддержкой юнитов и юнитов
конверсия. Значения параметров можно задать в виде числа с
Ед. изм. Параметры могут быть зарегистрированы заранее с предпочтительным
единица измерения, и все, что предписывает пользователь, значение и единица измерения
преобразован так, что единица станет зарегистрированной единицей.2 \), \ (t \) быть
время измеряется в с, и, следовательно, \ (с \) будет расстоянием, измеренным в м.
 Пул параметров 
 Во-первых, Parampool требует от нас определить пул   всех входных данных.
параметры, которые здесь просто представлены списком словарей, где каждый
словарь содержит информацию об одном параметре. Возможно
организовать входные параметры в древовидной структуре с подпулами, которые
сами могут иметь
субпулы,
но для нашего простого приложения нам просто нужна плоская структура с
три входных параметра:
\ (v_0 \), \ (a \) и \ (t \).Эти параметры помещаются в подпул под названием
"Главный". Пул создается по коду
 def define_input ():
    бассейн = [
        'Главный', [
            dict (name = 'начальная скорость', по умолчанию = 1.0, unit = 'm / s'),
            dict (name = 'acceleration', по умолчанию = 1.0, unit = 'm / s ** 2'),
            dict (name = 'time', по умолчанию = 10.0, unit = 's')
            ]
        ]

    из parampool.pool.UI import listtree2Pool
    pool = listtree2Pool (pool) # преобразовать список в объект Pool
    возвратный бассейн
 
 Для каждого параметра мы можем определить логическое имя, например,  начальная скорость ,
значение по умолчанию и единица измерения.Дополнительные свойства
также разрешены, см. документацию Parampool.
 Совет: укажите значения чисел по умолчанию как объекты с плавающей запятой
 Обратите внимание, что мы пишем не просто 1, а 1.0 по умолчанию.
Если бы использовалось 1, Parampool интерпретировал бы наш параметр как
целое число и поэтому преобразует ввод, например,  2,5 м / с  в  2 м / с .
Чтобы гарантировать, что параметр с действительным знаком становится объектом  float  внутри
пула, мы должны указать значение по умолчанию как действительное число:  1. или  1.0 .
(Тип входного параметра может быть также задан  явно  с помощью
свойство  str2type , например,  str2type = float .)
 Получение данных пула для вычислений 
 Мы можем сделать небольшую функцию для получения значений из пула
и вычисление \ (s \):
 дистанция def (бассейн):
    v_0 = pool.get_value ('начальная скорость')
    a = pool.get_value ('ускорение')
    t = pool.get_value ('время')
    s = v_0 * t + 0.5 * а * т ** 2
    вернуть s
 
 Функция  pool.get_value  возвращает числовое значение
названный параметр, после того, как единица была преобразована из того, что
Пользователь указал, что было зарегистрировано в пуле.
Например, если пользователь предоставляет аргумент командной строки  - время '2 ч' , Parampool преобразует это количество в секунды и  pool.get_value ('time')  вернет 7200.
 Чтение параметров командной строки 
 Для выполнения вычислений мы определяем пул, загружаем значения из
командная строка и позвоните по номеру  на расстояние :
 пул = define_input ()
из Parampool.menu.UI import set_values_from_command_line
pool = set_values_from_command_line (пул)

s = расстояние (бассейн)
print 's =% g'% s
 
 В именах параметров с пробелами должен использоваться символ подчеркивания вместо пробела.
в параметре командной строки, например, в  --Initial_velocity .
Теперь мы можем запустить
 Терминал> python distance.py --initial_velocity '10 km / h '\
          - ускорение 0 - время '1 ч
s = 10000
 
 Обратите внимание на ответ ( s ), что 10 км / ч преобразуется в м / с, а 1 ч - в с.
 Также можно получить значения параметров как  PhysicalQuantity  объекты из пула по телефону
 v_0 = pool.get_value_unit ('Начальная скорость')
 
 Следующий вариант функции  расстояние  вычисляет с
значений и единиц:
 def distance_unit (пул):
    # Вычислить с помощью единиц
    из parampool.PhysicalQuantities импортировать PhysicalQuantity как PQ
    v_0 = pool.get_value_unit ('начальная скорость')
    a = pool.get_value_unit ('ускорение')
    t = бассейн.get_value_unit ('время')
    s = v_0 * t + 0,5 * a * t ** 2
    вернуть s.getValue (), s.getUnitName ()
 
 Тогда мы можем сделать
 с, s_unit = Distance_unit (пул)
print 's =% g'% s, s_unit
 
 и получите результат с нужным блоком.
 Установка значений по умолчанию в файле 
 В больших приложениях с большим количеством входных параметров часто нравится
для определения (огромного) набора значений по умолчанию для конкретного случая, а затем
переопределите некоторые из них в командной строке.Такие наборы значений по умолчанию
может быть установлен в файле с использованием синтаксиса типа
 вспомогательный пул Главный
начальная скорость = 100! ярд / мин
ускорение = 0! м / с ** 2 # ускорение падения
конец
 
 Аппарат можно отдать после ! Символ  (и перед символом комментария  # ).
 Для чтения таких файлов нам нужно добавить строки
 из parampool.pool.UI import set_defaults_from_file
pool = set_defaults_from_file (пул)
 
 перед вызовом на  set_defaults_from_command_line .
 Если приведенные выше команды хранятся в файле  distance.dat , мы даем
информация об этом файле в программу через
option  --poolfile distance.dat . Запуск всего
 Терминал> python distance.py --poolfile distance.dat
s = 15,25 м
 
 сначала загружает скорость
100 ярдов / мин преобразовано в 1,524 м / с и нулевое ускорение
в систему пула и затем мы вызываем  distance_unit , который
загружает эти значения из пула вместе со значением по умолчанию для
время, установленное на 10 с.Тогда расчет будет \ (s = 1,524 \ cdot 10 + 0 = 15,24 \)
с блоком м. Мы можем изменить время и / или два других
параметры в командной строке:
 Терминал> python distance.py --poolfile distance.dat --time '2 h'
s = 10972,8 м
 
 В результате вычислений будет \ (s = 1,524 \ cdot 7200 + 0 = 10972,8 \).
Предлагаем вам поиграть с программой distance.py.
 Указание нескольких значений входных параметров 
 Parampool имеет интересную особенность: можно назначить несколько значений.
к входному параметру, тем самым облегчая приложению
пройти через все комбинации всех параметров.Мы можем продемонстрировать эту особенность, составив таблицу из \ (v_0 \), \ (a \), \ (t \) и
\ (s \) значения. В функции вычисления нам нужно вызвать  pool.get_values ​​ вместо  pool.get_value , чтобы получить список всех значений, которые
были указаны для рассматриваемого параметра. Вложением петель поверх
все параметры, мы посещаем все комбинации всех параметров как
указано пользователем:
 def Distance_table (бассейн):
    "" "Получение нескольких значений параметров из пула." ""
    таблица = []
    для v_0 в пуле.get_values ​​('начальная скорость'):
        для a в pool.get_values ​​('ускорение'):
            для t в pool.get_values ​​('time'):
                s = v_0 * t + 0,5 * a * t ** 2
                table.append ((v_0, a, t, s))
    таблица возврата
 
 Если для параметра было указано только одно значение,  pool.get_values ​​ возвращает только это значение, и будет только один проход в связанном
петля.
 После загрузки аргументов командной строки в наш объект  pool , мы можем вызвать  Distance_table  вместо  distance  or  distance_unit  and
напишите красиво отформатированную таблицу результатов:
 table = distance_table (бассейн)
print '| ----------------------------------------------- ------ | '
печать '| v_0 | а | т | с | '
print '| ----------------------------------------------- ------ | '
для v_0, a, t, s в таблице:
    печать '|% 11.3f | % 10.3f | % 10.3f | % 12.3f | ' % (v_0, a, t, s)
print '| ----------------------------------------------- ------ | '
 
 Вот пример выполнения,
 Терминал> python distance.py --time '1 ч и 2 ч и 3 ч' \
          - ускорение '0 м / с ** 2 и 1 м / с ** 2 и 1 ярд / с ** 2' \
      --initial_velocity '1 и 5'
| ------------------------------------------------- ---- |
| v_0 | а | т | s |
| ------------------------------------------------- ---- |
| 1.000 | 0,000 | 3600.000 | 3600.000 |
| 1.000 | 0,000 | 7200.000 | 7200.000 |
| 1.000 | 0,000 | 10800.000 | 10800.000 |
| 1.000 | 1.000 | 3600.000 | 6483600.000 |
| 1.000 | 1.000 | 7200.000 | 25927200.000 |
| 1.000 | 1.000 | 10800.000 | 58330800.000 |
| 1.000 | 0,914 | 3600.000 | 5928912.000 |
| 1.000 | 0,914 | 7200.000 | 23708448.000 |
| 1.000 | 0,914 | 10800.000 | 53338608.000 |
| 5.000 | 0,000 | 3600.000 | 18000.000 |
| 5.000 | 0,000 | 7200.000 | 36000.000 |
| 5.000 | 0,000 | 10800.000 | 54000.000 |
| 5.000 | 1.000 | 3600.000 | 6498000.000 |
| 5.000 | 1.000 | 7200.000 | 25956000.000 |
| 5.000 | 1.000 | 10800.000 | 58374000.000 |
| 5.000 | 0,914 | 3600.000 | 5943312.000 |
| 5.000 | 0,914 | 7200.000 | 23737248.000 |
| 5.000 | 0,914 | 10800.000 | 53381808.000 |
| ------------------------------------------------- ---- |
 
 Обратите внимание, что некоторые из нескольких значений имеют разные размеры.
из зарегистрированного измерения для этого параметра, а таблица
показывает, что преобразование в правильное измерение имело место.
 Создание графического пользовательского интерфейса 
 Для удовольствия мы можем легко создать графический пользовательский интерфейс.
через Parampool. Мы оборачиваем функцию  distance_unit  в функцию, которая
возвращает результат в красивом HTML-коде:
 def distance_unit2 (пул):
    # Перенести результат из distance_unit в HTML
    s, s_unit = Distance_unit (пул)
    return ' Distance: % .2f% s'% (s, s_unit)
 
 Кроме того, мы должны сделать файл  generate_distance_GUI.py  с
простое содержание
 из импорта parampool.generator.flask сгенерировать
с расстояния импорт distance_unit2, define_input

генерировать (distance_unit2, pool_function = define_input, MathJax = True)
 
 Запуск  generate_distance_GUI.py  создает веб-сайт на основе Flask.
интерфейс
для нашей функции  distance_unit , см. Рисунок Web GUI, где параметры могут быть указаны с единицами измерения.
Текстовые поля в этом графическом интерфейсе позволяют указывать параметры с
числа и единицы, e.g., ускорение с единицей измерения ярдов в минуту в квадрате,
как показано на рисунке. Слегка наведя указатель мыши слева от
текстовое поле вызывает появление маленького черного окошка с зарегистрированным устройством
этого параметра.
  Веб-интерфейс, в котором параметры могут быть указаны с помощью единиц 
 С примерами, показанными выше, читатель должен уметь использовать  PhysicalQuantity  объект и пакет Parampool в программах
и тем самым безопасно работать с юнитами. В следующем тексте, где мы обсуждаем
умение масштабировать подробно, мы просто будем работать в стандартных единицах СИ
и избегайте преобразования единиц измерения, чтобы больше не использовать  PhysicalQuantity  и Parampool.
 2.3: Измерения обычно встречающихся величин 
 В природе существует множество явлений, которые можно объяснить простыми соотношениями между наблюдаемыми явлениями.
 Пример 2.5 Период маятника
 Рассмотрим простой маятник, состоящий из массивного боба, подвешенного к фиксированной точке на веревке. Пусть  \ (\ text {T} \)  обозначает интервал времени (период маятника), в течение которого качель совершает один цикл колебаний. Как период простого маятника зависит от величин, определяющих маятник, и величин, определяющих движение?
  Раствор 
 Какие возможные количества задействованы? Длина маятника \ (\ text {l} \), масса маятника bob \ {\ text {m} \), ускорение свободного падения \ (\ text {g} \) и угловая амплитуда bob \ (\ theta_ {0} \) - это все возможные величины, которые могут вступать во взаимосвязь в течение периода колебания.Включили ли мы все возможные количества? Мы никогда не можем быть уверены, но давайте сначала поработаем с этим набором, и если нам нужно больше, нам придется подумать больше! Наша задача состоит в том, чтобы найти функцию \ (\ text {f} \) такую, что \ [T = f \ left (l, m, g, \ theta_ {0} \ right) \]. Сначала мы составляем список размеры наших количеств, как показано в таблице 2.4.
 Наименование количества
 Символ
 Размерная формула
 Время поворота
 \ (\ text {t} \)
 \ (\ text {T} \)
 Длина маятника
 \ (\ text {l} \)
 \ (\ text {L} \)
 Масса маятника
 \ (\ text {m} \)
 \ (\ text {M} \)
 Ускорение свободного падения
 \ (\ text {g} \)
 \ (L \ cdot T ^ {- 2} \)
 Угловая амплитуда качания
 \ (\ theta_ {0} \)
 Без размера
 Наше первое наблюдение состоит в том, что масса боба не может входить в наши отношения, поскольку наша конечная величина не имеет измерений массы, и никакая другая величина не имеет измерений массы.{1/2} \]
 измерений физических величин - учебный материал для IIT JEE 

  Введение в размеры физических величин 
 Природа физической величины описывается природой ее размеров. Когда мы наблюдаем за объектом, первое, что мы замечаем, - это его размеры. Фактически, мы также определяемся или наблюдаемся в отношении наших размеров, то есть роста, веса, количества мяса и т. Д. Размер тела означает, насколько оно соотносимо с точки зрения основных величин.Когда мы определяем размерность количества, мы обычно определяем его идентичность и существование. Становится ясно, что все во вселенной имеет измерение, а значит, и присутствие.
  Изображение 1: Размеры определяют форму объекта 

  Определение размеров физических величин 
 Размерность физической величины  определяется как степени, до которых возводятся фундаментальные величины, чтобы представить эту величину. Семь основных величин заключены в квадратные скобки [] для обозначения его размеров.
   Примеры  
 Размерность длины описывается как [L], размерность времени описывается как [T], размерность массы описывается как [M], размерность электрического тока описывается как [A], а размерность количества Величина может быть описана как [моль]. Добавляем еще один параметр температуры [K], а этот параметр силы света составляет [Cd]
.
 Рассмотрим физическую величину Q, которая зависит от основных величин, таких как длина, масса, время, электрический ток, количество вещества и температура, когда они возведены в степени a, b, c, d, e и f.Тогда размерность физической величины Q может быть задана как:
  [Q] = [L  a  M  b  T  c  A  d  моль  e  K  f ] 
 Мы обязательно используем [] для записи измерения физической величины. В реальной жизни все записано в единицах измерения массы, длины и времени. Обратите внимание на несколько примеров, приведенных ниже:
  1.  Объем твердого тела равен произведению длины, ширины и высоты.Его размер указан как:
.
 Объем = длина × ширина × высота
 Объем = [L] × [L] × [L] (поскольку длина, ширина и высота являются длинами)
 Объем = [л]  3 
 Поскольку объем зависит от массы и времени, степени времени и массы будут равны нулю при выражении его размеров, то есть [M]  0  и [T]  0 
 Окончательный размер объема будет [M]  0  [L]  3  [T]  0  = [M  0  L  3  T]
  2. Аналогичным образом размеры области будут [M]  0  [L]  2  [T]  0 
  3.  Скорость объекта - это расстояние, которое он преодолел за определенное время, и задается как:
 Скорость = Расстояние / Время
 Размер расстояния = [L]
 Измерение времени = [T]
 Размер скорости = [L] / [T]
 [Скорость] = [L] [T]  -1  = [LT  -1 ] = [M  0  LT  -  1]
  4. Ускорение тела определяется как скорость изменения скорости во времени, его размеры задаются как:
 Ускорение = Скорость / Время
 Размерность скорости = [LT  -1 ]
 Измерение времени = [T]
 Размер ускорения будет = [LT  -1 ] / [T]
 [Ускорение] = [LT –2 ] = [M  0  LT –2 ]
  Фундаментальная величина 
  Размер 
 Длина
 л
 Масса
 M
 Время
 Т
 Температура
 К
 Электрический ток
 A
 Сила света
 Cd
 Количество вещества
 моль
  5. Плотность тела определяется как масса на единицу объема, а его размер определяется как:
 Плотность = Масса / Объем
 Размер массы = [M]
 Размер объема = [L  3 ]
 Размерность плотности будет = [M] / [L  3 ]
 [Плотность] = [ML  -3 ] или [ML  -3  T  0 ]
  6.  Сила, приложенная к телу, является произведением ускорения и массы тела
 Сила = Масса × Ускорение
 Измерение массы = [M]
 Размер ускорения = [LT  -2 ]
 Размер силы будет = [M] × [LT  -2 ]
 [Сила] = [MLT  -2 ] 
 Правила записи размеров физической величины 
 Сила, [F] = [MLT -2 ]
 Скорость.[v] = [LT  -1 ]
 Заряд, (q) = [AT]
 Удельная теплоемкость, (с) = [L  2  T  2  K  -1 ]
 Газовая постоянная, [R] = [ML  2  T -2  K  -1  моль  -1 ]
 Мы следуем определенным правилам при выражении физической величины в единицах измерения, они следующие:
 Размеры всегда заключаются в [] скобки
 Если тело не зависит от какой-либо фундаментальной величины, мы принимаем его мощность равной 0
 При упрощении размеров мы помещаем все фундаментальные величины с их соответствующей мощностью в одинарные [] скобки, например, в качестве скорости мы пишем [L] [T]  -1  как [LT  -1 ]
 Мы всегда пытаемся получить производные величины в терминах фундаментальных величин при написании измерения.
 Законы экспонент используются при написании измерения физических величин, поэтому основное требование является обязательным.
 Если размер записан как есть, мы принимаем его мощность равной 1, что понятно
 Плоский угол и Телесный угол являются безразмерными величинами, то есть не зависят от основных величин 
 Преимущества габаритов 
 Прежде чем записывать измерения физической величины, необходимо кое-что знать, чтобы понять, зачем нам нужны измерения и каковы преимущества записи физической величины.Преимущества описания физического количества следующие:
 Описание размеров помогает понять взаимосвязь между физическими величинами и их зависимость от основных или фундаментальных величин, то есть, как размеры тела зависят от массы, времени, длины, температуры и т. Д.
 Размеры используются в анализе размеров, где мы используем их для преобразования и обмена единиц измерения
 Размеры используются для предсказания неизвестных формул путем простого изучения того, как определенное тело зависит от основных величин и до какой степени
 Облегчает измерение и изучение физических величин
 Мы можем идентифицировать или наблюдать количество только по его размерам
 Размеры определяют объекты и их существование 
 Ограничения размеров 
 Помимо полезного количества, существует множество ограничений размеров, а именно:
 Размеры нельзя использовать для тригонометрических и экспоненциальных функций
 Размеры никогда не определяют точную форму отношения
 Мы не можем найти значения некоторых констант в физических отношениях с помощью размерностей
 Размерно правильное уравнение не всегда может быть правильным 
 Таблица размеров 
 На определение размеров количеств уходит много времени.Итак, чтобы сэкономить время, мы изучаем некоторые основные измерения определенных величин, таких как скорость, ускорение и другие связанные производные величины.  Для примера , предположим, что вас просят найти размеры Силы, и вы помните, что измерение ускорения равно [LT  -2 ], вы можете легко указать, что размер силы как [MLT  -2 ] как сила равен произведение массы и ускорения тела.
 В таблице ниже показаны измерения нескольких производных величин, которые можно использовать непосредственно в задачах анализа размерностей.
  Кол-во 
  Формулы 
  Размеры 
 Скорость
 Рабочий объем / время
 [LT  -1 ]
 Разгон
 Скорость / Время
 [LT -2 ]
 Работы выполнены
 Сила × смещение
 [ML  2  T -2 ]
 Давление
 Сила / Площадь
 [ML -1  T -2 ]
 Мощность
 Работа выполнена / Время
 [ML  2  T -3 ]
 Плотность
 Масса / Объем
 [ML -3  T  0 ]
 Площадь
 Длина × ширина
 [L  2 ]
 
  Посмотрите это видео, чтобы получить дополнительную информацию  
 
  Дополнительная информация 
 Размеры физических величин
 Скаляров и векторов 
  Чтобы лучше понять науку о движении
необходимо использовать некоторые математические идеи из  векторный анализ .Большинство людей знакомятся с переносчиками в средней школе или колледже,
но для учащихся начальной и средней школы, а также для детей с математическими трудностями: 
  НЕ ПАНИКА! .  
 В векторном анализе есть много сложных частей, и мы не собираемся туда идти.
Мы собираемся ограничиться самыми основами.
Векторы позволяют нам смотреть на сложные, многомерные проблемы.
как более простая группа одномерных задач.Мы будем интересоваться в основном определениями
Слова немного странные, но идеи
очень мощный, как вы увидите.
Если вы хотите узнать больше о векторах, вы можете скачать
этот отчет о
векторный анализ.
 Математика и естественные науки были изобретены людьми для описания и
понять мир вокруг нас.
Мы живем в (по крайней мере) четырехмерном мире, управляемом
течение времени и трех пространственных измерений; вверх и вниз,
влево и вправо, вперед и назад.Мы наблюдаем, что есть некоторые количества и процессы в
наш мир, который зависит от направления  , в котором
они происходят, и есть некоторые количества, которые не зависят
по направлению. Например,
объем
объекта, трехмерное пространство, которое занимает объект,
не зависит от направления.
Если у нас есть железный блок объемом 5 кубических футов, мы перемещаем его вверх и вниз и
затем налево и направо, у нас все еще остается железный блок объемом 5 кубических футов.
С другой стороны,
место нахождения,
объекта действительно зависит от направления.Если мы переместим блок 5 кубических футов на 5 миль к
север, результирующее местоположение сильно отличается от
если мы переместим его на 5 миль к востоку.
Математики и ученые называют количество
зависящее от направления  векторная величина . Количество
которая не зависит от направления, называется скалярной величиной  .
 Векторные величины имеют две характеристики: величину и направление.
Скалярные величины имеют только величину.Когда
сравнение
две векторные величины одного типа, необходимо сравнить обе
величина и направление. Для скаляров вам нужно только
сравнивать
величина. При выполнении любой математической операции над векторной величиной
(например, сложение, вычитание, умножение ..) вы должны
рассмотреть возможность
как по величине, так и по направлению. Это делает работу с вектором
количества немного сложнее, чем скаляры.
 На слайде мы перечисляем некоторые из обсуждаемых физических величин.
в
Руководство по воздухоплаванию для новичков
и сгруппируйте их в векторные или скалярные величины.В частности
интерес,
силы
которые работают на летающих самолетах,
масса,
тяга, и
аэродинамические силы, все
векторные величины. Результирующий
движение
самолета с точки зрения водоизмещения, скорости и
ускорение - это тоже векторные величины.
Эти количества можно определить, применяя
Законы Ньютона
для векторов.
Скалярные величины включают большую часть
термодинамическое состояние
переменные, связанные с двигательной установкой, такие как
плотность,
давление и
температура порохов.В
энергия
Работа,
а также
энтропия
с двигателями также связаны скалярные величины.
 У векторов есть величина и направление, у скаляров - только величина.
Тот факт, что величина  величины  встречается как для скаляров, так и для векторов, может
привести к некоторой путанице.
Есть некоторые количества, например  скорость , которые имеют
очень специальные определения для ученых. По определению,
скорость - это скалярная величина вектора  скорости .Машина
при движении по дороге скорость составляет 50 миль в час. Его скорость
50 миль / ч в северо-восточном направлении. Это может быть очень
сбивает с толку, когда термины используются как синонимы! Другой пример
масса   и масса  . Вес - это сила, которая является вектором
и имеет величину и направление. Масса - скаляр.
Масса и масса
связаны друг с другом, но это не одно и то же.
 В то время как законы Ньютона описывают результирующее движение
твердого тела существуют специальные уравнения, описывающие движение
жидкостей,
газы и жидкости.Для любой физической системы
масса,
импульс, и
энергия
системы должны быть сохранены. Масса и энергия
- скалярные величины, а импульс - вектор
количество. Это приводит к  связанной системе  уравнений,
называется
Уравнения Навье-Стокса,
которые описывают, как жидкости ведут себя под воздействием внешних сил.
Эти уравнения являются жидким эквивалентом законов движения Ньютона.
и их очень сложно решить и понять.Упрощенная версия уравнений, названная
Уравнения Эйлера
может быть решена для некоторых проблем с жидкостями.
  Действия:  
  Экскурсии с гидом 
  Навигация .. 
 
 Руководство для начинающих Домашняя страница
 единиц и размерности 
 единиц и размерности
 Единицы и размерность 
 Содержание 
 Физические величины и связанные с ними размеры
 Основные физические величины
 Механические физические величины
 Электрические физические величины
 Алгебра размерности
 Преобразование систем единиц
 Определения основных единиц
 Определения производных единиц
 Константы преобразования единиц
 Физические константы
 Физические уравнения
 Физические величины и связанные с ними размеры 
   Ошибки могут возникать при написании уравнений для решения задач в классической
физика.Многие из этих ошибок можно предотвратить, выполнив измерение
проверьте уравнения. Все физические величины имеют фундаментальное измерение
это не зависит от единиц измерения. Основные физические размеры
являются: длина, масса, время, электрический заряд, температура и сила света.

   Существует ряд систем единиц измерения физических размеров.
Система MKS основана на измерении метра, килограмма и секунды. Система CGS
основывается на сантиметре, грамме, секунде измерения.Английская система основана на
на ногах, фунт, второе измерение. Несколько физических измерений и
связанными единицами измерения в этих трех системах являются:


        Система единиц физических величин
          Dimension MKS CGS английский


          длина метр сантиметр фут

          масса килограмм грамм фунт масса

          время секунда секунда секунда

          сила ньютон дин фунтал

          энергия джоуль эрг B.t.u.


   Проверка физического уравнения имеет два аспекта. Первый - это проверить
размерность. Размерность не зависит от системы единиц. В
во-вторых, необходимо проверить, что в уравнении используется согласованная система единиц.

   Примером проверки размерности является использование основного уравнения F = ma to
определить, что сила имеет размерную массу x длину / время в квадрате, тогда
              2
проверьте правильность размеров F = mv / r. Проверка осуществляется
расширение габаритов, e.грамм. масса x (длина / время) x (длина / время) / длина.
Объединение условий и уменьшение урожайности дает квадрат массы x длины / времени. Это согласен
с размерами, ожидаемыми для силы из основного уравнения F = ma. В качестве
Ожидается, что центростремительная сила имеет ту же размерность, что и сила от
Второй закон движения Ньютона.

   Приведенная ниже таблица организована таким образом, чтобы наименование физического количества отображалось с
сопутствующая информация. Второй столбец - один из типичных используемых символов.
для физического количества. Третий столбец - это размер физического
количество, выраженное в фундаментальных измерениях.Четвертый столбец
- название единицы в системе измерения MKS. Пятая колонна
- типичное уравнение модуля MKS. Независимая таблица представляет преобразование
коэффициенты из системы измерения MKS в другие системы измерения.

   Физика развивалась в течение многих лет многими людьми из самых разных
дисциплин. Таким образом, возникает неоднозначность и дублирование символов.
 
 Основные физические величины 
ФИЗИЧЕСКАЯ КОЛИЧЕСТВО СИМВОЛ РАЗМЕР ЕДИНИЦА ИЗМЕРЕНИЕ УРАВНЕНИЕ
_________________ ______ _________ ________________ ______________


длина s L метр м

масса м М килограмм кг

время t T секунда сек

электрический заряд q Q кулон c

сила света I C свеча кд

                                                                  о
температура T K градус кельвина K

угол тета нет радианы нет
 
 Физико-механические величины (производные) 
ФИЗИЧЕСКАЯ КОЛИЧЕСТВО СИМВОЛ РАЗМЕР ЕДИНИЦА ИЗМЕРЕНИЕ УРАВНЕНИЕ
_________________ ______ _________ ________________ ______________

                                    2 2
площадь A L квадратный метр

                                    3 3
объем V L стере м

скорость v L / T метр в секунду м / сек

угловая скорость omega 1 / T радиан в секунду 1 / сек

                                      2 2
ускорение a L / T метр на квадратный м / сек
                                               второй

                                      2 2
угловое ускорение альфа 1 / Т радиан за 1 / сек
                                               квадратная секунда

                                       2 2
сила F мл / т ньютон кг м / сек

                                     2 2 2 2
энергия E ML / T джоуль кг м / сек
работа W "
тепло Q "

                                     2 2 2 2
крутящий момент T ML / T ньютон-метр кг м / сек


                                     2 3
мощность P ML / T ватт джоуль / сек

                                      3 3
плотность D M / L килограмм на кг / м
                                               кубический метр

                                       2 2
давление P M / LT ньютон на кг / м сек.
квадратный метр модуля упругости

импульс p ML / T ньютон секунда кг м / сек
импульс

                                     2 2
инерция I ML / T джоуль-секунда кг · м / сек


световой поток phi C люмен (4Pi свеча cd sr
                                               для точечного источника)
                                      2 2
освещенность E C / L люмен на кд ср / м
                                               квадратный метр

                                     2 2 2 2 о
энтропия S ML / T K джоуль на градус кг м / сек K

                                    3 3
объемный расход Q л / т куб.м / сек
                                               в секунду

                                    2 2
кинематическая вязкость ню л / т квадратный метр м / сек
                                               в секунду

динамическая вязкость mu M / LT ньютон-секунда кг / м-сек
                                               за квадратный метр

                                      2 2 2 2
удельный вес гамма M / L T ньютон кг / м сек
                                               за кубический метр

 
 Электрические физические величины (производные) 

ФИЗИЧЕСКАЯ КОЛИЧЕСТВО СИМВОЛ РАЗМЕР ЕДИНИЦА ИЗМЕРЕНИЕ УРАВНЕНИЕ
_________________ ______ _________ ________________ ______________

электрический ток I Q / T ампер c / сек

                                     2 2 2 2
ЭДС, напряжение, потенциал E ML / T Q вольт кг м / с c

                                     2 2 2 2
электрическое сопротивление R ML / TQ Ом кг м / сек c

                                     2 3 2 3
проводимость сигма TQ / ML mho на метр сек c / кг · м

                                    2 2 2 2 2 2
емкость C T Q / ML фарад с / кг · м

                                     2 2 2 2
индуктивность L ML / Q генри кг м / c

                                       2 2
плотность тока J Q / TL ампер на с / сек м
                                               квадратный метр

                                      3 3
плотность заряда rho Q / L кулон на к / м
                                               кубический метр

магнитный поток, B M / TQ weber на Kq / sec c
   квадратный метр магнитной индукции

магнитная напряженность H Q / LT ампер на метр c / м · сек

магнитный векторный потенциал A ML / TQ Вебер / метр кг м / сек c

                                       2 2
напряженность электрического поля E ML / T Q вольт / метр или кг · м / сек c
                                               ньютон на кулон

                                      2 2
электрическое перемещение D Q / L кулон на см / м
                                               квадратный метр

                                       2 2
проницаемость мю ML / Q генри на метр кг м / c

                                    2 2 3 2 2 3
диэлектрическая проницаемость, epsi T Q / ML фарад на метр сек c / кг · м
  диэлектрическая постоянная

                                                                     -1
частота f Pi / Т герц сек

                                                                     -1
угловая частота омега 1 / T радиан в секунду с

длина волны лямбда L метры м
 
 Алгебра размерности 

   Размерность любой физической величины можно записать как

                  а б в г д е
                 L M T Q C K

где a, b, c, d, e и f - целые числа, например -4, -3, -2, -1, 0, 1, 2, 3, 4
и L - длина, M - масса, T - время, Q - заряд, C - сила света.
К - температура.Нулевой показатель степени означает, что размер не применяется.
к физическому количеству. Применяются обычные правила алгебры для показателей
для совмещения размеров.

   Чтобы сложить или вычесть две физические величины, они должны
иметь такое же измерение. Результирующая физическая величина имеет то же
Габаритные размеры. Физические величины с одинаковой размерностью в разных
системы единиц могут быть добавлены или вычтены путем умножения одного из
количества с помощью коэффициента преобразования единиц для получения совместимых единиц.Умножение двух физических величин приводит к новому физическому
количество, которое имеет сумму показателей размерностей исходной
две величины.

   Деление одной физической величины на другую приводит к новому физическому
величина, имеющая размерность показателя первой величины минус
показатели второй величины.

   Извлечение квадратного корня из физической величины приводит к новому физическому
величина, имеющая размерность с показателем, равным половине начальной размерности.Повышение физической величины до степени приводит к появлению новой физической величины.
имеющий размерность с показателями, умноженными на степень.

          например v имеет размерность L / T

                     2 2 2 2 -2
               тогда v имеет размерность L / T или L T


   Производная одной физической величины по отношению к другой физической величине.
количество приводит к новой физической величине с показателями степени
первое измерение минус показатели другого измерения.

         е.грамм. v имеет размерность L / T, t имеет размерность T,

                                           2
               тогда dv / dt имеет размерность L / T ускорения


   Интеграл одной физической величины в диапазоне другого физического
количество приводит к новой физической величине, имеющей измерение с
сумма показателей двух величин.

        
         например v имеет размерность L / T, t имеет размерность T,

               то интеграл v dt имеет размерность L
 
 Преобразование систем единиц 

   Этот раздел организован таким образом, чтобы соответствовать обсуждению физических
величины и уравнения физики.Определение шести основных
единицы физических величин представлены для системы единиц МКС. В
определение некоторых производных единиц затем представлено в системе MKS. В
определения в других системах единиц следуют определениям MKS. Это
за которой следует таблица коэффициентов пересчета между системой MKS и другими
системы единиц.


   Система MKS, основанная на счетчике, килограмм-секунде, была расширена, чтобы позволить
сила и энергия от электрических величин должны быть измерены в одном рационализированном
система единиц.Система была предложена Георгием в 1904 году.
IEC 1935 г. вступит в силу 1 января 1940 г. Переход от электрического к механическому
преобразование было выбрано исходя из проницаемости свободного пространства, которое необходимо

        -7
4Pi x 10 генри на метр.
 
 Определение основных единиц 

Метр, основная единица длины, определяемая как расстояние между двумя
                                                          о
указанные линии на определенном слитке из платино-иридия при 0 ° C при стандарте
атмосферное давление поддерживается в двух нейтральных точках 0.285 метров от
центр бара. Бар находится в Международном бюро весов.
и Меры возле Парижа, Франция.


Сантиметр, единица измерения длины cgs, определяемая как 1/100 метра.


Футы, английская единица измерения длины, определяемая как 0,3048 метра в США.


Дюйм, английская единица измерения длины, определяемая как 0,00254 метра в США.

                                       -10
Ангстрем, единица длины, определяемая как 10 метров.


Килограмм, основная единица массы, определяемая как масса определенного
цилиндр из платины - иридий хранится в Международном бюро весов и
Меры.Грамм, единица массы cgs, определяемая как 1/1000 килограмм.


Фунт, английская единица массы, фунт экирдупуа определяется как
0,4535924277 килограмм в США. Аптекарский или тройской фунт
5760/7000 фунтов стерлингов.


Вторая, фундаментальная единица времени, определяемая как одна 86400-я часть среднего
солнечный день. В настоящее время измеряется атомными часами, основанными на скорости ядерных
разлагаться.


Кулон, фундаментальная единица заряда, определяемая как заряд, необходимый для
получить один ньютон силы между двумя такими зарядами на расстоянии одного
метр.Свеча, основная единица силы света, определяемая как источник
интенсивность квадратного отверстия 1/60 сантиметра стандартного источника света
светящейся полости с температурой, равной температуре затвердевающей платины.
Точечный источник из одной свечи излучает один люмен на стерадиан.


Градусы Кельвина, основная единица измерения температуры, определяемая как ноль, где
молекулярная активность газов прекращается. Шкала основана на нулевых градусах.
Цельсия (Цельсия) для точки замерзания воды и 100 градусов
по Цельсию при температуре кипения воды.Ноль градусов по Цельсию - 273,16
градусы кельвина.


Радианы, основная единица угла, определяемая как угол, образованный
длина дуги окружности равна радиусу, образующему дугу.
 
 Определение производных единиц 

Ньютон, единица силы, определяемая как сила, необходимая для ускорения массы.
1 килограмм со скоростью 1 метр в секунду в секунду при непрерывном действии.


Дин, сгс единица силы, определяемая как сила, необходимая для ускорения массы.
                                                                  -5
1 грамм при скорости 1 сантиметр в секунду в секунду.Одна дина равна 10 ньютонам.


Фунтал, английская единица силы, определяемая как сила, необходимая для ускорения.
масса 1 фунт при скорости 1 фут в секунду в секунду. Один фунтал - это
          -10
7.23300 10 ньютонов. Фунтал, основанный на земном притяжении, равен 32,174 фунта.
Avoirdupois.


Джоуль, единица энергии, определяется как работа, выполняемая 1 ньютоном, действующим через
расстояние один метр.


Эрг, сгс единица энергии, определяемая как работа, выполняемая 1 дином, действующим через
                                         -7
расстояние в один сантиметр.Один эрг равен 10 джоулям.


Килограмм калорий, большая калория, единица энергии - это тепло, необходимое для
повысить температуру 1 килограмма воды с 1 градуса Цельсия на
заявленная температура. т.е. кг кал (22 ° C). Средняя килограммовая калорийность определяется как
1/100 тепла, необходимого для повышения температуры 1 кг воды
      о о
от 0 C до 100 C. Маленькая калорийность - это калорийность в граммах, равная 1/1000 от
большая калорийность. Один средний килограмм калории равен 0,000238889 джоуля.


Британская тепловая единица, Б.t.u, единица энергии, количество тепла, необходимое для подъема
температура 1 фунта воды 1 градус по Фаренгейту при заявленной
                           о
температура. т.е. B.t.u. (39 F). Средняя британская тепловая единица определяется как
1/180 тепла, необходимого для повышения температуры 1 фунта воды с
  о о
От 32 до 212 F. Одно среднее значение B.t.u. составляет 0,00009480 джоуль.


Мол, килограмм молекулы - это количество килограммов вещества, которое
соответствует его молекулярной массе, деленной на 1000. В системе cgs
единиц моль, грамм молекула, это количество граммов вещества, которое
соответствует его молекулярной массе.Масса отдельной молекулы в
килограммы - это килограмм молекулы, деленный на число Авогадро. Для атомов
молекулярная масса - это атомная масса.


Стерадиан, sr, представляет собой отношение площади пересекаемой поверхности
сфера до радиуса сферы в квадрате. 4Pi steradians означает
перехватывается общая площадь сферы.


Ватт, единица мощности, определяемая как работа, выполняемая с постоянной скоростью, равной единице.
джоуль в секунду.


Лошадиная сила (механическая), английская единица мощности, определяемая как выполненная работа.
со скоростью 550 фут-фунтов в секунду.Одна механическая мощность равна
745,705 Вт.


Лошадиная сила (электрическая), английская единица мощности, по определению точно
760 ватт.


Ампер, единица измерения электрического тока, определяемая как ток, который будет течь.
через цепь с сопротивлением один Ом при приложении одного вольт. В
международный стандарт определяется как текущий, который будет депонировать серебро
со скоростью 0,00111800 грамм в секунду. Один международный ампер - это примерно
0,999835 абсолютного ампера. Международные электрические единицы основаны на физических
стандарты, спецификации которых немного ошибочны.Инструменты, изготовленные после
1 января 1948 г. откалиброваны в абсолютных единицах.


Примечания:
        Используется единственная форма единиц, за исключением ступни и ступни.
        Имена собственные в единицах измерения и константах не пишутся с заглавной буквы.


Использованная литература:
             Коэффициенты пересчета и таблицы Циммермана и Лавина
             Электрические и магнитные поля, Стивен Аттвуд
             Элементы физики Шортли и Уильямса

 
 ПОСТОЯННЫЕ ПРЕОБРАЗОВАНИЯ ЕДИНИЦ 

получить единицы МКС от других единиц, чтобы получить другие единицы от единиц МКС

значение значение значение значение
в MKS = в другом x константа в другом = в MKS x константа
единицы единицы единицы единицы

                                 длина

метр = ангстрем x 1.0E-10 ангстрем = метр x 1.0E10

метр = мил x 0,254E-4 мил = метр x 39370,07874

метр = сантиметр x 0,01 сантиметр = метр x 100

метр = дюйм x 0,0254 дюйма = метр x 39,37007874

метр = фут x 0,3048 фут = метр x 3,280839895

метр = ярд x 0,
18288 ярд = метр x 1,0936111

метр = сажень x 1,8288036 сажень = метр x

метр = стержень x 5,0292099 стержень = метр x 0.19883839

метр = цепь (инспектор) x 20,12 цепи (инспектор) = метр x 66 футов

метр = цепь (инженер) x 30,48006 цепь (инженер) = метр x 100 футов

метр = фарлонг x 0.2011684E + 3 фарлонга = метр x 0,49709597E-2

метр = миля (статут) x 1,6093472E + 3 мили (статут) = метр x 0,6213699E-3 *

метр = миля (морская) x 1,8532487E + 3 миля (морская) = метр x 0,539593E-3

метр = лига (земля) x 4.82804E + 3 лига (земля) = метр x

метр = лига (морская) x 5.5596E + 3 лига (морская) = метр x

метр = световой год x 9.459936E + 15 световых лет = метр x



                                    масса


килограмм = грамм x 0,001 грамм = килограмм x 1000

килограмм = зерно (трой) x 0,6480E-4 гран (трой) = килограмм x

килограмм = пеннивейт (трой) x 1,5552E-3 пеннивейт (трой) = килограмм x
              24 зерна

килограмм = карат (трой) x 0,2E-3 3086 гран

килограмм = сомнения x 1.296E-3 scruple = килограмм x

килограмм = драм (avdp) x 1.772E-3 драм (avdp) = килограмм x

килограмм = унция (avdp) x 0.02834952 унция (avdp) = килограмм x 35,27

килограмм = унция (тройская) x 0,031 · 103481 унция (тройская) = килограмм x 32,15

килограмм = фунт (трой) x 0,37324177 фунт (трой) = килограмм x 2,6792285

килограмм = фунт (avdp) x 0,45359244 фунт (avdp) = килограмм x 2,204622341 *

килограмм = тонна (короткая) x 907,18486 тонна (короткая) = килограмм x 2000 фунтов *

килограмм = тонна (длинная) x 1016,047 тонна (длинная) = килограмм x 0,9842064E-3

килограмм = тонна (метрическая) x 1000 (метрическая) = килограмм x 0,001



                                     время


секунда = минута x 60 минут = секунда x

секунда = час x 3600 час = секунда x

второй = день x 0.86400E + 5 день = второй x

вторая = две недели x 1.2096E + 6 две недели = вторая x

второй = месяц x 2,628E + 6 месяц = ​​второй x

второй = год x год = второй x



                             электрический заряд



кулон = заряд электрона x заряд электрона = кулон x 1,60193E-19

кулон = фарадей x фарадей = кулон x 96,480

кулон = ампер-часы x ампер-часы = кулон x 3600



                                температура


o o o oL
 К = С + 273.16 С = К - 273,16

o o oL
 К = F = (К - 273,16) х 1,8 + 32,0


                                    угол



радиан = секунда (угловая) x 4,84814E-6 секунда (угловая) = радиан x

радиан = минута (угловая) x 0,0002 минута (угловая) = радиан x

радиан = градус (угловой) x 0,0174533 градус (угловой) = радиан x

радиан = оборот x 6,283 1853 оборот = радиан x

радиан = бам х



                            площадь


квадратный метр = квадратный сантиметр квадратный сантиметр = квадратный метр
               х 1.0E-4 x 10 000

квадратный метр = квадратный дюйм квадратный дюйм = квадратный метр
               х х

квадратный метр = квадратный фут квадратный фут = квадратный метр
               х 0,092 х

квадратный метр = квадратный ярд квадратный ярд = квадратный метр
               х х

квадратный метр = квадратная миля (статут) квадратная миля (статут) = квадратный метр
               х х

квадратный метр = акр x 4046.873 акра = квадратный метр x

квадратный метр = круговой мил x круговой мил = квадратный метр x 1,97352E + 6

квадратный метр = га x 1,0E + 4 га = квадратный метр x

квадратный метр = поселок x 93,24E + 6 поселок = квадратный метр x

квадратный метр = сарай x 1.0E-28


                              объем


кубический кубический кубический кубический
метр = сантиметр x 1.0E-6 сантиметр = метр x 1.0E + 6

кубический кубический кубический кубический
метр = дюйм x 0.16387162E-4 дюйма = метр x

кубический метр = кубический фут x 0,028317017 кубический фут = кубический метр x

кубический метр = кубический ярд x кубический ярд = кубический метр x

кубический кубический кубический кубический
метр = миля (статут) x миля (статут) = метр x

кубический метр = литр x 0,001 литр = кубический метр x 1000

кубический метр = жидкая унция x 0,295737E-4 жидкая унция = кубический метр x 0,33814E + 7

кубический метр = чашка x

кубический кубический
метр = пинта (жидкость) x 0.4731798E-3 пинта (жидкость) = метр x 21113,4

кубический метр = кварта (жидкость) x кварта (жидкость) = кубический метр x

кубический метр = галлон x 0,003785 галлона = кубический метр x

кубический метр = баррель x 1 / 0,1589873 баррель = кубический метр x 0,1589873

кубический метр = пинта (сухая) x 0,03524 / 64

кубический метр = кварта (сухая) x 0,03524 / 32

кубический метр = клев x 0,03524 / 4

кубический метр = бушель x 0,03524 бушель = кубический метр x

кубический метр = бочонок x (менее 10 галлонов)

кубический метр = шнур x 3,625

баррель = галлон x 31.5 (еда) x 42 (нефть)

                              скорость


метр в секунду = сантиметры в секунду x

метр в секунду = километр в час x

метр в секунду = дюймов в секунду x

метр в секунду = футов в секунду x

метр в секунду = мили в секунду x

метр в секунду = дюймы в минуту x

метр в секунду = футов в минуту x

метр в секунду = мили в час x

метр в секунду = узлы x



                            ускорение


метр на секунду в квадрате = сантиметр на секунду в квадрате x

метр на секунду в квадрате = футов на секунду в квадрате x

метр в секунду в квадрате = мили в час в квадрате x



                              сила



ньютон = дин x 1.0E-5

ньютон = фунт x 7,23300E-10

ньютон = фунт x 7,23300E-10 / 32,17 г



                             энергия



джоуль = эрг x 1,0E-7

джоуль = грамм калорий x 0,238889E-6

джоуль = килограмм калорий x 0,238889E-3

джоуль = грамм калорий x 0,238889E-6

джоуль = B.t.u x 0,9480E-4

джоуль = фут-фунт x 1,356

джоуль = киловатт-час x 3,6E + 6

джоуль = лошадиные силы-часы x 2,684E + 6



                              власть


ватт = килограмм калорий в секунду x

ватт = килограмм калорий в минуту x

ватт = мощность (механическая) x 745.705

ватт = мощность (электрическая) x 760

ватт = лошадиные силы (метрическая система) 1.014?

ватт = лошадиные силы (котел) x 9.804E + 3 33 520 БТЕ в час

ватт = B.t.u в минуту x 17,57

ватт = БТЕ в час x 17,57 * 60

ватт = фут-фунт в минуту x 0,2260E-3 33000 л.с.

ватт = фут-фунт в секунду x 1,356 550 л.с.



                             плотность

килограмм на кубический метр = фунт на кубический фут


                             давление



паскаль = ньютон на квадратный метр x 1

паскаль = фунтов на квадратный фут x

паскаль = тонна на квадратный фут x

паскаль = атмосфера (стандарт) x 1.013250E5

паскаль = футов воды x

паскаль = дюймы ртутного столба

паскаль = миллиметры ртутного столба x 1 / 133,3

паскаль = бар x 1.0E5

паскаль = миллибар x

паскаль = торр х


                             крутящий момент


метр ньютон = фут фунт x
 

                            скорость потока



кубический метр в секунду = галлон в минуту x 0,6309E-8

кубический метр в секунду = кубический фут в минуту x 0,4719E-3


                          удельная теплоемкость, энтропия


                   o oL
джоуль на килограмм K = B.t.u. за фунт F x 4.187E + 3



                          динамическая вязкость

равновесие = дин-секунда на квадратный сантиметр


                           кинематическая вязкость

сток = квадратный сантиметр в секунду


                           электрический ток


ампер = ампера x 10

ампер = статампер x 0,333333E-9
                                     
                         магнитный поток B

                         магнитная индукция

                        магнитодвижущая сила

                       напряженность магнитного поля H

                        диэлектрическая постоянная

                        постоянная диэлектрической проницаемости

                          скорость вращения


радиан в секунду = оборотов в секунду x

радиан в секунду = оборотов в минуту x


 
 ФИЗИЧЕСКИЕ ПОСТОЯННЫЕ 

   Есть ряд физических констант, которые используются в уравнениях

решать задачи по физике.Ошибки могут возникать из-за размерности

и / или единицы физической постоянной неизвестны. Таблица ниже

представляет некоторые физические константы с их типичным символом, размерностью,

номинальная стоимость и единица измерения в системе МКС.

ФИЗИЧЕСКАЯ ПОСТОЯННАЯ СИМВОЛ РАЗМЕР MKS ЗНАЧЕНИЕ ЕДИНИЦА
_________________ ______ _________ _________ ____

                                        3 3
плотность воздуха, нормальная rho M / L 1.293 кг / м
   условия


молекула воздуха, масса m M 4.81E-26 кг
                              а


молекула воздуха, w M 0,028952 кг / моль
 килограмм молекулярный вес


                                         2 2
атмосферное давление A M / LT 1.01325 ньютон / м


Число Авогадро N нет 6.023E + 23 молекулы в
  молекулы в моль моль


                                       2 2 o
Постоянная Больцмана k ML / T K 1.380E-23 джоуль / К


                                       2 2
электрон-вольт e ML / T 1.60210E-10 джоуль


                                       3 2 2 2 2
электростатическая постоянная k ML / T Q 8.987E + 9 нт м / кулон
  обратная диэлектрическая проницаемость м / фарад


элементарный заряд e Q 1.6021892E-19 кулон


масса электрона m M 9.1066E-31 кг
                              е

Фарадей f L / T 9.648456E + 4 кулон / моль


                                       2 2 o
газовая постоянная моля R ML / T K 8,3144 джоуль / K

                                        2 2
сила тяжести (земля) g L / T 9.80665 м / сек


масса атома водорода m M 1,6734E-27 кг
                              час


атом водорода w M 1.0079E-3 кг / моль
  килограмм атомный вес


                                       2 2
сопротивление свободного пространства Z ML / TQ 120Pi Ом
                              0


механический эквивалент Дж нет 4186,05 джоуль /
   тепла кг калорий


                                      2 2 3
диэлектрическая проницаемость (вакуум) epsi T Q / ML 8.854E-12 фарад / метр
                                 0


                                         2
проницаемость (вакуум) мю ML / Q 4Pi E-7 генри / метр
                               0


Pi, отношение окружности Pi нет 3.14159265 радиан
      к диаметру

                                       2
Постоянная Планка h ML / T 6.624E-34 джоуль-секунда


скорость света (в вакууме) c L / T 2.99792458E + 8 метров в секунду


скорость звука (воздуха) с Л / Т 331,45 м / сек


                                      2 2 2 2
универсальный гравитационный G L / MT 6.6720E-12 нт м / кг
    постоянный



Примечание: некоторые константы связаны с комбинациями других констант:
      электростатическая постоянная = диэлектрическая проницаемость 1 / 4Pi (вакуум)
      скорость света = 1 / sqrt (диэлектрическая проницаемость x проницаемость)
      полное сопротивление свободного пространства Z = sqrt (проницаемость / диэлектрическая проницаемость)
                               0

 
 ФИЗИЧЕСКИЕ УРАВНЕНИЯ 


                     НЕКОТОРЫЕ УРАВНЕНИЯ ФИЗИКИ


F = m сила равна массе, умноженной на ускорение,
                     Второй закон движения Ньютона


       2
F = m v / r сила равна массе, умноженной на квадрат скорости по радиусу,
                     центростремительная сила массы, движущейся по кругу


             2
F = G м м / с гравитационная сила между массой и массой на расстоянии s
       1 2 1 2
                     с универсальной гравитационной постоянной G


               2
g = G m / r ускорение свободного падения на земле
       земля земля


             2
F = k Q Q / s электрическая сила между зарядом и зарядом на расстоянии s
       1 2 1 2
                     с электростатической постоянной k.Если есть диэлектрик
                     затем умножьте на безразмерную диэлектрическую проницаемость.


F = 1 / 2Pi мю I I / с
               1 2
                     электрическая сила между двумя параллельными проводами, несущими
                     токи I и I с шагом s с проницаемостью
                               1 2
                     му. Это сила на один метр длины провода.


         2
F = B H s
                     электрическая сила в магнитном поле равна магнитной
                     магнитный поток, умноженный на магнитную напряженность, приложенную к области

         2
F = E D s
                     электрическая сила в электрическом поле равна электрической
                     умножение напряженности поля на приложенное электрическое смещение
                     в область


s = v t расстояние равно скорости, умноженной на время (линейно)


v = a t скорость равна ускорению, умноженному на время (линейно)


                      2
s = s + v t + 1/2 a t
     0 0
                     линейное расстояние равно начальному расстоянию плюс
                     начальная скорость умноженная на время плюс половина ускорения
                     умножить на квадрат времени

            2
v = sqrt (v + 2as)
 f 0
                    конечная скорость равна квадратному корню из
                    квадрат начальной скорости плюс двукратное ускорение
                    раз пройденное расстояние


v = sqrt (s g) критическая скорость любого объекта на орбите с
 c
                    расстояние s от источника гравитационного поля g


theta = omega t угол равен угловой скорости, умноженной на время (вращение)


omega = alpha t угловая скорость равна угловому ускорению, умноженному на время
                    (ротационный)

                                      2
тета = тета + омега т + 1/2 альфа т
             0 0
                    угловой поворот равен начальному углу плюс
                    начальная угловая скорость умноженная на время плюс половина
                    угловое ускорение, умноженное на квадрат времени

           2
w = sqrt (w + 2 альфа * угол)
 f 0
                    конечная угловая скорость равна квадратному корню из
                    квадрат начальной угловой скорости в два раза больше
                    угловое ускорение, умноженное на пройденный угол


E = I R напряжение равно току через резистор, умноженному на
                    сопротивление

I = C (E - E) / (t - t)
        2 1 2 1
                    ток через конденсатор равен емкости
                    раз изменение напряжения за изменение во времени

E = L (I - I) / (t - t)
        2 1 2 1
                    напряжение на катушке индуктивности равно индуктивности
                    раз изменение тока по сравнению с изменением во времени

C = epsi A / с
                    емкость в фарадах конденсатора с параллельными пластинами
                    равна диэлектрической проницаемости, умноженной на площадь, деленную на
                    интервал.L = n mu r (ln 8r / d - 7/4)
                    индуктивность в генри n витков провода диаметром
                    d плотно завернутый в спираль радиуса r с проницаемостью
                    mu приблизительно определяется этим уравнением.

H = 1/2 л / г
                    магнитная напряженность в центре токовой петли
                    равно 1/2 тока, деленного на радиус петли

B = mu H магнитный поток равен проницаемости, умноженной на
                    магнитная напряженность

D = epsi E электрическое смещение равно диэлектрической проницаемости
                    умноженное на напряженность электрического поля

P = E I мощность равна электрическому потенциалу, вызывающему ток

P = F s мощность равна силе, приложенной на расстоянии

       2 л
E = m c энергия от преобразования массы в энергию
                       (c = скорость света)

           2 л
E = 1/2 m v кинетическая энергия массы, движущейся со скоростью

E = m g s потенциальная энергия массы в гравитационном поле
                    на высоте s

E = 1/2 B H V энергия магнитного поля в объеме V с магнитным
                    поток B и магнитная напряженность H.Обычно это
                    интеграл приращения объема, умноженный на B, умноженный на H
                    в дополнительном объеме.

E = 1/2 D E V энергия электрического поля в объеме V с электрическим
                    смещения D и напряженности электрического поля E. Это
                    обычно это интеграл от приращения объема, умноженного на D
                    умножить на E в увеличивающемся объеме.

           2
E = 1/2 C V энергия, запасенная в конденсаторе с емкостью C, имеющей
                    напряжение V

           2
E = 1/2 L I энергии, запасенной в катушке индуктивности с индуктивностью L, имеющей
                    ток я


T = F s крутящий момент равен силе, приложенной на радиусе s

T = I альфа крутящий момент равен инерции вращения, умноженной на угловой
                    ускорение


                                 2
E = P V = R T = N k T = 1/3 Н · м v Закон идеального газа
                                 среднеквадратичное значение
                    Эти соотношения рассчитаны на один моль (килограмм-молекулу)
                    идеальный газ при абсолютном давлении P, объем V,
                    газовая постоянная R, число Авогадро N, число Больцмана
                    постоянная k, температура T в градусах кельвина, газ
                    масса молекулы m, среднеквадратичная скорость молекул
                    v в метрах в секунду.Каждый раздел уравнения
                     среднеквадратичное значение
                    представляет энергию в джоулях.

             2 2
P + 1/2 rho v + rho g z = P + 1/2 rho v + rho g z
 1 1 1 2 2 2

                    Это уравнение связывает давление P, скорость v и относительную
                    высота z для несжимаемой жидкости в трубе, наблюдаемая
                    в позиции 1 и позиции 2. rho - плотность
                    жидкость, а g - гравитационная постоянная.2
L = C rho v A / 2
     LL
                    подъемная сила равна безразмерному коэффициенту
                    высота подъема, умноженная на плотность воздуха, умноженная на квадрат скорости, умноженный на
                    площадь поверхности деленная на 2.

            2
D = C rho v A / 2
     D
                    сила сопротивления равна безразмерному коэффициенту
                    сопротивление, умноженное на плотность воздуха, умноженное на квадрат скорости, умноженное на
                    площадь поверхности деленная на 2.

ню = му / ро
                    кинематическая вязкость равна динамической вязкости в течение
                    плотность в жидкости

Р = Q (р - р)
        1 2 мощность P, необходимая для управления объемным расходом Q,
                    от давления p до давления p.1 1
о о
 С = К - 273,16
                    градусы по Цельсию равны градусам кельвина минус 273,16

o oL
 F = (К-273,16) x 9/5 + 32
                    градусы Фаренгейта как функция от градусов кельвина

 
 В начало 
 Последнее обновление 8.09.01
 Типы физических величин и их примеры 
 Физические величины - это те величины, которые можно измерить. По сути, существует два типа физических величин (основные величины или основные величины) и (производные величины).
 Это величины, которые используются для описания законов физики. Физические величины можно разделить на шесть категорий.
  Константа или соотношение 
 Такие величины имеют единственную величину, например, показатель преломления, диэлектрическую проницаемость и удельный вес. У таких количеств нет единиц.
  Скаляры 
 Эти величины имеют величину и единицу. Некоторые из них также могут иметь направление, но векторные законы не применяются.Примеры: заряд, масса, расстояние, скорость и ток.
  Векторы 
 Эти величины обладают величиной, единицей и направлением. Они также следуют закону сложения треугольников. Например, скорость, сила, импульс, крутящий момент и смещение.
  Фазоры 
 Они обладают величиной (амплитудой) и фазой. Постарайтесь следовать закону треугольника. Простое гармоническое движение (SHM), волны. Напряжение переменного тока и ток переменного тока являются векторами.
  Тензоры 
 Такие величины не имеют определенного направления, но имеют разные значения в разных направлениях. Например момент инерции. В анизотропных средах даже плотность, показатель преломления, диэлектрическая проницаемость, электрическая проводимость, напряжение, деформация и т. Д. Становятся тензорами. Физическая величина, имеющая только один компонент, называется скаляром или тензором нулевого ранга. Если он имеет более одного компонента, но меньше или равен четырем, он называется вектором или тензором ранга 1.Если компонент больше четырех, это называется тензором более высокого ранга.
  Коэффициенты преобразования 
 Некоторые физические величины преобразуются в другие при умножении на множитель. Например, в волне y  = y  0  sin (ωt -  kx ) , k - коэффициент преобразования. Когда k умножается на смещение или разность хода, он генерирует фазы или разность фаз. При частотной модуляции kE  m  f  c  = δ, k преобразует напряжение в угол и называется коэффициентом преобразования.Можно подумать о многих других коэффициентах пересчета. 
 В общем, физическая величина = величина x единица. Если единица измерения изменится, величина также изменится. Применяем n  1  u  1  = n  2  u  2 . 
 Физические величины можно разделить на основные и производные. 
  Фундаментальные величины  
 Величины, не зависящие от каких-либо других величин, называются «фундаментальными, абсолютными или основными величинами». Первоначально учитывались только три фундаментальные величины - длина, масса и время.С развитием науки добавились еще четыре физических величины. Это температура, электрический ток, сила света и количество вещества.
 Примеры физических величин 
 Масса
 Длина
 Время
 Электрический ток
 Объем
 Площадь
 Плотность
 Сила
 Энергия
 Мощность
 Электрический поток
 Электрический потенциал
 Скорость
 Скорость
 Разгон
 Импульс
 Крутящий момент
  Производные величины  
 Физические величины, полученные из фундаментальных величин, называются производными величинами, такими как скорость, ускорение, сила и импульс.