правило Ленца, уравнения Максвелла в интегральной форме, электромагнитная индукция
В статье расскажем что такое электромагнитная индукция, подробно опишем закон Фарадея и правило Ленца, а так же немного затронем тему уравнений Максвелла.
Электромагнитная индукция
Суть электромагнитной индукции заключается в том, что изменение магнитного поля, покрывающего электрическую цепь, вызывает возникновение электродвижущей силы в этой цепи, которая в случае замкнутой цепи вызывает протекание электрического тока. Если цепь, в которой мы должны генерировать электродвижущую силу, состоит из катушки и прикрепленного к ней амперметра, то источник изменяющегося магнитного поля, который включает в себя катушку, может быть адекватно перемещен постоянным магнитом или движущимся электромагнитом, в котором мы меняем ток питания. В каждом из этих случаев магнитное поле, которое пронизывает катушку, изменяется со временем.

В общем, изменение магнитного потока в цепи амперметра вызывает электрический ток в этой цепи.
Источником индуктивных явлений снова является сила Лоренца F, которая возникает, когда заряд q движется со скоростью v в магнитном поле B
F = q * v * B
Когда направляющая перемещается в поле B, подвижные носители нагрузки будут смещаться под действием силы Лоренца до тех пор, пока в проводнике не появится электрическое поле E, а сила, действующая на носители, F = q * E, уравнивает силу Лоренца. Когда линейный проводник длины l движется с постоянной скоростью v в однородном магнитном поле B, направленном перпендикулярно оси проводника и вектору скорости v , как на чертеже:

тогда мы сохраним условие баланса между силой Лоренца и силой отталкивания между зарядами в виде уравнения:
q*v*B = q*E ,
следовательно
v*B = E = V / l ,
где V — разность потенциалов на концах проводника длиной l. Следовательно, значение этой разности потенциалов:

Если вектор v не перпендикулярен полю B , но образует с ним угол N , то разность потенциалов на концах направляющей будет:
V = v * B * l * sin θ
Это означает, что перемещение проводника вдоль направления поля B не будет генерировать в нем электродвижущую силу. Нетрудно доказать, что в случае направляющей любой формы разность потенциалов между точками а и b направляющей равна:

Когда прямоугольная рамка со сторонами a и b вращается в однородном магнитном поле B с постоянной угловой скоростью T

это электродвижущая сила V, генерируемая с обеих сторон рамы:

Магнитные силы, действующие в двух других сторонах петли, перпендикулярны этим сторонам и не влияют на электродвижущую силу. Посредством соответствующего способа получения генерируемого напряжения можно реализовать простейшие модели генераторов переменного тока (а) и постоянного тока (b), как показано на рисунке:

В природе и технике существует огромное количество явлений, вызванных электромагнитной индукцией, то есть генерацией электродвижущей силы в пространстве, где существует изменяющееся магнитное поле. Все эти явления описываются одним замечательным, компактным уравнением, являющимся содержанием закона Фарадея.
Формулы и объяснение закона Фарадея
Большое открытие Майкла Фарадея (1791 — 1867) состояло в том, что он нашел правило, управляющие электромагнитной индукцией. В результате многолетних экспериментов Фарадей заявил, что электродвижущая сила E появляется в проводнике при изменении магнитного поля, окружающего этот проводник, величина генерируемой электродвижущей силы пропорциональна скорости магнитного поля, и что направление индуцированной электродвижущей силы зависит от направления, в котором изменяется магнитное поле. Все эти факты содержатся только в одном уравнении:

где dΦ B — элементарный поток магнитного поля

В общем случае, даже когда проводников нет, электродвижущая сила равна циркуляции электрического поля E вдоль замкнутого контура:

Таким образом , закон Фарадея может быть записан в обобщенной форме:

Обратите внимание, сколько факторов может изменить значение потока:

1. Изменение значения вектора B ;
2. Изменение значения площади поверхности d A ;
3. Путем изменения угла между B и d А ;
4. Одновременное изменение B и d А ;
5. Одновременное изменение В и угла ;
6. Одновременное изменение d A и угла.
Нельзя не заметить появившийся здесь знак минус! Этот знак минус в законе Фарадея был назван правилом Ленца, который можно понимать как правило неповиновения в электродинамике.
Правило Ленца
Правило Ленца (знак минуса в законе Фарадея) определяет, что индукционный электрический ток в проводнике, возникающий при изменении магнитного потока, направлен таким образом, что его магнитное поле противодействует изменению магнитного потока.
Закон индукции Фарадея вместе с правилом Ленца представляет собой анимацию, в которой движение постоянного магнита вызывает создание электродвижущей силы в катушке, покрытой полем магнита.


Индукционный ток может создаваться не только в обмотках, но и в сплошных металлических блоках, помещенных в изменяющиеся магнитные поля.
Пример: так называемый вихревой ток, схематически показанный на рисунке:

Когда постоянное магнитное поле приложено к вращающейся алюминиевой мишени, то в мишени создаются два семейства противоположно направленных токов. Магнитное поле вихревых токов направлено так, что часть диска, которая выходит из поля, будет втянута обратно в поле, а часть диска, которая входит в область поля, будет вытеснена из этого поля.
Вихревые токи часто нежелательны, например, в сердечниках трансформатора, где они вызывают потери тепла. Для ограничения вихревых токов сердечники трансформатора выполнены в виде стопок из листового металла.

Уравнения Максвелла в интегральной форме
Закон Фарадея содержит: обобщенный закон Ампера, закон Гаусса для электрического поля и закон Гаусса для магнитного поля в системе из четырех уравнений Максвелла. Эти уравнения были представлены применительно к макроскопическим контурам и замкнутым поверхностям. По этой причине мы говорим, что это уравнения Максвелла в интегральной форме. Давайте посмотрим на эти уравнения еще раз.
Закон Фарадея

Обобщенный закон Ампера

Закон Гаусса для электрического поля

Закон Гаусса для магнитного поля

Интегральные уравнения Максвелла описывают электрические и магнитные явления в макроскопическом масштабе. Ведь для их формулировки нужны контуры, замкнутые поверхности, токи и потоки полей. Однако чрезвычайно важно знать, что происходит с электрическими и магнитными полями в отдельных точках, то есть в микроскопическом масштабе. Тогда можно будет описать такие явления как электромагнитные волны.
Для микроскопического описания электрических и магнитных явлений используются уравнения Максвелла в дифференциальной форме. Чтобы получить их, мы применим две математические теоремы к уравнениям в интегральной форме: теорема Гаусса-Остроградского и теорема Стокса.
Следует отметить, что преобразование уравнений Максвелла между целочисленной и дифференциальной формами получается в результате только математических операций. Это означает физическую эквивалентность этих двух форм уравнений Максвелла.
Теорема Гаусса-Остроградского и теорема Стокса, несмотря на их кажущуюся сложность, концептуально совершенно просты и легко интуитивно принимаются. Обе эти тему будут представлены в следующей статье.
2. Закон Фарадея.
Обобщая опытные данные, Фарадей показал, что когда происходит изменение потока магнитной индукции через замкнутый контур в нем возникает индукционный ток, который указывает на наличие в цепи электродвижущей силы, эдс — электромагнитной индукции.
Величина тока и эдс определяется только скоростью изменения магнитного потока.
Пользуясь этими представлениями, Максвелл сформулировал закон Фарадея
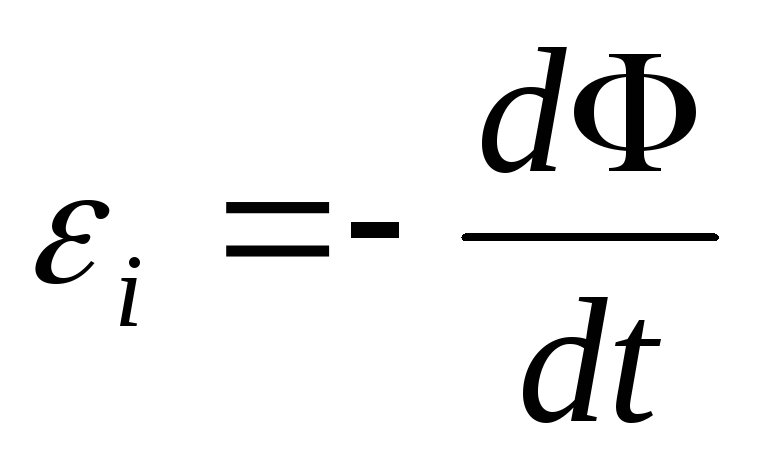
-электромагнитная индукция в контуре численно равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную этим контуром.
Знак – является математическим выражением правила Ленца для нахождения направления индукционного тока.
Правило Ленца: при всяком изменении магнитного потока сквозь замкнутый контур в последнем возникает ток такого направления, что его магнитное поле противодействует изменению магнитного потока.
3. Самоиндукция. Индуктивность контура.
Самоиндукцией называется возникновение эдс электромагнитной индукции в электрической цепи, вследствие изменения в ней электрического тока.
Это частный случай электромагнитной
индукции. По закону Био-Савара- Лапласа
при протекании в замкнутом контуре
тока, вокруг контура возникает магнитное
поле, магнитная индукция которого прямо
пропорциональна величине тока.
Поверхность, ограниченную контуром,
пронизывает собственный магнитный
поток  ,
прямо пропорциональный току
,
прямо пропорциональный току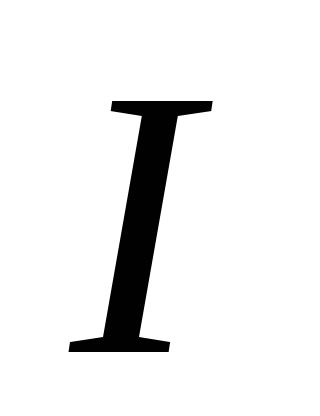
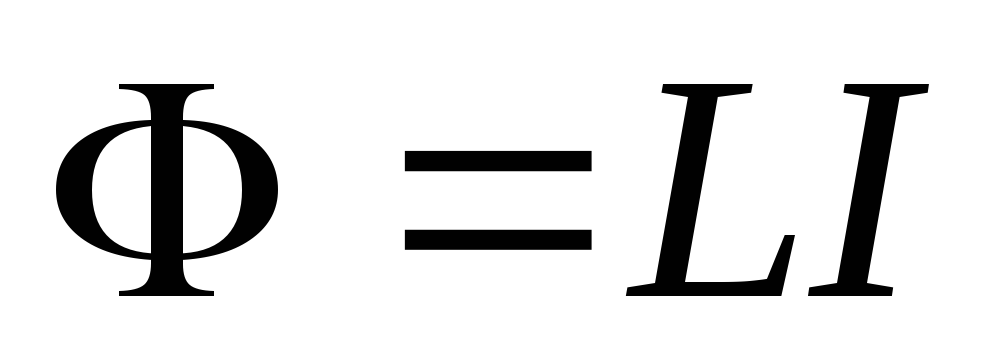 (1)
(1)
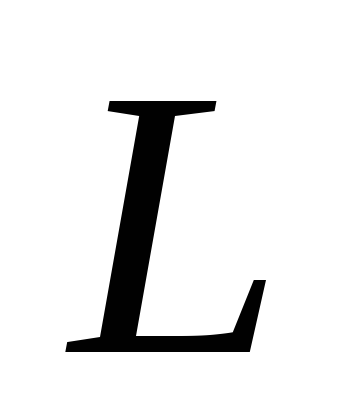 — коэффициент пропорциональности,
называемый индуктивностью контура.
— коэффициент пропорциональности,
называемый индуктивностью контура.
При изменении тока изменяется и  .
Следовательно в контуре будет
индуцироваться эдс самоиндукции. Из
(1) найдем единицу индукции,
.
Следовательно в контуре будет
индуцироваться эдс самоиндукции. Из
(1) найдем единицу индукции,
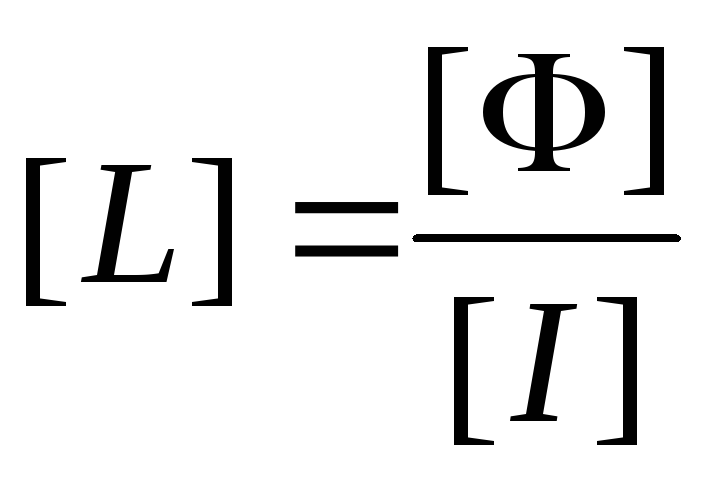
= Вб /А = Гн — единица индуктивности Генри.
1Гн индуктивность такого контура, магнитный поток самоиндукции которого при токе 1А равен 1Вб.
Применим к явлению самоиндукции закон Фарадея
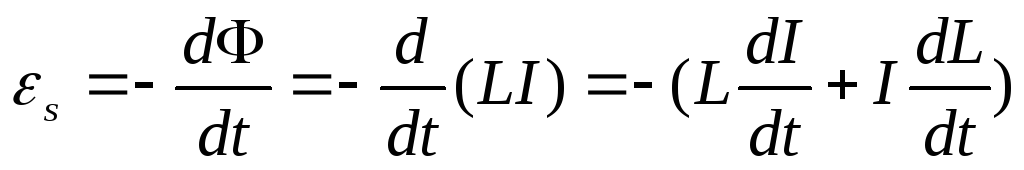 ,
,
при 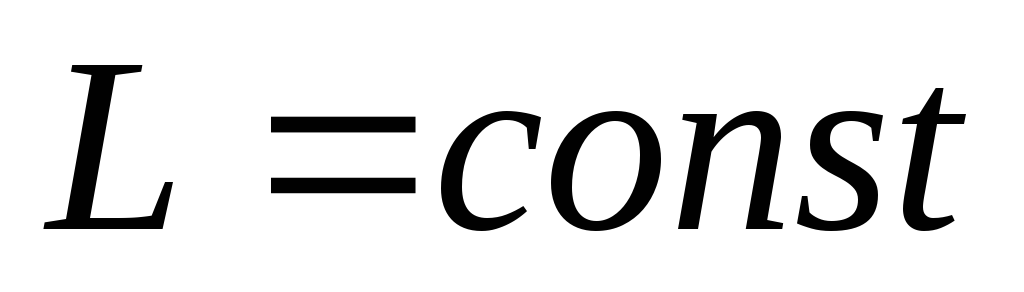 ,
,
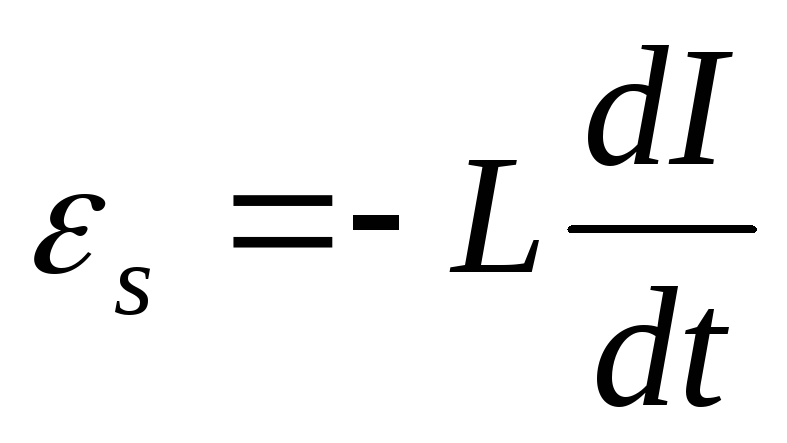 .
.
По правилу Ленца эдс самоиндукции противодействует изменению электрического тока в контуре, то есть замедляет его возрастание и убывание. Эдс и индуктивный ток пропорционален индуктивности контура. Индуктивность контура является мерой его инертности по отношению к изменению силы тока.
4. Взаимная индукция.
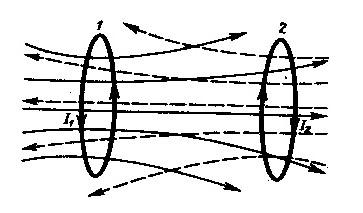
Явление взаимной индукции заключается в наведении эдс индукции во всех проводниках, находящихся вблизи цепи переменного тока.
| Рассмотрим
два неподвижных контура, расположенных
близко друг от друга.
|
Рис.2. |
При протекании тока 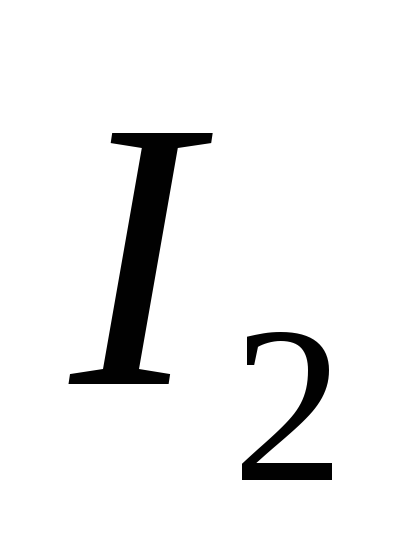 возникает магнитный поток, пронизывающий
контур 1
возникает магнитный поток, пронизывающий
контур 1
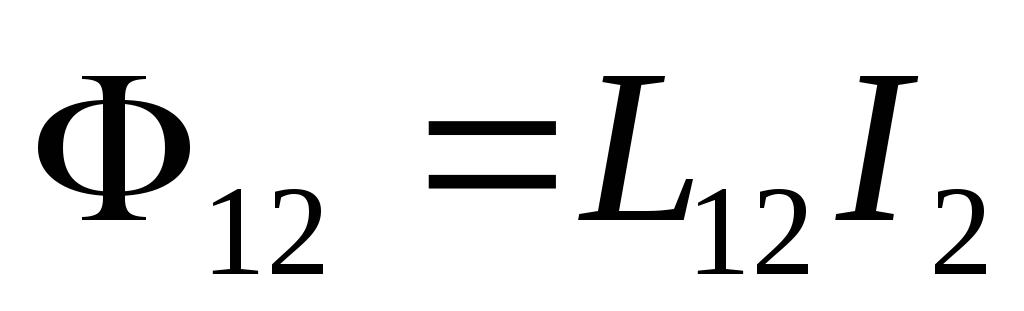
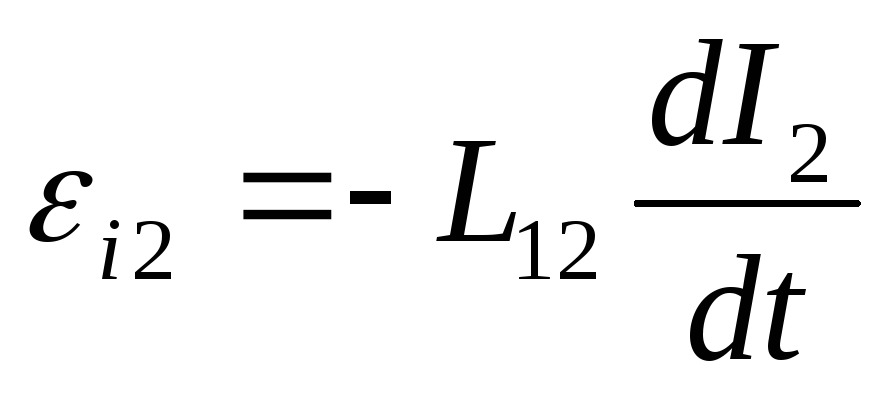 .
.
Явление возникновения эдс в одном из контуров при изменении силы тока в другом называется взаимной индукцией.
Коэффициенты 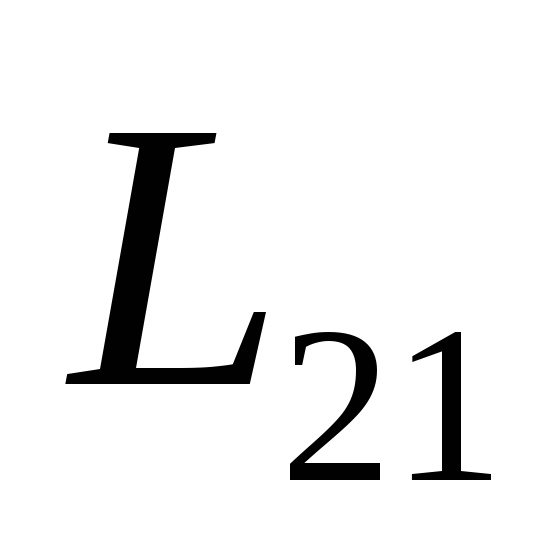
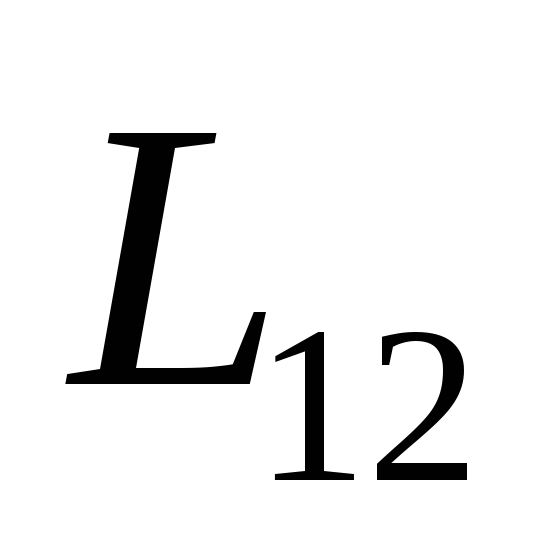 называются взаимной индуктивностью
контуров. Расчеты показывают, что
называются взаимной индуктивностью
контуров. Расчеты показывают, что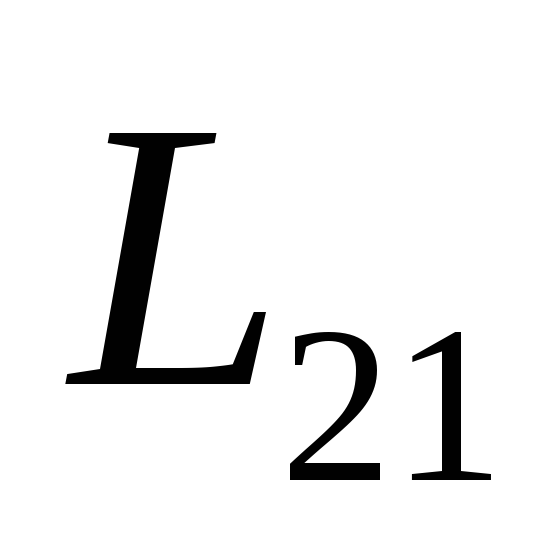 =
=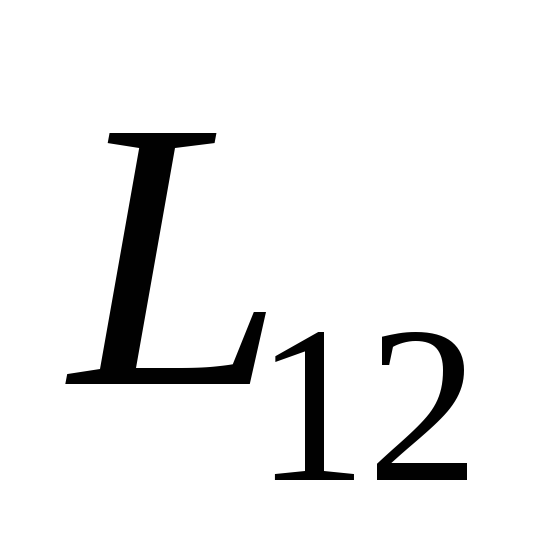 и зависят от магнитной проницаемости
среды
и зависят от магнитной проницаемости
среды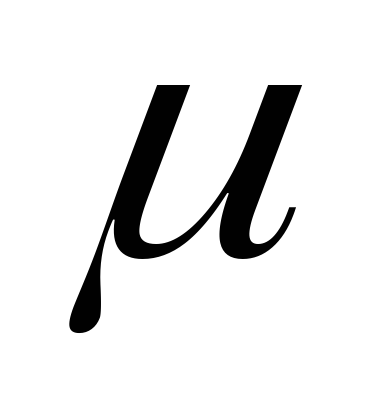 ,
от геометрической формы, размеров и
взаимного расположения контуров.
,
от геометрической формы, размеров и
взаимного расположения контуров.5. Энергия магнитного поля.
Проводник, по которому течет ток, окружен магнитным полем. Магнитное поле появляется и исчезает вместе с током. Часть энергии тока идет на создание магнитного поля, которое является как и электрическое носителем энергии.
Энергия магнитного поля равна работе, которая затрачивается током на создание этого поля.
Рассмотрим контур с индуктивностью 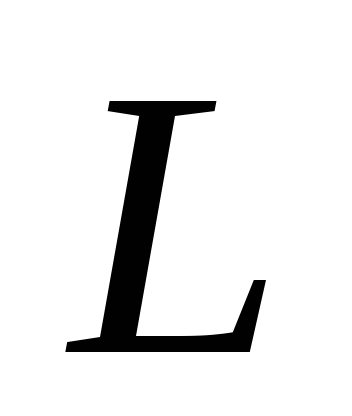 ,
по которому течет ток
,
по которому течет ток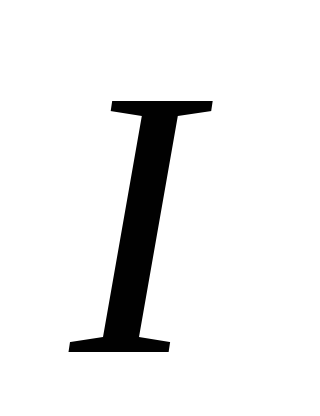 .
С данным контуром связан поток
.
С данным контуром связан поток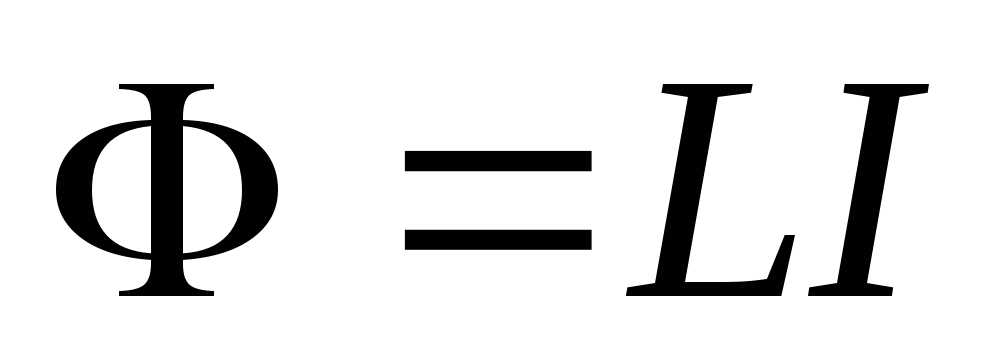 ,
при изменении тока на
,
при изменении тока на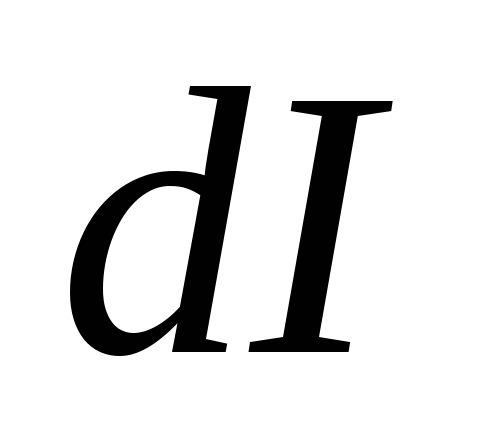 поток меняется на
поток меняется на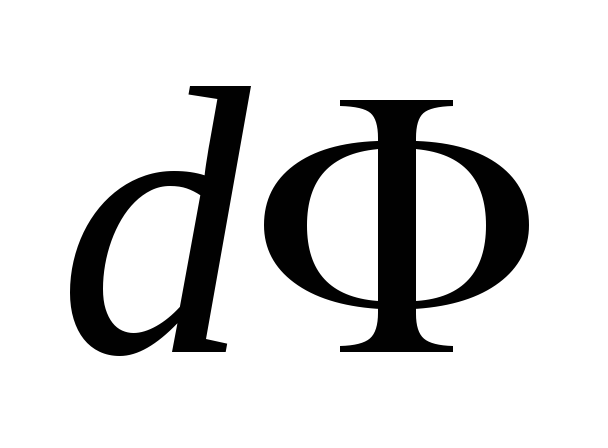
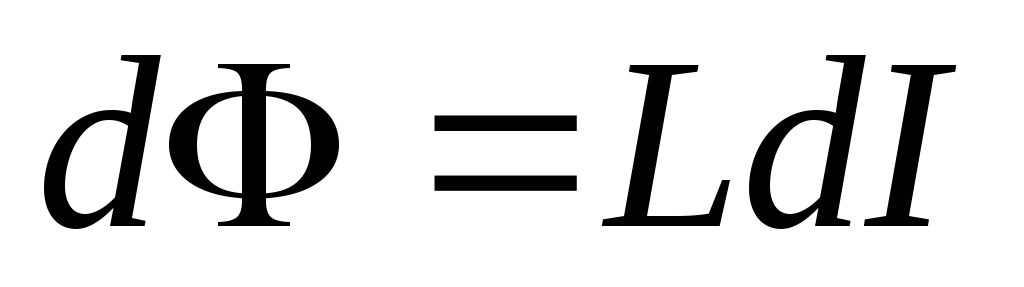 .
Для изменения потока нужно совершить
работу
.
Для изменения потока нужно совершить
работу 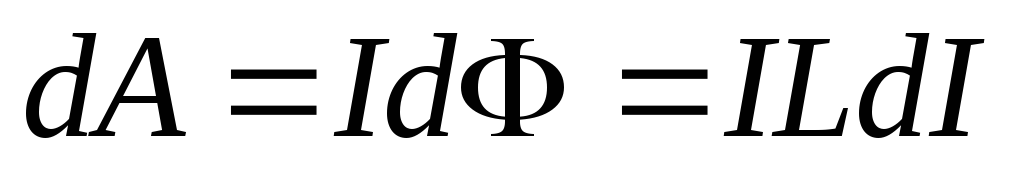 .
.
Тогда работа по созданию потока  будет равна
будет равна

Поэтому
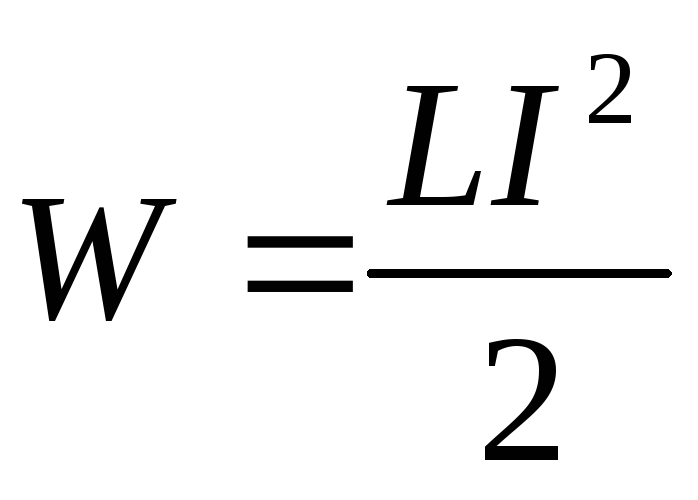 .
.
Закон электромагнитной индукции (закон Фарадея).
Лекция 26.
Электромагнитная индукция. Открытие Фарадея.
В 1831 г. М. Фарадеем было сделано одно из важнейших фундаментальных открытий в электродинамике – обнаружено явлениеэлектромагнитной индукции.
В замкнутом проводящем
контуре при изменении магнитного потока
(потока вектора 
Этот ток получил название индукционного.
Появление индукционного тока означает, что при изменении магнитного
Фарадей обнаружил, что индукционный ток можно вызвать двумя различными способами, которые удобно объяснить с помощью рисунка.
1-й способ: перемещение рамки  в магнитном поле неподвижной катушки
в магнитном поле неподвижной катушки (см.
рис.26.1).
(см.
рис.26.1).
2-й способ: изменение магнитного поля 
 ,
за счет ее движения или вследствие
изменения силы тока
,
за счет ее движения или вследствие
изменения силы тока в ней (или того и другого вместе). Рамка
в ней (или того и другого вместе). Рамка при этом неподвижна.
при этом неподвижна. В обоих этих случаях гальванометр  будет показывать наличие индукционного
тока в рамке
будет показывать наличие индукционного
тока в рамке
Направление индукционного тока и,
соответственно, знак э.д.с. индукции  определяются правилом Ленца.
определяются правилом Ленца.
Правило Ленца.
Индукционный ток всегда направлен так, чтобы противодействовать причине, его вызывающей.
Правило Ленца выражает важное физическое свойство – стремление системы противодействовать изменению ее состояния. Это свойство называют электромагнитной инерцией.
| (26.1) |
Природа электромагнитной индукции.
С целью выяснения физических причин, которые приводят к возникновению э.д.с. индукции, последовательно рассмотрим два случая.
1. Контур движется в постоянном магнитном поле.
| Пусть контур
с подвижной перемычкой длиной |
Рисунок 26.2 |
действовать сила
|
вызывающая перемещение электронов по перемычке вниз, т.е. потечет ток, направленный вверх.
Перераспределившиеся заряды создадут электрическое поле, которое возбудит ток и в остальных участках контура.
Это и есть индукционный ток.
Магнитная сила 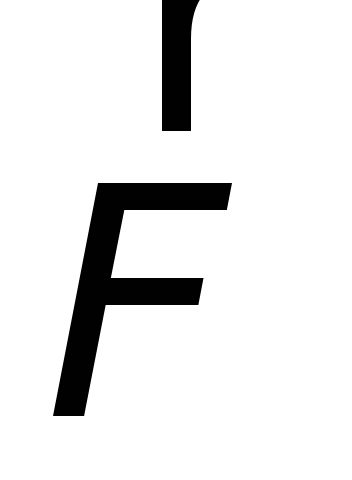 играет роль сторонней силы. Ей можно
сопоставить эквивалентное поле сторонних
сил
играет роль сторонней силы. Ей можно
сопоставить эквивалентное поле сторонних
сил
| (26.2) |
Электродвижущая сила,
создаваемая этим полем, называется электродвижущей
силой индукции  .
В нашем случае
.
В нашем случае
| (26.3) |
Здесь знак «минус» поставлен
потому, что стороннее поле 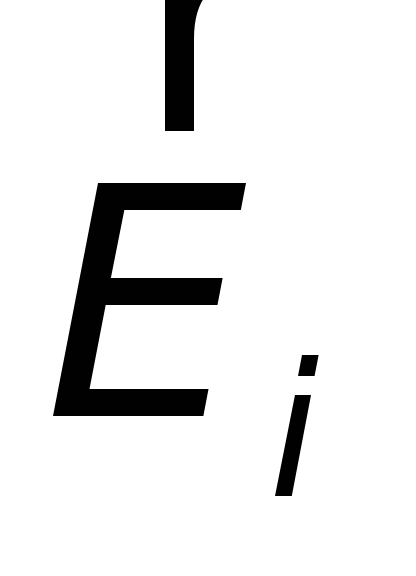 направлено против положительного обхода
контура, определяемого правилом правого
винта. Произведение
направлено против положительного обхода
контура, определяемого правилом правого
винта. Произведение есть скорость приращения площади контура
(приращение площади в единицу времени),
поэтому
есть скорость приращения площади контура
(приращение площади в единицу времени),
поэтому
|
где  — приращение магнитного потока сквозь
контур.
— приращение магнитного потока сквозь
контур.
Тогда,
| (26.4) |
Полученный результат можно обобщить
на случай произвольной ориентации
вектора индукции магнитного поля 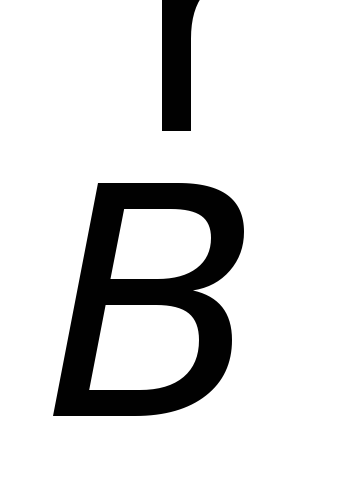 относительно плоскости контура и на
любой контур, движущийся (и/или
деформируемый) произвольным образом в
постоянном неоднородном внешнем
магнитном поле.
относительно плоскости контура и на
любой контур, движущийся (и/или
деформируемый) произвольным образом в
постоянном неоднородном внешнем
магнитном поле.
Итак, возбуждение э.д.с. индукции при
движении контура в постоянном магнитном
поле объясняется действием магнитной
составляющей силы Лоренца, пропорциональной  ,
которая возникает при перемещении
проводника.
,
которая возникает при перемещении
проводника.
2. Контур покоится в переменном магнитном поле.
Наблюдаемое на опыте возникновение индукционного тока свидетельствует о том, что и в этом случае в контуре появляются сторонние силы, которые теперь связаны с изменяющимся во времени магнитным полем. Какова же их природа? Ответ на этот принципиальный вопрос был дан Максвеллом.
Поскольку проводник покоится, то скорость
упорядоченного движения электрических
зарядов 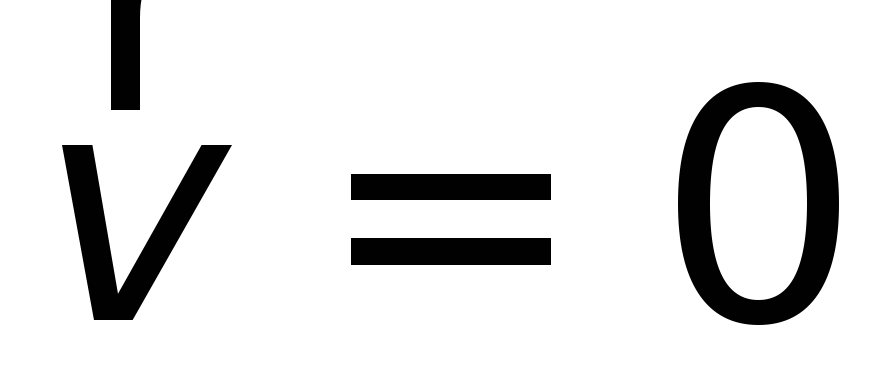 и, следовательно, магнитная сила,
пропорциональная
и, следовательно, магнитная сила,
пропорциональная ,
также равна нулю и уже не может привести
заряды в движение. Однако кроме магнитной
силы на электрический заряд может
действовать только сила со стороны
электрического поля, равная
,
также равна нулю и уже не может привести
заряды в движение. Однако кроме магнитной
силы на электрический заряд может
действовать только сила со стороны
электрического поля, равная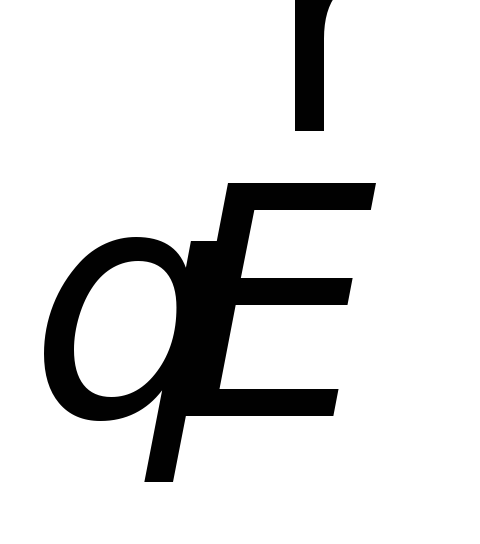 .
Поэтому остается заключить, чтоиндукционный ток обусловлен
электрическим полем
.
Поэтому остается заключить, чтоиндукционный ток обусловлен
электрическим полем 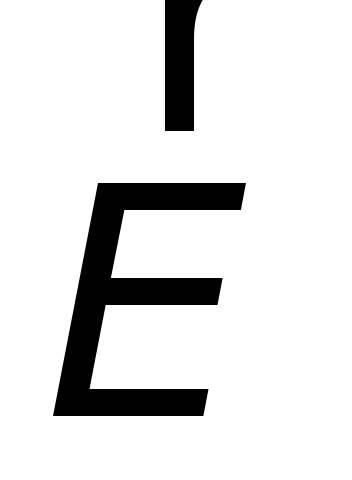 ,
возникающим при изменении во времени
внешнего магнитного поля. Именно
это электрическое поле и ответственно
за появление э.д.с. индукции в неподвижном
контуре. Согласно Максвеллу,изменяющееся
во времени магнитное поле порождает в
окружающем пространстве электрическое
поле. Возникновение электрического
поля не связано с наличием проводящего
контура, который лишь позволяет обнаружить
по возникновению в нем индукционного
тока существование этого поля.
,
возникающим при изменении во времени
внешнего магнитного поля. Именно
это электрическое поле и ответственно
за появление э.д.с. индукции в неподвижном
контуре. Согласно Максвеллу,изменяющееся
во времени магнитное поле порождает в
окружающем пространстве электрическое
поле. Возникновение электрического
поля не связано с наличием проводящего
контура, который лишь позволяет обнаружить
по возникновению в нем индукционного
тока существование этого поля.
Формулировка закона электромагнитной индукции, данная Максвеллом, принадлежит к числу наиболее важных обобщений электродинамики.
Всякое изменение магнитного поля во времени возбуждает в окружающем пространстве электрическое поле.
Математическая формулировка закона электромагнитной индукции в понимании Максвелла имеет вид:
Циркуляция вектора
напряженности 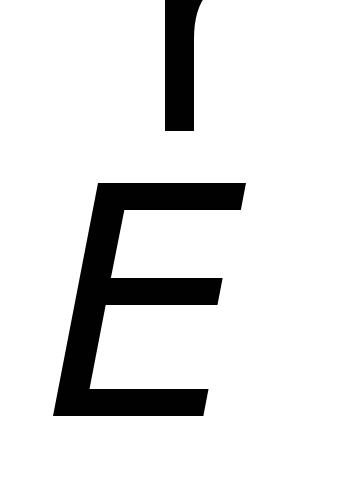 этого поля по любому неподвижному
замкнутому контуруопределяется выражением
этого поля по любому неподвижному
замкнутому контуруопределяется выражением
| (26.5) |
где  — магнитный поток, пронизывающий контур
— магнитный поток, пронизывающий контур .
.
Используемый для обозначения скорости изменения магнитного потока знак частной производной указывает на то, что контур является неподвижным.
Поток вектора  через поверхность, ограниченную контуром
через поверхность, ограниченную контуром ,
равен
,
равен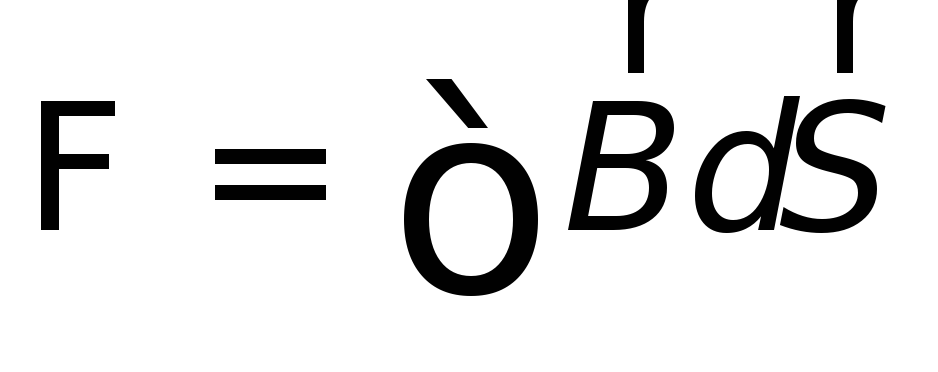 ,
поэтому выражение закона электромагнитной
индукции можно переписать следующим
образом:
,
поэтому выражение закона электромагнитной
индукции можно переписать следующим
образом:
| (26.6) |
Воспользовавшись теоремой Стокса можно получить закон электромагнитной индукции в дифференциальной форме:
| (26.7) |
Это одно из уравнений системы уравнений Максвелла.
Тот факт, что циркуляция электрического поля, возбуждаемого переменным во времени магнитным полем, отлична от нуля, означает, что рассматриваемое электрическое поле не потенциальное.Оно, как и магнитное поле, являетсявихревым.
В общем случае электрическое поле 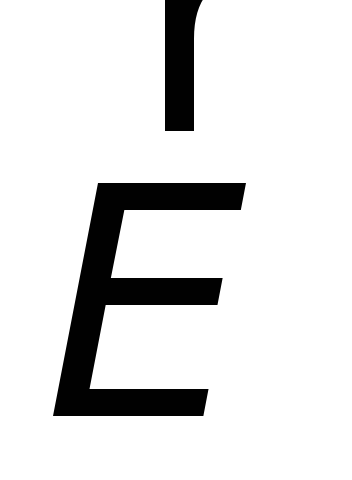 может быть представлено векторной
суммой потенциального (поля статических
электрических зарядов, циркуляция
которого равна нулю) и вихревого
(обусловленного изменяющимся во времени
магнитным полем) электрических полей.
может быть представлено векторной
суммой потенциального (поля статических
электрических зарядов, циркуляция
которого равна нулю) и вихревого
(обусловленного изменяющимся во времени
магнитным полем) электрических полей.
В основе рассмотренных нами явлений,
объясняющих закон электромагнитной
индукции, не просматривается общего
принципа, позволяющего установить
общность их физической природы. Поэтому
эти явления следует рассматривать как
независимые, а закон электромагнитной
индукции — как результат их совместного
действия. Тем более удивительным
оказывается тот факт, что э.д.с. индукции
в контуре всегда равна скорости изменения
магнитного потока сквозь контур. В тех
случаях, когда меняется и поле 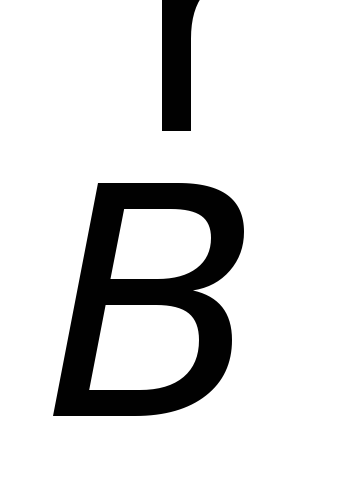 и расположение или конфигурация контура
в магнитном поле, э.д.с. индукции следует
рассчитывать по формуле
и расположение или конфигурация контура
в магнитном поле, э.д.с. индукции следует
рассчитывать по формуле
| (26.8) |
а закон электромагнитной индукции можно представить в виде
| (26.9) |
Выражение, стоящее в правой части этого равенства, представляет собой полную производную магнитного потока по времени: первое слагаемое связано с изменением магнитного поля во времени, второе – с движением контура.
Можно сказать, что во всех случаях индукционный ток вызывается полной силой Лоренца
|
Какая часть индукционного тока вызывается электрической, а какая магнитной составляющей силы Лоренца — зависит от выбора системы отсчета.
О работе сил Лоренца и Ампера.
Из самого определения работы следует, что сила, действующая в магнитном поле на электрический заряд и перпендикулярная его скорости, не может совершать работы. Однако при движении проводника с током, увлекающего за собой заряды, сила Ампера все же работу совершает. Наглядным подтверждением этого служат электромоторы.
Это противоречие исчезает, если принять
во внимание, что движение проводника в
магнитном поле неизбежно сопровождается
явлением электромагнитной индукции.
Поэтому наряду с силой Ампера работу
над электрическими зарядами совершает
и возникающая в проводнике электродвижущая
сила индукции. Т.о., полная работа сил
магнитного поля складывается из
механической работы, обусловленной
силой Ампера, и работы э.д.с., индуцируемой
при движении проводника. Обе работы
равны по модулю и противоположны по
знаку, поэтому их сумма равна нулю.
Действительно, работа амперовой силы
при элементарном перемещении проводника
с током в магнитном поле равна 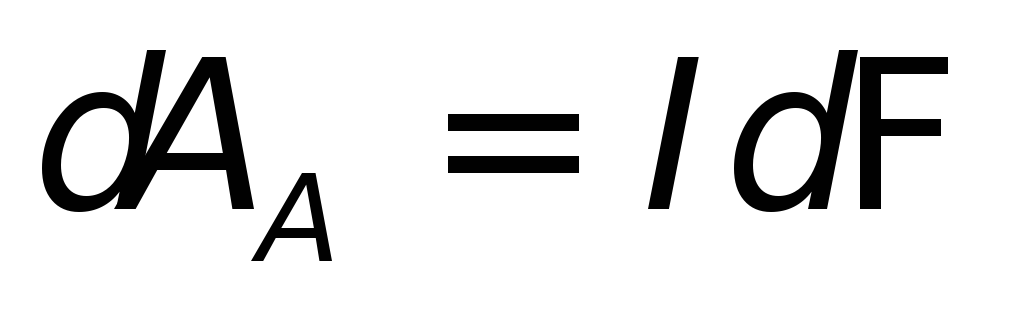 ,
за это же время э.д.с. индукции совершает
работу
,
за это же время э.д.с. индукции совершает
работу
| (26.10) |
тогда полная работа  .
.
Силы Ампера совершают работу не за счет энергии внешнего магнитного поля, которое может оставаться постоянным, а за счет источника э.д.с., поддерживающего ток в контуре.
Закон электромагнитной индукции Фарадея — Википедия
Материал из Википедии — свободной энциклопедии
Зако́н электромагни́тной инду́кции Фараде́я является основным законом электродинамики, касающимся принципов работы трансформаторов, дросселей, многих видов электродвигателей и генераторов.[1] Закон гласит:
или другими словами:
Генерируемая ЭДС пропорциональна скорости изменения магнитного потока.
При этом индукционный ток направлен таким образом, что его действие противоположно действию причины, вызвавшей этот ток (правило Ленца).[2]
История
Электромагнитная индукция была обнаружена независимо друг от друга Майклом Фарадеем и Джозефом Генри в 1831 году, однако Фарадей первым опубликовал результаты своих экспериментов[3][4].
В первой экспериментальной демонстрации электромагнитной индукции (август 1831) Фарадей обмотал двумя проводами противоположные стороны железного тора (конструкция похожа на современный трансформатор). Основываясь на своей оценке недавно обнаруженного свойства электромагнита, он ожидал, что при включении тока в одном проводе особого рода волна пройдёт сквозь тор и вызовет некоторое электрическое влияние на его противоположной стороне. Он подключил один провод к гальванометру и смотрел на него, когда другой провод подключал к батарее. В самом деле, он увидел кратковременный всплеск тока (который он назвал «волной электричества»), когда подключал провод к батарее, и другой такой же всплеск, когда отключал его.[5] В течение двух месяцев Фарадей нашёл несколько других проявлений электромагнитной индукции. Например, он увидел всплески тока, когда быстро вставлял магнит в катушку и вытаскивал его обратно, он генерировал постоянный ток во вращающемся вблизи магнита медном диске со скользящим электрическим проводом («диск Фарадея»)[6].

Электромагнитная индукция. Опыты Фарадея. Электромагнитные колебания и волны

1. Явление электромагнитной индукции было открыто английским ученым Майклом Фарадеем. Если соединить катушку с гальванометром и внести в катушку полосовой магнит северным полюсом, то стрелка гальванометра отклонится, что свидетельствует о существовании в катушке электрического тока. Когда магнит остановится в катушке, то ток прекратится (рис. 95). При выдвижении магнита из катушки в ней вновь появится электрический ток, но он будет иметь противоположное направление. Причиной возникновения электрического тока в катушке, является изменение магнитного поля, пронизывающего эту катушку, которое происходит при движении магнита.


Возможны различные способы изменения магнитного поля, пронизывающего контур проводника. Можно, например, перемещать не магнит, а катушку, т.е. надевать её на магнит. При этом также возникнет индукционный ток. Можно в большую катушку вставить малую катушку. Большую катушку соединить с гальванометром, а малую — с источником постоянного тока. При замыкании и размыкании цепи малой катушки можно наблюдать отклонение стрелки гальванометра. Таким образом, при любом изменении магнитного поля пронизывающего замкнутый проводник, в нём возникает индукционный ток.
Эти и другие опыты показывают, что ток появляется только при изменении магнитного поля, пронизывающего замкнутый проводник.
Явление возникновения тока в замкнутом проводнике при изменении магнитного поля, пронизывающего контур проводника, называется электромагнитной индукцией. Ток, возникающий в этом случае в цепи, называют индукционным током.
Таким образом, направление индукционного тока в катушке зависит от направления движения магнита.
2. Направление индукционного тока зависит от того, каким полюсом вносят магнит в катушку или выносят из нее, т.е. от направления магнитного поля. Если вносить магнит в катушку не северным полюсом, как это делалось в опыте, описанном выше, а южным полюсом, то стрелка гальванометра отклонится в сторону, противоположную той, в которую она отклонялась при внесении магнита северным полюсом. Направление индукционного тока будет разным в зависимости от того, вносят магнит в катушку или выносят его из катушки. Таким образом, направление индукционного тока зависит от направления движения магнита относительно катушки.
Вносить магнит в катушку можно быстрее и медленнее. Наблюдения позволяют сделать вывод о том, что сила индукционного тока зависит от скорости движения магнита, т.е. от скорости изменения магнитного поля. Сила индукционного тока тем больше, чем больше скорость изменения магнитного поля, пронизывающего контур проводника.
Если в самом проводнике изменяется сила тока, то вокруг проводника существует переменное магнитное поле. Это поле порождает в проводнике индукционный ток, который называется током самоиндукции, а явление возникновения такого тока — явлением самоиндукции.
Значение открытия явления магнитной индукции заключается в том, что в этом явлении наглядно наблюдается связь электрических и магнитных явлений, электрического и магнитного полей, что позволяет говорить о существовании единого электромагнитного поля.
3. Явление электромагнитной индукции лежит в основе работы генератора электрического тока — устройства, которое служит источником электрического тока и в котором происходит преобразование механической энергии в электрическую. Основными частями генератора являются магнит и расположенная между его полюсами насаженная на вал рамка.
Рамка приводится во вращение, пронизывающее её магнитное поле изменяется, и в катушке возникает индукционный ток. Этот ток снимается с рамки с помощью устройства, называемого коллектором, представляющим собой два полукольца, каждое из которых присоединяется к различным концам рамки, и щёток, касающихся колец. Промышленные генераторы имеют более сложное устройство, но все они состоят из вращающейся части (ротора), обычно в промышленном генераторе это электромагнит, создающий вращающееся магнитное поле, и неподвижной части (статора) — обмотки, в которой индуцируется электрический ток.
4. Максвеллом было теоретически показано, а Герцем экспериментально доказано, что изменяющееся магнитное поле порождает переменное электрическое поле, в свою очередь переменное электрическое поле порождает переменное магнитное поле, т.е. в пространстве происходят изменения (колебания) характеристик электромагнитного поля.
Электромагнитные колебания происходят в колебательной системе, называемой колебательным контуром. Колебательный контур — это электрическая цепь, состоящая из конденсатора и катушки индуктивности (рис. 96).


Если зарядить конденсатор и затем замкнуть его на катушку, то по цепи пойдёт электрический ток. При этом конденсатор начнёт разряжаться. Сначала сила тока в цепи будет увеличиваться, и появится ток самоиндукции, препятствующий увеличению основного тока и направленный против него. Через ½ часть периода конденсатор полностью разрядится, а сила тока в катушке станет максимальной. Затем сила тока начнет уменьшаться. Ток самоиндукции, который при этом возникнет, будет стремиться поддержать основной ток и будет направлен так же, как и он. Через ¼ часть периода ток прекратится, и конденсатор перезарядится. Затем пойдет обратный процесс.
Таким образом, в колебательном контуре происходят электромагнитные колебания, т.е. периодические изменения заряда, силы тока, электрического и магнитного полей. Колебания, происходящие в колебательном контуре, благодаря начальному запасу энергии в конденсаторе называются свободными. В процессе колебаний энергия извне в контур не поступает.
Минимальный промежуток времени, через который процесс в колебательном контуре полностью повторяется, называется периодом \( (T) \) электромагнитных колебаний. За период колебаний заряд на обкладках конденсатора изменяется от максимального значения до следующего максимального значения того же знака, или сила тока изменяется от максимального значения до следующего максимального значения при том же направлении тока.
Характеризуя электромагнитные колебания, часто говорят об их частоте. Частотой \( (\nu) \) колебаний называют число полных колебаний в одну секунду. Частота обратна периоду колебаний
Единицей частоты является 1 Гц. Частоту электромагнитных колебаний часто измеряют в килогерцах (1 кГц = 1000 Гц) и в мегагерцах (1 МГц = 1 000 000 Гц).
5. Подобно тому как механические колебания распространяются в пространстве в виде механических волн, электромагнитные колебания распространяются в пространстве в виде электромагнитных волн. Многочисленные эксперименты показывают, что электрическое и магнитное поля взаимосвязаны. Если в какой-либо точке пространства возникает переменное электрическое поле, то в соседних точках оно возбуждает переменное магнитное поле, которое, в свою очередь, возбуждает переменное электрическое поле и т.д. Таким образом, можно говорить об электромагнитном поле. Это поле и распространяется в пространстве.
Процесс распространения периодически изменяющегося электромагнитного ноля представляет собой электромагнитные волны.
Электромагнитные волны распространяются в вакууме со скоростью 300 000 км/с. Они характеризуются определённой длиной волны \( \lambda \). Длина волны — это расстояние, на которое перемещается электромагнитная волна за время, равное периоду колебаний \( (T) \). \( \lambda=cT \) или \( \lambda=c/\nu \), где \( c \) — скорость распространения электромагнитной волны, \( \nu \) — частота колебаний.
6. Электрически заряженные частицы могут колебаться с различной частотой. Соответственно, излучаемые при этом электромагнитные волны имеют разную длину волны. Поэтому диапазон частот электромагнитных волн очень широк: он лежит в пределах от 0 до 1022 Гц, а длина волны — в пределах от 10-14 м до бесконечности. По длине волны или по частоте электромагнитные волны можно разделить на восемь диапазонов. Обладая рядом общих свойств (интерференция, дифракция), волны разной частоты имеют и специфические свойства.
ПРИМЕРЫ ЗАДАНИЙ
Часть 1
1. В катушку, соединённую с гальванометром, вносят магнит. Направление индукционного тока зависит
А. От скорости перемещения магнита.
Б. От того, каким полюсом вносят магнит в катушку.
Правильный ответ
1) только А
2) только Б
3) и А, и Б
4) ни А, ни Б
2. В катушку, соединённую с гальванометром, вносят магнит. Сила индукционного тока зависит
А. от скорости перемещения магнита
Б. от того, каким полюсом вносят магнит в катушку
1) только А
2) только Б
3) и А, и Б
4) ни А, ни Б
3. Постоянный магнит вносят в катушку, замкнутую на гальванометр (см. рисунок).


Если выносить магнит из катушки с большей скоростью, то показания гальванометра будут примерно соответствовать рисунку


4. Две одинаковые катушки замкнуты на гальванометры. В катушку А вносят полосовой магнит, а из катушки Б вынимают такой же полосовой магнит. В какой катушке гальванометр зафиксирует индукционный ток?
1) только в катушке А
2) только в катушке Б
3) в обеих катушках
4) ни в одной из катушек
5. В первом случае магнит вносят в сплошное эбонитовое кольцо, а во втором случае выносят из сплошного медного кольца (см. рисунок).


Индукционный ток
1) возникает только в эбонитовом кольце
2) возникает только в медном кольце
3) возникает в обоих кольцах
4) не возникает ни в одном из колец
6. Внутри катушки, соединённой с гальванометром, находится малая катушка, подключённая к источнику постоянного тока. В каком из перечисленных опытов гальванометр зафиксирует индукционный ток?
А. В малой катушке выключают электрический ток.
Б. Малую катушку вынимают из большой.
1) только в опыте А
2) только в опыте Б
3) в обоих опытах
4) ни в одном из опытов
7. Внутри катушки, соединённой с гальванометром, находится малая катушка, подключённая к источнику тока. Первую секунду от начала эксперимента малая катушка неподвижна внутри большой катушки. Затем в течение следующей секунды её вынимают из большой катушки. Третью секунду малая катушка находится вне большой катушки. В течение четвертой секунды малую катушку вдвигают в большую. В какой(-ие) промежуток(-ки) времени гальванометр зафиксирует появление индукционного тока?
1) только 0-1 с
2) 1 с-2 с и 3 с-4 с
3) 0-1 с и 2 с-3 с
4) только 1 с-2 с
8. Внутри катушки, соединённой с гальванометром, находится малая катушка, подключённая к источнику тока. Оси катушек совпадают. Первую секунду от начала эксперимента малая катушка неподвижна внутри большой катушки. Затем в течение следующей секунды её вращают относительно вертикальной оси по часовой стрелке. Третью секунду малая катушка вновь остаётся в покое. В течение четвёртой секунды малую катушку вращают против часовой стрелки. В какие промежутки времени гальванометр зафиксирует появление индукционного тока в катушке?
1) индукционный ток может возникнуть в любой промежуток времени
2) индукционный ток возникнет в промежутках времени 1-2 с, 3-4 с
3) индукционный ток не возникнет ни в какой промежуток времени
4) индукционный ток возникнет в промежутках времени 0-1 с, 2-3 с
9. К электромагнитным волнам относятся:
A. Волны на поверхности воды.
Б. Радиоволны.
B. Световые волны.
Укажите правильный ответ.
1) только А
2) только Б
3) только В
4) Б и В
10. Какие из приведённых ниже формул могут быть использованы для определения скорости электромагнитной волны?
A. \( v=\lambda\nu \)
Б. \( v=\frac{\lambda}{\nu} \)
В. \( v=\frac{\lambda}{T} \)
Г. \( v=\lambda T \)
1) только А
2) только Б
3) А и В
4) В и Г
11. Установите соответствие между названием опыта (в левом столбце таблицы) и явлением, которое в этом опыте наблюдается (в правом столбце таблицы). В таблице под номером физической величины левого столбца запишите соответствующий номер выбранного вами элемента правого столбца.
ВЕЛИЧИНА
A) опыты Фарадея
Б) опыт Эрстеда
B) опыт Ампера
ХАРАКТЕР ИЗМЕНЕНИЯ ЗНАЧЕНИЯ ВЕЛИЧИНЫ
1) действие проводника с током на магнитную стрелку
2) электромагнитная индукция
3) взаимодействие проводников с током
12. Установите соответствие между техническими устройствами и физическими явлениями, лежащими в основе их работы.
ТЕХНИЧЕСКИЕ УСТРОЙСТВА
A) генератор электрического тока
Б) электрический двигатель
B) электромагнитное реле
ФИЗИЧЕСКИЕ ЯВЛЕНИЯ
1) взаимодействие постоянных магнитов
2) взаимодействие проводников с током
3) возникновение электрического тока в проводнике при его движении в магнитном поле
4) магнитное действие проводника с током
5) действие магнитного поля на проводник с током
Часть 2
13. На какую частоту нужно настроить радиоприёмник, чтобы слушать радиостанцию, которая передает сигналы па длине волны 2,825 м?
1) 106,2 кГц
2) 106,2 МГц
3) 847,5 кГц
4) 847,5 МГц
Ответы




Электромагнитная индукция. Опыты Фарадея. Электромагнитные колебания и волны
Оценка7
7..Явление электромагнитной индукции. Закон Фарадея. Правило Ленца.
Электромагнитная индукция — явление возникновения электрического тока в замкнутом контуре при изменении магнитного потока, проходящего через него.
Электромагнитная индукция была открыта Майклом Фарадеем 29 августа 1831 года. Он обнаружил, что электродвижущая сила, возникающая в замкнутом проводящем контуре, пропорциональна скорости изменения магнитного потока через поверхность, ограниченную этим контуром. Величина электродвижущей силы (ЭДС) не зависит от того, что является причиной изменения потока — изменение самого магнитного поля или движение контура (или его части) в магнитном поле. Электрический ток,
Закон Фарадея
Согласно закону электромагнитной индукции Фарадея (в СИ):
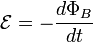
где
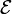 —
электродвижущая
сила, действующая вдоль произвольно
выбранного контура,
—
электродвижущая
сила, действующая вдоль произвольно
выбранного контура,
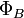
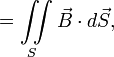 —
магнитный
поток через поверхность, натянутую
на этот контур.
—
магнитный
поток через поверхность, натянутую
на этот контур.
Знак «минус» в формуле отражает правило Ленца, названное так по имени русского физика Э. Х. Ленца:
Индукционный ток, возникающий в замкнутом проводящем контуре, имеет такое направление, что создаваемое им магнитное поле противодействует тому изменению магнитного потока, которым был вызван данный ток.
Для катушки, находящейся в переменном магнитном поле, закон Фарадея можно записать следующим образом:
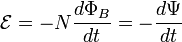
где
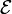 —
электродвижущая сила,
—
электродвижущая сила,
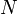 —
число витков,
—
число витков,
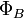 —
магнитный поток через один виток,
—
магнитный поток через один виток,
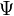 —
потокосцепление
катушки.
—
потокосцепление
катушки.
Правило Ленца определяет направление индукционного тока и гласит:
Индукционный ток всегда имеет такое направление, что он ослабляет действие причины, возбуждающей этот ток.
Физическая суть правила
Согласно
закону
электромагнитной индукции Фарадея
при изменении магнитного
потока 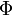 ,
пронизывающего электрический контур,
в нём возбуждается ток,
называемый индукционным. Величина
электродвижущей
силы,
ответственной за этот ток, определяется
уравнением[1]:
,
пронизывающего электрический контур,
в нём возбуждается ток,
называемый индукционным. Величина
электродвижущей
силы,
ответственной за этот ток, определяется
уравнением[1]:
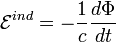
где знак «минус» означает, что ЭДС индукции действует так, что индукционный ток препятствует изменению потока. Этот факт и отражён в правиле Ленца.
Правило Ленца носит обобщённый характер и справедливо в различных физических ситуациях, которые могут отличаться конкретным физическим механизмом возбуждения индукционного тока. Так, если изменение магнитного потока вызвано изменением площади контура (например, за счёт движения одной из сторон прямоугольного контура), то индукционный ток возбуждается силой Лоренца, действующей на электроны перемещаемого проводника в постоянном магнитном поле. Если же изменение магнитного потока связано с изменение величины внешнего магнитного поля, то индукционный ток возбуждается вихревым электрическим полем, появляющимся при изменении магнитного поля. Однако в обоих случаях индукционный ток направлен так, чтобы скомпенсировать изменение потока магнитного поля через контур.
Если внешнее магнитное поле, пронизывающее неподвижный электрический контур, создаётся током, текущим в другом контуре, то индукционный ток может оказаться направлен как в том же направлении, что и внешний, так и в противоположном: это зависит от того, уменьшается или увеличивается внешний ток. Если внешний ток увеличивается, то растёт создаваемое им магнитное поле и его поток, что приводит к появлению индукционного тока, уменьшающего это увеличение. В этом случае индукционный ток направлен в сторону, противоположную основному. В обратном случае, когда внешний ток уменьшается со временем, уменьшение магнитного потока приводит к возбуждению индукционного тока, стремящегося увеличить поток, и этот ток направлен в ту же сторону, что и внешний ток.
Конспект «Электромагнитная индукция. Опыты Фарадея»
Электромагнитная индукция. Опыты Фарадея
Раздел ОГЭ по физике: 3.13. Электромагнитная индукция. Опыты Фарадея.
Опыт Эрстеда показал, что электрический ток создаёт в окружающем пространстве магнитное поле. Майкл Фарадей пришёл к мысли, что может существовать и обратный эффект: магнитное поле, в свою очередь, порождает электрический ток. В 1831 г. М. Фарадей обнаружил, что в замкнутом проводящем контуре при изменении магнитного поля возникает индукционный ток. (Индукция в данном случае – появление, возникновение.)
1) Опыт с двумя проволочными спиралями (катушками). Одна из таких спиралей присоединялась к гальванометру, который регистрировал слабые токи. Вторая спираль сообщалась с гальванической батареей. В момент замыкания и размыкания цепи второй катушки индикаторная стрелка гальванометра обязательно отклонялась.
2) Опыт по взаимодействию магнита и катушки с током: при внесении магнита в катушку в цепи возникает электрический ток, при вынесении также возникает ток, но другого направления. Сила тока зависит от скорости внесения (вынесения) магнита.
 Явление возникновения электрического поля при изменении магнитного поля называется электромагнитной индукцией.
Явление возникновения электрического поля при изменении магнитного поля называется электромагнитной индукцией.
Индукционный ток в катушке возникает при:
- перемещении постоянного магнита относительно катушки;
- перемещении электромагнита относительно катушки;
- перемещении сердечника относительно электромагнита, вставленного в катушку;
- регулировании тока в цепи электромагнита;
- замыкании и размыкании цепи.
Если в изменяющееся магнитное поле поместить замкнутый проводящий контур, то появление тока в контуре свидетельствует о действии в контуре сторонних электрических сил (или о возникновении в контуре ЭДС индукции).
Явление возникновения электрического тока в замкнутом проводящем контуре при изменении магнитного поля, пронизывающего контур, является следствием электромагнитной индукции.
Основные области применения электромагнитной индукции: генерирование тока (индукционные генераторы на всех электростанциях, динамо-машины), трансформаторы.

Конспект урока по физике 8 класса «Электромагнитная индукция. Опыты Фарадея».
Следующая тема: Электромагнитные колебания и волны.




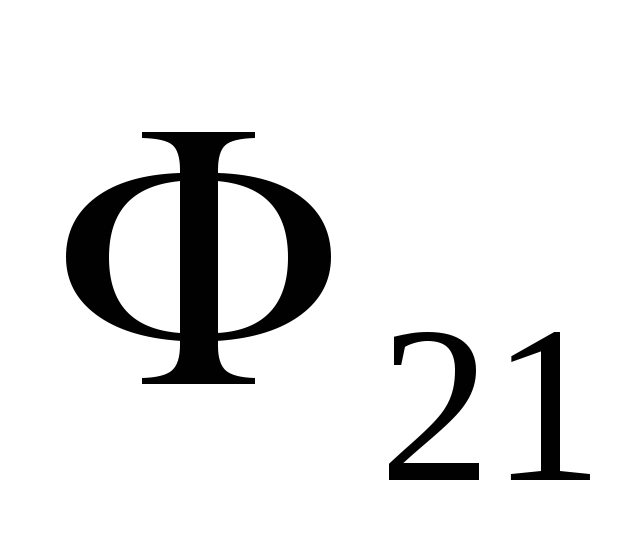 — часть потока, которая пронизывает
контур 2
— часть потока, которая пронизывает
контур 2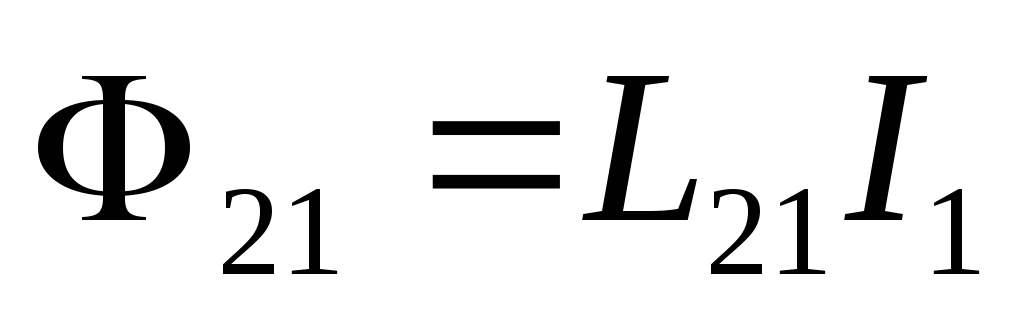
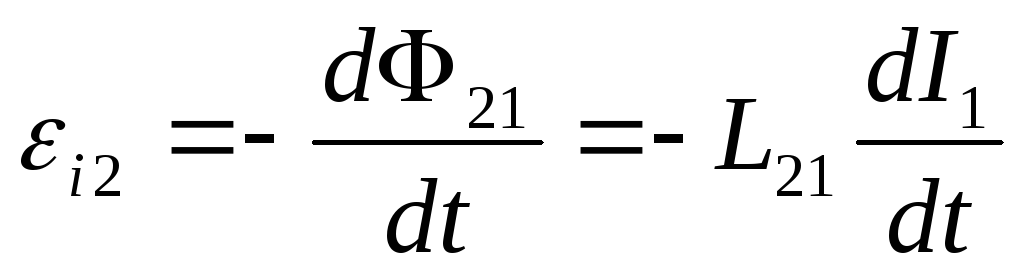
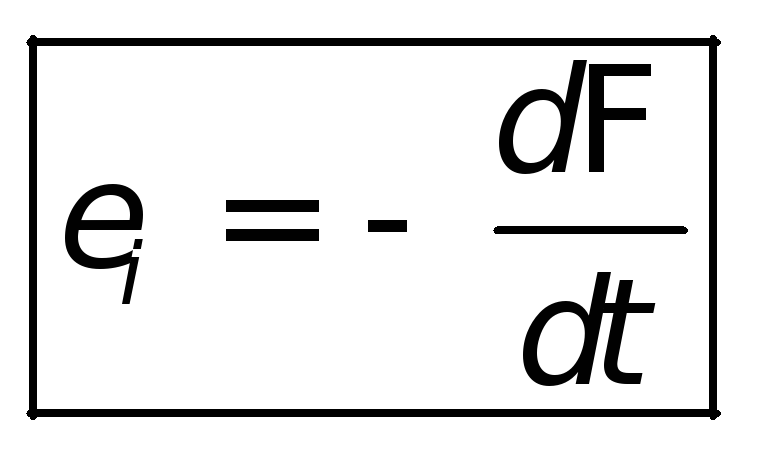

 находится в магнитном поле,
перпендикулярном плоскости контура
(см.Рисунок
26.2). Если двигать перемычку со
скоростью
находится в магнитном поле,
перпендикулярном плоскости контура
(см.Рисунок
26.2). Если двигать перемычку со
скоростью вправо, то с такой же скоростью начнут
двигаться и носители тока в перемычке
– электроны. В результате на каждый
электрон начинает
вправо, то с такой же скоростью начнут
двигаться и носители тока в перемычке
– электроны. В результате на каждый
электрон начинает ,
,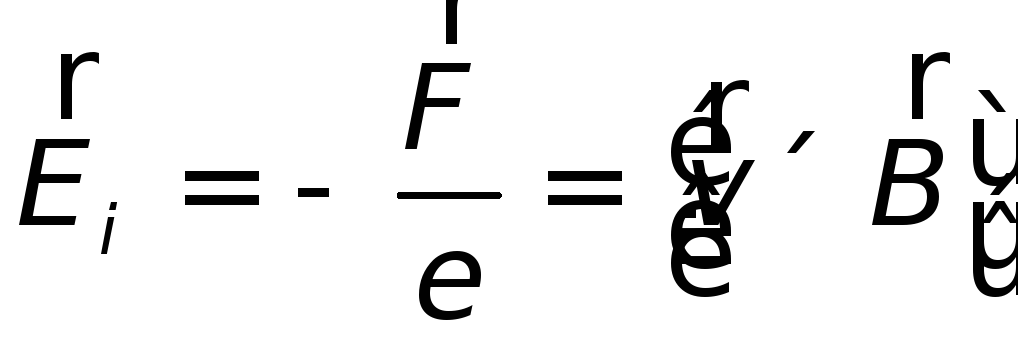 .
.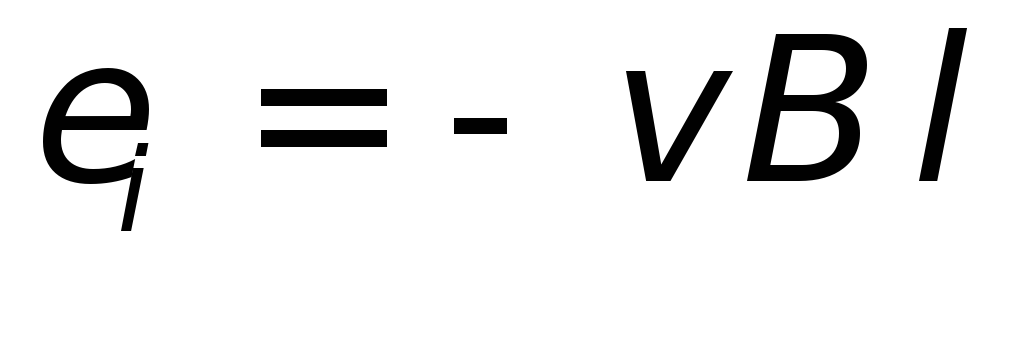 .
.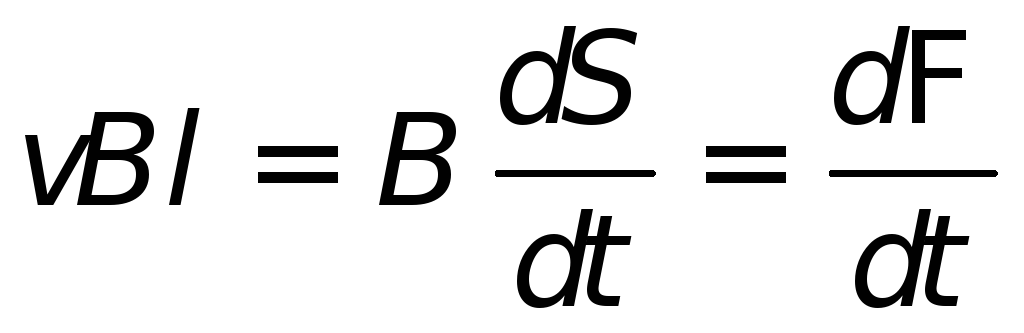 ,
,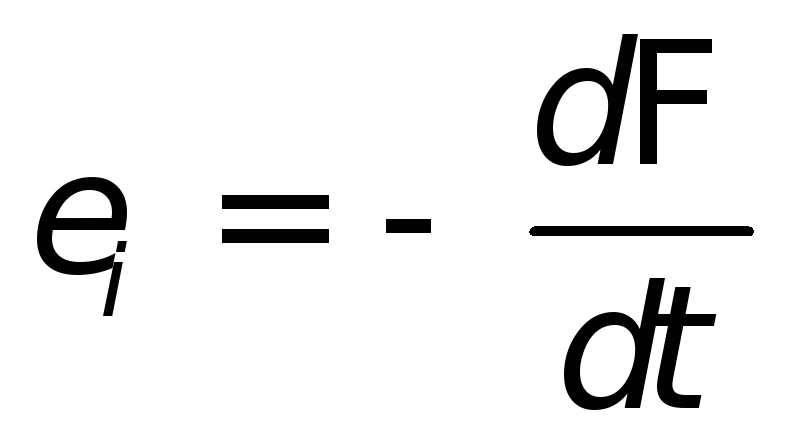 .
.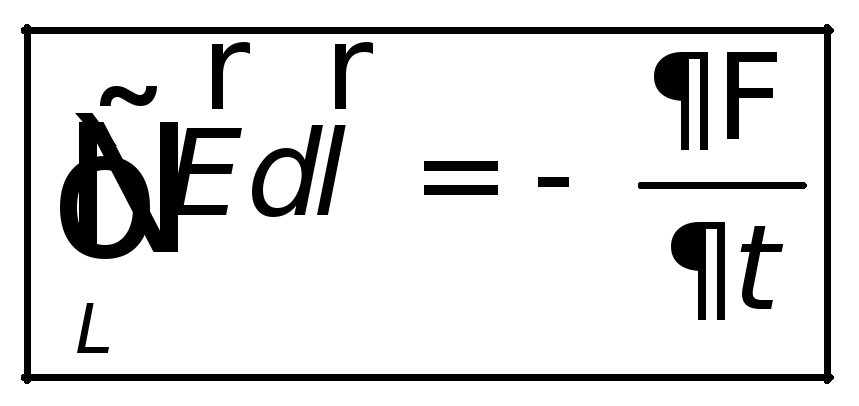 ,
,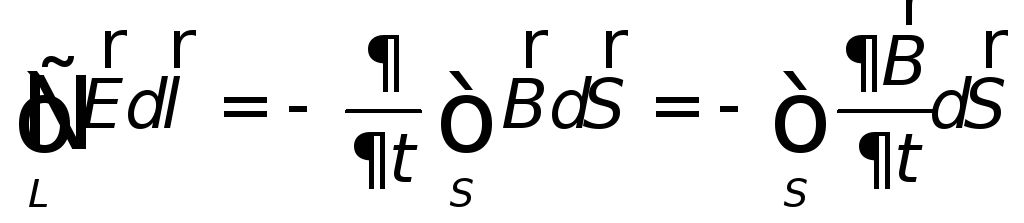 .
. .
. ,
,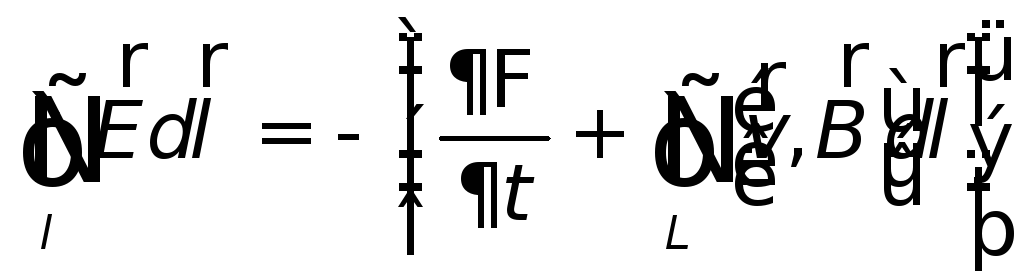 .
.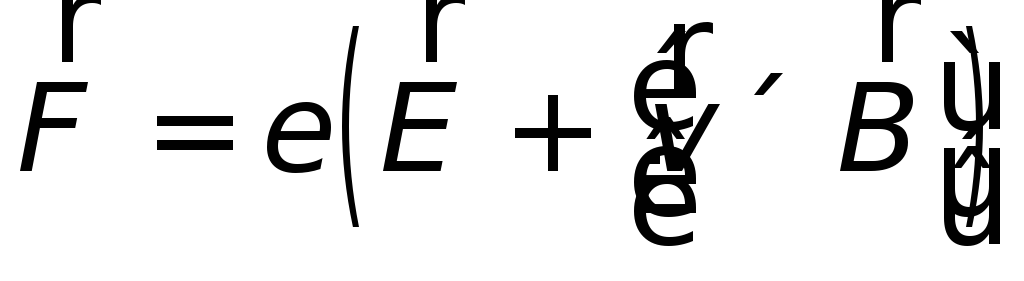 .
.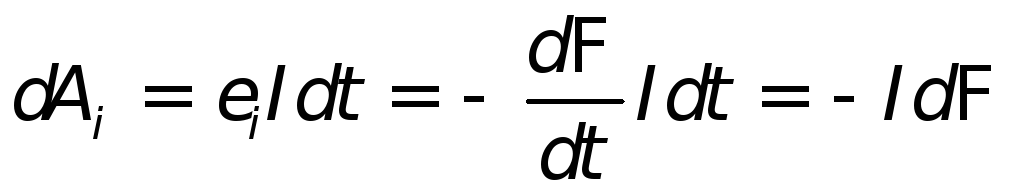 ,
,