Закон электромагнитной индукции Фарадея — Википедия. Что такое Закон электромагнитной индукции Фарадея

Зако́н электромагни́тной инду́кции Фараде́я является основным законом электродинамики, касающимся принципов работы трансформаторов, дросселей, многих видов электродвигателей и генераторов.^[1] Закон гласит:

или другими словами:

Генерируемая ЭДС пропорциональна скорости изменения магнитного потока.

При этом индукционный ток направлен таким образом, что его действие противоположно действию причины, вызвавшей этот ток (правило Ленца).^[2]

История

Электромагнитная индукция была обнаружена независимо друг от друга Майклом Фарадеем и Джозефом Генри в 1831 году, однако Фарадей первым опубликовал результаты своих экспериментов^[3][4].

В первой экспериментальной демонстрации электромагнитной индукции (август 1831) Фарадей обмотал двумя проводами противоположные стороны железного тора (конструкция похожа на современный трансформатор). Основываясь на своей оценке недавно обнаруженного свойства электромагнита, он ожидал, что при включении тока в одном проводе особого рода волна пройдёт сквозь тор и вызовет некоторое электрическое влияние на его противоположной стороне. Он подключил один провод к гальванометру и смотрел на него, когда другой провод подключал к батарее. В самом деле, он увидел кратковременный всплеск тока (который он назвал «волной электричества»), когда подключал провод к батарее, и другой такой же всплеск, когда отключал его.

[5] В течение двух месяцев Фарадей нашёл несколько других проявлений электромагнитной индукции. Например, он увидел всплески тока, когда быстро вставлял магнит в катушку и вытаскивал его обратно, он генерировал постоянный ток во вращающемся вблизи магнита медном диске со скользящим электрическим проводом («диск Фарадея»)

[6].

Фарадей объяснил электромагнитную индукцию с использованием концепции так называемых силовых линий. Однако, большинство учёных того времени отклонили его теоретические идеи, в основном потому, что они не были сформулированы математически.^[7] Исключение составил Максвелл, который использовал идеи Фарадея в качестве основы для своей количественной электромагнитной теории.^[7][8][9] В работах Максвелла аспект изменения во времени электромагнитной индукции выражен в виде дифференциальных уравнений. Оливер Хевисайд назвал это законом Фарадея, хотя он несколько отличается по форме от первоначального варианта закона Фарадея и не учитывает индуцирование ЭДС при движении. Версия Хевисайда является формой признанной сегодня группы уравнений, известных как уравнения Максвелла.

Эмилий Христианович Ленц сформулировал в 1834 году закон (правило Ленца), который описывает «поток через цепь» и даёт направление индуцированной ЭДС и тока в результате электромагнитной индукции.

Эксперимент Фарадея, показывающий индукцию между витками провода: жидкостная батарея (справа) даёт ток, который протекает через небольшую катушку (A), создавая магнитное поле. Когда катушки неподвижны, ток не индуцируется. Но когда маленькая катушка вставляется или извлекается из большой катушки (B), магнитный поток через катушку изменяется, вызывая ток, который регистрируется гальванометром (G).^[10]

Закон Фарадея как два различных явления

Некоторые физики отмечают, что закон Фарадея в одном уравнении описывает два разных явления: двигательную ЭДС, генерируемую действием магнитной силы на движущийся провод, и трансформаторную ЭДС, генерируемую действием электрической силы вследствие изменения магнитного поля. Джеймс Клерк Максвелл обратил внимание на этот факт в своей работе

О физических силовых линиях в 1861 году. Во второй половине части II этого труда Максвелл даёт отдельное физическое объяснение для каждого из этих двух явлений. Ссылка на эти два аспекта электромагнитной индукции имеется в некоторых современных учебниках.^[11] Как пишет Ричард Фейнман:^[12]

Таким образом, «правило потока» о том, что ЭДС в цепи равна скорости изменения магнитного потока через контур, применяется независимо от причины изменения потока: то ли потому что поле изменяется, то ли потому что цепь движется (или и то, и другое)…. В нашем объяснении правила мы использовали два совершенно различных закона для двух случаев  –    v×B{\displaystyle {\stackrel {\mathbf {v\times B} }{}}}   для «движущейся цепи» и   ∇ x E = −∂ tB{\displaystyle {\stackrel {\mathbf {\nabla \ x\ E\ =\ -\partial _{\ t}B} }{}}}   для «меняющегося поля».

Мы не знаем никакого аналогичного положения в физике, когда такие простые и точные общие принципы требовали бы для своего реального понимания анализа с точки зрения двух различных явлений.

— Ричард Фейнман,   Фейнмановские лекции по физике

Отражение этой очевидной дихотомии было одним из основных путей, которые привели Эйнштейна к разработке специальной теории относительности:

Известно, что электродинамика Максвелла — как её обычно понимают в настоящее время — при применении к движущимся телам приводит к асимметрии, которая, как кажется, не присуща этому явлению. Возьмем, к примеру, электродинамическое взаимодействие магнита и проводника. Наблюдаемое явление зависит только от относительного движения проводника и магнита, тогда как обычное мнение рисует резкое различие между этими двумя случаями, в которых либо одно, либо другое тело находится в движении. Ибо, если магнит находится в движении, а проводник покоится, в окрестности магнита возникает электрическое поле с определенной плотностью энергии, создавая ток там, где расположен проводник. Но если магнит покоится, а проводник движется, то в окрестности магнита никакое электрическое поле не возникает. В проводнике, однако, мы находим электродвижущую силу, для которой не существует соответствующей энергии самой по себе, но которая вызывает — предполагая равенство относительного движения в двух обсуждаемых случаях — электрические токи по тому же направлению и той же интенсивности, как в первом случае.

Примеры подобного рода вместе с неудачной попыткой обнаружить какое-либо движение Земли относительно «светоносной среды» предполагают, что явления электродинамики, а также механики не обладают свойствами, соответствующими идее абсолютного покоя.

— Альберт Эйнштейн, К электродинамике движущихся тел^[13]

Поток через поверхность и ЭДС в контуре

Определение поверхностного интеграла предполагает, что поверхность Σ поделена на мелкие элементы. Каждый элемент связан с вектором dA, величина которого равна площади элемента, а направление — по нормали к элементу во внешнюю сторону. Векторное поле F(r, t) определено во всём пространстве, а поверхность Σ ограничена кривой ∂Σ, движущейся со скоростью v. По этой поверхности производится интегрирование поля.

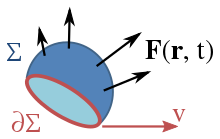
Закон электромагнитной индукции Фарадея использует понятие магнитного потока Φ_B через замкнутую поверхность Σ, который определён через поверхностный интеграл:

 :Φ=∬SBn⋅dS,{\displaystyle \Phi =\iint \limits _{S}\mathbf {B_{n}} \cdot d\mathbf {S} ,}

где dS — площадь элемента поверхности Σ(t), B — магнитное поле, а B·dS — скалярное произведение B и dS. Предполагается, что поверхность имеет «устье», очерченное замкнутой кривой, обозначенной ∂Σ(

t). Закон индукции Фарадея утверждает, что когда поток изменяется, то при перемещении единичного положительного пробного заряда по замкнутой кривой ∂Σ возникает ЭДС E{\displaystyle {\mathcal {E}}}, величина которой определяется по формуле:

|E|=|dΦdt| ,{\displaystyle |{\mathcal {E}}|=\left|{{d\Phi } \over dt}\right|\ ,}

где |E|{\displaystyle |{\mathcal {E}}|} — величина электродвижущей силы (ЭДС) в вольтах, а Φ_B — магнитный поток в веберах. Направление электродвижущей силы определяется законом Ленца.

Для плотно намотанной катушки индуктивности, содержащей N витков, каждый с одинаковым магнитным потоком Φ_B, закон индукции Фарадея утверждает, что:

|E|=N|dΦBdt|,{\displaystyle |{\mathcal {E}}|=N\left|{{d\Phi _{B}} \over dt}\right|,}

где N — число витков провода, Φ_B — магнитный поток в веберах на один виток.

При выборе пути ∂Σ(t) для нахождения ЭДС заметим, что путь должен удовлетворять двум основным требованиям: (i) путь должен быть замкнутым, и (ii) путь должен охватывать относительное движение частей контура (источник происхождения t-зависимости в ∂Σ(t)). К требованиям не относится то, что путь должен совпадать с линией тока, но, конечно, ЭДС, которая находится по закону потока, будет считаться по выбранному пути. Если путь не совпадает с линией тока, то подсчитанная ЭДС, возможно, будет не та ЭДС, которая вызывает ток.

Пример 1: пространственно меняющееся магнитное поле

Рис. 3. Замкнутый прямоугольный провод движется вдоль оси x со скоростью v в магнитном поле, которое изменяется вдоль x.

Рассмотрим случай на рисунке 3, на котором прямоугольная замкнутая проволочная петля, расположенная в плоскости xy, перемещается в направлении оси x со скоростью v. Центр петли x_C удовлетворяет условию v = dx_C / dt. Петля имеет длину ℓ в направлении оси y и ширину w в направлении оси x. Зависящее от времени пространственно меняющееся магнитное поле B(x) показано в направлении z. Магнитное поле на левой стороне равно B(x_C − w / 2), а на правой стороне B(x_C + w / 2). Электродвижущую силу можно найти либо с помощью закона Лоренца, либо, что эквивалентно, используя вышеизложенный закон индукции Фарадея.

Закон Лоренца

Заряд q в проводнике на левой стороне петли испытывает силу Лоренца q v × B k = −q v B(x_C − w / 2) j   (j, k — единичные векторы в направлениях y и z; см. векторное произведение векторов), что вызывает ЭДС (работу на единицу заряда) v ℓ B(x_C − w / 2) по всей длине левой стороны петли. На правой стороне петля аналогичное рассуждение показывает, что ЭДС равна v ℓ B(x_C + w / 2). Две противоположные друг другу ЭДС толкают положительный заряд по направлению к нижней части петли. В случае, когда поле B возрастает вдоль х, сила на правой стороне будет больше, а ток будет течь по часовой стрелке. Используя правило правой руки, мы получаем, что поле B, создаваемое током, противоположно приложенному полю.^[14] ЭДС, вызывающая ток, должна увеличиваться по направлению против часовой стрелки (в отличие от тока). Складывая ЭДС в направлении против часовой стрелки вдоль петли мы находим:

E=vℓ[B(xC+w/2)−B(xC−w/2)] .{\displaystyle {\mathcal {E}}=v\ell [B(x_{C}+w/2)-B(x_{C}-w/2)]\ .}

Закон Фарадея

В любой точке петли магнитный поток через неё равен:

ΦB=±∫0ℓdy∫xC−w/2xC+w/2B(x)dx{\displaystyle \Phi _{B}=\pm \int _{0}^{\ell }dy\int _{x_{C}-w/2}^{x_{C}+w/2}B(x)dx}

=±ℓ∫xC−w/2xC+w/2B(x)dx .{\displaystyle \qquad =\pm \ell \int _{x_{C}-w/2}^{x_{C}+w/2}B(x)dx\ .}

Выбор знака определяется по принципу, имеет ли нормаль к поверхности в данной точке то же направление, что и B, или противоположное. Если нормаль к поверхности имеет то же направление, что и поле B наведённого тока, этот знак отрицательный. Производная по времени от потока (найденная с помощью методов дифференцирования сложной функции или по правилу Лейбница дифференцирования интеграла) равна:

dΦBdt=(−)ddxC[∫0ℓdy ∫xC−w/2xC+w/2dxB(x)]dxCdt {\displaystyle {\frac {d\Phi _{B}}{dt}}=(-){\frac {d}{dx_{C}}}\left[\int _{0}^{\ell }dy\ \int _{x_{C}-w/2}^{x_{C}+w/2}dxB(x)\right]{\frac {dx_{C}}{dt}}\ }

=(−)vℓ[B(xC+w/2)−B(xC−w/2)] ,{\displaystyle \qquad =(-)v\ell [B(x_{C}+w/2)-B(x_{C}-w/2)]\ ,}

(где v = dx_C / dt является скоростью движения петли в направлении оси х), что приводит к:

E=−dΦBdt=vℓ[B(xC+w/2)−B(xC−w/2)] ,{\displaystyle {\mathcal {E}}=-{\frac {d\Phi _{B}}{dt}}=v\ell [B(x_{C}+w/2)-B(x_{C}-w/2)]\ ,}

как и в предыдущем случае.

Эквивалентность этих двух подходов является общеизвестной, и в зависимости от решаемой задачи более практичным может оказаться либо тот, либо другой метод.

Пример 2: проводник, движущийся в постоянном магнитном поле

Рис. 4. Два проводника замкнутые на проводящие обода образуют «рамку» вращающуюся с угловой скоростью ω в радиальном, направленном наружу магнитном поле B фиксированной величины. Ток подается щётками, касающимися верхнего и нижнего дисков с проводящими ободами.

На рис. 4 показан шпиндель, образованный двумя дисками с проводящими ободами, и проводники, расположенные вертикально между этими ободами. ток скользящими контактами подается на проводящие обода. Эта конструкция вращается в магнитном поле, которое направлено радиально наружу и имеет одно и то же значение в любом направлении. то есть мгновенная скорость проводников, ток в них и магнитная индукция, образуют правую тройку, что заставляет проводники вращаться.

Сила Лоренца

В этом случае на проводники действует Сила Ампера, а на единичный заряд в проводнике Сила Лоренца — поток вектора магнитной индукции B , ток в проводниках, соединяющих проводящие обода, направлен нормально к вектору магнитной индукции, тогда сила, действующая на заряд в проводнике, будет равна

F=qBv,{\displaystyle F=qBv\,,}

где v = скорости движущегося заряда^[15]

Следовательно, сила действующая на проводники

F=IBℓ,{\displaystyle {\mathcal {F}}=IB\ell ,}

где l — длина проводников

Здесь мы использовали B как некую данность, на самом деле она зависит от геометрических размеров ободов конструкции, и это значение можно вычислить, используя Закон Био — Савара — Лапласа . Данный эффект используется и в другом устройстве, называемом Рельсотрон

Закон Фарадея

Интуитивно привлекательный, но ошибочный подход к использованию правила потока выражает поток через цепь по формуле Φ_B = B w ℓ, где w — ширина движущейся петли.

Ошибочность такого подхода в том, что это не рамка в обычном понимании этого слова. Прямоугольник на р

Закон электромагнитной индукции Фарадея и его формулировка в дифференциальной форме

Фарадей был первым, кто обнаружил явление электромагнитной индукции. Это случилось в ходе опыта, когда он исследовал изменение потока магнитной индукции в замкнутом проводнике и выявил, что при этом вырабатывается электрический ток. Определение направления ЭДС индукции осуществляется согласно правилу, сформулированному Ленцем.

Определение 1

Направление индукционного потока препятствует изменению магнитного потока через создаваемое им поле.

Определение 2

Нейман определил закон электромагнитной индукции математически, и этой формулировкой мы пользуемся по сей день: εi=-dΦdt.

В нем не учитываются возможные движения контура. Соотношение dΦdt является выражением полной скорости изменения потока индукции, который охватывается проводником при его движении и деформации, а также при изменениях магнитного поля.

Закон Фарадея для электромагнитной индукции очень важен, поскольку он является выражением нового физического явления: когда магнитное поле изменяется, оно порождает электрическое, т.е. электрическое поле может возникать не только при помощи электрических зарядов. Здесь необходимо учитывать одно важное замечание:

Определение 3

Движение магнитов может порождать электрический ток даже при неподвижных проводниках.

Электромагнитная индукция является одним из фундаментальных природных законов, устанавливающим связь между магнитным или электрическим полями.

Закон Фарадея в дифференциальной форме

Чтобы сформулировать закон Фарадея в такой форме, нам потребуется вспомнить несколько базовых формул.

1. ЭДС индукции: εi=-υBl.
2. Магнитный поток: Φ=∫SBndS.
3. Теорема Стокса: ∮l=a→dl=∫Srotna→dS.

Используя данные выражения, мы можем записать следующую формулу:

∮C(Edl)=∫S(n rot E)dS=-1c∫Sn∂B∂tdS.

Здесь S обозначает поверхность, натянутую на контур S. Поскольку значение S является п

Электромагнитная индукция ℹ️ определение физического явления, формулы, единицы измерения, значение закона Фарадея, применение правила Ленца к направлению потока вектора

При изменении тока в электрической цепи возникает магнитное поле. Причиной этого является электромагнитная индукция. Это явление широко применяется на практике. 

В статье рассказывается о том, что это такое, и каковы его основные закономерности.

Явление электромагнитной индукции

При изменении тока происходит образование магнитного поля. Это явление, в свою очередь, влияет на движение электронов. 

Если рассматривать одиночный провод, расположенный прямо, то он будет создавать поле, направление силовых линий которого идёт по кругу в перпендикулярной ему плоскости.

Если в магнитном поле происходят изменения, то это увеличивает или ослабляет силу тока, который проходит по проводнику. Направление изменения зависит от того, как меняется поле. Это явление позволяет преобразовывать электрическую энергию в механическую или наоборот.

Учёный, которому принадлежит заслуга открытия взаимодействия электрического и магнитного полей — Майкл Фарадей. 

Были проведены опыты, которые показали, что изменение магнитного поля способно порождать движение электронов. Это явление впоследствии назвали индукционным током.

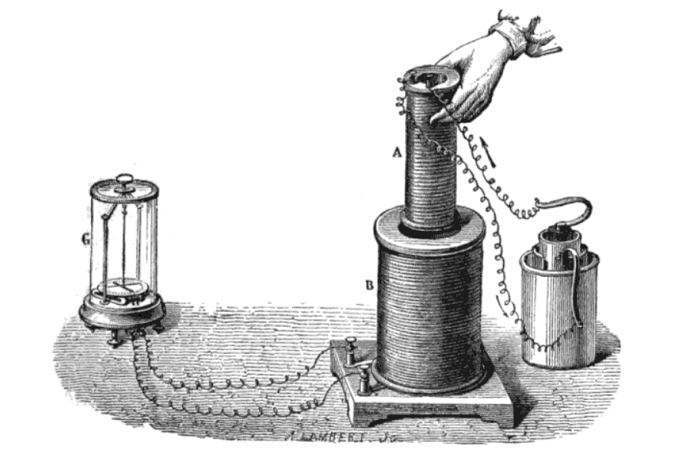
Опыты, выполненные этим учёным, выглядят следующим образом:

1. Фарадей сделал катушку с полой серединой. Её концы соединил с гальванометром. Взял в руки магнит и поместил его внутрь катушки. Если его вдвигать или выдвигать, то на гальванометре отклоняется стрелка, доказывая наличие тока. Чем быстрее выполняемое движение, тем выше его сила. Аналогичный эффект будет достигнут, если магнит будет неподвижен, но будет перемещаться соленоид.

2. В следующем опыте были использованы две катушки. Большая подключена к гальванометру, а вторая — к источнику. Одна из катушек была настолько узкой, чтоб могла проходить внутрь второй. Если её поместить туда и несколько раз включить и выключить ток, то на гальванометре стрелка отклонится, показывая наличие тока.

3. Если взять два соленоида под током и один из них подвигать рядом с другим, то в них также возникнет движение электронов.

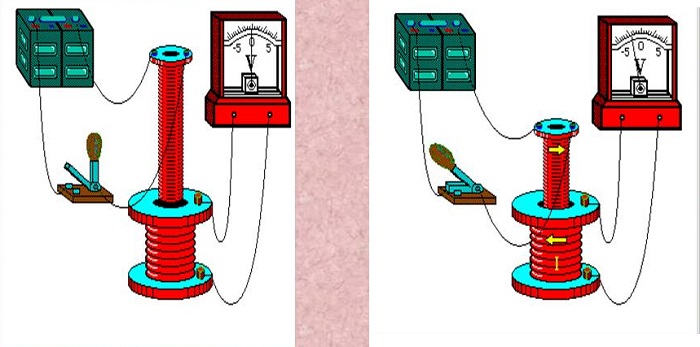
При проведении таких опытов более быстрое движение создаёт более сильное движение электронов.

Одновременно с Фарадеем аналогичные исследования осуществил Джозеф Генри, однако опубликовал свои результаты позже.

Объяснение явления

Движение носителей заряда — электронов происходит в том случае, когда на них действует электродвижущая сила, создаваемая разностью потенциалов. 

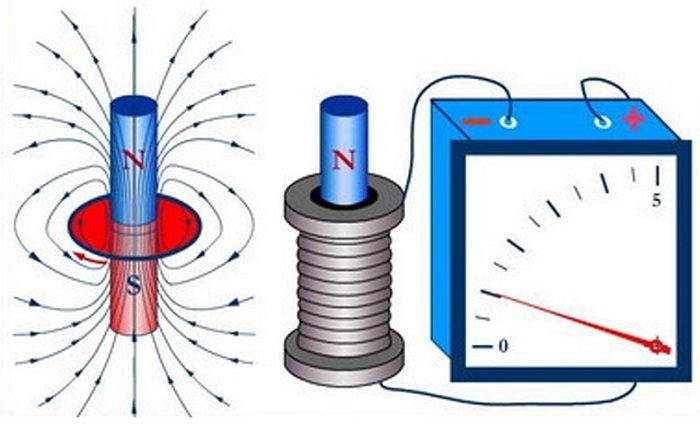
Возникновение тока под действием изменения магнитного поля происходит из-за того, что оно создаёт такую силу, которая носит название ЭДС индукции. Хотя явление индуктивности было обнаружено Фарадеем, он не дал ему теоретического объяснения. 

Теория электромагнитного поля в физике была создана Максвеллом в 1861 году. Этому явлению присущи такие черты:

• источником движения электронов является переменное магнитное поле;

• его наличие можно обнаружить по производимому воздействию на электрические заряды;

• это поле не является потенциальным;

• силовые линии поля представляют собой замкнутые кривые.

Работа магнитного поля выражается в создании электродвижущей силы для электронов.

Закон электромагнитной индукции Фарадея

Основной характеристикой магнитного поля является магнитный поток. Зрительно его можно представить, как силовые линии, пронизывающие перпендикулярную плоскую фигуру, ограниченную замкнутой линией. Эти линии выражают вектор магнитной индукции.

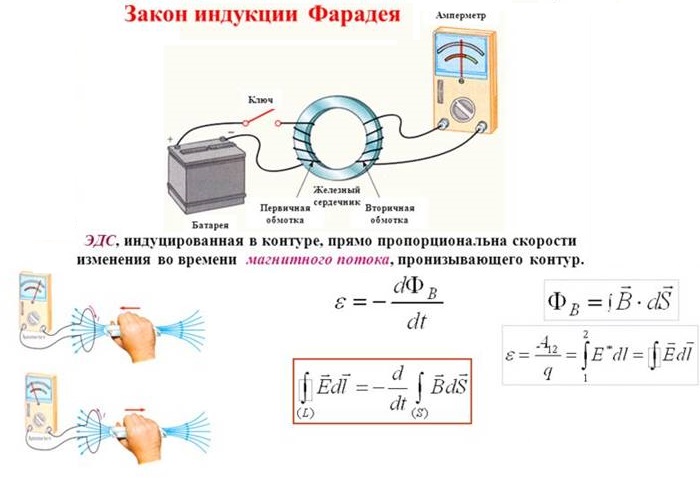
Произведение модуля этой величины на площадь для равномерного и однородного магнитного поля равно потоку поля через рассматриваемый контур.

При рассмотрении сложного поля, фигуру разбивают на небольшие участки, в которых поле равномерно и суммируют значения для каждого из них. Для вычисления в таких случаях используются методы дифференциального и интегрального исчисления.

Электромагнитная индукция измеряется в Тесла (Тл). Эта единица получила своё название в честь великого учёного-физика.

Закон Фарадея количественно описывает влияние магнитного поля на движение электронов. Он утверждает следующее: скорость изменения потока электромагнитного поля равна порождаемой им электродвижущей силе, воздействующей на электроны и создающей ток.

Нужно заметить, что когда магнитное поле порождается изменением силы тока, то возникающая электродвижущая сила воздействует на него противоположным образом. Это можно прояснить на таком примере. 

Если рассматривается провод, и в нём увеличивается сила тока, то это создаёт магнитное поле. Оно, в свою очередь, создаёт ЭДС, которая препятствует увеличению.

Правило Ленца

Это правило даёт возможность правильно определить направление индукционного тока в различных ситуациях. Оно формулируется следующим образом: направление тока, порождённого индукцией, создаёт такое изменение магнитного потока, препятствующее изменению внешнего поля, благодаря которому оно возникло.

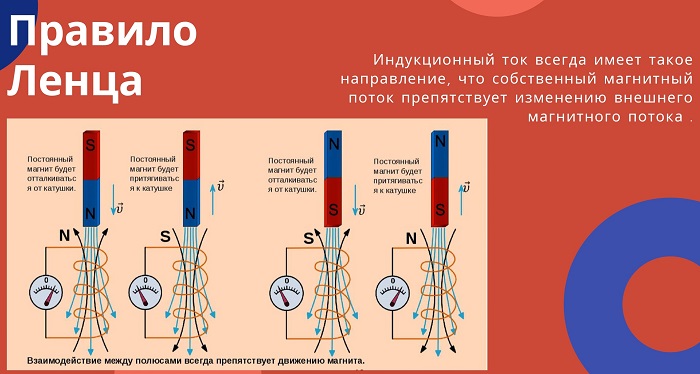
Это можно пояснить на следующем примере. Будет рассмотрена ситуация, когда внешнее магнитное поле со временем будет возрастать, а его силовые линии направлены вверх. 

Это произойдёт, например, в той ситуации, когда снизу к контуру, расположенному горизонтально, будут приближать магнит так, чтобы его северный полюс был обращён вверх. В этом случае магнитный поток будет увеличиваться, создавая электродвижущую силу.

В контуре будет создан индукционный ток. Он будет таким, чтобы магнитные силовые линии были противоположными по отношению к тем, которые характеризуют первоначальное. Теперь можно определить направление индукционного тока в контуре.

Как известно, если смотреть со стороны создаваемого поля, то он будет направлен по часовой стрелке. То есть, если смотреть сверху, направление будет против неё.

На этом примере можно увидеть, как с помощью правила Ленца можно определить направление магнитного поля и индукционного тока.

Самоиндукция

В этом случае рассматривается ситуация, когда изменение движения электронов порождает ЭДС, вызывающий индукционный ток в этом же проводнике. 

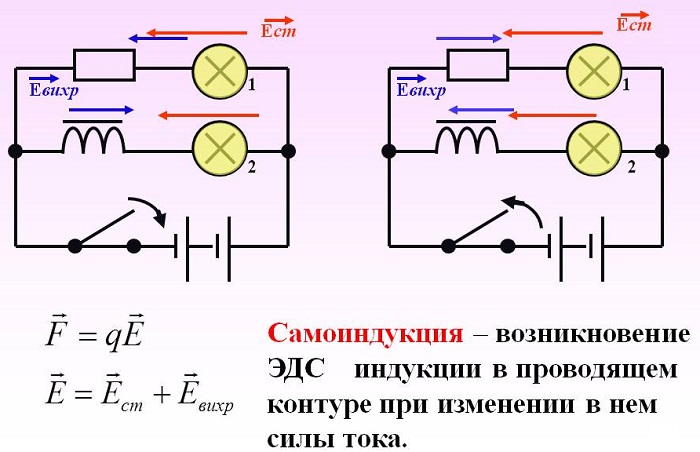
Взяв за основу правило Ленца, можно утверждать, что он имеет направление, противоположное первоначальному изменению.

Самоиндукция похожа на явление инерции. Тяжёлое тело невозможно остановить мгновенно. Также нельзя изменить силу тока за один миг до нужной величины из-за наличия явления самоиндукции.

Это свойство можно продемонстрировать следующим опытом. Нужно сделать две электрических цепи. В одной из них имеется источник и лампочка. Другая сделана аналогичным образом, но различие состоит в том, что в цепь добавлена катушка. 

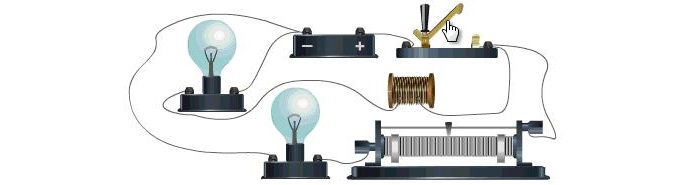
В первой цепи после включения лампочка загорается сразу. Во второй, учитывая наличие индуктивного элемента, это происходит с заметным опозданием.

После размыкания свет в первой лампочке отключается практически мгновенно, а во второй это происходит замедленно. Важно отметить, что в процессе выключения индукционный ток может превысить первоначальный. Поскольку в этой ситуации он направлен также, как и рабочий, то сила тока может возрасти. В некоторых цепях это может вызвать перегорание лампочки.

Индуктивность

Проводник, через который проходит изменяющийся ток, способен накапливать энергию путём использования магнитного поля. У прямолинейного отрезка провода эта способность имеет незначительную величину. 

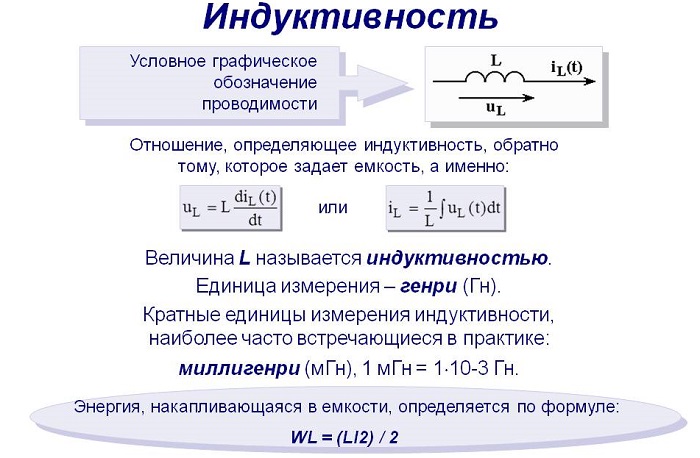
Однако, если речь идёт о катушке, то её величина гораздо сильнее. Эта характеристика называется индуктивностью. Она обозначается как «L» и играет важную роль при определении различных характеристик электромагнитного поля.

Магнитный поток в определённом контуре можно выразить посредством формулы Ф = L* I, а электродвижущую силу в виде E = L* (dI/dt).

Ток, проходящий через контур, способен создать электромагнитное поле, причём оно будет тем сильнее, чем быстрее будут происходить его изменения.

На практике для увеличения индуктивности катушки используют вставленные внутрь стержни из ферромагнетика.

Энергия магнитного поля

Электрический ток создаёт магнитное поле. При этом он затрачивает определённую энергию. Её величина равна той работе, которая была затрачена на создание поля. Она вычисляется по следующей формуле:

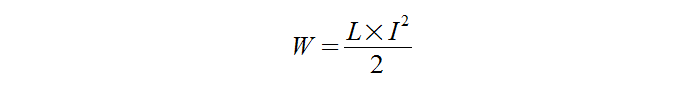
Здесь использовались такие обозначения:

Если магнитное поле по какой-то причине пропадёт, то его энергия выделится в той или иной форме.

Применение электромагнитной индукции

Это явление активно применяется в различных сферах жизни человеческого общества. 

Далее будут приведены несколько наиболее известных примеров:

• радиовещание невозможно без использования явления электромагнитной индукции;

• в медицине магнитотерапия является одним из эффективных методов лечения;

• при фундаментальных исследованиях для разгона элементарных частиц применяются синхрофазотроны, работа которых основана на явлении индуктивности;

• счётчики электричества, применяемые в быту для его учёта, используют рассматриваемое явление;

• для того, чтобы передавать произведённую электростанциями электрическую энергию на большие расстояния, применяются трансформаторы, работа которых построена на использовании электромагнитной индукции;

• в металлургии для плавки металла применяются индукционные печи.

Использование этого явления очень широко распространено. Приведённые примеры являются только частью различных вариантов использования.

Все формулы по теме «Электромагнитная индукция»

Для того чтобы кратко освежить в памяти формулы, относящиеся к магнитной индукции, далее приводится перечень наиболее важных из них.

Открытие законов, которые описывают поведение электромагнитного поля, является одним из важнейших достижений науки за всю историю. В современной жизни использование этого явления происходит практически во всех областях жизни общества.

Опыты Фарадея

В 1820 году было произведено открытие магнитного пола вокруг проводника Эрстедом. В то время производилось много опытов и экспериментов, связанных с электричеством. Фарадей эмпирически открыл явление электромагнитной индукции 29 августа 1831 года. Он обнаружил явление у стационарных проводников при замыкании и размыкании цепи.

Позже было доказано, что явление электромагнитной индукции появляется при движении катушек с токами друг с другом. Еще 17 октября из лабораторного журнала было видно обнаружение индукционного тока во время введения и удаления магнита из катушки. В течение месяца все особенности изучил Фарадей.

Именно он сумел объяснить явления диа- и парамагнетизма, объясняя это тем, что материалы, располагаемые в пределах магнитного поля ведут себя по-разному: ориентируются по полю, как пара- и ферромагнетики, или поперек, как диамагнетики.

Опыты Фарадея. Электромагнитная индукция

Опыты Фарадея известны из школьного курса, наглядно представленные на рисунке.

Рисунок 3.1. Возникновение электрического тока при поднесении или вытягивании катушки с левой стороны и возникновение электрического тока с двумя близко расположенными катушками справа.

Рисунок 3.2. Возникновение электрического тока при соединении катушек сердечником.

Определение 1

На данный момент опыты Фарадея называют классическими и применяют для обнаружения электромагнитной индукции:

1. Замыкание гальванометра на соленоиде. В соленоид опускается постоянный магнит, перемещая который, фиксируются отклонения стрелки гальванометра. Это говорит о наличии индукционного тока. Если увеличить скорость перемещения магнита относительно катушки, тогда стрелка гальванометра отклонится еще сильнее. Это говорит о том, что произошла замена полей. Магнит может быть неподвижным или передвижение соленоида происходит относительно магнита.
2. Две катушки. Производится установка одной в другую. Концы одной из них подключаются с гальванометром. Другая катушка подвергается прохождению тока. При его подаче и отключении стрелка гальванометра изменяет свое положение. В этом случае катушки должны находиться в движении относительно друг друга. Стрелка гальванометра уменьшает значение при его включении.

Определение 2

При изменении потока вектора индукции, пронизывающего проводящий контур, происходит возникновение электрического тока, что называется явлением электромагнитной индукции, а такой ток – индукционным.

Законы электролиза Фарадея — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 11 ноября 2019; проверки требует 1 правка. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 11 ноября 2019; проверки требует 1 правка. Майкл Фарадей, портрет Томаса Филипса, 1841—1842

Зако́ны электро́лиза Фараде́я являются количественными соотношениями, основанными на электрохимических исследованиях, опубликованных Майклом Фарадеем в 1836 году.^[1]

В учебниках и научной литературе можно найти несколько версий формулировки законов. В наиболее общем виде законы формулируются следующим образом:

• Первый закон электролиза Фарадея: масса вещества, осаждённого на электроде при электролизе, прямо пропорциональна количеству электричества, переданного на этот электрод. Под количеством электричества имеется в виду электрический заряд, измеряемый, как правило, в кулонах.
• Второй закон электролиза Фарадея: для данного количества электричества (электрического заряда) масса химического элемента, осаждённого на электроде, прямо пропорциональна эквивалентной массе элемента. Эквивалентной массой вещества является его молярная масса, делённая на целое число, зависящее от химической реакции, в которой участвует вещество.

Законы Фарадея можно записать в виде следующей формулы:

m = (QF)(Mz),{\displaystyle m\ =\ \left({Q \over F}\right)\left({M \over z}\right),}

где:

Заметим, что M/z{\displaystyle M/z} — это эквивалентная масса осаждённого вещества.

Для первого закона Фарадея M,F{\displaystyle M,\,F} и z{\displaystyle z} являются константами, так что, чем больше величина Q{\displaystyle Q}, тем больше будет величина m{\displaystyle m}.

Для второго закона Фарадея Q,F{\displaystyle Q,\,F} и z{\displaystyle z} являются константами, так что чем больше величина M/z{\displaystyle M/z} (эквивалентная масса), тем больше будет величина m{\displaystyle m}.

В простейшем случае используется постоянный ток и полный электрический заряд (прошедший через систему) за время электролиза равен: Q=It{\displaystyle Q=It} , что приводит к выражению:

m = (ItF)(Mz),{\displaystyle m\ =\ \left({It \over F}\right)\left({M \over z}\right),} где размерность тока I{\displaystyle I} ампер-час (ампер-секунда и др.) определяет размерность времени электролиза t{\displaystyle t}.

и тогда

n = (ItF)(1z),{\displaystyle n\ =\ \left({It \over F}\right)\left({1 \over z}\right),}

где:

• n{\displaystyle n} — выделенное количество вещества («количество молей»): n=m/M{\displaystyle n=m/M},
• t{\displaystyle t} — время действия постоянного тока.

В более сложном случае переменного электрического тока полный заряд Q{\displaystyle Q} тока I(τ){\displaystyle I(\tau )} суммируется за время τ{\displaystyle \tau }:

Q=∫0tI(τ) dτ.{\displaystyle Q=\int _{0}^{t}I(\tau )\ d\tau .}

Здесь t{\displaystyle t} — полное время электролиза, τ{\displaystyle \tau } переменная времени, ток I{\displaystyle I} является функцией от времени τ{\displaystyle \tau }.^[2]

• Serway, Moses, and Moyer, Modern Physics, third edition (2005).

Электролитические процессы

Явление э/м индукции. Магн. поток. Закон э/м индукции

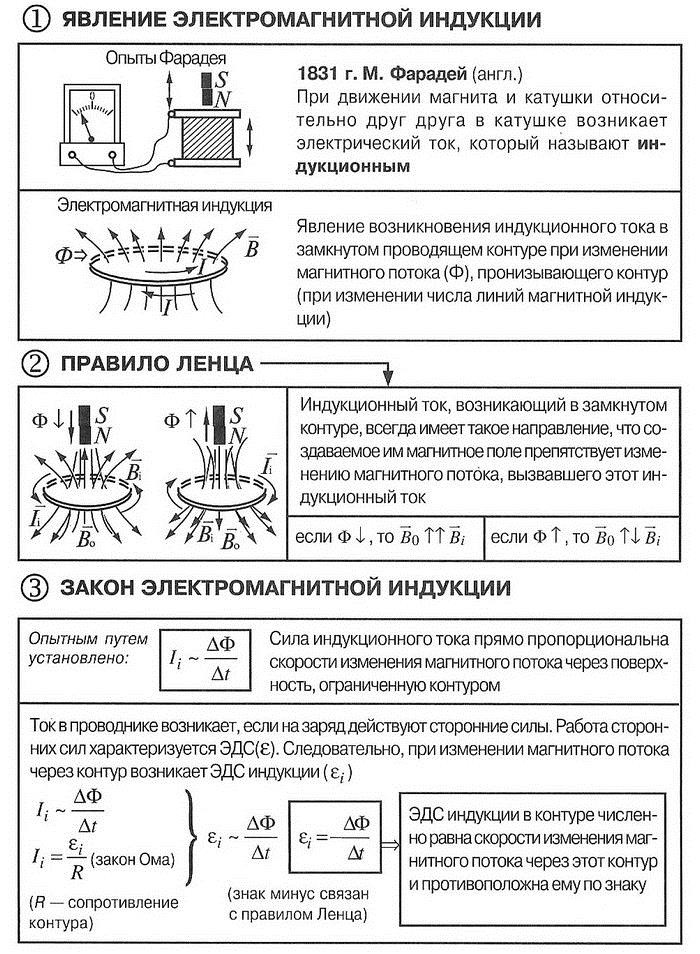
• Явление электромагнитной индукции

Электрические и магнитные поля порождаются одними и теми же источниками – электрическими зарядами, поэтому можно предположить, что между этими полями существует определенная связь. Это предположение нашло экспериментальное подтверждение в 1831 г. в опытах выдающегося английского физика М.Фарадея. Он открыл явление электромагнитной индукции.

Явление электромагнитной индукции лежит в основе работы индукционных генераторов электрического тока, на которые приходится вся вырабатываемая в мире электроэнергия.

• Магнитный  поток

Замкнутый контур, помещенный в однородное магнитное поле

Количественной характеристикой процесса изменения магнитного поля через замкнутый контур является физическая величина называемая магнитным потоком. Магнитным потоком (Ф) через замкнутый контур площадью (S) называют физическую величину, равную произведению модуля вектора магнитной индукции (В) на площадь контура (S) и на косинус угла  между вектором В и нормалью к поверхности:  Φ = BS cos α.   Единица магнитного потока Ф — вебер (Вб): 1 Вб = 1 Тл · 1 м².

Если вектор магнитной индукции перпендикулярен площади контура, то магнитный поток максимальный.

Если вектор магнитной индукции параллелен площади контура, то магнитный поток равен нулю.

• Закон электромагнитной индукции

Опытным путем был установлен закон электромагнитной индукции: ЭДС индукции в замкнутом контуре равна по модулю скорости изменения магнитного потока через поверхность, ограниченную контуром:   Эта формула носит название закона Фарадея.

Классической демонстрацией основного закона электромагнитной индукции является первый опыт Фарадея. В нем, чем быстрее перемещать магнит через витки катушки, тем больше возникает индукционный ток в ней, а значит, и ЭДС индукции.

• Правило Ленца

Зависимость направления индукционного тока от характера изменения магнитного поля через замкнутый контур в 1833 г. опытным путем установил русский физик Э.Х.Ленц. Согласно правилу Ленца, возникающий в замкнутом контуре индукционный ток своим  магнитным  полем противодействует тому изменению  магнитного потока, которым он вызван.  Более кратко это правило можно сформулировать следующим образом: индукционный ток направлен так, чтобы препятствовать причине, его вызывающей. Правило Ленца отражает тот экспериментальный факт, что    всегда имеют противоположные знаки (знак «минус» в формуле Фарадея).

Ленцем был сконструирован прибор, представляющий собой два алюминиевых кольца, сплошное и разрезанное, укрепленные на алюминиевой перекладине. Они могли вращаться вокруг оси, как коромысло. При внесении магнита в сплошное кольцо оно начинало «убегать» от магнита, поворачивая соответственно коромысло. При вынесении магнита из кольца оно стремилось «догнать» магнит. При движении же магнита внутри разрезанного кольца никакого движения не происходило. Ленц объяснял опыт тем, что магнитное поле индукционного тока стремилось компенсировать изменение внешнего магнитного потока.

Правило Ленца имеет глубокий физический смысл – оно выражает закон сохранения энергии.

Опыты Фарадея (электромагнитная индукция)

Электромагнитная индукция

В начале XIX столетия опыты в области электромагнетизма стали чуть ли не модой. Открытие в 1820 г. Эрстедом существование магнитного поля вокруг проводника с током вызвало небывалый резонанс в научных кругах. Проводилось множество экспериментов с электричеством.

29 августа 1831 г. Фарадеем эмпирически было открыто явление электромагнитной индукции. Первоначально данное явление Фарадей обнаружил для стационарных по отношению друг к другу проводников при замыкании и размыкании цепи. Чуть позднее ученый показал, что явление электромагнитной индукции обнаруживается при движении катушек с токами друг по отношению к другу. 17 октября Фарадей отметил в лабораторном журнале, что обнаружил индукционный ток во время введения и удаления магнита в (из) катушку. За один месяц Фарадей определил все основные особенности явления электромагнитной индукции.

Опыты Фарадея

В настоящее время классическими опытами Фарадея по обнаружению явления электромагнитной индукции являются следующие эксперименты:

1. Гальванометр замыкают на соленоид. В соленоид вдвигается (или выдвигается из него) постоянный магнит. При перемещении магнита фиксируют отклонение стрелки гальванометра, что означает возникновение индукционного тока. При увеличении скорости перемещения магнита по отношению к катушке отклонение стрелки увеличивается. Замена полюсов магнита вызывает изменение направления отклонения стрелки гальванометра. Отметим, что магнит можно оставить неподвижным и перемещать соленоид относительно магнита.
2. В этом эксперименте используются две катушки. Одна вставлена в другую. Концы одной из катушек соединяют с гальванометром. Через другую катушку пропускается электрический ток. Стрелка гальванометра претерпевает отклонения, когда происходит включение (выключение) тока, его изменение (увеличение или уменьшение) или если катушки движутся относительно друг друга. Направление отклонения стрелки гальванометра противоположны при включении и выключении тока (уменьшении – увеличении силы тока).

При обобщении результатов своих экспериментов Фарадей отметил, что индукционный ток возникает всякий раз, когда происходит изменение потока магнитной индукции, сцепленного с контуром. При этом величина индукционного тока не связана со способом изменения потока, а зависит от скорости его изменения. Эмпирически Фарадей доказывал, что величина угла отклонения стрелки гальванометра связана со скоростью перемещения магнита (скоростью изменения силы тока, скоростью перемещения катушек относительно друг друга).

Своими опытами Фарадей показал, что сила тока индукции в проводящем контуре пропорциональна скорости изменения количества линий магнитной индукции, которые проходят через поверхность, которую ограничивает рассматриваемый контур.

На основе опытов Фарадея Максвелл сформулировал основной закон электромагнитной индукции. В соответствии с этим законом электродвижущая сила индукции в замкнутом контуре равна скорости изменения магнитного потока () сквозь поверхность, которую ограничивает этот контур:

   

где , – магнитный поток ( – угол между вектором и нормалью к плоскости контра). Минус отображает правило Ленца.

Значение опытов Фарадея заключено в том, что через явления электромагнитной индукции проявляется взаимосвязь электрического и магнитного полей. Электрическое поле, которое возникает при изменении магнитного поля, имеет иную природу, нежели электростатическое поле. Оно не имеет непосредственной связи с электрическими зарядами, и его линии напряженности не могул на них начинаться и заканчиваться. Эти линии поля подобны линиям магнитной индукции и являются замкнутыми линиями. Это электрическое поле является вихревым.

Примеры решения задач